A Systematic Adaptive Mesh Refinement Method for Large Eddy Simulation of Turbulent Flame Propagation

Abstract

This paper presents a feature-based adaptive mesh refinement (AMR) method for Large Eddy Simulation of propagating deflagrations, using massive-scale parallel unstructured AMR libraries. The proposed method, named turbulent flame propagation-AMR (TFP-AMR), is able to track the transient dynamics of both the turbulent flame and the vortical structures in the flow. To handle the interaction of the turbulent flame brush with the vortical structures of the flow, a vortex selection criterion is derived from flame/vortex interaction theory. The method is built with the general intent to prioritise conservatively estimated parameters, rather than to rely on user-dependent parameters. In particular, a specific mesh adaptation triggering strategy is constructed, adapted to the strongly transient physics found in deflagrations, to guarantee that the physics of interest consistently reside within a region of high accuracy throughout the transient process. The methodology is applied and validated on several elementary cases representing fundamental bricks of the full problem: (1) a laminar flame propagation, (2) the advection of a pair of non-reacting vortices, (3) a flame/vortex interaction. The method is then applied to three different configurations of a three-dimensional complex explosion scenario in an obstructed chamber. All cases demonstrate the TFP-AMR capability to recover accurate results at reduced computational cost without requiring any ad hoc tuning of the AMR method or its parameters, thus demonstrating its genericity and robustness.

1 Introduction

Large Eddy Simulation (LES) of deflagrations are now possible at reasonably large Reynolds numbers thanks to the continuous increase in computational power (Vermorel et al. 2017; Volpiani et al. 2017). For such complex unsteady reacting phenomena, this approach offers a good compromise between Unsteady Reynolds-Averaged Navier–Stokes (URANS) and Direct Numerical Simulations (DNS) approaches in terms of precision-to-cost ratio. LES has great potential in safety applications, both for its prediction capabilities and as a tool to further understand the underlying physics of complex scenarios. In the context of industrial safety, deflagrations often occur in confined and obstructed spaces, where the sudden pressure rise responsible for the destructive effects—the overpressure—is driven by the process of Flame Acceleration (FA). The mechanisms involved in the different steps of FA are well documented, for instance in the review paper of Ciccarelli and Dorofeev (2008). In the case of deflagrations in confined and obstructed spaces, the two main FA mechanisms are (1) the burnt gases expansion combined with the geometrical confinement and (2) the Flame/Vortex Interaction (FVI). The strong temperature rise, due to the combustion process, results in the expansion of the burnt gases. The burnt gases are trapped between the walls of the confined geometry and, as a result, “push" the flame and the fresh gases ahead, increasing their velocity. The flame acts as a permeable piston, compressing the fresh gases as it accelerates. This is a purely laminar and hydrodynamic acceleration process. The flow velocity induced in the fresh gases ahead of the flame, due to the burnt gases expansion, leads to the generation of flow structures through mechanisms such as vortex shedding in the wake of the obstacles. As the flame arrives at the obstacles, it is strongly wrinkled by the vortical, turbulent structures present in the flow. This creates a strong increase of the flame surface and consumption rate as the flame transitions to the turbulent regime. This establishes a positive feedback loop of acceleration that is the main driver of the overpressure generation. Therefore, it is essential to correctly capture the flame, the vortices and their interaction to recover the correct overpressure. Several experimental studies have explored deflagrations in confined and obstructed geometries and provide a validation database for LES: for example the semi-confined, obstructed explosion chamber from the University of Sydney (Kent et al. 2005; Masri et al. 2012) or the closed GraVent explosion channel operated at TUMunich (Boeck et al. 2016). In the case of the laboratory-scale Sydney explosion chamber, LES have been able to correctly reproduce the aforementioned FA physics and to retrieve the experimental overpressure evolution (Vermorel et al. 2017), despite a significant computational cost.

When simulating steady or quasi-steady-state phenomena, static mesh refinement approaches can be used to reduce the computational cost. Criteria based on statistically averaged quantities (Dannenhoffer and Baron 1985; Daviller et al. 2017; Jouhaud et al. 2005; Toosi and Larsson 2020) can be employed to generate an optimal mesh, obtained thanks to an iterative converging procedure, that remains unchanged throughout the entire simulation. The physics of interest in deflagrations are, however, highly unsteady. In this kind of scenario, the flame may propagate along the whole computational domain and the vortical turbulent structures are generated, advected and dissipated during said flame evolution over a wide range of scales. In the specific context of LES, the flow and combustion filter size is directly linked to the local mesh cell size. Therefore, to ensure an accurate numerical resolution of the relevant flow and flame features, it is imperative that the flame and vortical structures always remain in regions with a constant, fine mesh resolution: static mesh refinement approaches are thus not applicable since a fine resolution is ultimately required in almost the entire computational domain. Instead, a homogeneous, fine static mesh is often used (Abdel-Raheem et al. 2015; Gubba et al. 2011; Vermorel et al. 2017), which leads to a prohibitive computational burden for large-scale configurations.

Whereas static mesh refinement strategy is not suitable for intrinsically transient phenomena—here, deflagrations—the Adaptive Mesh Refinement (AMR) approach has a great potential, as it can dynamically adapt the grid to provide high accuracy where it is needed. In the context of deflagrations, the main physical features previously described—the flame and the resolved vortices—are very localised in space and time, as they are mainly propagative phenomena. Therefore, significant computational savings are expected with AMR, as it should be able to drastically reduce the number of elements while preserving accuracy, provided that the high resolution regions can be properly identified through Quantities of Interest (QoI). The more localised the physical phenomena are in space and time, the higher the potential computational savings. For example, a deflagration in a high aspect ratio channel will be significantly more affordable to compute with AMR. To address the constraints of performing unsteady LES of deflagrations in complex, confined and obstructed geometries, the AMR methodology needs to fulfil the following properties:

• Massively parallel.

• Able to conform to complex boundaries: Some of the AMR methods are only compatible with structured or cartesian meshes (Berger and Oliger 1984; Berger and Colella 1989; Khokhlov et al. 1999; Maxwell 2016). Since a body-fitted framework is considered here, an unstructured mesh approach is best suited.

• Feature-based: The most common AMR approaches are based on error criteria (Antepara et al. 2015; Babuska and Miller 1981; Haldenwang and Pignol 2002; Rios et al. 2009; Wilkening and Huld 1999). The specific context of LES adds some difficulty to the definition of such errors. First, it must take into account the LES filter size, which is directly linked to the local grid size. Toosi and Larsson (2020) argue that, as LES is, by definition, under-resolved, convergence based on point-wise (in space and time) error estimation would lead to an unaffordable degeneration of the adapted mesh towards a DNS mesh. For non-reacting cases, they address this issue by including the effect of the subgrid closure in the definition of the error. For reacting cases, the effect of the combustion filter size and subgrid combustion model would also need to be accounted for, which might be a tedious task due to the high non-linearity of flame processes. A more practical approach consists in identifying important simulation features (named QoI in this work), for which high accuracy is required. We adopt a similar approach in the highly transient LES context of this study. QoI constructed from a priori knowledge of the physics are used to define the zones where a fine mesh resolution is required. The important features are identified in this case as the flame and the resolved vortical structures. In this framework, the target mesh resolution in region of high accuracy remains a parameter defined by the user, for example according to subgrid turbulence, subgrid flame-turbulence interaction criteria or, from a more practical point of view, based on overall computational budget.

• Based on systematic, user-independent mesh refinement criteria: AMR has been widely used for the simulation of turbulent propagating flames (Cant et al. 2022; Lapointe et al. 2020; Mehl et al. 2018, 2021; Verhaeghe et al. 2022; Wilkening and Huld 1999), but most of the methods proposed depend on case-specific thresholds. Indeed, most of the criteria to detect where a fine mesh is required are often based on dimensional quantities: velocity, temperature or species gradients (Cant et al. 2022; Rios et al. 2009), turbulent kinetic energy (Babuska and Miller 1981), vorticity (Iapichino et al. 2008; Lapointe et al. 2020) or heat release rate (Haldenwang and Pignol 2002; Lapointe et al. 2020). Even with proper nondimensionalisation, these require an arbitrary threshold that is highly case dependent, may not be valid across the wide range of scales found in highly transient deflagration configuration and cannot be known a priori. Even so, these approaches have been used in the context of deflagrations and shown good results. For example, Xiao and Oran (2020) used an AMR method based on velocity and density gradients for a turbulent flame propagation in a channel filled with obstacles. Sengupta (2023) used a similar AMR approach for an explosion in an obstructed chamber. Some authors proposed dimensionless formulations to detect the evolution of the vortices (Fabius and Amersfoort 2014; Kamkar et al. 2010; Pang et al. 2021; Zeoli et al. 2020) or the flame (Mehl et al. 2018, 2021; Verhaeghe et al. 2022). However, these methods do not explicitly link the flame and vortices detection criteria, in the context of turbulent propagating flames.

In this work, an AMR method to compute LES of turbulent propagating flames, named Turbulent Flame Propagation-AMR (TFP-AMR), is implemented in the massively parallel compressible solver AVBP (Gicquel et al. 2011). The AVBP solver is based on an explicit time advancement, cell-vertex/finite element method to solve the compressible reactive and unsteady multi-species Navier–Stokes equations on unstructured meshes. This solver has been used successfully to perform simulations of propagating deflagrations and detonations (Dounia et al. 2019; Jaravel et al. 2020; Quillatre et al. 2011, 2013; Vermorel et al. 2017; Volpiani et al. 2017). The AMR method presented uses a systematic criteria evaluation and is compatible with any node-based AMR library. The in-house AMR library kalpaTARU, developed at CERFACS is used.

The paper is organised as follows: in Sect. 2, the AMR methodology is presented and the key notions of QoI, criteria, mask and metric are defined. The AMR library kalpaTARU is also described. Then, in Sects. 3 and 4, the different frameworks, sensors and the mesh adaptation triggering strategy are presented. Three canonical test cases are used to illustrate the methodology and the shortcomings of several of the methods present in the literature: a 3-D, planar, laminar and premixed flame in Sect. 3.4; a pair of 2-D isentropic and incompressible advected vortices in Sect. 4.2 and a 2-D flame/vortex interaction, combining flames and vortices, in Sect. 4.4. Finally, in Sect. 5, the TFP-AMR is used to compute three configurations of the laboratory-scale explosion chamber from the University of Sydney (Kent et al. 2005; Masri et al. 2012). Several geometries and fuels are considered here to highlight the user-independent and systematic aspects of the TFP-AMR method, as well as its robustness. Finally, the capability to recover the same level of precision as a set of reference LES performed on a static homogeneous mesh, for a lower computational cost, is evaluated.

2 AMR Methodology

2.1 Framework and Definitions

The goals of the TFP-AMR framework are threefold: (1) to track the dynamic evolution of the physical phenomena of interest, (2) to establish when a mesh adaptation should be triggered and (3) to determine the grid size distribution required for the adaptation. Since this method focuses on deflagrations in confined and obstructed geometries, the physical features of interest are the flame and the resolved vortical structures that drive the FA stage. Of course, the QoI could potentially be extended depending on the physics of interest. For example, shocks can be additional targets when the FA stage is strong enough to produce shocks ahead of the flame, leading to shock/flame interactions and potentially deflagration to detonation transition.

Fig. 1

Schematic representation of a feature-based AMR workflow

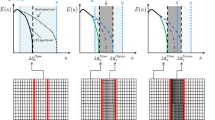
A schematic of a feature-based AMR workflow is presented in Fig. 1. To track the physical phenomena of interest to detect, a sensor needs to be defined. It identifies either the flame or the vortex structures in the present framework. It needs to be a physical, instantaneous and preferably dimensionless quantity, and constitutes the QoI. Based on QoI, criteria are applied to build a mask field M that goes from $M=1$ in regions where a fine mesh is required, to $M=0$ in regions where a coarse mesh is deemed sufficient. In this work, these criteria are based on threshold values: if a QoI becomes higher than a fixed threshold, the criterion is met, making the corresponding mask field take the value of $M=1$. Otherwise, $M=0$. From the local value of the mask field, the target cell size for AMR is, then, determined. Either the fine or the coarse mesh cell size targeted is imposed, building a complete target metric field. The local target edge size is, thus, defined as:

$$\begin{aligned} \Delta _x = \Delta _x^{\textrm{fine}} + \left( \Delta _x^{\textrm{coarse}} -\Delta _x^{\textrm{fine}} \right) \left( 1- M \right) , \end{aligned}$$

(1)

Additionally, a smooth transition between $\Delta _x^{\textrm{fine}}$ and $\Delta _x^{\textrm{coarse}}$ is ensured given an imposed growth ratio. When a mesh adaptation is required, the complete target metric field is fed to the AMR library. In this work, the kalpaTARU AMR library is used (Sect. 2.2). The library handles the parallel adaptation and generation of meshes whose cell size distribution follows the target metric field. The role of the mask field is illustrated in Fig. 2: the zone where the flame and vortical structures are present are flagged by the mask field being equal to one. There, a fine mesh resolution is set, the grid size progressively transitioning to coarse values in the zones that are not of interest and where the mask field is, therefore, equal to zero. The sensors and criteria that allow to build such mask fields for the flame and the vortices are built separately. They are presented in Sects. 3 and 4, respectively. They are combined in Sects. 4.4 and 5, where more details on how both QoI are used together are presented.

Fig. 2

Identification of the QoI and corresponding adapted mesh in a simple 2D configuration of flame/obstacle interaction. Left: the line integral convolution of the flow velocity vectors, coloured by the vorticity magnitude is shown, together with the heat release rate at the flame. Right: the QoI (flame and vortices) are identified by contours (red and blue, respectively) that delimit the region where $M=1$. These are presented together with the resulting adapted mesh. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.2 The kalpaTARU AMR Library

We provide a brief description of the parallel AMR library kalpaTARU (Topology-Aware adaptive Refinement and load-balancing framework for Unstructured meshes) used in this work. It is a massive-scale parallel unstructured mesh refinement and load-balancing library that exploits the knowledge of hardware topology for optimal load and data placement to achieve near optimal parallel efficiency. The online hierarchical mesh partitioner and load-balancing tool in the library is shown to scale to extremely large core counts and problem sizes (Mohanamuraly and Staffelbach 2020). The library leverages the load-balancing tool, coupling it with the serial mesh adaptation library MMG3D (Dapogny et al. 2014; Dobrzynski and Frey 2008) to perform distributed parallel mesh adaptation. An iterative approach similar to Benard et al. (2016) is used, where the bordering inter-processor elements are frozen during the first adaptation step and a mesh re-balancing step ensures these frozen elements are pushed to the internal regions going into the next adaptation step (see Fig. 3). An isotropic mesh adaptation strategy is implemented in this work, therefore, a single scalar metric field (Alauzet et al. 2003; Dobrzynski and Frey 2008) is used to enforce a desired edge length distribution. The algorithm terminates when a desired convergence threshold is reached, satisfying this user defined scalar metric. The complete iterative adaptation process is illustrated in Fig. 3 using a simple 2D mesh and metric field on four processors.

Fig. 3

Schematic of the iterative parallel adaptation process on four parallel MPI ranks; a initial mesh and user-defined metric field, b first adaptation step, c second adaptation step with re-partitioning and d final adapted mesh. The four processor boundaries are denoted by the cuts in the mesh and the relative elements sizes with respect to the metric contour is shown in the legend (not to scale)

To reduce the total number of iterations required to reach this threshold; vertex and edge weights in the graph-based partitioning (to re-balance the mesh) are set to high values in the vicinity of the processor boundary (typically a factor 10). Higher edge weights ensures that the graph partitioner pushes the frozen elements into the interior regions by avoiding edge cuts near their vicinity. Imposing higher vertex weights improves the load balance; since by definition these elements have not been adapted and will require more computation from the algorithm to match the criteria. At the end of each adaptation iteration, the solution is interpolated to the newly adapted mesh using a linear Barycentric interpolation. To interpolate noisy data, a linear least-squares interpolation was also implemented using the vertices in the immediate neighbourhood of the vertex edge stencil. Note that the results shown in this work are obtained only using the Barycentric interpolation. Since the AMR methodology imposes a target resolution depending on the mask (see Fig. 1), mesh resolution remains mostly constant (either $\Delta _x^{\textrm{coarse}}$ or $\Delta _x^{\textrm{fine}}$) thus ensuring very low interpolation errors. The kalpaTARU library is linked to the AVBP solver using a plain C language application programming interface (API). All input data like mesh, metric and solution fields are shared as memory pointers avoiding redundant data transfer and storage. After adaptation, adapted local mesh data is copied back into AVBP arrays directly.

3 AMR Framework for Propagating Flames

In this section, only the AMR aspects related to the flame are described. The methodology regarding vortical structures is presented in Sect. 4.

3.1 Flame Mask Definition

One of the principal physical phenomena of interest in a deflagration is the propagating flame. Within the reaction zone, sharp species and density gradients are found. It is, thus, imperative to have a sufficient mesh resolution to correctly resolve the flame front. To target the flame front, several sensors could be used as long as they are inexpensive to compute and have a dimensionless and bounded formulation. In this AMR framework, the QoI used to localise the flame is the flame sensor $\theta _{\textrm{F}}$ classically used in the DTFLES model (Legier et al. 2000). Further details on the model can be found in Supplementary Material. $\theta _{\textrm{F}}$ is computed at each iteration and depends on the type of chemical mechanism used. In the case of a global mechanism, it is defined as:

$$\begin{aligned} \theta _{\textrm{F}} = \tanh \left( \beta '\frac{\varTheta }{\varTheta _0}\right) , \quad \text {with} \quad \varTheta = {Y}_{\textrm{F}}^{n_{\textrm{F}}} {Y_{\textrm{O}}}^{n_{\textrm{O}}} \exp \left( - \chi \frac{E_{\textrm{a}}}{RT} \right) , \end{aligned}$$

(2)

where $\beta '$ is a model constant equal to 50. $Y_{\textrm{F}}$ and $Y_{\textrm{O}}$ are the fuel and oxidiser mass fractions, $n_{\textrm{F}}$ and $n_{\textrm{O}}$ the fuel and oxidiser chemical scheme reaction exponents, $E_{\textrm{a}}$ the activation energy, R the ideal gas constant and $\chi$ is a model parameter set to 1/2. $\varTheta _0$ is the maximum of $\varTheta$ for a 1D laminar flame computation at a given initial pressure $p_0$, initial temperature $T_0$ and equivalence ratio $\phi$. In the case of propagating deflagrations, the values of $\varTheta _0$ can be tabulated as a function of $p_0$, $T_0$ and $\phi$, as these may vary locally in space and time. By definition, $\theta _{\textrm{F}}$ is dimensionless and bounded: Its value goes from $\theta _{\textrm{F}}=1$ inside the flame front to $\theta _{\textrm{F}}=0$ outside, with a smooth transition following the hyperbolic tangent.

To target the zone where the mesh needs to be fine, a mask field is built on the basis of a threshold-type criterion. To target exclusively the flame front, a threshold value $\theta _{\textrm{F}}^{\textrm{lim}} = 1/2$ is applied to the flame sensor field. The mask field is then:

$$\begin{aligned} M(\theta _{\textrm{F}})={\left\{ \begin{array}{ll} 1 &{} \text {if } \theta _{\textrm{F}} \ge \theta _{\textrm{F}}^{\textrm{lim}} \\ 0 &{} \text {if } \theta _{\textrm{F}} < \theta _{\textrm{F}}^{\textrm{lim}} . \end{array}\right. } \end{aligned}$$

(3)

This definition of the mask field ensures that $\Delta _x$ is kept constant in the flame front, which is essential to the correct numerical resolution of a thickened flame in LES. It can be employed both in LES or DNS, independently of the DTFLES model itself. Note that the same methodology is applicable with any flame sensor definition, and is not restricted to the one from Eq. (2).

3.2 Mesh Adaptation Triggering Strategy

During the flame front propagation, successive mesh adaptations must ensure that the flame always remains in a fine region of the mesh. Otherwise, this would lead to a strong variation of the flow and combustion filter scales, which is detrimental for the accuracy of the LES. It would also lead to high interpolation errors during the mesh adaptation. However, as the mesh adaptation process represents a supplementary cost, if triggered too often, the accumulated costs from the adaptations can become prohibitive and overcome the gains due to the mesh size reduction. Several criteria exist in the literature to determine when to trigger adaptation. The simplest method is to set a fixed time frequency (Alauzet et al. 2003, 2007) or to use a minimum spatial displacement (Hartmann et al. 2008). These approaches are impractical since they rely on highly case-dependent values that cannot be known a priori. In addition, a single value may not be adequate to track the dynamics of the QoI throughout the simulation: in a deflagration, for example, the flame accelerates and the flame front absolute speed strongly increases, going from the order of $10^{-2}\,\textrm{m}/\textrm{s}$ in the initial laminar phase up to $10^{2}\,\textrm{m}/\textrm{s}$ at the final stages: the frequency of the mesh adaptations should therefore increase throughout the simulation, following the flame acceleration, which is not the case with this approach. A more automated approach, based on the mask field variation $M^*$, has been proposed in the thesis of Sengupta (2023) for AMR. It compares the initial mask $M_0$, i.e. the mask field computed before the first time step on the current mesh, with the current mask M, i.e. the mask field at the current time step. The relative mask variation $M^*$ is then computed as follows:

$$\begin{aligned} M^{\mathrm{*}} = \frac{\displaystyle \sum _{\mathrm{n=0}}^{\textrm{nnodes}} |\,M^{\textrm{n}}_0 -M^{\textrm{n}}\,|}{\displaystyle \sum _{\mathrm{n=0}}^{\textrm{nnodes}} M^{\textrm{n}}_0} . \end{aligned}$$

(4)

This ratio represents the spatial variation of the QoI relative to the fine mesh region. The higher the value, the higher fraction of the flame front is allowed to enter coarse mesh regions. The adaptation is triggered based on a threshold value $M^*_{\textrm{limit}}$ set by the user. The mask variation method has shown promising results provided that the threshold is properly tuned. However, it is still case-dependent and cannot be known a priori. If the value is set too low, the mesh adaptation is triggered too frequently, and if it is set too high, the flame can go out the fine mesh zone leading to high interpolation errors and to inaccurate results (Sengupta 2023) (see Sect. 3.4). Additionally, as the value of the threshold remains constant, if the dynamics of the QoI change along the simulation, this method may lead to problematic scenarios. For example, an initially laminar and therefore smooth-shaped flame, can locally accelerate or be wrinkled, propagating into coarse zones of the mesh without significantly increasing the value of $M^*$. A global criterion cannot provide a control on what happens locally. To illustrate this phenomenon, Fig. 4 shows a schematic representation of the interaction of a propagating flame with a section variation. An initially laminar and smooth flame is entrained by the high flow velocity created by the contraction at the obstacles. Even though most of the flame remains in a refined zone ($M=1$, $M_0=1$) and the refined zone may extend ahead of the flame ($M=0$, $M_0=1$), the flame tip is advected by the flow and elongates into a coarse mesh region ($M=1$, $M_0=0$). As this represents a small part of the flame, $M^*$ is very low and the mesh adaptation is not triggered.

Fig. 4

Illustration of the mask variation limitation. Schematic of a smooth flame entering coarse regions of the mesh locally due to a change in the flow dynamics

To avoid these issues, an alternative triggering method based on local information is proposed. It is based on the simple idea that, regions where the QoI detection criterion is fulfilled, are contained within fine mesh regions at every time step. This method is named mask inclusion in the following. The formulation is based on the comparison of the initial mask field $M_0$ and the QoI field ($\theta _{\textrm{F}}$ for the flame). As soon as the physical phenomenon of interest leaves the fine region of the mesh, an adaptation is triggered. To do so, the difference between the initial mask field $M_0$ and the QoI field is calculated at each time step at every grid node. For the flame sensor, the mesh adaptation is triggered as soon as the following condition is met:

$$\begin{aligned} \theta _{\textrm{F}}^{\textrm{n}} - M_0^{\textrm{n}} > \theta _{\textrm{F}}^{\textrm{lim}},\; \text {for\;any\;grid\;node n.} \end{aligned}$$

(5)

This apparently small formal change from averaged to local quantities has an important impact on the results. The mask inclusion triggering formulation ensures the correct resolution of the physics of interest in the high fidelity simulations targeted. Additionally, since the metric is directly dependent on the value of M, this allows for the QoI to be interpolated in between very similar fine mesh regions ($M=1$) when adapting the mesh, thus limiting interpolation errors. Simply setting a very low $M^*_{\textrm{limit}}$ is not sufficient and does not yield the desired behaviour as it is often local parts of the QoI that drive the dynamics of deflagrations, as illustrated in Fig. 4.

3.3 Mask Field Dilatation

The mask inclusion method described in Sect. 3.2 automatically triggers a mesh adaptation each time the flame leaves the refined zone, i.e. each time the flame moves locally by a single cell. To avoid an unreasonably high adaptation frequency, one solution is to extend the fine mesh region ahead of the flame, allowing more time in between adaptations (thus reducing the cost of mesh adaptations), but at the expense of a heavier mesh (increasing the cost of the solver). To this end, an operation, called dilatation in mathematical morphology, is applied to the mask field to enlarge the refined region (where $M=1$) by a fixed number of mesh cells ahead of the flame. If this procedure is relatively straight forward on structured meshes, it requires additional operations on unstructured meshes. A gather/scatter method with a maximum formulation is employed here. The method is described in Supplementary Material.

To limit the extension of the fine mesh zones due to the dilatation process, physical considerations can be introduced. Firstly, it should be noted that the flame wrinkling created by the FVI takes place on the unburnt gas side. Furthermore, the vortices on the burnt gas side have a shorter lifetime due to the increase in viscosity caused by the rise in temperature. Consequently, it is only necessary to perform the dilatation in the direction of flame propagation, i.e. in the direction of the unburnt gases, which can be easily detected with a progress variable c based on the fuel mass fraction. The progress variable goes from $c=0$ in the unburnt mixture to $c=1$ in the burnt gases. This allows for significant computational cost savings without compromising the reproduction of the key physics for the flame propagation. The mask field dilatation principle is illustrated in Fig. 5. At the bottom, the mask field is not dilated and the mesh cell size starts increasing according to the imposed growth ratio immediately ahead of the flame. At the top, the mask field is dilated by three cells, resulting in a fine mesh that extends ahead of the direction of flame propagation, i.e. in the fresh gases, identified by the progress variable c. The number of cells by which the mask field is dilated is obviously closely related to the total computational cost. Increasing the dilatation of the mask results, on the one hand, in a larger fine mesh zone and, consequently, in a higher computational cost for the solver. But, on the other hand, the mesh adaptation is triggered less frequently, reducing the mesh adaptation cost. Therefore, an optimum has to be found for each configuration. This is further discussed, in the case of the final application of this paper, in Supplementary Material. It should be noted that this choice should have only a marginal impact on the accuracy of the computation since the QoI remain on a fine mesh in all cases. In this work, the mask field dilatation is set to one cell.

Fig. 5

Example of a mask dilatation for a flame on an unstructured mesh. No mask field dilatation (bottom) and three cells dilatation (top) with the contour of flame sensor where $\theta _{\textrm{F}}$ = $\theta _{\textrm{F}}^{\textrm{lim}}$. The unburnt and burnt gases are indicated together with the associated values of progress variable. The direction of dilatation follows the propagation of the flame towards the fresh gases

3.4 Application in a 3-D, Planar, Thickened Laminar Flame Problem

To illustrate the different notions introduced in Sects. 3.2 and 3.3, several simulations of a 3-D, thickened flame propagation are carried out, as summarised in Table 1. Cases A and B are used to show the limitations of the mask variation triggering method and the importance of the dilatation whereas case C is supposed to be the best setup. Note that, in cases A and B, the value of $M^*_{\textrm{limit}}$ is set deliberately high to highlight its shortcomings for limiting cases. The test case consists in a fully premixed, laminar and planar flame, propagating into a $\hbox {CH}_{4}$-air mixture at ambient conditions.

Table 1 Matrix of AMR cases to evaluate the influence of the adaptation triggering method and dilatation

The Dynamic Thickened Flame Model for LES (DTFLES) (Legier et al. 2000) is used. This model applies an artificial thickening factor to the flame, allowing for the explicit resolution of the flame front. The two-step chemical scheme BFER (Franzelli 2011) is employed. The flame is resolved with 5 cells per thermal flame thickness. The flame is initialised using profiles extracted from a 1-D flame computed with the chemical kinetics solver Cantera (Goodwin et al. 2017). The boundary conditions (BC) use the Navier–Stokes Characteristic Boundary Conditions (NSCBC) formalism (Poinsot and Lele 1992) and are indicated in Fig. 6. In this case, the inlet velocity is set to $u_{\textrm{BC}} = s_{\textrm{L}}^0 - u_{\textrm{d}} = 0$ so that the flame propagates towards the inlet (from right to left) at an absolute velocity of $u_{\textrm{d}} = s_{\textrm{L}}^0 = 0.282\,\hbox {m}/\hbox {s}$. This is a canonical illustration of the AMR framework in the case of a propagating laminar flame, representative of the initial stage of a deflagration scenario. A first simulation on a static and homogeneous mesh with $\Delta _x= 258$ μm is performed. This case is considered as a reference (REF) to validate the AMR case results. The consumption speed $s_{\textrm{c}}$ (Poinsot and Veynante 2011) is the most relevant quantity in a laminar flame and is used to assess the accuracy of the results. The aim for the AMR methodology is to be able to recover the static case results by targeting the same mesh resolution of the reference case, $\Delta _x^{\textrm{fine}} =258$ μm, where the flame is detected. Outside this zone, the mesh is coarsened towards a resolution ten times larger ($\Delta _x^{\textrm{coarse}} = 2.58\,\hbox {mm}$). The transition from fine to coarse mesh regions is governed by a maximum growth rate ratio of 40%. The first adapted mesh, with the associated BC and a flame sensor iso-contour, is shown in Fig. 6.

Fig. 6

3D planar laminar flame test case: 2-D section of the initial adapted mesh with the domain boundary conditions. The flame front is delimited by an iso-contour of $\theta _{\textrm{F}}=\theta _{\textrm{F}}^{\textrm{lim}}$

The results are shown in Fig. 7. Since the flame of interest is an unstretched laminar flame, the consumption speed $s_{\textrm{c}}$ is expected to be equal to the laminar flame speed $s_{\textrm{L}}^0$. This behaviour is recovered by the REF simulation. AMR methods A and B exhibit spurious peaks in consumption speed along the propagation, at the instants of mesh adaptation. These peaks occur when the flame enters coarse mesh regions, as discussed in more detail in Supplementary Material. Setup C shows none of these peaks and gives, as expected, the best AMR results. The mask inclusion triggering criterion guarantees that the flame stays in the fine mesh region throughout the propagation. The computational cost of method C is reduced by 79% in comparison with the reference simulation on a static homogeneous mesh, with the cost of mesh adaptations representing only 1.2% of the total simulation cost. Of course the speed-ups shown here are strongly dependent on the ratio between the length of the fluid domain considered and the thickened flame thickness. The more the phenomena of interest are localised in space, the greater the acceleration factor provided by the AMR.

Fig. 7

3D planar laminar flame test case. Comparison of the temporal evolution of the consumption speed for the REF case (static mesh) and the different AMR methods A, B and C

4 AMR Framework for Propagating Vortices in Reactive and Non-reactive Flows

In typical deflagration scenarios in confined and obstructed channels, correctly capturing the vortical structures generated in the flow is essential to accurately predict the flame evolution. Vortical structures result from the interaction of the flow induced by the flame with obstructions, through mechanisms such as vortex shedding. In the LES framework, these large scale structures cascade to smaller scale structures down to the filter scale and interact back with the flame, constituting a driving mechanism for FA of turbulent flames in obstructed and confined geometries. This section, therefore, focuses on this critical aspect for AMR simulations. First, a vortex capturing strategy is constructed in the context of non-reactive simulations. The methodology is, then, adapted to reactive simulations with the aim of applying the method to LES of deflagrations: a vortex selection criterion is thus built based on theoretical arguments of FVI to identify relevant vortical structures, critical to predict the flame acceleration process.

4.1 Vortex Detection in Non-reactive Flows

Vortex structures can be identified as the regions of the flow where rigid rotation is predominant over deformation. That is precisely the idea behind the sensor used as QoI for the vortex capturing in the present AMR methodology: the Omega sensor. The formulation of this sensor was first introduced by Kamkar et al. (2010) and was modified more recently by Liu et al. (2016). This vortex detection sensor has the advantage of being inexpensive to compute and, most importantly, having a dimensionless and bounded formulation. It is therefore insensitive to the scale of the case of study: it separates the zones with predominant rigid rotation from the zones with predominant deformation regardless of the vortex size or intensity. Other quantities may be used similarly for vortex detection, such as the vorticity magnitude $\omega$ (Lapointe et al. 2020) Q-criterion (Hunt et al. 1988) or $\lambda _2$-criterion (Jeong and Hussain 1995) but require a case-dependent threshold that cannot be known a priori.

The Omega sensor is noted $\varPsi$ in this paper, to clearly differentiate it from the vorticity, commonly noted $\omega$. It is defined as the ratio of the Frobenius norm of the rotation tensor over the sum of the norms of the rotation and deformation tensors,

$$\begin{aligned} \varPsi = \frac{\Vert {\varvec{B}}\Vert ^{2}_{\textrm{F}}}{\Vert {\varvec{A}}\Vert ^{2}_{\textrm{F}}+ \Vert {\varvec{B}}\Vert ^{2}_{\textrm{F}}+ \epsilon } , \;\;\text {with} \;\; \Vert {\varvec{A}}\Vert ^{2}_{\textrm{F}}= \sum _{i=1}^N \sum _{j=1}^M A_{ij}^2 . \end{aligned}$$

(6)

$\varvec{A}$ and $\varvec{B}$ are, respectively, the symmetric (non-vortical) and antisymmetric (vortical) part of the velocity gradient tensor, as shown in their 2-D form in Eq. (7). The parameter $\epsilon$ was initially introduced by Liu et al. (2016) as a small positive scalar for numerical reasons, namely to avoid dividing by zero in regions without velocity gradients and to eliminate numerical noise.

$$\begin{aligned} \varvec{A} = \begin{bmatrix} \frac{\partial {u}}{\partial {x}} &{} \frac{1}{2} \left( \frac{\partial {u}}{\partial {y}} + \frac{\partial {v}}{\partial {x}} \right) \\ \frac{1}{2} \left( \frac{\partial {v}}{\partial {x}} + \frac{\partial {u}}{\partial {y}} \right) &{} \frac{\partial {v}}{\partial {y}} \end{bmatrix}; \; \varvec{B} = \begin{bmatrix} 0 &{} \frac{1}{2} \left( \frac{\partial {u}}{\partial {y}} - \frac{\partial {v}}{\partial {x}} \right) \\ \frac{1}{2} \left( \frac{\partial {v}}{\partial {x}} - \frac{\partial {u}}{\partial {y}} \right) &{} 0 \end{bmatrix} . \end{aligned}$$

(7)

The QoI $\varPsi$ takes values in the range (0,1), tending to $\varPsi =1$ in regions where the rotation is predominant and to $\varPsi =0$ where the deformation dominates, thus, being able to identify the vortex cores in the flow. To define the vortex detection criterion, a threshold $\varPsi ^{\textrm{lim}}$ needs to be introduced, so that vortex structures are identified in the regions where $\varPsi \ge \varPsi ^{\textrm{lim}}$. This criterion determines the vortical parts of the flow where the mask field will take the value $M(\varPsi )=1$:

$$\begin{aligned} M(\varPsi )={\left\{ \begin{array}{ll} 1 &{} \text {if } \varPsi \ge \varPsi ^{\textrm{lim}} \\ 0 &{} \text {if } \varPsi < \varPsi ^{\textrm{lim}} . \end{array}\right. } \end{aligned}$$

(8)

Even though this vortex detection method has been used successfully for mesh refinement applied to steady-state simulations (Pang et al. 2021), the formulation still has weaknesses. First, the value of the detection threshold varies from 0.5 to 0.6 in the literature, adding a user-dependent parameter. Secondly, the impact and physical meaning of the dimensional regularisation parameter $\epsilon$ have never been studied. In the literature, different options have been proposed for the definition of $\epsilon$. After the original use of a small positive number, Dong et al. (2018) proposed the expression:

$$\begin{aligned} \epsilon = c_\epsilon \; \textrm{max}\left( \Vert {\varvec{B}}\Vert ^{2}_{\textrm{F}}- \Vert {\varvec{A}}\Vert ^{2}_{\textrm{F}}\right) , \end{aligned}$$

(9)

with the dimensionless parameter $c_\epsilon =10^{-3}$, and the $\textrm{max}$ operator designating the maximum value in the fluid domain. This expression was applied on several non-reactive steady-state turbulent flow simulations. In the context of AMR for LES of highly unsteady phenomena, such as deflagrations, this global formulation seems ill-suited because of the strong spatial and temporal disparity of the problem. To improve the $\varPsi$ sensor in the particular context of this study, the impact of $\epsilon$ is assessed analytically hereafter. A definition of the value of $\epsilon$ is then proposed based on physical arguments of FVI.

To get a better understanding of the interpretation of the $\epsilon$ parameter, the exact expression of $\varPsi$ is derived for a simple canonical case, corresponding to an isentropic and incompressible vortex, solution of the 2-D Euler equations (Spiegel et al. 2015). Its stream function and the associated components of the velocity vector are given by:

$$\begin{aligned} \varphi = \varGamma \textrm{e}^{- \frac{1}{2} \left( \frac{r}{R} \right) ^2}; \; u = \frac{\partial {\varphi }}{\partial {y}}; \; v = - \frac{\partial {\varphi }}{\partial {x}}, \end{aligned}$$

(10)

where r is the radial coordinate $r = \sqrt{x^2+y^2}$, R is the vortex radius, $\varGamma$ is the vortex strength, to which the vortex circulation is proportional. The vortex is isotropic with respect to the polar coordinate. Injecting Eq. (10) in the definition of $\varPsi$ (Eq. 6) yields the analytical solution for the $\varPsi$ sensor for an isentropic, incompressible 2-D vortex:

$$\begin{aligned} \varPsi = \frac{ 1 }{ 1+ \left( 1 + \dfrac{2}{\hat{r}^2 -2} \right) ^2 + \epsilon \tau _{\textrm{v}}^{2} \dfrac{2 \textrm{e}^{\hat{r}^2}}{(\hat{r}^2 -2 )^2}}; \end{aligned}$$

(11)

where $\hat{r} = r/R$ is the radial coordinate of the vortex normalised by its radius and $\tau _{\textrm{v}} = R^2 / \varGamma$ is the vortex characteristic time scale, a positive scalar. $\varPsi$ is an isotropic field, variable with respect to the normalised radial coordinate, such that $\varPsi (\hat{r}) \in \left[ 0,1 \right]$. If $\epsilon \tau _{\textrm{v}}^{2} = 0$, the exponential perturbation in the denominator of Eq. (11) vanishes and the expression of $\varPsi$ becomes:

$$\begin{aligned} \varPsi = \frac{ 1 }{ 1+ \left( 1 + \dfrac{2}{\hat{r}^2 -2} \right) ^2}. \end{aligned}$$

(12)

This is represented by the solid curve in Fig. 8. Far from the vortex center, $\varPsi$ does not asymptote to zero as would be desirable:

$$\begin{aligned} \lim _{\hat{r} \rightarrow +\infty } \varPsi (\hat{r}, \epsilon \tau _{\textrm{v}}^{2}=0) = 1/2 . \end{aligned}$$

(13)

At the vortex center $\varPsi (\hat{r}=0, \epsilon \tau _{\textrm{v}}^{2}=0) = 1$. As soon as $\epsilon \tau _{\textrm{v}}^{2} > 0$, $\varPsi$ tends to zero far from the vortex center as desired:

$$\begin{aligned} \lim _{\hat{r} \rightarrow +\infty } \varPsi (\hat{r}, \epsilon \tau _{\textrm{v}}^{2}> 0) = 0 , \end{aligned}$$

(14)

as can be visualised in Fig. 8. At the vortex center, the value of $\varPsi$ is driven by the magnitude of $\epsilon \tau _{\textrm{v}}^{2}$:

$$\begin{aligned} \lim _{\epsilon \tau _{\textrm{v}}^{2} \rightarrow 0} \varPsi (\hat{r}=0) = 1 \; \; \text {and} \; \;\lim _{\epsilon \tau _{\textrm{v}}^{2} \rightarrow \infty } \varPsi (\hat{r}=0) = 0 . \end{aligned}$$

(15)

Thus, for a given vortex with a characteristic time $\tau _{\textrm{v}}$, the value of $\epsilon$ can be critical for its detection according to certain threshold $\varPsi \ge \varPsi ^{\textrm{lim}}$. In Fig. 8 for example, the case $\epsilon \tau _{\textrm{v}}^{2}=10$ would fall under the threshold $\varPsi \ge \varPsi ^{\textrm{lim}} = 1/2$.

Fig. 8

Normalised radial profile of the $\varPsi$ field. Effect of $\epsilon$ (cf. Eq. 11) on the values of $\varPsi$ for a 2-D isentropic vortex with a characteristic time $\tau _{\textrm{v}}$

The role of $\epsilon$ is therefore twofold: 1) it is a regularisation parameter that ensures the correct asymptotic behaviour of $\varPsi$ far from the vortex, where the sensor should tend to zero, and 2) even though the Omega sensor was intended to be scale independent, the value of the sensor in the vortex core is actually dependent on the ratio between $\epsilon ^{1/2}$ and the vortex time-scale $\tau _{\textrm{v}}$. This remains true in 3-D, as verified by simple dimensional analysis: $\left[ \Vert {\varvec{A}}\Vert ^{2}_{\textrm{F}}\right] =\left[ \Vert {\varvec{B}}\Vert ^{2}_{\textrm{F}}\right] = \left[ \epsilon \right] = \hbox {T}^{-2}$. Thus, $\epsilon ^{-1/2}$ can be seen as a cut-off time scale to define the vortical structures to detect. Therefore, taking a small value for $\epsilon$ is sufficient to detect all structures, regardless of their size or intensity, and to regularise the formulation by avoiding an ill-posed behaviour. The necessary condition is that $\tau _{\textrm{v}}^2 \epsilon \ll 1$ for every vortex if considering a threshold $\varPsi \ge \varPsi ^{\textrm{lim}}$ close to 1/2, as suggested in the literature (Dong et al. 2018) (see Fig. 8). This cut-off effect of $\epsilon$ is illustrated by applying the TFP-AMR methodology to non-reactive simulations of vortex advection in Sect. 4.2, confirming the importance of the choice of the formulation of $\epsilon$. Then, in Sect. 4.3 a new expression for $\epsilon$ is proposed for the case of reactive, unsteady simulations based on fundamental knowledge of flame/vortex interaction.

4.2 Application in a 2-D Vortex Advection Problem

The importance of the formulation used for $\epsilon$ is evaluated in the case of the advection of two isentropic, incompressible 2-D vortices (Eq. 10). The example presented here is particularly chosen to highlight the limitations of the formulation from Eq. (9). The unsteady Euler equations are solved on a 2-D domain, using a centered continuous Taylor–Galerkin scheme, third-order in space and fourth-order in time (TTG4A (Colin and Rudgyard 2000)). Inlet and pressure outlet boundary conditions use the NSCBC formalism (Poinsot and Lele 1992). There, two vortices V1 (top) and V2 (bottom), with different initial radii $R_1$ and $R_2$ and different initial strengths $\varGamma _1$ and $\varGamma _2$, are advected at a velocity $U_\infty$. V1 is a big vortex with weak intensity whereas V2 is a small vortex with strong intensity ($R_1 > R_2$ and $\varGamma _1 < \varGamma _2$). The main characteristics of these two vortices are given in Table 2. The reference advective time is defined as $\tau _{\textrm{adv}}=R_1/U_\infty = 0.39\,\hbox {ms}$. Since the vortices are an exact solution of the Euler equations and a high order numerical scheme is used, they should be simply advected over time in the computational domain, without any distortion or dissipation, if properly resolved.

Table 2 Characteristics of the two vortices V1 (weak, big) and V2 (strong, small), advected at a velocity $U_\infty =100\,\hbox {m}/\hbox {s}$

A reference case using a homogeneous static mesh is compared with two AMR methods that differ in the formulation chosen for $\epsilon$. The two AMR setups use the mask field built on $\varPsi$ as indicated in Eq. (8). The first setup (A) uses the formulation proposed by Dong et al. (2018). In the second setup (B), the value of $\epsilon = 10^{3}\,\hbox {s}^{-2}$ is chosen, so that $\epsilon \tau _{\textrm{v,1}}^2 = 2.6 \times 10^{-2} \ll 1$ and $\epsilon \tau _{\textrm{v,2}}^2 = 1.6 \times 10^{-5} \ll 1$. Note that, while many values are valid in this case, higher ones will be more effective in reducing spurious noise. Both methods are summarised in Table 3. In both cases, the mask field is dilated by one cell as for the flame sensor described in Sect. 3. The mask inclusion method is used to trigger the mesh adaptations. Analogously to the flame QoI (Sect. 3.2) the adaptation is triggered when vortices, defined by the QoI field ($\varPsi$), are no longer included in the region defined by the initial mask field $M_0$. This translates into the following condition:

$$\begin{aligned} \varPsi ^n - M_0^n > \varPsi ^{\textrm{lim}},\;\text {for\;any\;grid\;node\;n.} \end{aligned}$$

(16)

The transition from fine to coarse mesh regions is governed by a maximum growth rate ratio of 20%.

Table 3 Summary of the vortex advection AMR methods

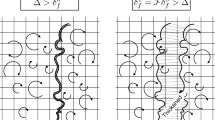
The adapted mesh and the vortices at several instants are shown in Fig. 9. The method used in case B is the only one capable of detecting and preserving vortex V1 (top vortex) because the value of $\epsilon$ has been chosen consistently with the vortex characteristics, such that $\epsilon \tau _{\textrm{v}}^2 \ll 1$ for both vortices. For case A, the vortex for which $\Vert {\varvec{B}}\Vert ^{2}_{\textrm{F}}-\Vert {\varvec{A}}\Vert ^{2}_{\textrm{F}}$ is maximal is V2, therefore it can be shown, by injecting Eq. (9) in Eq. (11), that only vortices where $\tau _{\textrm{v}} < c_\epsilon ^{-2} \tau _{\textrm{v,2}} \approx 32 \cdot \tau _{\textrm{v,2}}$ will be detected. V1, having $\tau _{\textrm{v,1}}/\tau _{\textrm{v,2}}=40$, is therefore not detected. On the other hand, as expected, both methods succeed in correctly detecting the vortex V2, since this is the vortex for which $\Vert {\varvec{B}}\Vert ^{2}_{\textrm{F}}-\Vert {\varvec{A}}\Vert ^{2}_{\textrm{F}}$ is maximal.

Fig. 9

Mesh evolution at three instants (columns) with $\varPsi$ isolines ($\varPsi =0.05\ \hbox {and}\ 0.5$ in blue and red, respectively). Regions where the criterion $\varPsi \ge \varPsi ^{\textrm{lim}} = 1/2$ is fulfilled are encompassed by the red isoline. Comparison between the different methods for the calculation of the vortex detection sensor (rows): A max epsilon; B constant epsilon. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The results can be analysed more in depth by looking at the evolution of the vorticity profiles in Fig. 10. Regarding vortex V1, only method B is able to conserve the vorticity peak. In the case of method A, the undetected and therefore insufficiently resolved vortex V1 is gradually dissipated as it propagates. Regarding vortex V2, the evolution of the vorticity profiles is identical in the two cases and the peak is well preserved: all methods being tuned to detect V2, the vortex is correctly resolved, as expected. Finally, the best method B reduces the computational cost by 94% in comparison with the reference case on a static homogeneous mesh.

Fig. 10

Normalised vorticity profiles on a line crossing the vortex center at several advective times for both vortices: V1, weak and big (a); V2 strong and small (b). Comparison between the different methods for the calculation of the vortex detection sensor in AMR and the reference static mesh. The vorticity is normalised with respect to $\omega _{\textrm{peak}}(t_0)$, the maximum value of the initial vorticity in the center of each vortex. The spatial coordinate is the distance to the vortex center $x_{\textrm{V}}$, normalised by the corresponding vortex radius

These tests confirm that the $\varPsi$ approach is very well suited for vortex detection, provided that the $\epsilon$ parameter, which acts as a cut-off, is adequately defined to capture the vortical structures of interest. The choice of $\epsilon$ might be tedious for a general case and may resort to user intervention. However in the context of FVI, this cut-off effect is an opportunity since the relevant vortical scales for the interaction with the flame can be identified a priori: the choice of $\epsilon$ can therefore be automated to avoid over –or under– selection of vortices, as presented in Sect. 4.3.

4.3 Vortex Detection and Selection in Reactive Flows

In this section, a formulation for the parameter $\epsilon$ is proposed for reactive flows, focusing on flame/vortex interaction. The objective is to ensure that all vortices that can have an impact on the resolved, thickened flame are correctly resolved on the computational grid. A clear physical meaning of $\epsilon$ is established and its value is related to the flame characteristic quantities that are known a priori, through FVI theory.

Recalling the expression of Eq. (11), $\epsilon$ acts as a filter with respect to the vortex characteristic time scale $\tau _{\textrm{v}}$. A vortex is detected by the sensor if, at any $\hat{r}$, $\varPsi (\hat{r}) \ge \varPsi ^{\textrm{lim}}$. Since $\varPsi$ is maximal at the vortex center ($\hat{r}=0$), a relation between $\tau _{\textrm{v}}$, $\varPsi ^{\textrm{lim}}$ and $\epsilon$ can be established for the detected vortex with the limit characteristic vortex time scale $\tau _{\textrm{v,limit}}$: $\varPsi (\hat{r}=0) = \varPsi ^{\textrm{lim}}$. Injecting this expression in Eq. (11), the following condition is obtained:

$$\begin{aligned} \epsilon \tau _{\textrm{v,limit}}^2 = \frac{2 (1- \varPsi ^{\textrm{lim}})}{\varPsi ^{\textrm{lim}} } . \end{aligned}$$

(17)

This relation determines which value of $\epsilon$ needs to be used so that every vortex whose characteristic time is bigger than $\tau _{\textrm{v,limit}}$ falls under the threshold for detection $\varPsi ^{\textrm{lim}}$ and is, thus, not detected. The question, then, becomes which reference value of $\tau _{\textrm{v,limit}}$ to use for the vortex selection. In a flame/vortex interaction perspective, the objective is to correctly detect all the vortex structures that may have an impact on the flame, i.e. that will induce a significant change in heat release. This problem has been widely studied in the literature, as it sets the bases for flame/turbulence interaction. Spectral diagrams of flame/vortex interaction have been constructed using both numerical calculations (Poinsot et al. 1991) and experimental techniques (Roberts et al. 1993), showing consistent qualitative trends. Different outcomes from a flame/vortex interaction can be identified, and will depend on the vortex scale R and its velocity $\varGamma /R$. In these diagrams, a cut-off limit (Gülder and Smallwood 1995) can be identified, which corresponds to vortices causing a change in total reaction rate of around 5%. This cut-off limit is related to the vortex Reynolds number ${ Re}_{\textrm{v}}$, defined as:

$$\begin{aligned} { Re}_{\textrm{v}} = \left( \frac{\varGamma /R}{s_{\textrm{L}}^0} \right) \left( \frac{R}{\mathcal {F} \delta _{\textrm{L}}^0} \right) =\left( \frac{R}{\mathcal {F} \delta _{\textrm{L}}^0} \right) ^2 \frac{\tau _{\textrm{c}}}{\tau _{\textrm{v}}} = \left( \frac{R}{\mathcal {F} \delta _{\textrm{L}}^0} \right) ^2 { Da}_{\textrm{v}}^{-1} , \end{aligned}$$

(18)

where $\delta _{\textrm{L}}^0$ is the laminar flame thickness and $\mathcal {F}$ is the thickening factor from the TFLES model. In this expression, the relation between ${ Re}_{\textrm{v}}$, the vortex characteristic time $\tau _{\textrm{v}}$ and the thickened flame chemical time scale $\tau _{\textrm{c}}$, for a given vortex with spatial scale R is shown. Note that the characteristic flame time in Eq. (18) corresponds to the thickened flame time $\mathcal {F} \delta _{\textrm{L}}^0 / s_{\textrm{L}}^0$ since only resolved fields are relevant in the LES context, as subgrid effects are handled by dedicated models. Still, the formulation correctly degenerates towards DNS, which corresponds to the limit case of a thickening value $\mathcal {F}=1$. ${ Da}_{\textrm{v}}$ represents the vortex Damköhler number, i.e. the ratio between the vortex characteristic time $\tau _{\textrm{v}}$ and the thickened flame chemical time scale $\tau _{\textrm{c}}$:

$$\begin{aligned} { Da}_{\textrm{v}} = \frac{\tau _{\textrm{v}}}{\tau _{\textrm{c}}} = \frac{\tau _{\textrm{v}}}{\mathcal {F} \delta _{\textrm{L}}^0 / s_{\textrm{L}}^0} = \left( \frac{s_{\textrm{L}}^0}{\varGamma /R} \right) \left( \frac{R}{\mathcal {F} \delta _{\textrm{L}}^0} \right) . \end{aligned}$$

(19)

Using the aforementioned spectral diagrams from the literature, the order of magnitude of the cut-off vortex Reynolds number can be roughly evaluated: Poinsot et al. (1991) numerically estimate the cut-off limit, which can be approximated to a value of ${ Re}_{\textrm{v,limit}} \approx 13$; Roberts et al. (1993) show an experimental evaluation of the cut-off limit corresponding to ${ Re}_{\textrm{v,limit}}=2.5$. Therefore, the order of magnitude retained here for this parameter is ${ Re}_{\textrm{v,limit}} = 10$. This will set a limit for the vortices that should be detected with the $\varPsi$ sensor. Additionally, the vortex scales that can be recovered in a given simulation will be bounded: on the lower end, by the mesh resolution $\Delta _x$; and on the higher end by the largest characteristic dimension in the simulated geometry L. These limits are illustrated in Fig. 11.

Using Eq. (18), the value of $\tau _{\textrm{v,limit}}$ to use for the vortex selection can be determined as a function of ${ Re}_{\textrm{v,limit}}$ for a given spatial scale R, here set to the largest characteristic dimension in the simulated geometry L:

$$\begin{aligned} \tau _{\textrm{v,limit}} = \left( \frac{L}{\mathcal {F} \delta _{\textrm{L}}^0} \right) ^2 { Re}_{\textrm{v,limit}}^{-1} \tau _{\textrm{c}} = { Da}_{\textrm{v,limit}} \tau _{\textrm{c}} . \end{aligned}$$

(20)

Fig. 11

Simplified spectral diagram of flame/vortex interaction

Figure 11 illustrates the aforementioned vortex selection criterion. In the diagram, the selection through the value of $\tau _{\textrm{v,limit}}$ is represented in dimensionless form through the ${ Da}_{\textrm{v,limit}}$ curve. There, the correspondence between ${ Re}_{\textrm{v,limit}}$ and ${ Da}_{\textrm{v,limit}}$ at the selected spatial scale L is shown. As the largest characteristic dimension in the simulated geometry L is chosen to be conservative, the vortex selection ensures that all vortices above the cut-off limit are detected, at the expense of detecting some of the vortices that will have no impact on the flame. Finally, $\epsilon$ can be written as a function of a limit vortex Reynolds number at the largest characteristic scale L, by injecting Eq. (20) in Eq. (17):

$$\begin{aligned} \epsilon = \dfrac{2 (1- \varPsi ^{\textrm{lim}})}{\varPsi ^{\textrm{lim}}} \dfrac{\left( s_{\textrm{L}}^0 \mathcal {F} \delta _{\textrm{L}}^0 \right) ^2}{L^4} \mathrm{Re}_{\textrm{v,limit}}^2. \end{aligned}$$

(21)

Then, the general formulation proposed is obtained by injecting Eq. (21) in Eq. (6):

$$\begin{aligned} \varPsi = \frac{\Vert {\varvec{B}}\Vert ^{2}_{\textrm{F}}}{\Vert {\varvec{A}}\Vert ^{2}_{\textrm{F}}+ \Vert {\varvec{B}}\Vert ^{2}_{\textrm{F}}+ \dfrac{2 (1- \varPsi ^{\textrm{lim}})}{\varPsi ^{\textrm{lim}}} \dfrac{\left( s_{\textrm{L}}^0 \mathcal {F} \delta _{\textrm{L}}^0 \right) ^2}{L^4} { Re}_{\textrm{v,limit}}^2 } . \end{aligned}$$

(22)

This expression combines the general vortex detection expression with a conservative flame/vortex interaction selection criterion. The last parameter whose value needs to be set is the threshold $\varPsi ^{\textrm{lim}}$. Since the goal is to detect only the parts of the flow where rotation is predominant, the value of $\varPsi ^{\textrm{lim}}$ can be set such that a 2-D isentropic vortex, for which $\tau _{\textrm{v}} \ll \tau _{\textrm{v,limit}}$, is captured up to its radius. That is $\varPsi (\hat{r}) \ge \varPsi ^{\textrm{lim}}$ only for $\hat{r} \in (0,1)$. By applying this condition to Eq. (11) and injecting the expression of $\epsilon$ from Eq. (21), the following expression is obtained:

$$\begin{aligned} \varPsi ^{\textrm{lim}} = \varPsi \left( \hat{r}=1 , \frac{\tau _{\textrm{v,limit}}}{\tau _{\textrm{v}}} \gg 1 \right) = \frac{1}{2} . \end{aligned}$$

(23)

Additionally, this value is conservative and consistent with the criterion chosen by Liu et al. (2016). It corresponds to regions of the flow where rotation is dominant, i.e. $\Vert {\varvec{B}}\Vert ^{2}_{\textrm{F}}> \Vert {\varvec{A}}\Vert ^{2}_{\textrm{F}}$.

To summarise, the proposed formulation is dimensionless and able to capture any region where rotation overtakes deformation. It is a local, bounded quantity between zero and one. With the proposed estimation for the parameter $\epsilon$, it is no longer ill-defined in regions without velocity gradients, naturally reducing numerical noise. Finally it allows to preserve all vortices that can have an impact on the flame, based on a priori known flame characteristic quantities: all coefficients are related to the physics of the problem, with conservative estimates (Table 4), and do not rely on user-dependent parameters.

Table 4 Summary of the final formulation for $\epsilon$ in reactive flows

4.4 Application in a 2-D Thickened Flame/Vortex Interaction Case

To validate the previously developed formulation for $\epsilon$ and to illustrate the combination of the flame and vortices criteria in the AMR framework, several thickened flame/vortex interaction simulations are conducted. This exercise has three objectives: (1) to show the ability of the AMR simulations to recover the results from a reference simulation on a static, homogeneously fine mesh; (2) to illustrate the previously discussed FVI dynamics, i.e. that it is the vortex Reynolds number $\mathrm{Re}_{\textrm{v}}$ that determines if a vortex strongly impacts a flame and (3) to show that the formulation for $\epsilon$ in reactive cases automatically adapts to the flame characteristics and ensures that vortices having a significant impact are detected. The configuration used is shown in Fig. 12a. A 2-D isentropic and incompressible vortex (as in Sect. 4.2) is convected towards a planar, thickened methane-air flame (as in Sect. 3.4 but in 2-D). The inlet flow velocity and, therefore, the vortex advection velocity is set to $U_\infty =s_{\textrm{L}}^0=0.282\,\hbox {m}/\hbox {s}$ so that the flame remains fixed in the domain, prior to the FVI. The size of the vortex is kept constant in all cases, with an initial radius $R=51.6\,\hbox {mm}$. The reference advective time is defined as $\tau _{\textrm{adv}}=R/U_\infty = 183\,\hbox {ms}$. The flame characteristics can be found in Sect. 3.4. The chemical kinetics and the initialisation procedure are identical to the ones used in Sect. 3.4. The thickened flame thermal thickness is resolved using 5 cells, so the level of thickening is adapted to the selected resolution in each case. The unsteady reacting Navier–Stokes equations are solved on a 2-D domain depicted in Fig. 12a, using a centered continuous Taylor–Galerkin scheme, third-order in space and fourth-order in time (TTG4A (Colin and Rudgyard 2000)), as in Sect. 4.2. The boundary conditions use the NSCBC formalism (Poinsot and Lele 1992).

Fig. 12

FVI setup and different cases studied

A total of six different cases are used for this test and are summarised in Table 5. Both static mesh and AMR simulations are performed for each case. In the AMR simulations, the transition from fine to coarse mesh regions is governed by a maximum growth rate ratio of 20%. The formulation of $\epsilon$ summarised in Table 4 is employed, using the appropriate flame-dependent quantities and selecting $L=R$, since a single vortex is present in this simplified configuration. The test cases are separated in two groups. Cases A1/A2/A3/A4/A4X share the same flame, with a thickening factor of $\mathcal {F}=60$. The strength of the vortex $\varGamma$ is progressively increased, so that the vortex Reynolds number $\mathrm{Re}_{\textrm{v}}$ also increases, following Eq. (18). According to the FVI literature presented in Sect. 4.3, the impact of the vortices on the resolved flame should increase with $\mathrm{Re}_{\textrm{v}}$ and become non-negligible for values of $\mathrm{Re}_{\textrm{v,limit}} \ge 10$. The AMR is expected to detect only the vortices with $\mathrm{Re}_{\textrm{v}} \ge { Re}_{\textrm{v,limit}} = 10$, which should have a significant impact (case A4). In case A4X, the vortex detection is willingly disabled to show the consequences of not detecting a strongly impacting vortex. The second group of test cases comprises cases A3/B3. They share the same vortex, with strength $\varGamma = 2.7 \times 10^{-2}\,\hbox {m}^{2}/\hbox {s}$. The thickening factor of the flame $\mathcal {F}$ is decreased from 60 (A3) to 20 (B3), so that the vortex Reynolds number $\mathrm{Re}_{\textrm{v}}$ increases, following Eq. (18). The thinner flame (B3) should be more sensitive to the vortex than the thicker one (A3), and the vortex detection should automatically adapt, accordingly. All cases are placed in the flame/vortex interaction diagram shown in Fig. 12b. To evaluate the impact of the vortex on the flame, the normalised consumption speed as a function of the reduced time $t/\tau _{\textrm{adv}}$ is used. Since the consumption speed is directly proportional to the total consumption rate, the increase in normalised consumption speed corresponding to the cut-off limit mentioned in Sect. 4.3 is also around 5%. The simulations are performed until the vortex has finished crossing the flame front, i.e. until $t/\tau _{\textrm{adv}}=5$.

Table 5 Summary of the flame/vortex interaction cases

To carry out these reactive simulations with vortex detection, the combined mask field is built additively from both the flame and vortex sensor. It is set to $M=1$ if either the flame or the vortex criteria are met (Eqs. 3 and 8). Additionally, following the reasoning presented in Sect. 3.1, as the flame vortex interaction primarily happens in the fresh gases side, the mask field is fixed to zero in the burnt gases side even if vortices are detected. Regarding the mesh adaptation, it is triggered when either one of the conditions in Eqs. (5) and (16) is met. The fine mesh size targeted is the same for both QoI (the flame and the vortex sensors). This is done to avoid space and time commutation errors (Mehl et al. 2021; Moureau 2004) in the present LES framework. Indeed, having different target size between the flame and vortex metric would lead to an inconsistency between the combustion model filter size and the flow filter size of the LES, which would require to adapt the subgrid models (Mehl et al. 2021).

Results from the different simulations are shown in Fig. 13. The first group of cases (A1/A2/A3/A4/A4X) is presented in Fig. 13a. As expected, the higher the $\mathrm{Re}_{\textrm{v}}$, the more the flame is affected by the vortex and the higher the increase in consumption speed. In cases A1 and A2, the variation in consumption speed is almost negligible, being under the cut-off limit of 5%. These vortices, with $\mathrm{Re}_{\textrm{v}} = 0.11\;{and}\;1.1 < \mathrm{Re}_{\textrm{v,limit}}$, have no major impact on the flame. That is the reason why, even though the vortices are not detected in AMR, the results remain very similar to the reference cases performed on a static refined mesh. For case A3, with $\mathrm{Re}_{\textrm{v}}= 3.3 < \mathrm{Re}_{\textrm{v,limit}}$, the flame starts to be affected by the vortex ($s_{\textrm{c}}/s_{\textrm{L}}^0 \approx 110\%$) and the AMR simulation does not recover the same results as the reference simulation, since the vortex is not detected. As the value of $\mathrm{Re}_{\textrm{v,limit}}=10$ comes from an approximate estimates from the literature (going from $\mathrm{Re}_{\textrm{v,limit}}=2.5$ (Roberts et al. 1993) to $\mathrm{Re}_{\textrm{v,limit}}=13$ (Poinsot et al. 1991)), discrepancies in values close to the threshold may be observed. Nevertheless, the order of magnitude of the parameter seems to yield reasonable results. Finally, case A4 ($\mathrm{Re}_{\textrm{v}} = 11 > \mathrm{Re}_{\textrm{v,limit}}$) shows a strong impact on the flame, as expected ($s_{\textrm{c}}/s_{\textrm{L}}^0 \approx 150\%$). The vortex is successfully detected in the AMR simulation and the evolution of the reference simulation is correctly recovered. Case A4X illustrates the importance of correctly detecting vortices that have a strong impact on the flame. In this case, the vortex detection is disabled, and the FVI is clearly underestimated.

Fig. 13

Temporal evolution of the flame consumption speed during the FVI. Solid lines: static mesh simulations; dashed lines: AMR simulations where the vortex is detected/refined; dotted lines: AMR simulations where the vortex is not detected/refined

The reference and AMR simulations are compared in more detail for cases A4 and A4X in Fig. 14. In case A4, both the flame and the vortex are detected in the AMR simulation, retrieving the same evolution as the reference case. The vortex is advected towards the flame and its vorticity levels are preserved. The velocity perturbation created by the vortex induces a strong flame wrinkling until the vortex enters the burnt gases, where the higher viscosity rapidly dissipates it. In the AMR simulation A4X, since the vortex is not detected, it evolves on a very coarse mesh, being highly dissipated before even interacting with the flame. As a consequence, a strong underestimation of the flame consumption speed is observed. The AMR simulation of case A4 allows for a reduction of 74% of the computational cost in comparison with the reference case on a static homogeneous mesh.

Fig. 14

Mesh evolution at three instants (columns). Comparison between the cases with $\mathcal {F}=60$, $\varGamma = 2.7 \times 10^{-2}\,\hbox {m}^{2}/\hbox {s}$ and $\mathrm{Re}_{\textrm{v}}=11$ (rows): (A4-REF) reference static mesh simulation; (A4-AMR) AMR simulation with vortex detection activated; (A4X) AMR simulation with vortex detection deactivated. Transparent vorticity field with progress variable isolines ($c=0.1\ \hbox {and}\ 0.9$) identify the vortex and the flame

To show the capability of the vortex detection method to adapt to the flame characteristics, the results from cases A3/B3 are shown in Fig. 13b. These two cases share the same vortex but the flame thickening factor is very different (60 and 20, respectively). As expected, in case B3 with the lower thickening ($\mathrm{Re}_{\textrm{v}} =11>\mathrm{Re}_{\textrm{v,limit}}$), the flame is strongly impacted by the vortex. The impact is somewhat similar to the one in case A4 ($s_{\textrm{c}}/s_{\textrm{L}}^0 \approx 150\%$). This shows that it is indeed $\mathrm{Re}_{\textrm{v}}$ that pilots the relative impact of a vortex on a flame. In both cases, the value of $\epsilon$ adapts to the change in $\mathcal {F}$, resulting in a successful detection of the impacting vortex. This allows for the AMR case to recover the evolution of the reference case. The simulation cost of case B3 is reduced by 88% with AMR compared with the static reference case.

5 Application of TFP-AMR in a Complex and Highly Turbulent Explosion Chamber with Variable Obstacles and Fuels

To validate the TFP-AMR methodology presented in the previous sections, several LES of explosions in a semi-open chamber with obstacles are performed. The goal is to show the genericity of the AMR methodology, recovering the results obtained on static and homogeneous meshes, regardless of the geometrical configuration or the type of fuel.

5.1 Setup Description

The baseline experimental setup is that of the laboratory-scale explosion chamber from the University of Sydney (Kent et al. 2005; Masri et al. 2012). It consists in a semi-confined chamber with a variable number of obstacles where deflagrations of different mixtures are studied (Fig. 15a). The chamber is filled with a perfectly premixed fuel-air mixture and ignited on the closed end. The obstacles consist of three removable grids that can be positioned at different distances from the ignition source and one fixed central obstruction with a square cross section. The number of obstacles will pilot the level of turbulence that is generated as the flame propagates in the chamber. This configuration presents several advantages that make it suitable for demonstrating the potential of the TFP-AMR method. Firstly, the experimental database includes different operating points in variable geometries, thus enabling the generic nature of the AMR approach developed here to be assessed and validated. Secondly, previous works have already shown the ability of LES to reproduce the physics of such phenomena (Vermorel et al. 2017; Volpiani et al. 2017) using static and homogeneous meshes, thus constituting a solid basis of comparison for the evaluation of AMR results.

Fig. 15

Explosion chamber setup from the University of Sydney

Table 6 Summary of the complex deflagration cases

For this work, three configurations are retained, as summarised in Table 6. Two different geometries are used. The first geometry (noted A) corresponds to a chamber with 1 grid of obstacles followed by a central obstacle (Fig. 15b top). The second (noted B) corresponds to a chamber with 3 grids of obstacles followed by a central obstacle (Fig. 15b bottom). In addition, two different flammable mixtures are also considered: a propane-air mixture at an equivalence ratio of $\phi = 1$ and a hydrogen-air mixture at an equivalence ratio of $\phi = 0.7$. The laminar flame speed is around four times higher in the case of hydrogen. Since the flame front propagation velocity and acceleration are proportional to the laminar flame speed, a faster and more violent deflagration is expected in the case of hydrogen. In this type of scenario, the overpressure is the key quantity that causes the destructive effects and is, therefore, the critical quantity to be predicted. In the experimental test rig, the pressure signal is recorded by a pressure transducer placed at the center of the closed end of the chamber, near the ignition location (Fig. 15a).

5.2 Numerical Setup

The LES numerical setup is close to that described in Vermorel et al. (2017). The computational domain includes the combustion chamber and a plenum, located at its outlet, which mimics the atmosphere. Both chamber and obstacle walls are modelled as non-slip walls. Plenum boundaries are set as atmospheric pressure outlets, using the NSCBC formalism (Poinsot and Lele 1992). The subgrid scale turbulence is modelled by the WALE model (Nicoud and Ducros 1999). Ignition is done through a hemisphere of burnt gases with a radius of 10 mm imposed at $t=0$ (Fig. 15a). The DTFLES combustion model is used with the efficiency formulation from Colin et al. (2000). A 6 species reduced 2-step chemical scheme is used for propane-air combustion (Quillatre et al. 2013). For hydrogen, previous work of Vermorel et al. (2017) used a reduced 1-step chemical scheme. To gain in accuracy and to show the validity of AMR using more complex chemistry, the scheme used in this study is the sub-mechanism for hydrogen combustion from the University of San Diego (San Diego 2016) (9 species, 42 reactions). Due to the more complex nature of the chemical scheme, the algebraic flame sensor from Eq. (2) cannot be used anymore. The sensor from Jaravel (2016), based on a transport equation, is used instead. Even though the formulation of the sensor itself is different, the resulting sensor field $\theta _{\textrm{F}}$ is analogous and can be used indistinctly as a QoI.

Simulations carried out on static meshes will be referred to as REF in the following. A constant mesh resolution of 0.5 mm is used in the chamber, with a smooth transition to a coarser mesh in the plenum filled with air at atmospheric conditions. For the AMR simulations, the target resolution, in the regions where flame and vortices are detected, is equal to that of the static mesh, to ensure a fair comparison. Outside said regions, the target resolution is set to 2.5 mm, corresponding to a maximum $\Delta _x^{\textrm{coarse}}/\Delta _x^{\textrm{fine}}$ ratio of 5. This ratio is imposed by geometric constraints since a minimum resolution of 2 numerical cells is required in the 5 mm gaps between two strips of a turbulence-generating grid. The transition from fine to coarse mesh is governed by a maximum growth rate ratio of 10%.

5.3 Results

A comparison of the flow fields between AMR and REF simulations is displayed in Fig. 16 for each of the cases of Table 6. For all three cases, the flame and flow physics of the reference simulation on homogeneous and static meshes are perfectly reproduced by AMR. The shape of the flame and the levels of heat release are almost identical. The flow ahead of the flame is a direct result of the FA and the chamber geometry. Therefore, the instantaneous vorticity fields are a consequence of the complete time-history of the FA. The correspondence between AMR and REF simulations shown here is, therefore, only possible if the complete time-history of the deflagration scenario has been correctly captured. One can also see that the explosion dynamics are significantly different in each of the three cases. Case B-$\hbox {H}_{2}$ generates higher vorticity magnitude levels than B-$\hbox {C}_{3}\hbox {H}_{8}$ since the laminar flame speed of hydrogen is much higher than the one of propane (Table 6). Case B-$\hbox {C}_{3}\hbox {H}_{8}$, in turn, creates higher vorticity levels than A-$\hbox {C}_{3}\hbox {H}_{8}$, due to the presence of a higher number of obstacles. These obstacles obstruct the flow in the fresh gases, creating vortex shedding and zones with predominant rotation in their wake. Not only the vorticity levels are recovered, but also the shape of the wake around obstacles is correctly reproduced with AMR. This is ensured by the conservative vortex selection criteria developed in Sect. 4.3.

Fig. 16

Comparison between AMR and REF simulations for the three cases of Table 6. All cases are compared at approximately the same flame tip position, corresponding to the arrival of the flame at the second row of obstacles in geometry B. Heat release rate at the flame front plus vorticity magnitude contours. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The overpressure evolution is shown in the left column of Fig. 17. For all cases, the overpressure curves from the experiments are shifted in time to match the maximum overpressure peak of the reference simulation, as commonly done in this type of comparison. This procedure also allows to keep the curves from the different simulations unchanged, thereby highlighting potential differences between the reference and AMR simulations. The maximum overpressure shows the expected tendency between the three cases, as it is highly dependent on the flame velocity and acceleration rate. Geometry B cases show higher overpressures because of the stronger turbulence generated by the presence of more obstacles. Case B-$\hbox {H}_{2}$ shows the highest overpressure due to its fastest flame propagation. The overpressures obtained with AMR show maximum peak levels and evolution very similar to those of the REF cases. All curves remain within the experimental envelop. This validates the capability of the AMR approach to recover precise results, independently of the case of study.

Fig. 17

Comparison between AMR and REF simulations for the three cases of Table 6 (rows). Temporal evolution of the overpressure at the ignition point (left column). Temporal evolution of the number of cells (right column): the symbols are placed every 10 mesh adaptations

The evolution of the number of cells is presented in the right column of Fig. 17. At the very start of the simulations, the number of elements in the AMR cases is around 8 times lower than the corresponding REF case, for the three cases. Then, a sharp increase in the number of cells is first observed, followed by a gradual increase until a maximum of around 80% of the static mesh size is reached. This trends can be explained in further detail by looking at the evolution of the mask fields that determine the evolution of the adapted mesh. This is represented for case B-$\hbox {H}_{2}$ in Fig. 18. Initially, as the flow is quiescent, only the hemispherical burnt gases kernel is detected and refined. Then, as the flame starts to propagate, vortices are detected around the obstacles. This leads to the first increase in the number of cells shown in Fig. 17. Since case A-$\hbox {C}_{3}\hbox {H}_{8}$ has fewer obstacles, the total number of cells is slightly lower than in the other two cases. Thereafter, the flame gradually accelerates and occupies more and more space in the computational domain, increasing the mesh size. The mask field successfully follows the evolution of the flame shape as well as the advected vortices in the wake of the obstacles. Eventually, the obstacles are immersed in the burnt gases and the flame is close to the chamber’s end. It is at this point that the number of cells reaches a maximum corresponding to 80% of the static mesh size. Note that the adapted mesh is refined only in the unburnt mixture and across the flame, as expected. At the end of the simulations, the flame leaves the chamber and the number of cells decreases accordingly.

Fig. 18

Snapshots of the evolution of the adapted mesh in the case B-$\hbox {H}_{2}$. Isolines of mask field $M=1$. The flame mask is shown in red and the vortex mask in blue. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

5.4 Computational Cost

For an AMR simulation, the total computational cost corresponds to the sum of the solver cost and the mesh adaptation cost. For each case, the REF case solver cost, AMR solver cost and AMR mesh adaptation cost are shown in Fig. 19. In all cases, the costs are compared at the occurrence of the third pressure peak in the REF simulation (Fig. 17). In the A-$\hbox {C}_{3}\hbox {H}_{8}$ case, for instance, both REF and AMR computational costs are compared for a physical time of 16.7 ms. The highest computational savings are observed for the case A-$\hbox {C}_{3}\hbox {H}_{8}$ (− 64.0%), followed by B-$\hbox {C}_{3}\hbox {H}_{8}$ (− 45.3%) and finally B-$\hbox {H}_{2}$ (− 31.7%). This result is a direct consequence of the different flame dynamics: the faster the deflagration, the lower the gains arising for having a reduced number of cells. Indeed, Fig. 17 shows that, in case A-$\hbox {C}_{3}\hbox {H}_{8}$, the AMR simulation takes around 10 ms to reach 50% of the number of cells in the REF case. In comparison, this number of cells is reached after 7.5 ms for case B-$\hbox {C}_{3}\hbox {H}_{8}$ and 2.5 ms for case B-$\hbox {H}_{2}$. This can be explained, first, by looking at the simulations results on geometry A. In this geometry, the flame takes a much longer time to reach the obstacles, remaining laminar, and therefore slower, for a longer time. This allows for a larger reduction in the number of cells because the flame only covers a small part of the computational domain for a longer time. In geometry B, the hydrogen flame is much faster than the propane one. Therefore, the flame goes across the obstacles much faster, triggering mesh adaptations at a higher rate. This leads to a significant increase in the relative impact of the mesh adaptation cost.

Fig. 19

Normalised computational cost for the A-$\hbox {C}_{3}\hbox {H}_{8}$ case (left—208 mesh adaptations), B-$\hbox {C}_{3}\hbox {H}_{8}$ case (middle—222 mesh adaptations) and B-$\hbox {H}_{2}$ case (right—243 mesh adaptations)

Of course, the computational cost savings are highly dependent on the type of configuration studied. In the Sydney experiments, the flame rapidly takes up a large part of the chamber. Higher savings would be observed in more favourable configurations, where the flame is more compact and the vortices are very localised in small regions of the domain, as in the experimental configurations studied by Boeck et al. (2016), for example. This complex larger-scale case was studied by Vanbersel et al. (2023) using the same methodology, showing computational cost savings of up to 88%. The size of the static mesh chosen for comparison with the AMR simulations also impacts the cost savings: the finer the resolution of the static mesh, the greater the potential savings with AMR.

6 Conclusion

In this work, a systematic and user-independent mesh adaptation method, called TFP-AMR (Turbulent Flame Propagation-AMR), has been presented. It uses the AMR libraries MMG3D and kalpaTARU, with unstructured tetrahedral meshes. This method is used to perform LES of deflagrations in complex, confined and obstructed geometries. It shows promising results on several test cases, without requiring any modification from the user: (1) a 3-D propagating flame, with a computational cost reduction of 80% compared to a reference simulation performed on a static mesh; (2) a 2-D vortex advection, with a computational cost reduction of 94%; (3) a 2-D thickened flame/vortex interaction, with a computational cost reduction between 74% and 88% and (4) three deflagration scenarios in obstructed geometries with different fuels, for a computational cost reduction between 32 and 64%. All simulations have shown the capability of the method to retrieve precise results for a lower cost.

The methodology used in this work is most adapted to deflagrations in confined and obstructed geometries, where the two physical phenomena of interest are the flame and the vortices. For other physics of interest, the proposed method can be easily extended by building suitable sensors and criteria in an analogous feature-based fashion. The approach could also be extrapolated to other mesh topologies. In the present method, a minimum number of parameters are left for the user to determine. Overall, they do not significantly affect the accuracy of the results, but may have slight room for improving the computational cost, depending on the use case. This method offers the possibility to compute complex and larger-scale configurations for a largely reduced computational cost, either in LES or DNS, and can be implemented with any AMR library.