1 Introduction

The use of high-fidelity simulation tools in industrial design has progressed in recent years. In particular, Large Eddy Simulation (LES) has enabled significant advances in the understanding of combustion systems, such as internal combustion engines (ICE) (Rutland 2017) and gas turbines (Gicquel et al. 2012). However, practical systems operate at high pressure and temperature, and the scales associated to combustion and turbulence are much smaller than affordable computational cell sizes. In the context of turbulent flames, modeling is thus needed to (i) enable a proper resolution of flame fronts; (ii) describe the interactions between subgrid scale (SGS) turbulence, not resolved on the mesh, and the flame (Fiorina et al. 2015). A wide variety of models have been proposed in the literature to tackle issues (i) and (ii). Common strategies include the following:

  • Statistical methods, where SGS interactions are modeled by considering presumed or transported probability density functions (Haworth 2010; Givi 2006).

  • Mixing-based methods, such as Linear Eddy Model (LEM) (Kerstein 1988) or One Dimensional Turbulence model (ODT) (Cao and Echekki 2008), are based on a multi-scale approach, where turbulence is incorporated in a stochastic manner and reactions are computed on fine embedded meshes.

  • Geometrical methods, where the flame is considered as a moving geometrical surface (Colin et al. 2000, 2003). In this case, SGS interactions are taken into account through the definition of a subgrid-scale flame surface.

For any LES turbulent combustion model, the accuracy deteriorates as the cell size increases. Indeed, for large cells, a significant part of the interactions between flame and turbulence has to be modeled. As the model involves uncertainties due to its underlying assumptions, the accuracy is expected to be smaller. A strategy to increase accuracy at a relatively low computational cost is to use Adaptive Mesh Refinement (AMR). The principle is to add computational cells dynamically where it is needed. AMR has been successfully applied to several physical problems, in particular those involving sharp interfaces such as primary break-up (Fuster et al. 2009; Liu et al. 2019) or rising bubbles (Antepara et al. 2019). AMR is particularly suitable for combustion as flames involve sharp gradients of temperature and species mass fractions in very localized regions of space. Several previous studies proposed the use of AMR to compute premixed (Xiao et al. 2018; Haldenwang and Pignol 2002; Mehl et al. 2018), non-premixed (Gao and Groth 2006, 2010) and spray flames (Xu et al. 2018). They have shown a significant reduction of the cell count with respect to traditional meshes for a similar accuracy.

Using AMR in combustion problems however introduces two resolution levels, namely a fine resolution for the flame and a coarser one for the surrounding flow. It thus raises questions regarding the applicability of standard turbulent combustion models, which do not intrinsically take into account differences in the turbulent flow resolution. The aim of the present paper is to investigate this issue and propose a model which explicitly integrates the impact of a difference in cell size between the flame and the surrounding flow. The study will be conducted in the context of a specific turbulent combustion model, namely the Thickened Flame Model (TFM) (Colin et al. 2000). TFM is a geometrical model which consists in artificially thickening the flame front to ensure its correct resolution on the mesh. It involves a subgrid-scale wrinkling factor to model SGS interactions. A coupling between TFM and AMR (TFM-AMR) has recently been proposed (Mehl et al. 2018) and will be considered here. The present work extends the model proposed in Mehl et al. (2018) by considering the implications of using AMR on the subgrid-scale wrinkling factor modeling. The TFM-AMR methodology is briefly described in Sect. 2. A new model is then proposed to properly take into account the effect of AMR on the turbulent flame propagation. The model is finally validated on a turbulent flame propagating in a Homogeneous Isotropic Turbulence (HIT) in Sect. 3.

2 TFM-AMR Model for Turbulent Premixed Combustion

2.1 TFM-AMR Model

TFM formulation Turbulent combustion modeling is addressed with the Thickened Flame Model (TFM), originally developed for the LES of turbulent premixed combustion by Colin et al. (2000). The flame front is thickened to ensure a good resolution of the reactive layer, and the impact of subgrid scale structures on the flame is modeled using an efficiency factor (Colin et al. 2000; Charlette et al. 2002a). A dynamic formulation of the TFM model is retained, where thickening is restricted to the flame front region (Légier et al. 2000). A gradient assumption is used to model turbulent fluxes outside the flame. The transport equation of a thickened species mass fraction \({\widetilde{Y}}_k\) reads:

$$\begin{aligned} \frac{\partial {\overline{\rho }} {\widetilde{Y}}_k }{\partial t} + \frac{\partial {\overline{\rho }} {\widetilde{u}}_i {\widetilde{Y}}_k }{\partial x_i} = \frac{\partial }{\partial x_i} \left( \left[ {\mathcal {F}}E {\overline{\rho }}{\widetilde{D}}_k + (1-S) \frac{\mu _t}{Sc_t} \right] \frac{\partial {\widetilde{Y}}_k }{\partial x_i} \right) + \frac{E}{{\mathcal {F}}} \overline{{\dot{\omega }}}_k \end{aligned}$$
(1)

where \({\mathcal {F}}\) is the thickening factor, E the efficiency factor, \(\mu _t\) the turbulent viscosity and \(Sc_t\) the turbulent Schmidt number. S is the flame sensor function estimated using a methodology derived by Jaravel (2016). In this approach, the flame front is first detected using a sensor \(S'\):

$$\begin{aligned} S' = \max \left[ \min \left( \beta \frac{\mid \overline{{\dot{\omega }}}_{\text {fuel}} \mid }{ {\dot{{\varOmega }}}_{fuel} (\phi ,p)} -1, 1 \right) ,0 \right] \end{aligned}$$
(2)

where \({\dot{{\varOmega }}}_{fuel}\) is the maximal fuel reaction rate tabulated from 1-D laminar premixed flames as a function of the equivalence ratio \(\phi\) and the pressure p. The sensor \(S'\) is consequently enlarged towards fresh and burned gases by a filtering operation described in Jaravel (2016). \(\beta\) is a parameter controlling the thickness of the sensor, set to \(\beta =2\) in this work.

The thickening factor is expressed as:

$$\begin{aligned} {\mathcal {F}} = 1 + \left( {\mathcal {F}}_{max} -1 \right) S \end{aligned}$$
(3)

where \({\mathcal {F}}_{max}\) is a grid-dependent quantity:

$$\begin{aligned} {\mathcal {F}}_{max} = \frac{n_{res} {\varDelta }_x^{\mathrm {flame}}}{\delta _l^0(\phi ,p)} \end{aligned}$$
(4)

\({\varDelta }_x^{\mathrm {flame}}\) is the cell size in the flame and \(n_{res}\) is the number of mesh points imposed in the flame front, typically set to a value between 5 and 10 in order to accurately compute reaction rates (Jaravel 2016). The laminar flame thickness \(\delta _l^0\) is tabulated from mono-dimensional premixed laminar flames for several equivalence ratios \(\phi\) and pressures p.

The efficiency factor is estimated as the ratio of the total flame wrinkling to the modeled resolved wrinkling of the thickened flame (Charlette et al. 2002a; Colin et al. 2000):

$$\begin{aligned} E = \frac{{\varXi }_{{\varDelta }}\left( \frac{{\varDelta }}{\delta _l^0}, \frac{{u'}_{{\varDelta }}}{S_l^0} \right) }{{\varXi }_{{\varDelta }}\left( \frac{{\varDelta }}{{\mathcal {F}}\delta _l^0},\frac{{u'}_{{\varDelta }}}{S_l^0} \right) } \end{aligned}$$
(5)

where \({\varDelta }\) is the flame filter size and \({\varXi }_{{\varDelta }}\) is the flame wrinkling factor at scale \({\varDelta }\). As done in previous studies (Charlette et al. 2002a), the choice \({\varDelta }= {\mathcal {F}} \delta _l^0\) is made and the efficiency factor reduces to \(E={\varXi }_{{\varDelta }}\left( \frac{{\varDelta }}{\delta _l^0} ,\frac{{u'}_{{\varDelta }}}{S_l^0} \right)\) as \({\varXi }_{{\varDelta }}\left( \frac{{\varDelta }}{{\mathcal {F}}\delta _l^0},\frac{{u'}_{{\varDelta }}}{S_l^0} \right) \simeq 1\). In the present work, the flame wrinkling factor is computed using the non-dynamic Charlette et al. formulation (Charlette et al. 2002a; Wang et al. 2011):

$$\begin{aligned} {\varXi }_{{\varDelta }} \left( \frac{{\varDelta }}{\delta _l^0}, \frac{{u'}_{{\varDelta }}}{S_l^0} \right) = \left( 1 + \min \left[ \frac{{\varDelta }}{\delta _l^0}-1, {\varGamma }_{\eta }^{{\varDelta }} \left( \frac{{\varDelta }}{\delta _l^0}, \frac{{u'}_{{\varDelta }}}{S_l^0}, Re_{{\varDelta }} \right) \frac{{u'}_{{\varDelta }}}{S_l^0} \right] \right) ^{\beta } \end{aligned}$$
(6)

\({\varGamma }_{\eta }^{{\varDelta }}\) is an efficiency function accounting for the effect of turbulent eddies with sizes ranging from the Kolmogorov scale \(\eta\) to the TFM filter size \({\varDelta }\). This function is here evaluated using the model developed in the work of Bougrine et al. (2014). \({u'}_{{\varDelta }}\) is the SGS velocity at scale \({\varDelta }\), \(Re_{{\varDelta }}={u'}_{{\varDelta }} {\varDelta }/ \nu\) the SGS Reynolds number and \(\beta\) a model parameter. The velocity \({u'}_{{\varDelta }}\) is computed from the resolved velocity field as Colin et al. (2000):

$$\begin{aligned} {u'}_{{\varDelta }} = c_2 {\varDelta }_x^3 \mid \nabla ^2 \left( \nabla \times {\widetilde{u}} \right) \mid \left( \frac{{\varDelta }}{n_x {\varDelta }_x} \right) ^{\frac{1}{3}} \end{aligned}$$
(7)

with \(c_2=2\) and \(n_x=10\).

Coupling TFM with AMR Recent work has focused on the coupling between TFM and adaptive mesh refinement, leading to the TFM-AMR modeling strategy (Mehl et al. 2018). The method enables to use fine cells within the flame front, thus decreasing the thickening factor value required to resolve the flame compared to conventional TFM simulations. A better prediction of the flame structure is then achieved (Mehl et al. 2018). In this study, the grid used to solve the flow is uniform with cell size \({\varDelta }_x^{\mathrm {flow}}\). The CONVERGE CFD solver used in the present work (Richards et al. 2017) features an AMR algorithm for cartesian grids. AMR is carried out by successively splitting cells so that the obtained cell size \({\varDelta }_x^{\mathrm {flame}}\) in the flame front reads:

$$\begin{aligned} {\varDelta }_x^{\mathrm {flame}} = \frac{{\varDelta }_x^{\mathrm {flow}}}{2^{n_{AMR}}} \end{aligned}$$
(8)

where \(n_{AMR}\) is the AMR level. In the TFM-AMR strategy, AMR is activated when the flame sensor is active (i.e. \(S>0\)). Using an adequate flame sensor, points are added in the reaction zones only, thus limiting the number of cells in the domain as compared to a homogeneous refinement of the region of interest. The level of refinement is set by defining a target thickening factor \({\mathcal {F}}_{\mathrm {target}}\) which reads:

$$\begin{aligned} {\mathcal {F}}_{\mathrm {target}} = \frac{n_{\mathrm {res}} {\varDelta }_x^{\mathrm {flame}}}{\delta _l^0(\phi ,p)} \end{aligned}$$
(9)

The AMR level is locally adapted so that the computed thickening matches \({\mathcal {F}}_{\mathrm {target}}\). The resulting AMR level may be expressed as:

$$\begin{aligned} n_{AMR} = \mathrm {int} \left[ \frac{1}{\log (2)} \log \left( \frac{n_{\mathrm {res}} {\varDelta }_x^{\mathrm {flow}} }{\delta _l^0(\phi ,p) {\mathcal {F}}_{\mathrm {target}} } \right) \right] \end{aligned}$$
(10)

where int refers to the nearest integer function. \(n_{AMR}\) varies here with the local equivalence ratio and the pressure. Note that, as the AMR mesh size \({\varDelta }_x^{AMR}\) belongs to a discrete set of values [See Eq. (8)], the target thickening factor is not reached exactly in each LES cell.

Two methods are possible to define the target thickening factor: (i) it may be defined as a constant user-specified value; (ii) it may be set through the specification of a targeted resolved flame thickness \(\delta _l^{1,\mathrm {target}}\). In case (ii), the target thickening is recast as \({\mathcal {F}}_{\mathrm {target}} = \delta _l^{1,\mathrm {target}} / \delta _l^0(\phi ,p)\). As the thickened flame thickness reads \(\delta _{l}^1=n_{\mathrm {res}} {\varDelta }_x^{\mathrm {flame}}\), this relationship is equivalent to Eq. (9). In one case, we target a constant thickening factor \({\mathcal {F}}_{\mathrm {target}}\), and the thickened flame thickness \(\delta _{l}^1\) may vary due to changes in \(\delta _l^0\). In the second situation, we target a thickened flame thickness \(\delta _l^{1,target}\), and the thickening factor \({\mathcal {F}}\) varies due to changes in \(\delta _l^0\). The second method is particularly adapted to situations where the laminar flame thickness strongly varies in time or space. Using method (i) in such cases might indeed lead to extremely high AMR levels when \(\delta _l^0\) gets small, as predicted by Eq. (8). The cases considered in this paper are purely premixed and at constant pressure, and thus feature constant flame scales (\(\delta _l^0\), \(S_l^0\)). Method (i) is thus retained. Method (ii) would be recommended for practical IC engine computations which have varying cylinder pressure.

2.2 Improved TFM-AMR Efficiency Function

Fig. 1
figure 1

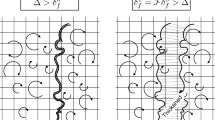
Illustration of the effect of AMR on turbulent energy spectrum. Case 1: Flow and flame are resolved on the same uniform mesh. Case 2: The flame is resolved on a mesh finer than the flow mesh, and \({\varDelta }=n_{res}{\varDelta }_x^{flame} > 2{\varDelta }_{x}^{\mathrm {flow}}\). Case 3: The flame is resolved on a mesh finer than the flow mesh, and \({\varDelta }=n_{res}{\varDelta }_x^{flame} < 2{\varDelta }_{x}^{\mathrm {flow}}\)

Full size image

2.2.1 AMR and Turbulent Flame Propagation

The accurate computation of turbulent premixed flames requires the correct prediction of both flame structure and flame propagation speed. While the TFM-AMR model improves the flame structure prediction by decreasing the thickening factor (Mehl et al. 2018), issues might arise when it comes to the prediction of the turbulent flame propagation. The TFM approach indeed relies on the computation of an efficiency factor E estimated from a local flame filter size \({\varDelta }= {\mathcal {F}} \delta _l^0\) (Eq. (5)). In particular, E is computed by integrating the contributions of subfilter turbulent eddies (with sizes \(\eta\) to \({\varDelta }\)) to the flame wrinkling. When \(n_{AMR}>0\), the flow is however resolved with a coarser grid than the flame and the associated LES cut-off filter size, estimated here as \(2{\varDelta }_{x}^{\mathrm {flow}}\), is larger than the LES cut-off \(2{\varDelta }_{x}^{\mathrm {flame}}\) defined by the flame front discretization; where \({\varDelta }_{x}^{\mathrm {flow}}\) and \({\varDelta }_{x}^{\mathrm {flame}}\) are the cell sizes in the flow and in the flame, respectively. The issue is illustrated in Fig. 1, where three cases may be distinguished:

  • Case 1 When no AMR is used to resolve the flame front, the standard TFM model applies. To compute E, scales are integrated from \(\eta\) to \({\varDelta }={\mathcal {F}} \delta _l^0=n_{res} {\varDelta }_{x}^{\mathrm {flame}}\). As there is no AMR, \({\varDelta }_{x}^{\mathrm {flow}}={\varDelta }_{x}^{\mathrm {flame}}\) and the filter size may thus also be computed as \({\varDelta }=n_{res} {\varDelta }_{x}^{\mathrm {flow}}\).

  • Case 2 AMR is used to compute the flame, introducing a LES resolution filter size \(2{\varDelta }_{x}^{\mathrm {flame}}\) in the flame. In this case, we assume \(2{\varDelta }_{x}^{\mathrm {flow}} < {\varDelta }= n_{res} {\varDelta }_{x}^{\mathrm {flame}}\). This means that like in case 1, turbulent scales are resolved on the flow mesh down to scale \({\varDelta }\) at least. \({\varDelta }\) is therefore the correct upper bound of integration of the efficiency function in Eq. (5), like for case 1. At the same time, scales ranging from \(2{\varDelta }_{x}^{\mathrm {flow}}\) down to \(2{\varDelta }_{x}^{\mathrm {flame}}\) are not resolved on the flow mesh but can be partially retrieved on the flame mesh if sufficient time is left for turbulence to cascade in the flame zone. Three sub-cases may then be distinguished:

    1. (a)

      No turbulent cascading in the AMR region: The characteristic turbulent time is much larger than the characteristic flame time. In this case, the smallest scales, close to \(2{\varDelta }_{x}^{\mathrm {flow}}\) on the flow mesh, do not have the time to cascade down to smaller scales as the flame propagates.

    2. (b)

      Partial turbulent cascading in the AMR region: Turbulent and flame times are of the same order of magnitude. This is an intermediate situation in which the cascade of turbulent scales is only partial and accordingly, the actual cut-off scale should be considered to lie between \(2{\varDelta }_{x}^{\mathrm {flow}}\) and \(2{\varDelta }_{x}^{\mathrm {flame}}\).

    3. (c)

      Full turbulent cascading in the AMR region: The turbulent time is much smaller than the flame time. In this case, the smallest scales (close to \(2{\varDelta }_{x}^{\mathrm {flow}}\)) on the flow mesh have enough time to cascade down to the smallest scale (\(2{\varDelta }_{x}^{\mathrm {flame}}\)) resolved on flame mesh because in a turbulent time, the flame has only traveled a negligible distance compared to the width of the refined region. This situation is equivalent to that of the propagation of a flame on a uniform mesh with cell size \({\varDelta }_{x}^{\mathrm {flame}}\).

    The estimation of \({u'}_{{\varDelta }}\) by Eq. (7) might therefore not be reliable because it is based on the existence of these small scales on a standard mesh (case c). Case 2 therefore requires at least an adaptation of the estimation of \({u'}_{{\varDelta }}\).

  • Case 3 AMR is used to compute the flame but this time \(2{\varDelta }_{x}^{\mathrm {flow}} > {\varDelta }\). As scales from \(2{\varDelta }_{x}^{\mathrm {flow}}\) down to \({\varDelta }\) are not resolved on the flow mesh and only partially on the flame mesh, the upper bound for integration of the efficiency function must be larger than \({\varDelta }\), which makes the standard expression Eq. (5) incorrect for this case. In addition, even more than in case 2, scales ranging from \({\varDelta }\) down to \(2{\varDelta }_{x}^{\mathrm {flame}}\) might be under-predicted on the flame mesh, therefore leading to an under-prediction of \({u'}_{{\varDelta }}\). In particular, the three sub-cases (a), (b) and (c) described for case 2 are applicable, as illustrated in Fig. 1. The cascading is indeed dependent on the relative importance of turbulent and flame time scales. The incorrect upper bound and under-prediction of velocity fluctuations both lead to an under-prediction of the turbulent flame wrinkling by the standard efficiency function if the turbulent cascading on the flame mesh is not fully achieved. Adequate modeling is therefore required for both aspects.

A new model, named AMR-E, is proposed to account for the impact of AMR on the flame propagation.

2.2.2 AMR-E Model

A model tackling the case \(2{\varDelta }_{x}^{\mathrm {flow}} > {\varDelta }\) (case 3 in Fig. 1) will readily deal with the case \(2{\varDelta }_{x}^{\mathrm {flow}} < {\varDelta }\) (case 2) by setting the upper integration bound to \({\varDelta }\). The emphasis in this section is therefore on case 3.

Effective TFM filter We saw that when the filter size \({\varDelta }\) is smaller than \(2{\varDelta }_{x}^{\mathrm {flow}}\), the integration of SGS scales in the calculation of the efficiency function is incomplete. The solution retained here is to consider an effective filter size \({\varDelta }_{\mathrm {eff}}\) that will be used as an appropriate upper bound for SGS scales. In particular, when AMR is used, \({\varDelta }_{\mathrm {eff}}\) will need to be larger than the TFM filter size \({\varDelta }\).

A legitimate choice for this bound would be \({\varDelta }_{\mathrm {eff}} = 2{\varDelta }_{x}^{\mathrm {flow}}\). But there are two major drawbacks to it: (i) The LES filter is in practice not a sharp cut-off at \(2{\varDelta }_{x}^{\mathrm {flow}}\), the spectral content of larger scales is likely also affected; (ii) the partial cascading of structures inside the AMR zone is not taken into account if we choose a fixed upper integration scale, and as will be seen in the application below, this effect cannot be ignored.

Issue (ii) is tackled by considering a transport equation for the test filter size \({\varDelta }_{\mathrm {eff}}\) which evolves in a characteristic time \(\tau _{t}\) (to be defined) towards the asymptotic filter size \({\widehat{{\varDelta }}}\) on the local mesh of cell size \({\varDelta }_x\):

$$\begin{aligned} \frac{\partial {\overline{\rho }} {\varDelta }_{\mathrm {eff}}}{\partial t} + \frac{\partial {\overline{\rho }} {\widetilde{u}}_i {\varDelta }_{\mathrm {eff}} }{\partial x_i} = {\overline{\rho }} \frac{{\widehat{{\varDelta }}}-{\varDelta }_{\mathrm {eff}}}{\tau _{t}} \end{aligned}$$
(11)

\({\widehat{{\varDelta }}}\) is defined as \({\widehat{{\varDelta }}}=\gamma {\varDelta }_x\) where according to issue (i), \(\gamma\) should be large enough to ensure that vortices with size larger than \({\widehat{{\varDelta }}}\) are fully resolved on the mesh. The linear relaxation source term in this equation thus mimics the turbulence cascade, that is, the filling of the turbulence spectrum when the local cell size \({\varDelta }_x\) goes from \({\varDelta }_{x}^{\mathrm {flow}}\) to \({\varDelta }_{x}^{\mathrm {flame}}\). An effective sub-filter velocity \({u'}_{\mathrm {eff}}\) is consequently defined as the fluctuations at scale \({\varDelta }_{\mathrm {eff}}\) and is computed using a similar transport equation:

$$\begin{aligned} \frac{\partial {\overline{\rho }} {u'}_{\mathrm {eff}}}{\partial t} + \frac{\partial {\overline{\rho }} {\widetilde{u}}_i {u'}_{\mathrm {eff}} }{\partial x_i} = {\overline{\rho }} \frac{\widehat{{u'}}-{u'}_{\mathrm {eff}}}{\tau _{t}} \end{aligned}$$
(12)

\(\widehat{{u'}}\) is the local velocity fluctuation at the test filter size and is computed by assuming that both \({\varDelta }\) and \({\widehat{{\varDelta }}}\) lie in the inertial part of the turbulent spectrum:

$$\begin{aligned} \widehat{{u'}} = {u'}_{{\varDelta }} \left( \frac{{\widehat{{\varDelta }}}}{{\varDelta }} \right) ^{\frac{1}{3}} \end{aligned}$$
(13)

where \({u'}_{{\varDelta }}\) is computed using Eq. (7). The cascading time is assumed to vary with the largest resolved turbulent scales:

$$\begin{aligned} \tau _t = \alpha \frac{{\varDelta }_{\mathrm {eff}}}{{u'}_{\mathrm {eff}}} \end{aligned}$$
(14)

where \(\alpha\) is a model parameter controlling the relaxation speed. Note that the effective filter size is clipped at \({\varDelta }\) when it becomes too small in order to preserve continuity with the standard TFM model.

To illustrate the behavior of the model, a time-scale analysis is carried out by introducing the following non-dimensional ratio:

$$\begin{aligned} {\varLambda }= \tau _f / \tau _t \end{aligned}$$
(15)

\(\tau _f\) is a characteristic time for the propagation of the turbulent flame defined as \(\tau _f={\mathcal {F}}\delta _l^0 / S_T\), where \(S_T\) is the turbulent flame speed including both resolved and unresolved wrinkling. Two limiting behaviors are observed: (i) if \({\varLambda }\ll 1\), the turbulent flame propagation is very fast compared to the turbulent cascading. In this case, there is not enough time for turbulent structures to cascade and a slow relaxation is predicted by Eq. (11), leading to \({\varDelta }_{\mathrm {eff}} \approx \gamma {\varDelta }_x^{\mathrm {flow}}\); (ii) if \({\varLambda }\gg 1\), the turbulent decay is much faster than the flame propagation and the relaxation is very fast. Small structures may then be generated on the fine mesh and \({\varDelta }_{\mathrm {eff}} \approx \gamma {\varDelta }_x^{\mathrm {flame}}\), which is clipped at \({\varDelta }= n_{res} {\varDelta }_x^{\mathrm {flame}}\) if \(\gamma <n_{res}\). The original TFM model is then retrieved. In the general case, the value of the effective filter size results from a balance between the turbulent propagation of the flame front and the turbulent cascading on the fine mesh.

Efficiency factor In addition, we propose a correction to the efficiency function Eq. (5). This expression in fact states that the total wrinkling of the real flame, i.e. non thickened from scales \(\eta\) to \({\varDelta }\), \({\varXi }_{{\varDelta }} \left( \frac{{\varDelta }}{\delta _l^0}, \frac{{u'}_{{\varDelta }}}{S_l^0} \right)\), equals the product of the modeled resolved wrinkling \({\varXi }_{{\varDelta }} \left( \frac{{\varDelta }}{{\mathcal {F}}\delta _l^0}, \frac{{u'}_{{\varDelta }}}{S_l^0} \right)\) times the SGS wrinkling E of the thickened flame. In this model, the estimated resolved wrinkling is given by Eq. (6) where function \({\varGamma }_{\eta }^{{\varDelta }}\) considers the efficiency of all vortices from \(\eta\) to \({\varDelta }\). This expression is approximate as the resolved flame can only be wrinkled by resolved vortices, that is, ranging from size \(2 {\varDelta }_x^{\mathrm {flame}}\) to \({\varDelta }\), while the Kolmogorov scale \(\eta\) can be much smaller than \(2{\varDelta }_x^{\mathrm {flame}}\). Therefore we propose a more accurate formulation for the modeled resolved wrinklingFootnote 1:

$$\begin{aligned} {\varXi }^{\mathrm {res}}_{{\varDelta }} \left( \frac{{\varDelta }}{{\mathcal {F}}\delta _l^0}, \frac{{u'}_{{\varDelta }}}{S_l^0} \right) = \left( 1 + \min \left[ \frac{{\varDelta }}{\delta _l^c}-1, {\varGamma }_{2{\varDelta }_x^{\mathrm {flame}}}^{{\varDelta }} \left( \frac{{\varDelta }}{{\mathcal {F}}\delta _l^0}, \frac{{u'}_{{\varDelta }}}{S_l^0}, Re_{{\varDelta }} \right) \frac{{u'}_{{\varDelta }}}{S_l^0} \right] \right) ^{\beta } \end{aligned}$$
(16)

where \({\varGamma }_{2{\varDelta }_x^{\mathrm {flame}}}^{{\varDelta }}\) is computed considering the flame/vortex interactions from scales \(2{\varDelta }_x^{\mathrm {flame}}\) to \({\varDelta }\). The flame cut-off length scale is here evaluated as:

$$\begin{aligned} \delta _l^c = \max \left( {\mathcal {F}} \delta _l^0, 2{\varDelta }_x^{\mathrm {flame}} \right) \end{aligned}$$
(17)

Using this new expression for the modeled resolved wrinkling and Eq. (6) for the total wrinkling, the efficiency function up to the effective scale \({\varDelta }_{\mathrm {eff}}\) becomes:

$$\begin{aligned} E = \frac{{\varXi }^{\mathrm {tot}}_{{\varDelta }_{\mathrm {eff}}} \left( \frac{{\varDelta }_{\mathrm {eff}}}{\delta _l^0}, \frac{{u'}_{\mathrm {eff}}}{S_l^0} \right) }{{\varXi }^{\mathrm {res}}_{{\varDelta }_{\mathrm {eff}}} \left( \frac{{\varDelta }_{\mathrm {eff}}}{{\mathcal {F}}\delta _l^0}, \frac{{u'}_{\mathrm {eff}}}{S_l^0} \right) } \end{aligned}$$
(18)

An effective cell size \({\varDelta }_x^\mathrm {eff}\) is required in Eq. (6) and (16). As on a fixed mesh of cell size \({\varDelta }_x\), \({\varDelta }_{\mathrm {eff}}\) is defined by \(\gamma {\varDelta }_x\), we define here \({\varDelta }_x^\mathrm {eff}\) by \({\varDelta }_{\mathrm {eff}} / \gamma\). Note finally that by redefining \({\varDelta }_{\mathrm {eff}}\) as \(\max \left( {\varDelta }_{\mathrm {eff}}, {\varDelta }\right)\), Eq. (18) remains valid when \(2 {\varDelta }_{x}^{\mathrm {flow}} < {\varDelta }\).

Fig. 2
figure 2

Mono-dimensional setup used in the a priori analysis. The refinement level is here \(n_{AMR}=3\)

Full size image

2.3 A Priori Analysis of the AMR-E Efficiency Function

2.3.1 A Priori Analysis

In order to illustrate the behavior of the AMR-E efficiency model, an a priori analysis is first carried out. Unlike for standard algebraic expressions of efficiency factor (Charlette et al. 2002a; Thiesset et al. 2016), the AMR-E efficiency cannot be computed directly from the filter size and the subfilter turbulent velocity. Instead, it requires the transport of \({\varDelta }_{\mathrm {eff}}\) and \({u'}_{\mathrm {eff}}\), which depend on conditions outside of the flame. A simplified mono-dimensional set-up, reproducing the behavior of the AMR-E model is thus proposed in the present work to perform a priori testing.

2.3.2 A Priori Analysis on a Monodimensional Steady Flame

A stationary flame in a frame moving at the turbulent flame speed \(S_T={\varXi }_{tot}S_l^0\) is considered, where \({\varXi }_{tot}\) is the total flame wrinkling factor. The flow is resolved with a cell size \({\varDelta }_x^{\mathrm {flow}}\) and \(n_{AMR}\) adaptive mesh refinement levels are applied to solve the flame, so that \({\varDelta }_x^{\mathrm {flame}}={\varDelta }_x^{\mathrm {flow}} / 2^{n_{AMR}}\). \({\varXi }_{tot}\) is assumed to be constant when AMR levels are added inside the flame front. In other words, the flame turbulent propagation speed is kept constant when AMR is applied. This is a desired property of the efficiency factor model which will be assumed here to perform the a priori analysis.

In the AMR algorithm, the mesh goes from level 0 to level \(n_{AMR}\) by successively splitting cells at AMR level \(1,2,\ldots ,n_{AMR}\). This is illustrated in Fig. 2 for a flame refinement level \(n_{AMR}=3\). \(x_0\) corresponds to the spatial location where the first cell split is done, \(x_1\) corresponds to the second split and \(x_{2}\) to the last cell split. The flame ends at location \(x_{3}\) so that \(x_{3} - x_{2} = {\mathcal {F}} \delta _l^0\) is the thickened flame thickness, which is an estimate here of the refined zone width. Transport equations for \({\varDelta }_{\mathrm {eff}}\) and \({u'}_{\mathrm {eff}}\) are solved in time by using the transformation \(t=x/({\varXi }_{tot}S_l^0)\). The initial filter size is \({\varDelta }_{\mathrm {eff}}(t=t_0) = {\varDelta }_0 = \gamma {\varDelta }_x^{\mathrm {flow}}\) and \({u'}_{\mathrm {eff}}(t=t_0)={u'}_0\) is the velocity fluctuation at scale \({\varDelta }_0\). Equations (11) and (12) are recast in one dimension as:

$$\begin{aligned} \frac{\partial {\varDelta }_{\mathrm {eff}}}{\partial t}= & {} \frac{{\widehat{{\varDelta }}}-{\varDelta }_{\mathrm {eff}}}{\tau _{t}} \end{aligned}$$
(19)
$$\begin{aligned} \frac{\partial {u'}_{\mathrm {eff}}}{\partial t}= & {} \frac{\widehat{{u'}}-{u'}_{\mathrm {eff}}}{\tau _{t}} \end{aligned}$$
(20)

For \(t \in [t_k,t_{k+1}[\) the 1-D transport equations correspond to locations \(x \in [x_k,x_{k+1}[\) where the cell size is \({\varDelta }_x^{k}={\varDelta }_x^{\mathrm {flow}} / 2^{k+1}\). The target value for the effective filter size is thus:

$$\begin{aligned} {\widehat{{\varDelta }}} = \frac{{\varDelta }_0}{2^{k+1}} \end{aligned}$$
(21)

By assuming that considered scales lie in the inertial part of the spectrum, the corresponding target velocity is:

$$\begin{aligned} \widehat{{u'}} = \frac{{u'}_0}{2^{\frac{k+1}{3}}} \end{aligned}$$
(22)

Equations (19) and (20) may finally be rewritten as:

$$\begin{aligned} \frac{\partial {\varDelta }_{\mathrm {eff}}}{\partial t}= & {} \frac{1}{\alpha } \left( \frac{{u'}_{\mathrm {eff}}}{{\varDelta }_{\mathrm {eff}}} \right) \left( \frac{{\varDelta }_0}{2^{k+1}}-{\varDelta }_{\mathrm {eff}} \right) \end{aligned}$$
(23)
$$\begin{aligned} \frac{\partial {u'}_{\mathrm {eff}}}{\partial t}= & {} \frac{1}{\alpha } \left( \frac{{u'}_{\mathrm {eff}}}{{\varDelta }_{\mathrm {eff}}} \right) \left( \frac{{u'}_0}{2^{\frac{k+1}{3}}} -{u'}_{\mathrm {eff}} \right) \end{aligned}$$
(24)

By solving Eqs. (23) and (24) for each of the intervals \([t_k,t_{k+1}[\), the evolution of \({\varDelta }_{\mathrm {eff}}\) and \({u'}_{\mathrm {eff}}\) in time is obtained. The a priori efficiency factor is finally obtained by applying Eq. (18) using \({\varDelta }_{\mathrm {eff}}(t=t_{n_{AMR}})\) and \({u'}_{\mathrm {eff}}(t=t_{n_{AMR}})\) as effective properties.

2.3.3 Results

The analysis is performed for flame and turbulence conditions representative of an internal combustion engine near ignition (\(p=30\) bar, \(T_0 = 700\) K, \(\phi =1.1\)). Flame properties are computed by assuming a premixed mixture of iso-octane (\(C_8H_{18}\)) and air. The same conditions will be considered in the validation case in Sect. 3. The flow cells have a size \({\varDelta }_x^{\mathrm {flow}}=0.5\) mm and the turbulent fluctuations have an intensity \({u'}_{10{\varDelta }_x} / S_l^0=15.2\), where \({u'}_{10{\varDelta }_x}\) are the fluctuations at scale \(10 {\varDelta }_x^{\mathrm {flow}}\). Imposing \({u'}_{10{\varDelta }_x}\) instead of \({u'}_0\) ensures that all the considered cases are compared at similar turbulent conditions, as \({u'}_0\) would otherwise depend on the model parameter \(\gamma\). Additionally, a case representative of atmospheric conditions (\(p=1\) bar, \(T_0 = 300\) K, \(\phi =1.1\)) is investigated in order to analyze the model in several circumstances. The thermo-chemical conditions are summarized in Table 1, while flame and turbulence characteristic scales are provided in Table 2.

Table 1 Thermo-chemical conditions used for the model evaluation
Full size table
Table 2 Flame scales and turbulent velocity of the two studied cases
Full size table

Computed profiles of \({\varDelta }_{\mathrm {eff}}\) and \({u'}_{\mathrm {eff}}\) are illustrated on the left of Fig. 3 for relaxation parameters α = 1, 3 and 5 in the engine conditions. The flame is resolved with \(n_{AMR}=3\) levels and the test filter size is here set using \(\gamma =3\). Position \(x=0\) corresponds to the first refinement level and vertical dashed lines indicate subsequent refinement levels. As the local filter size value decreases with each AMR level, the effective filter size and fluctuation velocity are monotonically decreasing. This mimics the cascading of turbulent structures taking place as the mesh is refined. The relaxation is faster for small values of \(\alpha\) as the characteristic relaxation time shrinks. The evolution of the efficiency factor with \(\alpha\) is illustrated on the right of Fig. 3. In the limit of very low \(\alpha\) values, E rapidly tends towards the value predicted by the standard Charlette et al. model (Eq. 5), which is in this case \(E=4.84\). It is explained by a very fast relaxation towards the local filter size and velocity fluctuation values. As the turbulent cascading is likely to be at least one eddy turnover-time, the lower bound \(\alpha \ge 1\) is proposed here. In the present case, E only slightly increases with \(\alpha\) when \(\alpha \ge 1\). The turbulent flame propagation is here much larger than the characteristic turbulent time (\({\varLambda }\ll 1\)) and the efficiency value is mostly dictated by the conditions outside of the flame front.

Fig. 3
figure 3

Computed profiles \({\varDelta }_{\mathrm {eff}}\) and \({u'}_{\mathrm {eff}}\) for the engine conditions. Circles (Filed blue circle): \(\alpha =1\). Squares (Filled orange square): \(\alpha =3\). Triangles (Filled green triangle): \(\alpha =5\)

Full size image

Figure 4 shows the same computation for the atmospheric conditions. In this case, the ratio \({u'}_{10{\varDelta }_x} / S_l^0\) is higher than for the engine conditions as the flame speed is lower, and the flame is thus more sensitive to the turbulence level. In terms of time scales, the gap between the turbulent flame propagation time and the turbulent time is reduced. The relaxation of \({\varDelta }_{\mathrm {eff}}\) and \({u'}_{\mathrm {eff}}\) is more pronounced, as seen in the left of Fig. 4, and the model thus adequately responds to a change in the flame time scale. For these conditions, the efficiency predicted by the standard model is \(E=1\).

Fig. 4
figure 4

Computed profiles \({\varDelta }_{\mathrm {eff}}\) and \({u'}_{\mathrm {eff}}\) for the atmospheric conditions. Circles (Filled blue circle): \(\alpha =1\). Squares (Filled orange square): \(\alpha =3\). Triangles (Filled green triangle): \(\alpha =5\)

Full size image

To analyze the AMR-E efficiency model further, estimations of E as a function of \(n_{AMR}\) are shown in Fig. 5a for \(\gamma =2, \ 3\) and 5 for the engine conditions. The AMR-E values are compared to the standard Charlette et al. model (solid black line). The relaxation parameter is here set to \(\alpha =1\). The corresponding modeled resolved wrinkling factors are shown in Fig. 5b for the three AMR-E cases. When AMR is not activated in the flame front (\(n_{AMR}=0\)), the AMR-E model degenerates towards the standard modeling approach. As \(n_{AMR}\) increases, the resolution inside the flame front increases and the thickening factor (dash-dotted lines) tends towards unity. In accordance with previous studies (Charlette et al. 2002a), the standard efficiency model also tends toward unity because the missing turbulent structures due to coarse resolution of the flow upstream of the flame are not taken into account in the computation of E. The AMR-E model, on the opposite, tends towards a value significantly larger than unity for large values of \(n_{AMR}\). This SGS wrinkling corresponds to the impact of turbulent eddies larger than \(2{\varDelta }_{x}^{\mathrm {flame}}\) which could theoretically wrinkle the flame at the resolved scale but which in practice are not present in the simulation due to the too slow turbulence cascade. Note that these significant values of the efficiency function can be found even when flame thickening is close to unity. The limit efficiency value is found to be relatively insensitive to the choice of \(\gamma\). This suggests that for high values of \(n_{AMR}\), the additional total wrinkling due to larger \(\gamma\) value is compensated by the increase of the modeled resolved wrinkling. For intermediate values of \(n_{AMR}\) (1 and 2 in the present case), the predicted efficiencies are larger for AMR-E than for the standard model and predictions vary with the choice of \(\gamma\). We observe that the resolved flame wrinkling \({\varXi }^{\mathrm {res}}_{{\varDelta }_{\mathrm {eff}}}\) increases with the value of \(\gamma\). This stems from the fact that larger scales are included in the estimation of E when \(\gamma\) is large. \(\gamma =2\) corresponds to the case where no resolved flame wrinkling is predicted (\({\varXi }^{\mathrm {res}}_{{\varDelta }_{\mathrm {eff}}}=1\)). This is explained by the model assumption stating that the smallest eddies interacting with the flame have a size \(2{\varDelta }_{\mathrm {eff}}/\gamma\), which in this case corresponds also to the maximal scale \({\varDelta }_{\mathrm {eff}}\).

Fig. 5
figure 5

Efficiency factor and modeled resolved wrinkling factor as a function of the AMR level for different values of the model parameter \(\gamma\)

Full size image

3 Simulations of Flame Propagation in Homogeneous Isotropic Turbulence (HIT)

In this section, the AMR-E efficiency model is applied to a 3-D turbulent propagating flame case. The numerical setup is first described in Sect. 3.1, followed by a discussion of the results in Sects. 3.2 and 3.3.

3.1 Validation Case and Computational Set-up

3.1.1 HIT Case Description

The model validation is performed on a numerical experiment, which enables to cover a wide range of model parameters. The case of a spherical flame propagating in a turbulent flow field is selected in order to mimic flame propagation in an IC engine. A cubic domain is first initialized with a Homogeneous Isotropic Turbulence (HIT). The initial HIT field is generated using an Inverse Fast Fourier Transformation method and an analytical Passot-Pouquet energy spectrum:

$$\begin{aligned} {\mathcal {E}}(\kappa ) = 16 \sqrt{\frac{2}{\pi }} \frac{{u'}^2}{\kappa _e} \left( \frac{\kappa }{\kappa _e} \right) ^4 \exp \left( -2 \left( \frac{\kappa }{\kappa _e} \right) ^2 \right) \end{aligned}$$
(25)

where \(\kappa\) is the wavenumber and \({\mathcal {E}}\) the associated energy spectrum density. The Passot-Pouquet spectrum is parametrized by the velocity root mean square (RMS) \({u'}_0\) and the wavenumber of the most energetic turbulent mode \(\kappa _e\). The selected RMS velocity is \({u'}_0 = 10\,\mathrm{m/s}\) for all the cases considered in this work. The wavenumber \(\kappa _e\) is set at a value of \(546.4\,\mathrm{m}^{-1}\), which leads to a turbulent integral scale \(L_t^0 = 5\,\mathrm{mm}\).

A fresh iso-octane (\(C_8H_{18}\)) air mixture at a fuel/air equivalence of 1.1 is considered. A sphere of burned gases is added at the box center and subsequently propagates in the domain. The sphere radius is initially set at a value larger than the thickened flame thickness, in order to avoid the need for an ignition model. The initial burned gas sphere is kept identical for all the simulations performed in this study and its radius \(r_0\) is set based on the highest encountered thickening factor, which corresponds to the case without AMR. By rewritting the thickened flame thickness as \({\mathcal {F}}\delta _l^0 = n_{res} {\varDelta }_x^{\mathrm {flame}}\), the choice \(r_0 = 3 n_{res}{\varDelta }_x^{\mathrm {flow}}\) is madeFootnote 2. An illustration of the setup is provided in Fig. 6. Two sets of thermo-chemical initial conditions are considered, corresponding to the engine and atmospheric conditions previously investigated in Sect. 2.3.3, and detailed in Table 1. A flame regime analysis for both conditions is provided in Appendix.

Fig. 6
figure 6

Illustration of the HIT setup

Full size image

3.1.2 Numerics

The CONVERGE CFD solver (Richards et al. 2017) is selected to solve the transport equations in the present work. It features an Adaptive Mesh Refinement (AMR) algorithm, which refines the grid dynamically where needed. A second-order spatial and temporal numerical scheme is used to solve the transport equations.

The box is discretized using a uniform mesh with cell size \({\varDelta }_x^{\mathrm {flow}}\). The cell size in the flame front \({\varDelta }_x^{\mathrm {flame}}\) is dictated by the TFM-AMR approach. The thickening target of the TFM-AMR model is used as an input of the TFM-AMR model, as detailed in Sect. 2.1. The box faces are treated as outlet boundary conditions in order to avoid a pressure increase in the domain. The Sigma model (Nicoud et al. 2011) is used for solving unresolved turbulent stresses.

In order to limit the computational cost, and as pollutants are not considered in the present study, a two-step chemical mechanism for \(C_8H_{18}\) is considered:

$$\begin{aligned} C_8H_{18} + \frac{17}{2} O_2 \longrightarrow 8 CO + 9 H_2O \end{aligned}$$
(R1)
$$\begin{aligned} CO + \frac{1}{2} O_2 \longrightarrow CO_2 \end{aligned}$$
(R2)

For each case (engine and atmospheric) the mechanism coefficients are optimized to reach the laminar flame speed predicted by the mechanism of An et al. (2016). Most fuel/air mixtures present a sensitivity of the laminar flame speed to stretch. As shown by Quillatre (2014), this leads to a sensitivity of the laminar flame speed to the thickening factor, which is prejudicial to a correct prediction of the flame dynamics. Although these authors proposed a correction of TFM to solve this issue, we prefer here to avoid the complexity brought by sensitivity to stretch by considering unity Lewis number flames. Such flames are obtained by considering the same molecular diffusivity for all species and energy.

3.1.3 Turbulent combustion modeling

Two versions of the TFM model are here evaluated: (i) the TFM-AMR model without AMR correction of the efficiency model, which corresponds to the standard usage of TFM; (ii) the TFM-AMR-E model. Both strategies are based on the algebraic formulation of the Charlette model, which requires the specification of the fractal dimension \(\beta\) of the flame. \(\beta\) is here a model constant which is not known for the present setup and is known to have a strong influence on flame propagation speed (Misradiis et al. 2014). Indeed, as the flame thickness is small (see Table 2), a Direct Numerical Simulation of the HIT is out of reach.

In this study, a large velocity fluctuation \({u'}_0 = 10 m/s\) is considered in order to obtain efficiency levels much larger than unity. This choice is made for two reasons. First, in practical industrial applications, the efficiency level is often quite large, meaning that today the acceptable mesh resolution is not sufficient to get highly resolved LES. Secondly, choosing a low velocity fluctuation would lead to efficiency factor values close to unity, making the comparison between the different efficiency models not meaningful. As a consequence, the HIT condition considered here could not be run at DNS resolution because of the excessive CPU cost it would induce. This means, the different efficiency models could not be compared to a reference DNS solution. Instead, it is still possible to discriminate between models considering that a competitive turbulent combustion model should have a similar behavior when the mesh resolution is modified, given that the mesh is fine enough to resolve the large turbulent structures with sufficient accuracy. In other words, the additional sub-grid scale wrinkling due to a coarsening of the mesh for instance, should be captured accurately by a good model. When this property is not satisfied, it can safely be argued that the model is not sufficiently accurate. Thus, in the present case involving AMR, the model should behave the same regardless of the flame refinement level. In the light of these elements, the following model evaluation approach is proposed:

  1. 1.

    A fixed value for the \(\beta\) parameter is set. The value \(\beta =0.75\) is here selected, as it is representative of values found in engine LES (Misradiis et al. 2014).

  2. 2.

    A preliminary study is carried out to assess the intrinsinc sensitivity of the Charlette wrinkling model to a uniform refinement of the mesh. The standard TFM model is used as no AMR is considered in this step. Two simulations are run with \({\varDelta }_x^{\mathrm {flow}}=0.5 \, \mathrm{mm}\) and \({\varDelta }_x^{\mathrm {flow}}=0.25 \, \mathrm{mm}\), respectively. This study is necessary to ensure the consistency of the AMR simulations comparison.Footnote 3

  3. 3.

    AMR-E and standard TFM models are compared for \({\varDelta }_x^{\mathrm {flow}}=0.5 \, \mathrm{mm}\) and different AMR refinement levels in the flame. Three cases will be considered: (i) No AMR in the flame, so that \({\varDelta }^{\mathrm{flame}}_{x}={\varDelta }_x^{\mathrm {flow}}\); (ii) one level of AMR in the flame, i.e. \({\varDelta }^{\mathrm{flame}}_{x}={\varDelta }_x^{\mathrm {flow}} / 2\); (iii) two levels of AMR in the flame, i.e. \({\varDelta }^{\mathrm{flame}}_{x}={\varDelta }_x^{\mathrm {flow}} / 4\).

  4. 4.

    A parametric study is finally performed on the AMR-E model parameters \(\alpha\) and \(\gamma\) in order to test the robustness of the model.

Table 3 Turbulent properties of the simulated HIT
Full size table

3.2 Analysis of Non-reacting Turbulent Decay

Before comparing the turbulent combustion models on the flame propagation case, the non-reacting HIT setup is analyzed. Turbulent scales obtained from the initial synthetic velocity field are summarized in Table 3. \(k_0 = (1 / 2) {u'}_0^2\) is the initial turbulent kinetic energy, \(L_t^0\) the integral length scale, \(\tau _t^0 = L_t^0 / {u'}_0\) the eddy turnover time and \(\eta _k^0\) the Kolmogorov length scale. According to turbulence theory, the time evolution of the turbulent kinetic energy (TKE) k and the TKE dissipation rate \(\epsilon\) are given by the following equations:

$$\begin{aligned} \frac{dk}{dt}= & {} - \epsilon \end{aligned}$$
(26)
$$\begin{aligned} \frac{d\epsilon }{dt}= & {} - C_2 \frac{\epsilon ^2}{k} \end{aligned}$$
(27)

where \(C_2 = 1.92\) is a modeling constant (Launder and Spalding 1972). Equations (26) and (27) can be integrated to give the following theoretical evolution of TKE in time:

$$\begin{aligned} \frac{k(t)}{k_0} = \left( 1 + \left( 1 - C_2 \right) \frac{t}{\tau _t^0} \right) ^{\frac{1}{1-C_2}} \end{aligned}$$
(28)

Two numerical simulations are carried out: (i) a simulation with a uniform cell size \({\varDelta }_x^{\mathrm {flow}} = 0.5\,\mathrm{mm}\) in the domain, ensuring a resolution \(L_t^0 / {\varDelta }_x^{\mathrm {flow}} = 10\) for the largest turbulent scales; (ii) a second simulation with a refined cell size \({\varDelta }_x^{\mathrm {flow}} = 0.25\,\mathrm{mm}\), leading to a resolution \(L_t^0 / {\varDelta }_x^{\mathrm {flow}} = 20\). The TKE evolution for both simulations is compared to the theoretical TKE in Fig. 7. An initial adaptation phase of the synthetic initial turbulent field is observed, which lasts between one and two turbulent times. Afterwards, the theoretical TKE decrease is globally well retrieved by the simulations.

Fig. 7
figure 7

Evolution of the normalized turbulent kinetic energy \(k/k_0\) as a function of the normalized time \(t / \tau _{t}^0\)

Full size image

3.3 Turbulent flame propagation analysis

The propagation of the spherical flame in the HIT is investigated in this section. Useful post-processing quantities are first defined in Sect. 3.3.1. Then, as discussed in Sect. 3.1.3, the analysis of the simulations is performed in three steps. In Sect. 3.3.2, a mesh refinement study is carried out to evaluate the intrinsic sensitivity of the Charlette algebraic model with respect to the cell size. A detailed comparison between AMR-E and standard TFM on cases involving AMR is made in Sect. 3.3.3. The relative importance of changing the SGS velocity computation and the new upper bound in the wrinkling integration is then evaluated in Sect. 3.3.4. Finally, a parametric study of the AMR-E model is provided in Sect. 3.3.5.

3.3.1 Definition of Flame-averaged Quantities

A deeper comprehension of the flame propagation can be achieved by defining quantitites averaged on the flame front. The total fuel reaction rate in the flame at a given instant, written \(<{\dot{\omega }}_{f,tot}>\), is evaluated by integrating the local fuel filtered reaction rate \(\overline{{\dot{\omega }}}_f\) as:

$$\begin{aligned}<{\dot{\omega }}_{f,tot}> = \int _{V} \frac{E}{{\mathcal {F}}} \overline{{\dot{\omega }}}_f dV =<E> <{\dot{\omega }}_{f,res}> \end{aligned}$$
(29)

where \(<{\dot{\omega }}_{f,res}>\) and \(<E>\) are defined as:

$$\begin{aligned} <{\dot{\omega }}_{f,res}>\,=\, & {} \int _{V} \frac{1}{{\mathcal {F}}} \overline{{\dot{\omega }}}_f dV \end{aligned}$$
(30)
$$\begin{aligned} <E>\,=\, & {} \frac{\int _{V} \frac{E}{{\mathcal {F}}} \overline{{\dot{\omega }}}_f dV}{\int _{V} \frac{1}{{\mathcal {F}}} \overline{{\dot{\omega }}}_f dV} \end{aligned}$$
(31)

\(<{\dot{\omega }}_{f, res}>\) represents the resolved contributions to the filtered reaction rate, and \(<E>\) the average efficiency factor in the flame. Additionally, the total heat release \(<{\dot{q}}>\) is defined as:

$$\begin{aligned} <{\dot{q}}>\, =\, \int _{V} \frac{E}{{\mathcal {F}}} \overline{{\dot{q}}} dV \end{aligned}$$
(32)

where:

$$\begin{aligned} {\dot{q}} \,=\, - \sum _{k} h_k {\dot{\omega }}_k \end{aligned}$$
(33)

is the local heat release rate.

For an arbitrary quantity \({\varPhi }\), a flame-averaged value may be computed as:

$$\begin{aligned}<{\varPhi }> = \frac{ \int _{V} {\varPhi }\frac{E}{{\mathcal {F}}} \overline{{\dot{\omega }}}_f dV}{<{\dot{\omega }}_{f,tot}>} \end{aligned}$$
(34)

3.3.2 Uniform Mesh Refinement Study

The sensitivity of the selected algebraic Charlette model to the cell size is evaluated in this section. A low sensitivity is a pre-requisite for a consistent evaluation of the AMR influence on flame propagation. Two simulations on uniform meshes are here compared: (i) a reference simulation with \({\varDelta }_x^{\mathrm {flow}} = 0.5\,\mathrm{mm}\); (ii) a fine simulation with \({\varDelta }_x^{\mathrm {flow}} = 0.25\,\mathrm{mm}\).

Fig. 8
figure 8

Comparison of heat release rate \(<{\dot{q}}>\) (on the left) and mean efficiency \(<E>\) (on the right) as a function of normalized time \(t / \tau _t^0\) for the reference and the fine cases on uniform meshes. The engine conditions are considered here. Black continuous line (−): reference case (\({\varDelta }_x^{\mathrm {flow}} = 0.5mm\)). Blue dashed line (- - -): fine case (\({\varDelta }_x^{\mathrm {flow}} = 0.25mm\))

Full size image

The heat release rate \(<{\dot{q}}>\) and the mean efficiency in the flame front \(<E>\) are represented as a function of the normalized time \(t / \tau _t^0\) in Fig. 8. The heat release rate increase is stronger for the reference case than for the fine case, and thus the flame propagates faster. By analyzing the average efficiency, on the right of Fig. 8, it is seen that the efficiency at \(t=0\) is significantly higher for the reference case than for the fine simulation. This is a direct consequence of Eq. (5), as the filter size \({\varDelta }\) and the SGS velocity \({u'}_{{\varDelta }}\) are smaller for the fine case. The high initial efficiency values are in fact due to the assumption that flame and turbulence are in equilibrium, which is a known shortcoming of algebraic wrinkling models (Charlette et al. 2002a). As the flame is initially perfectly spherical, there is no SGS wrinkling and the efficiency should be \(E=1\). This effect is not reproduced by the algebraic model which assumes that the flame is wrinkled by eddies with estimated speed \({u'}_{{\varDelta }}\). On the contrary, at times larger than \(0.8\tau _t^0\), the slope of heat release rate of the reference and fine cases get closer, indicating that the turbulence and flame are closer to the equilibrium assumption.

Fig. 9
figure 9

Comparison of heat release rate \(<{\dot{q}}>\) as a function of normalized burned gas radius \(r_{BG} / r_0\) for the reference and the fine cases on uniform meshes. On the left: engines conditions. On the right: atmospheric conditions. Black continuous line (−): reference case (\({\varDelta }_x^{\mathrm {flow}} = 0.5\,\mathrm{mm}\)). Blue dashed line (---): fine case (\({\varDelta }_x^{\mathrm {flow}} = 0.25\,\mathrm{mm}\))

Full size image

Alternatively, it is here proposed to analyze the flame as a function of an equivalent radius of burned gases. Hence, the heat release is compared for identical flame states and the effect of the initial speed-up of the flame due to excessive wrinkling is avoided. A burned gases radius is defined by summing the computational cells which are close to the burned gas state:

$$\begin{aligned} r_{BG} = \sum _{\begin{array}{c} k \\ \\ T_k>T_0+1000 \end{array}} V_k \end{aligned}$$
(35)

where \(V_k\) and \(T_k\) are the volume and temperature of the computational cell k, respectively. The criterion used to mark a cell as burned is \(T_k > T_0+1000\) K. The heat release rate is then plotted as a function of the normalized burned gases radius \(r_{BG} / r_0\) in Fig. 9 for both the engine (left) and atmospheric (right) conditions. A good agreement is found on the heat release rate evolution between the reference and fine cases for burned gases radius larger than \(2 r_0\) approximately. As a result, the sensitivity of the wrinkling model to the cell size can be considered low in the present conditions, as long as the error due to the flame/turbulence equilibrium assumption at early times is removed. In the remaining of this work, all results are shown as a function of \(r_{BG} / r_0\) in order to provide a fair comparison between simulations.

3.3.3 Comparison Between Standard and AMR-E Modeling Approach

The emphasis is now on the comparison between the standard TFM model and TFM-AMR-E in situations involving AMR. The flow is resolved with a cell size \({\varDelta }_x^{\mathrm {flow}} = 0.5\,\mathrm{mm}\) for all the considered cases. The largest turbulent scales are thus solved with 10 points. For both engine and atmospheric conditions, a case without AMR (i.e. mesh is uniform with cell size \({\varDelta }_x^{\mathrm {flow}}\)) is considered in addition to two cases with AMR at different levels. The selected AMR levels with corresponding cell sizes and TFM thickening factors are detailed in Table 4.Footnote 4 The AMR-E model parameters are here set to \(\alpha =1\) and \(\gamma =3\). The sensitivity of results to these parameters is investigated in Sec. 3.3.5.

Table 4 AMR levels considered in the present work
Full size table

The comparison between Standard TFM and TFM-AMR-E in terms of heat release rate is illustrated in Fig. 10, where the left plot corresponds to engine conditions and the right plot to atmospheric conditions. In the engine conditions, a strong impact of the AMR level on the flame propagation is observed for the standard TFM model (black dashed lines). This is explained here by an inadequate estimation of TFM scales: a partial cascading of the turbulent scales leads to an under-estimation of the efficiency E which in turn gives rise to a lower heat release rate. A good improvement is obtained when using the AMR-E model (blue continuous lines). Indeed, the simulations with AMR levels \(n_{AMR}=0\) and \(n_{AMR}=1\) slightly differ, and simulation with \(n_{AMR}=2\) closely matches the results obtained with \(n_{AMR}=1\). Additionally, cases without AMR (circles) show a good agreement between standard TFM and AMR-E.

At atmospheric conditions (right of Fig. 10), the impact of the AMR level on the flame propagation using standard TFM is not as significant as for engine conditions. Indeed, the relative difference of turbulent flame propagation and turbulent cascading time scales is lower in these conditions. AMR level \(n_{AMR}=2\) even matches the simulation without AMR (\(n_{AMR}=0\)), meaning that the additional LES resolved wrinkling due to the AMR refinement sufficiently enhances the flame wrinkling. The simulations of the atmospheric cases with the AMR-E model also lead to an acceptable sensitivity of the heat release rate to the AMR level. However, a slight difference is here observed between standard TFM and AMR-E for the cases without AMR. This is a consequence of the different definitions of the subgrid scale velocity, which is local for TFM and transported for AMR-E.

Fig. 10
figure 10

Total heat release rate \(<{\dot{q}}>\) as a function of the normalized burned gas radius \(r_{BG} / r_0\) for the engine (left) and atmospheric (right) conditions. Black dashed lines (---) correspond to standard TFM cases and blue continuous lines (−) to AMR-E. The different AMR levels are represented using different symbols. Circles (\(\bullet\)): \(n_{AMR}=0\). Squares (\(\blacksquare\)): \(n_{AMR}=1\). Triangles (\(\blacktriangle\)): \(n_{AMR}=2\)

Full size image
Fig. 11
figure 11

Instantaneous fields of TFM subgrid scale velocities (\({u'}_{{\varDelta }}\) for standard TFM and \({u'}_{\mathrm {eff}}\) for AMR-E) and efficiency E at a given instant. Results are represented for engine conditions with AMR level \(n_{AMR}=2\). Left column: standard TFM. Right column: AMR-E model

Full size image

The instantaneous fields at a given instant are analyzed next in order to emphasize the fundamental changes brought by the AMR-E formulation compared to the standard efficiency model. The simulations in engine conditions at the AMR level \(n_{AMR}=2\) are considered. Subgrid scale velocities \({u'}_{{\varDelta }}\) and \({u'}_{\mathrm {eff}}\), obtained for the standard TFM and AMR-E models, respectively, are shown on the top of Fig. 11, while the resulting efficiency factors are represented on the bottom. A sharp drop of \({u'}_{{\varDelta }}\) in the refined flame region is observed for the standard efficiency model. This stems from the fact that \({u'}_{{\varDelta }}\) is directly proportional to \(({\varDelta }_x^{flame})^2\). In contrast, the SGS velocity field predicted by the AMR-E model is much smoother and the value is not affected by the finer resolution inside the flame front. This is due to the fact that the flame propagation is much faster than turbulent cascading in engine conditions. As a result, the efficiency predicted by the AMR-E model is higher, and the flame travels faster inside the domain.

Fig. 12
figure 12

Flame averaged quantities for the engine conditions: mean total wrinkling \(<{\varXi }^{\mathrm {tot}}_{{\varDelta }_{\mathrm {eff}}}>\) (top left), mean modeled resolved wrinkling \(<{\varXi }^{\mathrm {res}}_{{\varDelta }_{\mathrm {eff}}}>\) (top right), mean efficiency \(<E>\) (bottom left), mean resolved fuel reaction rate \(<{\dot{\omega }}_{f,res}>\) (bottom right). Circles (\(\bullet\)): \(n_{AMR}=0\). Squares (\(\blacksquare\)): \(n_{AMR}=1\). Triangles (\(\blacktriangle\)): \(n_{AMR}=2\)

Full size image

As detailed in Sect. 2.2.2, the AMR-E efficiency is the ratio between the total subfilter wrinkling \({\varXi }^{\mathrm {tot}}_{{\varDelta }_{\mathrm {eff}}}\) and the modeled resolved wrinkling \({\varXi }^{\mathrm {res}}_{{\varDelta }_{\mathrm {eff}}}\). An analysis of the different contributions to the efficiency is proposed here. Mean total and modeled resolved wrinkling up to scale \({\varDelta }_{\mathrm {eff}}\) are computed by setting \({\varPhi }={\varXi }^{\mathrm {tot}}_{{\varDelta }_{\mathrm {eff}}}\) and \({\varPhi }={\varXi }^{\mathrm {res}}_{{\varDelta }_{\mathrm {eff}}}\) in Eq. 34.Footnote 5 Fig. 12 illustrates the evolution of \(<{\varXi }^{\mathrm {tot}}_{{\varDelta }_{\mathrm {eff}}}>\), \(<{\varXi }^{\mathrm {res}}_{{\varDelta }_{\mathrm {eff}}}>\), \(<E>\) and \(<{\dot{\omega }}_{f,res}>\) as a function of the burned gas radius for the engine conditions. The total flame wrinkling \(<{\varXi }^{\mathrm {tot}}_{{\varDelta }_{\mathrm {eff}}}>\) is the highest for \(n_{AMR}=0\) as (i) the upper integration scale \({\varDelta }_{\mathrm {eff}}\) is the highest; (ii) large scales are the most efficient to wrinkle the flame. Indeed, no relaxation is made in this case and thus \({\varDelta }_{\mathrm {eff}} = \gamma {\varDelta }_x^{\mathrm {flow}}\). When \(n_{AMR}>0\), the total wrinkling is lower as \({\varDelta }_{\mathrm {eff}}\) is relaxed towards the locally refined cell size. The total wrinkling for \(n_{AMR}=1\) and \(n_{AMR}=2\) are very close. Indeed, \({\varDelta }_{\mathrm {eff}}\) is comparable for these two cases as the flame turbulent time-scale is much smaller than the turbulent cascading time. Meanwhile, due to the decrease of the thickening factor for the finer flame, \({\varXi }^{\mathrm {res}}_{{\varDelta }_{\mathrm {eff}}}\) is higher for \(n_{AMR}=2\) than for \(n_{AMR}=1\). This gives rise to a lower efficiency \(<E>\) for \(n_{AMR}=2\). This lower predicted efficiency factor actually compensates an increase in the flame resolved reaction. This is emphasized on the bottom right of Fig. 12, where the mean resolved fuel reaction rate \(<{\dot{\omega }}_{f,res}>\) is shown for both mesh resolutions: it is indeed larger for the fine flame (red) than for the coarse flame (blue).

Fig. 13
figure 13

Flame averaged quantities for the atmospheric conditions: mean total wrinkling \(<{\varXi }^{\mathrm {tot}}_{{\varDelta }_{\mathrm {eff}}}>\) (top left), mean modeled resolved wrinkling \(<{\varXi }^{\mathrm {res}}_{{\varDelta }_{\mathrm {eff}}}>\) (top right), mean efficiency \(<E>\) (bottom left), mean resolved fuel reaction rate \(<{\dot{\omega }}_{f,res}>\) (bottom right). Circles (\(\bullet\)): \(n_{AMR}=0\). Squares (\(\blacksquare\)): \(n_{AMR}=1\). Triangles (\(\blacktriangle\)): \(n_{AMR}=2\)

Full size image

The same analysis is provided for the atmospheric conditions in Fig. 13. The total wrinkling \({\varXi }^{\mathrm {tot}}_{{\varDelta }_{\mathrm {eff}}}\) is here lower for \(n_{AMR}=2\) than for \(n_{AMR}=1\). Indeed, as the turbulent cascading time and the flame time are comparable, the AMR-E model relaxes the effective scales faster towards the local scales. The efficiency for the finest case (\(n_{AMR}=2\)) is then close to one, and we observe that the resolved reaction rate \(<{\dot{\omega }}_{f,res}>\) is significantly increased as the AMR resolution grows (bottom right in Fig. 13).

3.3.4 Impact of stand-alone SGS velocity modeling

As detailed in Sect. 2.2.2, The AMR-E model involves the change of the upper integration scale in the algebraic wrinkling model as well as a new definition for the SGS velocity, which takes into account the partial cascading of turbulence in the refined flame region. An analysis is carried out here in order to evaluate the impact of the new definition for the SGS velocity alone. For this purpose, an alternative formulation of E is defined : it is defined by the standard efficiency expression of Charlette but the reference velocity fluctuation \({u'}_{{\varDelta }}\) is replaced by \({u'}_{{\varDelta }}^{\mathrm {eff}}\) which is based on the effective velocity fluctuation \({u'}_{\mathrm {eff}}\). This efficiency reads:

$$\begin{aligned} E = \frac{{\varXi }_{{\varDelta }}\left( \frac{{\varDelta }}{\delta _l^0}, \frac{{{u'}}_{{\varDelta }}^{\mathrm {eff}}}{S_l^0} \right) }{{\varXi }_{{\varDelta }}\left( \frac{{\varDelta }}{{\mathcal {F}}\delta _l^0},\frac{{{u'}}_{{\varDelta }}^{\mathrm {eff}}}{S_l^0} \right) } \end{aligned}$$
(36)

In this equation, \({u'}_{{\varDelta }}^{\mathrm {eff}}\) is the effective velocity rescaled at the TFM filter size \({\varDelta }={\mathcal {F}}\delta _l^0\) using the inertial spectrum assumption:

$$\begin{aligned} {u'}_{{\varDelta }}^{\mathrm {eff}} = {u'}_{\mathrm {eff}} \left( \frac{{\varDelta }}{{\varDelta }_{\mathrm {eff}}} \right) ^{\frac{1}{3}} \end{aligned}$$
(37)

Equation (36) thus takes into account the partial cascading of turbulence in the AMR region through the use of the effective velocity \({u'}_{{\varDelta }}^{\mathrm {eff}}\). But interactions between the flame and vortices are considered up to scale \({\varDelta }\) as in the reference efficiency model, and hence scales from \({\varDelta }\) to \({\varDelta }_{\mathrm {eff}}\) are not taken into account in this model.

Fig. 14
figure 14

Instantaneous fields of subgrid scale velocity \({u'}_{\mathrm {eff}}\) and efficiency E at a given instant for the Charlette model computed using rescaled effective velocity (Eq. 36). Results are represented for engine conditions with AMR level \(n_{AMR}=2\)

Full size image
Fig. 15
figure 15

Heat release rate \(<{\dot{q}}>\) (left) and mean efficiency \(<E>\) (right) as a function of the normalized burned gas radius \(r_{BG} / r_0\) for engine conditions. Black dashed lines (---) correspond to standard TFM cases and blue continuous lines (−) to the Charlette model evaluated using rescaled effective SGS velocity (Eq. 36). The different AMR levels are represented using different symbols. Circles (\(\bullet\)): \(n_{AMR}=0\). Squares (\(\blacksquare\)): \(n_{AMR}=1\). Triangles (\(\blacktriangle\)): \(n_{AMR}=2\)

Full size image

Fields of effective SGS velocity \({u'}_{{\varDelta }}^{\mathrm {eff}}\) and the associated efficiency are shown in Fig. 14 for the model defined by Eq. (36) and AMR level \(n_{AMR}=2\). The SGS velocity is smooth as it is directly computed from the transported \({u'}_{\mathrm {eff}}\). The efficiency values are lower than the values previously obtained with the AMR-E model, shown in Fig. 11. The results using Eq. (36) are then compared to the standard Charlette model, which computes E from \({\varDelta }\) and \({u'}_{{\varDelta }}\), in Fig. 15. The total heat release rate \(<{\dot{q}}>\) and mean efficiency \(<E>\) are represented as a function of the burned gas radius. While the mean efficiency is increased by the use of \({u'}_{{\varDelta }}^{\mathrm {eff}}\) (right in Fig. 11), the heat release rate significantly drops as the flame is refined. The probable cause for this loss in flame propagation speed is the fact that the scales in the range \([{\varDelta }, {\varDelta }_{\mathrm {eff}}]\) are not sufficiently resolved and should be included in the TFM efficiency model. It is thus essential to use the newly defined model for E [Eq. (18)].

3.3.5 Influence of Model Parameters on AMR-E Model Predictions

The improvements brought by the AMR-E model compared to standard TFM in situations involving AMR have been demonstrated in the previous sections. We finally investigate the influence of the two main model parameters present in the AMR-E model: (i) the relaxation time-scale \(\alpha\); (ii) the filter size scaling factor \(\gamma\).

Influence of \(\alpha\) The partial cascading of turbulent scales is driven by a relaxation with time-scale \(\alpha \tau _t\) in the AMR-E model (see Eqs. (11) and (12)). The impact of \(\alpha\) on the results is investigated here. Computations are performed in the engine conditions, which are the most sensitive to the wrinkling modeling, and for an AMR level \(n_{AMR}=2\). The filter size parameter \(\gamma\) is set to 3. A comparison of simulations with \(\alpha \in \{1,3,5\}\) is provided in Fig. 16. The main observation is that the results are weakly sensitive to the value of \(\alpha\), which is in agreement with the conclusions drawn from the a priori study in Fig. 3. A slight decrease of the effective scales \(<{u'}_{\mathrm {eff}}>\) and \(<{\varDelta }_{\mathrm {eff}}>\) is observed as the value of \(\alpha\) decreases. This is explained by a faster relaxation in Eqs. (11) and (12). It leads to a slight decrease in the efficiency, leading to a negligible impact on the heat release rate.

Fig. 16
figure 16

Influence of the relaxation parameter \(\alpha\) on the heat release rate \({\dot{q}}\) (top left), the mean efficiency \(<E>\) (top right), the mean effective subgrid scale velocity \(<{u'}_{\mathrm {eff}}>\) (bottom left) and the mean effective filter size \(<{\varDelta }_{\mathrm {eff}}>\). Circles (\(\bullet\)): \(\alpha =1\). Squares (\(\blacksquare\)): \(\alpha =3\). Triangles (\(\blacktriangle\)): \(\alpha =5\)

Full size image

Influence of \(\gamma\) As exposed in Sect. 2.2.2, the AMR-E filter size is defined as \(\gamma {\varDelta }_x\), where \(\gamma\) is a model parameter. In practice, \(\gamma\) influences the upper integration scale in the efficiency function calculation. The impact of \(\gamma\) on the AMR-E results is here illustrated. Simulations with \(n_{AMR}=0 \ ,1 \ , 2\) with a fixed value \(\alpha =1\) for the relaxation parameter are carried out. The obtained heat release rates for \(\gamma \in \{2,3,5\}\) are shown in Fig. 17. Results for the standard TFM model, independent of \(\gamma\), are also reported on each plot. For \(\gamma =2\), a significant variation of the heat release rate with the AMR level is observed, which means in this case the AMR-E model is not capable of preserving a low sensitivity to the mesh resolution. Better results are obtained for \(\gamma =3\) and \(\gamma =5\). For \(\gamma =3\), the \(n_{AMR}=1\) simulation closely matches the \(n_{AMR}=2\) simulation, while for \(\gamma =5\) it is closest to the \(n_{AMR}=0\) simulation. Nevertheless, the sensitivity to the cell size is acceptable in both cases, meaning that the influence of the \(\gamma\) parameter on the model’s results is moderate for values in the range [3, 5]. Note that this could be expected as \({\widehat{{\varDelta }}}=\gamma {\varDelta }_x\) is defined as the scale above which eddies as fully resolved on the LES mesh. With standard finite volume discretization used here, numerical dissipation is high for scales close to the minimum resolved scale \(2 {\varDelta }_x\), thus explaining why \(\gamma =2\) performs poorly.

Fig. 17
figure 17

Heat release rate \(<{\dot{q}}>\) as a function of the normalized burned gas radius \(r_{BG} / r_0\) for several values of the parameter \(\gamma\). Left: \(\gamma =2\). Center: \(\gamma =3\). Right: \(\gamma =5\). Black dashed lines (---) correspond to standard TFM cases (independent of \(\gamma\)) and blue continuous lines (−) to AMR-E. Circles (\(\bullet\)): \(n_{AMR}=0\). Squares (\(\blacksquare\)): \(n_{AMR}=1\). Triangles (\(\blacktriangle\)): \(n_{AMR}=2\)

Full size image

4 Conclusion

Issues arising from the use of adaptive mesh refinement to resolve turbulent flame fronts have been investigated in this paper. It has been shown that for a specific turbulent combustion model, namely the Thickened Flame Model, an adaptation of the turbulent/chemistry interaction model is needed to account for the use of AMR to resolve the thin flame front. This is explained here by a partial cascading of turbulent structures in the refined flame front, while the TFM efficiency factor is built for uniform meshes and implicitly assumes a complete cascade. When used in typical engine conditions, the TFM model indeed strongly under-predicts the turbulent flame propagation. A new model, named TFM-AMR-E, has been proposed to account for the partial cascading. The underlying idea is to relax turbulent length and velocity scales towards the local ones in a characteristic turbulent time. This relaxation thus mimics partial cascading of turbulent structures. The AMR-E model is shown to have better properties than the standard TFM model when AMR is used to resolved the flame front. In particular, the propagation of a flame in a homogeneous isotropic turbulence has been successfully simulated using the AMR-E model with three different flame front resolution levels. A good behavior of the model when varying the flame cell size has been observed. Additionally, a good robustness of AMR-E with respect to its model parameters has been demonstrated on the simulated cases. The improvements brought by AMR-E are particularly important when the turbulent time-scale is large compared to the flame time (engine case) whereas the standard TFM model is sufficient to reach acceptable results when the turbulent time-scale is small compared to the flame time (atmospheric case).

The present issue, highlighted for the TFM model, is likely to hold for any turbulent combustion model. The AMR-E approach presented in this paper is however specific to models involving an efficiency factor to describe turbulence/chemistry interactions. Additional research is needed for different modeling formalisms. In the context of TFM, a weakness which has already been put into evidence in previous work (Wang et al. 2011) is the use of the model parameter \(\beta\), which is case-dependant. Dynamic models, designed to automatically compute \(\beta\) using similarity assumptions (Charlette et al. 2002b), have been proposed to tackle this problem. They have been applied with success in various situations such as deflagrations (Volpiani et al. 2017) or internal combustion engines (Mouriaux et al. 2017). Future research on the TFM-AMR model will focus on the coupling between dynamic efficiency modeling and AMR in order to increase the predictivity of the proposed modeling approach. Another issue, to our knowledge today untackled for TFM as for many other combustion models, is that the simultaneous use of two different filters in the equations (one for combustion, the other for the flow) leads to an inter-scale convective term in the species equation (Mercier et al. 2015) which is neglected and requires modeling. This error is already non negligible on a fixed mesh (Mercier et al. 2015), and thus requires a specific evaluation when AMR is used. In addition to simulations involving AMR, the presented model may also be of interest for unstructured meshes featuring a fine resolution in the flame front, and thus a strongly varying cell size.