Reaching consensus in group decision making with non-reciprocal pairwise comparison matrices

Abstract

In a complex group decision-making (GDM) process, decision makers (DMs) usually encounter some uncertainties. The uncertainty experienced by DMs could be characterized by the non-reciprocal property of pairwise comparisons. In this paper, the concept of non-reciprocal pairwise comparison matrices (NrPCMs) is introduced to generally capture the situation with the breaking of reciprocal property. The transformation relation between NrPCMs and interval multiplicative reciprocal matrices (IMRMs) is addressed. It is identified that NrPCMs together with IMRMs are inconsistent in nature. Then a consistency index of NrPCMs is constructed according to cosine similarity measures of two row/column vectors. An optimization-based method for eliciting priorities from NrPCMs is proposed. The properties of the proposed consistency index and prioritization method are investigated. Furthermore, a model of building consensus in GDM with NrPCMs is formed, where an optimization model is constructed and solved using a particle swarm optimization (PSO) algorithm. Some comparisons with the existing methods are reported by carrying out numerical examples. The obtained results reveal that NrPCMs provide a new yet effective way to capture the uncertainty experienced by DMs.

1 Introduction

As a typical choice model, the Analytic Hierarchy Process (AHP) has been developed and applied for more than forty years [1, 2]. The basic mathematical tool of the AHP model is pairwise comparison matrix (PCM), which is produced by the technique of pairwisely comparing criteria and alternatives. As shown in the axiomatic foundation of AHP [3], multiplicative reciprocal property is usually equipped for a PCM due to mathematical intuition. It is further noted that some uncertainty is always encountered by decision makers (DMs) in the process of comparing alternatives [4, 5]. An uncertainty-induced axiomatic foundation of the AHP model has been proposed [6], where the concept of reciprocal symmetry breaking was introduced to characterize the uncertainty. Moreover, the concept of interval multiplicative reciprocal matrices (IMRMs) has been proposed to capture the experienced uncertainty of DMs [7], which can be derived from PCMs with the breaking of reciprocal property.

It is worth noting that there is an inherent relationship between the concepts of PCMs and IMRMs. The concept of IMRMs is the extension of PCMs by considering the uncertainty of human-originated information [7]. It is further found that IMRMs can be decomposed into two matrices without multiplicative reciprocal property and derived by a PCM with reciprocal symmetry breaking [6]. However, the uncertainty-induced axiomatic foundation in [6] only considers the case with 0 < a_ija_ji ≤ 1 where a_ij denotes the comparison ratio between alternatives x_i and x_j for i ∈ I_n = {1,2,⋯ ,n}. In fact, for the reciprocal symmetry breaking, the mixed situation with 0 < a_ija_ji ≤ 1 and 1 < a_kla_lk < 81 could emerge. For convenience, the mixed matrices without multiplicative reciprocal property are recalled as non-reciprocal pairwise comparison matrices (NrPCMs). It is worth mentioning that the non-reciprocal property of pairwise comparisons has been considered theoretically and experimentally [8, 9]. Here we further link the non-reciprocal property to the uncertainty of decision information. That is, when the multiplicative reciprocal property of PCMs is relaxed, the generalized NrPCMs can be used to characterize decision information under uncertainty. Moreover, from the viewpoint of producing a NrPCM, the workload is equal to that of giving an IMRM. And NrPCMs exhibit a simpler form than IMRMs. Motivated by the above considerations, we focus on the concept of the generalized NrPCMs and its application to group decision making (GDM), since GDM under uncertain environments has still been a research hotspot [10,11,12,13,14,15]. In particular, the consistency index and prioritization method are studied for NrPCMs. The main contributions are worth mentioning below:

• The concept of NrPCMs is proposed generally. The transformation relation between IMRMs and NrPCMs is carefully addressed.

• The consistency index of NrPCMs is proposed. It is identified that NrPCMs are inconsistent in nature due to the lacking of multiplicative reciprocal property.

• The priority vector is derived from NrPCMs by constructing an optimization model.

• The proposed consistency index and prioritization method are used to propose a consensus model in GDM, where individual NrPCMs are optimized using the particle swarm optimization (PSO) algorithm.

The paper is organized as follows. In Section 2, a literature review is provided to give a solid foundation for the present study. Section 3 introduces some concepts related to PCMs, IMRMs and NrPCMs, respectively. The relationship between IMRMs and NrPCMs is studied and some interesting properties are reported. In Section 4, a consistency index is proposed for NrPCMs and some comparisons are given by numerical computations. Then the prioritization method is constructed to derive the priority vector from NrPCMs. Section 5 gives a consensus model with NrPCMs and offers some discussions on the effects of the parameters and comparisons with the existing methods. Finally, the conclusions and future research direction are covered in Section 6.

2 Literature review

Our contributions are related to the line of work that addresses consistency index, prioritization method and consensus reaching model [11, 16, 17]. It is found that DMs always provide inconsistent PCMs [1]. In order to quantify the inconsistency degrees of PCMs, an index should be proposed. The earliest contribution is attributed to Saaty’s consistency index (CI) and consistency ratio (CR) [1], which are constructed from a global view point to measure the deviation degree of inconsistent PCMs from a consistent one. The geometric consistency index (GCI) of PCMs was formalized in [18] using the average value of the squared difference between the logarithm of entries and the corresponding ratio of priorities. The consistency index C^∗ of a PCM was determined by the average of the determinants of 3 × 3 submatrices [19]. A statistical approach was proposed to measure the consistency level of PCMs in [20]. The cosine similarity measures of two column vectors in a PCM were used to obtain the cosine consistency index (CCI) in [21]. The CCI was further extended to the double cosine similarity consistency index (DCSCI) by considering row/column vectors in a PCM [22]. In general, the consistency indexes of PCMs have been analyzed and compared using an axiomatic approach [23]. Recently, the distance-based method has been used to measure the consistency and transitivity degrees of pairwise comparisons [24]. It is seen from the above analysis that the consistency indexes of PCMs have been widely studied according to various views. Moreover, consistency indexes of interval-valued comparison matrices have also attracted much attention [25]. For example, Conde and Pérez [26] have defined a consistency index of IMRMs by considering the existence of an associated PCM with consistency. Dong et al. [27] have constructed two consistency indexes of interval-valued comparison matrices where the deviation degree of a PCM from a consistent one. Liu et al. [28] have given a consistency index of IMRMs by considering the boundary matrices and the permutations of alternatives. The result in [28] shows that a consistent PCM is the limiting case of an IMRM. In addition, the cardinal and ordinal consistencies of fuzzy preference relations have also attracted a great deal of attention with some investigations of consistency index [29,30,31,32]. Here we construct the consistency index of NrPCMs and consider its extension to IMRMs.

Moreover, it is important to derive the priority vector from a preference relation. When considering a PCM, many methods have been proposed [33]; and here they are split into two classes. One is the direct computation methods using a mathematical theory. For example, based on the matrix eigenvalue theory, the eigenvector method was considered to be the only way to give the priorities and correct ranking of alternatives [34]. According to the statistical theory, the scaling method was proposed to elicit the priorities of alternatives [35]. The other is the distance-based optimization methods by constructing various objective functions. For instance, the logarithmic least squares method was proposed by Crawford and Williams to obtain the geometric mean priority vector of alternatives [36]. By considering the singular value decomposition (SVD) of a matrix, the priorities of alternatives were determined by explicitly solving an optimization problem [37]. A linear goal programming model was established to derive the priorities in [38] from a PCM. By maximizing the cosine similarity degree of two row vectors in a PCM, the priority vector was elicited in [21]. The cosine maximization method in [21] has been further extended to the double cosine similarity maximization method in [22]. The extended logarithmic least squares method was proposed to derive individual and collective priority vectors from multiplicative preference relations with self-confidence in [39]. In addition, when deriving the priority vector from IMRMs, the prioritization methods of PCMs have been extended to propose the corresponding techniques. It is seen that the sampling method has been given for deriving the interval weights from IMRMs [7]. The convex combination method has been proposed to directly compute the interval weights from an IMRM [28, 40]. Following the ideas of CI and GCI, two methods have been used to determine the interval weights of alternatives from IMRMs [41]. Recently, the eigenvector method has been further applied to derive the interval priority vector from IMRMs [42]. In addition, many mathematical programming models have been constructed to elicit the priority vector from IMRMs [43, 44]. In the present study, an optimization model will be established to elicit the priority vector from NrPCMs.

At the end, let us briefly review consensus reaching models in GDM. In order to achieve a widely accepted solution to a GDM problem, the consensus of experts should be considered [11, 45]. The consensus level is always measured by proposing an index or characterized by a function. For example, based on the distance between eigenvectors of individual and collective PCMs, the group consensus was computed in [10, 46]. The similarity degree between individual and collective fuzzy preference relations was used to define the consensus level of group in [47, 48]. The distance-based method was usually developed to capture the consensus degree between individual and collective judgements of DMs [49,50,51,52,53]. In the process of reaching consensus, two approaches are always adopted. One is the optimization-based method for reaching an optimal consensus level [10, 46,47,48, 54,55,56]. The other is to use the threshold of consensus index to give an acceptable consensus degree [49,50,51,52,53]. This paper focuses on the optimization-based consensus model with NrPCMs, which is solved using a PSO algorithm.

3 Preliminaries and notations

Suppose that there are a finite set of alternatives X = {x₁,x₂,…,x_n} in a decision making problem. The DM compares the alternatives in pairs and gives her/his opinions. In the following, we recall some basic definitions and offer some novel findings.

3.1 Basic definitions

When the judgements of DMs are expressed as positive real numbers, the concept of PCMs with multiplicative reciprocal property is given as follows:

Definition 1

Saaty [1] A PCM A = (a_ij)_n×n is multiplicative reciprocal, if a_ij = 1/a_ji and $a_{ij}\in \mathbb {R}^{+}$ for ∀i,j ∈ I_n.

In addition, by considering the strict transitivity of judgements, the consistent PCM is defined:

Definition 2

Saaty [1] A PCM A = (a_ij)_n×n is consistent if a_ij = a_ik ⋅ a_kj for ∀i,j,k ∈ I_n.

It is seen that when A = (a_ij)_n×n is consistent, the condition of a_ij = a_ik ⋅ a_kj yields the multiplicative reciprocal property a_ija_ji = 1 for ∀i,j ∈ I_n. In other words, the multiplicative reciprocal property is a necessary condition for the consistency of PCMs in Definition 2. When a PCM is not with multiplicative reciprocal property, it must be inconsistent.

Moreover, by considering the uncertainty experienced by DMs, the concept of IMRMs is provided below:

Definition 3

[7] An IMRM $\bar {A}$ is represented as

$$ \bar{A}=(\bar{a}_{ij})_{n\times n}= \left( \begin{array}{cccc} [1,1] & \left[a_{12}^{-},a_{12}^{+}\right] & {\cdots} & \left[a_{1n}^{-},a_{1n}^{+}\right]\\ \left[a_{21}^{-},a_{21}^{+}\right] & [1,1] & {\cdots} & \left[a_{2n}^{-},a_{1n}^{+}\right]\\ {\vdots} & {\vdots} & {\vdots} & {\vdots} \\ \left[a_{n1}^{-},a_{n1}^{+}\right] & \left[a_{n2}^{-},a_{n2}^{+}\right] & {\cdots} & [1,1] \end{array}\right) $$

(1)

where $a_{ij}^{-}$ and $a_{ij}^{+}$ are non-negative real numbers satisfying $a_{ij}^{-}\leq a_{ij}^{+},$ $a_{ij}^{-}\cdot a_{ji}^{+}=1$ and $a_{ij}^{+}\cdot a_{ji}^{-}=1$. The term $\bar {a}_{ij}$ indicates that the comparison ratio of alternatives x_i over x_j lies between $a_{ij}^{-}$ and $a_{ij}^{+}$.

It is seen that two boundary PCMs with multiplicative reciprocal property can be constructed from an IMRM $\bar {A}$ [40]. In addition, since the comparison ratio is considered to be uniformly distributed in $[a_{ij}^{-}, a_{ij}^{+}],$ the following two boundary matrices can be also determined:

$$ \begin{array}{@{}rcl@{}} &&A^{L}=(a_{ij}^{-})_{n\times n}= \left( \begin{array}{cccc} 1 & a_{12}^{-} & {\cdots} & a_{1n}^{-} \\ a_{21}^{-} & 1 & {\cdots} & a_{2n}^{-} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} \\ a_{n1}^{-} & a_{n2}^{-} & {\cdots} & 1 \end{array}\right), \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} &&A^{R}=(a_{ij}^{+})_{n\times n}= \left( \begin{array}{cccc} 1 & a_{12}^{+} & {\cdots} & a_{1n}^{+} \\ a_{21}^{+} & 1 & {\cdots} & a_{2n}^{+} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} \\ a_{n1}^{+} & a_{n2}^{+} & {\cdots} & 1 \end{array}\right). \end{array} $$

(3)

In general, we have $0<a_{ij}^{-}a_{ji}^{-}\leq 1$ and $a_{ij}^{+}a_{ji}^{+}\geq 1$ since $a_{ij}^{-}\leq a_{ij}^{+}$ for i,j ∈ I_n. The two matrices A^L and A^R are inconsistent, unless $\bar {A}$ degenerates to a consistent PCM with $a_{ij}^{-}=a_{ij}^{+}$ (i,j ∈ I_n). As compared to Definition 1, the difference in A^L and A^R is that the multiplicative reciprocal property has been relaxed. In the recent paper [6], the concept of reciprocal symmetry breaking has been proposed to consider the case without reciprocal property. The case of $0<a_{ij}^{-}a_{ji}^{-}\leq 1$ has been used to establish the novel axiomatic foundation of the AHP model under uncertainty. Here we generally consider the mixed situation, where the two cases of $0<a_{ij}^{-}a_{ji}^{-}\leq 1$ and $a_{ij}^{+}a_{ji}^{+}\geq 1$ may exist at the same time in a matrix. The concept of NrPCMs is proposed as follows:

Definition 4

If there is a pair of entries in a PCM A = (a_ij)_n×n such that the relation a_ij ⋅ a_ji = 1 is not satisfied, A is called a non-reciprocal pairwise comparison matrix (NrPCM).

One can find from Definition 4 that when a_ij ⋅ a_ji≠ 1 for at least a pair of i and j, a NrPCM is given. For a practical situation, when the DM compares alternatives x_i and x_j to give the judgement a_ij, the comparison ratio of x_j over x_i is written as a_ji. A NrPCM means that it is not necessary to satisfy the relation a_ij ⋅ a_ji = 1. For example, when considering the scale [1/9,9] and giving a_ij = 1/4, the value of a_ji could deviate from 4 to a certain degree. This deviation is attributed to the uncertainty experienced by DMs [7]. As compared to the process of giving IMRMs, the method of providing NrPCMs seem simpler and more direct. The reveal-valued comparison matrix is more intuitive than an interval-valued one. Hereafter, similar to the idea in [6], when talking about PCMs, it means that the multiplicative reciprocal property may be not satisfied. Clearly, A^L and A^R are two particular NrPCMs corresponding to $0<a_{ij}^{-}a_{ji}^{-}\leq 1$ and $a_{ij}^{+}a_{ji}^{+}\geq 1,$ respectively.

3.2 The relationship between NrPCMs and IMRMs

In what follows, let us discuss the relationship between NrPCMs and IMRMs. For a generalized PCM A = (a_ij)_n×n, it is convenient to define the uncertainty degree as

$$ h_{ij}=\frac{1}{a_{ij}\cdot a_{ji}},\quad i,j\in I_{n}. $$

(4)

When the scale [1/9,9] is used, it gives h_ij ∈ [1/81,81] for ∀i,j ∈ I_n. It is seen that the interval [1/81,81] can be easily transformed into [0,1] by only using a linear transformation. Here for the sake of simplicity, the interval [0,1] is not used for the uncertainty degree. Then the uncertainty matrix is determined as:

$$ H=(h_{ij})_{n\times n}. $$

(5)

Since h_ij = h_ji, we can find that H is a symmetric matrix. When h_ij = 1 for ∀i,j ∈ I_n, A = (a_ij)_n×n is a PCM with multiplicative reciprocal property. When there are a pair of i and j for holding h_ij≠ 1, A = (a_ij)_n×n is a NrPCM. Furthermore, we consider the relationship between the two PCMs A^L and A^R. Similar to (4) and (5), we give the following terms:

$$ h_{ij}^{-}=\frac{1}{a_{ij}^{-}a_{ji}^{-}},\quad h_{ij}^{+}=\frac{1}{a_{ij}^{+}a_{ji}^{+}},\quad i,j\in I_{n}, $$

(6)

and

$$ H^{L}=(h_{ij}^{-})_{n\times n},\quad H^{R}=(h_{ij}^{+})_{n\times n}. $$

(7)

According to the relations $a_{ij}^{-}\cdot a_{ji}^{+}=1$ and $a_{ij}^{+}\cdot a_{ji}^{-}=1,$ it gives

$$ h_{ij}^{-}=\frac{1}{a_{ij}^{-}}\cdot \frac{1}{a_{ji}^{-}}=a_{ij}^{+}\cdot a_{ji}^{+}=\frac{1}{h_{ij}^{+}}. $$

(8)

The above observation shows that the uncertainty degree of IMRMs can be characterized using the two symmetric matrices H^L and H^R, respectively. Hence, we have the following property:

Theorem 1

For an IMRM $\bar {A}=(\bar {a}_{ij})_{n\times n},$ letting $A^{L}=(a_{ij}^{-})_{n\times n}$ and $A^{R}=(a_{ij}^{+})_{n\times n},$ it follows

$$ A^{R}=A^{L}\circ H^{L},\quad A^{L}=A^{R}\circ H^{R}, $$

(9)

where the symbol “∘” denotes the Hadamard product of two matrices.

Proof

Since

$$ a_{ij}^{+}=a_{ij}^{-}\cdot \frac{a_{ij}^{+}}{a_{ij}^{-}}=a_{ij}^{-}\cdot \frac{1}{a_{ij}^{-}a_{ji}^{-}}=a_{ij}^{-}\cdot h_{ij}^{-}, $$

and

$$ a_{ij}^{-}=a_{ij}^{+}\cdot \frac{a_{ij}^{-}}{a_{ij}^{+}}=a_{ij}^{+}\cdot \frac{1}{a_{ij}^{+}a_{ji}^{+}}=a_{ij}^{+}\cdot h_{ij}^{+}, $$

for ∀i,j ∈ I_n, we get A^R = A^L ∘ H^L and A^L = A^R ∘ H^R. □

It is noted from the above analysis that both NrPCMs and IMRMs can be used to capture the uncertainty of DMs. Moreover, the transformation relationship between NrPCMs and IMRMs can be determined as follows:

Theorem 2

For a NrPCM A = (a_ij)_n×n, let

$$ a_{ij}^{-}=a_{ij}\cdot h_{ij},\quad a_{ij}^{+}=a_{ij}\quad \text{for}\quad a_{ij}\cdot a_{ji}\geq 1, $$

(10)

and

$$ a_{ij}^{-}=a_{ij},\quad a_{ij}^{+}=a_{ij}\cdot h_{ij} \quad \text{for} \quad a_{ij}\cdot a_{ji}<1, $$

(11)

where h_ij has been defined in (4). Then an IMRM $\bar {A}=([a_{ij}^{-}, a_{ij}^{+}])_{n\times n}$ is uniquely determined by (10) and (11).

Proof

If a_ij ⋅ a_ji ≥ 1, we can determine $h_{ij}=\frac {1}{a_{ij}\cdot a_{ji}}\leq 1,$ and

$$ a_{ij}^{-}=a_{ij}\cdot h_{ij}\leq a_{ij}=a_{ij}^{+}. $$

According to (10), it follows:

$$ a_{ij}^{-}=a_{ij}\cdot h_{ij},\quad a_{ij}^{+}=a_{ij}, $$

and

$$ a_{ji}^{-}=a_{ji}\cdot h_{ji},\quad a_{ji}^{+}=a_{ji}. $$

Therefore, it is calculated that

$$ a_{ij}^{-}\cdot a_{ji}^{+}=a_{ij}\cdot h_{ij}\cdot a_{ji}=a_{ij}\cdot a_{ji}\cdot \frac{1}{a_{ij}\cdot a_{ji}}=1, $$

and

$$ a_{ij}^{+}\cdot a_{ji}^{-}=a_{ij}\cdot a_{ji}\cdot h_{ji}=a_{ij}\cdot a_{ji}\cdot \frac{1}{a_{ji}\cdot a_{ij}}=1. $$

Similarly, when a_ij ⋅ a_ji < 1, we also obtain $a_{ij}^{-}\leq a_{ij}^{+},$ $a_{ij}^{-}\cdot a_{ji}^{+}=1$ and $a_{ij}^{+}\cdot a_{ji}^{-}=1$. Hence, an IMRM $\bar {A}=([a_{ij}^{-}, a_{ij}^{+}])_{n\times n}$ is constructed and the proof is completed. □

It is seen from Theorem 1 that an IMRM can be decomposed into two NrPCMs with the relations in (9). A NrPCM can be transformed into an IMRM according to Theorem 2. When all the entries in a NrPCM A = (a_ij)_n×n satisfy a_ij ⋅ a_ji ≥ 1 or 0 < a_ij ⋅ a_ji ≤ 1, A = (a_ij)_n×n is written as A^R or A^L and an IMRM is determined using (9). When the two cases of a_ij ⋅ a_ji ≥ 1 and 0 < a_ij ⋅ a_ji ≤ 1 are all existing, some computations should be made to obtain an IMRM in terms of Theorem 2. For example, we consider the following NrPCM:

$$ A_{1}=\left( \begin{array}{ccccc} 1 & 4 & 3 & 7 & 5 \\ 1/5 & 1 & 1/2 & 5 & 3 \\ 1/3 & 3 & 1 & 6 & 3 \\ 1/7 & 1/5 & 1/5 & 1 & 1/3 \\ 1/6 & 1/3 & 1/2 & 3 & 1 \end{array} \right). $$

It is seen that $a_{23}\cdot a_{32}=\frac {1}{2}\cdot 3=\frac {3}{2}>1,$ then $h_{23}=h_{32}=\frac {2}{3}$. According to (10), we have

$$ a_{23}^{-}=a_{23}\cdot h_{23}=\frac{1}{2}\cdot \frac{2}{3}=\frac{1}{3},\quad \ \ a_{23}^{+}=a_{23}=\frac{1}{2}, $$

and

$$ a_{32}^{-}=a_{32}\cdot h_{32}=3\cdot \frac{2}{3}=2,\quad \ \ a_{32}^{+}=a_{32}=3, $$

meaning that

$$\bar{a}_{23}=\left[\frac{1}{3},\frac{1}{2}\right],\quad\bar{a}_{32}=[2,3].$$

Because $a_{12}\cdot a_{21}=4\cdot \frac {1}{5}=\frac {4}{5}<1,$ then it gives $h_{12}=h_{21}=\frac {5}{4}$. The application of (11) yields

$$ a_{12}^{-}=a_{12}=4,\quad a_{12}^{+}=a_{12}\cdot h_{12}=4\cdot \frac{5}{4}=5, $$

and

$$ a_{21}^{-}=a_{21}=\frac{1}{5},\quad a_{21}^{+}=a_{21}\cdot h_{21}=\frac{1}{5}\cdot \frac{5}{4}=\frac{1}{4}, $$

implying that

$$\bar{a}_{12}=[4,5],\quad \bar{a}_{21}=\left[\frac{1}{5}, \frac{1}{4}\right].$$

For the case of $a_{13}\cdot a_{31}=3\cdot \frac {1}{3}=1,$ it is natural to give h₁₃ = h₃₁ = 1 and

$$\bar{a}_{13}=[3, 3],\ \ \bar{a}_{31}=\left[\frac{1}{3}, \frac{1}{3}\right].$$

According to the above computations, the IMRM $\bar {A}_{1}$ can be determined:

$$ \bar{A}_{1} = \!\left( \begin{array}{ccccc} \left[1, 1\right] & \left[4, 5\right] & \left[3, 3\right] & \left[7, 7\right] & \left[5, 6\right] \\ \!\!\left[1/5, 1/4\right] & \left[1, 1\right] & \left[1/3, 1/2\right] & \left[5, 5\right] & \left[3, 3\right] \\ \!\!\left[1/3, 1/3\right] & \left[2, 3\right] & \left[1, 1\right] & \left[5, 6\right] & \left[2, 3\right] \\ \!\!\left[1/7, 1/7\right] & \left[1/5, 1/5\right] & \left[1/6, 1/5\right] & \left[1, 1\right] & \left[1/3, 1/3\right] \\ \!\!\left[1/6, 1/5\right] & \left[1/3, 1/3\right] & \left[1/3, 1/2\right] & \left[3, 3\right] & \left[1, 1\right] \end{array}\!\!\right)\!. $$

4 Consistency index and prioritization method of NrPCMs

It is noted that NrPCMs are inconsistent due to the lack of multiplicative reciprocal property. It is important to propose a consistency index to quantify the inconsistency degree and a prioritization method of NrPCMs.

4.1 A consistency index based on cosine similarity measure

Following the ideas in [21, 22], the cosine similarity measure of two vectors is used to construct a consistency index of NrPCMs. For convenience, we recall the following definitions:

Definition 5

[21] For $\vec {v}_{i}=(v_{i1}, v_{i2}, \ldots , v_{in})$ and $\vec {v}_{j}=(v_{j1}, v_{j2}, \ldots$,v_jn), the cosine similarity measure is given as:

$$ CSM(\vec{v}_{i}, \vec{v}_{j})=\frac{\|\vec{v}_{i}\odot\vec{v}_{j}\|}{\|\vec{v}_{i}\|\cdot\|\vec{v}_{j}\|}= \frac{\|{\sum}_{k=1}^{n}v_{ik}v_{jk}\|}{\sqrt{{\sum}_{k=1}^{n}v_{ik}^{2}}\sqrt{{\sum}_{k=1}^{n}v_{jk}^{2}}}, $$

(12)

where the symbol ⊙ is the dot product of two vectors.

Then the properties of cosine similarity measure are given as follows [21]:

• $0\leq CSM(\vec {v}_{i}, \vec {v}_{j})\leq 1;$

• $CSM(\vec {v}_{i}, \vec {v}_{i})=1;$

• $CSM(\vec {v}_{i}, \vec {v}_{j})=1$ means that $\vec {v}_{i}$ and $\vec {v}_{j}$ are completely similar;

• $CSM(\vec {v}_{i}, \vec {v}_{j})=0$ implies that $\vec {v}_{i}$ and $\vec {v}_{j}$ are not similar at all;

• $CSM(\vec {v}_{i}, \vec {v}_{j})<CSM(\vec {v}_{i}, \vec {v}_{k})$ indicates that $\vec {v}_{k}$ is more like $\vec {v}_{i}$ than $\vec {v}_{j}$.

According to the cosine similarity measure, a consistency index of PCMs has been constructed:

Definition 6

[22] Assume that A = (a_ij)_n×n is a PCM. The row and column vectors of A = (a_ij)_n×n are written as $\vec {a}_{i\cdot }=(a_{i1}, a_{i2}, \ldots , a_{in})$ and $\vec {a}_{\cdot i}=(a_{1i}, a_{2i}, \ldots , a_{ni})^{T}$ for i ∈ I_n, respectively. The double cosine similarity consistency index (DCSCI) is defined as:

$$ DCSCI(A)=\frac{1}{n(n-1)}\sum\limits_{i<j}^{n}(2-r_{ij}-c_{ij}), $$

(13)

when $r_{ij}=CSM(\vec {a}_{i\cdot }, \vec {a}_{j\cdot })$ and $c_{ij}=CSM(\vec {a}_{\cdot i}, \vec {a}_{\cdot j})$.

One can see from the finding in [22] that the values of r_ij and c_ij could be different for a PCM with multiplicative reciprocal property. In the present study, in order to consider the non-reciprocal property of NrPCMs, the DCSCI should be modified. Therefore, we propose a consistency index of NrPCMs as follows:

Definition 7

For a generalized PCM A = (a_ij)_n×n, the consistency index is defined as:

$$ CSCI(A)=\frac{1}{2n^{2}}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\left( 2-\frac{r_{ij}+e_{ij}}{2}-\frac{c_{ij}+f_{ij}}{2}\right), $$

(14)

where $r_{ij}=CSM(\vec {a}_{i\cdot }, \vec {a}_{j\cdot }),$ $c_{ij}=CSM(\vec {a}_{\cdot i}, \vec {a}_{\cdot j}),$ $e_{ij}=CSM(\vec {a}_{i\cdot }, \vec {a}_{\cdot j}^{-1}),$ and $f_{ij}=CSM(\vec {a}_{\cdot i}, \vec {a}_{j\cdot }^{-1})$ with

$$ \vec{a}_{i\cdot}^{-1} = \left( \!\frac{1}{a_{i1}}, \frac{1}{a_{i2}},\cdots\frac{1}{a_{in}}\!\right)\!,\quad \vec{a}_{\cdot i}^{-1\!}=\!\left( \frac{1}{a_{1i}}, \frac{1}{a_{2i}}, \cdots, \frac{1}{a_{ni}}\!\right)^{\!T}. $$

(15)

It is noted from Definition 7 that the proposed consistency index for a generalized PCM considers the cosine similarity measures of two row vectors, two column vectors, the row vectors and the reciprocal vectors of column vectors, the column vectors and the reciprocal vectors of row vectors. The uncertainty of a NrPCM has been incorporated into the proposed consistency index. Now, we give the properties in the following result:

Theorem 3

Suppose that A = (a_ij)_n×n is a generalized PCM. The consistency index in (14) satisfies:

(1):

0 ≤ CSCI(A) ≤ 1;

(2):

CSCI(A) = 0 if and only if A is consistent according to Definition 2;

(3):

$CSCI(A)=\displaystyle \frac {n-1}{n}DCSCI(A)$ when A is with multiplicative reciprocal property.

Proof

(1) Since we have $0\leq CSM(\vec {v}_{i}, \vec {v}_{j})\leq 1$ for any two vectors, it is determined 0 ≤ CSCI(A) ≤ 1 according to (14).

(2) When A = (a_ij)_n×n is perfectly consistent, one has a_ij = a_ik ⋅ a_kj for ∀i,j,k ∈ I_n. Therefore, it follows

$$ a_{ij}\cdot a_{ji}=a_{ik}\cdot a_{kj}\cdot a_{jk}\cdot a_{ki}=a_{ik}\cdot a_{ki}\cdot a_{jk}\cdot a_{kj}=a_{ii}\cdot a_{jj}=1, $$

for ∀i,j ∈ I_n. Thus, we have

$$ \begin{array}{@{}rcl@{}} \!\!\!\!&&r_{ij} = \frac{{\sum}_{k=1}^{n}a_{ik}a_{jk}}{\sqrt{{\sum}_{k=1}^{n}a_{ik}^{2}}\sqrt{{\sum}_{k=1}^{n}a_{jk}^{2}}} = \frac{{\sum}_{k=1}^{n}a_{ij}a_{jk}^{2}}{\sqrt{{\sum}_{k=1}^{n}a_{ij}^{2}a_{jk}^{2}}\sqrt{{\sum}_{k=1}^{n}a_{jk}^{2}}}=1,\\ \!\!\!\!&&e_{ij}\!=\frac{{\sum}_{k=1}^{n}a_{ik}(1/a_{kj})}{\sqrt{{\sum}_{k=1}^{n}\!a_{ik}^{2}}\sqrt{{\sum}_{k=1}^{n}(1/a_{kj})^{2}}} = \frac{{\sum}_{k=1}^{n}a_{ik}a_{jk}}{\sqrt{{\sum}_{k=1}^{n}a_{ik}^{2}}\sqrt{{\sum}_{k=1}^{n}a_{jk}^{2}}} = r_{ij} = 1,\\ \!\!\!\!&&c_{ij}\!=\frac{{\sum}_{k=1}^{n}a_{ki}a_{kj}}{\sqrt{{\sum}_{k=1}^{n}\!a_{ki}^{2}}\sqrt{{\sum}_{k=1}^{n}a_{kj}^{2}}} = \frac{{\sum}_{k=1}^{n}a_{ki}^{2}a_{ij}}{\sqrt{{\sum}_{k=1}^{n}a_{ki}^{2}}\sqrt{{\sum}_{k=1}^{n}a_{ki}^{2}a_{ij}^{2}}}=1,\\ \!\!\!\!&&f_{ij}\!=\frac{{\sum}_{k=1}^{n}a_{ki}(1/a_{jk})}{\sqrt{{\sum}_{k=1}^{n}\!a_{ki}^{2}}\sqrt{{\sum}_{k=1}^{n}(1/a_{jk})^{2}}} = \frac{{\sum}_{k=1}^{n}a_{ki}a_{kj}}{\sqrt{{\sum}_{k=1}^{n}a_{ki}^{2}}\sqrt{{\sum}_{k=1}^{n}a_{kj}^{2}}}=c_{ij} = 1. \end{array} $$

This means that CSCI(A) = 0 by virtue of Definition 7.

On the contrary, the application of CSCI(A) = 0 leads to

$$\frac{r_{ij}+e_{ij}}{2}+\frac{c_{ij}+f_{ij}}{2}=2.$$

Moreover, in terms of Definition 5, it follows 0 ≤ r_ij,e_ij,c_ij,f_ij ≤ 1. Hence, we must have r_ij = e_ij = c_ij = f_ij = 1 for ∀i,j ∈ I_n. According to the properties of cosine similarity measure and Definition 7, A = (a_ij)_n×n is perfectly consistent.

(3) When A = (a_ij)_n×n is with multiplicative reciprocal property, one has

$$ a_{ij}=1/a_{ji},\quad i,j\in I_{n}. $$

Therefore, it follows:

$$ \begin{array}{@{}rcl@{}} e_{ij} &=& CSM(\vec{a}_{i\cdot}, \vec{a}_{\cdot j}^{-1}) \\ &=&\frac{{\sum}_{k=1}^{n}a_{ik}(1/a_{kj})}{\sqrt{{\sum}_{k=1}^{n}a_{ik}^{2}}\sqrt{{\sum}_{k=1}^{n}(1/a_{kj})^{2}}} \\ &=&\frac{{\sum}_{k=1}^{n}a_{ik}a_{jk}}{\sqrt{{\sum}_{k=1}^{n}a_{ik}^{2}}\sqrt{{\sum}_{k=1}^{n}a_{jk}^{2}}} \\ &=& r_{ij}, \end{array} $$

Similarly, we can get f_ij = c_ij for ∀i,j ∈ I_n. Based on Definition 5, the following relations hold:

$$ r_{ij}=r_{ji},\quad c_{ij}=c_{ji}. $$

Hence, we have

$$ \begin{array}{@{}rcl@{}} CSCI(A)&=& \frac{1}{2n^{2}}{\sum}_{i=1}^{n}{\sum}_{j=1}^{n}(2-\frac{r_{ij}+e_{ij}}{2}-\frac{c_{ij}+f_{ij}}{2}) \\ &=& \frac{1}{2n^{2}}{\sum}_{i=1}^{n}{\sum}_{j=1}^{n}(2-r_{ij}-c_{ij}) \\ &=& \frac{1}{n^{2}}{\sum}_{i<j}^{n}(2-r_{ij}-c_{ij}) \\ &=& \frac{n-1}{n}\frac{1}{n(n-1)}{\sum}_{i<j}^{n}(2-r_{ij}-c_{ij}) \\ &=& \frac{n-1}{n}DCSCI(A). \end{array} $$

□

It is found from Theorem 3 that the consistency index is based on the deviation degree of a generalized PCM from a consistent one. The more the value of CSCI(A) is, the more the inconsistency degree of A is. As compared to the DCSCI in [22], the only difference is the coefficient for a PCM A with multiplicative reciprocal property. This is attributable to the different coefficient when defining the two consistency indexes. Moreover, the acceptable consistency of NrPCMs should be considered according to the proposed consistency index in (14). Here we follow the idea of Saaty [1] to randomly generated 10,000 NrPCMs and give the mean value of CSCI as the random consistency index in Table 1 for n = 2,3,⋯ ,9, respectively. As compared to the random index of consistency index in [1], the main difference is the non-zero value for n = 2 here. Then the consistency ratio is defined as

$$ CR_{Nr}(A)=\frac{CSCI(A)}{\overline{CSCI}}. $$

(16)

When CR_Nr(A) ≤ 0.1, matrix A is considered to be acceptable. Otherwise, matrix A is unacceptable and could be adjusted to a new matrix with acceptable consistency.

Table 1 Random consistency index of NrPCM with order n

As an illustration, we compute the value of CSCI for the following NrPCM:

$$ A_{2}=\left( \begin{array}{cccccc} 1 & 3 & 3 & 1 & 3 & 4 \\ 1/4 & 1 & 7 & 3 & 1/6 & 1 \\ 1/3 & 1/6 & 1 & 1/5 & 1/5 & 1/6 \\ 1 & 1/3 & 4 & 1 & 1 & 1/3 \\ 1/3 & 5 & 3 & 1 & 1 & 3 \\ 1/4 & 1 & 6 & 3 & 1/2 & 1 \end{array} \right). $$

According to Definition 7, it gives

$$ R_{2}=\left( \begin{array}{cccccc} 1.0000 & 0.6106 & 0.7076 & 0.6574 & 0.8952 & 0.6448 \\ 0.6106 & 1.0000 & 0.9301 & 0.9440 & 0.6194 & 0.9967 \\ 0.7076 & 0.9301 & 1.0000 & 0.9896 & 0.6460 & 0.9266 \\ 0.6574 & 0.9440 & 0.9896 & 1.0000 & 0.5773 & 0.9423 \\ 0.8952 & 0.6194 & 0.6460 & 0.5773 & 1.0000 & 0.6403 \\ 0.6448 & 0.9967 & 0.9266 & 0.9423 & 0.6403 & 1.0000 \end{array}\right), $$

$$ C_{2}=\left( \begin{array}{cccccc} 1.0000 & 0.6032 & 0.6902 & 0.5550 & 0.8860 & 0.7378 \\ 0.6032 & 1.0000 & 0.5846 & 0.5210 & 0.7433 & 0.9304 \\ 0.6902 & 0.5846 & 1.0000 & 0.9792 & 0.5526 & 0.6221 \\ 0.5550 & 0.5210 & 0.9792 & 1.0000 & 0.4562 & 0.5594 \\ 0.8860 & 0.7433 & 0.5526 & 0.4562 & 1.0000 & 0.9148 \\ 0.7378 & 0.9304 & 0.6221 & 0.5594 & 0.9148 & 1.0000 \end{array}\right), $$

$$ E_{2}=\left( \begin{array}{cccccc} 0.9923 & 0.6281 & 0.7332 & 0.6267 & 0.8249 & 0.6348 \\ 0.5859 & 0.9979 & 0.9161 & 0.9491 & 0.7283 & 0.9977 \\ 0.6790 & 0.9240 & 0.9925 & 0.9853 & 0.7483 & 0.9237 \\ 0.6221 & 0.9367 & 0.9917 & 0.9970 & 0.6961 & 0.9381 \\ 0.9360 & 0.6355 & 0.6330 & 0.5605 & 0.9653 & 0.6377 \\ 0.6199 & 0.9990 & 0.9205 & 0.9419 & 0.7380 & 0.9997 \end{array}\right), $$

and

$$ F_{2}=\left( \begin{array}{cccccc} 0.9986 & 0.6104 & 0.7385 & 0.5570 & 0.8904 & 0.7707 \\ 0.6060 & 0.9979 & 0.6926 & 0.5210 & 0.7397 & 0.8534 \\ 0.7176 & 0.5518 & 0.9773 & 0.9796 & 0.5368 & 0.6305 \\ 0.5845 & 0.4848 & 0.9336 & 0.9999 & 0.4331 & 0.5730 \\ 0.8796 & 0.7688 & 0.6002 & 0.4566 & 0.9979 & 0.9497 \\ 0.7406 & 0.9428 & 0.6822 & 0.5594 & 0.9107 & 0.9848 \end{array}\right). $$

It is found that matrices R₂ and C₂ are symmetric, while matrices E₂ and F₂ are asymmetric. By virtue of (14), we arrive at CSCI(A₂) = 0.2179 and CR_Nr(A₂) = 0.5222 > 0.1, meaning that A₂ is not of acceptable consistency.

By the way, based on the relationship between NrPCMs and IMRMs, we can construct a novel consistency index of IMRMs as follows:

Definition 8

Suppose that two NrPCMs A^L and A^R are obtained from an IMRM $\bar {A}=(\bar {a}_{ij})_{n\times n}$. The consistency index of $\bar {A}$ is defined as:

$$ NCI(\bar{A})=\frac{CSCI(A^{L})+CSCI(A^{R})}{2}. $$

(17)

As shown in Theorem 3, the properties of $NCI(\bar {A})$ can be obtained straightforwardly and the detailed procedures have been omitted. In particular, it is observed that if and only if $NCI(\bar {A})=0,$ IMRM $\bar {A}$ degenerates to a consistent PCM. That is, the value of $NCI(\bar {A})$ can be considered as the deviation degree of $\bar {A}$ from a consistent PCM. The above observation is in agreement with the finding in [28]. For example, we consider the IMRM as follows [27, 28, 40]:

$$ \bar{A}_{2}= \left( \begin{array}{cccc} \left[1, 1\right] & \left[2, 5\right] & \left[2, 4\right] & \left[1, 3\right] \\ \left[1/5, 1/2\right] & \left[1, 1\right] & \left[1, 3\right] & \left[1.2\right] \\ \left[1/4, 1/2\right] & \left[1/3, 1\right] & \left[1, 1\right] & \left[1/2, 1\right] \\ \left[1/3, 1\right] & \left[1/2, 1\right] & \left[1, 2\right] & \left[1, 1\right] \end{array}\right). $$

The results in [28] have shown that $ICI(\bar {A}_{2})=0,$ $SICI(\bar {A}_{2})=0.3385$ and $WCI(\bar {A}_{2})=0.0483$. Here the application of (17) leads to $NCI(\bar {A}_{2})=0.0592$ and $ICI(\bar {A}_{2})<WCI(\bar {A}_{2})<NCI(\bar {A}_{2})<SICI(\bar {A}_{2})$.

4.2 An optimization method of eliciting priorities

When the judgements of DMs are expressed as NrPCMs, one of the important issues is on how to derive the priority vector of alternatives. Suppose that $\vec {\omega }=(\omega _{1}, \omega _{2}, \ldots , \omega _{n})^{T}$ with ${\sum }_{i=1}^{n}\omega _{i}=1$ and ω_i ≥ 0 (i ∈ I_n) is the priority vector obtained from a PCM A = (a_ij)_n×n. Moreover, let $\vec {t}=(t_{1}, t_{2}, \ldots , t_{n})$ and t_i ⋅ ω_i = 1. If A = (a_ij)_n×n is consistent, then $a_{ij}=\frac {\omega _{i}}{\omega _{j}}$ [1]. At the same time, one has $\vec {a}_{i\cdot }=\omega _{i}(\frac {1}{\omega _{1}}, \frac {1}{\omega _{2}}, {\ldots } \frac {1}{\omega _{n}})=\omega _{i}(t_{1}, t_{2}, \ldots , t_{n})$ and $\vec {a}_{\cdot j}=\frac {1}{\omega _{j}}(\omega _{1}, \omega _{2}, {\ldots } \omega _{n})^{T}$. In the following, based on the idea of constructing CSCI in (14), we propose an optimization model to elicit the priorities of alternatives.

First, by considering the non-reciprocal property of NrPCM A = (a_ij)_n×n, we construct a new matrix D = (d_ij)_n×n where

$$ d_{ij}=\frac{a_{ij}+\frac{1}{a_{ji}}}{2},\quad i,j\in I_{n}. $$

(18)

According to Definition 5, we have

$$ C_{j}=CSM(\vec{\omega}, \vec{d}_{\cdot j}),\quad R_{i}=CSM(\vec{t}, \vec{d}_{i \cdot}), $$

(19)

where $\vec {d}_{i\cdot }=(d_{i1}, d_{i2}, \ldots , d_{in})$ and $\vec {d}_{\cdot j}=(d_{1j}, d_{2j}, \ldots ,$ d_nj)^T for i,j ∈ I_n. It is further obtained that

$$ \begin{array}{@{}rcl@{}} C&=&\sum\limits_{j=1}^{n}C_{j}=\frac{{\sum}_{j=1}^{n}{\sum}_{i=1}^{n}\omega_{i}d_{ij}}{\sqrt{{\sum}_{i=1}^{n}{\omega_{i}^{2}}}\sqrt{{\sum}_{i=1}^{n}d_{ij}^{2}}}\\ &=&\frac{{\sum}_{j=1}^{n}{\sum}_{i=1}^{n}\omega_{i}\frac{a_{ij}+\frac{1}{a_{ji}}}{2}}{\sqrt{{\sum}_{i=1}^{n}{\omega_{i}^{2}}}\sqrt{{\sum}_{i=1}^{n}(\frac{a_{ij}+\frac{1}{a_{ji}}}{2})^{2}}}, \end{array} $$

(20)

$$ \begin{array}{@{}rcl@{}} R&=&\sum\limits_{i=1}^{n}R_{i}=\frac{{\sum}_{i=1}^{n}{\sum}_{j=1}^{n}t_{j}d_{ij}}{\sqrt{{\sum}_{j=1}^{n}{t_{j}^{2}}}\sqrt{{\sum}_{j=1}^{n}d_{ij}^{2}}}\\ &=&\frac{{\sum}_{i=1}^{n}{\sum}_{j=1}^{n}t_{j}\frac{a_{ij}+\frac{1}{a_{ji}}}{2}}{\sqrt{{\sum}_{j=1}^{n}{t_{j}^{2}}}\sqrt{{\sum}_{j=1}^{n}(\frac{a_{ij}+\frac{1}{a_{ji}}}{2})^{2}}}. \end{array} $$

(21)

Second, similar to the finding in [22], the optimization model is established as follows:

$$ \begin{array}{@{}rcl@{}} & & \max\ \ \ F=pC+qR \\ & &s.t. \left\{\begin{array}{l} {\sum}_{i=1}^{n}\omega_{i}=1, \\ t_{i}\omega_{i}=1,\ i\in I_{n}, \\ \omega_{i}\geq 0,\ i\in I_{n}, \end{array}\right. \end{array} $$

(22)

where p ≥ 0 and q ≥ 0 are constants. If A is with multiplicative reciprocal property, the optimization model (22) degenerates to that in [22]. For convenience, the proposed model is called as the cosine similarity maximization method (CSM). For the optimal solutions, we have the following result:

Theorem 4

Assume that the optimal solution to the optimization problem (22) is $\vec {\omega }^{\ast }=(\omega _{1}^{\ast }, \omega _{2}^{\ast }, \ldots , \omega _{n}^{\ast })^{T}$ and the optimal value is F^∗.

(1):

When p = 1 and q = 0, the optimal solution and value of the optimization model (22) are determined as:

$$ \omega_{i}^{\ast}=\frac{\hat{\omega}_{i}^{\ast}}{{\sum}_{j=1}^{n}\hat{\omega}_{j}^{\ast}},\quad i\in I_{n},\quad F^{\ast}=\sqrt{\sum\limits_{i=1}^{n}\left( \sum\limits_{j=1}^{n}u_{ij}\right)^{2}}, $$

(23)

where

$$ \begin{array}{@{}rcl@{}} \hat{\omega}_{i}^{\ast}&=&\frac{{\sum}_{j=1}^{n}u_{ij}}{\sqrt{{\sum}_{i=1}^{n}({\sum}_{j=1}^{n}u_{ij})^{2}}},\quad u_{ij}=\frac{d_{ij}}{\sqrt{{\sum}_{i=1}^{n}d_{ij}^{2}}},\\ d_{ij}&=&\frac{a_{ij}+\frac{1}{a_{ji}}}{2}. \end{array} $$

(24)

(2):

When p = 0 and q = 1, the optimal solution and value of the optimization model (22) are given as:

$$ \omega_{i}^{\ast}=\frac{1/\hat{t}_{i}^{\ast}}{{\sum}_{j=1}^{n}(1/\hat{t}_{j}^{\ast})},\quad i\in I_{n},\quad F^{\ast}=\sqrt{\sum\limits_{j=1}^{n}\left( \sum\limits_{i=1}^{n}v_{ij}\right)^{2}}, $$

(25)

where

$$ \begin{array}{@{}rcl@{}} \hat{t}_{j}^{\ast}&=&\frac{{\sum}_{i=1}^{n}v_{ij}}{\sqrt{{\sum}_{j=1}^{n}({\sum}_{i=1}^{n}v_{ij})^{2}}},\quad v_{ij}=\frac{d_{ij}}{\sqrt{{\sum}_{j=1}^{n}d_{ij}^{2}}},\\ d_{ij}&=&\frac{a_{ij}+\frac{1}{a_{ji}}}{2}. \end{array} $$

(26)

Proof

(1) When p = 1 and q = 0, letting

$$ \hat{\omega}_{i}=\frac{\omega_{i}}{\sqrt{{\sum}_{j=1}^{n}{\omega_{j}^{2}}}}\geq 0, \ \ i\in I_{n}, $$

and

$$ u_{ij}=\frac{d_{ij}}{\sqrt{{\sum}_{i=1}^{n}d_{ij}^{2}}}>0, \ \ i,j\in I_{n}, $$

we have

$$ \sum\limits_{i=1}^{n}\hat{\omega}_{i}^{2}=1,\quad \sum\limits_{i=1}^{n}u_{ij}^{2}=1. $$

Then the optimization model (22) is simplified as the following form:

$$ \begin{array}{@{}rcl@{}} & & \max\ \ F=\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{n}u_{ij}\hat{\omega}_{i}=\sum\limits_{i=1}^{n}\left( \sum\limits_{j=1}^{n}u_{ij}\right)\hat{\omega}_{i} \\ & &s.t.\ \left\{ \begin{array}{l} {\sum}_{i=1}^{n}\hat{\omega}_{i}^{2}=1, \\ \hat{\omega}_{i}\geq 0,\ i\in I_{n}. \end{array} \right. \end{array} $$

(27)

The model (27) can be solved by introducing the Lagrangian function as follows:

$$ \begin{array}{@{}rcl@{}} L(C,\lambda)&=&C+\lambda\left( \sum\limits_{i=1}^{n}\hat{\omega}_{i}^{2}-1\right)\\ &=&\sum\limits_{i=1}^{n}\left( \sum\limits_{j=1}^{n}u_{ij}\right)\hat{\omega}_{i}+\lambda\left( \sum\limits_{i=1}^{n}\hat{\omega}_{i}^{2}-1\right). \end{array} $$

By assuming

$$ \frac{\partial L(C,\lambda)}{\partial \hat{\omega}_{i}}=\sum\limits_{j=1}^{n}u_{ij}+2\lambda\hat{\omega}_{i}=0, \ \ i\in I_{n}, $$

it gives

$$ \hat{\omega}_{i}=-\frac{{\sum}_{j=1}^{n}u_{ij}}{2\lambda}. $$

According to ${\sum }_{i=1}^{n}\hat {\omega }_{i}^{2}=1,$ $\hat {\omega }_{i}\geq 0$ and u_ij > 0, one has λ < 0 and

$$ \sum\limits_{i=1}^{n}\left( \sum\limits_{j=1}^{n}u_{ij}/2\lambda\right)^{2}=\sum\limits_{i=1}^{n}\hat{\omega}_{i}^{2}=1. $$

Then it follows

$$ \lambda=-\sqrt{\sum\limits_{i=1}^{n}\left( \sum\limits_{j=1}^{n}u_{ij}\right)^{2}}/2, $$

and

$$ \begin{array}{@{}rcl@{}} \hat{\omega}_{i}^{\ast}&=-\frac{{\sum}_{j=1}^{n}u_{ij}}{2\lambda}=\frac{{\sum}_{j=1}^{n}u_{ij}}{\sqrt{{\sum}_{i=1}^{n}({\sum}_{j=1}^{n}u_{ij})^{2}}}, \ \ i\in I_{n},\\ F^{\ast}&=\sum\limits_{i=1}^{n}\left( \sum\limits_{j=1}^{n}u_{ij}\right)\hat{\omega}_{i}^{\ast} =\sqrt{\sum\limits_{i=1}^{n}\left( \sum\limits_{j=1}^{n}u_{ij}\right)^{2}}. \end{array} $$

We further normalize the vector $\hat {\omega }_{i}^{\ast }$ to give

$$ \omega_{i}^{\ast}=\frac{\hat{\omega}_{i}^{\ast}}{{\sum}_{j=1}^{n}\hat{\omega}_{j}^{\ast}}, \ \ i\in I_{n}. $$

(2) When p = 0 and q = 1, the proof is similar to the case (1) and the detailed procedure has been omitted for saving space. □

In general, when p≠ 0 and q≠ 0, the optimization model (22) should be solved using a resolution algorithm. For example, let us assume p + q = 1 and derive the priority vector from the following NrPCM:

$$ A_{2}= \left( \begin{array}{cccccc} 1 & 3 & 3 & 1 & 3 & 4 \\ 1/4 & 1 & 7 & 3 & 1/6 & 1 \\ 1/3 & 1/6 & 1 & 1/5 & 1/5 & 1/6 \\ 1 & 1/3 & 4 & 1 & 1 & 1/3 \\ 1/3 & 5 & 3 & 1 & 1 & 3 \\ 1/4 & 1 & 6 & 3 & 1/2 & 1 \end{array}\right). $$

The obtained results are shown in Table 2 according to the proposed method. In addition, it is seen that there are many methods to derive the priority vector from PCMs [33]. For the sake of simplicity, here we extend serval representative methods to A₂, such as the eigenvector method (EM) [35], the additive normalization method (AN) [1], the weighted least-squares method (WLS) [57] and the logarithmic least squares (LLS) method [36]. As shown in Table 2, the ranking of alternatives is dependent on the values of p or q. When p = 0, p = 0.25 and p = 0.5, the CSM-based ranking is in accordance with that using WLS. When p = 0.75, the ranking using CSM is in agreement with those using EV, AN and LLS. Furthermore, in order to assess the performance of various prioritization methods, we also use the following two error criteria [58]:

$$ ED(\vec{w})=\left[\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\left( a_{ij}-\frac{\omega_{i}}{\omega_{j}}\right)^{2}\right]^{1/2}, $$

and

$$ MV(\vec{\omega})=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}l_{ij}, $$

with

$$ l_{ij}=\left\{\begin{array}{cc} 1,& \omega_{i}>\omega_{j}, a_{ji}>1\ \text{or}\ a_{ij}<1,\\ 0.5,&\omega_{i}=\omega_{j}, a_{ji}\neq1\ \text{or}\ a_{ij}\neq1,\\ 0.5,&\omega_{i}\neq \omega_{j}, a_{ji}=1\ \text{or}\ a_{ij}=1,\\ 0, & otherwise. \end{array} \right. $$

The less the values of ED or MV, the better the performance of the prioritization method is. The obtained results are given in Table 3. It is seen that the proposed method is effective and better than the others according to the criterion ED.

Table 2 Priority vectors and rankings for A₂ under various prioritization methods

Table 3 Error measure values of prioritization methods for A₂

5 Reaching consensus in GDM with NrPCMs

One can see that the GDM models with PCMs and PSO have been widely studied [10, 46]. Here it is of much interest to apply the proposed consistency index and prioritization method to GDM with NrPCMs. A consensus reaching process is built, where an optimization model is constructed and solved using PSO [59, 60].

5.1 Consensus reaching model

Assume that a group of experts E = {e₁,e₂,…,e_m} (m ≥ 2) are invited to express their opinions on X = {x₁,x₂,…,x_n} (n ≥ 2). A set of NrPCMs $A^{(k)}=(a_{ij}^{(k)})_{n\times n}$ for k ∈ I_m = {1,2,⋯ ,m} are provided. In GDM, a consensus building process is necessary to improve the level of consensus within the group. To assess the level of consensus among DMs, we can examine the distance between individual and collective opinions. For obtaining the collective matrix, the weighted geometric mean method is applied to $A^{(k)}=(a_{ij}^{(k)})_{n\times n}$ (k ∈ I_m) [61, 62]. That is, we obtain $A^{c}=(a_{ij}^{c})_{n\times n}$ with

$$ a_{ij}^{c}=\prod\limits_{k=1}^{m}\left( a_{ij}^{(k)}\right)^{\lambda_{k}}, $$

(28)

where

$$ \sum\limits_{k=1}^{m}\lambda_{k}=1,\quad \lambda_{k}\geq0,\quad k\in I_{m}. $$

For the two matrices A^(k) and A^c, the similarity matrix can be computed as $SM^{kc}=(sm^{kc}_{ij})_{n\times n},$ where

$$ sm^{kc}_{ij}=(a_{ij}^{(k)}-a_{ij}^{c})^{2}. $$

(29)

Then the similarity degree between A^(k) and A^c is calculated as follows:

$$ cd_{k}=\frac{\sqrt{{\sum}_{i=1}^{n}{\sum}_{j=1}^{n}sm_{ij}^{kc}}}{n(n-1)},\quad k\in I_{m}. $$

(30)

Hence, the consensus degree of DMs is determined as:

$$ cd=\sum\limits_{k=1}^{m}\lambda_{k}\cdot cd_{k}. $$

(31)

Obviously, the smaller the value of cd is, the better the group consensus is.

Moreover, for reaching the optimal solution to a GDM problem accepted by the most experts, a DM could consider the opinions of the others and modify her/his initial judgments by multiple consultations. This means that DMs should have some flexibility to adjust their initial opinions [10, 54]. Following the idea in [46], it is assumed that the flexibility degree α_k is given to the DM e_k with the initial matrix A^(k). Then the entries in A^(k) can be adjusted such that

$$ \begin{array}{@{}rcl@{}} \text{Case I:}~~\tilde{a}_{ij}^{(k)}\in\left[\max\left( \frac{1}{9},a_{ij}^{(k)}-\frac{8\alpha_{k}}{9}\right), \min\left( 1,a_{ij}^{(k)}+\frac{8\alpha_{k}}{9}\right)\right], \end{array} $$

(32)

for $\frac {1}{9}\leq a_{ij}^{(k)}<1,$ and

$$ \begin{array}{@{}rcl@{}} \text{Case II:}~~\tilde{a}_{ij}^{(k)}\in\left[\max\left( 1, a_{ij}^{(k)}-8\alpha_{k}), \min(9, a_{ij}^{(k)}+8\alpha_{k}\!\right)\!\right]\!, \end{array} $$

(33)

for $1\leq a_{ij}^{(k)}\leq 9$ with α_k ∈ [0,1] (k ∈ I_n). It is convenient to express the set of all matrices with the entries satisfying (32) or (33) is expressed as P(A^(k)).

In order to build the consensus model in GDM, two objectives are usually considered: the group consistency level and the consensus degree among DMs [10, 45, 54, 56]. The former is due to the consideration of rationality for the judgements of DMs, and the latter is attributable to the wide acceptability of the final solution. For the former, by using the proposed consistency index of NrPCMs, the objective function is written as:

$$ Q_{1}=\sum\limits_{k=1}^{m}\lambda_{k}\cdot CSCI(A^{(k)}). $$

(34)

For the latter, the application of (31) leads to

$$ Q_{2}=cd. $$

(35)

Hence, we construct an optimization problem as follows:

$$ \min(Q_{1}, Q_{2}). $$

(36)

For the sake of simplicity, the multi-objective problem (36) is written as the linear form [46, 48]:

$$ \underset{A^{(k)}\in P(A^{(k)})}{\min} Q=\mu Q_{1}+\nu Q_{2}, $$

(37)

where μ and ν are non-negative real numbers. Furthermore, in order to reach a group consensus, we equip the constraint condition for the optimization model (37) as follows:

$$ Q_{2}\leq \delta, $$

(38)

where the term δ stands for the predetermined threshold of the consensus level. When solving the optimization model (37) under the condition (38), the consistency levels of individual and collective matrices can be controlled automatically. If one wants to further make A^c be with acceptable consistency, the following constraint condition can be equipped:

$$ CR_{Nr}(A^{c})\leq0.1. $$

(39)

5.2 Optimization of individual NrPCMs

It is noted that the PSO algorithm has been used to solve the nonlinear and complex optimization problems arising in GDM [10, 54, 55]. The PSO algorithm was proposed to simulate the behavior of birds flying for finding the food through swarm cooperation [59]. The PSO algorithm is initialized as a group of random particles, then to find the optimal solution through iterations. In each iteration, the particle updates itself by tracking two “extremum”: the local optimal solution $\vec {z}_{p}$ found by the particle itself and the global optimal solution $\vec {z}_{g}$ found by the population. The position of each particle changes according to the following formula:

$$ \begin{array}{@{}rcl@{}} \vec{v}(t+1)&=&w\cdot\vec{v}(t)+c_{1}\cdot rand()\cdot(\vec{z}_{p}-\vec{z}(t))\\ &&+c_{2}\cdot rand()\cdot(\vec{z}_{g}-\vec{z}(t)), \end{array} $$

(40)

$$ \begin{array}{@{}rcl@{}} \vec{z}(t+1)&=&\vec{z}(t)+\vec{v}(t+1). \end{array} $$

(41)

The terms c₁ and c₂ are positive constants, which are called learning factors, and are usually assigned to 2 [10, 54, 55, 59]. The symbol rand() means to generate the random numbers with uniform distribution in [0,1]. In the searching process, the balance between the local and global searching abilities plays an important role to the success of the algorithm. Properly changing the inertia weight w will have a good effect. When the inertia weight w is large, it is conducive to search the local optimum. When the inertia weight w is small, it is conducive to the convergence of the algorithm. Therefore, a large inertia weight it is generally assumed in the initial stage of optimization, and a small inertia weight is used in the later stage of optimization. For this reason, we adopt the linear change of inertia weight w as follows:

$$ w(t)=(w_{max}-w_{min})\cdot\frac{t_{max}-t}{t_{max}}+w_{min}, $$

(42)

where w_max is the initial factor usually assigned to 0.9; w_min is the factor at the maximum number of iterations usually assigned to 0.4; t_max is the maximum number of iterations, and t is the current number of iterations [10, 54, 55, 59]. The initial position and velocity of a particle are generated randomly, and updated according to (40) and (41), respectively.

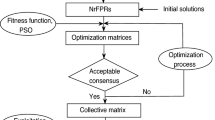
In this study, due to the non-reciprocal property of NrPCMs, the dimension of particles is mn(n − 1) and the searching range is given in (32) and (33), respectively. Based on the proposed consistency index and prioritization method, the new GDM algorithm is elaborated on as follows:

Step 1::

In a GDM problem, a group of experts E = {e₁,e₂,…,e_m} are invited to provide their opinions by pairwisely comparing alternatives in X = {x₁,x₂,…,x_n}.

Step 2::

NrPCM A^(k) is determined to represent the initial position of expert e_k with flexibility degree α_k for k ∈ I_m.

Step 3::

The fitness function Q is constructed and the constraint conditions (32) and (33) are considered.

Step 4::

The PSO algorithm is used to solve the optimization problem (37) with the constraint conditions in (38). The matrices A^(k) (k ∈ I_m) are optimized and written as $\tilde {A}^{(k)}$ (k ∈ I_m).

Step 5::

Using the optimized matrices $\tilde {A}^{(k)} (k\in I_{m})$, the collective one $\tilde {A}^{c}$ is obtained by using (28).

Step 6::

According to $\tilde {A}^{c}=(a_{ij}^{c})_{n\times n}$, the weight of alternatives is derived by using optimization model (22).

It is convenient to provide the algorithm to solve the GDM problem with NrPCMs by controlling the consistency and consensus levels. The resolution process of a GDM with NrPCMs is shown in Fig. 1.

Fig. 1

Resolution process of a GDM with NrPCMs

5.3 Numerical results and discussion

Now we carry out a numerical example to illustrate the above algorithm and investigate the effects of parameters α_k, p and q on the objective functions Q, Q₁ and Q₂, respectively. It is considered that four DMs E = {e₁,e₂,e₃,e₄} are invited to compare and analyze five alternatives in X = {x₁,x₂,x₃,x₄,x₅}. Four NrPCMs {A⁽¹⁾,A⁽²⁾,A⁽³⁾,A⁽⁴⁾} are provided as follows:

$$ \begin{array}{@{}rcl@{}} A^{(1)}=\left( \begin{array}{ccccc} 1 & 1/4 & 1/3 & 1/7 & 1/3 \\ 4 & 1 & 1/6 & 1/5 & 1/6 \\ 4 & 6 & 1 & 1/3 & 1/3 \\ 7 & 4 & 2 & 1 & 1/2 \\ 3 & 6 & 3 & 2 & 1 \end{array} \right), \\ A^{(2)}=\left( \begin{array}{ccccc} 1 & 1/2 & 1/6 & 1/3 & 1/2 \\ 2 & 1 & 1/5 & 1/2 & 4 \\ 4 & 5 & 1 & 1/4 & 1/2 \\ 3 & 2 & 1 & 1 & 3 \\ 2 & 1/2 & 3 & 1/3 & 1 \end{array} \right), \\ A^{(3)}=\left( \begin{array}{ccccc} 1 & 1/2 & 1/2 & 1/8 & 1/8 \\ 2 & 1 & 1/4 & 1/3 & 1/6 \\ 2 & 5 & 1 & 1/5 & 1/5 \\ 8 & 3 & 4 & 1 & 1/4 \\ 8 & 9 & 5 & 4 & 1 \end{array} \right), \\ A^{(4)}=\left( \begin{array}{ccccc} 1 & 1/2 & 1/3 & 1/6 & 1/2 \\ 2 & 1 & 1/5 & 1/2 & 1/3 \\ 3 & 4 & 1 & 1/4 & 1/4 \\ 7 & 2 & 4 & 1 & 1/2 \\ 2 & 3 & 4 & 1 & 1 \end{array} \right). \\ \end{array} $$

It is easy to compute the initial values of consistency index and consensus level as CSCI(A⁽¹⁾) = 0.1280, CSCI(A⁽²⁾) = 0.2324, CSCI(A⁽³⁾) = 0.0906, CSCI(A⁽⁴⁾) = 0.1423 and cd = 0.2740.

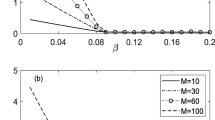
For convenience, it is assumed that each NrPCM is equipped with the same flexibility degree α and λ_k = 1/4 (k = 1,2,3,4). When the PSO algorithm is run, the selected values of some parameters are given in Table 4. Figure 2 is drawn to show the variations of the fitness function Q versus the generation number for (μ,ν) = (0.25,0.75) with α = 0.05,0.1,0.15 respectively. We can observe from Fig. 2 that the values of Q decrease with the increase of generation number. Then a stable value of Q is obtained for a sufficiently large generation number such as 100, meaning that the optimal value of Q is determined. In addition, with the increase of α, the value of Q decreases for a fixed generation number, indicating that the greater the flexibility degree is, the better the value of Q is. The above findings are in agreement with the existing results [10, 46, 47].

Table 4 Selected values of some quantities

Fig. 2

Plots of Q versus the generation number with (μ,ν) = (0.25,0.75) for α = 0.05,0.1,0.15, respectively

Furthermore, we investigate the effects of α on the values of Q, Q₁ and Q₂, respectively. The variations of Q, Q₁ and Q₂, versus α are shown in Fig. 3 by choosing (μ,ν) = (0.25,0.75) and performing 100 iterations. It is found from Fig. 3 that the values of Q, Q₁ and Q₂ generally decrease with the increase of α. Additionally, we analyze the effects of the parameters μ and ν on Q. As shown in Fig. 4, a series of (μ,ν) are selected to compute. It is noted that for a fixed value of μ (or ν), the values of Q decreases with the increase of ν (or μ). The above findings are in accordance with the phenomenon in [48]. This means that the values of μ and ν can be used to adjust the value of Q.

Fig. 3

Plots of the optimal values of Q, Q₁ and Q₂ versus α for the selected values of (μ,ν) = (0.25,0.75)

Fig. 4

Plots of the optimal values of Q versus α under the conditions of (a): μ = 0.25 together with the selected values of ν, and (b): ν = 0.75 together with the selected values of μ

At the end, the optimized individual matrices and the final collective ones can be determined. For example, by selecting (μ,ν) = (0.25,0.75), when α = 0.05, we have

$$ \begin{array}{@{}rcl@{}} \tilde{A}^{(1)}_{0.05}=\left( \begin{array}{ccccc} 1.0000 & 0.2944 & 0.2889 & 0.1873 & 0.2889 \\ 3.6000 & 1.0000 & 0.2111 & 0.2444 & 0.2111 \\ 3.6000 & 5.6000 & 1.0000 & 0.3778 & 0.3778 \\ 6.6000 & 4.4000 & 2.4000 & 1.0000 & 0.5444 \\ 3.4000 & 6.4000 & 3.4000 & 1.6000 & 1.0000 \end{array} \right), \\ \tilde{A}^{(2)}_{0.05}=\left( \begin{array}{ccccc} 1.0000 & 0.4556 & 0.2111 & 0.2889 & 0.4556 \\ 2.4000 & 1.0000 & 0.2444 & 0.4556 & 3.6000 \\ 3.6000 & 4.6000 & 1.0000 & 0.2056 & 0.5444 \\ 3.4000 & 2.4000 & 1.0000 & 1.0000 & 2.6000 \\ 2.4000 & 0.5444 & 2.6000 & 0.3778 & 1.0000 \end{array} \right), \\ \tilde{A}^{(3)}_{0.05}=\left( \begin{array}{ccccc} 1.0000 & 0.5444 & 0.5444 & 0.1111 & 0.1111 \\ 2.4000 & 1.0000 & 0.2944 & 0.2889 & 0.2111 \\ 2.4000 & 4.6000 & 1.0000 & 0.1556 & 0.1556 \\ 7.6000 & 3.2476 & 3.6000 & 1.0000 & 0.2944 \\ 7.6000 & 8.6000 & 4.6000 & 3.6000 & 1.0000 \end{array} \right), \\ \tilde{A}^{(4)}_{0.05}=\left( \begin{array}{ccccc} 1.0000 & 0.5444 & 0.3359 & 0.2111 & 0.4556 \\ 2.4000 & 1.0000 & 0.2444 & 0.4556 & 0.3778 \\ 3.4000 & 4.4000 & 1.0000 & 0.2944 & 0.2944 \\ 6.6000 & 2.4000 & 3.6000 & 1.0000 & 0.5444 \\ 2.4000 & 3.4000 & 3.6000 & 0.9556 & 1.0000 \end{array} \right), \\ \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \tilde{A}^{(c)}_{0.05}=\left( \begin{array}{ccccc} 1.0000 & 0.4465 & 0.3250 & 0.1887 & 0.2857 \\ 2.6560 & 1.0000 & 0.2469 & 0.3479 & 0.4962 \\ 3.2068 & 4.7785 & 1.0000 & 0.2442 & 0.3115 \\ 5.7922 & 3.0120 & 2.3616 & 1.0000 & 0.6902 \\ 3.4928 & 3.1771 & 3.4784 & 1.2008 & 1.0000 \end{array} \right). \end{array} $$

When α = 0.1, it gives the following results:

$$ \begin{array}{@{}rcl@{}} \tilde{A}^{(1)}_{0.1}=\left( \begin{array}{ccccc} 1.0000 & 0.3389 & 0.2444 & 0.1111 & 0.2444 \\ 3.2000 & 1.0000 & 0.2556 & 0.2475 & 0.2556 \\ 3.2000 & 5.2000 & 1.0000 & 0.4222 & 0.4222 \\ 6.2000 & 3.2000 & 2.4904 & 1.0000 & 0.5889 \\ 3.8000 & 5.2000 & 3.0083 & 1.2000 & 1.0000 \end{array} \right), \\ \tilde{A}^{(2)}_{0.1}=\left( \begin{array}{ccccc} 1.0000 & 0.4111 & 0.2556 & 0.2444 & 0.5889 \\ 2.8000 & 1.0000 & 0.2889 & 0.5889 & 3.2000 \\ 3.2000 & 4.2000 & 1.0000 & 0.3389 & 0.5889 \\ 3.8000 & 2.8000 & 1.0000 & 1.0000 & 2.2000 \\ 2.8000 & 0.5889 & 2.2000 & 0.4222 & 1.0000 \end{array} \right), \\ \tilde{A}^{(3)}_{0.1}=\left( \begin{array}{ccccc} 1.0000 & 0.5889 & 0.5889 & 0.2139 & 0.2139 \\ 2.6058 & 1.0000 & 0.3389 & 0.3418 & 0.2556 \\ 2.8000 & 4.3881 & 1.0000 & 0.2889 & 0.2889 \\ 7.2000 & 3.1868 & 3.2000 & 1.0000 & 0.3389 \\ 7.2000 & 8.2000 & 4.2000 & 3.2000 & 1.0000 \end{array} \right), \\ \tilde{A}^{(4)}_{0.1}=\left( \begin{array}{ccccc} 1.0000 & 0.5889 & 0.3767 & 0.2556 & 0.4111 \\ 2.8000 & 1.0000 & 0.2889 & 0.4111 & 0.2444 \\ 2.2000 & 4.4572 & 1.0000 & 0.3389 & 0.3389 \\ 6.2000 & 2.8000 & 3.2000 & 1.0000 & 0.5889 \\ 2.8000 & 3.6527 & 3.2000 & 0.9111 & 1.0000 \end{array} \right), \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \tilde{A}^{(c)}_{0.1}=\left( \begin{array}{ccccc} 1.0000 & 0.4688 & 0.3431 & 0.1963 & 0.3354 \\ 2.8435 & 1.0000 & 0.2916 & 0.3783 & 0.4754 \\ 2.8182 & 4.5462 & 1.0000 & 0.3440 & 0.3950 \\ 5.6948 & 2.9902 & 2.2472 & 1.0000 & 0.7131 \\ 3.8270 & 3.0947 & 3.0710 & 1.1025 & 1.0000 \end{array} \right). \end{array} $$

When α = 0.15, one arrives at the following matrices:

$$ \begin{array}{@{}rcl@{}} \tilde{A}^{(1)}_{0.15}=\left( \begin{array}{ccccc} 1.0000 & 0.3833 & 0.2000 & 0.2762 & 0.2000 \\ 2.8000 & 1.0000 & 0.3000 & 0.3333 & 0.3000 \\ 4.1044 & 4.8000 & 1.0000 & 0.4667 & 0.4667 \\ 5.8000 & 3.2815 & 2.3207 & 1.0000 & 0.6333 \\ 4.2000 & 4.8000 & 4.2000 & 3.2000 & 1.0000 \end{array} \right), \\ \tilde{A}^{2}_{0.15}=\left( \begin{array}{ccccc} 1.0000 & 0.4710 & 0.3000 & 0.2000 & 0.3667 \\ 2.7413 & 1.0000 & 0.3333 & 0.3841 & 2.8000 \\ 4.1525 & 4.0438 & 1.0000 & 0.3833 & 0.3667 \\ 4.2000 & 3.2000 & 1.0000 & 1.0000 & 1.8000 \\ 3.2000 & 0.6333 & 3.2158 & 0.4667 & 1.0000 \end{array} \right), \\ \tilde{A}^{3}_{0.15}=\left( \begin{array}{ccccc} 1.0000 & 0.6333 & 0.3667 & 0.2583 & 0.1111 \\ 2.2827 & 1.0000 & 0.3833 & 0.2000 & 0.3000 \\ 3.2000 & 4.0714 & 1.0000 & 0.3333 & 0.3333 \\ 6.8000 & 3.3939 & 2.8000 & 1.0000 & 0.3833 \\ 6.8000 & 7.8000 & 3.8000 & 2.8000 & 1.0000 \end{array} \right), \\ \tilde{A}^{4}_{0.15}=\left( \begin{array}{ccccc} 1.0000 & 0.6333 & 0.4667 & 0.3000 & 0.6333 \\ 2.4946 & 1.0000 & 0.3333 & 0.3667 & 0.4667 \\ 4.2000 & 4.2077 & 1.0000 & 0.3833 & 0.3833 \\ 5.8000 & 3.2000 & 2.8000 & 1.0000 & 0.6333 \\ 3.2000 & 3.4028 & 3.6150 & 1.0000 & 1.0000 \end{array} \right), \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \tilde{A}^{c}_{0.15}=\left( \begin{array}{ccccc} 1.0000 & 0.5187 & 0.3183 & 0.2558 & 0.2680 \\ 2.5713 & 1.0000 & 0.3362 & 0.3113 & 0.5856 \\ 3.8904 & 4.2703 & 1.0000 & 0.3888 & 0.3845 \\ 5.5674 & 3.2679 & 2.0653 & 1.0000 & 0.7253 \\ 4.1354 & 2.9971 & 3.6907 & 1.4300 & 1.0000 \end{array} \right). \end{array} $$

The values of consistency index and consensus level are given in Tables 5 and 6 under the selected flexibility degrees. The values of CSCI_c, Q₁, Q₂ and Q decrease with the increasing values of α. The phenomenon is in agreement with the observation in [47]. Moreover, for the optimized individual matrices, there are some different situations in the values of consistency indexes and consensus levels. For example, when α = 0.15, the values of CSCI₂ and cl₁ increase with the increasing values of α. The observation shows that although the individual levels of consistency and consensus may be worse, the global levels of consistency and consensus could be better. When the threshold of consensus level δ = 0.2 is selected, the group consensus is reached for α > 0.10 according to Table 6. However, we consider the threshold of CSCI for acceptable consistency in Table 1, the consistency degree of CSCI_c is not acceptable. In order to achieve the condition (39), we only need to increase the value of flexibility degree to α = 0.2. The detailed procedure is only based on the straightforward computation and it has been omitted.

Table 5 Values of consistency index for $\tilde {A}^{(1)}-\tilde {A}^{(4)}$ and Q₁ under (μ,ν) = (0.25,0.75) and various flexibility degrees

Table 6 Values of consensus level for $\tilde {A}^{(1)}-\tilde {A}^{(4)},$ Q₂ and Q under (μ,ν) = (0.25,0.75) and various flexibility degrees

The final issue of concern is the priorities and ranking of alternatives. For comparisons, the priorities and rankings of alternatives are given in Tables 7 and 8 by using the proposed method and the eigenvector method [1], where the collective matrices under α = 0.00,0.05,0.10 and α = 0.15 are considered. Here it should be pointed out that although the considered matrices could be with non-reciprocal property, the eigenvector method may still be suitable to derive the priorities of alternatives [6]. It is found from Tables 7 and 8 that for different values of α, the ranking of alternatives obtained by the two methods are the same.

Table 7 Priorities and rankings of alternatives for (μ,ν) = (0.25,0.75) and α = 0.00,0.05,0.10,0.15, respectively

Table 8 Priorities and rankings of alternatives with (μ,ν) = (0.25,0.75) and α = 0.00,0.05,0.10,0.15 using the eigenvector method (EM) [1]

5.4 Comparative analysis

In this paper, we constructed a consensus reaching model in GDM based on NrPCMs, where the consistency index, the prioritization method and the consensus level have been proposed. An optimization model has been constructed by controlling the consistency degrees of individual and collective matrices under the given consensus level of group. A thorough comparative analysis with the existing consensus models in GDM is worth making to show the advantages and disadvantages of the proposed one.

First, the uncertainty experienced by DMs is characterized using the non-reciprocal property of NrPCMs. Moreover, IMRMs [7] and intuitionistic multiplicative preference relations (IMPRs) [63] have the same capability as NrPCMs to describe the uncertainty. But the expression of NrPCMs is simpler than those of IMRMs and IMPRs, which is one of the advantages of NrPCMs. In addition, the workload of providing a NrPCM is less than giving an IMRM or an IMPR. From the mechanism of causing uncertainty, NrPCMs clearly show that the uncertainty is caused by the inherent indeterminacy of human-originated information when exchanging the order to paired alternatives.

Second, the consistency index is constructed by considering the cosine similarity degree between two row/column vectors in a NrPCM. Although this idea comes from the existing works [21, 22], the procedure of forming the consistency index is an extension of that in [22] by considering the non-reciprocal property of NrPCMs. When comparing with multiplicative reciprocal PCMs, the expression of NrPCMs and the method of computing the consistency index are more complex. Moreover, the prioritization method of NrPCMs is also an extension of the finding in [22]. The comparative analysis with EV, WLS, AN and LLS shows the advantage and disadvantage of the proposed method.

Third, the consensus reaching process is based on the optimization model by controlling the consistency degree of matrices and consensus level of group. The PSO algorithm is used to simulate the dynamic process of adjusting experts’ judgements. The developed consensus model follows the initial work of Pedrycz and Song [10]. In addition, here the collective matrix is obtained using an aggregation operator, which is different with that in [10], where the collective priority vector was used.

6 Conclusions

It is common to experience some uncertainty when comparing alternatives for decision makers (DMs). Interval multiplicative reciprocal matrices (IMRMs) have been used to characterize the experienced uncertainty. In this paper, the concept of non-reciprocal pairwise comparison matrices (NrPCMs) has been proposed to generally consider the case with the reciprocal symmetry breaking. Then the consistency index and prioritization method of NrPCMs have been established. A consensus model in group decision making (GDM) has been proposed where the opinions of DMs are expressed as NrPCMs. The main findings are covered as follows:

• The transformation relation between IMRMs and NrPCMs has been constructed due to the similar ability to capture the uncertainty experienced by DMs.

• It is concluded that NrPCMs and IMRMs are inconsistent in nature. The cosine similarity degree-based consistency index has been given to quantify the inconsistency degree of NrPCMs and IMRMs.

• The prioritization method has been constructed to elicit the priority vector from NrPCMs and it is effective as compared to some extended methods.

• The consensus model in GDM with NrPCMs has been reported by constructing an optimization problem, which is solved by the particle swarm optimization (PSO) algorithm.

We should point out that except for the transformation between IMRMs and NrPCMs, NrPCMs are related to intuitionistic multiplicative preference relations (IMPRs) [63], which could be investigated in the future. In addition, this paper only focuses on the typical consensus reaching model with NrPCMs, and some further studies could be made. For example, some GDM algorithms could be developed under uncertainty and incomplete decision information by following the idea shown in NrPCMs. Multiple-objective optimization models could be constructed and solved such that the Pareto solutions can be found. The effectiveness and performance of decision-making models could be evaluated by considering the differences of decision information. By considering the large-scale and cooperative/non-cooperative relationship of DMs [45, 50, 52], some GDM models could be proposed.