1 Introduction

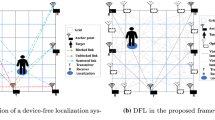
Target location is one of the most fundamental pieces of information in the Internet of Things (IoT). Traditional positioning technologies include the global positioning system (GPS), Bluetooth, ultrasonic, and radio frequency identification (RFID) [1], which often require electronic equipment installed on the targets, such as electronic identification tags and wireless sensor nodes. Hence the name device-based localization (DBL). However, DBL cannot be applied to targets unwilling or unable to carry those devices, e.g., the elderly or invaders. Device-free localization (DFL) emerges as promising technology since it does not require any device and can be widely adopted in many special applications with space constraints, such as elderly behavior recognition in smart homes, target detection in disaster rescue, and indoor invader surveillance in security defends, as shown in Fig. 1.

Fig. 1
figure 1

Illustration of a DFL system applied to security monitoring in a smart home with IoT

Full size image

To achieve DFL, multiple radio frequency (RF) sensors have been installed in advance to detect, locate and track targets in the area of interest. A typical DFL system consists of numerous pre-installed wireless sensor nodes, i.e., access points (APs), which act as transceivers to transmit and receive radio signals. When the target equivalent to an obstacle is at a different position in the area, the radio signal links passing through it are attenuated. Thus, the target location can be determined by detecting and estimating the weak signal changes.

Youssef et al. [2] first conceptualized device-free passive localization and formulated DFL as a fingerprint matching problem. Zhang et al. [3] proposed three geometric tracking approaches for eliminating noise and improving the tracking accuracy of DFL systems, i.e., midpoint, intersection, and best-cover algorithms. To solve the ill-posed inverse problem, Wilson and Patwari [4] regarded DFL as an inverse problem, for which they presented a linear model and utilized Tikhonov regularization to obtain resultant images for DFL by radio tomographic imaging (RTI). The above studies provided an early foundation for DFL research.

Related works inspired by image processing methods in computer vision and pattern recognition imply the feasibility of classification methods in solving localization problems, e.g., deep neural networks with autoencoders [5, 6]. Among the different classification methods, sparse coding has attracted the attention of many researchers due to its simple decision rules, high accuracy and high efficiency [7]. Localization can be transformed into sparse representation classification (SRC) problems for DFL systems [8]. In other words, sparse solutions of underdetermined systems can be reached by sparse coding algorithms with sparsity constraints, and the target location can be recovered by seeking the relationship between the solution and the index of the preset monitoring area grids occupied by the target [9,10,11,12].

Solving the DFL problem via sparse coding is a process of inferring the target location from the sparse coefficient solutions obtained from underdetermined systems with observed signals and base dictionaries. Recently explored approaches to DFL via sparse coding included orthogonal matching pursuit (OMP) [10, 13, 14], basis pursuit linear programming (BP-LP) [8, 14], and iterative shrinkage-thresholding algorithm (ISTA) [11, 15,16,17]. However, BP-LP [8] lacks efficiency of computations, and the OMP algorithm in [10] cannot provide sufficient DFL accuracy. Li et al. [9] considered a dictionary learning approach based on the difference in convex programming and further improved the DFL accuracy with a tracking neighborhood rule. Recently, Huang et al. [18] and Han et al. [19] proposed improved sparse coding algorithms (ISCAs) with log-regularizers, which positioned targets in more complex environments robustly. To overcome the low accuracy and insufficient robustness of DFL, Zhao et al. [20] considered a block sparse scheme, that achieved robust performance under severely noisy conditions. However, most of the above algorithms failed to consider the effect of high-dimensional data on computing efficiency. Recent work showed that sparse coding via the iterative shrinkage thresholding algorithm (SC-ISTA) [11] with the L1 Norm as penalty function has good localization accuracy and robustness. However, the L1 Norm applied in the above algorithm still has room for improvement in seeking a sparse solution to the L0 Norm.

Related research [19, 21,22,23,24,25] showed that using generalized penalty functions other than the L1 Norm to approximate the sparse solutions of the L0 Norm can achieve good performance with nonconvex minimization optimization. In a previous study [26], we proposed a sparse coding-iterative p-thresholding algorithm (SC-IpTA) and considered a thresholding function with parameter p as the penalty function to derive sparse solutions and achieve better DFL performance, where the accuracy and robustness of the proposed method were verified with localization results.

To some extent, the accuracy is restricted by the number of sensor nodes. To achieve improved accuracy and enlarged areas of interest, most methods resort to more sensor nodes, leading to greater measurement data volume. With the RF model [27], the total number of wireless links between sensor node pairs increases dramatically with the number of sensor nodes, which places a greater burden on computing and data storage. In order to cater to the real-time requirements of IoT, the time cost of DFL systems needs to be reduced.

With high dimensionality, data mining is susceptible to the curse of dimensionality, a natural countermeasure of which is dimension reduction, where the high-dimensional feature space is projected onto a low-dimensional subspace. The most common dimension reduction method is principal component analysis (PCA) [28], which seeks a small number of orthogonal basis vectors to represent the maximum variance of the variables in the dataset.

The dimensionality of dictionaries can be reduced through the orthogonal transformation with PCA, which converts a series of possibly correlated vectors to linearly unrelated vectors, termed principal components. In order to reduce dimensionality, new features should be identified to reveal the main characteristics of the original data, each of which is a linear combination of orthogonal features. Eigenvalue decomposition (EVD), commonly utilized for signal features extraction and data representation, has wide applications such as image compression.

Recently, the research on DFL has shifted its focus to efficient computation after dimension reduction. To reduce the amount of localization data and the storage costs of DFL systems, Liu et al. [29] proposed a two-level controlling redundancy reduction approach for indoor DFL based on PCA node reduction. On the basis of [9], Li et al. [30] further proposed an outlier suppression approach via non-convex robust PCA for safe localization with dimension reduction. Wang et al. [31] achieved device-free simultaneous wireless localization and activity recognition (DFLAR) with a wavelet feature using RSS signal features extracted by PCA. Shi et al. [32] presented a computationally efficient approach for device-free indoor location tracking systems based on channel state information (CSI) metrics, which proved efficient and robust for high-dimensional CSI vectors due to the PCA-based dimension reduction. However, those methods mentioned above only considered one single target. Huang et al. [11] performed sparse coding with subspace techniques in low-dimensional signal subspace, achieving high localization accuracy and robustness while reducing time cost.

In this paper, SC-IpTA based on generalized thresholding is first introduced, which achieves good accuracy with high robustness. Then, an enhanced generalized thresholding scheme based on dimension reduction is derived to improve the computational and storage efficiencies of DFL systems, which overcomes the increased computation complexity induced by the high-dimensional RSS sampling data. In the meantime, the multi-target performance of the proposed method is also analyzed.

Firstly, the original RSS data for a single target and multiple targets were collected from the Sensing and Processing Across Networks (SPAN) Lab at the University of Utah [27]. Then, the overcomplete dictionary D was constructed with RSS data via matrix transformation. After that, dimension reduction was performed for each row and column of matrix D with PCA to yield the subspace dictionary matrix D∗. In addition, the same operation is performed for the transformation from the observation vector b to b∗, as depicted in Fig. 2. Next, the objective function constructed by the regularized constraint term with a p generalized thresholding was formulated as a non-convex optimization problem. Finally, the sparsest solution of the underdetermined equation was obtained using SC-IpTA, and the target location was estimated.

Fig. 2
figure 2

The SRC model based on PCA

Full size image

Contributions of the paper are summarized in the following three aspects. 1) A subspace sparse coding iterative p-thresholding algorithm(SSC-IpTA) is proposed by reducing the dimension of learning dictionaries and retaining the trunk of the most important information to provide a higher computing efficiency and save data storage space. 2) The robustness of the algorithm is evaluated numerically under different ambient noise levels. 3) The multi-target accuracy of the proposed algorithm is verified.

The structure of the paper is as follows. In Section 2, DFL systems and SRC models are introduced. Section 3 elaborates on the improved SSC-IpTA. In Section 4, the performance of the proposed algorithm is evaluated. In Section 5, conclusions are drawn.

2 DFL systems and the SRC model

2.1 DFL systems

In DFL systems, multiple sensor nodes are installed opposite each other on the edge of the areas of interest, as shown in Fig. 3. In order to facilitate the inference of the target location, the area is divided into grids, namely reference points (RPs), and the target is assumed to be in one of the RPs. Each sensor sends radio while the rest receive RSS signals simultaneously, forming sensor pairs.As the target moves into a different RP, the wireless links passing through it are blocked, and the received RSS measurement configurations differ, showing the specific characteristics of the target location. Thus the target location can be inferred by detecting the changes in RSS signals.

Fig. 3
figure 3

A typical DFL system

Full size image

Since the above RSS measurement configurations represent different classes, they can be considered an image classification problem. In addition, the targets are far fewer than RPs in a typical DFL system.Hence the characteristics of sparsity. Therefore, the problem can be dealt with under SRC.

2.2 SRC model and sparse coding

SRC [33] is adopted to recover the observation signal from the underdetermined equation with overcomplete dictionaries with the constraints of the minimum reconstruction error. In addition, the observed vector b can be expressed as a linear combination of dictionary matrix D and sparse coefficient vector x, as shown in Fig. 2. The solutions of coefficient vector via sparse coding are featured with sparsity, i.e., most elements are zero. The DFL problem can be solved by mapping the index of the sparse coefficient vector with the target location.

Sparse coding is the process of computing coefficient vectors based on a set of observed signals and known dictionaries, i.e., solving inverse problems.

The linear equation for Fig. 3 can be represented as:

$$ \mathbf{b}^{m\times 1}={\mathbf{D}^{m \times N}\mathbf{x}^{N\times 1}} $$
(1)

DFL systems require more RP measurement repetitions to construct the dictionary for better accuracy of the target localization in the offline stage, which causes N to become larger than m. When N > m, the equation becomes an underdetermined system with none-unique solutions, making it an ill-posed problem. With proper sparse constraints, the sparsest solution can be obtained, and the problem becomes well-posed.

Since the sparsest solution based on the L0 Norm is an NP-hard problem [34], suboptimal solutions are solved by orthogonal matched pursuit (OMP) algorithms, which do not apply to the DFL problem with high-dimensional data due to inefficiency. According to [13] and [14], the sparsest solution can be obtained by relaxing the L0 Norm to an L1 Norm optimization problem. The regularization method is used to solve combinatorial optimization problems consisting of an error term and an L1 penalty function term, i.e.:

$$ \mathbf{x}^{*}={arg \min_{\substack{\mathbf{x}}}}\frac{1}{2}{\Vert\mathbf{b}-\mathbf{D}\mathbf{x}\Vert}^{2}_{2}+\tau{\Vert\mathbf{x}\Vert}_{1} $$
(2)

where τ is the regularization parameter.

Assuming that there are K APs, and 𝜃i,j represent the RSS measurements received by the i-th AP from the j-th AP, vector 𝜃i can be expressed as:

$$ \boldsymbol{\theta}_{i}=[\theta_{i,1},\theta_{i,2},\cdots,\theta_{i,\mit K}]^{H} $$
(3)

where 𝜃i,i is equivalent to the signal value transmitted by the i-th AP and H is the conjugate transpose operator. All 𝜃i representing RSS values of the links compose matrix Θ as follows.

$$ \mathbf{\Theta}= [\boldsymbol{\theta_{1}}, \boldsymbol{\theta_{2}}, \cdots, \boldsymbol{\theta_{K}}]^{H}\\ $$
(4)

The operation of the DFL system consists of two stages: offline training and online testing.

  1. 1)

    At the offline training stage, the area of interest of the DFL system is discretized into G RPs, each labeled with an RP index. Suppose the target is in the g-th RP and Z RSS matrices can be produced as follows:

    $$ \lbrace \mathbf{\Theta}_{g,1},\mathbf{\Theta}_{g,2},\cdots,\mathbf{\Theta}_{g,t},\cdots,\mathbf{\Theta}_{g,Z} \rbrace $$
    (5)

    where Θg,t is the t-th measurement RSS matrix of the g-th RP, and Z is the repeated number of sampling at each RP.

The RSS matrix can be transformed into a column vector dg,t. Thus, the following matrix Dg can be constructed with the Z sample vector of the g-th AP as the column.

Repeating the experiment Z trials produces G sample matrices, and N = G × Z sample vectors are combined to construct a matrix D.

  1. 2)

    At the online testing stage, the observed signal with the target in the area of interest is the vectorization of RSS matrix Θ.

The target assumed to be in the g-th RP, belongs to the g-th class. If sufficient sampling is taken in the g-th RP to ensure N > m, the observed signal vector b can be approximated using sampling matrix Dg.

$$ \mathbf{b}=\mathbf{D}_{g}\mathbf{x}_{g}={\sum}_{t=1}^{Z}\mathbf{d}_{g,t}x_{g,t} \quad (0\le g \le G) $$
(6)

In (6), xg = [xg,1,xg,2,⋯ ,xg,t,⋯ ,xg,Z] ∈RZ is the sparse coefficient vector, and xg,t ∈R is the coefficient of the element.

According to [11] and [26], the linear representation of the observation vector can be sparsely represented with N sample vectors of the dictionary.

$$ \mathbf{b}=\mathbf{D}_{g}\mathbf{x}_{g}=\mathbf{D}\mathbf{x} $$
(7)

where

$$ \begin{array}{llll} \mathbf x &=[0,\cdots,\mathbf x_{g},\cdots,0]^{H} \\ &=[0,\cdots,\underbrace{x_{g,1},x_{g,2},\cdots,x_{g,t},\cdots,x_{g,Z}}_{\mathbf{x}_{g}},\cdots,0]^{H} \end{array} $$
(8)

Equation (7) is a sparse representation problem that can be solved by SRC, which reconstructs the input observed signal with a few atoms selected from the overcomplete dictionary and achieves the minimum reconstruction error.

2.3 Sparse Coding-Iterative p-Thresholding Algorithm

To solve the L1 minimization problem in (2), Huang et al. [11] presented the SC-ISTA using the soft thresholding operator.

$$ (\mathbf{S}_{\tau}(\mathbf{x}))_{k}=\text{sgn} (\mathbf{x_{k}}) \max\{0,\mid \mathbf{x_{k}}\mid-\tau\} $$
(9)

To solve the optimization problem, we introduced a generalized thresholding operator in [26], as can be defined as follows:

$$ \mathbf{S}_{\tau}^{p}(\mathbf{x}_{i})=\text{sgn}(\mathbf{x}_{i}) \max\{0,\mid\mathbf{x}_{i}\mid-\tau \mid\mathbf{x}_{i}\mid^{p-1}\} $$
(10)

The algorithm can be developed using the thresholding function as:

$$ \mathbf{x}_{i+1} \gets \mathbf{S}_{\tau}^{p} (\mathbf{x}_{i}+\mathbf{D}^{T}\mathbf{b}-\mathbf{D}^{T}\mathbf{D}\mathbf{x}_{i}) $$
(11)

By solving (10) and (11), the sparse solution of (2) can be obtained.

$$ \mathbf{x}^{*}=\{\mathbf x_{1},\cdots,\mathbf x_{N}\}=\{\mathbf x_{1,1},\cdots,\mathbf x_{g,t},\cdots,\mathbf x_{G,Z}\} $$
(12)

where t = {1,⋯ ,Z}. With \(\mathbf x^{*}_{g}={\sum }_{t=1}^{Z}x^{*}_{g,t}\), (12) can be transformed as follows:

$$ \mathbf{x}^{*}=\{\mathbf x^{*}_{1},\cdots,\mathbf x^{*}_{g},\cdots,\mathbf x^{*}_{G}\} $$
(13)

where \(\mathbf {x}^{*}_{i}=\{ x^{*}_{i,1},\cdots , x^{*}_{i,Z}\}\).

The location of single target is estimated to be within the Φ-th RP, where Φ is the index of the maximal nonzero element determined as follows:

$$ {\Phi}=arg \max_{g}\{\mathbf x^{*}_{1},\cdots,\mathbf x^{*}_{g},\cdots,\mathbf x^{*}_{G}\} $$
(14)

For multiple targets, we can estimate T targets at the Φ1-th RP,..., ΦT-th RP, where Φ1,⋯ ,ΦT are the elements with decreasing order in x∗, given by:

$$ \{{\Phi}_{1},\cdots,{\Phi}_{T}\}=arg \max_{1,\cdots,T}\{\mathbf x^{*}_{1},\cdots,\mathbf x^{*}_{T},\cdots,\mathbf x^{*}_{G}\} $$
(15)

Indices {Φ1,⋯ ,ΦT} of the maximum nonzero elements of x∗ can be considered the target locations.

3 Proposed algorithm

Previous research has shown that existing OMP, BP, and ISTA take more time as the data grow, which affects their application in IoT scenarios with high real-time requirements. To address the issue, a subspace SC-IpTA (SSC-IpTA) is presented. Firstly, the columns and rows of the dictionary matrix constructed by the RSS measurements were reduced. Next, a new dictionary was built in the principal component subspace, the dimension number of which was determined by the cumulative energy ratio (CER). Then, the coefficient vector was obtained via the sparse coding algorithm. Lastly, the experimental evaluation was conducted to verify the algorithm’s performance.

The flowchart of the proposed SSC-IpTA is summarized in Fig. 4.

Fig. 4
figure 4

Flowchart of the DFL system based on SSC-IpTA

Full size image

The dictionary should be constructed and normalized after the original RSS data are ready in the offline training stage.

3.1 Column dimension Reduction for dictionary D

Dictionary D consisting of the original RSS data can be expressed as:

$$ \mathbf D=[\mathbf D_{1},\mathbf D_{2},\cdots,\mathbf D_{g},\cdots,\mathbf D_{G}] $$
(16)
$$ \mathbf D_{g}=[\mathbf d_{g,1},\cdots,\mathbf d_{g,i},\cdots,\mathbf d_{g,Z}]\in \mathbf R^{m\times Z} \quad (1\le g\le G) $$
(17)

where dg,i is the column vector of the i-th column of Dg. The main steps of column dimension reduction are summarized as follows.

  1. (1)

    Zero mean normalization for the dictionary

First, each column of D (denoted as Di ) subtracts the mean of D to form a new column.

$$ \mathbf D_{i} \gets \mathbf D_{i}-\frac{1}{G}\sum\limits^{G}_{i=1}\mathbf D_{i} $$
(18)

Then, the updated columns are divided by the standard variance, i.e.:

$$ \mathbf D^{\prime}_{i} \gets \frac{\mathbf D_{i}-\frac{1}{G}\sum\limits^{G}_{i=1}\mathbf D_{i}}{\sigma} $$
(19)

Where the standard variance is defined as:

$$ \sigma=\sqrt{(\frac{\sum\limits^{G}_{i=1}(\mathbf D_{i}-\frac{1}{G}\sum\limits^{G}_{i=1}\mathbf D_{i})^{2}}{G-1}} $$
(20)

Thus the normalized matrix is:

$$ \mathbf D_{nomal}=[\mathbf D^{\prime}_{1},\mathbf D^{\prime}_{2},\cdots,\mathbf D^{\prime}_{g},,\cdots,\mathbf D^{\prime}_{G}] $$
(21)

Each column of the matrix Dnomal represents the different groups of the normalized value of the RSS matrix sampling.

  1. (2)

    Calculation of the covariance matrix C

At the g-th RP, we have:

$$ \mathbf D^{\prime}_{g}=[\mathbf d^{\prime}_{g,1},\mathbf d^{\prime}_{g,2},\cdots,\mathbf d^{\prime}_{g,i},\cdots,\mathbf d^{\prime}_{g,Z}] $$
(22)

The covariance matrix C of \(\mathbf D^{\prime }_{g}\) in (24) is

$$ \mathbf C=\mathbf D^{\prime}_{g}\mathbf D^{'H}_{g} $$
(23)

or

$$ \mathbf C_{g}=\frac{1}{Z}{\sum}^{Z}_{j=1}\mathbf d^{\prime}_{g,j}\mathbf d^{'H}_{g,j} $$
(24)

where Cg ∈Rm×m.

  1. (3)

    Singular value decomposition (SVD) on the covariance matrix

After SVD, we have:

$$ \mathbf C_{g}=\mathbf U_{g}\sum\nolimits_{g}\mathbf V_{g} $$
(25)

where, Ug = {ug,1,ug,2,⋯ ,ug,m}, and Ug ∈Rm×m is the normalized singular vector matrix whose vectors denote the most important features of dictionary D. \({\sum }_{g}=diag\{\sigma _{1},\cdots ,\sigma _{m}\}\) is the singular value diagonal matrix, all singular values of which are sorted in descending order. The first column vector ug,1 is related to the maximum singular value σ1, denoting the most important feature of matrix Dg. As all RPs are transformed with SVD, all first column vectors of the matrix Ug of the overall RPs are selected to form a semi-transformation matrix U as follows:

$$ \mathbf U=\{\mathbf u_{1,1},\mathbf u_{2,1},\cdots,\mathbf u_{g,1},\cdots,\mathbf u_{G,1}\} $$
(26)

All vectors of matrix U correspond to the maximum singular values of the RPs.

3.2 Row dimension reduction for dictionary D and observed vector b

  1. (1)

    Firstly, the above semi-transformation matrix U is processed with zero mean normalization. Then, EVD is performed to produce the covariance matrix Δ of the normalized matrix Unomal.

    $$ \mathbf {\Delta}=\mathbf U_{nomal}\mathbf D^{H}_{nomal}=\mathbf W \sum\nolimits_{\lambda}\mathbf W^{H} $$
    (27)

    where W is the matrix constructed by the singular vector wi of the matrix Δ, which can be expressed as follows:

    $$ \mathbf W=\{\mathbf w_{1},\mathbf w_{2},\cdots,\mathbf w_{i},\cdots,\mathbf w_{m}\} $$
    (28)

    In (27), \({\sum }_{\lambda }\) is the diagonal matrix expressed as:

    $$ \begin{array}{llll} \sum\nolimits_{\lambda}&=diag\{\lambda_{1},\lambda_{2},\cdots,\lambda_{i},\cdots,\lambda_{m}\},\\ & \lambda_{1}\ge\lambda_{2}\ge\cdots\ge\lambda_{m} \end{array} $$
    (29)

    where the element λi on the main diagonal is the eigenvalue in descending order. We can select the first k eigenvectors to form the projecting matrix Wk as follows:

    $$ \mathbf W_{k}=\{\mathbf w_{1},\mathbf w_{2},\cdots,\mathbf w_{k}\} $$
    (30)
  2. (2)

    The selection of characteristic number k for the principal component space

Here, CER is defined as the ratio of all eigenvalues from 1 to k to the sum of all eigenvalues, i.e.:

$$ CER=\frac{\sum\limits^{k}_{i=1}\lambda_{i}}{\sum\limits^{m}_{i=1}\lambda_{i}} \ge\chi,\quad (1\le k\le m) $$
(31)

We should make a trade-off between dimension and localization precision by selecting the proper DFL CER higher than the threshold χ to meet the requirements. Here, χ = 99% and the corresponding k were selected to guarantee the localization performance. As a result, the matrix Wk ∈Rm×k can be determined as follows:

  1. (3)

    The low-dimensional dictionary matrix Dk and the low-dimensional vector bk can be obtained using the projecting matrix Wk.

    $$ \mathbf D_{k}=\mathbf{W^{H}_{k}}\mathbf U\in \mathbf R^{k\times G} $$
    (32)
    $$ \mathbf b_{k}=\mathbf{W^{H}_{k}}\mathbf b\in \mathbf R^{k\times 1} $$
    (33)

    Finally, low-dimensional sparse solutions can be obtained by solving the optimization problem in (34), which is similar to the procedure of SC-IpTA.

    $$ \mathbf{x}^{*}={arg \min_{\substack{\mathbf{x}}}}\frac{1}{2}{\Vert\mathbf b_{k}-\mathbf D_{k}\mathbf{x}\Vert}^{2}_{2}+\tau{\Vert\mathbf{x}\Vert}_{1} $$
    (34)

The pseudocode of SSC-IpTA is as follows.

figure c

4 Performance evaluation

4.1 Experimental setups

A dataset is dowloaded from the SPAN Lab [27]. The monitoring area is depicted in Fig. 5, which is 21 feet by 21 feet outdoor square divided into 35 RPs (the third grid for the bottom left is occupied by a tree). A total of 28 APs were installed on the parameters. A more detail configuration can be found in [11, 27]. In each grid, every 30 RSS measurement samples are gathered, of which 25 samples are used to construct the learning dictionary for training and the observation vector for testing, respectively. The experiments were performed in MATLAB R2019b and a 64-bit Windows 10 computer with 8 GB RAM and Intel E3-1230 CPU @ 3.3 GHz.

Fig. 5
figure 5

Experiment diagram of DFL based on the dataset of the SPAN lab

Full size image

4.2 Experiment metrics and other settings

To evaluate the performance of the proposed method, alternative algorithms such as SSC-OMP and SSC-ISTA were also applied with L0 and L1 regularization terms, respectively, as references.

Localization accuracy was employed as the metric to compare the performance of the algorithms. The accuracy is defined as the ratio of correctly estimated samples Nc to the total test samples Nt.

Assuming The actual target location in the i-th RP (xi,yi) and the corresponding estimated location coordinate is \((\bar {x}_{i},\bar {y}_{i})\), the distance between the two sets of coordinates is the localization error (LE). The average localization error (ALE) is the average value LE at each RP.

$$ ALE=\sum\limits^{G}_{i=1}\frac{\sqrt{(x_{i}-\bar{x}_{i})^{2}+(y_{i}-\bar{y}_{i})^{2}}}{G} $$
(35)

Since the RSS samples are inevitably interfered with by environment noise, different levels of Gaussian noise were added to enhance the robustness.

Table 1 lists the typical metrics for the experiment.

Table 1 Typical value of numerical computation
Full size table

4.3 Results and discussion

4.3.1 Performance analysis of single target localization in low-dimensional space

It is assumed that the target is in the 14th grid in Fig. 5, and the signal-to-noise ratios (SNRs) of the dictionary and the observed signal are both 20 dB.

Different levels of noise are added to the dictionary to evaluate the ALE of the algorithm at the observed signal SNR of 20 dB, as shown in Fig. 6. As k increases from 10 to 784, the ALE decreases from 12 feet to nearly zero. Especially when k = 15, the performance of SSC-IpTA (green line) is similar to that of SC-IpTA (pink line) without dimension reduction.

Fig. 6
figure 6

Comparison of ALE of the algorithm with the characteristic number k of 10, 15, 20, and 784

Full size image

As shown in Fig. 7, the accuracy of SSC-IpTA and the other algorithms improves as the characteristic number k increases. When k increases from 12 to 15, the accuracy of SSC-IpTA increases from 30% to almost 100%, which is superior to SSC-ISTA and comparable to SSC-OMP.

Fig. 7
figure 7

Comparison of accuracy between the SSC-IpTA and alternative algorithms with different characteristic numbers k

Full size image

According to Fig. 8, ALE decreases to zero as the SNR of the dictionary increases under the condition that k = 20 and the dimension of the dictionary is 20 × 35. The ALE of SSC-IpTA decreases rapidly as the SNR of the observed signal increases from 15 dB to 20 dB and to noiseless. At dictionary SNRs above 15 dB, ALE is approximately zero when the observed signal SNRs are 20 dB and noiseless.

Fig. 8
figure 8

Comparison of ALE between the algorithms with the observed signal SNR of noiseless, 20 dB, and 10 dB, k = 20, and the dictionary dimension of 20 × 35

Full size image

Table 2 shows the computation time of SC-OMP, SC-ISTA, and SC-IpTA at the RP index of 15 and the maximum number M of 200. The time cost of SC-ISTA is lower than those of SC-IpTA and SC-OMP before dimension reduction. In addition, the computing efficiencies of all algorithms are improved by two or three orders of magnitude with dimension reduction. Moreover, the efficiency of SSC-IpTA is superior to SSC-ISTA and SSC-OMP, thus satisfying the real-time requirements of IoT.

Table 2 Time costs of different algorithms
Full size table

4.3.2 Comparison with state-of-the-art DFL methods

The proposed method was compared with another two novel state-of-the-art DFL algorithms, ISCA [18] and BSCPO [20],based on the same dataset.

According to the Fig. 6 in [26], the performance of SC-IpTA can be improved by measureing the sparsity with the distinctive capability of the proposed generalized thresholding algorithm with adaptive parameter p. Meanwhile, most of the useful information can be extracted with PCA. The comparison results are presented in Table 3. The proposed algorithm achieve the highest localization accuracy at the dictionary data SNR of 15dB, the test signal SNR of 20 dB, and k = 15, i.e., the proposed method outperforms the other algorithms in terms of robustness and accuracy.

Table 3 Performance comparison with other algorithms
Full size table

4.3.3 Performance analysis of multi-targets localization

It is assumed that N(N > 1) targets, e.g., N = 2, are in the area of interest, one at RP-24 and the other at RP-28, as depicted in Fig. 9. As shown in Fig. 10, the accuracy levels of SSC-IpTA are compared under different k values and the dictionary SNRs of 17 dB, 18 dB, 19 dB, and 20 dB, respectively. the results show that when k is below 5, the accuracy is nearly zero. In contrast, when k is above 15, the accuracy reaches 60%. When k = 25, the performance is similar to that when k = 784, and the accuracy is almost up to 100%.

Fig. 9
figure 9

Illustration of the DFL system with multiple persons (N = 2)

Full size image
Fig. 10
figure 10

Accuracy of SSC-IpTA with different k values for multiple targets (N = 2)

Full size image

5 Conclusion

In order to improve the computation efficiency and reduce the time delay of DFL system while maintaining high accuracy, a generalized thresholding algorithm based on dimension reduction with PCA for DFL was proposed in this paper. The method formulates the sparse model based on the DFL problem into a subspace problem. Numerical results showed that the proposed algorithm could improve the computation efficiency of DFL systems and take significantly less time than other algorithms, implying its applicability to IoT scenarios with high real-time requirements.