1 Introduction

In decision support models and systems, the basic decision information usually comes from the judgements of decision makers (DMs) on alternatives [23]. For a finite set of alternatives X = {x1,x2,⋯ ,xn}, it is convenient to express the DMs’ opinions as a matrix such as multiplicative reciprocal matrices (MRMs) [30], additive complementary judgement matrices (ACJMs) or fuzzy preference relations (FPRs) [25, 33], linguistic preference relations (LPRs) [6, 10], intuitionistic fuzzy preference relations (IFPRs) [16, 44] and others [34, 40]. The derived preference relations are always used as the basic tools for analyzing a decision making problem and reaching a finial solution. Here we mainly focus on the consensus model where ACJMs are used to express individual decision information in a GDM problem.

It is noted that an ACJM is originated by applying the sense of fuzzy sets to the binary relations of alternatives [33, 54]. That is, when defining a mapping as follows:

$$ \mathcal{R}: X\times X\mapsto[0,1], $$
(1)

and writing \(\mathcal {R}(x_{i},x_{j})=r_{ij}\) for i,j ∈ In = {1,2,⋯ ,n}, a matrix R = (rij)n×n is determined. In general, it is supposed that the additively reciprocal property is satisfied with the relation of rij + rji = 1 (∀i,j ∈ In) [33]. Therefore, the matrix R(xi,xj) = rij is called as an ACJM to distinguish the concept of MRMs. One can see that the decision support models based on ACJMs have attracted a great deal of attention [8, 29, 47]. As shown in the above mentioned works, a completed ACJM is always used to make a decision analysis. It means that only when completing all pairwise comparisons of alternatives, the obtained matrix is considered to be applicable. However, in a practical case, the preference intensities rij (i,j ∈ In) are given by using a sequential pairwise comparisons of alternatives. For example, a comparison sequence could be chosen as follows:

$$ \begin{array}{@{}rcl@{}} &&x_{1}\leftrightarrow x_{2}, \quad x_{1}\leftrightarrow x_{3},\quad \cdots,\\ &&x_{1}\leftrightarrow x_{n},\quad\cdots,\quad x_{n-1}\leftrightarrow x_{n}. \end{array} $$
(2)

The preference intensity rij could be given by carefully studying the relation of xi and xj. After repeated comparisons, finally the DM could offer the values of the preference intensities. It is seen that the comparison process is complex and related to the knowledge, the experience, and the psychology of DMs. When a completed ACJM is used, the process of giving additive complementary pairwise comparisons rij has been neglected. In order to capture the complexity of a pairwise comparison process, it is worth noting that a sequential model based on leading principal submatrices of a reciprocal preference relation has been proposed in [20, 21]. Based on the developed sequential model [20, 21], the process of paired comparisons can be simulated, then the evolutionary processes associated with the inconsistency degrees of judgements and the priorities of alternatives in pairwise comparisons can be captured. Hence, the sequential model in [20, 21] has the advantages that (i) the process of giving pairwise comparisons could be described carefully; (ii) the irrational behavior of the DM could be checked accurately; (iii) the DM could be reminded timely to reconsider or modify her/his judgements. In the present study, we follow the idea in [20, 21] to consider the process of giving rij and propose a sequential model of ACPCs. It is an attempt to manage individual decision information with rationality and efficiency in a consensus reaching process of GDM.

Moreover, it is seen that two important issues are worth to be investigated in a GDM model with ACJMs. One is the consistency of decision information and the other is the process of building consensus. For the consistency of ACJMs, additive and multiplicative consistency definitions have been proposed in [33]. A functional consistency definition of ACJMs has been further developed in [11] by considering the relationship among entries. In addition, one can find that a consistent matrix corresponds to an ideal case and an inconsistent one is more common in a practical situation [30]. Hence, the inconsistency degree of an ACJM should be quantified and some indexes have been proposed [12, 37, 46, 50]. In particular, it is noted that the threshold of acceptable additive consistency for ACJMs has been discussed in [50] by using the distance-based method. When a comparison matrix is not acceptably consistent, the method of improving consistency should be proposed [42]. In order to improve the consistency of an inconsistent ACJM, many methods have been proposed [24, 37, 38, 41, 49]. For example, an iteration algorithm was proposed in [24] to repair the consistency degree of ACJMs by considering the distance to a consistent one. By defining a deviation measure, an algorithm was proposed in [37] to adjust an inconsistent ACJM to a new one with acceptable consistency. The PSO algorithm was applied to improve the consistency degree of ACJMs by equipping a granularity level in [1]. The ordinal consistency and multiplicative consistency of ACJMs were improved by proposing an ordinal consistency index in [51]. It is seen that the above-mentioned consistency improving methods are usually based on a completed ACJM. Here since a sequential model of additive complementary pairwise comparisons is utilized, the consistency improving method should be developed correspondingly.

On the other hand, for reaching the consensus in GDM with ACJMs, a great number of models have been proposed [12, 13, 33]. For instance, a feedback-mechanism-based iteration algorithm has been reported in [3, 12], where the process of improving the consensus level in GDM has been controlled. The group decision support model in [37] was based on the improvement of the consensus level of experts. With the knowledge of Abelian linearly ordered group, the generalized GDM consensus model has been addressed in [41], where the consensus index was used. Cabrerizo et al. [2] have introduced the concept of the information granularity and the consensus in GDM was reached by using the PSO algorithm. A consensus reaching process with individual consistency control has been proposed by Li et al. [15]. Liu et al. [22] have proposed a consensus model for GDM with ACJMs based on the technique for order preference by similarity to an ideal solution (TOPSIS). In addition, the social network analysis and the prospect theory have been introduced into the process of reaching consensus [7, 35, 39, 56]. The trust measures in the recommender systems were incorporated into the process of reaching consensus in GDM [4, 36, 55]. In this study, we further develop the method of reaching consensus in GDM with ACJMs by using the sequential model of ACPCs.

For the purpose of achieving the above objectives, the remaining parts of this paper is organized as follows. Section 2 briefly recalls the definitions of ACJMs and additive consistency index in [50]. A sequential model of ACPCs is proposed by comparing the existing one. In Section 3, a novel method of improving the additive consistency of ACJMs is proposed according to the developed sequential model. A novel optimization model is constructed to adjust an inconsistent ACJM to a new one with acceptable additive consistency. The PSO algorithm is adopted to effectively solve the constructed optimization model. It is found that the initial decision information can be kept as much as possible. Section 4 addresses a new method of building consensus based on individual consistency control in GDM. A feedback mechanism is established to remind DMs avoiding the irrational and illogical judgements. The novel finding is attributed to the fact that when individual ACJMs are acceptably additively consistent, the collective matrix is acceptably additively consistent by using the weighted averaging operator. Conclusions are covered in the last section.

2 Modeling additive complementary pairwise comparisons

Assume that there are a set of alternatives X = {x1,x2,⋯ ,xn}, and the binary relation is defined as (1). If the alternative xi is preferred to xj, the value of rij satisfies 0.5 < rij ≤ 1. If the alternative xj is preferred to xi, we have 0 ≤ rij < 0.5. If the alternative xi is indifferent to xj, it gives rij = 0.5. Moreover, when the preference intensity of xi over xj is given, it is considered that the preference intensity of xj over xi is determined simultaneously. Then the additively reciprocal property is satisfied with rij + rji = 1 [33]. In addition, one can see that the process of creating the preference intensities rij (i,j ∈ In) means that of pairwisely comparing the alternatives. By considering the property of rij + rji = 1, we call the process of giving rij (i,j ∈ In) as that of realizing ACPCs.

2.1 A completed model of ACPCs

When the ACPCs for all alternatives are completed, an ACJM R = (rij)n×n is formed. In the known literature, the completed ACJM is usually used as a basic tool for decision analyzing and modelling [7, 12, 20, 33, 39]. For convenience, the definition of an ACJM is given as follows:

Definition 1

[33] R = (rij)n×n is called an ACJM, where rij ∈ [0,1] and rij + rji = 1 for ∀i,j ∈ In.

Furthermore, the ideal case of ACPCs is to keep the perfect consistency. That is, we have the following definition:

Definition 2

[33] An ACJM R = (rij)n×n is additively consistent if

$$ r_{ij}=r_{ik}+r_{kj}-0.5, \quad \forall i, j, k\in I_{n}. $$
(3)

However, it is difficult to provide a consistent matrix R = (rij)n×n due to the complexity of decision environments. Hence, a consistency index is requisite to measure the inconsistency degree of an ACJM [12, 37, 46, 50]. Here we recall the additive consistency index (ACI) proposed in [50] as follows:

Definition 3

[50] Let R = (rij)n×n be an ACJM. The matrix \(\bar {R}=(\bar {r}_{ij})_{n\times n}\) with additive consistency is determined from R = (rij)n×n according to the following relation:

$$ \bar{r}_{ij}=\frac 1n \sum\limits_{k=1}^{n} (r_{ik}+r_{kj})-0.5. $$
(4)

The additive consistency index (ACI) of R is defined as follows:

$$ ACI(R)=\sqrt{\frac {2} {n(n-1)}\sum\limits_{i=1}^{n-1}\sum\limits_{j=i+1}^{n}(r_{ij}-\bar{r}_{ij})^{2}}. $$
(5)

Meanwhile, the threshold of ACI for an ACJM with acceptable consistency is proposed as [50]

$$\overline{ACI}=\sigma_{0}\sqrt{\frac {2} {n(n-1)}\lambda_{\alpha}},$$

where λα is the critical value of the χ2 distribution under the significance level α. The values of \(\overline {ACI}\) for different n are shown in Table 1 when setting α = 0.1 and σ0 = 0.2. If \(ACI(R)\leq \overline {ACI},\) the matrix R is considered to be with acceptable additive consistency; otherwise, the matrix R is not acceptably additively consistent.

Table 1 The values of \(\overline {ACI}\) for different n when α = 0.1 and σ0 = 0.2 [50]
Full size table

2.2 A sequential model of ACPCs

It is seen that the completed model of ACPCs offers a final ACJM R = (rij)n×n. The other information of comparing alternatives has been neglected. The complex decision behavior of DMs in producing rij (i,j ∈ In) has been packaged as an unknown whole. With the requirement of intensively managing individual decision information, the packaged unknown behavior of DMs is worth to be unpacked. It is seen that a sequential model of pairwise comparison process within the framework of AHP has been proposed in [20, 21]. Here we follow the idea in [20, 21] to offer a sequential model of ACPCs and simulate the process of comparing alternatives. That is, the process of ACPCs is based on the following steps:

(1):

The first alternative marked as x1 is offered to DMs to give the preference intensity r11 = 0.5; and the matrix is obtained as

Hereafter the symbol C stands for the criterion of DMs.

(2):

The second alternative x2 is considered to produce r12 and r22 = 0.5. According to the additively reciprocal property r21 = 1 − r12, the matrix is determined as

(3):

The alternatives x3,x4,⋯ ,xn are used to form a series of matrices written as R3,R4,⋯ , and Rn.

When the full process of ACPCs is completed, the final matrix Rn is expressed as:

In the above process, an ACJM R = (rij)n×n is decomposed as the leading principal submatrices R1,R2,⋯ ,Rn. Moreover, the process of \(R_{1}\rightarrow R_{2}\rightarrow \cdots \rightarrow R_{n}\) contains a great deal of individual decision information. Some possible meanings according to the sequential model are given as follows:

  • The values of rij (i,j ∈ In) could be with some uncertainty such as fuzzy numbers and a possibility distribution. Some other properties could be offered to the term rij (i,j ∈ In) such as the times of modifying its values for DMs.

  • The preference intensities rij (i,j ∈ In) could be provided by DMs under repetitive thought and modification.

  • The relationship between two adjacent submatrices Ri and Ri+ 1 could reflect the logic of decision information for i = 1,2,⋯ ,n − 1.

  • The complex decision behavior of DMs could exhibit due to the complexity of decision environments.

In general, the sequential model of individual decision information can be used to record the full decision behavior of DMs in a decision support system. The typical model with a completed matrix could be improved to possess the ability of characterizing the complex decision behavior of DMs.

3 An implication of sequential additive complementary pairwise comparisons

In the following, the sequential model of ACPCs is used to propose a novel method of improving additive consistency of inconsistent ACJMs, which can be considered as its implication to the reasonability of individual judgements.

3.1 The relationship between two adjacent submatrices

It is seen that the consistency is one of the important properties of a preference relation. By considering the additive consistency of two adjacent submatrices, we obtain the following result:

Theorem 1

Suppose that R1, R2, ⋯ , and Rn are the leading principal submatrices of an ACJM R = (rij)n×n. When Rk (k = 2,⋯ ,n) is additively consistent, Rt (1 ≤ t < k) is additively consistent.

Proof

Let the matrix Rk be additively consistent. Based on the relation (3), one has rij = ris − rsj + 0.5 (i,j,s = 1,2,⋯ ,k). When i,j,s ≤ k, the relation (3) still holds, implying that Rt is additively consistent. The proof is completed. □

According to Theorem 1, the inconsistency of Rk leads to the inconsistency of Rs (s > k). Although the additive consistency of Rk means the additive consistency of Rt (t < k), the additive consistency of Rk does not imply the additive consistency of Rs (s > k). Moreover, it is noted that the additive consistency of ACJMs is only the ideal case and acceptable additive consistency is more applicable in a practical decision problem. However, acceptable additive consistency of Rk and Rk+ 1 does not exhibit a logical relationship analogous to the observation in Theorem 1. For example, we consider the following ACJM:

$$ \bar{R}_{1}=\left( \begin{array}{cccc} 0.5 & 0.3 & 0.2 & 0.3 \\ 0.7 & 0.5 & 0.1 & 0.4 \\ 0.8 & 0.9 & 0.5 & 0.9 \\ 0.7 & 0.6 & 0.1 & 0.5 \end{array} \right). $$

It can be computed that \(ACI(\bar {R}_{1})=0.0913<0.1212\). For the leading principal submatrix:

$$ \bar{R}_{2}=\left( \begin{array}{ccc} 0.5 & 0.3 & 0.2\\ 0.7& 0.5 & 0.1\\ 0.8& 0.9 &0.5 \end{array} \right), $$

we obtain \(ACI(\bar {R}_{2})=0.1>0.0882\). Obviously, according to the criterion in Table 1 [50], the matrix \(\bar {R}_{1}\) is of acceptable additive consistency and \(\bar {R}_{2}\) is not of acceptable additive consistency. The above observation is in agreement with the finding in [20] for the leading principal submatrices of MRMs. Moreover, similar to the method in [20], the first implication of the sequential model is to give an additive consistency improving method for inconsistent ACJMs. There are the following two situations:

  • When Rk is with acceptable additive consistency and Rk+ 1 is not acceptably additively consistent, the entries of ri(k+ 1) (i = 1,2,⋯ ,k) are only adjusted to obtain a new Rk+ 1 with acceptable additive consistency.

  • When Rk and Rk+ 1 are all not acceptably additively consistent, we can obtain a new Rk+ 1 with acceptable additive consistency by adjusting partial entries of Rk+ 1 such as ri(k+ 1) (i = 1,2,⋯ ,k) and others belonging to Rk.

It is obvious that the second situation is more generic than the first one. As an example, we consider the following matrix:

$$ \bar{R}_{3}=\left( \begin{array}{cccc} 0.50 & 0.30 & 0.40 & 0.60 \\ 0.70 & 0.50 & 0.20 & 0.60 \\ 0.60 & 0.80 & 0.50 & 0.30 \\ 0.40 & 0.40 & 0.70 & 0.50 \end{array} \right), $$

and its submatrix:

$$ \bar{R}_{4}=\left( \begin{array}{ccc} 0.5 & 0.3 & 0.4\\ 0.7& 0.5 & 0.2\\ 0.6& 0.8 &0.5 \end{array} \right). $$

The values of additive consistency index can be computed as \(ACI(\bar {R}_{3})=0.1732>0.1212\) and \(ACI(\bar {R}_{4})=0.1333>0.0882,\) respectively. By adjusting the entries r14 = 0.60, r24 = 0.60 and r43 = 0.70, it follows

$$ \bar{R}_{5}=\left( \begin{array}{cccc} 0.5000 & 0.3000 & 0.4000 & 0.5000 \\ 0.7000 & 0.5000 & 0.2000 & 0.5219 \\ 0.6000 & 0.8000 & 0.5000 & 0.4500 \\ 0.5000 & 0.4781 & 0.5500 & 0.5000 \end{array} \right), $$

with \(ACI(\bar {R}_{5})=0.1212 \leq 0.1212\). In addition, when adjusting the entries in \(\bar {R}_{4},\) we have

$$ \bar{R}_{6}=\left( \begin{array}{cccc} 0.5000 & 0.4468 & 0.4469 & 0.6000 \\ 0.5532 & 0.5000 & 0.3500 & 0.6000 \\ 0.5531 & 0.6500 & 0.5000 & 0.3000 \\ 0.4000 & 0.4000 & 0.7000 & 0.5000 \end{array} \right), $$

with \(ACI(\bar {R}_{6})=0.1212 \leq 0.1212\). The method of improving the additive consistency of inconsistent ACJMs will be used to propose a group decision support model, where the feedback mechanism will be constructed from the additive consistency of individual decision information to the consensus reaching in GDM.

3.2 A method of improving additive consistency

In order to adjust an inconsistent ACJM to a new one with acceptable additive consistency, a feasible approach should be proposed. By considering the convenience and high efficiency of decision support systems, it is suitable to ask DMs to give as little information as possible when improving the consistency of decision information. Following the idea in [1, 21], the DM only need to offer a flexibility degree such that the consistency degree of ACJMs can be improved. For the purpose of achieving a fast yet effective adjustment, we construct an algorithm similar to that in [21]. There are two important situations to be considered. One is the standard of acceptable ACJMs, and the other is to keep the initial information as much as possible. Hence, the first function is written as:

$$ Q_{1}=ACI(\bar{R}), $$
(6)

where \(\bar {R}\) stands for the adjusted ACJM. The less the value of Q1 is, the higher the additive consistency degree of the matrix \(\bar {R}\). As shown in Table 1, the standard of acceptable ACJMs can be used. The second function is defined as:

$$ Q_{2}=\sum\limits_{i,j=1; i\neq j}^{n}\frac{|r_{ij}-\bar{r}_{ij}|}{n^{2}-n}. $$
(7)

where \(\bar {r}_{ij}\) belongs to \(\bar {R}=(\bar {r}_{ij})_{n\times n}\). Obviously, the less the value of Q2 is, the more the initial decision information is kept.

From the viewpoint of optimization, it seems that one should minimize simultaneously the values of Q1 and Q2. The simplest method is to address the following linear combination [18, 19, 21]:

$$ Q=pQ_{1}+qQ_{2}, $$
(8)

where p and q are two nonnegative constants. When p = 0 or q = 0, then we have Q = qQ2 or Q = pQ1, meaning that only one of the two situations is considered. However, for a GDM problem, it is unnecessary to require individual decision information to be perfectly consistent. It is sufficient to make individual decision information be acceptable additive consistency. Hence, by considering the threshold of acceptable additive consistency, here we construct the following optimization problem:

$$ \min_{\bar{R}} Q_{2} $$
(9)

subject to the following condition:

$$ Q_{1}=\overline{ACI}. $$
(10)

On the other hand, the attitude of DMs towards the adjustment of ACJMs should be considered. Similar to those in [2, 21, 27], the flexibility degree β of DMs is equipped. The other constraint conditions are given as follows [22]:

$$ \begin{array}{@{}rcl@{}} \text{Case I:}\bar{r}_{ij}\in\left[\max\left( 0.5,r_{ij}-\beta\right), \min\left( 1,r_{ij}+\beta\right)\right], \end{array} $$
(11)

for 0.5 ≤ rij ≤ 1, and

$$ \begin{array}{@{}rcl@{}} \text{Case II:}\bar{r}_{ij}\in\left[\max\left( 0,r_{ij}-\beta), \min(0.5,r_{ij}+\beta\right)\right], \end{array} $$
(12)

for 0 ≤ rij ≤ 0.5. According to the additively reciprocal property of \(\bar {R},\) it is sufficient to consider one of Cases I and II. In order to solve the optimization problem (9) subject to (10) and (11)/(12), The penalty function method [32] is applied to rewrite the optimization problem as

$$ \min_{\bar{R}} Q_{c}=Q_{2}+M\left|Q_{1}-\overline{ACI}\right|, $$
(13)

where M is a sufficiently large positive number. For numerically computations, Case I is chosen and the PSO algorithm [14, 28, 31] is performed to solve the nonlinear optimization problem (13). Moreover, it is noted that there are many methods to solve an optimization problem, for example, the typical mathematical analysis and the metaheuristic methods [5, 32]. In the present study, we are motivated by the successful applications of the PSO algorithm to various nonlinear optimization problems [27, 28, 55]. The PSO algorithm is still chosen to obtain the optimal solution of the constructed one (13). The numerical results in the next subsection reveal that the PSO algorithm is effective in solving (13). In particular, we should point out that the value of M is chosen in advance when performing the PSO algorithm. The effects of the values of M on the optimal solution have been investigated in the following numerical computations.

In what follows, combining the sequential model of ACPCs and the optimization model (13), we elaborate on a new algorithm (Algorithm I) to improve additive consistency of inconsistent ACJMs.

Step 1::

Consider an ACJM R = (rij)n×n without acceptable additive consistency and write the submatrix Rn− 1.

Step 2::

Check the acceptable additive consistency of Rn− 1. When Rn− 1 is acceptably additively consistent, the entries rkn (k = 1,2,⋯ ,n − 1) are chosen to be adjusted. When Rn− 1 is not acceptably additively consistent, the entries in Rn− 1 are chosen to be adjusted.

Step 3::

Construct the optimization problem (13) by considering (11) with the flexibility degree β.

Step 4::

Run the PSO algorithm to solve the constructed optimization problem.

Step 5::

Obtain an ACJM with acceptable additive consistency.

The above algorithm can be used to derive an ACJM with acceptable additive consistency by keeping the initial decision information as much as possible. Except for the given ACJM, the DM only needs to provide the value of the flexibility degree β. The adjustment process can be completed with a fast yet effective way. Based on the above algorithm, we have the following result:

Theorem 2

Under Algorithm I, there is a flexibility degree β such that a matrix with acceptable additive consistency can be obtained from an inconsistent ACJM R = (rij)n×n by keeping the initial information as much as possible.

Proof

According to (4), one can obtain a matrix with additive consistency from any an ACJM R = (rij)n×n. Acceptable additive consistency is a deviation from additive consistency. Hence, there is a flexibility degree β such that a matrix with acceptable additive consistency is determined by using an inconsistent ACJM R = (rij)n×n. Moreover, the optimization model (13) and the PSO algorithm mean that the obtained matrix can keep the initial information as much as possible. □

3.3 Numerical examples and discussion

Now let us carry out some numerical computations for verifying the algorithm to improve additive consistency of ACJMs. The effects of the parameters β and M on the optimal solutions of Qc and Q1 are investigated respectively. For example, an inconsistent ACJM is given as follows [37]:

$$ \bar{R}_{7}=\left( \begin{array}{cccccc} 0.50 & 0.20 & 0.10 & 0.50 & 0.80 & 0.90\\ 0.80 & 0.50 & 0.20 & 0.90 & 0.60 & 1.00\\ 0.90 & 0.80 & 0.50 & 0.80 & 0.60 & 0.60\\ 0.50 & 0.10 & 0.20 & 0.50 & 1.00 & 0.80\\ 0.20 & 0.40 & 0.40 & 0.00 & 0.50 & 0.40\\ 0.10 & 0.00 & 0.40 & 0.20 & 0.60 & 0.50 \end{array} \right). $$

Based on the standard of acceptable additive consistency in Table 1, it is easily found that the 5 × 5 and 6 × 6 leading principle matrices are unacceptably consistent. According to the above proposed algorithm, there are the following two approaches to the additive consistency improvement of \(\bar {R}_{7}:\)

  • Adjusting the entries of the 5 × 5 leading principle matrix;

  • Modifying the entries in the fifth and the sixth columns and rows of \(\bar {R}_{7}\).

Moreover, we consider all the entries bigger than 0.5 and the additively reciprocal property. The relation (11) is used when running the PSO algorithm to solve the optimization problem (13). The sizes of swarm and the maximal generation number are chosen as 100. Under each step of β, the optimal solution of Qc is determined for a fixed parameter M.

Figure 1 is drawn to show the variations of the optimal solution of Qc versus β for the selected values of the parameter M under the cases of (a) and (b), respectively. It is seen from Fig. 1 that with the increasing of β, the values of the optimal solution of Qc are decreasing, then tending to a stable one for any parameter M. This means that for a sufficiently large value of β, the inconsistent matrix \(\bar {R}_{7}\) can be adjusted to a new one with \(Q_{1}=\overline {ACI}\). For a small value of β satisfying \(Q_{1}>\overline {ACI},\) the parameter M has great influences on the value of Qc. In addition, the variations of Q1 versus M are shown in Fig. 2 for the selected values of β under the cases of (a) and (b), respectively. With the increasing of the values of M, the values of Q1 are tending a constant for a fixed β, meaning that a sufficiently lager value of M can be determined to obtain the optimal value of Q1. Comparisons between the cases of (a) and (b) in Figs. 1 and 2 show that the two approaches exhibit the similar effects on adjusting an inconsistent matrix to an acceptable one.

Fig. 1
figure 1

Variations of the optimal solution of Qc versus β for the selected values of the parameter M under the cases of (a) and (b), respectively

Full size image
Fig. 2
figure 2

Variations of Q1 versus M for the selected values of β under the cases of (a) and (b), respectively

Full size image

On the other hand, it is noted that many other methods have been proposed to improve the additive consistency of ACJMs [24, 37, 38, 41, 46,47,48, 50, 51]. One of the important issues is how to determine the effectiveness of the consistency improving method. Here, the departure of the original matrix R = (rij)n×n from the modified one \(\bar {R}=(\bar {r}_{ij})_{n\times n}\) is measured by the following criteria [42]:

$$ \begin{array}{@{}rcl@{}} &&\text{Cr1: }\delta=\max\limits_{i,j}\left\{\left|r_{ij}-\bar{r}_{ij}\right|\right\}, \end{array} $$
(14)
$$ \begin{array}{@{}rcl@{}} &&\text{Cr2: }\sigma=\frac{\sqrt{{\sum}_{i=1}^{n}{\sum}_{j=1}^{n}\left( r_{ij}-\bar{r}_{ij} \right)^{2}}}{n}. \end{array} $$
(15)

The determined matrix is considered to be acceptable when δ < 0.2 and σ < 0.1. As shown in Figs. 1 and 2, it is feasible to obtain an acceptably consistent matrix by choosing β = 0.1 and M = 10 to run the PSO algorithm under the cases of (a) and (b), respectively. Figure 3 is depicted to show the variations of Qc versus the generation number under the cases of (a) and (b), respectively. One can see from Fig. 3 that with the increasing of the generation number, the values of Qc drop down to a stable one. This implies that the optimal solution of Qc is determined by choosing a sufficiently large generation number. For example, when the generation number is 100, the adjusted matrices with additively acceptable consistency can be written as

$$ \bar{R}_{8}=\left( \begin{array}{cccccc} 0.5000 & 0.2870 & 0.0244 & 0.5870 & 0.7213 & 0.9000\\ 0.7130 & 0.5000 & 0.1348 & 0.8601 & 0.6072 & 1.0000\\ 0.9756 & 0.8652 & 0.5000 & 0.7325 & 0.5957 & 0.6000\\ 0.4130 & 0.1399 & 0.2675 & 0.5000 & 0.9901 & 0.8000\\ 0.2787 & 0.3928 & 0.4043 & 0.0099 & 0.5000 & 0.4000\\ 0.1000 & 0.0000 & 0.4000 & 0.2000 & 0.6000 & 0.5000 \end{array} \right) $$

for Case (a) and

$$ \bar{R}_{9}=\left( \begin{array}{cccccc} 0.5000 & 0.2000 & 0.1000 & 0.5000 & 0.7884 & 0.9497\\ 0.8000 & 0.5000 & 0.2000 & 0.9000 & 0.5918 & 0.9370\\ 0.9000 & 0.8000 & 0.5000 & 0.8000 & 0.5818 & 0.5905\\ 0.5000 & 0.1000 & 0.2000 & 0.5000 & 0.9616 & 0.7239\\ 0.2116 & 0.4082 & 0.4182 & 0.0384 & 0.5000 & 0.3218\\ 0.0503 & 0.0630 & 0.4095 & 0.2761 & 0.6782 & 0.5000 \end{array} \right) $$

for Case (b). It is easy to compute that \(\delta (\bar {R}_{8})=0.0870,\) \(\sigma (\bar {R}_{8})=0.0457,\)\(\delta (\bar {R}_{9})=0.0761,\) and \(\sigma (\bar {R}_{9})=0.0308\). The obtained results satisfy the criteria δ < 0.2 and σ < 0.1, meaning that the consistency improving method is effective and convincing.

Fig. 3
figure 3

Variations of the fitness function Qc versus the generation number with β = 0.1 and M = 10 under the cases of (a) and (b), respectively

Full size image

4 A novel group decision support model with a feedback mechanism

The aim of the sequential model of ACPCs is to finely managing individual decision information. A real-time feedback mechanism can be established to remind DMs avoiding the irrational and illogical behavior. Then a consensus reaching process in GDM is proposed by controlling individual consistency level of decision information.

4.1 A real-time feedback mechanism of individual decision information

Let us assume that there are a set of alternatives X = {x1,x2,⋯ ,xn} and a group of experts E = {e1,e2,⋯ ,em} in a GDM problem. The process of providing DMs’ opinions can be recorded in real time. Based on the sequential model of ACPCs, the expert ek gives a series of ACJMs as \(R^{(k)}_{s}=(r_{ij}^{(k)})_{s\times s}\) for s ∈ In and k ∈ Im = {1,2,⋯ ,m}. The decision behavior of the expert ek can be captured by the process of providing \(R^{(k)}_{s}\). Moreover, we compute the priorities of alternatives by using \(R^{(k)}_{s}=(r_{ij}^{(k)})_{s\times s}\) and the simple formula in [9] is used for xi with

$$ \omega_{i}^{(k)}=\frac{2}{s}\sum\limits_{j=1}^{s}r_{ij}^{(k)}. $$
(16)

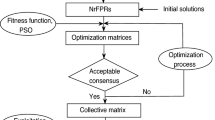
Then the corresponding priority vector is \(\omega ^{(k)}=(\omega _{1}^{(k)}, \omega _{2}^{(k)}, \cdots , \omega _{s}^{(k)})\) and it is normalized into [0,1], then \(\sum \limits _{i=1}^{s}\omega _{i}^{(k)}=1\). In the following, the real-time feedback mechanism is established by offering two reference quantities to DMs. One is the values of additive consistency index and the other is the ranking of the compared alternatives. The algorithm of the real-time feedback mechanism is shown in Fig. 4 and elaborated on as follows:

Step 1::

The expert ek is asked to input her/his opinions on a series of alternatives \(x_{1}\rightarrow x_{2}\rightarrow \cdots \rightarrow x_{n}\) in a decision support system.

Step 2::

When the matrix \(R^{(k)}_{s}\) is completed, the values of additive consistency index of \(R^{(k)}_{t}\) (1 ≤ t ≤ s) and the rankings of alternatives are output by using a figure.

Step 3::

The values of additive consistency index and the rankings of the compared alternatives can remind the DM revise her/his opinions.

Step 4::

When the DM offers a flexibility degree β, the adjustment procedure of improving the consistency starts automatically.

Step 5::

When the DM does not want to adjust her/his judgements, the final matrix is originated.

Remark 1

The feedback mechanism is based on the sequential model of ACPCs. The value of the additive consistency index and the ranking of alternatives can be offered with the process of giving the preference intensities of alternatives. The DMs can be reminded in real time such that their final opinions are rational enough.

Fig. 4
figure 4

Real-time feedback mechanism of individual decision information

Full size image

The advantage of the feedback mechanism lies in the reminding for DMs in real time such that the complexity of decision process can be decomposed and captured. As an example, we investigate the following final matrix:

The leading principal submatrices of \(\bar {R}_{10}\) are analyzed and the priority process of alternatives is illustrated. For convenience, the normalized priority vector of alternatives is determined according to (16) in the following computations. By considering the comparison process of \(x_{1}\rightarrow x_{2}\rightarrow \cdots \rightarrow x_{n},\) The leading principal submatrices of \(\bar {R}_{10}\) are written as Ri(i = 1,2,⋯ ,5), where

It is easy to compute that ACI(R4) = 0.1429 > 0.1212 and ACI(R5) = 0.1440 > 0.1359, meaning that R4 and R5 are of unacceptable additive consistency. In addition, one can see that the ranking of x2 ≻ x4 ≻ x1 ≻ x3 for R4 is changed to x2 ≻ x4 ≻ x3 ≻ x5 ≻ x1 for R5. The order of x3 and x1 has been changed due to the introduction of x5. The information related to the additive consistency index and the ranking of alternatives can be feedback to the DM. When the DM wants to modify the judgements such that the derived matrix is of acceptably additive consistency, two approaches are provided. One is to adjust the entries in the fourth and fifth columns and rows of \(\bar R_{10},\) then the modified matrix \(\bar R_{11}\) is obtained as follows:

with \(ACI(\bar R_{11})=0.1359\). The ranking of alternatives is determined as x2 ≻ x4 ≻ x3 ≻ x5 ≻ x1. The other is to modify the entries in the 4 × 4 leading principle matrix of \(\bar R_{10}\). The new matrix \(\bar {R}_{12}\) is given as follows:

with \(ACI(\bar R_{12})=0.1359\). The ranking of alternatives is obtained x2 ≻ x4 ≻ x3 ≻ x5 ≻ x1. Then following the idea in [20], the priority processes of alternatives for \(\bar {R}_{11}\) and \(\bar {R}_{12}\) are drawn in Fig. 5. Regardless of \(\bar {R}_{11}\) and \(\bar {R}_{12},\) there is an intersection point of the lines for x1 and x3. This implies that the standard of acceptable additive consistency cannot eliminate the phenomenon of rank reversal. The finding is similar to the result about the acceptable consistency of pairwise comparison matrices in the AHP [20].

Fig. 5
figure 5

The priority processes of alternatives for \(\bar {R}_{11}\) (a) and \(\bar {R}_{12}\) (b)

Full size image

Furthermore, when the DM wants to avoid the occurrence of the rank reversal phenomenon, the standard of weak transitivity should be used [24]. For example, applying the method in [24], \(\bar {R}_{11}\) and \(\bar {R}_{12}\) are readjusted to \(\bar {R}_{13}\) and \(\bar {R}_{14}\) with transitivity as follows:

One can compute that \(ACI(\bar R_{13})=ACI(\bar R_{14})=0.0408<0.1359,\) meaning the two matrices are of acceptable additive consistency. Figure 6 shows that the priority processes of alternatives for \(\bar R_{13}\) and \(\bar R_{14}\). It is seen from Fig. 6 that there is not any intersection point, meaning that the phenomenon of rank reversal does not occur.

Fig. 6
figure 6

The priority processes of alternatives for \(\bar {R}_{13}\) (a) and \(\bar {R}_{14}\) (b)

Full size image

In the proposed feedback mechanism, the values of additively consistency index and the priority processes are offered such that the DMs can adjust their opinions in real times.

4.2 Building consensus based on individual consistency control

Based on the feedback mechanism, the final matrices can be considered as the optimal results derived from a sequence of rational comparisons of DMs. The remaining issue is how to build the consensus among the experts and reach the final solution. It is assumed that the collective matrix is obtained by using the weighted averaging operator [37, 51]. That is, let \(R^{(k)}=(r_{ij}^{(k)})_{n\times n}\) be the k th ACJM provided by the expert ek and λk ∈ [0,1] be the corresponding weight for k ∈ Im. Then the collective ACJM Rc is determined as:

$$ R^{c}=(r_{ij}^{c})_{n\times n}=\sum\limits_{t=1}^{m} {\lambda_{t}R^{(t)}}, $$
(17)

where

$$r_{ij}^{c}=\sum\limits_{t=1}^{m}\lambda_{t}r_{ij}^{(t)},\quad \sum\limits_{t=1}^{m}\lambda_{t}=1.$$

In addition, by considering the acceptable additive consistency of R(k) (k ∈ Im), we have the following result:

Theorem 3

When individual ACJMs R(k) (k ∈ Im) are with acceptable additive consistency satisfying

$$ACI(R^{(k)})\leq \overline{ACI},$$

the collective one Rc exhibits acceptable additive consistency.

Proof

With the knowledge (5) and (17), we have the following equality:

$$ ACI(R^{c})=\sqrt{\frac {2}{n(n-1)}\sum\limits_{i=1}^{n-1}\sum\limits_{j=i+1}^{n}\left( r_{ij}^{c}-\bar{r}_{ij}^{c}\right)^{2}}, $$
(18)

where

$$\bar{r}_{ij}^{c}=\frac {1}{n} \sum\limits_{k=1}^{n} (r_{ik}^{c}+r_{kj}^{c})-0.5.$$

Then, it is computed that

$$ \begin{array}{@{}rcl@{}} (r_{ij}^{c}-\bar{r}_{ij}^{c})^{2} &=&\left[r_{ij}^{c}-\frac 1n \sum\limits_{k=1}^{n} (r_{ik}^{c}+r_{kj}^{c})+0.5\right]^{2} \\ &=&\left[\sum\limits_{t=1}^{m} {\lambda_{t}r_{ij}^{(t)}}-\frac{1}{n} \sum\limits_{k=1}^{n} \left( \sum\limits_{t=1}^{m} \lambda_{t} r_{ik}^{(t)}+\sum\limits_{t=1}^{m} \lambda_{t} r_{kj}^{(t)}\right)+0.5\right]^{2}\\ &=&\left[\sum\limits_{t=1}^{m}\lambda_{t}\left( r_{ij}^{(t)}-\frac{1}{n} \sum\limits_{k=1}^{n} \left( r_{ik}^{(t)}+r_{kj}^{(t)}\right)+0.5\right)\right]^{2}\\ &=&\left[\sum\limits_{t=1}^{m}\lambda_{t} \left( r_{ij}^{(t)}-\bar{r}_{ij}^{(t)}\right)\right]^{2}\\ &\leq&\sum\limits_{t=1}^{m}\lambda_{t}\left( r_{ij}^{(t)}-\bar{r}_{ij}^{(t)}\right)^{2}, \end{array} $$
(19)

where the relation 2ab ≤ a2 + b2 and the equality \({\sum }_{t=1}^{m}\lambda _{t}=1\) have been used. Therefore, one has

$$ \begin{aligned} ACI(R^{c})&\leq \sqrt{\sum\limits_{t=1}^{m}\lambda_{t}\frac {2} {n(n-1)}\sum\limits_{i=1}^{n-1}\sum\limits_{j=i+1}^{n} \left( r_{ij}^{(t)}-\bar{r}_{ij}^{(t)}\right)^{2}}\\ &\leq\sqrt{\sum\limits_{t=1}^{m} \lambda_{t}\overline{ACI}^{2}}\\ &=\overline{ACI}. \end{aligned} $$

This means that the matrix Rc is acceptably additively consistent and the proof is completed. □

The observation in Theorem 3 shows that when the consistency levels of individual matrices are controlled to be acceptable, the collective matrix is also with acceptable additive consistency. It is worth noting that the similar result to Theorem 3 has been observed by Xu [43] for the aggregation of MRMs using the geometric averaging operator. Here we use the additive consistency index of ACJMs in [51] to develop the interesting result. Moreover, it is seen that the aggregation operators have been developed widely to aggregate individual decision information [12, 43, 52, 53]. When the induced ordered weighted averaging operator is used to aggregate R(k) (k ∈ Im), the similar result as Theorem 3 can be obtained. The detail procedure has been neglected due to the straight extension of the finding in Theorem 3.

In what follows, similar to the existing works [37, 51], we define the consensus level (CL) by using the distance-based method as follows:

$$ CL(R^{(k)})=\sum\limits_{i,j=1; i\neq j}^{n} \frac{|{r}_{ij}^{c}- {r_{ij}^{(k)}}|}{n^{2}-n}, $$
(20)

where \(R^{c}=({r}_{ij}^{(c)})_{n\times n}\) and \(R^{(k)}=({r}_{ij}^{(k)})_{n\times n}\) represent the collective and individual matrices, respectively. When CL(R(k)) = 0, there is the greatest consensus between R(k) and Rc. With the increasing of the values of CL, the consensus level is decreasing. In addition, a threshold of the consensus level can be set such as \(\overline {CL}\). When the consensus level CL(R(k)) is bigger than \(\overline {CL},\) the adjustment formula is suggested as follows [37]:

$$ \bar{R}^{(k)}=\gamma R^{(k)}+(1-\gamma)R^{c}, \quad \gamma\in[0,1]. $$
(21)

When γ = 0, one has \(\bar {R}^{(k)}=R^{c};\) when γ = 1, it gives \(\bar {R}^{(k)}=R^{(k)}\). In other words, when the value of γ is changed from 1 to 0, the new matrix \(\bar {R}^{(k)}\) approaches to Rc. Hence, there is a value of γ such that the consensus level of \(\bar {R}^{(k)}\) is smaller than \(\overline {CL}\). Furthermore, we have the following result:

Theorem 4

If the matrices Rk and Rc are with acceptable additive consistency, \(\bar {R^{k}}\) determined by (21) is acceptably additively consistent.

Proof

The proof can be obtained by assuming λ1 = γ and λ2 = 1 − γ in Theorem 3. □

Fig. 7
figure 7

Building consensus with individual consistency control

Full size image

At the end, it is convenient to show the consensus reaching process in Fig. 7. Except for the method of improving additive consistency of individual matrices, the key step is the consensus reaching process. Under the control of acceptable additive consistency, the final matrices are all with acceptable additive consistency and acceptable consensus level.

4.3 Case studies and comparison

In this subsection, let us carry out two examples to illustrate the consensus model and compare with the other methods.

Example 1

It is supposed that there are four alternatives {x1,x2,x3,x4}. Four experts with the same weights ωi = 0.25 (i = 1,2,3,4) evaluate their opinions as the following ACJMs [3, 15, 37]:

$${R}^{(1)}=\left( \begin{array}{cccc} 0.50 & 0.20 & 0.60 & 0.40 \\ 0.80 & 0.50 & 0.90 & 0.70 \\ 0.40 & 0.10 & 0.50 & 0.30 \\ 0.60 & 0.30 & 0.70 & 0.50 \end{array} \right), {R}^{(2)}=\left( \begin{array}{cccc} 0.50 & 0.70 & 0.90 & 0.50 \\ 0.30 & 0.50 & 0.60 & 0.70 \\ 0.10 & 0.40 & 0.50 & 0.80 \\ 0.50 & 0.30 & 0.20 & 0.50 \end{array} \right),$$
$${R}^{(3)}=\left( \begin{array}{cccc} 0.50 & 0.30 & 0.50 & 0.70 \\ 0.70 & 0.50 & 0.10 & 0.30 \\ 0.50 & 0.90 & 0.50 & 0.25 \\ 0.30 & 0.70 & 0.75 & 0.50 \end{array} \right), {R}^{(4)}=\left( \begin{array}{cccc} 0.50 & 0.25 & 0.15 & 0.65 \\ 0.75 & 0.50 & 0.60 & 0.80 \\ 0.85 & 0.40 & 0.50 & 0.50 \\ 0.35 & 0.20 & 0.50 & 0.50 \end{array} \right).$$

It is easy to compute that ACI(R(1)) = 0, ACI(R(2)) = 0.1707, ACI(R(3)) = 0.2165, and ACI(R(4)) = 0.1190. Considering the threshold \(\overline {ACI}=0.1212,\) one can see that the matrices R(2) and R(3) should be revised to those with acceptable additive consistency. Based on the proposed group decision support model, the following steps should be completed.

In the first step, we improve the consistency levels of R(2) and R(3) by using the proposed method for improving additive consistency. The revised matrices of R(2) and R(3) are given as follows:

$${R}^{(2)}_{r}=\left( \begin{array}{cccc} 0.5000 & 0.7000 & 0.9000 & 0.6000 \\ 0.3000 & 0.5000 & 0.6000 & 0.6792 \\ 0.1000 & 0.4000 & 0.5000 & 0.7000 \\ 0.5000 & 0.3208 & 0.3000 & 0.5000 \end{array} \right),$$
$${R}^{(3)}_{r}=\left( \begin{array}{cccc} 0.5000 & 0.3000 & 0.5000 & 0.5200 \\ 0.7000 & 0.5000 & 0.2800 & 0.3378 \\ 0.5000 & 0.7200 & 0.5000 & 0.4178 \\ 0.4800 & 0.6622 & 0.5822 & 0.5000 \end{array} \right).$$

Using R(1), \({R}^{(2)}_{r},\) \({R}^{(3)}_{r}\) and R(4), the collective ACJM Rc is obtained by considering (17) and λi = 0.25 (i = 1,2,3,4) as follows:

$$ R^{c}=\left( \begin{array}{cccc} 0.5000 & 0.3837 & 0.5544 & 0.5495 \\ 0.6163 & 0.5000 & 0.5669 & 0.6154 \\ 0.4456 & 0.4331 & 0.5000 & 0.4945 \\ 0.4505 & 0.3846 & 0.5055 & 0.5000 \end{array} \right). $$

According to (20), the consensus levels are computed as CL(R(1)) = 0.1101, \(CL(R^{(2)}_{r})=0.1691,\) \(CL(R^{(3)}_{r})=0.1348\) and CL(R(4)) = 0.1130.

Second, the threshold of the consensus level should be set such as \(\overline {CL}=0.1\). Then, the matrices R(1), \({R}^{(2)}_{r},\) \({R}^{(3)}_{r}\) and R(4) should be modified by using the formula (21). For example, by choosing γ1 = 0.9050, γ2 = 0.5900, γ3 = 0.7400 and γ4 = 0.8850, we have

$$R^{(1)}_{1}=\left( \begin{array}{cccc} 0.5000 & 0.2704 & 0.5745 & 0.4619 \\ 0.7296 & 0.5000 & 0.7678 & 0.6743 \\ 0.4255 & 0.2322 & 0.5000 & 0.3774 \\ 0.5381 & 0.3257 & 0.6226 & 0.5000 \end{array} \right),$$
$$R^{(2)}_{1}=\left( \begin{array}{cccc} 0.5000 & 0.5703 & 0.7583 & 0.5793 \\ 0.4297 & 0.5000 & 0.5864 & 0.6530 \\ 0.2417 & 0.4136 & 0.5000 & 0.6157 \\ 0.4207 & 0.3470 & 0.3843 & 0.5000 \end{array} \right),$$
$$R^{(3)}_{1}=\left( \begin{array}{cccc} 0.5000 & 0.3218 & 0.5141 & 0.5277 \\ 0.6782 & 0.5000 & 0.3546 & 0.4100 \\ 0.4859 & 0.6454 & 0.5000 & 0.4377 \\ 0.4723 & 0.5900 & 0.5623 & 0.5000 \end{array} \right), $$
$$R^{(4)}_{1}=\left( \begin{array}{cccc} 0.5000 & 0.2887 & 0.2771 & 0.6166 \\ 0.7113 & 0.5000 & 0.5951 & 0.7469 \\ 0.7229 & 0.4049 & 0.5000 & 0.4952 \\ 0.3834 & 0.2531 & 0.5048 & 0.5000 \end{array} \right).$$

It is computed that \(CL(R^{(1)}_{1})=0.0997,\) \(CL(R^{(2)}_{1})=0.0998,\) \(CL(R^{(3)}_{1})=0.0998\) and \(CL(R^{(4)}_{1})=0.1\). Then, the collective matrix \({R^{c}_{1}}\) can be determined as follows:

$$ {R^{c}_{1}}=\left( \begin{array}{cccc} 0.5000 & 0.3628 & 0.5310 & 0.5464 \\ 0.6372 & 0.5000 & 0.5760 & 0.6210 \\ 0.4690 & 0.4240 & 0.5000 & 0.4815 \\ 0.4536 & 0.3790 & 0.5185 & 0.5000 \end{array} \right). $$

In what follows, the consensus levels are recomputed as \(CL(R^{(1)}_{1})=0.0949,\) \(CL(R^{(2)}_{1})=0.1074,\) \(CL(R^{(3)}_{1})=0.0921\) and \(CL(R^{(4)}_{1})=0.0928\). One can see that the matrix \(R^{(2)}_{1}\) should be adjusted. After some computations, it gives

$$ R^{(2)}_{2}=\left( \begin{array}{cccc} 0.5000 & 0.5509 & 0.7370 & 0.5762 \\ 0.4491 & 0.5000 & 0.5855 & 0.6501 \\ 0.2630 & 0.4145 & 0.5000 & 0.6032 \\ 0.4238 & 0.3499 & 0.3968 & 0.5000 \end{array} \right). $$

Then the collective matrix \({R^{c}_{2}}\) is determined as follows:

$$ {R^{c}_{2}}=\left( \begin{array}{cccc} 0.5000 & 0.3579 & 0.5257 & 0.5456 \\ 0.6421 & 0.5000 & 0.5757 & 0.6203 \\ 0.4743 & 0.4243 & 0.5000 & 0.4784 \\ 0.4544 & 0.3797 & 0.5216 & 0.5000 \end{array} \right). $$

Finally, it is seen that all the consensus levels are determined and smaller than the threshold. The consensus reaching process is completed. Applying (16), one has ω1 = 0.2411, ω2 = 0.2923, ω3 = 0.2346, and ω4 = 0.2320. So the ranking of alternatives is x2 ≻ x1 ≻ x3 ≻ x4.

In order to make a comparison, some results are given in Table 2 by using the existing methods. It is seen from Table 2 that the optimal solution x2 is in accordance with the findings in [3, 15, 37]. Moreover, the ranking x2 ≻ x1 ≻ x4 ≻ x3 is in agreement with that in [37]. There exists a small difference for the ranking of x3 and x4 as compared to the results in [3, 15], which is attributed to the application of different consensus reaching processes.

Table 2 Comparison with the other methods for Example 1
Full size table

Example 2

It is seen that the proposed consensus model has been verified in Example 1. We further notice that an application to a practical case should be considered [17, 26, 37, 45]. Now let us investigate the practical problem about how to evaluate and select suitable locations for a shopping center in Istanbul, Turkey [26, 37, 45]. It is noted that the growth in population yields the spending demand in Istanbul [26]. This means that attractive shopping centers are requisite to match the requirements of people. An investor company wants to locate an appropriate shopping center by establishing strategies. Five experts are invited to provide decision information to evaluate six feasible locations xi(i = 1,2,⋯ ,6) [26]. By carefully comparing the six locations in pairs, the ACJMs are given as follows:

$$ {G}^{(1)}=\left( \begin{array}{cccccc} 0.50 & 0.40 & 0.20 & 0.60 & 0.70 & 0.60\\ 0.60 & 0.50 & 0.40 & 0.60 & 0.90 & 0.70\\ 0.80 & 0.60 & 0.50 & 0.60 & 0.80 & 1.00\\ 0.40 & 0.40 & 0.40 & 0.50 & 0.70 & 0.60\\ 0.30 & 0.10 & 0.20 & 0.30 & 0.50 & 0.30\\ 0.40 & 0.30 & 0.00 & 0.40 & 0.70 & 0.50 \end{array} \right), $$
$$ {G}^{(2)}=\left( \begin{array}{cccccc} 0.50 & 0.30 & 0.30 & 0.50 & 0.80 & 0.70\\ 0.70 & 0.50 & 0.40 & 0.70 & 1.00 & 0.80\\ 0.70 & 0.60 & 0.50 & 0.50 & 0.90 & 0.90\\ 0.50 & 0.30 & 0.50 & 0.50 & 0.60 & 0.70\\ 0.20 & 0.00 & 0.10 & 0.40 & 0.50 & 0.40\\ 0.30 & 0.20 & 0.10 & 0.30 & 0.60 & 0.50 \end{array} \right), $$
$$ {G}^{(3)}=\left( \begin{array}{cccccc} 0.50 & 0.50 & 0.60 & 0.60 & 0.70 & 0.90\\ 0.50 & 0.50 & 0.30 & 0.80 & 0.70 & 0.80\\ 0.40 & 0.70 & 0.50 & 0.70 & 0.70 & 0.80\\ 0.40 & 0.20 & 0.30 & 0.50 & 0.80 & 0.60\\ 0.30 & 0.30 & 0.30 & 0.20 & 0.50 & 0.20\\ 0.10 & 0.20 & 0.20 & 0.40 & 0.80 & 0.50 \end{array} \right), $$
$$ {G}^{(4)}=\left( \begin{array}{cccccc} 0.50 & 0.20 & 0.10 & 0.50 & 0.80 & 0.90\\ 0.80 & 0.50 & 0.20 & 0.90 & 0.60 & 1.00\\ 0.90 & 0.80 & 0.50 & 0.80 & 0.60 & 0.60\\ 0.50 & 0.10 & 0.20 & 0.50 & 1.00 & 0.80\\ 0.20 & 0.40 & 0.40 & 0.00 & 0.50 & 0.40\\ 0.10 & 0.00 & 0.40 & 0.20 & 0.60 & 0.50 \end{array} \right), $$
$$ {G}^{(5)}=\left( \begin{array}{cccccc} 0.50 & 0.30 & 0.30 & 0.70 & 0.80 & 0.50\\ 0.70 & 0.50 & 0.20 & 0.70 & 0.80 & 0.60\\ 0.70 & 0.80 & 0.50 & 0.70 & 0.70 & 0.80\\ 0.30 & 0.30 & 0.30 & 0.50 & 0.90 & 0.70\\ 0.20 & 0.20 & 0.30 & 0.10 & 0.50 & 0.40\\ 0.50 & 0.40 & 0.20 & 0.30 & 0.60 & 0.50 \end{array} \right). $$

The values of ACI are computed as ACI(G(1)) = 0.0789, ACI(G(2)) = 0.0730, ACI(G(3)) = 0.1193, ACI(G(4)) = 0.2033 and ACI(G(5)) = 0.1193. In terms of the threshold \(\overline {ACI}=0.1530,\) it is found that G(4) is unacceptable and should be revised to \({G}^{(4)}_{r}\) with acceptable additive consistency as:

$$ {G}^{(4)}_{r}=\left( \begin{array}{cccccc} 0.5000 & 0.2870 & 0.0244 & 0.5870 & 0.7213 & 0.9000\\ 0.7130 & 0.5000 & 0.1348 & 0.8601 & 0.6072 & 1.0000\\ 0.9756 & 0.8652 & 0.5000 & 0.7325 & 0.5957 & 0.6000\\ 0.4130 & 0.1399 & 0.2675 & 0.5000 & 0.9901 & 0.8000\\ 0.2787 & 0.3928 & 0.4043 & 0.0099 & 0.5000 & 0.4000\\ 0.1000 & 0.0000 & 0.4000 & 0.2000 & 0.6000 & 0.5000 \end{array} \right). $$

Making use of G(1), G(2), G(3), \({G}^{(4)}_{r}\) and G(5), the collective ACJM Gc is obtained by using (17) and λi = 0.2 (i = 1,2,3,4,5) as follows:

$$ {G}^{c}=\left( \begin{array}{cccccc} 0.5000 & 0.3574 & 0.2849 & 0.5974 & 0.7443 & 0.7200\\ 0.6426 & 0.5000 & 0.2870 & 0.7320 & 0.8014 & 0.7800\\ 0.7151 & 0.7130 & 0.5000 & 0.6465 & 0.7391 & 0.8200\\ 0.4026 & 0.2680 & 0.3535 & 0.5000 & 0.7980 & 0.6800\\ 0.2557 & 0.1986 & 0.2609 & 0.2020 & 0.5000 & 0.3400\\ 0.2800 & 0.2200 & 0.1800 & 0.3200 & 0.6600 & 0.5000 \end{array} \right). $$

Then the consensus levels can be computed as CL(G(1)) = 0.0816, CL(G(2)) = 0.0850, CL(G(3)) = 0.0814, \(CL(G^{(4)}_{r})=0.1374\) and CL(G(5)) = 0.0697, respectively.

In the following, let us still set the threshold of the consensus level as \(\overline {CL}=0.1\). One can see that \(G^{(4)}_{r}\) should be adjusted by (21). When choosing γ = 0.72, we obtain

$$ G^{(4)}_{1}=\left( \begin{array}{cccccc} 0.5000 & 0.3064 & 0.0960 & 0.5899 & 0.7276 & 0.8505\\ 0.6936 & 0.5000 & 0.1767 & 0.8249 & 0.6606 & 0.9395\\ 0.9040 & 0.8233 & 0.5000 & 0.7088 & 0.6351 & 0.6605\\ 0.4101 & 0.1751 & 0.2912 & 0.5000 & 0.9373 & 0.7670\\ 0.2724 & 0.3394 & 0.3649 & 0.0627 & 0.5000 & 0.3835\\ 0.1495 & 0.0605 & 0.3395 & 0.2330 & 0.6165 & 0.5000 \end{array} \right). $$

The consensus level is calculated as \(CL(G^{(4)}_{1})=0.0996\). Then, we determine the collective matrix \({G^{c}_{1}}\) as follows:

$$ {G^{c}_{1}}=\left( \begin{array}{cccccc} 0.5000 & 0.3613 & 0.2992 & 0.5980 & 0.7455 & 0.7101 \\ 0.6387 & 0.5000 & 0.2953 & 0.7250 & 0.8121 & 0.7679 \\ 0.7008 & 0.7047 & 0.5000 & 0.6418 & 0.7470 & 0.8321 \\ 0.4020 & 0.2750 & 0.3582 & 0.5000 & 0.7875 & 0.6734 \\ 0.2545 & 0.1879 & 0.2530 & 0.2125 & 0.5000 & 0.3367 \\ 0.2899 & 0.2321 & 0.1679 & 0.3266 & 0.6633 & 0.5000 \end{array} \right). $$

Furthermore, we give CL(G(1)) = 0.0761, CL(G(2)) = 0.0810, CL(G(3)) = 0.0840, \(CL(G^{(4)}_{1})=0.1071,\) and CL(G(5)) = 0.0712, respectively. It is noted that the matrix \(G^{(4)}_{1}\) should be adjusted and a new matrix is obtained as:

$$ G^{(4)}_{2}=\left( \begin{array}{cccccc} 0.5000 & 0.3110 & 0.1131 & 0.5906 & 0.7292 & 0.8387 \\ 0.6890 & 0.5000 & 0.1867 & 0.8165 & 0.6733 & 0.9251\\ 0.8869 & 0.8133 & 0.5000 & 0.7032 & 0.6445 & 0.6749\\ 0.4094 & 0.1835 & 0.2968 & 0.5000 & 0.9247 & 0.7591\\ 0.2708 & 0.3267 & 0.3555 & 0.0753 & 0.5000 & 0.3795\\ 0.1613 & 0.0749 & 0.3251 & 0.2409 & 0.6205 & 0.5000 \end{array} \right). $$

Hence, the collective matrix \({G^{c}_{2}}\) is determined as follows:

$$ {G^{c}_{2}}=\left( \begin{array}{cccccc} 0.5000 & 0.3622 & 0.3026 & 0.5981 & 0.7458 & 0.7077\\ 0.6378 & 0.5000 & 0.2973 & 0.7233 & 0.8147 & 0.7650\\ 0.6974 & 0.7027 & 0.5000 & 0.6406 & 0.7489 & 0.8350\\ 0.4019 & 0.2767 & 0.3594 & 0.5000 & 0.7849 & 0.6718\\ 0.2542 & 0.1853 & 0.2511 & 0.2151 & 0.5000 & 0.3359\\ 0.2923 & 0.2350 & 0.1650 & 0.3282 & 0.6641 & 0.5000 \end{array} \right). $$

Now it is found that all the consensus levels are smaller than the threshold and the consensus reaching process is completed. Applying (16), one has ω1 = 0.1709, ω2 = 0.2255, ω3 = 0.2775, ω4 = 0.1345, ω5 = 0.0871, and ω6 = 0.1045. For the sake of comparisons, some existing results are shown in Table 3. One can see that the ranking of alternatives are the same with x3 ≻ x2 ≻ x1 ≻ x4 ≻ x6 ≻ x5.

Table 3 Comparison with the other methods for Example 2
Full size table

5 Conclusions

In group decision support systems, it is important to finely manage individual decision information and reach a fast yet effective consensus. We suppose that a group of experts compare a set of alternatives in pairs and evaluate their opinions as the preference intensities with additively reciprocal property in this paper. The sequential model of additively pairwise comparisons is proposed to finely manage individual decision information. A novel additive consistency improving method has been offered by constructing a novel optimization model. A feedback mechanism is established such that the irrational and illogical individual decision behavior can be reminded. Under the control of individual consistency degree, a consensus model in GDM has been established. Some main findings are shown as follows:

  • The sequential model of ACPCs has been proposed to record the decision information and behavior of experts. The irrational and illogical judgements can be checked such that the DMs can be reminded in real time to adjust their opinions.

  • When individual ACJMs are of acceptable additive consistency, the collective one obtained by using the weighted averaging operator is with acceptable additive consistency.

  • The consensus of a group of experts can be reached under a fixed level by controlling the consistency degrees of individual judgements.

One can find that the proposed method has the advantage of reminding the DMs to give more rational judgements. It is further seen that the particle swarm optimization (PSO) is used to achieve a fast yet intelligent adjustment of individual inconsistent decision information. The disadvantage of the proposed method is that the consensus process should be run repeatedly for many times. In the future, the proposed model could be extended to solve large GDM problems and propose some decision making models with incomplete decision information.