1 Introduction

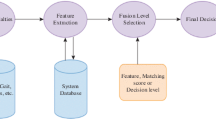
Single modal recognition systems are not always promising due to partial observability and data variability [3]. To compensate for this drawback, high performance recognition systems in a simultaneous manner collect data from different sources (e.g. audio and video) since none of them can solely characterize all input states [2, 5]. The main issue in multimodal systems is to develop an efficient fusion method to fuse the features from different modalities in order to enrich a discriminative feature set [1, 2, 4]. Fusion techniques are applied to several bimodal recognition systems like automatic audio-visual speech recognition [5], human computer interaction [6, 49], biometric systems [7, 51], video indexing [8], object tracking [9] and emotion recognition [10–12, 48].

Information fusion can take place at the decision [18] or feature levels [28]. At the decision level, elicited features of each modality are applied to a specific classifier and the final result is obtained through classifiers’ decision fusion. The well-known methods at this level are single winner, majority voting, Bayesian and Dempster-Shafer [29]. Nevertheless, decision fusion cannot take the correlation of modalities into account which reduces the performance of this approach compared to the feature fusion approach in a significant manner.

Though feature fusion methods are a bit complicated, they have the advantage of unveiling the implicit linear/nonlinear correlation among the sources. The feature fusion procedure is similar to that of the human brain, since data from different sensors (e.g. ears, eyes) are fused in the brain to draw an accurate decision. Since the neurons’ function is nonlinear, the brain fusion takes the benefit of nonlinear mapping. Observing the ability of the brain fusion encourages the research teams to develop mathematical methods for data fusion of different sources. In early feature fusion methods, features of different modalities were arranged in a high dimensional feature vector. In fact, no conceptual fusion was made except putting features beside each other and constructing a long vector. After feature fusion, these high dimensional vectors were fed to a classifier in order to assign a label to each vector.

The number of estimated parameters in some classification schemes like neural networks or Bayesian based classifiers depends on the feature size, that is, there exist, a direct relation between an increase in the number of features, and their computational complexity. In parametric classifiers the number of which depend on the input size have a serious problem in handling the datasets which contain low number of high dimensional samples. This problem is named small sample size (SSS) problem, and to solve it, a great volume of training data is necessary for a valid learning. One of the controversial issues in the multimodal recognition systems is the existence of statistical correlation among the features of different modalities. In one sense independency between modalities can diminish the redundancy and improve the recognition performance, and in the other, this correlation should not be observed as a negative factor, because it sometimes leads to a better data analysis, denoising and enhancement [12, 21, 24]. Besides the discussion of pros and cons of this correlation, it is better to estimate the statistical correlation among the features which are elicited from different sources. If this correlation is in a measured accurate manner the redundant features can be estimated; otherwise, even strong learners cannot consider all interactions among great number of features, hence a possible decrease in classifiers’ performance. For instance, during a certain activity in audio-visual recognition systems facial expression and speech signal affect each other, which lead to the availability of a degree of correlation [2, 5, 12, 13, 50].

Canonical correlation analysis (CCA) [14] is a well-known fusion method that elicits common features (latent variables) between two sets of feature vectors. In CCA, these sets are projected into a new domain, named correlation space. By maximizing the sets cross-correlation in this space, latent variables of two modalities are extracted to be applied to a classifier.

Cross-modal factor analysis (CFA) [15] is another linear statistical method for extracting latent features from two sources. CFA adopts a criterion which minimizes the Frobenius norm between two data streams in the transformed domain.

CCA and CFA are adopted in practical recognition systems such as face detection during talking [16], biometric [17, 18], audio-visual speaker detection [19] medical imaging [7, 47] and audio-visual synchronization [20].

To enable conventional fusion methods capture linear/ nonlinear dependencies, the nonlinear kernels are applied to project the features into the kernel space and then fuse them together. For this purpose, the kernel CCA (KCCA) [21] and kernel CFA (KCFA) [12] are introduced as the nonlinear versions of CCA and CFA respectively. They have been and are being applied in various data fusion applications like specific radar emitter identification [22], audiovisual biometric aliveness checking [23] and audiovisual emotion recognition [12]. Real applications involved in a high degree of variability cannot obtain promising results through the deterministic fusion methods, since during audio/video data recording some artificial and natural variations are inevitable. For instance, the authors in [12] applied KCCA to elicit the latent variables of audio and video modalities but their findings were not convincing.

To overcome the data variability, the authors in [24] proposed the probabilistic CCA (PCCA) method in order to digest this variability. Since PCCA is a linear method, it finds a linear projection, to map the data in the correlation space on which the variance is maximized [25–27].

Attempt is made here to propose the kernel version of PCCA (KPCCA) to capture both the dependencies and data variability in nonlinear correlation space. Although applying a nonlinear kernel increases the ability of fusion methods, the dimension of kernel matrix directly depends on the number of samples, that is provided that the number samples are low, the estimating of covariance matrix will be encountered by SSS problem; on the contrary provided that the number of samples are high, the dimension of kernel matrix increase.

The gradual evolution of KPCCA is assessed here by developing a sparse version of KPCCA (SKPCCA) which scarifies the elements of covariance matrix in order to avoid SSS problem. Here, SKPCCA solves the KPCCA problem at the cost of diminishing the rank of covariance matrix by a well-known sparse technique. The computational burden of SKPCCA is remarkably decreased compared to that of KPCCA.

In the final stage, a feature fusion method upon the framework of SKPCCA is proposed which seeks to fuse the latent variables of different modalities instead of just concatenate them together in a long feature vector in a conceptual sense. In this proposed method, the latent variables of the two modalities are unified into one vector with a size equal to the size of latent variable of the corresponding modality with numerous samples.

The remainder of this paper is organized as follows: the methods of identifying latent variables in the correlation space are explained in Section 2; the main proposed method with its major continuance component are introduced in Section 3; the applied datasets and the feature extraction techniques are discussed in Section 4; the empirical results and their comparisons with the state-of-the-art methods are presented in Section 5 and the article is concluded in Section 6.

2 Background methods

In a multimodal recognition system, instead of analyzing the data of each modality alone, the main concern is estimating a joint correlation subspace where the features (latent variables) can be extracted. There exist several fusion techniques for constructing this subspace; in this study only a few will be of concern.

2.1 CCA and KCCA methods

CCA [14] is known as the most famous statistical fusion method which finds a linear map for projecting features of two modalities in the correlation space in a manner that their cross-correlation is maximized. Given two feature sets of x and y, CCA estimates two linear projections W x and W y , respectively. These two projecting are named canonical correlation matrices which are determined by maximizing their cross-correlation in a manner that W x and W y become diagonal (compact) in the projected space.

To capture nonlinear correlations between two sources, CCA is equipped with kernel (KCCA) [21]. The optimization criterion of which is described as follows:

$$\begin{array}{@{}rcl@{}} {\underset{\alpha,\beta}{\max}}\frac{\boldsymbol{\alpha }^{T}\mathbf{K}_{\mathrm{x}}\mathbf{K}_{\mathrm{y}}\boldsymbol{\beta }}{\sqrt {\left[ \boldsymbol{\alpha }^{T}\mathbf{K}_{\mathrm{x}}\mathbf{K}_{\mathrm{x}}\boldsymbol{\alpha } \right]\left[ \boldsymbol{\beta }^{T}\mathbf{K}_{\mathrm{y}}\mathbf{K}_{\mathrm{y}}\boldsymbol{\beta } \right]} } \end{array} $$
(1)

where K x and K y are the kernel matrices of x and y, respectively.

The KCCA criterion is optimized through the generalized eigen-value decomposition method. When kernel functions are non-invertible, conventional regularization techniques are applied to convert (1) into (2) [30]:

$$\begin{array}{@{}rcl@{}} {\underset{\alpha,\beta}{\max}}\frac{\boldsymbol{\alpha }^{T}\mathbf{K}_{\mathrm{x}}\mathbf{K}_{\mathrm{y}}\boldsymbol{\beta }}{\sqrt {\left[ \boldsymbol{\alpha }^{T}\mathrm{(}\mathbf{K}_{\mathrm{x}}^{\mathrm{2}}\mathrm{ +\tau }\mathbf{K}_{\mathrm{x}}\mathrm{)}\boldsymbol{\alpha } \right]\left[ \boldsymbol{\beta }^{T}\mathrm{(}\mathbf{K}_{\mathrm{y}}^{\mathrm{2}}\mathrm{ +\tau }\mathbf{K}_{\mathrm{y}}\mathrm{)}\boldsymbol{\beta } \right]} } \end{array} $$
(2)

where 0≤τ≤1. The computation details of CCA and KCCA are expressed in Appendix IA.

2.2 CFA and KCFA methods

The cross-modal factor analysis (CFA) technique is proposed by [15]. In this technique, features are extracted from two modalities followed by determining two separate linear maps for projecting their features into the cross-modal space. The main difference between CFA and CCA is in their objective functions. CFA minimizes the Frobenius norm between the projected features while CCA maximizes their correlation.

CFA is capable of detecting linear relations between two feature sets while it suffers from the lack of capturing nonlinear correlations between them. Similar to KCCA, the kernelized version of CFA is introduced as KCFA by [12] in order to enhance its detection ability. In a similar manner, before applying CFA, the feature sets of two modalities are implicitly projected to the high dimensional kernel space, where the standard CFA is applied. To explain the KCFA routine the projected feature vectors in the cross-modal associated domain are computed as:

$$\begin{array}{@{}rcl@{}} \frac{1}{\sqrt {\boldsymbol{\alpha }_{j}^{T}\mathbf{K}_{\mathrm{x}}\boldsymbol{\alpha }_{j}} }\boldsymbol{\alpha }_{j}^{T}\left[ {\begin{array}{llll} K\left( x^{\prime},x_{1} \right) \\ K\left( x^{\prime},x_{2} \right) \\ \mathellipsis \\ K(x^{\prime},x_{n}) \\ \end{array}} \right] \end{array} $$
$$\begin{array}{@{}rcl@{}} \frac{1}{\sqrt {\boldsymbol{\beta }_{i}^{T}\mathbf{K}_{y}\boldsymbol{\beta }_{i}} }\boldsymbol{\beta }_{i}^{T}\left[ {\begin{array}{llll} K\left( y^{\prime},y_{1} \right) \\ K\left( y^{\prime},y_{2} \right) \\ \mathellipsis \\ K(y^{\prime},y_{n}) \\ \end{array}} \right] \end{array} $$
(3)

where α j and β i are the eigenvectors of K y K x and K x K y , respectively. Further details are expressed in Appendix IA

The main drawback of CCA, KCCA, CFA and KCFA is the absence of considering the uncertainty of input observations of x and y since no deterministic correlation space can be found for two sets of uncertain features.

2.3 Probabilistic CCA

To deal with the uncertainty problem of CCA, a probabilistic version of CCA (PCCA) is proposed by [24] where the projected latent variables provide maximum variance in the joint correlation space (Fig. 1). To insert this uncertainty parameter, they assigned a specific Gaussian function for each single source of data, which is expressed as:

$$\begin{array}{@{}rcl@{}} z&\sim&\mathcal{N}\left( {\mathrm{0,}I}_{d} \right)\mathrm{ \quad 1\le }d\mathrm{\le }\min \left( p\mathrm{,}q \right) \end{array} $$
$$\begin{array}{@{}rcl@{}} &&\mathbf{x\vert }z=\mathcal{N}\left( {z\mathbf{W}}_{x}^{T} +\mu_{x},\varphi_{x} \right) \end{array} $$
$$\begin{array}{@{}rcl@{}} &&\mathbf{y\vert }z=\mathcal{N}({z\mathbf{W}}_{y}^{T} +\mu_{y}, \varphi_{y}) \end{array} $$
(4)

where, z is the latent variable of the two modalities of x and y and μ and φ are the mean and covariance of each modality, respectively. They revealed that the posterior expectation of z given x and y is determined as follows [24]:

$$\begin{array}{@{}rcl@{}} {\varphi }_{x}&=&C_{xx}-\mathbf{W}_{x}\mathbf{W}_{x}^{T} \end{array} $$
$$\begin{array}{@{}rcl@{}} { \varphi }_{y}&=&C_{yy}-\mathbf{W}_{y}\mathbf{W}_{y}^{T} \end{array} $$
$$\begin{array}{@{}rcl@{}} E\left( z \vert \mathbf{x}\right) &=& \mathbf{x}\mathbf{W}_{x}M_{x}^{-1} , M_{x}=I+ \mathbf{W}_{x}^{T}\varphi_{x}^{-1}\mathbf{W}_{x} \end{array} $$
$$\begin{array}{@{}rcl@{}} E\left( z \vert \mathbf{y}\right) &=& \mathbf{y}\mathbf{W}_{y}M_{y}^{-1} , M_{y}=I+ \mathbf{W}_{y}^{T}\varphi_{y}^{-1}\mathbf{W}_{y} \end{array} $$
(5)

where W x and W y are the early d canonical directions of x and y and C x x and C y y are the covariance matrices of x and y respectively.

Fig. 1
figure 1

Graphical model for showing the relations of two modalities and its latent variable z[24]

Full size image

Another solution for (4) can be reached by applying the expectation maximization (EM) scheme [24]. This method provides a general solution for PCCA scheme which yields the following updated described in (6):

$$\begin{array}{@{}rcl@{}} \mathbf{W}_{\mathbf{t}\mathrm{\mathbf{+1}}}\!\!&=&\!\! C\mathrm{\varphi }_{t}^{\mathrm{-1}}\mathbf{W}_{\mathbf{t}}M_{t}^{\mathrm{-1}}\left( M_{t}^{\mathrm{-1}}\mathrm{+}M_{t}^{\mathrm{-1}}\mathbf{W}_{t}^{T}\mathrm{\varphi }_{t}^{\mathrm{-1}}C\mathrm{\varphi }_{t}^{\mathrm{-1}}\mathbf{W}_{\mathbf{t}}M_{t}^{\mathrm{-1}} \right)^{\mathrm{-1}} \end{array} $$
$$\begin{array}{@{}rcl@{}} \mathrm{\varphi }_{t+1}\!\!&=&\!\! \left( {\begin{array}{*{20}c} \left( C\,-\,C\mathrm{\varphi }_{t}^{-1}\mathbf{W}_{\mathbf{t}}M_{t}^{-1}\mathbf{W}_{t+1}^{T} \right)_{11} & 0\\ 0 & \left( C-C\mathrm{\varphi }_{t}^{-1}\mathbf{W}_{\mathbf{t}}M_{t}^{-1}\mathbf{W}_{t+1}^{T} \right)_{22}\\ \end{array} } \right)\\ \end{array} $$
(6)

where \(M_{t}\mathrm {=}I\mathrm {+ }\mathbf {W}_{t}^{T}\mathrm {\varphi }_{t}^{\mathrm {-1}}\mathbf {W}_{t}\).

3 Proposed method

The proposed method and its constituent components are presented in detail following a gradual evolution inflicted on PCCA.

3.1 The kernel PCCA (KPCCA)

Although PCCA performs well in finding linear correlations between two sets of x and y contaminated by the variability factors, its performance decreases when their correlation is nonlinear. To solve this problem, first the features are passed through nonlinear kernels of (ϕ(x) and ψ(y ) ), next, PCCA is applied to them in order to elicit the latent variables [31] (Fig. 2).

$$\begin{array}{@{}rcl@{}} &&z\mathrm{\sim \mathcal{N}}\left( {\mathrm{0,}I}_{d} \right) \end{array} $$
$$\begin{array}{@{}rcl@{}} \phi \left( \mathbf{x} \right)\mathbf{\vert }z&=&\mathcal{N}\left( {z\mathbf{W}}_{x}^{T} +\mu_{x},\varphi_{x} \right) \end{array} $$
$$\begin{array}{@{}rcl@{}} \psi (\mathbf{y})\mathbf{\vert }z&=&\mathcal{N}({z\mathbf{W}}_{y}^{T} +\mu_{y}\varphi_{y}) \end{array} $$
(7)

In KPCCA, similar to KCCA, W x and W y are determined through W x =ϕ(x)T α and W y =ψ(y)T β followed by implementing the procedure in Bach and Jordan method [4] to obtain the parameters. By inserting W x and W y into (5), the posterior expectation of parameters is estimated as:

$$\begin{array}{@{}rcl@{}} {\varphi }_{x}\!&=&\!{\phi \left( \mathbf{x} \right)}^{T}\left( I\,-\,\boldsymbol{\alpha }\boldsymbol{\alpha }^{T} \right)\phi \left( \mathbf{x} \right)\,=\,{\phi \left( \mathbf{x} \right)}^{T}\mathrm{\Omega }_{\mathrm{x}}\phi \left( \mathbf{x} \right) \end{array} $$
$$\begin{array}{@{}rcl@{}} {\varphi }_{y}\!&=&\!{\psi \left( \mathbf{y} \right)}^{T}\left( I\,-\,\boldsymbol{\beta }\boldsymbol{\beta }^{T} \right)\psi \left( \mathbf{y} \right)\,=\,{\psi (\mathbf{y})}^{T}\mathrm{\Omega }_{\mathrm{y}}\psi (\mathbf{y}) \end{array} $$
$$\begin{array}{@{}rcl@{}}E\left( z \vert \mathbf{x}\right) \!&=&\! \phi \left( \mathbf{x} \right){.[\phi \left( \mathbf{x} \right)}^{T}\boldsymbol{\alpha ]}M_{x}^{-1}\,=\,\mathbf{K}_{x}\boldsymbol{\alpha }M_{x}^{-1} , \end{array} $$
$$\begin{array}{@{}rcl@{}} M_{x}\!&=&\!I\!+ \boldsymbol{\alpha }^{T}\left( I\!-\boldsymbol{\alpha }\boldsymbol{\alpha }^{T} \right)^{-1}\boldsymbol{\alpha \,=\,}I+ \boldsymbol{\alpha }^{T}\left( \mathrm{\Omega }_{\mathrm{x}} \right)^{-1}\boldsymbol{\alpha } \end{array} $$
$$\begin{array}{@{}rcl@{}} E\left( z \vert \mathbf{y}\right) \!&=&\! \psi \left( \mathbf{y} \right){.[\psi \left( \mathbf{y} \right)}^{T}\boldsymbol{\beta ]}M_{y}^{-1}\,=\,\mathbf{K}_{y}\boldsymbol{\beta }M_{y}^{-1} , \end{array} $$
$$\begin{array}{@{}rcl@{}} M_{y}\!&=&\!I\,+\, \boldsymbol{\beta }^{T}\left( I\,-\,\boldsymbol{\beta }\boldsymbol{\beta }^{T} \right)^{-1}\boldsymbol{\beta =}I+ \boldsymbol{\beta }^{T}\left( \mathrm{\Omega }_{\mathrm{y}} \right)^{-1}\boldsymbol{\beta } \end{array} $$
(8)

where Ωx = I−α α Tand Ωy = I−β β T.

Fig. 2
figure 2

Graphical representation of the proposed method

Full size image

The general solution to estimate these transformation matrices is achieved by applying EM algorithm in (6). By inserting W x =ϕ(x)T α and W y =ψ(y)T β into (6), and by defining \(\mathrm {\pi }\left (\mathrm {\mathbf {O}} \right )=\left [ {\begin {array}{*{20}c} \phi \left (\mathbf {x} \right ) & \mathbf {0}\\ \mathbf {0} & \psi \left (\mathbf {y} \right )\\ \end {array} } \right ] \quad \mathbf {\gamma }=[ \boldsymbol {\alpha \beta }]^{T}\)and φ =π(O)TΩπ(O) (where \(\mathrm {\Omega =}\left [ {\begin {array}{*{20}c} \mathrm {\Omega }_{\mathrm {x}} & \mathbf {0}\\ \mathbf {0} & \mathrm {\Omega }_{\mathrm {y}}\\ \end {array} } \right ]\mathbf {)}\)and by assuming that K x and K y are invertible, (6) is yield:

$$\begin{array}{@{}rcl@{}} {\mathrm{\pi }\left( \mathrm{\mathbf{O}} \right)}^{T}\mathbf{\gamma }_{\mathbf{t}\mathrm{\mathbf{+1}}}\!\!&=&\!\!{\mathrm{\pi }\left( \mathrm{\mathbf{O}} \right)}^{T}\mathrm{[}\mathrm{\Omega }_{\mathrm{t}}^{\mathrm{-1}}\mathbf{\gamma }_{\mathbf{t}}M_{t}^{\mathrm{-1}}\left( M_{t}^{\mathrm{\!-1}}\mathrm{\!+}M_{t}^{\mathrm{\!-1}}\mathbf{\gamma }_{t}^{T}\mathrm{\Omega }_{\mathrm{t}}^{\mathrm{\!-1}}\mathrm{\Omega }_{\mathrm{t}}^{\mathrm{\!-1}}\mathbf{\gamma }_{\mathbf{t}}M_{t}^{\mathrm{\!-1}} \right)^{\mathrm{\!-1}}\mathrm{]} \end{array} $$
$$\begin{array}{@{}rcl@{}} { \varphi }_{t+1}\!\!&=&\!\!{\mathrm{\pi }\left( \mathrm{\mathbf{O}} \right)}^{T}\mathrm{\Omega }_{\mathrm{t+1}}\mathrm{\pi }\left( \mathrm{\mathbf{O}} \right) \end{array} $$
$$\begin{array}{@{}rcl@{}}\!\!&=&\!\!{\mathrm{\pi }\left( \mathrm{\mathbf{O}} \right)}^{T}\left( {\begin{array}{*{20}c} \left( I\,-\,\mathrm{\Omega }_{\mathrm{t}}^{\!-1}\mathbf{\gamma }_{\mathbf{t}}M_{t}^{\!-1}\mathbf{\gamma }_{t\,+\,1}^{T} \right)_{11} & 0\\ 0 & \left( I\,-\,\mathrm{\Omega }_{\mathrm{t}}^{\!-1}\mathbf{\gamma }_{\mathbf{t}}M_{t}^{\!-1}\mathbf{\gamma }_{t+1}^{T} \right)_{22}\\ \end{array} } \right)\\ &&\times\mathrm{\pi }\left( \mathrm{\mathbf{O}} \right) \end{array} $$
(9)

consequently, (9) can be modified into (10) as follow:

$$\begin{array}{@{}rcl@{}} \boldsymbol{\gamma }_{\mathbf{t}\mathrm{\mathbf{+1}}} \!&=&\!\mathrm{\Omega }_{\mathrm{t}}^{\mathrm{-1}}\boldsymbol{\gamma }_{\mathbf{t}}M_{t}^{\mathrm{-1}}\left( M_{t}^{\mathrm{-1}}\mathrm{+}M_{t}^{\mathrm{-1}}\boldsymbol{\gamma }_{t}^{T}\mathrm{\Omega }_{\mathrm{t}}^{\mathrm{-1}}\mathrm{\Omega }_{\mathrm{t}}^{\mathrm{-1}}\boldsymbol{\gamma }_{\mathbf{t}}M_{t}^{\mathrm{-1}} \right)^{\mathrm{-1}} \end{array} $$
$$\begin{array}{@{}rcl@{}} \mathrm{\Omega }_{\mathrm{t+1}}\!&=&\!\left( {\begin{array}{*{20}c} \left( I-\mathrm{\Omega }_{\mathrm{t}}^{-1}\boldsymbol{\gamma }_{\mathbf{t}}M_{t}^{-1}\boldsymbol{\gamma }_{t+1}^{T} \right)_{11} & 0\\ 0 & \left( I-\mathrm{\Omega }_{\mathrm{t}}^{-1}\boldsymbol{\gamma }_{\mathbf{t}}M_{t}^{-1}\boldsymbol{\gamma }_{t+1}^{T} \right)_{22}\\ \end{array} } \right)\\ \end{array} $$
(10)

The above equations illustrate the learning procedure of transformation matrices (α and β) applied for obtaining latent variables of both the modalities. It is obvious that if K x and K y are not invertible and the above equations would not be solved. An alternative solution is the regularization approach similar to KCCA [30]. In methods where a prior knowledge on W∼N(0,r −1 I s ) is considered, the regularization parameter r is determined by applying EM algorithm [27, 32]. Applying the described regularization method yield the following iterative solution for γ:

$$\begin{array}{@{}rcl@{}} \boldsymbol{\gamma }_{\mathbf{t}\mathrm{\mathbf{+1}}}&=&\mathrm{\Omega }_{\mathrm{t}}^{\mathrm{-1}}\boldsymbol{\gamma }_{\mathbf{t}}M_{t}^{\mathrm{-1}}\left( M_{t}^{\mathrm{-1}}\mathrm{+}M_{t}^{\mathrm{-1}}\boldsymbol{\gamma }_{t}^{T}\mathrm{\Omega }_{\mathrm{t}}^{\mathrm{-1}}\mathrm{\Omega }_{\mathrm{t}}^{\mathrm{-1}}\boldsymbol{\gamma }_{\mathbf{t}}M_{t}^{\mathrm{-1}}\right.\\ &&\hspace*{5pc}\left.\mathrm{+}r\lambda_{\mathrm{\varphi }}\lambda_{\mathbf{K}} \right)^{\mathrm{-1}} \end{array} $$
(11)

where λ φ = t r a c(φ) and λ K = t r a c(K x ) + t r a c(K y ).

3.2 The sparse KPCCA (SKPCCA)

In kernel based methods, the dimension of projected features in the kernel space (K x and K y ) is related to the number of data samples. When the dimension size is low, the full-covariance matrices of Ωx and Ωy can be estimated properly; otherwise, the covariance matrices cannot be estimated accurately due to limited number of samples. The innovative manner to solve this problem, where additional latent variables z x and z y are avoided in constructing high dimensional inputs are introduced by [25, 26]:

$$\begin{array}{@{}rcl@{}} &&z_{x}z_{y}z \sim \mathcal{N}\left( {0,I}_{d} \right) \end{array} $$
$$\begin{array}{@{}rcl@{}} \phi \left( \mathbf{x} \right)\mathbf{\vert }zz_{x}&=&\mathcal{N}\left( {z\mathbf{W}}_{x}^{T}+{z_{x}\mathbf{V}}_{x}^{T} +\mu_{x},{\sigma_{x}^{2}}I \right) \end{array} $$
$$\begin{array}{@{}rcl@{}} \psi (\mathbf{y})\mathbf{\vert }zz_{y}&=&\mathcal{N}({z\mathbf{W}}_{y}^{T}+{z_{y}\mathbf{V}}_{y}^{T} +\mu_{y}{\sigma_{Y}^{2}}I) \end{array} $$
(12)

where, \({\sigma _{I}^{2}}\) is the variance parameter and V x and V y are the two extra projection matrices for individual sources of x and y respectively. Here, by marginalizing z x and z y , a model similar to (11) is developed which generates the following full-rank covariance matrix: \(\mathrm {\Omega }_{i}=\mathbf {\nu }_{i}\mathbf {\nu }_{i}^{T}+{\sigma _{I}^{2}}I(\mathbf {V=}~{\mathrm {\phi }(\mathrm {i})}^{T}\mathbf {\nu }\) ). This model is able to solve the SSS problem [26] and for calculating the covariance matrices of Ωx and Ωy, it leads to a better estimation of the transform matrix γ. The pseudo code of SKPCCA is illustrated in Algorithm 1.

figure a

3.3 The new feature fusion method

Conventional feature fusion methods concatenate latent variables of two sources (Fig. 3a) and construct high dimensional feature vectors in the correlation space. These large-scale vectors are applied to a classifier. This procedure has two drawbacks: availability of redundancy between the modalities and not coping with large-scale feature vectors.

Fig. 3
figure 3

Fusion level approaches (a) Feature fusion (b) Decision fusion (c) Proposed fusion method

Full size image

To solve this dimensionality problem, a new feature fusion method is proposed which mathematically fuses latent variables of both the modalities into a unified lowdimensional feature vector (Fig. 3c).

To explain this method in a mathematically manner, conditional expectation of unified latent variables x and y is optimized according to [24]. By considering W x =ϕ(x)T α, and W y =ψ(y)T β, (13) is obtained:

$$\begin{array}{@{}rcl@{}} E\left( z \vert {\mathbf{x,y}}\right) \!\!&=&\!\!\left[ {\begin{array}{*{20}c} \mathbf{K}_{x}\mathbf{\alpha } & \mathbf{K}_{y}\boldsymbol{\beta }\\ \end{array} } \right]\!\left[ {\begin{array}{*{20}c} {(I-{P_{d}^{2}})}^{-1} &\! {(I-{P_{d}^{2}})}^{-1}P_{d}\\ {(I-{P_{d}^{2}})}^{-1}P_{d} &\! {(I-{P_{d}^{2}})}^{-1}\\ \end{array} } \right]\\ &&\times\left[ {\begin{array}{*{20}c} M_{x}^{-1}\\ M_{y}^{-1} \end{array} } \right] \end{array} $$
(13)

where, α and β are the two matrices applied in highdimensional concatenated features of x and y, in order to unify them at z, where, \(P_{d}=M_{x}^{-1}\ast \left (M_{y}^{-1} \right )^{T}\). A low-dimensional feature vector is obtained as the input classifier. The schematic of the above mentioned gradual evolution is illustrated in (Fig. 3c).

4 Real applications

Research findings in this field indicate that the fusion of information from acoustic and facial expression modalities improve the performance of both speech and emotion recognition systems [4, 5, 12]. Acoustic signals or video frames cannot provide a promising result on their own since each contains partial information on the subject during speaking. The variability factors affect the recording quality (e.g. noise, head pose etc.) reduce the recognition accuracy.

4.1 Speech recognition

The best descriptive audio signal feature is Cepstral coefficients [33], categorized as nonlinear features, elicited in short windows and represent the vocal tract state. Variants of the Cepstrum features include the popular Mel-Warped Cepstrum or Mel-frequency Cepstral Coefficients (MFCCs) [28] and the perceptual linear predictor (PLP) [34]. To extract the audio features, the additive background noise is eliminated [35] and the clean signals are divided into successive windows with the lengths are named as time frames. A windowing function, like Hamming, is usually applied to ongoing speech signals and the first 12 MFCC coefficients are extracted from each windowed signal.

In extracting informative features from lip motion of a subject, a proper detection method should be adopted in order to estimate lip contour in successive video frames. To detect lip contour, [33] proposed a method which partitions a given face image (colored image) into lip and non-lip regions based on the intensity and color features. By applying spatial fuzzy C-mean clustering to these features and simulating a simple geometric lip model, the lip contour reveals. The geometric lip model described by (14) is presented in Fig. 4.

$$\begin{array}{@{}rcl@{}} y_{\mathrm{1}}&=&h_{\mathrm{1}}\left( \left( \frac{x\mathrm{-}sy_{\mathrm{1}}}{w} \right)^{\mathrm{2}} \right)^{\mathrm{1+}\delta^{\mathrm{2}}}\mathrm{-}h_{\mathrm{1}} , \end{array} $$
$$\begin{array}{@{}rcl@{}} y_{\mathrm{2}}&=&\frac{\mathrm{-}h_{\mathrm{2}}}{\left( w\mathrm{-}x_{off} \right)^{\mathrm{2}}}\left( \left| x\mathrm{-}sy_{\mathrm{2}} \right|\mathrm{-}x_{off} \right)^{\mathrm{2}}\mathrm{+}h_{\mathrm{2}} \end{array} $$
(14)

where x∈[−w,w] at (0,0).

Fig. 4
figure 4

Geometric lip model

Full size image

After fitting the lip model on each image, a lip contour is characterized with six parameters (features), which are applied in successive frames, Fig 5.

Fig. 5
figure 5

Lip feature extraction

Full size image

Our audio-visual feature extraction process is drawn in Fig. 6.

Fig. 6
figure 6

Audio-Video feature extraction process for speech recognition

Full size image

4.2 Emotion recognition

To extract audio features, first the Hamming window is applied to the short time frame (512 samples) in order to preserve the stationary property of the signal. Successive windows have 50 % overlap. Next, the background noise is reduced by applying a threshold to the energy of wavelet coefficients in different scales and the ones with energy less than the threshold are removed and the signal is reconstructed again [35]. To obtain appropriate features, the pith period and the energy of the signal in each window [36] and spectral features (first 13 Mel-Frequency Cepstral Coefficients (MFCC)) [12, 37] are extracted. Finally, all extracted acoustic features on each time frame are arranged as a feature vector.

In each video frame, the features of facial expression are extracted from the face region. Since successive windowed signals have 50 % overlap something that the video frames, are without; the visual features are elicited from the nearest audio time. One challenge of feature extraction from each frame is to determine the accuracy rate of face region detection algorithm. In this article, the Haar cascade technique [38] is applied for the face detection.

Images of successive frames are all normalized into a frame size of 64×64 pixels.Gabor wavelet is very effective for describing spatial frequencies in images [39]. Accordingly, a Gabor filter bank with 5 scales and 8 orientations is used to extract the facial expression features [12, 40] which construct a very high dimensional feature vector. Thus, each sub-band of the sample is reduced to a size of 32×32 pixels followed by applying Principle Component Analysis (PCA) in them in order to reduce the number of features and elicit a rich feature set, as shown in Fig. 7.

Fig. 7
figure 7

Audio-Video feature extraction process for emotion recognition

Full size image

5 Experimental results

To evaluate the performance of the proposed algorithms, the following databases are applied: M2vts database [41] for audio visual speech recognition and eNTERFACE [42] and Ryerson (RML) databases [11] for audio visual emotion recognition.

The parameters of HMM classifiers are estimated in the cross-validation phase. The number of states is changed from 1 to 6 and the number of Gaussian components is changed from 1 to 5 within each state. The best HMM result for the speech datasets is achieved through 3 hidden states and 1 Gaussian mixture per state. Similarly, the best HMM results for the emotion recognition dataset are achieved through 6 hidden states and 3 Gaussian mixtures within each state. To find the variance parameter of Gaussian kernel, different values (σ= 2, 6, 10, 14, and 20) are evaluated where σ=14 for both applications has led to the best solution. The experiments are conducted by considering different values of the regularization parameter r ranged from 0.2 to 1.

5.1 Results on speech data

The audio-visual database (M2VTS) [41], contains 185 recordings of 37 subjects (12 females and 25 males) and provides 5 shots per person. During each shot, the subjects are asked to count from ‘0’ to ‘9’ and their audio and video data is recorded by the sampling rate of 48 KHz and frame rate of 25Hz, respectively. In this database, the speaker dependent recognition rate is applied to deal with high complexity and memory requirements of kernel methods.

The experimental results for audio-visual speech recognition accuracy using MFCC and PLP acoustic features for feature fusion and decision fusion, are shown in Figs. 8 and 9, respectively. In this proposed algorithm, the dimension sizes 1, 2 and 3 are of concern for ν space. The results obtained from the tests indicate that for ν=3, the best result is achieved. It is observed that in lower dimensions, KPCCA provides better results than KCCA, KCFA and SKPCCA because it can estimate a fullcovariance matrix representing all information about the residual dimensions. Evidently, KPCCA provides similar results to SKPCCA in highdimensions.

Fig. 8
figure 8

Experimental results of Feature Fusion method. Top Left: M2vts database with MFCC features on KCCA and KCFA methods. Top Right: M2vts database with MFCC features on KPCCA and SKPCCA methods. Bottom Left: M2vts database with PLP features on KCCA and KCFA methods. Bottom Right: M2vts database with PLP features on KPCCA and SKPCCA methods

Full size image
Fig. 9
figure 9

Experimental results of Decision Fusion method. Top Left: M2vts database with MFCC features on KCCA and KCFA methods. Top Right: M2vts database with MFCC features on KPCCA and SKPCCA methods. Bottom Left: M2vts database with PLP features on KCCA and KCFA methods. Bottom Right: M2vts database with PLP features on KPCCA and SKPCCA methods

Full size image

5.2 Results on emotion data

Emotion databases (eNTERFACE and RML) consist of six basic human prototypical emotions (anger, disgust, fear, happy, sad and surprise) [43, 44]. The eNTERFACE database contains 44 subjects who showing 5 believable reactions to each emotion with the acoustic sampling rate of 48 KHz and visual frame rate of 25. Ryerson database contains 8 subjects, speaking 6 languages that generate 3 believable reactions to all the situations with acoustic sampling rate of 22050 Hz, and visual frame rate of 30. In eNTERFACE and RML datasets, each sample is truncated to 2 and 1.2-second-long, respectively, and divided into 10 segments. The dimensionality of the audio and visual features is empirically set to 200. To overcome the high complexity and memory requirements of kernel methods, 10 subjects are randomly selected for each experiment. These subjects are divided in two sets: 70 % for training 30 % for testing. This process is repeated 10 times, and the average results are presented in Figs. 10 and 11.

Fig. 10
figure 10

Experimental results of Feature Fusion method. Top Left: eNTERFACE on KCCA and KCFA methods. Top Right: eNTERFACE on KPCCA and SKPCCA methods. Bottom Left: RML on KCCA and KCFA methods. Bottom Right: RML on KPCCA and SKPCCA methods

Full size image
Fig. 11
figure 11

Experimental results of Decision Fusion method. Top Left: eNTERFACE on KCCA and KCFA methods. Top Right: eNTERFACE on KPCCA and SKPCCA methods. Bottom Left: RML on KCCA and KCFA methods. Bottom Right: RML on KPCCA and SKPCCA methods

Full size image

The emotion recognition accuracy of the conventional methods together with this proposed method for eNTERFACE and Ryerson (RML) databases are presented in Figs. 10 and 11. In SKPCCA the different dimension sizes are considered at 0, 25, 50 and 100 for the ν space and the results indicate that for ν=50, the best result is achieved.

Although KPCCA provides proper results when handling low dimensional data, it cannot perform well when encountering high dimensional inputs. This deficiency arises from the estimation of great number of parameters (fullcovariance Ω) with small number of train samples. It is observed that SKPCCA outperforms KCCA, KCFA and KPCCA due to estimating a low rank (sparse) covariance matrix in highdimensional space with adequate number of samples.

5.3 The results of the proposed FF-SKPCCA method

As explained before, the conventional feature fusion methods synchronously concatenate latent variables of audio and visual modalities (Fig. 3a) which might lead to the curse of dimensionality problem. For example, in RML database which contains low reactions of each situation, the number of samples is not enough for the training phase; therefore, a decrease is expected in the results when conventional feature fusion methods are applied (Fig. 10).

To solve the above mentioned problems, the proposed feature fusion for KPCCA is applied to RML and other datasets. According to Figs. 12 and 13, it is observed that this proposed method overcomes both the problems of redundant features and curse of dimensionality, in comparison with the conventional feature fusion methods (Figs. 8 and 10). This proposed FF-SKPCCA reveals that fusion of latent variables into a unified set, instead of concatenating them, can generate informative and lowdimensional feature vectors for describing the subjects’ state.

Fig. 12
figure 12

Experimental results of New Fusion method. Top Left: M2vts database with MFCC features. Top Right: M2vts database with PLP features. Bottom Left: eNTERFACE database. Bottom Right: RML database

Full size image
Fig. 13
figure 13

Comparison overall recognition accuracy between KCCA, KCFA, KPCCA, SKPCCA and FF-SKPCCA. Top Left: M2vts database with MFCC features. Top Right: M2vts database with PLP features Bottom Left: eNTERFACE database. Bottom Right: RML database

Full size image

The recognition accuracy of all conventional and proposed methods for emotion databases (eNTERFACE and RML) and speech database (M2vts with MFCC and PLP acoustic features) are demonstrated in Fig. 13. To make a fair comparison, maximum accuracy in each dimension for regularization parameters is shown. It is observed that at lowdimensions, FF-SKPCCA method does not provide proper results, in contrast when input dimension increases, this algorithm improves the performance considerably. In fact fusing different feature vectors is totally different from concatenating them; because by increasing both the number of modalities and the number of features, the recognition accuracy declines. Thus, FF-SKPCCA is designed to conceptually fuse the latent variables from different modalities instead of concatenating them, which leads to a reduction in both the redundancy and curse of dimensionality.

To have a better comparison among these methods, their results for each emotion class (eNTERFACE and RML contain 6 classes) and speech class (M2vts contain 10 classes) are illustrated in bar-charts in Fig. 14. Note that, for both the emotion datasets, the FF-SKPCCA in average provides better performance than the conventional methods. However, regarding M2vts database, the FF-SKPCCA outperforms the compared methods for all cases significantly by improving the speech recognition accuracy in a significant manner.

Fig. 14
figure 14

Comparison between KCCA, KCFA, KPCCA, SKPCCA and FF-SKPCCA. Top Left: M2vts database with MFCC features. Top Right: M2vts database with PLP features. Bottom Left: eNTERFACE database. Bottom Right: RML database

Full size image

6 Conclusion

Information fusion systems are in their infancy with respect to artificial intelligence. Naturally, they encounter different problems like coping with input variability, lack of detecting nonlinear dependencies and sensitivity to high dimensional inputs. To overcome these drawbacks, an almost coverall fusion algorithm for bimodal emotion and speech recognition systems is developed mathematically. This newly introduced KPCCA method provides good results on low-dimensional inputs but its performance is not sufficient for high dimensional ones. SKPCCA is capable of better handling high-dimensional inputs when the covariance matrix is sparse and its results on the emotion datasets confirm this claim. FF-SKPCCA, by fusing the latent variables of two modalities and generate a low-dimensional set of latent variables solves the problems of redundancy and curse of dimensionality. Experimental results on several datasets demonstrated that FF-SKPCCA outperforms its counterparts in most cases.