1 Introduction

The network is ubiquitous. Network facilitates us with enormous convenience to better communicate with others. Network is changing our daily life unprecedentedly. The term “network” here mainly refers to the mobile communication networks. Besides the communication networks, there are a lot of other networks in real life, such as the power or the traffic transportation networks, the metabolic networks, etc. To do research on these complex networks is of great importance from the perspective of theoretical analysis and real applications.

A direct way to analyze complex networks is to represent networks by graphs. A graph is comprised of a set of nodes and edges. The nodes represent the objects that consist of the networks and the edges denote the relations among the objects. By analyzing the characteristics of a graph one can get to know the properties of a network. Networks have many famous properties, such as the small-world property [26], the scale-free property [2], etc., and among them the network community structure property [10] has been proved to be an eminent one. The network community property is in accordance with the Chinese old saying that “birds of a feather flock together”. A feather is like a community. In graph language, a community is referred to as a subgraph which holds the condition that within a community the similarities between the nodes are high while between different communities the similarities are low.

The community structure is very important for many networks. Consequently, to discover the community structures of complex networks has aroused great interests of scholars. So far, a large amount of methods have been proposed to detect the community structures of networks [8, 15, 23, 28]. One of the landmark contribution should owe to Girvan and Newman for their work in [10]. In their work, the modularity index has been put forward. The modularity index has been widely used to evaluate the goodness of a network partition. Following this work, many methods based on the modularity index have been cranked out [8]. The essence of community discovery is a clustering problem and a clustering problem can be effectively solved by heuristic optimization methods. With respect to this, a massive amount of creative works based on heuristic optimization algorithms have been done [5, 8]. To solve the signed network community detection problem, Cai et al. in [4] have proposed a particle swarm optimization algorithm which aims to maximize the signed modularity index [11]. However, the modularity based index exists the resolution limitation [9], i.e., by purely optimizing the modularity based index one cannot discover small communities whose sizes are smaller than a scale which depends on the total size of the network and on the degree of inter connectedness of the community. Apart from this, each sigle run of the algorithm in [4] can only produce one network community structure which is inconvenient for the decision maker. To avoid these two drawbacks, Gong et al. in [12] have put forward a state-of-the-art multiobjective discrete particle swarm optimization (MODPSO) algorithm for complex network clustering. Although the MODPSO algorithm is quite promising for community discovery, its search ability still needs improvement from the viewpoint of multiobjective optimization. Besides, from the viewpoint of network community discovery, the established optimization model also can be improved.

In this paper, to better solve the problem of community discovery from signed networks, a novel algorithm based on multiobject particle swarm optimization is newly proposed. The main contributions of this paper are as follows:

  1. 1.

    A new multiobjective optimization model is suggested for the signed network community discovery problem. The newly proposed model is based on the link density of a node. By optimizing the model one can ensure that both the positive link density within a community and the negative link density between different communities are big, which is in accordance with the signed community property.

  2. 2.

    A novel multiobject particle swarm optimization (MOPSO) algorithm based on the decomposition strategy is developed to solve the established multiobjective optimization model. In the newly developed algorithm, an efficient subproblem update strategy is proposed to enhance population diversity.

  3. 3.

    Extensive experiments compared against several state-of-the-art signed network community discovery algorithms are carried out. The experiments demonstrate that the proposed optimization model is effective and the devised subproblem update strategy does improve the performance of the proposed algorithm for signed network community discovery.

The rest of the paper is organized as follows. Section 2 gives the related backgrounds including the statement of the network community discovery problem and the brief introduction of MOPSO. Section 3 presents the proposed algorithm for network clustering in detail. Section 4 shows the experimental studies of the proposed method, and the conclusions are finally drawn in Section 5.

2 Related backgrounds

2.1 Problem description

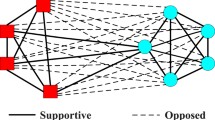
A signed network is normally represented by a signed graph that is comprised of a set of nodes and edges. The edges contain two types, the positive edges and the negative edges. The task of signed network community detection is to divide a signed network into different clusters based on certain principles. Each cluster is called a community. Fig. 1 shows an example of a signed network with 9 nodes and 16 edges.

Fig. 1
figure 1

A graphical illustration of a an example of a signed network, b an example of the corresponding community structure

Full size image

Currently, there is no uniform definition of what a community is. In academic domain, a community is regarded as a subset of a network that holds the condition that the similarities within a community are big while the similarities between different communities are small.

Gong et al. in [12] gave a condition that a signed community should satisfy. Given a signed network modeled as G=(V,P L,N L), where V is the set of nodes and PL and NL are the sets of positive and negative links, respectively. Let A be the adjacency matrix of G and l i j be the link between nodes i and j.

Given that S⊂G is a subgraph where node i belongs to. Let \((d_{i}^{+})^{in}={\sum }_{j\in S,l_{ij}\in PL}A_{ij}\) and \((d_{i}^{-})^{in}={\sum }_{j\in S,l_{ij}\in NL}|A_{ij}|\) be the positive and negative internal degrees of node i, respectively. Then S is a signed community in a strong sense if

$$ \forall i\in S,\quad (d_{i}^{+})^{in}>(d_{i}^{-})^{in} $$
(1)

Let \((d_{i}^{-})^{out}={\sum }_{j\notin S,l_{ij}\in NL}|A_{ij}|\) and \((d_{i}^{+})^{out}={\sum }_{j\notin S,l_{ij}\in PL}A_{ij}\) be the negative and positive external degrees of node i, respectively. Then S is a signed community in a weak sense if

$$ \left\{ \begin{array}{l} {\sum}_{i\in S}(d_{i}^{+})^{in}>{\sum}_{i\in S}(d_{i}^{+})^{out}\\ {\sum}_{i\in S}(d_{i}^{-})^{out}>{\sum}_{i\in S}(d_{i}^{-})^{in} \end{array}\right. $$
(2)

The above condition indicates that, in a strong sense, a node has more positive links than negative links within the community; in a weak sense, the positive links within a community and the negative links between different communities are all dense.

As can be seen from Fig. 1 that the task of community discovery from a signed network is to separate the whole network into many communities. However, how to evaluate the goodness of a separation is still an open issue.

For a signed network, in order to give a quantitative standard to a signed community structure, Gómez et al. in [11] presented a reformulation of the modularity metric which was originally proposed by Girvan and Newman [10]. The reformulated index is called the signed modularity (SQ) which reads:

$$ SQ\,=\,\frac{1}{2w^{+}\,+\,2w^{-}}\sum\limits_{i,j}\left( \!w_{ij}\,-\,\left( \!\frac{w_{i}^{+}\!w_{j}^{+}}{2w^{+}}\,-\, \frac{w_{i}^{-}\!w_{j}^{-}}{2w^{-}}\!\right)\!\right)\!(\delta(i,j) $$
(3)

where w i j is the weight of the signed adjacency matrix, \(w_{i}^{+}(w_{i}^{-})\) denotes the sum of all positive (negative) weights of node i. If nodes i and j are in the same group, δ(i,j)=1, otherwise, 0. Normally by assumption we take it that the larger the value of SQ is, the better the separation of the community structure is.

2.2 Multiobjective particle swarm optimization

Particle swarm optimization (PSO) is a well known stochastic searching algorithm. PSO has been widely applied to solve a wide range of hard optimization problems [18]. PSO is an eminent optimization technique among the swarm intelligence algorithms which are originated from the social behaviors such as fish schooling and birds flocking. It was first proposed by Eberhart and Kennedy [13] in 1995.

PSO is also a population based algorithm. It optimizes a problem by having a swarm of individuals each of which is called a particle. Each particle has a position and a velocity vector. The position represents a candidate solution to the optimization problem. The velocity denotes the tendency for one particle to change its current position. The flight status of a particle is updated by simple rules.

Given that the size of the particle swarm is pop and the dimension of the search space is n. Let V i ={v i1,v i2,…,v i n } and X i ={x i1,x i2,…,x i n } be the ith (i=1,2,...,p o p) particle’ velocity and position vectors, respectively. Then the rules for particle i to adjust its status are as the following:

$$ \boldsymbol{V}_{i}\leftarrow\boldsymbol{V}_{i}+c_{1}r_{1}(\boldsymbol{P}_{i}-\boldsymbol{X}_{i})+c_{2}r_{2} (\boldsymbol{G}-\boldsymbol{X}_{i}) $$
(4)
$$ \boldsymbol{X}_{i}\leftarrow\boldsymbol{X}_{i}+\boldsymbol{V}_{i} $$
(5)

where P i ={p i1,p i2,…,p i n } is the ith particle’s personal best position and G={g 1,g 2,…,g n } is the best position of the swarm. Parameter c 1 and c 2 are the learning factors, and r 1,r 2∈[0,1] are two random numbers.

It can be seen from the above descriptions that the canonical PSO is designed for continuous optimization problems. Many efforts have been made to extend the basic PSO into discrete contexts, and many discrete PSO (DPSO) algorithms have been proposed [1, 6, 14, 20]. In real applications, many optimization problems involve more than one optimization objective. These problems are the so called multiobjective optimization problems (MOPs). In order to solve MOPs, multiobjective PSO (MOPSO) algorithms have emerged. In the existing literatures, the framework of a general MOPSO is shown in Fig. 2.

Fig. 2
figure 2

Pseudocode of a general MOPSO algorithm

Full size image

Most of the existing MOPSOs apply some sort of mutation operator to promote diversity after performing the flight. It is obvious that the scheme of the basic PSO has to be modified if we want to apply PSO to MOPs, because for a MOP, we aim to find a set of different solutions. With respect to the leaders selection, the straight forward method is random selection, but it is not good to guide the flight. Another most simple approach is to adopt aggregating functions (i.e., weighted sums of the objectives) or approaches that optimize each objective separately. Other techniques based on the concept of Pareto optimality can also be utilized as a selection method, such as the density measure [7].

3 Proposed method for signed network community discovery

3.1 Framework of the proposed algorithm

Considering that the positive links within a signed community and the negative links between different communities should be dense, we separately model the two conditions as two objectives and consequently, a bi-objective optimization model is newly established in this paper. Let C={c 1,c 2,...,c k } be a network partition where k is the number of communities. The two objectives are shown as the following:

$$ \min\, F(\cdot)\left\{ \begin{array}{c} f_{1}=-\sum\limits_{i=1}^{k}\frac{L^{+}(c_{i},c_{i})-L^{+}(c_{i}, \overline{c_{i}})}{|c_{i}|}\\ f_{2}=-\sum\limits_{i=1}^{k}\frac{L^{-}(c_{i},\overline{c_{i}})-L^{-}(c_{i},c_{i})}{|c_{i}|} \end{array}\right. $$
(6)

where \(L^{+}(c_{i},c_{j})={\sum }_{i\in c_{i},j\in c_{j}}A_{ij},(A_{ij}>0)\), \(L^{-}(c_{i},c_{j})={\sum }_{i\in c_{i},j\in c_{j}}|A_{ij}|,(A_{ij}<0)\), and \(\overline {c_{i}}=C-c_{i}\).

In the proposed optimization model, to minimize f 1 we can maximize the positive links within a signed community while to minimize f 2 we can maximize the negative links between different communities.

In order to minimize these two objectives simultaneously, decomposition strategy is employed to decompose the optimization problem into many scalar optimization problems. Because in this paper the two objectives are discrete, what is more, it is hard to decide whether they are concave or not. Based on these, the Tchebycheff approach is adopted in our algorithm to decompose the multiobjective optimization problem into scalar optimization problems. The Tchebycheff decomposition technique is written as:

$$ \begin{array}{c} g^{te}(\boldsymbol{x}|\boldsymbol{w},\boldsymbol{z}^{*})=\max_{1\leq i\leq k}w_{i}|f_{i}(\boldsymbol{x})-z_{i}^{*}|\\ subject\, to\,\boldsymbol{x}\in{\Omega} \end{array} $$
(7)

where \(\boldsymbol {z}^{*}=(z_{1}^{*},z_{2}^{*},\cdots ,z_{k}^{*})\) is the reference point \(z_{i}^{*}=\{\min f_{i}(\boldsymbol {x})|\boldsymbol {x}\in {\Omega }\}\).

Algorithm 1 shows the framework of the proposed algorithm (denoted by PSOSCD) for signed network community discovery. In step 2 and step 12, we have developed a position repair operation which aims to save computational time. The detailed operations are shown in Section 3.4. In step 11, in order to better preserve population diversity, in this paper we have devised a novel replacement strategy to update the neighboring subproblems of x i . The detailed operations are shown in Section 3.5.

figure b

3.2 Particle coding/decoding scheme

A particle represents a solution to the optimization problem. The update rules in (4) and (5) are for the particles to reproduce offspring solutions. For the community detection problem, this paper adopts the string based coding scheme in which the position vector of a particle is an integer permutation while the veloity vector is a binary coded permutation. The adopted representation schema is shown in Fig. 3.

Fig. 3
figure 3

A schematic illustration of the string based particle representation schema

Full size image

It can be seen from the figure that the string based coding scheme is direct and it is easy to decode. What most important is that this kind of scheme does not need to specific the community size in advance.

3.3 Particle update rules

From Fig. 3 we can notice that the (4) and (5) no longer fit for the community detection problem. In this paper we have redefined (4) and (5). The redefined rules are shown as follows:

$$ \boldsymbol{V}_{i}\leftarrow\varphi(\omega\boldsymbol{V}_{i}+c_{1}r_{1}(\boldsymbol{P}_{i}\cap\boldsymbol{X}_{i})+ c_{2}r_{2}(\boldsymbol{G}\cap\boldsymbol{X}_{i})) $$
(8)
$$ \boldsymbol{X}_{i}\leftarrow\boldsymbol{X}_{i}\cup\boldsymbol{V}_{i} $$
(9)

In the above equations, the symbol “ ∩” is the XOR operator. The function φ(t) is defined as follows:

$$ \varphi(t)=\left\{ \begin{array}{ccc} 1 & if & rand(0,1)\leq1/(1+e^{-t})\\ 0 & if & rand(0,1)>1/(1+e^{-t}) \end{array}\right. $$
(10)

The operation rule for the symbol “ ∪” in (9) is defined in the following way:

$$ \left\{ \begin{array}{l} X_{i}\circleddash V_{i}=X_{i}^{\prime}=\{x_{i1}^{\prime},x_{i2}^{\prime},...,x_{in}^{\prime}\}\\ x_{ij}^{\prime}=x_{ij}\,\,\, if\,\,\, v_{i}=0\\ x_{ij}^{\prime}=\arg\max_{r}{\sum}_{k\in N_{j}}\delta(x_{ik},r)\,\,\, if\,\,\, v_{i}=1 \end{array}\right. $$
(11)

where N j is the neighbor set of node j. If a=b, δ(a,b)=1, otherwise, 0.

Figure 4 graphically depicts the detailed operations of the update rules. It can be seen that the particle status update rules make use of the topology information of a signed network, which makes the proposed algorithm feasible for addressing the community discovery task.

Fig. 4
figure 4

A graphical illustration of the operations of the update rules

Full size image

3.4 Position repair

From the coding system described above one may notice a phenomenon that two different position vectors may correspond to the same network community structure. Figure 5 shows an example of this phenomenon.

Fig. 5
figure 5

An example of two different position vectors that correspond to the same network community structure

Full size image

In Fig. 5, X i and P i are the ith particle’s current and historically best positions respectively. After decoding, X i and P i represent the same network community structure. Based on (8) and (9) we will get a non-zero vector V i , and X i will be changed which takes time. In order to save computational time, we have devised a position repair operation whose pseudocodes are shown in Algorithm 2.

figure c

As shown in Fig. 5, after we repair the position, X i and P i become the same and based on (8) a zero vector is obtained. Then there is no need to compute the new position vector and the computational time is saved.

3.5 Replacement operation

The replacement operation aims to replace the subproblems with better offspring solutions. In this paper, in order to better preserve population diversity, we have proposed a novel subproblems update strategy. Given that \(\boldsymbol {x}_{i}^{t+1}\) is a newly generated solution, in our proposed update strategy, only T subproblems are updated. The pseudocode of the proposed strategy is shown in Algorithm 3.

figure d

The parameter T cannot be to large. On one hand, if T is too big, it will cost a lot of computational time. On the other hand, since T subproblems will be replaced by the newly generated good individual, if T is too big, the population diversity will decrease immediately.

4 Experimental testing

4.1 Experimental settings

In this part, the proposed PSOSCD algorithm will be tested on both benchmark signed networks and real-world signed networks. Several state-of-the-art signed network community discovery methods have been selected to compare with the proposed approach. The proposed algorithm is coded in C++, and the experiments are carried out on an Inter(R) Celeron(R)M CPU 550 machine, 3.2GHz, with 4GB memory.

The comparison methods are the MODPSO algorithm [12] and the MOEA-SN algorithm [3]. For all the algorithms, the population size pop, and the maximal algorithm iteration number gmax are all set to 200. The crossover and mutation possibilities are set to 0.8 and 0.2, respectively. In PSOSCD, the learning factors c 1 and c 2 are both set to 1.494, and the inertia weight ω is set to 0.729.

In order to estimate the similarity between the true network partition and the discovered one, the widely used Normalized Mutual Information (NMI) metric [27] is adopted. Given that A and B are two partitions of a network, then the NMI between A and B is written as:

$$ NMI=\frac{-2{\sum}_{i=1}^{C_{A}}{\sum}_{j=1}^{C_{B}}C_{ij}log(C_{ij}N/C_{i.}C_{.j})}{{\sum}_{i=1}^{C_{A}}C_{i.} log(C_{i.}/N)+{\sum}_{j=1}^{C_{B}}C_{.j}log(C_{.j}/N)} $$
(12)

where N is the number of nodes of the network, C is a confusion matrix. C i j equals to the number of nodes shared in common by community i in partition A and by community j in partition B. C A (or C B ) is the number of clusters in partition A (or B), C i. (or C .j ) is the sum of elements of C in row i (or column j). If N M I(A,B)=1, then we say that A and B are the same.

4.2 Testing on synthetic signed networks

Lancichinetti et al. in [17] have cranked out the so called LFR model for generating unsigned benchmark networks for testing purpose. In this paper, this model has been extended to generate signed benchmark networks. The extended model is denoted by S N(n,k a v g ,k m a x , γ,β,s m i n ,s m a x ,μ,p−,p+). By tuning the parameters in SN we can control the structure of the generated network. The meanings of the parameters are listed in Table 1.

Table 1 Meanings of the parameters in the extended LFR model for generating signed benchmark networks
Full size table

In this paper, we have generated 216 benchmark networks to test the performance of the proposed algorithm. Table 2 lists the parameters for the generated benchmark networks.

Table 2 Parameter settings for the 216 generated signed benchmark networks
Full size table

Because the real community structures of the benchmark networks are known, we use the NMI index to evaluate the performance of the algorithms. For the benchmark networks, we run the proposed algorithm and the comparison algorithms for 30 times and the averaged NMI values are recorded.

Figure 6 shows the averaged NMI values for the 216 signed benchmark networks. When the parameter μ increases, then the links within a community will be less, consequently the community structure becomes more and more vague, and it is harder and harder for an algorithm to detect the ground truths of the benchmark networks.

Fig. 6
figure 6

Averaged NMI values for the 216 signed benchmark networks

Full size image

The structure of each signed network is mainly decided by the parameters μ, p−, and p+. If μ is bigger than 0.5, then there is hardly community structure in the network. Since we limit the range of μ from 0 to 0.5, consequently the network structure is mainly decided by the parameters p− and p+. From Fig. 6 we can see that when p− is small, the obtained NMI values are high, close to or equal 1. With p− increases, the negative edges within a community is becoming denser, i.e., the community structure is becoming vague which makes it difficult for any methods to discover the community structures. Reflected in the figure, the NMIvalues decrease.

The experiments on the extended LFR signed benchmark networks indicate that the proposed algorithm works well on the benchmark networks. In the next subsection we are going to show the performances of the proposed algorithm on real-world signed networks.

4.3 Testing on real-world signed networks

Six real-world signed networks have been employed to test the community discovery performances of the proposed algorithm and the comparison algorithms. The statistics of each network are given in Table 3.

Table 3 Statistics of the signed networks. E + and E − denote the positive and negative edges, respectively
Full size table

In Table 3, the real community structures of the SPP and the GGS network are known. In our experiments, each of the algorithm has been independently tested for 30 times.

4.3.1 Impact of the parameter T

In our proposed subproblem update operation, there is a parameter T which affects the performance of our proposed algorithm. In this part we will test its impact.

Because different values of parameter T will lead to different Pareto fronts, since the true Pareto front for each network is unknown, in order to evaluate the goodness of the Pareto front yielded by the proposed algorithm, we adopt the hypervolume index (HI) [29] which calculates the area of the space covered by the Pareto front. The HI index, also known as the S metric or the Lebesgue measure, is calculated as follows:

$$ \text{HI}(PS,\boldsymbol{y}_{ref})=\mathcal{L}\left( \cup_{\boldsymbol{y}\in PS}\left\{ \boldsymbol{y}^{\prime}|\boldsymbol{y}\prec\boldsymbol{y}^{\prime}\prec\boldsymbol{y}_{ref}\right\} \right), $$
(13)

where PS is the set of Pareto-optimal solutions; \(\boldsymbol {y}_{ref}\in \mathbb {R}^{m}\) (m is the number of objectives) denotes the reference point that should be dominated by all Pareto-optimal solutions; \(\mathit {\mathcal {L}}\) denotes the Lebesgue measure; and ≺ represents dominance.

In our experiments, HI has been normalized and the reference point y r e f is set to (1.2, 1.2). We test our proposed algorithm with different configurations of the parameter T. We record the hypervolumes of the Pareto fronts when experimenting on the six real-world networks. The results over 30 runs are recorded in Table 4.

Table 4 Hypervolumes of the PFs generated by the proposed algorithm with different settings of the parameter T
Full size table

The parameter T determines the number of neighboring solutions which will be updated by a new offspring solution. If T is very big, it will be very time consuming and the whole population diversity will be lost because a good new offspring solution will update the majority of the solutions. If T is so small, the convergence speed will be slow because at each update step only a small number of solutions will be updated. The results in Table 4 suggest that T=2 seems to be the best. Based on this, in all the experiments, we set T=2 for our proposed algorithm.

4.3.2 Efficacy of the replacement operation

In this paper we have devised a new replacement operation to update the neighboring subproblems. In order to test the effectiveness of the proposed strategy, we compare the Pareto fronts obtained by PSOSCD and its variant PSOSCD-v1 which does not use the update strategy. We run both PSOSCD and PSOSCD-v1 for 30 times. The Pareto fronts with the biggest hypervolumes are shown in Fig. 7.

Fig. 7
figure 7

Pareto fronts obtained by the algorithms with biggest hypervolumes

Full size image

It can be seen from Fig. 7a that, for the SPP network, PSOSCD yields the same Pareto front as PSOSCD-v1 does. In our experiments we have found that each single run of these two algorithms always output the same results when experimenting on the SPP network, which indicates that the impact of the replacement operation is not significant. One reason that can explain this is because of the simple structure of the SPP network which makes the algorithm easy to find the optimal solutions.

From Fig. 7b to f we can clearly see that PSOSCD yields better Pareto fronts on the rest five real signed networks than PSOSCD-v1 does. The above experiments demonstrate that the proposed replacement operation can greatly enhance the population diversity.

4.3.3 Community discovery performance

In view of that the parameter T is determined and the efficacy of the replacement operation is validated, next step we will show the community discovery performance of our proposed algorithm.

For each network, we select the solution on the Pareto front that has the biggest signed modularity value as the final output of our proposed algorithm. Table 5 lists the statistical results when experimenting on the two small scale networks with known community structures.

Table 5 Statistical results over 30 runs on the signed networks with known ground truth
Full size table

From Table 5 we can see that, for the SPP and the GGS networks, all the algorithms perform similarly good, but the proposed algorithm performs the best. These two signed networks are small in size. It is easy for the algorithms to find the optimal solutions.

Figures 8 and 9 display the community structures obtained by our proposed algorithm when experimenting on the SPP and the GGS networks.

Fig. 8
figure 8

Detected community structures of the SPP network

Full size image
Fig. 9
figure 9

Detected community structures of the GGS network

Full size image

Each single run of the proposed algorithm can yield a set of solutions each of which denotes a network community structure. In Figs. 8 and 9 we respectively display two community structures of the corresponding network.

It can be seen that apart from the ground truth community structures, our proposed algorithm also discovered other interesting community structures. For the SPP network, it has discovered a structure with three communities in which the node SNS has been separated as an independent community. Because the node SNS has two negative linkages with the nodes in its original community, consequently, the discovered structure with three communities is meaningful. The similar phenomenon also happens to the GGS network. Apart from the ground truth structure, it also discovered other meaningful community structures which can facilitate intelligent decision making.

Table 6 lists the experimental results for the four networks with unknown ground truth. Because these four networks have no ground truth, we cannot compare the detected community structures with any reference structures. Besides, since the scales of these networks are big, it is hard to display their community structures. However, from the viewpoint of the signed modularity we can notice that, the maximum values and the averaged values obtained by our proposed algorithm are higher than those obtained by the rest algorithms, which indicates that the discovered community structures are better than those discovered by the comparison algorithms.

Table 6 Statistical results over 30 runs on the signed networks with unknown ground truth
Full size table

All the experiments have proved the validity of the proposed algorithm. The proposed optimization model is effective for the signed network community discovery problem. The developed PSOSCD algorithm which makes use of the decomposition strategy solves the proposed model well. Meanwhile, the newly cranked out subproblems update strategy enhances the population diversity.

5 Conclusion

Community discovery from signed networks is an important task in complex network analytics. This paper modeled the task of signed network community discovery as a multiobjective optimization problem. Considering the very nature of a signed community, in this paper, a new multiobjective optimization model based on the link density was put forward. In order to solve the newly proposed model, a novel multiobjective particle swarm optimization algorithm was devised. The proposed algorithm divided the multiobjective optimization problem into many scalar optimization subproblems by using the Tchebycheff decomposition technique. Each subproblem was optimized through the particle swarm optimization technique. In order to enhance the diversity of the swarm, a novel subproblem update tactic was proposed. Each single run of the proposed algorithm can yield a set of equally good solutions each of which represents a certain community structure of the tested signed network. Extensive experiments compared against several state-of-the-art approaches on both synthetic and real-world signed networks demonstrated that the proposed optimization model was effective and the devised algorithm was promising for solving the signed network community detection problem.

In this paper, the proposed optimization model is promising for undirected and unweighted signed networks. However, in reality many signed networks are directed and have weights. What is more, the topologies of many signed networks may evolve with the time. In our future work, more efforts will be made to study the community detection problem under these contexts.