1 Introduction

Rational Queueing, i.e. the branch of Queueing Theory that treats problems of economic flavor where the various agents (customers and/or administrators-servers) are strategic, is a flourishing scientific area for more than 50 years. The inception of the area goes back to the pioneering papers of Naor (1969), and Edelson and Hildebrand (1975) who studied the join-or-balk dilemma of arriving customers at the M/M/1 queue. Naor (1969) focused on the observable case, where the arriving customers have the possibility to observe the queue length before making their decisions, whereas (Edelson and Hildebrand, 1975) considered the unobservable case, where the decisions are based solely on the knowledge of the parameters of the system. Since then there is a growing part of the literature that deals with strategic considerations in queueing. The fundamental models, problems and results in this area can be found in the monograph by Hassin and Haviv (2003). The recent progress has been summarized in Hassin (2016) while a relevant overview of optimal design problems in queueing systems can be found in Stidham (2009).

A fundamental question in the Rational Queueing literature is the impact of the information that is provided to the customers. Several recent works summarize some important findings and challenges regarding this question, see e.g. chapter 4 in the book of Hassin (2016) and the review papers by Ibrahim (2018) and Economou (2021), Economou (2022). For more details see the literature review in Sect. 2. Most studies about the impact of information on the strategic behavior in a queueing system focus on the number of present customers which is the key information that is provided to the customers. This is indeed a crucial information so that the customers estimate the congestion of the system with accuracy. However, the provision of this information to the customers has an undesirable effect: It makes the effective arrival process (i.e. the process that records the entrances at the system) quite irregular. Indeed, under such an information mechanism the customers continuously enter till they reach a certain threshold and then the entrances are interrupted frequently as long as the system is highly congested. As a remedy to this situation we suggest that the effective arrival process can become more regular if the customers are informed about other customers’ joining decisions. Knowing the joining behavior of recently arrived customers can help customers to coordinate at a certain degree.

Apart from the smoothing of the effective arrival process, the provision of information about other customers’ decisions seems advantageous in several cases that occur in practice. The first case is when there are independent web-based systems that receive the arriving customers that do not have information about what is going on in the core service system. This is typical when petitions for service are deposited through a web-platform and the service consists of several stages that are not monitored by the platform. In such a case the platform can provide information about previous arrivals and joining decisions but not about the actual congestion. Another case is when the customers do not trust the server provider for the information that he provides, so they report their decisions/evaluations to independent sources that are accessible by other customers.

Taking into account the aforementioned points, the aim of the present paper is to initiate a path for the study of the impact of information about other customers’ decisions on the join-or-balk dilemma in a queueing system. To keep the framework as simple as possible, we consider the Markovian single-server queue (i.e. the M/M/1 queue) with strategic customers that receive information about the decision of the most recent arrival. This is the first step towards a more thorough investigation in the case where the customers are informed about the decisions of a number of recent arrivals. However, the simplicity of the framework allows to go more deeply and prove analytically various interesting results.

The main contributions of the paper are summarized below:

  1. 1.

    We study the performance of the system when the population of potential customers follow an arbitrary strategy.

  2. 2.

    We characterize the customer equilibrium strategies and show how their form changes as the normalized service value increases from 0 to \(\infty \).

  3. 3.

    We compare the equilibrium strategies, the equilibrium social welfare and the equilibrium throughput with the corresponding quantities of the unobservable and observable systems.

  4. 4.

    We derive conclusions about the benefits of providing customers with information about other customers’ decisions and point to further generalizations and problems.

The rest of the paper is structured as follows: In Sect. 2 we present an extensive literature review regarding the problem of information provision to strategic customers of a queueing system. In Sect. 3 we describe in detail the queueing model under study, its performance and economic parameters, and present the strategic framework for the interaction of the customers. The performance evaluation of the model under an arbitrary strategy is studied in Sect. 4. Subsequently, in Sect. 5, we characterize the customer equilibrium strategies and show how they can be computed from the system parameters. The comparison of the equilibrium strategies and the corresponding equilibrium throughput and social welfare with the benchmark models (observable and unobservable) is carried out in Sect. 6. We present several results that are proved analytically and also demonstrate other results that have been consistently observed in a large number of numerical experiments. The study is finished with a list of conclusions and managerial take-away messages that are presented in Sect. 7. We also discuss some extensions and directions for future research there.

2 Literature review

The present paper belongs to a body of work in the Operations Research and the Operations Management literature that focuses on the effect of information on strategic customer behavior in service systems. Two key references from this thread of research are the pioneering papers of Hassin (1986) and Chen and Frank (2004) who compared the equilibrium performance of the observable and unobservable versions of an M/M/1 queue with strategic customers who make their join-or-balk decisions upon arrival. The main take-away message from these papers is that it is better in some cases to reveal the queue length and in other cases to conceal it.

Various authors considered models that lie between the two extreme versions (observable and unobservable) of queueing models with strategic customers who face the join-or-balk dilemma. More specifically, the following categories of models have appeared in the literature (see Economou, 2021,2022):

  • Systems with imperfect observation structure In such systems, the customers receive imperfect information about the queue length. For example, Economou and Kanta (2008) and Guo and Zipkin (2009) considered imperfectly observable versions of the M/M/1 queue, where the state-space of the queue length is partitioned into subsets and the arriving customers are not informed about the exact queue length, but rather about the subset it belongs to. When the subsets are singletons, the imperfectly observable model reduces to the observable M/M/1 queue, whereas if there is only one subset we have the unobservable case. In another study, Hassin and Koshman (2017) considered the M/M/1 queue where the arriving customers are informed about whether the number of present customers exceeds a critical level or not. They showed that this kind of information can be used to maximize the profit generated by the system.

  • Systems with delayed observation structure In such systems, the customers observe the queue length with some delay. Burnetas et al. (2017) considered the M/M/1 with delayed observations, where the customers decide whether to join or balk without knowing the queue length, but later on they are informed about their current position and may renege. In a similar direction, Hassin and Roet Green (2020) studied a model where the customers observe the queue length before reaching it, using probably some web-based application, and decide whether to go to the service facility or not. However, when they arrive at the system they are informed about the current queue length and make their second decision, to join or balk. Models with delayed observations reduce to the corresponding observable or unobservable models, when the delay tends respectively to 0 or to \(\infty \).

  • Systems with mixed observation structure In such models, only a fraction of the customers observe the queue length. Economou and Grigoriou (2015) and Hu et al. (2018) studied the join-or-balk dilemma in the framework of an M/M/1 queue, where the population of customers is divided into observing and uninformed (non-observing) customers. The observable and unobservable models correspond to the extreme cases where the fraction of uninformed customers is 0 and 1 respectively.

  • Systems with alternating observation structure Under such an information structure, a system alternates between observable and unobservable periods. Dimitrakopoulos et al. (2021) studied the M/M/1 queue with strategic customers who decide whether to join or balk upon arrival, in the case where the system remains observable for an exponentially distributed period, and subsequently becoming unobservable for another exponentially distributed period (with a different mean duration) and so on. They showed that alternating a system between observable and unobservable periods can be advantageous for increasing the equilibrium throughput and/or the equilibrium social welfare.

  • Systems with non-standard or augmented observation structure In such systems, the customers observe system features other than or in addition to queue length. For example, in systems with a controllable or unreliable server, the customers may observe the state of the server upon arrival (see e.g. Burnetas & Economou, 2007). In other situations, the system feature that can be observed is the state of a random environment that influences the arrival and service rates (see e.g. Economou & Manou, 2013). Moreover, another example of such systems corresponds to the situation where customers are informed about the elapsed or remaining service time in process. This type of information is usually provided in transportation systems (see e.g. Logothetis and Economou (2023)).

Some other significant studies regarging the influence of information on strategic customer behavior in queueing systems have been reported in Allon et al. (2011), Armony and Maglaras (2004), Cui and Veeraraghavan (2016), Debo and Veeraraghavan (2014), Guo and Zipkin (2007), Hassin and Roet-Green (2017), Hassin and Snitkovsky (2020), Haviv and Kerner (2007), Haviv and Oz (2016), Haviv and Oz (2018), Ibrahim et al. (2017), Inoue et al. (2023), Kerner (2011), Veeraraghavan and Debo (2009), Veeraraghavan and Debo (2011), Wang et al. (2018), Wang and Hu (2019), and Yu et al. (2018). In these works the authors examine various dimensions of the information impact on the customers, e.g., its function to signal quality of services, its relationship with customers’ heterogeneity, its interplay with customers’ beliefs and herding behavior, its role for the coordination of customers’ behavior with social objectives, estimation procedures etc. For detailed overviews and comments see Chapter 3 in Hassin (2016) and the recent papers Economou (2021), Economou (2022) and Ibrahim (2018).

3 The model

We consider a single server queue with infinite waiting space, where strategic customers arrive according to a Poisson process at rate \(\lambda \) and have independent exponential service times with rate \(\mu \), independent of the arrival process. The queue discipline is the First-Come-First-Served (FCFS). We define \(\rho =\frac{\lambda }{\mu }\) to be the utilization factor of the model.

Arriving customers at this M/M/1 queue face the dilemma of whether to join or balk with the objective of maximizing their own utilities. Each customer receives a reward of R units upon service completion and accumulates waiting costs at rate C as long as she stays in the system. We define \(\nu =\frac{R\mu }{C}\) to be the normalized service value, which corresponds to the ratio of the service value over the mean cost of a service time.

The operational and economic parameters of the system are assumed to be common knowledge for all customers. This is a reasonable assumption when the population of customers visits the system recurrently. Moreover, upon arrival, each customer is informed about the decision of the last arrival before her, being join (1) or balk (0), and then makes her own decision. Therefore, a customer’s mixed strategy is specified by a vector \((q_0,q_1)\), where \(q_i\) is the joining probability, if the previous arrival made the decision i, for \(i=0,1\).

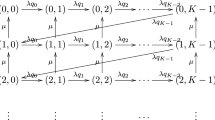
Under a given population strategy \((q_0,q_1)\), to obtain a Markovian description of the system, we should keep track of the evolution of the number of customers in the system and the decision of the the most recent arrival. Let N(t) be the number of customers in the system at time t and I(t) be the decision of the last arrival before time t. Then, a moment of reflection reveals that \(\{(N(t),I(t))\}\) is a continuous-time Markov chain with state space

$$\begin{aligned} \mathcal {S}=\{(n,i):n\ge 0, i=0,1\} \end{aligned}$$
(3.1)

and non-zero transition rates

$$\begin{aligned} q_{(n,0),(n+1,1)}= & \lambda q_0,\;\;\; n\ge 0, \end{aligned}$$
(3.2)
$$\begin{aligned} q_{(n,1),(n+1,1)}= & \lambda q_1,\;\;\; n\ge 0,\end{aligned}$$
(3.3)
$$\begin{aligned} q_{(n,1),(n,0)}= & \lambda (1-q_1),\;\;\; n\ge 0,\end{aligned}$$
(3.4)
$$\begin{aligned} q_{(n,i),(n-1,i)}= & \mu ,\;\;\; n\ge 1,i=0,1. \end{aligned}$$
(3.5)

The transition diagram is shown in Fig. 1.

Fig. 1
figure 1

Transition diagram of \(\{(N(t),I(t))\}\) under a given population strategy \((q_0,q_1)\)

Full size image

We will refer to this model as the last-customer’s-decision (lcd) model when we compare it with other models that have been reported in the literature as the unobservable (un) and the observable (obs) models.

4 Performance evaluation

The information process \(\{I(t)\}\) which records the decisions of the customers is a 2-state continuous-time Markov chain on \(\{0,1\}\) with rates \(q_{0,1}=q_0\) and \(q_{1,0}=1-q_1\). Let \((p_I(0),p_I(1))\) be its steady-state distribution. Then, we have

$$\begin{aligned} p_I(0)=\frac{1-q_1}{1-q_1+q_0} \text{ and } p_I(1)=\frac{q_0}{1-q_1+q_0}. \end{aligned}$$
(4.1)

To obtain the performance measures of the model, we should compute the steady-state distribution \((p(n,i):n\ge 0,i=0,1)\) of \(\{(N(t),I(t))\}\). The balance equations are

$$\begin{aligned} \lambda q_0 p(0,0)= & \lambda (1-q_1) p(0,1)+\mu p(1,0),\end{aligned}$$
(4.2)
$$\begin{aligned} \lambda p(0,1)= & \mu p(1,1),\end{aligned}$$
(4.3)
$$\begin{aligned} (\lambda q_0+\mu ) p(n,0)= & \lambda (1-q_1) p(n,1)+\mu p(n+1,0),\;\;\; n\ge 1,\end{aligned}$$
(4.4)
$$\begin{aligned} (\lambda +\mu ) p(n,1)= & \lambda q_0 p(n-1,0)+\lambda q_1 p(n-1,1)+\mu p(n+1,1),\;\;\; n\ge 1. \qquad \end{aligned}$$
(4.5)

Let

$$\begin{aligned} P_i(z)=\sum _{n=0}^{\infty } p(n,i) z^n,\;\;\; |z|\le 1,\;\;\; i=0,1, \end{aligned}$$
(4.6)

be the partial generating function of the number of present customers when the last customer’s decision is i, \(i=0,1\). Theorem 4.1 provides the stability condition for the model and closed-form expressions for \(P_i(z)\), for \(i=0,1\).

Theorem 4.1

The continuous-time Markov chain \(\{(N(t),I(t))\}\) is positive recurrent if and only if

$$\begin{aligned} \rho <1+\frac{1-q_1}{q_0}. \end{aligned}$$
(4.7)

When the stability condition holds, the partial generating functions of the steady-state distribution, \(P_i(z)\), \(i=0,1\), are given by

$$\begin{aligned} P_0(z)= & \frac{1-q_1}{1-q_1+q_0}\cdot \frac{\rho q_0+\rho +1-\rho _2-\rho q_1 z}{\rho q_0+\rho +1-\rho _2-\rho q_1}\cdot \frac{1-\rho _2}{1-\rho _2 z},\end{aligned}$$
(4.8)
$$\begin{aligned} P_1(z)= & \frac{q_0}{1-q_1+q_0}\cdot \frac{1+(\rho -\rho _2)z}{1+\rho -\rho _2}\cdot \frac{1-\rho _2}{1-\rho _2 z}, \end{aligned}$$
(4.9)

where \(\rho _2=\rho _2(q_0,q_1)\) is given by

$$\begin{aligned} \rho _2=\rho _2(q_0,q_1)=\frac{\rho q_0+\rho +1-\sqrt{\left( \rho q_0 +\rho +1\right) ^2-4\left( \rho ^2q_0+\rho q_1\right) }}{2}. \end{aligned}$$
(4.10)

Proof

The stability condition can be justified directly and intuitively as follows: Let \(\alpha \) denote the steady-state probability that an arriving customer joins the queue. Then, conditioning on whether the previous arriving customer joined or balked, we have that

$$\begin{aligned} \alpha =\alpha q_1 +(1-\alpha ) q_0 \end{aligned}$$

which yields

$$\begin{aligned} \alpha =\frac{q_0}{1-q_1+q_0}. \end{aligned}$$

For stability, we need \(\rho \alpha <1\) which is written as (4.7). Formal derivations of (4.7) are presented in the sequel, using the generating function approach and the mean-drift criterion for homogeneous QBD processes.

To derive the formulas (4.8) and (4.9) for the probability generating functions \(P_0(z)\) and \(P_1(z)\), we apply the standard generating function approach. Multiplying equation (4.4) by \(z^n\), summing all these equations, for \(n\ge 1\), and adding Eq. (4.2) yields:

$$\begin{aligned} (\lambda q_0 +\mu )P_0(z)-\mu p(0,0)= & \lambda (1-q_1) P_1(z) +\mu \sum _{n=0}^{\infty } p(n+1,0) z^n\nonumber \\= & \lambda (1-q_1) P_1(z)+\frac{\mu }{z}(P_0(z)-p(0,0)). \end{aligned}$$
(4.11)

Multiplying by z and rearranging terms, we derive the equation:

$$\begin{aligned} \left[ (\lambda q_0+\mu )z-\mu \right] P_0(z)-\lambda (1-q_1) z P_1(z)=\mu (z-1) p(0,0). \end{aligned}$$
(4.12)

Similarly, multiplying Eq. (4.5) by \(z^n\), summing all these equations, for \(n\ge 1\), and adding Eq. (4.3) yields:

$$\begin{aligned} (\lambda +\mu )P_1(z)-\mu p(0,1)= & \lambda q_0 z P_0(z)+\lambda q_1 z P_1(z)+\frac{\mu }{z}(P_1(z)-p(0,1)), \end{aligned}$$
(4.13)

which easily reduces to

$$\begin{aligned} -\lambda q_0 z^2 P_0(z)+\left[ (\lambda +\mu )z-\lambda q_1 z^2-\mu \right] P_1(z)=\mu (z-1) p(0,1). \end{aligned}$$
(4.14)

Equations (4.12)–(4.14) form a linear system for \((P_0(z),P_1(z))\):

$$\begin{aligned} \left[ \begin{array}{cc} (\lambda q_0+\mu )z-\mu & -\lambda (1-q_1) z \\ -\lambda q_0 z^2 & (\lambda +\mu ) z-\lambda q_1 z^2 - \mu \end{array}\right] \left[ \begin{array}{c} P_0(z)\\ P_1(z) \end{array} \right] = \mu (z-1) \left[ \begin{array}{c} p(0,0)\\ p(0,1) \end{array} \right] . \qquad \end{aligned}$$
(4.15)

The determinant of the system can be written after some algebraic manipulation in the form

$$\begin{aligned} D(z)=(1-z)\left[ \left( \lambda ^2q_0+\lambda \mu q_1\right) z^2-\left( \lambda \mu q_0+\lambda \mu +\mu ^2\right) z+\mu ^2\right] =(1-z)z^2 C(1/z), \nonumber \\ \end{aligned}$$
(4.16)

where the polynomial C(x) is given by

$$\begin{aligned} C(x)=\left( \lambda ^2q_0+\lambda \mu q_1\right) -\left( \lambda \mu q_0+\lambda \mu +\mu ^2\right) x+\mu ^2 x^2. \end{aligned}$$
(4.17)

The roots of C(x) are given as

$$\begin{aligned} \rho _{1,2}=\frac{\lambda \mu q_0+\lambda \mu +\mu ^2\pm \sqrt{\Delta }}{2\mu ^2} \end{aligned}$$
(4.18)

where

$$\begin{aligned} \Delta= & \left( \lambda \mu q_0+\lambda \mu +\mu ^2\right) ^2-4\mu ^2 \left( \lambda ^2 q_0+\lambda \mu q_1\right) \nonumber \\= & \left( \lambda \mu q_0-\lambda \mu +\mu ^2\right) ^2+4\lambda \mu ^3 (1-q_1)\ge 0. \end{aligned}$$

We can now easily see that \(\rho _2\) assumes the simplified form (4.10) by dividing the numerator and denominator of (4.18) by \(\mu ^2\). Therefore, (4.16) can be written as

$$\begin{aligned} D(z)=(1-z)z^2\mu ^2\left( \frac{1}{z}-\rho _1\right) \left( \frac{1}{z}-\rho _2\right) =\mu ^2(1-z)(1-\rho _1 z)(1-\rho _2 z). \end{aligned}$$
(4.19)

Cramer’s rule applied to the system (4.15) for the unknown variable \(P_0(z)\) yields:

$$\begin{aligned} P_0(z)= & \frac{\mu (z-1)\det \left[ \begin{array}{cc} p(0,0) & -\lambda (1-q_1) z \\ p(0,1) & (\lambda +\mu ) z-\lambda q_1 z^2 - \mu \end{array}\right] }{D(z)}\nonumber \\= & \frac{\left[ \lambda q_1 z^2-(\lambda +\mu )z+\mu \right] p(0,0)-\lambda (1-q_1)zp(0,1)}{\mu (1-\rho _1 z)(1-\rho _2 z)}. \end{aligned}$$
(4.20)

Similarly, for \(P_1(z)\), we have:

$$\begin{aligned} P_1(z)= & \frac{\mu (z-1)\det \left[ \begin{array}{cc} (\lambda q_0+\mu )z-\mu & p(0,0) \\ -\lambda q_0 z^2 & p(0,1) \end{array}\right] }{D(z)}\nonumber \\= & \frac{-\lambda q_0 z^2p(0,0)+[\mu -(\lambda q_0+\mu )z)]p(0,1)}{\mu (1-\rho _1 z)(1-\rho _2 z)}. \end{aligned}$$
(4.21)

Regarding the stability condition, note that for C(x), given by (4.17), we have that \(C(0)=\lambda ^2 q_0+\lambda \mu q_1>0\), whereas \(C(1)=\lambda ^2 q_0+\lambda \mu q_1-\lambda \mu -\lambda \mu q_0<C(0)\). There are two cases: Either condition (4.7) holds (in which case \(C(1)<0\)) or does not hold (in which case \(C(1)\ge 0\)). In the former case, we have that C(x) has a root in (0, 1), i.e., \(0<\rho _2<1<\rho _1\), whereas in the latter we have \(0<1\le \rho _2<\rho _1\).

Therefore, if condition (4.7) does not hold, we have that \(\rho _1^{-1}\) and \(\rho _2^{-1}\) reside both in the closed unit disk and are roots of the denominators in (4.20) and (4.21). Hence, they should be also roots of the corresponding numerators, since the partial probability generating functions \(P_1(z)\), \(P_2(z)\) converge in the closed unit disk. Since the numerators are second degree polynomials, we conclude that they should also factorize as constant multiples of \((1-\rho _1 z)(1-\rho _2 z)\). Hence, \(P_0(z)\), \(P_1(z)\) are constants and setting \(z\rightarrow \infty \) yields \(p(0,0)=p(0,1)=0\), so \(P_1(z)\), \(P_2(z)\) are identically zero. Therefore, in this case, the CTMC \(\{(N(t),I(t))\}\) has not a steady-state distribution, and we conclude that condition (4.7) is necessary for stability.

Assume, now, that (4.7) holds. Then \(\rho _1^{-1}\) resides in the closed unit disk and hence it is also root of the two numerators of \(P_0(z)\) and \(P_1(z)\). Hence, the numerator \(N_0(z)\) of \(P_0(z)\) in (4.20) is written as \(N_0(z)=N_0(z)-N_0(\rho _1^{-1})\). Grouping similar terms yields

$$\begin{aligned} N_0(z)= & \left[ \lambda q_1 z^2-(\lambda +\mu )z+\mu \right] p(0,0)-\lambda (1-q_1)zp(0,1)\nonumber \\ & \quad \;\;\; -\left[ \lambda q_1 \rho _1^{-2}-(\lambda +\mu )\rho _1^{-1}+\mu \right] p(0,0)+\lambda (1-q_1)\rho _1^{-1}p(0,1)\nonumber \\= & \left\{ \lambda (1-q_1)\rho _1^{-1}p(0,1)-\left[ \lambda q_1 \left( z+\rho _1^{-1}\right) -(\lambda +\mu )\right] \rho _1^{-1}p(0,0)\right\} (1-\rho _1 z). \nonumber \\ \end{aligned}$$
(4.22)

Then, plugging \(N_0(z)\) given by (4.22) in (4.20) and simplifying yields

$$\begin{aligned} P_0(z)=\frac{\lambda (1-q_1)p(0,1)-\left[ \lambda q_1 \left( z+\rho _1^{-1}\right) -(\lambda +\mu )\right] p(0,0)}{\mu \rho _1(1-\rho _2z)}. \end{aligned}$$
(4.23)

Moreover, \(N_0\left( \rho _1^{-1}\right) =0\) yields

$$\begin{aligned} p(0,1)=\frac{\mu \rho _1^2-(\lambda +\mu )\rho _1+\lambda q_1}{\lambda (1-q_1)\rho _1}p(0,0). \end{aligned}$$
(4.24)

Substituting (4.24) in (4.23) and simplifying yields

$$\begin{aligned} P_0(z)=\frac{\mu \rho _1-\lambda q_1z}{\mu \rho _1(1-\rho _2z)}p(0,0). \end{aligned}$$
(4.25)

Finally, p(0, 0) can be determined using (4.1):

$$\begin{aligned} \frac{1-q_1}{1-q_1+q_0}=p_I(0)=P_0(1)=\frac{\mu \rho _1-\lambda q_1}{\mu \rho _1(1-\rho _2)}p(0,0), \end{aligned}$$

which shows that

$$\begin{aligned} p(0,0)=\frac{\mu \rho _1(1-\rho _2)(1-q_1)}{(\mu \rho _1-\lambda q_1)(1-q_1+q_0)}. \end{aligned}$$
(4.26)

Substituting (4.26) in (4.25) yields

$$\begin{aligned} P_0(z)=\frac{1-q_1}{1-q_1+q_0}\cdot \frac{\mu \rho _1-\lambda q_1z}{\mu \rho _1-\lambda q_1}\cdot \frac{1-\rho _2}{1-\rho _2z}. \end{aligned}$$
(4.27)

Now, since \(\rho _1\) and \(\rho _2\) are roots of C(x), by Vieta’s formulas we have \(\rho _1+\rho _2=\frac{\lambda \mu q_0+\lambda \mu +\mu ^2}{\mu ^2}\) which shows that

$$\begin{aligned} \rho _1=\rho q_0+\rho +1-\rho _2. \end{aligned}$$
(4.28)

Substituting \(\rho _1\), given by (4.28), in (4.27) and simplifying yields (4.8).

Equation (4.9) is proved along the same lines. Again, when (4.7) is valid, we have that the numerator \(N_1(z)\) of \(P_1(z)\) in (4.21) has a root at \(z=\rho _1^{-1}\). Therefore, \(N_1(z)=N_1(z)-N(\rho _1^{-1})\) and grouping similar terms yields the factorization

$$\begin{aligned} N_1(z)=\left\{ (\lambda q_0+\mu )\rho _1^{-1} p(0,1)+\lambda q_0 (z+\rho _1^{-1})\rho _1^{-1}p(0,0)\right\} (1-\rho _1 z). \end{aligned}$$
(4.29)

Moreover, \(N_1\left( \rho _1^{-1}\right) =0\) yields

$$\begin{aligned} p(0,1)=\frac{\lambda q_0}{\mu \rho _1^2-(\lambda q_0+\mu )\rho _1}p(0,0). \end{aligned}$$
(4.30)

Substituting (4.29) and (4.30) in (4.21) and simplifying yields

$$\begin{aligned} P_1(z)=\frac{(\mu \rho _1-\lambda q_0-\mu )z+\mu }{\mu (1-\rho _2z)}p(0,1). \end{aligned}$$
(4.31)

We can now determine p(0, 1), using (4.31) and (4.1):

$$\begin{aligned} p(0,1)=\frac{\mu (1-\rho _2)q_0}{(\mu \rho _1-\lambda q_0)(1-q_1+q_0)}. \end{aligned}$$
(4.32)

Substituting (4.32) in (4.31) yields

$$\begin{aligned} P_1(z)=\frac{q_0}{1-q_1+q_0}\cdot \frac{(\mu \rho _1-\lambda q_0-\mu )z+\mu }{\mu \rho _1-\lambda q_0}\cdot \frac{1-\rho _2}{1-\rho _2z}. \end{aligned}$$
(4.33)

Now, substituting \(\rho _1\), given by (4.28), in (4.33) yields (4.9).

The stability condition (4.7) can be proved independently of the generating functions approach by noting that the process \(\{(N(t),I(t))\}\) is a QBD process and applying the mean-drift criterion for the stability of such processes (see e.g. Nelson, 1995, Chapter 9). Indeed, the phase process of the QBD is \(\{I(t)\}\) with steady-state distribution given by (4.1). The mean drift of the QBD process is

$$\begin{aligned} p_I(0)(\lambda q_0-\mu )+p_I(1)(\lambda q_1-\mu )=\frac{\lambda q_0}{1-q_1+q_0}-\mu . \end{aligned}$$
(4.34)

According to the mean-drift criterion, a QBD process is positive recurrent if and only if the mean drift is strictly negative, which reduces to \(\frac{\lambda q_0}{1-q_1+q_0}-\mu <0\) in the present case. This is equivalent to the validity of (4.7). \(\square \)

Consider, now, a tagged arriving customer and let S be her sojourn time in the system. Moreover, let \(Q^-\) and \(I^-\) be the number of customers in the system and the decision of the last arrival before her. Due to the Poisson arrivals (PASTA property) we have that the joint distribution of \((Q^-,I^-)\) coincides with the steady-state distribution of \(\{(Q(t),I(t)\}\) in continuous time. Therefore, the conditional probability that the tagged customer will see n customers in the system, given that the last arrival before her made the decision i is

$$\begin{aligned} \Pr [Q^-=n|I^-=i]=\frac{p(n,i)}{p_I(i)},\;\;\; n\ge 0,\;\;\; i=0,1. \end{aligned}$$
(4.35)

Therefore, we can easily see that

$$\begin{aligned} E[S|I^-=i]=\sum _{n=0}^{\infty } \frac{n+1}{\mu }\cdot \frac{p(n,i)}{p_I(i)}=\frac{E[Q|I=i]+1}{\mu }=\frac{P'_i(1)/p_I(i)+1}{\mu }. \end{aligned}$$
(4.36)

Let \(S_i(q_0,q_1)\) be the net benefit of a tagged arriving customer who sees \(I^-=i\) upon arrival and decides to join, given that the population of customers follows a strategy \((q_0,q_1)\). Then, we have that

$$\begin{aligned} S_i(q_0,q_1)=R-\frac{C}{\mu }E[S|I^-=i]. \end{aligned}$$
(4.37)

Using (4.37), (4.36) and Theorem 4.1, we can derive explicit formulas for the quantities \(S_i(q_0,q_1)\), \(i=0,1\).

Corollary 4.1

The net benefit functions of a tagged customer who sees upon arrival that the last decision before her was \(i=0\) or \(i=1\) and decides to enter are given by

$$\begin{aligned} S_0(q_0,q_1)= & R-\frac{C}{\mu }\left( \frac{1}{1-\rho _2}-\frac{\rho \rho _2 q_1}{\rho ^2 q_0+\rho (1-\rho _2)q_1}\right) , \end{aligned}$$
(4.38)
$$\begin{aligned} S_1(q_0,q_1)= & R-\frac{C}{\mu }\left( \frac{1}{1-\rho _2}+\frac{\rho (\rho -\rho _2)q_0+\rho q_1-\rho _2}{\rho (\rho -\rho _2)q_0+\rho q_1}\right) . \end{aligned}$$
(4.39)

Proof

We evaluate the derivatives of \(P_i(z)\), \(i=1,2\) at \(z=1\) using (4.8) and (4.9). Then, we substitute them in (4.37) and (4.36). \(\square \)

Using the formulas (4.1) we can easily derive the throughput of the system under a given customer strategy \((q_0,q_1)\). In conjunction with (4.38) and (4.39) we can also obtain the social welfare per time unit generated by the system.

The throughput generated from a customer strategy \((q_0,q_1)\) is given by

$$\begin{aligned} TH^{lcd}(q_0,q_1)=p_I(0)\lambda q_0+ p_I(1)\lambda q_1=\frac{\lambda q_0}{1-q_1+q_0} \end{aligned}$$
(4.40)

and the corresponding welfare is

$$\begin{aligned} SW^{lcd}(q_0,q_1)= & p_I(0)\lambda q_0S_0(q_0,q_1)+ p_I(1)\lambda q_1S_1(q_0,q_1)\nonumber \\= & \frac{\lambda q_0 (1-q_1) S_0(q_0,q_1)+\lambda q_0 q_1 S_1(q_0,q_1)}{1-q_1+q_0}. \end{aligned}$$
(4.41)

5 Equilibrium customer behavior

Formulas (4.38) and (4.39) show that

$$\begin{aligned} S_0(q_0,q_1)>S_1(q_0,q_1). \end{aligned}$$
(5.1)

This inequality shows that if a population follows a given strategy \((q_0,q_1)\), then a tagged customer who is informed that the last customer balked anticipates a higher net benefit than a customer who is informed that the last customer joined. This implies that, for an equilibrium strategy \(\left( q_0^{lcd-e},q_1^{lcd-e}\right) \), we should necessarily have \(q_0^{lcd-e}\ge q_1^{lcd-e}\). Moreover, inequality (5.1) implies that the only possible forms for an equilibrium strategy are (0, 0), \((q_0^*,0)\), (1, 0), \((1,q_1^*)\) and (1, 1), with \(q_0^*,q_1^*\in (0,1)\). This is proved in the following result.

Lemma 5.1

Regarding the equilibrium strategy, we have the following cases:

  1. 1.

    (0, 0) is equilibrium strategy if and only if \(S_0(0,0)\le 0\).

  2. 2.

    \((q_0^*,0)\) with \(q_0^*\in (0,1)\) is equilibrium strategy if and only if \(S_0(q_0^*,0)=0\).

  3. 3.

    (1, 0) is equilibrium strategy if and only if \(S_1(1,0)\le 0 \le S_0(1,0)\).

  4. 4.

    \((1,q_1^*)\) with \(q_1^*\in (0,1)\) is equilibrium strategy if and only if \(S_1(1,q_1^*)=0\).

  5. 5.

    (1, 1) is equilibrium strategy if and only if \(S_1(1,1)\ge 0\).

Proof

Denote by \(BR(q_0,q_1)\) the best response of a tagged customer against a given strategy \((q_0,q_1)\) of the population of customers. Since the best response of the customer depends on the signs of the quantities \(S_i(q_0,q_1)\) and inequality (5.1) holds, we have the following form for the best response correspondence:

$$\begin{aligned} BR(q_0,q_1)=\left\{ \begin{array}{ll} {(0,0)} & \text{ if } S_0(q_0,q_1)<0, \\ {(q'_0,0):q'_0\in [0,1]} & \text{ if } S_0(q_0,q_1)=0, \\ {(1,0)} & \text{ if } S_1(q_0,q_1)<0<S_0(q_0,q_1), \\ {(1,q'_1):q'_1\in [0,1]} & \text{ if } S_1(q_0,q_1)=0, \\ {(1,1)} & \text{ if } S_1(q_0,q_1)>0. \end{array} \right. \end{aligned}$$
(5.2)

The equilibrium strategies are best responses against themselves, therefore the only possible forms of equilibrium strategies are the forms in (5.2).

Now, (0, 0) is equilibrium if and only if \((0,0)\in BR(0,0)\), which is equivalent to \(S_0(0,0)\le 0\), because of (5.2). This yields Case 1 of the Lemma.

A strategy \((q_0^*,0)\) is equilibrium if and only if \((q_0^*,0)\in BR(q_0^*,0)\), which is equivalent to \(S_0(q_0^*,0)= 0\), because of (5.2). This yields Case 2 of the Lemma.

The other cases are treated along the same lines. \(\square \)

It is illuminating to think of the various cases of Lemma 5.1 as follows: In case 1 all customers balk. In case 2 a customer who joins is followed by at least one customer who balks. In case 3 the customers alternate, one joins and the next balks. In case 4 a customer who balks is followed by at least one customer who joins. In case 5 all customers join.

Lemma 5.1 shows that the key for the computation of the equilibrium strategies for a specific instance of the model (for given parameters \(\lambda \), \(\mu \), R and C) is the calculation of the quantities \(S_0(0,0)\), \(S_0(1,0)\), \(S_1(1,0)\), \(S_1(1,1)\) and the solution of the equations \(S_0(x,0)=0\) and \(S_1(1,x)=0\) in (0, 1). To this end we can use the formulas (4.38) and (4.39). Then we can derive the following characterization of the equilibrium strategy, as the normalized service value \(\nu \) assumes values from 0 to \(\infty \).

Theorem 5.1

An equilibrium customer strategy for the lcd model exists and is unique for any values of the underlying parameters. If \(\rho <1\), then we have the following cases regarding the equilibrium strategy \(\left( q_0^{lcd-e},q_1^{lcd-e}\right) \):

  1. 1.

    \(\nu \in [0,1]\). Then \(\left( q_0^{lcd-e},q_1^{lcd-e}\right) =(0,0)\).

  2. 2.

    \(\nu \in \left( 1,\frac{2}{1-2\rho +\sqrt{1+4\rho }}\right) \). Then \(\left( q_0^{lcd-e},q_1^{lcd-e}\right) =(q_0^*,0)\) with

    $$\begin{aligned} q_0^*=\frac{1}{\frac{1}{\nu }+\rho -1}-\frac{1}{\nu \rho }. \end{aligned}$$
    (5.3)
  3. 3.

    \(\nu \in \left[ \frac{2}{1-2\rho +\sqrt{1+4\rho }},\frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }}\right] \). Then \(\left( q_0^{lcd-e},q_1^{lcd-e}\right) =(1,0)\).

  4. 4.

    \(\nu \in \left( \frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }},\frac{1}{1-\rho }\right) \). Then \(\left( q_0^{lcd-e},q_1^{lcd-e}\right) =(1,q_1^*)\) with

    $$\begin{aligned} q_1^*=\frac{3-\rho -\frac{2}{\nu -1}+(1-\rho )\sqrt{1+\frac{4}{\rho (\nu -1)}}}{2}. \end{aligned}$$
    (5.4)
  5. 5.

    \(\nu \in \left[ \frac{1}{1-\rho },\infty \right) \). Then \(\left( q_0^{lcd-e},q_1^{lcd-e}\right) =(1,1)\).

Proof

We characterize each possible form of an equilibrium strategy.

Case 1 Equilibrium strategy (0, 0).

(0, 0) is equilibrium strategy if and only if \(S_0(0,0)\le 0\). However, under population strategy (0, 0), the system is continuously empty, so \(S_0(0,0)=R-\frac{C}{\mu }\). Hence, (0, 0) is equilibrium strategy, if an only if \(R\le \frac{C}{\mu }\), which is equivalent to \(\nu \le 1\).

Case 2 Equilibrium strategy \((q_0^*,0)\), with \(q_0^*\in (0,1)\).

For \(q_0^*\in (0,1)\), \((q_0^*,0)\) is equilibrium strategy if and only if \(S_0(q_0^*,0)=0\). By (4.38), we have that

$$\begin{aligned} S_0(q_0^*,0)=R-\frac{C}{\mu }\cdot \frac{1}{1-\sigma (q_0^*)}, \end{aligned}$$
(5.5)

where \(\sigma (q_0)=\rho _2(q_0,0)\). Using (4.10) and after some algebraic simplifications, we derive that

$$\begin{aligned} \sigma (q_0)=\frac{\rho q_0+\rho +1-\sqrt{(\rho q_0-\rho +1)^2+4\rho }}{2}. \end{aligned}$$
(5.6)

Therefore, we should have

$$\begin{aligned} R-\frac{C}{\mu }\cdot \frac{1}{1-\sigma (q_0^*)}=0\;\;\; \text{ and } \;\;\; q_0^*\in (0,1). \end{aligned}$$

Differentiating (5.6) with respect to \(q_0\) yields

$$\begin{aligned} \frac{d}{dq_0}\sigma (q_0)=\frac{\rho }{2}\left( 1-\frac{\rho q_0^*-\rho +1}{\sqrt{(\rho q_0^*-\rho +1)^2+4\rho }}\right) >0. \end{aligned}$$

which shows that \(\sigma (q_0)\) is strictly increasing. Therefore,

$$\begin{aligned} q_0^*\in (0,1)\Leftrightarrow \sigma (q_0^*)\in (\sigma (0),\sigma (1))=\left( 0,\frac{2\rho +1-\sqrt{1+4\rho }}{2}\right) . \end{aligned}$$

Moreover, \(R-\frac{C}{\mu (1-\sigma )}\) is clearly strictly decreasing in \(\sigma \). Hence

$$\begin{aligned} & q_0^*\in (0,1)\\\Leftrightarrow & R-\frac{C}{\mu (1-\sigma (1))}< R-\frac{C}{\mu (1-\sigma (q_0^*))}<R-\frac{C}{\mu (1-\sigma (0))}\\\Leftrightarrow & R-\frac{C}{\mu (1-(2\rho +1-\sqrt{1+4\rho })/2)}< 0<R-\frac{C}{\mu }\\\Leftrightarrow & \frac{C}{\mu }< R<\frac{C}{\mu (1-(2\rho +1-\sqrt{1+4\rho })/2)}\\\Leftrightarrow & 1< \frac{R\mu }{C}<\frac{2}{1-2\rho +\sqrt{1+4\rho }} \end{aligned}$$

which yields the interval for \(\nu \) in Case 2.

Moreover, \(q_0^*\) can be found in closed form in this case. Indeed, the defining equation for \(q_0^*\), \(R-\frac{C}{\mu (1-\sigma (q_0^*))}=0\), can be written as \(1-\sigma (q_0^*)=\frac{C}{R\mu }=\frac{1}{\nu }\). Using (5.6), we arrive, after some algebraic manipulations, at

$$\begin{aligned} (\rho q_0^*-\rho +1)^2+4\rho =\left( \frac{2}{\nu }+\rho +\rho q_0^*-1\right) ^2. \end{aligned}$$
(5.7)

Therefore, factorizing the difference of the two squares, we obtain

$$\begin{aligned} \left( \frac{2}{\nu }+2\rho q_0^*\right) \left( \frac{2}{\nu }+2\rho -2\right) =4\rho \end{aligned}$$

and, solving for \(q_0^*\), we obtain (5.3), which concludes Case 2.

Case 3 Equilibrium strategy (1, 0).

(1, 0) is equilibrium strategy if and only if \(S_1(1,0)\le 0\le S_0(1,0)\). When \((q_0,q_1)=(1,0)\), equations (4.38) and (4.39) assume the form:

$$\begin{aligned} S_0(1,0)= & R-\frac{C}{\mu }\cdot \frac{1}{(1-\tau )}, \end{aligned}$$
(5.8)
$$\begin{aligned} S_1(1,0)= & R-\frac{C}{\mu }\left( \frac{\rho (\rho -\tau )-\tau }{\rho (\rho -\tau )}+\frac{1}{1-\tau }\right) , \end{aligned}$$
(5.9)

where \(\tau =\rho _2(1,0)\). Using (4.10), we derive that

$$\begin{aligned} \tau =\frac{2\rho +1-\sqrt{1+4\rho }}{2}. \end{aligned}$$
(5.10)

Therefore, (1, 0) is equilibrium if and only if

$$\begin{aligned} R-\frac{C}{\mu }\left( \frac{\rho (\rho -\tau )-\tau }{\rho (\rho -\tau )}+\frac{1}{1-\tau }\right) \le 0\le R-\frac{C}{\mu }\cdot \frac{1}{(1-\tau )}. \end{aligned}$$

After some rearrangement of terms and simplifications, this is shown to be equivalent to

$$\begin{aligned} \frac{C}{\mu }\cdot \frac{2}{1-2\rho +\sqrt{1+4\rho }}\le R\le \frac{C}{\mu }\cdot \frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }}, \end{aligned}$$

and multiplying by \(\frac{\mu }{C}\) and substituting \(\nu =\frac{R\mu }{C}\) concludes with Case 3.

Case 4 Equilibrium strategy \((1,q_1^*)\), with \(q_1^*\in (0,1)\).

For \(q_1^*\in (0,1)\), \((1,q_1^*)\) is equilibrium strategy if and only if \(S_1(1,q_1^*)=0\). By (4.39), we have that

$$\begin{aligned} S_1(1,q_1^*)= & R-\frac{C}{\mu }\left( \frac{\rho (\rho -\upsilon (q_1^*))+\rho q_1^*-\upsilon (q_1^*)}{\rho (\rho -\upsilon (q_1^*))+\rho q_1^*}\right. \nonumber \\ & \quad \left. +\frac{1}{1-\upsilon (q_1^*)}\right) , \end{aligned}$$
(5.11)

where \(\upsilon (q_1)=\rho _2(1,q_1)\). Using (4.10) and after some algebraic simplifications, we derive that

$$\begin{aligned} \upsilon (q_1)=\frac{2\rho +1-\sqrt{1+4\rho (1-q_1)}}{2}. \end{aligned}$$
(5.12)

Note, now, that \(\upsilon (q_1^*)\) is a root of (4.17) for \(q_0=1\) and \(q_1=q_1^*\), hence

$$\begin{aligned} \rho q_1^*=(2\rho +1)\upsilon (q_1^*)-(\upsilon (q_1^*))^2-\rho ^2. \end{aligned}$$
(5.13)

Using (5.13), we can easily see that \(\rho (\rho -\upsilon (q_1^*))+\rho q_1^*=(\rho +1-\upsilon (q_1^*))\upsilon (q_1^*)\). Therefore, (5.11) is written equivalently as

$$\begin{aligned} S_1(1,q_1^*)= & R-\frac{C}{\mu }\left( 1-\frac{1}{\rho +1-\upsilon (q_1^*)}+\frac{1}{1-\upsilon (q_1^*)}\right) \nonumber \\= & R-\frac{C}{\mu }-\frac{C\rho }{\mu }\cdot \frac{1}{(\rho +1-\upsilon (q_1^*))(1-\upsilon (q_1^*))} \end{aligned}$$
(5.14)

Therefore, \((1,q_1^*)\) is equilibrium if and only if

$$\begin{aligned} R-\frac{C}{\mu }-\frac{C\rho }{\mu }\cdot \frac{1}{(\rho +1-\upsilon (q_1^*))(1-\upsilon (q_1^*))}=0\;\;\; \text{ and } \;\;\; q_1^*\in (0,1). \end{aligned}$$

Note, now, that the function

$$\begin{aligned} g(\upsilon )=R-\frac{C}{\mu }\left( 1-\frac{1}{\rho +1-\upsilon }+\frac{1}{1-\upsilon }\right) =R-\frac{C}{\mu }-\frac{C\rho }{\mu }\cdot \frac{1}{(\rho +1-\upsilon )(1-\upsilon )} \nonumber \\ \end{aligned}$$
(5.15)

is strictly decreasing in \(\upsilon \), whereas \(\upsilon (q_1)\) given by (5.12) is clearly strictly increasing in \(q_1\). Therefore,

$$\begin{aligned} q_1^*\in (0,1)\Leftrightarrow \upsilon (q_1^*)\in (\upsilon (0),\upsilon (1))=(\tau ,\rho ). \end{aligned}$$

Hence, \((1,q_1^*)\) with \(q_1^* \in (0,1)\) is equilibrium if and only if

$$\begin{aligned} & \tau<\upsilon (q_1^*)<\rho \nonumber \\\Leftrightarrow & S_1(1,1)<S_1(1,q_1^*)<S_1(1,0)\nonumber \\\Leftrightarrow & R-\frac{C}{\mu (1-\rho )}< 0<R-\frac{C}{\mu }\left( 1-\frac{1}{\rho +1-\tau }+\frac{1}{1-\tau }\right) \nonumber \\\Leftrightarrow & 1-\frac{1}{\rho +1-\tau }+\frac{1}{1-\tau }< \frac{R\mu }{C} <\frac{1}{(1-\rho )}. \end{aligned}$$
(5.16)

Substituting \(\tau \) given by (5.10) and using \(\nu =\frac{R\mu }{C}\) shows that this is equivalent to

$$\begin{aligned} \frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }}<\nu <\frac{1}{1-\rho } \end{aligned}$$

which yields the interval for \(\nu \) in Case 4.

Moreover, \(q_1^*\) can be found explicitly in this case. Indeed, the defining equation for \(q_1^*\) is \(S_1(1,q_1^*)=0\), which can be written equivalently as

$$\begin{aligned} R-\frac{C}{\mu }-\frac{C\rho }{\mu }\cdot \frac{1}{(\rho -1)\upsilon (q_1^*)-\rho ^2+\rho +1-\rho q_1^*}=0, \end{aligned}$$
(5.17)

because of (5.14) and (5.13). Solving for \(\upsilon (q_1^*)\) yields

$$\begin{aligned} \upsilon (q_1^*)=\frac{1}{1-\rho }\left( 1+\rho -\rho ^2-\rho q_1^* -\frac{C\rho }{R\mu -C}\right) . \end{aligned}$$
(5.18)

Equating the two expressions for \(\upsilon (q_1^*)\) given by (5.12) and (5.18) yields a quadratic equation for \(q_1^*\). Solving this equation and choosing the root that belongs to (0, 1) yields (5.4), which concludes Case 4.

Case 5 Equilibrium strategy (1, 1).

(1, 1) is equilibrium strategy if and only if \(S_1(1,1)\ge 0\). Under strategy (1, 1), the system behaves as an M/M/1 queue with arrival rate \(\lambda \) and service rate \(\mu \); hence \(S_1(1,1)=R-\frac{C}{\mu (1-\rho )}\). Therefore, (1, 1) is equilibrium if and only if \(R-\frac{C}{\mu (1-\rho )}\ge 0\), which is equivalent to \(\nu =\frac{R\mu }{C}\ge \frac{1}{1-\rho }\), which concludes Case 5. \(\square \)

When \(\rho \ge 1\), Theorem 5.1 continues to be valid with appropriate adaptations. More concretely, some cases cease to exist. Indeed, from the stability condition (4.7), we see that strategies of the form \((1,q_1)\), with \(q_1\in [0,1]\), cannot be equilibrium strategies when \(\rho \ge 2\). Moreover, the strategy (1, 1) cannot be equilibrium strategy for \(\rho \ge 1\). Therefore, for \(\rho \in [1,2)\), the cases 1–3 of the Theorem are still valid and the case 4 holds for \(\nu \in \left( \frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }},\infty \right) \). For \(\rho \in [2,\infty )\), the case 1 of the Theorem is valid and the case 2 holds for \(\nu \in (1,\infty )\).

Now, we can use the formulas (4.40) and (4.41) to obtain the equilibrium throughput and the equilibrium social welfare as \(\nu \) increases from 0 to \(\infty \).

Corollary 5.1

Regarding the equilibrium throughput, \(TH^{lcd-e}\), and the equilibrium social welfare per time unit, \(SW^{lcd-e}\), we have the following cases, when \(\rho <1\):

  1. 1.

    \(\nu \in [0,1]\). Then

    $$\begin{aligned} TH^{lcd-e}=0 \end{aligned}$$
    (5.19)

    and

    $$\begin{aligned} SW^{lcd-e}=0. \end{aligned}$$
    (5.20)
  2. 2.

    \(\nu \in \left( 1,\frac{2}{1-2\rho +\sqrt{1+4\rho }}\right) \). Then

    $$\begin{aligned} TH^{lcd-e}=\frac{\lambda q_0^*}{1+\lambda q_0^*}, \end{aligned}$$
    (5.21)

    where \(q_0^*\) is given by (5.3) and

    $$\begin{aligned} SW^{lcd-e}=0. \end{aligned}$$
    (5.22)
  3. 3.

    \(\nu \in \left[ \frac{2}{1-2\rho +\sqrt{1+4\rho }},\frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }}\right] \). Then

    $$\begin{aligned} TH^{lcd-e}=\frac{\lambda }{2} \end{aligned}$$
    (5.23)

    and

    $$\begin{aligned} SW^{lcd-e}=C\left( \frac{\rho }{2}\nu -\frac{\rho }{1-2\rho +\sqrt{1+4\rho }}\right) . \end{aligned}$$
    (5.24)
  4. 4.

    \(\nu \in \left( \frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }},\frac{1}{1-\rho }\right) \). Then

    $$\begin{aligned} TH^{lcd-e}=\frac{\lambda }{2-q_1^*}, \end{aligned}$$
    (5.25)

    where \(q_1^*\) is given by (5.4) and

    $$\begin{aligned} SW^{lcd-e}=C\rho \frac{1-q_1^*}{2-q_1^*}\left( \nu -\frac{\rho +(1-v(q_1^*))^2q_1^*}{[\rho +(1-v(q_1^*))q_1^*](1-v(q_1^*))}\right) , \end{aligned}$$
    (5.26)

    where \(q_1^*\) is given by (5.4) and

    $$\begin{aligned} v(q_1^*)=\frac{2\rho +1-\sqrt{1+4\rho -4\rho q_1^*}}{2}. \end{aligned}$$
    (5.27)
  5. 5.

    \(\nu \in \left[ \frac{1}{1-\rho },\infty \right) \). Then

    $$\begin{aligned} TH^{lcd-e}=\lambda \end{aligned}$$
    (5.28)

    and

    $$\begin{aligned} SW^{lcd-e}=C\rho \left( \nu -\frac{1}{1-\rho }\right) . \end{aligned}$$
    (5.29)

Proof

We substitute the equilibrium probabilities \(q_0\) and \(q_1\) in the formulas (4.40) and (4.41), according to the various cases of Theorem 5.1. After some algebraic simplifications we derive the various formulas of the Corollary. \(\square \)

6 Comparisons with other information structures

In this section we present some results concerning the comparison of the lcd model with the un (Edelson & Hildebrand, 1975) and obs (Naor, 1969) models. Let \(q^{un-e}\) be the equilibrium probability of the un model which is given as

$$\begin{aligned} q^{un-e}=\left\{ \begin{array}{ll} 0 & \text{ if } \nu \in [0,1], \\ \frac{\nu -1}{\nu \rho } & \nu \in \left( 1,\frac{1}{1-\rho }\right) ,\\ 1 & \text{ if } \nu \in \left[ \frac{1}{1-\rho },\infty \right) , \end{array} \right. \end{aligned}$$
(6.1)

(see e.g., Hassin & Haviv, 2003 Table 3.1) and \(TH^{un-e}\), \(SW^{un-e}\) be the corresponding equilibrium throughput, equilibrium social welfare. Moreover, we denote by \(TH^{obs-e}\) and \(SW^{obs-e}\) the throughput and the social welfare of the obs model when customers enter according to Naor’s individually optimal threshold \(\left\lfloor \frac{R\mu }{C}\right\rfloor =\lfloor \nu \rfloor \).

To present several numerical results concerning the comparison of the various models, we will consider a numerical experiment with parameters \(\lambda =0.8\), \(\mu =1\), \(C=1\) and \(R\in [0,6]\), which we will refer to as the ‘standard numerical scenario’. Note that in this scenario we have that \(\rho =0.8\), and \(\nu \in [0,6]\). This numerical scenario is typical. Indeed, we have considered a large number of other parameter values and the numerical results are similar, in the sense that the various figures have similar shapes leading to the same findings and interpretations.

We articulate the presentation of the analytical and the numerical results in three subsections, for the equilibrium probabilities, the equilibrium throughput and the equilibrium social welfare.

6.1 Comparison of the equilibrium probabilities

The equilibrium joining probabilities for the lcd and the un models satisfy a universal inequality. The inequality states that the join probability of the un model is always between the two join probabilities of the lcd model. In addition, the equilibrium join probability for customers who follow balking (respectively joining) customers in the lcd model is greater than or equal (respectively less than or equal) to the equilibrium join probability of the un model.

Theorem 6.1

Let \(\left( q_0^{lcd-e},q_1^{lcd-e}\right) \) be the equilibrium strategy for an lcd model, given according to the various cases of Theorem 5.1, and \(q^{un-e}\) the equilibrium strategy for the corresponding un model, given by (6.1). Then

$$\begin{aligned} q_0^{lcd-e}\ge q^{un-e} \ge q_1^{lcd-e}. \end{aligned}$$
(6.2)

Proof

Let \(S(q_0,q_1)\) be the net benefit of a tagged customer who joins given that the strategy of the population is \((q_0,q_1)\). Then, conditioning on the last decision before her arrival and using (4.1) we have that

$$\begin{aligned} S(q_0,q_1)=\frac{1-q_1}{1-q_1+q_0}S_0(q_0,q_1)+\frac{q_0}{1-q_1+q_0}S_1(q_0,q_1). \end{aligned}$$
(6.3)

Moreover, the functions \(S_0(q_0,q_1)\), \(S_1(q_0,q_1)\) and \(S(q_0,q_1)\) are all decreasing in \(q_0\) and \(q_1\).

We now consider the various cases of Theorem 5.1 separately.

Case 1 (\(\nu \in [0,1]\)):

In this case, we have \(q_0^{lcd-e}=q_1^{lcd-e}=q^{un-e}=0\) and the inequality (6.2) is valid.

Case 2 \(\left( \nu \in \left( 1,\frac{2}{1-2\rho +\sqrt{1+4\rho }}\right) \right) \):

In this case, the equilibrium \(q_0^{lcd-e}\) is characterized by the equation \(S_0\left( q_0^{lcd-e},0\right) =0\), whereas \(q^{un-e}\) is characterized by the equation \(S\left( q^{un-e},q^{un-e}\right) =0\). Using (6.3), we have that

$$\begin{aligned} 0=S\left( q^{un-e},q^{un-e}\right) =\left( 1-q^{un-e}\right) S_0\left( q^{un-e},q^{un-e}\right) +q^{un-e}S_1\left( q^{un-e},q^{un-e}\right) . \end{aligned}$$

But \(S_0\left( q^{un-e},q^{un-e}\right) >S_1\left( q^{un-e},q^{un-e}\right) \) (because of (5.1)), so necessarily \(S_0\left( q^{un-e},q^{un-e}\right) >0\). Now, \(S_0(q_0,q_1)\) is decreasing in \(q_0\) and \(q_1\); hence \(S_0(q^{un-e},0)\ge S_0\left( q^{un-e},q^{un-e}\right) >0\). However, note that \(S_0(q_0^{lcd-e},0)=0\) (by the defining equation of \(q_0^{lcd-e}\)) and we conclude that \(S_0(q^{un-e},0)>S_0(q_0^{lcd-e},0)\). Using the monotonicity of \(S_0(q_0,q_1)\), we conclude that \(q^{un-e}<q_0^{lcd-e}\). On the other hand, we have that for this case \(q_1^{lcd-e}=0\le q^{un-e}\) and the inequality (6.2) is valid.

Case 3 \(\left( \nu \in \left[ \frac{2}{1-2\rho +\sqrt{1+4\rho }},\frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }}\right] \right) \):

In this case, we have that \(q_0^{lcd-e}=1\), \(q_1^{lcd-e}=0\), whereas \(q^{un-e}\in (0,1)\). Hence, the inequality (6.2) is valid.

Case 4 \(\left( \nu \in \left( \frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }},\frac{1}{1-\rho }\right) \right) \):

In this case, the equilibrium \(q_1^{lcd-e}\) is characterized by the equation \(S_1\left( 1,q_1^{lcd-e}\right) =0\), whereas \(q^{un-e}\) is characterized by the equation \(S\left( q^{un-e},q^{un-e}\right) =0\). Using (6.3), we have that

$$\begin{aligned} 0=S\left( q^{un-e},q^{un-e}\right) =\left( 1-q^{un-e}\right) S_0\left( q^{un-e},q^{un-e}\right) +q^{un-e}S_1\left( q^{un-e},q^{un-e}\right) . \end{aligned}$$

But \(S_0\left( q^{un-e},q^{un-e}\right) >S_1\left( q^{un-e},q^{un-e}\right) \) (because of (5.1)), so necessarily \(S_1\left( q^{un-e},q^{un-e}\right) <0\). Now, \(S_1(q_0,q_1)\) is decreasing in \(q_0\) and \(q_1\); hence \(S_1(1,q^{un-e})\le S_1\left( q^{un-e},q^{un-e}\right) <0\). However, note that \(S_1(1,q_1^{lcd-e})=0\) (by the defining equation of \(q_1^{lcd-e}\)) and we conclude that \(S_1(1,q^{un-e})<S_1(1,q_1^{lcd-e},0)\). Using the monotonicity of \(S_1(q_0,q_1)\), we conclude that \(q^{un-e}>q_1^{lcd-e}\). On the other hand, we have that for this case \(q_0^{lcd-e}=1\ge q^{un-e}\) and the inequality (6.2) is valid.

Case 5 \(\left( \nu \in \left[ \frac{1}{1-\rho },\infty \right) \right) \):

In this case, we have \(q_0^{lcd-e}=q_1^{lcd-e}=q^{un-e}=1\) and the inequality (6.2) is valid. \(\square \)

To illustrate the result we consider the standard numerical scenario that we described in the beginning of the Section and plot the equilibrium joining probabilities as functions of the service value. The graphs are shown in Fig. 2.

Fig. 2
figure 2

Equilibrium joining probabilities for \(\rho =0.8\), \(\nu \in [0,6]\)

Full size image

6.2 Comparison of the equilibrium social welfare functions

An analytical comparison result shows that the lcd model outperforms the un model with respect to the equilibrium social welfare functions.

Theorem 6.2

Let \(SW^{lcd-e}\) be the equilibrium social welfare for an lcd model, given according to the various cases of Corollary 5.1, and \(SW^{un-e}\) the equilibrium strategy for the corresponding un model. Then we have the following cases:

  1. 1.

    \(\nu \in \left[ 0,\frac{2}{1-2\rho +\sqrt{1+4\rho }}\right] \). Then

    $$\begin{aligned} SW^{lcd-e}=SW^{un-e}=0. \end{aligned}$$
    (6.4)
  2. 2.

    \(\nu \in \left( \frac{2}{1-2\rho +\sqrt{1+4\rho }},\frac{1}{1-\rho }\right) \). Then

    $$\begin{aligned} SW^{lcd-e}>SW^{un-e}=0. \end{aligned}$$
    (6.5)
  3. 3.

    \(\nu \in [\frac{1}{1-\rho },\infty )\). Then

    $$\begin{aligned} SW^{lcd-e}=SW^{un-e}=C\rho \left( \nu -\frac{1}{1-\rho }\right) >0. \end{aligned}$$
    (6.6)

Consider a model with fixed \(\lambda \), \(\mu \) and C and let R vary. Denote by \(SW^{lcd-e}(\nu )\) and \(SW^{un-e}(\nu )\) the equilibrium social welfare of the lcd and the unobservable model as functions of the normalized service value \(\nu =\frac{R\mu }{C}\). Then, the difference \(SW^{lcd-e}(\nu )-SW^{un-e}(\nu )\) is a unimodal function of \(\nu \) which attains its maximum at \(\frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }}\).

Proof

When \(\nu \in \left[ 0,\frac{2}{1-2\rho +\sqrt{1+4\rho }}\right] \), we have that \(SW^{lcd-e}=0\) (Cases 1 and 2 of Corollary 5.1). Moreover \(q^{un-e}\) is either 0 or such that it leaves zero net benefit to a customer who joins (see formula (6.1)). Hence \(SW^{un-e}=0\) and we conclude with Case 1 of the Theorem.

When \(\nu \in \left( \frac{2}{1-2\rho +\sqrt{1+4\rho }},\frac{1}{1-\rho }\right) \), then we have Cases 3 and 4 of Theorem 5.1. In Case 3, we have that the equilibrium strategy is (1, 0) and \(S_0(1,0)>0>S_1(1,0)\), so for the equilibrium social welfare (see (4.41)) we have:

$$\begin{aligned} SW^{lcd-e}=SW^{lcd}(1,0)= & \lambda S_0(1,0)>0. \end{aligned}$$

In Case 4, we have that the equilibrium strategy is \((1,q_1^*)\) and \(S_0(1,q_1^*)>0=S_1(1,q_1^*)\), so for the equilibrium social welfare (see (4.41)) we have:

$$\begin{aligned} SW^{lcd-e}=SW^{lcd}(1,q_1^*)= & p_I(0)\lambda S_0(1,q_1^*)+ p_I(1)\lambda q_1^*S_1(1,q_1^*)>0. \end{aligned}$$

Moreover \(q^{un-e}\) is such that it leaves zero net benefit to a customer who joins (see formula (6.1)). Hence \(SW^{un-e}=0\) and we conclude with Case 2 of the Theorem.

When \(\nu \in \left[ \frac{1}{1-\rho },\infty \right) \), all customers join in equilibrium under both the lcd and the un models so the two social welfare functions coincide and are given by formula (5.29). This implies Case 3 of the Theorem.

Now, we have immediately that the difference \(SW^{lcd-e}(\nu )-SW^{un-e}(\nu )\) is 0 when \(\nu \in \left[ 0,\frac{2}{1-2\rho +\sqrt{1+4\rho }}\right] \) or \(\nu \in \left[ \frac{1}{1-\rho },\infty \right) \) (Cases 1 and 3 of the present Theorem). In the remaining case where \(\nu \in \left( \frac{2}{1-2\rho +\sqrt{1+4\rho }},\frac{1}{1-\rho }\right) \), we consider two subcases that correspond to Cases 3 and 4 of Theorem 5.1. In the first subcase, where \(\nu \in \left( \frac{2}{1-2\rho +\sqrt{1+4\rho }},\frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }}\right] \), we have that \(SW^{lcd-e}(\nu )-SW^{un-e}(\nu )=SW^{lcd-e}(\nu )\) which is given by (5.24) which is a linear function of \(\nu \) with positive rate \(\frac{C\rho }{2}\). Therefore, \(SW^{lcd-e}(\nu )-SW^{un-e}(\nu )\) is increasing for \(\nu \in \left( \frac{2}{1-2\rho +\sqrt{1+4\rho }},\frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }}\right] \). In the second subcase, where \(\nu \in \left[ \frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }},\frac{1}{1-\rho }\right) \), we have that the equilbrium strategy is \((1,q_1^*(\nu ))\). Using (4.41), we have

$$\begin{aligned} SW^{lcd-e}(\nu )-SW^{un-e}(\nu )= & SW^{lcd-e}(\nu )=SW^{lcd}(1,q_1^*(\nu ))\nonumber \\= & \frac{\lambda (1-q_1^*(\nu )) S_0(1,q_1^*(\nu ))+\lambda q_1^*(\nu ) S_1(1,q_1^*(\nu ))}{2-q_1^*(\nu )}\nonumber \\= & \lambda \cdot \frac{1-q_1^*(\nu )}{2-q_1^*(\nu )}\cdot S_0(1,q_1^*(\nu )), \end{aligned}$$
(6.7)

since \(S_1(1,q_1^*(\nu ))=0\). Now, the functions \(\frac{1-q_1}{2-q_1}\) and \(S_0(1,q_1)\) are both decreasing and positive so \(\lambda \frac{1-q_1}{2-q_1}S_0(1,q_1)\) is decreasing. Moreover, \(q_1^*(\nu )\) is increasing in \(\nu \). Therefore, we conclude that \(SW^{lcd-e}(\nu )-SW^{un-e}\) is decreasing for \(\nu \in \left[ \frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }},\frac{1}{1-\rho }\right) \). This shows the unimodality of \(SW^{lcd-e}(\nu )-SW^{un-e}\) and its maximum is attained for \(\nu =\frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }}\). \(\square \)

Theorem 6.2 shows that for low and high values of the service value, the social welfare functions coincide and consequently providing information about the last customer decision for this range of \(\nu \) does not improve the economic performance of a system. However, for intermediate values of \(\nu \), there is some difference which is maximized for the normalized service value \(\nu =\frac{5\rho +1-(\rho +1)\sqrt{1+4\rho }}{3\rho -\rho \sqrt{1+4\rho }}\). This value constitutes the boundary between Cases 3 and 4 of Theorem 5.1, that is it is the value where the equilibrium strategy changes from (1, 0) to \((1,q_1^*)\) with \(q_1^*\). Therefore, we see that providing the information about the last customer’s decision is particularly valuable for normalized service values near to this boundary point.

Unfortunately, due to the nature of the social welfare function of the observable model (see e.g. Economou, 2021 p.148), an analytical comparison between the equilibrium social welfare between the observable and the lcd models does not seem possible. Nevertheless, in all numerical experiments, the observable model outperforms the lcd model. In Fig. 3, we show the graphs of the equilibrium social welfare functions, as the service value varies, for the standard numerical scenario.

Fig. 3
figure 3

Equilibrium social welfare functions for \(\rho =0.8\), \(\nu \in [0,6]\)

Full size image

6.3 Comparison of the equilibrium throughput functions

The analytical comparison of the throughput functions for the lcd, the un and the obs models seems particularly difficult (if not impossible) due to the corresponding involved formulas (see Corollary 5.1 for the lcd model - Cases 2 and 4 and the corresponding formulas for the obs and un models). Extensive numerical experiments have consistently shown the following findings as the normalized service value, \(\nu \), varies (assuming that the parameters \(\lambda \), \(\mu \) and C, are kept fixed):

  1. 1.

    \(TH^{obs-e}(\nu )>TH^{lcd-e}(\nu )>TH^{un-e}(\nu )\), for low values of \(\nu \) (but greater than 1).

  2. 2.

    \(TH^{obs-e}(\nu )<TH^{lcd-e}(\nu )<TH^{un-e}(\nu )\), for high values of \(\nu \) (but smaller than \(\frac{1}{1-\rho }\)).

  3. 3.

    \(TH^{obs-e}(\nu )<TH^{lcd-e}(\nu )=TH^{un-e}(\nu )\), for \(\nu \ge \frac{1}{1-\rho }\).

  4. 4.

    The functions \(TH^{lcd-e}(\nu )\) and \(TH^{un-e}(\nu )\) cross only once in \(\left( 1,\frac{1}{1-\rho }\right) \). More concretely, there exists \(\nu ^*\) such that \(TH^{lcd-e}(\nu )>TH^{un-e}(\nu )\), for \(\nu \in (1,\nu ^*)\), whereas \(TH^{lcd-e}(\nu )<TH^{un-e}(\nu )\), for \(\nu \in \left( \nu ^*,\frac{1}{1-\rho }\right) \).

These findings are illustrated in Fig. 4, where we see the graphs of the equilibrium throughput functions for the standard numerical scenario.

Fig. 4
figure 4

Equilibrium throughput functions for \(\rho =0.8\), \(\nu \in [0,6]\)

Full size image

7 Conclusions and extensions

In this paper we studied the effect of providing information about last customer’s decision on strategic customers who face the dilemma of whether to join or balk at the arrival instants of an M/M/1 queue. This kind of information smooths the effective arrival process and has been shown to be beneficial for the social welfare in comparison to the unobservable model, in particular for intermediate values of the service reward. Therefore, in systems where the information about the queue length cannot be communicated to the customers (as it is the case of several models that we discussed in the introduction), the provision of information about the last customer’s decision is advantageous.

The present study constitutes the first step towards a more complete understanding of the pros and cons of communicating the decisions of other customers to the strategic customers of a service system. There are a number of directions for the generalization and extension of this idea.

In the framework of the join-or-balk dilemma for the arrivals at an M/M/1 queue, the most natural extension is to consider the situation where the customers are informed upon arrival about the decisions of more than one recent arrivals. There is a whole family of models in this area that are currently under investigation (see e.g. Economou, 2024). For example, each arriving customer may be informed about the join-or-balk decisions of the N more recent arrivals. Then, in this ‘generalized Bernoulli’ model, the information I(t) is an N-vector of 0 s and 1 s and a customer’s strategy is a vector \(\textbf{q}=(q_{i_1,i_2,\ldots ,i_n}:(i_1,i_2,\ldots ,i_n)\in \{0,1\}^N)\). Another possibility is that arriving customers are informed about the number of joining customers since the last customer who balked. In this ‘geometric’ model the information I(t) is a non-negative integer and a customer’s strategy is an infinite sequence \(\textbf{q}=(q(0),q(1),q(2),\ldots )\). The performance evaluation of the underlying queueing models under an arbitrary strategy and the characterization and computation of equilibrium customer strategies seem challenging problems in the area of Rational Queueing.