Optimal control of a dynamic production-inventory system with various cost criteria

Abstract

In this article, we investigate the dynamic control problem of a production-inventory system. Here, demands arrive at the production unit according to a Poisson process and are processed in an FCFS manner. The processing time of the customer’s demand is exponentially distributed. Production manufacturers produce items on a make-to-order basis to meet customer demands. The production is run until the inventory level becomes sufficiently large. We assume that the production time of an item follows an exponential distribution and that the amount of time for the produced item to reach the retail shop is negligible. In addition, we assume that no new customer joins the queue when there is void inventory. Moreover, when a customer is waiting in an infinite FIFO queue for service, he/she does not leave the queue even if the inventory is exhausted. This yields an explicit product-form solution for the steady-state probability vector of the system. The optimal policy that minimizes the discounted/average/pathwise average total cost per production is derived using a Markov decision process approach. We find an optimal policy using value/policy iteration algorithms. Numerical examples are discussed to verify the proposed algorithms.

1 Introduction

Inventory theory has useful applications in various day-to-day real-life scenarios. One such application is production control, in which decision-makers focus on controlling costs while satisfying customer demands and maintaining their goodwill. Over the last decade, research on complex integrated production-inventory systems or service-inventory systems has found much attention, often in connection with the research on integrated supply chain management, see He et al. (2002), He and Jewkes (2001), Helmes et al. (2015), Krishnamoorthy et al. (2015), Krishnamoorthy and Narayanan (2013), Malini and Shajin (2020), Pal et al. (2012), Sarkar (2012) and Veatch and Wein (1994). In these articles, the authors considered (s, S)/(s, Q)-type policy to study their inventory models.

Sigman and Simchi-Levi (1992) and Melikov and Molchanov (1992) introduced the integrated queueing-inventory models. Whereas the article by Sigman and Simchi-Levi (1992) considered the Poisson arrival of demands, arbitrarily distributed service time, and exponentially distributed replenishment lead time. Also, they showed that the resulting queueing-inventory system is stable if and only if the service rate is higher than the customer arrival rate. The authors considered that the customers might join the system even when the inventory level is zero and discussed the case of non-exponential lead-time distribution. Berman et al. (1993) followed them with deterministic service times and formulated the model as a dynamic programming problem. For more inventory models with positive service times, see Berman and Kim (1999, 2004), Arivarignan et al. (2002), Krishnamoorthy et al. (2006a, 2006b), for a recent extensive survey of the literature we refer in Krishnamoorthy et al. (2021), it provides the summary of work done until 2019.

We recall the remarkable work of Schwarz et al. (2006). They propose product form solutions for the system state distribution under the assumption that customers do not join when the inventory level is zero, where the service/lead time is exponentially distributed, and demands follow a Poisson distribution. Krishnamoorthy and Narayanan (2013) reduced the Schwarz et al. (2006) model to a production-inventory system with single-batch bulk production of the quantum of inventory required. The production-inventory with service time and protection for a few of the final phases of production and service is discussed in Sajeev (2012).

Saffari et al. (2011) considered an M/M/1 queue with inventoried items for service, where the control policy followed is (s, Q) and the lead time is a mixed exponential distribution. They assumed that when inventory stock is empty, fresh arrivals are lost to the system, and thus, they obtain a product form solution for the system state probability. Schwarz et al. (2007) studied an inventory system with queueing networks. The authors assumed that at each service station, an order for replenishment is made when the inventory level at that station drops to its reorder level; hence, no customer is lost to the system. Zhao and Lian (2011) used dynamic programming to obtain the necessary and sufficient conditions for a priority queueing inventory system to be stable.

In all the papers quoted above, customers are provided with an item from the inventory after the completion of service. In Krishnamoorthy et al. (2015), customers may not get an inventory after the completion of service. They studied the optimization problem and obtained the optimal pairs (s, S) and (s, Q) corresponding to the expected minimum costs.

In this study, we do not use any common inventory control policies such as (s, S)/ (s, Q)-type. We consider the problem of finding the optimal production rates for discounted/long-run average/pathwise average cost criteria of the dynamic production-inventory system. Here, we consider an $M/M/1/ \infty$ production-inventory system with positive service time. Customers’ demands arrive one at a time according to Poisson processes. Service and production times follow an exponential distribution. Each production is 1 units, and the production process is run until the inventory level becomes sufficiently large (infinity). It is assumed that the amount of time for the item produced to reach the retail shop is negligible. We assume that no customer joins a queue when the inventory level is zero. This assumption leads to an explicit product-form solution for the steady-state probability vector using a simple approach. In this paper, we have directly obtained a product-form solution for the steady-state probability vector from the balance equation. Readers are referred to Neuts (1989, 1994), Chakravarthy and Alfa (1986), and Chakravarthy (2022a, 2022b) where the authors obtain a such product-form solution for the steady-state probability vector using matrix analytic methods.

In this paper, we find an optimal stationary policy by policy/value iteration algorithm. We see that there are many studies on inventory production control theory on continuous-time controlled Markov decision processes (CTCMDPs) for discounted/ average/ pathwise average cost criteria (see Federgruen & Zipkin, 1986a; b; Helmes et al., 2015). However, the articles discussed algorithms for finding an optimal stationary policy are, Federgruen and Zhang (1992), He et al. (2002), He and Jewkes (2001). The fixed costs of ordering items or setting up a production process arise in many real-life scenarios. In their presence, the most widely used ordering policy in the stochastic inventory literature is the (s, S) policy. In this context, we mention two important survey papers for discrete/continuous-time regarding (s, S) replenishment policy; see Perera and Sethi (2022a, 2022b) for a comprehensive survey report with the vast literature accumulating the articles over seven decades on the discounted/average cost criterion on discrete/continuous time cases.

The motivation for studying discounted problems comes mainly from economics. For instance, if $\delta$ denotes a rate of discount, then $(1 +\delta )L$ would be the amount of money one would have to pay to obtain a loan of L dollars over a single period. Similarly, the value of a note promises to pay L dollars t time steps into the future would have a present value of $\frac{L}{(1+\delta )^t}=\alpha ^tL$, where $\alpha :=(1+\delta )^{-1}$ denotes the discount factor. This is the case for finite-horizon problems. But in some cases, for instance, processes of capital accumulation for an economy, or some problems with inventory or portfolio management, do not necessarily have a natural stopping time in the definable future, see Hernández-Lerma and Lasserre (1996) and Puterman (1994). Now when decisions are made frequently, the discount rate is very close to 1, or when performance criteria cannot easily be described in economic terms, the the decision maker may prefer to compare policies on the basis of their average expected reward instead of their expected total discounted reward, see Piunovsky and Zhang (2020).

The ergodic problem for controlled Markov processes refers to the problem of minimizing the time-average cost over an infinite time horizon. Hence, the cost over any finite initial time segment does not affect ergodic cost. This makes the analytical analysis of ergodic problems more difficult. However, the sample-path cost $r(\cdot ,\cdot ,\cdot )$, defined by (13), corresponding to an average-cost optimal policy that minimizes the expected average cost may fluctuate from its expected value. To consider these fluctuations, we discuss the pathwise average-cost (PAC) criterion. This study investigates a dynamic production-inventory control problem for the discounted/average/pathwise average cost criterion. We find the optimal production rate through a value/policy iteration algorithm. Finally, numerical examples are included to verify the proposed algorithms.

The remainder of this paper is organized as follows. First, we define the production control problem in Sect. 2. In Sect. 3, we discuss the steady-state analysis of this model and describe the evaluation of the control system. In addition, we define our cost criterion and assumptions required to obtain an optimal policy. Section 4 discusses the discount cost criterion. Here, we find a solution for the optimality equation corresponding to the discounted cost criterion and provide its value/policy iteration algorithms. The next section deals with the optimality equation and policy iteration algorithm corresponding to the average cost criterion. We perform the same analysis in Sect. 6 for the pathwise average cost criterion, as in Sect. 5. Finally, in Sect. 7, we provide concluding remarks and highlight the directions for future research.

Notations

• ${\mathcal {N}}(t)$: number of customers in the system at time t.

• ${\mathcal {I}}(t)$: inventory level in the system at time t.

• $e: (1, 1, \ldots , 1,\ldots )$ a column vector of $1^{\prime }s$ of appropriate order.

• ${\mathbb {N}}_0={\mathbb {N}}\cup \{0\}$, where ${\mathbb {N}}$ is set of all natural numbers.

• $C_b({\mathbb {N}}_0\times {\mathbb {N}}_0)$ is the collection of all bounded functions on ${\mathbb {N}}_0\times {\mathbb {N}}_0$.

2 Problem description

We consider an $M/M/1/ \infty$ dynamic production-inventory system (Fig. 1) with positive service time. Demands by customers for the item occur according to a Poisson process of rate $\lambda$ and each demand asks for one item from the inventory. Processing the customer request requires a random amount of time, which is exponentially distributed with parameter $\mu$ and the requested item will be provided to the customer at the end of his/her service completion. Each production is of one unit and the production process is kept run until the inventory level becomes sufficiently large (infinity). To produce an item, it takes an amount of time that is exponentially distributed with the parameter $\beta$. We assume that no external customer is allowed to join the queue when the inventory level becomes zero; such demands are considered lost sales. We assume that the waiting customers will remain in the queue when the inventory level is empty. It is assumed that the amount of time for the item produced to reach the retail shop is negligible. Thus the system is a continuous-time Markov chain (CTMC) $\left\{ {\mathcal {X}}(t);t\ge 0\right\} =\left\{ \left( {\mathcal {N}}(t),{\mathcal {I}}(t)\right) ; t\ge 0\right\}$ with state space $\varvec{\Omega }=\bigcup \nolimits _{n = 0}^\infty {{\mathcal {L}}(n)},$ where ${\mathcal {L}}(n)$ is called the $n^{th}$ level of the CTMC, is given by, $\left\{ (n,i); i \in {\mathbb {N}}_0\right\} .$

Now the transition rates in the CTMC are:

• $(n,i)\rightarrow (n+1,i)$: rate is $\lambda$, $n\in {\mathbb {N}}_0$, $i\in {\mathbb {N}}$

• $(n,i)\rightarrow (n-1,i-1)$: rate is $\mu$, $n,i\in {\mathbb {N}}$

• $(n,i)\rightarrow (n,i+1)$: rate is $\beta$, $n,i\in {\mathbb {N}}_0.$

• All other transition rates are zero.

Write,

$$\begin{aligned} P\{{\mathcal {N}}(t)=n, {\mathcal {I}}(t)=i\} = P_{n, i}(t). \end{aligned}$$

These satisfy the system of difference-differential equations:

$$\begin{aligned} P^{\prime }_{n,0}(t)&= - \beta P_{n,0}(t) + \mu P_{n+1,1}(t), \quad n\in {\mathbb {N}}_0. \end{aligned}$$

(1)

$$\begin{aligned} P^{\prime }_{n,i}(t)&= - (\lambda +\beta +\mu ) P_{n,i}(t) + \mu P_{n+1,i+1}(t) + \lambda P_{n-1,i}(t) + \beta P_{n, i-1},~n,i \in {\mathbb {N}}. \end{aligned}$$

(2)

The invariant probability measure is obtained under the conditions $\lambda <\mu$ and $\beta <\lambda$ which will be shown in the subsequent section.

Write,

$$\begin{aligned} \lim _{t\rightarrow \infty } P_{n, i}(t)= P_{n, i}, \quad n,i \in {\mathbb {N}}. \end{aligned}$$

Thus, the above set of Eqs. (1) and (2) becomes,

$$\begin{aligned}{} & {} -\beta P_{n,0}+ \mu P_{n+1,1} =0, \quad n \in {\mathbb {N}}_0 \end{aligned}$$

(3)

$$\begin{aligned}{} & {} -(\lambda +\beta +\mu )P_{n,i} + \mu P_{n+1,i+1} + \lambda P_{n-1,i} + \beta P_{n, i-1} = 0, \quad n, i \in {\mathbb {N}}. \end{aligned}$$

(4)

We can solve these equations to find the steady-state probability distribution (Fig. 1).

Fig. 1

Dynamic production-inventory system

The infinitesimal generator of this CTMC $\left\{ {\mathcal {X}}(t);t\ge 0\right\}$ is

$$\begin{aligned} {\varvec{Q}}= \left[ {\begin{array}{*{20}c} {B } &{} {A_0 } &{} {} &{} {} &{} {} &{} {} \\ {A_2 } &{} {A_1 } &{} {A_0 } &{} {} &{} {} &{} {} \\ {} &{} {} {A_2 } &{} {A_1 } &{} {A_0 } &{} \dots \\ {} &{} {} &{} {} {\ddots } &{} {\ddots } &{} {\ddots } \\ \end{array}} \right] , \end{aligned}$$

(5)

where B contains transition rates within ${\mathcal {L}}(0)$; $A_0$ is the arrival matrix that represents the transition rates of customer arrival i.e., $A_0$ represents the transition from level n to level $n+1,$ for any $n \in {\mathbb {N}}_0$; $A_1$ represents the transitions within ${\mathcal {L}}(n)$ for any $n \in {\mathbb {N}}$ and $A_2$ is the service matrix that represents the transition rates of service times i.e., $A_2$ represents transitions from ${\mathcal {L}}(n)$ to ${\mathcal {L}}(n-1), \ n \in {\mathbb {N}}.$ The transition rates are

$$\begin{aligned} \left[ B\right] _{kl}= & {} \left\{ \begin{array}{ll} -\beta , &{} \quad \text {for }l= k = 0, \\ -(\lambda +\beta ), &{} \quad \text {for }l = k; \ k=1, 2,\ldots , \infty ,\\ \beta , &{} \quad \text {for }l = k+1; \ k=0, 1,\ldots , \infty ,\\ 0, &{} \quad \text {otherwise,}\\ \end{array} \right. \\ \left[ A_{0}\right] _{kl}= & {} \left\{ \begin{array}{ll} \lambda , &{} \quad \text {for }l = k; \ k=1, 2,\ldots , \infty ,\\ 0, &{} \quad \text {otherwise,}\\ \end{array} \right. \\ \left[ A_{1}\right] _{kl}= & {} \left\{ \begin{array}{ll} -\beta , &{} \quad \text {for }l = k = 0, \\ -(\lambda +\beta +\mu ), &{} \quad \text {for }l = k; \ k = 1, 2,\ldots ,\infty , \\ \beta , &{} \quad \text {for }l = k+1; \ k = 0,1,\ldots , \infty ,\\ 0, &{} \quad \text {otherwise,}\\ \end{array} \right. \\ \left[ A_{2}\right] _{kl}= & {} \left\{ \begin{array}{ll} \mu , &{} \quad \text {for }l = k-1; \ k = 1, 2,\ldots , \infty ,\\ 0, &{} \quad \text {otherwise.}\\ \end{array} \right. \end{aligned}$$

All other remaining transition rates are zero.

Note: All entries (block matrices) in ${\varvec{Q}}$ have infinite order, and these matrices contain transition rates within the level (in the case of diagonal entries) and between levels (in the case of off-diagonal entries).

3 Analysis of the system

In this section, we discuss the invariant probability measure of a production-inventory model with consideration of stability conditions of the system. We know that the limiting distribution is the unique solution of the system of balance equations when we add the normalizing equation. To obtain the limiting distribution, we assume that $P_{n,i}$ be a solution of (3)–(4). Let $P_{n,i}=Cx^ny^i$ and using (3)–(4), we have

$$\begin{aligned} (\lambda +\beta +\mu )xy=\lambda y+\beta x+\mu x^2 y^2~\text {and}~\beta =\mu xy. \end{aligned}$$

Thus,

$$\begin{aligned} \beta \mu x^2-(\lambda +\mu )\beta x+\beta \lambda =0. \end{aligned}$$

After factorization, we get

$$\begin{aligned} (x-1)(\mu x-\lambda )=0. \end{aligned}$$

(6)

From above equtaion, we have $x=\frac{\lambda }{\mu }$ and $y=\frac{\beta }{\lambda }$. By normalization,

$$\begin{aligned} 1=\sum _{n=0}^{\infty }\sum _{i=0}^{\infty }P_{n,i}=C\sum _{n=0}^{\infty } \sum _{i=0}^{\infty }\left( \frac{\lambda }{\mu }\right) ^n\left( \frac{\beta }{\lambda }\right) ^i=C\frac{1}{\left( 1-\frac{\lambda }{\mu }\right) \left( 1-\frac{\beta }{\lambda }\right) }. \end{aligned}$$

(7)

This implies, $C=\left( 1-\frac{\lambda }{\mu }\right) \left( 1-\frac{\beta }{\lambda }\right)$ and hence

$$\begin{aligned} P_{n,i}=\left( 1-\frac{\lambda }{\mu }\right) \left( 1-\frac{\beta }{\lambda } \right) \left( \frac{\lambda }{\mu }\right) ^n\left( \frac{\beta }{\lambda }\right) ^i. \end{aligned}$$

(8)

Consequently, the stability conditions of the dynamic production-inventory model are given by $\lambda <\mu$ and $\beta <\lambda$. The invariant measure of the CTMC $\left\{ {\mathcal {X}}(t);t\ge 0\right\} =\left\{ \left( {\mathcal {N}}(t),{\mathcal {I}}(t)\right) ; t\ge 0\right\}$ is given by

$$\begin{aligned} {\varvec{P}}=({\varvec{P}}_{\varvec{0}}, {\varvec{P}}_{\varvec{1}},{\varvec{P}}_{\varvec{2}},\dots ), \end{aligned}$$

(9)

where the sub-vectors of ${\varvec{P}}$ are further partitioned as,

$$\begin{aligned} {\varvec{P}}_{\varvec{n}}=(P_{n,0}, P_{n,1}, P_{n,2}, \dots ), \quad n \in {\mathbb {N}}_0, \end{aligned}$$

where $P_{n,i}$ is given in (8). The existence of such invariant measure is ensured by Assumptions 1 and Condition A (which is satisfied by our transition rates); see Remark 2, p. 12–13, for details. For more details about steady-state control of queues exploiting the product form stationary distributions, see, e.g., the recent work of Rahul (2022), Krishnamoorthy et al. (2015), Malini and Shajin (2020) and Neuts (1994).

It is very natural to assume that our production rate function never goes to zero because of heavy starting cost, and at any time, it depends on the number of items in the inventory and the number of demands in the queue, i.e., it is a map

$$\begin{aligned} {\beta }: {\mathbb {N}}_0\times {\mathbb {N}}_0 \rightarrow [\gamma ,R], \end{aligned}$$

where ${\mathbb {N}}_0:=\{0,1,2,\ldots \}$, and $\gamma , R$ are some positive constant. Here in our model, state space is ${\varvec{\Omega }}=\bigcup \nolimits _{n = 0}^\infty \left\{ (n,i); i \in {\mathbb {N}}_0\right\}$, and the action space is $A=[\gamma ,R]$ also let for any state $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$, the corresponding admissible action space is $A(n,i)=[\gamma ,R]$. Now, consider a Borel subset of ${\mathbb {N}}_0\times {\mathbb {N}}_0\times [\gamma ,R]$ denoted by $K:=\{(n,i, {\tilde{\beta }}):n,i\in {\mathbb {N}}_0, {\tilde{\beta }}\in [\gamma ,R]\}$. Recall (p. 6–7) corresponding to state (n, i) and ${\tilde{\beta }}\in [\gamma ,R]$, we denote the transition rates as $\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}$.

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\pi ^{{\tilde{\beta }}}_{(0,i)(0,j)}=(B)_{ij}\\ &{}\pi ^{{\tilde{\beta }}}_{(n,i)(n+1,j)}=(A_0)_{ij}~\text { for any}~n\in {\mathbb {N}}_0\\ &{}\pi ^{{\tilde{\beta }}}_{(n,i)(n,j)}=(A_1)_{ij}~\text { for any}~n\in {\mathbb {N}}\\ &{}\pi ^{{\tilde{\beta }}}_{(n,i)(n-1,j)}=(A_2)_{ij}~\text { for any}~n\in {\mathbb {N}}. \end{array}\right. \end{aligned}$$

(10)

All other transition rates are zero. Note that,

$$\begin{aligned}&\sum _{(m,j)\in {\mathbb {N}}_0\times {\mathbb {N}}_0}\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}\equiv 0,~\forall (n,i, {\tilde{\beta }})\in K \end{aligned}$$

(11)

and

$$\begin{aligned} \displaystyle {\sup _{(n,i) \in {\mathbb {N}}_0 \times {\mathbb {N}}_0 }}\pi ^*_{(n,i)}&={\sup _{(n,i) \in {\mathbb {N}}_0 \times {\mathbb {N}}_0 }}\sup _{{\tilde{\beta }}\in [\gamma ,R]} \pi ^{{\tilde{\beta }}}_{(n,i)}\nonumber \\&={\sup _{(n,i) \in {\mathbb {N}}_0 \times {\mathbb {N}}_0 }} \sup _{{\tilde{\beta }}\in [\gamma ,R]} \Big [ -\pi _{(n,i)(n,i)}^{{\tilde{\beta }}} \Big ]=R+\mu + \lambda <\infty . \end{aligned}$$

(12)

Define $r(n,i,\beta )$ as the cost function in the long run corresponding to production rate function $\beta$. Then the cost function is of the form:

$$\begin{aligned} r(n,i,\beta )&=h\cdot i+c_1\cdot \mu \cdot I_{\{n>0\}}+c_2 \cdot \beta \cdot I_{\{i>S\}}+c_3\cdot \lambda I_{\{i=0\}} \nonumber \\&\quad +c_4\cdot (n-1)I_{\{n\ge 2\}}, \end{aligned}$$

(13)

where h is the holding cost per item per unit of time in the warehouse, $c_1$ is the service cost per customer, $c_2$ is the storage/penalty cost per item per production when the inventory level is beyond S, $c_3$ is the cost incurred due to loss per customer when the item of the inventory is out of stock, and $c_4$ is the waiting cost per customer when there are more than one customer in the system. Note that our cost function is continuous in the third argument for each fixed first $(n,i) \in {\mathbb {N}}_0\times {\mathbb {N}}_0$. Here our aim is to minimize our accumulated cost overall production rate functions, i.e.,

$$\begin{aligned} {\mathscr {U}}_{SM}:=\{{\beta } ~ \vert \; {\beta }: {\mathbb {N}}_0\times {\mathbb {N}}_0 \rightarrow [\gamma ,R]\}. \end{aligned}$$

This is the collection of all deterministic stationary strategies/policies. Note that we can write ${\mathscr {U}}_{SM}$ as the countable product space $[\gamma ,R]$. So, Tychonoff’s theorem (see Guo & Hernández-Lerma, 2009, Proposition A. 6) yields that ${\mathscr {U}}_{SM}$ is compact.

Evolution of the control system: Next, we give an informal description of the evolution of the CTCMCs as follows. The controller observes continuously the current state of the system. When the system is in state $(n,i)\in {\varvec{\Omega }}$ at time $t\ge 0$, he/she chooses action ${\tilde{\beta }}\in [\gamma ,R]$ according to some control. As a consequence of this, the following happens:

• 1. the controller incurs an immediate cost at rate $r(n,i, {\tilde{\beta }})$; and

• 2. the system stays in state (n, i) for a random time, with rate of leaving (n, i) given by $\pi _{(n,i)}^{{\tilde{\beta }}}$, and then jumps to a new state $(m,j)\ne (n,i)$ with the probability determined by $\dfrac{\pi _{(n,i)(n,i)}^{{\tilde{\beta }}}}{\pi _{(n,i)}^{{\tilde{\beta }}}}$ (see Guo & Hernández-Lerma 2009, Proposition B.8, for details).

When the state of the system transits to the new state (m, j), the above procedure is repeated. The controller tries to minimize his/her costs with respect to some performance criterion defined by (16), (17) and (18) below.

For each ${\beta }\in {\mathscr {U}}_{SM}$, the associated rates are defined as

$$\begin{aligned} \pi _{(n,i)(m,j)}^{\beta }:=\pi _{(n,i)(m,j)}^{{\beta }(n,i)}~\text { for }~(n,i),(m,j)\in {\mathbb {N}}_0\times {\mathbb {N}}_0~\text {for}~t\ge 0. \end{aligned}$$

(14)

Let $Q({\beta }):=\left[ \pi _{(n,i)(m,j)}^{{\beta }}\right]$ be the associated matrix of transition rates with the $((n,i),(m,j))^\text {th}$ element $\pi _{(n,i)(m,j)}^{{\beta }}$. Any (possible sub stochastic and homogeneous) transition function ${\tilde{p}}(s,(n,i),t,(m,j),{\beta })$ such that

$$\begin{aligned} \lim _{\gamma \rightarrow 0^{+}}\frac{{\tilde{p}}(t,(n,i),t+\gamma ,(m,j),{\beta }) -\delta _{(n,i)(m,j)}}{\gamma }=\pi _{(n,i)(m,j)}^{{\beta }} \end{aligned}$$

is called a Q-processes with the transition rate matrices $Q({\beta })$, where $\delta _{(n,i)(m,j)}$ is the Kronecker delta. Under Assumption 1 (a), we will denote by $\{Y(t,{\tilde{\beta }})\}$ the associated right-continuous Markov chain with values in ${\mathbb {N}}_0\times {\mathbb {N}}_0$ and for each ${\beta }\in {\mathscr {U}}_{SM}$, the regular Q process simply denoted as $p(s,(n,i),t,(m,j),{\beta })$, see Guo and Hernández-Lerma (2009).

Also, for each initial state $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$ at time $s=0$, we denote our probability space as $(\Omega ,{\mathscr {F}}, P^{{\beta }}_{(n,i)})$, where ${\mathscr {F}}$ is Borel $\sigma$-algebra over $\Omega$ and $P^{{\beta }}_{(n,i)}$ denotes the probability measure determined by $p(s,(n,i),t,(m,j),{\beta })$. Denote $E^{{\beta }}_{(n,i)}$ as the corresponding expectation operator. For any real-valued measurable function u on K and ${\beta }\in {\mathcal {U}}_{SM}$, let

$$\begin{aligned} u(n,i,{\beta }):=u(n,i,{\beta }(n,i))~\forall ~(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0~\text {and}~t\ge 0, \end{aligned}$$

(15)

whenever the integral is well defined. For any measurable function $V\ge 1$ on ${\mathbb {N}}_0\times {\mathbb {N}}_0$, we define the V-weighted supremum norm $\Vert \cdot \Vert$ of a real-valued measurable function u on ${\mathbb {N}}_0\times {\mathbb {N}}_0$ by

$$\begin{aligned} \Vert u\Vert _V:=\sup _{(n, i) \in {\mathbb {N}}_0\times S_n}\biggl \{\frac{\textrm{u}(\textrm{n}, \textrm{i})}{V(n,i)}\biggr \}, \end{aligned}$$

and the Banach space $B_V({\mathbb {N}}_0\times {\mathbb {N}}_0):=\{u:\Vert u\Vert _V<\infty \}$.

Now we briefly describe the problems we consider in this paper.

3.1 Discounted cost problem

For ${\beta } \in {\mathscr {U}}_{SM}$, define $\alpha$-discounted cost criterion by

$$\begin{aligned} I_{\alpha }^{{\beta }} (n,i)\ = \ E_{(n,i)}^{{\beta }} \left[ \int _{0}^{\infty }e^{-\alpha t} r(Y(t),{\beta }(Y(t))) dt \right] \end{aligned}$$

(16)

where $\alpha >0$ is the discount factor, $Y(\cdot )$ is the Markov chain corresponding to ${\beta } \in {\mathscr {U}}_{SM}$ with $Y(0)=(n,i)$, $E_{(n,i)}^{ {{\beta }}}$ denote the corresponding expectation and r is defined as in (13). Here the controller wants to minimize his cost over ${\mathscr {U}}_{SM}$.

Definition

A control ${\beta }^*\in {\mathscr {U}}_{SM}$ is said to be optimal if

$$\begin{aligned} I_\alpha ^{*}(n,i):=I_{\alpha }^{{\beta }^*} ( n,i)=\inf _{{{\beta }} \in {\mathscr {U}}_{SM}}I_{\alpha }^{{{\beta }}} (n,i). \end{aligned}$$

3.2 Ergodic cost criterion

For ${\beta } \in {\mathscr {U}}_{SM}$, the ergodic cost criterion is defined by

$$\begin{aligned} J(n,i, {\beta }) \ = \ \limsup _{T \rightarrow \infty } \frac{1}{T} E_{(n,i)}^{{\beta }} \Big [ \int ^T_0 r(Y(t), {\beta }(Y(t))) dt \Big ] \,, \end{aligned}$$

(17)

where r is defined as in (13) and $Y(\cdot )$ is the process corresponding to the control ${{\beta }} \in {{\mathscr {U}}_{SM}}$ and $E_{(n,i)}^{ {{\beta }}}$ denote the expectation where control ${\beta }$ used with $Y(0)=(n,i)$. Here the controller wants to minimize his cost over ${\mathscr {U}}_{SM}$.

Definition

A control ${\beta }^*\in {\mathscr {U}}_{SM}$ is said to be optimal if

$$\begin{aligned} J^*(n,i):=J(n,i, {\beta }^{*})=\inf _{{\beta } \in {\mathscr {U}}_{SM}} J(n,i, {\beta }). \end{aligned}$$

3.3 Pathwise average cost criterion

Pathwise average cost (PAC) criterion $J_c(\cdot ,\cdot ,\cdot )$ is defined as follows: for all ${\beta }\in {\mathscr {U}}_{SM}$ and $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$,

$$\begin{aligned} J_c(n,i,{\beta }):=\limsup _{T\rightarrow \infty }\frac{1}{T} \int _{0}^{T}r(Y(t),{\beta }(Y(t)))dt. \end{aligned}$$

(18)

Definition

A policy ${\beta }^{*}\in {\mathscr {U}}_{SM}$ is said to PAC-optimal if there exists a constant $g^{*}$ such that

$$\begin{aligned} P^{{\beta }^{*}}_{(n,i)}(J_c(n,i,{\beta }^{*})\le g^{*})=1~\text {and}~P^{{\beta }}_{(n,i)}(J_c(n,i,{\beta })\ge g^{*})=1, \end{aligned}$$

for all $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$ and ${\beta }\in {\mathscr {U}}_{SM}$.

To ensure the regularity of a Q-process and finiteness of the cost criteria (16), (17) and (18), we take the following assumption.

Assumption 1

• (a) There exist a nondecreasing function $W\ge 1$ on ${\mathbb {N}}_0 \times {\mathbb {N}}_0$ and constants $c_1>0$ and $b_1\ge 0$ such that for any $\ (n,i) \in {\mathbb {N}}_0 \times {\mathbb {N}}_0, ~\text {and}~\ {\tilde{\beta }}\in [\gamma ,R]$, the following holds:

  $$\begin{aligned} \Pi _{(n,i)}^{{\tilde{\beta }}} W(n,i) =\sum _{(m,j)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0}\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}W(m,j)\le -c_1 W(n,i) + b_1\delta _{(n,i)(0,0)}, \, \end{aligned}$$

  where $\delta _{(n,i)(m,j)}$ is the Dirac delta measure.

• (b) For every $(n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0$ and some constant $M >0$, $r(n,i,{\tilde{\beta }}) \le M W(n,i)$.

Remark 1

• (1) Assumption 1 (a) and its variants are used to study ergodic control problems, see, Guo and Hernández-Lerma (2009), Meyn and Tweedie (1993) and Pal and Pradhan (2019).

• (2) Assumption 1 (b) and its variants are very useful Assumption for unbounded costs in control theory, see Golui and Pal (2022), Guo and Hernández-Lerma (2009). For bounded cost as in Ghosh and Saha (2014), Kumar and Pal (2015), Assumption 1 (b) is not required. By (10) and (13), we have that the functions, $r(n,i,{{\tilde{\beta }}}),\; \pi _{(n,i)(m,j)}^{{{\tilde{\beta }}}}$, and $\sum _{(m,j)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0}\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}W(m,j)$ are all continuous in ${\tilde{\beta }}$ for each fixed $(n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0,$ with W as in Assumption 1. To ensure the existence of optimal stationary strategies, we need this continuity (see, for instance, Ghosh & Saha, 2014; Kumar & Pal, 2013; 2015 and their references).

Now to prove the existence of an optimal stationary policy for discounted cost criterion, we need the following Assumption, see Guo and Hernández-Lerma (2009, chapter 6).

Assumption 2

There exists a nonnegative function $W'$ on ${\mathbb {N}}_0 \times {\mathbb {N}}_0$ and constants $c'>0, \; b'\ge 0$, and $M' > 0$ such that

$$\begin{aligned}&\pi _{(n,i)}^* W(n,i) \le M' W'(n,i) , \ (n,i) \in {\mathbb {N}}_0 \times {\mathbb {N}}_0, \\&\sum _{(m,j)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0}\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}W'(m,j) \le c' W'(n,i) + b' , \ (n,i) \in {\mathbb {N}}_0 \times {\mathbb {N}}_0, \ {\tilde{\beta }} \in [\gamma ,R]. \end{aligned}$$

We now state an important condition that is satisfied by our transition rates given by (10).

Condition A For each $\beta \in {\mathscr {U}}_{SM}$, the corresponding Markov process $\{Y(t)\}$ with transition function $p((n,i),t,(m,j),\beta )$ is irreducible, which means that, for any two states $(n,i)\ne (m,j)$, there exists a set of distinct states $(n,i)=(m_1,i_1),\ldots ,(m_k,i_k)$ such that

$$\begin{aligned} \pi _{(m_1,i_1)(m_2,i_2)}^{\beta (m_1,i_1)}\ldots \pi _{(m_k,i_k)(m,j)}^{\beta (m_k,i_k)}>0. \end{aligned}$$

Remark 2

• (1) Condition A is satisfied by our transition rates given by (10).

• (2) Under Assumptions 1 and Condition A, for each $\beta \in {\mathscr {U}}_{SM}$, by Guo and Hernández-Lerma (2009, Propositions C.11 and C.12), we say that the MC $\{Y(t)\}$ has a unique invariant probability measure, $\vartheta _\beta$ which satisfies

  $$\begin{aligned} \vartheta _\beta (m,j)=\lim _{t\rightarrow \infty }p((n,i),t,(m,j),\beta ), \end{aligned}$$

  (independent of $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0)$ for all $(m,j)\in {\mathbb {N}}_0\times {\mathbb {N}}_0.$ Thus by Assumption 1 (a) and Guo and Hernández-Lerma (2009, Lemma 6.3 (i)), we have

  $$\begin{aligned} \vartheta _\beta (W):=\sum _{(m,j)}W(m,j)\vartheta _\beta (m,j)\le \frac{b_1}{c_1}<\infty , \end{aligned}$$

  and so,

  $$\begin{aligned} \vartheta _\beta (u):=\sum _{(m,j)}u(m,j)\vartheta _\beta (m,j)<\infty ,~\forall \beta \in {\mathscr {U}}_{SM}~\text {for any}~ u\in B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0). \end{aligned}$$

  (19)

To get the existence of average cost optimal (ACO) stationary strategy, in addition to Assumptions 1 and 2, we impose the following condition. This assumption is very important to study an ergodic control problem, see Guo and Hernández-Lerma (2009, chapter 7). Under this assumption, the Markov chain is uniformly ergodic.

Assumption 3

The control model is uniformly ergodic, which means the following: there exist constants $\delta >0$ and $L_2>0$ such that [using the notation in (19)]

$$\begin{aligned} \sup _{\beta \in {\mathscr {U}}_{SM}}\vert E^{\beta }_{(n,i)}u(Y(t))-\vartheta _\beta (u)\vert \le L_2 e^{-\delta t}\Vert u\Vert _W W(n,i) \end{aligned}$$

for all $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$, $u\in B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$, and $t\ge 0$.

For the existence of pathwise average cost optimal (PACO) stationary strategy, in addition to Assumptions 1, 2 and 3, we impose the following conditions.

Assumption 4

Let $W\ge 1$ be as in Assumption 1. For $k=1,2$, there exist nonnegative functions $W^{*}_k\ge 1$ on ${\mathbb {N}}_0$ and constants $c^{*}_k>0$, $b^{*}_k\ge 0$, and $M^*_k>0$ such that for all $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$ and ${\tilde{\beta }}\in [\gamma , R]$,

• (a) $W^2(n,i)\le M^*_1W_1^*(n,i)$ and $\displaystyle \sum _{(m,j)}\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}W^*_1(n,j)\le -c_1^*W^*_1(n,i)+b_1^{*}$.

• (b) $[\pi _{(n,i)}^* W(n,i)]^2\le M^*_2W_2^*(n,i)$ and $\sum _{(m,j)}\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}W^*_2(m,j)\le -c_2^*W^*_2(n,i)+b^*_2.$

4 Analysis of discounted cost problem

In this section, we study the infinite horizon discounted cost problem given by the criterion (16) and prove the existence of the optimal policy. Corresponding to the cost criterion (16), we recall the following function

$$\begin{aligned} I^*_{\alpha }(n,i)= \inf _{{\beta } \in {\mathscr {U}}_{SM}}I_{\alpha }^{{\beta }} (n,i). \end{aligned}$$

Using the dynamic programming heuristics, the Hamilton-Jacobi-Bellman (HJB) equations for discounted cost criterion are given by

$$\begin{aligned} \alpha I^*_{\alpha }(n,i)= & {} \inf _{{\tilde{\beta }}\in [\gamma ,R]} \Big [ \Pi _{(n,i)}^{{\tilde{\beta }}} I^*_{\alpha }(n,i) + r(n,i,{\tilde{\beta }}) \Big ]\, \end{aligned}$$

(20)

where $\Pi _{(n,i)}^{{\tilde{\beta }}} f(n,i):= \displaystyle {\sum _{(m,j)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0}} \pi _{(n,i)(m,j)}^{{\tilde{\beta }}}f(m,j)$, for any function f(n, i).

Define an operator $T:B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)\rightarrow B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$ as

$$\begin{aligned} Tu(n,i):= \mathop {\inf }\limits _{{\tilde{\beta }}\in [\gamma ,R]} \biggl [\dfrac{r(n,i,{\tilde{\beta }})}{R+\alpha +\lambda +\mu } +\dfrac{R+\lambda +\mu }{R+\alpha +\lambda +\mu } \mathop {\sum }\limits _{(m,j)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0}p^{{\tilde{\beta }}}_{(n,i)(m,j)}u(m,j) \biggr ],\nonumber \\ \end{aligned}$$

(21)

for $u\in B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$ and $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$, where

$$\begin{aligned} p^{{\tilde{\beta }}}_{(n,i)(m,j)}:=\frac{\pi ^{{\tilde{\beta }}}_{(n,i) (m,j)}}{R+\lambda +\mu }+\delta _{(n,i)(m,j)} \end{aligned}$$

is a probability measure on ${\mathbb {N}}_0\times {\mathbb {N}}_0$ for each $(n,i,{\tilde{\beta }})\in {\mathbb {N}}_0\times {\mathbb {N}}_0\times [\gamma , R]$ and $\delta _{(n,i)(m,j)}$ is the Dirac-delta function.

Next, we prove the optimality theorem for the discounted cost criterion. In this theorem, we find the existence of a solution of the discounted-cost optimality equation (DCOE) and the optimal stationary policy.

Theorem 1

Suppose that Assumptions 1 and 2 hold. Define $u_0:=0$, $u_{k+1}:=Tu_k$. Then the following hold.

• (a) The sequence $\{u_k\}_{k\ge 0}$ is monotone nondecreasing, and the limit $u^*:=\lim _{k\rightarrow \infty }u_k$ is in $B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$.

• (b) The function $u^*$ in (a) satisfies the fixed-point equation $u^*=Tu^*$, or, equivalently, $u^*$ verifies the DCOE, that is

  $$\begin{aligned} \alpha u^*(n,i)=\inf _{{\tilde{\beta }} \in [\gamma ,R]}\biggl \{r(i,n,{\tilde{\beta }})+\mathop {\sum }\limits _{(m,j)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0}\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}u^*(m,j)\biggr \}~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0.\nonumber \\ \end{aligned}$$

  (22)

• (c) There exist stationary policies $\beta _k$ (for each $k\ge 0$) and $\beta ^*_{\alpha }$ attaining the minimum in the equations $u_{k+1}=Tu_k$ and the DCOE (22), respectively. Moreover, $u^*=I^*_{\alpha }$. and the policy $\beta ^*_\alpha$ is discounted-cost optimal.

• (d) Every limit point in ${\mathscr {U}}_{SM}$ of the sequence $\{\beta _k\}$ in (c) is a discounted-cost optimal stationary policy.

Proof

• (a) We first prove the monotonicity of $\{u_k\}_{k\ge 0}$. Let $u_0=0$. Since $r\ge 0$, $u_1(n,i)\ge u_0(n,i)$ for all $(n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0$. Consequently, the monotonicity of T gives

  $$\begin{aligned} u_k=T^ku_0\le T^ku_1=u_{k+1}~\text { for every}~k\ge 1. \end{aligned}$$

  So, the sequence $\{u_k\}_{k\ge 0}$ is a monotone increasing sequence. So, the limit $u^*$ exists. Also, by direct calculations we get

  $$\begin{aligned} \vert u_k(n,i)\vert \le \frac{b_1M}{\alpha (\alpha +c_1)}+\frac{MW(n,i)}{\alpha +c_1}\le \frac{(\alpha +b_1)M}{\alpha (\alpha +c_1)}W(n,i)~\forall k\ge 0~\text {and}~(n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0, \end{aligned}$$

  which implies that $\sup _{k\ge 0}\Vert u_k\Vert _W$ is finite. Hence $u^*\in B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$.

• (b) By the monotonicity of T, $Tu^*\ge Tu_k=u_{k+1}$ for all $k\ge 0$, and thus

  $$\begin{aligned} Tu^*\ge u^*. \end{aligned}$$

  (23)

  Now, there exists $\beta _k\in {\mathscr {U}}_{SM}$ such that

  $$\begin{aligned} u_{k+1}(n,i)= \biggl [\dfrac{r(n,i,\beta _k)}{R+\alpha +\lambda +\mu }+\dfrac{R +\lambda +\mu }{R+\alpha +\lambda +\mu } \mathop {\sum }\limits _{(m,j)}p^{\beta _k}_{(n,i)(m,j)}u_k(m,j) \biggr ], \end{aligned}$$

  for all $k\ge 0$. Since ${\mathscr {U}}_{SM}$ is compact, there exist a policy $\beta ^*\in {\mathscr {U}}_{SM}$ and a subsequence of k for which $\lim _{k\rightarrow \infty }\beta _k=\beta ^*$. So, by the generalized Fatou’s lemma by taking $k\rightarrow \infty$, we get

  $$\begin{aligned} u^*(n,i)\ge \biggl [\dfrac{r(n,i,\beta ^*)}{R+\alpha +\lambda +\mu }+\dfrac{R +\lambda +\mu }{R+\alpha +\lambda +\mu } \mathop {\sum }\limits _{(m,j)}p^{\beta ^*}_{(n,i)(m,j)}u^*(m,j) \biggr ]~\forall (n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0, \end{aligned}$$

  which gives $u^*\ge Tu^*$. So, $u^*= Tu^*$, and so we get DCOE (22).

• (c) Since we have that $u_k$ and $u^*$ are in $B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$, from Guo and Hernández-Lerma (2009, Proposition A.4), we see that the functions in (21) and (22) are continuous in ${\tilde{\beta }}\in [\gamma ,R]$. Hence the first claim of part (c) holds. Moreover, for all $\forall (n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0$ and $\beta \in {\mathscr {U}}_{SM}$, it follows from (22) that

  $$\begin{aligned} \alpha u^*(n,i)\le \biggl \{r(n,i,\beta )+\Pi ^{\beta }_{(n,i)}u^*(n,i)\biggr \}~\text { for all}~ (n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0 \end{aligned}$$

  (24)

  with equality if $\beta =\beta ^*_\alpha$. Hence, (24), together with Guo and Hernández-Lerma (2009, Theorem 6.9 (b)), yields that

  $$\begin{aligned} I_\alpha ^{\beta ^*_\alpha }(n,i)=u^*(i)\le I_\alpha ^{\beta }(n,i)~\text { for all}~ (n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0~\text {and}~t\ge 0. \end{aligned}$$

  Hence, we prove part (c).

• (d) By part (a) and the generalized dominated convergence theorem in Guo and Hernández-Lerma (2009, Proposition A.4), every limit point $\beta \in {\mathscr {U}}_{SM}$ of $\{\beta _k\}$ satisfies

  $$\begin{aligned} u^*(n,i) = \biggl [\dfrac{r(n,i,\beta )}{R+\alpha +\lambda +\mu } +\dfrac{R+\lambda +\mu }{R+\alpha +\lambda +\mu } \mathop {\sum }\limits _{(m,j)}p^\beta _{(n,i)(m,j)}u^*{(m,j)} \biggr ], \end{aligned}$$

  which is equivalent to

  $$\begin{aligned} \alpha u^*(n,i)= \biggl \{r(n,i,\beta )+\Pi ^{\beta }_{(n,i)}u^*(n,i)\biggr \}~\forall (n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0. \end{aligned}$$

  Thus by (b) and Guo and Hernández-Lerma (2009, Theorem 6.9 (c)), $I^\beta _\alpha (n,i)=u^*(n,i)=I^*_\alpha (n,i)$ for every $(n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0$.

$\square$

4.1 The discounted-cost value iteration algorithm

Now using the value iteration algorithm, we find an optimal production rate $\beta ^{*}_\alpha$ for the discounted-cost criterion. Since this optimal production rate $\beta ^{*}_\alpha$ cannot be computed explicitly, we explore the possibility of algorithmic computation. Thus, in the presence of Theorem 1, one can use the following value iteration algorithm for computing $\beta ^{*}_\alpha$.

A Value Iteration Algorithm 4.1 By the value iteration algorithm, we will find an optimal production rate $\beta ^{*}_\alpha$, described briefly as follows:

• Step 0 Let $v_0 {(n,i)}= {0}$, for all $(n,i) \in {\mathbb {N}}_0\times {\mathbb {N}}_0$.

• Step 1 For $k\ge 1$, define

  $$\begin{aligned} v_k{(n,i)} = \mathop {\inf }\limits _{{\tilde{\beta }} \in [\gamma ,R]} \biggl [\dfrac{r(n,i,{\tilde{\beta }})}{R+\alpha +\lambda +\mu } +\dfrac{R+\lambda +\mu }{R+\alpha +\lambda +\mu } \mathop {\sum }\limits _{(m,j)}p^{{\tilde{\beta }}}_{(n,i) (m,j)}v_{k-1}{(m,j)}\biggr ],\nonumber \\ \end{aligned}$$

  (25)

  where $(n,i),(m,j)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$, $p^{{\tilde{\beta }}}_{(n,i)(m,j)}:=\frac{\pi ^{{\tilde{\beta }}}_{(n,i) (m,j)}}{R+\lambda +\mu }+\delta _{(n,i)(m,j)}$.

• Step 2 Choose $\beta _k\in {\mathscr {U}}_{SM}$ attaining the minimum in the right-hand side of (25).

• Step 3 $v_{*}{(n,i)}=\mathop {\lim }\limits _{k\rightarrow \infty }v_k{(n,i)},$ for all $(n,i) \in {\mathbb {N}}_0\times {\mathbb {N}}_0$.

• Step 4 Every limit point in ${\mathscr {U}}_{SM}$ of the sequence $\lbrace \beta _k \rbrace$ is a discounted-cost optimal stationary policy.

4.2 Numerical example

Now, we discuss the results obtained from the implementation of the discounted-cost value iteration algorithm. Unless specified otherwise, the experiment parameters remain consistent as follows: $\lambda =4.5$, $\mu =5$, $\alpha =0.7$, $h=100$, $c_1=20$, $c_2=30$, $c_3=40$, $c_4=10$, $S=2$ and $[\gamma ,R] = [0.1, 2]$ discretized as $\{0.1, 0.2, 0.3, \dots , 1.9, 2\}$ for computational purposes. We assume $n \le 25$ and $i \le 25$ in the computational experiments to enhance the interpretability while allowing substantial numerical insights. Figure 2 shows the speed of convergence of the value function for selected states and different $\alpha$ values. Reducing the value of $\alpha$ leads to an increase in the number of iterations k required to achieve $\epsilon$-convergence, as evident from Fig. 2, as well as in (25).

Fig. 2

$\epsilon$-Convergence of $v_k$ for selected state(s) as k increases, where $\epsilon = 0.01$

Fig. 3

Discounted-cost value iteration results for each state (n, i) at convergence

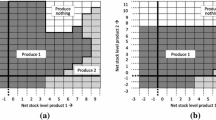
The optimal policy table for the discounted-cost criterion using the above mentioned parameters is shown in Fig. 3. A lower production rate is advised in most states where the majority of customer demands can be fulfilled using the existing inventory. We notice that a high production rate is optimal for some states where there is zero/low inventory. In addition, we see that the optimal policy is in accordance with the current state as well as future transitions. It is intriguing to observe that the optimal production rates often approach either the lower or upper bounds of the permissible production rates, i.e., $\gamma =0.1$ or $R=2$, respectively. The optimal value function ($v_{*}{(n,i)}$) reveal that as the inventory level i increases, the discounted cost also rises.

Fig. 4

Discounted-cost value iteration results when $\mu = 20$

Fig. 5

Discounted-cost value iteration results $\mu = 40$

It is important to note that the optimal policy has a strong correlation with the service rate of the system $\mu$. As $\mu$ increases, the expected service time reduces and thus the production frequency should be increased in consideration of future demands. Figures 3, 4, and 5 provide supporting evidence for this by varying $\mu$ with rest of the fixed parameters. When $\mu =40$, the optimal state values increase when there is a larger number of customers waiting for service, which is an infrequent event for a lower $\frac{\lambda }{\mu }$ value.

Fig. 6

Discounted-cost value iteration results when $\alpha = 0.3$

Fig. 7

Discounted-cost value iteration results when $\alpha = 0.9$

The discount factor $\alpha$ is another parameter used to measure the value of future costs which impacts the optimal policies significantly. A smaller $\alpha$ value not only prolongs the computational time to algorithm convergence but also influences the optimal production rates and optimal state values, as depicted in Figs. 6 and 7, where the remaining parameters are fixed.

4.3 The discounted-cost policy iteration algorithm

Now if the state and action spaces are both finite then using Lemma 1 and Theorem 2 below, one can find an optimal production rate $\beta _\alpha ^{*}$ by using the policy iteration algorithm given below.

In order to solve the discounted-cost problem through the policy iteration algorithm, we define some sets. For every $\beta \in {\mathscr {U}}_{SM}$, $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$, and ${\tilde{\beta }}\in [\gamma ,R]$, let

$$\begin{aligned} D_{\beta }(n,i,{\tilde{\beta }}):=r(n,i,{\tilde{\beta }}) +\sum _{(m,j)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0}\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}I^{\beta }_{\alpha }(m,j) \end{aligned}$$

(26)

and

$$\begin{aligned} E_\beta (n,i):=\{{\tilde{\beta }}\in [\gamma ,R]:D_\beta (n,i,{\tilde{\beta }})<\alpha I^{\beta }_{\alpha }(n,i) \}. \end{aligned}$$

(27)

We then define an improvement policy $\beta ^{\prime }\in {\mathscr {U}}_{SM}$ (depending on $\beta$) as follows:

$$\begin{aligned} \beta ^{\prime }(n,i)\in E_\beta (n,i)~\text {if}~E_\beta (n,i)\ne \emptyset ~\text {and}~\beta ^{\prime }(n,i):=\beta (n,i)~\text {if}~E_\beta (n,i)=\emptyset . \end{aligned}$$

(28)

Note: Now if the number of customers is m and the number of items is also m, then corresponding to fixed $\beta \in {\mathscr {U}}_{SM}$, let I is the ${m^2\times m^2}$ standard identity matrix. Also, define ${\hat{I}}^{\beta }_{\alpha }:=[{I}^{\beta }_{\alpha }(n,i)]_{m^2\times 1}$ and ${\hat{r}}(\beta ):=[r(n,i,\beta )]_{m^2\times 1}$ are column vectors (here $\beta$ is fixed but (n, i) will vary). Note that, if the state and action spaces are finite, then Assumption 1 (which is required for the next Lemma 1 and Theorem 2) of the present manuscript is satisfied by suitable Lyapunov function and constants.

Next, we state a Lemma whose proof is in Guo and Hernández-Lerma (2009, Lemma 4.16, Lemma 4.17).

Lemma 1

Suppose that Assumption 1 holds. Then for the finite CTMDP model, $I^\beta _{\alpha }$ is a unique bounded solution to the equation

$$\begin{aligned} \alpha u(n,i)= & {} r(n,i,\beta )+\sum _{(m,j)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0}\pi ^{{\beta }}_{(n,i)(m,j)}u(m,j)~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0,~\nonumber \\ {}{} & {} \text { for every}~\beta \in {\mathscr {U}}_{SM}. \end{aligned}$$

(29)

Also, for any given $\beta \in {\mathscr {U}}_{SM}$, let $\beta ^{\prime }\in {\mathscr {U}}_{SM}$ be defined as in (28) and suppose that $\beta ^{\prime }\ne \beta$. Then $I_\alpha ^\beta \ge I_\alpha ^{\beta ^{\prime }}$.

The Policy Iteration Algorithm 4.1

• Step 1 Pick an arbitrary $\beta \in {\mathscr {U}}_{SM}$. Let $k=0$ and take $\beta _k:=\beta$

• Step 2 (Policy evaluation) Obtain ${\hat{I}}^{\beta _k}_{\alpha }=[\alpha I-Q(\beta _k)]^{-1}{\hat{r}}(\beta _k)$ (by Lemma 1), where $Q(\beta _k)=\left[ \pi ^{\beta _k}_{(n,i)(m,j)}\right]$ , I is the identity matrix, ${\hat{I}}^{\beta _k}_{\alpha }$ and ${\hat{r}}$ are column vecors.

• Step 3 (Policy improvement) Obtain a policy $\beta _{k+1}$ from (28) (with $\beta _k$ and $\beta _{k+1}$ in lieu of $\beta$ and $\beta ^{\prime }$, respectively.

• Step 4 If $\beta _{k+1}=\beta _k$, then stop because $\beta _{k+1}$ is discounted-cost optimal (by Theorem 2 below). Otherwise, increase k by 1 and return to Step 2.

To get the optimal policy from the above policy iteration algorithm, we prove the following Theorem.

Theorem 2

Suppose that Assumption 1 holds. Then for each fixed discounted factor $\alpha >0$, the discounted-cost policy iteration algorithm yields a discounted-cost optimal stationary policy in a finite number of iterations.

Proof

Let $\{\beta _k\}$ be the sequence of policies in the discounted-cost policy iteration algorithm above. Then, by Lemma 1, we have $I_\alpha ^{\beta _k}\succeq I^{\beta _{k+1}}_\alpha$. Thus, each policy in the sequence $\{\beta _k, k=0,1,\ldots \}$ is different. Since the number of policies is finite, the iterations must stop after a finite number. Suppose that the algorithm stops at a policy denoted by $\beta ^*_\alpha$. Then $\beta ^*_\alpha$ satisfies the optimality equation

$$\begin{aligned} \alpha I_\alpha ^*(n,i)=\inf _{{\tilde{\beta }}\in [\gamma ,R]}\biggl [{r(n,i,{\tilde{\beta }})}+ \mathop {\sum }\limits _{(m,j)}\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)} I_\alpha ^*{(m,j)} \biggr ]. \end{aligned}$$

(30)

Thus, by Guo and Hernández-Lerma (2009, Theorem 4.10), $\beta ^*_\alpha$ is discounted-cost optimal. $\square$

Note As expected, the above policy iteration algorithm with a discrete action space given by $\{0.1, 0.2, 0.3, \dots , 1.9, 2\}$ provides the same optimal solution as the value iteration algorithm in Fig. 3. Differences may appear in the optimal policy tables (corresponding to each algorithm) when there are alternate optimal production rates for one or more states. The speed of convergence of the policy iteration depends on the initial choice of arbitrary $\beta (n,i)$ for each state (n, i).

5 Analysis of ergodic cost criterion

In this section, we prove that under Assumptions 1, 2 and 3, the average cost optimality equation (ACOE) (or HJB equation) given by (31) has a solution. Also, we find the optimal stationary policy by using the policy iteration algorithm for this cost criterion.

Next, we prove the optimality theorem for the ergodic cost criterion.

Theorem 3

Suppose that Assumptions 1, 2 and 3 hold. Then:

• (a) There exists a solution $(g^*,{\tilde{u}})\in {\mathbb {R}}\times B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$ to the ACOE

  $$\begin{aligned} g^*=\inf _{{\tilde{\beta }} \in [\gamma ,R]}\biggl \{r(n,i,{\tilde{\beta }})+\sum _{(m,j)}{\tilde{u}}(m,j) \pi _{(n,i)(m,j)}^{{\tilde{\beta }}}\biggr \}~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0. \end{aligned}$$

  (31)

  Moreover, the constant $g^*$ coincides with the optimal average cost function $J^*$, i.e.,

  $$\begin{aligned} g^*=J^*(n,i)~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0, \end{aligned}$$

  and ${\tilde{u}}$ is unique up to additive constants.

• (b) A stationary policy $\beta ^*\in {\mathscr {U}}_{SM}$ is AC optimal if and only if it attains the minimum in ACOE (31) i.e.,

  $$\begin{aligned} g^*=\biggl \{r(n,i,\beta ^*)+\sum _{(m,j)}{\tilde{u}}(m,j)\pi _{(n,i) (m,j)}^{\beta ^*}\biggr \}~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0. \end{aligned}$$

  (32)

Proof

We prove parts (a) and (b) together. Take the $\alpha$-discounted cost optimal stationary policy $\beta ^*_\alpha$ as in Theorem 1. Hence $I_\alpha ^{\beta ^*_\alpha }(n,i)=I_\alpha ^{*}(n,i)$. Now define $u_\alpha ^{\beta ^*_\alpha }(n,i):=I_\alpha ^{\beta ^*_\alpha }(n,i) -I_\alpha ^{\beta ^*_\alpha }(n_0,i_0)$, where $(n_0,i_0)$ is a fixed reference state. Now we apply the vanishing discounted approach. By Guo and Hernández-Lerma (2009, Lemma 7.7, Proposition A.7), we get a sequence $\{\alpha _k\}$ of discounted factors such that $\alpha _k\downarrow 0$, a constant $g^*$ and a function ${\bar{u}}\in B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$ such that

$$\begin{aligned} \lim _{k\rightarrow \infty }\alpha _k I^*_{\alpha _k}(n_0,i_0)=g^*~\text {and}~\lim _{k\rightarrow \infty } u^{\beta ^*_{\alpha _k}}_{\alpha _k}(n,i)={\bar{u}}(n,i)~\forall (n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0. \end{aligned}$$

(33)

Now for all $k\ge 1$ and $(n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0$, by Theorem 1, we have

$$\begin{aligned}&\frac{\alpha _k I^*_{\alpha _k}(n_0,i_0)}{R+\lambda +\mu } +\frac{\alpha _n u^{\beta ^*_{\alpha _k}}_{\alpha _k}(n_0,i_0)}{R+\lambda +\mu }+u^{\beta ^*_{\alpha _k}}_{\alpha _k}(n,i)\\&\quad \le \frac{r(n,i,{\tilde{\beta }})}{R+\lambda +\mu } +\sum _{(m,j)}u^{\beta ^*_{\alpha _k}}_{\alpha _k}(n,i) \biggl [\frac{\pi _{(n,i)(m,j)}^{{\tilde{\beta }}}}{R+\lambda +\mu }+\delta _{(n,i)(m,j)}\biggr ] \end{aligned}$$

for all $(n,i,{\tilde{\beta }})\in K$. Using this and (33), we get

$$\begin{aligned} \frac{g^*}{R+\lambda +\mu }+{\bar{u}}(n,i)\le \frac{r(n,i,{\tilde{\beta }})}{R+\lambda +\mu }+\sum _{(m,j)} {\bar{u}}(m,j)\biggl [\frac{\pi _{(n,i)(m,j)}^{{\tilde{\beta }}}}{R+\lambda +\mu }+\delta _{(n,i)(m,j)}\biggr ] \end{aligned}$$

for all $(n,i,{\tilde{\beta }})\in K$. Thus we get

$$\begin{aligned} g^*\le \inf _{{\tilde{\beta }} \in [\gamma ,R]}\biggl \{r(n,i,{\tilde{\beta }})+\sum _{(m,j)} {\bar{u}}(m,j)\pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}\biggl \}. \end{aligned}$$

(34)

Now there exists $\beta _k\in {\mathscr {U}}_{SM}$ such that for all $(n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0$, we have

$$\begin{aligned}&\frac{\alpha _k I^*_{\alpha _k}(n,i_0)}{R+\lambda +\mu }+\frac{\alpha _k u^{\beta ^*_{\alpha _k}}_{\alpha _k}(n,i_0)}{R+\lambda +\mu } +u^{\beta ^*_{\alpha _k}}_{\alpha _k}(n,i)\nonumber \\&\quad = \frac{r(n,i,\beta _{k})}{R+\lambda +\mu }+\sum _{(m,j)} u^{\beta ^*_{\alpha _k}}_{\alpha _k}(n,i)\biggl [\frac{\pi _{(n,i) (m,j)}^{\beta _{k}}}{R+\lambda +\mu }+\delta _{(n,i)(m,j)}\biggr ]. \end{aligned}$$

(35)

Since ${\mathscr {U}}_{SM}$ is compact, there exists $\beta ^{\prime }\in {\mathscr {U}}_{SM}$ such that

$$\begin{aligned} \lim _{k\rightarrow \infty }\beta _{k}(n,i)=\beta ^{\prime }(n,i)~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0. \end{aligned}$$

So, by the dominated convergence theorem, taking $k\rightarrow \infty$ in (35), we get

$$\begin{aligned} \frac{g^*}{R+\lambda +\mu }+{\bar{u}}(n,i)= \frac{r(n,i,\beta ^{\prime })}{R+\lambda +\mu }+\sum _{(m,j)} \biggl [\frac{\pi _{(n,i)(m,j)}^{\beta ^{\prime }}}{R+\lambda +\mu } +\delta _{(n,i)(m,j)}\biggr ]{\bar{u}}(m,j) \end{aligned}$$

for all $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$. Hence we get

$$\begin{aligned} g^*&= r(n,i,\beta ^{\prime })+\sum _{(m,j)}\pi ^{\beta ^{\prime }}_{(n,i)(m,j)}{\bar{u}}(m,j)\nonumber \\&\ge \inf _{{\tilde{\beta }} \in [\gamma ,R]}\biggl \{r(n,i,{\tilde{\beta }})+\sum _{(m,j)} \pi ^{{\tilde{\beta }}}_{(n,i)(m,j)}{\bar{u}}(m,j)\biggl \}. \end{aligned}$$

(36)

From (34) and (36), we get (31). Now we prove that $g^{*}=J^*(n,i)$ for every $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$. Take an arbitrary $\beta \in {\mathscr {U}}_{SM}$. Then from (31), we get for $\beta \in {\mathscr {U}}_{SM}$,

$$\begin{aligned} g^*\le \biggl \{r(n,i,\beta )+\sum _{(m,j)}\pi ^{\beta }_{(n,i) (m,j)}{\bar{u}}(m,j)\biggl \}~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0. \end{aligned}$$

Then by Guo and Hernández-Lerma (2009, Proposition 7.3), we get $g^*\le J(n,i,\beta )$. Hence $g^*\le J^{*}(n,i)$ for every $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$. Now there exists $\beta ^*\in {\mathscr {U}}_{SM}$ for which

$$\begin{aligned} g^*= \biggl \{r(n,i,\beta ^*)+\sum _{(m,j)}{\bar{u}}(m,j) \pi ^{\beta ^*}_{(n,i)(m,j)}\biggr \}~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0. \end{aligned}$$

Hence, by Guo and Hernández-Lerma (2009, Proposition 7.3), we get $g^{*}=J(n,i,\beta ^*)$. Hence $g^{*}=J(n,i,\beta ^*)=J^{*}(n,i)$ for all $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$. Consequently, $\beta ^*$ is AC-optimal.

Now by Guo and Hernández-Lerma (2009, (7.3)), we have

$$\begin{aligned} J(n,i,\beta )=\sum _{(m,j)}r(m,j,\beta )\vartheta _\beta (m,j)=g(\beta )~\forall f\in {\mathscr {U}}_{SM}~\text {and}~(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0, \end{aligned}$$

(37)

where $g(\beta ):=\sum _{(m,j)}r(m,j,\beta )\vartheta _\beta (m,j)$.

Now we prove the necessary part for a deterministic stationary policy to be AC optimal by contradiction. So, suppose that $\beta ^{*}\in {\mathscr {U}}_{SM}$ is an AC optimal that does not attain the minimum in the ACOE (31). Then there exist $(n^{\prime },i^{\prime })\in {\mathbb {N}}_0\times {\mathbb {N}}_0$ and a constant $d>0$ (depending on $(n^{\prime },i^{\prime })$ and $\beta ^*$) such that

$$\begin{aligned} g^*\le r(n,i,\beta ^*)-d\delta _{(n^{\prime },i^{\prime })(m,j)} +\sum _{(m,j)}\pi ^{\beta ^*}_{(n,i)(m,j)}{\bar{u}}(m,j)~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0. \end{aligned}$$

(38)

By the irreducibility condition of the transition rates, the invariant measure $\vartheta _{\beta ^*}$ of $p((n,i),t,(m,j),\beta ^*)$ is supported on all of ${\mathbb {N}}_0\times {\mathbb {N}}_0$, meaning that $\vartheta _{\beta ^*}(m,j)>0$ for every $(m,j)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$. So, as in the proof of (37), from (38) and Guo and Hernández-Lerma (2009, Proposition 7.3), we have

$$\begin{aligned} g^*\le g(\beta ^*)-d \vartheta _{\beta ^*}(n^{\prime },i^{\prime })< g(\beta ^*), \end{aligned}$$

(39)

which is a contradiction. So, $\beta ^*$ is AC-optimal.

By similar arguments as in Guo and Hernández-Lerma (2009, Theorem 7.8), we get the uniqueness of the solution of ACOE (31). $\square$

The Bias of a stationary policy Let $\beta \in {\mathscr {U}}_{SM}$. We say that a pair $(g^{\prime },h_\beta )\in {\mathbb {R}}\times B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$ is a solution to the Poisson equation for $\beta \in {\mathscr {U}}_{SM}$ if

$$\begin{aligned} g^{\prime }=r(n,i,\beta )+\sum _{(m,j)}h_\beta (m,j)\pi ^{\beta }_{(n,i)(m,j)}~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0. \end{aligned}$$

Define $g(\beta )=\sum _{(m,j)}r(m,j,\beta )\vartheta _\beta (m,j)$.

Then by recalling Guo and Hernández-Lerma (2009, (7.13)), the expected average cost (loss) of $\beta$ is

$$\begin{aligned} J(n,i,\beta )=\sum _{(m,j)}r(m,j,\beta )\vartheta _\beta (m,j) =g(\beta )=\vartheta _{\beta }(r(\cdot ,\cdot ,\beta )),~(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0. \end{aligned}$$

(40)

Next we define the bias (or “potential”-see Guo and Hernández-Lerma (2009, Remark 3.2)) of $\beta \in {\mathscr {U}}_{SM}$ as

$$\begin{aligned} h_\beta (n,i):=\int _{0}^{\infty }[E^\beta _{(n,i)}r(Y(t),\beta )-g(\beta )]dt~\text { for } ~(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0. \end{aligned}$$

(41)

Next we state a Proposition whose proof is in Guo and Hernández-Lerma (2009, Proposition 7.11).

Proposition 4

Under Assumptions 1, 2 and 3, for every $\beta \in {\mathscr {U}}_{SM}$, the solution to the Poisson equation for $\beta$ are of the form

$$\begin{aligned} (g(\beta ),h_\beta +z)~\text {with}~z~\text {any real number}. \end{aligned}$$

Moreover, $(g(\beta ),h_\beta )$ is the unique solution to the Poisson equation

$$\begin{aligned} g(\beta )=r(n,i,\beta )+\sum _{(m,j)}h_\beta (m,j)\pi ^{\beta }_{(n,i)(m,j)}~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0 \end{aligned}$$

(42)

for which $\vartheta _\beta (h_\beta )=0$.

5.1 The average-cost policy iteration algorithm

In view of Theorem 5 given below, one can use the policy iteration algorithm for computing the optimal production rate $\beta ^{*}$ that is described as follows:

The Policy Iteration Algorithm 5.1

• Step 1 Take $k=0$ and $\beta _k\in {\mathscr {U}}_{SM}$.

• Step 2 Solve for the invariant probability measure $\ \vartheta _{\beta _k}$ from the system of equations (see Guo and Hernández-Lerma (2009, Remark 7.12 or Proposition C.12))

  $$\begin{aligned}&\sum _{(n,i)}\pi ^{\beta _k}_{(n,i)(m,j)}\vartheta _{\beta _k}(n,i)=0~\text {for}~(m,j)\in {\mathbb {N}}_0\times {\mathbb {N}}_0,\\&\sum _{(m,j)}\vartheta _{\beta _k}(m,j)=1, \end{aligned}$$

  then calculate the loss, $g(\beta _k)=\sum _{(m,j)}r(m,j,\beta _k)\vartheta _{\beta _k}(m,j)$ and finally, the bias, $h_{\beta _k}$ from the system of linear equations (see Proposition 4)

  $$\begin{aligned} \displaystyle \left\{ \begin{array}{ll} &{} r(n,i,\beta _k)+\sum _{(m,j)}\pi ^{\beta _k}_{(n,i)(m,j)}h(m,j)=g(\beta _k)\\ &{}\sum _{(m,j)}h(m,j)\vartheta _{\beta _k}(m,j)=0. \end{array}\right. \end{aligned}$$

• Step 3 Define the new stationary policy $\beta _{k+1}$ in the following way: Set $\beta _{k+1}(n,i):=\beta _k(n,i)$ for all $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$ for which

  $$\begin{aligned}&r(n,i,\beta _k(n,i))+\sum _{(m,j)}\pi ^{\beta _k}_{(n,i)(m,j)}h_{\beta _k}(m,j)\nonumber \\&\quad =\inf _{{\tilde{\beta }}\in [\gamma , R]} \biggl \{r(n,i,{\tilde{\beta }})+\sum _{(m,j)}\pi ^{{\tilde{\beta }}}_{(n,i) (m,j)}h_{\beta _k}(m,j)\biggr \}; \end{aligned}$$

  (43)

  otherwise (i.e., when (43) does not hold), choose $\beta _{k+1}(n,i)\in [\gamma ,R]$ such that

  $$\begin{aligned}&r(n,i,\beta _{k+1}(n,i))+\sum _{(m,j)}\pi ^{\beta _{k+1}}_{(n,i) (m,j)}h_{\beta _k}(m,j)\nonumber \\&\quad =\inf _{{\tilde{\beta }}\in [\gamma , R]} \biggl \{r(n,i,{\tilde{\beta }})+\sum _{(m,j)}\pi ^{{\tilde{\beta }} }_{(n,i)(m,j)}h_{\beta _k}(m,j)\biggr \}. \end{aligned}$$

  (44)

• Step 4 If $\beta _{k+1}$ satisfies (43) for all $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$, then stop because (by Theorem 5 below) $\beta _{k+1}$ is average cost (AC) (or pathwise average cost optimal (PACO)); otherwise, replace $\beta _k$ with $\beta _{k+1}$ and go back to Step 2.

Remark 3

Now we discuss how the policy iteration algorithm works.

Let $\beta _0\in {\mathscr {U}}_{SM}$ be the initial policy in the policy iteration algorithm (see Step 1), and let $\{\beta _k\}$ be the sequence of stationary policies obtained by the repeated application of the algorithm.

If

$$\begin{aligned} \beta _k=\beta _{k+1}~ \text {for some}~k, \end{aligned}$$

then it follows from Proposition 4 that the pair $(g(\beta _k),h_{\beta _k})$ is a solution to the ACOE, and thus, by Theorem 3, $\beta _k$ is AC optimal. Hence, to analyze the convergence of the policy iteration algorithm, we will consider the case

$$\begin{aligned} \beta _k\ne \beta _{k+1}~\text {for every}~k\ge 0. \end{aligned}$$

(45)

Define, for $k\ge 1$ and $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$,

$$\begin{aligned} \varepsilon (n,i,\beta _k)&:=\biggl [r(n,i,\beta _{k-1})+\sum _{(m,j)} \pi ^{\beta _{k-1}}_{(n,i)(m,j)}h_{\beta _{k-1}}(m,j)\biggr ]\\&\quad -\biggl [r(n,i,\beta _k)+\sum _{(m,j)}\pi ^{\beta _k}_{(n,i) (m,j)}h_{\beta _{k-1}}(m,j)\biggr ], \end{aligned}$$

which by Proposition 4 can be expressed as

$$\begin{aligned} \varepsilon (n,i,\beta _k)=g(\beta _{k-1})-\biggl [r(n,i,\beta _k) +\sum _{(m,j)}\pi ^{\beta _k}_{(n,i)(m,j)}h_{\beta _{k-1}}(m,j)\biggr ]. \end{aligned}$$

(46)

Observe (by Step 3 above) that $\varepsilon (n,i,\beta _k)=0$ if $\beta _k(n,i)=\beta _{k-1}(n,i)$, whereas $\varepsilon (n,i,\beta _k)>0$ if $\beta _k(n,i)\ne \beta _{k-1}(n,i)$.

Hence, $\varepsilon (n,i,\beta _k)$ can be interpreted as the “improvement” of the nth iteration of the algorithm.

5.2 Numerical example

Figure 8 shows the results obtained from the above algorithm using the same parameters as in the previous experiments with the exception of $\alpha$. Due to computational challenge in obtaining results for $n,i\le 25$, we limit our numerical example with $n,i\le 10$ for the average-cost policy iteration algorithm. Unlike the discounted cost case where current and immediate state transition rewards are prioritized, average cost criterion calculates optimal policies according to the long run expected value of each state. We can observe that the optimal production rates align precisely with the boundary values $\gamma$ and R even in this example case of the average cost criterion. This is likely due to the presence of multiple alternate optimal solutions. In cases where one of these optimal solutions comprises the boundary values of $\beta$, the algorithm tends to converge towards such policies quickly.

Fig. 8

Optimal policy corresponding to average-cost policy iteration algorithm

Next by Guo and Hernández-Lerma (2009, Lemma 7.13), we have the following Lemma.

Lemma 2

Under Assumptions 1, 2 and 3, suppose that (45) is satisfied. Then the following statements hold

• (a) The sequence $\{g(\beta _k)\}$ is strictly decreasing and it has a finite limit.

• (b) For every $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$, $\varepsilon (n,i,\beta _k)\rightarrow 0$ as $k\rightarrow \infty$.

To get the optimal policy from the policy iteration algorithm 5.1, we prove the following Theorem.

Theorem 5

Suppose that Assumptions 1, 2 and 3 hold, and let $\beta _1\in {\mathscr {U}}_{SM}$ be an arbitrary initial policy for the policy iteration Algorithm 5.1. Let $\{\beta _k\}\subset {\mathscr {U}}_{SM}$ be the sequence of policies obtained by the policy iteration Algorithm 5.1. Then one of the following results holds.

• (a) Either

  • (i) the algorithm converges in a finite number of iterations to an AC optimal policy;

    Or

  • (ii) as $k\rightarrow \infty$, the sequnce $\{g(\beta _k)\}$ converges to the optimal AC function value $g^*$, and any limit point of $\{\beta _k\}$ is an AC optimal stationary policy.

• (b) There exists a subsequence $\{\beta _l\}\subset \{\beta _k\}$ for which

  $$\begin{aligned}&g(\beta _l)\rightarrow g~[\text {Lemma}~2],~\beta _l\rightarrow \beta ,~\text {and}\nonumber \\&h_{\beta _l}\rightarrow h~\text {[pointwise]}. \end{aligned}$$

  In addition, the limiting triplet $(g,\beta ,h)\in {\mathbb {R}}\times {\mathscr {U}}_{SM}\times B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$ satisfies

  $$\begin{aligned} g&=r(n,i,\beta )+\sum _{(m,j)}\pi ^{\beta }_{(n,i)(m,j)}h(m,j)\nonumber \\&=\inf _{{\tilde{\beta }}\in [\gamma , R]}\biggl \{r(n,i,{\tilde{\beta }})+\sum _{(m,j)}\pi ^{{\tilde{\beta }}}_{(n,i) (m,j)}h(m,j)\biggr \}. \end{aligned}$$

  (47)

Proof

Note that it is enough to prove part (b).

Let $\{\beta _k\}$ satisfy (45). In view of Lemma 2, since ${\mathscr {U}}_{SM}$ is compact and $h_{\beta _l}\in B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$, there exists a subsequence $\{\beta _l\}$ of $\beta _k$ such that $h_{\beta _l}$ converges pointwise to some $h\in B_W({\mathbb {N}}_0 \times {\mathbb {N}}_0)$. So, we have

$$\begin{aligned}&g(\beta _l)\rightarrow g,~\beta _l\rightarrow \beta ,~\text {and}\nonumber \\&h_{\beta _l}\rightarrow h. \end{aligned}$$

(48)

Now, by Proposition 4 and the definition of the improvement term $\varepsilon (n,i,\beta _{l+1})$ in (46), we have

$$\begin{aligned} g(\beta _{l})&=\biggl [r(n,i,\beta _l)+\sum _{(m,j)}\pi ^{\beta _l}_{(n,i) (m,j)}h_{\beta _{l}}(m,j)\biggl ]\nonumber \\&=\min _{{\tilde{\beta }}\in [\gamma , R]}\biggl \{r(n,i,{\tilde{\beta }})+\sum _{(m,j)}\pi ^{{\tilde{\beta }}}_{(n,i) (m,j)}h{(m,j)}\biggr \}+\varepsilon (n,i,\beta _{l+1}). \end{aligned}$$

(49)

Taking $l\rightarrow \infty$, we have

$$\begin{aligned} g&=\biggl [r(n,i,\beta )+\sum _{(m,j)}\pi ^{\beta }_{(n,i) (m,j)}h_{\beta }(m,j)\biggr ]\nonumber \\&=\inf _{{\tilde{\beta }}\in [\gamma , R]}\biggl \{r(n,i,{\tilde{\beta }})+\sum _{(m,j)}\pi ^{{\tilde{\beta }}}_{(n,i) (m,j)}h{(m,j)}\biggr \}~\forall (n,i)\in {\mathbb {N}}_0 \times {\mathbb {N}}_0. \end{aligned}$$

(50)

Hence $\beta$ is AC optimal and g is the optimal AC function. $\square$

6 Average optimality for pathwise costs

In Sect. 5, we have studied the optimality problem under the expected average cost $J(n,i,\beta )$. However, the sample-path reward $r(Y(t), \beta )$ corresponding to an average-reward optimal policy that minimizes an expected average cost may have fluctuations from its expected value. To take these fluctuations into account, we next consider the pathwise average-cost (PAC) criterion.

In the next theorem, we find the existence of the solution of the pathwise average cost optimality equation (PACOE).

Here we give an outline of the proof of the following optimality Theorem; for details, see Guo and Hernández-Lerma (2009, Theorem 8.5).

Theorem 6

Under Assumptions 1, 2, 3 and 4, the following statements hold.

• (a) There exist a unique $g^*$, a function $u^*\in B_W({\mathbb {N}}_0\times {\mathbb {N}}_0)$, and a stationary policy $\beta ^*\in {\mathscr {U}}_{SM}$ satisfying the average-cost optimality equation (ACOE)

  $$\begin{aligned} g^*&=\inf _{{\tilde{\beta }}\in [\gamma ,R]}\biggl \{r(n,i,{\tilde{\beta }}) +\sum _{(m,j)}u(m,j)\pi _{(n,i)(m,j)}^{{\tilde{\beta }}}\biggr \}\nonumber \\&=r(n,i,\beta ^*(n,i))+\sum _{(m,j)}u(m,j)\pi _{(n,i)(m,j)}^{\beta ^*}~\forall (n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0. \end{aligned}$$

  (51)

• (b) The policy $\beta ^*$ in (a) is PAC-optimal, and $P^{\beta ^*}_{(n,i)}(J_c(n,i,\beta ^*)=g^*)=1$ for all $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$, with $g^*$ as in (a).

• (c) A policy in ${\mathscr {U}}_{SM}$ is PAC-optimal iff it realizes the minimum in (51).

Proof

• (a) Note that part (a) has been obtained in Theorem 3, see Guo and Hernández-Lerma (2009, Remark 8.4). The proof is based on the fact that if $\beta _k$, $g(\beta _k)$, and $h_{\beta _k}$ are as in (43)–(46), then there exist a subsequence $\{\beta _{k_l}\}$ of $\beta _k$, $\beta ^*\in {\mathscr {U}}_{SM}$, $u^*\in B_W({\mathbb {N}}_0\times {\mathbb {N}}_0)$, and a constant $g^*$ such that for each $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$,

  $$\begin{aligned} \lim _{l\rightarrow \infty }h_{\beta _{k_l}}=:u^*,~ \lim _{l\rightarrow \infty } \beta _{k_l}=\beta ^*,~\text {and}~ \lim _{l\rightarrow \infty }g(\beta _{k_l})=g^*. \end{aligned}$$

  (52)

  The triplet $(g^*,u^*,\beta ^*)$ satisfies (51).

• (b) To prove (b), for all $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$, $\beta \in {\mathscr {U}}_{SM}$ let

  $$\begin{aligned} \Delta (n,i,\beta (n,i))&:=r(n,i,\beta (n,i))+\sum _{(m,j)}u^*(m,j) \pi _{(n,i)(m,j)}^{\beta }-g^*, \end{aligned}$$

  (53)
  $$\begin{aligned} {\bar{h}}(n,i,\beta )&:=\sum _{(m,j)}u^*(m,j)\pi ^{\beta }_{(n,i)(m,j)}. \end{aligned}$$

  (54)

  We define the (continuous-time) stochastic process

  $$\begin{aligned} M(t,\beta ):=\int _{0}^{t}{\bar{h}}(Y(y),\beta )dy-u^*(Y(t))~\text { for }~t\ge 0. \end{aligned}$$

  (55)

  By similar arguments as in Guo and Hernández-Lerma (2009, Theorem 8.5), we have

  $$\begin{aligned} M(t,\beta )=-\int _{0}^{t}r(Y(y),\beta )dy +\int _{0}^{t}\Delta (Y(y),\beta )dy-u^*(Y(t))+t g^*. \end{aligned}$$

  (56)

  Then from (14), (51) and (53) we get $\Delta (n,i,\beta )\le 0$ and $\Delta (n,i,\beta ^*)=0$ for all $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$. Thus by Guo and Hernández-Lerma (2009, Theorem 8.5, equations (8.31), (8.32)) and (56), we get

  $$\begin{aligned}&P^{\beta }_{(n,i)}(J_c(n,i,\beta )\ge g^*)=1~\text {and}\nonumber \\&P^{\beta ^*}_{(n,i)}(J_c(n,i,\beta ^*)=g^*)=1. \end{aligned}$$

  (57)

  Since $\beta \in {\mathscr {U}}_{SM}$ and $(n,i)\in {\mathbb {N}}_0\times {\mathbb {N}}_0$ are arbitrary, we get part (b).

• (c) See Theorem 3 (b) or Guo and Hernández-Lerma (2009, Theorem 8.5 (c)).

$\square$

6.1 The pathwise average-cost policy iteration algorithm

In view of Theorem 6 and Proposition 7 given below, one can use the policy iteration algorithm for computing the optimal production rate $\beta ^{*}$. To compute this optimal production rate $\beta ^*$, we describe the following policy iteration algorithm.

The Policy Iteration Algorithm 6.1 See the Policy Iteration Algorithm 5.1 for computing the optimal production rate $\beta ^{*}$.

Next in view of Theorem 6 (c), we have the following Proposition.

Proposition 7

Suppose that Assumptions 1, 2, 3 and 4 hold. Then any limit point $\beta ^*$ of the sequence $\{\beta _k\}$ obtained by the Policy Iteration Algorithm 5.1 is PAC-optimal.

Remark 4

 

• (1) If the state and action spaces are finite, then all assumptions of the present manuscript are satisfied by some suitable Lyapunov functions and constants. In this case, one can easily apply control theory for continuous-time Markov chain to obtain the value and policy iteration algorithms, by analogous results of this article, for details see Guo and Hernández-Lerma (2009).

• (2) The policy iteration algorithm is the same for both average cost and pathwise average cost criteria, see policy iteration Algorithm 5.1 and policy iteration Algorithm 6.1. We observe from the numerical computation for policy iteration Algorithm 6.1 corresponding to the pathwise average cost criterion, it gives the same result as we have obtained for policy iteration Algorithm 5.1. As a result, for both cases, we get the same optimal policy. Consequently, we have omitted the numerical result from Sect. 6.

7 Dynamic production-inventory system through semi-Markov processes

One can use semi-Markov theory to deal with a production-inventory model when the state and action spaces are finite using the following construction. In our model, we have considered a single-product inventory system in which the demand process is described by a Poisson process and the inventory position can be replenished at any time. Here, the decision epochs are the demand epochs and they occur randomly in time. Now let us consider the action space to be limited to, let us say, maximally three choices, e.g. $\beta _L<\beta _N<\beta _H$ (for all states), standing for respectively a low, a normal, and a high production rate with larger production costs for higher production rates and switching costs for changing the production rate. Then we set up a semi-Markov decision model (SMDM) with state space

$$\begin{aligned} {\mathscr {S}}=\{(n,i,\beta ,e):n=0,1,2,\ldots ; i=0,1,2,\ldots ; \beta \in \{\beta _L,\beta _N,\beta _H\};e=0,1,2\}, \end{aligned}$$

where e is the type of event that triggers a state change: $e = 0$ stands for the arrival of new demand, $e = 1$ stands for a service completion, and $e = 2$ stands for the completion of production. The action set is $A(n,i,e)=\{\beta _L,\beta _N,\beta _H\}$ for each state. Next, calculate the transition probabilities, distribution of time until the next transition from a state $(n,i,\beta ,e)$ to another state $(n^{\prime },i^{\prime },\beta ^{\prime },e^{\prime })$, distribution of the holding time at a state $(n,i,\beta ,e)$, the expected times and expected costs, respectively, as $p[(n^{\prime },i^{\prime },\beta ^{\prime },e^{\prime })\vert (n,i,\beta ,e),\beta ^{\prime }]$, $F_{t}((n,i,\beta ,e), \beta ^{\prime }, (n^{\prime },i^{\prime },\beta ^{\prime },e^{\prime }))$, $H_{t}((n,i,\beta ,e), \beta ^{\prime })$, $\tau (n,i,\beta ,e,\beta ^{\prime })$, and $\eta (n,i,\beta ,e,\beta ^{\prime })$ with the following meaning.

• $p[s^{\prime }\vert s,a]$ is the probability that the next state is $s^{\prime },$ given that in state s, action a is chosen.

• Given that the next state to be entered is state $s^{\prime }$, the time until the transition from s to $s^{\prime }$ occurs has distribution $F_{t}(s,a,s^{\prime })$, given that action a is chosen.

• Let $H_{t}(s,a)$ denote the distribution of time that the semi-Markov process spends time in state s before making a transition, given that action a is chosen. That is, by conditioning on the next state, we obtain

  $$\begin{aligned} H_{t}(s,a)=\sum _{s^{\prime }}p[s^{\prime }\vert s,a]F_{t}(s,a,s^{\prime }). \end{aligned}$$

• $\tau (s,a)$ is the expected time until the next decision epoch, given that in state s, action a is chosen.

• $\eta (s,a)$ is the expected cost incurred until the next decision epoch, given that in state s, action a is chosen.

Note that $\tau (n,i,\beta ,e,\beta ^{\prime })>0$ for all $n,i,\beta ,e,\beta ^{\prime }$. As before, a stationary policy R is a rule which adds to each state $(n,i,\beta ,e)$ a single action $R(n,i,\beta ,e)\in A(n,i,e)$ and always prescribes to take this action whenever the system is observed in state $(n,i,\beta ,e)$ at a decision epoch. Since the state space is finite, it can be shown that under each stationary policy, the number of decisions made in any finite time interval is finite with probability 1. If we let $\xi (t)$ denote the state at any time, then $\{\xi (t),t\ge 0\}$ is called a semi-Markov process. Also, let

$$\begin{aligned} \zeta _n=\textit{the state of the system at the}~n^{\textit{th}}~ \textit{decision epoch.} \end{aligned}$$

Then it follows that under a stationary policy R the embedded stochastic process $\zeta _n$ is a discrete-time Markov chain with one-step transition probabilities $p[(n^{\prime },i^{\prime },\beta ^{\prime },e^{\prime })\vert (n,i,\beta ,e),R]$. Define the random variable Z(t) by

$$\begin{aligned} Z(t)=\textit{the total costs incurred up to time}~t,~ t\ge 0. \end{aligned}$$

Fix now a stationary policy R. Denote by $E_{(n,i,\beta ,e), R}$ the expectation operator when the initial state $\zeta _0=(n,i,\beta ,e)$ and the policy R is used. Then the limit

$$\begin{aligned} g_{(n,i,\beta ,e)}(R)=\lim _{t\rightarrow \infty }\frac{1}{t}E_{(n,i,\beta ,e), R}[Z(t)] \end{aligned}$$

exists for all $(n,i,\beta ,e)\in {\mathscr {S}}$. If the embeded Markov chain $\{\zeta _n\}$ has no two disjoint closed sets, by Tijms (2003, Theorem 7.11, Chapter 7), we have

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{Z(t)}{t}=g(R)~\textit{with probability 1} \end{aligned}$$

for each initial state $\zeta _0=(n,i,\beta ,e)$, where the constant g(R) is given by

$$\begin{aligned} g(R)=\frac{\sum _{(n^{\prime },i^{\prime },\beta ^{\prime },e^{\prime })\in {\mathscr {S}}} \eta ((n^{\prime },i^{\prime },\beta ^{\prime },e^{\prime }),R)\vartheta _{R}(n^{\prime },i^{\prime }, \beta ^{\prime },e^{\prime })}{\sum _{(n^{\prime },i^{\prime },\beta ^{\prime },e^{\prime })\in {\mathscr {S}} }\tau ((n^{\prime },i^{\prime },\beta ^{\prime },e^{\prime }),R) \vartheta _{R}(n^{\prime },i^{\prime },\beta ^{\prime },e^{\prime })} \end{aligned}$$

with $\vartheta _{R}(n^{\prime },i^{\prime },\beta ^{\prime },e^{\prime })$ denoting the equilibrium distribution of the Markov chain $\{\zeta _n\}$. Then, using policy-iteration and value-iteration algorithm as in Tijms (2003, Chapter 7), we can easily get the required optimal production rate of the production inventory system for the corresponding semi-Markov process.

8 Conclusions

In this article, we have examined a production-inventory dynamic control system for discounted, average, and pathwise average cost criterion for risk-neutral cost (i.e., the expectation of the total cost) criterion. Here, the demands arrive at the production workshop according to a Poisson process, and the processing time of the customer’s demands is exponentially distributed. Each production is one unit and the production is kept running until the inventory level becomes sufficiently large, and the production is on a make-to-order basis. We assume that the production time of an item follows an exponential distribution and that the amount of time for the item produced to reach the retail shop is negligible. In addition, we have assumed that no new customer joins the queue when there is a void inventory. This yields an explicit product-form solution for the steady-state probability vector of the system. We further discuss the policy and value iteration algorithms for each cost criterion. Using these algorithms, we obtain the optimal production rate that minimizes the discounted/average/pathwise average total cost per production using a Markov decision process approach. Through numerical experiments, we validate the discussed algorithms and analyze how different parameters affect the optimal policies. Finally, we briefly discuss the dynamic production-inventory system through semi-Markov process as a special case.

Our proposed model with service time, production time, or lead time following a general distribution can be direct extensions of this work. Another potential research would be to conduct the same analysis under the risk-sensitive utility (i.e., the expectation of the exponential of the total cost) cost criterion, which provides more comprehensive protection from risk than the risk-neutral case.