1 Introduction

Convergence-type trading strategies have become one of the most popular trading strategies that are used to capitalize on market inefficiencies, or deviations from “equilibrium,” especially with the rapid developments in algorithmic and high-frequency trading. For a typical convergence trade, temporary mispricing is exploited by simultaneously buying relatively underpriced assets and selling short relatively overpriced assets in anticipation that at some future date their prices will have become closer and thus one can profit by the extent of the convergence. A prime example of a convergence trade is the pairs trading strategy that involves a long position and a short position in a pair of similar stocks that have moved together historically and hence an investor can profit from the relative value trade arising from the cointegration between asset price dynamics involved in the trade. Other examples of convergence-type trading strategies are risk arbitrage (known also as merger arbitrage) that speculates on successful completion of a merger of two companies, or cash and carry trade that tries to benefit from pricing inefficiencies between spot market and futures market of the same underlying stock or commodity by simultaneously placing opposite bets on spot and futures markets.

In this work, we extend the convergence trade model given by Liu and Timmermann (2013) that investigates the dynamic optimal portfolio allocation via expected utility maximization from terminal wealth, with two co-integrated assets with pricing errors and a market index. Liu and Timmermann (2013) show that under recurring and non-recurring “arbitrage” opportunities, optimal portfolio allocations could deviate from conventional long-short delta-neutral strategies and it can be optimal to hold both risky assets long (or short) at the same time. We extend Liu and Timmermann (2013) mainly in two directions. First, we assume that pricing errors related to the co-integrated assets are affine functions of the spread and modulated by a continuous-time, finite-state Markov chain, which is taken to be unobservable and hence needs to be filtered out. Having an affine structure on the pricing errors allows us to model liquidity effects related to the market microstructure. Moreover, taking pricing errors (or “alphas” as commonly referred in finance literature) dependent on a hidden Markov chain captures certain salient features of convergence trade. Although most of the existing literature assumes that pricing errors are fully observable, in reality, those errors, albeit having a stochastic nature, cannot be known precisely or may depend on some unobservable state variables that change according to certain factors in the economy or the market. By modeling those pricing errors as functions of an unobservable regime-switching factor, we would like to build a more realistic representation for convergence trading. The second extension of our model is that we allow capital asset pricing model (CAPM) betas of two risky assets to be different. This characteristic enables us to show the optimal portfolio allocation for beta-neutral pairs trading, which is designed to keep the portfolio’s beta zero all the time and hence achieve market neutrality. Hence, in this way we can represent a common market practice among pairs traders who use to form beta-neutral portfolio to avoid market risk. Moreover, allowing for different betas also enables us to account for betting against beta strategies that involve going short with high-beta stocks and going long with low-beta ones. Betting against beta type strategies are often associated with fluctuating low alpha (Frazzini and Pedersen 2014), which also justifies our choice of modeling pricing errors under regime switching and partial information.

There is a growing stream of literature about optimal convergence trading. Liu and Longstaff (2003) provide a partial equilibrium examination of convergence trading strategies, where the mispricing is modeled using a Brownian bridge. Jurek and Yang (2007) incorporate an Ornstein–Uhlenbeck process to model the spread for non-myopic investors and solve the dynamic portfolio allocation for constant relative risk aversion and recursive Epstein–Zin utility function. By building on the results of Jurek and Yang (2007), Liu and Timmermann (2013) solve a similar problem by focusing both on recurring and non-recurring arbitrage opportunities in a continuous error-correction model with two co-integrated assets and a market index. Lei and Xu (2015) extend Liu and Timmermann (2013) by incorporating transaction costs. Inspired by the dynamic pairs trading model of Mudchanatongsuk et al. (2008), Tourin and Yan (2013) develop an optimal portfolio strategy to invest in two risky assets and the money market account, assuming that log-prices are co-integrated, and solve the optimal portfolio allocation problem for the exponential utility. Cartea and Jaimungal (2016) extend Tourin and Yan (2013) to allow the investor to trade in multiple co-integrated assets. Chiu and Wong (2011) investigate the optimal dynamic trading of co-integrated assets using the classical mean-variance portfolio selection criterion. Angoshtari (2016) studies the necessary and sufficient conditions for well-posedness and no-arbitrage for the model of Liu and Timmermann (2013) by focusing on the concept of investor nirvana.

Considering similar problems under regime-switching and/or partial information, studies that focus on the dynamic portfolio choice problem are rather limited in the literature. Lee and Papanicolaou (2016) solve the optimal pairs trading problem within a power utility setting, where the drift uncertainty is modeled by a continuous time Gaussian mean-reverting process and necessitates Kalman filtering to extract estimates of the unobservable state process. Altay et al. (2018) extend the pairs trading model of Mudchanatongsuk et al. (2008) by incorporating regime switching under partial information and risk penalization. Classical portfolio selection problems, which do not cover portfolios involving co-integrated assets, in a full or partial information and/or Markov regime-switching framework can be found, for example, in Zhou and Yin (2003), Bäuerle and Rieder (2004), and Sotomayor and Cadenillas (2009) for the full information case with Markov regime switching or Bäuerle and Rieder (2005), Björk et al. (2010) and Frey et al. (2012) for the partial information case.

In summary, we have the following key contributions. First, we compute the optimal unrestricted and beta-neutral strategies both in full and partial information settings for a log-utility trader by using dynamic programming. Second, we characterize the value function as the unique (classical) solution of the Hamilton–Jacobi–Bellman (HJB) equation, which is reduced to a system of ordinary differential equations (ODE) in the full information case, and given by a system of partial differential equations (PDE) in the partial information case. We also provide verification results for both cases. Third, to solve the convergence trade problem under partial information we compute the filtering equation by applying the innovations approach, see Sect. 4. Having the filter dynamics enables us to study the equivalent reduced problem where unobservable states of the Markov chain are replaced by their optional projections over the available filtration. Comparing optimal strategies under full and partial information, we obtain that the certainty equivalence principle holds, i.e., the optimal portfolio strategy in the latter case can be obtained by replacing the unobservable state variable with its filtered estimate. Finally, we analyze numerically an example with a two-state Markov chain and demonstrate certain features of our proposed model. In particular, we illustrate the dominance of unrestricted strategies over beta-neutral strategies. Moreover, we show that a trader who uses averaged data (in terms of parameters) is not performing better than the trader who uses a Markov modulated model in a full information setting. For the partial information case, our example suggests that there is a non-negative information premium, indicating that the fully informed trader has an advantage over the partially informed one.

The remainder of the paper is organized as follows. Section 2 introduces the model setting and the notation. In Sect. 3 we study the portfolio optimization problem in a full information setting with regime switching and compare the optimal strategies with those implied by Liu and Timmermann (2013) model. In Sect. 4 we solve the utility maximization problem under partial information. In Sect. 5, we provide a numerical analysis of an example with a two-state Markov chain. We conclude with Sect. 6. In order to improve the flow of the paper we provide proofs of all results in the “Appendix”.

2 Model setting and notation

We study a modification of the continuous-time error-correction model of Liu and Timmermann (2013) in a regime-switching setup under both full and partial information. Precisely we fix a probability space \((\varOmega , {\mathcal {G}}, {\mathbf {P}})\) and a finite-time horizon T which coincides with the terminal time of an investment. We also introduce a complete and right-continuous filtration \({\mathbb {G}}=\{{\mathcal {G}}_t, \ t \in [0,T]\}\), representing the global information flow, and assume that all processes defined below are adapted to \({\mathbb {G}}\).

Let Y be a continuous-time finite-state Markov chain taking values in \({\mathcal {E}}=\{e_1, \dots , e_K\}\), for \(K\ge 2\), where, without loss of generality, we assume that \(e_i\) is the ith canonical vector in \({\mathbb {R}}^K\), for every \(i\in \{1, \dots , K\}\). We denote by \(Q=(q^{ij})_{i,j\in \{1, \dots , K\}}\) the infinitesimal generator of Y, with \(q^{ij}>0\) for every \(i\ne j\) and \(q^{ii}=-\sum _{j \ne i}q^{ij}\), and let \(\varPi =(\varPi ^1, \dots \varPi ^K)\) be its initial distribution.

Remark 1

The finite-state nature of the Markov chain implies that for every \(t\in [0,T]\), and every function \(f:{\mathcal {E}}\rightarrow {\mathbb {R}}\) we have \(f(Y_t)=\sum _{i=1}^K f^i {{\mathbf {1}}}_{\{Y_t=e_i\}}\) where \(f^{i}=f(e_i)\), for every \(i\in \{1, \dots , K\}\).

We consider a market model where a trader can invest in a riskless asset with constant rate of return \(r\ge 0\) and three risky assets with price processes \(S^{(m)}, S^{(1)}\) and \(S^{(2)}\). The first asset represents the market index and the other two are co-integrated assets. We assume that the price dynamics of market index is given by

$$\begin{aligned} \frac{\mathrm dS^{(m)}_t}{S^{(m)}_t}=(r+\mu _m)\,\mathrm dt+\sigma _m\,\mathrm dB^{(m)}_t, \quad S^{(m)}_0>0, \end{aligned}$$
(1)

where \(\mu _m\in {\mathbb {R}}\) is the market risk premium, \(\sigma _m>0\) is the market volatility and \(B^{(m)}\) is a standard Brownian motion. Co-integrated asset prices are described by the following SDEs,

$$\begin{aligned} \frac{\mathrm dS^{(1)}_t}{S^{(1)}_t}&=(r+\beta _1 \mu _m)\,\mathrm dt+\beta _1\sigma _m\,\mathrm dB^{(m)}_t+\sigma \,\mathrm dB^{(0)}_t+b_1\,\mathrm dB^{(1)}_t - \lambda _1(Y_t) \left( X_t -\alpha _1(Y_t)\right) \mathrm dt, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\mathrm dS^{(2)}_t}{S^{(2)}_t}&=(r+\beta _2 \mu _m)\,\mathrm dt + \beta _2\sigma _m\,\mathrm dB^{(m)}_t + \sigma \,\mathrm dB^{(0)}_t + b_2\,\mathrm dB^{(2)}_t + \lambda _2(Y_t) \left( X_t -\alpha _2(Y_t)\right) \mathrm dt, \end{aligned}$$
(3)

with \(S^{(1)}_0>0\) and \(S^{(2)}_0>0\). Coefficients \(\beta _1 \in {\mathbb {R}}, \beta _2 \in {\mathbb {R}}, b_1>0, b_2>0\) and \(\sigma >0\) are constant parameters and \((B^{(0)}, B^{(1)}, B^{(2)})\) is a three-dimensional standard Brownian motion independent of \(B^{(m)}\).

At any time \(t \in [0,T]\), we define the spread between co-integrated assets by \(X_t=\log {S^{(1)}_t}-\log {S^{(2)}_t}\). The process X represents the mean-reverting component of pricing errors. We assume that \(\lambda _1(Y_t)+\lambda _2(Y_t)>0\) \({\mathbf {P}}\)-a.s. for every \(t \in [0,T]\), so that X becomes a stationary process with the dynamics

$$\begin{aligned} \mathrm dX_t&=\Big (\varGamma _1-\lambda _1(Y_t)(X_t-\alpha _1(Y_t)) -\lambda _2(Y_t)(X_t-\alpha _2(Y_t))\Big )\,\mathrm dt \nonumber \\&+\left( \beta _1-\beta _2\right) \sigma _m\,\mathrm dB^{(m)}_t+b_1 \mathrm dB^{(1)}_t-b_2\,\mathrm dB^{(2)}_t,\quad X_0\in {\mathbb {R}}, \end{aligned}$$
(4)

where

$$\begin{aligned} \varGamma _1:=\left( \beta _1-\beta _2\right) \mu _m-\frac{1}{2}\left( (\beta _1^2-\beta _2^2)\sigma _m^2+b_1^2-b_2^2 \right) . \end{aligned}$$
(5)

Note that X is a mean-reverting process with regime-switching mean-reversion level

$$\begin{aligned} \theta (Y_t)=\frac{\varGamma _1+\lambda _1(Y_t)\alpha _1(Y_t) +\lambda _2(Y_t)\alpha _2(Y_t)}{\lambda _1(Y_t)+\lambda _2(Y_t)}, \quad t \in [0,T]. \end{aligned}$$
(6)

We observe that in (2) and (3), the infinitesimal expected returns are

$$\begin{aligned} (r+\beta _1 \mu _m)\,\mathrm dt-\lambda _1(Y_t) \left( X_t -\alpha _1(Y_t)\right) \mathrm dt \end{aligned}$$

and

$$\begin{aligned} (r+\beta _2 \mu _m)\,\mathrm dt+\lambda _2(Y_t) \left( X_t -\alpha _2(Y_t)\right) \mathrm dt, \end{aligned}$$

respectively. The form of infinitesimal returns implies that if \(\lambda _j(\cdot )\) is chosen to be identical to zero or \(X_t\) is equal to \(\alpha _j(\cdot )\), for every \(j\in \{1,2\}\), asset price dynamics satisfy the CAPM relation, meaning that CAPM establishes the expected returns correctly and there is no mispricing in either asset. On the other hand, if, for example, \(-\lambda _1(Y)(X-\alpha _1(Y))>0\), the first asset has a higher expected return than it is justified by its exposure to market risk, and hence has a positive alpha, meaning that it is undervalued. By choosing \(\lambda _1\), \(\lambda _2\) and \(\alpha _1\), \(\alpha _2\) depending on the hidden Markov chain Y, we therefore, postulate that pricing errors depend on some common factor in the economy or in the market that can not be directly observed by the trader. Also, as it is suggested by Liu and Timmermann (2013), one can interpret those pricing errors as reflecting momentarily positive or negative liquidity shocks, which may vanish in liquid markets. For example, because of liquidity effects, stocks listed in S&P 500 have overstated betas (Vijh 1994), which in turn affects pricing errors. By assuming a regime-switching framework for pricing errors, we are also able to model these types of features.

We should also remark that if we take \(\beta _1=\beta _2\), \(b_1=b_2\) and \(\alpha _1(\cdot )=\alpha _2(\cdot )=0\), the model becomes a regime-switching version of the original one suggested by Liu and Timmermann (2013) which involves two assets with the same payoff traded at different prices. Under these assumptions the spread is a mean reverting process around zero. However, in our extended setting, the mean-reversion level of the process X has a more involved expression, see Eq. (6), which is due to the fact that we allow co-integrated assets to have different betas and different correlations with the market index, and that mispricing errors are assumed to be affine functions of the spread rather than just proportional.

To concentrate more on the financial motivation behind our model setup, we can justify the role of \(\alpha _1\) and \(\alpha _2\) from a market microstructural point of view. That role is mainly due to the affine specification of the Markov modulated error correction terms. Suppose for the sake of simplicity and comparison purposes with the Liu and Timmerman model that \(\varGamma _1=0\) and \(\lambda _i(\cdot )=1\), for \(i=1,2\). With this parameter choice, we obtain a model where the long-run mean of the spread process is \((\alpha _1(Y_t)+\alpha _2(Y_t))/2\) and depends on the Markov chain Y. This allows us to model a situation in which the long-run mean of the spread can be switched on (\(\alpha _i\ne 0\)) or off (\(\alpha _i =0\)). From a financial point of view, this setting is able, for example, to capture the liquidity effects related to Siamese twin companies. These are dual-listed companies that are incorporated in different countries and listed in different exchanges simultaneously while operating as a single entity, their shares have same control rights and dividends are based on the same cash flow. Therefore for such companies, most of the mispricing between two stocks is due to liquidity effects arising from the microstructural features of stock exchanges where individual shares are traded; see De Jong et al. (2009) for more on stock price differentials of dual-listed companies. Although these liquidity effects may vanish, implying that the spread converges to zero, they may also lead to a certain degree of persistent error between two stocks in certain states of the economy, manifesting itself in alphas that are different than zero. This type of modeling is not possible, if, for example, the corresponding errors are just proportional to the spread X, because having \(\varGamma _1=0\) would imply zero long-run mean for the spread process in all states of Y.

3 Optimal convergence trade under regime switching

Let \(W^{h}\) be the value of a portfolio \(h=(h^{(m)}, h^{(1)}, h^{(2)})\), where quantities \(h^{(m)}_t, h^{(1)}_t\) and \(h^{(2)}_t\) denote fractions of the wealth invested at any time \(t \in [0,T]\) in the market index \(S^{(m)}\) and in the co-integrated assets with prices \(S^{(1)}\) and \(S^{(2)}\), respectively. Consequently the percentage of wealth invested in the riskless asset is \(1-h^{(m)}-h^{(1)}-h^{(2)}\). We introduce now the suitable set of strategies.

Definition 1

A \({\mathbb {G}}\)-admissible portfolio strategy is a self-financing, \({\mathbb {G}}\)-predictable strategy \(h=(h^{(m)}, h^{(1)}, h^{(2)})\) such that

$$\begin{aligned} \mathbb {E}\left[ \int _0^T \left( {h^{(m)}_t}^2+{h^{(1)}_t}^2+{h^{(2)}_t}^2\right) \mathrm dt\right] <\infty . \end{aligned}$$
(7)

The set of \({\mathbb {G}}\)-admissible strategies is denoted by \({\mathcal {A}}\).

For every \(h=(h^{(m)}, h^{(1)},h^{(2)}) \in {\mathcal {A}}\), the dynamics of the convergence trading portfolio is given by

$$\begin{aligned} \frac{\mathrm dW^h_t}{W^h_t}= & {} \left( r+\left( h^{(m)}_t+h^{(1)}_t\beta _1+h^{(2)}_t\beta _2 \right) \mu _m+h^{(2)}_t\lambda _2(Y_t)(X_t-\alpha _2(Y_t))\right. \\&-\left. h^{(1)}_t\lambda _1(Y_t)(X_t-\alpha _1(Y_t)) \right) \mathrm dt +\sigma _m\left( h^{(m)}_t+h^{(1)}_t\beta _1+h^{(2)}_t\beta _2\right) \mathrm dB^{(m)}_t\\&+ \sigma \left( h^{(1)}_t+h^{(2)}_t \right) \mathrm dB^{(0)}_t +b_1h^{(1)}_t \mathrm dB^{(1)}_t+b_2h^{(2)}_t \mathrm dB^{(2)}_t, \end{aligned}$$

with \(W_0^h>0\).

We consider a trader with logarithmic preferences and who aims to maximize the expected utility from terminal wealth at time T in a market with regime switching. In this section, we assume that the trader may directly observe the state of the Markov chain Y that influences the dynamics of price processes and the spread. Formally, we address the following optimization problem

$$\begin{aligned} \text{ Maximize } \ {\mathbf {E}}^{t,w,x,i}[\log W_T^h] \ \text{ over } \text{ all } \ h \in {\mathcal {A}}, \end{aligned}$$
(8)

where \({\mathbf {E}}^{t,w,x,i}\) denotes the conditional expectation given \(W_t=w\), \(X_t=x\) and \(Y_t=e_i\). We define the value function corresponding to problem (8) as

$$\begin{aligned} V(t,w,x,i):=\underset{h\in {\mathcal {A}}}{\sup }\,\,{\mathbf {E}}^{t,w,x,i} \left[ \log {W_T^h}\right] . \end{aligned}$$
(9)

Notice that for a given \(h\in {\mathcal {A}}\), \(W^h\) is a controlled process. For notational simplicity, from now on we suppress the dependence on h and write W instead of \(W^h\).

In Theorem 1, we apply dynamic programming to solve the optimization problem. Our goal is to identify the optimal strategy as well as to characterize the value function as the unique solution of the corresponding HJB equation. This approach permits to examine the value function of the control problem in detail. One could alternatively derive the stochastic representation of the value function and characterize it up to the solution of a system of partial differential equations via Feynman–Kac type arguments for Markov-modulated diffusion processes; see, e.g., Baran et al. (2013) and Escobar et al. (2015).

In the sequel, we use the following notation for partial derivatives: for every function \(g:[0,T]\times {\mathbf {R}}_{+}\times {\mathbf {R}}\rightarrow {\mathbf {R}},\) we write, for instance, \(\frac{\partial g}{\partial t}=g_t\). Moreover, according to Remark 1 we have that \(\lambda _j(e_i)=\lambda _j^i\) and \(\alpha _j(e_i)=\alpha _j^i\), for \(j\in \{1,2\}\) and \(i\in \{1,\dots ,K\}\).

Theorem 1

Consider a trader endowed with a logarithmic utility function. Then the optimal portfolio strategy \(h^*=({h^{(1)}}^{*},{h^{(2)}}^{*},{h^{(m)}}^{*})\in {\mathcal {A}}\) is

$$\begin{aligned} {h^{(1)}}^{*}(t,x,i)= & {} -\frac{\lambda _1^{i}(x-\alpha _1^i) +\lambda _2^{i}(x-\alpha _2^i)\varrho _2}{b_1^2+b_2^2\varrho _2}, \end{aligned}$$
(10)
$$\begin{aligned} {h^{(2)}}^{*}(t,x,i)= & {} \frac{\lambda _2^{i}(x-\alpha _2^i) +\lambda _1^{i}(x-\alpha _1^i)\varrho _1}{b_2^2+b_1^2\varrho _1}, \end{aligned}$$
(11)
$$\begin{aligned} {h^{(m)}}^{*}(t,x,i)= & {} \frac{\mu _m}{\sigma _m^2}-\beta _1{h^{(1)}}^{*}(t,x,i)-\beta _2{h^{(2)}}^{*}(t,x,i), \end{aligned}$$
(12)

with \(\varrho _1=\frac{\sigma ^2}{ \sigma ^2+b_1^2}\) and \(\varrho _2=\frac{\sigma ^2}{ \sigma ^2+b_2^2}\). The value function is of the form

$$\begin{aligned} V(t, w, x, i )=\log (w)+m(t,i)x^2+n(t,i)x+u(t,i), \end{aligned}$$
(13)

where functions m(t, i), n(t, i) and u(t, i) for \(i\in \{1, \dots , K\}\) solve the following system of ordinary differential equations

$$\begin{aligned}&m_t(t,i)-2(\lambda _1^i+\lambda _2^i)m(t,i)+\sum _{j=1}^K m(t,j) q^{ij}+\varTheta _1^i =0, \end{aligned}$$
(14)
$$\begin{aligned}&n_t(t,i)-(\lambda _1^i+\lambda _2^i)n(t,i)+\sum _{j=1}^K n(t,j) q^{ij}+2(\varGamma _1+\lambda _1^i\alpha _1^i+\lambda _2^i\alpha _2^i)m(t,i)-\varTheta _2^i=0, \end{aligned}$$
(15)
$$\begin{aligned}&u_t(t,i)+ \sum _{j=1}^K u(t,j) q^{ij}+\varGamma _2m(t,i)+(\varGamma _1+\lambda _1^i\alpha _1^i+\lambda _2^i\alpha _2^i) n(t,i)+\varTheta _3^i=0, \quad {} \end{aligned}$$
(16)

with terminal conditions \(m(T,i)=0\), \(n(T,i)=0\) and \(u(T,i)=0\) for all \(i\in \{1,\dots ,K \}\), and where \(\varGamma _1\) is given in (5) and

$$\begin{aligned} \varTheta _1^i&:=\frac{b_1^2(\lambda _2^i)^2 + b_2^2(\lambda _1^i)^2 +\sigma ^2\left( \lambda _1^i+\lambda _2^i\right) ^2}{2\left( b_1^2b_2^2 +\sigma ^2(b_1^2+b_2^2)\right) },\\ \varTheta _2^i&:= \frac{\alpha _1^i\lambda _1^i(\lambda _1^i(b_2^2+\sigma ^2) +\lambda _2^i\sigma ^2)+\alpha _2^i\lambda _2^i(\lambda _2^i(b_1^2+\sigma ^2) +\lambda _1^i\sigma ^2)}{b_1^2b_2^2 +\sigma ^2(b_1^2+b_2^2)},\\ \varTheta _3^i&:=\frac{(\alpha _1^i\lambda _1^ib_2)^2+(\alpha _2^i\lambda _2^ib_1)^2 +\sigma ^2(\alpha _1^i\lambda _1^i+\alpha _2^i\lambda _2^i)^2}{2\left( b_1^2b_2^2 +\sigma ^2(b_1^2+b_2^2)\right) }+r+\frac{\mu _m^2}{2\sigma _m^2},\\ \varGamma _2&=\sigma _m^2(\beta _1-\beta _2)^2+b_1^2+b_2^2. \end{aligned}$$

The proof of the Theorem 1 is provided in the “Appendix”.

3.1 Discussion on the optimal trading strategy

The optimal trading strategy is Markov modulated and has a typical structure of a mean-variance portfolio weights. More specifically, the numerator of each portfolio weight \(h^{(j)^{*}}\), \(j\in \{1,2\}\), depends on the regime-switching parameters, \(\lambda _1(Y),\lambda _2(Y)\) and \(\alpha _1(Y),\alpha _2(Y)\), related to the co-integration between \(S^{(1)}\) and \(S^{(2)}\), or equivalently, to pricing errors. The denominator, on the other hand, is akin to the idiosyncratic risk components, \(b_1\), \(b_2\) and \(\sigma \). We should also emphasize that \({h^{(1)}}^{*}\) and \({h^{(2)}}^{*}\) do not depend on market parameters, \(\beta _1\), \(\beta _2\), \(\mu _m\) and \(\sigma _m\), since the market exposure of each asset is covered by investing in the market index. The coefficients \(\varrho _1\) and \(\varrho _2\) can be seen as the relative idiosyncratic variation of \(S^{(1)}\) (resp. \(S^{(2)}\) ) with respect to \(S^{(2)}\) (resp. \(S^{(1)}\)). The role of \(\varrho _1\) is actually to scale the contribution of pricing error and the independent idiosyncratic variance of \(S^{(2)}\) in \({h^{(1)}}^{*}\). Naturally, \(\varrho _2\) has the analogous interpretation. Note that when \(\sigma =0\), meaning that there is no correlation between \(S^{(1)}\) and \(S^{(2)}\), those contributions vanish and the optimal portfolio weights in each stock only depend on their own pricing errors and idiosyncratic risks. The structure of the market portfolio weight is similar to that in Liu and Timmermann (2013) and given by the sum of Sharpe’s ratio of the market index and a linear combination of \({h^{(1)}}^{*}\) and \({h^{(2)}}^{*}\), weighted by their corresponding betas. Another important feature implied by our model is that, although the market index dynamics is independent of the Markov chain, the optimal investment strategy in the market index \({h^{(m)}}^{*}\) is Markov modulated. This characteristic, indeed is not directly related to the market index, but arises as a consequence of the fact that optimal investments in co-integrated assets, \({h^{(1)}}^{*}\) and \({h^{(2)}}^{*}\), are prone to different regimes.

We observe that \({h^{(1)}}^{*}\) and \({h^{(2)}}^{*}\) are linear functions of the spread and depend on mispricing errors of stocks \(S^{(1)}\) and \(S^{(2)}\). When the spread touches the value \(\alpha ^i_1\), the dependence of optimal strategies on mispricing error of the first stock vanishes. The same holds for \(\alpha ^i_2\). Consequently if, for some state of the Markov chain it holds that \(\alpha ^i_1=\alpha ^i_2=\alpha \), then the investor’s optimal choice, when the spread takes the value \(\alpha \), would be to allocate all her wealth in the market index. Roughly speaking, when \(x=\alpha \) an investor cannot not take advantages from mispricing errors and then the only profitable investment would be the market index and riskless asset. In this case any investment in stocks \(S^{(1)}\) and \(S^{(2)}\) would not be convenient since the risk of the entire portfolio would be larger then the investment in the market index only, but with the same expected return. More precisely, for \(x=\alpha \) the infinitesimal return of the portfolio is \(\left( r+\frac{\mu _m^2}{\sigma _m^2}\right) \mathrm dt\) and it is easily seen that by choosing the optimal strategy \({h^{(1)}}^{*}={h^{(2)}}^{*}=0\) and \({h^{(m)}}^{*}=\frac{\mu _m}{\sigma _m^2}\), the portfolio volatility is \(\frac{\mu _m}{\sigma _m}\). Any other portfolio with non-zero weights in stocks \(S^{(1)}\) and \(S^{(2)}\) would have higher volatility, given by \(\sqrt{\frac{\mu _m^2}{\sigma _m^2}+\sigma ^2(h^{(1)}+h^{(2)})^2+(b_1{h^{(1)}})^2+(b_2{h^{(2)}})^2}\).

Remark 2

By setting the parameter values

$$\begin{aligned} b_1=b_2=b, \quad \beta _1=\beta _2=\beta , \quad \lambda ^i_1=\lambda _1, \quad \lambda ^i_2=\lambda _2, \quad \alpha ^i_1=\alpha ^i_2=0 \end{aligned}$$
(17)

for \(i\in \{1, \dots , K\}\), one gets the optimal trading strategies implied by the model of Liu and Timmermann (2013) in the case of logarithmic utility, which are explicitly given by

$$\begin{aligned} {h^{(1)}}^{*}(t,x)= & {} -\frac{(\lambda _1 +\varrho \lambda _2)x}{b^2(1+\varrho )}, \end{aligned}$$
(18)
$$\begin{aligned} {h^{(2)}}^{*}(t,x)= & {} \frac{(\lambda _2 +\varrho \lambda _1)x}{b^2(1+\varrho )}, \end{aligned}$$
(19)
$$\begin{aligned} {h^{(m)}}^{*}(t,x)= & {} \frac{\mu _m}{\sigma _m^2}-\beta \left( {h^{(1)}}^{*}(t,x)+{h^{(2)}}^{*}(t,x)\right) \, \end{aligned}$$
(20)

with \(\varrho =\frac{\sigma ^2}{ \sigma ^2+b^2}.\) To gain a better intuition on the characteristics of our model, we investigate the following cases;

  1. i.

    Consider the parameter restrictions in (17) except for Markov modulated \(\lambda _1^i\) and \(\lambda _2^i\), for \(i\in \{1, \dots , K\}\). This leads to a simple regime-switching version of Liu and Timmermann (2013) model. The optimal strategies, in this case, preserve the same structure of (18)–(20), meaning that the investor allocates her portfolio according to the same rule of Liu and Timmermann (2013), conditional on the state of the Markov chain.

  2. ii.

    If we take only regime-switching \(\alpha ^i_1\) and \(\alpha ^i_2\), for \(i\in \{1, \dots , K\}\), we see that the optimal strategy has two components:

    $$\begin{aligned} {h^{(1)}}^{*}(t,x,i)= & {} -\frac{(\lambda _1 +\varrho \lambda _2)x}{b^2(1+\varrho )} +\frac{\lambda _1\alpha ^i_1 +\varrho \lambda _2\alpha ^i_2}{b^2(1+\varrho )},\\ {h^{(2)}}^{*}(t,x,i)= & {} \frac{(\lambda _2 +\varrho \lambda _1)x}{b^2(1+\varrho )}-\frac{\lambda _2\alpha ^i_2 +\varrho \lambda _1\alpha ^i_1}{b^2(1+\varrho )},\\ {h^{(m)}}^{*}(t,x,i)= & {} \frac{\mu _m}{\sigma _m^2}-\beta \left( {h^{(1)}}^{*}(t,x)+{h^{(2)}}^{*}(t,x)\right) . \end{aligned}$$

    Relations above imply that to account for the mispricing errors, optimal strategies in (18)–(20) need to be adjusted. For example, assuming that the spread is larger than \(\alpha ^i_1\) and \(\alpha ^i_2\) and that also \(\lambda _1,\lambda _2>0\), the correction for mispricing suggests that an investor should short sell a smaller amount of stock \(S^{(1)}\) and buy a smaller amount of stock \(S^{(2)}\). This is intuitively reasonable since in this case the first asset is overpriced and the second one is underpriced.

Note that for Liu and Timmermann (2013) model, under recurring arbitrage opportunities, \(({h^{(1)}}^{*},{h^{(2)}}^{*})\), are zero as soon as the process \(X_t\) hits its mean reversion level. This is due to two observations. The first observation is that the errors, and hence optimal strategies, are just proportional to X, and the second one is that the long run mean of the spread is zero. In our model, the mean reversion level of the spread is Markov modulated, given by \(\theta (Y)\), and error terms are affine functions of the spread. Therefore, we have a clear interpretation of the optimal strategies when the spread \(X_t\) hits \(\alpha _1\) or \(\alpha _2\). For example, if the spread hits \(\alpha _1\), the portion of the portfolio weights related to the first asset, i.e., in \({h^{(2)}}^{*}\) the term \(\frac{\lambda _1^{i}(x-\alpha _1^i)}{b_2^2+b_1^2\varrho _1}\), vanishes. Similar results apply when X hits \(\alpha _2\). If for example \(\alpha _1=\alpha _2=\alpha \), the investor chooses not to invest in \(S^{(1)}\) or \(S^{(2)}\) when X reaches the level \(\alpha \), since there is no mispricing between two co-integrated assets. Basically this implies that the portfolio contribution arising from the relative mispricing errors vanishes when the spread hits that error term and consequently, we may not expect \(({h^{(1)}}^{*},{h^{(2)}}^{*})\) to vanish as soon as X hits \(\theta (Y)\).

3.2 Optimal beta-neutral investment

To achieve market neutrality, traders may chose investment strategies so that the resulting portfolio has zero (CAPM) beta. The goal of this section is to characterize this type of trading strategies which are called beta-neutral. We should also remind the reader that this type of strategies can also be used for “betting against betas” type strategies in which an high beta asset (short leg) is deleveraged so that its beta decreases to 1 and a low beta asset (long leg) is leveraged so that its beta becomes 1. We start with a formal definition.

Definition 2

A \({\mathbb {G}}\)-admissible beta-neutral portfolio strategy is a \({\mathbb {G}}\)-predictable self-financing strategy \(h^{\beta }=(h^{(\beta ,1)},h^{(\beta ,2)},h^{(\beta ,m)})\) such that

$$\begin{aligned} \beta _1h^{(\beta ,1)}_t+\beta _2h^{(\beta ,2)}_t=0, \quad t \in [0,T], \end{aligned}$$

and satisfies \(\mathbb {E}\left[ \int _0^T\left( {h^{(\beta ,m)}_t}^2+{h^{(\beta ,1)}_t}^2\right) \mathrm dt\right] <\infty \). We denote the set of \({\mathbb {G}}\)-admissible beta-neutral strategies by \({\mathcal {A}}^{\beta }\).

In the next theorem we compute the optimal beta-neutral investment strategies and the corresponding value function. The proof of this result replicates that of Theorem 1 and it is therefore omitted.

Theorem 2

Consider a trader with a logarithmic utility function. Then the optimal beta-neutral investment strategy \({h^{\beta }}^{*}=({h^{(\beta ,1)}}^{*},{h^{(\beta ,2)}}^{*},{h^{(\beta ,m)}}^{*}) \in {\mathcal {A}}^{\beta }\) is given by

$$\begin{aligned}&{h^{(\beta ,1)}}^{*}(t,x,i)= -\frac{\lambda _1^i(x-\alpha _1^i)+\frac{\beta _1}{\beta _2}\lambda _2^i(x-\alpha _2^i)}{b_1^2+\frac{\beta _1^2}{\beta _2^2}b_2^2+\sigma ^2\left( 1-\frac{\beta _1}{\beta _2}\right) ^2}, \end{aligned}$$
(21)
$$\begin{aligned}&{h^{(\beta ,2)}}^{*}(t,x,i)=-\frac{\beta _1}{\beta _2}{h^{(\beta ,1)}}^{*}(t,x,i), \end{aligned}$$
(22)
$$\begin{aligned}&{h^{(\beta ,m)}}^{*}(t,x,i)=\frac{\mu _m}{\sigma _m^2}. \end{aligned}$$
(23)

The value function is of the form

$$\begin{aligned} V(t, w, x, i )=\log (w)+m(t,i)x^2+n(t,i)x+u(t,i),\end{aligned}$$
(24)

where the functions m(t, i), n(t, i) and u(t, i) for \(i\in \{1, \dots , K\}\) solve the following system of ordinary differential equations

$$\begin{aligned}&m_t(t,i)-2(\lambda _1^i+\lambda _2^i)m(t,i)+\sum _{j=1}^K m(t,j) q^{ij}+\varPhi _1^i =0, \end{aligned}$$
(25)
$$\begin{aligned}&n_t(t,i)-(\lambda _1^i+\lambda _2^i)n(t,i)+\sum _{j=1}^K n(t,j) q^{ij}+2(\varGamma _1+\lambda _1^i\alpha _1^i+\lambda _2^i\alpha _2^i)m(t,i)-\varPhi _2^i=0, \end{aligned}$$
(26)
$$\begin{aligned}&u_t(t,i)+ \sum _{j=1}^K u(t,j) q^{ij}+\varGamma _2m(t,i)+(\varGamma _1+\lambda _1^i\alpha _1^i+\lambda _2^i\alpha _2^i)n(t,i)+\varPhi _3^i=0, \quad {} \end{aligned}$$
(27)

with terminal conditions \(m(T,i)=0\), \(n(T,i)=0\) and \(u(T,i)=0\) for all \(i\in \{1,\dots ,K \}\), and where \(\varGamma _1\) and \(\varGamma _2\) are as given in Theorem 1 and

$$\begin{aligned} \varPhi _1^i&:=\frac{\left( \beta _2\lambda _1^i+\beta _1\lambda _2^i\right) ^2}{2\left( b_1^2\beta _2^2+b_2^2\beta _1^2+\sigma ^2\left( \beta _1-\beta _2\right) ^2\right) },\\ \varPhi _2^i&:=\frac{\left( \alpha _1^i\beta _2\lambda _1^i+\alpha _2^i\beta _1 \lambda _2^i\right) \left( \beta _1 \lambda _2^i+\beta _2\lambda _1^i\right) }{b_1^2\beta _2^2+b_2^2\beta _1^2 +\sigma ^2\left( \beta _1-\beta _2\right) ^2},\\ \varPhi _3^i&:=\frac{\left( \alpha _1^i\beta _2\lambda _1^i+\alpha _2^i\beta _1 \lambda _2^i\right) ^2}{2\left( b_1^2\beta _2^2+b_2^2\beta _1^2 +\sigma ^2\left( \beta _1-\beta _2\right) ^2\right) } +r+\frac{\mu _m^2}{2\sigma _m^2}. \end{aligned}$$

Remark 3

Notice that the ratio \(\beta _1/\beta _2\) plays the role of \(\varrho _2\) in Theorem 1. In addition, setting \(\beta _1=\beta _2\) in the current context corresponds to the so-called delta-neutral strategies. This is a class of investment strategies that satisfy \(h^{(\delta ,1)}=-h^{(\delta ,2)}\) that is, the same amount of capital is invested in each of the co-integrated stocks. In this setting the optimal delta-neutral strategy is given by

$$\begin{aligned} {h^{(\delta ,1)}}^{*}(t,x,i)= & {} -{h^{(\delta ,2)}}^{*}(t,x,i) =-\frac{\lambda _1^i(x-\alpha _1^i)+\lambda _2^i(x-\alpha _2^i)}{b_1^2+b_2^2},\\ {h^{(\delta ,m)}}^{*}(t,x,i)= & {} \frac{\mu _m}{\sigma _m^2}. \end{aligned}$$

4 Optimal convergence trade under partial information

The goal of this section is to study the utility maximization problem related to convergence trade from the point of view of a partially informed investor. Therefore we now assume that the investor cannot directly observe the state of the Markov chain Y, and that her information comes from the observation of price processes \(S^{(m)}, S^{(1)}\) and \( S^{(2)}\). Mathematically, the available information flow is given by the filtration \({\mathbb {F}}:=\{{\mathcal {F}}_t, \ t \in [0,T]\}\), where \({\mathcal {F}}_t=\sigma (S^{(1)}_u, S^{(2)}_u, S^{(m)}_u, \ 0 \le u \le t)\). Since the investor chooses how to allocate her wealth according to the available information, we will now consider the following set of admissible strategies.

Definition 3

An \({\mathbb {F}}\)-admissible portfolio strategy is a self-financing and \({\mathbb {F}}\)-predictable strategy \(h=(h^{(m)}, h^{(1)}, h^{(2)})\) that satisfies integrability condition (7), and \({\mathcal {A}}^{{\mathbb {F}}}\) is the set of all \({\mathbb {F}}\)-admissible strategies.

In order to solve the optimization problem under partial information we first need to infer information about the state of the Markov chain Y from the observation process \((S^{(1)},S^{(2)},S^{(m)})\), using filtering techniques. The idea is to determine the conditional distribution of the unobservable state process Y, given the observed history. To this, for every function \(f:E \rightarrow {\mathbb {R}}\) we define the filter \(\pi (f)\) as the optional projection of the process f(Y) on the available filtration, i.e.

$$\begin{aligned} \pi _t(f)={\mathbf {E}}\left[ f(Y_t)|{\mathcal {F}}_t\right] , \quad t \in [0,T]. \end{aligned}$$

Due to the nature of process Y, we get that

$$\begin{aligned} \pi _t(f)=\sum _{i=1}^K f(e_i){\mathbf {P}}\left( Y_t=e_i |{\mathcal {F}}_t\right) , \quad t \in [0,T]. \end{aligned}$$

Therefore, solving the filtering problem amounts to compute conditional state probabilities,

$$\begin{aligned} \pi ^{i}_t:={\mathbf {P}}\left( Y_t=e_i |{\mathcal {F}}_t\right) , \quad t \in [0,T], \end{aligned}$$

for every \(i\in \{1,\dots ,K\}\). In the sequel we will use the notation \(\varvec{\pi }\) to indicate the K-dimensional process \((\pi ^{1}, \dots , \pi ^{K} )^\top \) and \(\pi _t(f)={\mathbf {f}}^\top \varvec{\pi }_t=\sum _{i=1}^K f^i\pi ^i_t\) where \(\mathbf{f}=(f^1, \dots , f^K)^\top \) and \(f^i=f(e_i)\) for every \(i\in \{1, \dots , K\}\). We characterize processes \(\pi ^i\) for \(i \in \{1, \dots , K\}\) using the innovations approach. This is a standard technique that allows to formulate the filtering problem in the context of martingale theory, see, e.g. Fujisaki et al. (1972). Concretely, in our setting, we will derive conditional state probabilities via a system of coupled stochastic differential equations driven by a (multidimensional) Brownian motion in the observation filtration \({\mathbb {F}}\), called the innovation process. The name innovation comes from the fact that “new information” on the signal from t to \(t+\varDelta t\) is given by the increment of the innovation process between t and \(t+\varDelta t\), and it is independent of the observed history up to time t. To begin, we introduce the processes

$$\begin{aligned} R^{(1)}_t&=-\int _0^t\lambda _1(Y_s) (X_s-\alpha _1(Y_s)) \mathrm ds +\sigma B^{(0)}_t + b_1 B^{(1)}_t, \quad t \in [0,T],\\ R^{(2)}_t&=\int _0^t\lambda _2(Y_s)( X_s-\alpha _2(Y_s)) \mathrm ds +\sigma B^{(0)}_t + b_2 B^{(2)}_t, \quad t \in [0,T], \end{aligned}$$

and observe that the triplets \((S^{(1)}, S^{(2)}, S^{(m)})\) and \((R^{(1)}, R^{(2)}, S^{(m)})\) generate the same information flow. Define \(({\mathbb {G}}, {\mathbf {P}})\)-Brownian motions \(Z^{(1)}\) and \(Z^{(2)}\) by

$$\begin{aligned} Z^{(1)}_t=\frac{\sigma B^{(0)}_t + b_1 B^{(1)}_t}{\sigma _1}, \qquad Z^{(2)}_t=\frac{\sigma B^{(0)}_t + b_2 B^{(2)}_t}{\sigma _2},\quad t \in [0,T],\end{aligned}$$

where \(\sigma _1=\sqrt{\sigma ^2+b^2_1}\) and \(\sigma _2=\sqrt{\sigma ^2+b^2_2}\). Note that \(Z^{(1)}\) and \(Z^{(2)}\) are correlated Brownian motions with correlation coefficient \(\rho =\frac{\sigma ^2}{\sigma _1\sigma _2}\in [0,1]\) and that there exists a \(({\mathbb {G}}, {\mathbf {P}})\)-Brownian motion \({\widetilde{Z}}^{(2)}\) independent of \(Z^{(1)}\) such that \(Z^{(2)}=\rho Z^{(1)}+\sqrt{1-\rho ^2}{\widetilde{Z}}^{(2)}\). We now introduce the innovation process \(I=(I^{(1)}, I^{(2)})^\top \) in the following way. Define

$$\begin{aligned} \mu _1(X_t, Y_t)&= -\lambda _1(Y_t) (X_t-\alpha _1(Y_t)), \quad t \in [0,T],\\ \mu _2(X_t, Y_t)&=\lambda _2(Y_t) (X_t-\alpha _2(Y_t)), \quad t \in [0,T], \end{aligned}$$

and denote by \(\pi _t(\mu _i)={\mathbf {E}}\left[ \mu _i(X_t,Y_t)|{\mathcal {F}}^S_t\right] =\varvec{\mu }_i(X_t)^\top \varvec{\pi }_t\) where, for \(i\in \{1,2\}\) and \(t \in [0,T]\) vector \(\varvec{\mu }_i(X_t)=(\mu _i(X_t, e_1), \dots ,\mu _i(X_t, e_K) )\); then we get that

$$\begin{aligned} I^{(1)}_t&= Z^{(1)}_t+\int _0^t \frac{\mu _1(X_u, Y_u) - \varvec{\mu }_1(X_u)^\top \varvec{\pi }_u }{\sigma _1} \mathrm du, \\ I^{(2)}_t&= {\widetilde{Z}}^{(2)}_t + \int _0^t \frac{\sigma _1 (\mu _2(X_u, Y_u) - \varvec{\mu }_2(X_u)^\top \varvec{\pi }_u)-\rho \sigma _2 (\mu _1(X_u, Y_u) - \varvec{\mu }_1(X_u)^\top \varvec{\pi }_u)}{\sigma _1\sigma _2\sqrt{1-\rho ^2}} \mathrm du, \end{aligned}$$

for every \(t \in [0,T]\). In the sequel we will use also the matrix/vector form of the process I, given by

$$\begin{aligned} I_t=Z_t+\int _0^t\varSigma ^{-1}(A(X_u,Y_u)-\pi _u(A))\mathrm du, \quad t \in [0,T], \end{aligned}$$
(28)

where \(Z=(Z^{(1)}, {\widetilde{Z}}^{(2)})^\top \), \(A(X,Y)=(\mu _1(X,Y), \mu _2(X,Y))^\top \),

$$\begin{aligned} \varSigma =\left( \begin{array}{cc} \sigma _1&{}0\\ \sigma _2 \rho &{} \sigma _2 \sqrt{1-\rho ^2} \end{array}\right) . \end{aligned}$$

Remark 4

The innovation process I in (28) has two important features. First, I is an \(({\mathbb {F}}, {\mathbf {P}})\)-Brownian motion; see, for instance, (Bain and Crisan 2009, Proposition 2.30). Second, by the independence between the Markov chain Y and the vector \((B^{(m)},B^{(0)}, B^{(1)}, B^{(2)})\) driving the observation we get that the filtration generated by \((S^{(m)}, R^{(1)}, R^{(2)})\) and that generated by \((S^{(m)}, I^{(1)}, I^{(2)})\) are the same; see Allinger and Mitter (1981, Theorem 1). Then, we can apply (Jacod and Shiryaev 1987, Theorem III.4.34-(a)) and get that every \(({\mathbb {F}}, {\mathbf {P}})\)-local martingale M admits the following representation

$$\begin{aligned} M_t=M_0+\int _0^t\gamma _u\, \mathrm dI_u,\quad t\in [0,T], \end{aligned}$$
(29)

for some \({\mathbb {F}}\)-predictable 2-dimensional process \(\gamma \) such that

$$\begin{aligned} \int _0^T\Vert \gamma _u\Vert ^2\,\mathrm du<\infty , \quad {\mathbf {P}}-\text {a.s.} \end{aligned}$$

The filtering equation is computed in the next proposition. The proof of this result is given in “Appendix”.

Proposition 1

For every \(i \in \{1, \dots , K\}\), conditional state probabilities of the process Y satisfy the following system of SDEs

$$\begin{aligned} \mathrm d\pi _t^i= \sum _{j=1}^K q^{ji}\pi ^j_t \mathrm dt + H^{i}(X_t,\varvec{\pi }_t) \mathrm dI_t \end{aligned}$$
(30)

with \(\pi _0^i=p_0\), where for \(i=1, \dots , K\), \(H^{i}(X, \varvec{\pi }):=\{H^{i}(X_t, \varvec{\pi }_t), t\ge 0\}\) is the 2-dimensional process with components

$$\begin{aligned} H^{i,(1)}(X_t, \varvec{\pi }_t)&= \frac{\pi ^i_t (\mu _1(X_t, e_i)-\varvec{\mu }_1(X_t)^\top \varvec{\pi }_t)}{\sigma _1}, \\ H^{i,(2)}(X_t, \varvec{\pi }_t)&=\frac{\pi ^i_t\left( \sigma _1(\mu _2(X_t, e_i)-\varvec{\mu }_2(X_t)^\top \varvec{\pi }_t)-\sigma _2\rho (\mu _1(X_t, e_i)-\varvec{\mu }_1(X_t)^\top \varvec{\pi }_t)\right) }{\sigma _1\sigma _2\sqrt{1-\rho ^2}}, \end{aligned}$$

for every \(t \in [0,T]\) with \(\sigma _1=\sqrt{\sigma ^2+b^2_1}\) and \(\sigma _2=\sqrt{\sigma ^2+b^2_2}\).

Having the dynamics of the filtered probabilities enables us to derive a semimartingale decomposition for the co-integrated asset price processes with respect to the information filtration. Precisely, we have that

$$\begin{aligned} \frac{\mathrm dS^{(1)}_t}{S^{(1)}_t}&=(r+\beta _1 \mu _m)\mathrm dt +\beta _1\sigma _m \mathrm dB^{(m)}_t+\sigma _1 \mathrm dI^{(1)}_t + \varvec{\mu }_1(X_t)^\top \varvec{\pi }_t \mathrm dt, \end{aligned}$$
(31)
$$\begin{aligned} \frac{\mathrm dS^{(2)}_t}{S^{(2)}_t}&=(r+\beta _2 \mu _m)\mathrm dt+\beta _2\sigma _m \mathrm dB^{(m)}_t +\sigma _2 \rho \mathrm dI^{(1)}_t +\sigma _2 \sqrt{1-\rho ^2}\mathrm dI^{(2)}_t +\varvec{\mu }_2(X_t)^\top \varvec{\pi }_t \mathrm dt, \end{aligned}$$
(32)

with \(S^{(1)}_0>0\) and \(S^{(2)}_0>0\), and the market index price process \(S^{(m)}\) which is not affected by the Markov chain, preserves its dynamics. This leads to the following stochastic differential equations for the spread and the wealth processes

$$\begin{aligned} \mathrm dX_t&=\left( \varGamma _1+\left( \varvec{\mu }_1(X_t)^\top \varvec{\pi }_t -\varvec{\mu }_2(X_t)^\top \varvec{\pi }_t \right) \right) dt\nonumber \\&+\left( \beta _1-\beta _2\right) \sigma _m \mathrm dB^{(m)}_t+(\sigma _1 -\rho \sigma _2)\mathrm dI^{(1)}_t-\sigma _2\sqrt{1-\rho ^2} \mathrm dI^{(2)}_t, \quad X_0\in {\mathbb {R}}, \end{aligned}$$
(33)
$$\begin{aligned} \frac{\mathrm dW^h_t}{W^h_t}&=\left( r + \left( h^{(m)}_t +h^{(1)}_t\beta _1 +h^{(2)}_t\beta _2 \right) \mu _m + \left( h^{(1)}_t \varvec{\mu }_1(X_t)^\top \varvec{\pi }_t +h^{(2)}_t \varvec{\mu }_2(X_t)^\top \varvec{\pi }_t \right) \right) \mathrm dt\nonumber \\&+\sigma _m\left( h^{(m)}_t+h^{(1)}_t\beta _1+h^{(2)}_t\beta _2\right) \mathrm dB^{(m)}_t+ (\sigma _1 h^{(1)}_t +\rho \sigma _2 h^{(2)})\,\mathrm dI^{(1)}_t\nonumber \\&+\sigma _2 \sqrt{1-\rho ^2} h^{(2)}_t \mathrm dI^{(2)}_t, \quad W_0^h>0, \end{aligned}$$
(34)

respectively. Moreover, thanks to uniqueness of the solution of the filtering equation we can consider the \((K+2)\)-dimensional process \((W,X,\varvec{\pi })\) as the state process and introduce the equivalent optimal control problem under full information, called the separated problem; see, e.g., Fleming and Pardoux (1982). The optimization problem we address now is

$$\begin{aligned} \text{ Maximize } \quad {\mathbf {E}}^{t,w,x, {\mathbf {p}}}[\log {W_T}] \quad \text{ over } \text{ all } \ h\in {\mathcal {A}}^{\mathbb {F}}\end{aligned}$$
(35)

where \({\mathbb {E}}^{t,w,x,{\mathbf {p}}}\) denotes the conditional expectation given \(W_t=w\), \(X_t=x\) and \(\varvec{\pi }_t={\mathbf {p}}\), where \((w,x,{\mathbf {p}})\in {{\mathbb {R}}}_+ \times {\mathbb {R}} \times \varDelta _K\), with \(\varDelta _K\) denoting the \((K-1)\)-dimensional simplex. Next, we resort to the HJB approach to solve problem (35). We define the value function by

$$\begin{aligned} V(t,w,x,{\mathbf {p}}):=\underset{h\in {\mathcal {A}}^{\mathbb {F}}}{\sup }\,\,{\mathbf {E}}^{t,w,x,{\mathbf {p}}} \left[ \log {W_T}\right] . \end{aligned}$$
(36)

In order to get explicit form for the value function up to the solution of a system of PDEs we restrict to the case where \(\lambda _1(y)=\lambda _1\in {\mathbb {R}}\) and \(\lambda _2(y)=\lambda _2\in {\mathbb {R}}\). In this case coefficients \(H^{(i),1}(X, \varvec{\pi })\) and \(H^{(i),2}(X, \varvec{\pi })\), for \(i=1,\dots ,K\) in Eq. (30) do not depend on X and are given by

$$\begin{aligned} H^{i,(1)}(X_t, \varvec{\pi }_t)&= H^{i, (1)}(\varvec{\pi }_t)= \frac{\lambda _1 \pi ^i_t (\alpha _1^i-\varvec{\alpha }_1^\top \varvec{\pi }_t)}{\sigma _1}, \\ H^{i,(2)}(X_t, \varvec{\pi }_t)&= H^{i, (2)}(\varvec{\pi }_t)=\frac{-\lambda _2\sigma _1\pi ^i_t(\alpha _2^i-\varvec{\alpha }_2^\top \varvec{\pi }_t) -\sigma _2\lambda _1\rho \pi ^i_t(\alpha _1^i-\varvec{\alpha }_1^\top \varvec{\pi }_t)}{\sigma _1\sigma _2\sqrt{1-\rho ^2}}, \end{aligned}$$

for every \(t \in [0,T]\).

Theorem 3

Suppose that \(\lambda _1(y)=\lambda _1\in {\mathbb {R}}\) and \(\lambda _2(y)= \lambda _2\in {\mathbb {R}}\) with \(\lambda _1+\lambda _2>0\) and assume that the investor has logarithmic utility preferences. Then the optimal portfolio strategy \(h^*=({h^{(1)}}^{*},{h^{(2)}}^{*},{h^{(m)}}^{*})\in {\mathcal {A}}^{{\mathbb {F}}}\) is

$$\begin{aligned} {h^{(1)}}^{*}(t,x,{\mathbf {p}})= & {} \frac{\varvec{\mu }_1(x)^\top {\mathbf {p}}-\varvec{\mu }_2(x)^\top {\mathbf {p}}\varrho _2}{b_1^2+b_2^2\varrho _2}, \end{aligned}$$
(37)
$$\begin{aligned} {h^{(2)}}^{*}(t,x,{\mathbf {p}})= & {} \frac{\varvec{\mu }_2(x)^\top {\mathbf {p}}-\varvec{\mu }_1(x)^\top {\mathbf {p}}\varrho _1}{b_2^2+b_1^2\varrho _1}, \end{aligned}$$
(38)
$$\begin{aligned} {h^{(m)}}^{*}(t,x,{\mathbf {p}})= & {} \frac{\mu _m}{\sigma _m^2}-\beta _1{h^{(1)}}^{*}(t,x,{\mathbf {p}})-\beta _2{h^{(2)}}^{*}(t,x,{\mathbf {p}}). \end{aligned}$$
(39)

The value function is of the form

$$\begin{aligned} V(t, w, x, {\mathbf {p}})=\log (w)+{{\bar{m}}}(t)x^2+{{\bar{n}}}(t,{\mathbf {p}})x+{{\bar{u}}}(t,{\mathbf {p}}), \end{aligned}$$
(40)

where function \({{\bar{m}}}(t)\) solves the ordinary differential equation

$$\begin{aligned}&{{\bar{m}}}_t(t) -2 {{\bar{m}}}(t) (\lambda _1+\lambda _2)+ \varTheta _1 =0 \end{aligned}$$
(41)

with terminal condition \({{\bar{m}}}(T)=0\) and functions \({{\bar{n}}}(t,{\mathbf {p}})\) and \({{\bar{u}}}(t,{\mathbf {p}})\) solve the following system of partial differential equations

$$\begin{aligned}&{{\bar{n}}}_t(t,{\mathbf {p}}) - {{\bar{n}}}(t, {\mathbf {p}}) (\lambda _1+\lambda _2)+ \sum _{i,j=1}^K {{\bar{n}}}_{p^i}(t,{\mathbf {p}}) q^{ji}p^j + 2(\varGamma _1+\lambda _1\varvec{\alpha }_1^\top {\mathbf {p}}+\lambda _2\varvec{\alpha }_2^\top {\mathbf {p}}) {{\bar{m}}}(t)\nonumber \\&\qquad +\frac{1}{2}\sum _{i,j=1}^K {{\bar{n}}}_{p^ip^j}(t,{\mathbf {p}})\left( H^{i, (1)}({\mathbf {p}}) H^{j, (1)}({\mathbf {p}})+H^{i, (2)}({\mathbf {p}}) H^{j, (2)}({\mathbf {p}})\right) - \varTheta _2({\mathbf {p}})=0, \end{aligned}$$
(42)
$$\begin{aligned}&{{\bar{u}}}_t(t,{\mathbf {p}})+ \varGamma _2 {{\bar{m}}}(t) + (\varGamma _1+\lambda _1\varvec{\alpha }_1^\top {\mathbf {p}}+\lambda _2\varvec{\alpha }_2^\top {\mathbf {p}}) {{\bar{n}}}(t,{\mathbf {p}})+ \varTheta _3({\mathbf {p}})\nonumber \\&\qquad +\sum _{i=1}^K {{\bar{u}}}_{p^i}(t,{\mathbf {p}}) q^{ji} p^j+\frac{1}{2}\sum _{i,j=1}^K {{\bar{u}}}_{p^ip^j}(t,{\mathbf {p}})(H^{i, (1)}({\mathbf {p}}) H^{j, (1)}({\mathbf {p}})+H^{i, (2)}({\mathbf {p}}) H^{j, (2)}({\mathbf {p}})) \nonumber \\&\qquad + \sum _{i=1}^K {{\bar{n}}}_{p^i}(t,{\mathbf {p}}) \left( \frac{b_1^2}{\sqrt{\sigma ^2+b_1^2}}H^{i, (1)}({\mathbf {p}}) - \frac{\sqrt{\sigma ^2(b_1^2+b_2^2)+b_1^2b_2^2}}{\sqrt{\sigma ^2+b_1^2}} H^{i, (2)}({\mathbf {p}})\right) =0 \end{aligned}$$
(43)

with terminal conditions \({{\bar{n}}}(T,{\mathbf {p}})=0\) and \({{\bar{u}}}(T,{\mathbf {p}})=0\) and where \(\varGamma _1\) and \(\varGamma _2\) are the same of Theorem 1 and

$$\begin{aligned} \varTheta _1&:=\frac{(\sigma ^2+b_2^2)\lambda _1^2+(\sigma ^2+b_1^2) \lambda _2^2+2\sigma ^2 \lambda _1\lambda _2}{2(\sigma ^2b_1^2+\sigma ^2b_2^2+b_1^2b_2^2)},\\ \varTheta _2({\mathbf {p}})&:= \frac{\lambda _1 \varvec{\alpha }_1^\top {\mathbf {p}}(\lambda _1(b_2^2+\sigma ^2) +\lambda _2\sigma ^2)+\lambda _2\varvec{\alpha }_2^\top {\mathbf {p}}(\lambda _2(b_1^2+\sigma ^2)+\lambda _1\sigma ^2)}{b_1^2b_2^2 +\sigma ^2(b_1^2+b_2^2)},\\ \varTheta _3({\mathbf {p}})&:=\frac{(\lambda _1 b_2\varvec{\alpha }_1^\top {\mathbf {p}})^2+(\lambda _2 b_1\varvec{\alpha }_2^\top {\mathbf {p}})^2+\sigma ^2(\lambda _1 \alpha _1^\top {\mathbf {p}}+\lambda _2\alpha _2^\top {\mathbf {p}})^2}{2\left( b_1^2b_2^2 +\sigma ^2(b_1^2+b_2^2)\right) }+r+\frac{\mu _m^2}{2\sigma _m^2}. \end{aligned}$$

The proof of Theorem 3 is given in “Appendix”. We observe here that the function \({{\bar{m}}}\) driving the quadratic term is independent of \({\mathbf {p}}\). Mathematically this is due to the fact that \(\lambda _1\) and \(\lambda _2\) are assumed to be constant and therefore the trader does not account for the effect of partial information on the quadratic level of the current spread. The optimal portfolio strategy under partial information shares similar properties of the full information one (see Remark 3.1), except that unobserved parameters are replaced by the filtered estimates. That is, the certainty equivalence principle holds for the optimization problem under partial information; see Kuwana (1995) and Bäuerle and Rieder (2004).

4.1 Optimal beta-neutral investment under partial information

For comparison purposes we also investigate the structure of strategies leading to zero (CAPM) beta in the partial information setting. This means to consider investment strategies of the form outlined below.

Definition 4

An \({\mathbb {F}}\)-admissible beta-neutral investment strategy is an \({\mathbb {F}}\)-predictable self-financing investment strategy \(h^{\beta }=({h^{(\beta ,1)}},{h^{(\beta ,2)}},{h^{(\beta ,m)}})\) such that

$$\begin{aligned} \beta _1h^{(\beta ,1)}_t+\beta _2h^{(\beta ,2)}_t=0, \quad t \in [0,T] \end{aligned}$$
(44)

with \(\mathbb {E}\left[ \int _0^T \left( {h^{(\beta ,m)}_t}^2 +{h^{(\beta ,1)}_t}^2\right) \mathrm dt\right] <\infty \). We denote by \({\mathcal {A}}^{{\mathbb {F}},\beta }\) the set of all \({\mathbb {F}}\)-admissible beta-neutral strategies.

The optimal beta-neutral investment strategy under restricted information and the corresponding value function are given in Theorem 4 below. The proof is similar to that of Theorem 3 and it is therefore omitted.

Theorem 4

Assume that \(\lambda _1(y)=\lambda _1\in {\mathbb {R}}\) and \(\lambda _2(y)=\lambda _2\in {\mathbb {R}}\) with \(\lambda _1+\lambda _2>0\) and consider a trader with a logarithmic utility function. Then, the optimal beta-neutral strategy under partial information \({h^{\beta }}^{*}=({h^{(\beta ,1)}}^{*},{h^{(\beta ,2)}}^{*},{h^{(\beta ,m)}}^{*}) \in {\mathcal {A}}^{ {\mathbb {F}},\beta }\) is

$$\begin{aligned}&{h^{(\beta ,1)}}^{*}(t,x,{\mathbf {p}})= -\frac{\lambda _1(x-\varvec{\alpha }_1^\top {\mathbf {p}}) +\frac{\beta _1}{\beta _2}\lambda _2(x-\varvec{\alpha }_2^\top {\mathbf {p}})}{b_1^2+b_2^2 \frac{\beta _1^2}{\beta ^2_2}+\sigma ^2\left( 1-\frac{\beta _1}{\beta _2}\right) ^2}, \\&{h^{(\beta ,2)}}^{*}(t,x,{\mathbf {p}})=-\frac{\beta _1}{\beta _2}{h^{(\beta ,1)}}^{*}(t,x,i),\\&{h^{(\beta ,m)}}^{*}(t,x,{\mathbf {p}})=\frac{\mu _m}{\sigma _m^2}. \end{aligned}$$

The value function is of the form

$$\begin{aligned} V(t, w, x, {\mathbf {p}})=\log (w)+{{\bar{m}}}(t)x^2+{{\bar{n}}}(t,{\mathbf {p}})x+{{\bar{u}}}(t,{\mathbf {p}}), \end{aligned}$$

where function \({{\bar{m}}}(t)\) solves the ordinary differential equation

$$\begin{aligned}&{{\bar{m}}}_t(t) -2{{\bar{m}}}(t) (\lambda _1+\lambda _2) + \varPhi _1=0, \end{aligned}$$

with the terminal condition \({{\bar{m}}}(T)=0\) and functions \(\bar{n}(t,{\mathbf {p}})\) and \({{\bar{u}}}(t,{\mathbf {p}})\) solve the following system of partial differential equations

$$\begin{aligned}&{{\bar{n}}}_t(t,{\mathbf {p}}) +2 {{\bar{m}}}(t)(\varGamma _1+\lambda _1\varvec{\alpha }_1+\lambda _2\varvec{\alpha }_2) - {{\bar{n}}}(t, {\mathbf {p}}) (\lambda _1+\lambda _2)+ \sum _{i,j=1}^K {{\bar{n}}}_{p^i}(t,{\mathbf {p}}) q^{ji}p^j \\&\qquad +\frac{1}{2}\sum _{i,j=1}^K {{\bar{n}}}_{p^ip^j}(t,{\mathbf {p}})\left( H^{i, (1)}({\mathbf {p}}) H^{j, (1)}({\mathbf {p}})+H^{i, (2)}({\mathbf {p}}) H^{j,(2)}({\mathbf {p}})\right) - \varPhi _2({\mathbf {p}})=0, \\&{{\bar{u}}}_t(t,{\mathbf {p}})+ (\varGamma _1+\lambda _1\varvec{\alpha }_1+\lambda _2\varvec{\alpha }_2) {{\bar{n}}}(t,{\mathbf {p}}) +\varGamma _2 {{\bar{m}}}(t) + \varPhi _3({\mathbf {p}})\\&\qquad +\sum _{i,j=1}^K {{\bar{u}}}_{p^i}(t,{\mathbf {p}}) q^{ji} p^j +\frac{1}{2}\sum _{i,j=1}^K{{\bar{u}}}_{p^ip^j}(t,{\mathbf {p}})(H^{i, (1)}({\mathbf {p}}) H^{j, (1)}({\mathbf {p}})+H^{i, (2)}({\mathbf {p}}) H^{j,(2)}({\mathbf {p}})) \\&\qquad + \sum _{i=1}^K {{\bar{n}}}_{p^i}(t,{\mathbf {p}}) \left( \frac{b_1^2}{\sqrt{\sigma ^2+b_1^2}}H^{i, (1)}({\mathbf {p}}) - \frac{\sqrt{\sigma ^2(b_1^2+b_2^2)+b_1^2b_2^2}}{\sqrt{\sigma ^2+b_1^2}} H^{i, (2)}({\mathbf {p}})\right) =0 \end{aligned}$$

with terminal conditions \({{\bar{n}}}(T,{\mathbf {p}})=0\) and \({{\bar{u}}}(T,{\mathbf {p}})=0\) and where \(\varGamma _1\) and \(\varGamma _2\) are the same of Theorem 1 and

$$\begin{aligned} \varPhi _1&:=\frac{\left( \beta _2\lambda _1+\beta _1\lambda _2\right) ^2}{2\left( b_1^2\beta _2^2+b_2^2\beta _1^2+\sigma ^2\left( \beta _1-\beta _2\right) ^2\right) },\\ \varPhi _2({\mathbf {p}})&:=\frac{\left( \beta _2\lambda _1 \varvec{\alpha }_1^\top {\mathbf {p}}+\beta _1\lambda _2\varvec{\alpha }_2^\top {\mathbf {p}}\right) \left( \beta _1\lambda _2+\beta _2\lambda _1\right) }{b_1^2\beta _2^2+b_2^2\beta _1^2+\sigma ^2\left( \beta _1-\beta _2\right) ^2},\\ \varPhi _3({\mathbf {p}})&:=\frac{\left( \beta _2\lambda _1\varvec{\alpha }_1^\top {\mathbf {p}}+\beta _1\lambda _2\varvec{\alpha }_2^\top {\mathbf {p}}\right) ^2}{2\left( b_1^2\beta _2^2+b_2^2\beta _1^2+\sigma ^2\left( \beta _1-\beta _2\right) ^2\right) } +r+\frac{\mu _m^2}{2\sigma _m^2}. \end{aligned}$$

Finally we again observe that choosing \(\beta _1=\beta _2\) we recover delta-neutral strategies in partial information which are given by

$$\begin{aligned} {h^{(\delta ,1)}}^{*}(t,x,{\mathbf {p}})= & {} -{h^{(\delta ,2)}}^{*}(t,x,{\mathbf {p}}) =-\frac{\lambda _1(x-\varvec{\alpha }_1^\top {\mathbf {p}})+\lambda _1(x-\varvec{\alpha }_1^\top {\mathbf {p}})}{b_1^2+b_2^2},\\ {h^{(\delta ,m)}}^{*}(t,x,{\mathbf {p}})= & {} \frac{\mu _m}{\sigma _m^2}. \end{aligned}$$

5 Numerical study with a 2-state Markov chain

In this section, we consider a 2-state Markov chain Y, that is, \({\mathcal {E}}=\{e_1, e_2\}\). Here we resort to a numerical approach in order to get qualitative characteristics of optimal strategies and the value function both under full and partial information. In the sequel, we fix the values for the following parameters as \(w=1\), \(r=0.02\), \(\beta _1=1.2\), \(\beta _2=1.05\), \(\sigma _m=.35\), \(\mu _m=0.05\) and \(\sigma =0.2\).

5.1 Optimization problem under full information

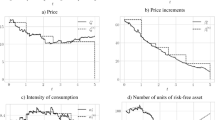
We first consider the full information setting where the trader is assumed to observe the state of the Markov chain. We begin with a simulation of a data set from which we generate a Markov chain and the price processes, respectively. In Fig. 1 we investigate the behavior of the optimal investment strategy for the simulated data. Clearly, we see that strategies depend on different regimes and present jumps at the jump times of the Markov chain. We also observe that the resulting optimal portfolio weights for the first and second assets change sign through time. In particular, we have long-long, long-short and short-short type optimal portfolios, which may indicate the flexibility of our modeling framework.

Fig. 1
figure 1

Optimal trading strategy for simulated data. Parameter values: \(b_1=0.3\), \(b_2=0.5, \lambda _1^1=0.5, \lambda _1^2=-0.3, \lambda _2^1=-0.1, \lambda _2^2=0.6, \alpha _1=\alpha _2= 0, x=0.01, q^{12}=0.7, q^{21}=0.2\)

Full size image

Next we investigate the properties of the value function. To do this, we solve the system of ODEs in Theorem 1 numerically. Figure 2 summarizes our results. To explain the outcomes, let \(({\overline{p}},1-{\overline{p}})\) denote the stationary distribution of the Markov chain Y. We consider two traders, one of which ignores the Markov modulated nature of the underlying parameters and use the averaged data \({\overline{\lambda }}_i={\overline{p}}\lambda _i^1+(1-{\overline{p}})\lambda _i^2\). The second trader, on the other hand, behaves optimally under our Markov modulated model. We set \(q^{12}=0.7\) and \(q^{21}=0.2\), and compute \({\overline{p}}={q^{21}}/(q^{12}+q^{21})=0.22\). Then, we get \({\overline{\lambda }}_1=-0.12\) and \({\overline{\lambda }}_2=0.45\). In Fig. 2 we plot \(V^{Av}(t,x)\), the value function obtained in the model assuming averaged data, and \({\mathbb {E}}^{{\overline{p}}}[V(t,x,Y_t)]={\overline{p}} V(t,x,1)+(1-{\overline{p}})V(t,x,2)\). We observe that \({\mathbb {E}}^{{\overline{p}}}[V(t,x,Y_t)]>V^{Av}(t,x)\), that is, averaged data do not suffice to obtain the optimal value for the convergence trade problem and hence on the average, the second trader performs better than the first one. We repeat this analysis for the case of beta-neutral trading and obtain same qualitative results.

Figure 2 also illustrates the dominance of the unrestricted strategies over the beta-neutral ones. This is quite natural since by restricting the set of admissible strategies, the trader could not realize all the benefits resulting from the co-integration between \(S^{(1)}\) and \(S^{(2)}\). The gap between values depends on the choice of parameters and in particular it increases in initial spread, x, and time to maturity, \(T-t\).

Fig. 2
figure 2

Optimal value corresponding to Markov regime-switching (RS) case and averaged data (AV) case for unrestricted and \(\beta \)-neutral trading as a function of initial spread (x) (upper panel) and time to maturity (T-t) (lower panel). Parameter values: \(b_1=0.3\), \(b_2=0.5\), \(\lambda _1^1=0.5\), \(\lambda _1^2=-0.3\), \(\lambda _2^1=-0.1\), \(\lambda _2^2=0.6\), \(\alpha _1=\alpha _2= 0\), \(x=0.5\), \(q^{12}=0.7\), \(q^{21}=0.2\)

Full size image

5.2 Optimization problem under partial information

We now consider the partial information case. Since conditional state probabilities \(\pi ^1\) and \(\pi ^2\) satisfy \(\pi ^1_t+\pi ^2_t=1\) for every \(t \in [0,T]\), we can reduce the number of state variables for the optimization problem. In the following we denote by \(p=p^1\) and \(1-p=p^2\). In Fig. 3 we plot the optimal strategies followed by a fully informed investor who observes the state of the underlying Markov chain Y and the partially informed one who can only estimate the state of Y through observation of prices, for the simulated data. The plot in Fig. 4 provides the corresponding path of the spread process X.

Fig. 3
figure 3

Comparison of optimal strategy under full (\(h^{(\cdot )}\)) and partial information (\(h^{(\cdot )}_p\)) for simulated data. Parameter values: \(\lambda _1\equiv 1.9\), \(\lambda _2\equiv 1.8\), \(\alpha _1^1=-0.4\), \(\alpha _1^2=0.2\), \(\alpha _2^1=-0.5\), \(\alpha _2^2=0.5\), \(p_0=0.3\), \(x=0.01\)

Full size image
Fig. 4
figure 4

Spread process versus Markov modulated pricing errors. Parameter values: \(\lambda _1\equiv 1.9\), \(\lambda _2\equiv 1.8\), \(\alpha _1^1=-0.4\), \(\alpha _1^2=0.2\), \(\alpha _2^1=-0.5\), \(\alpha _2^2=0.5\), \(x=0.01\)

Full size image

We see from Fig. 4 that, for instance, at the beginning of the investment period the spread is below the values \(\alpha _1(Y_t)\) and \(\alpha _2(Y_t)\), meaning that the first stock is undervalued and the second is overvalued. Figure 3 shows that a fully informed investor goes long in the first asset and short-sells the second one until the first jump occurs, which is consistent with Fig. 4. Notice that just before the first jump, the spread stays above the level \(\alpha _1(Y_t)\) for a short period of time, meaning that the first asset is overvalued. However the investor still goes long in the first asset, and the reason is due to the relative mispricing with the second asset. This is inline with the analytical result provided in equations (10)–(12).

When the first jump occurs characteristics of stocks change. The informed investor immediately reacts to the regime switch and changes her position from long to short in the first stock and from short to long in the second one. This is not the case for the uninformed investor who cannot observe the true values of the mispricing errors. She needs time for learning from the observation of stock prices and adjust her portfolio weights. How fast she can catch the state of the Markov chain mainly depends on two parameters. First, the amplitude of noise and second the speed of mean reversion of the spread towards its long-run mean. Figure 5 shows optimal investment strategies under full (solid lines) and partial information (dashed lines) for a parameter set where \(\sigma \) is large relative to \(\lambda _1+\lambda _2\). In this situation the effect of the noise dominates the drift and the partially informed investor is not able to estimate mispricing errors correctly. That means her investment strategy strongly deviates from the one under full information. Figure 3, instead represents the case where \(\sigma \) is small relative to \(\lambda _1+\lambda _2\). In this case, we see that the spread converges faster to its mean reversion level and consequently the filter approaches the true state of the Markov chain. The uninformed investor is, therefore, able to detect the signal and the investment strategy becomes closer to the one under full information.

Fig. 5
figure 5

Comparison of optimal strategy under full (\(h^{(\cdot )}\)) and partial information (\(h^{(\cdot )}_p\)) for simulated data (impact of mean-reversion speed). Parameter values: \(\lambda _1\equiv 0.2\), \(\lambda _2\equiv 0.3\), \(\alpha _1^1=-0.4\), \(\alpha _1^2=0.2\), \(\alpha _2^1=-0.5\), \(\alpha _2^2=0.5\), \(p_0=0.3\), \(x=0.01\)

Full size image

Now we measure the advantage of the fully informed investor over the partially informed one. In order to do that, we introduce the process L defined by

$$\begin{aligned} L_t={\mathbb {E}}\left[ V^f(t,W_t,X_t,Y_t)-V^p(t,W_t,X_t, \varvec{\pi }_t)|\{W_t=w\}\vee {\mathcal {F}}_t\right] , \ t\in [0,T] , \end{aligned}$$

where \(V^f\) represents the value function corresponding to the full information setting and \(V^p\) that corresponding to the partial information one. The process L represents the loss of utility due to partial information (see, e.g., Lee and Papanicolaou 2016 for the definition). The form of value functions and the Markov property of the pair \((X,\varvec{\pi })\) imply that there exists a function \(l(t, x, {\mathbf {p}})\) such that \(L_t=l(t, X_t, \varvec{\pi }_t)\), \({\mathbf {P}}-a.s.\) for every \(t\in [0,T]\). In Fig. 6 we plot the loss of utility in the 2-state Markov chain case. We observe that this is always greater than or equal to zero, meaning that information premium exists and it is always non-negative. Moreover it is larger when conditional state probabilities are close to 0.5. This reflects the fact that more uncertainty about the state of the Markov chain leads to higher losses in utility.

Fig. 6
figure 6

Loss of utility due to partial information as a function of estimated state probability (p) and time to maturity (T–t). Parameter values: \(\lambda _1\equiv 0.3\), \(\lambda _2\equiv 0.4\), \(\alpha _1^1=0.5\), \(\alpha _1^2=-0.2\), \(\alpha _2^1=0.2\), \(\alpha _2^2=-0.3\), \(x=0.05\), \(q^{12}=0.2\), \(q^{21}=0.5\)

Full size image

Possible Estimation Method. Although, we have focused more on the theoretical side of the convergence trading within a regime-switching and partial information framework in this study, here we find it useful to mention possible estimation methods that may be necessary for the practical and the data-driven side of the investment problem. In our co-integrated asset dynamics framework, the application of the model to data amounts to the filtering of unobserved states of the Markov chain as well as estimating the regime-switching unknown model parameters. In the literature, several Markov regime-switching cointegration models have been studied; see e.g., Krolzig (1997) and Hansen and Seo (2002). More recently, Elliott and Bradrania (2017) consider the estimation of a discrete-time pairs trading model that includes regime changes in the dynamics, where they utilized the Expectation-Maximization [EM] algorithm (see also Elliott 1993 or Damian et al. 2018 for details). This methodology provides an iterative procedure to compute maximum likelihood estimates. Each iteration of the EM algorithm consists of two steps. In the (E)xpectation-step, the likelihood function is averaged over the unobserved states given the observed data and the current estimates of parameters. In the (M)aximization-step, the parameter values that maximize this likelihood function are obtained based on the previously estimated values. Given the need for a substantial effort to tailor this method to our setting, we leave obtaining the corresponding EM algorithm and application to real data for future research.

6 Conclusion

In this paper, we have considered an extension of the model proposed by Liu and Timmermann (2013). We have studied the optimization problem for a trader with logarithmic utility preferences under different levels of information. We have assumed that the mean-reverting component of pricing errors depends on a hidden Markov switching factor which may or may not be directly observed by the investor.

In the full information setting, that is when the state of the Markov chain is observable, we have computed the optimal strategy and characterized the value function as the unique (classical) solution of the HJB equation. In this framework, we can reduce the HJB to a system of ODEs. We have analysed optimal strategies under full information and related our results to those implied by Liu and Timmermann (2013) model, to underline the effect of Markov modulated mispricing errors. We have also discussed the structure of beta-neutral strategies, achieved by taking long and short positions in such a way that the impact of the overall market on the portfolio is minimized. In the partial information case, we have transformed the original problem into the so-called reduced (or separated) problem via filtering by replacing unobservable states of the Markov chain with their optional projections over the available filtration. Then we have addressed the resulting control problem by dynamic programming, and we have represented the value function in terms of the solution of a system of PDEs. Beta-neutral strategies are also obtained in the partial information framework. Finally, we have studied a numerical example with a two-state Markov chain. We have provided a comparison between optimal decisions of fully informed and partially informed investors. We have concluded that averaged data are not sufficient to obtain the optimal value in the full information case, and that there is always positive premium due to information superiority when we compare the optimal value under full and partial information.