1 Introduction

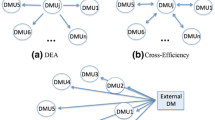
Data envelopment analysis (DEA) is a methodology for measuring the relative efficiencies in a group of decision-making units (DMUs) that consume multiple inputs to produce multiple outputs. Many applications and theoretical developments of DEA models have been reported since its appearance (for example, the review of Liu et al. 2013). The most prominent feature of a DEA is to provide a self-evaluation in which each DMU can choose the most favorable input and output weights to obtain the highest efficiency score. If the score is unity, then this DMU is nondominated; otherwise, it is dominated. However, the evaluation may lead to the situation in which many DMUs are evaluated as efficient, and the efficient units cannot be further discriminated. This would make the task of ranking DMUs more difficult.

Several studies have investigated to tackle this problem (Adler et al. 2002; Kao and Hung 2005; Ramón et al. 2010). Since all DMUs being evaluated have different preferences of DEA weights, Sexton et al. (1986) and Doyle and Green (1994) proposed the approach of using a cross-efficiency evaluation to discriminate among the DMUs. The idea of this approach is that the weights selected by each DMU are applied to calculate the efficiency of every other DMU. In other words, each DMU is required to be not only self- but also peer-evaluated. In this case, every DMU has n efficiencies, called cross efficiencies, calculated from the weights selected by all n DMUs, including itself. The final efficiency of a DMU is the average of the n efficiency scores. The results are thus more discriminative.

The advantages of cross-efficiency evaluation are ranking the DMUs in a unique order (Doyle and Green 1994) and effectively discriminating among DMUs (Boussofiane et al. 1991). Due to these advantages, this evaluation technique has been widely used in many applications, for example, technology selection (Sun 2002), economic-environmental performance (Lu and Lo 2007), supply chain management (Yu et al. 2010), public resource management (Falagario et al. 2012), resource allocation (Du et al. 2014), portfolio selection (Lim et al. 2014), premium allocation for academic faculty (Oral et al. 2014), baseball player ranking (Oukil and Amin 2015), and two-sided mergers and acquisition fits (Shi et al. 2017).

The main difficulty with the cross evaluation is that multiple solutions commonly prevail in a DEA, which lead to different cross efficiency scores and consequently different rankings of the DMUs. One remedy, as suggested by Sexton et al. (1986), is to use the secondary goals to help select a set of weights from the alternative solutions. In addition to the well-known aggressive and benevolent formulations (Sexton et al. 1986; Doyle and Green 1994) that use an additional criterion for the selection of weights, other secondary-goal techniques are proposed and discussed. Örkcü et al. (2015) and Wu et al. (2016) provided good reviews for the secondary goal approaches in a cross-efficiency evaluation. There is another line of literature developed in which all the possible weight sets in the weight space were considered in the proposed approaches, and a cross-efficiency interval was derived for a DMU being evaluated (Yang et al. 2012; Alcaraz et al. 2013; Ramόn et al. 2014; Liu 2018).

In the real world, observations are usually difficult to measure precisely. One way to manipulate imprecise data directly is to represent the uncertain values by the membership functions of the fuzzy set theory (Zimmermann 1996). Under the framework of a DEA, different approaches for measuring efficiency in fuzzy environments have been proposed. A comprehensive bibliography of these approaches and applications can be found in Hatami-Marbini et al. (2011) and Emrouznejad and Tavana (2014). However, as indicated in Sirvent and León (2014), the ranking of DMUs based on the ordering of fuzzy DEA efficiency scores can be criticized for the same reasons as those resulting from conventional DEA efficiencies. Dotoli et al. (2015) also noted that the existing fuzzy DEA models do not allow for discrimination among the efficient DMUs. A fuzzy cross-efficiency evaluation, which measures both the fuzzy self- and peer-evaluations, is able to eliminate the weaknesses of fuzzy DEA models, and this justifies the need for a fuzzy cross-efficiency evaluation for ranking the performance of DMUs in a fuzzy environment.

While Dotoli et al. (2015), Chen and Wang (2016), and Ruiz and Sirvent (2017) developed their own specific methodologies, these studies share one common property that they all employed the secondary goal approach to make a choice of weights among the alternative optimum solutions. Different approaches for determining the weights may produce different cross-efficiencies. Knowing which method to use depends on the underlying assumptions. Instead of using the secondary goal approach in those studies, we propose a novel approach that considers all possible weights of all the DMUs at the same time, which originates from the idea of Ramόn et al. (2014), to calculate the fuzzy cross-efficiency for ranking DMUs in a fuzzy environment. The advantages of the proposed approach compared to the existing approaches are that the fuzzy cross-efficiency of a DMU is calculated directly without the need to calculate the average cross efficiency from n DMUs, and a choice of weights is not required.

In the development of a fuzzy DEA, the α-level approach is a technique that is used to transform fuzzy DEA models into a pair of parametric programs for finding the lower and upper bounds of the fuzzy efficiency scores (Hatami-Marbini et al. 2011). This approach is very similar to that of interval programming, where it allows us to specify a model with interval coefficients (Oliveira and Antunes 2007). At a given α-level, the pair of parametric programs becomes a pair of conventional linear programs. Solving this pair of linear programs produces the lower and upper bounds of the fuzzy efficiency score. By enumerating the different α-levels, the membership function of the efficiency scores can be approximated. In addition, since convex fuzzy numbers can be represented as forms of α-level sets, any type of convex fuzzy number can be used as fuzzy input and output data in this approach. This is the reason why the α-level-based approach is the most popular approach for the development of a fuzzy DEA and fuzzy cross-efficiency models (Hatami-Marbini et al. 2011; Emrouznejad and Tavana 2014; Dotoli et al. 2015). In this study, the α-level based approach is incorporated into the idea of Ramόn et al. (2014) to investigate the fuzzy cross-efficiency evaluation for ranking DMUs.

The next section reviews several studies related to the cross-efficiency, fuzzy DEA, and fuzzy cross-efficiency evaluation. Then, in Sect. 3, we briefly introduce the crisp cross-efficiency evaluation methodology, and we formulate a fuzzy cross-efficiency evaluation based on the α-level-based approach in Sect. 4. After that, three examples are used in Sect. 5 to illustrate the fuzzy cross-efficiency measures. Finally, in Sect. 6, some conclusions are drawn from the discussions in the preceding sections.

2 Literature review

This section is classified into three subsections for the reviews of cross-efficiency evaluation, fuzzy DEA, and fuzzy cross-efficiency evaluation to provide a simple overview of the existing literature.

2.1 Cross-efficiency evaluation

Among all methods for discussing the issue of the discriminative power of a DEA, the most popularly studied method is the cross-efficiency evaluation method (Wu et al. 2016).Despite the extensive use of the cross-efficiency method, it has some limitations arising from the classic DEA. Doyle and Green (1994) stated that non-uniqueness decreases the usefulness of the cross-efficiency method and recommended the use of a secondary goal for a cross efficiency evaluation related to the non-uniqueness of the optimal weights in a DEA. They proposed aggressive and benevolent cross efficiency models to achieve the secondary goal.

Liang et al. (2008) proposed using the DEA game cross-efficiency evaluation method. Their method contains the DEA game cross efficiency model and an algorithm which can generate a set of cross-efficiency scores that constitute a Nash equilibrium point for the DMUs. Lam (2010) developed a methodology that applies discriminant analysis, a super-efficiency DEA model and a mixed-integer linear programming method to choose the suitable weight sets to be used in computing the cross-evaluation, and each obtained weight set can reflect the relative strengths of the efficient DMU under consideration. Wang and Chin (2010) investigated a neutral DEA model for cross-efficiency evaluation. Their neutral DEA model determined one set of input and output weights for each DMU from its own point of view without being an aggressive or benevolent formulation for the other DMUs. Ramón et al. (2010) initiated an idea to avoid the unreasonable weights instead of expecting that their effects would be cancelled out in the amalgamation of the weights. Specifically, their approach allows the inefficient DMUs to make a choice of weights that prevented them from using unrealistic weighting schemes. Jahanshahloo et al. (2011) incorporated a symmetric technique into the DEA cross-efficiency evaluation and presented a secondary goal model that can choose symmetric weights for DMUs. Örkcü and Bal (2011) exploited a goal programming method for the second stage of the cross-efficiency evaluation depending on the multiple criteria DEA model, which had three different efficiency concepts: the classical DEA, minmax, and minsum efficiency criteria.

Wang et al. (2012) proposed some alternative DEA models to minimize the virtual disparity in the cross-efficiency evaluation, and the proposed DEA models determined the input and output weights of each DMU in a neutral way. Lim (2012) introduced minimax and maximin formulations of cross-efficiency in the DEA, and the secondary goal was replaced with the minimization (or maximization) of the best (or worst) cross-efficiency of the peer DMUs. A bisection algorithm was developed for finding the cross-efficiency. Wu et al. (2012) developed a weight-balanced DEA model in which the secondary goal was to reduce the large differences in the weighted data and decrease the number of zero weights. Oral et al. (2015) used the advantage of multiple optimal solutions to integrate both the first- and second-order voices of all DMUs and suggested a model that was most appreciative for all DMUs being cross-evaluated by all others. Örkcü et al. (2015) modified the model of Lam (2010) to reduce the solution steps during the solution procedure, and the model became a linear programming model to make it easier to use and to reduce the computational complexity.

Wu et al. (2016) incorporated a target identification model to obtain reachable targets for all DMUs. Then, several secondary goal models were proposed for the weight selection considering both the desirable and undesirable cross-efficiency targets of all DMUs. Al-Siyabi et al. (2018) employed the DEA cross-efficiency evaluation and proposed a mean–variance goal programming model for minimizing the risk of changing the DEA weights for the identification of high performing DMUs. Oukil (2018) exploited the properties of multiple weighting schemes, which were generated over the cross-evaluation process in developing a methodology, and the robustness of the proposed methodology was evaluated using OWA combinations involving different minimax disparity models and different levels of optimism of the decision maker.

Apart from the secondary goal approach, there is an alternative strategy that does not take into account the choice of an aggressive or benevolent strategy. Instead, all possible weight sets in the weight space are considered in the computation of the cross efficiency. Yang et al. (2012) calculated both the minimal and maximal game cross-efficiency scores for each given DMU according to the idea of Liang et al. (2008) and gave a measure of the overall acceptability of the obtained cross-efficiency scores for ranking the DMUs. Alcaraz et al. (2013) considered all the possible choices of weights that all DMUs could make, and for each DMU, determined a range for its possible ranking rather than a single ranking. Ramόn et al. (2014) developed a pair of models that allowed for all possible weights for all DMUs to obtain a cross-efficiency interval for each DMU. The existing order relations for interval numbers were used to rank the DMUs. Liu (2018) considered the cross-efficiency intervals and their variances for ranking the DMUs. The aggressive and benevolent formulations were chosen at the same time, and the signal-to-noise ratio was constructed as a numerical index for ranking the DMUs. These approaches performed the cross-efficiency evaluations without the need to make any choice of DEA weights.

2.2 Fuzzy DEA

DEA, which was developed by Charnes et al. (1978), is a well-established nonparametric approach used to evaluate the relative efficiency of a set of comparable entities with multiple inputs and outputs. Numerous DEA theoretical and application studies have been reported. Initially, the DEA was meant to be used with crisp observations. To handle imprecise data, the notion of fuzziness has been introduced, and several fuzzy formulations of the traditional DEA models have been proposed.

Kao and Liu (2000) transformed a fuzzy DEA model to a family of conventional crisp DEA models by applying the α-level-based approach. A pair of parametric programs is formulated to describe the family of crisp DEA models, by which the membership functions of the efficiency measures were approximated. Guo and Tanaka (2001) proposed a fuzzy DEA model for symmetrical triangular fuzzy inputs and outputs. For a given possibility level, h, it provided an efficiency score that is a nonsymmetrical triangular fuzzy number. León et al. (2003) utilized possibilistic programming techniques to address fuzzy efficiency. By using the ranking methods based on the comparison of α-levels, the resulting auxiliary crisp problems can be solved. Lertworasirkul et al. (2003) developed a possibility approach for solving a fuzzy DEA model, and they transformed the fuzzy DEA model into a possibility linear programming problem by using the possibility measures of the fuzzy event.

Jahanshahloo et al. (2004) investigated a fuzzy ranking method for solving a slack-based measurement model in a DEA when the input–output data were triangular fuzzy numbers. Hatami-Marbini et al. (2010) presented a four-phase fuzzy DEA framework based on the theory of the displaced ideal. Two hypothetical DMUs, namely, the ideal and nadir DMUs, were constructed and used as reference points to evaluate a set of DMUs based on their Euclidean distance from these reference points. Shokouhi et al. (2010) introduced a robust DEA model that seeks to maximize efficiency under the assumption of a worst-case efficiency defined by the uncertainty set and its supporting constraint, and a Monte-Carlo simulation is used to compute the conformity of the rankings in the model. Zerafat Angiz et al. (2010) proposed an α-level based approach to retain the fuzziness of the model by maximizing the membership functions of the inputs and outputs.

2.3 Fuzzy cross-efficiency evaluation

Fuzzy DEA models lack sufficient discriminative power to rank efficient DMUs with fuzzy data since they measure the DMUs only by self-evaluation. Fuzzy cross-efficiency evaluation, which performs fuzzy self- and peer-evaluations, can eliminate the weaknesses of fuzzy DEA models, and it is an effective tool for ranking DMUs in fuzzy environments. As noted in Sirvent and León (2014), different approaches exist to calculate the efficiency score in a fuzzy DEA, and it is not possible to develop a general approach to fuzzy cross-efficiency. In other words, each method of the fuzzy cross-efficiency evaluation depends on the specific features of the fuzzy DEA model and the underlying assumptions.

Dotoli et al. (2015) integrated the fuzzy DEA technique with the cross-efficiency method to evaluate DMUs under uncertainty, and the secondary goals approach proposed by Doyle and Green (1994) was applied to deal with the alternate optima for the DEA weights to calculate the fuzzy cross-efficiency, which was subsequently defuzzified by means of a center of area method for ranking. Chen and Wang (2016), according to the idea of Dimitris and Yiannis (2002), measured the fuzzy efficiency score as the self-evaluation. Similar to Dotoli et al. (2015), the approach of Doyle and Green (1994) was employed for the selection of the weights to calculate the fuzzy peer-evaluated efficiencies of DMUs, and the averages of the self- and peer-evaluated efficiencies were regarded as the final cross-efficiency of a DMU being evaluated. Ruiz and Sirvent (2017) proposed a fuzzy cross-efficiency evaluation based on the possibility approach by Lertworasirkul et al. (2003), and the idea of Doyle and Green (1994) was used to develop the aggressive and benevolent formulations for determining the sets of weights to calculate the fuzzy cross-efficiency of the DMUs.

3 Crisp cross-efficiency

Nomenclature

   

\( E_{dd} \)

CCR efficiency score for DMU d

\( v_{id} \)

weight of input i for DMU d

\( \tilde{E}_{dd} \)

fuzzy CCR efficiency for DMU d

\( x_{ij} \)

input variable i consumed by DMU j

\( (E_{dd} )_{\alpha }^{L} \)

lower bound of fuzzy CCR efficiency at α-level for DMU d

\( y_{rj} \)

output variable r produced by DMU j

\( (E_{dd} )_{\alpha }^{U} \)

upper bound of fuzzy CCR efficiency at α-level for DMU d

\( X_{ij} \)

input data i consumed by DMU j

\( E_{dk} \)

cross-efficiency of DMU k calculated from weights selected by DMU d

\( Y_{rj} \)

output data r produced by DMU j

\( \bar{E}_{k} \)

average cross-efficiency of DMU k

\( \tilde{X}_{ij} \)

fuzzy input data i consumed by DMU j

\( E_{k}^{A} \)

aggressive cross-efficiency for DMU k

\( \tilde{Y}_{rj} \)

fuzzy output data r produced by DMU j

\( E_{k}^{B} \)

benevolent cross-efficiency for DMU k

\( (X_{ij} )_{\alpha }^{L} \)

lower bound of input data i consumed by DMU j at α-level

\( \tilde{E}_{k}^{A} \)

fuzzy aggressive cross-efficiency for DMU k

\( (X_{ij} )_{\alpha }^{U} \)

upper bound of input data i consumed by DMU j at α-level

\( \tilde{E}_{k}^{B} \)

fuzzy benevolent cross-efficiency for DMU k

\( (Y_{rj} )_{\alpha }^{L} \)

lower bound of output data r produced by DMU j at α-level

\( (E_{k}^{A} )_{\alpha }^{L} \)

lower bound of fuzzy aggressive efficiency for DMU k at α-level

\( (Y_{rj} )_{\alpha }^{U} \)

upper bound of output data r produced by DMU j at α-level

\( (E_{k}^{B} )_{\alpha }^{U} \)

upper bound of fuzzy benevolent efficiency for DMU k at α-level

\( \hat{x}_{idj} \)

variable transformation for \( v_{id} x_{ij} , \)

\( \forall \) i, d, j

\( u_{rd} \)

weight of output r for DMU d

\( \hat{y}_{rdj} \)

variable transformation for \( u_{rd} y_{rj} , \)

\( \forall \) r, d, j

Let Xij and Yrj denote the ith input, i = 1,…, m, and rth output, r = 1,…, s, respectively, of the jth DMU, j = 1,…, n. The DEA model proposed by Charnes et al. (1978) for calculating the efficiency of DMU d under the assumption of constant returns to scale, referred to as the CCR model, is:

$$ \begin{aligned} E_{dd} & = \hbox{max} \quad \frac{{\sum\limits_{r = 1}^{s} {u_{rd} Y_{rd} } }}{{\sum\limits_{i = 1}^{m} {v_{id} X_{rd} } }} \\ & {\text{s}} . {\text{t}} .\quad \sum\limits_{i = 1}^{m} {v_{id} X_{id} } = 1 \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} Y_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} X_{ij} } \le 0,\quad j = 1, \ldots ,n \\ & \quad \quad u_{rd} , \, v_{id} \ge 0,r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(1)

where \( u_{rd} \) and \( v_{id} \) are the weights selected by DMU d to calculate its efficiency \( E_{dd} \). Model (1) is a linear fractional program that can be transformed into the following linear program:

$$ \begin{aligned} E_{dd} & = \hbox{max} \sum\limits_{r = 1}^{s} {u_{rd} Y_{rd} } \\ & {\text{s}} . {\text{t}} .\quad \sum\limits_{i = 1}^{m} {v_{id} X_{id} } = 1 \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} Y_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} X_{ij} } \le 0,\quad j = 1, \ldots ,n \\ & \quad \quad u_{rd} , \, v_{id} \ge 0,r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(2)

Model (2) is a self-evaluation of DMU d. As different DMUs may select different \( u_{rd} \) and \( v_{id} \) to measure efficiency, the idea of cross-efficiency is to use the weights selected by all n DMUs to calculate the cross-efficiency of each DMU, and use the average as the final efficiency measure. To be specific, if \( v_{id}^{*} \) (i = 1,…,m) and \( u_{rd}^{*} \) (r = 1,…,s) is an optimal solution of (2) for a given DMU d. Let \( E_{dk} \) denote the efficiency of DMU k calculated from the weights selected by DMU d. We then have the cross-efficiency

$$ E_{dk} = \frac{{\sum\nolimits_{r = 1}^{s} {u_{rd}^{*} Y_{rk} } }}{{\sum\nolimits_{i = 1}^{m} {v_{id}^{*} X_{ik} } }}, $$
(3)

The cross-efficiency of DMU k is the average of \( E_{dk} \), d = 1,…, n, that is,

$$ \bar{E}_{k} = \frac{1}{n}\sum\limits_{d = 1}^{n} {E_{dk} } \, $$
(4)

Ramón et al. (2014) took all the possible weights into account for all the DMUs simultaneously and produced a cross-efficiency interval of each DMU being evaluated. Interestingly, since all the possible weights of all the DMUs were considered at the same time, the lower and upper bounds of the cross-efficiency interval for DMU k are calculated only once via the following aggressive and benevolent models, respectively:

$$ \begin{aligned} E_{k}^{A} = \, & \hbox{min} \frac{1}{n}\left( {\sum\limits_{d = 1}^{n} {\sum\limits_{r = 1}^{s} {u_{rd} Y_{rk} } } } \right) \\ & {\text{s}} . {\text{t}} .\sum\limits_{i = 1}^{m} {v_{id} X_{ik} } = 1,\quad d = 1, \ldots ,n \\ & \quad \sum\limits_{r = 1}^{s} {u_{rd} Y_{rd} } - E_{dd} \sum\limits_{i = 1}^{m} {v_{id} X_{id} } = 0,\quad d = 1, \ldots ,n \\ & \quad \sum\limits_{r = 1}^{s} {u_{rd} Y_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} X_{ij} } \le 0,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad u_{rd} , \, v_{id} \ge 0,\quad d = 1, \ldots ,n,\quad r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(5)
$$ \begin{aligned} E_{k}^{B} = \, & \hbox{max} \frac{1}{n}\left( {\sum\limits_{d = 1}^{n} {\sum\limits_{r = 1}^{s} {u_{rd} Y_{rk} } } } \right) \\ & {\text{s}} . {\text{t}} . \sum\limits_{i = 1}^{m} {v_{id} X_{ik} } = 1,\quad d = 1, \ldots ,n \\ & \quad \sum\limits_{r = 1}^{s} {u_{rd} Y_{rd} } - E_{dd} \sum\limits_{i = 1}^{m} {v_{id} X_{id} } = 0,\quad d = 1, \ldots ,n \\ & \quad \sum\limits_{r = 1}^{s} {u_{rd} Y_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} X_{ij} } \le 0,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad u_{rd} , \, v_{id} \ge 0,\quad d = 1, \ldots ,n,\quad r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(6)

The only difference between (5) and (6) is the direction of optimization: one is for minimization and the other is for maximization. The set of weights derived from these two models may not be the same as that obtained from (2). Models (5) and (6) produce the smallest and largest cross-efficiency scores for DMU k, respectively, while maintaining the efficiency of DMU d at its current level of \( E_{dd} \). These two models are designed for calculating the cross-efficiencies when the input and output data are crisp values. If the observations in (5) and (6) are expressed as fuzzy numbers, then Models (5) and (6) become the fuzzy cross-efficiency evaluation methods.

In the next section, we adopt the idea of Ramón et al. (2014) to develop a novel fuzzy cross-efficiency evaluation model, where the observations are represented as fuzzy numbers.

4 Fuzzy cross-efficiency

In a set of DMUs, assume that the input and output data are approximately known and can be represented as convex fuzzy numbers \( \tilde{X}_{ij} \) and \( \tilde{Y}_{rj} \), respectively. In the case of a fuzzy environment, Model (2) becomes:

$$ \begin{aligned} \tilde{E}_{dd} & = \hbox{max} \sum\limits_{r = 1}^{s} {u_{rd} \tilde{Y}_{rd} } \\ & {\text{s}} . {\text{t}} . \quad \sum\limits_{i = 1}^{m} {v_{id} \tilde{X}_{id} } = 1 \\ & \quad\quad \sum\limits_{r = 1}^{s} {u_{rd} \tilde{Y}_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} \tilde{X}_{ij} } \le 0,\quad j = 1, \ldots ,n \\ & \quad\quad u_{rd} , \, v_{id} \ge 0,r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(7)

Similarly, Models (5) and (6) with fuzzy inputs and outputs can be formulated, respectively, as

$$ \begin{aligned} \tilde{E}_{k}^{A} & = \hbox{min} \frac{1}{n}\left( {\sum\limits_{d = 1}^{n} {\sum\limits_{r = 1}^{s} {u_{rd} \tilde{Y}_{rk} } } } \right) \\ & \quad {\text{s}} . {\text{t}} . \sum\limits_{i = 1}^{m} {v_{id} \tilde{X}_{ik} } = 1,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} \tilde{Y}_{rd} } - \tilde{E}_{dd} \sum\limits_{i = 1}^{m} {v_{id} \tilde{X}_{id} } = 0,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} \tilde{Y}_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} \tilde{X}_{ij} } \le 0,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad \quad u_{rd} , \, v_{id} \ge 0,\quad d = 1, \ldots ,n,\quad r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(8)
$$ \begin{aligned} \tilde{E}_{k}^{B} & = \hbox{max} \frac{1}{n}\left( {\sum\limits_{d = 1}^{n} {\sum\limits_{r = 1}^{s} {u_{rd} \tilde{Y}_{rk} } } } \right) \\ & \quad {\text{s}} . {\text{t}} . \sum\limits_{i = 1}^{m} {v_{id} \tilde{X}_{ik} } = 1,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} \tilde{Y}_{rd} } - \tilde{E}_{dd} \sum\limits_{i = 1}^{m} {v_{id} \tilde{X}_{id} } = 0,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} \tilde{Y}_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} \tilde{X}_{ij} } \le 0,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad \quad u_{rd} , \, v_{id} \ge 0,\quad d = 1, \ldots ,n,\quad r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(9)

Since the α-level based approach is the most popular approach for the development of fuzzy DEA models (Hatami-Marbini et al. 2011), this approach is used to formulate the mathematical models proposed in this study. Denote \( (X_{ij} )_{\alpha } \) = [\( (X_{ij} )_{\alpha }^{L} \),\( (X_{ij} )_{\alpha }^{U} \)], \( (Y_{rj} )_{\alpha } \) = [\( (Y_{rj} )_{\alpha }^{L} \),\( (Y_{rj} )_{\alpha }^{U} \)], and \( (E_{dd} )_{\alpha } \) = [\( (E_{dd} )_{\alpha }^{L} \), \( (E_{dd} )_{\alpha }^{U} \)] as the α-levels of \( \tilde{X}_{ij} \), \( \tilde{Y}_{rj} \), and \( \tilde{E}_{dd} \), respectively.

At a specific α-level, Kao and Liu (2000) have shown that the minimal and maximal efficiency scores for DMU d in (7) are given by the following formulations, respectively:

$$ \begin{aligned} (E_{dd} )_{\alpha }^{L} & = \hbox{max} \sum\limits_{r = 1}^{s} {u_{rd} (Y_{rd} )_{\alpha }^{L} } \\ & \quad {\text{s}} . {\text{t}} . \sum\limits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{U} } = 1 \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} (Y_{rd} )_{\alpha }^{L} } - \sum\limits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{U} } \le 0 \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} (Y_{rj} )_{\alpha }^{U} } - \sum\limits_{i = 1}^{m} {v_{id} (X_{ij} )_{\alpha }^{L} } \le 0,\quad j = 1, \ldots ,n,\quad j \ne d \\ & \quad \quad u_{rd} , \, v_{id} \ge 0,\quad r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(10)
$$ \begin{aligned} (E_{dd} )_{\alpha }^{U} & = \hbox{max} \sum\limits_{r = 1}^{s} {u_{rd} (Y_{rd} )_{\alpha }^{U} } \\ & \quad {\text{s}} . {\text{t}} . \sum\limits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{L} } = 1 \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} (Y_{rd} )_{\alpha }^{U} } - \sum\limits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{L} } \le 0 \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} (Y_{rj} )_{\alpha }^{L} } - \sum\limits_{i = 1}^{m} {v_{id} (X_{ij} )_{\alpha }^{U} } \le 0,\quad j = 1, \ldots ,n,\quad j \ne d \\ & \quad \quad u_{rd} , \, v_{id} \ge 0,\quad r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(11)

Model (10) is a DEA model with exact data, where the levels of the input and output data are set unfavorably for DMU d and in favor of the other units. For DMU d, the input data are adjusted to their upper bounds and the output data to their lower bounds. For the other DMUs, the inputs are favorably adjusted to their lower bounds and the outputs to their upper bounds. In this manner, DMU d is placed in the worst possible position compared to the other units. Contrary to (10), Model (11) has the levels of inputs, and the outputs are adjusted in favor of DMU d and aggressively against the other units. For DMU d, the inputs and outputs are set to their lower bounds and upper bounds, respectively. Unfavorably for the other units, the inputs and outputs are contrarily adjusted to their upper bounds and lower bounds, respectively, and DMU d is placed the best possible position compared to the other units.

Models (8) and (9) are the aggressive and benevolent formulations which are to find the smallest and largest cross-efficiency scores for DMU k with fuzzy input and output data. At a specific α-level, they can be expressed as:

$$ (E_{k}^{A} )_{\alpha }^{L\phantom{A}}\kern-3pt = \mathop {\hbox{min} }\limits_{\begin{aligned} (E_{dd} )_{\alpha }^{L} \le e_{dd} \le (E_{dd} )_{\alpha }^{U} \\ (X_{ij} )_{\alpha }^{L} \le x_{ij} \le (X_{ij} )_{\alpha }^{U} \\ (Y_{rj} )_{\alpha }^{L} \le y_{rj} \le (Y_{rj} )_{\alpha }^{U} \\ \forall d,i,j,r \\ \end{aligned} } \left( {\varvec{x},\varvec{y},\varvec{e}} \right) $$
(12)
$$ (E_{k}^{B} )_{\alpha }^{U} = \mathop {\hbox{max} }\limits_{\begin{aligned} (E_{dd} )_{\alpha }^{L} \le e_{dd} \le (E_{dd} )_{\alpha }^{U} \\ (X_{ij} )_{\alpha }^{L} \le x_{ij} \le (X_{ij} )_{\alpha }^{U} \\ (Y_{rj} )_{\alpha }^{L} \le y_{rj} \le (Y_{rj} )_{\alpha }^{U} \\ \forall d,i,j,r \\ \end{aligned} } \left( {\varvec{x},\varvec{y},\varvec{e}} \right) $$
(13)

where \( E_{k}^{A} \)(x,y,e) and \( E_{k}^{B} \)(x,y,e) are defined in Models (5) and (6), respectively. Note that \( E_{k}^{A} \)(x,y,e) and \( E_{k}^{B} \)(x,y,e) are two mathematical programs with minimum and maximum operations as the objective functions, respectively. Therefore, Models (12) and (13) are two-level mathematical programs.

Based on each set of \( x_{ij} \), \( y_{rj} \), and \( e_{dd} \) defined by the first level, the second-level program is able to calculate the cross-efficiency. In other words, the smallest and largest cross-efficiency scores are determined by the values of \( x_{ij} \), \( y_{rj} \), and \( e_{dd} \) in Models (12) and (13), respectively. These two models can be rewritten as follows:

$$ (E_{k}^{A} )_{\alpha }^{L} = \mathop {\hbox{min} }\limits_{\begin{aligned} (E_{dd} )_{\alpha }^{L} \le e_{dd} \le (E_{dd} )_{\alpha }^{U} \\ (X_{ij} )_{\alpha }^{L} \le x_{ij} \le (X_{ij} )_{\alpha }^{U} \\ (Y_{rj} )_{\alpha }^{L} \le y_{rj} \le (Y_{rj} )_{\alpha }^{U} \\ \forall d,i,j,r \\ \end{aligned} } \cdot \left\{ \begin{array}{l} \hbox{min} \, \frac{1}{n}\left( {\sum\limits_{d = 1}^{n} {\sum\limits_{r = 1}^{s} {u_{rd} y_{rk} } } } \right) \hfill \\ {\text{s}} . {\text{t}} .\hfill \\ \quad \quad \sum\limits_{i = 1}^{m} {v_{id} x_{ik} } = 1,\quad d = 1, \ldots ,n \hfill \\ \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} y_{rd} } - e_{dd} \sum\limits_{i = 1}^{m} {v_{id} x_{id} } = 0,\quad d = 1, \ldots ,n \hfill \\ \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} y_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} x_{ij} } \le 0,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \hfill \\ \quad \quad u_{rd} , \, v_{id} \ge 0,\quad d = 1, \ldots ,n,\quad r = 1, \ldots ,m,\quad i = 1, \ldots ,m \, \hfill \\ \end{array} \right. $$
(14)
$$ (E_{k}^{B} )_{\alpha }^{U} = \mathop {\hbox{max} }\limits_{\begin{aligned} (E_{dd} )_{\alpha }^{L} \le e_{dd} \le (E_{dd} )_{\alpha }^{U} \\ (X_{ij} )_{\alpha }^{L} \le x_{ij} \le (X_{ij} )_{\alpha }^{U} \\ (Y_{rj} )_{\alpha }^{L} \le y_{rj} \le (Y_{rj} )_{\alpha }^{U} \\ \forall d,i,j,r \\ \end{aligned} } \cdot \, \left\{ \begin{array}{l} \hbox{max} \, \frac{1}{n}\left( {\sum\limits_{d = 1}^{n} {\sum\limits_{r = 1}^{s} {u_{rd} y_{rk} } } } \right) \hfill \\ {\text{s}} . {\text{t}} .\hfill \\ \quad \quad \sum\limits_{i = 1}^{m} {v_{id} x_{ik} } = 1,\quad d = 1, \ldots ,n \hfill \\ \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} y_{rd} } - e_{dd} \sum\limits_{i = 1}^{m} {v_{id} x_{id} } = 0,\quad d = 1, \ldots ,n \hfill \\ \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} y_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} x_{ij} } \le 0,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \hfill \\ \quad \quad u_{rd} , \, v_{id} \ge 0,\quad d = 1, \ldots ,n,\quad r = 1, \ldots ,m,\quad i = 1, \ldots ,m \, \hfill \\ \end{array} \right. $$
(15)

Since the inner level and outer level programs of (14) and (15) have the same directions of optimization, that is, minimization and maximization, respectively, we can combine these programs into one-level mathematical programs. The objective functions of the inner and outer programs are treated as the overall objective functions, and the constraints at the two levels are regarded as the overall constraints. In other words, Models (14) and (15) are reduced to the following formulations:

$$ \begin{aligned} (E_{k}^{A} )_{\alpha }^{L} & = \hbox{min} \frac{1}{n}\left( {\sum\limits_{d = 1}^{n} {\sum\limits_{r = 1}^{s} {u_{rd} y_{rk} } } } \right) \\ & \quad{\text{s}} . {\text{t}} . \sum\limits_{i = 1}^{m} {v_{id} x_{ik} } = 1,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} y_{rd} } - e_{dd} \sum\limits_{i = 1}^{m} {v_{id} x_{id} } = 0,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} y_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} x_{ij} } \le 0,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad \quad (E_{dd} )_{\alpha }^{L} \le e_{dd} \le (E_{dd} )_{\alpha }^{U} ,\quad d = 1, \ldots ,n, \\ & \quad \quad (X_{ij} )_{\alpha }^{L} \le x_{ij} \le (X_{ij} )_{\alpha }^{U} ,\quad i = 1, \ldots ,m,\quad j = 1, \ldots ,n \\ & \quad \quad (Y_{rj} )_{\alpha }^{L} \le y_{rj} \le (Y_{rj} )_{\alpha }^{U} ,\quad r = 1, \ldots ,s,\quad j = 1, \ldots ,n \\ & \quad \quad u_{rd} , \, v_{id} \ge 0,\quad d = 1, \ldots ,n,\quad r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(16)
$$ \begin{aligned} (E_{k}^{B} )_{\alpha }^{U} & = \hbox{max} \frac{1}{n}\left( {\sum\limits_{d = 1}^{n} {\sum\limits_{r = 1}^{s} {u_{rd} y_{rk} } } } \right) \\ & \quad {\text{s}} . {\text{t}} . \sum\limits_{i = 1}^{m} {v_{id} x_{ik} } = 1,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} y_{rd} } - e_{dd} \sum\limits_{i = 1}^{m} {v_{id} x_{id} } = 0,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {u_{rd} y_{rj} } - \sum\limits_{i = 1}^{m} {v_{id} x_{ij} } \le 0,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad \quad (E_{dd} )_{\alpha }^{L} \le e_{dd} \le (E_{dd} )_{\alpha }^{U} ,\quad d = 1, \ldots ,n, \\ & \quad \quad (X_{ij} )_{\alpha }^{L} \le x_{ij} \le (X_{ij} )_{\alpha }^{U} ,\quad i = 1, \ldots ,m,\quad j = 1, \ldots ,n \\ & \quad \quad (Y_{rj} )_{\alpha }^{L} \le y_{rj} \le (Y_{rj} )_{\alpha }^{U} ,\quad r = 1, \ldots ,s,\quad j = 1, \ldots ,n \\ & \quad \quad u_{rd} , \, v_{id} \ge 0,\quad d = 1, \ldots ,n,\quad r = 1, \ldots ,s,\quad i = 1, \ldots ,m \\ \end{aligned} $$
(17)

Because of the nonlinear terms \( u_{rd} y_{rk} \), \( v_{id} x_{ik} \) ¸ \( u_{rd} y_{rd} \), \( v_{id} x_{id} \), \( u_{rd} y_{rj} \), \( v_{id} x_{ij} \), and \( e_{dd} \sum\nolimits_{i = 1}^{m} {v_{id} x_{id} } \), Models (16) and (17) are nonlinear programs. In this case we let \( \hat{x}_{idj} = v_{id} x_{ij} , \) \( \forall i,d,j, \) and \( \hat{y}_{rdj} = u_{rd} y_{rj} \), \( \forall r,d,j, \) and multiply the associated terms in the constraints \( (X_{ij} )_{\alpha }^{L} \le x_{ij} \le (X_{ij} )_{\alpha }^{U} \) and \( (Y_{rj} )_{\alpha }^{L} \le y_{rj} \le (Y_{rj} )_{\alpha }^{U} \) with \( v_{id} \) and \( u_{rd} \), respectively, that is, \( v_{id} (X_{ij} )_{\alpha }^{L} \le \hat{x}_{idj} \)\( \le v_{id} (X_{ij} )_{\alpha }^{U} \), i = 1,…,m, d = 1,…, n, j = 1,…, n, and \( u_{rd} (Y_{rj} )_{\alpha }^{L} \le \hat{y}_{rdj} \le \)\( u_{rd} (Y_{rj} )_{\alpha }^{U} \), r = 1,…,s, d = 1,…, n, j = 1,…,n. Nevertheless, the term \( e_{dd} \sum\nolimits_{i = 1}^{m} {v_{id} x_{id} } \) still needs to be dealt with. Fortunately, we have \( \hat{x}_{idd} = v_{id} x_{id} \) and \( \sum\nolimits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{L} } (E_{dd} )_{\alpha }^{L} \)\( \le \)\( \sum\nolimits_{i = 1}^{m} {e_{dd} \hat{x}_{idd} } \) = \( \sum\nolimits_{i = 1}^{m} {e_{dd} v_{id} x_{id} } \)\( \le \)\( \sum\nolimits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{U} } (E_{dd} )_{\alpha }^{U} \). By letting \( \hat{w}_{idd} = e_{dd} \hat{x}_{idd} \) transform the set of constraints, \( (E_{dd} )_{\alpha }^{L} \le e_{dd} \le \)\( (E_{dd} )_{\alpha }^{U} \), d = 1,…, n, into \( \sum\nolimits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{L} } (E_{dd} )_{\alpha }^{L} \)\( \le \)\( \sum\nolimits_{i = 1}^{m} {\hat{w}_{idd} } \)\( \le \)\( \sum\nolimits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{U} } (E_{dd} )_{\alpha }^{U} \), d = 1,…, n, Models (16) and (17) can be reformulated as follows:

$$ \begin{aligned} (E_{k}^{A} )_{\alpha }^{L} & = \hbox{min} \frac{1}{n}\left( {\sum\limits_{d = 1}^{n} {\sum\limits_{r = 1}^{s} {\hat{y}_{rdk} } } } \right) \\ & \quad {\text{s}} . {\text{t}} . \sum\limits_{i = 1}^{m} {\hat{x}_{idk} } = 1,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {\hat{y}_{rdd} } - \sum\limits_{i = 1}^{m} {\hat{w}_{idd} } = 0,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {\hat{y}_{rdj} } - \sum\limits_{i = 1}^{m} {\hat{x}_{idj} } \le 0,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad \quad \sum\limits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{L} (E_{dd} )_{\alpha }^{L} } \le \sum\limits_{i = 1}^{m} {\hat{w}_{idd} } \le \sum\limits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{U} (E_{dd} )_{\alpha }^{U} } ,\quad d = 1, \ldots ,n \\ & \quad \quad v_{id} (X_{ij} )_{\alpha }^{L} \le \hat{x}_{idj} \le v_{id} (X_{ij} )_{\alpha }^{U} ,\quad i = 1, \ldots ,m,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad \quad u_{rd} (Y_{rj} )_{\alpha }^{L} \le \hat{y}_{rdj} \le u_{rd} (Y_{rj} )_{\alpha }^{U} ,\quad r = 1, \ldots ,s,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad \quad u_{rd} , \, v_{id} \ge 0,\quad d = 1, \ldots ,n,\quad r = 1, \ldots ,s,\quad i = 1, \ldots ,m. \\ \end{aligned} $$
(18)
$$ \begin{aligned} (E_{k}^{B} )_{\alpha }^{U} & = \hbox{max} \frac{1}{n}\left( {\sum\limits_{d = 1}^{n} {\sum\limits_{r = 1}^{s} {\hat{y}_{rdk} } } } \right) \\ & \quad {\text{s}} . {\text{t}} . \sum\limits_{i = 1}^{m} {\hat{x}_{idk} } = 1,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {\hat{y}_{rdd} } - \sum\limits_{i = 1}^{m} {\hat{w}_{idd} } = 0,\quad d = 1, \ldots ,n \\ & \quad \quad \sum\limits_{r = 1}^{s} {\hat{y}_{rdj} } - \sum\limits_{i = 1}^{m} {\hat{x}_{idj} } \le 0,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad \quad \sum\limits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{L} (E_{dd} )_{\alpha }^{L} } \le \sum\limits_{i = 1}^{m} {\hat{w}_{idd} } \le \sum\limits_{i = 1}^{m} {v_{id} (X_{id} )_{\alpha }^{U} (E_{dd} )_{\alpha }^{U} } ,\quad d = 1, \ldots ,n \\ & \quad \quad v_{id} (X_{ij} )_{\alpha }^{L} \le \hat{x}_{idj} \le v_{id} (X_{ij} )_{\alpha }^{U} ,\quad i = 1, \ldots ,m,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad \quad u_{rd} (Y_{rj} )_{\alpha }^{L} \le \hat{y}_{rdj} \le u_{rd} (Y_{rj} )_{\alpha }^{U} ,\quad r = 1, \ldots ,s,\quad d = 1, \ldots ,n,\quad j = 1, \ldots ,n \\ & \quad \quad u_{rd} , \, v_{id} \ge 0,\quad d = 1, \ldots ,n,\quad r = 1, \ldots ,s,\quad i = 1, \ldots ,m. \\ \end{aligned} $$
(19)

Models (18) and (19) are linear programs that guarantee globally optimal solutions. The optimal values of \( (E_{k}^{A} )_{\alpha }^{L} \) and \( (E_{k}^{B} )_{\alpha }^{U} \) solved from (18) and (19), respectively, are the lower and upper bounds of the cross-efficiency at a specific α-level.

When the observations are all crisp numbers in (18), Models (18) and (5) have the same objective function and constraints. The similar case also applies in Models (19) and (6). In other words, when the observations are all deterministic values in (18) and (19), these two models boil down to (5) and (6), respectively.

Since the derived cross-efficiency scores of the DMUs are fuzzy numbers, we need to rank these fuzzy cross-efficiency scores for discriminating the DMUs. In the literature some methods for ranking fuzzy numbers (Chen and Klein 1997; Chu and Tsao 2002; Abbasbandy and Hahhari 2009; Wang et al. 2009; Boulmakoul et al. 2017) are discussed. Most of the ranking methods, which are based on area measurement or the corresponding integral values, require the exact forms of the membership functions of the fuzzy numbers to be ranked, and we cannot apply these methods if the membership functions of the fuzzy numbers are not explicitly known. Since the method of Chen and Klein (1997) does not require the exact membership functions of the fuzzy numbers, it is an appropriate method for ranking the fuzzy cross-efficiency scores derived in this study. Chen and Klein (1997) devised the following index for ranking fuzzy numbers:

$$ I(\tilde{E}_{j} ) = \frac{{\sum\nolimits_{p = 0}^{\infty } {((E_{j} } )_{{\alpha_{p} }}^{U} - \beta )}}{{\left[ {\sum\nolimits_{p = 0}^{\infty } {((E_{j} } )_{{\alpha_{p} }}^{U} - \beta ) - \sum\nolimits_{p = 0}^{\infty } {((E_{j} } )_{{\alpha_{p} }}^{L} - \gamma )} \right]}} $$
(20)

where \( \beta = { \hbox{min} }_{j, \, p} \{ (E_{j} )_{{\alpha_{p} }}^{L} \} \) and \( \gamma = \max_{j, \, p} \{ (E_{j} )_{{\alpha_{p} }}^{U} \} \). Chen and Klein (1997) believe that three or four α-levels are sufficient to discriminate the differences. The larger the value of the ranking index \( I(\tilde{E}_{j} ) \), the larger the fuzzy number is. According to the ranking indices, we can discriminate the cross-efficiency scores of the DMUs accordingly.

5 Illustrative examples

In this section we use three examples to illustrate the idea proposed in this paper. Specifically, the stronger discriminative power of the fuzzy cross-efficiency scores is demonstrated. Generally, convex fuzzy numbers can be represented as the forms of α-level sets, and any type of convex fuzzy numbers (for example, trapezoidal fuzzy numbers) can thus be used in the proposed approach. For simplicity, we use the fuzzy triangular fuzzy numbers to represent the fuzzy input and output data, which are denoted as (a, b, c), where a, b, and c are the coordinates of the three vertices of the triangle, for the illustrated examples.

5.1 Example 1

In this example, we have a sample of five DMUs with two fuzzy inputs and two fuzzy outputs, as shown in Table 1. To show the generality of the proposed method, there are crisp input and output data distributed in DMUs 1, 2, and 3, and these deterministic observations can be treated as degenerated fuzzy numbers, with only one point in their associated domains.

Table 1 Fuzzy inputs and outputs for DMUs
Full size table

We need to calculate the CCR efficiency scores of the DMUs first before measuring their associated cross-efficiencies. By applying Models (10) and (11), the lower bound \( (E_{dd} )_{\alpha }^{L} \) and upper bound \( (E_{dd} )_{\alpha }^{U} \) of the fuzzy CCR efficiency scores are derived. Enumerating this process for all DMUs at α = 0.0, 0.1, …, 1.0, we obtain the fuzzy CCR efficiency scores at different α-levels, as shown in Table 2. Although the inputs and outputs are fuzzy numbers, DMUs 1, 3, and 5 are evaluated as CCR-efficient at all α-levels, making the ranking task more difficult.

Table 2 The bounds of the fuzzy CCR efficiency scores for Example 1
Full size table

Now we use (18) and (19) to measure the fuzzy cross-efficiency scores for all DMUs, with the calculation results for α = 0.0, 0.1, …, 1.0 presented in Table 3. Since they are derived from (18) and (19) at distinctive α-levels, their associated membership functions are not explicitly known. In this case the approach of Chen and Klein (1997), which is discussed in the previous section, is suitable for ranking these fuzzy cross-efficiencies. With the eleven α-levels of the fuzzy cross-efficiency scores listed in Table 3, the variable of p in (20) is set to 10, that is, p = 0, 1,…, 10, for the derivation of the ranking index \( I(\tilde{E}_{j} ) \). Putting the obtained cross-efficiencies into (20), the ranking indices of the five DMUs are calculated, with the result shown in the second-to-last column of Table 3. Based on the ranking indices, the fuzzy cross-efficiency scores are discriminated accordingly. Since the larger the ranking index the larger the cross-efficiency score is: the top one is DMU 5, followed by DMUs 1 and 3 subsequently.

Table 3 The bounds of the fuzzy cross-efficiency scores and their ranks of DMUs
Full size table

The cross-evaluation method has stronger discriminative power than the self-evaluation method, in that the nondominated DMUs, which cannot be discriminated by the latter method, can be discriminated by the former method. This is because the self-evaluation method calculates the efficiency of every DMU from only its own viewpoint, while the cross-evaluation method calculates the efficiencies from the viewpoints of all DMUs. In most studies, the final efficiency of a DMU is the average of the n efficiency scores. However, since all the possible weights of all the DMUs are considered simultaneously, similar to the method of Ramón et al. (2014), this study calculates the lower and upper bounds of the fuzzy cross-efficiency only once at a specified α-level. With the different α-levels, the shape of the fuzzy cross-efficiency can be approximately derived. Although the inputs and outputs are fuzzy numbers, the methodology proposed in this paper is able to calculate and discriminate the fuzzy cross-efficiency scores of the DMUs.

5.2 Example 2

In investigating the performance of FMS candidates with fuzzy data, Liu (2008) used the cost and floor space requirements as the inputs and the improvements in the qualitative factor, work-in-process (WIP), numbers of tardy jobs, and yield as the outputs. The associated fuzzy data set was modified from Shang and Sueyoshi (1995). In this section, we also use the data of Liu (2008), as shown in Table 4, to measure the fuzzy cross-efficiency scores of the twelve FMS candidates.

Table 4 Data used to measure the fuzzy cross-efficiency scores of FMS alternatives
Full size table

To measure the fuzzy cross-efficiency, Models (10) and (11) are first used to calculate the lower and upper bounds of the fuzzy CCR efficiency scores, respectively, for each FMS with α = 0.0, 0.1, …, 1.0, and the calculated results are listed in Table 5. Specifically, FMS candidates 2, 5, and 9 have a perfect efficiency of 1.0, and their ranks are indistinguishable. Even for those FMS candidates with different fuzzy efficiency scores, they are not comparable with each other because they are calculated from their own weights. Now, every FMS employs (18) and (19) to calculate the associated fuzzy cross-efficiency at a specific α-level. Repeating this process obtains the fuzzy cross-efficiency for all twelve FMS candidates, with the results shown in Table 6.

Table 5 The bounds of the fuzzy CCR efficiency scores for FMS alternatives
Full size table
Table 6 The bounds of the fuzzy cross-efficiency scores and their ranks of FMS alternatives
Full size table

As expected, all efficiencies in the cross-evaluation part are less than or equal to the corresponding efficiencies in the self-evaluation part. This is because the efficiencies in the self-evaluation part are calculated from the most favorable weights, while in the cross-evaluation part, they are calculated from the weights determined by the twelve FMS candidates. In particular, No. 9 is the most sensitive to the selection of DEA weights. In the self-evaluation part, this candidate has a perfect efficiency score of 1.0, while in the cross-evaluation part, the associated efficiency score is between 0.140 and 1.0. This result is similar to that of Ramón et al. (2014). When the α-level = 1.0, the dataset of Table 4 becomes the original inputs and outputs of Shang and Sueyoshi (1995), which also served as an illustrated example of Ramón et al. (2014). In this case, the calculated cross-efficiency scores shown in Table 6 under the heading of “α = 1.0” are the same as those of Ramón et al. (2014). This echoes the statement that when the observations are all deterministic numbers in (18) and (19), these two models boil down to (5) and (6), respectively.

Similar to Example 1, since the derived cross-efficiency scores are fuzzy numbers, Eq. (20) is applied to derive the associated ranking indices, with the results shown in Table 6 under the heading of “Index”. The numbers in the last column of Table 6 are the rankings of the corresponding FMS candidates. Clearly, FMS 5 is in first place from the viewpoint of every FMS. It is thus the one that should be selected for production.

5.3 Example 3

In this example, the proposed methodology is applied to a practical case for robot selection in the H-company. The company, whose stock is listed on the Taipei Exchange, is a leading manufacturer in the closed-circuit television industry (CCTV) in Taiwan, providing a wide variety of high quality and cost effective products, including LCD monitors, car rear view cameras, digital video recorders and other peripherals that offer a wide variety of CCTV applications for industry and transportation vehicles. The modernized production environment and state-of-the-art equipment allow the company to manufacture different products on the same production line. Recently, the customer demands for the global market have changed rapidly, and the company faces fierce competition from competitors. To be able to fill the diversity of customized orders in the shortest time, the company intends to use a robotic system to enhance its manufacturing flexibility to satisfy customer demands. Eighteen candidate robots are considered as feasible alternatives for increasing the manufacturing flexibility. A committee is established to discuss and determine the required input and output factors for the assessment of the candidate robots, and this committee is also responsible for the evaluation of the technical and qualitative attributes of the robots and the selection of the most suitable one.

The most widely considered performance attributes for industrial robots are total cost, floor space, load capacity, repeatability, and velocity (Talluri and Yoon 2000; Karsak and Ahiska 2005). Total cost includes the purchase and estimated operating and maintenance costs of the robot. The floor space is the total area that the robot system occupies for operations. The load capacity is the maximum load that the robot can lift, which includes the actual load and the gripper weight. Repeatability is a measure of the ability of the robot to return to the target point and is defined as the radius of the circle sufficiently large to include all points to which the robot actually goes on repeated trials. The velocity of the robot is the distance covered by the robot arm. The technical characteristics are quantitative performance measures that have been widely used in robot selection problems. However, some factors, such as the vendor-related attributes, also have a critical effect on the justification and selection of robots. Following the idea of Karsak and Ahiska (2005), the vendor’s service quality and throughput improvement are considered in the decision processes of the H-company.

Since the total cost includes the estimated future operating and maintenance costs, this item is treated as an uncertain number. Due to the lack of sufficient historical total cost data, it is not easy to estimate the probability distribution of this item. One approach widely used in the absence of data is to ask experts for their subjective estimates of the data. The fuzzy number of the total cost, which can therefore be constructed from the pessimistic, optimistic, and most possible estimates solicited from the experts, is used to express its uncertainty.

The vendor service quality, which is a subjective judgement of the committee, is a linguistic variable that is represented by several different linguistic terms. Linguistic terms usually have meanings that are vague and not mathematically operable. Moreover, in reality, there is no clear-cut boundary between different linguistic terms. Therefore, using fuzzy numbers instead of crisp values to represent the linguistic terms is more appropriate (Chen et al. 1992). The vendor service quality can be classified into five levels. According to Chen et al. (1992), the fuzzy numbers (0, 0.2, 0.4), (0.2, 0.4, 0.6), (0.4, 0.6, 0.8), (0.6, 0.8, 1), and (0.8, 1, 1) are used to represent the terms very bad, bad, moderate, good, and very good, respectively. Similar to the total cost, the factor ‘improvement in throughput’ is uncertain data, which is also represented as a fuzzy number. The notation used in this paper is (a,b,c) for a triangular fuzzy number, where a, b, and c are the coordinates of the three vertices of the triangle.

In the performance evaluation, the total cost and floor space are treated as inputs because, from the committee’s viewpoint, they represent the investment required to purchase and operate the robotic system. The load capacity, repeatability, velocity, vendor service quality, and improvement in throughput are regarded as outputs because they are measures that indicate the ability of the system to perform various tasks with satisfactory quality. In a DEA analysis, a large value of an output is considered to be better than a small value. Since a robot with the capability of operating with low repeatability contributes positively to the performance of the manufacturing processes, we used the inverse of repeatability in the DEA evaluation. There are 18 robot candidates, with the data shown in Table 7, which is confirmed by the committee. We use this dataset to illustrate how our model is applied in a practical application of the fuzzy cross-efficiency evaluation for the selection of a robot.

Table 7 Data used to measure the fuzzy cross-efficiency scores of robot candidates
Full size table

According to (10) and (11), the data contained in Table 7 are used to calculate the fuzzy CCR efficiency scores, with the results presented in Table 8. Similar to Examples 1 and 2, ten candidates are being evaluated as CCR-efficient and cannot be further discriminated among. Now, we use (18) and (19) to calculate the associated fuzzy cross-efficiency at a specific α-level for each robot. By executing this process for eleven distinct α-levels, the fuzzy cross-efficiencies are obtained, with the results shown in columns three to thirteen of Table 9. Since the fuzzy cross-efficiency score lies in a range, the different values of the α-level show the different intervals of the scores. Moreover, the greater the value of the α-level, the narrower the interval is. Specifically, the α-level = 0 shows the range in which the cross-efficiency will appear, and the α-level = 1.0 shows the cross-efficiency that is the most likely. For example, while the cross-efficiency of Robot No. 8 in Table 9 is fuzzy, it is impossible for its value to exceed 0.998 or fall below 0.390. At the other extreme, at the α-level = 1, the most likely cross-efficiency value of this robot lies within 0.613 and 0.898.

Table 8 The bounds of the fuzzy CCR efficiency scores for robot candidates
Full size table
Table 9 The bounds of the fuzzy cross-efficiency scores and their ranks of robot candidates
Full size table

Since we have derived the fuzzy cross-efficiency scores of the 18 robot candidates, Eq. (20) is used to calculate their associated ranking indices. In this example, the parameters are set as \( \beta = 0.134 \) and \( \gamma = 1.0 \), as in (20) and the ranking indices \( I(\tilde{E}_{j} ) \) of the 18 robot candidates are calculated, as shown in the second-to-last column of Table 9. Based on the ranking indices, the 18 robot candidates are ranked accordingly. Since the larger the ranking index, the better the robotic system is, clearly, Robot No. 13 is the best, followed by Robots No. 3 and 4. In other words, Robot No. 13 is the most preferred robot for the committee in the H-company.

6 Conclusion

The traditional self-evaluation DEA models use the most favorable weights determined by a DMU to calculate its efficiency. They are strong in identifying inefficient units but weak in discriminating efficient units. To improve the discriminative power and make the efficiency scores comparable, the cross-evaluation methodology has been proposed in the literature. In the real world, the observations are usually difficult to measure precisely, or the observations need to be estimated. When the observations are uncertain, one approach is to represent the uncertain values by fuzzy numbers. Since the existing fuzzy DEA models cannot discriminate among efficient DMUs, we need to develop a fuzzy cross-efficiency evaluation for ranking the performance of DMUs in a fuzzy environment.

The existing approaches of fuzzy cross-efficiency evaluation employed the secondary goals approach to determine the weights for measuring fuzzy cross-efficiencies. However, the different approaches for determining the weights may produce different cross efficiencies. In this paper, we propose a novel approach that considers all possible weights of all DMUs at the same time to calculate the fuzzy cross-efficiency directly without the need to calculate the average cross efficiency from n DMUs. More importantly, a choice of weights is not required. A pair of two-level mathematical programs is developed to calculate the fuzzy cross-efficiency. By variable substitutions, this pair of two-level mathematical programs is transformed into a pair of one-level linear programs, and the lower and upper bounds of the fuzzy cross-efficiency can thus be easily derived by solving this pair of linear programs. Since the obtained cross-efficiency scores are fuzzy numbers, a fuzzy number ranking method is used to derive the ranking indices of the efficiency scores, and the ranking of the DMUs is determined accordingly.

Three examples are used to illustrate the idea proposed in this paper, and the obtained results find that all efficiency scores at specific α-levels in the cross-evaluation process are less than or equal to the corresponding ones in the self-evaluation process. This is because the efficiencies in the self-evaluation part are calculated from the most favorable weights, while in the cross-evaluation part, they are calculated from the weights determined by all DMUs. The illustrated examples demonstrate that the cross-evaluation method proposed in this paper has discriminative power in ranking the DMUs when the observations are represented as fuzzy numbers.

In the examples of this study, the fuzzy input and output data are represented as triangular fuzzy numbers. However, convex fuzzy numbers can be treated as forms of α-level sets; thus, any type of convex fuzzy number can be applied in this study. This might help initiate more applications of the fuzzy cross-efficiency evaluation.