Abstract
In the 2 years since our last 4OR review of distance geometry methods with applications to proteins and nanostructures, there has been rapid progress in treating uncertainties in the discretizable distance geometry problem; and a new class of geometry problems started to be explored, namely vector geometry problems. In this work we review this progress in the context of the earlier literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This contribution provides an update on the state of the art reviewed in our 2016 4OR paper (Billinge et al. 2016) on the topic of assigned (aDGP) and unassigned (uDGP) distance geometry problems. Here we give a summary of the definitions, notations and results in Billinge et al. (2016); and we discuss two important advances that have emerged over the past two years: (i) development of mathematical methods to treat uncertainty in the distances in aDGP, using distance intervals, (ii) generalization of the mathematical description to a new class of problems called vector geometry problems (VGPs) for both the assigned (aVGP) and unassigned (uVGP) variants. VGPs arise in the use of Patterson methods in crystallography and in vector PDF methods related to the nanostructure problem (see Sect. 5.3).
The general form of the problems we consider consists of finding a graph embedding based on a set of vectors of dimension d in an embedding space of dimension K. We call this problem the d-K geometry problem (d-K-GP). The vector information consists of distances and angles, with the distances always given, and \(d-1\) bond angles given. In this review we restrict attention to two subclasses of d-K-GPs, the distance geometry problem (DGP) which is the 1-K-GP case; and the vector geometry problem (VGP) which corresponds to the K-K-GP case. In the latter case, the vectors have the same dimension as the embedding space, so that \(K-1\) bond angles are given. For most of the discussion we also restrict attention to embedding dimensions \(K=1,2,3\).
Before starting our discussion, we mention some previous publications available in the scientific literature, which review some developments in this research domain. A wide survey on the DGP is given in Liberti et al. (2014); an edited book and a journal special issue completely devoted to DGP solutions methods and to its applications can be found in Mucherino et al. (2013) and Mucherino et al. (2015), respectively. Classic books on aDGP include Crippen and Havel’s book (Crippen and Havel 1988), Donald’s book (Donald 2011), and more recent books (Lavor et al. 2017; Liberti and Lavor 2017). Applications to signal processing are reviewed in Dokmanic et al. (2015) and Dokmanic and Lu (2016).
Let V be a set of n objects and
be the function that assigns positions (coordinates) in a Euclidean space of dimension \(K>0\) to the n objects belonging to the set V, whose elements are called vertices. The function x is referred to as a realization.
For DGPs, let \(\mathcal {D} = ( d_1, d_2, \dots , d_m )\) be a finite sequence consisting of m distances, called a distance list, where repeated distances, i.e. \(d_i = d_j\) for \(i \ne j\), are allowed. Distances in \(\mathcal {D}\) can be represented either with a nonnegative real number (when the distance is exact) or by an interval \([\underline{d},\bar{d}]\), where \(0< \underline{d} < \bar{d}\).
For VGPs, let \(\mathcal {D}_s = (\pm \, \mathbf {s}_1, \pm \, \mathbf {s}_2, \dots , \pm \, \mathbf {s}_m )\) be a finite sequence consisting of m interparticle vectors, where repeated vectors, \(\pm \, \mathbf {s}_i = \pm \, \mathbf {s_j}\), are allowed. Note that for every vector \(\mathbf {s}_i\) in the list, its negative \(-\, \mathbf {s}_i\) also appears. For a complete graph of n points, the cardinality of \(\mathcal {D}_s\) is then \(n(n-1)\).
Considering the set of all possible unordered pairs \(\{u,v\}\) of vertices in V, called \(\hat{E}\), we define an injective function \(\ell \), called assignment function, given by
that relates an index of an element of the distance list \(\mathcal {D}\) or the vector list \(\mathcal {D}_s\) to an unordered pair of vertices of V. Thus, \(\ell (j) = \{u,v\}\) means that the j-th entry of \(\mathcal{D}\) (or \(\mathcal{D}_s\)) is assigned to \(\{u,v\}\) and we denote its corresponding edge weight by \(d(u,v) = d_{\ell ^{-1}(\{u,v\})} = d_j\) (or associated vector by \(\mathbf {s}(u,v) = \mathbf {s}_{\ell ^{-1}(\{u,v\})} = \mathbf {s}_j\)). We will use the compact notation \(d_{uv}\) for d(u, v) and similarly for \(\mathbf {s}\).
First consider DGPs. From the assignment function \(\ell \), we can define the edge set E as the image of \(\ell \), that is \(E = \ell (\{1,\dots ,m\}) \subset \hat{E}\). The edge weight function \(d:E \rightarrow \{d_1, \dots , d_m \}\) is given, also from the assignment function, by
Using \(V,\,E,\,d\) we define a simple weighted undirected graph \(G = (V,E,d)\).
We give the following definition for the unassigned DGP (uDGP) (Duxbury et al. 2016).
Definition 1
Given a list \(\mathcal {D}\) of m distances, the unassigned Distance Geometry Problem (uDGP) in dimension \(K>0\) asks to find an assignment function \(\ell : \{1,\dots ,m\} \rightarrow \hat{E}\) and a realization \(x: V \rightarrow \mathbb {R}^K\) such that
Let \(d_{uv}\) be the short notation for d(u, v). Since precise values for distances may not be available, the equality constraint in (1) becomes
where \(\underline{d}_{uv}\) and \(\overline{d}_{uv}\) are, respectively, the lower and upper bounds on the distance \(d_{uv}\) (\(\underline{d}_{uv} = \overline{d}_{uv}\) when \(d_{uv}\) is an exact distance).
When distances are already assigned to pairs of vertices, we can assume that the associated graph G is known a priori. We give the following definition for the assigned case (Liberti et al. 2014).
Definition 2
Given a weighted undirected graph \(G=(V,E,d)\), the assigned Distance Geometry Problem (aDGP) in dimension \(K>0\) asks to find a realization \(x : V \rightarrow \mathbb {R}^K\) such that
As in Definition 1, the equality constraint in (2) becomes an inequality constraint when interval distances are considered.
We point out that several methods for uDGP and aDGP are based on a global optimization approach, where a penalty function is defined so that its optimization is equivalent to having all distance constraints satisfied (Liberti et al. 2014). When all distances are exact, one possible penalty function related to the constraint (2) is
Turning to the vector problems, we consider first the definition of uVGP.
Definition 3
Given a list \(\mathcal {D}_s\) of m vector interpoint separations, the unassigned Vector Geometry Problem (uVGP) in dimension \(K>0\) asks to find an assignment function \(\ell : \{1,\dots ,m\} \rightarrow \hat{E}\) and a realization \(x: V \rightarrow \mathbb {R}^K\) such that
When vector separations are assigned to pairs of vertices, we can assume that the associated graph G is known a priori.
Definition 4
Given a weighted undirected graph \(G=(V,E,s)\), the assigned Vector Geometry Problem (aVGP) in dimension \(K>0\) asks to find a realization \(x : V \rightarrow \mathbb {R}^K\) such that
As in Definition 1, the equality constraint in (5) becomes an inequality constraint when interval distances are considered.
An optimization formulation for cases where vector separations are exact (5) may utilize the penalty function
Since precise values for interpoint vectors may not be available, the equality constraint in (4) becomes
where \(\underline{\mathbf {s}}_{uv}\) and \(\overline{\mathbf {s}}_{uv}\) are, respectively, the lower and upper bounds on the vector \(\mathbf {s}_{uv}\) (\(\underline{\mathbf {s}}_{uv} = \overline{\mathbf {s}}_{uv}\) when \(\mathbf {s}_{uv}\) has exact entries).
We conclude this introductory section by briefly reviewing the main applications in this research domain. In dimension 1, the clock synchronization problem can be formulated as a DGP (Freris et al. 2010; Wu et al. 2011). The problem consists in computing the internal clock time for sensors in a given network by exploiting their own offset with respect to a predefined clock, which is used as a reference. When all offsets are precisely provided, the identification of solutions can be performed by a tree search (see Sect. 4.7), even when the numerical information about the offsets is not precise. More applications in the one-dimensional space can be found in Jaganathan and Hassibi (2013).
In dimension 2, the sensor network localization problem is the one of positioning the sensors of a given network by using the available relative distances. Such distances can be estimated by measuring the power for a 2-way communication between pairs of sensors (Biswas et al. 2006; Biswas and Ye 2006; Ding et al. 2010; Wang et al. 2008).

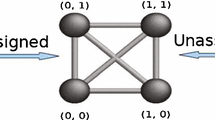
(Image from Gujarathi 2014)
(Color online) Schematic of the differences between uDGP and aDGP, for a simple case
In dimension 3, conformations of protein molecules and nanostructures can be obtained by exploiting information about distances between atom pairs that can be either derived from experimental techniques, such as Nuclear Magnetic Resonance (NMR) experiments (Almeida et al. 2013; Malliavin et al. 2013) or from the pair distribution function (PDF) method (Juhás et al. 2006). A recent and interesting application is related to determining small-field astrometric point-patterns (Santiago et al. 2018).
The aVGP problem arises from the Patterson function which is a Fourier transform of the intensity of the elastic scattering from single crystals; as found experimentally by using x-ray, neutron or electron beams. The Patterson function gives a assignment of vectors to edges in a graph and it can also be used to construct a vector matrix completion problem where the entries in the matrix, which we call vM, are the vectors associated with each edge in the graph. For example, the matrix in Table 2.3.1.1 of Rossmann and Arnold (2006) can be used to construct vM.
In most applications mentioned above, the available distances are pre-assigned to the vertex pairs. For example, the DGP usually solved in the context of molecular conformations using NMR data starts from a known graph structure and proceeds to find a graph embedding. However, the information that is actually given by the NMR experiments consists of a list \(\mathcal {D}\) of distances, that are only subsequently assigned to atom pairs. Therefore, the Molecular Distance Geometry Problem (MDGP) can also be considered as a uDGP. Figure 1 gives a schematic illustration of the input data for a uDGP, as well as for an aDGP. The aDGP is NP-hard (Saxe 1979). Moreover, the uDGP class is particularly challenging because the graph structure and the graph embedding both need to be determined at the same time. As noted above, the aDGP is strictly related to the problem of finding missing entries of a Euclidean distance matrix (Moreira et al. 2018). The vector matrix, vM, is similar to the conventional distance matrix except that the entries are vectors instead of scalar distances. This defines a new type of matrix completion problem.
This survey is arranged as follows. In the next section (Sect. 2) the basic definitions and theorems essential to build up algorithms are introduced. In Sect. 2.2, two basic theorems for VGP are presented here for the first time. Section 3 describes algorithms developed for the uDGP; including the treatment of experimental error. In Sect. 4, the discretizable distance geometry problem with intervals is discussed in detail and an exact algorithm for the one-dimensional case is given in Sect. 4.7. Applications to the protein structure problem and to the nanostructure problem are presented in Sect. 5, while Sect. 6 provides a summary of the main points and discussion of future research directions that look promising to us.
2 Graph rigidity and unique embeddability
2.1 Introduction
Our aim is to find a set of n positions for a given set of objects (vertices in V), in the Euclidean space having dimension \(K>0\), that are consistent with a given list \(\mathcal {D}\) of distances or vectors \(\mathcal {D}_s\) (see Introduction). In other words, we are interested in finding an embedding x for which a list of distances or vectors, pre-assigned or not to pairs of vertices, is satisfied. The first question we may ask ourselves is related to the uniqueness of the DGP solution. Given a list \(\mathcal {D}\) or the list \(\mathcal {D}_s\), is there more than one realization?
Clearly, if only a few (compatible) distances or vectors are given, many solutions can be found that are consistent with the constraints. The opposite extreme case is the one where the full set of \(n(n-1)/2\) distances or vectors is given. The number of translational degrees of freedom of an embedding of n vertices in \(\mathbb {R}^K\) is nK, while \(K(K+1)/2\) is the number of degrees of freedom associated with translations and rotations of a rigid body in K dimensions. As a consequence, when all available distances are exact, since \(n(n-1)/2 \gg nK - K(K+1)/2\) for large values of n, it is a likely event to have a unique realization. The constraint due to vectors in a clique is K times \(n(n-1)/2\) which is more strongly constrained than the scalar distance case. Thus if we are given the complete set of exact interpoint distances or vectors for a large point set, it is typical that the resulting graph embedding is unique.
A related question was raised by Patterson (1944) in his early work considering the determination of crystal structures from scattering data, and there is a large subsequent literature (Gommes et al. 2012). An important result is that there is a subclass of instances that are homometric, which means that elastic scattering data, and hence the full set of interpoint vector distances, is not sufficient to determine a unique realization (Jain and Trigunayat 1977; Schneider et al. 2010). Patterson’s original paper discussed the vector separations \(x(u)-x(v)\), whereas the uDGP considers the distances \(||x(u)-x(v)||\). Two distinct point sets are weakly homometric when their complete sets of interpoint distances are the same (Senechal 2008), where point sets related by rigid rotations, translations or reflections are not distinct within the context of this discussion. We then have two definitions concerning homometric structures:
Definition 5
If a list of interpoint vectors, \(\mathcal {D}_s\), is sufficient to yield a unique framework, then the vector list is not homometric (NH).
Definition 6
If a set of interpoint distances, \(\mathcal {D}\), is sufficient to yield a unique framework, then the distance list is not weakly homometric (NWH).
Weakly homometric point sets are of interest in the uDGP and in a variety of contexts (Skiena et al. 1990; Boutin and Kemper 2007; Senechal 2008). Figure 2 shows two three-dimensional conformations that are weakly homometric with a hexagon. When the distance list has a large number of entries in comparison to the number of degrees of freedom, the probability of having homometric variants decreases rapidly, though no rigorous tests are available. Similarly this is also true of VGP problems, and the cases found by Patterson (1944) are crystals with special symmetries.
However if the number of distances or edges is sufficiently small, there are subclasses of problems where a discrete number of homometric or weakly homometric structures may occur. This has been called the discretizable distance geometry problem (DDGP) for DGP cases, and it has extensions to the VGP cases as discussed below. This is especially important in discovering discrete families of structures in proteins, as discussed in detail later (in Sects. 4, 5).

(Reproduced with permission from Juhás et al. 2006)
(Color online) The hexagon has three distinct distances with degeneracies (6—grey, 6—blue, 3—green). The two three-dimensional conformations in the figure are weakly homometric with the hexagon
A beautiful and rich literature on uniqueness of structures is based on the theory of generic graph rigidity. The beauty of this theory is based on the fact that generic graph rigidity is a topological property where the rigidity of all graph realizations that are generic is dependent only on the graph connectivity and not on the specifics of the realization (Connelly 1991; Hendrickson 1992; Graver et al. 1993). Conditions for a unique graph realization have been determined precisely for generic cases, where it has been proven that a unique solution exists if and only if the kernel of the stress matrix has dimension \(K+1\), the minimum possible (Connelly 1991; Hendrickson 1992; Connelly 2005; Jackson and Jordan 2005; Gortler et al. 2010). A second approach is to use rigorous constraint counting methods that have associated algorithms based on bipartite matching. Combinatorial algorithms of this type to test for generic global rigidity (Hendrickson 1992; Connelly 2013), based on Laman’s theorem (Laman 1970) and its extensions (Tay 1984; Connelly 2013), are also efficient for testing the rigidity of a variety of graphs relevant to materials science, statistical physics and the rigidity of proteins (Jacobs and Thorpe 1995; Jacobs and Hendrickson 1997; Moukarzel and Duxbury 1995; Moukarzel 1996; Thorpe and Duxbury 1999; Rader et al. 2002).
In the following, we will concentrate on constructing graph realizations using Globally Rigid Build-up (GRB) methods that have sufficient distance or vector constraints to ensure generic global rigidity at each step in the process; or on less constrained cases where a binary tree of possible DDGP structures is developed using build up strategies and branch and prune methods (BP) (Lavor et al. 2013).
These buildup procedures can be applied to both generic and non-generic cases. GRB methods have been developed for the aDGP case (Dong and Wu 2002; Wu and Wu 2007; Voller and Wu 2013), and more recently for the uDGP case (Gujarathi et al. 2014; Duxbury et al. 2016). GRB methods iteratively add a site and \(K+1\) (or more) edges to an existing globally rigid structure. In two dimensions this approach is called trilateration for the distance list cases. GRB methods for NH and NWH problems are polynomial for the case of precise distance lists satisfying the additional condition that all substructures are unique, for both the assigned and unassigned cases (see Sect. 3), in contrast to the most difficult DGP cases defined by Saxe (1979), where the DGP is NP-hard. The NP-hard instances of DGP with precise distances correspond to families of locally rigid structures that are consistent with an exponentially growing number of different nanostructures as the size of the structure grows (Lavor et al. 2012a). If global rigidity is only imposed at the final step in the process, the algorithm must search an exponential number of intermediate locally rigid structures from which the final unique structure is selected, for example using the BP algorithm (see Sect. 4.1). If globally rigid substructures occur at intermediate steps however, the complexity of the search can be reduced, as has been demonstrated in recent branch and prune approaches (Liberti et al. 2014).
Significant extensions of GRBs are required to fully treat imprecise distance lists that occur in experimental data. One promising approach, the LIGA algorithm, utilizes a stochastic build-up heuristic with backtracking and tournament strategies to mitigate experimental errors (Juhás et al. 2006, 2008). LIGA has been used to successfully reconstruct \(C_{60}\) and several crystal structures using distance lists extracted from experimental x-ray or neutron scattering data (Juhás et al. 2006, 2008; Juhas et al. 2010). More recently progress has been made in finding feasible solutions for discretizable distance geometry problems with intervals, as summarized in Gonçalves et al. (2017).
The theorems presented below summarize the results necessary for polynomial-time build-up algorithms for the exact distance cases of aDGP, uDGP, aVGP and uVGP. This theory also provides useful background in understanding other algorithms for finding nanostructure from experimental data (see Sect. 5.3), such as the LIGA algorithm (see Sect. 3.2).
An important concept in the following is that of a redundant edge in a graph. If a redundant edge is removed from a graph, the graph remains stable to local distortions. Therefore the distance associated with a redundant edge must have a length that does not produce local distortions in the structure. Randomly chosen distances do not have that property, but distances derived from random point sets do. Distances derived from random point sets are thus compatable, in the sense that if they are placed in their correct positions, they fit perfectly.
2.2 Globally rigid buildup for precise DGP problems
A Globally rigid buildup (GRB) process that ensures global rigidity for systems that are not weakly homometric at each step of the algorithm is stated in Theorems 1 and 2 below. First, we need the following definitions.
Definition 7
A compatable subcluster is a substructure that has at least one redundant bond and which does not violate any of the distance constraints in the substructure.
Definition 8
A distance list is strongly generic if all compatable substructures that have at least one redundant edge are NWH.
Theorem 1
(Follows from Dong and Wu 2002)
A GRB algorithm in \(\mathbb {R}^2\) that adds three compatible distances connecting a new site to an existing globally rigid structure yields a structure that is globally rigid, if the three sites of the existing structure at which the three added distances connect are not on the same line.
Theorem 2
(Dong and Wu 2002)
A GRB algorithm in \(\mathbb {R}^3\) that adds four compatible distances connecting a new site to an existing globally rigid structure yields a structure that is globally rigid, if the four sites of the existing structure at which the four distances connect are not in the same plane.
Theorems 1 and 2 provide sufficient conditions for generating a unique realization from a strongly generic distance list, provided there are enough distances in the list to enable the process to proceed to a complete reconstruction. Algorithms for uDGP are described in more detail in Sect. 3.
2.3 Assigned and unassigned vector geometry problems (aVGP, uVGP)
In the unassigned vector geometry problem (uVGP) a list of interpoint vectors is given. In this case both the underlying graph and the point positions need to be determined. Figure 3 illustrates the difference between aVGP and uVGP.
GRB methods for aVGP and uVGP follow straightforwardly from the aDGP and uDGP cases described in the previous subsection. We start with definition of compatable vectors.
Definition 9
An assignment of a set of interpoint vectors to a graph is compatable if this assignment leads to no violation of the constraints imposed by the vectors. A globally rigid substructure and the associated set of compatible distances or vectors is called a compatable substructure.
A strongly generic vector list is defined as:
Definition 10
A vector list is strongly generic if all compatable substructures containing at least one redundant edge (vector) are part of the correct unique reconstruction. That is, the reconstruction is unique and all possible compatable redundant substructures are part of the unique reconstruction.
For exact strongly generic vector lists, GRB leads to correct reconstruction due to the following Theorem.
Theorem 3
For an exact strongly generic vector list derived from a set of n points in K Euclidean dimensions, completion of the following buildup yields the unique reconstruction of a point set.
-
1.
Start with a correct unique globally rigid substructure.
-
2.
Recursively add a new point and two compatable vectors to the structure; ensuring that the 2K implied connecting vertices have a subset of \(K+1\) of these vertices that do not lie in a Euclidean subspace of dimension \(K-1\).
-
3.
If this process yields an embedding of n points in K dimensions, the process terminates with a unique final structure.
Proof
First note that a vector in K dimensions defines K constraints, one distance and \(K-1\) angles. However the \(K-1\) angular constraints can be captured using \(K-1\) implied distance constraints. These implied distance constraints have one endpoint as the newly added point, and the others as implied points in the existing substructures. When two edges (vectors) and a new vertex are added to an existing rigid substructure, 2 connecting vertices are used, and \(2(K-1)\) implied connecting vertices and distances are also defined. There are then 2K connecting vertices and edges, of which K are redundant. This vertex and vector addition is thus highly overconstrained. If any subset of \(K+1\) of the true or implied connecting vertices do not lie in a subspace of dimension \(K-1\), then the vertex position is unique if the vector list is strongly generic. This follows from Theorems 1 and 2; and Definitions 9 and 10. \(\square \)
For VGP, two points connected by a vector provide a unique starting structure, making VGP buildup efficient in comparison to DGP. An upper bound on the time taken to execute an algorithm based on Theorem 1 for complete precise sets of interpoint vectors is given by.
Theorem 4
GRB for VGP is polynomial \((O(n^t))\) for complete precise vector sets; where for aVGP the exponent \(t_a = 1\), while for uVGP \(t_u\le 3\).
Proof
An aVGP algorithm based on Theorem 3 consists of adding a new point and two vectors at each step. Since the graph is given and the vectors are assigned to the edges of the graph, sequential addition of a vertex using two edges at each step yields an exact reconstruction. In this case, the algorithm reconstructs the point set in computational time O(n), so that \(t_a=1\). Checking that all vectors are compatable with a reconstruction is \(O(n^2)\).
In the uVGP case, vectors with positive and negative signs occur in the vector list. To ensure global rigidity, two vectors from the vector list are checked for compatability, including a check of the four possible signs of the four vectors \((++,+-,-+,--)\). Checking of all pairs of vectors in the list for compatability is bounded above by \(n^2\). Reconstruction is complete when n single vertex GRB steps have occurred. The time to reconstruct is then \(O(n^3)\), so that \(t_u = 3\). \(\square \)
3 Algorithms for the uDGP
In some applications, the information about the pairs of vertices that corresponds to a given known distance is not provided. In other words, while the distance is known, the identity of the two vertices having such a relative distance is not. In this case, the graph G is actually unknown, and the only input is the list \(\mathcal {D}\) of distances (see Definition 1 and Fig. 1). This is the uDGP and it has received much less attention than the aDGP. In this section we survey two algorithms that have recently been developed for uDGPs. The first (TRIBOND Gujarathi et al. 2014) is related to a GRB approach that is based on extensions of the results of Theorems 1 and 2 to the uDGP case. The second algorithm (LIGA Juhás et al. 2006) is also a build-up approach, however it is stochastic and relies on backtracking to resolve incorrect structures generated during buildup. LIGA is a heuristic designed to treat distance lists extracted from experimental data, which requires robustness to errors in the distances and missing distances. To develop the GRB approach, we start with a definition and a theorem (full details are found in Duxbury et al. 2016).
Definition 11
Let \(\mathcal {D}\) be a distance list with m elements. Amongst all the possible assignments of \(\mathcal{D}\) to the set \(\hat{E}\) of the underlying graph, \(\ell : \{1,\dots ,m\} \rightarrow \hat{E}\), there is one assignment that corresponds to the structure from which the distance list was calculated. We call that assignment the true assignment (TA).
In general, for distance lists containing precise and compatible distances, assignments different from the TA leading to a feasible aDGP may exist. However, for a NWH distance list, the only assignment that leads to a aDGP having a solution is the TA.
Theorem 5
The smallest generic graph that has a redundant edge and is globally rigid in dimensions \(K=2,3\) is the clique of size \(K+2\).
Proof
Cliques in three dimensions satisfy the molecular conjecture so constraint counting can be used (Laman 1970; Connelly 2013). By constraint counting, a generic graph with n vertices, having no floppy modes and \(n(n-1)/2\) edges has one redundant edge if:
which gives \(n = K+2\). nK is the number of degrees of freedom of the nodes in the structure, while \(K(K+1)/2\) is the set of global degrees of freedom that occur for any rigid body and is not affected by the edge constraints. \(\square \)
Theorem 5 states that the smallest globally rigid structure in two dimensions has four vertices and in three dimensions has five vertices, as presented in Fig. 4. We call these structures the core of the buildup, and in order to start a build-up procedure, a core compatible with the input distance list must be found. This is the most time consuming step in the reconstruction for uDGPs. If the distances are imprecise, larger cores should be used for the buildup process to reduce the chances of incorrect starting structures.

(Reproduced with permission from Duxbury et al. 2016)
(Color online) Examples of cores in \(K=2\) (left) and \(K = 3\) (right). A core is the smallest cluster that contains a redundant bond in a generic graph rigidity sense. For the two dimensional case (left figure), the horizontal bond is the base (in black), the bonds below it (in blue) make up the base triangle while those above it (in red) make up the top triangle. The vertical bond is the bridge bond (in green). The extension to \(K = 3\) requires a base triangle (black), feasible tetrahedra compatible with the base triangle (blue, red) and finally a bridging bond (green) that is consistent with the target distance list
3.1 GRB algorithm for uDGPs (TRIBOND)
The input to the TRIBOND algorithm consists of a distance list \(\mathcal {D}\) and the number n of vertices to be embedded. The first step in the algorithm is finding a core, and from Theorem 5 we know that a core in two dimensions has four sites and in three dimensions five sites. The procedures that TRIBOND uses to find cores are illustrated in Fig. 4. Once a core has been found, build-up is carried out utilizing Theorems 1 or 2 to ensure that the conformation remains globally rigid at each step in the process.
A sketch of the TRIBOND algorithm is given in Algorithm 1. The framework F is the structure that is built, starting with the CORE and increased in size by adding one vertex position at a time. In this discussion, it is assumed that the distance list is complete and precise, so that there are \(n(n-1)/2\) precise distances in \(\mathcal {D}\).

If TRIBOND runs to completion it generates the correct unique structure for distance lists that are NWH. However, during buildup, incorrect “decoy” positions may be generated leading to failure of buildup. A decoy position is a vertex position that is consistent with the input distance list at an intermediate stage of the buildup, but which fails to be part of a correct completed structure. Although for cases that we have studied decoy positions are unlikely, distance lists leading to decoy positions can be constructed. A restricted set of distance lists has no intermediate decoy positions, and we define such distance lists to be strongly generic (see Definition 8).
Strongly generic distance lists have no decoy positions and for these cases, for a list \(\mathcal {D}\) of exact distances, TRIBOND runs deterministically to completion. Moreover, we find that in practice distance lists of random point sets can be reconstructed in polynomial time (Gujarathi et al. 2014; Duxbury et al. 2016), though random restarts are needed in some cases. Due to the need for random restarts, in general TRIBOND is a combinatorial heuristic algorithm. For strongly generic distance lists, it is straightforward to find a polynomial upper bound on TRIBOND by estimating the worst-case computational time for core-finding and for buildup. Since the number of ways of choosing six distances from the set of \(m = n(n-1)/2\) unique distances is \({m\atopwithdelims ()6}\), a brute force search would find a core in computational time \(\uptau _{core} < {m\atopwithdelims ()6} \sim n^{12}\), which demonstrates that the algorithm is polynomial in two dimensions. Similar arguments show that TRIBOND is polynomial in any embedding dimension for strongly generic distance lists, though the polynomial exponent is large.
These arguments are useful to show that the computational complexity of TRIBOND is polynomial for strongly generic distance lists for any K (Gujarathi et al. 2014; Duxbury et al. 2016), however these upper bounds on the algorithmic efficiency are loose. In practice, the scaling of the computational time with the size of random point sets in the plane is approximately \(n^{3.3}\) and point sets with over 1000 sites have been reconstructed on a laptop (see Gujarathi et al. 2014).
3.2 LIGA: a robust heuristic for uDGP
The LIGA heuristic is efficient for precise and imprecise uDGPs with a relatively low number of distinct distances. The input of the algorithm may only consist of the distance list \(\mathcal {D}\). In some cases, the number of vertices, n, in the solution is given as well; in other cases, only approximate information about the number of vertices may be given. Using LIGA, the structure of \(C_{60}\) and a range of crystal structures (Juhás et al. 2006, 2008; Juhas et al. 2010) have been solved using distances extracted from x-ray or neutron scattering experiments (see Sect. 5.3). This algorithm uses a combination of ideas from dynamic programming with backtracking, and tournaments (see Algorithm 2). The input to LIGA is the ordered distance list \(\mathcal {D}\), the number of vertices n, and the size of the population s that is kept for each cluster size in the algorithm. LIGA builds up a candidate structure by starting with a single vertex and adding additional vertices one at a time. The algorithm keeps a population of candidate structures at each size and uses promotion and relegation procedures to move toward higher quality nanostructures (see Juhás et al. 2008).
A key feature of the LIGA algorithm is the choice of a cost function. If we have n vertices and m distances in \(\mathcal {D}\), with \(m \le n(n-1)/2\), then the cost of constructing a model substructure with label i is the following:
where \(d^{model}_{uv}\) is a distance in the model and \(t_{\ell ^{-1}(\{u,v\})}\) is a distance in \(\mathcal {D}\). The minimum is taken over all ways of assigning model distances to nearest distances and the sum is over all distances in the model. A pseudocode for LIGA is given in Algorithm 2.

Promotion is the process of changing the level of a candidate substructure (also called “cluster”) by adding one or more vertices to it. LIGA generates possible positions for new vertices using three different methods:
-
1.
Line trials This method places new sites in-line with two existing vertices in the cluster.
-
2.
Planar trials This method adds vertices in plane to account for occurrence of vertex planes in crystal structures.
-
3.
Pyramid trials Three vertices in a subcluster are randomly selected based on their fitness to form a base for a pyramid of four vertices. The remaining vertex is constructed using three randomly chosen lengths from the list of distances. As there are 3! ways of assigning three lengths to three vertices, and because a pyramid vertex can be placed above or below the base plane, this method generates 12 candidate positions.
Each of these methods is repeated many times (typically, 10,000 times in our trials) to provide a large pool of possible positions for a new vertex. For each of the generated sites, LIGA calculates the associated cost increase for the enlarged candidate and filters the ‘good’ positions with the new cost in a low cost window. The positions outside the cost window are discarded and the winner is chosen randomly from the remaining possibilities with a probability proportional to 1/cost (the cost of a vertex is the contribution to Eq. (8) of the edges incident to the vertex). The winner vertex is added to the candidate substructure, and the distances it uses are removed from \(\mathcal {D}\). The costs of other vertices in the pool are recalculated with respect to the new candidate subcluster and the shortened distance table. If the candidate has fewer than n vertices and there are any vertices inside the cost window, a new winner is selected and added. This can lead to an avalanche of added vertices, potentially reducing the long-term overhead associated with generating larger high-quality candidates.
Each level is set to contain a fixed number of candidates, but at the beginning they are completely or partially empty. When a winner for promotion is selected from a level that is not full it adds a copy of itself to that level in addition to being promoted. Similarly, when a loser is selected for relegation from a division that is not full it adds a copy of itself to that division before being relegated. Finally, after a winner is promoted it checks to see if there are any empty levels below its new level. If this is the case then it adds an appropriately relegated clone of itself to those empty levels.
4 Discretizable distance geometry
BuildUp methods are potentially able to find solutions to DGP instances in polynomial time (Dong and Wu 2002; Wu and Wu 2007). In fact, at every iteration of the corresponding algorithms, one unique position for the current vertex can be computed. In other words, the search space is discrete and reduced to one singleton per vertex. However, in order to make this possible in dimension K, a vertex order on the vertices of G must exist so that every vertex v shares edges with at least \(K+1\) predecessors.
The work in Carvalho et al. (2008) showed for the first time that weaker assumptions are actually necessary for performing the discretization of the search space. These weaker assumptions allow in fact to consider real-life instances of the DGP (Liberti et al. 2010; Lavor et al. 2012b). In this context, an important theoretical contribution was the formalization of the concept of discretization orders (Lavor et al. 2012).
DGP instances need to satisfy the following assumptions in order to perform the discretization. To simplify notations, let us focus in this paragraph on the three-dimensional case. The main requirement is that the vertices need to be sorted in a way such that there are at least three reference vertices for each of them, aside, obviously, the first three. We say that a vertex u is a reference for another vertex v when u precedes v in the given vertex order, and the distance \(d_{uv}\) is known. In such a case, indeed, candidate positions for v belong to the sphere centered in u and having radius \(d_{uv}\). When the reference distance \(d_{uv}\) is given through a real-valued interval, the sphere becomes a spherical shell. If three reference vertices are available for v, then candidate positions (for v) belong to the intersection of three spherical shells. The easiest situation is the one where the three available distances are exact, and the intersection gives, in general, two possible positions for v (Lavor et al. 2012a). However, if only one of the three distances is allowed to take values into a certain interval, then the intersection gives two arcs, generally disjoint, where sample points can be chosen (Lavor et al. 2013). In both situations, the discretization can be performed. The discretization allows to define a search domain that has the structure of a tree, where possible positions for the same vertex are grouped on the same layer of the tree.
Let \(G=(V,E,d)\) be a simple weighted undirected graph representing an instance on the DGP in dimension \(K>0\). Let \(n = |V| > K\), and \(E'\) be the subset of edges in E related to exact distances; as a consequence, the subset \(E \setminus E'\) contains all edges that are related to distances represented by suitable intervals. We suppose that a vertex ordering is associated to the vertex set V, so that a rank is associated to each vertex. The Discretizable DGP (DDGP) is a class of instances of the DGP for which there exists a vertex order \((v_1,v_2,\dots ,v_n)\) that satisfies the following assumptions (Lavor et al. 2012a, 2013; Mucherino et al. 2012a):
-
(a)
\(G[\{ v_1,v_2,\dots ,v_K \}]\) is a clique;
-
(b)
\(\forall v \in \{ v_{K+1},\dots , v_n \}\), there exist K vertices \(u_1, u_2, \dots , u_K \in V\) such that
-
1.
\(u_1 < v\), \(u_2 < v\), ..., \(u_K < v\);
-
2.
\(\{ \{u_1,v\}, \{u_2,v\}, \dots , \{u_{K-1},v\} \} \subset E'\) and \(\{u_K,v\} \in E\);
-
3.
\(\mathcal {V}_S(u_1,u_2,\dots ,u_K) > 0\), if \(K > 1\),
-
1.
where \(G[\cdot ]\) is the subgraph induced by a subset of vertices of V, “\(u < v\)” means that u precedes v in the vertex order, and \(\mathcal {V}_S(\cdot )\) is the volume of the simplex generated by an embedding of the vertices \(u_1, u_2, \dots , u_K\). Notice that a unique realization (modulo congruent transformations) for such vertices can be identified, before the solution of the instance, as far as they form a K-clique in G; if not, this verification cannot be performed in advance. However, when dealing with real-life instances, the volume \(\mathcal {V}_S\) can be zero with probability 0, and it is therefore common use to neglect this assumption (Lavor et al. 2013).
Assumption (a) allows us to fix the positions of the first K vertices, avoiding to consider congruent solutions that can be obtained by total translations, rotations and reflections (except the total reflection around the (hyper-)plane defined by these K vertices). Assumption (b.1) ensures the existence of the K reference vertices for every vertex \(v_i\), with \(i > K\), and assumptions (b.2) ensures that at most one of the K reference distances is represented by an interval. We call “reference distances” the ones that are used in the discretization process; additional distances can also be available and exploited for the pruning process (see below). Finally, assumption (b.3) makes it sure that \(\left\{ u_1,\dots ,u_K\right\} \) is an affinely independent set, which implies, in case of exact distances, that the spheres provide finitely many points.
Under the assumptions (a) and (b), the DGP can be discretized. The search domain becomes a tree containing, layer by layer, the possible positions for a given atom. In this tree, the number of branches increases exponentially layer by layer. After the discretization, the DGP can be seen as a combinatorial problem.
4.1 The Branch-and-Prune (BP) algorithm
The Branch-and-Prune (BP) algorithm was initially proposed in 2008 for solving DDGP problems with exact distances (Liberti et al. 2008). Subsequently, it was extended to deal with instances containing uncertainty, which are often represented by suitable intervals; i.e. lower and upper bounds are available for such distances (Lavor et al. 2013).

Algorithm 3 is a sketch of the BP algorithm for DDGP instances in dimension \(K>0\). The algorithm takes as input the graph G representing a DDGP instance, the discretization factor D, and the current vertex v; once the initial clique is realized and fixed into a unique configuration, the algorithm recursively calls itself from the vertex ranked \(K+1\) in the vertex order, in order to perform the exploration of the search tree. By computing the sphere intersections, two disjoint arcs are obtained in the general case, which are subsequently “discretized” by choosing a set of D equidistant sample points. For each sample point, a new branch of the tree is added at the next layer, and the feasibility of the branch is immediately verified by checking the unique point it currently contains. If the branch is infeasible, then it is pruned. Otherwise, the algorithm invokes itself for an exploration of the layer \(v+1\).
As it is easy to see from the above discussion, the BP algorithm has two main phases: the branching phase, where vertex positions are computed and new tree branches are initialized, and the pruning phase, where the feasibility of such newly generated positions is verified. Even if tree branches grow exponentially layer by layer, the pruning devices allow BP to focus the search on the feasible parts of the tree. The easiest and probably most natural pruning device is the Direct Distance Feasibility (DDF) criterion (Lavor et al. 2012a), which consists in verifying the \(\upvarepsilon \)-feasibility of the constraints:
All distances related to edges \(\{ w,v \}\), with \(w < v\) and that are not used in the discretization, are named pruning distances, because they can be used by DDF for discovering infeasibilities. Several pruning devices can be integrated in BP, that can be based on either pure geometric features of molecules, or rather on chemical and biological properties (Cassioli et al. 2015; Mucherino et al. 2011; Worley et al. 2018).
While the branching phase of BP algorithm can be implemented in different efficient ways (see for example the discussions in Mucherino et al. 2012a; Gonçalves and Mucherino 2014), some questions are still open on the way the pruning phase is executed. As far as all available distances are exact (as in the original version of the paper published in Liberti et al. 2008), then the BP algorithm is able to perform a complete exploration of the search tree, and to provide a finite set of solutions (see for example the computational experiments presented in Lavor et al. (2012a)). This set of solutions is complete, in the sense that no realization can be a solution to the DDGP if it is not included in this solution set. However, this high efficiency of the algorithm is lost when it is necessary to deal with interval distances. In such a case, BP basically turns into a heuristic, so that the complete enumeration of the solution set is not possible any longer, and the propagation of the errors caused by the distance approximations can lead to convergence problems.
In terms of computational time, the BP algorithm needs more and more computational power as the imprecision of the available distances increases (larger range of the corresponding intervals). In the last years, we have been working therefore on parallel implementations of the algorithm. In Gramacho et al. (2012), we considered general instances of the DDGP; we focused instead on DDGP instances having vertex orders satisfying the consecutivity assumption in Mucherino et al. (2010).
In the next section, we will discuss the methods that we employ for the computation of vertex coordinates. In Sect. 4.3, we will describe a technique for reducing the size of the arcs obtained with the sphere intersections by using the information about the pruning distances before performing the branching phase of the algorithm. Thereafter, we will give a larger emphasis on possible methods for improving the pruning phase of the BP algorithm (see Sect. 4.4). Our focus will mainly be on recently published results; the reader interested in additional information can find a wider discussion on the management of errors in the BP algorithm in Costa et al. (2017), D’Ambrosio et al. (2017), Gonçalves (2018), Gonçalves et al. (2017) and Souza et al. (2013). In Sect. 4.5, we will discuss how to exploit tools for local (continuous) optimization for correcting the errors that are introduced in the branching phase of the BP algorithm. Section 4.6 will be devoted to the various discretization orders that have been proposed over the last years for the DDGP. In Sect. 4.7, we will focus on the one-dimensional case, and we will present a variant of the BP algorithm that is able to deal efficiently with interval data. Finally, we will briefly discuss the symmetry properties of BP trees in Sect. 4.8.
4.2 Computing vertex coordinates
In the BP algorithm (see sketch in Algorithm 3), when candidate vertex positions for the vertex v are searched, it is supposed that K reference vertices for v are already positioned on the current branch of the search tree. In the following, in order to avoid including too complex notations, the discussion will focused on the three-dimensional case, i.e. for \(K=3\). However, both methods discussed below can be extended for any \(K \ge 1\) (the reader is referred to Gonçalves 2018; Maioli et al. 2017).
When \(K=3\), the discretization assumptions ensure that there exist 3 reference vertices \(\{u_1,u_2,u_3\}\) for the current vertex v. In order to simplify the notations, we will refer to \(\{a,b,c\}\) as the set of reference vertices.
Whenever the three reference distances belong to \(E'\), three spheres are defined, whose intersection gives 2 points, with probability 1 (Lavor et al. 2012a). The two points \(x_v^+\) and \(x_v^-\) for vertex v are symmetric with respect to the plane defined by the reference vertices. When one of the three distances belongs instead to \(E \setminus E'\), the intersection involves two spheres and one spherical shell, which results in two arcs (see Fig. 5). These two arcs correspond to two intervals, \([\underline{\upomega }_v^+, \overline{\upomega }_v^+]\) and \([\underline{\upomega }_v^-, \overline{\upomega }_v^-]\), for the angle \(\upomega _v\). In order to discretize these intervals, D points can be selected from the two arcs. This selection can be performed in different ways: (i) D equally spaced distances can be extracted from the intervals; (ii) D equally spaced angles can be extracted from the angle intervals; (iii) D equidistant points can be selected from the obtained arcs. All these techniques are simple to implement, and they are equivalent in terms of complexity. In all situations, after performing this selection, the problem is reduced to the one of computing the intersection among three spheres. Therefore, we will suppose in the following that the available discretization distances are exact.
From the equations of the spheres in the three-dimensional space, we can deduce that the points belonging to the intersection of the three spheres can be obtained by solving the following system of quadratic equations:
This particular quadratic system can be solved by calculating the solutions of two linear systems (Coope 2000). However, solution methods for both quadratic and linear systems can lead to numerical instabilities (Mucherino et al. 2012a).
A different method, proposed in Gonçalves and Mucherino (2014), is based on the fact that the reference vertices \(\left\{ a,b,c\right\} \) define a local coordinate system centered at the vertex a (Gonçalves and Mucherino 2014; Thompson 1967), illustrated in Fig. 6. In this coordinate system, a is the origin, the x-axis is defined in such a way that b is on its negative side, and the y-axis (orthogonal to the x-axis) is defined such that the vertex c is on the xy-plane and has negative y coordinate (see Fig. 6). We remark that this setting allows us to have a clockwise orientation for the angles \(\upomega _v\), in a way that the minimum distance between c and v is achieved when \(\upomega _v = 0\) (equivalently, we have the maximal achieved distance when \(\upomega _v = \uppi \)). Naturally, the z-axis is normal to the xy-plane. In the following, we will refer to this coordinate system as the system defined in a.
Similarly, we define a matrix \(U_a \in \mathbb {R}^{3 \times 3}\) which is able to convert position coordinates from the system defined in a to the system defined by the canonical system (the one defined by the initial clique). Let \(v_1\) be the vector from b to a and \(v_2\) be the vector from b to c (see Fig. 6). The x-axis for the system in a can be defined by \(v_1\), and the unit vector in this direction is \(\hat{x} = v_1/\Vert v_1 \Vert \). Moreover, the vectorial product \(v_1 \times v_2\) gives the vector that defines the z-axis, whose corresponding unit vector is \(\hat{z}\). Finally, the vectorial product \(\hat{x} \times \hat{z}\) provides the vector that defines the y-axis (let the unit vector be \(\hat{y}\)).
These three unit vectors are the columns of the matrix \(U_{a} = \left[ \hat{x} \ \ \hat{y} \ \ \hat{z} \right] \), whose role is to directly convert vertex positions from the coordinate system defined in a to the canonical system. Once the matrix \(U_{a}\) has been computed, the canonical Cartesian coordinates for a candidate position for the vertex v can be obtained by:
where \(\uptheta _v\) is the angle formed by the two segments (v, a) and (a, b), and \(\upomega _v\) is the angle formed by the two planes defined by the triplets (a, b, c) and (b, a, v). The two angles \(\uptheta _v\) and \(\upomega _v\), correspond to the spherical coordinates of vertex v.
Thus, the two possible positions for the vertex v, \(x_v^+\) and \(x_v^-\), correspond to the two possible opposite values, \(\upomega _v^+\) and \(\upomega _v^-\), for the angle \(\upomega _v\). More precisely, the sine and cosine of the angles \(\uptheta _v\) and \(\upomega _v\) can be computed by exploiting the positions of the reference vertices a, b and c, as well as the discretization distances \(d_{a,v}\), \(d_{b,v}\) and \(d_{c,v}\) (recall this information is available because the discretization assumptions are satisfied). More details in Gonçalves and Mucherino (2014) and Gonçalves et al. (2017).
4.3 Arc reduction technique
As previously discussed, in dimension \(K=3\), D sample positions can be extracted from the two arcs that are obtained when intersecting two spheres with one spherical shell. This allows to approximate the original search tree, containing either positions or arcs on its nodes, with another tree containing only vertex positions. In this section, we describe a procedure that can be executed before selecting the D sample positions per arc, so that all these selected positions are at least feasible for the DDF pruning device. This procedure allows therefore to avoid generating sample positions that can immediately be discarded at the same layer when applying the DDF pruning device.
Our adaptive scheme is based on the idea to identify, before the branching phase of the algorithm, the subset of positions on the two computed arcs that is feasible with respect to all pruning distances that can be verified at the current layer (Gonçalves et al. 2014). Let us suppose that, at the current layer v, the distance \(d_{cv}\) is represented by the interval \([\underline{d}_{cv}, \overline{d}_{cv}]\). By using Eq. (11), two intervals for the angle \(\upomega _v\) can be identified: \([\underline{\upomega }_v^+, \overline{\upomega }_v^+] \subset [0,\uppi ]\) and \([\underline{\upomega }_v^-, \overline{\upomega }_v^-] \subset [\uppi ,2\uppi ]\), such that the distance constraints
are satisfied.
Let us suppose there is a vertex \(u \in \{ w<v \ |\ v \notin \{a,b,c \} \}\), such that the distance \(d_{uv}\) is known and lies in the interval \([\underline{d}_{uv},\,\overline{d}_{uv}]\). The solution set of the inequalities
consists of intervals for \(\upomega _v\) that are compatible with the distance \(d_{uv}\). A discussion about how to solve the inequalities (12) is given in details in Gonçalves et al. (2014), where all possible scenarios are taken into consideration.
The feasible positions for the vertex v can be therefore obtained by intersecting the two previously computed arcs (in bold in Fig. 6), and several spherical shells, each of them defined by considering one pruning distance between v and \(u < v\). The final subset of \(\mathcal {C}\), which is compatible with all available distances, can be found by intersecting the arcs obtained for each pruning distance with the two initial disjoint arcs, given by Eq. (12). From this final set, we can extract 2D sample positions, that all satisfy the DDF pruning device.
We remark that similar results can be obtained by applying a novel methodology based on Clifford Algebra (Alves and Lavor 2017; Alves et al. 2018; Lavor et al. 2015, 2018), having as a main advantage the fact that the equations of the arcs obtained by the intersections can be written in algebraic form.
4.4 Limitations of BP algorithm
Recent computational experiments have shown that taking equidistant sample points on feasible arcs (or equidistant samples from interval distances), even after the intersection with the available pruning distances, is not enough to allow the BP algorithm to solve some instances within a predefined precision (Gonçalves et al. 2017). The sampled distances are taken independently in each layer of the tree and, in particular for small D values, it is not likely that they are compatible with each other and with other pruning distances available at deeper layers.
The underlying issue is related to the conditions a given set of distances must verify in order to admit a realization in \(\mathbb {R}^k\). We present below a result of Havel et al. (1983) based on Cayley–Menger determinants (Sippl and Scheraga 1986) that is extensively discussed in Blumenthal (1953).
Definition 12
Given a matrix \(D \in \mathbb {R}^{(m+1) \times (m+1)}\) whose entries \(D_{ij} = d_{ij}^2\) correspond to the squares of the distances between points \(\left\{ v_0, v_1, \dots , v_m\right\} \), the Cayley-Menger determinant of these \(m+1\) points is defined as
where \(\mathbf{1}^T = (1,1,\dots ,1)^T \in \mathbb {R}^{m+1}\).
Theorem 6
A \((n + 1)\)-clique admits a realization in \(\mathbb {R}^k\) for \(k \le n\), if and only if all non-vanishing Cayley-Menger determinants of \(m+1\) points have sign \((-1)^{m+1}\) for all \(m = 1, 2, \dots , k\), while the value of all Cayley-Menger determinants of more than \(k+1\) points must be zero.
For example, if we want to determine whether a set of \(n+1\) points with distance matrix \(D \in \mathbb {R}^{(n+1) \times (n+1)}\) admits realizations in \(\mathbb {R}^3\), we must verify the following conditions:
-
\(CM(v_0, v_1) \ge 0\), for all pairs \(\left\{ v_0, v_1\right\} \);
-
\(CM(v_0, v_1,v_2) \le 0\), for all triplets \(\left\{ v_0, v_1,v_2\right\} \);
-
\(CM(v_0, v_1, v_2, v_3) \ge 0\), for all quadruplets \(\left\{ v_0, v_1, v_2, v_3\right\} \);
-
\(CM(v_0, v_1, v_2, v_3, v_4) = 0\), for all set of five points \(\left\{ v_0, v_1, v_2, v_3, v_4\right\} \);
-
\(CM(v_0, v_1, v_2, v_3, v_4, v_5) = 0\), for all set of six points \(\left\{ v_0, v_1, v_2, v_3,v_4, v_5\right\} \).
Now, suppose we know exactly all the distances between five points, except for two of them, that are represented by a real interval: \(x \in [ \underline{x}, \overline{x} ]\) and \(y \in [\underline{y}, \overline{y} ]\). It is not hard to check that the condition \(CM(v_0, v_1, v_2, v_3, v_4) = 0\) is a nonlinear equation and generally, the solution set for such equation, w.r.t. x and y, constitute a curve (Gonçalves et al. 2017). It is clear then, that not every pair of points in \([ \underline{x}, \overline{x} ] \times [ \underline{y}, \overline{y} ]\) will be feasible, and it is likely that uniformly sampling distances values in such intervals will not lead to a solution, mainly if the number of samples is small.
For this reason, we can see the current version of the BP algorithm, which takes samples on interval distances or on feasible arcs, as a heuristic that is only able to provide approximate solutions, in general.
Another difficulty found in previous experiments is related to long-range pruning distances. Long-range distance restraints (or long pruning distances for short) are related to atoms that are at least 4 amino-acids apart in the protein sequence. Even if far in the protein sequence, some atom pairs may be in condition to be detected by an experimental technique. For example, if we consider NMR, it is typical to detect distances between atoms that are very far in the sequence, but quite close in space (\(\le 5~\AA \)).
Furthermore, since other interval distances are also employed in the discretization, the sampled positions in the feasible arcs for previous atoms are only approximations for their true positions, and such a sequence of approximate positions may lead to an infeasibility at a further layer. For this reason, the longest-range pruning distances may fail to be verified (even if they are represented by an interval).
An error introduced during the intersection discretization, in a certain tree layer, might make every sampled candidate position infeasible with pruning distances in a further layer. This phenomenon is more evident when considering long-range distance restraints.
Considering the “sampling problem” that may lead to the violation of long pruning distances, one possibility to avoid pruning out all branches of the search tree and to obtain approximate solutions to the DDGP is to relax those distance constraints. For this, we define the set
where M is a positive integer used to identify long-range distance restraints. Our relaxation consists in avoiding the application of the DDF feasibility test, as well as the intersection scheme (arc reduction) to pruning distances in \(\mathcal{L}\).
Naturally, when such pruning distances are neglected, some information is lost and this can have an impact on the found solutions. In fact, long-range distance restraints are the main responsible for the global fold. Thus, in order to mitigate this effect, we introduce another pruning criterion based on the partial Mean Distance Error (MDE) at the current layer k,
where
Let \(n = |V|\) and note that \(J_n = E\). Thus, by monitoring the \(PMDE_k(X)\) for \(k<n\), we can control the quality of partial realizations. This suggests the PMDE pruning device: if at layer k, \(PMDE_k(X) > \hat{\upvarepsilon }\), then the candidate partial realization may be pruned. We set \(\hat{\upvarepsilon } > \upvarepsilon \), where \(\upvarepsilon \) is the tolerance used in DDF.
When this new pruning device is introduced, a solution found by BP is actually an approximate solution in the sense that it satisfies all distances related to \(E \setminus \mathcal{L}\) (with tolerance \(\upvarepsilon \)), while some distances related to \(\mathcal{L}\) can be violated.
4.5 Solution refinement by continuous optimization
Since some long pruning distances are not considered in the “relaxed BP”, in general, such distance constraints are not satisfied at any incongruent realization found by the algorithm (Gonçalves et al. 2017). Thus, in order to refine the solutions found by BP, following the ideas of Glunt et al. (1993), we consider the following optimization problem:

where \(X \in \mathbb {R}^{n \times 3}\) is a matrix whose rows correspond to the atom positions \(x_v \in \mathbb {R}^3\), \(y \in \mathbb {R}^{|E|}\) and \(\uppi _{uv}\) is a non-negative weight of the distance constraint related to the edge \(\{u,v\}\).
As shown in de Leeuw (1988) and discussed in Glunt et al. (1993, 1994), the function \(\upsigma (X,y)\) is differentiable at (X, y) if and only if \(\Vert x_u - x_v \Vert >0 \) for all \(\{u, v\} \in E\) such that \(\uppi _{uv} y_{uv} >0\). In such case, the gradient, with respect to X, can be written as
where the matrix V is defined by
In expression (17), the matrix \(B(X,y) = [b_{uv}(X,y)]\) is a function of (X, y) defined by
The only kind of constraints defining the feasible set
are box constraints on the variables y. Therefore, it is simple to compute the projection of a pair (X, y) onto \(\Omega \):
where \(\tilde{y}_{uv} = \min \left\{ \overline{d}_{uv} \, , \, \max \left\{ \underline{d}_{uv} \, , \, y_{uv} \right\} \right\} \), for all \(\left\{ u,v\right\} \in E\).
Considering this structure, we tackle the optimization problem (16) with a non-monotone spectral projected gradient method (SPG) proposed by Birgin et al. (2000). In our implementation, a spectral parameter (Barzilai and Borwein 1988) is employed to scale the negative gradient direction before the projection onto the feasible set, followed by a non-monotone line-search, as described in Zhang and Hager (2004), to ensure a sufficient decrease of the objective function at every iteration.
The main steps are summarized in Algorithm 4. In Step 2, it is described a safeguarded expression for the spectral parameter \(\mu _k\) used to scaled the gradient direction.Footnote 1 The safeguards are necessary in order to show that the search directions \(D_k\) satisfy certain properties used to demonstrate global convergence (that every limit point of the sequence generated by Algorithm 4 is a stationary point of (16) Birgin et al. 2000; Zhang and Hager 2004).
Steps 4 and 5 implement the non-monotone line-search (Zhang and Hager 2004). While the non-monotone Armijo condition is not satisfied we reduce \(\upalpha \) by half. Following the non-monotone line search in Zhang and Hager (2004), by setting \(\upeta _k = 0\) one obtains, a classical monotone line-search whereas \(\upeta _k = 1\) implies a non-monotone line search where \(C_k\) corresponds to the average of objective function values over the previous iterations.
Although the algorithm only stops when \(\Vert D_k\Vert \le \upvarepsilon \) (\(\Vert D_k\Vert =0\) only occurs if \((X_k, y_k)\) is a stationary point), in practice we employ other stopping criteria. For example, since we know the global minima of \(\upsigma (X,y)\) is zero, we could also stop when \(\upsigma ( X_k, y_k) < \upvarepsilon _f\).

We recall that (16) is a non-convex global optimization problem, thus the starting point for SPG is crucial. So, we take the approximate solutions given by relaxed BP as starting points to SPG: in other words, SPG acts as a refinement tool.
4.6 Vertex orders
As pointed out in the beginning of Sect. 4, it is a fundamental pre-processing step for the solution of DDGPs by the BP approach to identify a suitable discretization order for the vertices of the DGP graph \(G=(V,E,d)\). Discretization orders for the DDGP have been identified over the last years by employing different approaches. In Costa et al. (2014) and Lavor et al. (2013), handcrafted orders were presented for the protein backbone and the side chains belonging to the 20 amino acids that can take part to the protein synthesis. More recently, in Mucherino (2015b), orders were identified by searching for total paths on pseudo de Bruijn graphs containing cliques of the original graph G. These orders were all conceived for satisfying an additional assumption, which requires that the reference vertices, together with the current vertex v, form a subset of vertices having consecutive ranks in the vertex ordering. We call this assumption the consecutivity assumption. The following class of vertex orders satisfies the consecutivity assumption.
Definition 13
A repetition order (re-order) is a sequence \(r:\mathbb {N}\rightarrow V\cup \{0\}\) with length \(|r|\in \mathbb {N}\) (for which \(r_i=0\) for all \(i>|r|\)) such that:
-
\(G[\{r_1,r_2,\dots ,r_K\}]\) is a clique
-
for all \(i\in \{K+1,\ldots ,|r|\}\) the sets \(\{r_{i-K+1},r_i\},\{r_{i-1},r_i\}\) are exact edges;
-
for all \(i\in \{K+1,\ldots ,|r|\}\) the set \(\{r_{i-K},r_i\}\) is either a singleton (i.e. \(r_{i-K}=r_i\)) or an edge of E.
Notice that the edges \(\{r_{i-K},r_i\}\), when they do not correspond to singletons, they can be related to either exact distances or to distances represented by intervals.
Another way to construct discretization orders is given by the greedy algorithm firstly proposed in Lavor et al. (2012) and subsequently extended for interval distances in Mucherino (2013). This algorithm is able to find orders where the consecutivity assumption is not ensured. A heuristic has also been proposed for finding discretization orders without consecutivity assumption, which outperformed the greedy algorithm on large instances, but for which there is no guarantee of convergence (Gramacho et al. 2013).
More recently, we have been working on discretization orders that are optimal w.r.t. a certain number of objectives (Mucherino 2015a). In Gonçalves et al. (2015), we found some optimal orders for the protein backbones by using Answer Set Programming (ASP). In Gonçalves and Mucherino (2016), we extended the previously proposed greedy algorithm and we proved that it can still find orders in polynomial time when the objectives are simple functions. In Sect. 5.1.1, we will present a new handcrafted order for protein backbones where several constraints arising in structural biology are taken into consideration.
4.7 The one-dimensional case
In the one-dimensional case, the BP framework has the particular feature to allow to perform a deterministic search even when non-exact distances are available (Mucherino 2018). Let G be an instance of the aDGP in dimension \(K=1\), such that the discretization assumptions are satisfied. In this case, the discretization assumption basically ensures that a vertex ordering on V exists so that, for every vertex \(v \in V\) which is not the first in the order, there exists at least one vertex \(u < v\) such that \(\{ u,v \} \in E\). At every level of the tree search, the set of feasible positions for the current vertex can be obtained by intersecting real-valued intervals, which correspond to a set of intervals on which the algorithm can branch. Differently from the case where \(K>1\), it is not necessary to discretize the position intervals, i.e. to select sample points from these intervals (see Sect. 4.1).
There are two important remarks related to the one-dimensional case, which are direct consequence of the fact that position intervals do not need to be discretized during the search, and that vertex positions can be obtained only after having performed the search. Firstly, the solutions that the algorithm can output in these settings are composed by real-valued intervals and not by positions. We define therefore the following function:
which associates a real-valued interval to every vertex of the graph G. Notice that \(\mathcal {I}(\mathbb {R})\) is the set of all real-valued intervals in \(\mathbb {R}\). Secondly, it is necessary to consider, in these settings, distances between pairs of intervals and not distances between singletons. We define the minimal and the maximal distance between two position intervals \([z_u^L,z_u^U]\) and \([z_v^L,z_v^U]\) as follows:
\(\hbox {BP}_1\) is an adaptation of the BP algorithm (see Sect. 4.1) for the one-dimensional case, which can deal with instances consisting of interval distances. However, the solutions given by BP\(_1\) are sets of functions z (see Eq. (18)) satisfying the following property:
From one obtained function z, it is possible to subsequently extract valid realizations x of G. In the following, the functions z will be referred to as a “BP\(_1\) solutions”, which do not correspond to the realizations.

A sketch of the BP\(_1\) algorithm is given in Algorithm 5. At each recursive call, it begins by generating the two initial position intervals, by considering the reference vertex w that is the closest to the current v in the vertex order. The existence of at least one reference vertex is guaranteed by our assumptions. Then, the pruning phase of BP (as in Algorithm 3) is executed, but this phase takes into consideration intervals in BP\(_1\). After the intersections, if the resulting \(I_v\) is empty, then the current branch is infeasible, and the search is back-tracked (there is no branching over intervals at line 20). Once the intersections are performed, a new pruning device, particularly adapted for BP1, is executed: we named this new device the back-tracking pruning. In fact, it is able to refine (or completely discard) intervals of positions that were obtained at previous layers of the search tree. Naturally, the position intervals that are concerned are those adjacent to the current v. The branching phase is left at the end, when all infeasible positions, up to the current layer, have been removed from the intervals. In \(\hbox {BP}_1\), branching is performed over the final number of intervals in \(I_v\), and \(\hbox {BP}_1\) is invoked for each of them and with \(v+1\) as current vertex.
It is important to remark that, when some previous position intervals are refined by the back-tracking pruning, the current branch is re-initialized at the higher layer where a position interval was modified. If this position interval is now empty, then the current branch can be pruned. Otherwise, its construction can be restarted from this layer, so that all intermediate position intervals can be updated.
4.8 Symmetries of the search tree
Given a DDGP instance for which a discretization order exists that satisfies the “consecutivity assumption”, then this instance admits an even number of solutions (Lavor et al. 2012a). Our computational experiments confirmed this result. Moreover, the solution sets found by the BP algorithm always satisfies a stronger property: the cardinality of the set of solutions is always a power of 2 (Mucherino et al. 2012c).
This theoretical result remained unproved for a long time. At a certain point, we found indeed a counterexample, i.e. an instance, artificially generated in a special way, for which the total number of solutions is not a power of 2. Subsequently, we were able to prove that the Lebesgue measure of the subset of instances for which this property is not satisfied is 0 (Liberti et al. 2013, 2011). As a consequence, we can say that, in practice, real-life instances should always have a power of 2 number of solutions. This result has been formally proved for the DDGP instances with vertex orders satisfying the consecutivity assumption (Liberti et al. 2014); we are currently working for extending this result to the DDGP (Abud et al. 2018).
The “power of 2” property is due to the presence of various symmetries in BP binary trees (Lavor et al. 2012a). First of all, there is a symmetry at layer 4 of all BP trees, which makes even the total number of solutions. We usually refer to this symmetry as the first symmetry. At layer 4, there are no distances for pruning, and the two branches rooted at node 3 are perfectly symmetric. In other words, any solution found on the first branch is related to another solution on the second one, which can be obtained by inverting, at each layer, left with right branches, and vice versa.
In the DDGP with consecutivity assumption, as for the first symmetry, each partial reflection symmetry appears every time there are no pruning distances concerning some layer v. In such a case, the number of feasible branches on layer v is duplicated with respect to the one of the previous layer \(v-1\), and pairs of branches rooted at the same node \(x_{v-1}\) are perfectly symmetric. Figure 7 shows a BP tree containing 3 symmetries.
A solution to a DDGP instance can be represented in different ways, such as a path on the tree and a list of binary choices 0–1 (we suppose here that all distances are exact). Since solutions sharing symmetric branches of the tree have symmetric local binary representations, we can derive a very easy strategy for generating all solutions to a DDGP from one found solution and the information on the symmetries in the corresponding tree (Mucherino et al. 2011). Let us consider for example the solution in Fig. 7 corresponding to the second leaf node (from left to right). The binary vector corresponding to this solution is
where we suppose that 0 represents the choice left, and 1 represents right (the first three zeros are associated to the first three fixed vertices of the graph). Since there is a symmetry at layer 6, another solution to the problem can be easily computed by repeating all choices from the root node until the layer 5, and by inverting all other choices. On the binary vector, repeating means copying, and inverting means flipping. So, another solution to the problem is
This solution corresponds to the third feasible leaf node in Fig. 7.
This property can be exploited for speeding up the solution to DDGPs. The procedure we mentioned above can indeed be used for reconstructing any solution to the problem. Thus, once one solution to the problem is known, all the others can be obtained by exploiting information on the symmetries of BP trees. The set
contains all layers v of the tree where there is a symmetry (Mucherino et al. 2011). As a consequence, |B| is the number of symmetries that are present in the tree. Naturally, since the first symmetry is present in all BP trees, \(|B| \ge 1\). The total number of solutions is, with probability 1, equal to \(2^{|B|}\).
If the current layer corresponds to the vertex \(v \in B\), for each \(x_{v-1}\) on the previous layer, both the newly generated positions for \(x_v\) are feasible. If \(v \not \in B\), instead, only one of the two positions can be part of a branch leading to a solution. The other position is either infeasible or it defines a branch that will be pruned later on at a further layer v, in correspondence with a pruning distance whose graph edge \(\{u,w\}\) is such that \(u+3<v\le w\). Therefore, we can exploit such information for performing the selection of the branches that actually define a solution to the problem. When \(v \not \in B\) (only one position is feasible), it is not known a priori which of the two branches (left/right) is the correct one. This is the reason why at least one solution must be computed before having the possibility of exploiting the symmetries for computing all the others.
We remark that the symmetry properties of BP trees can be exploited for speeding up the algorithm, as shown in Mucherino et al. (2012b). Very recently, a parallel version of BP which exploits the presence of symmetries was proposed in Fidalgo et al. (2018).
5 Applications
5.1 DGP for protein molecules
The distance information from NMR experiments are distances between nuclei in proteins (Almeida et al. 2013; Crippen and Havel 1988; Wuthrich 1989; Hendrickson 1995; Nilges and O’Donoghue 1998), though these distances have significant errors so they are treated as restraints rather than constraints (Clore and Gronenborn 1997; Brunger et al. 1998; Nilges and O’Donoghue 1998). More recently, a variety of other approaches to distance measurements in biological and inorganic materials have been developed and there is considerable promise for continuing progress in this area (Guerry and Herrmann 2011; Bouchevreau et al. 2013). Considerable experimental work is carried out to determine the pair of nuclei assigned to each distance extracted from the NMR data, allowing the problem to be represented by a graph \(G=(V,E,d)\), where V represents the set of atoms and E is the set of atom pairs for which a distance is available.
5.1.1 Identifying vertex orders for protein backbones
In this section, we consider graphs related to the backbone of a protein, from which its general structure is determined. The backbone is defined by a sequence of three atoms, \(N,C_{\upalpha },C\), where each \(C_{\upalpha }\) is bonded to another group of atoms (the side chains of the protein) that distinguishes one amino acid from another. We also consider the atoms attached to \(N,C_{\upalpha },C\), respectively \(H,H_{\upalpha },O\). More details about protein graphs including side chains are given in Costa et al. (2014) and Sallaume et al. (2013).
Since we are interested in determining the structure of the backbone of a protein, the sequence of atoms \(N^{i},C_{\upalpha }^{i},C^{i}\), for \(i=1,\dots ,p\) (where p is the number of amino acids), would be the first candidate for defining a DMDGP (Discretizable Molecular Distance Geometry Problem) order. However, for this kind of order, it is not guaranteed that we have all the distances \(d_{i-3,i}\) necessary to define a DMDGP instance. On the other hand, NMR experiments, in general, provide distances between hydrogen atoms that are close enough. An order involving only hydrogens was defined in Lavor et al. (2011), but it does not work well because of uncertainty in NMR data. This has been partially addressed by simultaneously using hydrogen atoms bonded to the backbone and the backbone itself (Lavor et al. 2013).
As it was done in Lavor et al. (2013), the idea is to allow the repetition of some vertices in the order, so that at least three adjacent predecessors can always be chosen to be contiguous. Such orders are called re-orders, and they are defined in Sect. 4.6. In this section, we will give a specific definition in dimension \(K=3\). First of all, the set of edges E of the protein graph \(G=(V,E,d)\) is partitioned into \(E=E^{\prime }\cup E^{\prime \prime }\), where \(\{u,v\}\in E^{\prime }\) if \(d_{uv}\in (0,\infty )\), and \(\{u,v\}\in E^{\prime \prime }\) if \(d_{uv}=[ \underline{d}_{uv},\overline{d}_{uv}]\), with \(0<\underline{d}_{uv}<\overline{ d}_{uv}\). Note that the function d is now more general: the interval values represent the uncertainties in NMR data. As we will see, \(E^{\prime }\) represents pairs of atoms separated by one and two covalent bonds and \( E^{\prime \prime }\) represents pairs of hydrogen atoms whose distances are provided by NMR.
Therefore, a re-order in dimension 3 is a sequence \(r : \mathbb {N} \mapsto V \cup \{0\}\), with length \( |r| \in \mathbb {N}\) (for which \(r_i = r(i) =0\) for all \(i > |r|\)), such that
-
1.
\(\{r_1, r_2\}, \{r_1, r_3\}, \{r_2, r_3\} \in E^{\prime }\);
-
2.
\(\forall i \in \{4, \dots , |r|\}\), \(\{r_{i-1}, r_i\}, \{r_{i-2}, r_i\} \in E^{\prime }\);
-
3.
\(\forall i \in \{4, \dots , |r|\}\), \(\{r_{i-3}, r_i\} \in E^{\prime }\cup E^{\prime \prime }\) or \(r_{i-3} = r_i\).
The first property says that \(d_{r_1 r_2}, d_{r_1 r_3}, d_{r_2 r_3} \in (0, \infty )\) and the second one says that \(d_{r_{i-1} r_i}, d_{r_{i-2} r_i} \in (0, \infty )\), for \(i = 4, \dots , |r|\). That is, all of them must be precise distances and greater than zero.
From the third property, there are three possibilities for \(d_{r_{i-3} r_i}\) , \(i = 4, \dots , |r|\):
-
\(d_{r_{i-3} r_i} = 0\), meaning that there is a vertex repetition (\( r_{i-3} = r_i\));
-
\(d_{r_{i-3} r_i} \in (0, \infty )\), when \(r_{i-3}, r_i\) are related to atoms separated by one or two covalent bonds;
-
\(d_{r_{i-3}r_{i}}=[\underline{d}_{r_{i-3}r_{i}},\overline{d} _{r_{i-3}r_{i}}]\), with \(0<\underline{d}_{r_{i-3}r_{i}}<\overline{d} _{r_{i-3}r_{i}}\) (these distances are called interval distances).
Any re-order corresponds to a DMDGP order, where some of the pairs \( \{r_{i},r_{j}\}\), with \(|i-j|\ge 3\), may not correspond to precise distances, but rather to intervals.
The most important property of the re-order described below is that it allows branches (in the BP search) only at hydrogen atoms that are bonded to the protein backbone. Previous re-orders (Gonçalves et al. 2017; Lavor et al. 2013) do not have this property.
Let us define a graph \(G=(V,E,d)\) associated to the backbone of a protein (\(\{N^{k},C_{\upalpha }^{k},C^{k}\}\), for \(k=1,\dots ,p\)), including oxygen atoms \(O^{k}\), bonded to \(C^{k}\), and hydrogen atoms \(H^{k}\) and \( H_{\upalpha }^{k}\), bonded to \(N^{k}\) and \(C_{\upalpha }^{k}\), respectively (see Fig. 8, for \(p=3\)).
The hand-crafted vertex order (hc order) is the following:
where \(i=2,\dots ,p-1\), \(H^{1^{\prime }}\) is the second hydrogen bonded to \( N^{1}\) and \(O^{p^{\prime }}\) is the second oxygen bonded to \(C^{p}\).
In Lavor et al. (2018), it was proved that hc is a re-order and the following theorem was established.
Theorem 7
Using the hc order, the rigid geometry hypothesis, the peptide plane properties, the chirality property, and the set of distances between the pairs of hydrogen atoms
where \(i=2,\dots ,p-1\) and p is the number of amino acids of a protein, the branches in the search tree occur only at hydrogen atoms given by
The two main consequences of this theorem, as explained in Lavor et al. (2018), are the following: (a) If the distances related to the pairs (20) are precise values, the search space of the associated DGP is finite, represented as a binary tree; (b) If the distances related to the pairs (20) are precise values and there is at least one additional (also precise) distance (from NMR data) for each hydrogen in the list (21) to previous hydrogens, there is only one DGP solution that can be found in linear time.
Although precise and additional distances are very strong hypotheses, this kind of information emphasizes the relationship of the cardinality of the DGP solution set with the computational complexity of the problem.
Since atoms \(H^{i},H_{\upalpha }^{i}\) are in the same amino acid, the associated distance \(d(H^{i},H_{\upalpha }^{i})\) is likely to be detected by NMR. Although atoms \(H_{\upalpha }^{i-1},H^{i}\) are in consecutive amino acids, there is just one torsion angle (the one defined by \( \{N^{i-1},C_{\upalpha }^{i-1},C^{i-1},N^{i}\}\)) related to the position of \( H^{i}\), because the peptide plane “constrains” the torsion angle defined by \(\{C_{\upalpha }^{i-1},C^{i-1},N^{i-1},C_{\upalpha }^{i}\}\) to be \(\uppi \) radians. In the worst case, supposing that the distance \(d(H_{\upalpha }^{i-1},H^{i})\) is not available, we can use “implicit” information associated with the fact that the distance was not detected (Agra et al. 2017) or some estimations given in Wüthrich (1986).
5.1.2 Some numerical results
The previous section shows that, by considering the theoretical model for the protein backbone along with experimental distance data provided by NMR, it is possible to devise a suitable vertex order that allows for the discretization. Then, we can employ the variant of BP algorithm (Algorithm 3) described in Sect. (4.4) to obtain approximate solutions for the DGP.
We present some results obtained by the relaxed version of BP (see Sect. 4.4) and the improvements achieved by the refinement step with SPG (Sect. 4.5).
The artificial instances are the same as those in Gonçalves et al. (2017). Based on protein files from the PDB, we compute all distances between the atoms and to generate an instance we keep those between atoms separated by one or two covalent bonds and those between atoms of the same peptide plane; such distances are considered as exact. Distances between hydrogen atoms that are smaller than 5 Å are also considered as random intervals of size 1 Å containing their actual value.
In Algorithm 4, we have used the safeguards \(\mu _{min} = 10^{-8}\) and \(\mu _{max}=10^8\), \(\upgamma = 10^{-4}\). The iterations were stopped when \(\Vert \nabla \upsigma (X_k,y_k) \Vert < \upvarepsilon _g = 10^{-7}\) or \(\upsigma (X_k,y_k) < \upvarepsilon _f = 10^{-9}\) or when the number of iterations reach 20,000. For the non-monotone line search we chose \(\upeta _k = 0.99\). We have considered all the weights \(\uppi _{uv}\) equal to one. In BP the tolerance in the DDF test was \(\upvarepsilon = 10^{-3}\) and in the PMDE test \(\hat{\upvarepsilon } = 10^{-2}\).
Our initial points for SPG have the form \((X_0,y_0)\), where \(X_0\) is a solution given by BP and
Table 1 reports the numerical results. It presents for each instance, its PDB name, number of atoms |V| and number of available distances (exact and interval ones) |E|. Concerning BP, we report the smallest number of samples D taken in the feasible arcs that allow it to find a solution and the maximum length (in the vertex order) M of the pruning distances considered in the DDF feasibility test and in the arc reduction procedure. The symbol “−” means that none pruning distance was neglected. It is important to remark that we have stopped BP after reaching the first leaf node. The table also brings the CPU time in seconds spent by BP to find this first solution and by SPG to refine it. The quality of the solutions is measured by the value of the stress function \(\upsigma (X,y)\), which indicates how well the distance constraints are satisfied, and by the RMSD (root mean squared deviation) with respect to the actual protein structure from the PDB.
As one can see from the figures of Table 1, when all pruning distances are taken into account the improvement in the solution quality after the refinement is very small, if any. On the other hand, as the number of neglected distances increases (M decreases) the solutions provided by BP have a relatively high value for the stress function, indicating that those distance constraints are not well satisfied. For most of these instances, we can observe a considerable improvement after the SPG refinement, not only in terms of the stress (almost five orders of magnitude), but also in terms of RMSD (highlighted in boldface in the table). For example, the actual backbone structure for the instance 2JWU is shown in Fig. 9 in blue, superimposed with the solution found by BP on the left and with the refined solution on the right.
5.2 DGP and VGP in nanostructures
The Nanostructure Problem is the problem of finding, at high precision, the atomic positions of molecular, biomolecular or solid state systems when it is difficult or impractical to grow a single crystal or even a polycrystal sample (Billinge and Levin 2007). The meaning of high precision is context dependent, however a typical requirement in a solid state system is the determination of the positions of all atoms in a nanostructure to better than 2% for each interatomic distance in the nanostructure, and in some cases even higher resolution is necessary. High resolution is required as the function of nanostructured materials and complex molecules is highly sensitive to small changes in the interatomic distances, making it essential to determine nanostructure to high precision to enable understanding and design of materials. Nanostructure problems are encountered in a wide variety of materials, including complex molecules, nanoparticles, polymers, proteins, non-crystalline motifs embedded in a crystalline matrix and many others (see Fig. 10 for three examples). We consider single phase problems where one nanostructure is dominant, though extensions to multiphase nanostructures are possible once the single phase case can be solved efficiently.

(Reproduced with permission from Billinge and Levin 2007)
(Color online) Examples of nanostructured materials. a Nanostructured bulk materials. b Intercalated mesoporous materials. c Discrete nanoparticles. In each case, ball-and-stick renditions of possible structures are shown on the top, and TEM images of examples are shown on the bottom
The pair-distribution function (PDF) method is a versatile and readily available approach to probing the local atomic structure of nanostructured materials (Egami and Billinge 2012). PDF results can be extracted from x-ray, neutron or electron total scattering data and in many cases the data can be collected efficiently. The major bottleneck in PDF analysis is the extraction of nanostructures from the data, as standard techniques are based on either refinement from a good initial guess (Farrow et al. 2007); or on simulated annealing (McGreevy and Pusztai 1988; Evrard and Pusztai 2005; Tucker et al. 2007).
A more systematic approach to finding good starting structures is a high priority in the field and provides the motivation for developing ab-initio DG approaches (Gujarathi et al. 2014; Juhás et al. 2006). Alternative experimental approaches such as high resolution transmission electron microscopy (see Fig. 10) are very useful for larger scale morphological studies, but they do not yield the high precision atomic structures available from diffraction and scattering approaches. Local structural information can also be found using extended x-ray absorption fine-structure (EXAFS) and related near-edge absorption spectroscopies, solid-state NMR, and scanning probe methods at sample surfaces. An innovative emerging approach utilizes ultrafast x-ray laser pump-probe “diffract and destroy” methods which require a separate suite of analysis algorithms (Gaffney and Chapman 2007).
A longer term goal in the field is to develop modeling frameworks incorporating all of the available experimental probes to yield consensus best local atomic structures, and the most recent software packages are moving in this direction. Here, we focus on the determination of local atomic structure from PDF data.
The ideal PDF contains a list of the interatomic distances in a material for both crystalline or non-crystalline cases (see the next subsection). There is a very extensive literature describing PDF experiments on a wide range of complex nanostructured materials (Egami and Billinge 2012). Nanostructures consistent with the experimental PDF data are usually discovered using one of two approaches: (i) By using physical intuition or theoretical modeling to propose a starting structure, followed by structure refinement (Farrow et al. 2007) or (ii) Use of global optimization methods to find structures, most often using a simulated annealing approach that in this literature is called Reverse Monte Carlo (RMC) (McGreevy and Pusztai 1988; Tucker et al. 2007). Nanostructures found to be consistent with the PDF data are then tested further by checking their properties against known results from other experimental structural characterization approaches such as TEM, STM etc, and experimental results for electrical, mechanical, thermodynamic, optical, magnetic and other physical properties. Quantum mechanical calculations to predict the structure and properties of complex materials are utilized in making these comparisons. Though the RMC method is a global optimization approach it is of limited use in finding unique nanostructures, due to the strong metastability of the nanostructure optimization problem. However, RMC is widely utilized to find populations of local nanostructures consistent with materials with varying local atomic structures, such as structural glasses and liquids.
Attempts at finding unique global minimum nanostructures of solid state materials using DG approaches is recent (see Sect. 3), despite the long history of finding global minimum atomic structures using Bragg diffraction from single crystals. This is partly due to the fact that only recently PDF methods have become sufficiently refined to provide high quality distance lists.
5.3 The pair distribution function
The distances between atoms in a material are contained in the pair distribution function (PDF). The PDF is found by taking a Fourier transform of the structure factor (see Eq. 23 below) which is extracted from the experimentally measured total scattering of x-rays, neutrons or electrons from a sample (Egami and Billinge 2012; Billinge and Kanatzidis 2004). The PDF method is widely used to study nanostructures (Egami and Billinge 2012; Billinge and Kanatzidis 2004; Billinge and Levin 2007) and several software packages to find atomic structures that are consistent with PDF data are available (Evrard and Pusztai 2005; Farrow et al. 2007; Tucker et al. 2007). Despite the successes of these methods, finding high quality nanostructures from experimental PDF data remains challenging and subject to interpretation. There is a need for efficient computational methods that have a stronger mathematical foundation and performance guarantees. DG methods provide one avenue to achieve these more rigorous approaches to nanostructure determination. As we show below, a perfect PDF would yield all of the interatomic distances in the sample. However there are many limitations in the real PDF data. First, the data is truncated at an upper interatomic distance that is typically 3.5 nm or less, and the data is imprecise leading to overlap of peaks and hence difficulty in extracting distances that are close in length.
The ideal pair distribution function is defined by
The delta function in this expression yields a set of peaks in g(r), that are located at the values of the interatomic distances. Here, \(r_{jl}\) is the distance between atoms j and l located at positions \(\mathbf {r}_j\) and \(\mathbf {r}_l\) so that \(r_{jl} = ||\mathbf {r}_l-\mathbf {r}_j||\). n is the total number of atoms in the structure, where \(j=1,\ldots ,n\) and \(l=1,\ldots ,n\). \(f_j\) is the scattering power of the atom at position \(\mathbf {r}_j\), and \(f_j^*\) is its complex conjugate. The scattering power is found by taking a Fourier transform of the electron charge density (for x-ray or electron scattering) or the nuclear potential (neutron scattering).
The measured structure factor, extracted from scattering experiments in the kinematical limit where multiple scattering is ignored, is given by (see Sivia 2011, Chapter 3)
where \(\mathbf Q = \mathbf k - \mathbf k '\) is the scattering wavevector which is the difference of the incoming and outgoing wavevectors of the particle that is scattered. For elastic scattering, the magnitudes of the scattering wavevectors are the same, \(k = k'\), where k is the magnitude of \(\mathbf k \). The term \(j=l\) is called the self-scattering term, and is usually treated separately and normalized in the following way,
\((\langle f \rangle )^2\) is the mean square averaged scattering power, where the average is taken over all scatterers in the system. PDF analysis is usually used when the material samples are amorphous or powders so that the scattering is independent of sample orientation and an average over the scattering angles yields
where Q is the magnitude of \(\mathbf Q \) and \(r_{jl}\) is the magnitude of \(\mathbf {r}_{jl}\).
For convenience in comparing different materials, the PDF above is often normalized so that it approaches one at large distances. From the relations (22) and (25), it is easy to see that the structure factor (the experimentally measured quantity) is related to the pair distribution function through
From the point of view of DG, the key feature of the pair distribution function as defined in Eq. (22) is that it contains a list of interatomic distances without any specific reference to the particular atoms at the endpoints of each distance, so finding atomic structure from the PDF requires solution to a uDGP.
The vector PDF is given by,
The vector PDF contains a list of interatomic vectors without specific reference to the particular atoms at the endpoints of each distance, so that a uVGP needs to be solved. It is interesting to note that Patterson methods used in solving structure from crystals leads to an aVGP problem (see Sect. 5.5).
The experimental PDF does not have delta function peaks as occurs in the ideal PDF of Eq. (22). The experimental peak width is determined by both physical processes and experimental resolution (Egami and Billinge 2012). In structures with high symmetry, such as Ni which crystallizes into a face-centered cubic structure, distances of the same length occur frequently and the degeneracy of each distance can be estimated from the area of each peak. Extraction of high quality distance lists requires high purity samples, high resolution detectors and careful data analysis.
5.4 Solution to uDGP for a fullerene molecule
An illustration of the solution to the \(C_{60}\) fullerene using the LIGA algorithm for uDGP is presented in Fig. 11, showing that it is possible to reconstruct interesting nanostructures from unassigned distance lists extracted from real experimental PDF data. A large number of other structures have been reconstructed using LIGA using precise distance lists and also from experimental data (Juhas et al. 2010). LIGA works well when structures have high symmetry leading to a limited number of unique distances. However, LIGA has difficulty with structures that have a large number of different distances due to the stochastic nature of its vertex addition procedures. The emergence of DGP GRB methods, such as those used in TRIBOND, provide new avenues for improving LIGA (see Sect. 3.2).
Reconstruction of a buckeyball from experimental neutron scattering data. a–c Are various forms of the experimental data, starting with the raw structure factor data. The imprecise distance list of d extracted from this data is the only information that is used to find the correct structure
When the distance list \(\mathcal {D}\) is obtained from experimental PDF data (see Sect. 5.3), they may contain significant errors in the multiplicity and values of the distances (see Fig. 11). This is a problem especially because underestimated multiplicities may greatly increase the cost of the correct structure. Under such circumstances it is advantageous to relax or even ignore multiplicities altogether. In the first case, the distance table is constructed with distance multiplicities increased by a fixed percentage, and thus it contains more lengths than actually present in the searched structure. In the second case, the program allows any distance to be compared with the model structure an arbitrary number of times. This is in effect the same as setting infinite multiplicities for all lengths in the target set. It is also possible to relax the condition of a fixed target size n, in which case the largest cluster size keeps growing. However since the distances have a fixed maximum length, the cost of the large structures grows significantly, indicating the true largest cluster consistent with the input distance list.
One clear lesson emerging from experiences with the TRIBOND and LIGA algorithms, and which has also been emphasized in recent work on BP methods for DGPs, is that the ordering of vertices used in reconstruction from distance information is very important. This leads to the viewpoint that it is more effective to find a smaller number of high precision distances in a core, than it is to find a larger number of low precision distances that are not closely related.
5.5 VGP and the Patterson function
Patterson (1934) realized that x-ray scattering data from single crystals could be used to find the vector distances between atoms in the unit cell of the crystal. The Patterson function is defined through the relation.
It is essentially the Fourier transform of the scattering intensities and does not include the phase. The Patterson function is also equivalent to the electron density convolved with its inverse:
A Patterson map of n random points has \(n(n - 1)\) unique peaks, excluding the central (origin) peak and any overlap.
The peaks positions in the Patterson function give the interatomic distance vectors and the peak heights are proportional to the product of the number of electrons in the atoms concerned. For each vector between atoms i and j there is an oppositely oriented vector of the same length (between atoms j and i). Though the phase is not explicitly used in the analysis, Patterson realized that if the interatomic vectors could be used to find the atomic structure, then the “phase” problem would be solved. There was thus a great deal of excitement about this method. However despite early successes on small molecules Patterson methods were found to be best when used to find the locations of heavy atoms which give the strongest peaks in the Patterson map.
6 Conclusions
We updated our earlier review on some methods for the assigned and the unassigned distance geometry problems (aDGP and uDGP); particularly methods that determine graph embeddings by iteratively growing substructures. Starting with a general discussion on graph rigidity, we have presented two main approaches to the DGP. The first approach, for the uDGP, is strongly based on the concept of finding unique substructures during iterative growth of a final unique realization. The second, the discretizable distance geometry problem was initially conceived for the aDGP, and reduces the search space to a discrete one having the structure of a tree. We focused our attention on two particular applications: the identification of conformations of protein molecules and determining the nanostructures of complex materials.
The discretizable distance geometry problem is unique in that it maps out different conformational states in proteins. These states are typically related to each other by large scale motion of rigid regions of the protein, making it difficult to explore them using conventional methods. The use of these different conformational states as initial states for conventional methods is an interesting direction for future work. Significant progress has also been outlined in treating uncertainty intervals, particularly toward finding feasible solutions in systems with intervals. An alternative approach in emerging work is to consider lists of incompatable distances chosen according to typical experimental uncertainties, and to look for optimal structures.
The unassigned distance geometry problem is relatively unexplored and the build up methods, like TRIBOND and LIGA are first generation algorithms. Though LIGA is able to treat errors in experimental distance lists, the method is not designed to handle low symmetry structures, like polymers or proteins, or even solid state nanoparticles with little symmetry. Nevertheless LIGA finds structures that are optimal and for high symmetry structures is very effective, for example the fullerene case. From a modeling perspective, the GRB studies clearly show that the most time consuming part of the TRIBOND and LIGA algorithms is finding a good starting core, so this is an interesting direction for future studies. There are a variety of strategies to implant a known core into a system so that the unknown structure can be determined with respect to it. Larger known cores also help mitigate errors in buildup due to experimental uncertainties.
The vector geometry problem introduced here does not seem to be an active area of research in the mathematics and OR communities, though its importance to protein structure determination has been known since the very early days of x-ray crystallography. The Patterson function found from scattering data from crystals leads to the set of interatomic vectors in the atomic structure, and the inverse problem is to find the atom locations from these vectors. We showed that the buildup methods developed for the DGP can be adapted to the VGP and that the latter problem is computationally more efficient. The interatomic vectors found from the Patterson function are assigned leading to a new matrix completion problem where the entries in the matrix are the interatomic vectors. The PDF is also being extended to the vector case, and from the vector PDF an unassigned list of interatomic vectors is found. The aVGP and uVGP thus have interesting experiment connections, and for this reason and their interesting mathematical structure makes them intriguing directions for future work.
Further discussion of interesting future directions can be found in Gonçalves et al. (2017), Liberti and Lavor (2016, 2018).
Notes
\(\langle (X,y), (\hat{X},\hat{y}) \rangle := \text {tr} (X \hat{X}^T) + y^T \hat{y}\).
References
Abud, G., Alencar, J., Lavor, C., Liberti, L., & Mucherino, A. (2018). The \(k\)-discretization and \(k\)-incident graphs for discretizable distance geometry. Optimization Letters. https://doi.org/10.1007/s11590-018-1294-2.
Agra, A., Figueiredo, R., Lavor, C., Maculan, N., Pereira, A., & Requejo, C. (2017). Feasibility check for the distance geometry problem: An application to molecular conformations. International Transactions in Operational Research, 24, 1023–1040.
Almeida, F. C. L., Moraes, A. H., & Gomes-Neto, F. (2013). An overview on protein structure determination by NMR, historical and future perspectives of the use of distance geometry methods. In A. Mucherino et al. (Eds.), (Vol. 102, pp. 377–412).
Alves, R., & Lavor, C. (2017). Geometric algebra to model uncertainties in the discretizable molecular distance geometry problem. Advances in Applied Clifford Algebra, 27, 439–452.
Alves, R., Lavor, C., Souza, C., & Souza, M. (2018). Clifford algebra and discretizable distance geometry. Mathematical Methods in the Applied Sciences, 41(11), 4063–4073.
Barzilai, J., & Borwein, J. (1988). Two-point step size gradient methods. IMA Journal of Numerical Analysis, 8, 141–148.
Billinge, S. J. L., Duxbury, Ph M, Gonçalves, D. S., Lavor, C., & Mucherino, A. (2016). Assigned and unassigned distance geometry: Applications to biological molecules and nanostructures. Quarterly Journal of Operations Research, 14(4), 337–376.
Billinge, S. J. L., & Kanatzidis, M. G. (2004). Beyond crystallography: the study of disorder, nanocrystallinity and crystallographically challenged materials with pair distribution functions. Chemical Communications (Cambridge, England), 7, 749–760.
Billinge, S. J. L., & Levin, I. (2007). The problem with determining atomic structure at the nanoscale. Science, 316(5824), 561–565.
Birgin, E. G., Martínez, J. M., & Raydan, M. (2000). Nonmonotone spectral projected gradient methods on convex sets. SIAM Journal on Optimization, 10, 1196–1211.
Biswas, P., Lian, T., Wang, T., & Ye, Y. (2006). Semidefinite programming based algorithms for sensor network localization. ACM Transactions in Sensor Networks, 2, 188–220.
Biswas, P., & Ye, Y. (2006). A distributed method for solving semidefinite programs arising from ad hoc wireless sensor network localization (pp. 69–84). Boston: Springer.
Blumenthal, L. M. (1953). Theory and applications of distance geometry (p. 347). Oxford: Clarendon Press.
Bouchevreau, B., Martineau, C., Mellot-Draznieks, C., Tuel, A., Suchomel, M. R., Trebosc, J., et al. (2013). An NMR-driven crystallography strategy to overcome the computability limit of powder structure determination: A layered aluminophosphate case. International Journal of Computational Geometry and Applications, 19, 5009–5013.
Boutin, M., & Kemper, G. (2007). Which point configurations are determined by the distribution of their pairwise distances. International Journal of Computational Geometry and Applications, 17(1), 31–43.
Brunger, A. T., Adams, P. D., Clore, G. M., DeLano, W. L., Gros, P., Grosse-Kunstleve, R. W., et al. (1998). Crystallography & NMR system: A new software suite for macromolecular structure determination. Acta Crystallographica Section D: Biological Crystallography, 54(595), 905–921.
Carvalho, R. S., Lavor, C., & Protti, F. (2008). Extending the geometric build-up algorithm for the molecular distance geometry problem. Information Processing Letters, 108, 234–237.
Cassioli, A., Bardiaux, B., Bouvier, G., Mucherino, A., Alves, R., Liberti, L., et al. (2015). An algorithm to enumerate all possible protein conformations verifying a set of distance restraints. BMC Bioinformatics, 16(23), 1–15.
Clore, G. M., & Gronenborn, A. M. (1997). New methods of structure refinement for macromolecular structure determination by NMR. PNAS, 95, 5891–5898.
Connelly, R. (1991). On generic global rigidity, in: Applied geometry and discrete mathematics. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, 4, 147–155.
Connelly, R. (2005). Generic global rigidity. Discrete Computational Geometry, 33, 549–563.
Connelly, R. (2013). Generic global rigidity of body-bar frameworks. Journal of Combinational Theory Series B, 103, 689–705.
Coope, I. D. (2000). Reliable computation of the points of intersection of \(n\) spheres in \(n\)-space. ANZIAM Journal, 42, 461–477.
Costa, T., Bouwmeester, H., Lodwick, W., & Lavor, C. (2017). Calculating the possible conformations arising from uncertainty in the molecular distance geometry problem using constraint interval analysis. Information Sciences, 415–416, 41–52.
Costa, V., Mucherino, A., Lavor, C., Cassioli, A., Carvalho, L., & Maculan, N. (2014). Discretization orders for protein side chains. Journal of Global Optimization, 60, 333–349.
Crippen, G. M., & Havel, T. F. (1988). Distance geometry and molecular conformation. New York: Wiley.
D’Ambrosio, C., Ky, V., Lavor, C., Liberti, L., & Maculan, N. (2017). New error measures and methods for realizing protein graphs from distance data. Discrete & Computational Geometry, 57, 371–418.
de Leeuw, J. (1988). Convergence of the majorization method for multidimensional scaling. Journal of Classification, 5, 163–180.
Ding, Y., Krislock, N., Qian, J., & Wolkowicz, H. (2010). Sensor network localization, euclidean distance matrix completions, and graph realization. Optimization and Engineering, 11(1), 45–66.
Dokmanic, I., & Lu, Y. M. (2016). Sampling sparse signals on the sphere: Algorithms and applications. IEEE Transactions on Signal Processing, 64(1), 189–202.
Dokmanic, I., Parhizkar, R., Ranieri, J., & Vetterli, M. (2015). Euclidean distance matrices: Essential theory, algorithms, and applications. IEEE Signal Processing Magazine, 32(6), 12–30.
Donald, B. R. (2011). Algorithms in structural molecular biology (p. 464). Boston: MIT Press.
Dong, Q., & Wu, Z. (2002). A linear-time algorithm for solving the molecular distance geometry problem with exact interatomic distances. Journal of Global Optimization, 22, 365–375.
Duxbury, P. M., Granlund, L., Gujarathi, S. R., Juhas, P., & Billinge, S. J. L. (2016). The unassigned distance geometry problem. Discrete Applied Mathematics, 204, 117–132.
Egami, T., & Billinge, S. J. L. (2012). Underneath the Bragg peaks: Structural analysis of complex materials (2nd ed.). Oxford: Pergamon Press, Elsevier.
Evrard, G., & Pusztai, L. (2005). Reverse Monte Carlo modelling of the structure of disordered materials with RMC++: A new implementation of the algorithm in C++. Journal of Physics: Condensed Matter, 17, S1–S13.
Farrow, C. L., Juhas, P., Liu, J. W., Bryndin, D., Boz̈in, E. S., Bloch, J., et al. (2007). Pdffit2 and pdfgui: Computer programs for studying nanostructure in crystals. Journal of Physics: Condensed Matter, 19(33), 335219.
Fidalgo, F., Gonçalves, D. S., Lavor, C., Liberti, L., & Mucherino, A. (2018). A symmetry-based splitting strategy for discretizable distance geometry problems. Journal of Global Optimization, 71(4), 717–733.
Freris, N. M., Graham, S. R., & Kumar, P. R. (2010). Fundamental limits on synchronizing clocks over networks. IEEE Transactions on Automatic Control, 56(6), 1352–1364.
Gaffney, K. J., & Chapman, H. N. (2007). Imaging atomic structure and dynamics with ultrafast x-ray scattering. Science, 36(5830), 1444–1448.
Glunt, W., Hayden, T. L., & Raydan, M. (1993). Molecular conformation from distance matrices. Journal of Computational Chemistry, 14, 114–120.
Glunt, W., Hayden, T. L., & Raydan, M. (1994). Preconditioners for distance matrix algorithms. Journal of Computational Chemistry, 15, 227–232.
Gommes, C. J., Jiao, Y., & Torquato, S. (2012). Microstructural degeneracy associated with a two-point correlation function and its information contents. Physical Review E, 85, 051140.
Gonçalves, D. S. (2018). A least-squares approach for discretizable distance geometry problems with inexact distances. Optimization Letters. https://doi.org/10.1007/s11590-017-1225-7.
Gonçalves, D., & Mucherino, A. (2014). Discretization orders and efficient computation of cartesian coordinates for distance geometry. Optimization Letters, 8, 2111–2125.
Gonçalves, D. S., & Mucherino, A. (2016). Optimal partial discretization orders for discretizable distance geometry. International Transactions in Operational Research, 23(5), 947–967.
Gonçalves, D. S., Mucherino, A., & Lavor, C. (2014). An adaptive branching scheme for the branch & prune algorithm applied to distance geometry. In IEEE conference proceedings, federated conference on computer science and information systems (FedCSIS14), workshop on computational optimization (WCO14), Warsaw, Poland (pp. 463–469).
Gonçalves, D. S., Mucherino, A., Lavor, C., & Liberti, L. (2017). Recent advances on the interval distance geometry problem. Journal of Global Optimization, 69(3), 525–545.
Gonçalves, D. S., Nicolas, J., Mucherino, A., & Lavor, C. (2015). Finding optimal discretization orders for molecular distance geometry by answer set programming. In S. Fidanova (Ed.), Recent advances in computational optimization. Studies in computational intelligence (Vol. 610, pp. 1–15). Cham: Springer.
Gortler, S., Healy, A., & Thurston, D. (2010). Characterizing generic global rigidity. American Journal of Mathematics, 132(4), 897–939.
Gramacho, W., Gonçalves, D., Mucherino, A., & Maculan, N. (2013). A new algorithm to finding discretizable orderings for distance geometry. In Proceedings of distance geometry and applications (DGA13) (pp. 149–152). Manaus, Amazonas, Brazil.
Gramacho, W., Mucherino, A., Lavor, C., & Maculan, N. (2012). A parallel bp algorithm for the discretizable distance geometry problem. In In IEEE conference proceedings, workshop on parallel computing and optimization (PCO12), 26th IEEE international parallel & distributed processing symposium (IPDPS12) (pp. 1756–1762). Shanghai, China.
Graver, J., Servatius, B., & Servatius, H. (1993). Combinatorial rigidity, graduate studies in mathematics (Vol. 2). American Mathematical Society.
Guerry, P., & Herrmann, T. (2011). Advances in automated NMR protein structure determination. Quarterly Reviews of Biophysics, 44(3), 257–309.
Gujarathi, S. (2014). Ab initio nanostructure determination. Ph.D. thesis, Michigan State University.
Gujarathi, S. R., Farrow, C. L., Glosser, C., Granlund, L., & Duxbury, P. M. (2014). Ab-initio reconstruction of complex Euclidean networks in two dimensions. Physical Review, 89, 053311.
Havel, T. F., Kuntz, I. D., & Crippen, G. M. (1983). The theory and practice of distance geometry. Bulletin of Mathematical Biology, 45, 665–720.
Hendrickson, B. (1992). Conditions for unique graph realizations. SIAM Journal of Computing, 21, 65–84.
Hendrickson, B. (1995). The molecule problem: Exploiting structure in global optimization. SIAM Journal on Optimization, 5(4), 835–857.
Jackson, B., & Jordan, T. (2005). Connected rigidity matroids and unique realization graphs. Journal of Combinatorial Theory Series B, 94, 1–29.
Jacobs, D. J., & Hendrickson, B. (1997). An algorithm for two-dimensional rigidity percolation: The pebble game. Journal of Computational Physics, 137, 346–365.
Jacobs, D. J., & Thorpe, M. F. (1995). Generic rigidity percolation: The pebble game. Physical Review Letteers, 75(22), 4051–4054.
Jaganathan, K., & Hassibi, B. (2013). Reconstruction of integers from pairwise distances. In IEEE conference proceedings, international conference on acoustics, speech and signal processing (ICASSP13) (pp. 5974–5978). Vancouver (BC), Canada.
Jain, P. C., & Trigunayat, G. C. (1977). Resolution of ambiguities in Zhdanov notation: Actual examples of homometric structures. Acta Crystallographica, A33, 257–260.
Juhás, P., Cherba, D. M., Duxbury, P. M., Punch, W. F., & Billinge, S. J. L. (2006). Ab initio determination of solid-state nanostructure. Nature, 440(7084), 655–658.
Juhás, P., Granlund, L., Duxbury, P. M., Punch, W. F., & Billinge, S. J. L. (2008). The LIGA algorithm for ab initio determination of nanostructure. Acta Crystallographica. Section A, Foundations of crystallography, 64(Pt 6), 631–640.
Juhas, P., Granlund, L., Gujarathi, S. R., Duxbury, P. M., & Billinge, S. J. L. (2010). Crystal structure solution from experimentally determined atomic pair distribution functions. Journal of Applied Crystallography, 43, 623–629.
Laman, G. (1970). On graphs and rigidity of plane skeletal structures. Journal of Engineering Mathematics, 4, 331–340.
Lavor, C., Alves, R., Figueiredo, W., Petraglia, A., & Maculan, N. (2015). Clifford algebra and the discretizable molecular distance geometry problem. Advances in Applied Clifford Algebras, 25, 925–942.
Lavor, C., Lee, J., Lee-St.John, A., Liberti, L., Mucherino, A., & Sviridenko, M. (2012). Discretization orders for distance geometry problems. Optimization Letters, 6(4), 783–796.
Lavor, C., Liberti, L., Donald, B., Worley, B., Bardiaux, B., Malliavin, T., & Nilges, M. (2018). Minimal NMR distance information for rigidity of protein graphs. Discrete Applied Mathematics. https://doi.org/10.1016/j.dam.2018.03.071.
Lavor, C., Liberti, L., Lodwick, W., & Mendonça da Costa, T. (2017). An introduction to distance geometry applied to molecular geometry. Number 54 pages in springerbriefs in computer science. New York: Springer.
Lavor, C., Liberti, L., Maculan, N., & Mucherino, A. (2012a). The discretizable molecular distance geometry problem. Computational Optimization and Applications, 52, 115–146.
Lavor, C., Liberti, L., Maculan, N., & Mucherino, A. (2012b). Recent advances on the discretizable molecular distance geometry problem. European Journal of Operational Research, 219, 698–706.
Lavor, C., Liberti, L., & Mucherino, A. (2013). The interval BP algorithm for the discretizable molecular distance geometry problem with interval data. Journal of Global Optimization, 56, 855–871.
Lavor, C., Mucherino, A., Liberti, L., & Maculan, N. (2011). On the computation of protein backbones by using artificial backbones of hydrogens. Journal of Global Optimization, 50, 329–344.
Lavor, C., Xambo-Descamps, S., & Zaplana, I. (2018). A geometric algebra invitation to space-time physics, robotics and molecular geometry. Number 130 pages in springerbriefs in mathematics. New York: Springer.
Liberti, L., & Lavor, C. (2016). Six mathematical gems from the history of distance geometry. International Transactions in Operational Research, 23, 897–920.
Liberti, L., & Lavor, C. (2017). Euclidean distance geometry (p. 133). Berlin: Springer.
Liberti, L., & Lavor, C. (2018). Open research areas in distance geometry. In A. Migdalas & P. Pardalos (Eds.), Open problems in mathematics, optimization and data science. Berlin: Springer.
Liberti, L., Lavor, C., Alencar, J., & Resende, G. (2013). Counting the number of solutions of \(^{K}\)dmdgp instances. Lecture Notes in Computer Science, 8085, 224–230.
Liberti, L., Lavor, C., & Maculan, N. (2008). A branch-and-prune algorithm for the molecular distance geometry problem. International Transactions in Operational Research, 15, 1–17.
Liberti, L., Lavor, C., Maculan, N., & Mucherino, A. (2014). Euclidean distance geometry and applications. SIAM Review, 56(1), 3–69.
Liberti, L., Lavor, C., Mucherino, A., & Maculan, N. (2010). Molecular distance geometry methods: From continuous to discrete. International Transactions in Operational Research, 18(1), 33–51.
Liberti, L., Masson, B., Lee, J., Lavor, C., & Mucherino, A. (2011). On the number of solutions of the discretizable molecular distance geometry problem. In Wang, W., Zhu, X., & Du, D-Z. (eds), Proceedings of the 5th annual international conference on combinatorial optimization and applications (COCOA11). Lecture notes in computer science (Vol. 6831, pp. 322–342). Zhangjiajie, China.
Liberti, L., Masson, B., Lee, J., Lavor, C., & Mucherino, A. (2014). On the number of realizations of certain Henneberg graphs arising in protein conformation. Discrete Applied Mathematics, 165, 213–232.
Maioli, D., Lavor, C., & Gonçalves, D. (2017). A note on computing the intersection of spheres in \(\mathbb{R}^{n}\). ANZIAM Journal, 59, 271–279.
Malliavin, T. E., Mucherino, A., & Nilges, M. (2013). Distance geometry in structural biology: New perspectives. In A. Mucherino et al. (Eds.), (Vol. 102, pp. 329–350). Springer.
McGreevy, R. L., & Pusztai, L. (1988). Reverse Monte Carlo simulation: A new technique for the determination of disordered structures. Molecular Simulation, 1, 359–367.
Moreira, N., Duarte, L., Lavor, C., & Torezzan, C. (2018). A novel low-rank matrix completion approach to estimate missing entries in Euclidean distance matrix. Computational and Applied Mathematics. https://doi.org/10.1007/s40314-018-0613-7.
Moukarzel, C. (1996). An efficient algorithm for testing the generic rigidity of graphs in the plane. Journal of Physics A: Mathematical and General, 29, 8079–8098.
Moukarzel, C., & Duxbury, P. M. (1995). Stressed backbone and elasticity of random central-force system. Physical Review Letters, 75(22), 4055–4058.
Mucherino, A. (2013). On the identification of discretization orders for distance geometry with intervals. Lecture notes in computer science. In Nielsen, F., & Barbaresco, F. (Eds.), Proceedings of geometric science of information (GSI13), Paris, France (Vol. 8085, pp 231–238).
Mucherino, A. (2015a). Optimal discretization orders for distance geometry: a theoretical standpoint. In Lecture notes in computer science, proceedings of the 10th international conference on large-scale scientific computations (LSSC15) (pp. 234–242), Sozopol, Bulgaria.
Mucherino, A. (2015b). A pseudo de bruijn graph representation for discretization orders for distance geometry. Lecture notes in computer science. Lecture notes in bioinformatics series. In Ortuño, F., & Rojas, I. (Eds.), Proceedings of the 3rd international work-conference on bioinformatics and biomedical engineering (IWBBIO15), Granada, Spain (Vol. 9043, pp. 514–523).
Mucherino, A. (2018). On the exact solution of the distance geometry with interval distances in dimension 1. In Fidanova, S. (Ed), Recent advances in computational optimization, studies in computational intelligence (Vol. 717, pp. 123–134).
Mucherino, A., de Freitas, R., & Lavor, C. (2015). Distance geometry and applications. Special Issue of Discrete Applied Mathematics, 197, 1–144.
Mucherino, A., Lavor, C., & Liberti, L. (2011). A symmetry-driven bp algorithm for the discretizable molecular distance geometry problem. In IEEE conference proceedings, computational structural bioinformatics workshop (CSBW11), international conference on bioinformatics & biomedicine (BIBM11) (pp. 390–395). Atlanta, GA, USA.
Mucherino, A., Lavor, C., & Liberti, L. (2012a). The discretizable distance geometry problem. Optimization Letters, 6, 1671–1686.
Mucherino, A., Lavor, C., & Liberti, L. (2012b). Exploiting symmetry properties of the discretizable molecular distance geometry problem. Journal of Bioinformatics and Computational Biology, 10(3), 1242009.
Mucherino, A., Lavor, C., Liberti, L., & Maculan, N. (2012). On the discretization of distance geometry problems. In ITHEA conference proceedings, mathematics of distances and applications 2012 (MDA12) (pp. 160–168). Varna, Bulgaria.
Mucherino, A., Lavor, C., Liberti, L., & Maculan, N. (Eds.). (2013). Distance geometry: Theory, methods, and applications. New York: Springer.
Mucherino, A., Lavor, C., Liberti, L., & Talbi, E. -G. (2010). A parallel version of the branch & prune algorithm for the molecular distance geometry problem. In IEEE conference proceedings, ACS/IEEE international conference on computer systems and applications (AICCSA10) (pp. 1–6). Hammamet, Tunisia.
Mucherino, A., Lavor, C., Malliavin, T., Liberti, L., Nilges, M., & Maculan, N. (2011). Influence of pruning devices on the solution of molecular distance geometry problems. Lecture notes in computer science. In Pardalos, P. M., & Rebennack, S. (Eds.), Proceedings of the 10th international symposium on experimental algorithms (SEA11), Crete, Greece (Vol. 6630, pp. 206–217).
Nilges, M., & O’Donoghue, S. I. (1998). Ambiguous NOEs and automated NOE assignment. Progress in Nuclear Magnetic Resonance Spectroscopy, 32(2), 107–139.
Patterson, A. L. (1934). A fourier series method for the determination of the components of interatomic distances in crystals. Physical Review, 46(5), 372–376.
Patterson, A. L. (1944). Ambiguities in the x-ray analysis of crystal structures. Physical Review, 65, 195–201.
Rader, A. J., Hespenheide, B. M., Kuhn, L. A., & Thorpe, M. F. (2002). Protein unfolding: Rigidity lost. PNAS, 99, 3540–3545.
Rossmann, M. G., & Arnold, E. (2006). Patterson and molecular replacement techniques. International Tables for Crystallography, B, 235–263.
Sallaume, S., Martins, S., Ochi, L., Gramacho, W., Lavor, C., & Liberti, L. (2013). A discrete search algorithm for finding the structure of protein backbones and side chains. International Journal of Bioinformatics Research and Applications, 9, 261–270.
Santiago, C., Lavor, C., Monteiro, S., & Kroner-Martins, A. (2018). A new algorithm for the small-field astrometric point-pattern matching problem. Journal of Global Optimization. https://doi.org/10.1007/s10898-018-0653-y.
Saxe, J. (1979). Embeddability of weighted graphs in k-space is strongly NP-hard. Conference in Communications Control and Computing (pp. 480–489).
Schneider, M. N., Seibald, M., Lagally, P., & Oeckler, O. (2010). Ambiguities in the structure determination of antimony tellurides arising from almost homometric structure models and stacking disorder. Journal of Applied Crystallography, 43, 1011–1020.
Senechal, M. (2008). A point set puzzle revisited. European Journal of Combinatorics, 29, 1933–1944.
Sippl, M. J., & Scheraga, H. A. (1986). Cayley-menger coordinates. Proceedings of the National Academy of Sciences of the United States (PNAS), 83, 2283–2287.
Sivia, D. S. (2011). Elementary scattering theory. Oxford: Oxford University Press.
Skiena, S., Smith, W., & Lemke, P. (1990). Reconstructing sets from interpoint distances. In Sixth ACM symposium on computational geometry (pp. 332–339).
Souza, M., Lavor, C., Muritiba, A., & Maculan, N. (2013). Solving the molecular distance geometry problem with inaccurate distance data. BMC Bioinformatics, 14, S71–S76.
Tay, T. S. (1984). Rigidity of multi-graphs I: Linking rigid bodies in n-space. Journal of Combinatorial Theory Series B, 36, 95–112.
Thompson, H. (1967). Calculation of cartesian coordinates and their derivatives from internal molecular coordinates. Journal of Chemical Physics, 47, 3407–3410.
Thorpe, M. F., & Duxbury, P. M. (Eds.). (1999). Rigidity theory and applications. New York: Springer.
Tucker, M. G., Keen, D. A., Dove, M. T., Goodwin, A. L., & Huie, Q. (2007). RMCProfile: Reverse Monte Carlo for polycrystalline materialss. Journal of Physics: Condensed Matter, 19, 335218.
Voller, Z., & Wu, Z. (2013). Distance geometry methods for protein structure determination. In A. Mucherino et al. (Eds.) (Vol. 102, pp. 139–159).
Wang, Z., Zheng, S., Ye, Y., & Boyd, S. (2008). Further relaxations of the semidefinite programming approach to sensor network localization. SIAM Journal on Optimization, 19(2), 655–673.
Worley, B., Delhommel, F., Cordier, F., Malliavin, T., Bardiaux, B., Wolff, N., Nilges, M., Lavor, C., & Liberti, L. (2018). Tuning interval branch-and-prune for protein structure determination. Journal of Global Optimization. https://doi.org/10.1007/s10898-018-0635-0.
Wu, D., & Wu, Z. (2007). An updated geometric build-up algorithm for solving the molecular distance geometry problems with sparse data. Journal of Global Optimization, 37, 661–672.
Wu, Y.-C., Chaudhari, Q., & Serpedin, E. (2011). Clock synchronization of wireless sensor networks. IEEE Signal Processing Magazine, 28(1), 124–138.
Wüthrich, K. (1986). NMR of proteins and nucleic acids (p. 320). New York: Wiley.
Wuthrich, K. (1989). The development of nuclear magnetic resonance spectroscopy as a technique for protein structure determination. Accounts of Chemical Research, 22(1), 36–44.
Zhang, H., & Hager, W. W. (2004). A nonmonotone line search technique and its applications to unconstrained optimization. SIAM Journal of Optimization, 14(4), 1043–1056.
Acknowledgements
The authors are thankful to the editors for their invitation to submit an updated version of our survey that was previously published in 2016 in the Quarterly Journal of Operations Research. We wish to thank FAPESP and CNPq for financial support. Support for work at Michigan State University by the MSU foundation is gratefully acknowledged. Collaborations with Pavol Juhas, Luke Granlund, Saurabh Gujarathi, Chris Farrow and Connor Glosser are much appreciated. PMD, CL and AM would like to thank Leo Liberti for interesting and motivating discussions. Work in the Billinge group was supported by the U.S. National Science Foundation through grant DMREF-1534910.
Author information
Authors and Affiliations
Corresponding author
Additional information
This is an updated version of the paper “Assigned and unassigned distance geometry: applications to biological molecules and nanostructures” that appeared in 4OR—Q J Oper Res (2016) 14: 337–376.
Rights and permissions
About this article
Cite this article
Billinge, S.J.L., Duxbury, P.M., Gonçalves, D.S. et al. Recent results on assigned and unassigned distance geometry with applications to protein molecules and nanostructures. Ann Oper Res 271, 161–203 (2018). https://doi.org/10.1007/s10479-018-2989-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-018-2989-6