Effect of two-echelon trade credit on pricing-inventory policy of non-instantaneous deteriorating products with probabilistic demand and deterioration functions

Abstract

Usually, the profit of companies will increase if they employ trade credit financing policy to encourage customer to purchase more. This paper develops a model for pricing and inventory control of non-instantaneous deteriorating items under two-echelon trade credit in which the vendor provides a credit period to the retailer and the retailer in turn offers a delay in payment to his/her customer. The price-dependent probabilistic demand function and partially backlogged shortages are adopted. Also, deterioration is shown by three different probability distribution function including (1) uniform distribution, (2) triangular distribution, and (3) beta distribution. The theoretical results are designed to determine the optimal selling price and the optimal inventory control variables so that the retailer’s total profit is maximized. Also, the necessary and sufficient conditions to prove the existence and uniqueness of the optimal solution are provided. Moreover, an algorithm is extended to describe the solution procedure. Numerical example, sensitivity analysis, and a simulation approach are presented to illustrate the performance of the algorithm and the theoretical results. Several managerial insights are also driven from computational results. The results indicate that the retailer’s total profit increases by considering the non-instantaneous deteriorating phenomenon and the trade credit policy.

1 Introduction

Deterioration of items is the process of decay, spoilage, damage, obsolescence, and loss of utility in such a way that the items are not in a condition of being used for its original purpose like as: medicine, fruits, vegetables, blood banks, volatile liquids (Wee 1993). For example, in the retail industry, shrinkage consisting of employee theft, executive mistakes, supplier deception, and shoplifting, leads to loss in inventory amounts to 1.7 % of annual sales, which equals to 31.3 billion dollars (Chen and Chen 2007). The deterioration affects the inventory system of retailers. I.e. the retailer has to order more items than the market demand because some of the items will be deteriorated. Moreover, some works have combined the inventory control problem of deteriorating items with pricing. The pricing policy is one of the most important factors to improve the net income and profit of companies (Fattahi et al. 2015a, b). For example, the net income of Philips would be improved by 28.7 %, if 1 % price realization improvement happened (Dolan and Simon 1996). In this paper, we present a pricing and inventory control problem for non-instantaneous deteriorating items which means items that maintain their original condition for a particular period. Therefore, deterioration does not occur for certain period of time, such as: Medicines, first hand vegetables, and fruits. Wu et al. (2006) defined this concept as “non-instantaneous deteriorating”. For these products, if the retailer assumes that the deterioration starts to occur as soon as the items are received, the retailer may adopt inappropriate inventory policy because of overvaluing the total relevant inventory cost. Therefore, the non-instantaneous deteriorating attribute plays an important role in the inventory control problem.

Moreover, we consider three following subjects in our study:

• 1. The probabilistic demand function $\xi _{1}R\left( p \right) +\xi _{2}$ is considered in which the distribution function of random variables $\xi _{1}$ and $\xi _{2}$ are deterministic and independent of time.

• 2. Three different probabilistic deterioration functions including uniform, beta, and triangular distribution have been considered to show the deterioration of the products.

• 3. In the traditional inventory control models, it is presumed that the retailer must pay to the vendor for the purchased goods as soon as the goods are received. Nowadays, promotional operations such as advertising and trade credit financing help the firms to increase sales and profits. To encourage the retailer to buy more, in practice, vendors allow a fixed period to settle the payment without interest for their customers which increases sales and decreases on-hand inventory of vendors. In fact, permissible delay in payment reduces the holding inventory cost because the amount of capital invested in inventory for the credit period is decreased. Moreover, before the end of the credit period, the retailer can sell the goods and accumulate revenue and earn interest. Thus, the permissible delay in payment policy has a significant role in business environment. Recently, some business use “two-echelon trade credit period” means the retailer that enjoy a delay period in payment by vendor, offers a fixed credit period to his/her customer. In this paper, we consider two-echelon trade credit period.

This paper develops a model for pricing and inventory control of non-instantaneous deteriorating item considering the probabilistic demand and deterioration function, and two-echelon trade credit. Shortages are accepted and partially backlogged in which the backlogging rate is variable and dependent on the waiting time for the next replenishment. We adopt the price-dependent probabilistic demand function. The major objective is to jointly determine selling price and variables of inventory control to maximize the retailer’s total profit. This paper contributes to the literature in the following aspects. First, we consider probabilistic demand function as $\xi _{1}R\left( p \right) +\xi _{2}$ in the problem of pricing and inventory control of non-instantaneous deteriorating items. Second, we formulate the problem based on the two- echelon trade credit period policy. Third, we apply three different probabilistic deterioration rates which illustrate the real condition better than the other works in this area.

The rest of the paper is structured as follows. Section 2 presents literature review. Section 3 defines assumptions and notations employed throughout the paper. Section 4 formulates the mathematical model. In this section, the required conditions to obtain an optimal solution are presented. Section 5 introduces a solution algorithm to solve the proposed model and to extract the optimal value of model’s variables. Section 6 solves a numerical example. Section 7 runs sensitivity analysis for model’s parameters and discusses some managerial insights. Also, some simulation results have been shown in this section. Finally, finding results and future research are provided in Sect. 8.

2 Literature review

Numerous researchers have studied the inventory control models of deteriorating commodities. As a pioneer researchers, Ghare and Schrader (1963) studied an exponentially deteriorating inventory model. Philip (1974) extended this model considering deterioration rate as a three parameters Weibull distribution. After that, many studies have worked on the deteriorating goods. Abad (1996,2001) studied pricing and inventory control policy for deteriorating products under variable rate of deterioration and partially backlogging shortages. Chang et al. (2006) presented an economic order quantity (EOQ) model for deteriorating items with partial backlogging and log-concave demand. Dye (2007) extended joint pricing and replenishment policy for deteriorating goods with price-dependent demand. Jaber et al. (2009) established a mathematical model for inventory policy of deteriorating items under minimizing entropy. Goyal and Giri (2001), Bakker et al. (2012), and Pahl and Voß (2014) have provided excellent review papers on deteriorating inventory problems.

Some papers consider the non-instantaneous deterioration products which starts with Wu et al. (2006). Chang et al. (2010) generalized Wu et al. (2006) with maximizing objective function, setting the maximum inventory level and establishing the theoretical results and solution algorithm. Shah et al. (2013) developed an inventory model for non-instantaneous deteriorating goods in which demand function depends on the advertising and the selling price. Maihami and Nakhai Kamalabadi (2012) studied the pricing and replenishment policy for non-instantaneous deteriorating items considering time and price dependent demand function. Ghoreishi et al. (2014) consider the optimal pricing and ordering policy for non-instantaneous deteriorating products with inflation and customer returns. Kapoor (2014) developed a model for non-instantaneous deteriorating items with price and time dependent demand. Valliathal and Uthayakumar (2011) considered the problem with shortages. Tat et al. (2015) consider the inventory control of non-instantaneous deteriorating products with vendor managed inventory (VMI) policy. Gupta et al. (2013) developed the problem by considering the stock-dependent demand. Geetha and Udayakumar (2015) extended a model for the problem of lot-sizing of the non-instantaneous deteriorating items with price and advertisement dependent demand. Palanivel and Uthayakumar (2015) extended Geetha and Udayakumar (2015) by assuming inflation. Tyagi et al. (2014) analyzed the replenishment policy of non-instantaneous deteriorating items with stock dependent demand and variable holding cost. Other works in this area are: Dye (2013), Valliathal and Uthayakumar (2013), Udayakumar and Geetha (2014), Singh and Rathore (2015), and Tayal et al. (2015).

Recently, to better illustrate the real condition, some researchers consider the stochastic subjects such as probabilistic demand and deterioration functions (Govindan and Fattahi 2015). Maihami and Karimi (2014) developed a model for pricing and inventory control of non-instantaneous deteriorating items under stochastic demand and promotional effort. Shah (1977) determined the inventory control policy of deteriorating goods with both exponential and Weibull distribution function. Other works that consider stochastic functions are as follows: Datta and Pal (1988), Hariga (1996), Federgruen and Heching (1999), Petruzzi and Dada (1999), Skouri and Papachristos (2003), Chen and Simchi-Levi (2004), Pang (2011), Sarkar (2012), Zhu (2012), Wang et al. (2013), Abdelsalam and Elassal (2014), Fattahi et al. (2015a, b), and Govindan (2015).

The delay in payment in the inventory model was first introduced by Haley and Higgins (1973). Goyal (1985) embedded delay in payment in a traditional Economic Order Quantity (EOQ) inventory model. Ouyang et al. (2006) considered delay in payments policy for non-instantaneous deteriorating items. Tsao and Sheen (2008) analyzed the problem of pricing and inventory control for deteriorating products with promotional effort and supplier’s trade credit. Geetha and Uthayakumar (2010) considered an EOQ inventory model for non-instantaneously deteriorating goods under partially backlogging shortages and credit period. Other important works in this area are: Hwang and Shinn (1997), Liao et al. (2000), Sarker et al. (2000), Chang et al. (2001), Chang (2004), Teng et al. (2005), and Maihami and Abadi (2012).

All the aforementioned papers assumed that the vendor would offer the retailer a delay period but the retailer would not offer the trade credit period to the customer. In some business, this assumption is not real. The customer who purchases the items enjoys a fixed credit period offered by his/her retailer. This policy called “two-echelons trade credit period”. Huang (2003) was the first researcher who considered the retailer will adopt the trade credit period to stimulate his/her customer demand. Chung and Huang (2007) modified Huang (2003) considering a two-warehouse inventory system. Liao et al. (2013) extended Chung and Huang (2007) analyzing situation that the rate of deteriorating in rented warehouse (RM) exceeds that of owned warehouse (OW). Min et al. (2010) presented an inventory policy for deteriorating goods under two-level trade credit period and stock-dependent demand. Urban (2012) extended model of Min et al. (2010) relaxing the boundary condition and constraining the maximum inventory level. Thangam (2012) determined the optimal price discounting and lot-sizing policy in a supply chain of perishable items with two-level trade credit and advanced payment scheme. Shah et al. (2013) studied the replenishment policy for deteriorating goods under stock sensitive demand, limited capacity and two-level trade credit. Chung et al. (2014) explored an EPQ inventory model for deteriorating items with two-level credit period in which the items are deteriorated over time and follow an exponential distribution. The comparative Table 1 shows the important attribute of the main papers in the related research area.

Based on Table 1, the main contribution of this paper are revealed. This study considers the optimal pricing and inventory control policy for non-instantaneous deteriorating products with two-echelon credit period and probabilistic demand and deterioration functions. The most relevant papers to our work are Maihami and Karimi (2014), Ghoreishi et al. (2014), Shah et al. (2013), and Sarkar (2012). Maihami and Karimi (2014) considered the problem of pricing and inventory control of non-instantaneous deteriorating products with probabilistic demand and promotional efforts. While, we consider two-echelon credit period and probabilistic deterioration rates. Also, we consider different probabilistic demand function. Ghoreishi et al. (2014) considered the problem with inflation and customer returns. They have not applied any stochastic subjects. Besides, the delay in payments policy has not been considered in their work. Shah et al. (2013) presented a model for non-instantaneous deteriorating items with generalized function for holding cost and deterioration without considering the probabilistic functions and delay in payments policy. Sarkar (2012) developed a model for deteriorating goods with delay in payments and time dependent functions for demand and deterioration. However, we consider non-instantaneous deteriorating products, price dependent probabilistic function, probabilistic deteriorating function, and two-echelon delay in payments policy which are different from Sarkar (2012).

Table 1 The important attributes of the main papers in the literature of this work

3 Notations and assumptions

Table 2 shows the notations are employed throughout the paper.

Table 2 Mathematical notations

Also, we use the following assumptions to formulate the proposed model.

• (1) The inventory system includes single non-instantaneous deteriorating item.

• (2) Replenishment rate is infinite and lead time is zero.

• (3) Shortages are allowed. We assume that only a fraction of demand is backlogged. Abad (1996) denoted this fraction as $\beta \left( t \right) =\frac{1}{1+\delta t}, (\delta \,>\,0)$, where t is the waiting time up to the next replenishment and backlogging parameter $\delta$ is a positive constant. It should be noted that if $\beta \left( t \right) =1$ (or 0) for all t, then the shortage is totally backlogged (or lost).

• (4) The demand rate $\xi _{1}R\left( p \right) +\xi _{2}$ includes following parts:

  • $R\left( p \right)$: a decreasing and deterministic linear function of the selling price p.

  • $\xi _{1}$ and $\xi _{2}$: non-negative and continuous random variables ($E\left( \xi _{1} \right) =\mu _{1}$ and $E\left( \xi _{2} \right) =\mu _{2})$ which they have a determined and time-independent distribution function.

• (5) Over the inventory cycle time, the parameters of demand rate are static.

• (6) Three continuous probability distribution functions including (a) uniform distribution, (b) triangular distribution, and (c) beta distribution has been considered.

• (7) The length of time in which there is no shortage is larger than or equal to the length of time in which the product exhibits no deterioration, i.e. ${t_{1}}>t_{d}$.

• (8) The fix credit period offered by the supplier to the retailer is equal or greater than that allowed by the retailer to his/her customers, i.e. $Y\ge Z$. If $Y \,< \,Z$, the retailer cannot earn any interest.

• (9) The length of credit period offered by the supplier to the retailer (Y) and the length of credit period offered by the retailer to the customer (Z) are greater than the length of time which the product exhibits no deterioration ($t_{d})$, i.e. $Y\ge t_{d}$ and $Z\ge t_{d}$.

• (10) The length of credit period offered by the supplier to the retailer (Y) and the length of credit period offered by the retailer to the customer (Z) are less than the length of period with positive inventory (${t_{1}})$, i.e. $Y\le {t_{1}}$ and $Z\le {t_{1}}$.

• (11) When $Y\le {t_{1}}$, the retailer pays for interest charges on goods in stock with rate $I_{p}$ over the interval $\left[ Y,{t_{1}} \right]$.

• (12) The retailer can earn interest from the time that his/her customer pays for the purchased items until the end of the credit period offered by the supplier. This period is from $t=Z$ to $t=Y$ with rate $I_{e}$ under the condition of trade credit.

4 Development of mathematical model

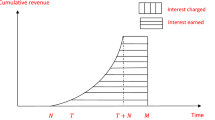
To develop the mathematical model, the following inventory system has been applied. At the beginning of each inventory cycle, Q units of products arrive at the system which are depleted to zero due to combined effects of demand and deterioration. Then, shortage occurs until the end of the order cycle. The whole process is repeated. Figure 1 depicts the considered inventory system.

Fig. 1

Schematic illustration of the inventory system

The inventory level is diminishing only due to demand during the time interval $\left[ {0,t}_{d} \right]$. Next, the inventory level is declining to zero owing to demand and deterioration over the time interval $\left[ t_{d}{,t}_{1} \right]$. Finally, during the time interval $\left[ {t_{1}},T \right]$ shortage happens due to demand function and partial backlogging.

During the time interval $\left[ {0,t}_{d} \right]$, the inventory status is governed by the following differential equation

$$\begin{aligned} \frac{dI_{1}(t)}{dt}=-\left( \xi _{1}R\left( p \right) +\xi _{2} \right) ,\quad 0\le t\le t_{d} \end{aligned}$$

(1)

With the boundary condition $I_{1}\left( 0 \right) =I_{0}$, the solution of Eq. (1) is

$$\begin{aligned} I_{1}\left( t \right) =-\left( \xi _{1}R(p)+\xi _{2} \right) +I_{0} ,\quad 0\le t\le t_{d} \end{aligned}$$

(2)

During the time interval $\left[ t_{d}{,t}_{1} \right]$, the inventory level reduces owing to demand rate as well as deterioration. Hence, the differential equation representing the inventory status is given by

$$\begin{aligned} \frac{dI_{2}(t)}{dt}+\theta I_{2}\left( t \right) =-\left( \xi _{1}R\left( p \right) +\xi _{2} \right) ,\quad t_{d}\le t\le {t_{1}} \end{aligned}$$

(3)

With the boundary condition $I_{2}\left( {t_{1}} \right) =0$, the solution of Eq. (3) is

$$\begin{aligned} I_{2}(t)=\frac{\left( \xi _{1}R\left( p \right) +\xi _{2} \right) }{\theta }\left[ e^{\theta \left( {t_{1}}-t \right) }-1 \right] ,\quad t_{d}\le t\le {t_{1}} \end{aligned}$$

(4)

Continuity of I(t) at ${t=t}_{d}$ implies that $I_{1}(t_{d} )=I_{2}(t_{d})$. Thus, the maximum inventory level for each cycle $I_{0}$ is

$$\begin{aligned} I_{0}=\frac{\left( \xi _{1}R\left( p \right) +\xi _{2} \right) }{\theta }\left[ e^{\theta \left( {t_{1}}-t \right) }-1 \right] +\left( \xi _{1}R\left( p \right) +\xi _{2} \right) t_{d} \end{aligned}$$

(5)

Substituting Eq. (5) in Eq. (2), yields

$$\begin{aligned} I_{1}(t)=\left( \xi _{1}R\left( p \right) +\xi _{2} \right) \left( \frac{e^{\theta \left( {t_{1}}-t_{d} \right) }-1}{\theta }+t_{d}-t \right) , \quad 0\le t\le t_{d} \end{aligned}$$

(6)

During the shortage interval $\left[ {t_{1}},T \right] ,$ the demand is partially backlogged according to the fraction $\beta (T-t)$. Therefore, the inventory level at time t is given by the following differential equation:

$$\begin{aligned} \frac{dI_{3}(t)}{dt}=-\left( \xi _{1}R\left( p \right) +\xi _{2} \right) \beta \left( T-t \right) =\frac{-\left( \xi _{1}R\left( p \right) +\xi _{2} \right) }{1+\delta \left( T-t \right) },\quad {t_{1}}\le t\le T \end{aligned}$$

(7)

With the boundary condition $\hbox {I}_{3}\left( \hbox {t} \right) =0$ , the solution for Eq. (7) is

$$\begin{aligned} \hbox {I}_{3}\left( \hbox {t} \right) =-\left( \frac{\left( \xi _{1}R\left( p \right) +\xi _{2} \right) }{\delta }\right) \{\ln {[1+\delta {(T-t}_{1})]}-\ln [1+\delta (T-t)]\} , \quad {t_{1}}\le t\le T \end{aligned}$$

(8)

By substituting $t=T$ into Eq. (8), the maximum amount of demand backlogging will be calculated as follows:

$$\begin{aligned} S=-\hbox {I}_{3}\left( \hbox {t} \right) =\left( \frac{\left( \xi _{1}R\left( p \right) +\xi _{2} \right) }{\delta }\right) \{\ln {[1+\delta {(T-t}_{1})]} \end{aligned}$$

(9)

The summation of S and $I_{0}$ forms the order quantity per cycle Q as follows:

$$\begin{aligned} Q=S+I_{0}= & {} \frac{\left( \xi _{1}R\left( p \right) +\xi _{2} \right) }{{\uptheta }}\left[ e^{\uptheta \left( \hbox {t}_{1}-t_{d} \right) }-1 \right] \nonumber \\&+\left( \xi _{1}R\left( p \right) +\xi _{2} \right) t_{d}+\left( \frac{\left( \xi _{1}R\left( p \right) +\xi _{2} \right) }{\delta } \right) \ln {[1+\delta {(T-t}_{1})]} \end{aligned}$$

(10)

In this study, we consider the deterioration function based on Sarkar (2013). It is assumed that the deterioration function $\uptheta$ follows three different types of probability distribution function as ${\uptheta =\hbox {E}}\left[ f(x) \right]$, where f(x) follows (1) uniform distribution, (2) triangular distribution, and (3) beta distribution. In the following, we compute the total profit for each deterioration function.

4.1 Case 1: uniform distribution

${\uptheta }$ is based on the uniform distribution as ${\uptheta =\hbox {E}}\left[ f(x) \right] =\frac{\alpha _{1}+\alpha _{2}}{2},\alpha _{1}{>}0,\alpha _{2}{>}0$, and $\alpha _{1}{<}\alpha _{2}$. Now, based on the obtained inventory levels, we can calculate the inventory costs and the sales revenue per inventory cycle, which are shown in Table 3.

Table 3 The inventory costs and the sales revenue per inventory cycle

The expected interest payable the account is settled at $t=Y$ and the retailer starts paying the capital opportunity cost for the items in inventory with rate $I_{p}$. Thus, the expected interest payable (opportunity cost per cycle) is as follows:

$$\begin{aligned}&\hbox {The expected interest payable}=E\left( cI_{p}\int _Y^{t_{1}} {I_{2}(t)dt} \right) \nonumber \\&\quad =\frac{cI_{p}\left( \xi _{1}R\left( p \right) +\xi _{2} \right) }{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left[ -\frac{1}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( 1-e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) } \right) -(\hbox {t}_{1}-Y) \right] \end{aligned}$$

(16)

The expected interest earned during the time interval $\left[ Z,Y \right]$, the retailer sells the goods and earns the interest with rate $I_{e}$. Thus, the expected interest earned per cycle is as follows:

$$\begin{aligned} \hbox {The expexted interest earned}= & {} E\left( pI_{e}\int _Z^Y {\left( \xi _{1}R\left( p \right) +\xi _{2} \right) tdt} \right) \nonumber \\= & {} pI_{e}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left( \frac{Y^{2}-Z^{2}}{2} \right) \end{aligned}$$

(17)

Thus, the retailer’s total profit ${\textit{TP}}_{1}\left( p, {{t_{1}}},T \right)$ is determined by the following equation:

$$\begin{aligned} {\textit{TP}}_{1}\left( p, {{t_{1}}},T \right)= & {} \left( \frac{1}{T} \right) \times \left( \hbox {expected sales revenue}-\hbox {constant ordering cost}\right. \nonumber \\&-\,\hbox {expected holding cost} -\hbox {expected backorder cost}\nonumber \\&-\,\hbox {expected lost sale cost}-\hbox {expected purchasing cost}\nonumber \\&\left. +\,\hbox {expexted interest earned}-\hbox {expected interest payable} \right) \nonumber \\= & {} \frac{1}{T}\left[ \left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left\{ \left( \mathrm{p}-\mathrm{c}+\frac{s+\delta o}{\delta } \right) \left[ {{t_{1}}}+\frac{\ln \left[ 1+\delta \left( T-{{t_{1}}} \right) \right] }{\delta } \right] \right. \right. \nonumber \\&-\,\frac{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( c+ht_{d} \right) +h}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) ^{2}}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) -1 \right] \nonumber \\&\left. -\,ht_{d}{{t_{1}}}+\frac{ht_{d}^{2}}{2}-\frac{\left( s+\delta o \right) }{\delta }T-\frac{A}{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) } \right\} \nonumber \\&-\,\frac{cI_{p}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left[ -\frac{1}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( 1-e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) } \right) -\left( \hbox {t}_{1}-Y \right) \right] \nonumber \\&\left. +\,pI_{e}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left( \frac{Y^{2}-Z^{2}}{2} \right) \right] \end{aligned}$$

(18)

4.2 Case 2: triangular distribution

In this case, ${\uptheta }$ is based on the triangular distribution as $\uptheta =\hbox {E}\left[ f(x) \right] =\frac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{3}$. Where f(x) is a continuous probability distribution with lower limit $\alpha _{1}$, upper limit $\alpha _{2}$, and mode $\alpha _{3}$, where $\alpha _{1}{<}\alpha _{2}$ and $\alpha _{1}\le \alpha _{3}\le \alpha _{2}$. By the same computations as Case 1, the total profit for case 2 is

$$\begin{aligned}&{\textit{TP}}_{2}\left( p, {{t_{1}}},T \right) =\frac{1}{T}\left[ \left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left\{ \left( p-c+\frac{s+\delta o}{\delta } \right) \left[ {{t_{1}}}+\frac{\ln \left[ 1+\delta \left( T-{{t_{1}}} \right) \right] }{\delta } \right] \right. \right. \nonumber \\&\quad \quad \quad \left. -\,\frac{\left( \frac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{2} \right) \left( c+ht_{d} \right) +h}{\left( \frac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{2} \right) ^{2}}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-\left( \frac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{2} \right) \left( {{t_{1}}}-t_{d} \right) -1 \right] \right. \nonumber \\&\quad \quad \quad \left. -\,ht_{d}{{t_{1}}}+\frac{ht_{d}^{2}}{2}-\frac{\left( s+\delta o \right) }{\delta }T-\frac{A}{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) } \right\} \nonumber \\&\quad \quad \quad -\,\frac{cI_{p}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{\left( \frac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{2} \right) }\left[ -\frac{1}{\left( \frac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{2} \right) }\left( 1-e^{\left( \frac{\alpha _{1}+\alpha _{2}+\alpha _{3}}{2} \right) \left( \hbox {t}_{1}-Y \right) } \right) -\left( \hbox {t}_{1}-Y \right) \right] \nonumber \\&\quad \quad \quad \left. +\,pI_{e}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left( \frac{Y^{2}-Z^{2}}{2} \right) \right] \end{aligned}$$

(19)

4.3 Case 3: beta distribution

In the case 3, ${\uptheta }$ follows beta distribution as $\uptheta =\hbox {E}\left[ f(x) \right] =\frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}}$. Where f(x) is a continuous probability distribution on the interval (0, 1) and $\alpha _{1}{>}0$, $\alpha _{2}{>}0$. By the same computations as Case 1, the total profit for case 3 is

$$\begin{aligned}&{\textit{TP}}_{3}\left( p, {{t_{1}}},T \right) =\frac{1}{T}\left[ \left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left\{ \left( p-c+\frac{s+\delta o}{\delta } \right) \left[ {{t_{1}}}+\frac{\ln \left[ 1+\delta \left( T-{{t_{1}}} \right) \right] }{\delta } \right] \right. \right. \nonumber \\&\quad \quad \quad -\,\frac{\left( \frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}} \right) \left( c+ht_{d} \right) +h}{\left( \frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}} \right) ^{2}}\left[ e^{\left( \frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}} \right) \left( {{t_{1}}}-t_{d} \right) }-\left( \frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}} \right) \left( {{t_{1}}}-t_{d} \right) -1 \right] \nonumber \\&\quad \quad \quad \left. -\,ht_{d}{{t_{1}}}+\frac{ht_{d}^{2}}{2}-\frac{\left( s+\delta o \right) }{\delta }T-\frac{A}{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) } \right\} \nonumber \\&\quad \quad \quad -\,\frac{cI_{p}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{\left( \frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}} \right) }\left[ -\frac{1}{\left( \frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}} \right) }\left( 1-e^{\left( \frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}} \right) \left( \hbox {t}_{1}-Y \right) } \right) -\left( \hbox {t}_{1}-Y \right) \right] \nonumber \\&\quad \quad \quad \left. +\,pI_{e}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left( \frac{Y^{2}-Z^{2}}{2} \right) \right] \end{aligned}$$

(20)

4.4 Theoretical analysis

In this section, our main objective is to compute optimal solution for $\left( p, {{t_{1}}},T \right)$ such that the total profit for each case is maximized. In the following, we present some theoretical results to obtain the optimal solutions. It should be noted that we obtain the results for case 1 (uniform distribution for deterioration). The procedure to obtain the optimal solution for case 2 and 3 is similar to case 1.

For any given p, to maximize the ${\textit{TP}}_{1}\left( p, {{t_{1}}},T \right)$, it is necessary to solve $\frac{{\textit{TP}}_{1}\left( p, {{t_{1}}},T \right) }{\partial {{t_{1}}}}=0$ and $\frac{{\textit{TP}}_{1}\left( p, {{t_{1}}},T \right) }{\partial T}=0$, simultaneously. That is,

$$\begin{aligned} \frac{\partial {\textit{TP}}_{1}\left( p, {{t_{1}}},T \right) }{\partial {{t_{1}}}}= & {} \frac{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{\hbox {T}}\left\{ \left( {\hbox {p}}-{\hbox {c}}+\frac{\left( \hbox {s}+\updelta \hbox {o} \right) }{{\updelta }} \right) \left[ \frac{{\updelta }\left( \hbox {T}-\hbox {t}_{1} \right) }{{1+\updelta }\left( \hbox {T}-\hbox {t}_{1} \right) } \right] \right. \nonumber \\&-\,\frac{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {c+h}\hbox {t}_{\mathrm{d}} \right) +\hbox {h}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left[ \hbox {e}^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) }-1 \right] \nonumber \\&\left. -\,\hbox {h}\hbox {t}_{\mathrm{d}}-\left( \frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right) \right\} {=0} \end{aligned}$$

(21)

$$\begin{aligned} \frac{\partial {\textit{TP}}_{1}\left( p, {{t_{1}}},T \right) }{\partial T}= & {} \frac{1}{\hbox {T}^{2}}\left[ \left\{ \left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left( {\hbox {p}}-{\hbox {c}}+\frac{\hbox {s}+\updelta \hbox {o}}{{\updelta }} \right) \right. \right. \nonumber \\&\left. \times \,\left[ \frac{\hbox {T}}{{1+\updelta }\left( \hbox {T}-\hbox {t}_{1} \right) }\right. -\hbox {t}_{1}-\frac{\hbox {ln}\left[ 1+\updelta \right. (\hbox {T}-\hbox {t}_{1})}{{\updelta }} \right] \nonumber \\&\left. +\,\frac{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {c+h}\hbox {t}_{\mathrm{d}} \right) +\hbox {h}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) ^{2}}\times \left[ \hbox {e}^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) }-\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) -1 \right] \right. \nonumber \\&\left. +\,\hbox {h}\hbox {t}_{\mathrm{d}}\hbox {t}_{1}-\frac{\hbox {h}\hbox {t}_{\mathrm{d}}^{2}}{2}+\frac{\hbox {A}}{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) } \right\} -\frac{1}{2}I_{e}p\left( \mu _{1}R\left( p \right) +\mu _{2} \right) (Y^{2}-Z^{2})\nonumber \\&\left. +\frac{cI_{p}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) (-\hbox {t1}+Y-\frac{1-e^{(\hbox {t1}-Y)\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) })}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } \right] {=0} \end{aligned}$$

(22)

For notational convenience, let

$$\begin{aligned} N\equiv \frac{\left( \frac{\alpha _{1}+\alpha _{2}}{2}\right) (c+ht_{d})+h}{\left( \frac{\alpha _{1}+\alpha _{2}}{2}\right) }>0, \quad M\equiv \frac{s+\delta _{o}}{\delta }>0 \end{aligned}$$

Then, Eqs. (21) and (22) become

$$\begin{aligned}&\hbox {T}= \hbox {t}_{1}+\frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right\} } \nonumber \\\end{aligned}$$

(23)

$$\begin{aligned}&\quad \quad \quad \left\{ \left( {\hbox {p}}-{\hbox {c}}+{\hbox {M}} \right) \left[ \frac{\hbox {T}}{1+\updelta \left( \hbox {T}-\hbox {t}_{1} \right) }-\hbox {t}_{1}-\frac{\hbox {ln}[1+\updelta (\hbox {T}-\hbox {t}_{1})}{{\updelta }} \right] +\frac{\hbox {N}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right. \nonumber \\&\quad \quad \quad \times \,\left[ \hbox {e}^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) }-\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) -\hbox {1} \right] \nonumber \\&\quad \quad \quad +\,\hbox {h}\hbox {t}_{\mathrm{d}}\hbox {t}_{1}-\frac{\hbox {h}\hbox {t}_{\mathrm{d}}^{2}}{2}+\frac{\hbox {A}}{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }-\frac{1}{2}I_{e}p\left( \mu _{1}R\left( p \right) +\mu _{2} \right) (Y^{2}-Z^{2})\nonumber \\&\quad \quad \quad \left. +\frac{cI_{p}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left( -\hbox {t1}+Y-\frac{1-e^{(\hbox {t1}-Y)\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) }{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } \right\} =0 \end{aligned}$$

(24)

We have $T>{{t_{1}}}$. Thus, from Eq. (23), it can be obtained

$$\begin{aligned} \frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\theta }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{\updelta \left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d}\right\} +\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }>0 \end{aligned}$$

Because $\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) >0$, we conclude that

$$\begin{aligned} {\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d} \right\} +\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) >0 \end{aligned}$$

which gives:

$$\begin{aligned} {{t_{1}}}{<}\left( 1\big /\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \hbox {ln}\left( \frac{p-c+M+N-ht_{d}-\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) {\updelta }}}{\frac{N}{e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) t_{d}}}-\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) {\updelta }e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) Y}}} \right) \equiv \hbox {t}_{1}^{\hbox {b}} \end{aligned}$$

Substituting Eq. (23) into Eq. (24), we obtain

$$\begin{aligned}&\left\{ \left( \hbox {p}-\hbox {c}+\hbox {M} \right) \left[ \frac{\hbox {t}_{1}+\frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right\} }}{1+\updelta \left( \hbox {t}_{1}+\frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right\} }-\hbox {t}_{1} \right) }\right. \right. \nonumber \\&\quad \quad \quad \left. -\hbox {t}_{1}-\frac{\hbox {ln}[1+\updelta (\hbox {t}_{1}+\frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right\} }-\hbox {t}_{1})}{{\updelta }} \right] \nonumber \\&\quad \quad \quad +\frac{\hbox {N}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\times \left[ \hbox {e}^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) }-\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) -1 \right] +\hbox {h}\hbox {t}_{\mathrm{d}}\hbox {t}_{1}\nonumber \\&\quad \quad \quad -\frac{\hbox {h}\hbox {t}_{\mathrm{d}}^{2}}{2}+\frac{\hbox {A}}{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }-\frac{1}{2}I_{e}p\left( \mu _{1}R\left( p \right) +\mu _{2} \right) (Y^{2}-Z^{2})\nonumber \\&\quad \quad \quad \left. +\frac{cI_{p}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) (-\hbox {t1}+Y-\frac{1-e^{(\hbox {t1}-Y)\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) })}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } \right\} =0 \end{aligned}$$

(25)

Next, to obtain ${{t_{1}}}\in \left[ t_{d},t_{1}^{b} \right)$, which satisfies (25), let

$$\begin{aligned} \hbox {F}\left( {{t_{1}}} \right)= & {} \left\{ \left( \hbox {p}-\hbox {c}+\hbox {M} \right) \left[ \frac{\hbox {t}_{1}+\frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right\} }}{{1+\updelta }\left( \hbox {t}_{1}+\frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right\} }-\hbox {t}_{1} \right) }\right. \right. \nonumber \\&\left. -\,\hbox {t}_{1}-\frac{\hbox {ln}[1+\updelta (\hbox {t}_{1}+\frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right\} }-\hbox {t}_{1})}{{\updelta }} \right] \nonumber \\&+\,\frac{\hbox {N}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }{\times }\left[ \hbox {e}^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) }-\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) -\hbox {1} \right] +\hbox {h}\hbox {t}_{\mathrm{d}}\hbox {t}_{1}\nonumber \\&-\,\frac{\hbox {h}\hbox {t}_{\mathrm{d}}^{2}}{2}+\frac{\hbox {A}}{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }-\frac{1}{2}I_{e}p\left( \mu _{1}R\left( p \right) +\mu _{2} \right) (Y^{2}-Z^{2})\nonumber \\&\quad \left. +\,\frac{cI_{p}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) (-\hbox {t1}+Y-\frac{1-e^{(\hbox {t1}-Y)\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) })}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } \right\} =0 \end{aligned}$$

(26)

We take the first-order derivative $\hbox {F}\left( {{t_{1}}} \right)$ with respect to ${{t_{1}}}$, which gives

$$\begin{aligned}&\frac{dF\left( {{t_{1}}} \right) }{d{{t_{1}}}}=\left( -1+e^{\left( \hbox {t}_{1}-\hbox {t}_{d} \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) N+h\hbox {t}_{d}+\frac{c\left( -1+e^{\left( \hbox {t}_{1}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } \right) I_{p}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\\&\quad +\,\left( -c+M+p\right) \left( -1-\left( e^{\left( \hbox {t}_{1}-\hbox {t}_{d}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) ^{2}\right. \right. \\&\quad \,\times \left( -\left( -\left( M+p\right) \hbox {t}_{1}\delta +\left( -1+e^{\left( \hbox {t}_{1}-\hbox {t}_{d} \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) \right. \right. \\&\left. \quad \times \,N\left( -1+\hbox {t}_{1}\delta \right) +h\hbox {t}_{d}\left( -1+\hbox {t}_{1}\delta \right) \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) +c\left( \left( -1+e^{\left( \hbox {t}_{1}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) I_{p}\left( 1+\hbox {t}_{1}\delta \right) \right. \\&\quad \left. \left. -\,\hbox {t}_{1}\delta \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) \left( -c^{2}e^{\hbox {t}_{d}\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }I_{p}+e^{Y\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N\left( M+p\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right. \\&\quad \left. \left. +\,c\left( e^{\hbox {t}_{d}\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }I_{p}\left( M+2N+p-2h\hbox {t}_{d}\right) -e^{Y\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N\left( 2I_{p}+\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) \right) \right) \\&\quad \big /\left( \delta \left( \left( M+N-e^{\left( \hbox {t}_{1}-\hbox {t}_{d} \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N+p-h\hbox {t}_{d}\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right. \right. \\&\quad \left. -\,c\left( I_{p}-e^{\left( \hbox {t}_{1}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }I_{p}+\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) \left( \left( M+p \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right. \\&\quad -\,c\left( -2\left( -1+e^{\left( \hbox {t}_{1}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } \right) I_{p}\right. \left. \left. \left. +\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) ^{2}\right) \\ \end{aligned}$$

$$\begin{aligned}&\quad +\left( e^{\left( \hbox {t}_{1}-\hbox {t}_{d}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) ^{2}\left( c^{2}e^{\hbox {t}_{d}\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }I_{p}-e^{Y\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N\left( M+p\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right. \right. \nonumber \\&\quad +\,c\left( -e^{\hbox {t}_{d}\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\hbox {IP}\left( M+2N+p-2h\hbox {td}\right) \right. \left. \left. \left. +\,e^{Y\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N\left( 2I_{p}+\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) \right) \right) \nonumber \\&\quad \big /\left( \delta \left( \left( M+N-e^{\left( \hbox {t}_{1}-\hbox {t}_{d} \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N+p-h\hbox {t}_{d}\right) \right. \right. \nonumber \\&\quad \times \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) -c\left( I_{p}-e^{\left( \hbox {t}_{1}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }I_{p}\left. \left. +\,\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) \right. \nonumber \\&\quad \left. \times \left( \left( M+p\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) -c\left( -2\left( -1+e^{\left( \hbox {t}_{1}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) I_{p}+\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) \right) \nonumber \\&+\left( \left( \left( M+N-e^{\left( \hbox {t}_{1}-\hbox {t}_{d} \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N+p-h\hbox {t}_{d}\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right. \right. \nonumber \\&\left. -\,c\left( I_{p}-e^{\left( \hbox {t}_{1}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }I_{p}+\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) \nonumber \\&\quad \left( 1+\frac{ce^{\left( \hbox {t}_{1}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }I_{p}+e^{\left( \hbox {t}_{1}-\hbox {t}_{d} \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }{\delta \left( -c+M+N-e^{\left( \hbox {t}_{1}-\hbox {t}_{d} \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } N+p-h\hbox {t}_{d}+\frac{c\left( -1+e^{\left( \hbox {t}_{1}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } \right) I_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } \right) }\right. \nonumber \\&\quad +\left( \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( -ce^{\left( \hbox {t}_{1}-Y \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }I_{p}+e^{\left( \hbox {t}_{1}-\hbox {t}_{d} \right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right. \nonumber \\&\quad \times \left( c\left( -1+e^{\left( \hbox {t}_{1}-Y\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) I_{p}\right. \left. \left. +\left( \left( -1+e^{\left( \hbox {t}_{1}-\hbox {t}_{d}\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) +h\hbox {t}_{d}\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) \nonumber \\&\quad \big /\left( \delta \left( \left( M+N-e^{\left( \hbox {t}_{1}-\hbox {t}_{d}\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N+p-h\hbox {t}_{d}\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right. \right. \nonumber \\&\left. \left. \left. \left. -c\left( I_{p}-e^{\left( \hbox {t}_{1}-Y\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }I_{p}+\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) ^{2}\right) \right) \right) \bigg /\left( \left( M+p\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right. \nonumber \\&\left. \left. -c\left( -2\left( -1+e^{\left( \hbox {t}_{1}-Y\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) I_{p}+\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) \right) \right) \end{aligned}$$

(27)

Due to high complexity of $\frac{dF\left( {{t_{1}}} \right) }{d{{t_{1}}}}$, it is unlikely to prove the negativity of $\frac{dF\left( {{t_{1}}} \right) }{d{{t_{1}}}}$ analytically. However, we numerically observe that $\frac{dF\left( {{t_{1}}} \right) }{d{{t_{1}}}}<0$. Thus, $F\left( {{t_{1}}} \right)$is a strictly decreasing function with respect to ${{t_{1}}}$ in the interval $\left[ t_{d},t_{1}^{b} \right) \, \hbox {andlim}_{t_{1}\rightarrow t_{1}^{b}} {F\left( {{t_{1}}} \right) =-\infty }$. Let

$$\begin{aligned} \Phi \left( p \right) \equiv F\left( t_{d} \right)= & {} \left( \hbox {p}-\hbox {c}+\hbox {M} \right) \left( \frac{t_{d}+\frac{ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) \right\} }}{{1+\updelta }\left( \frac{+ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) \right\} } \right) }-t_{d}\right. \nonumber \\&\quad \left. -\frac{\hbox {ln}[1+\updelta \left( \frac{ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) \right\} } \right] }{{\updelta }}\right) +\frac{\hbox {h}\hbox {t}_{\mathrm{d}}^{2}}{2}\nonumber \\&\quad +\frac{\hbox {A}}{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }-\frac{1}{2}I_{e}p\left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left( Y^{2}-Z^{2}\right) \nonumber \\&\quad +\frac{cI_{p}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left( -t_{d}+Y-\frac{1-e^{\left( t_{d}-Y\right) \left( \mu _{1}R\left( p \right) +\mu _{2} \right) }}{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }\right) }{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) } \end{aligned}$$

(28)

which gives the following results:

Theorem 1

for any given p,

• (a) If $\Phi \left( p \right) \ge 0$, then there is a unique solution of ${\hbox {(t}}_{1}\hbox {,T)}$ which satisfies Eqs. (21) and (22).

• (b) If $\Phi \left( p \right) <0$, then there is not solution of ${\hbox {(t}}_{1}\hbox {,T)}$ which satisfies Eqs. (21) and (22).

Proof

see Appendix 1 for details. $\square$

Theorem 2

for any given p,

• (a) If ${\Phi }\left( p \right) \ge 0$, then $TP(p,{{t_{1}}},T)$ is concave and reaches its global maximum at the point $\left( {{t_{1}}},T \right) =(t_{1}^{*},T^{*})$, which $(t_{1}^{*},T^{*})$ is the optimal solution of Eqs. (21) and (22).

• (b) If ${\Phi }\left( p \right) <0$, then ${\textit{TP}}_{1}(p,{{t_{1}}},T)$ has a maximum value at the point of $\left( {{t_{1}}},T \right) =(t_{1}^{*},T^{*})$, which

  $$\begin{aligned} t_{1}^{*}=t_{d} \hbox { and } T^{*}=t_{d}+\frac{ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-{\hbox {c}}+{\hbox {M}}-ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) \right\} } \end{aligned}$$

Proof

see Appendix 2 for details. $\square$

Now, we should identify the conditions which for any $t_{1}^{*}$ and $T^{*}$, there would be a unique optimal selling price. ${\textit{TP}}_{1}(p,t_{1}^{*},T^{*})$ is a function of p. Thus, the necessary condition to maximize ${{\textit{TP}}_{1}(p,t}_{1}^{*},T^{*})$ is $\frac{\partial {\textit{TP}}_{1}(p,t_{1}^{*},T^{*})}{\partial p}=0$, which gives

$$\begin{aligned}&\frac{\partial {\textit{TP}}_{1}(p,t_{1}^{*},T^{*})}{\partial p}=\frac{\mu _{1}R^{'}(p) }{T^{*}}\left\{ \left( p-c+M \right) \left[ t_{1}^{*}+\frac{ln\left[ 1+\delta \left( T^{*}-t_{1}^{*} \right) \right] }{\delta } \right] -\frac{N}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right. \nonumber \\&\quad \times \left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{1}^{*}-t_{d} \right) }-\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{1}^{*}-t_{d} \right) -1 \right] \nonumber \\&\quad \left. -\,ht_{d}t_{1}^{*}+\frac{ht_{d}^{2}}{2}-MT^{*}+\frac{1}{2}\hbox {I}_{e}p\left( Y^{2}-Z^{2} \right) +\frac{c\hbox {I}_{p}(-t_{1}^{*}+Y-\frac{1-e^{(t_{1}^{*}-Y)\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) })}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } \right\} \nonumber \\&\quad +\frac{\left( \mu _{1}R^{'}(p)+\mu _{2} \right) }{T^{*}}\left\{ t_{1}^{*}+\frac{ln\left[ 1+\delta \left( T^{*}-t_{1}^{*} \right) \right] }{\delta } \right\} -\frac{1}{2}\hbox {I}_{p}\left( \mu _{1}R\left( p \right) +\mu _{2} \right) (Y^{2}-Z^{2})=\hbox {0}\nonumber \\ \end{aligned}$$

(29)

Also, we take the second-order derivative of ${\textit{TP}}_{1}(p,t_{1}^{*},T^{*})$ with respect to p as follows:

$$\begin{aligned}&\frac{\partial {\textit{TP}}_{1}(p,t_{1}^{*},T^{*})}{\partial p^{2}}=\frac{\mu _{1}R^{\prime \prime }(p)}{T^{*}}\left\{ \left( p-c+M \right) \left[ t_{1}^{*}+\frac{ln\left[ 1+\delta \left( T^{*}-t_{1}^{*} \right) \right] }{\delta } \right] \right. \nonumber \\&\quad -\,\frac{N}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{1}^{*}-t_{d} \right) }-\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{1}^{*}-t_{d} \right) -1\right] \nonumber \\&\quad \left. -\,ht_{d}t_{1}^{*}+\frac{ht_{d}^{2}}{2}-MT^{*} \right\} +\frac{2\mu _{1}R^{'}(p)}{T^{*}}\left\{ t_{1}^{*}+\frac{ln\left[ 1+\delta \left( T^{*}-t_{1}^{*} \right) \right] }{\delta }+\frac{\hbox {I}_{e}(Y^{2}-Z^{2})}{2} \right\} \nonumber \\ \end{aligned}$$

(30)

where $R^{'}(p)$ and $R^{''}(p)$ are the first-order and the second-order derivative of R(p) with respect to p, respectively.

From Eq. (30), it is clear that $\frac{\partial {\textit{TP}}_{1}(p,t_{1}^{*},T^{*})}{\partial p^{2}}<0$. Since, we assume that deterministic part of demand function R(p) is a decreasing linear function of p. Thus, $R^{''}\left( p \right) =0$ and $R^{'}(p)<0$ and Eq. (28) becomes $\frac{2\mu _{1}R^{'}(p)}{T^{*}}\left\{ t_{1}^{*}+\frac{ln\left[ 1+\delta \left( T^{*}-t_{1}^{*} \right) \right] }{\delta }+\frac{\hbox {I}_{e}(Y^{2}-Z^{2})}{2} \right\}$. Due to $\left\{ t_{1}^{*}+\frac{ln\left[ 1+\delta \left( T^{*}-t_{1}^{*} \right) \right] }{\delta }+\frac{\hbox {I}_{e}(Y^{2}-Z^{2})}{2} \right\} >0,$ we conclude that $\frac{2\mu _{1}R^{'}(p)}{T^{*}}\left\{ t_{1}^{*}+\frac{ln\left[ 1+\delta \left( T^{*}-t_{1}^{*} \right) \right] }{\delta }\right.$ $\left. +\frac{\hbox {I}_{e}(Y^{2}-Z^{2})}{2} \right\} <0$. Consequently, for a given $(t_{1}^{*},T^{*})$, ${\textit{TP}}_{1}(p,t_{1}^{*},T^{*})$ is a concave function of p. Therefore, there exists a unique optimal selling price $p^{*}$ that satisfies Eq. (29).

Based on the aforementioned theoretical analysis, the following solution algorithm is presented to solve the proposed model.

5 Solution algorithm

Step 1: set $i=0$ and initialize the value of $p_{i}=p_{1}$.

Step 2: calculate

$$\begin{aligned} {\Phi }\left( p_{i} \right)= & {} \left( \hbox {p}-\hbox {c}+\hbox {M} \right) \left( \frac{t_{d}+\frac{ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) }{{\updelta }\left\{ p_{i}-\hbox {c}+\hbox {M}-ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) \right\} }}{{1+\updelta }\left( \frac{+ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}_{i}-\hbox {c}+\hbox {M}-ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) \right\} } \right) }\right. \nonumber \\&\left. -\,t_{d}-\frac{\hbox {ln}\left[ 1+\updelta (\frac{ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) }{{\updelta }\left\{ p_{i}-\hbox {c}+\hbox {M}-ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) \right\} } \right] }{{\updelta }}\right) \nonumber \\&+\,\frac{\hbox {h}\hbox {t}_{\mathrm{d}}^{2}}{2}+\frac{\hbox {A}}{\left( \mu _{1}R\left( p_{i} \right) +\mu _{2} \right) }-\frac{1}{2}I_{e}p_{i}\left( \mu _{1}R\left( p_{i} \right) +\mu _{2} \right) (Y^{2}-Z^{2})\nonumber \\&+\,\frac{cI_{p}\left( \mu _{1}R\left( p_{i} \right) +\mu _{2} \right) (-t_{d}+Y-\frac{1-e^{(t_{d}-Y)\left( \mu _{1}R\left( p_{i} \right) +\mu _{2} \right) }}{\left( \mu _{1}R\left( p_{i} \right) +\mu _{2} \right) })}{\left( \mu _{1}R\left( p_{i} \right) +\mu _{2} \right) } \end{aligned}$$

• (i) If ${\Phi }\left( p_{i} \right) \ge 0$, find the optimal value of $(t_{1}^{*},T^{*})$ by solving Eqs. (21) and (22). Substitute the value of $(t_{1}^{*},T^{*})$ into Eq. (29) and solve it to obtain $p_{i+1}$; go to step 3.

• (ii) If ${\Phi }\left( p_{i} \right) <0$, $t_{1}^{*}=t_{d},T^{*}=t_{d}+\frac{ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) }{{\updelta }\left\{ {\hbox {p}}-{\hbox {c}}+{\hbox {M}}-ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-1 \right) \right\} }$. Substitute $(t_{1}^{*},T^{*})$ into Eq. (29) and solve it to obtain $p_{i+1}$; go to step 3.

Step 3: if the difference between $p_{i}$ and $p_{i+1}$is small enough (i.e., $\left| {p_{i}-p}_{i+1} \right| \le {10}^{-4})$, set ${p^{*}=p}_{i+1}$; $p^{*},t_{1}^{*}, \hbox { and } T^{*}$ is the optimal solution and stop. Otherwise, put $i=i+1$ and go back to step 2.

Step 4: calculate $Q^{*}$ and ${\textit{TP}}_{1}^{*}$ from Eqs. (10) and (18), respectively.

Theorem 3

the proposed algorithm is convergent.

Proof

see Appendix 3 for details. $\square$

6 Numerical example

This section solves a numerical example to illustrate the solution procedure and the proposed algorithm. We apply Mathematica version 9.0 to solve the example. Table 4 gives the parameters and functions used in the example.

Table 4 Parameters and functions used in the numerical example

The solution algorithm starts with $p_{1}=600$. Table 5 shows the numerical results. It is clear that after six iterations the optimal value of model’s variables are: $p^{*}=513.5443, t_{1}^{*}=0.1816$, $T^{*}=0.5607\, {\textit{TP}}^{*}=237{,}192,$ and $Q^{*} =23.8226$.

Table 5 The solution of numerical example

The numerical example is solved for different starting values of $p\in \{ 460, 480, 500, 520, 560, 580, 699 \}$. As shown in Fig. 2, the computational results indicate that retailer’s total profit function ${\textit{TP}}^{*}$ is strictly concave respect to selling price p. Therefore, we conclude that the local maximum solution obtained from the algorithm is the global maximum solution. Moreover, we plot the three-dimensional retailer’s total profit for $p^{*}=513.5443$. As shown in Fig. 3, ${\textit{TP}}_{1}$ is clearly a concave function of T and ${{t_{1}}}$. Hence, the obtained solution is a global maximum solution.

Fig. 2

Graphical illustration of ${\textit{TP}}_{1}(p\left| t_{1}^{*},T^{*}) \right.$

Fig. 3

Total profit function ${\hbox {TP}}_{1}$ with respect to $\hbox {t}_{1}$ and $\hbox {T}$

7 Sensitivity analysis and managerial recommendations

This section presents the effect of change in the model’s parameters on the variables of problem. Moreover, some managerial recommendations are provided. The sensitivity analysis is performed by changing each of the parameters, taking one parameter at a time and keeping the other parameters unchanged.

We solve the numerical example for different value of $t_{d}$. Table  6 shows the numerical results. If $t_{d}=0$, the model converts to the instantaneous deterioration items case and the optimal retailer’s total profit is 220,998. It means that the non-instantaneous deteriorating items make an improvement in the optimal retailer’s total profit. Moreover, when the fresh product time increases, the retailer’s optimal total profit increases. That is, the longer the fresh product time is, the greater total profit would be. Thus, if the retailer can extend the length of time the items has no deterioration (for example by improvement in the stock equipment), the retailer’s total profit will increase apparently.

Table 6 The effect of non-instantaneous deteriorating phenomenon on the variables

We perform sensitivity analysis for different values of trade credit periods. Table 7 shows the numerical results.

Table 7 The numerical results for different values of the customer’s trade credit period offered by retailer Z and the retailer’s trade credit period offered by supplier Y

When the value of supplier’s trade credit to the retailer Y increases, it is trivial, that the retailer’s optimal total profit increases; since, the retailer has more time to accumulate the sales revenue and earns interest. However, when the difference between Y and Z decreases, the retailer’s total profit will decrease. If $Z=Y=0$, the model becomes no-trade credit policy system and the optimal total profit is 235,456. This means that the trade credit policy has a significant effect on the retailer’s total profit. Moreover, when $Z=Y=0.04$, the retailer’s total profit is 237,654. This implies that even the retailer adopts the credit period to his/her customer equal to supplier’s credit period to the retailer, the retailer’s total profit is greater than the no-trade credit policy system. The retailer’s order quantity $Q^{*}$ increases when Z increases. This means that the retailer could increase the sales quantity by adopting policy of delay in payment for his/her customer. We explain this phenomenon that when Z increases, the retailer will order more items to accumulate more interest to make restitution the loss of interest earned. However, when the optimal order quantity increases the total profit decreases.

Table 8 shows the effect of change in the values of interest payable and the interest earned on the variables.

Table 8 The numerical results for different values of ${\hbox {I}}_{p}$ and $\hbox {I}_{e}$

The retailer’s total profit ${\textit{TP}}^{*}$ decreases when the interest payable ${\hbox {I}}_{p}$ is high. Also, increase in ${\hbox {I}}_{p}$ yields decrease in $t_{1}^{*}$, $T^{*}$, and $Q^{*}$. From managerial viewpoint, it is concluded that the retailer should order less amount of stock when the interest payable is high. When the value of parameter $\hbox {I}_{e}$ increases, $p^{*}$ and ${\textit{TP}}^{*}$ increase while $t_{1}^{*}$, $T^{*}$, and $Q^{*}$ decrease. This identifies that when the interest earned is high, the retailer’s total profit is high.

We perform sensitivity analysis for parameters $A, c, h, s, o, and \, \theta$ by changing each value of the parameters by $+50, +25, -25$, and $-50$ %. Table 9 shows the numerical results.

Table 9 The numerical results for different values of A, c, h, s, o, and $\theta$

On the basis of the results of this table, the following managerial insights can be achieved:

• 1. An increase in the value of the purchasing cost c results in an increase in the optimal selling price $p^{{*}}$ and the optimal length of order cycle $T^{{*}}$, but a decrease in the optimal order quantity $Q^{{*}}$ and the optimal total profit ${\textit{TP}}^{{*}}$. Moreover, the optimal selling price $p^{{*}}$and the optimal total profit are more sensitive to the purchasing cost than the other parameters. Thus, to decline the selling price and to obtain more total profit, the retailer should try to take a discount from his/her supplier.

• 2. The optimal order quantity $Q^{{*}}$ and the optimal total profit ${\textit{TP}}^{{*}}$ decrease as the value of $\theta$ increases. It means that to make more profit, the retailer should follow some actions to reduce the deterioration rate.

• 3. A higher value of ordering cost value A results in a higher optimal selling price $p^{{*}}$, the optimal length of order cycle $T^{{*}}$, and the optimal order quantity $Q^{{*}}$, but lower value for the optimal total profit per unit time ${\textit{TP}}^{{*}}$. This identifies that to reduce the numbers of orders, the retailer should increase the length of order cycle. Also, when the ordering cost is high, the retailer should increase the order quantity.

• 4. When the value of holding cost h increases, the optimal selling price $p^{{*}}$ increases; but, the optimal length of order cycle $T^{{*}}$, the optimal order quantity $Q^{{*}}$, and the optimal total profit ${\textit{TP}}^{{*}}$decrease. This finding indicates that to avoid higher holding costs, the retailer should diminishes the length of order cycle and the order quantity.

• 5. An increase in the value of the backorder cost s and lost sale cost o will result in an increase in the optimal length of time in which there is no inventory shortage $t_{1}^{*}$. From a managerial interpretation, this result signifies that when the backorder and lost sale costs are high, the retailer should avoid shortages.

7.1 Sensitivity analysis of probabilistic functions

In this section, we use simulation approach to analyse the effect of the probabilistic demand and deterioration rates. First we consider the uniform distribution for deterioration. The numerical example has been solved for different distribution function of $\xi _{1}$and $\xi _{2}$ (Table 10). For simulation, we generate 500 random numbers of probabilistic demand function of $\xi _{1}$and $\xi _{2}$, then the total profit for each random number has been obtained. The average of 500 obtained total profit values has been considered as final solution of simulation method which has been shown in column 5 of Table 10. Also, we calculate the difference between results of our model and simulation method in column 6.

Table 10 Compare of simulation method and our model for different normal distribution of $\xi _{1}$and $\xi _{2}$ and uniform distribution for deterioration rate

As an example, we plot the histogram chart of simulation results for distribution function N(2, 1) as Fig. 4.

Fig. 4

Histogram chart of total profit for 500 generated random number for N(2, 1) and uniform distribution for deterioration rate

Table 11 Compare of simulation method and our model for different normal distribution of $\xi _{1}$ and $\xi _{2}$ and beta distribution for deterioration rate

The same computations have been done to beta and triangular distribution of deterioration rate which are shown in Tables 11 and  12 and Figs. 5 and 6.

The above analysis shows the following results:

• 1. We use the mean of distribution function of $\xi _{1}$ and $\xi _{2}$ to formulate model. The difference between total profit of our model and the simulation results for three cases (percentage gaps) are in the reasonable distance. Thus, using the mean of distribution function of $\xi _{1}$ and $\xi _{2}$ in the formulation does not change the results significantly. This finding approves the validation of the proposed model and obtained solutions.

• 2. When the deterioration functions and parameters of normal distribution function of demand changes, the total profit of our model and simulation method will change. Thus, accurate estimation of parameters of distribution function of demand and deterioration functions needs to obtain the correct value of variables.

• 3. In three cases, for our model and simulation results, the total profit significantly depend on the mean of normal distribution. When mean increases, the total profit will increase drastically. Thus, to obtain the correct value of variables, determine the accurate value of mean of distribution for $\xi _{1}$and $\xi _{2}$ is an important issue.

Table 12 Compare of simulation method and our model for different normal distribution of $\xi _{1}$and $\xi _{2}$ and triangular distribution for deterioration rate

Fig. 5

Histogram chart of total profit for 500 generated random number for N(2, 1) and beta distribution for deterioration rate

Tables 13 and 14 show the results of our model and simulation method for exponential and uniform distribution function of demand when the deterioration distribution function is uniform.

Fig. 6

Histogram chart of total profit for 500 generated random number for N(2, 1) and triangular distribution for deteriorating rate

Table 13 Compare of simulation method and our model for different exponential distribution of $\xi _{1}$ and $\xi _{2}$ and uniform distribution for deterioration rate

Table 14 Compare of simulation method and our model for different uniform distribution of $\xi _{1}$ and $\xi _{2}$ and uniform distribution for deterioration rate

It is clear that the results of our model and simulation results are change comparing to normal distribution function for demand (Table  10). Thus, the kind of distribution function of demand could change the results. Moreover, similar to normal distribution, the gap percentages are reasonable and our model has enough validation to perform different distribution functions for demand.

To analyse the effect of variance, we solve our model and simulation method for normal distribution with different variance. Table 15 shows the results.

Table 15 The effect of variance on the solution of our model and simulation method

We used the mean of distribution function of $\xi _{1}$ and $\xi _{2}$ to formulate our model. Thus, the change in the variance does not affect the optimal solution (Column 5 of Table 15). While, if the variance changes, the solution of simulation method will change. However, gap percentages between our model and simulation method are little and can be ignored. Thus, we conclude that change in variance of distribution function of demand does not remarkably effect on our solutions and the proposed model is valid.

8 Concluding remarks and future scope

This paper established a pricing and inventory control model for non-instantaneous deteriorating products with partially backlogging shortage. We assumed price-dependent probabilistic demand rate and probabilistic deterioration functions. Moreover, the two-echelon trade credit policy was adopted which means the vendor offers the retailer a trade credit period and also the customer receives a credit period offered by his/her retailer. In the proposed model, we determined the necessary and sufficient conditions to solve the problem and have developed a solution algorithm to obtain optimal selling price and optimal inventory control parameters. Finally, we solved numerical example and performed sensitivity analysis to illustrate the proposed model and the algorithm.

The results indicated that considering the non-instantaneous deteriorating concept improves the retailer’s total profit. If the ordering cost is high, the retailer should increase the order quantity. The two-echelon trade credit policy effectively increases the retailer’s total profit. When the retailer’s trade credit period to his/her customer increases, the retailer’s order quantity will increase. Also, if the interest payable is high, the retailer’s total profit will decrease. Increase in the value of interest earned increases the optimal selling price and the optimal total profit. In addition, the simulation results validated the proposed model and obtained solution.

Our novelty of our model is in the modelling a problem that investigates pricing and inventory control for non-instantaneous deteriorating items with price-dependent probabilistic demand function, two-echelon trade credit policy, probabilistic deterioration rates, and partially backlogged shortage. In this regard, several breakthrough with broader magnitude can be proposed. For example, we can extend the model for non-zero lead time. Also, a problem of pricing and inventory control of non-instantaneous deteriorating can be studied in two or more echelons supply chain. Moreover, the supply chain of non-instantaneous deteriorating products with multiple-vendor and multiple-retailer can be considered.

Appendices

Appendix 1: Proof of Theorem 1

Proof of part (a): We show that $F({{t_{1}}})$ is a strictly decreasing function in ${{t_{1}}}{\in }\left[ t_{d},t_{1}^{b} \right)$ and $\hbox {lim}_{t_{1}\rightarrow t_{1}^{b}}{F\left( {{t_{1}}} \right) {=-\infty }}$. Thus, if ${\Phi }\left( p \right) {\equiv }F\left( t_{d} \right) {\ge 0}$, the intermediate value theorem implies that there exists a unique value of $\hbox {t}_{1}$ ($\hbox {t}_{1}^{{*}})$ such that $F\left( \hbox {t}_{1}^{{*}} \right) =0$. Solving Eq. (24), the unique value $\hbox {t}_{1}^{{*}}$ is calculated. When the value of $\hbox {t}_{1}^{{*}}$ is identified, solving Eq. (23), the value of T ($T^{*})$ is computed.

Proof of part (b): If ${\Phi }\left( p \right) \equiv F\left( t_{d} \right) <0$, then $F\left( {{t_{1}}} \right)$ is a strictly decreasing function of ${{t_{1}}}\in \left[ t_{d},t_{1}^{b} \right)$. So, for all ${{t_{1}}}\in \left[ t_{d},t_{1}^{b} \right)$, $F\left( {{t_{1}}} \right) <0$. Therefore, we cannot find a value of ${{t_{1}}}\in \left[ t_{d},t_{1}^{b} \right)$ such that $F\left( {{t_{1}}} \right) =0$.

Appendix 2: Proof of Theorem 2

Proof of part (a): Let $\left( {{t_{1}}},T \right) =(t_{1}^{*},T^{*})$ be the solution of Eqs. (21) and (22). We have

$$\begin{aligned}&{\frac{\partial ^{2}{\textit{TP}}_{1}\left( p,{{t_{1}}},T\right) }{\partial t_{1}^{2}}|}_{\left( t_{1}^{*},T^{*}\right) }\\&\quad =\frac{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{T^{*}}\left\{ \frac{{-\updelta }\left( {\hbox {p}}-{\hbox {c}}+{\hbox {M}} \right) }{\left[ {1+\updelta }\left( T^{*}-t_{1}^{*} \right) \right] ^{2}}-\hbox {N}\hbox {e}^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{1}^{*}-t_{d} \right) }-ce^{\left( {t_{1}^{*}}-Y\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }I_{p} \right\} <O\\&{\frac{\partial ^{2}{\textit{TP}}_{1}\left( p,{{t_{1}}},T\right) }{\partial T^{2}}|}_{\left( t_{1}^{*},T^{*}\right) }=\frac{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{T^{*}}\nonumber \\&\quad \times \left( \frac{{-\updelta }\left( {\hbox {p}}-{\hbox {c}}+{\hbox {M}} \right) }{\left[ {1+\updelta }\left( T^{*}-t_{1}^{*} \right) \right] ^{2}}-\frac{2\left( -\frac{1}{2}\hbox {I}_{e}p\left( Y^{2}-Z^{2} \right) +\frac{c\hbox {I}_{p}\left( -t_{1}^{*}+Y-\frac{1-e^{\left( t_{1}^{*}-Y\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) }{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) }{T^{{*}^{2}}}\right) <0\\&{\frac{\partial ^{2}{\textit{TP}}_{1}\left( p,{{t_{1}}},T\right) }{\partial T\partial {{t_{1}}}}|}_{\left( t_{1}^{*},T^{{*}}\right) }\\&\quad =\frac{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{T^{{*}}}\left\{ \frac{{\updelta }\left( {\hbox {p}}-{\hbox {c}}+{\hbox {M}} \right) }{\left[ {1+\updelta }\left( T^{{*}}-t_{1}^{*} \right) \right] ^{2}}+\frac{c\left( -1+e^{\left( t_{1}^{*}-Y\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) \hbox {I}_{p}}{T^{{*}}\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) } \right\} \end{aligned}$$

Therefore, the determinant of the Hessian matrix is

$$\begin{aligned}&{\frac{\partial ^{2}TP\left( p,{{t_{1}}},T\right) }{\partial t_{1}^{2}}|}_{\left( t_{1}^{*},T^{*}\right) }\times {\frac{\partial ^{2}{\textit{TP}}_{1}\left( t_{1,}T,p \right) }{\partial T^{2}}|}_{\left( t_{1}^{*},T^{*}\right) }-{\left[ {\frac{\partial ^{2}{\textit{TP}}_{1}\left( t_{1,}T,p \right) }{\partial T\partial t_{1,}}|}_{\left( t_{1}^{*},T^{*}\right) }\right] }^{2}\\&\quad =\left( \frac{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{T^{*}} \right) ^{2}\left( \left( {\left( \frac{\left( -c+M+p\right) \delta }{{\left( 1+T^{*}\delta -t_{1}^{*}\delta \right) }^{2}}+\frac{c\left( -1+e^{\left( t_{1}^{*}-Y\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) \hbox {I}_{p}}{T^{*}\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) }^{2}\right. \right. \\&\quad \quad +\left( -ce^{\left( t_{1}^{*}-Y\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\hbox {I}_{p}-e^{\left( t_{1}^{*}-\hbox {td}\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }N-\frac{\left( -c+M+p\right) \delta }{{\left( 1+T^{*}\delta -t_{1}^{*}\delta \right) }^{2}}\right) \left( -\frac{\left( -c+M+p\right) \delta }{{\left( 1+T^{*}\delta -t_{1}^{*}\delta \right) }^{2}}\right. \\&\left. \left. \left. \quad +\frac{\hbox {I}_{e}p\left( Y^{2}-Z^{2}\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) ^{2}-2c\hbox {I}_{p}\left( -1+e^{\left( t_{1}^{*}-Y\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }-t_{1}^{*}\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) +Y\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \right) }{T^{{*}^{2}}\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) ^{2}}\right) \right) \right) >0 \end{aligned}$$

It means that the Hessian matrix H at point $\left( t_{1}^{*},T^{*} \right)$ is negative definite. As a result, we find that the point $\left( t_{1}^{*},T^{*} \right)$ is a global maximum.

Proof of part (b): For any given p, if ${\Phi }\left( p \right) <0$, then $F\left( {{t_{1}}} \right) <0$ for all ${{t_{1}}}\in \left[ t_{d},t_{1}^{b} \right)$. Therefore,

$$\begin{aligned}&\frac{d{TP}_{1}\left( p,{{t_{1}}},T\right) }{dT}=\frac{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{T^{2}}\\&\quad \left( \left( \hbox {p}-\hbox {c}+\hbox {M} \right) \left( \frac{\hbox {t}_{1}+\frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right\} }}{1+\updelta \left( \hbox {t}_{1}+\frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right\} }-\hbox {t}_{1}\right) }-\hbox {t}_{1}\right. \right. \\&\quad \left. -\frac{\hbox {ln}[1+\updelta \left( \hbox {t}_{1}+\frac{\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] +ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) }{{\updelta }\left\{ \hbox {p}-\hbox {c}+\hbox {M}-\hbox {N}\left[ e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( {{t_{1}}}-t_{d} \right) }-1 \right] -ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-Y \right) }-1 \right) \right\} }-\hbox {t}_{1}\right) }{{\updelta }}\right) \\&\quad \quad +\frac{\hbox {N}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\times \left[ \hbox {e}^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) }-\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( \hbox {t}_{1}-\hbox {t}_{\mathrm{d}} \right) -1 \right] +\hbox {h}\hbox {t}_{\mathrm{d}}\hbox {t}_{1}-\frac{\hbox {h}\hbox {t}_{\mathrm{d}}^{2}}{2}+\frac{\hbox {A}}{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }\\&\quad \quad \left. -\frac{1}{2}I_{e}p\left( \mu _{1}R\left( p \right) +\mu _{2} \right) \left( Y^{2}-Z^{2}\right) +\frac{cI_{p}\left( \mu _{1}R\left( p \right) +\mu _{2}\right) \left( -\hbox {t1}+Y-\frac{1-e^{\left( \hbox {t1}-Y\right) \left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) }{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\right) \\&\quad =\frac{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) F\left( {{t_{1}}} \right) }{T^{2}} \end{aligned}$$

It is clear that $\frac{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) }{T^{2}}{>}0$ and we showed that $F\left( {{t_{1}}} \right) {<}0$. Therefore, $\frac{\left( \mu _{1}R\left( p \right) +\mu _{2} \right) F\left( {{t_{1}}} \right) }{T^{2}}{<}0$, which means that ${\textit{TP}}_{1}(p,{{t_{1}}},T)$ is a strictly decreasing function of T. Thus, when T is minimum, ${\textit{TP}}_{1}(p,{{t_{1}}},T)$ attains its maximum value. From Eq. (23), the minimum value of T occurs at

$$\begin{aligned} \hbox {T}= t_{d}+\frac{ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-\hbox {1} \right) }{{\updelta }\left\{ {\hbox {p}}-{\hbox {c}}+{\hbox {M}}-ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-\hbox {1} \right) \right\} } \end{aligned}$$

As ${{t_{1}}}=t_{d}$, ${\textit{TP}}_{1}(p,{{t_{1}}},T)$ has a maximum value at point $(t_{1}^{*},T^{{*}})$, where $t_{1}^{*}=t_{d}$ and

$$\begin{aligned} T^{{*}}=t_{d}+\frac{ht_{d}+\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-\hbox {1} \right) }{{\updelta }\left\{ {\hbox {p}}-{\hbox {c}}+{\hbox {M}}-ht_{d+}\frac{cI_{p}}{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) }\left( e^{\left( \frac{\alpha _{1}+\alpha _{2}}{2} \right) \left( t_{d}-Y \right) }-\hbox {1} \right) \right\} } \end{aligned}$$

Appendix 3: Proof of Theorem 3

Using step 1, the initial total profit function with staring value of $\hbox {t}_{1}^{0}, \hbox {T}^{0},{\hbox {and}\,\hbox {p}}_{{0}}$ is computed. For notational convenience, let

$$\begin{aligned} {\textit{TP}}_{1}\left( \hbox {t}_{1}^{{0}}\hbox {, }\hbox {T}^{{0}}, \hbox {p}_{{0}} \right) = {\Pi }^{\hbox {(o)}} \end{aligned}$$

Using step 2, $\hbox {p}_{{0}}$ is fixed and the value of $\hbox {t}_{1}^{1}\hbox { and }\hbox {T}^{1}$ is obtained. Therefore, the new total profit function is resulted.

$$\begin{aligned} {\textit{TP}}_{1}\left( \hbox {t}_{1}^{1}, \hbox {T}^{1}, \hbox {p}_{0} \right) ={\Pi }^{(1)} \end{aligned}$$

Applying Theorem 1, we determined that ${\textit{TP}}_{1}\left( \hbox {t}_{1}^{1}, \hbox {T}^{1}, \hbox {p}_{{0}} \right)$ is concave and takes its global solution at ${\hbox {(t}}_{1}^{1}, \hbox {T}^{1})$. So, ${\textit{TP}}_{1}\left( \hbox {t}_{1}^{1}, \hbox {T}^{1}, \hbox {p}_{0} \right) \ge {\textit{TP}}_{1}\left( \hbox {t}_{1}^{0},\hbox {T}^{0},\hbox {p}_{0}\right)$.

If ${\textit{TP}}_{1}\left( \hbox {t}_{1}^{1},\hbox {T}^{1}, \hbox {p}_{{0}} \right) ={\textit{TP}}_{1}\left( \hbox {t}_{1}^{{0}},\hbox {T}^{{0}},\hbox {p}_{{0}} \right)$, then the algorithm is convergent. Else,

$$\begin{aligned} {\textit{TP}}_{1}\left( \hbox {t}_{1}^{1},\hbox {T}^{1},\hbox {p}_{{0}} \right) {>}{\textit{TP}}_{1}\left( \hbox {t}_{1}^{{0}},\hbox {T}^{{0}},\hbox {p}_{{0}} \right) \Longrightarrow {\Pi }^{(1)}{>}{\Pi }^{\hbox {(o)}} \end{aligned}$$

Now, by fixing $\hbox {t}_{1}^{1}{\hbox { and T}}^{1}$, we solve Eq. (27) and the new selling price $\hbox {p}_{1}$ is obtained. Thus, the new total profit function is found.

$$\begin{aligned} {\textit{TP}}_{1}\left( \hbox {t}_{1}^{1},\hbox {T}^{1},\hbox {p}_{1} \right) ={\Pi }^{(2)} \end{aligned}$$

Using Theorem 2, we proved that ${\textit{TP}}_{1}\left( \hbox {t}_{1}^{1},\hbox {T}^{1},\hbox {p}_{1} \right)$ is concave and obtained its global solution at $\hbox {p}_{1}$. Therefore,

$$\begin{aligned} {\textit{TP}}_{1}\left( \hbox {t}_{1}^{1},\hbox {T}^{1},\hbox {p}_{1} \right) \ge {\textit{TP}}_{1}\left( \hbox {t}_{1}^{1},\hbox {T}^{1},\hbox {p}_{{0}} \right) \end{aligned}$$

If ${\textit{TP}}_{1}\left( \hbox {t}_{1}^{1},\hbox {T}^{1},\hbox {p}_{1} \right) ={\textit{TP}}_{1}\left( \hbox {t}_{1}^{1},\hbox {T}^{1},\hbox {p}_{{0}} \right)$, then the algorithm is convergent. Else,

$$\begin{aligned} {\textit{TP}}_{1}\left( \hbox {t}_{1}^{1},\hbox {T}^{1},\hbox {p}_{1} \right) {>}{\textit{TP}}_{1}\left( \hbox {t}_{1}^{1},\hbox {T}^{1},\hbox {p}_{{0}} \right) \Longrightarrow {\Pi }^{(2)}{>}{\Pi }^{(1)} \end{aligned}$$

Using the above approach, we obtain the strictly increasing sequence of ${\textit{TP}}_{1}\left( {{t_{1}}}\hbox {,T,p} \right)$as follows:

$$\begin{aligned} {\Pi }^{(n)}{>}{\Pi }^{({\hbox {n}}-1)}{>}\cdots >{\Pi ^{(1)}}{>}{\Pi }^{\hbox {(o)}} \end{aligned}$$

We assume that the retailer’s total profit is finite; i.e. the retailer’s total profit has an upper bound. It implies that the obtained strictly increasing sequence of ${\textit{TP}}_{1}\left( {{t_{1}}}\hbox {,T,p} \right)$ has an upper bound. On the other hand, a strictly increasing sequence with an upper bound is convergent.