1 Introduction

A microstrip diplexer implements frequency-domain multiplexing. Therefore, a planar high-performance diplexer with a compact size is widely demanded by the modern wireless communication systems. A high data-rate communication link is forced to employ wide passbands. To obtain an important advantage, a link with low data rate may deliberately use a wider bandwidth too. Ultra-wideband (UWB) is a technology to transmit data over a large bandwidth (> 0.5 GHz). Accordingly, a diplexer with wide bandwidths (having the high data-rate capability) can play a key role in UWB communication systems.

Several types of microstrip diplexers have been introduced for various applications [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. However, they have relatively narrow bandwidths and occupied large areas. The proposed diplexers in [1, 2] have low insertion losses at both channels while in [1] the frequency selectivity at the upper channel is relatively poor. Using common shorted stubs, a microstrip diplexer has been presented in [3]. It has several transmission zeros at the stopband. It operates at 2.4 GHz and 1.8 GHz for WLAN and GSM applications, respectively.

Nevertheless, the introduced diplexers in [3,4,5,6,7,8,9,10,11,12,13,14,15,16] could not decrease the insertion losses acceptably. In [4] and [5], coupled stepped impedance resonators and interdigital capacitors have been utilized, respectively, to design microstrip diplexers working at GSM and WLAN frequency bands. A diplexer has been designed in [6] based on a novel microstrip structure using four coupled lines integrated by step impedance cells, but it has low isolation. An unbalanced-to-balanced microstrip diplexer has been presented in [7] based on stub-loaded dual-mode resonators.

In [8], the coupled lines have been integrated to create a diplexer with several transmission zeros, which improve the stopband properties. In [9], microstrip triangular open-loop resonators have been employed to achieve a diplexer for the 4G application. A microstrip ring resonator coupled to the transmission lines has been used in [10]. In comparison to the other reported diplexers, it could expand the bandwidth slightly.

In [11], a high isolation diplexer has been designed using coupled square and rectangular open-loop resonators. To obtain a dual-frequency diplexer operated at 1.95 GHz and 2.14 GHz, two stub-loaded U-shape resonators have been integrated by a T-shape junction in [12]. In [13], two channels have been constructed by the electrically-coupling half-wavelength resonators, which have a problem of low selectivity at upper passband. The authors in [14] could improve the isolation between two channels using an integrated waveguide substrate.

In [15], spiral cells are coupled to design a diplexer with good return losses but high insertion losses at both channels. In [16], the lumped elements are loaded inside four open loops which lead to the complexity of manufacturing, a non-planar structure, increase the size and increase the measurement errors. In [20], a microstrip diplexer with two opposite very large and very narrowband widths has been proposed. It occupies a large implementation area with a high return loss in its wider channel.

Recently, artificial neural network (ANN) has been widely used in many engineering applications [21, 22]. As a powerful mathematical tool, ANN can be used in classification, patterns modeling, prediction, and optimization problems. In [23], ANN and ANFIS (adaptive neuro-fuzzy inference system) models have been developed in a microstrip subsystem to model and predict matching condition. This subsystem consists of a microstrip bandpass filter and a low noise amplifier (LNA), which can be used for WLAN applications. In [24], radial basis function (RBF) neural network has been used to design bandpass filters in shielded printed technology. For this purpose, a nonlinear equation has been obtained to relate the dimensions of the resonators to the coupling coefficients and quality factor. In [25], an ANN method has been used for designing a microstrip bandpass filter. For this means, dimensions and S-parameters of the microstrip bandpass filter have been used as the inputs and outputs of the ANN model, respectively.

In this paper, we use an ANN technique to design a microstrip diplexer with two wide bandwidths for L-Band and S-Band applications. Using a type of ANN, i.e., multilayer perceptron (MLP) a high-performance diplexer is designed and fabricated, which can solve the problems of the other reported diplexers in terms of reducing the size and improving the insertion losses, while the other parameters are acceptable. The wide fractional bandwidths (FBWs) of the proposed diplexer make it appropriate for UWB applications. The widest FBWs are obtained in this work. Meanwhile, it has two flat passbands with low group delays that is widely demanded by the high data-rate communication links.

The design process is prepared as follows: first, a microstrip resonator is proposed based on coupled lines and patch cells. Then, an LC model of the proposed resonator is presented and analyzed to find its most effective parameters. Next, using the proposed ANN model an optimization method is performed to design two bandpass filters by tuning the resonant frequency, bandwidth and miniaturization. Finally, using the obtained bandpass filters a high-performance diplexer is designed and fabricated.

2 Proposed resonator

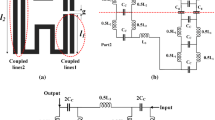
To create a passband channel, we need a passive LC circuit. The LC equivalent circuit of coupled lines includes several capacitors and inductors. The coupling effect can be presented by small coupling capacitors while the microstrip lines have inductance features [26]. Due to having an LC model of coupled lines, they have been used to create a bandpass frequency response. Hence, we will use the stub loaded coupled lines to obtain a bandpass frequency response. A patch cell with capacitance properties can save size. Therefore, it is suitable to join the coupled line and complete the equivalent LC circuit of a bandpass filter (BPF).

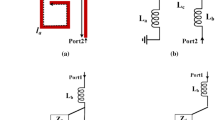
Accordingly, we prefer to select a coupled-line loaded by rectangular patch cell as shown in Fig. 1(a). For the proposed resonator, an approximated equivalent LC circuit is depicted in Fig. 1(b), where the patch cells are replaced by the capacitor CP and the equivalent model of coupled-line includes the capacitors Cc and inductors Lc [26]. The stubs with the physical lengths l1 and l6 are replaced by an inductor of La. Similarly, we replaced the inductors Lb instead of the stubs with the physical lengths l3 and l4. The LC circuit of bents and steps are ignored because they are only important at the frequencies above 10 GHz. Moreover, the equivalent circuit of the coupled lines is not exact. In the exact LC model, the number of coupling capacitors will be increased significantly.

Fig. 1
figure 1

Proposed resonator: a layout configuration, b LC circuit, c replacing the exact model of coupled lines in the LC circuit, d frequency response

Full size image

The resonance frequency can be obtained by calculating the input impedance Zin and then putting Zin =0. Accordingly, we have a single mode resonator achieved by having a short circuit. To calculate the input impedance Zin, the approximate model is replaced by an exact model shown in Fig. 1(c). In the exact model, an inductor of Ld is an equivalent of a small differential section of the coupled-line and the capacitors Cd depict the coupling of lines. Since the number of inductors and capacitors goes to infinity, it can be assumed that Zin~Zin1. According to this, the input impedance can be calculated as follows:

$$\begin{aligned} z_{in} = \frac{{(z_{in} + 2\omega jL_{d} C_{p} ) \times \frac{1}{{j\omega C_{d} }}}}{{z_{in} + 2\omega jL_{d} C_{p} + \frac{1}{{j\omega C_{d} }}}} + j\omega (L_{a} + L_{b} ) + \frac{1}{{j\omega C_{p} }} \Rightarrow \hfill \\ \hfill \\ z_{in}^{2} + z_{in} bj + c = 0\,\,\,\,\,for:\left\{ \begin{aligned} b = 2\omega L_{d} C_{p} + \frac{1}{{\omega C_{d} }} - \omega (L_{a} + L_{b} ) \hfill \\ c = \omega^{2} (L_{a} + L_{b} )2L_{d} C_{p} - 2L_{d} + \frac{1}{{\omega^{2} C_{d} C_{p} }} - \frac{{2L_{d} C_{p} + L_{a} + L_{b} }}{{C_{d} }} \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned}$$
(1)

To calculate the angular resonance frequencies ωo, we can set zin=0 as follows:

$$\begin{aligned} z_{in} = 0 \Rightarrow - bj \pm \sqrt { - b^{2} - 4c} = 0 \Rightarrow - b \pm \sqrt {b^{2} + 4c} = 0 \Rightarrow c = 0 \Rightarrow \hfill \\ \hfill \\ \omega_{o}^{4} - \frac{{2L_{d} C_{p} + L_{a} + L_{b} }}{{2L_{d} C_{p} C_{d} (L_{a} + L_{b} )}}\omega_{o}^{2} + \frac{{1 - 2L_{d} C_{d} C_{p} }}{{2L_{d} C_{P}^{2} C_{d} (L_{a} + L_{b} )}} = 0 \Rightarrow \hfill \\ \hfill \\ \omega_{o} = \sqrt {\frac{{2L_{d} C_{p} + L_{a} + L_{b} }}{{4L_{d} C_{p} C_{d} (L_{a} + L_{b} )}}(1 \pm \sqrt {1 - 2L_{d} C_{P}^{2} C_{d} (L_{a} + L_{b} )\frac{{1 - L_{d} C_{p} C_{d} (L_{a} + L_{b} )}}{{(2L_{d} C_{p} + L_{a} + L_{b} )^{2} }}} )} \hfill \\ \end{aligned}$$
(2)

Applying some approximations will help us to find the effective parameters in tuning resonant frequency. According to the transmission line formulas, when the inductors La and Lb are with millimetric dimensions, they are usually in nH, but Ld is the smaller parameter. On the other hand, the coupling capacitors are very small in PF. These estimates are based on the approximated dimensions of the microstrip lines that we usually set them in mm. Based on the above discussion, applying two approximations leads to the following simplifications:

$$\begin{aligned} L_{d} C_{p} C_{d} (L_{a} + L_{b} )\langle \langle 1 \Rightarrow \omega_{o} \approx \sqrt {\frac{{2L_{d} C_{p} + L_{a} + L_{b} }}{{4L_{d} C_{p} C_{d} (L_{a} + L_{b} )}}\left( {1 \pm \sqrt {1 - \frac{{2L_{d} C_{P}^{2} C_{d} (L_{a} + L_{b} )}}{{(2L_{d} C_{p} + L_{a} + L_{b} )^{2} }}} } \right)} \hfill \\ \sqrt {\frac{{2L_{d} C_{P}^{2} C_{d} (L_{a} + L_{b} )}}{{(2L_{d} C_{p} + L_{a} + L_{b} )^{2} }}} \langle \langle 1 \Rightarrow \omega_{o} \approx \sqrt {\frac{{2L_{d} C_{p} + L_{a} + L_{b} }}{{2L_{d} C_{p} C_{d} (L_{a} + L_{b} )}}} = \sqrt {\frac{1}{{C_{d} (L_{a} + L_{b} )}} + \frac{1}{{2L_{d} C_{p} C_{d} }}} \hfill \\ \hfill \\ \end{aligned}$$
(3)

According to Eq. (3), the resonant frequency depends on patch capacitor (CP), coupled line (Cd and Ld), and the stubs with the physical lengths l1, l3, l4 and l6, which are modeled by La and Lb. To find more effective parameters, we apply a new approximation as follows:

$$L_{a} + L_{b} \,\rangle \rangle \,2L_{d} C_{p} \Rightarrow \omega_{o} \approx \sqrt {\frac{1}{{2C_{d} L_{d} C_{p} }}}$$
(4)

Equation (4) shows that coupled lines and patch cells are the most important parameters in determining the resonant frequency. Due to having the angular resonance frequency in GHz, the coupling capacitor should be large. Therefore, we have to choose the dimensions of patch cells somewhat large, while we are careful to save the overall size. Then, the space between coupled lines and the dimensions of them will be selected to obtain a target resonant frequency by Eq. (4).

Knowing the behavior of the resonator will help in the diplexer design. Using this method, the resonant frequency will be tuned without size increment. The frequency response of the proposed resonator is presented in Fig. 1(d), where it operates at 2.7 GHz with a fractional bandwidth of 18.8% and a relatively large insertion loss. It is simulated on an RT/Duroid 5880 substrate with εr = 2.22, h = 0.7874 mm.

In other to control the bandwidth of the proposed resonator, an optimization method can be performed. We can calculate the highest -3 dB cut-off frequency. Hence, obtaining the network function \(H(j\omega_{o} )\) is essential. When the maximum amplitude \(\left| {H(j\omega_{o} )} \right|\) is reduced to \(0.707\left| {H(j\omega_{o} )} \right|\), we get the cut-off frequency. Finally, the dimensions must be tuned to obtain the highest cut-off frequency. Applying the optimization method shows that the bandwidth can be controlled by adjusting the patches. Figures 2(a)–(c) depict the bandwidth as a function of the dimensions of patch cells. The data obtained from Fig. 2 show that selecting the smaller patch cell can improve the bandwidth and insertion loss.

Fig. 2
figure 2

Frequency response of the resonator as a function of: a l5, b w2, and c l5 and w2

Full size image

By adding two rectangular patches inside the proposed resonator, a BPF is designed as shown in Fig. 3(a). The corresponding dimensions of the proposed BPF (in mm) are listed in Table 1. The other dimensions are exactly in accordance with the proposed resonator. Figure 3(b) depicts the frequency response of the proposed BPF. It operates at 1.87 GHz with a wide fractional bandwidth of 20.3% and a low insertion of 0.17 dB. It is clear that adding two rectangular patches can improve the frequency response without size increasing.

Fig. 3
figure 3

Proposed BPF: a layout configuration, and b frequency response

Full size image
Table 1 Dimensions of the proposed BPF in mm
Full size table

3 Diplexer design using ANN

In this section, we propose an accurate ANN model for designing a microstrip diplexer. As mentioned before, to tune the resonant frequency of the proposed BPF the best method is changing of the effective lengths and widths of microstrip cells used in the BPF layout. Therefore, if we change the overall scale of the BPF dominations all effective lengths and widths of microstrip cells used in the BPF layout are changed subsequently. Thus, we selected frequency (per GHz) and the scale of the BPF dominations as the inputs and S-parameters (scattering parameters) i.e. S11 and S21as the outputs of the proposed ANN model.

As shown in Fig. 4, a multilayer perceptron (MLP) neural network model is used which is the most used ANN. The presented MLP network has three layers i.e. input, hidden and output. More details about MLP neural networks can be found in [27, 28].

Fig. 4
figure 4

Proposed MLP network

Full size image

To develop the MLP model, a set of about 2000 data is used as the training and testing data. The data set is obtained by ADS full-wave EM simulator. About 70% of the data set is used for training and the rest is used to test and validate the proposed model. To build the best ANN model the main issue was to obtain an MLP network with high accuracy and less complicated structure. For this purpose, we tested many MLP structures with one and two hidden layers. Also, we changed the number of neurons in each hidden layers from 2 to 15 and the number of epochs from 50 to 500. Trainlm algorithm was chosen as the adaption learning function for all tested ANNs. At the end of this process, the best MLP network was obtained after 200 epochs with ten neurons in one hidden layer.

Figure 5 shows the obtained results of the proposed MLP model. In this figure, CF (correlation coefficient) is given by the following equation:

Fig. 5
figure 5

Results of the proposed MLP model in comparison with ADS software

Full size image
$$CF = 1 - \left[ {\frac{{\sum\limits_{i = 1}^{N} {(X_{i} (Sim) - X_{i} (\Pr ed))^{2} } }}{{\sum\limits_{i = 1}^{N} {(X_{i} (Sim))^{2} } }}} \right]$$
(5)

Where N is the number of data and ‘X(Simp) and ‘X(Pred)’ are the simulated (ADS) and predicted (ANN) values, respectively. As shown in Fig. 5, the MLP results are very close to the simulation results which show the proposed ANN model is very accurate.

Since ANN is a mathematical approach, we can obtain two equations for S21 and S11 based on the proposed MLP model:

$$\begin{aligned} {\text{S}}_{21} & = - \,0.74*{\text{Tansig}}\left( { - \,25.2*{\text{F}} + 28.5*{\text{Scale}} + 43.93} \right) - 8.85*{\text{Tansig}} \\ & \quad \times \left( { - 0.29*{\text{F}} - 1.87*{\text{Scale}} + 3.285} \right) - 0.83*{\text{Tansig}}\left( { - 9.00*{\text{F}} + 30.9*{\text{Scale}} - 16.51} \right) \\ & \quad + 1.68*{\text{Tansig}}\left( {18.95*{\text{F}} - 32.4*{\text{Scale}} - 21.30} \right) \\ & \quad + 1.6493*{\text{Tansig}}\left( { - 13.9*F - 27.7*{\text{Scale}} + 55.80} \right) \\ & \quad + 0.98*{\text{Tansig}}\left( { - 37.1*{\text{F}} + 91.3*{\text{Scale}} + 12.95} \right) \\ & \quad + 2.95*{\text{Tansig}}\left( {14.63*{\text{F}} + 28.1*{\text{Scale}} - 57.24} \right) \\ & \quad + 43.6*{\text{Tansig}}\left( { - 2.84*{\text{F}} - 3.05*{\text{Scale}} + 8.255} \right) \\ & \quad + 33.5*{\text{Tansig}}\left( { - 1.27*{\text{F}} - 3.44*{\text{Scale}} + 6.462} \right) \\ & \quad + 57.3*{\text{Tansig}}\left( {3.020*{\text{F}} + 4.25*{\text{Scale}} - 9.643} \right) - 20.6 \\ S_{11} & = - 11.1*{\text{Tansig}}\left( { - 25.2*{\text{F}} + 28.5*{\text{Scale}} + 43.93} \right) \\ & \quad + 6.10*{\text{Tansig}}\left( { - 0.29*{\text{F}} - 1.87*{\text{Scale}} + 3.285} \right) \\ & \quad + 0.86*{\text{Tansig}}\left( { - 9.00*{\text{F}} + 30.9*{\text{Scale}} - 16.51} \right) \\ & \quad - 24.2*{\text{Tansig}}\left( {18.95*{\text{F}} - 32.4*{\text{Scale}} - 21.30} \right) \\ & \quad - 109.07*{\text{Tansig}}\left( { - 13.9*{\text{F}} - 27.7*{\text{Scale}} + 55.80} \right) \\ & \quad - 12.5*{\text{Tansig}}\left( { - 37.1*{\text{F}} + 91.3*{\text{Scale}} + 12.95} \right) \pm 109*{\text{Tansig}} \\ & \quad \times \left( {14.63*{\text{F}} + 28.1*{\text{Scale}} - 57.24} \right) - 8.14*{\text{Tansig}} \\ & \quad \times \left( { - 2.84*{\text{F}} - 3.05*{\text{Scale}} + 8.255} \right) - 4.33*{\text{Tansig}} \\ & \quad \times \left( { - 1.27*{\text{F}} - 3.44*{\text{Scale}} + 6.462} \right) - 9.42*{\text{Tansig}} \\ & \quad \times \left( {3.020*{\text{F}} + 4.25*{\text{Scale}} - 9.643} \right) - 2.90 \\ \end{aligned}$$
(6)

Where Tansig is the transfer function for the hidden layer given by the following equation:

$$\text{Tan} sig(x) = \frac{2}{{1 + e^{ - 2x} }} - 1$$
(7)

The main advantage of the presented ANN model is its ability to calculate the outputs in a very short time. For example, if a simulation in ADS software takes few minutes to run; the proposed MLP network can do it in about 1 ms for the same condition. With this ability we can test many different microstrip layouts using the ANN method in a short time to obtain the best response for a special application. Using this method, we used the proposed MLP network to obtain two high-performance BPFs and place them into a single structure as a diplexer.

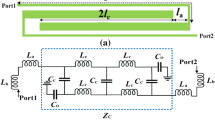
The proposed diplexer with its corresponding dimensions in mm is presented in Fig. 6. The designed diplexer includes two similar filters that their basic structures have already been analyzed and explained. These filters are integrated with a simple T-junction structure.

Fig. 6
figure 6

Layout of the proposed diplexer

Full size image

4 Simulation and measurement results

We used ADS full-wave EM simulator and MATLAB software to design and simulate the proposed diplexer. The designed diplexer is implemented on an RT/Duroid 5880 substrate with εr = 2.22, h = 0.7874 mm and tan(δ) = 0.0009. The measurements are done by Agilent network analyzer N5230A. The obtained S21 and S31 of the designed diplexer are shown in Fig. 7(a), whereas, Fig. 7(b) depicts the isolation and S11 with a photograph of the fabricated diplexer. The overall size of the diplexer is 40.5 mm × 23.7 mm = 0.054 λ 2g , where λg is the guided wavelength calculated at 1.6 GHz.

Fig. 7
figure 7

Simulation and measurement results: a S21 and S31, and b S11, S23 and a photograph of the fabricated diplexer

Full size image

The -3 dB bandwidth of the first channel is from 1.47 to 1.74 GHz, while another − 3 dB passband is from 2 to 2.23 GHz. The first resonant frequency is tuned at 1.6 GHz, which is located at the middle of passband with the simulated insertion and common port return losses of 0.1 dB and 33 dB respectively. The second resonance frequency is at 2.1 GHz, which is approximately located in the middle of passband with the simulated insertion and return losses better than 0.16 dB and 22 dB, respectively. The measured insertion losses are about 0.5 dB greater than the simulated results due to copper and junction losses. Both channels are wide, with the fractional bandwidths 16.8% and 11% that make it appropriate for wideband applications.

The results show that the isolation between channels is better than − 22 dB. The performance and size of the proposed diplexer are compared with the previous diplexers in Table 2. In this table, IL, FBW and FO are insertion loss, fractional bandwidth and operation frequency, respectively, where the indexes 1 and 2 indicate the first and second passbands, respectively. As depicted in Table 2, the minimum size, lowest insertion loss and widest fractional bandwidths are obtained in this work. Only the presented diplexer in [20] has a wider channel than our diplexer. However, another channel of this diplexer is narrow while it has a larger area and larger insertion losses.

Table 2 Comparison with the previous works (*: approximated values)
Full size table

Group delay is a type of distortion, which shows the phase linearity and passband flatness. However, there is no significant distortion as indicated by group delay < 10 ns while the insertion loss is low [29]. The group delay of the proposed diplexer is presented in Fig. 8. It shows that the maximum group delays at the first and second channels are 2.2 ns and 2.6 ns respectively. A comparison of the maximum group delays is shown in Table 3. As shown in this table, a good group delay is obtained in this work.

Fig. 8
figure 8

Group delay of the proposed diplexer

Full size image
Table 3 Group delay in comparison with previous works (MGD: maximum group delay; NCs: the number of channels)
Full size table

5 Conclusion

A compact microstrip diplexer with low insertion losses and wide FBWs was designed and fabricated using an accurate and fast artificial neural network model. The proposed diplexer consists of coupled lines loaded by patch cells; the patches could save size significantly. It has two flat channels with a maximum group delay of 2.6 ns. Therefore, the proposed diplexer can be used when we have high or low data rate communication links. Furthermore, the widest FBW obtained in the previous works was for one channel only, whereas, the obtained FBWs of the proposed diplexer in this work are 16.8% and 11% at the lower and upper channels, respectively. The passbands can cover L-Band and S-Band frequency spectrums. These advantages were obtained while the other parameters in terms of return losses, isolation and selectivity were acceptable.