1 Introduction

Multi-channel microstrip devices such as multiplexers, multi-channel diplexers, antennas, and filters [1,2,3,4,5,6,7,8,9] have been extensively in demand by modern communication systems.

Since multi-channel diplexers are usually designed based on multi-mode filters, designing multi-channel filters is a challenge. Furthermore, after the multi-band antenna components stage, we need this type of filter to suppress undesired signals. Therefore, quad-band bandpass filters (QB-BPFs) are more attractive to modern multi-service communication systems.

Accordingly, several types of microstrip QB-BPFs have been reported in [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. They are designed for various applications such as WLANs, GPS, WiMAX, GSM, and WCDMA. Open-stubs loaded by shorted stepped-impedance resonators have been used in [10] to design a QB-BPF to work at 1.19, 3.33, 5.87, and 8.39 GHz for wireless applications. In [11], a novel meandering structure has been utilized to design a QB-BPF with large return loss. A microstrip QB-BPF in [12] has been investigated by integrating the coupled lines and stub-loaded resonators. Similar to the presented filter in [11], it has low return losses. In [13], to design two QB-BPFs with good selectivity and narrow channels, a novel circular resonator having been employed. In [14], a switchable QB-BPF has been introduced, which consists of step impedance and coupling structures.

In [15], the stub-loaded resonators having been used to create four channels with very large insertion and return losses. Quad and dual-band BPFs have been introduced based on a triangular stepped-impedance resonator in [16]. Nevertheless, it has very large losses on all channels. On the other hand, there is poor isolation between its second and third channels. Due to having an elliptic function frequency response, there are several transmission zeros (TZs), which could improve the stop-band features. In [17], coupled open-loop resonators have been used to obtain four bandpass channels with high selectivity but small return losses at their first, third, and fourth channels. The authors in [18] have presented a QB-BPF using stub loaded stepped-impedance resonator. The disadvantage of this filter is its small return losses at the first and last channels. In [19], a QB-BPF that employing quad-mode stub-loaded resonators has been proposed. The common disadvantage of the introduced QB-BPFs in [10,11,12,13,14,15,16,17,18,19,20,21] is occupying large areas while they have large insertion losses. In [22], a quad-band microstrip BPF is designed and fabricated using defect ground structure (DGS), stub-loaded resonator (SLR), and stepped impedance resonators (SIR). It has relatively low insertion losses and compact size and can be utilized in LTE-TDD, DTH, and 5G communication systems. In [23], a microstrip Line QB-BPF is fabricated using microstrip line technology and dimensions based on the initial terms of the Fibonacci sequence. In [24], a method based on frequency transformation function is presented to design a QB-BPF.

Recently, artificial neural networks (ANNs) as powerful mathematical tools have been widely used in many applications such as classification, prediction, and optimization problems [25, 26]. In [27], the design of microstrip antennas using ANN has been proposed. In [28], the applicability of ANN modeling for analyzing and synthesizing of microstrip antennas has been reviewed. In [29], ANN and adaptive neuro-fuzzy inference system (ANFIS) models have been developed in a microstrip subsystem to model and predict matching conditions. This subsystem consists of a microstrip BPF and an LNA, which can be used for WLAN applications. In [30], radial basis function (RBF) neural network has been used to design BPFs in shielded printed technology. For this purpose, a nonlinear equation has been obtained to relate the dimensions of the resonators to the coupling coefficients and quality factor. In [31], an ANN method has been used for designing a microstrip BPF. For this means, the dimensions and S-parameters of the microstrip bandpass filter have been used as the inputs and outputs of the ANN model, respectively. In [32], an ANN model is used for designing a microstrip stepped impedance low-pass filter (LPF) and a parallel coupled-line BPF. The LPF has a cut-off frequency of 1 GHz and the BPF has fractional bandwidth (FBW) of 25% and a central frequency of 2.45 GHz. In [33], a novel adaptive neuro-fuzzy inference system (ANFIS) model is presented to design and fabricate a microstrip diplexer for wideband wireless applications. This microstrip diplexer has flat channels and low insertion losses.

In this paper, a microstrip QB-BPF is introduced using a novel structure. The layout of the proposed QB-BPF is obtained using ANN. To develop the ANN model, a multilayer perceptron (MLP) structure is used. After testing many different structures and by using the best obtained MLP model, a novel method to obtain a high-performance QB-BPF is introduced. The introduced method can be easily used for designing other microstrip devices. The designed QB-BPF works at 0.7 GHz for the broadcast TV and low power TV (LPTV) service, 2.2 GHz for the advanced wireless service and fixed microwave service, 3.8 GHz for IEEE 802.16 WiMAX, and 5.6 GHz for upper WiMAX band applications [34]. The proposed structure is well miniaturized so that its size is 93% smaller than the reported most compact QB-BPF, while it has very small insertion loss and high return loss at all channels, and relatively flat frequency response.

The design process is structured as follows: First, an LC model of the proposed resonator is presented. Second, the condition to: obtain perfect impedance matching, tune the resonance frequency, and improve the quality factor, is achieved simultaneously. Third, by adding the compact meandrous spiral cells, the basic layout of a BPF is created. Finally, by using an ANN model, the best configuration of the proposed basic layout is obtained, which has the maximum number of channels with good insertion and return losses.

2 Basic filter design

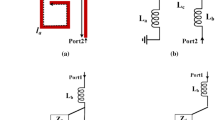
The transition between two ports and creating a filtering frequency response need an LC circuit. Microstrip coupled lines can provide passbands due to having inductive and capacitive properties [2]. Therefore, we used them to create passbands. Figure 1a depicts a simple basic structure consisting of the coupled-line with a physical length of 2lc and two additional microstrip cells with the physical lengths la and lb. An approximated LC circuit of Fig. 1a is shown in Fig. 1b by ignoring the equivalents of bents and steps. Eliminating the effect of bents and steps in the LC model is because of their low effects at frequencies less than 10 GHz.

Fig. 1
figure 1

Basic microstrip structure: a layout, and b equivalent LC circuit

Full size image

In Fig. 1b, the approximated equivalent LC circuit of coupled lines with two open ends is shown by an impedance of Zc. The equivalent circuit of the coupled lines consists of the inductors and capacitors Lc and Cc. Each Lc is an equivalent of the physical length lc and the coupling effect is presented by three capacitors of Cc [13]. According to this, the coupled lines can create a passband due to having inductors and capacitors in their LC equivalent circuit. This is an approximated model of the coupled lines. In the exact model, the number of lumped elements will increase. The physical lengths la and lb are replaced by La and Lb respectively. The capacitors Co are instead of the open ends of coupled lines. To express the input/output coupling, external quality factor (Qe) is defined as follows [35, 36]:

$$ Q_{e} = \frac{{2f_{o} }}{{(\Delta f)_{{3{\text{dB}}}} 10^{{\frac{ - IL}{{20}}}} }}\quad {\text{for}}:{\text{IL}} = - 20\log S_{21} $$
(1)

where IL and (Δf)3 dB are the insertion loss (in dB) and − 3 dB bandwidth, respectively. The ABCD matrix of the proposed structure from port1 to port 2 is calculated as follows [36, 37]:

$$ T = \left[ {\begin{array}{*{20}l} A \hfill & B \hfill \\ C \hfill & D \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} 1 \hfill & {\omega (L_{{\text{a}}} + L_{{\text{b}}} )} \hfill \\ 0 \hfill & 1 \hfill \\ \end{array} } \right]\; \times \;\left[ {\begin{array}{*{20}l} 1 \hfill & {Z_{{\text{c}}} } \hfill \\ 0 \hfill & 1 \hfill \\ \end{array} } \right]\; \times \;\left[ {\begin{array}{*{20}l} 1 \hfill & {j\omega (L_{{\text{a}}} + L_{{\text{b}}} )} \hfill \\ 0 \hfill & 1 \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} 1 \hfill & {j2\omega (L_{{\text{a}}} + L_{{\text{b}}} ) + Z_{{\text{c}}} } \hfill \\ 0 \hfill & 1 \hfill \\ \end{array} } \right] $$
(2)

where ω is an angular frequency. We assume that at the resonance frequency fo, the angular resonance frequency is ωo = 2πfo. To minimize the insertion loss and improve the quality factor, obtaining the condition of perfect impedance matching is effective. Having a reflection coefficient (Г) of zero results in obtaining the perfect impedance matching. Accordingly, to achieve the perfect impedance matching at a resonance frequency, we can write:

$$ \Gamma = \frac{A + B - C - D}{{A + B + C + D}} = 0 \Rightarrow j4\pi \,f_{o} (L_{{\text{a}}} + L_{{\text{b}}} ) + Z_{{\text{c}}} = 0 \Rightarrow f_{o} = \frac{{jZ_{{\text{c}}} }}{{4\pi \,(L_{{\text{a}}} + L_{{\text{b}}} )}} $$
(3)

The resonance frequency achieved by Eq. (3) can be calculated when the input impedance of the basic structure is zero. From Eq. (1) it is clear that to increase the external quality factor, the insertion loss should be very low as well as having a wide fractional bandwidth. To minimize the insertion loss, the condition of impedance matching in Eq. (3) should be performed. Ideally, for IL = 0 and from Eqs. (1) and (3), the external quality factor is obtained as follows:

$$ Q_{{\text{e}}} \, = \,\frac{{jZ_{c} }}{{2\pi (\Delta f)_{{3{\text{dB}}}} \,(L_{{\text{a}}} + L_{{\text{b}}} )}} $$
(4)

As a result of the above discussion, the resonance frequency is set at the desired point by controlling the ratio Zc/(La + Lb) while at the same time the perfect impedance matching can be obtained and the quality factor can be improved. The frequency response of the designed basic structure is presented in Fig. 2. This frequency response is obtained for la = 1 mm, lb = 12.5 mm with a width of 0.1 mm, 2lc = 8.8 mm with a width of 0.6 mm while the space between coupled lines is 0.1 mm. An RT/duroid®6002 substrate with relative dielectric constant (εr) = 2.93, thickness (h) = 30 mil, and a loss tangent (tan (δ)) = 0.0013 is used. The frequency response shows that the proposed basic structure has a low insertion loss of 0.1 dB at a center frequency of 2.095 GHz. By employing the basic structure, a BPF can be designed. Figure 3 illustrates the proposed BPF layout with its corresponding dimensions in mm.

Fig. 2
figure 2

Simulation result of the basic microstrip structure

Full size image
Fig. 3
figure 3

Proposed BPF layout

Full size image

In this layout, the meandrous spiral structures and patch feeds are added to the basic structure. The meandrous spirals have inductive features and the patches have capacitive properties while applying both of them can save the overall size. Moreover, there are several couplings between the thin microstrip lines that are close to each other. These couplings produce additional capacitors, which can help the equivalent LC circuit to obtain more passbands.

The frequency response of the proposed BPF layout as a function of the dimensions L, S, W1, and W2 are depicted in Fig. 4. As shown in Fig. 4, the third and fourth channels are heavily influenced by the lengths L and S as increasing in these lengths decreases the selectivity. Furthermore, an excessive increase in these lengths can destroy the last two channels. Changing the width W1 can shift the first resonance frequency, but if we decrease it to zero the second, third and fourth channels will disappear. As shown in Fig. 4, the last two channels are influenced by changing W2 while the first and second channels are almost unchanged.

Fig. 4
figure 4

Frequency responses as functions of L, S, W1, and W2

Full size image

From Fig. 4 it can be seen that by changing L, S, W1, and W2, it is possible to create a multichannel BPF with specific resonant frequencies. Therefore, in the next section, we apply an ANN model to create a multichannel BPF with the maximum number of channels and good insertion and return losses.

3 Proposed ann model

As mentioned in the previous section, the basic layout of the proposed BPF is tunable and also capable of creating different number of bandpass channels. The dimensions L, S, W1, and W2 have effect on resonant frequencies and the number of channels of the BPF. The other parameters that can affect both resonant frequencies and number of bandpass channels are the type and thickness of the substrate. In Fig. 4 the effects of L, S, W1, and W2 on the frequency response for a limited range of these parameters are shown. Rogers RT/duroid®6002 substrate with εr = 2.93, h = 31 mil and tan (δ) = 0.0013 is used. One way to create a multichannel BPF is to test all possible changes of the effective parameters on the resonant frequencies, i.e. L, S, W1, W2, and substrate type and thickness.

Since changing these effective parameters and then simulating the obtained layout in ADS software is difficult and very time-consuming, the use of an ANN model is proposed in this paper. For this purpose, the frequency, dimensions: L, S, W1, and W2 (in mm), substrate type, and substrate thickness (in mil) are used as the inputs of the ANN model. The outputs are S-parameters, i.e. S11 and S21 (in dB). The selected ranges of the inputs and outputs are shown in Table 1.

Table 1 Proposed inputs/outputs for the ANN model
Full size table

The aim of this paper is to design and simulate a BPF layout automatically with specified parameters such as size, passbands and etc. The conventional software like ADS can be used to design and simulate microstrip devices. But these devices are completely nonlinear and simulation of them is time-consuming. Also, the current tools like ADS software cannot be used to automatically design of microstrip devices. Therefore, we used MLP type of ANNs. ANNs can be used to extract patterns and detect trends that are too complex to be noticed by either humans or other computer methods and softwares. A trained ANN can be thought of as an "expert" to derive meaning from complicated or imprecise data. On the other hand, MLP can be applied to complex non-linear problems. It works with large input data and provides quick predictions after training. In MLP the same accuracy ratio can be achieved even with smaller data.

In Table 1, the defined input parameters ranges are selected as follows; the frequency range is between 0 and 7 GHz to cover most of the wireless applications, e.g., WLANs, GPS, WiMAX, GSM, and WCDMA. The dimensions range of L, S, W1, and W2 are selected as the practical ranges and to keep the BPF layout compact. The substrate types and dimensions are the most available commercially. The ranges of output parameters (S11 and S21) are the practical maximum and minimum values. Four types of substrates are used to develop the ANN model. Based on the substrate datasheets, the thickness of each substrate is selected and changed.

The dataset that used to develop the proposed ANN model is obtained by ADS software (about 15,000 input/output data). We divided this dataset into three groups: training data (about 70%), testing data (about 20%), and validation data (about 10%). We used multilayer perceptron (MLP) neural network structure because it is the most widely used ANN and usually has better performance in comparison to other ANN structures. Many different structures were tested for obtaining the best MLP model. We changed the number of hidden layers from 1 to 5 and the number of neurons in hidden layers from 5 to 20. The number of epochs is changed from 500 to 5000.

For each MLP structure the following training algorithms are tested:

  • Trainbr

  • Trainoss

  • Trainrp

  • Trainlm

The learning rate, which is an important parameter, is changed from 0.1 to 0.8.

After testing many MLP models, the best MLP structure with the minimum error is obtained with the following parameters:

  • Number of hidden layers: 4

  • Number of neurons in each hidden layer: 15

  • Learning rate: 0.5

  • Number of epochs: 3000

  • Adaption learning function: Trainlm

  • Activation function: Tansig

where Tansig function is given by:

$$ {\text{Tan}} {\text{sig}}(x) = \frac{2}{{1 + e^{ - 2x} }} - 1 $$
(5)

The proposed MLP structure is shown in Fig. 5.

Fig. 5
figure 5

Proposed MLP model

Full size image

The following equations relate the inputs to the outputs of the MLP model, where Yi, Zi, Ki, and Mi (i = 1, 2, …, 15) are the outputs of the first, second, third, and fourth hidden layers respectively.

$$ \left[ \begin{gathered} Y1 \hfill \\ Y2 \hfill \\ Y3 \hfill \\ Y4 \hfill \\ Y5 \hfill \\ Y6 \hfill \\ Y7 \hfill \\ Y8 \hfill \\ Y9 \hfill \\ Y10 \hfill \\ Y11 \hfill \\ Y12 \hfill \\ Y13 \hfill \\ Y14 \hfill \\ Y15 \hfill \\ \end{gathered} \right] = \,{\text{Tan}} {\text{sig}}\left( {\left[ {\begin{array}{*{20}l} { - 1.8} \hfill & { - 10.1} \hfill & {0.8} \hfill & {1.5} \hfill & { - 3.4} \hfill & {0.3} \hfill & {0.1} \hfill \\ {1.4} \hfill & {0.7} \hfill & { - 2.6} \hfill & {10.0} \hfill & { - 2.6} \hfill & {0.4} \hfill & { - 0.6} \hfill \\ {1.2} \hfill & { - 14.4} \hfill & {3.6} \hfill & {0.5} \hfill & {1.2} \hfill & {0.9} \hfill & { - 0.3} \hfill \\ {2.2} \hfill & {8.9} \hfill & {0.4} \hfill & {4.6} \hfill & { - 0.4} \hfill & { - 0.2} \hfill & { - 1.2} \hfill \\ { - 1.7} \hfill & {3.5} \hfill & {2.6} \hfill & {8.2} \hfill & { - 1.8} \hfill & {1.2} \hfill & {0.1} \hfill \\ { - 1.9} \hfill & { - 5.3} \hfill & { - 0.6} \hfill & {8.0} \hfill & {2.7} \hfill & {0.3} \hfill & {0.0} \hfill \\ {1.6} \hfill & {11.2} \hfill & { - 1.4} \hfill & {8.3} \hfill & {0.4} \hfill & { - 1.3} \hfill & {0.3} \hfill \\ { - 0.7} \hfill & { - 9.3} \hfill & { - 2.8} \hfill & { - 5.9} \hfill & {4.3} \hfill & {0.9} \hfill & {0.1} \hfill \\ {0.6} \hfill & {0.5} \hfill & { - 1.0} \hfill & {3.1} \hfill & {4.7} \hfill & {0.1} \hfill & { - 0.1} \hfill \\ {4.2} \hfill & { - 10.1} \hfill & {3.0} \hfill & {6.8} \hfill & { - 2.7} \hfill & {1.8} \hfill & { - 0.4} \hfill \\ {0.8} \hfill & { - 7.6} \hfill & {3.0} \hfill & {7.8} \hfill & { - 2.0} \hfill & {0.4} \hfill & { - 0.1} \hfill \\ { - 1.7} \hfill & { - 0.3} \hfill & {0.8} \hfill & { - 7.3} \hfill & {4.2} \hfill & {1.5} \hfill & {0.1} \hfill \\ {0.2} \hfill & {12.6} \hfill & { - 0.3} \hfill & { - 4.7} \hfill & {3.5} \hfill & { - 0.6} \hfill & {0.0} \hfill \\ {1.2} \hfill & { - 7.1} \hfill & { - 1.9} \hfill & {7.7} \hfill & { - 3.6} \hfill & {0.7} \hfill & { - 0.2} \hfill \\ {0.1} \hfill & { - 5.4} \hfill & { - 0.6} \hfill & { - 6.0} \hfill & { - 3.4} \hfill & {0.6} \hfill & {0.5} \hfill \\ \end{array} } \right]*\left[ \begin{gathered} f \hfill \\ L \hfill \\ S \hfill \\ W1 \hfill \\ W2 \hfill \\ {\text{Substrate}} \hfill \\ {\text{Thickness}} \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} 4.2 \hfill \\ 2.9 \hfill \\ 0.9 \hfill \\ - 8.5 \hfill \\ 0.1 \hfill \\ - 4.0 \hfill \\ - 10.1 \hfill \\ 1.0 \hfill \\ - 8.3 \hfill \\ 2.7 \hfill \\ - 3.7 \hfill \\ - 2.2 \hfill \\ - 5.6 \hfill \\ - 1.5 \hfill \\ 9.1 \hfill \\ \end{gathered} \right]} \right) $$
(6)
$$ \left[ \begin{gathered} Z1 \hfill \\ Z2 \hfill \\ Z3 \hfill \\ Z4 \hfill \\ Z5 \hfill \\ Z6 \hfill \\ Z7 \hfill \\ Z8 \hfill \\ Z9 \hfill \\ Z10 \hfill \\ Z11 \hfill \\ Z12 \hfill \\ Z13 \hfill \\ Z14 \hfill \\ Z15 \hfill \\ \end{gathered} \right] = \text{Tan} {\text{sig}}\left( {\left[ {\begin{array}{*{20}l} {0.22} \hfill & { - 0.73} \hfill & {2.61} \hfill & {1.10} \hfill & {1.00} \hfill & {1.95} \hfill & {0.38} \hfill & { - 0.86} \hfill & { - 3.74} \hfill & {1.93} \hfill & { - 3.24} \hfill & { - 0.44} \hfill & {1.38} \hfill & {2.31} \hfill & { - 1.28} \hfill \\ { - 0.49} \hfill & {1.62} \hfill & { - 0.44} \hfill & { - 0.68} \hfill & {0.37} \hfill & {1.71} \hfill & { - 0.17} \hfill & { - 0.96} \hfill & {2.28} \hfill & {0.20} \hfill & {1.71} \hfill & {3.27} \hfill & {2.65} \hfill & {1.26} \hfill & { - 0.21} \hfill \\ { - 1.35} \hfill & { - 3.93} \hfill & { - 2.53} \hfill & { - 1.25} \hfill & {0.20} \hfill & {0.52} \hfill & { - 0.29} \hfill & { - 0.75} \hfill & {1.02} \hfill & { - 1.45} \hfill & {2.59} \hfill & {1.90} \hfill & {1.51} \hfill & {4.46} \hfill & {0.13} \hfill \\ {0.33} \hfill & {0.37} \hfill & {0.39} \hfill & { - 0.13} \hfill & { - 0.23} \hfill & { - 2.41} \hfill & { - 1.09} \hfill & { - 3.04} \hfill & { - 0.74} \hfill & { - 1.65} \hfill & {0.00} \hfill & {1.23} \hfill & {0.22} \hfill & {1.13} \hfill & {0.18} \hfill \\ { - 0.39} \hfill & { - 0.11} \hfill & { - 0.40} \hfill & { - 1.21} \hfill & { - 0.88} \hfill & { - 0.98} \hfill & { - 2.53} \hfill & {0.38} \hfill & {1.65} \hfill & { - 1.19} \hfill & {1.61} \hfill & { - 3.97} \hfill & { - 2.28} \hfill & { - 0.74} \hfill & {0.78} \hfill \\ { - 0.77} \hfill & { - 1.91} \hfill & { - 2.59} \hfill & { - 1.25} \hfill & {2.04} \hfill & { - 0.52} \hfill & { - 0.07} \hfill & { - 0.92} \hfill & {0.78} \hfill & { - 0.46} \hfill & { - 1.60} \hfill & {1.71} \hfill & { - 1.30} \hfill & {0.99} \hfill & { - 0.28} \hfill \\ {1.44} \hfill & {0.63} \hfill & {5.48} \hfill & {1.90} \hfill & {1.50} \hfill & { - 0.35} \hfill & {1.79} \hfill & {2.05} \hfill & { - 1.77} \hfill & { - 0.12} \hfill & { - 5.65} \hfill & { - 4.78} \hfill & { - 0.19} \hfill & { - 2.78} \hfill & { - 3.36} \hfill \\ { - 0.21} \hfill & {1.27} \hfill & { - 1.55} \hfill & {2.88} \hfill & { - 0.05} \hfill & { - 0.03} \hfill & {0.04} \hfill & {2.82} \hfill & { - 0.08} \hfill & {5.21} \hfill & {2.15} \hfill & { - 2.01} \hfill & { - 1.40} \hfill & { - 1.00} \hfill & { - 1.70} \hfill \\ {0.85} \hfill & {0.38} \hfill & { - 0.82} \hfill & {0.54} \hfill & { - 2.07} \hfill & {0.06} \hfill & { - 2.72} \hfill & {2.65} \hfill & { - 3.27} \hfill & { - 2.50} \hfill & {0.22} \hfill & { - 1.40} \hfill & {1.37} \hfill & {0.09} \hfill & { - 1.07} \hfill \\ { - 0.13} \hfill & { - 0.72} \hfill & {0.43} \hfill & { - 0.47} \hfill & { - 0.94} \hfill & {0.78} \hfill & {0.58} \hfill & { - 0.73} \hfill & { - 2.57} \hfill & {1.55} \hfill & {2.71} \hfill & {1.07} \hfill & {1.43} \hfill & {2.04} \hfill & {1.60} \hfill \\ {1.10} \hfill & { - 2.48} \hfill & {3.76} \hfill & {2.13} \hfill & { - 0.59} \hfill & { - 1.02} \hfill & {0.68} \hfill & {0.49} \hfill & { - 0.97} \hfill & {1.79} \hfill & { - 3.23} \hfill & {1.26} \hfill & { - 2.67} \hfill & { - 1.34} \hfill & { - 1.34} \hfill \\ {0.10} \hfill & { - 1.20} \hfill & {1.32} \hfill & {1.13} \hfill & {0.80} \hfill & { - 2.58} \hfill & {0.46} \hfill & {3.07} \hfill & {0.61} \hfill & {1.82} \hfill & {2.06} \hfill & { - 3.21} \hfill & {1.39} \hfill & {0.02} \hfill & { - 1.56} \hfill \\ { - 2.49} \hfill & { - 1.44} \hfill & { - 1.55} \hfill & { - 1.14} \hfill & {0.21} \hfill & { - 0.03} \hfill & { - 0.64} \hfill & { - 1.86} \hfill & {1.11} \hfill & { - 1.11} \hfill & { - 2.45} \hfill & {1.47} \hfill & {0.16} \hfill & {1.16} \hfill & {1.02} \hfill \\ { - 1.62} \hfill & { - 1.81} \hfill & { - 0.82} \hfill & { - 1.21} \hfill & {0.84} \hfill & { - 0.19} \hfill & { - 5.78} \hfill & {0.27} \hfill & { - 1.40} \hfill & {0.25} \hfill & { - 0.96} \hfill & { - 1.45} \hfill & { - 1.16} \hfill & {0.60} \hfill & {1.61} \hfill \\ {0.44} \hfill & { - 0.19} \hfill & { - 0.48} \hfill & {1.50} \hfill & { - 1.41} \hfill & {0.16} \hfill & { - 0.16} \hfill & { - 0.97} \hfill & { - 0.99} \hfill & { - 0.61} \hfill & {0.10} \hfill & { - 0.49} \hfill & { - 0.92} \hfill & {3.05} \hfill & { - 0.02} \hfill \\ \end{array} } \right]\;*\;\left[ \begin{gathered} Y1 \hfill \\ Y2 \hfill \\ Y3 \hfill \\ Y4 \hfill \\ Y5 \hfill \\ Y6 \hfill \\ Y7 \hfill \\ Y8 \hfill \\ Y9 \hfill \\ Y10 \hfill \\ Y11 \hfill \\ Y12 \hfill \\ Y13 \hfill \\ Y14 \hfill \\ Y15 \hfill \\ \end{gathered} \right]\; + \;\left[ \begin{gathered} 1.05 \hfill \\ 1.89 \hfill \\ 2.03 \hfill \\ 0.95 \hfill \\ 1.15 \hfill \\ 0.39 \hfill \\ - 2.84 \hfill \\ - 1.75 \hfill \\ - 1.23 \hfill \\ 0.17 \hfill \\ - 1.12 \hfill \\ - 0.71 \hfill \\ - 0.69 \hfill \\ 2.66 \hfill \\ 1.00 \hfill \\ \end{gathered} \right]} \right) $$
(7)
$$ \left[ \begin{gathered} K1 \hfill \\ K2 \hfill \\ K3 \hfill \\ K4 \hfill \\ K5 \hfill \\ K6 \hfill \\ K7 \hfill \\ K8 \hfill \\ K9 \hfill \\ K10 \hfill \\ K11 \hfill \\ K12 \hfill \\ K13 \hfill \\ K14 \hfill \\ K15 \hfill \\ \end{gathered} \right] = {\text{Tan}} {\text{sig}}\left( {\left[ {\begin{array}{*{20}l} { - 2.40} \hfill & { - 6.72} \hfill & { - 3.48} \hfill & {7.70} \hfill & {1.25} \hfill & { - 0.08} \hfill & {3.02} \hfill & {2.46} \hfill & { - 3.11} \hfill & { - 4.17} \hfill & {3.31} \hfill & {1.45} \hfill & {2.14} \hfill & { - 5.45} \hfill & { - 0.09} \hfill \\ { - 1.79} \hfill & {1.20} \hfill & { - 0.70} \hfill & {2.29} \hfill & { - 0.83} \hfill & {0.45} \hfill & { - 0.51} \hfill & {1.46} \hfill & {0.04} \hfill & {0.32} \hfill & { - 1.01} \hfill & { - 1.02} \hfill & { - 2.06} \hfill & { - 3.13} \hfill & {0.68} \hfill \\ {0.06} \hfill & { - 3.02} \hfill & { - 0.17} \hfill & { - 3.60} \hfill & {2.34} \hfill & {0.00} \hfill & {0.12} \hfill & {1.43} \hfill & {1.44} \hfill & {4.28} \hfill & { - 2.85} \hfill & { - 0.43} \hfill & { - 0.38} \hfill & {5.83} \hfill & {4.33} \hfill \\ {1.38} \hfill & {0.19} \hfill & {3.56} \hfill & { - 2.20} \hfill & { - 0.28} \hfill & { - 1.98} \hfill & { - 3.05} \hfill & { - 2.06} \hfill & {2.05} \hfill & {0.48} \hfill & { - 0.78} \hfill & { - 2.37} \hfill & {1.84} \hfill & {2.67} \hfill & {3.36} \hfill \\ { - 1.31} \hfill & {0.14} \hfill & { - 0.69} \hfill & {3.35} \hfill & {1.18} \hfill & { - 0.43} \hfill & { - 1.92} \hfill & { - 3.52} \hfill & { - 0.60} \hfill & {0.55} \hfill & {2.22} \hfill & {0.84} \hfill & {1.96} \hfill & {4.64} \hfill & {1.23} \hfill \\ { - 0.23} \hfill & { - 0.86} \hfill & {1.12} \hfill & { - 3.73} \hfill & {1.70} \hfill & { - 3.28} \hfill & { - 2.15} \hfill & {3.03} \hfill & { - 2.07} \hfill & { - 1.01} \hfill & {0.02} \hfill & {0.14} \hfill & {1.15} \hfill & {1.96} \hfill & {0.35} \hfill \\ { - 0.62} \hfill & {0.21} \hfill & {1.61} \hfill & { - 2.82} \hfill & {0.30} \hfill & { - 1.58} \hfill & { - 2.28} \hfill & {0.12} \hfill & { - 0.85} \hfill & { - 0.65} \hfill & {0.29} \hfill & { - 2.17} \hfill & {2.57} \hfill & {2.39} \hfill & {3.60} \hfill \\ { - 1.94} \hfill & {2.88} \hfill & { - 0.50} \hfill & {2.01} \hfill & {0.54} \hfill & { - 3.49} \hfill & { - 3.01} \hfill & { - 0.88} \hfill & { - 0.25} \hfill & {1.61} \hfill & {1.91} \hfill & { - 1.23} \hfill & {1.55} \hfill & { - 1.57} \hfill & { - 1.05} \hfill \\ {0.20} \hfill & { - 2.58} \hfill & { - 1.43} \hfill & {1.39} \hfill & {0.43} \hfill & {0.87} \hfill & {0.78} \hfill & { - 0.80} \hfill & {0.39} \hfill & { - 1.43} \hfill & {3.92} \hfill & { - 1.30} \hfill & {1.07} \hfill & {2.99} \hfill & {0.78} \hfill \\ {3.10} \hfill & {1.52} \hfill & {0.60} \hfill & {4.34} \hfill & {0.26} \hfill & {0.46} \hfill & {0.17} \hfill & {0.41} \hfill & { - 0.47} \hfill & { - 0.55} \hfill & {0.93} \hfill & {1.10} \hfill & { - 1.22} \hfill & {0.03} \hfill & { - 2.62} \hfill \\ {2.77} \hfill & {1.92} \hfill & {1.91} \hfill & { - 0.16} \hfill & { - 0.62} \hfill & {0.70} \hfill & { - 0.16} \hfill & { - 2.81} \hfill & {0.52} \hfill & { - 2.20} \hfill & {3.85} \hfill & { - 1.27} \hfill & { - 2.44} \hfill & {0.33} \hfill & {0.30} \hfill \\ { - 0.65} \hfill & {1.55} \hfill & {1.18} \hfill & { - 1.93} \hfill & {1.98} \hfill & {0.18} \hfill & {0.15} \hfill & { - 1.58} \hfill & {1.56} \hfill & { - 0.28} \hfill & {0.88} \hfill & { - 0.40} \hfill & { - 0.62} \hfill & {1.03} \hfill & {0.17} \hfill \\ {0.30} \hfill & { - 1.88} \hfill & {1.49} \hfill & { - 0.94} \hfill & { - 0.19} \hfill & {0.36} \hfill & {7.05} \hfill & {6.60} \hfill & {1.14} \hfill & {2.40} \hfill & {0.69} \hfill & {0.18} \hfill & {1.24} \hfill & {1.65} \hfill & { - 8.13} \hfill \\ {0.47} \hfill & { - 1.27} \hfill & {0.20} \hfill & { - 1.81} \hfill & { - 0.70} \hfill & { - 1.99} \hfill & { - 0.67} \hfill & { - 3.89} \hfill & {0.46} \hfill & {1.42} \hfill & {1.84} \hfill & {0.27} \hfill & {0.70} \hfill & { - 0.67} \hfill & {1.19} \hfill \\ {1.86} \hfill & {1.56} \hfill & { - 1.57} \hfill & {3.01} \hfill & { - 0.61} \hfill & {0.11} \hfill & {1.10} \hfill & { - 3.28} \hfill & {1.47} \hfill & {3.95} \hfill & { - 0.54} \hfill & { - 3.67} \hfill & {0.90} \hfill & {1.97} \hfill & {1.25} \hfill \\ \end{array} } \right]\;*\;\left[ \begin{gathered} Z1 \hfill \\ Z2 \hfill \\ Z3 \hfill \\ Z4 \hfill \\ Z5 \hfill \\ Z6 \hfill \\ Z7 \hfill \\ Z8 \hfill \\ Z9 \hfill \\ Z10 \hfill \\ Z11 \hfill \\ Z12 \hfill \\ Z13 \hfill \\ Z14 \hfill \\ Z15 \hfill \\ \end{gathered} \right]\; + \;\left[ \begin{gathered} - 1.92 \hfill \\ 0.42 \hfill \\ - 2.11 \hfill \\ 0.20 \hfill \\ 1.99 \hfill \\ - 3.63 \hfill \\ 1.62 \hfill \\ 0.93 \hfill \\ - 0.67 \hfill \\ 0.82 \hfill \\ 0.69 \hfill \\ - 0.30 \hfill \\ 5.81 \hfill \\ 2.12 \hfill \\ - 3.29 \hfill \\ \end{gathered} \right]} \right) $$
(8)
$$ \left[ \begin{gathered} M1 \hfill \\ M2 \hfill \\ M3 \hfill \\ M4 \hfill \\ M5 \hfill \\ M6 \hfill \\ M7 \hfill \\ M8 \hfill \\ M9 \hfill \\ M10 \hfill \\ M11 \hfill \\ M12 \hfill \\ M13 \hfill \\ M14 \hfill \\ M15 \hfill \\ \end{gathered} \right] = \text{Tan} {\text{sig}}\left( {\left[ {\begin{array}{*{20}l} { - 3.24} \hfill & {0.66} \hfill & { - 0.03} \hfill & { - 0.47} \hfill & { - 1.58} \hfill & {0.66} \hfill & {1.46} \hfill & { - 1.92} \hfill & { - 0.13} \hfill & { - 1.93} \hfill & { - 1.16} \hfill & {1.58} \hfill & {1.58} \hfill & {0.14} \hfill & {0.15} \hfill \\ {2.59} \hfill & { - 0.01} \hfill & { - 2.06} \hfill & {1.67} \hfill & {0.49} \hfill & { - 0.42} \hfill & {0.26} \hfill & {1.91} \hfill & {0.33} \hfill & { - 0.40} \hfill & { - 0.69} \hfill & { - 0.86} \hfill & { - 1.02} \hfill & {0.68} \hfill & { - 1.12} \hfill \\ { - 0.83} \hfill & {1.60} \hfill & { - 0.92} \hfill & { - 1.02} \hfill & {2.00} \hfill & {0.04} \hfill & { - 0.58} \hfill & { - 0.93} \hfill & { - 2.14} \hfill & {1.20} \hfill & {0.73} \hfill & { - 0.88} \hfill & {0.56} \hfill & { - 1.86} \hfill & { - 0.93} \hfill \\ { - 1.07} \hfill & {3.21} \hfill & { - 2.53} \hfill & { - 1.66} \hfill & { - 2.47} \hfill & {1.16} \hfill & {2.74} \hfill & { - 1.81} \hfill & { - 0.97} \hfill & { - 0.75} \hfill & {4.28} \hfill & { - 0.72} \hfill & {3.30} \hfill & { - 0.15} \hfill & {2.77} \hfill \\ { - 1.75} \hfill & {4.34} \hfill & {0.51} \hfill & { - 0.94} \hfill & { - 0.95} \hfill & { - 0.01} \hfill & {0.32} \hfill & {2.75} \hfill & {2.58} \hfill & { - 1.91} \hfill & { - 0.84} \hfill & {3.72} \hfill & { - 0.59} \hfill & {3.18} \hfill & { - 1.29} \hfill \\ {1.70} \hfill & { - 1.27} \hfill & {0.29} \hfill & { - 1.53} \hfill & {3.10} \hfill & {0.51} \hfill & { - 0.83} \hfill & { - 0.81} \hfill & { - 0.57} \hfill & { - 2.11} \hfill & { - 4.22} \hfill & {0.61} \hfill & { - 2.65} \hfill & {2.47} \hfill & { - 0.74} \hfill \\ { - 3.17} \hfill & { - 3.69} \hfill & { - 2.67} \hfill & { - 5.73} \hfill & { - 0.81} \hfill & {0.74} \hfill & { - 3.10} \hfill & { - 2.90} \hfill & { - 2.78} \hfill & {0.24} \hfill & { - 0.32} \hfill & {0.04} \hfill & {0.41} \hfill & { - 0.45} \hfill & {0.07} \hfill \\ { - 0.34} \hfill & {3.27} \hfill & { - 1.96} \hfill & {0.14} \hfill & {0.46} \hfill & {3.92} \hfill & {2.68} \hfill & {2.88} \hfill & { - 1.68} \hfill & { - 1.24} \hfill & {0.56} \hfill & {0.99} \hfill & { - 2.77} \hfill & {2.27} \hfill & {5.69} \hfill \\ { - 0.30} \hfill & {1.90} \hfill & {0.05} \hfill & {0.14} \hfill & {0.19} \hfill & { - 1.55} \hfill & { - 0.06} \hfill & { - 4.80} \hfill & { - 2.24} \hfill & {3.65} \hfill & { - 0.13} \hfill & { - 1.04} \hfill & {1.74} \hfill & { - 3.24} \hfill & {0.94} \hfill \\ { - 0.54} \hfill & {2.00} \hfill & {3.47} \hfill & { - 1.06} \hfill & { - 2.75} \hfill & {2.81} \hfill & {4.35} \hfill & {4.93} \hfill & {6.70} \hfill & {0.77} \hfill & { - 2.85} \hfill & { - 0.50} \hfill & {6.78} \hfill & {0.41} \hfill & {1.97} \hfill \\ { - 0.57} \hfill & {1.11} \hfill & { - 0.96} \hfill & {2.04} \hfill & { - 2.11} \hfill & {5.10} \hfill & { - 0.42} \hfill & { - 0.33} \hfill & { - 2.25} \hfill & {6.06} \hfill & {1.13} \hfill & {2.02} \hfill & {3.87} \hfill & {8.59} \hfill & {1.27} \hfill \\ { - 0.80} \hfill & {0.12} \hfill & {1.52} \hfill & { - 3.78} \hfill & {0.42} \hfill & { - 3.55} \hfill & { - 1.13} \hfill & { - 0.30} \hfill & {2.41} \hfill & { - 2.11} \hfill & { - 0.27} \hfill & {0.01} \hfill & {1.62} \hfill & { - 1.01} \hfill & {6.47} \hfill \\ {2.76} \hfill & { - 4.09} \hfill & {1.75} \hfill & {0.16} \hfill & {0.17} \hfill & {0.65} \hfill & {1.45} \hfill & {0.60} \hfill & {0.20} \hfill & { - 1.14} \hfill & { - 0.69} \hfill & { - 3.05} \hfill & { - 1.30} \hfill & {1.76} \hfill & {1.57} \hfill \\ { - 0.15} \hfill & {0.65} \hfill & { - 2.40} \hfill & {1.15} \hfill & {0.86} \hfill & {0.73} \hfill & { - 1.23} \hfill & { - 3.21} \hfill & { - 2.70} \hfill & {1.37} \hfill & { - 0.29} \hfill & { - 2.37} \hfill & {1.32} \hfill & { - 3.76} \hfill & {2.22} \hfill \\ { - 0.76} \hfill & { - 0.06} \hfill & { - 1.68} \hfill & { - 0.79} \hfill & {0.29} \hfill & { - 0.80} \hfill & {0.85} \hfill & { - 2.33} \hfill & { - 2.40} \hfill & {2.09} \hfill & {1.38} \hfill & { - 1.10} \hfill & {0.72} \hfill & { - 3.12} \hfill & {0.14} \hfill \\ \end{array} } \right]\;*\;\left[ \begin{gathered} K1 \hfill \\ K2 \hfill \\ K3 \hfill \\ K4 \hfill \\ K5 \hfill \\ K6 \hfill \\ K7 \hfill \\ K8 \hfill \\ K9 \hfill \\ K10 \hfill \\ K11 \hfill \\ K12 \hfill \\ K13 \hfill \\ K14 \hfill \\ K15 \hfill \\ \end{gathered} \right]\, + \;\left[ \begin{gathered} 2.00 \hfill \\ - 4.27 \hfill \\ 1.75 \hfill \\ - 5.91 \hfill \\ 4.10 \hfill \\ - 0.91 \hfill \\ 0.06 \hfill \\ - 1.05 \hfill \\ 1.85 \hfill \\ - 6.41 \hfill \\ - 1.75 \hfill \\ - 1.49 \hfill \\ - 4.64 \hfill \\ - 2.10 \hfill \\ - 2.67 \hfill \\ \end{gathered} \right]} \right)$$
(9)
$$ \left[ {\begin{array}{*{20}l} {S11 } \hfill & {S21} \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} { - 1.3} \hfill & { - 2.37} \hfill & {6.66} \hfill & {1.53} \hfill & { - 0.16} \hfill & { - 2.9} \hfill & {1.56} \hfill & {1.82} \hfill & {1.8} \hfill & { - 1.4} \hfill & { - 2.08} \hfill & { - 1.66} \hfill & {4.9} \hfill & {3.55} \hfill & { - 5.09} \hfill \\ {0.48} \hfill & {0.46} \hfill & { - 1.66} \hfill & {0.35} \hfill & {1.78} \hfill & {2.72} \hfill & { - 2.17} \hfill & { - 1.26} \hfill & { - 1.08} \hfill & {1.4} \hfill & {1.64} \hfill & {1.69} \hfill & { - 1.22} \hfill & {1.68} \hfill & { - 2.12} \hfill \\ \end{array} } \right]\,*\,\left[ \begin{gathered} M1 \hfill \\ M2 \hfill \\ M3 \hfill \\ M4 \hfill \\ M5 \hfill \\ M6 \hfill \\ M7 \hfill \\ M8 \hfill \\ M9 \hfill \\ M10 \hfill \\ M11 \hfill \\ M12 \hfill \\ M13 \hfill \\ M14 \hfill \\ M15 \hfill \\ \end{gathered} \right]\, + \,\left[ {\begin{array}{*{20}l} { - 1.63 } \hfill & {0.83} \hfill \\ \end{array} } \right] $$
(10)

In Fig. 6, the comparison between the ADS simulation and proposed ANN method is shown, where CF (correlation coefficient) and MAE (mean absolute error) are given by:

$$ {\text{CF}} = 1 - \left[ {\frac{{\sum\nolimits_{{i = 1}}^{N} {(X_{i} ({\text{Sim}}) - X_{i} ({\text{Pred}}))^{2} } }}{{\sum\nolimits_{{i = 1}}^{N} {(X_{i} ({\text{Sim}}))^{2} } }}} \right]$$
(11)
$$ {\text{MAE}} = \frac{1}{N}\sum\nolimits_{{i = 1}}^{N} {\left| {X_{i} ({\text{Sim}}) - X_{i} ({\text{Pred}})} \right|} $$
(12)

where ‘X(Pred)’ and ‘X(Sim)’ are the predicted (MLP) and simulated (ADS) values respectively, and N is the number of all data. From Fig. 6 it can be seen that the proposed MLP model is very accurate in comparison with the ADS simulation.

Fig. 6
figure 6

Comparison of ADS simulation with the proposed ANN method

Full size image

The main advantage of the proposed ANN model is its very fast response compared to the ADS software. For example, if an ADS simulation takes a few minutes to simulate a BPF layout, the proposed ANN model can do it in a few milliseconds. Also, the obtained ANN model can predict the outputs of new input datasets that are not within the training and testing data. Therefore, based on its high accuracy and fast prediction speed we used this MLP model to obtain high-performance multichannel BPFs with different layouts.

For this purpose, the following algorithm is used:

The aim is to create a multichannel BPF which has n bandpass channels at f1, f1,…,fn (in GHz). Therefore, the algorithm takes the number of n preferred bandpass channels from the user and tries to create an n-channel BPF by changing the input parameters shown in Table 1. For this purpose, the algorithm changes L, S, W1, W2, substrate type, and thickness of the substrate in their specific ranges. Then, the proposed ANN model obtains S11 and S21 by using Eqs. (6–10).

A bandpass channel must have a large value of S21 (in dB) and a small value of S11 (in dB). It must also have a reasonable fractional bandwidth (FBW). There is a reasonable distance between two consecutive bandpass channels. In addition, at least one large value of S11 (small value of S21) must exist as transmission zero between two consecutive bandpass channels. At the beginning of this process, the algorithm receives all the above conditions from the user. For example, we determined for the algorithm that if all of the following conditions occur, it indicates that the desired bandpass channel has been created:

  1. 1-

    Any bandpass channel must have S21 > − 1.5 dB and S11 < − 15 dB.

  2. 2-

    For each bandpass channel, FBW% > 5%.

  3. 3-

    The distance between two consecutive bandpass channels must be greater than 0.3 GHz.

  4. 4-

    At least one transmission zero with S21 < − 15 dB and S11 > − 3 dB must exist between two consecutive bandpass channels.

  5. 5-

    Five bandpass channels are needed, i.e. 0.75 GHz, 2.5 GHz, 4.2 GHz, 3.7 GHz, and 5.7 GHz.

At first, the algorithm takes preferred bandpass channels and the above conditions. Then, all possible values of the input parameters (f, L, S, W1, W2, substrate type, and substrate thickness) are tested using the proposed ANN model for obtaining the maximum number of preferred bandpass channels. At the end of this process, a high-performance multichannel BPF can be created.

The prediction of S11 and S21 for some values of the input parameters is shown in Fig. 7. Using the proposed method, a high-performance QB-BPF is designed in this paper. Figure 8 shows the proposed QB-BPF. To obtain the preferred bandpass channels, the proposed method selected L = 0.3 mm, S = 1 mm, W1 = 0.6 mm, W2 = 1.4 mm, Rogers RT/duroid® 6002 substrate, and substrate thickness of 30 mil. Using these conditions, the following bandpass channels are obtained: 0.7 GHz, 2.7 GHz, 3.8 GHz, and 5.6 GHz.

Fig. 7
figure 7

ANN prediction of S11 and S21 for different values of the input parameters

Full size image
Fig. 8
figure 8

Proposed QB-BPF layout (all dominations are in mm)

Full size image

At the four resonance frequencies, the current density distribution of the introduced filter is presented in Fig. 9. As shown in Fig. 9, the spirals have the most significant effect on creating the second and third channels. The effect of coupling capacitors of the central coupled lines is important.

Fig. 9
figure 9

Current density distribution of the presented QB-BPF at 0.7, 2.2, 3.8, and 5.6 GHz

Full size image

4 Simulation and measurement results

We used ADS software and the MLP model to design and simulate the presented filter. To fabricate the proposed QB-BPF, a Rogers RT/duroid® 6002 substrate with εr = 2.93, h = 30 mil, and tan (δ) = 0.0013 is used. N5230A Network Analyzer is used to obtain the measurement results. The simulation and measurement results of the designed QB-BPF and a photograph of fabricated QB-BPF are shown in Fig. 10. It operates at 0.7 GHz (0.49–0.87 GHz), 2.2 GHz (1.94–2.36 GHz), 3.8 GHz (3.52–4.1 GHz), and 5.6 GHz (5.44–5.71 GHz).

Fig. 10
figure 10

Frequency response of the designed filter and a photo of the fabricated QB-BPF

Full size image

The overall size of the proposed structure is 7.7 mm × 15.3 mm = 0.0012 λg2, where λg is the guided wavelength calculated at 0.7 GHz. The simulated insertion losses are 0.023 dB, 0.088 dB, 0.086 dB, and 0.3 dB at the first, second, third, and fourth bands, respectively. Because of the copper and junction losses, the measured results are a little more than simulations with a maximum tolerance of 0.5 dB. The return losses are good at all channels so that they are 34.8 dB, 27.2 dB, 28.9 dB, and 21.4 dB at the first, second, third, and fourth channels, respectively. The fractional bandwidths at the four channels are about 55%, 19.7%, 15.3%, and 4.8%, respectively.

The performance and size of our QB-BPF are compared with the previously published designs. Table 2 depicts the comparison results.

Table 2 Comparison of the proposed design with the previously published works
Full size table

As it can be seen in Table 1, in comparison with the QB-BPF presented in [22], our design has better insertion and return losses. Also, it is 37.5 times smaller in size. Compared to the proposed designs in [23, 24], our QB-BPF has better insertion and return losses. In the previous designs, the smallest QB-BPF is introduced in [12]. The size of this filter is only 0.0189 λg2. However, our filter is 15.75 times smaller than it. The best insertion losses in the previous designs are achieved by [23]. But, our design has better insertion losses. Good insertion and return losses are obtained by the QB-BPF presented in [23]. In comparison with this previous work, our QB-BPF has better insertion losses and wider fractional bandwidths. Also, the proposed design in this paper is more than 41 times smaller.

According to the comparison results listed in Table 2, the proposed filter has the smallest size, the lowest insertion losses, and good return losses. Moreover, there are several TZs with a minimum level of − 45 dB, which improve the selectivity and isolation between channels. The TZs are about − 60 dB, − 55 dB, − 45 dB, and − 52 dB at 1 GHz, 3 GHz, 5.2 GHz, and 6.5 GHz, respectively.

Group delay is another important parameter of the filters and diplexers, which represents the phase linearity and passband flatness. A passband with high group delay has a type of distortion, where some of the frequencies are amplified by different amounts [37]. However, there is no significant distortion as indicated by group delay < 10 ns while the insertion loss is low [38]. The group delay of the designed QB-BPF at its passbands is presented in Fig. 11. According to the obtained results, the maximum group delay is 2.2 ns at all channels. The maximum group delay of the proposed filter is compared with the previous BPFs and diplexers in Table 3. In Table 3, MGD and NCs are the maximum group delays at all channels and the number of channels, respectively.

Fig. 11
figure 11

Group delay of the designed QB-BPF at its passbands

Full size image
Table 3 Maximum group delay of the proposed filter in comparison to the previously published designs
Full size table

5 Conclusion

This paper presents a novel ANN-based method for designing and simulating microstrip multichannel bandpass filters. Using the proposed ANN model, a compact quad-band bandpass filter is designed, which consists of coupled lines and meandrous spirals. The introduced filter has low insertion losses of 0.023 dB, 0.088 dB, 0.086 dB, and 0.3 dB. Also, it has high return losses of 34.8 dB, 27.2 dB, 28.9 dB, and 21.4 dB making it appropriate for electromagnetic energy harvesting. Moreover, there are several transition zeros with a minimum level of -45 dB, which improve the frequency selectivity and isolation between the channels. Flat frequency response with a maximum 2.2 ns group delay at all channels is achieved. Therefore, the proposed quad-channel bandpass filter has all of the requirements demanded by modern multi-service communication systems.