1 Introduction

ADCs are essential parts in systems in which signal processing is performed. Pipeline ADCs offer attractive combination of speed, resolution and power consumption. These properties make them the most powerful and efficient data converters for applications such as wireless communication, image recognition and medical instrumentation. Monolithic, high-resolution pipeline ADCs are difficult to obtain due to imperfections in analog components. Designing high performance analog circuits and component matching become increasingly difficult as CMOS technologies are scaled to smaller geometries. Without using some form of calibration, these limitations make it difficult to implement a conventional pipeline ADC with an effective number of bits greater than 10 in the present VLSI technologies [1]. Different calibration techniques have been proposed to improve overall performance of an ADC. Calibration techniques can be of digital nature [2–5], analog nature [6], or mixed (analog and digital) nature [7]. These techniques are categorized into one of the followings:

  1. (I)

    Calibrations performed in factory: These methods, such as capacitor trimming, are one-time events and re-calibration is not possible.

  2. (II)

    Foreground calibrations: These techniques [8] interrupt the routine work of the ADC to perform calibration. One of advantages of the foreground calibration is possibility of re-calibration.

  3. (III)

    Background calibrations: In some applications, interruption of the ADC to perform calibration is not desirable and hence on-line calibration has been proposed [2, 3]. It can track environmental changes such as temperature drifts, component aging and supply voltage fluctuations.

As technology moves to nano-scale, large leakage currents, small intrinsic gain of transistors and limited signal swings impose stringent challenges for analog calibration. In contrast with analog domain, digital circuits become smaller, faster and consume less power in submicron CMOS technologies. Therefore in recent years many types of digital calibration schemes have been proposed. Many of these calibration techniques compensate only some specific errors [2–5] and the need for calibration processor that addresses all errors still remains.

This paper describes a novel technique based on post-processing of the output bits of an ADC. The basic idea is to force some small number of pre-defined inputs to the ADC and obtain corresponding outputs. In fact, pre-defined inputs are digitized by the ADC and influenced by component errors consequently. This data set is used to find a suitable correction function that acts as an inverse model of ADC errors. Since each input sample can be applied to the ADC at scheduled intervals, this approach does not need to disturb the converter routine work. A function approximation algorithm can estimate the model during normal conversion routine. The extracted model is updated in background frequently to track parameter variations due to environmental influences.

This paper organized as follows. The proposed processor architecture is introduced in Sect. 2. Section 3 describes the hardware implementation details. Simulation and implementation results are presented in Sect. 4, and the conclusions are discussed in Sect. 5.

2 The proposed processor architecture

2.1 Architecture overview

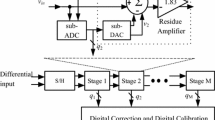
Block diagram of a pipeline ADC with proposed calibration processor is illustrated in Fig. 1. In the ADC, twelve bits of resolution is obtained through ten stages each having 1.5-bit/stage and a 2-bit last stage. The processor is shown inside the dashed box and consists of two RAMs, a function approximation unit and a digital DEMUX. The first five stages are calibrated because system level simulation result shows that the converter error is dominated by the first stages and no calibration is necessary for the least significant stages.

Fig. 1
figure 1

Proposed processor architecture

Full size image

The calibration procedure starts by feeding some pre-defined inputs to the ADC. These inputs are stored in the first RAM in form of digital codes. As shown in Fig. 1, the desired data (digital codes) are converted to analog domain by an external DAC and then passed through the ADC stages. The DAC is only used when pre-defined inputs are feeding to the ADC. These inputs are affected by component errors. The resulting digital outputs (actual data) are stored in the second RAM in the same order. Using this method, a set of inputs and a set of corresponding outputs are obtained. These two sets are then fed to the function approximation unit. It is worth to mention that in an ideal condition in which the ADC has no errors, we expect that an actual data set is equal to a desired data set. In this case, the function is an identity function. But in real situation, the actual data set are not similar to the desired data set since component errors disturb the ADC ideal function. In such cases, the extraction of an error model is essential. The main idea of the proposed technique is that the error model extraction is realized by using small number of the measured codes. It is remarkable that the extracted model is not constant and updated frequently to track parameter variations. In fact, the data stored in the first RAM are fed to the ADC at scheduled intervals and the data of the second RAM will change due to variations in the ADC parameters.

2.2 Function approximation algorithm

As mentioned before, two sets of codes in form of (x, F(x)) are stored in the two different RAMs for function approximation. Several techniques can be applied to approximate a function. Since the ADC has a nonlinear error model, a function approximation algorithm should be able to model relatively complex nonlinear function as an inverse model. In this work, a neural network and an interpolation scheme are tested for function approximation. The best approach in terms of performance has been used for hardware implementation.

2.2.1 Neural network

Neural networks have been used for ADC calibration in [9, 10]. In [9], a self-calibrating ADC employing a T-Model neural network is described. Errors of the converter are corrected by a simple error back propagation algorithm. The technique described in [10] can be considered as an improvement of the phase plane compensation technique. In fact, the error compensation tables represent ADC error partial discrete models, one for each signal dynamic.

In our work, the neural network has been used as a function approximation unit. The network inputs are the converter outputs and the network outputs are the calibrated output. The RBF (Radial Basis Function) [11] and the FFNN (Feed Forward Neural Network) [12] architectures have been used for network set up. After set up networks, the data stored in RAMs are used for training.

The simulation result shows that for calibration of a pipeline ADC, a FF network gives better result than a RBF network. The common algorithm for training of a FF network, gradient descent, is often too slow. Newton’s method is one of the algorithms that can converge fast [13]. The basic step of Newton’s method is:

$$ x_{k + 1} = x_{k} - A_{k}^{ - 1} g_{k} $$
(1)

where A −1k is the Hessian matrix (the second derivatives) of the performance index at the current values of the weights and biases. Unfortunately, it is complex and expensive to compute a Hessian matrix. Quasi-Newton (or secant) methods are a class of algorithms based on Newton’s method which does not require calculation of the second derivatives [14]. The Levenberg–Marquardt algorithm is one of these methods to approach the second-order training speed without necessity to compute the Hessian matrix [12, 15]. This algorithm uses the below approximation to a Hessian matrix in the following Newton-like update:

$$ x_{k + 1} = x_{k} - \left[ {J^{T} J + \mu .I} \right]^{ - 1} J^{T} e $$
(2)

where J is a Jacobian matrix that contains the first derivatives of the network errors with respect to the weights and biases, μ is the step parameter, and e is a vector of network errors. The simulation result shows that using this algorithm, the network converges within 10–20 iterations.

As explained in [1], the effects of decision boundaries imperfection cause several gaps in the converter transfer function. In this case, in the vicinity of certain input levels, major change occurs in the converter output. If the proposed method can eliminate these errors, the performance of overall calibration system will improve. Simulation results show that by use of a neural network with one hidden layer, the effect of these errors remains and cannot be removed completely. Although the performance of calibration system using two hidden layers neural network is improved, the computational complexity is also increased. In addition to above problem, another difficulty in using a neural network for ADC calibration is the lack of fast versatility with new data. As previously mentioned, the approximated function in the proposed system should be updated continuously to adapt to the new conditions. In a neural network, any change in the conditions, the training algorithm should run again on the entire training data. This feature increases power consumption and calibration time.

2.2.2 Interpolation

Interpolation is a method of constructing new data points within the range of a discrete set of known ones. There are different interpolation methods. In the proposed processor, we need a nonlinear complicated function. In such cases, a more flexible way is to divide the entire interval into a number of subintervals and to look for a piecewise approximation by polynomials of low degree. In this work, the Spline [16] and the Cubic Hermite [17] interpolations have been tested to find an appropriate algorithm. Both methods use an interpolating polynomial in each subinterval for piecewise interpolation of the overall function. Spline constructs the polynomial in almost the same way Hermite constructs it. However, Spline chooses the slopes at the partition points differently, namely to make even second derivative continuous. This has the following effects:

  1. 1.

    Spline produces a smoother result.

  2. 2.

    Spline produces a more accurate result if the data consists of values of a smooth function.

  3. 3.

    Hermite has no overshoots and less oscillation if the data are not smooth.

  4. 4.

    Hermite is less expensive to set up.

Since the effects of decision boundaries imperfection cause several gaps in the converter transfer function, a noncontinuous function should be approximated. By considering of the mentioned characteristics of each method, it seems that better results can be obtained by using of Hermite interpolation. The simulation results verify this conclusion. Also by use of Hermite algorithm, better results are obtained in comparison to the approximation using neural networks. Moreover, this algorithm does not have the mentioned problems of neural networks.

The procedure to perform hermite interpolation algorithm can be described as follows [17]:

At first, the entire interval, I = [a,b], are divided into a number of subintervals such as π = [xi,xi+1]. Each subinterval is a partition of “I” so that I:a = x1 < x2 < … < xi < xi+1<… < xn-1 < xn = b. Let (fi;i = 1,2,…n) be a given data set at the partition points. Our purpose is to construct on π a piecewise cubic function P(x) such that P(x) = fi;i = 1,2,…n. In each subinterval P(x) is a cubic polynomial which can be represented as follows:

$$ P(x) = \alpha_{3} (i)\left( {x - x_{i} } \right)^{3} + \alpha_{2} (i)\left( {x - x_{i} } \right)^{2} + \alpha_{1} (i)\left( {x - x_{i} } \right) + f_{i} $$
(3)

Let:

$$ d_{i} = P^{\prime } \left( {x_{i} } \right) $$
(4)
$$ del_{i} = \frac{{f_{i + 1} - f_{i} }}{{x_{i + 1} - x_{i} }} $$
(5)
$$ h_{i} = x_{i + 1} - x_{i} $$
(6)

Coefficients α3, α2, α1 can be calculated as follows:

$$ \alpha_{1} (i) = d_{i} $$
(7)
$$ \alpha_{2} (i) = \frac{{3\,del_{i} - 2\,d_{i} + d_{i + 1} }}{{\left( {x - x_{i} } \right)}} $$
(8)
$$ \alpha_{3} (i) = \frac{{d_{i + 1} + d_{i} - 2\,del_{i} }}{{\left( {x - x_{i} } \right)^{2} }} $$
(9)

Therefore an algorithm for constructing a piecewise cubic interpolant to {(xi,fi);i = 1,2,…n} is essentially a procedure to calculate the derivative values d1, d2,…, dn. In [17], a shape preserving method is discussed to calculate derivative values. More details on this method are described below.

$$ d_{i + 1} = \frac{{d_{\min } (i)}}{{w_{1} (i)\frac{{del_{i} }}{{d_{\max } (i)}} + w_{2} (i)\frac{{del_{i + 1} }}{{d_{\max } (i)}}}} $$
(10)
$$ d_{\max }^{\left( i \right)} = \max \left( {del_{i} ,del_{i + 1} } \right) $$
(11)
$$ d_{\min }^{\left( i \right)} = \min \left( {del_{i} ,del_{i + 1} } \right) $$
(12)
$$ w_{1} = \frac{{2h_{i} + h_{i + 1} }}{{3\left( {h_{i} + h_{i + 1} } \right)}} $$
(13)
$$ w_{2} = \frac{{h_{i} + 2h_{i + 1} }}{{3\left( {h_{i} + h_{i + 1} } \right)}} $$
(14)

The initial and the final derivative values are calculated as:

$$ d_{1} = \frac{{\left( {2h_{1} + h_{2} } \right)\,del_{1} - h_{1} \,del_{2} }}{{h_{1} + h_{2} }} $$
(15)
$$ d_{2} = \frac{{\left( {2h_{n - 1} + h_{n - 2} } \right)\,del_{n - 1} - h_{n - 1} \,del_{n - 2} }}{{h_{n - 1} + h_{n - 2} }} $$
(16)

Figure 2 shows the data flow of the coefficient calculation algorithm.

Fig. 2
figure 2

Data flow of the coefficient calculation algorithm

Full size image

The proposed method for calculation of derivative values is characterized by its efficiency, in terms of time required to determine the interpolant, storage required to represent it, and/or time required to evaluate it [17].

Unlike the global algorithms in which the approximation is defined by the same analytical expression on the whole interval, the main advantage of this algorithm is to locally interpolate the data points. In such a method, a single change in the data will affect the interpolant only in neighborhood. This property of this algorithm can be used to update each subinterval separately. Figure 3 gives the timing diagram for the coefficient calculation algorithm.

Fig. 3
figure 3

Timing diagram for the coefficient calculation algorithm

Full size image

A state machine controls the sequence of the events. This part uses a clock counter to control the timing of all coefficient calculation steps. The coefficient calculation algorithm is performed for each pre-defined input. As shown in Fig. 3, 7 clock cycles are needed for coefficient calculation procedure of each pre-defined input (except the first and the last data). Also, 3 and 4 clock cycles are necessary for the first and the last data respectively.

2.3 Pre-defined input distribution

As cited above, in the first step of calibration process some pre-defined digital codes should be stored in the first RAM. For precise approximation, these codes should be distributed over entire input range. One approach is to use a uniform distribution in which data points are selected from intervals with identical length. The simulation results show that at least 5% of all possible codes are needed to obtain satisfactory results. The possible codes are equal to 2N where N is the number of code bits. For example, in a 12-bit ADC, there are 4,096 possible codes and approximately 200 data are needed.

A nonuniform distribution is another approach which can be applied to reduce the number of data points. This technique can be useful because of the effect of decision boundaries of each stage on the ADC overall transfer curve [1]. As described in [1], in the neighborhood of the certain input levels, we observe a gap in the overall transfer curve of the ADC. These code gaps result from each stage errors. In fact, around certain input levels, the effect of errors is increased. Figure 4 illustrated error variation versus input codes.

Fig. 4
figure 4

Error distribution versus input codes

Full size image

In a non-uniform distribution, we can increase code density in the vicinity of the mentioned input levels and decrease code density in the other points. The non-uniform distribution is shown in Fig. 5.

Fig. 5
figure 5

Predefined input codes non-uniform distribution

Full size image

Simulation results show that non-uniform distribution is a more efficient than the uniform distribution and the same results can be obtained by less number of possible codes.

3 Hardware implementation

As described in Sect. 2, the role of the digital processor is to approximate a function that represents the inverse model of ADC errors. A function approximation unit is the most important part of this processor and its accuracy determines the overall accuracy of the proposed system. As mentioned in pervious section, because of its good properties, Hermite interpolation has been employed for hardware implementation. In fact, the purpose of implementation is to realize the Eq. 4. To realize this function, three tasks should be performed.

  1. 1.

    Coefficients calculation.

  2. 2.

    A search algorithm to find the corresponding subinterval that each new input belong to it.

  3. 3.

    Calculation of the Eq. 4.

Implementation of the function approximation unit is shown in Fig. 6. As illustrated, three blocks is designed to perform the mentioned tasks.

Fig. 6
figure 6

Details of the function approximation unit

Full size image

The input data to this unit are divided into two parts. The first part is the data stored in the RAMs and the second part is the converter outputs. By using the data stored in RAMs, the α3, α2, α1 are calculated by the algorithm described in Sect. 2. This algorithm has been implemented as shown in Fig. 7. This section requires high precision calculations since its accuracy determines the accuracy of the whole function approximation unit. To avoid floating point calculations, initially the processor input values are multiplied by a constant factor and after the completion of the calculations, the final number is divided to this factor again. This constant factor can be a power of 2 so that, the shift operation can be performed in, instead of multiplying at the first and dividing at the end.

Fig. 7
figure 7

Implementation of coefficient calculation algorithm

Full size image

As illustrated in Fig. 7, this unit has various components which include adders, subtractors, multipliers, comparator, divider, address pointer and a set of registers. A multiplexer is connected to the input of each block and the incoming signal to the block is controlled by its MUX. Each multiplexer has a control input that determines which input is to be transferred to the output. Also, each register and address pointer block have an enable input. A control unit is designed to generate the control bits from an input clock signal. This part is a state machine that controls the timing of all coefficient calculation steps. After calculation, the α3, α2, α1 are stored in the coefficient RAM. Since the operation of the coefficient calculation unit is performed in the background, its working frequency can be less than the converter sampling frequency. This feature reduces the power consumption of this unit.

In the second part, after each entry of the ADC outputs to the processor, their values are compared with the second RAM (Actual Data) values. This task is carried out by a search block. For this part, a binary search algorithm has been implemented to identify the corresponding subinterval. Subsequently, the Eq. 4 is applied to calculate the calibrated output which is the output of the interpolation block. The search and the interpolation block are illustrated in Fig. 8. Since these two blocks work along with converter, its frequency should be the same as the ADC sampling frequency. To achieve this feature, pipeline architecture has been used in design of these units. In this architecture, the calculations related to each section are divided into several parts and each part of the calculation is performed by separate blocks.

Fig. 8
figure 8

Implementation of search and interpolation units

Full size image

Although it seems that the power consumption of the proposed architecture is of a major concern, but it is remarkable that the most part of the processor are work with a lower frequency three times smaller than the converter sampling frequency. In fact, coefficients calculation process performed in the background for the small number of the measured codes. This process updates the coefficient RAM with lower rate than the ADC sampling rate and only the search and the interpolation unit work along with converter. This property reduces the total power consumption of the processor.

Table 1 gives the utilization of hardware resources for processor.

Table 1 Utilization of hardware resources
Full size table

4 Measured results

To verify the proposed calibration scheme, a 12-bit pipelined ADC based on 1.5-bit per stage architecture is simulated in the SIMULINK. Gain, sub-DAC reference voltages, systematic offset and nonlinearity are the controllable variables of the simulated pipelined ADC. Each stage has a gain error of 2%, a reference voltage error of 1%, a systematic offset error of 2% and a third order non-linearity of 1%. The value of those errors can be different in each stage. Figure 9 shows the output spectrum of the ADC before and after calibration.

Fig. 9
figure 9

Output spectrum: (a) before calibration (b) after calibration

Full size image

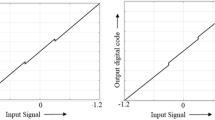
The input range for converter is set to 2 V (p–p) and the reference voltage for the converter is set to 1 V. A sampling frequency of 100 MHz and the sinusoidal input signal of 20 MHz with the amplitude of 1 V are used. Figure 10 shows the uncorrected and the corrected INL profile for the ADC.

Fig. 10
figure 10

INL: (a) before calibration (b) after calibration

Full size image

Figure 11 shows the variation of SNR and SFDR with varying input frequency before and after calibration.

Fig. 11
figure 11

Measured performances versus input frequency sampled at 100MS/s (a) SNR (b) SFDR

Full size image

Table 2 represents the system level simulation of the different function approximation algorithms. In the simulation, 2.5% of possible codes with uniform distribution are used as a pre-defined input. As given, by use of the Hermite Interpolation algorithm, the better result can be obtained. The improvements in the performance after hardware implementation are summarized in Table 3 for the 2.5% and the 5% of possible codes as a pre-defined input set. Table 4 shows the comparison of the proposed calibration technique to some other reported calibration techniques. This table shows that by use of the proposed architecture, extra improvements can be obtained in higher sampling frequencies. Table 5 illustrates the comparison of the gate count for design with some other FPGA based calibration methods. Table 6 summarizes the simulated performance.

Table 2 Comparison of the different function approximation algorithms
Full size table
Table 3 Performance summary before and after calibration for 2.5% and 5% of possible codes
Full size table
Table 4 Comparison of the proposed architecture with some other reported calibration methods
Full size table
Table 5 Comparison of the gate count for design with some other methods
Full size table
Table 6 Performance summary
Full size table

5 Conclusion

A Digital processor for full calibration of pipelined ADCs was presented. In this technique, the modifications of the ADC components are not necessary. The proposed processor employs a function approximation unit to find a function that acts as an inverse model of ADC errors. This error modeling is performed by using small number of the measured codes. Linear and nonlinear gain errors, component mismatch and sub-DAC nonlinearity in a pipeline ADC can be compensated by use of this method. Some function approximation algorithms were tested to find the best results. In the proposed technique, the use of cubic hermite interpolation was led to better results in performance and hardware costs. Therefore, this algorithm was selected for hardware implementation. The algorithm is simple and the interpolant is affected locally by changes in the data. This feature reduces the calibration time and power consumption. Compared to the other calibration methods, the technique presented in this paper is distinguished by its efficiency in terms of time required to determine the interpolant and storage required to represent it. By use of the proposed calibration architecture, extra improvements in higher frequency can be obtained. For a simulated ADC, the SNDR of the converter is improved by 25 dB and the SFDR is improved by 45 dB. The proposed technique is applicable to higher resolution pipeline architecture and the required area to implement the necessary digital logic scales down with the new process technologies.