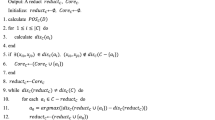Incremental reduction algorithm with acceleration strategy based on conflict region

Abstract

Attribute reduction plays a vital role in many areas of data mining and knowledge discovery. In the real world, several data sets may vary dynamically and many incremental reduction algorithms have been proposed to update reduct. Further improvement of the performance of the incremental reduction approach is an important task that can help to increase the efficiency of knowledge discovery in dynamic data systems. This paper researches incremental reduction algorithms via an acceleration strategy to compute new reduct based on conflict region. We firstly introduce the concepts and propositions of the conflict region and give a static reduction algorithm based on the conflict region. Consequently, incremental mechanisms based on the conflict region and an acceleration strategy for reduction are discussed. Then, two incremental reduction algorithms for updating new reduct when one single object and multi-objects are added to decision systems are developed. Finally, experiments on different data sets from UCI show the effectiveness and efficiency of the proposed algorithms in decision systems with the addition of objects.

1 Introduction

Feature selection (also called attribute reduction) is one of the important research contents in data mining, machine learning, intelligent data analysis and pattern recognition. In the real world, information expands quickly and plenty of features are stored in datasets. Some of the features in high-dimensional datasets are irrelevant or redundant, which typically deteriorates the performance of knowledge discovery algorithms.

Rough set theory is a powerful mathematical tool introduced by Pawlak (1982) to address imprecise, incomplete or vague information. Many researchers have contributed to its development and applications. Attribute reduction is one of the fundamental aspects of rough set theory, which can find a subset of attributes (denoted as the reduct) that provides the same descriptive, discernibility or classification ability as the original condition attribute set. In the last two decades, many attribute reduction techniques have been developed. These techniques mainly include the discernibility matrix-based reduction approaches (Skowron and Rauszer 1992; Wei et al. 2013; Yao and Zhao 2009; Zhang et al. 2003), the discernibility and indiscernibility-based reduction approaches (Li and Yao 2010; Qian et al. 2011; Susmaga and Słowiński 2015; Teng et al. 2010; Zhao et al. 2007), the positive region-based reduction approaches (Liu et al. 2009; Qian et al. 2010; Shen and Jensen 2004; Xu et al. 2006), the information entropy and its variation entropy-based reduction approaches (Hu et al. 2007; Liang and Xu 2002; Miao and Hu 1999; Qian et al. 2009), etc. These studies have offered interesting insights into attribute reduction and have been successfully applied to decision systems. However, most of the above reduction approaches can only be suitable for static data sets. When data sets vary with time, these algorithms must be re-implemented to obtain new reduct, which consumes a huge amount of computational time and space. It is very time-consuming or even infeasible to run repeatedly the static reduction algorithms. Hence, these static reduction algorithms are very inefficient when dealing with dynamic data tables.

Many scholars have noticed the shortcoming of the static reduction methods for dynamic data sets. Thereupon, based on rough set theory, some incremental learning approaches, instead of static reduction approaches, have been applied to obtain new reduct for dynamic systems. The incremental attribute reduction from dynamic decision systems can be broadly classified into three classes. The first class is the study on updating attribute reduction caused by variation of the object set (Chen et al. 2013; Fan et al. 2009; Huang et al. 2013; Jing et al. 2016a), the second class is the study on updating attribute reduction caused by variation of the attribute set (Jing et al. 2016b; Li et al. 2007, 2013; Zhang et al. 2012), and the third class is the study on updating attribute reduction caused by variation of the attribute values (Chen et al. 2010, 2012; Huang et al. 2016; Li and Li 2015).

Many papers concentrate on attribute reduction for dynamic variation of the object set in decision systems. Liu (1999) proposed an incremental reduction algorithm for the minimal reduct. This algorithm can only be applied to information systems without decision systems. Hu et al. (2005) presented a positive region-based attribute reduction algorithm to update the reduct via an incremental technique. Yang (2007) provided an incremental updating reduction algorithm based on an improved discernibility matrix in decision systems. However, it only considers the situation in which only a single object is entered into the systems. Xu et al. (2011) provided a dynamic attribute reduction algorithm based on integer programming in the decision systems. They considered multiple objects being entered into the system, but the entering of multiple objects is just seen as the cumulative change of a single object, which is inefficient when an object set is added into the decision systems. Regarding multiple objects being added into the decision systems, Liang et al. (2014) introduced incremental mechanisms for three representative information entropies and presented a group incremental approach to feature selection based on three information entropies. Wang et al. (2013a) developed incremental feature selection algorithms for decision systems that dynamically increase the attribute set based on three representative entropies. Moreover, Wang et al. (2013b) proposed attribute reduction algorithms for data sets with dynamically varying data values based on three representative entropies. Lang et al. (2014) presented an incremental approach to attribute reduction of dynamic set-valued information systems with respect to three aspects: variations of the attribute set, immigration and emigration of objects, and alterations of the attribute value. Shu and Shen (2014a) proposed incremental reduction algorithms for when an attribute set is added into and deleted from incomplete decision systems. In addition, Shu and Shen (2014b) presented efficient incremental feature selection algorithms for a single object and multiple objects with varying feature values, respectively. Zeng et al. (2015) presented a new hybrid distance for many types of data in hybrid information systems and researched updating mechanisms for reduction with variation of the attribute set and proposed two incremental feature selection algorithms with fuzzy rough set approaches.

From the above, the incremental technique improves the efficiency of reduction algorithms with dynamic systems. Can we further improve the performance of incremental reduction algorithms? This motivates us to develop efficient incremental reduction algorithms. In our previous work, we introduced the conflict region and proposed bidirectional heuristic reduction based on the conflict region (Ge et al. 2015). Moreover, it has been observed in many fields that the case of adding objects into decision systems is common. In this paper, we continue with this work and improve the approach to research incremental reduction algorithms with an acceleration strategy based on the conflict region for adding a single object and multiple objects. We firstly introduce the concept of the conflict region and the corresponding properties and give a static attribute reduction algorithm based on the conflict region. Then, we discuss the incremental mechanisms for adding a single object and multiple objects into decision systems based on the conflict region. Two incremental feature selection algorithms with an acceleration strategy for adding a single object and multiple objects are put forward. Finally, the performances of the incremental reduction algorithms are evaluated using several UCI datasets.

The contributions of this paper are as follows: (1) two incremental attribute reduction algorithms (IRACR-M and IRACR-S), used for adding multiple objects into decision systems rather than performing the static reduction algorithm repeatedly, are presented; (2) an acceleration strategy is presented by reducing the sort times to further increase the efficiency of the incremental reduction algorithms; and (3) the efficiency and effectiveness of the proposed algorithms are demonstrated on different UCI data sets.

The structure of the remainder of this paper is as follows. Section 2 briefly reviews preliminary notions in the rough set theory. Section 3 introduces the concept of the conflict region and gives a reduction algorithm based on the conflict region. Based on the conflict region, Sect. 4 designs the incremental reduction algorithm for adding a single object with the acceleration strategy and the incremental reduction algorithms for adding an object set with the acceleration strategy. Section 5 constructs a series of comparative experiments to evaluate the effectiveness and efficiency of our proposed incremental reduction algorithms. Finally, Sect. 6 gives conclusions that are drawn from this study.

2 Preliminaries of rough sets

In this section, we will review several basic concepts in rough set theory and the reduct of the positive region in the decision table.

2.1 Basic concepts of rough sets

Let $I=(U,A,V,f)$ be an information system, where $U=\{x_{1},x_{2},{\ldots },x_{n}\}$ is a non-empty finite set of objects called the universe; $A=\{a_{1},a_{2},{\ldots },a_{m}\}$ is a non-empty and finite set of attributes; $V=\{V_{a}\vert \, \forall \, a\in A\}$ is a set of a value domain of attributes, where $V_{a}$ is a value set of the attribute $a; f:U\times A \rightarrow V$ is called an information function ($f(x,a)\in V_{a}$ for each $a \in A)$.

For any $R\subseteq C$, the indiscernibility relation is defined as:

$$\begin{aligned} \hbox {IND}(R)=\{(x,y)\in U\times U \vert f (x,a)=f(y,a),\quad \forall \, a \in R \} \end{aligned}$$

That is, x and y are indiscernible with respect to R if and only if they have the same values for all attributes in R. The relation IND(R) is reflexive, symmetric and transitive and hence is an equivalence relation. $U{/}\hbox {IND}(R)=\{[x]_{R}{\vert }x\in U\}$(just as U / R) indicates the partitions of U induced by R, which denotes the equivalence class determined by x with respect to R, i.e., $[x]_{R}=\{y{\vert }y\in U,(x,y)\in \hbox {IND}(R)\}$.

For Pawlak’s rough set model, given an equivalence relation R on the universe U and a subset $X\subseteq U$, we have the lower approximation and upper approximation of X as follows

$$\begin{aligned} R_{-} (X)= & {} \bigcup \{x\vert [x]_{R}\subseteq X\},\\ R^{-}(X)= & {} \bigcup \{ x\vert [x]_{R}\cap X\ne \varPhi \}. \end{aligned}$$

The pair($R_-(X),R^{-}(X))$ is referred to as the rough set approximation of X, where $R_-(X)$ is the smallest definable set containing X and $R^{-}(X)$is the largest definable set contained in X.

From the rough set approximation, the positive region, negative region and boundary region of X can be defined:

$$\begin{aligned} \hbox {POS}_{R}(X)= & {} R_{-} (X),\\ \hbox {BND}_{R}(X)= & {} R^{-}(X)-R_{-} (X),\\ \hbox {NEG}_{R}(X)= & {} U -R^{-}(X). \end{aligned}$$

The positive region and negative region consist of objects whose descriptions allow for deterministic decisions regarding their membership in X. The boundary region consists of objects whose descriptions allow for non-deterministic decisions regarding their membership in X.

2.2 The positive region reduct of the decision table

A decision table can be denoted by $S=(U,C\bigcup D,V,f)$, where $C \bigcap D= \varPhi$; C and D are called the condition attribute set and decision attribute set, respectively. Assume the objects are partitioned into r mutually exclusive crisp subsets $\{D_{1},D_{2},\ldots , D_{r}\}$ by the decision attributes set D. Regarding $R\subseteq C$, denoted by POS$_{R}(D,U)=\bigcup _{i=1}^r R_- D_i$, it is called the positive region of D with respect to the condition attribute set R .

Given a decision table $S=(U,C \bigcup D,V,f)$, if $\exists x_{i},x_{j}\in U(i\ne j)$ and $f(x _{i},C)=f(x_{j},C)\wedge f(x_{i},D)\ne f(x _{j},D)$, then the decision table S is an inconsistent decision table and $x_{i}$, $x_{j}$ are called inconsistent objects; otherwise, the decision table S is a consistent decision table.

The attribute a is relatively indispensable in condition attribute set C if $\hbox {POS}_{C-\{a\}}(D,U) \ne \hbox {POS}_{C}(D,U)$; otherwise, a is said to be relatively dispensable in C. The set of relatively indispensable attributes is called core attribute set CORE(C).

Definition 1

Let $S=(U,C\bigcup D,V,f)$ be a decision table and $R\subset C$. For each $a \in C-R$, the joined significance measures of the attribute a based on the positive region in S can also be defined as

$$\begin{aligned} \textit{SIG}_{\mathrm{POS}}{}^{+}(a,R,D,U)= & {} {\upgamma }_{R^{\cup } \{a\}}(D,U)-{\upgamma }_{R}(D,U), \hbox { or}\\ \textit{SIG}_{\mathrm{POS}}{}^{+}(a,R,D,U)= & {} {\vert }\hbox {POS}_{R^{\cup } \{a\}}(D,U){\vert } -{\vert }\hbox {POS}_{R}(D,U){\vert } \end{aligned}$$

where $\upgamma _{R}(D,U)={\vert }\hbox {POS}_{R}(D,U){\vert }{/}{\vert }U{\vert }$.

Definition 2

Let $S=(U,C \bigcup D,V,f)$ be a decision table and $R\subseteq C$. For each $a \in R$, the weeded significance measures of the attribute a based on the positive region in S can also be defined as

$$\begin{aligned} { SIG}_{\mathrm{POS}}{}^{-}(a,R,D,U)= {\vert }\hbox {POS}_{R}(D,U){\vert }-{\vert }\hbox {POS}_{R-\{a\}}(D,U){\vert } \end{aligned}$$

Proposition 1

Given a decision table $S=(U,C \bigcup D,V,f)$, for $a \in C$, if $\textit{SIG}_{\mathrm{POS}}{}^{-}$$(a,C,D,U)>$0, then $a \in \hbox {CORE}(C)$.

Attribute reduction is one of the applications for the rough set theory; it is a condition attributes sub-set that can provide the same information for classification purposes as the entire set of original condition attributes. Hu and Cercone (1995) proposed a heuristic feature selection algorithm, called positive-region reduct, that keeps the positive region of the target decision unchanged. The classic positive region reduct of D with respect to C can be illustrated as follows.

Definition 3

Let $S=(U,C \bigcup D,V,f)$ be a decision table and $R\subseteq C$. R is a positive region reduct of D with respect to C, which is satisfied with

• (1) $\hbox {POS}_{C}(D,U)=\hbox {POS}_{R}(D,U)$;

• (2) $\forall \, a \in R,\hbox { POS}_{R}(D,U)\ne \hbox {POS}_{R-\{a\}}(D,U)$.

The first condition ensures that the reduct has the same positive region information as the whole set of condition attributes. The second condition ensures that the reduct is minimal and there are no redundant attributes in the reduct. Namely, condition (1) states that the attributes in R are sufficient, while condition (2) implies that every attribute in R is necessary.

3 Attribute reduction algorithm based on the conflict region

In this section, we will introduce the concepts and propositions of the conflict region and give attribute significance measures based on the conflict region. Then, a static attribute reduction algorithm based on the conflict region will be proposed.

3.1 The concepts and propositions of the conflict region

The expression of the approximations, positive region, negative region and boundary region is a subset of U; however, we can use the granular structure information to express the above notions and redefine the lower approximation and upper approximation by using the equivalence classes of the universe, which are referred to as the quotient of the lower approximation and upper approximation of X.

Definition 4

Let $I=(U,A,V,f)$ be an information system, $X \subseteq U$ and $R\subseteq A$. The quotients of the lower approximation and upper approximation of X are defined as follows, respectively.

$$\begin{aligned} {\widetilde{R}}_-(X)= & {} \{[x]_{R} \vert [x]_{R} \in U{/}R ,[x]_{R} \subseteq X\},\\ {\widetilde{R}}^{-}(X)= & {} \{[x]_{R} \vert [x]_{R} \in U{/}R ,[x]_{R} \cap X \ne \varPhi \}. \end{aligned}$$

where ${\widetilde{R}}_- (X)$ is the set of the equivalence classes defined by U / R, which are the subsets of X. ${\widetilde{R}}^{-}(X)$ is the set of the equivalence classes defined by U / R, which have a non-empty intersection with X. According to Definition 4, we give an expression of the lower and upper approximations as subsets of U / R rather than subsets of U.

Definition 5

Let $I=(U,A,V,f)$ be an information system, $X \subseteq U$ and $R\subseteq A$. The quotient of the positive region, boundary region and negative region of X are defined as follows, respectively.

$$\begin{aligned} \hbox {QPOS}_{R}(X)= & {} {\widetilde{R}}_{-} (X),\\ \hbox {QBND}_{R}(X)= & {} {\widetilde{R}}^{-}(X)-{\widetilde{R}}_- (X),\\ \hbox {QNEG}_{R}(X)= & {} U{/}R-{\widetilde{R}}^{-}(X) \end{aligned}$$

where $U{/}R=\{X_{1},X_{2},{\ldots },X_{r}\}$ denotes the quotient set of U by R.

Definition 6

Let $S=(U,C \bigcup D,V,f)$ be a decision table and $R\subseteq C$. We define the conflict region of D with respect to the condition attribute set R as follows (Ge et al. 2012).

$$\begin{aligned} \hbox {CON}_{R}(D,U)=U-\bigcup \nolimits _{i=1}^r R_- D_i =U-\hbox {POS}_{R}(D,U) \end{aligned}$$

$\hbox {POS}_{R}(D,U)$ indicates all objects defined by U / R that for sure can induce a certain decision class. $\hbox {CON}_{R}(D,U)$ indicates objects defined by U / R that can induce different decision class.

Definition 7

Let $S=(U,C \bigcup D,V,f)$ be a decision table and $R\subseteq C$. We give the quotient set of positive region and conflict region of D with respect to R as follows, respectively.

$$\begin{aligned} \hbox {QPOS}_{R}(D,U)= & {} \bigcup \nolimits _{i=1}^r {\widetilde{R}}_- D_i ,\\ \hbox {QCON}_{R}(D,U)= & {} U{/}R-\bigcup \nolimits _{i=1}^r {\widetilde{R}}_- D_i = U{/}R - \hbox {QPOS}_{R}(D,U). \end{aligned}$$

$\hbox {QPOS}_{R}(D,U)$ indicates the set of all equivalence classes defined by U / R that can for sure induce a certain decision. $\hbox {QCON}_{R}(D,U)$ indicates the set of all equivalence classes defined by U / R that can induce a partial decision.

Proposition 2

Let $S=(U,C \bigcup D,V,f)$ be a decision table. If S is consistent, then $\hbox {CON}_{R}(D,U)=\varPhi$ and $\hbox {QCON}_{R}(D,U)=\varPhi$; otherwise, $\hbox {CON}_{R}(D,U) \ne \varPhi$ and $\hbox {QCON}_{R}(D,U) \ne \varPhi$.

Proposition 3

Let $S=(U,C \bigcup D,V,f)$ be a decision table and $P\subseteq R\subseteq C$. The following properties hold.

• (1) $\hbox {POS}_{P}(D,U)\subseteq \hbox {POS}_{R}(D,U)$ and $\hbox {CON}_{R}(D,U) \subseteq \hbox {CON}_{P}(D,U)$,

• (2) ${\vert }\hbox {POS}_{P}(D,U){\vert }\le {\vert }\hbox {POS}_{R}(D,U){\vert }$ and ${\vert }\hbox {CON}_{R}(D,U){\vert }\le {\vert }\hbox {CON}_{P}(D,U){\vert }$,

• (3) ${\vert }\hbox {QPOS}_{P}(D,U){\vert }\le {\vert }\hbox {QPOS}_{R}(D,U){\vert }$ and ${\vert }\hbox {QCON}_{P}(D,U){\vert }\le {\vert }\hbox {QCON}_{R}(D,U){\vert }$.

Definition 8

Let $S=(U,C \bigcup D,V,f)$ be a decision table and $R\subset C$. For each $a \in C-R$, the joined significance measures of the attribute a based on the conflict region in S can also be defined as (Ge et al. 2012):

$$\begin{aligned} \textit{SIG}_{\mathrm{CON}}{}^{+}(a,R,D,U)={\vert }\hbox {CON}_{R}(D,U){\vert }-{\vert }\hbox {CON}_{R^{\cup } \{a\}}(D,U){\vert } \end{aligned}$$

Definition 9

Let $S=(U,C \bigcup D,V,f)$ be a decision table and $R\subseteq C$. For each $a \in R$, the weeded significance measures of the attribute a based on the conflict region in S can also be defined as: (Ge et al. 2012)

$$\begin{aligned} \textit{SIG}_{\mathrm{CON}}{}^{-}(a,R,D,U)= {\vert }\hbox {CON}_{R-\{a\}}(D,U){\vert }-{\vert }\hbox {CON}_{R}(D,U){\vert } \end{aligned}$$

According to Definition 9, when an attribute is removed from the attribute set R, the significance measure of the attribute with respect to R can be obtained. If ${SIG}_{\mathrm{CON}}{}^{-}(a,R,D,U)>0$, then the attribute a is indispensable; otherwise, if ${SIG}_{\mathrm{CON}}{}^{-}(a,R,D,U)=0$, it is dispensable.

Therefore, according to Definition 9, we can delete dispensable attributes from the attribute set R while reserving other important attributes. Deleting redundant attributes from the obtained attribute subset guarantees the completeness of the attribute subset.

Proposition 4

Given a decision table $S=(U,C \bigcup D,V,f)$, for $a \in C$, if ${SIG}_{\mathrm{CON}}{}^{-}$$(a,R,D,U)>0$, then $a \in$CORE(C) (Ge et al. 2012).

Definition 10

Given a decision table $S=(U,C \bigcup D,V,f)$ and $R\subseteq C$, R is the positive region reduct of S, which satisfies the following two conditions.

• (1) ${\vert }\hbox {CON}_{R}(D,U){\vert }={\vert }\hbox {CON}_{C}(D,U){\vert }$;

• (2) $\forall \, a \in R, {\vert }\hbox {CON}_{R-\{a\}}(D,U){\vert }\ne {\vert }\hbox {CON}_{R}(D,U){\vert }$.

The first condition guarantees that the reduct R has the same conflict information as the whole attribute set C; the second condition guarantees that there are no redundant attributes in the reduct R.

Example 1

Table 1 illustrates a decision table S, where $U{=}\{x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7},x_{8},x_{9}\}$, $C=\{a,b,c,d\}$ is the condition attribute set, and D is the decision attribute set. Let $P=\{{ bc}\}$ and $R=\{{ bcd}\}$.

We can obtain $U{/}P=\{\{x_{1},x_{7}\}, \{x_{2},x_{5}\},\{x_{4},x_{8}\},\{x_{3},x_{6},x_{9}\}\}$, $U{/}R=\{\{x_{2}\},\{x_{3},x_{9}\},$$\{x_{5}\},\{x_{6}\},\{x_{1},x_{7}\}, \{x_{4},x_{8}\}\}$, $U{/}C=\{\{x_{2}\},\{x_{3},x_{9}\},$$\{x_{5}\},\{x_{6}\},\{x_{1},x_{7}\},\{x_{4},x_{8}\}\}$ and $U{/}D=\{\{x_{4}\},\{x_{1},x_{5},x_{6},x_{8}\},\{x_{2},x_{3},x_{7},x_{9}\}\}$, where $D_{1}=\{x_{4}\}$, $D_{2}=\{x_{1},x_{5},x_{6},x_{8}\}$, $D_{3}=\{x_{2},x_{3},x_{7},x_{9}\}$ and $r=3$.

Assume $X=\{x_{1},x_{2},x_{4},x_{5},x_{7}\}$, we can have

${\widetilde{P}}_- (X)=\{\{x_{1},x_{7}\},\{x_{2},x_{5}\}\}$ and ${\widetilde{P}}^{-}(X)=\{\{x_{1},x_{7}\},\{x_{2},x_{5}\},\{x_{4},x_{8}\}\}$;

${\widetilde{R}}_- (X)=\{\{x_{1},x_{7}\},\{x_{2}\},\{x_{5}\}\}$ and ${\widetilde{R}}^{-}(X)=\{\{x_{1},x_{7}\},\{x_{2}\},\{x_{4},x_{8}\},\{x_{5}\}\}$;

$\hbox {QPOS}_{P}(X)={\widetilde{P}}_- (X)=\{\{x_{1},x_{7}\},\{x_{2},x_{5}\}\}$, $\hbox {QBND}_{P}(X)={\widetilde{P}}^{-}(X)-{\widetilde{P}}_- (X)=\{\{x_{4},x_{8}\}\}$ and $\hbox {QNEG}_{P}(X)=U{/}P-{\widetilde{P}}_- (X)=\{\{x_{3},x_{9}\}\}$;

$\hbox {QPOS}_{R}(X)={\widetilde{R}}_- (X)=\{\{x_{1},x_{7}\},\{x_{2}\},\{x_{5}\}\}$, $\hbox {QBND}_{R}(X)={\widetilde{R}}^{-}(X)-{\widetilde{R}}_- (X)=\{\{x_{4},x_{8}\}\}$ and $\hbox {QNEG}_{R}(X)=U{/}R-{\widetilde{R}}^{-}(X)=\{\{x_{3},x_{9}\}\}$.

Moreover, we can obtain

$\hbox {POS}_{P}(D,U)=\bigcup \nolimits _{i=1}^r P_- D_i ={\varPhi }$,

$\hbox {CON}_{P}(D,U)=U-\bigcup \nolimits _{i=1}^r P_- D_i =U-\hbox {POS}_{P}(D,U)=\{x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},$$x_{7},x_{8},x_{9}\}$,

$\hbox {QPOS}_{P}(D,U)=\bigcup \nolimits _{i=1}^r {\widetilde{P}}_- D_i ={\varPhi }$,

$\hbox {QCON}_{P}(D,U)=U{/}P-\bigcup \nolimits _{i=1}^r {\widetilde{P}}_- D_i =U{/}P-\hbox {QPOS}_{P}(D,U)=\{\{x_{1},x_{7}\},\{x_{2},x_{5}\},$$\{x_{4},x_{8}\},\{x_{3},x_{6},x_{9}\}\}$,

$\hbox {POS}_{R}(D,U)=\bigcup \nolimits _{i=1}^r R_- D_i =\{x_{2},x_{3},x_{5},x_{6},x_{9}\}$,

$\hbox {CON}_{R}(D,U)=U-\bigcup \nolimits _{i=1}^r R_- D_i =U-\hbox {POS}_{R}(D,U)=\{x_{1},x_{7},x_{4},x_{8}\}$,

$\hbox {QPOS}_{R}(D,U)=\bigcup \nolimits _{i=1}^r {\widetilde{R}}_- D_i =\{\{x_{2}\},\{x_{3},x_{9}\},\{x_{5}\},\{x_{6}\}\}$,

$\hbox {QCON}_{R}(D,U)=U{/}R-\bigcup \nolimits _{i=1}^r {\widetilde{R}}_- D_i =U{/}R-\hbox {QPOS}_{R}(D,U)=\{\{x_{1},x_{7}\},\{x_{4},x_{8}\}\}$,

$\hbox {POS}_{C}(D,U)=\bigcup \nolimits _{i=1}^r C_- D_i =\{x_{2},x_{3},x_{5},x_{6},x_{9}\}$,

$\hbox {CON}_{C}(D,U)=U-\bigcup \nolimits _{i=1}^r C_- D_i =U-\hbox {POS}_{C}(D,U)=\{x_{1},x_{7},x_{4},x_{8}\}$.

Since, ${\vert }\hbox {CON}_{R}(D,U){\vert }={\vert }\hbox {CON}_{C}(D,U){\vert }$ and $\forall \, a \in R$, ${\vert }\hbox {CON}_{R-\{a\}}(D,U){\vert }\ne {\vert }\hbox {CON}_{R}(D,U){\vert }, R$ is a reduct of S. Nevertheless, P is not a reduct of S.

Table 1 A decision table s

3.2 Static attribute reduction algorithm based on the conflict region

According to the research of Sect. 3.1, in this subsection, we will design a static heuristic attribute reduction algorithm based on the conflict region. The reduction algorithm includes three components: core attributes computation, attribute subset generation and redundant attributes detection. The description of the algorithm is as follows.

The time complexity analysis The radix sort algorithm is used to compute equivalence classes. The time complexity of computing the core attributes is $O({\vert }C{\vert }^{2}{\vert }U{\vert })$ in Step 1. Step 2 is to compute conflict region $\hbox {CON}_{R}(D,U)$, whose time complexity are $O({\vert }\hbox {CORE}{\vert }{\vert }U{\vert })$ in the worst case. In Step 3, the indispensable attributes are computed and added into the selected attribute subset in turn, the time complexity is $\sum _{i=1}^{|C-{\mathrm{CORE}}|} {|U|(|C-\hbox {CORE}|-i+1)}$. In Step 4, in the worst case, the time complexity of deleting redundant attributes from the obtained attribute subset R is $O({\vert }C{\vert }^{2}{\vert }U{\vert })$. Hence, the time complexity of Algorithm SRACR is $2O({\vert }C{\vert }^{2}{\vert }U{\vert })+O({\vert }\hbox {CORE}{\vert }{\vert }U{\vert })+ \sum _{i=1}^{|C-{\mathrm{CORE}}|} {|U|(|C-\hbox {CORE}|-i+1)}$.

Example 2

Table 1 illustrates a decision table S, where $U=\{x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7},x_{8},x_{9}\}$, $C=\{a,b,c,d$} is the condition attribute set and D is the decision attribute set.

We have $U{/}C=\{\{x_{1},x_{7}\},\{x_{2}\},\{x_{3},x_{9}\},\{x_{4},x_{8}\},\{x_{5}\},\{x_{6}\}\}$, where $\{x_{1},x_{7}\}$ and $\{x_{4},x_{8}\}$ are two inconsistent object set. Hence, Table 1 is an inconsistent decision table, and we have $\hbox {POS}_{C}(D,U)=\{x_{2},x_{3},x_{5},x_{6},x_{9}\}$ and $\hbox {CON}_{C}(D,U)=\{x_{1},x_{7},x_{4},x_{8}\}$.

We can get $\hbox {CON}_{C-\{a\}}(D,U)=\hbox {CON}_{C-\{c\}}(D,U) =\hbox {CON}_{C-\{d\}}(D,U)=\{x_{1},x_{7},x_{4},x_{8}\}$, and $\hbox {CON}_{C-\{b\}}(D,U)= \{x_{1},x_{7},x_{4}$, $x_{8},x_{6}\}$. Since $\textit{SIG}_{\mathrm{CON}}{}^{-}(b,C,D,U)=$${\vert }\hbox {CON}_{C-\{b\}}(D,U){\vert }-{\vert } \hbox {CON}_{C}(D,U){\vert }=1>0, b\in \hbox {CORE}(C)$. Let $R=\{b\}$. We get $\textit{SIG}_{\mathrm{CON}}{}^{+}(a,R,D,U)$=6 and $\textit{SIG}_{\mathrm{CON}}{}^{+}(c,R,D,U)= \textit{SIG}_{\mathrm{CON}}{}^{+}(d,R,D,U)=0$. We should select a to add into $R=\{{ab}\}$ and get $\hbox {CON}_{R}(D,U)=\{x_{1},x_{7},x_{4},x_{8}\}$. And then, we have ${\vert }\hbox {CON}_{R}(D,U){\vert }={\vert }\hbox {CON}_{C}(D,U){\vert }$. The attribute a can not be deleted from R. Hence, a reduct of S is $R=\{{ ab}\}$, where $U{/}R=\{\{x_{1},x_{7}\},\{x_{2},x_{3},x_{9}\},\{x_{4},x_{8}\},\{x_{5},x_{6}\}\}$.

4 Incremental attribute reduction algorithm based on the conflict region when adding one object

With variation of the decision systems, new objects are added into the original decision system due to the arrival of new information, which results in the existing reduct possibly becoming invalid. The static (non-incremental) attribute reduction approach is to re-perform Algorithm 1 to acquire new reduct, which is often very costly or even intractable. To overcome this shortcoming, it is necessary to develop the incremental reduction algorithm to avoid re-computation by utilizing previous results.

In this section, we focus on discussing attribute reduction updating mechanisms and an acceleration strategy when adding one object into the decision system.

4.1 Incremental updating mechanisms based on the conflict region when adding one object

When a new object is added into the decision system, instead of re-computing the reduct, the incremental reduction approach can be applied to obtain the new reduct to improve the performance of the attribute reduction algorithm. In this sub-section, we introduce the incremental mechanisms for updating the conflict region when adding one object instead of re-computing the new decision table. To further improve the efficiency of the incremental reduction algorithm, we research an acceleration strategy of reducing the number of the radix sort for equivalence partition. Finally, we design an incremental reduction algorithm with the acceleration strategy based on the conflict region when adding one object and list some examples to show the effectiveness of the proposed algorithm.

Given a decision table $S=(U,C \bigcup D,V,f)$ and a reduct R, we can get $U{/}R=\{X_{1},X_{2},{\ldots },X_{m}\}$ and $U{/}C=\{Y_{1},Y_{2},{\ldots },Y_{n}\}$. Assume that a new object $x_{new}$ is added into the decision table S. We can get $S'=(U\bigcup \{x_{new}\},C \bigcup D,V,f)$. Let $U'=U\bigcup \{x_{new}\}$, $U'{/}R=\{X_{1},{\ldots },X_{i}',{\ldots },X_{m}\}$ and $U'{/}C=\{Y_{1},{\ldots },Y_{j}',{\ldots },Y_{n}\}$. Four cases exist as follows for adding the object $x_{new }$ into the decision table S.

• Case (a) : $\exists j\in [1,\ldots ,n], Y_{j}'= Y_{j}\bigcup \{x_{new}\}$, ${\vert }Y_{j}{/}D{\vert }=1$ and ${\vert }Y_{j}'{/}D{\vert }=1$;

• Case (b) : $\exists j\in [1,\ldots ,n], Y_{j}'= Y_{j} \bigcup \{x_{new}\}$, ${\vert }Y_{j}{/}D{\vert }\ne 1$ and ${\vert }Y_{j}'{/}D{\vert }\ne 1$;

• Case (c) : $\exists j\in [1,\ldots ,n]$, $Y_{j}'= Y_{j} \bigcup \{x_{new}\}$, ${\vert }Y_{j}{/}D{\vert }=1$ and ${\vert }Y_{j}'{/}D{\vert }\ne 1$;

• Case (d) : $j=n+1$, i.e., $Y_{j}'=\{x_{new}\}$.

Case(a) shows that the object $x_{new}$ belongs to an existing non-conflict class; Case(b) shows that the object $x_{new}$ belongs to an existing conflict class; Case(c) shows that the object $x_{new}$ results in the generation of a new conflict region; Case(d) shows that the object $x_{new}$ produces a new non-conflict region.

Proposition 5

Given a decision table S and $R\subseteq C$, let $\hbox {CON}_{R}(D,U)$ be the conflict region of D with respect to R. A new object $x_{new}$ is added into S to get $S'=(U',C \bigcup D,V,f)$, where $U'=U\bigcup \{x_{new}\}$ and $U'{/}R=\{X_{1},{\ldots },X_{i}',{\ldots },X_{m}\}$. Let $\exists i\in [1,{\ldots },m]$, $X_{i}'=X_{i} \bigcup \{x_{new}\}$; we have the following propositions.

• (1) ${\vert }X_{i}{/}D{\vert }=1$ and ${\vert }X_{i}'{/}D{\vert }=1$, then $\hbox {CON}_{R}(D,U')=\hbox {CON}_{R}(D,U)$, $\hbox {QCON}_{R}(D,U')=\hbox {QCON}_{R}(D,U)$ and ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{R}(D,U){\vert }$;

• (2) ${\vert }X_{i}{/}D{\vert }=1$ and ${\vert }X_{i}'{/}D{\vert }\ne 1$, then $\hbox {CON}_{R}(D,U')=\hbox {CON}_{R}(D,U) \bigcup X_{i}'$, $\hbox {QCON}_{R}(D,U')=\hbox {QCON}_{R}(D,U) \bigcup X_{i}$’ and ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{R}(D,U){\vert }+{\vert }X_{i}'{\vert }$;

• (3) ${\vert }X_{i}{/}D{\vert }\ne 1$ and ${\vert }X_{i}'{/}D{\vert }\ne 1$, then $\hbox {CON}_{R}(D,U')=\hbox {CON}_{R}(D,U)\bigcup \{x_{new}\}$, $\hbox {QCON}_{R}(D,U')=\hbox {QCON}_{R}(D,U)-X_{i} \bigcup X_{i}'$ and ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{R}(D,U){\vert }+1$.

• (4) $i=m+1$, then $\hbox {CON}_{R}(D,U')=\hbox {CON}_{R}(D,U)$, $\hbox {QCON}_{R}(D,U')=\hbox {QCON}_{R}(D,U)$ and ${\vert }\hbox {CON}_{R}(D,U'){\vert }= {\vert }\hbox {CON}_{R}(D,U){\vert }$;

Proposition 6

Given a decision table S, let $\hbox {CON}_{C}(D,U)$ be the conflict region of D with respect to C. A new object $x_{new}$ is added into S to get $S'=(U',C \bigcup D,V,f)$, where $U'=U\bigcup \{x_{new}\}$ and $U'{/}C=\{Y_{1},{\ldots },Y_{j}',{\ldots },Y_{n}\}$. Let $\exists j\in [1..n]$, $Y_{j}'=Y_{j} \bigcup \{x_{new}\}$; we have the following propositions.

• (1) ${\vert }Y_{j}{/}D{\vert }=1$ and ${\vert }Y_{j}'{/}D{\vert }=1$, then $\hbox {CON}_{C}(D,U')=\hbox {CON}_{C}(D,U)$ and ${\vert }\hbox {CON}_{C}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U){\vert }$;

• (2) ${\vert }Y_{j}{/}D{\vert }=1$ and ${\vert }Y_{j}'{/}D{\vert }\ne 1$, then $\hbox {CON}_{C}(D,U')=\hbox {CON}_{C}(D,U) \bigcup Y_{j}'$ and ${\vert }\hbox {CON}_{C}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U){\vert }+{\vert }Y_{j}'{\vert }$;

• (3) ${\vert }Y_{j}{/}D{\vert }\ne 1$ and ${\vert }Y_{j}'{/}D{\vert }\ne 1$, then $\hbox {CON}_{C}(D,U')=\hbox {CON}_{C}(D,U)\bigcup \{x_{new}\}$ and ${\vert }\hbox {CON}_{C}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U){\vert }+1$;

• (4) $j=n+1$, then $\hbox {CON}_{C}(D,U')=\hbox {CON}_{C}(D,U)$ and ${\vert }\hbox {CON}_{C}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U){\vert }$.

Theorem 1

Given a decision table S, R is a reduct of S. Let $\hbox {CON}_{R}(D,U)$ and $\hbox {CON}_{C}(D,U)$ be the conflict region of D with respect to R and C, respectively. A new object $x_{new}$ is added into the decision table S to get $S'=(U',C \bigcup D,V,f)$, where $U'=U\bigcup \{x_{new}\}$, $U'{/}R=\{X_{1},{\ldots },X_{i}',{\ldots },X_{m}\}$ and $U'{/}C=\{Y_{1},{\ldots },Y_{j}',{\ldots },Y_{n}\}$. Let $\exists i\in [1..m]$, $X_{i}'=X_{i} \bigcup \{x_{new}\}$, and $\exists j\in [1..n], Y_{j}'=Y_{j} \bigcup \{x_{new}\}$; the following properties hold.

• (1) If $x_{new}$ satisfies Case(a), then ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }$;

• (2) If $x_{new}$ satisfies Case(b), then ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }$;

• (3) If $x_{new}$ satisfies Case(c), then ${\vert }\hbox {CON}_{R}(D,U'){\vert }\ge {\vert }\hbox {CON}_{C}(D,U'){\vert }$;

• (4) If $x_{new}$ satisfies Case(d), then ${\vert }\hbox {CON}_{R}(D,U'){\vert } \ge {\vert }\hbox {CON}_{C}(D,U'){\vert }$.

Proof

• (1) In this case, new conflict objects with respect to C and R are not generated, respectively. Thus, $\hbox {CON}_{C}(D,U)=\hbox {CON}_{C}(D,U')$ and $\hbox {CON}_{R}(D,U)=\hbox {CON}_{R}(D,U')$. Hence, ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }$.

• (2) In this case, $\exists x \in \hbox {CON}_{C}(D,U)$ satisfies $f(x,C)=f(x_{new},C)\wedge f(x,D) \ne f(x_{new},D)$ such that $\hbox {CON}_{C}(D,U')=\hbox {CON}_{C}(D,U)\bigcup \{x_{new}\}$. Likewise, $\exists y\in \hbox {CON}_{R}(D,U)$ satisfies $f(y,R)=f(x_{new},R)\wedge \, f(y,D) \ne f(x_{new},D)$ such that $\hbox {CON}_{R}(D,U')=\hbox {CON}_{R}(D,U)\bigcup \{x_{new}\}$. Hence, ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }$.

• (3) In this case, $\exists x \in Y_{j}$ satisfies $f(x,C)=f(x_{new},C)\wedge f(x,D) \ne f(x_{new},D)$, such that $\hbox {CON}_{C}(D,U')= \hbox {CON}_{C}(D,U) \bigcup Y_{j} \bigcup \{x_{new}\}$. Suppose $x_{new} \in X_{i}'$; there exist two cases as follows.

  • (1) $\exists y\in X_{i}$ and $X_{i} \supset Y_{j}$, then $\hbox {CON}_{R}(D,U')=\hbox {CON}_{R}(D,U) \bigcup X_{i} \bigcup \{x_{new}\}$, such that ${\vert }\hbox {CON}_{R}(D,U'){\vert }> {\vert }\hbox {CON}_{C}(D,U'){\vert }$;

  • (2) $\exists y\in X_{i}$ and $X_{i} =Y_{j}$, then $\hbox {CON}_{R}(D,U')=\hbox {CON}_{R}(D,U) \bigcup X_{i} \bigcup \{x_{new}\}$, such that ${\vert }\hbox {CON}_{R}(D,U'){\vert }= {\vert }\hbox {CON}_{C}(D,U'){\vert }$.

• (4) In this case, $x_{new}$ is a whole new object that is not the same as any objects of S such that $\hbox {CON}_{C}(D,U')=\hbox {CON}_{C}(D,U)$. However, there may exist three cases as follows.

  • (a) $i=m+1$, then ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }$;

  • (b) $i\le m$, ${\vert }X_{i}{/}D{\vert }=1$ and ${\vert }X_{i}'{/}D{\vert }=1$, then ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }$;

  • (c) $i\le m$, ${\vert }X_{i}{/}D{\vert }\ne 1$ and ${\vert }X_{i}'{/}D{\vert }\ne 1$, then $\hbox {CON}_{R}(D,U')=\hbox {CON}_{R}(D,U) \bigcup X_{i}'$ such that ${\vert }\hbox {CON}_{R}(D,U'){\vert }> {\vert }\hbox {CON}_{C}(D,U'){\vert }$.

Proposition 7

Given a decision table S, a new object $x_{new}$ is added into S to get $S'=(U',C \bigcup D,V,f)$, $\hbox {CON}_{R}(D,U')$ and $\hbox {QCON}_{R}(D,U')$, where $U'=U\bigcup \{x_{new}\}$. Let $R\subset C$; for $a \in C-R$, $\hbox {CON}_{R\bigcup \{a\}}(D,U')$ can be illustrated as follows.

$$\begin{aligned} {\vert }\hbox {CON}_{R\bigcup \{a\}}(D,U'){\vert }= {\vert }\bigcup \{Z {\vert } W\in \hbox {QCON}_{R}(D,U')\wedge Z\in W{/}a\wedge {\vert }Z{/}D{\vert }\ne 1\}{\vert } \end{aligned}$$

Proposition 8

Given a decision table S, let $R\subset C$; a new object $x_{new}$ is added into S to obtain $S'$. For each $a \in C-R$, the joined significance measures of the attribute a based on the conflict region in $S'$ can also be defined as follows.

$$\begin{aligned} \textit{SIG}_{\mathrm{CON}}{}^{+}(a,R,D,U')= & {} {\vert }\hbox {CON}_{R}(D,U'){\vert } - {\vert }\hbox {CON}_{R\bigcup \{a\}}(D,U'){\vert }\\= & {} {\vert }\hbox {CON}_{R}(D,U'){\vert } - {\vert }\bigcup \{Z {\vert } W\in \hbox {QCON}_{R}(D,U')\\&\quad \quad \wedge Z\in W{/}a\wedge {\vert }Z{/}D{\vert }\ne 1\}{\vert } \end{aligned}$$

4.2 The acceleration strategy for deleting redundant attributes

As we know, if a subset R* of C only satisfies condition(1) of the reduct definition, the attributes in R* are sufficient. Namely, the condition(1) is not a necessary condition for the reduct of S and R* is only a superset of a reduct. There may exist one real reduct R of S and $R\subseteq R$*. Hence, we should check whether there exist redundant attributes in R*.

Generally, for an attribute a of reduct-superset R*, if $\textit{SIG}_{\mathrm{CON}}{}^{-}(a,R*,D,U')=0$, the attribute a is redundant and should be deleted from the attribute set R*. The time complexity of this operation is $O({\vert }R{\vert }^{2}{\vert }U{\vert })$ and the number of radix sort is ${\vert }R{\vert }({\vert }R{\vert }-1)$. This operation of checking every attribute in R* will require plenty of computational time. Can we further improve the performance of incremental reduction algorithms? This motivates us to research an acceleration approach by reducing sort times in the process of checking redundant attributes to improve efficiency. In the following, we discuss the acceleration strategy based on the conflict region for updating reduct.

Given a decision table $S=(U,C \bigcup D,V,f)$, C is a condition attribute set that includes $c_{1},c_{2},{\ldots },c_{i},\ldots ,$etc. U / C is a partition of the universe with respect to C. We can use radix sort to compute the equivalence classes of U / C. For $U{/}C-\{c_{i}\}$ and $U{/}C-\{c_{i+1}\}, {\vert }C{\vert }-2$ times sorts are repetitive (i.e., $c_{i+2},{\ldots },c_{|C|},c_{1},{\ldots },c_{i-1})$ and have only one different sort. We all know that the radix sort is stable; thus we can obtain $U{/}(C-\{c_{i+1}\})$ derived from $U{/}(C-\{c_{i}\})$ (Qian et al. 2011; Zhou et al. 2007).

Proposition 9

For a decision table $S=(U,C \bigcup D,V,f)$, RS($U,C-\{c_{i+1}\})=\hbox {RS}(\hbox {RS}(U,C-\{c_{i}\}),\{c_{i}\}$).

Proof

RS($U,C-\{c_{i+1}\}$) denotes the result of the radix sort with respect to the attributes order $c_{i+2},{\ldots },c_{|C|},c_{1},{\ldots },c_{i}$. We divide two steps to obtain RS(RS($U,C-\{c_{i}\}),\{c_{i}\}$). That is, firstly, we can obtain RS($U,C-\{c_{i}\}$) by radix sort with respect to the attributes order $c_{i+1},{\ldots },c_{|C|},c_{1},{\ldots },c_{i-1}$; then, based on RS($U,C-\{c_{i}\}$) we complete the radix sort by the attribute $c_{i}$. Therefore, the result of radix sort with respect to the attributes order $c_{i+1},c_{i+2}$,...,$c_{|C|},c_{1},{\ldots },c_{i}$ is equivalent to merging the above two steps of sort operations. Because the radix sort is a stable sort, RS($U,C-\{c_{i+1}\}$) is equivalent to RS(RS($U,C-\{c_{i}\}),\{c_{i}\}$). Hence, Proposition 9 holds.

From Proposition 9 we can significantly reduce the number of the radix sort between $U{/}C-\{c_{i}\}$ and $U{/}C-\{c_{i+1}\}$. Hence, we can employ Proposition 9 to carry out the operation of checking redundant attributes from the previous result of attribute reduction to accelerate the efficiency of incremental reduction algorithms.

4.3 Incremental reduction algorithm based on the conflict region when adding one object

Based on the above discussion, we present an incremental reduction algorithm (IRACR-O) with the acceleration strategy when adding one object into the decision table. The algorithm includes three main steps:

• (1) The first step (Steps 1–2 in algorithm IRACR-O) is to update $\hbox {CON}_{R}(D,U')$, $\hbox {QCON}_{R}(D,U')$ and $\hbox {CON}_{C}(D,U')$ when adding one object;

• (2) The second step (Step 3 in algorithm IRACR-O) is to select new attributes from the remaining attributes to add into the attribute subset, until the new attribute subset satisfies ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }$;

• (3) The third step (Steps 4–5 in algorithm IRACR-O) is to delete the redundant attributes of the new attribute subset with the acceleration strategy.

The time complexity analysis In Step 1, when adding one object into the decision system, the time complexity of computing the partition of the whole object set under the attribute sets R and C is $O({\vert }C{\vert }{\vert }U{\vert })$; the time complexity of Step 2 is $O({\vert }X_{i}'{\vert })$ in the worst case. In general, we only execute the ‘while’ loop structure once and can select an attribute to satisfy the termination condition of the loop structure. Hence, the time complexity of Step 3 is $O({\vert }C-R{\vert }{\vert }X_{i}'{\vert })$; In Steps 4–5, the selected attributes are checked to delete redundant attributes with the acceleration strategy, the time complexity of Step 4 –5 is $O({\vert }C{\vert }{\vert }U'+ 1{\vert })$. Hence, the total time complexity of algorithm IRACR-O is 2$O({\vert }C{\vert }{\vert }U'{\vert })+O({\vert }X_{i}'{\vert })+ O({\vert }C-R{\vert }{\vert }X_{i}'{\vert })$.

The performance analysis From IRACR-O, we can find that the incremental reduction algorithm improves the performance of the reduction algorithm compared with the non-incremental reduction algorithm SARCR when adding one object.

• (1) In Step 2, the new conflict regions ($\hbox {CON}_{R}(D,U')$ and $\hbox {CON}_{C}(D,U'))$ are computed via an incremental approach based on the existing conflict region.

• (2) In Step 3, the new attribute subset is generated from the original reduct, which generally only needs to execute the loop structure once to get the attributes subset R that satisfies ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }$.

• (3) From Steps 4–5, the acceleration strategy with reduction of the radix sort time is used to improve the performance of deleting redundant attributes.

When multiple objects immigrate into the decision system, we need to execute Steps 1–3 of Algorithm 2 repeatedly and execute Step 4 once to update reduct. The incremental reduction algorithm for adding multiple objects is as follows.

The time complexity analysis Suppose that l objects are added into the decision system. From the analysis of the time complexity of algorithm 2, we know that the time complexity of Step 1 is $l^{*}(O({\vert }C{\vert }{\vert }U{\vert })+O({\vert }X_{i}'{\vert })+O({\vert }C-R{\vert }{\vert }X_{i}'{\vert }))$; In Steps 2–3, the operations of checking the redundant attributes of obtain selected attribute subset R and deleting the redundant attributes form R with the acceleration strategy are performed, whose time complexity is $O({\vert }C{\vert }{\vert }U'+1{\vert })$. Hence, the time complexity of algorithm IRACR-M is $l^{*}(O({\vert }C{\vert }{\vert }U{\vert }) +O({\vert }X_{i}'{\vert })+O({\vert }C-R{\vert }{\vert }X_{i}'{\vert })) +O({\vert }C{\vert }{\vert }U'+1{\vert })$.

Example 3

(Continuation of Example 1) For Table 1, $R=\{{ab}\}$ is a reduct of the decision table S, and we can get $U{/}R=\{\{x_{1},x_{7}\},\{x_{2},x_{3},x_{9}\},\{x_{4},x_{8}\},\{x_{5},x_{6}\}\}$ and $U{/}C=\{\{x_{1},x_{7}\},\{x_{2}\},\{x_{3},x_{9}\},\{x_{4},x_{8}\},\{x_{5}\},\{x_{6}\}\}$, where $X_{1}=\{x_{1},x_{7}\}$, $X_{2}=\{x_{2},x_{3},x_{9}\}$, $X_{3}=\{x_{4},x_{8}\}$, $X_{4}=\{x_{5},x_{6}\}$, $Y_{1}=\{x_{1},x_{7}\}$, $Y_{2}=\{x_{2}\}$, $Y_{3}=\{x_{3},x_{9}\}$, $Y_{4}=\{x_{4},x_{8}\}$, $Y_{6}=\{x_{5}\}$ and $Y_{6}=\{x_{6}\}$. A new object $y_{1}=(0,1,0,0,1)$ is added to Table 1.

Execute IRACR-O; we can find that $X_{2}=\{x_{2},x_{3},x_{9}\}$ and $X_{2}'=\{x_{2},x_{3},x_{9},y_{1}\}$, where ${\vert }X_{2}{/}D{\vert }=1$ and ${\vert }X_{2}'{/}D{\vert }\ne 1$. Hence, we update $\hbox {CON}_{R}(D,U')=\{x_{1},x_{7},x_{4},x_{8},x_{2},x_{3},x_{9},y_{1}\}$ and $\hbox {CON}_{C}(D,U')=\{x_{1},x_{7},x_{4},x_{8},x_{2},y_{1}\}$ and can get ${\vert }\hbox {CON}_{R}(D,U'){\vert }=8,$${\vert \hbox {CON}_{C}(D,U'){\vert }=6}$ and ${\vert }\hbox {CON}_{R}(D,U'){\vert }\ne {\vert }\hbox {CON}_{C}(D,U'){\vert }$. Thus, we need to execute Step3 to add attributes for $C-R$ into R. In the first circulation, we can get $\textit{SIG}_{\mathrm{CON}}{}^{+}(c,R,D,U')=2$ and ${SIG}_{\mathrm{CON}}{}^{+}(d,R,D,U')=2$. Then, we select c into R, and have $R=\{{ ab}\}\bigcup \{c\}=\{{abc}\}$. Thus, we have ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }=6$. Redundant attributes in R do not exist. Hence, the new reduct is $R=\{{ abc}\}$.

Example 4

(Continuation of Example 1) For Table 1, $R=\{{ab}\}$ is a reduct of the decision table S, and the three objects (i.e., $y_{1}=(0,1,0,0,1)$, $y_{2}=(0,1,0,1,1)$ and $y_{3}=(1,0,1,0,2))$ are added into Table 1.

(1) We suppose that the adding order is $y_{1},y_{2},y_{3}$ and execute IRACR-M. From Example $_{3}$, we can get $R=\{{abc}\}$, $\hbox {CON}_{R}(D,U')=\hbox {CON}_{C}(D,U')=\{x_{1},x_{7},x_{4},x_{8},x_{2},y_{1}\}$ and $\hbox {QCON}_{R}(D,U')=\{\{x_{1},x_{7}\},\{x_{4},x_{8}\}$, $\{x_{2},y_{1}\}\}$.

Then, adding $y_{2}$ into the decision table, we can find that $X_{2}=\{x_{2},y_{1}\}$ and $X_{2}'=\{x_{2},y_{1},y_{2}\}$, where ${\vert }X_{2}{/}D{\vert }\ne 1$ and ${\vert }X_{2}'{/}D{\vert }\ne 1$. We update $\hbox {CON}_{R}(D,U')=\{x_{1},x_{7},x_{4},x_{8},x_{2},y_{1},y_{2}\}$ and $\hbox {CON}_{C}(D,U')=\{x_{1},x_{7},x_{4},x_{8},x_{2},y_{1}\}$; ${\vert }\hbox {CON}_{R}(D,U'){\vert }\ne {\vert }\hbox {CON}_{C}(D,U'){\vert }$. We select d into R and have $R=\{{abc}\}\bigcup \{d\}=\{{abcd}\}$.

Next, adding $y_{3}$ into the decision table, we have $\hbox {CON}_{R}(D,U')=\{x_{1},x_{7},x_{2},y_{1},x_{4},x_{8},y_{3}\}$ and $\hbox {CON}_{C}(D,U')= \{x_{1},x_{7},x_{2},y_{1},x_{4},x_{8},y_{3} \}$; ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }$.

Finally, according to Steps 2–3, we find that a in R can be deleted. Hence, the new reduct is $R=\{{bcd}\}$.

(2) We suppose that the adding order is $y_{3},y_{2},y_{1}$ and execute the algorithm IRACR-M.

Similar to the above analysis, when $y_{3}$ is added into the decision table, we can get $\hbox {CON}_{R}(D,U')= \{x_{1},x_{7},x_{4},x_{8},y_{3}\}$ and $\hbox {CON}_{R}(D,U')=\{ x_{1},x_{7},x_{4},x_{8},y_{3}\}$ such that $R=\{{ab}\}$.

Then, adding $y_{2}$ into the decision table, we can have $\hbox {CON}_{R}(D,U')=\{x_{1},x_{7},x_{4},x_{8},$$y_{3},x_{2},y_{2}\}$ and $\hbox {CON}_{C}(D,U')=\{x_{1},x_{7},x_{4},x_{8},y_{3}\}$, where ${\vert }\hbox {CON}_{R}(D,U'){\vert }\ne {\vert }\hbox {CON}_{C}(D,U'){\vert }$. We have ${SIG}_{\mathrm{CON}}{}^{+}(c,R,D,U')=0$ and ${SIG}_{\mathrm{CON}}{}^{+}(d,R,D,U')=2$. We select d into R and have $R=\{{ ab}\}\bigcup \{d\}=\{{ abd}\}$, $\hbox {CON}_{R}(D,U')=\{x_{1},x_{7},x_{4},x_{8},y_{3}\}$ and $\hbox {CON}_{C}(D,U')=\{x_{1},x_{7},x_{4},x_{8},y_{3}\}$.

Next, adding $y_{1}$ into the decision table, we have $\hbox {CON}_{R}(D,U')=\{x_{1},x_{7},x_{2},y_{1},x_{4},x_{8},$$y_{3}\}$ and $\hbox {CON}_{C}(D,U')= \{x_{1},x_{7},x_{2},y_{1},x_{4},x_{8},y_{3} \}$; ${\vert }\hbox {CON}_{R}(D,U'){\vert }={\vert }\hbox {CON}_{C}(D,U'){\vert }$.

Finally, redundant attributes in R do not exist. Hence, the new reduct is $R=\{{abd}\}$.

For Example 4, we can find that the results of the two reduction processes are not coincident because of the different orders in which objects are added.

5 Incremental attribute reduction based on the conflict region when adding the object set

In real-life applications, it is not often the case that only one object is added into the decision system. Generally, an object set (i.e., multiple objects) is added into the decision system. From Algorithm 2, obviously, immigration of multiple objects can be seen as the cumulative immigration of a single object. If we re-execute Algorithm 2 many times to update the reduct, it will consume plenty of time. In this sub-section, to improve the efficiency of the incremental attribute reduction algorithm when adding multiple objects, we will develop an incremental reduction algorithm in an efficient manner to obtain the new reduct that avoids repeated execution.

For a decision table $S=(U,C \bigcup D,V,f)$, a reduct R, $U{/}R=\{X_{1},X_{2},{\ldots },X_{m}\}$ and $U{/}C=\{Y_{1},Y_{2},{\ldots },Y_{n}\}$, we assume that an object set $U_{new}$ is added into the decision table S; we can get $S'=(U \bigcup U_{new},C \bigcup D,V,f)$. Let $U'=U \bigcup U_{new}$, $U'{/}R=\{X_{1}',{\ldots },X_{s}',X_{s+1}',{\ldots },X_{m}'\}$ and $U'{/}C=\{Y_{1}',{\ldots },Y_{t}',Y_{t+1}',{\ldots },Y_{n}'\}$, where $\forall i\in [1,\ldots ,s], {\vert }X_{i}'{/}D{\vert }\ne 1$; $\forall i\in [s+1,\ldots ,m], {\vert }X_{i}'{/}D{\vert }=1$; $\forall j\in [1,\ldots ,t], {\vert }Y_{j}'{/}D{\vert }\ne 1$; $\forall j\in [t+1,\ldots ,n], {\vert }Y_{j}'{/}D{\vert }=1$. Hence, we have $\hbox {CON}_{R}(D,U')=\bigcup \{X_{i}'{\vert } i\in [1,\ldots ,s]\}$ and $\hbox {CON}_{C}(D,U')=\bigcup \{Y_{j}'{\vert } i\in [1,{\ldots },t]\}$.

Proposition 10

Given a decision table S, R is a reduct of S and the object set $U_{new}$ is added into S. Let $U'=U'\bigcup U_{new}$, $U'{/}R=\{X_{1}',{\ldots },X_{s}',X_{s+1}',{\ldots },X_{m^{\prime }}'\}$ and $U'{/}C=\{Y_{1}',{\ldots },Y_{t}',Y_{t+1}',{\ldots },Y_{n^{\prime }}'\}$. For each $a \in C-R$, the joined significance measures of the attribute a based on the conflict region can also be defined as follows.

$$\begin{aligned} {SIG}_{\mathrm{CON}}{}^{+}(a,R,D,U')= & {} {\vert }\hbox {CON}_{R}(D,U'){\vert } - {\vert }\bigcup \{Z {\vert } W\in \hbox {QCON}_{R}(D,U')\wedge \\&\quad Z\in W{/}a\wedge {\vert }Z{/}D{\vert }\ne 1\}{\vert } \end{aligned}$$

In the following, we present an incremental reduction algorithm with the acceleration strategy when adding an object set into the decision table.

The time complexity analysis Step 1 is to compute $\hbox {CON}_{R}(D,U')$, $\hbox {QCON}_{R}(D,U')$ and $\hbox {CON}_{C}(D,U')$ when adding multiple objects, whose time complexity is $O({\vert }C{\vert }{\vert }U'{\vert })$. Step 3 is to check the selected attribute whether satisfies the stopping condition, whose time complexity 3 is $O({\vert }C-R{\vert }^{2}{\vert }\hbox {CON}_{R}(D,U'){\vert })$; In Steps 4–5, the selected attributes are checked to delete redundant attributes with the acceleration strategy. So the time complexity of Steps 4–5 is $O({\vert }C{\vert }{\vert }U'{\vert })$. Hence, the total time complexity of algorithm IRACR-S is $3O({\vert }C{\vert }{\vert }U'{\vert })+ O({\vert }C-R{\vert }^{2}{\vert }\hbox {CON}_{R}(D,U'){\vert })$.

The performance analysis We can find that IRACR-S improves the efficiency of the incremental reduction algorithm compared with IRACR-M when adding multiple objects into the decision system.

• (1) For IRACR-S, we only need to execute Step 1 at a time to update the conflict region.

• (2) For adding multiple objects, in Step 3, we only need to run the ‘while’ loop-structure once to obtain the selected attributes, while in IRACR-M, for adding every object of the object set, we should run the ‘while’ loop-structure once.

Example 5

(Continuation of Example 1) For Table 1, $R=\{{ab}\}$ is a reduct of the decision table S; we have $U{/}R=\{\{x_{1},x_{7}\},\{x_{2},x_{3},x_{9}\},\{x_{4},x_{8}\},\{x_{5},x_{6}\}\}$ and $U{/}C=\{\{x_{1},x_{7}\},\{x_{2}\},\{x_{3},x_{9}\},\{x_{4},x_{8}\},\{x_{5}\},\{x_{6}\}\}$. Let $X_{1}=\{x_{1},x_{7}\}$, $X_{2}=\{x_{2},x_{3},x_{9}\}$, $X_{3}=\{x_{4},x_{8}\}$, $X_{4}=\{x_{5},x_{6}\}$, $Y_{1}=\{x_{1},x_{7}\}$, $Y_{2}=\{x_{2}\}$, $Y_{3}=\{x_{3},x_{9}\}$,$Y_{4}=\{x_{4},x_{8}\}$, $Y_{5}=\{x_{5}\}$ and $Y_{6}=\{x_{6}\}$; we add an object set $U_{new}=\{y_{1},y_{2},y_{3}\}$ into Table 1, where $y_{1}=(0,1,0,0,1)$, $y_{2}=(0,1,0,1,1)$, $y_{3}=(1,0,1,0,2)$.

For IRACR-S, we have $U'=\{x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7},x_{8},x_{9},y_{1},y_{2},y_{3}\}$ and can get $U'{/}R=\{\{x_{5},x_{6}\},\{x_{1},x_{7}\}, \{x_{4},x_{8},y_{3}\}, \{x_{2},x_{3},x_{9},y_{1},y_{2}\}\}$ and $U'{/}C=\{\{x_{6}\},\{y_{2}\},$$\{x_{3},x_{9}\},\{x_{1},x_{7}\},\{x_{2},y_{1}\},\{x_{4},x_{8},y_{3}\}\}$. Obviously, $U'{/}R\bigcup \{c\}= \{\{x_{5}\},\{x_{6}\}, \{x_{3},x_{9}\},$$\{x_{1},x_{7}\},\{x_{2},y_{1},y_{2}\},\{x_{4},x_{8},y_{3}\}\}$ and $U'{/}R\bigcup \{d\}=\{\{x_{5}\},\{x_{6}\},\{x_{1},x_{7}\},\{x_{4},x_{8},y_{3}\},$$\{x_{2},x_{3},x_{9}\},\{y_{1},y_{2}\}\}$. We can get ${SIG}_{\mathrm{CON}}{}^{+}(c,R,D,U')$$=2$ and ${SIG}_{\mathrm{CON}}{}^{+}(d,R,D,U') =0$. Thus, we select c to merge into $R=\{{ ab}\}\bigcup \{c\}=\{{abc}\}$ and update $\hbox {CON}_{R}(D,U')$ to get ${\vert }\hbox {CON}_{R}(D,U'){\vert }=8$. Next, we have $U'{/}\{{ abc}\}=\{\{x_{5}\},\{x_{6}\},\{x_{3},x_{9}\},\{x_{1},x_{7}\},\{x_{4},x_{8},y_{3}\}, \{x_{2},y_{1},y_{2}\}\}$ and select d to merge into $R=\{{ abc}\}\bigcup \{d\}= \{{abcd}\}$. According to Steps 4–5, we find that the attribute a in R is a redundant attribute and must be deleted. Hence, the new reduct is $R=\{{bcd}\}$.

Table 2 gives the comparison of the time complexity for static and incremental algorithms when adding multiple objects.

Table 2 The comparison of time complexity for static and incremental algorithms when adding l objects

Step(1) is to compute the core attribute set and $\hbox {CON}_{C}(D,U)$ for SRACR and to update $\hbox {CON}_{C}(D,U')$ and $\hbox {CON}_{R}(D,U')$ for IRACR-M and IRACR-S; Step(2) is to add the attributes into the subset R; Step(3) is to delete the redundant attributes from the subset R.

From Table 2, when adding l objects into the decision table, we can find that the time complexity of IRACR-M is smaller than that of SRACR and that the time complexity of IRACR-S is smaller than that of IRACR-M. Hence, we can draw the conclusions that the proposed incremental algorithm IRACR-S is more efficient than the non-incremental algorithm SRACR and is also more efficient than the proposed incremental algorithm IRACR-M.

To further illustrate the efficiency of the proposed incremental reduction algorithms with the acceleration strategy, we present comparisons of the sorting number for four incremental reduction algorithms (IARC-S (Liang et al. 2014), GIARC-S (Liang et al. 2014), IRACR-M and IRACR-S) in Table 3.

Table 3 Comparison of sorting number among four incremental reduction algorithms

In Table 3, for convenience, let ${\theta }$ denote ${\theta } =\sum _{i=0}^{|C-R|-1} {(|C|-(|R|+i))}$. Step(1) is to update ME$(D{\vert }C)$ and ME($D{\vert }B)$ for IARC-S and GIARC-S and to update $\hbox {CON}_{C}(D,U')$ and $\hbox {CON}_{R}(D,U')$ for IRACR-M and IRACR-S; Step(2) is to add the attributes into the subset R; Step(3) is to delete the redundant attributes from the subset R.

From Table 3, because of using the acceleration strategy, the sorting numbers of IRACR-M and IRACR-S are both $2{\vert }R{\vert }$ in step(3), which are less than one of IARC-S and GIARC-S. Hence, the sorting number of IRACR-M is less than one of IARC-S and the sort time of IRACR-S is lower than the sorting numbers of the other three algorithms. It can be known that the sort for the decision systems is a pivotal and frequent operation in the process of attribute algorithms. The computation of reducing the number of the sort can improve the efficiency of reduction algorithms. Hence, the proposed incremental reduction algorithms IARC-S and GIARC-S make use of the acceleration to further improve the efficiency of reduction algorithms.

6 Experiments

In this section, we present a series of experiments to demonstrate the effectiveness and efficiency of the proposed algorithms. The experiment data use 11 UCI data sets (https://archive.ics.uci.edu/ml/datasets.html) whose basic information is outlined in Table 4. All of the experiments have been carried out on a personal computer with Windows XP, Pentium Dual-CORE CPU i5-3470 3.20GHZ and 3.47GB memory. The software used is Microsoft Visual Studio 2005, and the programming language is C++.

Table 4 Descriptions of data sets

6.1 A comparison of static and incremental reduction algorithms when adding data

To evaluate the efficiency of the proposed incremental reduction algorithms, we compare the incremental reduction algorithms (IRACR-M, IRACR-S) with the static reduction algorithm SRACR when adding data sets. For each data set in Table 4, 50% of the objects of the original data set are selected as the basic data set. Then, we divide the remaining 50% of the objects into ten equal parts. The first part is regarded as the 1st data set, the combination of the first part and the second part is viewed as the 2nd data set, the combination of the 2nd data set and the third part is regarded as the 3rd data set, $\cdot \cdot \cdot$, the combination of all eight parts is viewed as the tenth data set, i.e., 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50% of the universe. Next, we add ten data sets into the basic data set and run the static reduction algorithm (SRACR) and two incremental reduction algorithms (IRACR-M and IRACR-S). The results are shown in Fig. 1. In each sub-figure (a–i) of Fig. 1, the x-coordinate pertains to the ratio of adding the data set, while the y-coordinate concerns the computational time.

Fig. 1

The comparison of static and incremental algorithms when adding objects

It is easy to see from Fig. 1 that for each data set, the computational time of IRACR-M is much smaller than that of SRACR and the computational time of IRACR-S is much smaller than that of the incremental reduction algorithm IRACR-M. Namely, the performance of IRACR-M is higher than that of SRACR and the performance of IRACR-S is most efficient among the three algorithms.

From Fig. 1 it is easy to find that with the increment of the condition attributes number, the slope of the curve for algorithms IRACR-M and IRACR-S decreases. For example, the slopes of the data sets Gene, Ticdata2000 and Semeion are close to zero due to including more condition attributes.

To more clearly compare the efficiency between IRACR-M and IRACR-S, for data sets Landsat-trn, Gene, Semeion, Ticdata2000 and Handwritten, Fig. 2 gives the more detailed trend of IRACR-M and IRACR-S as the size of the data sets increases. We can see from these figures that IRACR-S takes less time to select a new feature subset than IRACR-M. For example, the computational time of IRACR-M achieves 0.076 s for the Gene data set, while IRACR-S needs 0.0345 s. The main reason is that IRACR-M needs to be carried out repeatedly to handle multiple objects, while IRACR-S only deals with multiple objects at a time instead of repetitive operations.

Fig. 2

The comparison of two incremental algorithms when adding objects

6.2 Comparison with reduct results of static and incremental reduction algorithms

To compare the results of incremental and static reduction algorithms, for each data set in Table 4, we randomly select 50% of the objects as the basic data set. Then, the remaining 50% of the objects are added into the corresponding basic data set. The generated reducts are shown in Table 5.

It is easy to see from Table 5 that the results of reducts for SRACR, IRACR-M and IRACR-S are not entirely identical; the reason is that the different orders of objects being added into the decision table result in different significances of the selected features in SRACR, IRACR-M and IRACR-S such that the feature subsets selected by the reduction algorithms are not wholly the same.

Table 5 Comparison of reduct results for three algorithms

Moreover, we can observe that IRACR-S can find relatively smaller or equal-sized attributes reduct than IRACR-M. For example, for data sets Mushroom, Ticdata2000 and Semeion, the sizes of attributes in the reduct by IRACR-S are less than that of IRACR-M. This is because for IRACR-S, the selected most significant attributes apply to the whole adding object set, while the selected most significant attributes only rely on the current one object for IRACR-M. Relative to IRACR-M, IRACR-S can more fully select the significant attributes from the integrity of the adding object set, which results in one needing to select smaller attributes than IRACR-M.

6.3 Performance comparison of the essential step for the static and incremental reduction algorithm

When an object set is added, the static reduction algorithm includes the following three steps.

Step 1 :

 Compute the core attributes set;

Step 2 :

 Select the most significant attributes to add into the alternative attribute subset;

Step 3 :

 Delete the redundant attributes from the alternative attribute subset.

The mains steps of the incremental reduction algorithm are as follows.

Step 1 :

 Select the most significant attributes to add into the alternative attribute subset;

Step 2 :

 Delete the redundant attributes from the alternative attribute subset.

To concretely illustrate the performance of the static algorithm and incremental algorithms when an object set is entered into the decision system, we compare the time consumed for the main steps of three attribute reduction algorithms (SRACR, IRACR-M and IRACR-S) for each data set in Table 4. We select 60% of the objects of the original data set as the basic data set and add 10% of the objects of the universe into the basic data set. The details of the computational time of the main steps of the static and incremental reduction algorithms for nine data sets are shown in Table 6 and Fig. 3 . In Table 6, ‘Core’ denotes the time consumption of computing core attributes, ‘Add’ denotes the time consumption of adding the attributes into the reduct, ‘Del’ denotes the time consumption of deleting the redundant attributes, and ‘Total’ denotes the whole time consumption of the reduction algorithm.

Table 6 Comparison of performances of three reduction algorithms

Each column denotes the whole computational time of the reduction algorithm. In the sub-figures of Fig. 3, the red part denotes the running time of computing core attributes for the static algorithm, the blue part represents the running time of selecting attributes in the reduct, and the green part denotes the running time of deleting redundant attributes.

It is clear that the static reduction algorithm spends a lot of time on computing core attributes. Meanwhile, for the incremental reduction algorithm, the computational time of selecting attributes and deleting redundant attributes is less than that of the static reduction algorithm. These reasons illustrate that the incremental reduction algorithm is faster than the static reduction algorithm with respect to finding the reduct.

Fig. 3

The comparison of the running time for the static and incremental algorithms of the main steps

6.4 The performance comparison with other incremental algorithms

To further illustrate the efficiency of the IRACR-M and IRACR-S algorithms, in this sub-section, our proposed algorithms are compared with other existing incremental reduction algorithms. We select the incremental reduction algorithm based on the positive region in (Hu et al. 2005), denoted as IRPR, and only select four incremental reduction algorithms (IARC-S and GIARC-S, IARC-C and GIARC-C) (Liang et al. 2014). IARC-S and IARC-C are incremental algorithms for reduct based on Shannon’s entropy and the combination entropy, respectively. GIARC-S and GIARC-C are group incremental algorithms for reduct based on Shannon’s entropy and the combination entropy, respectively. Actually, the algorithms IRACR-M, IARC-S and IARC-C are the incremental reduction algorithms for adding one object, and the algorithms IRACR-S, GIARC-S and GIARC-C are the group incremental reduction algorithms for adding the object set.

For each data set in Table 4, we randomly select 50% of the objects as the basic data set. Then, the remaining 50% of objects are added to the corresponding basic data set. The comparison results of the computational time are shown in Table 7 and Fig. 4.

Table 7 Comparison with other incremental algorithms

Fig. 4

The comparison of the running time with other incremental algorithms

From Table 7 and Fig. 4, we can easily find that the computational time of IRACR-M is much less than those of IARC-S and IARC-C and that the computational time of IRACR-S is much less than those of GIARC-S and GIARC-C. The computational times of IRACR-M and IRACR-S are both much less than that of IRPR. Hence, the experimental results indicate that IRACR-M is much more efficient than IARC-S and IARC-C and that IRACR-S is much more efficient than GIARC-S and GIARC-C.

6.5 Comparison of classification accuracies for five algorithms

To evaluate the classification performance with respect to generated reducts by the proposed incremental reduction algorithms (IRACR-M, IRACR-S), we use the results of the corresponding reduction algorithms to train the C4.5 classifier based on tenfold cross-validation method. IRACR-M, IRACR-S are used to select the attribute reducts when randomly selecting 50% of the objects as the basic data set and the remaining 50% of the objects as adding objects. The classification accuracy with respect to the raw data and the reduct result generated by different algorithms are shown in Table 8.

Table 8 Comparison of classification accuracy for three algorithms

From Table 8, it can be seen that when adding objects into the decision systems, the average classification accuracy of the reduct selected by algorithms IRACR-M and IRACR-S is closed to that of algorithm SRACR on most data sets and the classification accuracy of IRACR-S are better than that of Initial reduct and SRACR on many data sets. The experimental results indicate that algorithm IRACR-M and IRACR-S can find a feasible reduct as algorithm SRACR and selecting a feasible reduct based on the incremental algorithms IRACR-M and IRACR-S can consume much shorter computational time.

7 Conclusions

In many real-world tasks, the objects of decision systems may vary dynamically. Quickly updating attribute reduction is a significant task for knowledge discovery. In this paper, firstly, the concept and properties of the conflict region are presented. When a single object and an object set are added into the decision systems, the incremental mechanisms for the conflict region are discussed. To further improve the efficiency of incremental reduction algorithms, we give an acceleration strategy and develop incremental feature selection algorithms with the acceleration strategy based on the conflict region in terms of adding a single object and an object set. Theoretical analysis and experimental results for UCI datasets have shown that the proposed algorithms can effectively reduce computational time to improve the performance of updating reduct. In the future, we will extend the acceleration strategy to the variation of the attribute set and discuss quickly incremental reduction algorithms when the attribute set varies.