The parameterized complexity of manipulating Top Trading Cycles

Abstract

We study the problem of exchange when agents are endowed with heterogeneous indivisible objects, and there is no money. In this setting, no rule satisfies Pareto-efficiency, individual rationality, and strategy-proofness; there is no consensus in the literature on satisfactory second-best mechanisms. A natural generalization of the ubiquitous Top Trading Cycles (TTC) satisfies the first two properties on the lexicographic domain, rendering it manipulable. We characterize the computational complexity of manipulating this mechanism; we show that it is $\mathbf {W[P]}$-hard by reduction from MONOTONE WEIGHTED CIRCUIT SATISFIABILITY. We provide a matching upper bound for a wide range of preference domains. We further show that manipulation by groups (when parameterized by group size) is $\mathbf {W[P]}$-hard. This provides support for TTC as a second-best mechanism. Lastly, our results are of independent interest to complexity theorists: there are few natural $\mathbf {W[P]}$-complete problems and, as far as we are aware, this is the first such problem arising from the social sciences.

1 Introduction

Gale’s Top Trading Cycles (TTC) is ubiquitous [37]. It is used extensively as a key building block for the design of mechanisms in real-life applications including kidney exchange, school choice, airplane arrival slots exchange, probabilistic assignment, and mixed-ownership economies.^1,2 For example, in the design of kidney exchange mechanisms, the proposed Top Trading Cycles and Chains mechanism satisfies the usual desirable axiomatic properties and features substantial welfare gains in terms of both number and quality of transplants compared to other mechanisms [35]. The mechanism loses its incentive compatibility properties when moving to more general environments, though, and this is the setting of our paper.

Our precise setting is the problem of exchange between agents endowed with heterogeneous indivisible objects when there is no money. When each agent owns and eventually consumes one object, TTC is the unique mechanism satisfying Pareto-efficiency, individual rationality, and strategy-proofness, and selects the core allocation at each profile of preferences and endowments [24, 26, 34, 39, 44].³

Consider now the more general case in which each agent owns and consumes possibly multiple objects. There are numerous applications to this type of model: Dual-donor kidney exchange, liver exchange, employee shift trading, and dynamic assignment mechanisms (i.e., a stream of assignments is a bundle indexed by time).⁴ Unfortunately, no mechanism satisfies all three properties [39], and there is no consensus on satisfactory second-best mechanisms. The frontier of viable mechanisms remains a relevant and open question with welfare implications.

Our paper contributes to this discussion. A natural generalization of TTC (which we will refer to also as TTC) satisfies Pareto-efficiency and individual rationality on the lexicographic domain of preferences, rendering it manipulable. In this generalization, agents attempt to obtain their next most preferred available object and trade objects in cycles—repeatedly until no objects are remaining.

We characterize the computational complexity of manipulating TTC. We argue that a parameterized complexity approach is appropriate: The size of endowments is a natural parameter that may remain bounded or grow much more slowly than the number of participants. In general, the complexity of computational problems may depend heavily on parameters other than the total size of the input. Parameterized complexity thus offers a finer comparison of computational problems and reflects real-world constraints.⁵

Our main result is that the problem of manipulating TTC is $\mathbf {W[P]}$-hard when parameterized by the size of the endowments (Theorem 3.1). Furthermore, we provide a matching upper bound that holds for a large class of preference domains, including the additive domain (Theorem 4.1). Intuitively, as the market grows, even if agents’ endowments are below some finite bound, our result shows that manipulation of TTC is computationally difficult. We also consider group manipulability, wherein a number of agents can attempt to benefit by making a joint misreport to the mechanism. We show that TTC is $\mathbf {W[P]}$-hard to manipulate by groups, when parameterized by the size of the group (Theorem 5.1). This does not follow directly from the previous result, but the proof technique is similar. These results give support to TTC as a candidate second-best mechanism satisfying Pareto-efficiency and individual rationality (on the lexicographic domain).

The result is also of independent interest in computer science. To the best of our knowledge, there are no known problems derived from social science applications known to be $\mathbf {W[P]}$-complete. Natural problems that are complete for a given class are useful for reductions and help us understand the class. Populating parameterized complexity classes with problems from applications demonstrates the significance of parameterized complexity for practitioners.

We also remark that while the result is encouraging for TTC, complexity of manipulation would be complementary to—as opposed to substituting for—other oft-considered large market properties such as asymptotic strategy-proofness where the benefit from manipulation vanishes as the market grows [5, 23].

1.1 Related literature

Responding to the incompatibility of Pareto-efficiency, individual rationality, and strategy-proofness as shown by Sönmez [39], the literature has developed in several different directions. Closest to ours, Fujita et al. [18, 19] show that in the conditionally lexicographic domain of preferences TTC selects from the core, implying Pareto-efficiency and individual rationality, and is $\mathbf {NP}$-hard to manipulate. When Pareto-efficiency is weakened to range-efficiency, Pápai [32] provides a characterization of the entire class of mechanisms (the “fixed-deal exchange rules” where possible exchanges are predetermined). Alternatively, Sonoda et al. [42] and Sun et al. [43] cover several interesting domains where agents may have “tops-only”, m-chotomous, or correlated (referred to as asymmetric) preferences, and show the extent of compatibility as well as implications for single-valuedness of the core. If agents are restricted a priori to particular sets of trading partners, then compatibility may also be recovered [31, 45]. Finally, other authors also study tradeoffs in an environment where objects have types [21, 22, 27, 38].

2 Model

Let $\mathcal {N}$ be a finite set of agents, and $\mathcal {O}$ be a finite set of objects. Each agent $i\in \mathcal {N}$ has an endowment of objects $\omega _i \subset {\mathcal {O}}$. An endowment profile $\omega =(\omega _i)_{i\in \mathcal {N}}\in ( 2^\mathcal {O})^\mathcal {N}$ is a list of endowments for the agents such that $\bigcup _{i\in \mathcal {N}} \omega _i = \mathcal {O}$, and for each $i,j\in \mathcal {N}$ such that $i\ne j$, it holds that $\omega _i \cap \omega _j = \emptyset$. If $\alpha \in \omega _i$, then we say that agent i is the owner of $\alpha$ and that $ow(\alpha )=i$. Each agent $i\in \mathcal {N}$ has a preference relation $R_i$ over subsets of objects; that is, $R_i$ is a complete, transitive, and anti-symmetric binary relation over $2^\mathcal {O}$. Let $\mathcal {R}$ be the set of all such preference relations. We denote the strict component of $R_i$ by $P_i$, i.e. for each $X,Y\subseteq {\mathcal {O}}$, it holds that $X \mathrel {P}_i Y$ if and only if $X \mathrel {R}_i Y$ and $\lnot Y \mathrel {R_i} X$. A preference profile $R=(R_i)_{i \in \mathcal {N}} \in \mathcal {R}^\mathcal {N}$ is a list of preference relations for the agents.

An economy is a tuple $\mathcal {E}=(\mathcal {N},\mathcal {O}, \omega , R)$. An allocation $z=(z_i)_{i \in \mathcal {N}} \in ( 2^\mathcal {O})^\mathcal {N}$ for economy $\mathcal {E}$ is a list specifying for each agent a subset of objects, such that $\bigcup _{i\in \mathcal {N}} z_i = \mathcal {O}$, and for each $i,j\in \mathcal {N}$ such that $i\ne j$, it holds that $z_i \cap z_j = \emptyset$. Note that the endowment is an allocation. A rule $\phi$ maps each economy $\mathcal {E}$ to an allocation for $\mathcal {E}$. We denote by $\phi _i(\mathcal {E})$ the allocation of agent i under $\phi$ at $\mathcal {E}$; if $\phi (\mathcal {E})=z$, then $\phi _i(\mathcal {E}) = z_i$. We also refer to $z_i$ as an agent’s allocation.

Preference domains We define two natural subdomains of preference relations. An agent may prescribe for each object a utility level; subsequently, for each set of objects, their total utility is the summation of utilities over objects in the set. Formally, a preference relation $R_i$ is additive if there is $u_{i}:\mathcal {O}\rightarrow {\mathbb {R}}$ such that for each $X,Y\subseteq \mathcal {O}$, it holds that $X\,R_{i}\,Y$ if and only if $\sum _{\alpha \in X}u_{i}(\alpha )\ge \sum _{\alpha \in Y}u_{i}(\alpha )$. It is also possible that higher-ranked objects are worth significantly more than lower-ranked objects. In this case, in comparing two sets of objects, an agent first compares the respective top-ranked objects in each set, then the second... and so on, until one set contains a more preferred object. A special case of additivity is thus when $R_{i}$ is lexicographic: for each $X,Y\subseteq \mathcal {O}$, it holds that $X\,P_{i}\,Y$ if and only if there is $\beta \in X\setminus Y$ such that for each $\alpha \in Y$ with $\alpha \mathrel {P_{i}} \beta$, we have $\alpha \in X$.⁶

For the remainder of the paper, we assume that all agents have lexicographic preferences. Note that in such preferences, the ordering over objects uniquely determines the ordering over sets of obects.⁷ Furthermore, no two orderings over objects induces the same ordering over sets of objects. Thus it is sufficient to focus on agents’ preferences over objects. We write $R_i=(a,b,c,\Box )$ to mean that within objects, $R_i$ prefers a above each other object, followed by b, followed by c, followed (in arbitrary order) by objects in $\omega _i \setminus \{a,b,c\}$, followed (in arbitrary order) by objects in ${\mathcal {O}} \setminus (\omega _i \cup \{a,b,c\})$.⁸ We write $R_i=(a,b,c)$ to similarly mean that within objects $R_i$ prefers a to b, b to c, and c to all other objects. Finally, if $\alpha \mathrel {R_i} \beta$ for all $\beta$ in some subset of objects $\mathcal {O}'\subseteq {\mathcal {O}}$ , we say that agent i topranks $\alpha$ in $\mathcal {O}'$ (if $\mathcal {O}'=\mathcal {O}$ we say simply that i topranks $\alpha$).

Properties of rules Let $\mathcal {E}$ be an economy. Following standard notation we write $(R'_i,R_{-i})$ to be the preference profile obtained from R by replacing $R_i$ with $R'_i\ne R_i$. We say that $R'_i$ is a misreport for agent i. Let $\mathcal {E}'=(\mathcal {N},\mathcal {O}, \omega , R_i',R_{-i})$; a misreport $R'_i$ is beneficial under $\phi$ at $\mathcal {E}$ if $\phi _i(\mathcal {E}') \mathrel {P_i} \phi _i(\mathcal {E})$. A rule $\phi$ is strategy-proof if for each economy $\mathcal {E}$, no agent has a beneficial misreport under $\phi$ at $\mathcal {E}$. We also consider manipulation by groups. For each $\mathcal {M}\subseteq \mathcal {N}$, let $R_\mathcal {M}'=(R_i')_{i\in \mathcal {M}}$ be a group misreport for group $\mathcal {M}$, where for some $i\in \mathcal {M}$, $R'_i\ne R_i$. Let $\mathcal {E}'=(\mathcal {N},\mathcal {O}, \omega , R_\mathcal {M}',R_{-\mathcal {M}})$. A group misreport $R_\mathcal {M}'$ is beneficial under $\phi$ at $\mathcal {E}$ if for each $i\in \mathcal {M}$, it holds that $\phi _i(\mathcal {E}') \mathrel {R_i} \phi _i(\mathcal {E})$, and for some $j\in \mathcal {M}$, it holds that $\phi _j(\mathcal {E}') \mathrel {P_j} \phi _j(\mathcal {E})$. A rule $\phi$ is group strategy-proof if for each economy $\mathcal {E}$, there is no group $\mathcal {M}\subseteq N$ with a beneficial group misreport under $\phi$ at $\mathcal {E}$. These properties imply that no agent(s) have incentive to lie about their preferences even if they have full information about the preferences of the other agents. One trivial example of a group strategy-proof (and thus strategy-proof) rule is the “No Deal” rule—for each $\mathcal {E}$, let $\phi (\mathcal {E}) = \omega$—but this rule is suboptimal in terms of welfare as agents may benefit from trade. We say that an allocation z is Pareto-dominated at $\mathcal {E}$ if there is an allocation $z'$ for $\mathcal {E}$ such that for each $i\in \mathcal {N}$, it holds that $z'_i \mathrel {R}_i z_i$, and for some $j\in \mathcal {N}$, it holds that $z'_j \mathrel {P}_j z_j$. We say that an allocation is Pareto-efficient at $\mathcal {E}$ if it is not Pareto-dominated at $\mathcal {E}$, and that a rule is Pareto-efficient if for each economy $\mathcal {E}$, it recommends an allocation that is Pareto-efficient at $\mathcal {E}$. If an agent is worse off after the trade according to their own preference relation, then there is no incentive to take part. A rule is said to be individually rational if for each economy $\mathcal {E}$, and each agent $i\in \mathcal {N}$, it holds that $\phi _i(\mathcal {E}) \mathrel {R_i} \omega _i$.

We give some examples of rules. The No Deal rule is individually rational and (group) strategy-proof, but not Pareto-efficient. The rule where for each economy, we give all of the objects to agent 1 is Pareto-efficient and (group) strategy-proof, but not individually rational. Finally, TTC is a rule that is Pareto-efficient and individually rational, but not (group) strategy-proof.

Graph theory A (directed) graph is a set V of vertices and a set E of edges which are ordered pairs of vertices. The edge (u, v) is said to start at u and end at v. If there is such an edge, then we say that u is a predecessor of v and that v is a successor of u. The in-degree of a vertex u, denoted in(u), is the number of edges that end at u; the out-degree, denoted out(u), is the number of edges that start at u. A source is a vertex of in-degree 0; a sink is a vertex of out-degree 0. A (directed) walk in a graph is a sequence $(v_1,\ldots ,v_{j})$ where $v_i$ is a vertex and $(v_i,v_{i+1})$ is an edge for $1\le i < j$. A path is a walk where no vertex is repeated. A cycle is a path plus an edge from $v_j$ to $v_1$.

Top Trading Cycles We define the rule central to our study by means of an algorithm. In the first step, each agent points to their most preferred singleton object. If there is a cycle, then agents trade along that cycle. The process is repeated with the remaining agents and objects, until no agents remain. For the special case when each agent owns one object, the rule coincides with Gale’s TTC of [37].

Top Trading Cycles Algorithm

Input: An economy $\mathcal {E}=(\mathcal {N},\mathcal {O},\omega ,R)$.

Output: An allocation z for $\mathcal {E}$.

Initialize $V_1=\mathcal {O}$. For each $t\ge 1$:

Step ${\varvec{t}}$:

• 1. Let $H_{t}$ be the directed graph on $V_{t}$ with an edge $(\alpha ,\beta )$ in $E_{t}$ if and only if $ow(\alpha )$ topranks $\beta$ in $V_{t}$.

• 2. If $V_t$ is empty, then stop.

• 3. Otherwise, select an arbitrary cycle $(\gamma _1,\gamma _2,\ldots ,\gamma _j)$ in $H_t$.

  • (a) Add $\gamma _1$ to $z_{ow(\gamma _j)}$, and add $\gamma _{i+1}$ to $z_{ow(\gamma _i)}$ for $1 \le i < j$.

  • (b) Let $V_{t+1}=V_t \setminus \{\gamma _1,\ldots ,\gamma _j\}$.

We refer to Step t.3 in which the objects in the cycle $(\gamma _1,\dots ,\gamma _j)$ are allocated and removed, and the preference graph updated, as resolving the cycle $(\gamma _1,\dots ,\gamma _j)$. To see that the order in which we resolve cycles doesn’t matter, observe that this is obvious when the endowments are singletons (TTC is core-selecting [37]; the core is single-valued [34]). Inspecting the TTC protocol described above, we see that TTC does not distinguish between a single agent with a multiple endowment and multiple agents with singleton endowments who happen to have the same preference relation. The allocation to the single agent in the former case is precisely the disjoint union of the allocations to the multiple agent in the latter. Furthermore, all other agents’ allocations remain the same. Thus, after splitting all agents, we observe that the allocation is unique. This implies that any sequence of cycle selections results in the same allocation.⁹

Figure 1 gives an example of an economy with three agents, and shows the result of resolving one of its trading cycles. In this economy, $N=\{1,2,3\}$, $\omega _1=\{\gamma ,\delta \}$, $\omega _2=\{\alpha \}$, $\omega _3=\{\beta \}$, $R_1=(\alpha ,\beta ,\Box )$, $R_2=(\gamma ,\delta ,\beta ,\Box )$, and $R_3=(\gamma ,\Box )$. We adopt the convention throughout the paper that a directed edge

between an object $\alpha$ and an object $\beta$ indicates that, amongst the remaining objects in the economy, the owner of $\alpha$ prefers the object $\beta$ to any other object. Similarly,

denotes second preference,

denotes third preference,

denotes fourth preference, and

denotes fifth preference. We only depict the preferences of an agent up to their endowment and we may omit a loop (i.e. a directed edge from an object $\alpha$ to itself) for clarity unless confusion may arise. We have included two additional examples of economies depicted in this way, and full descriptions of the steps of applying TTC in Figs. 10 and 11 in the Appendix A.

Fig. 1

In the economy on the left, the owner of $\alpha$ topranks $\gamma$, whose owner topranks $\alpha$, so $(\alpha ,\gamma )$ is a trading cycle. On the right we show the result of resolving the cycle

We note that TTC is Pareto-efficient on the lexicographic domain, but not on the additive domain. To see this, consider an economy with two agents 1 and 2 in which $\omega _1=\{a\}$ and $\omega _2=\{b,c\}$. Suppose that $u_1(a)=4$, $u_1(b)=3$, $u_1(c)=2$, $u_2(a)=10$, $u_2(b)=2$, $u_2(c)=1$. In this economy, TTC allocates each agent their own endowment; the total utility of the allocation to agent 1 is therefore $u_1(a)=4$ and the total utility to agent 2 is $u_2(b)+u_2(c)=3$. However, swapping bundles makes both better off: $u_1(b)+u_1(c)=5$ and $u_2(a)=10$. We remark that TTC is individually rational on both domains.

When each agent owns only one object, TTC is strategy-proof; however, when agents own multiple objects, it is not. In Fig. 1, when agent 1 reports the lie $R_1'=(\beta ,\alpha ,\Box )$, TTC assigns them $\{\alpha ,\beta \}$. Since $\beta$ is ranked higher than $\delta$, agent 1 is better off and thus has a beneficial misreport.

In Fig. 2 we provide an example of a particular beneficial misreport. The intuition of the example will carry over into the proof of our main result. The idea is as follows: an agent ranks several “undesired” objects first in order to acquire more preferred objects later. There are two forces at play: Agent 1 has multiple opportunities to get $\alpha$ because $\gamma$ ranks two objects in the endowment of agent 1, so getting $\alpha$ can be delayed. Getting $x_1$ and $x_2$ first then “unlocks” the opportunity to get $\beta$ [the path $(\beta ,y_1,y_2,e_\beta )$].

Fig. 2

In this economy, agent 1 has a beneficial misreport. Agent 1 owns $e_1,e_2,e_\alpha ,$ and $e_\beta$. Their true preference relation, not shown, is $(\alpha ,\beta ,e_\alpha ,e_\beta ,e_1,e_2,\Box )$. If agent 1 reports the truth, their allocation is $\{\alpha ,e_\alpha ,e_\beta ,e_2\}$. If they report $(x_1,x_2,\alpha ,\beta ,\Box )$, then their allocation is $\{\alpha ,\beta ,x_1,x_2\}$

Since manipulation of TTC is possible, we next examine if computing a beneficial misreport is computationally tractable.

Computational complexity We are interested in the complexity of the following problem:

BENEFICIAL MISREPORT (BM)

INPUT: An economy $\mathcal {E}$.

QUESTION: Does agent 1 have a beneficial misreport under TTC at $\mathcal {E}$?

For simplicity’s sake, we always assume that agent 1 is the would-be liar. Since we are mainly interested in proving (conditional) lower bounds on the complexity of manipulating TTC, we focus on the decision version of the problem, which is $\mathbf {NP}$-hard as shown by Fujita et al. [18]. Since the outcome of TTC depends only on the reported preferences over singletons, we may assume that the input to BM includes only a total ordering of the objects for each agent apart from agent 1. It is necessary to compare bundles in the consumption space according to the true preference of agent 1 in order to solve BM, and we assume that the preference of agent 1 comes in the form of an algorithm that takes $f(k)\cdot |\mathcal {E}|^{O(1)}$ computational steps to compare two bundles of size k, where $|\mathcal {E}|$ is the number of bits needed to represent $\mathcal {E}$ and f is some computable function. We argue that this is a reasonable assumption. Choosing between two bundles of size k does not depend on the existence of alternative bundles, which implies the existence of an algorithm to compare bundles of size k whose runtime does not depend on the total size of the economy.

Parameterized complexity For a full treatment of the topic of parameterized complexity, we refer the reader to the textbook by Downey and Fellows [13]. For completeness, we recall some important terminology and definitions.

We define a parameterized language to be a subset of $\Sigma ^* \times {\mathbb {N}}$ for some alphabet $\Sigma$. If (s, k) is a member of a parameterized language L we say that k is the parameter. An algorithm that decides whether (s, k) is a member of L in time $f(k)\cdot |s|^{O(1)}$ for some computable function f is said to be an fpt-algorithm for L. The class of languages decidable by an fpt-algorithm is called $\mathbf {FPT}$. We call the decision problem associated with a parameterized language a parameterized problem (these terms are commonly used interchangeably).

A reduction between (classical) decision problems $\Pi _1$ and $\Pi _2$ is an algorithm which takes a string $s_1$ and produces a string $s_2$ such that $s_1$ is a yes-instance of $\Pi _1$ if and only if $s_2$ is a yes-instance of $\Pi _2$. A problem $\Pi$ is $\mathbf {NP}$-hard if there is a special kind of resource-bounded reduction from any problem in $\mathbf {NP}$ to $\Pi$. There are several choices for the definition of this reduction; the reader unfamiliar with this concept is directed to, e.g., [29]. Proving that $\Pi$ is $\mathbf {NP}$-hard is a conditional lower bound for the run time of an algorithm that solves $\Pi$. An analogous notion of a reduction and a corresponding conditional lower bound exists in the parameterized setting. An fpt-reduction between parameterized languages $L_1$ and $L_2$ is an algorithm which, for some computable functions f and g, takes $(s_1,k_1)$ as input and, in time at most $f(k)\cdot |s_1|^{O(1)}$, produces $(s_2,g(k_1))$ as output, such that $(s_1,k_1)\in L_1$ if and only if $(s_2,g(k_1))\in L_2$.

The class $\mathbf {W}[1]$ contains $\mathbf {FPT}$ and can be defined as the set of parameterized languages that can be reduced, by an fpt-reduction, to the language associated with the following decision problem.

SHORT NONDETERMINISTIC TURING MACHINE HALTING

INPUT: A nondeterministic multitape Turing machine M.

PARAMETER: An integer k.

QUESTION: Is it possible for M to reach a halting state in at most k steps?

It is considered extremely unlikely that $\mathbf {FPT}= \mathbf {W}[1]$. A parameterized problem $\Pi$ is $\mathbf {W}[1]$-hard if every problem in $\mathbf {W}[1]$ can be reduced, by an fpt-reduction, to $\Pi$. The $\mathbf {W}[1]$-hardness of a given problem is evidence of its intractability. For example, the problem of deciding whether a given graph contains a clique of size k (that is, k vertices every pair of which is adjacent), parameterized by k, is $\mathbf {W}[1]$-complete [12].

The class $\mathbf {W}[1]$ is the first level of the so-called $\mathbf {W}$-hierarchy of complexity classes: $\mathbf {FPT}\subseteq \mathbf {W}[1] \subseteq \mathbf {W}[2] \subseteq \ldots \subseteq \mathbf {W}[t] \subseteq \ldots \subseteq \mathbf {W[P]}$. We omit the technical definition of each level of the $\mathbf {W}$-hierarchy but, for example, deciding the existence of a dominating set of size k, parameterized by the size of the solution, is a $\mathbf {W}[2]$-complete problem. We are particularly interested in the class $\mathbf {W[P]}$, which contains the class W[t] for all t. The following theorem gives a characterization of $\mathbf {W[P]}$ that we will make use of later.

Theorem 2.1

([11] but see [9, 10]) A parameterized problem $\Pi$ is in $\mathbf {W[P]}$ if and only if there exists a Turing machine M that decides $\Pi$ such that, on input (x, k), M performs at most g(k)q(|x|) steps and at most $g(k)\log _2 |x|$ nondeterministic steps, where g is a computable function and q is a polynomial.

To state the defining problem of $\mathbf {W[P]}$, and the problem we will use to prove that BM is $\mathbf {W[P]}$-hard when parameterized by the size of the endowment to agent 1, we introduce some notions from circuit complexity.

Boolean circuits A Boolean circuit $\mathcal {C}$ is a directed acyclic graph with one sink. We call the vertices of $\mathcal {C}$ gates and the edges wires. The sources of $\mathcal {C}$, are labelled with Boolean variables $x_1,\ldots ,x_n$ (or $g_1,\dots ,g_n$); we call these input gates. The sink, $g_N$, is called the output gate. The remaining gates, denoted $g_{n+1},\ldots ,g_{N-1}$ are called the internal gates. Each of the gates $g_{n+1},\ldots ,g_N$ is labeled $\vee ,\wedge$ or $\lnot$. A $\lnot$-gate must have in-degree 1, otherwise the degrees are unrestricted. For brevity, we omit the word “Boolean” and refer simply to “circuits”. An assignment to a circuit assigns Boolean values to the input gates. We denote Boolean truth by the symbol 1 and falsehood by 0. It is convenient to refer to an assignment as a subset X of the input gates, namely the subset that is assigned 1. We evaluate a circuit $\mathcal {C}$ at an assignment X by assigning values to all of the gates recursively, according to their labels and to the assigned values of their predecessors. A $\lnot$-gate whose predecessor is assigned the value b is assigned the negation of b, denoted by $\lnot b$. An $\vee$-gate whose predecessors are assigned the values $b_1,\ldots ,b_j$ is assigned the logical disjunction of these values. An $\wedge$-gate whose predecessors are assigned the values $b_1,\ldots ,b_j$ is assigned the logical conjunction of these values. The value assigned to $g_N$ is the output of $\mathcal {C}$ given the assignment X, denoted $\mathcal {C}(X)$. If $\mathcal {C}(X)=1$ we say that X is satisfying and that X satisfies $\mathcal {C}$. The size of X is called its weight.

WEIGHTED CIRCUIT SATISFIABILITY (WCSAT)

INPUT: A circuit $\mathcal {C}$.

PARAMETER: An integer k.

QUESTION: Does $\mathcal {C}$ have a satisfying assignment of weight k?

A circuit with no $\lnot$-gates is said to be monotone; such a circuit is depicted in Fig. 3. The WCSAT problem is $\mathbf {W[P]}$-complete even when the input is restricted to monotone circuits [3]. We call this restricted problem MWCSAT.

Fig. 3

A monotone circuit with two input gates

Observation 2.2

If a monotone circuit has a satisfying assignment of weight at most k, then it has a satisfying assignment of weight exactly k.

We introduce the following terminology and a useful corollary of the previous observation. Let $x_i$ be an input gate of a monotone circuit $\mathcal {C}$ and let $g_j$ be a successor of $x_i$. Let X be an assignment to $\mathcal {C}$. We define an evaluation of $\mathcal {C}$ at X that is faulty on the wire $(x_i,g_j)$ in the sense that $g_j$ is assigned a value as if $x_i$ were assigned 0, regardless of X. Formally, if $g_j$ is an $\vee$-gate, then the value it is assigned is the logical disjunction of the values of its predecessors except that of $x_i$; if $g_j$ is an $\wedge$-gate, it is assigned 0. We then proceed with the evaluation in the normal way, and denote the result by $\mathcal {C}_{i,j}(X)$. We may extend the definition of a faulty evaluation to an arbitrary subset W of the wires starting at input gates, and denote the result by $\mathcal {C}_W(X)$.

Observation 2.3

Let $\mathcal {C}$ be a monotone circuit, W be a subset of the wires starting at the input gates of $\mathcal {C}$, and X be an assignment for $\mathcal {C}$. Then, $\mathcal {C}_W(X)=1$ implies $\mathcal {C}(X)=1$.

3 The main result

In this section, we state and prove our main result: BM is $\mathbf {W[P]}$-hard.

Theorem 3.1

BM, parameterized by the size of the endowment, is $\mathbf {W[P]}$-hard.

We prove the theorem by a reduction from MWCSAT. Let $\mathcal {C}$ be a monotone circuit and recall that we call its input gates $x_1,\ldots ,x_n$, its internal gates $g_{n+1}, \ldots ,g_{N-1}$, and its output gate $g_N$. We construct an economy $\mathcal {E}_\mathcal {C}$ with agent 1 having $k{+}2$ objects, such that agent 1 has a beneficial misreport if and only if $\mathcal {C}$ has a satisfying assignment of weight k.

In order to clarify the proof, we describe the construction in two stages. First, in Sect. 3.1, we show how to construct an economy $\mathcal {E}'_\mathcal {C}$ such that a weight-k satisfying assignment for $\mathcal {C}$ can be converted into a beneficial misreport for agent 1. Then, in Sect. 3.2 we show how to modify $\mathcal {E}'_\mathcal {C}$ to get the economy $\mathcal {E}_\mathcal {C}$ in which the converse holds.

3.1 Constructing economy $\mathcal {E}'_{\mathcal {C}}$

In both of our economies, agent 1 is endowed with $k+2$ objects and every other agent is endowed with exactly one object. To simplify our notation, we identify each such agent with the object they own, whenever this can be done unambiguously. For example, when we say that $\alpha$ topranks $\gamma$, we will mean that the owner of the object $\alpha$ topranks the object $\gamma$. We represent the preference relations of all agents as a list of singletons.

We now describe the set of objects and agents in $\mathcal {E}'_\mathcal {C}$. Firstly, we include agent 1 and the objects in the endowment to agent 1; namely, $\omega _1=\{e_1,\ldots ,e_k, e_\alpha ,e_\beta \}$. For each input gate $x_i$ we add objects $x_i^1,\ldots ,x_i^{out(i)}$, and we say these objects represent $x_i$; to simplify our notation, we will write $x_i^*$ instead of $x_i^{out(i)}$. For each gate $g_p$ with $n<p<N$ we add objects $g_p^1,\ldots ,g_p^{out(p)}$ and also $h_p^1,\ldots ,h_p^{in(p)}$. Only the objects $g_p^1,\ldots ,g_p^{out(p)}$ are said to represent $g_p$; the remaining objects are called the auxiliary objects of $g_p$. For the output gate $g_N$, we add a special object y which represents $g_N$ in this case. We add auxiliary objects $h_N^1,\ldots ,h_N^{in(N)}$ for $g_N$ just as for the other gates. Finally, we add objects $\alpha ,\beta ,\gamma ,\gamma _1,\ldots ,\gamma _k$.

We will construct $\mathcal {E}_\mathcal {C}'$ so that TTC allocates agent 1 the bundle $\{\alpha ,e_\alpha ,e_\beta ,e_k,\ldots ,e_2\}$ and, furthermore, that agent 1 will prefer a bundle B to this allocation if and only if both $\alpha$ and $\beta$ are in B. Thus let

$$\begin{aligned} R_1 = (\alpha ,\beta ,e_\alpha ,e_\beta ,e_k,e_{k-1},\ldots ,e_1,\square ) \end{aligned}$$

be the preference relation of agent 1. The only good preferred by agent 1 to any good in the allocation is $\beta$. Since $R_1$ is lexicographic, it is clear that agent 1 must obtain $\alpha$ and $\beta$ to benefit from any misreport.

The key intuitive idea behind our construction is that if (say) $\{x_{i_1},\ldots ,x_{i_k}\}$ is a satisfying assignment to $\mathcal {C}$, then agent 1 can benefit by reporting $R'_1=(x_{i_1}^*,\ldots ,x_{i_k}^*, \alpha ,\beta ,\square )$. If $\{ x_{i_1},\ldots ,x_{i_k}\}$ is not a satisfying assignment, and agent 1 reports $R'_1$, then we want y and $\beta$ to ultimately form a trading cycle when we run TTC; that is, agent 1 is unable to obtain $\beta$. On the other hand, if it is a satisfying assignment, we want that $\gamma _1,\ldots , \gamma _k$ and y are in trading cycles without $\beta$, so that the allocation of agent 1 will be $\{\alpha , \beta ,$ $x_{i_1}^*,\ldots ,x_{i_k}^*\}$. We will show that if there exists a beneficial misreport for agent 1, then there exists one of the form $R'_1$.

We now describe the preference relations of the other agents. In order to keep our notation simple, we refer to the agents by the name of their object. Since each agent, except agent 1, owns one object this will be unambiguous. Let

$$\begin{aligned} \begin{aligned} R_\alpha&= (\gamma ,\square ), \\ R_\beta&= (\gamma ,\gamma _1,\ldots ,\gamma _k,y, e_\beta ,\square ), \\ R_\gamma&= (e_1,\ldots ,e_k,e_\alpha ,\square ), \text { and} \\ R_{\gamma _i}&= (e_i,\beta ,\square ) \end{aligned} \end{aligned}$$

for each $i\in \{1,\dots ,k\}$. These preference relations imply that the allocation to agent 1 when they report the truth $R_1$ is as stated above: Observe that $(\alpha ,\gamma ,e_1)$ is a trading cycle. When this cycle is resolved, $\beta$ topranks $\gamma _1$ and vice versa, creating a trading cycle; so $\beta$ is not in the allocation for agent 1.

We now define the preferences of the agents owning objects representing $x_i$. In the definitions below, $g_p$ is a successor of $x_i$. According to some arbitrary ordering over the predecessors and successors of each gate, $g_p$ is the jth successor of $x_i$ and, in turn, $x_i$ is the qth predecessor of $g_p$. Let

$$\begin{aligned} \begin{aligned} R_{x_i^j}&= (\gamma _1,\ldots ,\gamma _k,h_p^q,\square )&\text {if }&j = 1\text { and} \\ R_{x_i^j}&= (x_i^{j-1},h_p^q,\square )&\text {if }&j> 1. \end{aligned} \end{aligned}$$

We now describe the preferences of agents that represent internal gates and their auxiliary agents. See Fig. 4 for an example of the construction.

Fig. 4

Left: an $\wedge$-gate gadget; Right: an $\vee$-gate gadget. In both cases the gate is $g_4$; its predecessors are $g_1,g_2$, and $g_3$; its successors are $g_5$ and $g_6$. It happens that $g_4$ is the first successor of each of its predecessors, and also the first predecessor of each of its successors

In the following definitions, $g_p$ is an $\wedge$-gate with a predecessor $g_i$ (which may possibly be an input gate $x_i$) and a successor $g_w$. The gate $g_i$ is the qth predecessor of $g_p$, and $g_p$ is the jth successor of $g_i$. The gate $g_w$ is the uth successor of $g_p$, and $g_p$ is the vth predecessor of $g_w$. Let

$$\begin{aligned} \begin{aligned} R_{h_p^q}&= (g_i^j,h_p^{q+1},\square )&\text {if }&q< in(p), \\ R_{h_p^q}&= (g_i^j,g_p^{out(p)},\square )&\text {if }&q= in(p), \\ R_{g_p^u}&= (h_p^1,h_w^v,\square )&\text {if }&u= 1, \text { and} \\ R_{g_p^u}&= (g_p^{u-1},h_w^v,\square )&\text {if }&1< u \le out(p). \end{aligned} \end{aligned}$$

The preference relations of agents representing $\vee$-gates are similar. Now let $g_p$ be an $\vee$-gate with a predecessor $g_i$ (which may possibly be an input gate $x_i$) and a successor $g_w$. As before, $g_i$ is the qth predecessor of $g_p$, $g_p$ is the jth successor of $g_i$, $g_w$ is the uth successor of $g_p$ and $g_p$ is the vth predecessor of $g_w$. Let

$$\begin{aligned} \begin{aligned} R_{h_p^q}&= (g_i^j,g_p^{out(p)},\square ), \\ R_{g_p^u}&= (h_p^1,\dots ,h_p^{in(p)},h_w^v,\square )&\text {if }&u= 1, \text { and} \\ R_{g_p^u}&= (g_p^{u-1},h_w^v,\square )&\text {if }&1<u \le out(p). \end{aligned} \end{aligned}$$

Finally we deal with the output gate $g_N$. The preference relations of the auxiliary agents for $g_N$ are similar to those above, simply replace $g_N^1$ with y in the definitions (think of $g_N$ as a gate with one output, and y as a relabeling of $g_N^1$). The preference relation of y is simply $(h_N^1,\beta ,\square )$ if $g_N$ is an $\wedge$-gate or $(h_N^1,\dots ,h_N^{in(N)},\beta ,\square )$ if $g_N$ is an $\vee$-gate.

Figure 5 gives a full example of the construction in the case $k=1$.¹⁰ The circuit corresponding to the economy in the figure is the circuit with two input gates $x_1$ and $x_2$, and an output gate which is an $\wedge$-gate. Agent 1 has $k+2$ objects denoted by $e_\alpha ,e_\beta$ and $e_1$, which are depicted as squares in the figure. If agent 1 tells the truth, then they are allocated $\{\alpha ,e_\alpha ,e_\beta \}$. The preferences of agent 1 are not shown in the figure, though, as the goal of agent 1 is to find a beneficial misreport if one exists. Note that the circuit has no satisfying assignment of weight 1, and that the misreports $R'_1=(x_1^*,\alpha ,\beta ,\square )$ and $R''_1=(x_2^*,\alpha ,\beta ,\square )$ are not beneficial. As $x_1^*=x_1^1$ and $x_2^*=x_2^1$, these misreports give agent 1 $\{x_1^1,\alpha ,e_\beta \}$ and $\{x_2^1,\alpha ,e_\beta \}$, respectively. We detail the steps of TTC for misreport $R_1'$ in Appendix A.2.¹¹

Fig. 5

The economy $\mathcal {E}'_\mathcal {C}$ where $\mathcal {C}$ is the circuit with one $\wedge$-gate $g_3$ and two input gates $x_1$ and $x_2$, with $k=1$ (agent 1 has endowment size $k+2=3)$. The true preference of agent 1, not shown, is $(\alpha ,\beta ,e_\alpha ,e_\beta ,e_1)$

Note that there is a beneficial misreport for agent 1 in the depicted economy (and indeed any economy constructed as we have described). If agent 1 reports $R_1'''=(y,\alpha ,\beta ,\square )$, then they are allocated $\{y,\alpha ,\beta \}$. We return to this issue in the next section. For now, we prove that the strategy of obtaining a set of objects corresponding to an assignment produces a beneficial misreport if and only if the assignment is satisfying.

Proposition 3.2

Let $X=\{x_{i_1},\ldots ,x_{i_k}\}$ be an assignment to $\mathcal {C}$ and let $R'_1=$ $(x_{i_1}^*,\ldots ,x_{i_k}^*,$ $\alpha ,\beta ,\square )$ be a misreport. Then $R'_1$ is beneficial if and only if X is satisfying.

Proof

We run TTC on $\mathcal {E}'_\mathcal {C}$ with agent 1 misreporting $R'_1$. Intuitively, a particular (non-output) gate in $\mathcal {C}$ has value 1 in the evaluation of the assignment if and only if the objects representing the gate are traded in the same cycle. Once all the objects representing a gate are traded we say that the gate is fixed. If all the objects representing a gate were traded in the same cycle, we will say that the gate is fixed with value 1, and with value 0 otherwise. Recall that we may choose the order in which to resolve cycles. We first resolve cycles including objects representing input gates. After dealing with the input gates, we deal with gates whose predecessors are all fixed.

In the initial preference graph, there is just one trading cycle $(e_1,x_{i_1}^*,\ldots ,x_{i_1}^1,\gamma _1)$. We resolve this cycle, and fix $x_{i_1}$ with value 1. The updated preference graph contains several trading cycles; we proceed by resolving the cycle $(e_j,x_{i_j}^*,\ldots ,x_{i_j}^1,\gamma _j)$ and fixing $x_{i_j}$ with value 1 for $j=2,\dots ,k$. At the end of this process, each gate in X is fixed with value 1.

Now, for each gate $x_i$ that is not in X, there is a trading cycle $(x_i^1,h_p^q)$, where $g_p$ is the 1st successor of $x_i$, and $x_i$ is the qth predecessor of $g_p$. We resolve this cycle, and update the preference graph. There is now a trading cycle $(x_i^2,h_{p'}^{q'})$, where $g_{p'}$ is the 2nd successor of $x_i$, and $x_i$ is the $q'$th predecessor of $g_{p'}$. Resolving this cycle and repeating for the remaining successors of $x_i$, we then fix $x_i$ with value 0. We do the same for all the input gates outside of X, and so all of the input gates are fixed.

We continue by fixing any $\wedge$-gate whose predecessors were all fixed. Let $g_p$ be such a gate; we show that $g_p$ is fixed with value 1 if and only if all its predecessors were fixed with value 1. Suppose first that each predecessor was fixed with value 1. Let the qth predecessor of $g_p$ be $g_j$; since it was fixed with value 1 the objects representing it were traded in the same cycle. In particular, if $g_p$ is the $\ell$th successor of $g_j$, the object $g_j^\ell$ was traded in the cycle with $g_j^1,\dots ,g_j^{out(j)}$ and not with $h_p^q$. Therefore, $h_p^q$ is in the current preference graph, and currently topranks $h_p^{q+1}$, unless $q=in(p)$, in which case it topranks $g_p^{out(p)}$. Thus there is a trading cycle $(g_p^{out(p)},\dots ,g_p^1,h_p^1,\dots ,h_p^{in(p)})$. We resolve this cycle, fixing $g_p$ with value 1 as required. Now suppose that $j'$ is the smallest integer such that the predecessor $g_{j'}$ was fixed with value 0, and suppose that $g_{j'}$ is the $q'$th predecessor of $g_p$. Then the objects representing $g_{j'}$ were not traded in the same cycle. We claim that $(g_{j'}^{\ell '},h_p^{q'})$ was a trading cycle already resolved in a previous step of TTC. Indeed, if $g_{j'}$ was in fact an input gate, then this follows from the previous paragraph. Since there must be a gate all of whose predecessors are input gates, the claim will follow by induction. Since $h_p^{q'}$ has been traded, $(h_p^{q'-1})$ is a trading cycle in the current preference graph, which we resolve. After repeating this step $q'{-}1$ times, $h_p^1$ is traded. Suppose the first successor of $g_p$ is $g_{r}$ and $g_p$ is the sth predecessor of $g_{r}$. Then $g_p^1$ topranks $h_{r}^{s}$ in the current preference graph, since $h_p^1$ was traded. Since $h_{r}^{s}$ topranks $g_p^1$ by definition, there is a trading cycle $(g_p^1,h_{r}^{s})$. Resolving this cycle completes the induction to give the claim. Thus, the objects representing $g_p$ are not traded in the same cycle, which is what we wanted: $g_p$ is fixed with value 0.

The procedure is similar for $\vee$-gates. Let $g_p$ be such a gate; we show that $g_p$ is fixed with value 0 if and only if all its predecessors were fixed with value 0. Suppose first that each predecessor was fixed with value 0. Let the qth predecessor of $g_p$ be $g_j$, and suppose $g_p$ is the $\ell$th sucessor of $g_j$. By the same inductive reasoning as in the previous paragraph, we may assume that $(g_{j}^\ell ,h_p^q)$ was a trading cycle resolved in a previous step. Let the first successor of $g_p$ be $g_{r}$ and suppose that $g_p$ is the sth predecessor of $g_{r}$. Then $g_p^1$ topranks $h_{r}^{s}$ in the current preference graph, since $h_p^1,\dots ,h_p^{in(p)}$ were removed. Since $h_{r}^{s}$ topranks $g_p^1$ by definition, there is a trading cycle $(g_p^1,h_{r}^{s})$. After resolving this cycle, we see that the objects representing $g_p$ are not traded in the same cycle, which is what we wanted: $g_p$ is fixed with value 0. Now let $j'$ be the smallest integer such that the predecessor $g_{j'}$ was fixed with value 1, and suppose that $g_{j'}$ is the $q'$th predecessor of $g_p$. Then the objects representing $g_{j'}$ were traded in the same cycle. As in the previous paragraph, $h_p^{q'}$ is in the current preference graph, but since $g_p$ is an $\vee$-gate, $h_p^{q'}$ topranks $g_p^{out(p)}$. Thus there is a trading cycle $(g_p^{out(p)},\dots ,g_p^1,h_p^{q'})$. We resolve this cycle, fixing $g_p$ with value 1 as required.

After repeating the above for all gates, we may observe that, if X is satisfying, then $g_N$ will be fixed with value 1, and the object y was in a cycle with its auxiliary objects and not in the remaining preference graph. Otherwise, y will be fixed with value 0, and there will be a trading cycle $(y,\beta )$, which will prevent agent 1 from getting $\beta$.

To complete the proof, we consider $\alpha$ and $\beta$. Since each of the objects in the endowment to agent 1 has been traded, $\gamma$ topranks $e_\alpha$. Agent 1 now topranks $\alpha$, so there is a trading cycle $(\alpha ,\gamma ,e_\alpha )$. We resolve this cycle, which adds $\alpha$ to the allocation to agent 1 as required. Consider the current preference graph. Since $\gamma$ was traded when the previous cycle was resolved, $\beta$ topranks $e_\beta$ if and only if y was already traded. Therefore, if X is satisfying, we will have a trading cycle $(\beta ,e_\beta )$ and resolving it will add $\beta$ to the allocation to agent 1. Otherwise, we will have a trading cycle $(\beta ,y)$ and the allocation of agent 1 does not include $\beta$. This completes the proof that $R'_1$ is beneficial if and only if X is satisfying. $\square$

We have proved that if $\mathcal {C}$ has a satisfying assignment of weight k then agent 1 has a beneficial misreport in $\mathcal {E}'_\mathcal {C}$. However, the converse may not hold. Indeed $R''_1=(y,\gamma _2,\ldots ,\gamma _k,\alpha ,\beta ,\square )$ is a beneficial misreport for $\mathcal {E}'_\mathcal {C}$ for any $\mathcal {C}$ and thus the main theorem is not yet proved. Before we overcome this difficulty, we make the following observation.

Observation 3.3

Let $X=\{x_{i_1},\dots ,x_{i_k}\}$ be an assignment to $\mathcal {C}$. For each $j\in \{1,\dots ,k\}$, let $\eta _j\in \{\gamma _j,x_{i_j}^1,\dots ,x_{i_j}^*\}$, and let $R'_1=(\eta _1,\ldots ,\eta _k,\alpha ,\beta ,\square )$. Then if $R'_1$ is beneficial so is $R''_1=(x_{i_1}^*,\ldots ,x_{i_k}^*,\alpha ,\beta ,\square )$.

Proof

By Proposition 3.2, running TTC with $R''_1$ is equivalent to evaluating $\mathcal {C}$ at the assignment $X=\{x_{i_1},\ldots ,x_{i_k}\}$. Running TTC with $R'_1$ is equivalent to a faulty evaluation of $\mathcal {C}$ at X, with some faulty wires starting at input gates. The claim follows from Observation 2.3. $\square$

3.2 Constructing economy $\mathcal {E}_{\mathcal {C}}$

In order to complete the proof of Theorem 3.1, we modify $\mathcal {E}'_\mathcal {C}$ to obtain the final construction $\mathcal {E}_\mathcal {C}$. Let the circuit structure of $\mathcal {E}'_\mathcal {C}$ be the set of objects representing gates, the set of auxiliary objects, and the preference relations of their respective owners. In the previous section, we observed that it is possible for agent 1 to destroy the circuit structure in $\mathcal {E}'_\mathcal {C}$, e.g., by topranking y, so that running TTC is not equivalent to evaluating some assignment to $\mathcal {C}$. We will show how to prevent this outcome by duplicating the circuit structure in $\mathcal {E}'_\mathcal {C}$ $k{+}1$ times.

For each object in the circuit structure of $\mathcal {E}'_\mathcal {C}$ we include $k{+}1$ copies in $\mathcal {E}_\mathcal {C}$. We distinguish these copies by adding a label from 1 to $k{+}1$ to their subscripts. For instance, the copies of $g_i^j$ are denoted $g_{i,1}^j,\ldots ,g_{i,k+1}^j$. The copies of the output gates are denoted $y_1,\ldots ,y_{k+1}$. We will use $x_i^*$ to denote only the last copy of $x_i^{out(i)}$; that is, $x_i^*=x_{i,k+1}^{out(i)}$.

We now describe the preference relations of the copies. For the $\ell$th copy of the objects representing an internal gate or any auxiliary object (including those of the output gate), we obtain a preference relation from that of its original in $\mathcal {E}'_\mathcal {C}$ by adding $\ell$ to the subscript and putting all objects that are not in the $\ell$th copies after itself. Similarly, $R_{y_\ell }=(h_{N,\ell }^1,\beta ,\Box )$ if $g_N$ is an $\wedge$-gate and $R_{y_\ell }=(h_{N,\ell }^1,\dots ,h_{N,\ell }^{in(N)},\beta ,\Box )$ if $g_N$ is an $\vee$-gate.

We treat the copies of objects representing input gates differently. The first copy of $x_i^1$ has a similar preference relation to its original, but the $\ell$th copy topranks the $\ell {-}1$th copy of $x_i^{out(i)}$. The copies of $x_i^j$ for $j>1$ have similar preference relations to their originals, the effect of which is that all the copies of all the objects representing the input gate $x_i$ form a directed path in the graph of first preferences. As in the original definitions, in what follows $g_p$ is a successor of $x_i$. In particular, it is the jth successor of $x_i$ and $x_i$ is the qth predecessor of $g_p$. Let

$$\begin{aligned} \begin{aligned} R_{x_{i,1}^j}&= (\gamma _1,\ldots ,\gamma _k,h_{p,1}^q,\square )&\text {if }&j= 1,\\ R_{x_{i,\ell }^1}&= (x_{i,\ell -1}^{out(i)},h_{p,\ell }^q,\square )&\text {if }&1<\ell \le k+1,\text { and}\\ R_{x_{i,\ell }^j}&= (x_{i,\ell }^{j-1},h_{p,\ell }^q,\square )&\text {if }&j>1 \& 1\le \ell \le k+1. \end{aligned} \end{aligned}$$

An example of the result of this duplication process is given in Fig. 6.

Fig. 6

The economy $\mathcal {E}_\mathcal {C}$ where $\mathcal {C}=x_1\wedge x_2$, as in Fig. 5, in which $k=1$. Here, $k=5$, chosen to illustrate the general construction. We omit the objects $\alpha$, $\beta$, $\gamma$, $e_\alpha$, and $e_\beta$ for clarity

The final modification that we make is to change the preference relation of $\beta$ to $R_\beta = (\gamma ,\gamma _1,\ldots ,\gamma _k,$ $y_1,\ldots ,y_{k+1},e_\beta ,\beta ,\square )$.

Proof of Theorem 3.1

Let $\mathcal {C}$ be a monotone circuit and $\mathcal {E}_\mathcal {C}$ be the economy obtained from $\mathcal {E}'_\mathcal {C}$ by the modifications described above. We will show that $\mathcal {C}$ has a satisfying assignment of weight k if and only if agent 1 has a beneficial misreport in $\mathcal {E}_\mathcal {C}$. Furthermore, $\mathcal {E}_\mathcal {C}$ can be constructed in time $g(k)\cdot |\mathcal {C}|$. We will conclude that there is a parameterized reduction from MONOTONE WCSAT to BM, as required.

Let $X=\{x_{i_1},\ldots ,x_{i_k}\}$ be an assignment for $\mathcal {C}$.

Claim 3.4

$R'_1=(x^*_{i_1},\ldots ,x^*_{i_k},\alpha ,\beta ,\square )$ is a beneficial misreport for agent 1 in $\mathcal {E}_\mathcal {C}$ if and only if $R'_1$ is beneficial for agent 1 in $\mathcal {E}'_\mathcal {C}$.

The above claim follows by the construction of $\mathcal {E}_\mathcal {C}$. To see this, consider the first step of TTC for this economy. As $x_{i_1}^*=x_{i_1,k+1}^{out(i_1)}$, the only cycle that forms is

$$\begin{aligned} (e_1,x_{i_1,k+1}^{out(i_1)},\dots ,x_{i_1,k+1}^{1},x_{i_1,k}^{out(i_1)},x_{i_1,k}^{out(i_1)-1},\dots ,x_{i_1,1}^{1},\gamma _1). \end{aligned}$$

Note then that for each copy of the circuit structure, the respective input gate $x_{i_1}$ takes value 1 (i.e. for copy $\ell <k+1$, the objects $\{x_{i_1,\ell }^{out(i_1)},\dots ,x_{i_1,\ell }^1\}$ are in the cycle as in Proposition 3.2).¹² A symmetric statement holds for each other input gate $\{x_{i_2},\dots ,x_{i_k}\}$. After we resolve each such trading cycles, we can run TTC in any of the copies of the circuit structure independently of the others in a way that is identical to the proof of Proposition 3.2. As a corollary, if $\mathcal {C}$ has a satisfying assignment of weight k then agent 1 has a beneficial misreport in $\mathcal {E}_\mathcal {C}$ as required.

We must show that if there is some beneficial misreport for agent 1, then there is a satisfying assignment for $\mathcal {C}$ of weight k. Let $R'_1$ be such a misreport, and consider running TTC on $\mathcal {E}_\mathcal {C}$ with agent 1 misreporting $R'_1$. We define a corresponding assignment for $\mathcal {C}$ later. Let $A=\{\alpha ,\beta ,\delta _1,\ldots ,\delta _k\}$ be the allocation of agent 1 when they report $R'_1$. We may assume that the first $k{+}2$ objects in $R'_1$ coincide with A; therefore, for each object $\epsilon \in \mathcal {O}\setminus A$, and each $\epsilon '\in A$, we have that $\epsilon ' \mathrel {R'_1} \epsilon$. We may also assume, without loss of generality, that $\delta _j \mathrel {R'_1} \delta _{j+1}$ for all j. We make the following useful observations about A and $R'_1$: Agent i cannot simultaneously obtain objects $a\in A$ and $\gamma$, and in order to obtain A, agent i must report a certain order of objects.

Observation 3.5

$\gamma \not \in A$.

Proof

Since $\alpha$ topranks $\gamma$, they are either traded in the same cycle or $\gamma$ is traded before $\alpha$. If $\gamma$ is traded before $\alpha$ then $(\alpha )$ will be a trading cycle, and the owner of $\alpha$ retains $\alpha$. So $\alpha \notin A$, a contradiction. $\square$

Observation 3.6

$\alpha \mathrel {R}'_1 \beta$.

Proof

If $\beta \mathrel {R}'_1 \alpha$, then since $\beta$ topranks $\gamma$, we have that $\gamma$ is necessarily traded before $\alpha$. Then the argument in Observation 3.5 applies. $\square$

Observation 3.7

$\delta _i \mathrel {R'_1} \alpha$ for $1\le i \le k$.

Proof

Let i be the smallest integer such that $\alpha \mathrel {R'_1} \delta _i$. By construction, the trading cycle containing $\alpha$ must be $(\alpha ,\gamma , e_i)$. After removing this cycle, $(\beta ,\gamma _i)$ is a trading cycle, which is a contradiction to $\beta \in A$. $\square$

The above observations show that $R'_1$ takes the form $(\delta _1,\ldots ,\delta _k,\alpha ,\beta ,\square )$ and that each $\delta _j$ is in some copy of the circuit structure (or $\delta _j=\gamma _j$, although we will see below that this effectively represents giving a lower weight assignment to $\mathcal {C}$; in this case the result will follow from Observation 2.2). Figure 8 in Appendix A.1 provides a reference example economy for which the reasoning of Observation 3.7 can be applied.

Intuitively, agent 1 makes k trading cycles each in some copy of the circuit structure of $\mathcal {E}_\mathcal {C}$ representing the circuit, and then tries to get $\alpha$ and $\beta$. Since there are $k{+}1$ copies of the circuit structure, there is at least one copy where $\delta _1,\dots ,\delta _k$ are not objects in the circuit structure. In this copy, the trading cycles including its objects only interact with input gates. Thus, its circuit structure is preserved, and agent 1 needs to avoid a trading cycle between its copy of y and $\beta$. We describe formally how to extract a satisfying assignment of weight k from this interaction below.

We apply TTC according to the following ordering of the trading cycles. For each $j=1,\ldots ,k$, we remove the trading cycle $C_j$ containing $\delta _j$ and $e_j$ and update the preference graph. We call these the initial cycles. There are at most k input gates $x_i$ such that some copy of some object representing $x_i$ has been removed. We call these $X=\{x_{i_1},\ldots ,x_{i_{k'}}\}$ where $k'\le k$. Our goal is to prove that X is a satisfying assignment for $\mathcal {C}$. By Observation 2.2, it will follow that $\mathcal {C}$ has a satisfying assignment of weight exactly k.

In order to achieve our goal, we continue our application of TTC in $\mathcal {E}_\mathcal {C}$ with agent 1 reporting $R'_1$. Observe that there must be some z with $1\le z\le k{+}1$ such that none of the zth copies of the objects representing internal gates and auxiliary objects have been removed. As we remove trading cycles representing zth copies of objects, we fix the value of the gates similarly to the proof of Proposition 3.2. Let $x_i$ be a gate not in X, and consider the object $x_{i,1}^1$. Since $\gamma _1,\ldots ,\gamma _k$ have been removed, and $x_{i,1}^1$ has not, there is a trading cycle $(x_{i,1}^1,h_{p,1}^q)$ where the first successor of $x_i$ is the qth predecessor of $g_p$. If $z\not =1$, we remove this cycle, and then there is a trading cycle $(x_{i,1}^2,h_{p',1}^{q'})$ which we remove, and so on up to $(x_{i,1}^{out(i)},h_{p'',1}^{q''})$. Now there is a trading cycle $(x_{i,2}^1,h_{p,2}^q)$ which we remove. We continue this process until we reach $x_{i,z}^1$. When we resolve the cycles $(x_{i,z}^1,h_{p,z}^q), \ldots , (x_{i,z}^{out(i)},h_{p'',z}^{q''})$ we fix the gate $x_i$ with value 0 (much as we did in the proof of Proposition 3.2). We repeat this process for each $x_i\not \in X$.

Now consider a gate $x_i\in X$ (in other words $i\in \{i_1,\ldots ,i_k\}$) and consider the zth copies of the objects representing $x_i$. There are three cases to consider. If all the objects $x_{i,z}^1,\ldots ,x_{i,z}^{out(i)}$ were removed in the same initial cycle, then we can simply fix $x_i$ with value 1 and continue. If none of the objects $x_{i,z}^1,\ldots ,x_{i,z}^{out(i)}$ have been traded (in other words, if an initial cycle removed $x_{i,\ell }^q,\ldots ,x_{i,\ell }^1,x_{i,\ell -1}^{out(i)},\dots , x_{i,\ell -1}^1,\dots ,x_{i,1}^{out(i)},\dots ,x_{i,1}^1$ for some q and for some $\ell <z$) then we can fix $x_i$ with value 0 and repeat the above process, eventually resolving $(x_{i,z}^1,h_p^q)$ where the first successor of $x_i$ is the qth predecessor of $g_p$, and so on. In the third case, some of the objects $x_{i,z}^1,\ldots ,x_{i,z}^{out(i)}$ have been traded and some have not. Note that this can only happen if $\delta _j=x_{i,z}^r$ for some j and r so that there was an initial cycle $(e_j,x_{i,z}^r,x_{i,z}^{r-1}, \ldots ,x_{i,z}^1,x_{i,z-1}^{out(i)},\ldots ,x_{i,1}^1,\gamma _j)$. In this case we fix $x_i$ with value 1, but now we have a trading cycle $(x_{i,z}^{r+1},h_{p,z}^{q})$, where $g_p$ is the $r+1$th successor of $x_i$, and $x_i$ is the qth predecessor of $g_p$. When we resolve this cycle, we will say that $g_{p}$ received the value 0 from $x_i$, and that the wire from $x_i$ to $g_{p}$ is faulty. We repeat this process for each $r'$ from $r+1$ to out(i). It will follow that continuing to run TTC in the zth copy of the circuit structure is equivalent to a (possibly faulty) evaluation of the assignment X.

Consider a gate $g_p$ all of whose predecessors are input gates. Following the proof of Proposition 3.2, if $g_p$ is an $\wedge$-gate, then there will be a trading cycle $(h_{p,z}^1,\ldots ,h_{p,z}^{in(p)},$ $g_{p,z}^{out(p)}, \ldots , g_{p,z}^2,$ $g_{p,z}^1)$ only if each predecessor of $g_p$ was assigned the value 1. Similarly, if $g_p$ is an $\vee$-gate, there will be a trading cycle $(h_{p,z}^i,g_{p,z}^{out(p)},\ldots , g_{p,z}^2,$ $g_{p,z}^1)$ only if at least one of the predecessors of $g_p$ was assigned the value 1; namely, its ith predecessor. The rest of the proof is identical to Proposition 3.2. Since $R'_1$ is beneficial, eventually $(\beta ,e_\beta )$ is a trading cycle. Therefore, $(y_z,\beta )$ is never a trading cycle; in other words, the output gate $g_N$ must be fixed with value 1 after we run TTC. We conclude that X is a satisfying assignment for $\mathcal {C}$.

It remains only to justify that the construction of $\mathcal {E}_\mathcal {C}$ can be performed in $g(k)\cdot |\mathcal {C}|^{O(1)}$ steps for some computable function g; that is, the reduction described above is truly an fpt-reduction. For each of the N gates of $\mathcal {C}$, at most N objects and agents are created in $\mathcal {E}'_\mathcal {C}$, each with a preference relation that is a list of objects of length at most $k{+}2$. We duplicate these $k{+}2$ times in $\mathcal {E}_\mathcal {C}$. This takes at most $f(k)\cdot O(N^2\log _2 N)$ time for some computable f. Agent 1 has $k{+}2$ objects and a preference relation of length $k{+}4$. There are $k{+}3$ remaining objects and agents which each have a preference relation of length at most $k{+}4$. Constructing these objects and agents takes $f'(k)\cdot O(\log _2 N)$ time for some computable $f'$. Combining the above shows that the reduction takes $g(k)\cdot |\mathcal {C}|^{O(1)}$ steps as required. $\square$

4 The upper bound

In this section, we show that BM is a member of $\mathbf {W[P]}$ and is thus $\mathbf {W[P]}$-complete.

Theorem 4.1

BM is $\mathbf {W[P]}$-complete.

Proof

Let $\mathcal {E}=(\mathcal {N},\mathcal {O},\omega ,R)$ be an economy. We show that there exists a Turing machine M that decides the existence of a beneficial misreport in $\mathcal {E}$ that performs at most $g(k)q(|\mathcal {E}|)$ steps and at most $g(k)\log _2 |\mathcal {E}|$ nondeterministic steps, for some computable g and polynomial q. By Theorem 2.1, this gives the upper bound that matches the lower bound of the previous section, and thus the result.

Our proof relies on the fact that a beneficial misreport for an agent with an endowment of size k has a canonical form that takes $O(k\left\lceil \log _2 |\mathcal {O}|\right\rceil )$ bits to specify. To prove this claim, it is necessary to fix a precise order in which cycles are removed by the TTC algorithm. In particular, for each economy $\mathcal {E}$ we fix a total ordering over the set of its objects $\mathcal {O}$. We can thus refer to the first object in $\mathcal {O}$. Observe that for each object $\alpha$ in $V_t$ there is a unique directed walk with no repeated edges starting at $\alpha$; we call this the trading walk starting at $\alpha$. Since every element of $V_t$ has outdegree 1, this walk must contain a cycle. We define the cycle chosen to be resolved in Step t.3 of the TTC algorithm to be the one contained in the trading walk starting at the first object in $V_t$. We can now define the trading time $tt_{\mathcal {E}}(\alpha )$ of an object $\alpha$ in a run of TTC on $\mathcal {E}$ to be the least integer t such that $\alpha \in V_t \setminus V_{t+1}$. When the economy is unambiguous, we write $tt(\alpha )=tt_{\mathcal {E}}(\alpha )$. The following observation says that, if an agent i receives an object $\beta$ at a particular step, then all objects that are preferable to $\beta$ under $R_i$ must have had an earlier trading time.

Observation 4.2

Let $\mathcal {E}$ be an economy, $i\in \mathcal {N}$ be an agent, and z be the allocation that TTC recommends for $\mathcal {E}$. For each $\beta \in z_i$, and each $\alpha \in {\mathcal {O}} \setminus \{\beta \}$, if $\alpha \mathrel {P_i} \beta$, then $tt(\alpha ) < tt(\beta )$.

We are now ready to show that every beneficial misreport is equivalent to one that can be specified efficiently, in the sense that they yield the same allocation. In particular, the following claim shows that it is enough to guess the first k objects of a beneficial misreport.

Claim 4.3

Suppose the allocation of agent 1 under TTC at $(R'_1,R_{-1})$ is $z_1=\{\gamma _1,\ldots ,\gamma _k\}$ and that $\gamma _i\mathrel {R'_1}\gamma _{i+1}$ for $1\le i < k$. Let $R''_1=(\gamma _1,\ldots ,\gamma _k,\square )$. Then the allocation of agent 1 at $(R''_1,R_{-1})$ is also $z_1$.

Proof

Let $\mathcal {E}'$ and $\mathcal {E}''$ be the (otherwise identical) economies in which agent 1 reports $R'_1$ and $R''_1$ respectively. For $t=1,2,\ldots$ let $H'_t$ and $H''_t$ be the graphs generated by running TTC on $\mathcal {E}'$ and $\mathcal {E}''$ respectively. Let $tt'(\alpha )$ and $tt''(\alpha )$ be the trade times of $\alpha$ during a run of TTC on $\mathcal {E}'$ and $\mathcal {E}''$ respectively. By Observation 4.2, $tt'(\gamma _1)<tt'(\gamma _i)$ and $tt''(\gamma _1) < tt''(\gamma _i)$ for $1< i \le k$. Consider $H'_{tt'(\gamma _1)}$. None of the cycles that were resolved to obtain $H'_2,\ldots ,H'_{tt'(\gamma _1)-1}$ have included any of $\gamma _1,\ldots ,\gamma _k$. Therefore we may assume without loss of generality that the same cycles are resolved to obtain $H''_2,\ldots ,H''_{tt''(\gamma _1)-1}$ and thus $H''_{tt''(\gamma _1)}$ and $H'_{tt'(\gamma _1)}$ are identical. Since $\gamma _1$ is allocated to agent 1 in $\mathcal {E}'$, it must also be allocated to agent 1 in $\mathcal {E}''$. The claim follows by induction. $\square$

Observe that TTC runs in polynomial time since in each step we reduce the total number of objects by at least one. In particular, there exists a Turing machine $M_{TTC}$ that runs in time $O(|\mathcal {E}|^c)$ for some constant c, takes as input a binary string representing the list of preferences over singletons of each agent, and returns an allocation by running TTC on the economy given by that string. Our Turing machine M will use $M_{TTC}$ as a subroutine. We omit the details but M has three phases.

• Phase 1 In this phase, M prepares an input string for $M_{TTC}$. First, M nondeterministically writes a binary string representing an ordered list of k objects onto one of its tapes, which is the beginning of $R'_1$. Since there are $|\mathcal {O}|$ objects in total, this string has length $O(k \left\lceil \log _2 |\mathcal {O}|\right\rceil )$. The rest of $R'_1$ can be prepared deterministically by ordering the remaining objects by their representation as a binary string. Finally the rest of the input to $M_{TTC}$ is prepared by writing the preferences of the other agents.

• Phase 2 In this phase, M runs $M_{TTC}$ on the input written on the tape in the previous phase, and also on the true preferences. It writes the true allocation A and the allocation $A'$ under $R'_1$ on one of its tapes.

• Phase 3 In this phase, M compares A and $A'$ according to $R_1$. If $A' \mathrel {R_1} A$, then M accepts. Otherwise, M rejects.

Phase 1 uses $O(k \left\lceil \log _2 |\mathcal {O}|\right\rceil )$ nondeterministic steps; in particular, it takes no more than $g(k)\log _2 |\mathcal {E}|$ bits of nondeterminism. By Claim 4.3 a beneficial misreport will be guessed in Phase 1 if one exists. Listing the remaining elements to complete the construction of $R'_1$ in the deterministic part of Phase 1 takes linear time. Phase 2 takes polynomial time by the definition of $M_{TTC}$, and Phase 3 takes polynomial time by the definition of BM. Therefore M fulfils the requirements of Theorem 2.1 as required. $\square$

5 Group manipulation

Consider now the possibility of manipulation by a group of agents. For intuition, we depict a scenario in Fig. 7 that extends upon that of Fig. 2. Now, instead of only one agent who must obtain an undesirable object to get a more desirable one, we have two agents who each must obtain an undesirable object for each of them to get their respective more desirable objects. In general, a group misreport may consist of agents in the group who simply state their true preference. Thus, in this scenario, if there is a third agent who benefits even if they state their true preference, then there is also a beneficial group misreport for the three agents.

Fig. 7

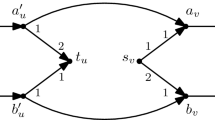
Agent 1 owns $\{e_\alpha ,e_0,e_\beta \}$ and agent 2 owns $\{e'_\alpha ,e'_0,e'_\beta \}$. Let $R_1=(\alpha ,\beta ,e_\alpha ,e_\beta ,e_0,\Box )$, and $R_2=(\alpha ',\beta ',e_\alpha ',e_\beta ',e_0',\Box )$. If agent 2 tells the truth, then agent 1 can only get $\{\alpha ,e_\alpha ,e_\beta \}$ (by telling the truth). If agent 2 lies by reporting $R_2'=(x',\alpha ',\beta ',\Box )$, then agent 1 can benefit by reporting the lie $R_1'=(x,\alpha ,\beta ,\Box )$: In the subsequent preference profile $(R_1',R_2',R_{-\{1,2\}})$, agent 1 receives $\{x,\alpha ,\beta \}$, and agent 2 receives $\{x',\alpha ',\beta '\}$. In this group misreport, agents 1 and 2 additionally obtain $\beta$ and $\beta '$ (respectively) through the cycle $(e_\beta ,\beta ,y,e_\beta ',\beta ',y',e_\beta )$

Formally, we consider the following problem:

GROUP MANIPULATION (GM)

INPUT: An economy $\mathcal {E}$, an integer m.

QUESTION: Do agents $1,\ldots , m$ have a beneficial group misreport under TTC at $\mathcal {E}$?

The natural parameters for GM are the size of the group and the size of the union of the endowments of the group. If we parameterize GM by the latter, then we obtain a $\mathbf {W[P]}$-hard problem as a corollary of our main result. If the number of manipulating agents is not part of the parameter, we can choose its size in the definition of the reduction. Thus the group can be of size one, and the exact same construction works.

We now adapt the proof of Theorem 3.1 to show that GM, parameterized by the size of the group k, is $\mathbf {W[P]}$-hard. In that proof, agent 1 had to obtain k unwanted objects in order to obtain a preferred bundle. Those k choices corresponded to choosing an assignment of weight k to a circuit. We adapt this idea by dividing the k choices among the manipulating agents. The agents each must obtain one unwanted object. Their choices will collectively correspond to an assignment of weight k to a circuit. As in Theorem 3.1, they will benefit if and only if they are able to find a satisfying assignment.

Theorem 5.1

GM, parameterized by the size of the manipulating group, is $\mathbf {W[P]}$-hard.

Proof

We reduce from MWCSAT. Let $\mathcal {C}$ be a monotone circuit. Recall the construction of $\mathcal {E}_\mathcal {C}$ from the proof of the main theorem. We adapt this construction to obtain an economy $\mathcal {E}^*_\mathcal {C}$. To construct $\mathcal {E}_\mathcal {C}$, we modified $\mathcal {E}'_\mathcal {C}$ by duplicating the circuit structure $k{+}1$ times. We do the same operation but instead we make 2k duplications. In order to explain our construction better, we label the copies with the pairs $(0,1),(1,1),\ldots ,(0,k),(1,k)$ and refer to the copy with label (b, i) as the (b, i)th copy. In particular, we denote the 2k duplications of y by $y^{0,i},y^{1,i}$ for $1\le i \le k$. We further duplicate the objects $\alpha ,\beta ,\gamma ,e_\alpha ,e_\beta$, and label the copies $\alpha ^i,\beta ^i,\gamma ^i,e_\alpha ^i,e_\beta ^i$ for $i=1,\ldots ,k$. The endowment of manipulating agent i is $\{e_i,e_\alpha ^i, e_\beta ^i\}$. The preference relations of the manipulating agents and the owners of the duplicated objects over singletons are given below.

$$\begin{aligned}&R_i&=& (\alpha ^i,\beta ^i,e_\alpha ^i,e_\beta ^i,\square )\\&R_{\alpha ^i}&=& (\gamma ^i,e_\alpha ^i, \square )\\&R_{\beta ^i}&=& (\gamma ^i,\gamma _i,y^{1,i},y^{2,i},e_\beta ^i,\square ) \end{aligned}$$

Finally, we change the preferences of the owners of $\gamma ^i,y^{0,i}$, and $y^{1,i}$ for each i by replacing $\beta$ in their preference relation with $\beta ^i$.

The true allocation of manipulating agent i is $\{\alpha ^i, e_\alpha ^i,e_\beta ^i\}$, and each manipulating agent can only improve upon this allocation by obtaining both $\alpha ^i$ and $\beta ^i$. The proof of the following proposition is analogous to that of Proposition 3.2.

Proposition 5.2

Let $X=\{x_{i_1},\ldots ,x_{i_k}\}$ be an assignment to $\mathcal {C}$ and let $(R_j')_{j=1}^k$ be a group misreport defined by $R'_j=(x^*_{i_j},\alpha ^i,\beta ^i)$ for each j. Then, $(R'_j)_{j=1}^k$ is beneficial if and only if X is satisfying.

It remains to show that if the manipulating agents have a beneficial group misreport, then there is a satisfying assignment for $\mathcal {C}$. The reasoning follows that of the proof of the main theorem. Let $A=\{A_1,\ldots ,A_k\}=\{\{\alpha ^1,\beta ^1,\delta _1\},\ldots ,\{\alpha ^k,\beta ^k,\delta _k\}\}$ be the assignments to the manipulating agents. The following observation is completely analogous to Observations 3.5, 3.6, and 3.7.

Observation 5.3

For $i=1,\ldots ,k$:

• 1. $\gamma ^i\not \in A_i$

• 2. $\alpha ^i \mathrel {R'_i} \beta ^i$

• 3. $\delta _i \mathrel {R'_i} \alpha ^i$

As in the proof of the main theorem, the above observation shows that the misreport must take a certain form. For agent i, we have that $R'_i=(\delta _i,\alpha ^i,\beta ^i)$, where $\delta _i$ is part of the circuit structure (again it could be the case that $\delta _i=\gamma _i$ but this will simply result in a lower weight assignment to $\mathcal {C}$).

Let z be the smallest integer such that, for some $b\in \{0,1\}$, none of the objects $\delta _1,\ldots ,\delta _k$ are elements of the (b, z)th copy. The rest of the proof is identical to that of the main theorem. By running TTC we perform a (possibly faulty) evaluation of an assignment to $\mathcal {C}$ of weight k. Since $(y^{b,z},\beta ^z)$ is not a trading cycle, the assignment must be satisfying, as required. $\square$

Appendix A

In this section we provide several fully worked examples of the constructions defined in the main text. Previously, in Figs. 5 and 6, we considered a simple circuit with no internal gates, and depicted the corresponding economies $\mathcal {E}'_\mathcal {C}$ and $\mathcal {E}_\mathcal {C}$. In Figs. 8 and 9 we consider a circuit with one internal gate (Fig. 3), and provide the full constructions of the corresponding $\mathcal {E}'_\mathcal {C}$ and $\mathcal {E}_\mathcal {C}$. In Figs. 10 and 11 we detail several steps of TTC for two different circuits and their resulting economy $\mathcal {E}'_\mathcal {C}$ constructions.

Fig. 8

The economy $\mathcal {E}'_\mathcal {C}$ for a circuit with one internal gate

Fig. 9

The economy $\mathcal {E}_\mathcal {C}$ “duplicates” certain elements of $\mathcal {E}'_\mathcal {C}$

Fig. 10

Four steps of TTC for an economy $\mathcal {E}'_\mathcal {C}$

1.1 Appendix A.1: a circuit with one internal gate

Consider the circuit from Fig. 3 equivalent to the formula $x_1\wedge (x_1\vee x_2)$. It is degenerate in a certain sense: it is equivalent to the circuit with a single gate $x_1$ serving as input and output. Thus there is only one satisfying assignment of weight 1, in which $x_1=1$ and $x_2=0$. In Fig. 8, we depict the corresponding economy $\mathcal {E}'_\mathcal {C}$ following the definitions in Sect. 3.1.

By design, there is a beneficial misreport of a particular form corresponding to the satisfying assignment of weight 1. Consider the possible preference relations that agent 1 can report. Recall that their true preference is $R_1= (\alpha ,\beta ,e_\alpha ,e_\beta ,e_k,e_{k-1},\ldots ,e_1)$. If agent 1 reports the truth, then they receive $\{\alpha ,e_\alpha ,e_\beta \}$. If agent 1 reports $R'_1=(x_1^2,\alpha ,\beta ,\square )$ (which represents the satisfying assignment $x_1=1$), then they receive $\{x_1^2,\alpha ,\beta \}$ and are better off. If agent 1 reports $R''_1=(x_2^1,\alpha ,\beta ,\square )$ (which represents a non-satisfying weight 1 assignment $x_2=1$), then they receive $\{x_2^1,\alpha ,e_\beta \}$ and are worse off.

Next, we show the result of the duplication process to construct $\mathcal {E}_\mathcal {C}$ for $k=1$ in Fig. 9. As in Fig. 6, we omit the objects $\alpha$, $\beta$, $\gamma$ , $e_\alpha$, and $e_\beta$ in this diagram for readability.

1.2 Appendix A.2: steps of TTC for economy from Fig. 5

The economy from Fig. 5 is the construction $\mathcal {E}'_\mathcal {C}$ where circuit $\mathcal {C}$ is equivalent to $x_1\wedge x_2$ and $k=1$. Recall that the true preference of agent 1 is $R_1=(\alpha ,\beta ,e_\alpha ,e_\beta ,e_1)$, and that they are allocated $\{\alpha ,e_\alpha ,e_\beta \}$.

In Fig. 10, we show the result of applying TTC when agent 1 misreports to $R'_1=(x_1^*,\alpha ,\beta ,\square )$. For readability, we omit drawing agent 1’s preference except where necessary. In the top left, we depict Step 1 of TTC. Since agent 1 topranks $x_1^*=x^1_1$, we have the cycle $(x_1^*,\gamma _1,e_1)$. All objects that agent 1 owns point to $x_1^*$ as well, but we omit these directed edges. We resolve this cycle. In the top right of the figure, we depict Step 2. We remove objects that were in a cycle in Step 1 (now greyed) and update all agents’ preferences over remaining objects. For example, since $e_1$ is gone, the owner of $\gamma$ now topranks $e_\alpha$. Agent 1 owns $e_\alpha$ which now topranks and points to $\alpha$. Two cycles appear: $(x_2^1,h_3^2)$ and $(\alpha ,\gamma ,e_\alpha )$. We select the former to resolve. In Step 3 (bottom left), we update preferences, and since $h_1^3$ only ranked one object in the previous step, they now toprank their own object. Again there are two cycles: $(h_1^3)$ and $(\alpha ,\gamma ,e_\alpha )$. We select the former to resolve. In Step 4 (bottom right), $(\alpha ,\gamma ,e_\alpha )$ is the only cycle. In Step 5 (not shown), $(y,\beta )$ form a cycle. Thus, we have that agent 1 is allocated $\{x_1^*,\alpha ,e_\beta \}$. This outcome is worse than the outcome if they had told the truth.

Note that in Step 2, removing $h_3^2$ from the graph corresponds to the second predecessor of the $\wedge$-gate $g_3$ taking value 0. Thus, the output $\wedge$-gate $g_3$ takes value 0. The result, by design, is that y cycles with $\beta$, taking away the opportunity for agent 1 to receive $\beta$.

1.3 Appendix A.3: steps of TTC for economy another circuit

In Fig. 11, we show the construction of $\mathcal {E}'_\mathcal {C}$ where $\mathcal {C}$ is the circuit equivalent to $x_1 \vee x_2$ and $k=1$. The true preference of agent 1 is $R_1=(\alpha ,\beta ,e_\alpha ,e_\beta ,e_1)$, and they are allocated $\{\alpha ,e_\alpha ,e_\beta \}$. We show the result of applying TTC when agent 1 misreports to $R'_1=(x_1^*,\alpha ,\beta ,\square )$. Note that this is a satisfying assignment of weight 1 for the circuit. By design, the misreport $R'_1=(x_1^*,\alpha ,\beta ,\square )$ will be beneficial.

Fig. 11

Four steps of TTC for an economy $\mathcal {E}'_\mathcal {C}$ with an $\vee$ output gate

In the top left, we depict Step 1 of TTC. Since agent 1 topranks $x_1^*=x^1_1$, we have the cycle $(x_1^*,\gamma _1,e_1)$. We resolve this cycle. All objects that agent 1 owns point to $x_1^*$ as well, but again we omit these directed edges. In Step 2 (top right), given updated preferences, we have three cycles: $(h^2_3,x_2^1)$, $(y,h_3^1)$, and $(\alpha ,\gamma ,e_\alpha )$. We select the first cycle to resolve. In Step 3 (bottom left), cycles are $(y,h_3^1)$, and $(\alpha ,\gamma ,e_\alpha )$. Again, we select the first cycle to resolve. In Step 4 (bottom right), $(\alpha ,\gamma ,e_\alpha )$ is the only cycle. In Step 5 (not shown), $(\beta ,e_\beta )$ form a cycle. Thus, we have that agent 1 is allocated $\{x_1^*,\alpha ,\beta \}$. This outcome is preferred to the one where they told the truth.