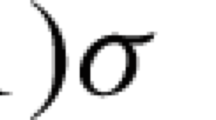Mean curvature flow of area decreasing maps between Riemann surfaces

Abstract

In this article, we give a complete description of the evolution of an area decreasing map $f{: }M\rightarrow N$, induced by the mean curvature of their graph, in the situation where M and N are complete Riemann surfaces with bounded geometry, M being compact, for which their sectional curvatures $\sigma _M$ and $\sigma _N$ satisfy $\min \sigma _M\ge \sup \sigma _N$.

1 Introduction

Let $(M,{{\text {g}}_M})$ and $(N,{{\text {g}}_N})$ be complete Riemann surfaces, with $(M,{{\text {g}}_M})$ being compact. A smooth map $f{: }M\rightarrow N$ is called area decreasing if $|{\text {Jac}}(f)|\le 1$, where ${\text {Jac}}(f)$ is the Jacobian determinant of f (for short just Jacobian). Being area decreasing means that the map f contracts two-dimensional regions of M. If $|{\text {Jac}}(f)|<1$, the map is called strictly area decreasing, and if $|{\text {Jac}}(f)|=1$ the map is said area preserving. Note that in the latter case ${\text {Jac}}(f)=\pm 1$ depending on whether f is orientation preserving or orientation reversing map. In this article, we deform area decreasing maps f by evolving their corresponding graphs

$$\begin{aligned} \varGamma (f):=\big \{(x,f(x))\in M\times N:x\in M\big \}, \end{aligned}$$

under the mean curvature flow in the Riemannian product 4-manifold

$$\begin{aligned} \left( M\times N,{{\text {g}}_{M\times N}}=\pi ^*_M{{\text {g}}_M}+\pi ^*_N{{\text {g}}_N}\right) , \end{aligned}$$

where here $\pi _M:M\times N\rightarrow M$ and $\pi _N:M\times N\rightarrow N$ are the natural projection maps. Our main goal is to show the following theorem which generalizes all the previous known results for area decreasing maps between Riemann surfaces evolving under the mean curvature flow.

Theorem A

Let $(M,{{\text {g}}_M})$ and $(N,{{\text {g}}_N})$ be complete Riemann surfaces, M being compact and N having bounded geometry. Let $f:M\rightarrow N$ be a smooth area decreasing map. Suppose that the sectional curvatures $\sigma _M$ of ${{\text {g}}_M}$ and $\sigma _N$ of ${{\text {g}}_N}$ are related by $\min \sigma _M\ge \sup \sigma _N$. Then, there exists a family of smooth area decreasing maps $f_t:M\rightarrow N$, $t\in [0,\infty )$, $f_0=f$, such that the graphs $\varGamma (f_t)$ of $f_t$ move by mean curvature flow in $(M\times N,{{\text {g}}_{M\times N}})$. Furthermore, there exist only two possible categories of initial data sets and corresponding solutions:

• I) The curvatures $\sigma _M$ and $\sigma _N$ are constant and equal and the map $f_0$ is area preserving. In this category, each $f_t$ is area preserving and $\varGamma (f_t)$ smoothly converges to a minimal Lagrangian graph $\varGamma (f_\infty )$ in $M\times N$, with respect to the symplectic form

  $$\begin{aligned} \varOmega _{M\times N}:=\pi ^*_M\varOmega _M\mp \pi ^*_N\varOmega _N, \end{aligned}$$

  depending on whether $f_0$ is orientation preserving or reversing, respectively. Here $\varOmega _M$ and $\varOmega _N$ are the positively oriented volume forms of M and N, respectively.

• II) All other possible cases. In this category, for $t>0$ each map $f_t$ is strictly area decreasing. Moreover, depending on the sign of $\sigma :=\min \sigma _M$ we have the following behavior:

  • a) If $\sigma >0$, then the family $\varGamma (f_t)$ smoothly converges to the graph of a constant map.

  • b) If $\sigma =0$ and N is compact, then $\varGamma (f_t)$ smoothly converges to a totally geodesic graph $\varGamma (f_\infty )$ of $M\times N$. The same result still holds if N is non-compact and f is homotopic to a minimal map.

  • c) If $\sigma <0$ and N is compact, then $\varGamma (f_t)$ smoothly converges to a minimal surface $M_{\infty }$ of $M\times N$. The same result still holds if N is non-compact and f is homotopic to a minimal map.

Remark 1.1

Some parts of Theorem A, especially in the case where $\sigma _M$ and $\sigma _N$ are constant, are already known. More precisely:

• a) If the initial data set belongs to category (I), then N is compact because $f_0$ is a local diffeomorphism. On the other hand, the maps $f_t$ will be area preserving for all t since this is a special case of the Lagrangian mean curvature flow (see [39] or the survey paper [36]). Now the statement of category (I) follows from the results of Smoczyk [37] and Wang [40].

• b) If the initial data set belongs to category (II), that is either $f_0$ is not area preserving everywhere or $\sigma _M=\sigma =\min \sigma _M=\sigma _N$ does not hold at each point, then (as will be shown in Lemma 3.2) $f_t$ will be strictly area decreasing for all $t>0$. Then if N is compact, II(a) was shown in [23].

• c) In the category (IIc), the minimal surface $M_{\infty }$ is not necessarily totally geodesic. One reason is that there is an abundance of examples of minimal graphs that are generated by area decreasing maps between two negatively curved compact hyperbolic surfaces. For instance, any holomorphic map between compact hyperbolic spaces is area decreasing due to the Schwarz–Pick–Yau Lemma [42] and its graph is minimal.

• d) If the surface N is non-compact and negatively curved, in general, is not expected convergence of the flow without any assumption on the homotopy type of f. For example, take as f a map from the flat torus $\mathbb {S}^1\times \mathbb {S}^1$ into a non-contractible circle on N which does not have geodesics that are homotopic to $\mathbb S^1$. Note that there are plenty of non-trivial (even harmonic) maps from any Riemann surface of positive genus to $\mathbb {S}^1$ (see [4, Example 3.3.8]). The assumption that f is homotopic to a minimal map forces the evolving images $f_t(M)$, $t\ge 0$, to stay within a fixed compact domain of N; see also [20, Conclusion C, p. 674].

Another aim of the present paper is to obtain curvature decay estimates. In particular, we prove the following theorem.

Theorem B

Let $(M,{{\text {g}}_M})$ and $(N,{{\text {g}}_N})$ be Riemann surfaces as in Theorem A and $f:M\rightarrow N$ a smooth strictly area decreasing map. Suppose that the sectional curvatures $\sigma _M$ of ${{\text {g}}_M}$ and $\sigma _N$ of ${{\text {g}}_N}$ are related by $\sigma :=\min \sigma _M\ge \sup \sigma _N$. Then, we have the following decay estimates for the mean curvature flow of the graph of f in $(M\times N,{{\text {g}}_{M\times N}})$:

• a) If $\sigma >0$, then there exists a uniform time-independent constant C such that the norm of the second fundamental form A satisfies

  $$\begin{aligned} |A|^2\le {C}{t^{-1}}. \end{aligned}$$

• b) If $\sigma =0$, then there exists a uniform time-independent constant C such that the norms of the second fundamental form and of the mean curvature satisfy

  $$\begin{aligned} \quad \quad |A|^2\le C,\quad \int _{M}|A|^2\varOmega _{{\text {g}}(t)}\le {C}{t}^{-1}\quad \text {and} \quad |H|^2\le C t^{-1}, \end{aligned}$$

  where $\varOmega _{{\text {g}}(t)}$ is the positively oriented volume form of $(M,{\text {g}}(t))$.

• c) If $\sigma <0$, then there exists a uniform time-independent constant C such that

  $$\begin{aligned} |A|^2\le C. \end{aligned}$$

Remark 1.2

Similar decay estimates for the norm of the second fundamental form in the case $\sigma >0$ were obtained also by Lubbe [25]. Explicit curvature decay estimates have been obtained by the authors [29] for the norm of the mean curvature vector field of length decreasing maps between Riemannian manifolds of arbitrary dimensions and by Smoczyk, Tsui and Wang in [35] in the case of strictly area decreasing Lagrangian maps between flat Riemann surfaces.

2 Geometry of graphical surfaces

In this section, we recall some basic facts about graphical surfaces. Some of these can be found in our previous papers [29,30,31]. In order to make the paper self-contained, let us recall very briefly some of them here.

2.1 Notation

Let $F:\varSigma \rightarrow L$ be an isometric embedding of an m-dimensional Riemannian manifold $\big (\varSigma ,{\text {g}}\big )$ to a Riemannian manifold $\big (L,\langle \cdot \,,\cdot \rangle \big )$ of dimension l. We denote by ${\nabla }$ the Levi-Civita connection associated to ${\text {g}}$ and by $\widetilde{\nabla }$ the corresponding Levi-Civita of $\langle \cdot \,,\cdot \rangle$. The differential ${\text {d}}F$ is a section in $F^{*}TL\otimes T^*\varSigma$. Let $\nabla ^F$ be the connection induced by F on this bundle. The covariant derivative of ${\text {d}}F$ is called the second fundamental tensor A of F, i.e.,

$$\begin{aligned} A(v_1,v_2):=\big (\nabla ^{F}{\text {d}}F\big ) (v_1,v_2)=\widetilde{\nabla }_{{\text {d}}F(v_1)}{\text {d}}F(v_2)-{\text {d}}F\big (\nabla _{v_1}v_2\big ), \end{aligned}$$

for any $v_1,v_2\in T\varSigma$. Note that the second fundamental form maps to the normal bundle $\mathcal {N}\varSigma$. The second fundamental form with respect to a normal direction $\xi$ is denoted by $A^{\xi }$, that is $A^{\xi }(v_1,v_2):=\langle A(v_1,v_2),\xi \rangle$, for any pair $v_1,v_2\in T\varSigma$. The trace H of A with respect to ${\text {g}}$ is called the mean curvature vector field of the graph. If H vanishes identically, then the embedding F is called minimal.

The normal bundle $\mathcal {N}\varSigma$ admits a natural connection which we denote by $\nabla ^{\perp }$. Let us denote by ${R}$, $\widetilde{{R}}$ and ${R}^{\perp }$ the curvature operators of $T\varSigma$, TL and $\mathcal {N}\varSigma$, respectively. Then, these tensors are related with A through the Gauß–Codazzi–Ricci equations. Namely:

• a) Gauß equation

  $$\begin{aligned} {R}(v_1,v_2,v_3,v_4)= & {} F^{*}\widetilde{{R}}(v_1,v_2,v_3,v_4)\\&+\langle A(v_1,v_3),A(v_2,v_4)\rangle -\langle A(v_2,v_3),A(v_1,v_4)\rangle , \end{aligned}$$

  for any $v_1,v_2,v_3,v_4\in T\varSigma$.

• b) Codazzi equation

  $$\begin{aligned} \big (\nabla ^{\perp }_{v_1}A\big )(v_2,v_3)-\big (\nabla ^{\perp }_{v_2}A\big )(v_1,v_3) =-\sum _{\alpha =m+1}^{l}\widetilde{R}(v_1,v_2,v_3,\xi _{\alpha })\xi _{\alpha }, \end{aligned}$$

  where $v_1,v_2,v_3\in T\varSigma$ and $\{\xi _{m+1},\dots ,\xi _{l}\}$ is a local orthonormal frame field in the normal bundle of F.

• c) Ricci equation

  $$\begin{aligned} {R}^{\perp }(v_1,v_2,\xi ,\eta )= & {} \widetilde{R}\big ({\text {d}}F(v_1),{\text {d}}F(v_2),\xi ,\eta \big )\\&+\sum _{k=1}^m\big \{A^{\xi }(v_1,e_k)A^{\eta }(v_2,e_k) -A^{\eta }(v_1,e_k)A^{\xi }(v_2,e_k)\big \}, \end{aligned}$$

  where here $v_1,v_2\in T\varSigma$, $\xi ,\eta \in \mathcal {N}\varSigma$ and $\{e_1,\dots ,e_m\}$ is a local orthonormal frame field with respect to ${\text {g}}$.

2.2 Graphs

Suppose now that the manifold L is a product of two Riemann surfaces $(M,{{\text {g}}_M})$ and $(N,{{\text {g}}_N})$ and that $f:M\rightarrow N$ is a smooth map. The induced metric on the product manifold will be denoted by

$$\begin{aligned} {{\text {g}}_{M\times N}}:=\langle \cdot \,,\cdot \rangle ={{\text {g}}_M}\times {{\text {g}}_N}. \end{aligned}$$

Define the embedding $F:M\rightarrow M\times N$, given by

$$\begin{aligned} F(x):=({{\mathrm{Id}}}\times f)(x)=\bigl (x,f(x)\bigr ), \end{aligned}$$

for $x\in M$. The graph of f is defined to be the submanifold $\varGamma (f):=F(M)$. Since F is an embedding, it induces another Riemannian metric ${\text {g}}:=F^*{{\text {g}}_{M\times N}}$ on M. Following Schoen’s [32] terminology, we call f a minimal map if its graph is a minimal submanifold of $M\times N$. The natural projections $\pi _{M}:M\times N\rightarrow N$, $\pi _{N}:M\times N\rightarrow N$ are submersions. Note that the tangent bundle of the product manifold $M\times N$ splits as a direct sum $T(M\times N)=TM\oplus TN.$ The metrics ${{\text {g}}_M},{{\text {g}}_{M\times N}}$ and ${\text {g}}$ are related to

$$\begin{aligned} {{\text {g}}_{M\times N}}=\pi _M^*{{\text {g}}_M}+\pi _N^*{{\text {g}}_N}\quad \text {and}\quad {\text {g}}={{\text {g}}_M}+f^*{{\text {g}}_N}. \end{aligned}$$

The Levi-Civita connection $\tilde{\nabla }$ of the product manifold is related to the Levi-Civita connections $\nabla ^{{{\text {g}}_M}}$ and $\nabla ^{{{\text {g}}_N}}$ by $\widetilde{\nabla }=\pi _M^*\nabla ^{{{\text {g}}_M}}\oplus \pi _N^*\nabla ^{{{\text {g}}_N}}$. The curvature operator $\widetilde{R}$ is related to the curvature operators ${R}_M$ and ${R}_N$ by

$$\begin{aligned} \widetilde{R}=\pi ^{*}_{M}{R}_M\oplus \pi ^{*}_{N}{R}_N. \end{aligned}$$

The Levi-Civita connection of ${\text {g}}$ will be denoted by $\nabla$, its curvature tensor by ${R}$ and it sectional curvature by $\sigma _{{\text {g}}}$. We denote the sectional curvatures of $(M,{{\text {g}}_M})$ and $(N,{{\text {g}}_N})$ by $\sigma _M$ and $\sigma _N$, respectively.

2.3 Singular decomposition

Let us recall here some basic Linear Algebra constructions. Fix a point $x\in M$. Let $\lambda ^2\le \mu ^2$ be the eigenvalues of $f^*{{\text {g}}_N}$ with respect to ${{\text {g}}_M}$ at x and denote by $\{\alpha _1,\alpha _2\}$ a positively oriented orthonormal (with respect to ${{\text {g}}_M}$) basis of eigenvectors. The corresponding values $0\le \lambda \le \mu$ are called singular values of f at x. Then, there exists an orthonormal (with respect to ${{\text {g}}_N}$) basis $\{\beta _{1},\beta _{2}\}$ of $T_{f(x)}N$ such that

$$\begin{aligned} {\text {d}}f(\alpha _{1})=\lambda \beta _{1}\quad \text {and}\quad {\text {d}}f(\alpha _{2})=\mu \beta _{2}. \end{aligned}$$

Indeed, in the case where the values $\lambda$ and $\mu$ are strictly positive, one may define them as

$$\begin{aligned} \beta _1:=\frac{{\text {d}}f(\alpha _1)}{|{\text {d}}f(\alpha _1)|}\quad \text {and}\quad \beta _2: =\frac{{\text {d}}f(\alpha _2)}{|{\text {d}}f(\alpha _2)|}. \end{aligned}$$

In the case where $\lambda$ vanishes and $\mu$ is positive, define first $\beta _2$ by

$$\begin{aligned} \beta _2:=\frac{{\text {d}}f(\alpha _2)}{|{\text {d}}f(\alpha _2)|} \end{aligned}$$

and take as $\beta _1$ a unit vector perpendicular to $\beta _2$. In the special case where both $\lambda$ and $\mu$ are zero, we may take an arbitrary orthonormal basis of $T_{f(x)}N$. This procedure is called the singular decomposition of the differential ${\text {d}}f$ of the map f. Observe that

$$\begin{aligned} v_1:=\frac{\alpha _1}{\sqrt{1+\lambda ^2}}\quad \text {and}\quad v_2:=\frac{\alpha _2}{\sqrt{1+\mu ^2}} \end{aligned}$$

are orthonormal with respect to the metric ${\text {g}}$. Hence, the vectors

$$\begin{aligned} e_{1}:=\frac{1}{\sqrt{1+\lambda ^2}}\big (\alpha _1\oplus \lambda \beta _1\big ) \quad \text {and}\quad e_{2}:=\frac{1}{\sqrt{1+\mu ^2}}\big (\alpha _2\oplus \mu \beta _2\big ) \end{aligned}$$

form an orthonormal basis with respect to the metric ${{\text {g}}_{M\times N}}$ of the tangent space ${\text {d}}F\left( T_{x}M\right)$ of the graph $\varGamma (f)$ at x. Moreover, the vectors

$$\begin{aligned} e_{3}:=\frac{1}{\sqrt{1+\lambda ^2}}\big (-\lambda \alpha _1\oplus \beta _1\big ) \quad \text {and}\quad e_{4}:=\frac{1}{\sqrt{1+\mu ^2}}\big (-\mu \alpha _2\oplus \beta _2\big ) \end{aligned}$$

form an orthonormal basis with respect to ${{\text {g}}_{M\times N}}$ of the normal space $\mathcal {N}_{x}M$ of the graph $\varGamma (f)$ at the point f(x). Observe now that

$$\begin{aligned} e_1\wedge e_2\wedge e_3\wedge e_4=\alpha _1\wedge \alpha _2\wedge \beta _1\wedge \beta _2. \end{aligned}$$

Consequently, $\{e_3,e_4\}$ is an oriented basis of the normal space $\mathcal {N}_xM$ if and only if $\{\alpha _1,\alpha _2,\beta _1,\beta _2\}$ is an oriented basis of $T_xM\times T_{f(x)}N$.

The area functional A(f) of the graph is given by

$$\begin{aligned} A(f):=\int _M \sqrt{\det ({{\text {g}}_M}+f^*{{\text {g}}_N})}\,\varOmega _M=\int _M \sqrt{(1+\lambda ^2)(1+\mu ^2)}\,\varOmega _M. \end{aligned}$$

2.4 Jacobians of the projection maps

As before let $\varOmega _M$ denote the Kähler form of the Riemann surface $(M,{{\text {g}}_M})$ and $\varOmega _N$ the Kähler form of $(N,{{\text {g}}_N})$. We can extend $\varOmega _M$ and $\varOmega _N$ to two parallel 2-forms on the product manifold $M\times N$ by pulling them back via the projection maps $\pi _M$ and $\pi _N$. That is we may define the parallel forms

$$\begin{aligned} \varOmega _1:=\pi ^*_M\varOmega _M\quad \text {and}\quad \varOmega _2:=\pi ^*_N\varOmega _N. \end{aligned}$$

Define now two smooth functions $u_1$ and $u_2$ given by

$$\begin{aligned} u_1:=*(F^*\varOmega _1)=*\big \{(\pi _M\circ F)^*\varOmega _M\big \}=*({{{\mathrm{Id}}}}^*\varOmega _M) \end{aligned}$$

and

$$\begin{aligned} u_2:=*(F^*\varOmega _2)=*\big \{(\pi _N\circ F)^*\varOmega _N\big \}=*(f^*\varOmega _N) \end{aligned}$$

where here $*$ stands for the Hodge star operator with respect to the metric ${\text {g}}$. Note that $u_1$ is the Jacobian of the projection map from $\varGamma (f)$ to the first factor of $M\times N$ and $u_2$ is the Jacobian of the projection map of $\varGamma (f)$ to the second factor of $M\times N$. With respect to the basis $\{e_1,e_2,e_3,e_4\}$ of the singular decomposition, we can write

$$\begin{aligned} u_1=\frac{1}{\sqrt{(1+\lambda ^2)(1+\mu ^2)}}\quad \text {and}\quad |u_2|=\frac{\lambda \mu }{\sqrt{(1+\lambda ^2)(1+\mu ^2)}}. \end{aligned}$$

Note also that

$$\begin{aligned} {\text {Jac}}(f):=\frac{*(f^*\varOmega _N)}{*({{\mathrm{Id}}}^*\varOmega _M)}=\frac{u_2}{u_1}. \end{aligned}$$

Moreover, the difference between $u_1$ and $|u_2|$ measures how far f is from being area preserving. In particular:

$$\begin{aligned} u_1-|u_2|\ge 0\Leftrightarrow & {} f \text { is area decreasing},\\ u_1-|u_2|> 0\Leftrightarrow & {} f \text { is strictly area decreasing},\\ u_1-|u_2|= 0\Leftrightarrow & {} f \text { is area preserving}. \end{aligned}$$

2.5 The Kähler angles

There are two natural complex structures associated with the product space $(M\times N,{{\text {g}}_{M\times N}})$, namely

$$\begin{aligned} J_1:=\pi ^*_MJ_M-\pi ^*_NJ_N\quad \text {and}\quad J_2:=\pi ^*_MJ_M+\pi ^*_NJ_N, \end{aligned}$$

where $J_M, J_N$ are the complex structures on M and N defined by

$$\begin{aligned} \varOmega _M(\cdot \,,\cdot )={{\text {g}}_M}(J_M\,\cdot \,,\cdot ),\quad \varOmega _N(\cdot \,,\cdot )={{\text {g}}_N}(J_N\,\cdot \,,\cdot ). \end{aligned}$$

Chern and Wolfson [14] introduced a function which measures the deviation of the tangent plane ${\text {d}}F(T_xM)$ from a complex line of the space $T_{F(x)}(M\times N)$. More precisely, if we consider $(M\times N,{{\text {g}}_{M\times N}})$ as a complex manifold with respect to $J_1$, then its corresponding Kähler angle $a_1$ is given by the formula

$$\begin{aligned} \cos a_1=\varphi :={{\text {g}}_{M\times N}}\big (J_1{\text {d}}F(v_1),{\text {d}}F(v_2)\big )=u_1-u_2. \end{aligned}$$

For our convenience, we require that $a_1\in [0,\pi ]$. Note that in general $a_1$ is not smooth at points where $\varphi =\pm 1$. If there exists a point $x\in M$ such that $a_1(x)=0$, then ${\text {d}}F(T_xM)$ is a complex line of $T_{F(x)}(M\times N)$ and x is called a complex point of F. If $a_1(x)=\pi$, then ${\text {d}}F(T_xM)$ is an anti-complex line of $T_{F(x)}(M\times N)$ and x is said anti-complex point of F. If $a_1(x)=\pi /2$, the point x is called Lagrangian point of the map F. In this case $u_1=u_2$. Similarly, if we regard the product manifold $(M\times N,{{\text {g}}_{M\times N}})$ as a Kähler manifold with respect to the complex structure $J_2$, then its corresponding Kähler angle $a_2$ is defined by the formula

$$\begin{aligned} \cos a_2=\vartheta :={{\text {g}}_{M\times N}}\big (J_2{\text {d}}F(v_1),{\text {d}}F(v_2)\big )=u_1+u_2. \end{aligned}$$

The graph $\varGamma (f)$ in the product Kähler manifold $(M\times N,{{\text {g}}_{M\times N}},J_i)$ is called symplectic with respect to the Kähler form related to $J_i$, if the corresponding Kähler angle satisfies $\cos a_i>0$. Therefore, a map f is strictly area decreasing if and only if its graph is symplectic with respect to both Kähler forms. There are many interesting results on symplectic mean curvature flow of surfaces in four-dimensional manifolds in the literature (see, for example, the papers [11,12,13, 18, 19, 24]).

2.6 Structure equations

Around each point $x\in \varGamma (f)$, we choose an adapted local orthonormal frame $\{e_1,e_2;e_3,e_4\}$ such that $\{e_1,e_2\}$ is tangent and $\{e_3,e_4\}$ is normal to the graph. The components of A are denoted as $A^{\alpha }_{ij}:=\langle A(e_i,e_j),e_{\alpha }\rangle$. Latin indices take values 1 and 2, while Greek indices take the values 3 and 4. For instance, we write the mean curvature vector in the form $H=H^3e_3+H^4e_4.$ By Gauß’ equation we get

$$\begin{aligned} 2\sigma _{{\text {g}}}=2u^2_1\sigma _M+2u_{2}^2\sigma _N+|H|^2-|A|^2. \end{aligned}$$

From the Ricci equation, we see that the curvature $\sigma _n$ of the normal bundle of $\varGamma (f)$ is given by the formula

$$\begin{aligned} \sigma _n:={R}^{\perp }_{1234} ={\widetilde{R}}_{1234} +A^3_{11}A^4_{12}-A^3_{12}A^{4}_{11}+A^3_{12}A^4_{22}-A^3_{22}A^4_{12}. \end{aligned}$$

The sum of the last four terms in the above formula is equal to minus the commutator $\sigma ^{\perp }$ of the matrices $A^3=(A^3_{ij})$ and $A^4=(A^4_{ij})$, i.e.,

$$\begin{aligned} \sigma ^{\perp }:=\left\langle [A^3,A^4]e_1,e_2\right\rangle =-A^3_{11}A^4_{12}+A^3_{12}A^{4}_{11}-A^3_{12}A^4_{22}+A^3_{22}A^4_{12}.\end{aligned}$$

(2.1)

3 A priori estimates for the Jacobians

Let M and N be Riemann surfaces, $f:M\rightarrow N$ a smooth map and let $F:M \rightarrow M\times N$, $F := {{\mathrm{Id}}}\times f$, be the parameterization of the graph $\varGamma (f)$. Consider the family of immersions $F:M\times [0, T )\rightarrow M\times N$ satisfying the mean curvature flow

$$\begin{aligned} \left\{ \begin{array}{ll} {\text {d}}F_{(x,t)}(\partial _t)=H(x,t), &{}\\ F(x,0)=F(x), &{} \end{array} \right. \end{aligned}$$

where $(x,t)\in M\times [0, T )$, H(x, t) is the mean curvature vector field at $x\in M$ of the immersion $F_t:M\rightarrow M\times N$ given by $F_t(\cdot ):=F(\cdot ,t)$ and T is the maximal time of existence of the solution. The compactness of M implies that the evolving submanifolds stay graphs on an interval $[0,T_g)$ with $T_g\le T$. This means that there exist smooth families of diffeomorphisms $\phi _t\in {\text {Diff}}(M)$ and maps $f_t:M\rightarrow N$ such that $F_t\circ \phi _t = {{\mathrm{Id}}}\times f_t$, for any time $t\in [0,T_g)$.

3.1 Evolution equations of first-order quantities

In the next lemma, we recall the evolution equation of a parallel 2-form on the product manifold $M\times N$. The proofs can be found in [41].

Lemma 3.1

Let $\varOmega$ be a parallel 2-form on the product manifold $M\times N$. Then, the function $u:=*(F^{*}\varOmega )$ evolves in time under the equation

$$\begin{aligned} \partial _{t}u=\varDelta u+|A|^2u-2\sum _{\alpha ,\beta , k}A^{\alpha }_{ki}A^{\beta }_{kj}\varOmega _{\alpha \beta } +\sum _{\alpha }\big ({\widetilde{R}}_{212\alpha }\varOmega _{\alpha 2}+{\widetilde{R}}_{121\alpha }\varOmega _{1\alpha }\big ) \end{aligned}$$

where $\{e_1,e_2;e_3,e_4\}$ is an arbitrary adapted local orthonormal frame.

As a consequence of Lemma 3.1, we deduce the following:

Lemma 3.2

The functions $u_1$ and $u_2$ defined in Sect. 2.4 satisfy the following coupled system of parabolic equations

$$\begin{aligned} \partial _{t}u_1-\varDelta u_1= & {} |A|^2u_1+2\sigma ^{\perp } u_2+\sigma _M\left( 1-u^2_1-u^2_2\right) u_1-2\sigma _Nu_1u^2_2,\\ \partial _{t}u_2-\varDelta u_2= & {} |A|^2u_2+2\sigma ^{\perp } u_1+\sigma _N\left( 1-u^2_1-u^2_2\right) u_2-2\sigma _Mu^2_1u_2. \end{aligned}$$

Moreover, $\varphi$ and $\vartheta$ satisfy the following system of equations

$$\begin{aligned} \partial _{t}\varphi -\varDelta \varphi= & {} \big (|A| ^2-2\sigma ^{\perp }\big )\varphi +\tfrac{1}{2}\big (\sigma _M(\varphi +\vartheta )+\sigma _N(\varphi -\vartheta )\big ) (1-\varphi ^2),\\ \partial _{t}\vartheta -\varDelta \vartheta= & {} \big (|A|^2+2\sigma ^{\perp }\big )\vartheta +\tfrac{1}{2}\big (\sigma _M(\varphi +\vartheta )-\sigma _N(\varphi -\vartheta )\big )(1-\vartheta ^2). \end{aligned}$$

In particular, if all the maps $f_t$ are area preserving, then the curvatures $\sigma _M$ and $\sigma _N$ necessarily must satisfy the relation $\sigma _M=\sigma _N\circ f_t$ for any $t\in [0,T_g)$.

Proof

The evolution equations of $u_1$ and $u_2$ follow as an immediate consequence of Lemma 3.1. Suppose now that each $f_t$ is an area preserving map. Then, $\varphi =u_1-u_2=0$ in space and time. Combining the two equations from above, we deduce that the curvatures of M and N are related to $\sigma _M=\sigma _N\circ f_t$, and so $f_t$, $t\in [0,T_g)$, are even curvature preserving maps. This completes the proof of lemma. $\square$

3.2 Estimating the Jacobians

We will give here several a priori estimates for the functions $u_1$ and $u_2$ and the Kähler angles.

Lemma 3.3

Suppose that $f:M\rightarrow N$ is a smooth map between complete Riemann surfaces, M being compact. Then, the mean curvature flow of $\varGamma (f)$ stays graphical as long as it exists and the function $u_2/u_1$ stays bounded.

Proof

From the first equation of Lemma 3.2, we deduce that there exists a time-dependent and bounded function h such that

$$\begin{aligned} \partial _{t}u_1-\varDelta u_1\ge h\,u_1. \end{aligned}$$

Then, from the parabolic maximum principle, we get that $u_{1}(x,t) >0$, for any $(x,t)\in M\times [0,T)$. Therefore, the solution remains graphical as long as the flow exists. $\square$

Lemma 3.4

Let $f:(M,{{\text {g}}_M})\rightarrow (N,{{\text {g}}_N})$ be an area decreasing map. Suppose that the curvatures of $(M,{{\text {g}}_M})$ and $(N,{{\text {g}}_N})$ satisfy $\sigma :=\min \sigma _M\ge \sup \sigma _N$. Then, the following statements hold.

• a) The conditions ${\text {Jac}}(f)\le 1$ or ${\text {Jac}}(f)\ge -1$ are both preserved under the mean curvature flow.

• b) The area decreasing property is preserved under the flow.

• c) If there is a point $(x_0,t_0)\in M\times (0,T_g)$ where ${\text {Jac}}^2(f)=1$, then ${\text {Jac}}^2(f)\equiv 1$ in space and time and $\sigma _M=\sigma =\sigma _N$.

Proof

From Lemma 3.2, we deduce that

$$\begin{aligned} {\partial _{t}}\varphi -\varDelta \varphi= & {} \big \{|A|^2-2\sigma ^{\perp }+\sigma _N(1-\varphi ^2)\big \}\varphi \\&+\frac{1}{2}(\sigma _M-\sigma _N)(\varphi +\vartheta )(1-\varphi ^2). \end{aligned}$$

Note that the quantities $1-\varphi ^2$ and $\varphi +\vartheta$ are nonnegative. Hence, because of our curvature assumptions, the last line of the above equality is nonnegative. Thus, there exists a time-dependent function h such that

$$\begin{aligned} \partial _{t}\varphi -\varDelta \varphi \ge h\,\varphi . \end{aligned}$$

From the parabolic maximum principle we deduce that $\varphi$ stays nonnegative in time. Moreover, from the strong parabolic maximum principle it follows that if $\varphi$ vanishes somewhere, then it vanishes identically in space and time. Hence, the sign of $\varphi$ is preserved by the flow. Similarly, we prove the results concerning $\vartheta$. This completes the proof. $\square$

Now we want to explore the behavior of the function

$$\begin{aligned} \rho =\varphi \vartheta =u^2_1-u^2_2 \end{aligned}$$

under the graphical mean curvature flow.

Lemma 3.5

Let $(M,{{\text {g}}_M})$ and $(N,{{\text {g}}_N})$ be complete Riemann surfaces with $(M,{{\text {g}}_M})$ being compact such that their curvatures $\sigma _M$ and $\sigma _N$ are related by the inequality $\sigma :=\min \sigma _M\ge \sup \sigma _N$. Suppose that $f:M\rightarrow N$ is a strictly area decreasing map.

• a) If $\sigma \ge 0$, then there exists a positive constant $c_0$ such that

  $$\begin{aligned} \rho \ge \frac{c_0e^{\sigma t}}{\sqrt{1+c^2_0e^{2\sigma t}}}, \end{aligned}$$

  for any (x, t) in space-time.

• b) If $\sigma <0$, then there exists a positive constant $c_0$ such that

  $$\begin{aligned} \rho \ge \frac{c_0e^{2\sigma t}}{\sqrt{1+c^2_0e^{4\sigma t}}}, \end{aligned}$$

  for any (x, t) in space-time.

Proof

From Lemma 3.2 we get,

$$\begin{aligned} \partial _{t}\rho -\varDelta \rho =2\rho |A|^2-2\langle \nabla \varphi ,\nabla \vartheta \rangle +2(1-\rho )\sigma _Mu^2_1-2(1+\rho )\sigma _Nu^2_2. \end{aligned}$$

Note that

$$\begin{aligned} -2\rho \langle \nabla \varphi ,\nabla \vartheta \rangle +\frac{1}{2}|\nabla \rho |^2= & {} \frac{1}{2}\big (|\nabla (\varphi \vartheta )|^2-4\varphi \vartheta \langle \nabla \varphi ,\nabla \vartheta \rangle \big )\\= & {} \frac{1}{2}\big (\varphi ^2|\nabla \vartheta |^2+\vartheta ^2|\nabla \varphi |^2-2\varphi \vartheta \langle \nabla \varphi ,\nabla \vartheta \rangle \big )\\\ge & {} \frac{1}{2}\big (|\varphi \nabla \vartheta |-|\vartheta \nabla \varphi |\big )^2. \end{aligned}$$

Since by assumption $\sigma _M\ge \sigma \ge \sigma _N$, we deduce that

$$\begin{aligned} \partial _{t}\rho -\varDelta \rho \ge -\frac{1}{2\rho }|\nabla \rho |^2+2\sigma \rho \left( 1-u^2_1-u^2_2\right) . \end{aligned}$$

One can algebraically check that

$$\begin{aligned} 1-\rho ^2\le 2\left( 1-u^2_1-u^2_2\right) \le 2(1-\rho ^2). \end{aligned}$$

(3.1)

Suppose at first that $\sigma \ge 0$. Then,

$$\begin{aligned} \partial _{t}\rho -\varDelta \rho \ge -\frac{1}{2\rho }|\nabla \rho |^2+\sigma \rho (1-\rho ^2). \end{aligned}$$

From the comparison maximum principle, we obtain

$$\begin{aligned} \rho \ge \frac{c_0e^{\sigma t}}{\sqrt{1+c^2_0e^{2\sigma t}}}, \end{aligned}$$

where $c_0$ is a positive constant.

In the case where $\sigma <0$, from Eq. (3.1) we deduce that

$$\begin{aligned} \partial _{t}\rho -\varDelta \rho \ge -\frac{1}{2\rho }|\nabla \rho |^2+2\sigma \rho (1-\rho ^2), \end{aligned}$$

from where we get the desired estimate. $\square$

Let us state here the following auxiliary result which will be used later for several estimates. The proof is straightforward.

Lemma 3.6

Let $f:(M,{{\text {g}}_M})\rightarrow (N,{{\text {g}}_N})$ be an area decreasing map. Let $\eta$ be a positive smooth function depending on $\rho$ and let $\zeta$ be the function given by

$$\begin{aligned} \zeta :=\log \eta (\rho ). \end{aligned}$$

Then,

$$\begin{aligned} \partial _{t}\zeta -\varDelta \zeta= & {} \frac{2\rho \eta _{\rho }}{\eta }|A|^2 +\frac{\eta _{\rho }}{\eta }\Big (-2\langle \nabla \varphi ,\nabla \vartheta \rangle +\frac{1}{2\rho }|\nabla \rho |^2\Big )\\&-\frac{1}{2\rho \eta ^2}\big (\eta \eta _{\rho }+2\rho \eta \eta _{\rho \rho } -\rho \eta _{\rho }^2\big )|\nabla \rho |^2+\frac{1}{2}|\nabla \zeta |^2\\&+\frac{2\eta _{\rho }}{\eta }\Big ((1-\rho )\sigma _Mu^2_1-(1+\rho )\sigma _Nu^2_2\Big ). \end{aligned}$$

4 A priori decay estimates for the mean curvature

We will show in this section that under our curvature assumptions, in the strictly area decreasing case, the norm of the mean curvature vector stays uniformly bounded as long as the flow exists.

Lemma 4.1

Let $f:M\rightarrow N$ be an area decreasing map. Suppose that the curvatures of M and N satisfy $\sigma :=\min \sigma _M\ge \sup \sigma _N$. Let $\delta :[0,T)\rightarrow \mathbb {R}$ be a positive increasing real function and $\tau$ the time-dependent function given by

$$\begin{aligned} \tau :=\log \big (\delta |H|^2+\varepsilon \big ), \end{aligned}$$

where $\varepsilon$ is a nonnegative number. Then,

$$\begin{aligned} \partial _{t}\tau -\varDelta \tau\le & {} \frac{2\delta }{\delta |H|^2+\varepsilon }|H|^2|A|^2 +\frac{\delta '}{\delta |H|^2+\varepsilon }|H|^2\\&+\frac{2\delta }{\delta |H|^2+\varepsilon }|H|^2\sigma _M\left( 1-u^2_1-u^2_2\right) +\frac{1}{2}|\nabla \tau |^2. \end{aligned}$$

Proof

Recall from [36, Corollary 3.8] that the squared norm $|H|^2$ of the mean curvature vector evolves in time under the equation

$$\begin{aligned} \partial _{t}|H|^2-\varDelta |H|^2= & {} 2|A^H|^2-2|\nabla ^{\perp }H|^2\\&+2{\widetilde{R}}(H,e_1,H,e_1)+ 2{\widetilde{R}}(H,e_2,H,e_2), \end{aligned}$$

where $\{e_1,e_2\}$ is a local orthonormal frame with respect to ${\text {g}}$. Using the special frames introduced in Sect. 2.3 we see that

$$\begin{aligned}&{\widetilde{R}}(H,e_1,H,e_1)+{\widetilde{R}}(H,e_2,H,e_2)=(H^2)^2{\widetilde{R}}_{4141}+(H^1)^2{\widetilde{R}}_{3131}\\&\quad =u^2_1\big (\mu ^2\sigma _M+\lambda ^2\sigma _N\big )(H^4)^2 +u^2_1\big (\lambda ^2\sigma _M+\mu ^2\sigma _N\big )(H^3)^2\\&\quad =\sigma _Mu^2_1\big (\lambda ^2+\mu ^2\big )|H|^2 -(\sigma _M-\sigma _N)u^2_1\big (\lambda ^2(H^4)^2+\mu ^2(H^3)^2\big )\\&\quad \le \sigma _M\big (1-u^2_1-u^2_2\big )|H|^2. \end{aligned}$$

Note that from Cauchy–Schwarz inequality we have $|A^H|\le |A||H|$. Moreover, observe that at points where the mean curvature vector is nonzero, from Kato’s inequality, we have that

$$\begin{aligned} |\nabla ^{\perp }H|^2\ge |\nabla |H||^2. \end{aligned}$$

Consequently, at points where the norm |H| of the mean curvature is not zero the following inequality holds

$$\begin{aligned} \partial _{t}|H|^2-\varDelta |H|^2\le -2|\nabla |H||^2+2|A|^2|H|^2 +2\sigma _M\left( 1-u^2_1-u^2_2\right) |H|^2. \end{aligned}$$

Now let us compute the evolution equation of the function $\tau$. We have,

$$\begin{aligned} \partial _{t}\tau -\varDelta \tau= & {} \frac{\delta \big (\partial _{t}|H|^2-\varDelta |H|^2\big )}{\delta |H|^2+\varepsilon } +\frac{\delta ^2|\nabla |H|^2|^2}{(\delta |H|^2+\varepsilon )^2} +\frac{\delta '|H|^2}{\delta |H|^2+\varepsilon }\\\le & {} -\frac{2\delta }{\delta |H|^2+\varepsilon }|\nabla |H||^2 +\frac{\delta ^2}{(\delta |H|^2+\varepsilon )^2}|\nabla |H|^2|^2\\&+\frac{2\delta }{\delta |H|^2+\varepsilon }|H|^2|A|^2 +\frac{\delta '}{\delta |H|^2+\varepsilon }|H|^2\\&+\frac{2\delta }{2\delta |H|^2+\varepsilon }|H|^2\sigma _M\big (1-u^2_1-u^2_2\big ). \end{aligned}$$

Note that

$$\begin{aligned} -\frac{2\delta }{\delta |H|^2+\varepsilon }|\nabla |H||^2 +\frac{1}{2}\frac{\delta ^2}{(\delta |H|^2+\varepsilon )^2}|\nabla |H|^2|^2\le 0. \end{aligned}$$

Therefore,

$$\begin{aligned} \partial _{t}\tau -\varDelta \tau\le & {} \frac{1}{2}|\nabla \tau |^2 +\frac{2\delta }{\delta |H|^2+\varepsilon }|H|^2|A|^2\\&+\frac{\delta '}{\delta |H|^2+\varepsilon }|H|^2 +\frac{2\delta }{\delta |H|^2+\varepsilon }|H|^2\sigma _M\big (1-u^2_1-u^2_2\big ), \end{aligned}$$

and this completes the proof. $\square$

Theorem 4.1

Let $f:(M,{{\text {g}}_M})\rightarrow (N,{{\text {g}}_N})$ be an area decreasing map, where M is compact and N a complete Riemann surface. Suppose that the curvatures of M and N satisfy $\sigma :=\min \sigma _M\ge \sup \sigma _N$. Then, the following statements hold.

• a) There exists a positive time-independent constant C such that

  $$\begin{aligned} |H|^2\le C, \end{aligned}$$

  as long as the flow exists.

• b) If $\sigma \ge 0$, the following improved decay estimate holds

  $$\begin{aligned} |H|^2\le C t^{-1}, \end{aligned}$$

  where C is again a positive constant.

Proof

Consider the time-dependent function $\varTheta$ given by

$$\begin{aligned} \varTheta :=\log ({\delta |H|^2+\varepsilon })-\log {\rho }, \end{aligned}$$

where $\delta$ is a positive increasing function. Making use of the estimate

$$\begin{aligned} |H|^2\le 2|A|^2 \end{aligned}$$

and from the evolution equations of Lemmas 3.6 and 4.1 we deduce that

$$\begin{aligned} \partial _{t}\varTheta -\varDelta \varTheta\le & {} \frac{1}{2}\langle \nabla \varTheta ,\nabla \tau +\nabla \rho \rangle \\&+\frac{\delta '|H|^2-\varepsilon |H|^2 -2\varepsilon \sigma \big (1-u^2_1-u^2_2\big )}{\delta |H|^2+\varepsilon }. \end{aligned}$$

Choosing $\delta =1$ and $\varepsilon =0$, we obtain that

$$\begin{aligned} \partial _{t}\varTheta -\varDelta \varTheta \le \frac{1}{2}\langle \nabla \varTheta ,\nabla \tau +\nabla \rho \rangle . \end{aligned}$$

From the maximum principle, the norm |H| remains uniformly bounded in time regardless of the sign of the constant $\sigma$. In the case where $\sigma \ge 0$, choosing $\varepsilon =1$ and $\delta =t$, we deduce that $\varTheta$ remains uniformly bounded in time which gives the desired decay estimate for H. $\square$

5 Blow-up analysis and convergence

5.1 Cheeger–Gromov compactness for metrics

Let us recall here the basic notions and definitions. Fore more details, see the books [26, Chap. 5], [15, Chap. 3] and [1, Chap. 9].

Definition 5.1

($C^{\infty }-convergence$) Let $(E,\pi ,\varSigma )$ be a vector bundle endowed with a Riemannian metric ${\text {g}}$ and a metric connection $\nabla$ and suppose that $\{\xi _k\}_{k\in \mathbb {N}}$ is a sequence of sections of E. Let U be an open subset of $\varSigma$ with compact closure $\overline{U}$ in $\varSigma$. Fix a natural number $p\ge 0$. We say that $\{\xi _k\}_{k\in \mathbb {N}}$ converges in $C^p$ to $\xi _{\infty }\in \varGamma (E|_{\overline{U}})$, if for every $\varepsilon >0$ there exists $k_0=k_0(\varepsilon )$ such that

$$\begin{aligned} \sup _{0\le \alpha \le p}\sup _{x\in \overline{ U}}\big |\nabla ^{\alpha } (\xi _k-\xi _{\infty })\big |<\varepsilon \end{aligned}$$

whenever $k\ge k_0$. We say that $\{\xi _k\}_{k\in \mathbb {N}}$ converges in $C^{\infty }$ to $\xi _{\infty }\in \varGamma (E|_{\overline{U}})$ if $\{\xi _k\}_{k\in \mathbb {N}}$ converges in $C^{p}$ to $\xi _{\infty }\in \varGamma (E|_{\overline{U}})$ for any $p\ge 0$.

Definition 5.2

($C^{\infty }$-convergence on compact sets) Let $(E,\pi ,\varSigma )$ be a vector bundle endowed with a Riemannian metric ${\text {g}}$ and a metric connection $\nabla$. Let $\{U_n\}_{n\in \mathbb {N}}$ be an exhaustion of $\varSigma$ and $\{\xi _{k}\}_{k\in \mathbb {N}}$ be a sequence of sections of E defined on open sets $A_{k}$ of $\varSigma$. We say that $\{\xi _{k}\}_{k\in \mathbb {N}}$ converges smoothly on compact sets to $\xi _{\infty }\in \varGamma (E)$ if:

• a) For every $n\in \mathbb {N}$ there exists $k_0$ such that $\overline{U}_n\subset A_k$ for all natural numbers $k\ge k_0$.

• b) The sequence $\{\xi |_{\overline{U}_k}\}_{k\ge k_0}$ converges in $C^{\infty }$ to the restriction of the section $\xi _{\infty }$ on $\overline{U}_n$.

In the next definitions, we recall the notion of smooth Cheeger–Gromov convergence of sequences of Riemannian manifolds.

Definition 5.3

(Pointed Riemannian manifolds) A pointed Riemannian manifold $(\varSigma ,{\text {g}},x)$ is a Riemannian manifold $(\varSigma ,{\text {g}})$ with a choice of origin or base point $x\in \varSigma$. If the metric ${\text {g}}$ is complete, we say that $(\varSigma ,{\text {g}},x)$ is a complete pointed Riemannian manifold.

Definition 5.4

(Cheeger–Gromov smooth convergence) A sequence of complete pointed Riemannian manifolds $\{(\varSigma _k,{\text {g}}_k,x_k)\}_{k\in \mathbb {N}}$ smoothly converges in the sense of Cheeger–Gromov to a complete pointed Riemannian manifold $(\varSigma _{\infty },{\text {g}}_{\infty },x_{\infty })$, if there exists:

• a) An exhaustion $\{U_k\}_{k\in \mathbb {N}}$ of $\varSigma _{\infty }$ with $x_{\infty }\in U_k$, for all $k\in \mathbb {N}$.

• b) A sequence of diffeomorphisms $\varPhi _k:U_k\rightarrow \varPhi _k(U_k)\subset \varSigma _k$ with $\varPhi _k(x_{\infty })=x_k$ and such that $\{\varPhi _k^*{\text {g}}_k\}_{k\in \mathbb {N}}$ smoothly converges in $C^{\infty }$ to ${\text {g}}_{\infty }$ on compact sets in $\varSigma _{\infty }$.

The family $\{(U_k,\varPhi _k)\}_{k\in \mathbb {N}}$ is called a family of convergence pairs of the sequence $\{(\varSigma _k,{\text {g}}_k,x_k)\}_{k\in \mathbb {N}}$ with respect to the limit $(\varSigma _{\infty },{\text {g}}_{\infty },x_{\infty })$.

When we say smooth convergence, we will always mean smooth convergence in the sense of Cheeger–Gromov. The family of convergence pairs is not unique. Two such families $\{(U_k,\varPhi _k)\}_{k\in \mathbb {N}}$, $\{(W_k,\varPsi _k)\}_{k\in \mathbb {N}}$ are equivalent in the sense that there exists an isometry $\mathcal {I}$ of the limit $(\varSigma _{\infty },{\text {g}}_{\infty },x_{\infty })$ such that, for every compact subset K of $\varSigma _{\infty }$ there exists a natural number $k_0$ such that for any natural $k\ge k_0$:

• a) the mapping $\varPhi ^{-1}_k\circ \varPsi _k$ is well defined over K and

• b) the sequence $\{\varPhi ^{-1}_k\circ \varPsi _k\}_{k\ge k_0}$ smoothly converges to $\mathcal {I}$ on K.

In the matter of fact, the limiting pointed Riemannian manifold $(\varSigma _{\infty },{\text {g}}_{\infty },x_{\infty })$ of the Definition 5.4 is unique up to isometries (see [26, Lemma 5.5]).

Definition 5.5

A complete Riemannian manifold $(\varSigma ,{\text {g}})$ is said to have bounded geometry, if the following conditions are satisfied:

• a) For any integer $j\ge 0$ there exists a uniform positive constant $C_j$ such that $|\nabla ^j{R}|\le C_j$.

• b) The injectivity radius satisfies ${\text {inj}}_{{\text {g}}}(\varSigma )>0$.

The following proposition is standard and will be useful in the proof of the long-time existence of the graphical mean curvature flow.

Proposition 5.1

Let $(\varSigma ,{\text {g}})$ be a complete Riemannian manifold with bounded geometry. Suppose that $\{a_k\}_{k\in \mathbb {N}}$ is an increasing sequence of real numbers that tends to $+\infty$ and let $\{x_k\}_{k\in \mathbb {N}}$ be a sequence of points on $\varSigma$. Then, the sequence $(\varSigma ,a^2_k{\text {g}},x_k)$ smoothly subconverges to the standard Euclidean space $(\mathbb {R}^m,{\text {g}}_{{\text {euc}}},0)$.

We will use the following definition of uniformly bounded geometry for a sequence of pointed Riemannian manifolds.

Definition 5.6

We say that a sequence $\{(\varSigma _k,{\text {g}}_k,x_k)\}_{k\in \mathbb {N}}$ of complete pointed Riemannian manifolds has uniformly bounded geometry if the following two conditions are satisfied:

• a) For any integer $j\ge 0$ there exists a uniform constant $C_j$ such that for each $k\in \mathbb {N}$ it holds $|\nabla ^j{R}_k|\le C_j$, where $R_k$ is the curvature operator of ${\text {g}}_k$.

• b) There exists a uniform constant $c_0$ such ${\text {inj}}_{{\text {g}}_k}(\varSigma _k)\ge c_0>0$.

In the next result, we state the Cheeger–Gromov compactness theorem for sequences of complete pointed Riemannian manifolds. The version that we present here is due to Hamilton (see, for example, [17] or [15, Chaps. 3 and 4]).

Theorem 5.1

(Cheeger–Gromov compactness) Let $\{(\varSigma _k,{\text {g}}_k,x_k)\}_{k\in \mathbb {N}}$ be a sequence of complete pointed Riemannian manifolds with uniformly bounded geometry. Then, the sequence $\{(\varSigma _k,{\text {g}}_k,x_k)\}_{k\in \mathbb {N}}$ subconverges smoothly to a complete pointed Riemannian manifold $(\varSigma _{\infty },{\text {g}}_{\infty },x_{\infty })$.

Remark 5.1

Due to an estimate from Cheeger et al. [6], the above compactness theorem still holds under the weaker assumption that the injectivity radius is uniformly bounded from below by a positive constant only along the base points $\{x_k\}_{k\in \mathbb {N}}$, thereby avoiding the assumption of the uniform lower bound for ${\text {inj}}_{{\text {g}}_k}(\varSigma _k)$.

5.2 Convergence of immersions

Let us begin our exposition with the geometric limit of a sequence of isometric immersions.

Definition 5.7

(Convergence of isometric immersions) Suppose that $F_k:(\varSigma _k,{\text {g}}_k,x_k)\rightarrow (P_k,{h}_k,y_k)$ is a sequence of isometric immersions, such that $F(x_k)=y_k$, for any $k\in \mathbb {N}$. We say that the sequence $\{F_k\}_{k\in \mathbb {N}}$ converges smoothly to an isometric immersion $F_{\infty }: (\varSigma _{\infty },{\text {g}}_{\infty },x_{\infty })\rightarrow (P_{\infty },{h}_{\infty },y_{\infty })$ if the following conditions are satisfied:

• a) The sequence $\{(\varSigma _k,{\text {g}}_k,x_k)\}_{k\in \mathbb {N}}$ smoothly converges to $(\varSigma _{\infty },{\text {g}}_{\infty },x_{\infty })$.

• b) The sequence $\{(P_k,{h}_k,y_k)\}_{k\in \mathbb {N}}$ smoothly converges to $(P_{\infty },{h}_{\infty },y_{\infty })$.

• c) If $\{(U_k,\varPhi _k)\}_{k\in \mathbb {N}}$ is a family of convergence pairs of $\{(\varSigma _k,{\text {g}}_k,x_k)\}_{k\in \mathbb {N}}$ and $\{(W_k,\varPsi _k)\}_{k\in \mathbb {N}}$ is a family of convergence pairs of $\{(P_k,{h}_k,y_k)\}_{k\in \mathbb {N}}$, then for each $k\in \mathbb {N}$, it holds $F_k\circ \varPhi _k(U_k)\subset \varPsi _k(W_k)$ and $\varPsi _k^{-1}\circ F\circ \varPhi _k$ smoothly converges to $F_{\infty }$ on compact sets.

The following result holds true (see, for example, [16, Corollary 2.1.11] or [9, Theorem 2.1]).

Lemma 5.1

Suppose that (P, h) is a complete Riemannian manifold with bounded geometry. Then, for any $C>0$ there exists a positive constant $r>0$ such that ${\text {inj}}_{{\text {g}}}(\varSigma )>r$ for any isometric immersion $F:(\varSigma ,{\text {g}})\rightarrow (P,{h})$ such that the norm $|A_F|$ of its second fundamental form satisfies $|A_F|\le C$.

The last lemma and the Cheeger–Gromov compactness theorem allow us to obtain a compactness theorem in the category of sequences of immersions (see for instance [16, Theorem 2.0.12]).

Theorem 5.2

(Compactness for immersions) Let $\{(\varSigma _k,{\text {g}}_k,x_k)\}_{k\in \mathbb {N}}$ and $\{(P_k,{h}_k,y_k)\}_{k\in \mathbb {N}}$ be two sequences of complete Riemannian manifolds with dimensions m and l, respectively. Let $F_k: (\varSigma _k,{\text {g}}_k,x_k)\rightarrow (P_k,{h}_k,y_k)$ be a family of isometric immersions with $F_k(x_k)=y_k$. Assume that:

• a) Each $\varSigma _k$ is compact.

• b) The sequence $\{(P_k,{h}_k,y_k)\}_{k\in \mathbb {N}}$ has uniformly bounded geometry.

• c) For each integer $j\ge 0$, there exists a uniform constant $C_j$ such that

  $$\begin{aligned} |(\nabla ^{F_k})^jA_{F_k}|\le C_j, \end{aligned}$$

  for any $k\in \mathbb {N}$. Here $A_{F_k}$ stands for the second fundamental form of the immersion $F_k$.

Then, the sequence of immersions $\{F_k\}_{k\in \mathbb {N}}$ subconverges smoothly to a complete isometric immersion $F_{\infty }:(\varSigma _{\infty },{\text {g}}_{\infty },x_{\infty })\rightarrow (P_{\infty },{h}_{\infty },y_{\infty })$.

5.3 Modeling the singularities

The next theorem shows how one can built smooth singularity models for the mean curvature flow by rescaling properly around points where the second fundamental form attains its maximum. The proof relies on the compactness theorem of Cheeger–Gromov and on the compactness theorem for immersions. For more details see [10, Theorem 2.4 and Proposition 2.5].

Theorem 5.3

(Blow-up limit) Let $\varSigma$ be a compact manifold and suppose that $F:\varSigma \times [0,T)\rightarrow (P,{h})$ is a solution of mean curvature flow, where P is a Riemannian manifold with bounded geometry and $T\le \infty$ is the maximal time of existence. Suppose that there exists a sequence of points $\{(x_k,t_k)\}_{k\in \mathbb {N}}$ in $\varSigma \times [0,T)$ with $\lim t_k=T$ and such that the sequence $\{a_k\}_{k\in \mathbb {N}}$, where

$$\begin{aligned} a_k:=\max _{(x,t)\in \varSigma \times [0, t_k]}|A(x,t)|=|A(x_k,t_k)|, \end{aligned}$$

tends to infinity. Then:

• a) The maps $F_k:\varSigma \times [-a^{2}_kt_k,0] \rightarrow (P,a^2_k{h})$, $k\in \mathbb {N}$, given by

  $$\begin{aligned} F_k(x,s):=F_{k,s}(x):=F\left( x,{s}/{a^{2}_k}+t_k\right) , \end{aligned}$$

  form a sequence of mean curvature flow solutions. Moreover, we have $|A_{F_{k}}|\le 1$ and $|A_{F_{k}}(x_{k},0)|=1$, for any $k\in \mathbb {N}$.

• b) For any $s\le 0$, the sequence $\{(\varSigma ,F_{k,s}^*(a^2_k{h}),x_k)\}_{k\in \mathbb {N}}$ smoothly subconverges to a complete pointed Riemannian manifold $(\varSigma _{\infty },{\text {g}}_{\infty },x_{\infty })$ that does not depend on the choice of s. Moreover, the sequence of pointed manifolds $\{(P,a^2_k{h},F_k(x_k,s))\}_{k\in \mathbb {N}}$ smoothly subconverges to the standard Euclidean space $(\mathbb {R}^{l},{\text {g}}_{{\text {euc}}},0)$.

• c) There is a mean curvature flow $F_{\infty }:\varSigma _{\infty }\times (-\infty ,0]\rightarrow \mathbb {R}^l$, such that for each fixed time $s\le 0$, the sequence $\{F_{k,s}\}_{k\in \mathbb {N}}$ smoothly subconverges to $F_{\infty , s}$. This convergence is uniform with respect to the parameter s. Additionally, $|A_{F_{\infty }}|\le 1$ and $|A_{F_{\infty }}(x_{\infty },0)|=1$.

• d) If $\dim \varSigma =2$ and $H_{F_{\infty }}=0$, then the limiting Riemann surface $\varSigma _{\infty }$ has finite total curvature. In the matter of fact, the limiting surface $\varSigma _{\infty }$ is conformally diffeomorphic to a compact Riemann surface minus a finite number of points and is of parabolic type.

5.4 Long-time existence

We shall see that under our assumptions the graphical mean curvature flow exists for all time.

Theorem 5.4

Let $(M,{{\text {g}}_M})$ and $(N,{{\text {g}}_N})$ be Riemann surfaces as in Theorem A and $f:M\rightarrow N$ a strictly area decreasing map. Evolve the graph of f under the mean curvature flow. Then, the norm of the second fundamental form of the evolved graphs stays uniformly bounded in time and so the graphical mean curvature flow exists for all time.

Proof

Suppose to the contrary that |A| is not uniformly bounded. Then, there exists a sequence $\{(x_k,t_k)\}_{k\in \mathbb {N}}$ in $M\times [0,T)$ with $\lim t_k=T\le \infty$, with

$$\begin{aligned} a_k:=\max _{(x,t)\in M \times [0, t_k]}|A(x,t)|=|A(x_k,t_k)|, \end{aligned}$$

and such that $\{a_k\}_{k\in \mathbb {N}}$ tends to infinity. Now perform scalings as in Theorem 5.3. A direct computation shows that the mean curvature vector $H_{k}$ of $F_k$ is related to the mean curvature H of F by

$$\begin{aligned} H_{k}(x,s)=a^{-2}_kH\left( x,s/a^{2}_k+t_k\right) , \end{aligned}$$

for any $(x,s)\in M\times [-a^{2}_kt_k,0]$. Let $F_{\infty }:\varSigma _{\infty }\times (-\infty ,0]\rightarrow \mathbb {R}^{4}$ be the blow-up flow of Theorem 5.3. Since |H| is uniformly bounded and the convergence is smooth, from Theorem 5.3(d) it follows that $F_{\infty }:\varSigma _{\infty }\rightarrow \mathbb {R}^{4}$ is a complete minimal immersion of parabolic type. Hence, any nonnegative superharmonic function must be constant. Since the convergence is smooth, the corresponding Kähler angles $\varphi _{\infty }$, $\vartheta _{\infty }$ of $F_{\infty }$ with respect to the complex structures $J=(J_{\mathbb {R}^2},-J_{\mathbb {R}^2})$ and $J_2=(J_{\mathbb {R}^2},J_{\mathbb {R}^2})$ of $\mathbb {R}^{4}$ are nonnegative. As in Lemma 3.2 we get that

$$\begin{aligned}&\varDelta \varphi _{\infty }+\big (|A_{F_{\infty }}|^2-2\sigma ^{\perp }_{F_{\infty }}\big )\varphi _{\infty }=0, \end{aligned}$$

(5.1)

$$\begin{aligned}&\varDelta \vartheta _{\infty }+\big (|A_{F_{\infty }}|^2+2\sigma ^{\perp }_{F_{\infty }}\big )\vartheta _{\infty }=0, \end{aligned}$$

(5.2)

where $-\sigma ^{\perp }_{F_{\infty }}$ is the normal curvature of $F_{\infty }$. Moreover,

$$\begin{aligned} |\nabla \varphi _\infty |^2 =(1-\varphi _\infty ^2)\Big (\big (\big (A_{F_\infty }\big )^3_{11}+\big (A_{F_\infty }\big )^4_{12}\big )^2 +\big (\big (A_{F_\infty }\big )^3_{12}-(A_{F_\infty })^4_{11}\big )^2\Big ),\end{aligned}$$

(5.3)

$$\begin{aligned} |\nabla \vartheta _\infty |^2 =(1-\vartheta _\infty ^2)\Big (\big (\big (A_{F_\infty }\big )^3_{11}-(A_{F_\infty })^4_{12}\big )^2 +\big (\big (A_{F_\infty }\big )^3_{12}+(A_{F_\infty })^4_{11}\big )^2\Big ). \end{aligned}$$

(5.4)

Note that from (2.1) one can easily derive the inequalities

$$\begin{aligned} |A_{F_{\infty }}|^2\pm 2\sigma ^{\perp }_{F_{\infty }}\ge 0. \end{aligned}$$

From (5.1) and (5.2)M we deduce that $\varphi _{\infty }$ and $\vartheta _{\infty }$ are superharmonic and consequently they must be constants. Thus, the functions $(u_1)_{\infty }$ and $(u_2)_{\infty }$ are also constants. We will distinguish three cases:

Case A. Suppose at first that $\varphi _{\infty }> 0$ and $\vartheta _{\infty }>0$. Then, from (5.1) and (5.2) we deduce that

$$\begin{aligned} |A_{F_{\infty }}|^2\pm 2\sigma ^{\perp }_{F_{\infty }}= 0 \end{aligned}$$

which implies that $|A_{F_{\infty }}|=0$. This contradicts the fact that there is a point where $|A_{F_{\infty }}|=1$.

Case B. Suppose that both constants $\varphi _{\infty }$ and $\vartheta _{\infty }$ are zero. Then, from the Eqs. (5.3) and (5.4) we obtain that $A_{F_\infty }$ vanishes identically, which is a again a contradiction.

Case C. Suppose now that only one of the constants $\varphi _\infty$, $\vartheta _\infty$ is zero. Let us assume that $\varphi _{\infty }=0$ and $\vartheta _{\infty }>0$. The case $\varphi _{\infty }>0$ and $\vartheta _{\infty }=0$ is treated in a similar way. Since $\varphi _\infty =0$, $F_\infty :\varSigma _\infty \rightarrow \mathbb {R}^{4}$ must be a minimal Lagrangian immersion. Note that in this case necessarily $(u_1)_\infty =(u_2)_\infty =\mathrm {const}>0$. It is well known (see, for example, [8] or [38]) that minimal Lagrangian surfaces in $\mathbb {C}^{2}$ are holomorphic curves with respect to one of the complex structures of $\mathbb {C}^{2}$. In the matter of fact (see, for example, [3, Theorem A, p. 495]), we can explicitly locally reparameterize the minimal Lagrangian immersion $F_{\infty }$ in the form

$$\begin{aligned} F_{\infty }=\frac{1}{\sqrt{2}}e^{i\beta /2}\big (\mathcal {F}_1-i\overline{\mathcal {F}_2},\mathcal {F}_2+i\overline{\mathcal {F}_1}\big ), \end{aligned}$$

where $\beta$ is a constant and $\mathcal {F}_1$, $\mathcal {F}_2:\mathbb {D}\subset \mathbb {C}\rightarrow \mathbb {C}$ are holomorphic functions defined in a simply connected domain $\mathbb {D}$ such that

$$\begin{aligned} |(\mathcal {F}_1)_z|^2+|(\mathcal {F}_2)_z|^2>0. \end{aligned}$$

The Gauß image of $F_{\infty }$ lies in the slice $\mathbb {S}^{2}\times \{(e^{i\beta },0)\}$ of the product $\mathbb {S}^2\times \mathbb {S}^2$. In the matter of fact, all the information on the Gauß image of $F_{\infty }$ is encoded in the map $\mathcal {G}:\mathbb {D}\rightarrow \mathbb {S}^{2}=\mathbb {C}\cup \{\infty \}$ given by $\mathcal {G}={(\mathcal {F}_1)_z}/{(\mathcal {F}_2)_z}$. Because $(u_1)_{\infty }=\mathrm {const}>0$ we get that $F_{\infty }$ is the graph of an area preserving map h. Then,

$$\begin{aligned} \mathcal {F}_1=({z+i\overline{h}})/2,\quad \mathcal {F}_2 =(-i\overline{z}+h)/2\quad \text {and}\quad |h_z|^2-|h_{\bar{z}}|^2=1. \end{aligned}$$

Therefore,

$$\begin{aligned}\mathcal {G}={(\mathcal {F}_1)_z}/{(\mathcal {F}_2)_z}=(1-i{h}_{\bar{z}})/{h_z}. \end{aligned}$$

A straightforward computation shows that

$$\begin{aligned} |\mathcal {G}|^2=\frac{\big |1+i\overline{h_{\bar{z}}}\big |^2}{|h_z|^2} =\frac{1+|h_{\bar{z}}|^2 +i\big (\overline{h_{\bar{z}}}-h_{\bar{z}}\big )}{1+|h_{\bar{z}}|^2} =1+\frac{2{\text {Im}}(h_{\bar{z}})}{1+|h_{\bar{z}}|^2}\le 2. \end{aligned}$$

Hence, the image of $\mathcal {G}$ is contained in a bounded subset of $\mathbb {C}\cup \{\infty \}$. But then, due to a result of Osserman [27, Theorem 1.2] the immersion $F_{\infty }$ must be flat, which is a contradiction.

Hence, the norm of the second fundamental form is uniformly bounded in time. This completes the proof of the theorem. $\square$

Remark 5.2

In the case where $F_{\infty }(\varSigma _{\infty })$ is an entire minimal graph, in the proof of the above theorem, one could use the Bernstein type theorems proved by Hasanis, Savas-Halilaj and Vlachos in [21, 22] to show flatness of $F_{\infty }$.

5.5 Convergence of the flow

Now we shall prove the convergence of the graphical mean curvature flow.

Theorem 5.5

Let $(M,{{\text {g}}_M})$ and $(N,{{\text {g}}_N})$ be Riemann surfaces as in Theorem A and let $f:M\rightarrow N$ be a strictly area decreasing map. Evolve the graph of the map f under the mean curvature flow. Then, the graphical mean curvature flow smoothly convergence to a minimal surface $M_{\infty }$ of $(M\times N,{{\text {g}}_{M\times N}})$.

Proof

For the proof of the theorem, we will distinguish two cases:

Case A. Suppose at first that N is compact. In this case, the product manifold $M\times N$ is compact. Since

$$\begin{aligned} \partial _{t}\varOmega _{{\text {g}}(t)}=-\int _M|H|^2\varOmega _{{\text {g}}(t)} \end{aligned}$$

and since the graphical flow exists for all time we have that there exists a time-independent constant C such that

$$\begin{aligned} \int _0^{\infty }\left( \int _M|H|^2\varOmega _{{\text {g}}(t)}\right) dt\le C. \end{aligned}$$

Therefore, there exists a sequence $\{t_k\}_{k\in \mathbb {N}}$ such that

$$\begin{aligned} \lim _{k\rightarrow \infty }\int _M|H|^2\varOmega _{{\text {g}}(t_k)}=0. \end{aligned}$$

(5.5)

From Theorem 5.4, the norms of the second fundamental forms of the evolving submanifolds, as well as their derivatives, are uniformly bounded in time. Because of compactness of $M\times N$, after passing to a sub-sequence of $\{t_k\}_{k\in \mathbb {N}}$ if necessary, we deduce that our flow sub-converges smoothly to a smooth surface $M_{\infty }$ of $M\times N$ (see, for example, [5, Theorem 1.1 and p. 1371]) which in view of (5.5) should be minimal. Due to a deep result of Simon [34, Corollary 2, p. 536], it follows that our flow converges smoothly and uniformly to $M_{\infty }$.

Case B. Suppose now that the Riemann surface N is non-compact.

Sub-Case ${B}_1$. Let us consider at first the case where $\sigma =\min \sigma _M>0$. Recall from Lemma 3.5(a) that there exists a positive constant $c_0$ such that for any $(x,t)\in M\times [0,\infty )$, it holds

$$\begin{aligned} \frac{1-\lambda ^2\mu ^2}{(1+\lambda ^2)(1+\mu ^2)}=\rho \ge \frac{c_0e^{\sigma t}}{\sqrt{1+c^2_0e^{2\sigma t}}}. \end{aligned}$$

Observe that

$$\begin{aligned} \rho (1+\mu ^2)=\frac{1-\lambda ^2\mu ^2}{1+\lambda ^2}\le 1. \end{aligned}$$

Consequently,

$$\begin{aligned} \lambda ^2\le \mu ^2\le {\rho }^{-1}-1\le c_0^{-1}e^{-\sigma t} \end{aligned}$$

and so

$$\begin{aligned} |{\text {d}}f_t|^2=\lambda ^2+\mu ^2\le 2c_0^{-1}e^{-\sigma t}. \end{aligned}$$

Claim 1. The diameter ${\text {diam}}(f_t(M))$ of $f_t(M)$ tends to zero as time goes to infinity.

Indeed. Fix a time $t>0$. Since $f_t(M)$ is compact, there are points $p_t,q_t\in M$ such that ${\text {diam}}(f_t(M))$ is realized by the distance of the points $f_t(p_t)$ and $f_t(q_t)$ in $(N,{{\text {g}}_N})$. Let $\gamma _t:[0,\ell _t]\rightarrow (M,{{\text {g}}_M})$ be a unit speed geodesic which connect the points $p_t$ and $q_t$. Using the Cauchy–Schwarz inequality we have

$$\begin{aligned} {\text {diam}}(f_t(M))\le & {} \mathrm{length}(f_t\circ \gamma _t)=\int _0^{\ell _t}|{\text {d}}f(\gamma '_t(s))|\hbox {ds}\\\le & {} \ell _t\big ({\max }|{\text {d}}f_t|\big )\le \mathrm{diam}(M,{{\text {g}}_M})\sqrt{2}c_0^{-1/2}e^{-\sigma t/2}. \end{aligned}$$

This completes the proof of the claim.

Let $\mathscr {B}(q,r)$ be the geodesic ball of N with radius r centered at a point $q\in N$ and $d_q:\mathscr {B}(q,r)\rightarrow \mathbb {R}$ be the function given by

$$\begin{aligned} d_q(y):={\text {dist}}_N(q,y), \end{aligned}$$

where ${\text {dist}}_N$ is the topological metric on N. Because the Riemannian manifold N has bounded geometry, due to a theorem of Whitehead (see [7, Theorem 5.14, p. 103] or [28, Theorem 29, p. 177]) there exists a positive constant $r_0<{\text {inj}}_{{{\text {g}}_N}}(N)$, depending only on the geometry of $(N,{{\text {g}}_N})$, such that the distance function of geodesic balls of radius $r_0$ is strictly convex. Because the diameter of the sets $f_t(M)$ is tending to zero, there exists a sufficiently large time $t_0$, such that the image of $f_{t_0}(M)$ is trapped in a geodesic ball $\mathscr {B}(p,r_0/2)$ centered at a point $p\in N$ with radius $r_0/2$.

Claim 2. The images $f_t(M)$ stays within the geodesic ball $\mathscr {B}(p,r_0/2)$ for all times $t>t_0$.

Suppose to the contrary that there exist $t_{1}>t_0$ for which the moving images $f_{t}(M)$ touch for the first time the boundary of the geodesic ball $\mathscr {B}(p,r_0/2)$. Define the smooth function $\omega _p:M\times [t_0,t_1]\rightarrow \mathbb {R}$ given by

$$\begin{aligned} \omega _p(x,t):=d^2_p(f_t(x))={\text {dist}}^2_N(p,f_t(x)). \end{aligned}$$

Note that the family of maps $\{f_t\}_{t\in [0,\infty )}$ evolves under the equation

$$\begin{aligned} {\text {d}}f(\partial _{t})-\mathscr {T}(f)=0 \end{aligned}$$

where $\mathscr {T}$ is the tension field of maps between the Riemannian manifolds $(M,{\text {g}}(t))$ and $(N,{{\text {g}}_N})$. In local coordinates $(x_1,x_2)$ of M and $(y_1,y_2)$ of N, the operator $\mathscr {T}$ has the form

$$\begin{aligned} \mathscr {T}(f)= & {} g^{ij}\big (\nabla ^f_{\partial _i}{\text {d}}f\big )\partial _j\\= & {} g^{ij}\big \{\partial _i\partial _j f^{\alpha }-{}^{{\text {g}}}\varGamma _{ij}^k\partial _kf^{\alpha } +\big ({}^{{{\text {g}}_N}}\varGamma _{\beta \gamma }^{\alpha }\circ f\big ) \partial _if^{\beta }\partial _j f^{\gamma }\big \}\partial _{\alpha }, \end{aligned}$$

where $(f^1,f^2)$ are the components of f with respect to the given charts, $\nabla ^f$ is the connection on the induced by f bundle on the surface M, $g^{ij}$ the coefficients of the induced time-dependent graphical metric ${\text {g}}$, ${}^{{\text {g}}}\varGamma _{ij}^k$ are the Christoffel symbols with respect to ${\text {g}}$ and ${}^{{{\text {g}}_N}}\varGamma _{\beta \gamma }^{\alpha }$ the Christoffel symbols with respect to the metric ${{\text {g}}_N}$. Moreover, $\alpha ,\beta ,\gamma ,i,j\in \{1,2\}$ and there is a summation whenever repeated indices appear. By a straightforward computation, we deduce that

$$\begin{aligned} \partial _{t}\omega _p-\varDelta \omega _p= -{{{\mathrm{trace}}}}_{{\text {g}}(t)}{\text {Hess}}d^2_p\big ({{\text {d}}f_t}(\cdot ),{\text {d}}f_t(\cdot )\big ), \end{aligned}$$

for any $(x,t)\in M\times [t_0,t_1]$. Because $d_p:\mathscr {B}(p,r_0)\rightarrow \mathbb {R}$ is strictly convex, its Hessian ${\text {Hess}}d_p$ is strictly positive definite. Thus,

$$\begin{aligned} \partial _{t}\omega _p-\varDelta \omega _p= -{{{\mathrm{trace}}}}_{{\text {g}}(t)}{\text {Hess}}d^2_p\big ({{\text {d}}f_t}(\cdot ),{\text {d}}f_t(\cdot )\big )\le 0. \end{aligned}$$

From the parabolic comparison principle, we deduce that

$$\begin{aligned} \omega _p(x,t)\le \omega _{p}(x,t_0)<r_0/2, \end{aligned}$$

for any point $(x,t)\in M\times [t_0,t_1]$, which leads to a contradiction. This completes the proof of the claim.

Because the images $f_t(M)$, $t\ge t_0$, stay inside the geodesic ball $\mathscr {B}(p,r_0)$, we deduce that all the graphs $\varGamma (f_t)$, $t\ge 0$, are trapped in a bounded region of $M\times N$. Again from the result of Simon [34, Corollary 2, p. 536], we deduce smooth convergence of the flow to a minimal surface $M_{\infty }$ of the product $(M\times N,{{\text {g}}_{M\times N}})$.

Sub-Case ${B}_2$. Let us consider now the case $0\ge \sigma =\min \sigma _M\ge \sigma _N$. By assumption the initial map $f:M\rightarrow N$ is homotopic to a smooth minimal map $\psi _{}:M\rightarrow N$. Define the time-dependent function $\omega _{\psi }:M\times (0,\infty )\rightarrow \mathbb {R}$ given by

$$\begin{aligned} \omega _{\psi }(x,t):={\text {dist}}^2_{N\times N}\big (\psi (x),f_t(x)\big ), \end{aligned}$$

where ${\text {dist}}_{N\times N}$ is the distance function on the product $(N\times N,{{\text {g}}_N}\times {{\text {g}}_N})$. Because N has non-positive curvature and because the maps $\psi$ and f are homotopic to each other, it follows that the function $\omega _{\psi }$ is smooth (details can be found in [33, Section 2]). Note that the functions $\psi$ and f satisfy the differential equations

$$\begin{aligned} \mathscr {T}(\psi )=0\quad \text {and}\quad {\text {d}}f(\partial _{t})-\mathscr {T}(f)=0. \end{aligned}$$

Then, by a direct computation we see that the function $\omega _{\psi }$ evolves in time under the equation

$$\begin{aligned} \partial _{t}\omega _{\psi }-\varDelta \omega _{\psi }=-{{{\mathrm{trace}}}}_{{\text {g}}(t)}{\text {Hess}} {\text {dist}}_{N\times N}^2 \big ({{\text {d}}}(\psi \times f_t)(\cdot ), {{\text {d}}}(\psi \times f_t)(\cdot )\big ). \end{aligned}$$

Since $\sigma _N\le 0$, from [33, Proposition 1, p. 366], the Hessian of the function ${\text {dist}}_{N\times N}^2$ is nonnegative. Therefore,

$$\begin{aligned} \partial _{t}\omega _{\psi }-\varDelta \omega _{\psi }\le 0. \end{aligned}$$

Hence, from the parabolic maximum principle it follows that $\omega _{\psi }$ stays bounded in time. Therefore, the images $f_t(M)$, $t\ge 0$, stay in a bounded region of N and as a consequence, all the graphs $\varGamma (f_t)$, $t\ge 0$, are trapped in a bounded region of the product $M\times N$. Again from the theorem of Simon [34, Corollary 2, p. 536], we deduce smooth convergence to a minimal surface $M_{\infty }$ of the manifold $(M\times N,{{\text {g}}_{M\times N}})$. This completes the proof of the theorem. $\square$

6 Proof of Theorem B

In this section, we will prove the decay estimates claimed in Theorem B. Let us start by proving the following auxiliary lemma.

Lemma 6.1

Let $f:(M,{{\text {g}}_M})\rightarrow (N,{{\text {g}}_N})$ be an area decreasing map, where M and N are Riemann surfaces as in Theorem A. Suppose that $\sigma :=\min \sigma _M>0$. Consider the time-dependent function g given by

$$\begin{aligned} g:=\log \big (t|A|^2+1\big ). \end{aligned}$$

Then, g satisfies the following inequality

$$\begin{aligned}&\partial _{t}g-\varDelta g\le 3|A|^2+\frac{1}{2}|\nabla g|^2+C(1+\sqrt{t})\sqrt{1-\rho ^2}, \end{aligned}$$

where C is a positive constant.

Proof

Recall from [41, Proposition 7.1] that

$$\begin{aligned} \partial _{t}|A|^2= & {} \varDelta |A|^2-2|\nabla ^{\perp }A|^2\\&+2\sum _{i,j,k,l}\Big (\sum _{\alpha }A^{\alpha }_{ij}A^{\alpha }_{kl}\Big )^2 +2\sum _{\alpha ,\beta ,i,j} \Big (\sum _{k}\big (A^{\alpha }_{ik}A^{\beta }_{jk} -A^{\beta }_{ik}A^{\alpha }_{jk}\big )\Big )^2\\&+4\sum _{\alpha ,i,j,k,l}\Big (A^{\alpha }_{ij}A^{\alpha }_{kl} -\delta _{kl}\sum _{p}A^{\alpha }_{ip}A^{\alpha }_{jp}\Big )\widetilde{R}_{kilj}\\&+2\sum _{\alpha ,\beta ,i,j,k}\Big (4A^{\alpha }_{jk}A^{\beta }_{ik} \widetilde{R}_{\alpha \beta ji} +A^{\alpha }_{jk}A^{\beta }_{jk}\widetilde{R}_{\alpha i\beta i}\Big )\\&+2\sum _{\alpha , i,j,k}A^{\alpha }_{jk} \Big (\big ({\nabla }_{i}\widetilde{R}\big )_{\alpha jki} +\big ({\nabla }_{k}\widetilde{R}\big )_{\alpha iji} \Big ), \end{aligned}$$

where the indices are with respect to an arbitrary adapted local orthonormal frame $\{e_1,e_2;e_3,e_4\}$. From [2, Theorem 1], we have that

$$\begin{aligned} 2\sum _{i,j,k,l}\Big (\sum _{\alpha }A^{\alpha }_{ij}A^{\alpha }_{kl}\Big )^2 +2\sum _{\alpha ,\beta ,i,j} \Big (\sum _{k}\big (A^{\alpha }_{ik}A^{\beta }_{jk} -A^{\beta }_{ik}A^{\alpha }_{jk}\big )\Big )^2\le 3|A|^4. \end{aligned}$$

Consider now the term

$$\begin{aligned} \mathcal {A}_1:= & {} 4\sum _{i,j,k,l,\alpha }\Big (A^{\alpha }_{ij}A^{\alpha }_{kl}-\delta _{kl}\sum _{p} A^{\alpha }_{ip}A^{\alpha }_{jp}\Big ){\widetilde{R}}_{kilj}\\&+2\sum _{i,j,k,\alpha ,\beta }\Big (4A^{\alpha }_{jk}A^{\beta }_{ik}{\widetilde{R}}_{\alpha \beta ji}+A^{\alpha }_{jk}A^{\beta }_{jk}{\widetilde{R}}_{\alpha i\beta i}\Big ). \end{aligned}$$

In terms of the frame fields introduced in Sect. 2.3, we get that

$$\begin{aligned} \mathcal {A}_1= & {} -4\big (\sigma _Mu^2_1+\sigma _Nu^2_2\big )\big (|A_{11}-A_{22}|^2 +4|A_{12}|^2\big )\\&+2u^2_1\big (\lambda ^2\sigma _M+\mu ^2\sigma _N\big )|A^3|^2 +2u^2_1\big (\mu ^2\sigma _M+\lambda ^2\sigma _N\big )|A^4|^2\\&-16u_1|u_2|(\sigma _M+\sigma _N)\sigma ^{\perp }\\\le & {} -4u^2_2\sigma _N\big (|A_{11}-A_{22}|^2 +4|A_{12}|^2\big )+2u^2_1(\lambda ^2+\mu ^2)\sigma _M|A|^2\\&-16u_1|u_2|(\sigma _M+\sigma _N)\sigma ^{\perp }. \end{aligned}$$

Since the evolving graphs are area decreasing, we see that

$$\begin{aligned} 2u^2_2=2\lambda ^2\mu ^2u^2_1\le 2\lambda \mu u^2_1\le (\lambda ^2+\mu ^2)u^2_1=1-u^2_1-u^2_2. \end{aligned}$$

Additionally,

$$\begin{aligned} 2u_1|u_2|=2\lambda \mu u^2_1\le u^2_1(\lambda ^2+\mu ^2)\le 1-u^2_1-u^2_2. \end{aligned}$$

Because the Riemann surfaces M and N have bounded geometry, we deduce that there exists a constant $C_1$ such that

$$\begin{aligned} \mathcal {A}_1\le C_1\left( 1-u^2_1-u^2_2\right) |A|^2. \end{aligned}$$

Denote by $\mathcal {A}_2$ the term

$$\begin{aligned} \mathcal {A}_2:=2\sum _{\alpha , i,j,k}A^{\alpha }_{jk} \Big (\big ({\nabla }_{i}\widetilde{R}\big )_{\alpha jki} +\big ({\nabla }_{k}\widetilde{R}\big )_{\alpha iji} \Big ). \end{aligned}$$

Similarly, we deduce that there exists a constant $K_2$ such that

$$\begin{aligned} \mathcal {A}_2\le K_2|A|u^2_1\big (\lambda +\mu +\lambda ^3\mu +\lambda \mu ^3+\lambda ^2\mu ^2\big ). \end{aligned}$$

Because by assumption the map f is area decreasing and since $u_1<1$, we obtain

$$\begin{aligned} \mathcal {A}_2\le & {} K_2|A|u^2_1\big (\lambda +\mu +\lambda ^2+\mu ^2+\lambda \mu \big )\\\le & {} K_2|A|u^2_1\left( \sqrt{2(\lambda ^2+\mu ^2)}+\frac{3}{2}(\lambda ^2+\mu ^2)\right) \\\le & {} K_2|A|\left( \sqrt{2\left( 1-u^2_1-u^2_2\right) }+\frac{3}{2}\big (1-u^2_1-u^2_2\big )\right) \\\le & {} \Bigl (\sqrt{2}+\frac{3}{2}\Bigr )K_2|A|\sqrt{1-u^2_1-u^2_2}. \end{aligned}$$

Going back to the evolution equation of $|A|^2$, we deduce that there are constants $C_1$ and $C_2$ such that

$$\begin{aligned}&\partial _{t}|A|^2-\varDelta |A|^2\le -2|\nabla ^{\perp }A|^2+3|A|^4\\&\quad +C_1|A|^2\left( 1-u^2_1-u^2_2\right) +C_2|A|\sqrt{1-u^2_1-u^2_2}. \end{aligned}$$

By straightforward computations, we have

$$\begin{aligned} \partial _{t}g= & {} \varDelta g+\frac{t}{t|A|^2+1}\big (\partial _{t}|A|^2-\varDelta |A|^2\big )+\frac{|A|^2}{t|A|^2+1}+|\nabla g|^2\\\le & {} \varDelta g+|\nabla g|^2-\frac{2 t}{t|A|^2+1}|\nabla ^{\perp }A|^2 +\frac{3 t|A|^2+1}{ t|A|^2+1}|A|^2\\&+C_1\left( 1-u^2_1-u^2_2\right) \frac{t|A|^2}{t|A|^2+1} +C_2\sqrt{1-u^2_1-u^2_2}\,\frac{ t|A|}{t|A|^2+1}\\\le & {} \varDelta g+\frac{1}{2}|\nabla g|^2-\frac{2 t}{ t|A|^2+1}|\nabla |A||^2+\frac{1}{2}|\nabla g|^2+3|A|^2\\&+C_1\left( 1-u^2_1-u^2_2\right) \frac{t|A|^2}{t|A|^2+1} +C_2\sqrt{1-u^2_1-u^2_2}\,\frac{t|A|}{t|A|^2+1}. \end{aligned}$$

Consequently,

$$\begin{aligned} \partial _{t}g\le & {} \varDelta g+\frac{1}{2}|\nabla g|^2+3|A|^2\\&+C_1\sqrt{1-u^2_1-u^2_2 }\,\frac{t|A|^2}{t|A|^2+1} +C_2\sqrt{1-u^2_1-u^2_2 }\,\frac{\sqrt{t}\sqrt{t}|A|}{t|A|^2+1}\\\le & {} \varDelta g+\frac{1}{2}|\nabla g|^2+3|A|^2+C\big (1+\sqrt{t}\big )\sqrt{1-\rho ^2} \end{aligned}$$

where C is a positive constant. This completes the proof. $\square$

In the following result, we give the decay estimates for the norm of the second fundamental form.

Theorem 6.1

Let $(M,{{\text {g}}_M})$ be a complete Riemann surfaces as in Theorem A and let $f:M\rightarrow N$ be a strictly area decreasing map. Let $\sigma :=\min \sigma _M$. Then, the following statements hold true:

• a) If $\sigma >0$, then there exists a constant C such that

  $$\begin{aligned} |A|^2\le {C}{t^{-1}}. \end{aligned}$$

• b) If $\sigma =0$, then there exists a constant C such that

  $$\begin{aligned} \int _M|A|^2\,\varOmega _{{\text {g}}(t)}\le Ct^{-1}. \end{aligned}$$

Proof

Recall from Theorem 5.4 that |A| is uniformly bounded and that the flow exists for all time. Let us now consider the following cases depending on the sign of $\sigma$.

(a) Suppose at first that $\sigma >0$. Consider the function $\varPhi$ given by the formula

$$\begin{aligned} \varPhi :=g-\zeta =\log \frac{t|A|^2+1}{\eta (\rho )}, \end{aligned}$$

where here $\eta (\rho )$ is a positive increasing function depending on $\rho$ that will be determined later. From Lemmas 3.6 and 6.1, the evolution equation of $\varPhi$ is

$$\begin{aligned} \partial _{t}\varPhi\le & {} \varDelta \varPhi +\frac{3\eta -2\rho \eta _{\rho }}{\eta }|A|^2+C\big (1+\sqrt{t}\big )\sqrt{1-\rho ^2}\\&+\frac{1}{2}\langle \nabla \varPhi ,\nabla g+\nabla \zeta \rangle +\frac{1}{2\rho \eta ^2}\big (\eta \eta _{\rho } +2\rho \eta \eta _{\rho \rho }-\rho \eta _{\rho }^2\big )|\nabla \rho |^2\\&-\frac{2\eta _{\rho }}{\eta }\big ((1-\rho )\sigma _Mu^2_1-(1+\rho )\sigma _Nu^2_2\big ). \end{aligned}$$

Hence,

$$\begin{aligned} \partial _{t}\varPhi\le & {} \varDelta \varPhi +\frac{3\eta -2\rho \eta _{\rho }}{\eta }|A|^2+C\big (1+\sqrt{t}\big )\sqrt{1-\rho ^2}\\&+\frac{1}{2}\langle \nabla \varPhi ,\nabla g+\nabla \zeta \rangle +\frac{1}{2\rho \eta ^2}\big (\eta \eta _{\rho } +2\rho \eta \eta _{\rho \rho }-\rho \eta _{\rho }^2\big )|\nabla \rho |^2\\&-\frac{2\sigma \rho \eta _{\rho }}{\eta }\big (1-u^2_1-u^2_2\big ). \end{aligned}$$

Since $\sigma >0$, we get that

$$\begin{aligned} \partial _{t}\varPhi\le & {} \varDelta \varPhi +\frac{3\eta -2\rho \eta _\rho }{\eta }|A|^2+C\big (1+\sqrt{t}\big )\sqrt{1-\rho ^2}\\&+\frac{1}{2}\langle \nabla \varPhi ,\nabla g+\nabla \zeta \rangle +\frac{1}{2\rho \eta ^2}\big (\eta \eta _{\rho } +2\rho \eta \eta _{\rho \rho }-\rho \eta ^2_{\rho }\big )|\nabla \rho |^2. \end{aligned}$$

Let us choose for $\eta$ the smooth function given by

$$\begin{aligned} \eta (\rho ):=\left( -\frac{1}{3}+\sqrt{\rho }\,\right) ^2. \end{aligned}$$

Since the flow exists for all time, from Lemma 3.5(a) and from the fact that $\rho \le 1$ we see that $\rho$ tends to 1 uniformly as time tends to infinity. Thus, there exists a $t_0>0$ such that $\eta (\rho )>0$ for all $t\in [t_0,+\infty )$. Moreover, for this choice of $\eta$, we see that

$$\begin{aligned} \frac{3\eta -2\rho \eta _{\rho }}{\eta }=\frac{3\big (\sqrt{\rho }-1\big )}{3\sqrt{\rho }-1}\le 0. \end{aligned}$$

By making again use of Lemma 3.5(a), we deduce that there exists a positive constant $c_0$ such that

$$\begin{aligned} \partial _{t}\varPhi -\varDelta \varPhi -\frac{1}{2}\langle \nabla \varPhi ,\nabla g+\nabla \zeta \rangle\le & {} C\big (1+\sqrt{t}\big )\sqrt{1-\rho ^2} \le \frac{C\big (1+\sqrt{t}\big )}{\sqrt{1+c^2_0 e^{2\sigma t}}}\\\le & {} \frac{C}{c_0}\big (1+\sqrt{t}\big )e^{-\sigma t}. \end{aligned}$$

Let y be the solution of the ordinary differential equation

$$\begin{aligned} y'(t)=\frac{C}{c_0}\big (1+\sqrt{t}\big )e^{-\sigma t},\quad y(0)=\max _{x\in M} \varPhi (x,0). \end{aligned}$$

From the parabolic maximum principle, it follows that $\varPhi (x,t)\le y(t)$ for any $(x,t)\in M\times [0,\infty )$. Therefore, $\varPhi$ is uniformly bounded because the solution y is bounded. This implies that there exists a constant, which we denote again by C, such that

$$\begin{aligned} t|A|^2\le C. \end{aligned}$$

(b) Suppose that $\sigma =0$. Denote by $\varOmega _{{\text {g}}(t)}$ the volume forms of the induced metrics. Because of the formula

$$\begin{aligned} \partial _{t}\left( \int _{M}\varOmega _{{\text {g}}(t)}\right) =-\int _{M} |H|^2\varOmega _{{\text {g}}(t)}\le 0, \end{aligned}$$

we obtain that

$$\begin{aligned} \int _M\varOmega _{{\text {g}}(t)}\le \int _M\varOmega _{{\text {g}}(0)}={\text {constant}}. \end{aligned}$$

Now from Theorem 4.1(b) it follows that there is a nonnegative constant C such that

$$\begin{aligned} \int _M |H|^2\varOmega _{{\text {g}}(t)}\le \frac{C}{t}\int _M\varOmega _{{\text {g}}(t)} \le \frac{C}{t}\int _M\varOmega _{{\text {g}}(0)}. \end{aligned}$$

Due to our assumptions, we have that $u^2_2\le u^2_1\le 1$ and $\min \sigma _M\ge 0\ge \sup \sigma _N$. Moreover, recall that

$$\begin{aligned} \varOmega _{{\text {g}}(t)}=\sqrt{(1+\lambda ^2)(1+\mu ^2)}\varOmega _M=\frac{1}{\,u_1}\varOmega _M. \end{aligned}$$

From the Gauß equation (2.6) and the Gauß-Bonnet formula, we get

$$\begin{aligned} \int _M|A|^2\varOmega _{{\text {g}}(t)}= & {} \int _M|H|^2\varOmega _{{\text {g}}(t)}\\&+2\int _M\big (\sigma _Mu^2_1+\sigma _Nu^2_2\big )\varOmega _{{\text {g}}(t)} -2\int _M \sigma _{{\text {g}}(t)}\varOmega _{{\text {g}}(t)}\\\le & {} 2\int _M\sigma _Mu^2_1\varOmega _{{\text {g}}(t)} -2\int _M \sigma _{{\text {g}}(t)}{\text {Vol}}_{{\text {g}}(t)} +\int _M|H|^2{\text {Vol}}_{{\text {g}}(t)}\\\le & {} 2\int _M\sigma _Mu_1\varOmega _{{\text {g}}(t)} -2\int _M \sigma _{{\text {g}}(t)}\varOmega _{{\text {g}}(t)} +\int _M|H|^2{\text {Vol}}_{{\text {g}}(t)}\\\le & {} 2\int _M\sigma _M\varOmega _M -2\int _M \sigma _{{\text {g}}(t)}\varOmega _{{\text {g}}(t)} +\int _M|H|^2\varOmega _{{\text {g}}(t)}\\= & {} \int _M|H|^2\varOmega _{{\text {g}}(t)}. \end{aligned}$$

From the above inequality, we get the decay estimate of the $L^2$-norm of |A|. This completes the proof of part (b). $\square$

From Theorems 5.4, 4.1 and 6.1, we immediately obtain the results stated in Theorem B.

7 Proof of the Theorem A

Let $(M,{{\text {g}}_M})$ and $(N,{{\text {g}}_N})$ be Riemann surfaces satisfying the assumptions of Theorem A and let $\sigma =\min \sigma _M$. Let $f:M\rightarrow N$ be an area decreasing map. Then, the property of being area decreasing is preserved by the flow and, moreover, the flow remains graphical for all time. In the matter of fact, there are two options: either the map f is immediately deformed into a strictly area decreasing one or each map $f_t$, $t\in [0,T)$, is area preserving, N is compact and the curvatures of M and N are constant and satisfy $\sigma _M=\sigma =\sigma _N$. The area preserving case is completely solved in [37] and [40]. Thus, it remains to examine the case where f becomes strictly area decreasing. In this case, from Theorem 5.4 we know that the graphical mean curvature flow, independently of the sign of $\sigma$, smoothly converges to a minimal surface $M_{\infty }$.

Suppose that $\sigma >0$. In this case, the flow is smoothly converging to a graphical minimal surface $M_{\infty }=\varGamma (f_{\infty })$ of $M\times N$. Due to Theorem 6.1(b), $M_{\infty }$ must be totally geodesic and $f_{\infty }$ is a constant map.

Assume that $\sigma =0$. As in the previous case, we have smooth convergence of the flow to a minimal graphical surface $M_{\infty }=\varGamma (f_{\infty })$ of $M\times N$, where $f_{\infty }$ is a strictly area decreasing map. From the integral inequality of Theorem 6.1(b), we deduce that

$$\begin{aligned} \int _M|A_{\infty }|^2=0. \end{aligned}$$

Consequently, $M_{\infty }$ must be a totally geodesic graphical surface.