“I find the whole oscillation most mysterious.”—The closing words of a 60-page mathematical analysis of the Hudson Bay Company’s hare and lynx fur data by Egbert R. Leigh, Jr. in 1968.

1 Introduction

The Hudson Bay Company’s fur trade data (Hewitt 1921; MacLulich 1937; Elton and Nicholson 1942; Leigh 1968; Odum and Barrett 1971) for the Canadian lynx and snowshoe hares is the oldest, the longest, and the most well-known data set in ecology. It has been extremely controversial and remains enigmatic to this day. Every book on introductory ecology must pay tribute to it, most (e.g. May 1973) would cite it as an example to support the classical predator–prey theory by Lotka (1925) and Volterra (1926), but only a few (e.g. Britton 2003) would point it out correctly that it does not. Unlike the classical theory which predicts the peak density of the predator to follow that of the prey, the peak volume of the hare pelt on average follows that of the lynx for some of the years. This paradox was discovered by Leigh (1968) and made widely known by Gilpin with an article titled ‘Do hares eat lynx?’ (Gilpin 1973). The net phase difference is more than 2 years with the lynx pelt data phase-advanced by 1 year on average from the hare pelt (Leigh 1968; Gilpin 1973; Bulmer 1974) but the field lynx population phase-lagged by 1 year from the field hare population (Keith 1963; O’Donoghue et al. 1998; Stenseth et al. 1998; Huffaker 1958) with maturation delay of the lynx being the main cause. Data aggregation cannot be the problem because pelts from different boreal regions of Canada were shown to be spatially synchronized in time (Blasius et al. 1999). Could some odd trading practice by the trappers, or the bookkeeping practice by the Hudson Bay Company, or both shift the lynx phase by 2 years? This is highly unlikely for two reasons: statistical averaging over large data set usually erase peculiarities and the absence of evidence for idiosyncratic practices by the company is probably the absence of such systematic practices. The phase divergence in opposite directions is so ‘mysterious’ (Leigh 1968) that it prompted a recent statistical study (Zhang et al. 2007) to suggest that the pelt data is the result of ‘intrinsic self-regulation’ of both hare and lynx (Fig. 1).

Fig. 1
figure 1

Pelt data. Hudson Bay Company’s hare and lynx pelt data from Leigh (1968) and Odum and Barrett (1971). There is insignificant difference for the hare pelt between the two sets. But for the period of 1875–1903, one of the two for the lynx pelt seems out of place. The lows of the Odum data in those years seem much higher than those from the period before and the period after. Also, unlike a rather sharp drop after reaching it maximum in other years, the high return around 1876 lingered, as if the trappers hesitated to go for the maximum return. If the Odum data is the benchmark, then Leigh under-counted the lynx pelt for many years of the period rather than shifted the time series backward

Full size image

Biologists never stopped trying to explain away the hares-eat-lynx (HEL) paradox (Finerty 1979; Weinstein 1977; Winterhalder 1980; Royama 1992; Krebs et al. 2001; Vik et al. 2008). Royama (1992, p. 233) went for an easy solution that Leigh (1968) made a booking error by shifting his lynx data 1-year out of phase. There were various data segments in the literature from Hewitt (1921), to MacLulich (1937), Elton and Nicholson (1942), leading to the longest compilation appeared in Odum and Barrett (1971) (referred to as the Odum Data for simplicity in this paper). By comparing Leigh’s tabulation to Odum’s it seems Royama’s explanation is a good one. However, upon further examination on his suggested corrections, the paradox persists even if Leigh’s lynx data is shifted out of phase. Specifically, unless Leigh shifted his data by at least 2 years, Royama’s suggested fix would only put the lynx data in synchrony with the hare data, turning Gilpin’s old quip into a new muse ‘Does lynx turn vegan?’, see Fig. 2. That is, if Leigh made a tabulation error by a 1-year shift, the paradox would not simply disappear. Furthermore, when Odum’s data is plotted for the same period of 1875–1903 as Guilpin did, the lynx was still not doing the job of eating the hares.

Fig. 2
figure 2

Did Leigh Err? Top Left: Leigh’s tabulation for the period of 1875–1903. The plots between the top left and the bottom right show some possible tabulation errors suggested by Royama. Backing the lynx data by 1 year (i.e. changing 1876’s return to 1875’s return, and so on) would only deepen the paradox. Advancing it 1 year would make the lynx an herbivore. Only by forwarding it 3 years would the data fit the classical theory perfectly. Bottom Right: Odum’s data for the same 1875–1903 period which makes the lynx an herbivore by the classical theory. Especially, the local loop near the top-right corner is of the HEL kind, of left-handed orientation. Squares mark the start of the orbits

Full size image

Although trappers were suspected to play a role for the HEL paradox (Finerty 1979; Weinstein 1977; Winterhalder 1980), all statistical and mathematical studies in the literature (e.g. Bulmer 1974; Schaffer 1984; Stenseth et al. 1997, 1998; Blasius et al. 1999; Gamarra and Solé 2000; King and Schaffer 2001; Stone and He 2007; Zhang et al. 2007; Vik et al. 2008) have made an inexplicable assumption that the pelt numbers is a proportional proxy of the populations in the wild, effectively rendering the trapper’s role nonessential. Figure 2 of Stenseth et al. (1998) was cited as an empirical basis for this assumption but the opposite can be equally inferred. Even at the conceptual level this proxy assumption is incredibly simplistic for obvious reasons. Just to name a few: trappers were not naturalists but resource exploiters who were economically vested in if not entirely depended on the animals for survival—taking out the animals in large quantity irreplaceably for food and trade; and like a natural predator they adjusted their tactics in pursuit of their preys (Finerty 1979; Weinstein 1977; Winterhalder 1980). These facts alone suggest that the trappers were too deeply embedded in the system to be excluded from any mathematical model aimed at explaining their catch data or the hare-lynx interaction in the wild that the data implies. After all, the pelt data should be more about the trapping business than about the hare-lynx system in the field. In the field, the prey drives the predator. As of trapping, the lynx pelt drives the hare pelt because lynx fur is economically more valuable. In both cases, whichever is the driver leads the cycle. This is exactly what we will demonstrate in this paper. Namely, if the trappers preferred the lynx fur then the pelt cycle must be the HEL kind and if the preference is reversed then the pelt cycle is the classical kind.

Before we do that in a comprehensive way we first consider as a motivation a toy model in three trophics, prey x, predator y, and intraguild top-predator z:

$$\begin{aligned}&\displaystyle {\frac{dx}{dt}=x\left( b - mx - \frac{a_1y}{1+h_1a_1x} - {u_1z}\right) }\nonumber \\&\displaystyle {\frac{dy}{dt}=y\left( \frac{b_1a_1x}{1+h_1a_1x} - d_1 - m_1y - {u_2z}\right) }\nonumber \\&\displaystyle {\frac{dz}{dt}=z\left( {r_1u_1x+r_2u_2y} - d_3 \right) .} \end{aligned}$$
(1)

It is a simple intraguild predator–prey model for which the top-predator is only of the Holling Type I. Figure 3 shows for two different parameter sets the catch cycle of the top-predator for which one parameter set is what we think should be but the other cycle is of the HEL kind. The former is because the per-predator per-prey catch rate of the prey by the top-predator is higher than that of the predator (\(u_1\gg u_2\)) and the latter is because of the opposite (\(u_2\gg u_1\)). These theoretical possibilities together with the supposition that trappers valued the lynx pelt more than the hare pelt imply the HEL phenomenon. If ecologists had known this, would they have tried to make the HEL paradox to go away? It is very likely that Leigh has been right all along. His version of the Hudson Bay Company’s data is qualitatively good according to such trapper-included models. It would be questionable if the data did not show the HEL effect for any of the years.

Fig. 3
figure 3

Trappers preference determines catch cycle chirality. Top panel: Equation (1) with \(u_1=0.1,u_2=1,r_1=0.01,r_2=0.1\), the top-predator applies a greater predatorial pressure on the predator (\(u_2\gg u_1\)). The killed prey and predator orbit (in \(u_1xz\) v.s. \(u_2yz\) labelled as Catch) cycles clockwise, i.e. the paradoxical prey-eats-predator direction. Circles mark the initial points of the orbits. Bottom panel: With \(u_1=1,u_2=0.01,r_1=0.1,r_2=0.1\), the top-predator applies a greater predatorial pressure on the prey (\(u_1\gg u_2\)). The killed prey and predator orbit cycles counterclockwise, the same as the population orbit. The other parameter values are the same for both cases, \(b=1,m=1,a_1=0.5,h_1=10,b_1=0.8,d_1=0.01,m_1=0.01,d_3=0.0015\)

Full size image

Because of the HEL paradox the failure of the classical Lotka–Volterra theory for the hare-lynx system was spectacular. It constantly reminded us how little we knew about population cycles in nature. Leigh’s work (1968) was the first and the only but unsuccessful attempt to fit a population model to the fur data in the past. The HEL legacy he left behind was long lasting. It led to questions about the place of mathematical models in ecology (Hutchinson 1975; Hall 1988). (Statistical analysis is not considered strictly as mathematical modeling here but rather an extension of observation or a tool of observation by experimentalists.) The HEL problem has raised some basic questions. For example, can a piece of mathematics be called a mathematical model without ever being best-fitted to an empirical data? How to objectively select them from seemingly innumerable and often arbitrary choices? And what is knowable and what is not when a model of high dimensions is fitted to a low dimensional data set?

In this paper we will consider several models for the Canadian hare-lynx problem. We will make the following distinctions. First, arbitrary equations or functions will not be considered as model candidates for the data. This is the implied premise upon which any inverse problem is based for any scientific problem. For example, time-dependent polynomials of arbitrary degrees will not be considered despite they can fit any data perfectly since the coefficients of such polynomials almost always do not have meanings for the physical processes to be modeled. Likewise, the celestial mechanics model for the N-body problem will not be considered either for ecological problems because of its lack of mechanistic link to the latter even though it may fit better to the hare-lynx data than some of the ecological models do. In other words, the concept of a model is restricted only to those mathematical equations and functionals which either have some mechanistic justifications or are well accepted for the intended physical processes. A model without being best-fitted to a data is referred to as a conceptual model. A conceptual model that is best-fitted to a data is referred to as a provisional model. A provisional model that is the best amongst all provisional models is referred to as the benchmark model.

To best fit a model to a data is to have the least error between the predicted by the model and the observed from the data. To determine system parameter values for the least error is to solve the so-called inverse problem in mathematics, and the most effective method to solve inverse problems is by Newton’s gradient search method for which the most effective implementation is the line search method (Rohner 1996; Ruszczynski 2006). The model selection protocol outlined above is referred to as benchmarking. All provisional models in this paper are determined by the line search method. We will demonstrate that all models without the trappers do not exhibit the HEL effect but all models with the trappers do, and of all the models with or without the trappers, the hare-lynx-competitor-trapper (HLCT) model has the least error, hence is qualified to be the benchmark model.

When a model fits a data well, it used to raise and still does this suspicion that it is a case of ‘over-fit’ because the model contains too many parameters or too many variables. The concern about ‘over-fit’ and the issue about polynomial pseudo models used to and still spread like an urban legend in the inverse problem community. In our opinion, any so-called ‘over-fit’ is always a bad fit if arbitrary functionals are used as it must not be allowed. Within the class of mechanistic models, ‘over-fit’ is a non-issue. As shown by our result, no matter how many different trophic levels, or how many species, or how many parameters a population model contains, as long as the trappers are not included in the model or the trapping rates are not used as the fit functionals, the best-fit time series will always result in the classical LEH oscillation rather than the paradoxical HEL oscillation and therefore produce a worse fit than our HLCT model does. In other words, having more variables or parameters does not always lead to a better fit. What does matter is to find the minimalistic, regardless of size, but mechanistic models to fit the data. Any model simpler than minimalistic but worse in fit is simplistic. Any model larger than minimalistic but worse in fit is unnecessarily complex.

We will introduce for the first time to our best knowledge a sensitivity analysis of the best fit to show expectedly that the trappers valued the lynx pelt more than the hare pelt, and to show unexpectedly that they did not interfere in each other’s trapping activities. We will also introduce for the first time an uncertainty analysis of fitting high dimensional models to low dimensional data to show that despite the dimensional deficiency some system parameters can be uniquely determined by the best fit.

2 Method

In this paper we will first introduce various conceptual models in differential equations with as much mechanistic justifications as possible. We will then use Newton’s gradient search method and an effective implementation—the line search method—to best fit each conceptual model to the lynx-hare data from Leigh (1968) and Gilpin (1973). It is by the benchmark model that our observations and conclusions about the Canadian hare-lynx system will be derived.

2.1 Models

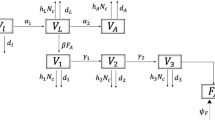
For variable notations we will denote by t the time in year with \(t=0\) corresponding to 1875, the first data year of Leigh (1968) and Gilpin (1973). We will use H(t), L(t) for the head counts of hare and lynx in the wild at time t that we often breviate to H, L, suppressing the time variable. According to Stenseth et al. (1997), lynx is just one of many predators of the hare, including wolf, wolverine, red fox, great horned owl, hark owl, and other avian predators (Rohner 1996; Stenseth et al. 1997). Although coyote is also a predator of the hare but it was a recent immigrant to the region post the Hudsons Bay Companys data (O’Donoghue et al. 1998). Hence variable \(C=C(t)\) is used as a proxy for the combined predatory effect by all predators other than the lynx. Instead of a natural number it is simply a nonnegative real number used as an aggregated index to measure this alternative predatory effect on the hare and the competing effect against the lynx. Similarly, variable \(T=T(t)\) is used as an index for the trappers, a proxy for the trapping effect on the hare and the lynx rather than the head count or family count or tribe count of the trappers. We note that just because there was no concurrent data available for the other predators nor for the trappers does not mean they had no impacted on the hare-lynx dynamics or they should not be included in a model. We take up the assumption that these four state variables are the minimal prerequisites for any model intended to explain the Hudson Bay Company’s data. The variable and parameter definitions together with their units are listed in Table 1. The theoretical model is given as follows:

$$\begin{aligned}&\displaystyle {\frac{d{H}}{dt}=H\left( b - mH - \frac{a_1L}{1+h_1a_1H} - \frac{a_2C}{1+h_2a_2H} - \frac{u_1T}{1+v_1u_1H+v_2u_2L}\right) }\nonumber \\&\displaystyle {\frac{d{L}}{dt}=L\left( \frac{b_1a_1H}{1+h_1a_1H} - d_1 - m_1L - \frac{u_2T}{1+v_1u_1H+v_2u_2L}\right) }\nonumber \\&\displaystyle {\frac{d{C}}{dt}=C\left( \frac{b_2a_2H}{1+h_2a_2H} - d_2 - m_2C\right) }\nonumber \\&\displaystyle {\frac{d{T}}{dt}=T\left( \frac{r_1u_1H+r_2u_2L}{1+v_1u_1H+v_2u_2L} - d_3 - m_3T\right) .} \end{aligned}$$
(2)

Explanation for the model is as follows. Without the predators and trappers (\(L=C=T=0\)), the hare population is modeled as a logistic growth with the intrinsic growth rate b and the intraspecific competition coefficient m (which can be justified by the field study of Krebs et al. 1995). We will use Holling’s Type II functional form (Holling 1959) for the predation rate of the lynx on the hare with the encounter rate \(a_1\) and the handling time \(h_1\). Parameter \(b_1\) is the consumption-to-birth ratio (biomass conversion coefficient) of the lynx and parameters \(d_1,m_1\) are its natural death rate and intraspecific competition rate respectively. Similar parameters notations, \(a_2,h_2,b_2,d_2,m_2\), apply to the C-equation.

Table 1 Model variables and parameters
Full size table

Like the predators, the trapping rates (the pelt harvest rates) of the hare and the lynx per unit index of the trapper are the joint Holling Type II functional forms (Murdoch 1973; Lawton et al. 1974), \(\frac{u_1H}{1+v_1u_1H+v_2u_2L},\frac{u_2L}{1+v_1u_1H+v_2u_2L}\), with the encounter rates \(u_1, u_2\) and the handling times \(v_1,v_2\) of the hare and lynx, respectively. However, unlike for the predator equations, parameters \(r_1,r_2\) for the trapper’s equation are the intrinsic pelt-to-recruit ratios, \(d_3\) is the trapper’s quit rate, and \(m_3\) is the trapper’s intraspecific competition rate. That is, the system of equations models not only the ecological interactions of the hare, lynx, and other predators, but also the economical interactions of the trappers with the natural system. The trapper equation is the same as those for the predators in form but the interpretations for its parameters are economical rather than ecological.

The continuous model Eq. (2) is referred to as the hare-lynx-competitor-trapper (HLCT) model. We will also consider the following models which it contains: the hare-lynx-trapper (HLT) model with \(C\equiv 0\) for the HLCT equation; the hare-lynx-competitor (HLC) model with \(T\equiv 0\); and the HLCT1 model which has the same equation (2) except that the trapping rates are of Holling’s Type I forms with the zero handling times \(v_1=v_2=0\). For comparison purpose we will also consider the vegetation-hare-lynx (VHL) model used in Blasius et al. (1999), King and Schaffer (2001) and Stone and He (2007).

2.2 Gradient Search and Line Search for Least Error

Empirical data for a physical process P is a collection of time and real numbers, denoted in general by

$$\begin{aligned} (t_{ij},y_{ij}), \qquad i=1,2,\dots ,k_j,\ j=1,2,\dots ,\ell \end{aligned}$$

Here the second subindex j is for different type of data, say \(j=1\) for the population of a prey and \(j=2\) for the population of a predator. We will refer to it as the jth data type for a total of \(\ell\) many types. Each data type is collected at the same or different data acquisition times but we will assume without loss of generality that \(t_{ij}\) is increasing in i and the earliest collecting time is set to 0, i.e. \(t_{(i+1)j}> t_{ij}\ge 0\).

In this paper we will only consider differential equations as mathematical models for the process,

$$\begin{aligned}&\displaystyle {\frac{dx}{dt}=F(x,p)}\nonumber \\&\displaystyle {x(0)=x_0} \end{aligned}$$
(3)

where t has the same time dimensional unit as \(t_{ij}\), p the model parameters, \(x(t)=(x_1,x_2,\dots ,x_n)(t)\) is the state variables of the model at time t. For each j, we consider a fit functional, \(f_j(t_{ij},p,x_0)\), to the jth data type \((y_{1j},y_{2j},\dots y_{k_jj})\), and consider the weighted Euclidean error between the predicted and the observed:

$$\begin{aligned} E_{(F,f)}(p,x_0)=\sqrt{\sum _{j=1}^\ell \sum _{i=1}^{k_j}w_{ij}^2 |f_j(t_{ij},p,x_0)-y_{ij}|^2} \end{aligned}$$

where the weight parameter \(w_{ij}\) has the reciprocal unit of \(y_{ij}\) to scale each term dimensionless. For example, we can use \(w_{ij}\equiv 1/\max _{1\le i\le k_j}\{|y_{ij}|\}\) assuming not all \(y_{ij}=0\) in i, or analogous to the \(\chi\)-square test we can use \(w_{ij}=1/|y_{ij}|\) assuming all \(y_{ij}\ne 0\). The usage of dimensional weights is essential when the best fit is sought for multiple data types for which the error, \(E_{(F,f)}(p,x_0)\), has to be dimensional free for consistency. We also note that the state variable x(t) may or may not coincide in part or whole with the data type y. That is, \(f_j\), for any \(1\le j\le \ell\), may or may not have the same dimensional unit as \(x_k\) for any \(1\le k\le n\).

By definition, the best fit of the model F to the data has the least error

$$\begin{aligned} \varepsilon (F,f)=\min _{(p,x_0)}E_{(F,f)}(p,x_0)=E_{(F,f)}(p^*,x_0^*) \end{aligned}$$

at some \((p^*,x_0^*)\), referred to as the global minimizer, among all choices of the initial conditions \(x_0\) and parameter values p. Therefore, by definition, a model F is a benchmark model if

$$\begin{aligned} \varepsilon (F,f)\le \varepsilon (G,g) \end{aligned}$$

holds for all provisional models G (with the same fit weights \(w_{ij}\)). A benchmark model is only temporary as it can be replaced by new and better provisional models. We note that it is often the case that we cannot prove a minimizer we found by a particular method is indeed the global minimizer but instead the best local minimizer with respect to the search method, and hence is referred to as a provisional global minimum. Thus, the provision and benchmark designation for models in this paper is contingent upon the search method we used.

Finding local minima of the error function \(E(p,x_0)\) is the same as finding local minima of the error function squared \(E^2(p,x_0)\). The search is done in the parameter and initial state space \((p,x_0)\), often along a fastest descending path. The methods we will use are all based on Newton’s gradient search method. That is, we seek to determine a path in the parameter and initial state space, \((p,x_0)(s)\), so that it follows the negative gradient of \(E^2(p(s),x_0(s))\) in search of a local minimum of the squared error:

$$\begin{aligned}&\displaystyle {\frac{\partial (p,x_0)}{\partial s} =-\nabla E^2(p,x_0)}=\displaystyle { -2\sum _{j=1}^\ell \sum _{i=1}^{k_j}w_{ij}^2[f_j(t_{ij},p,x_0)-y_{ij}]D_{(p,x_0)}(f_j(t_{ij},p,x_0))}\\&(p(0),x_0(0))=(p_0,x_{0,0}) \end{aligned}$$

where \(D_zf(z)\) denotes the derivative of function f with respect to its variable z, and \((p_0,x_{0,0})\) denotes the initial search point. A local minimizer is found if the path converges

$$\begin{aligned} (p^*,x_0^*)=\lim _{s\rightarrow \infty }(p(s),x_0(s)) \end{aligned}$$

and a local minimum is declared numerically after a sufficiently large number s. We note that at each search point, \(x(t,x_0(s),p(s))\) is a solution to the model differential equations Eq. (3). Thus, as a function of (t, s), \(x(t,x_0(s),p(s))\) in fact is the solution to a partial differential equation induced from the gradient search for which more details are given in the “Appendix”.

It is known that if the squared error has non-unique local extrema, a gradient search may not yield the global minimizer. In fact, finding the global minimizer is still an active research in the area of scientific computations. Another drawback for the gradient search method is that it can be time consuming in solving the resulting PDEs. A practical approach to both speeding up the search and to finding a better minimizer, which we will also adopt, is the line search method. Without loss of generality, we assume all the parameters and the initial states are non-negative. The line search method we will use in this paper works as follows.

For every initial guess \((p_0,x_{0,0})\), we consider a hypercube centered at the initial guess with \(0<p<2p_0,0<x_0<2x_{0,0}\), componentwise. We will then partition each interval into a fixed even number, say 2N, of subintervals of equal length, with N discrete partitioning points to each side of the center. We will then search for a smaller error \(E(p,x_0)\) along this and each coordinate line through the center \((p_0,x_{0,0})\) at these discrete points. For example, for the first parameter \(p_1\) there are \(2N+1\) discrete partitioning points \(q_i\) with \(q_0=0\), \(q_N=p_{1,0}\) the initial guess, and \(q_{2N}=2p_{1,0}\) the end of the line search segment for the parameter \(p_1\). With all other parameters and initial states fixed at the initial guess value \((p_0,x_{0,0})\), we compute \(E(p,x_0)\) with \(p_i=p_{i,0},i\ne 1, x_0=x_{0,0}\) but \(p_1=q_k\) for all \(k=0,1,2,\dots 2N\). This generates \(2N+1\) many values for \(E(p,x_0)\). Do the same for all other parameters and initial states to generate a total of \((2N+1)\times [{\text{number\ of\ parameters\ and\ initial\ states}}]\). Of which we select the smallest value of \(E(p,x_0)\) and thus the next new initial guess \((p_0,x_{0,0})\). We repeat this process until either the successive errors are within certain stoppage tolerance or if it runs out a predetermined number of iterations. The output of this line search is our provisional global minimizer \((p^*,x^*_0)\).

One can also run a gradient search after the line search just to increase the accuracy of such provisional minimizer, which we did use. Notice that if we know the error function \(E(p,x_0)\) has all local minima inside a bounded region, then both the gradient search and the line search must converge to a local minimizer. In fact, all searches carried out for this paper converged, and it is in this sense each best fitted model is the provisional model for the Canadian hare-lynx system.

2.3 Best-Fit Sensitivity

Suppose a provisional global minimizer \((p^*,x_0^*)\) has been found for the error function \(E(p,x_0)\), a next question is how sensitive does the error depend on changes in the parameters and initial states? This question can be formulated by the Taylor expansion of the error function. To be more specific, we first assume without loss of generality that the minimizer occurs in the interior of the parameter and initial state space \((p,x_0)>0\) componentwise. The justification is as follows. If the minimizer occurs on a boundary with one of the parameters \(p_i=0\), then that parameter can be effectively dropped from the model and we can restrict the model only to those system parameters whose minimizer components are strictly greater than zero. Similarly if the minimizer occurs on a boundary with one of the initial states \(x_j=0\), then the state of the model will stay invariant with the \(x_j\)-population zero for all future time, and hence it can be dropped from the model to consider only a smaller system of equations. Hence, sensitivity of the best fit is referred in this paper to only those effective parameters and initial states for which the minimizer occurs in their interiors of definition. As a result, the first partial derivatives of the error function E at the minimizer are all zeros.

We now define the sensitivity of the best fit. As an example, consider the case of the first parameter \(p_1\) and expand E at the minimizer

$$\begin{aligned} E(p,x_0)=E(p^*,x_0^*)+\displaystyle {\frac{1}{2}\frac{\partial ^2E}{\partial p_1^{\ 2}}(p^*,x_0^*)(p_1-p_1^*)^2}+\cdots , \end{aligned}$$

where the dots represents the expanding terms for the other parameters and initial states. Because \(p_1^*>0\) we can rewrite it as follows making the squared change dimensionless

$$\begin{aligned} E(p,x_0)=E(p^*,x_0^*)+\displaystyle {\frac{(p_1^*)^2}{2}\frac{\partial ^2E}{\partial p_1^{\ 2}}(p^*,x_0^*)\frac{(p_1-p_1^*)^2}{(p_1^*)^2}}+\cdots , \end{aligned}$$

By definition, the coefficient of the squared percentage change \(\frac{(p_1-p_1^*)^2}{(p_1^*)^2}\) is the sensitivity of the error with respect to the \(p_1\) parameter:

$$\begin{aligned} S_{p_1}:=\displaystyle {\frac{(p_1^*)^2}{2}\frac{\partial ^2E}{\partial p_1^{\ 2}}(p^*,x_0^*)} \end{aligned}$$
(4)

Similar definition applies to other parameters and initial states, denoted by \(S_{p_i}\) and \(S_{x_{j,0}}\) respectively. Note that all sensitivities are greater than or equal to zero because E is an interior local minimum at the point \((p^*,x_0^*)\).

It is important to note that the sensitivity can be used to compare deviations of the error from the best fit with changes of all parameters and initial states. For example, for the same squared relative changes in parameter \(p_1\) and \(p_2\) with \(\frac{(p_1-p_1^*)^2}{(p_1^*)^2}=\frac{(p_2-p_2^*)^2}{(p_2^*)^2}\), the inequality \(S_{p_1}>S_{p_2}\) implies that the error function \(E(p,x_0)\) is greater than its minimum \(E(p^*,x_0^*)\) along the \(p_1\) axis than along the \(p_2\) axis. In this sense we can say the best fit of the model to the data is more sensitive to the parameter \(p_1\) than to the parameter \(p_2\). Similar pair-wise comparison applies to all parameters and initial states. We also note that the S-sensitivity can be easily approximated from the line search method when at least three discrete points are used for each of the search range \([0,2(p^*,x_0^*)]\) componentwise, enough for a discrete approximation of that component’s second order partial derivative of the error function.

2.4 Dimensional Analysis: Best-Fit Uncertainty and Sensitivity Certainty

It is often the case that due to practical limitations, empirical data are collected in fewer independent dimensions than the dimensions of the physical system. The Canadian lynx-hare system is such an example for which the pelt data in lynx and hare are available but in reality the foodweb to which these two species are embedded has far more independently state variables from vegetation to competing herbivores and carnivores and to trappers. Intuitively, there ought to be some degree of freedom allowed for the best-fitted parameter values of any provisional model. The questions are which parameters can be uniquely determined and which parameters cannot, and for the latter what is the degree of uncertainty, and will such uncertainty affect the best-fit sensitivity \(S_{p,x_0}\)? These questions can be answered by the following theorem of dimensional analysis whose proof is a straightforward application of the Buckingham’s \(\pi\) Theorem (e.g. Logan 1996).

Theorem

Consider an \(\ell\)-dimensional data set

$$\begin{aligned} (t_{ij},y_{ij})\ \ \hbox{for}\ \ i=1,2,\dots ,k_j,\ j=1,2,\dots ,\ell , \end{aligned}$$

an n -dimensional differential equation model \(x'=F(x,p)\) with \(x\in {\mathbb {R}}^n\), \(p\in {\mathbb {R}}^m\), \(n\ge \ell\), and scalar fit functionals \(f_j(t_{ij},p,x_0)\). Assume the differential equations and the errors of fit, \(f_j(t_{ij},p,x_0)-y_{ij}\), are unit-free. Then there exist scalings \(\tau (p), K_i(p),q_j=g_j(p)\), and \(s_j(p)\) so that the model and the weighted squared error

$$\begin{aligned} E^2(p,x_0)={\sum _{j=1}^\ell \sum _{i=1}^{k_j}w_{ij}^2(f_j(t_{ij},p,x_0),p)-y_{ij})^2} \end{aligned}$$

are transformed to a dimensionless model \({\bar{x}}'=G({\bar{x}},q)\) and its corresponding squared error

$$\begin{aligned} E^2(q,{\bar{x}}_0,s,\tau )={\sum _{j=1}^\ell \sum _{i=1}^{k_j}w_{ij}^2(s_j{\bar{f}}_j( t_{ij}\tau ,\bar{x}_0,q)-y_{ij})^2} \end{aligned}$$

with \({\bar{f}}_j\) being dimensionless but \(s_j\) having the same dimensional unit as \(y_{ij}\), \({\bar{t}}=t\tau (p)\), \({\bar{x}}({\bar{t}}) = x({\bar{t}}/\tau (p))/K_i(p)\), \(q=g(p)\in {\mathbb {R}}^{[m-n-1]_+}\), where \([m-n-1]_+\) is zero if \(m-n-1\le 0\) and \(m-n-1\) otherwise.

We note that all physical systems are unit-free, namely equivalent under dimensional unit conversions, and hence the theorem should applies to mechanistic conceptual models. The degree of freedom for the best fit is explained as follows. Notice that when \(m-n-1\ge 0\), a best fit by the dimensionless model to the data in the scaled \((m-n-1)+n+\ell +1=m+\ell\) many quantities \((q,\bar{x}_0,s,\tau )\) corresponds to an \((n-\ell )\)-dimensional manifold of the same error value in the \(m+n\) dimensional parameter and initial condition space in \((p,x_0)\). That is, \(n-\ell\), which is the difference between the dimensional dimension \(m+n\) and the scaled, dimensionless dimension \(m+\ell\), is the degree of freedom for the best fit of the model to the dimensional data. In other words, if \(n>\ell\), we must expect infinitely many choices in the dimensional parameters to give the same best error fit. For particular model, the question is to determine which parameters can be uniquely determined for the best fit and which parameters cannot because of the inherent freedom for the fit.

We also note that for unit-free models the best fit sensitivity \(S_{p,x_0}\) is independent of the best fit uncertainty. This can be easily proved by the same argument for the Buckingham’s \(\pi\) Theorem. More specifically, the relationship between the dimensional and the dimensionless parameters and variables are algebraic, and the dependence of the uncertain parameters and initial states on the free parameters and initial states is also algebraic. As a result the free parameters and initial states are canceled out in the sensitivity values with respect to all the uncertain parameters and initial states. That is, even though the global minimizers in the parameters and initial states are not unique, their sensitivities are.

2.5 Chirality: HEL Versus LEH Orientation

When the time-dependent populations or pelts of hare and lynx are plotted in the HL-plane, the trajectory may proceed in a general counterclockwise direction, i.e. the lynx-eats-hare (LEH) orientation, or respectively in a general clockwise direction, i.e. the HEL orientation. Describing it differently the LEH chase is also right-handed, or right chiral, and the HEL chase is left-handed, or left chiral. Chirality is a quantity designed for the handedness of the orientation. In particular, a positive chirality is for a right-handed LEH chase and a negative chirality is for a left-handed HEL chase. Here is how the chirality of the hare-lynx trajectory is defined.

Let \(t_i,i=0,1,2,\dots ,n\), be an increasing sequence in time, and \(H_i,L_i\) be the population for the hare and lynx respectively at the time \(t_i\). To define their chirality, let \(\vec v_i=(H_i-H_{i-1},L_i-L_{i-1})\) be the direction or secant vector from point \((H_{i-1},L_{i-1})\) on the projected HL-plane to point \((H_i,L_i)\). Now with respect to the direction \(\vec v_i\) the next movement by the projected HL-trajectory takes place in the direction of \(\vec v_{i+1}\), which can either right-handedly (counterclockwise) rotate up or left-handedly (clockwise) rotate down, or neither. The chirality, \(c_i\), at the time \(t_i\), is defined to be the coefficient of the curl vector from \(\vec v_i\) to \(\vec v_{i+1}\). More specifically, if \(\vec a=(a_1,a_2)\) and \(\vec b=(b_1,b_2)\), then the curl of \(\vec a\) to \(\vec b\) is \({\mathbf{curl}}(\vec a,\vec b):=(a_1b_2-a_2b_1){\mathbf{k}}\) with \({\mathbf{k}}=(0,0,1)\) the standard vector base for the z-axis, and the sign of the curl coefficient, \(a_1b_2-a_2b_1={\mathbf{curl}}(\vec a,\vec b)\cdot {\mathbf{k}}\), tells whether the orientation from \(\vec a\) to \(\vec b\) is right chiral (\({\mathbf{curl}}(\vec a,\vec b)\cdot {\mathbf{k}}>0\)) or left chiral (\({\mathbf{curl}}(\vec a,\vec b)\cdot {\mathbf{k}}<0\)). That is, we define the local or point chirality of the HL-trajectory at time \(t_i\) to be

$$\begin{aligned} c_i={\mathbf{curl}}(\vec v_i,\vec v_{i+1})\cdot {\mathbf{k}},\ \ \hbox{for}\ \ i=1,2,\dots ,n. \end{aligned}$$

The chirality for the trajectory is defined to be the time-averaged point chirality:

$$\begin{aligned} {\bar{c}}(H,L)=\frac{1}{t_n-t_0}\sum _{i=1}^nc_i\Delta t_i \end{aligned}$$

with \(\Delta t_i=t_i-t_{i-1}\). Note that this definition applies to sequences from numerical simulations as well as to the pelt data. It is in this sense that we say the HL-trajectory or data is right chiral if \({\bar{c}}(H,L)>0\) or left chiral if \({\bar{c}}(H,L)<0\) for the rest of the paper.

3 Result

We now apply the method outlined above to the HLCT conceptual model Eq. (2) and its various subsystems for comparison purposes. We will use both data sets by Leigh and Odum. Specifically, we fit the models to the period from 1875 to 1903 considered by Gilpin and others because of its peculiarity and use the best-fits to fit the longer period data from 1847 to 1903, which is the entire time duration for the Leigh data. The goal is to find the benchmark model and its practical implications.

Now denote the truncated data by \(H_{T,i},L_{T,i}\), the pelt for hare and lynx respectively in the ith year, with \(t_i=i,i=0,1,2,\dots ,28\), since the year of 1875. Since they are tallied annually we can take them as the annual catch rates by the trappers. As a result we will use the trapper’s catch rates for the fit functionals:

$$\begin{aligned}&\displaystyle { H_T(t_i):=f_H(t_i,x_0,p)=\frac{u_1H(t_i,x_0,p)T(t_i,x_0,p)}{1+v_1u_1H(t_i,x_0,p)+v_2u_2L(t_i,x_0,p)}}\\&\displaystyle { L_T(t_i):=f_L(t_i,x_0,p)=\frac{u_2L(t_i,x_0,p)T(t_i,x_0,p)}{1+v_1u_1H(t_i,x_0,p)+v_2u_2L(t_i,x_0,p)}}\\ \end{aligned}$$

and the corresponding squared error:

$$\begin{aligned} \displaystyle {E^2(p,x_0)=\sum _{i=0}^{28}\left[ \left( \frac{f_H(t_i,x_0,p)-H_{T,i}}{H_{T}^*}\right) ^2 +\left( \frac{f_L(t_i,x_0,p)-L_{T,i}}{L_{T}^*}\right) ^2\right] } \end{aligned}$$

for which \(t_{i1}=t_{i2}=t_i=i, w_{i1}=1/H_T^*,w_{i2}=1/L_T^*, i=0,1,2,\dots ,28\) and

$$\begin{aligned} x_0=(H_0,L_0,C_0,T_0),\ \displaystyle {H_T^*=\max \{H_{T,i}\},\ L_T^*=\max \{L_{T,i}\}}. \end{aligned}$$

By the dimensional analysis theorem above we know for the HLCT model it has a degree-2 uncertainty for the best fit. To determine those uncertain parameters and initial states we transform the dimensional model Eq. (2) into a dimensionless model with a change of parameters and states. More specifically, the transformation and the inverse transformation are given in Table 2. For example, the entries from the Scaled Parameters column are defined by the last Scaling column which defines the transformation from the dimensional parameters to the dimensionless ones, such as \(\eta _1=h_1a_1K_H\) with \(K_H=b/m\). Similarly, the third column defines the inverse transformation from the dimensionless parameters to the dimensional ones in the first column, such as \(h_1=\eta _1K_L/(\tau K_H)\) with \(K_H=s_1/(\alpha _1\tau ),K_L=s_2/(\tau \beta _1)\). The dimensionless variables and dimensionless time are \({\bar{H}}=H/K_H,{\bar{L}}=L/K_L,\bar{C}=C/K_C,{\bar{T}}=T/K_T,{\bar{t}}=t\tau\). To simplify notations we drop the bars for the new variables and time and obtain the following dimensionless model for Eq. (2):

$$\begin{aligned}&\displaystyle {\frac{d{H}}{dt}=H\left( 1 - H - \frac{L}{1 + \eta _1H}-\frac{C}{1 + \eta _2H} - \frac{\alpha _1T}{1 + \tau _1H + \tau _2L}\right) }\nonumber \\&\displaystyle {\frac{d{L}}{dt}=\beta _1L\left( \frac{H}{1 + \eta _1H} -\delta _1 - \mu _1L -\frac{T}{1 + \tau _1H +\tau _2L}\right) }\nonumber \\&\displaystyle {\frac{d{C}}{dt}=\beta _2C\left( \frac{H}{1 + \eta _2H} - \delta _2 - \mu _2C\right) }\nonumber \\&\displaystyle {\frac{d{T}}{dt}=\rho T\left( \frac{\gamma _1H+ L}{1 + \tau _1H + \tau _2L} - \delta _3 - \mu _3T\right) } \end{aligned}$$
(5)

together with the fit functionals and the squared error

$$\begin{aligned}& {{\bar{f}}_H({\bar{t}}_i,{\bar{x}}_0,q)=\frac{H({\bar{t}}_i,{\bar{x}}_0,q)T({\bar{t}}_i,{\bar{x}}_0,q)}{1 + \tau _1H({\bar{t}}_i,{\bar{x}}_0,q) + \tau _2L({\bar{t}}_i,{\bar{x}}_0,q)}}\\ & {{\bar{f}}_L({\bar{t}}_i,{\bar{x}}_0,q)=\frac{L({\bar{t}}_i,{\bar{x}}_0,q)T({\bar{t}}_i,{\bar{x}}_0,q)}{1 + \tau _1H({\bar{t}}_i,{\bar{x}}_0,q) + \tau _2L({\bar{t}}_i,{\bar{x}}_0,q)}}\\ &{E^2(q,\bar{x}_0,s,\tau )=\sum _{i=0}^{28}\left[ \left( \frac{s_1\bar{f}_H(t_i\tau ,{\bar{x}}_0,q)-H_{T,i}}{H_{T}^*}\right) ^2 +\left( \frac{s_2{\bar{f}}_L(t_i\tau ,\bar{x}_0,q)-L_{T,i}}{L_{T}^*}\right) ^2\right] }\\ &{{\bar{x}}_0 =(H_0/K_H,L_0/K_L,C_0/K_C,T_0/K_T)},\ {\bar{t}}_i=t_i\tau . \end{aligned}$$

Notice here that \(t_i=i\) and \({\bar{t}}_i=i\tau\) retain their dimensional and dimensionless identities for being a fixed sequence each rather than a variable.

Table 2 Dimensional and dimensionless scalings
Full size table

A combined PDE search and line search for the dimensionless model yielded a provisional global minimizer for the dimensionless parameters listed in the second last column of Table 2 from \(\tau\) down to \(s_2\). Translating it to the dimensional variables and state scalings we obtain the parameterized values in the second column of Table 2. As predicted by the theorem, four parameters (\(m,a_1,a_2,u_2\)) are scaled away but two more, \(s_1,s_2\), are created by the transformation as can be seen in the Scaled Parameter column, which in turn creates two free, parameterizing, auxiliary parameters which we take them to be \(K_C, K_T\), the ‘carrying capacities’ for the other predator and the trapper respectively. Notice that their units remain to be free—they can be head-count, biomass, or for the case of \(K_T\), a pure index for the trapping business from the perspective of Hudson Bay Company. For the provisional global minimizer in the space of the dimensional parameters and initials, we see clearly from the second and the third columns that some parameters are uniquely determined by the global minimization of the squared error but some are not, namely the uncertain parameters and initial states. That is, different choices for the parameterizing pair, \(K_C,K_T\), will give rise to different values for those uncertain parameters but to the same minimum error value \(E(p^*,x^*_0)=0.4896\).

The minimizer in the parameters and initial states was found for the dimensionless model first, and then translated for the dimensional model. The dimensional minimizer was then checked and re-searched independently by both methods for the dimensional model, only after which were the sensitivities calculated and listed in the Best-Fit Sensitivity column.

Figures 4, 5 and 6 highlight some of the numerical result. Figure 4 clearly shows that the hare and lynx populations left in the wild is right-chiral and the respective catch by the trapper is left-chiral. Figure 4d also shows a typical gradient or line search in action. Figures 5 and 6 show more on the best-fit result. Specifically, twenty subinterval partitions are used for each of the line segment, \((0,2p_0)\) and \((0,2x_0)\), and as a result the provisional minimizer sits at the center of each segment with ten searching points to each side. Because the same proportionality is used for each interval length and the same window size is used for all plots of the error function against the search intervals regardless the values of the components of the minimizer, these plots give a graphical depiction to the dimensionless sensitivity and a graphical comparison of the sensitivities among all parameters and initials. For example, between the recruitment parameters \(r_1,r_2\) of the hare and lynx, respectively, the best fit is less sensitive to hare pelt than to lynx pelt because \(S_{r_1}<S_{r_2}\). This is represented by the top two graphs of Fig. 5 for which the concavity is more pronounced for the \(r_2\) parameter than for the \(r_1\) parameter. Similar comparisons can be done for all parameters and initial states, which are also captured by the sensitivity scores from Table 2.

Fig. 4
figure 4

Best fit by line search. a The best fit of the annual captured rates, \(H_T,L_T\), by the HLCT model to the pelt data, together with the hare and lynx populations, H, L(dashed curves). The best fit relative error is \(0.4896/29\approx 0.0169\) per data-point. b Top panel: The point-wise right chirality of the model hare-lynx population in the wild and the left chirality of the model hare-lynx trap rate. Bottom panel: the period-power plot for the lynx pelt data and that of the predicted lynx-trap rate as a result of the best fit. Both match exactly at the principle period mode around a 9.3-year cycle, and qualitatively at the secondary period mode about a 4.5-year cycle. c A hare-lynx phase plot to replicate the time-series plot of (a). It shows a 100:1 peak ratio between the wild population and the pelt for hare and a weak 2:1 peak ratio for the lynx. d By the line search method, the trapped lynx rate \(L_T\) as a function of the searching iteration in 10 steps. The companion search plot for hare is not shown

Full size image
Fig. 5
figure 5

Best-fit sensitivity and insensitivity. Four searching section curves of the error function (with square makers) are shown when the line search algorithm stopped upon finding the best fit. Averaged chiralities are also plotted which consistently shows the model population is right chiral (with circle markers) and trapper’s catch rate is left chiral (without markers). Since each parameter’s search interval length is twice the global minimum if it is not zero, showing it in a fixed picture frame amounts to showing each parameter in its relative or dimensionless scale. The best-fit error is the lest sensitive to parameter \(m_3\), leading to the interpretation that there was little competition or interference among the trappers

Full size image
Fig. 6
figure 6

Trapping preference by sensitivity analysis. The same type of sensitivity plot as Fig. 5 but for four trapper-related parameters \(u_1,v_1,u_2,v_2\). Wherever the catch chirality curve becomes flat at 0 but the population chirality curve is not, there is no trapped animal, i.e., all trappers quit their trapping business, which happens if there is not enough lynx to find (low \(u_2\)) or taking too much time to handle (high \(v_2\))

Full size image

A surprising finding from the last plot of Fig. 5 is that the intra-competition parameter \(m_3\) for the trappers can be set to zero with little change to the best fit. That is, as an interpretation there was little interference among the trappers. As a result, parameter \(m_3\) can be effectively dropped from the HLCT model. The sensitivity graphs for parameters \(r_1\) and \(r_2\) show that the catch on lynx gives rise to a much higher recruitment rate for trappers in \(r_2\) than \(r_1\) for the catch on hare. It also shows the lynx-recruitment rate is much more sensitive than the hare-recruitment rate to the best-fit error. This lynx-biased preference by the trappers is further demonstrated in Fig. 6. For which the discovery rate of the lynx by the trappers, \(u_2\), are higher and more sensitive than the hare’s rate \(u_1\). Also, it takes a longer handling time to process the lynx fur (\(v_2\)) than the hare fur (\(v_1\)), and again the best-fit is more sensitive to the former than to the latter. All suggest that trappers prefer lynx pelt to hare pelt. This is quite consistent with the hypothesis that lynx fur was economically more valuable.

Figure 7 shows various results for the full Leigh data from 1847 to 1903. Figure 7a shows the pelt data and its chirality. Prominent features are the followings: (i) the 1875–1903 data is predominantly left-chiral, the main motivation for Guilpin’s work; (ii) except for the second cycle every cycle peak is left-chiral, i.e. the chirality curve dipping below the horizontal axis; (iii) the averaged chirality for the entire period (the average value of the chirality function) is also negative (left-chiral). Figure 7b shows that for the same parameter values as in Table 2 the HLCT model’s fit to the full data, which is surprisingly good on its own right. Figure 7c shows the HLC-phase space of the model for the same parameter values but without the trapper (\(T_0=0\)). It shows if the ecological system were left alone, the field populations would be on a limit cycle, providing a support for the parameter values of Table 2 since we also expect the system to be cyclic without trapping.

Fig. 7
figure 7

Long data. a The full pelt data by Leigh and its chirality, which is mostly negative. b One best-fit for the same parameter values as Table 2 with the initial values: \(H_0=11425.75, L_0=61.03818, C_0=1.32106, T_0=0.21467\) for a per-data-point fit error 0.01799. c The system without the trapper (\(T_0=0\)), showing a stable limit cycle, situated far away from all extinction surfaces, \(H=0, L=0\), and \(C=0\). The nullcline surface for the H-equation and the other nullclines on the surfaces are also shown together with the limit cycle orbit. All variables are scaled by their ‘carrying capacity’ values \(K_H,K_L,K_C\), respectively. d Switching the trapping preference switches the chirality. Here \(sH_T,sL_T\) denote trapper’s catches when the parameter values are switched between \(u_1,v_1,r_1\) and \(u_2,v_2,r_2\) (see text for details). Chirality is most pronounced near the peaks of the catch cycle

Full size image

Figure 7d shows a comparative study on the catch chirality if trapper’s preference is changed. In particular, the \(H_T\)–\(L_T\) chirality is for the catch of Fig. 7b. The \(sH_T\)–\(sL_T\) chirality is for the catch of the model but for a different set of parameter values. Specifically, we first just swapped the values between \(u_1,v_1,r_1\) and \(u_2,v_2,r_2\). This switched preference from the lynx to the hare for the trapper drives the species to extinction because of a too high predation intensity on the hare. We then reduced the trapping intensity on the hare to one-third of the switched values, i.e. \(u_1=u_2/3,v_1=3v_2,r_1=r_2/3\) (with the handling time lengthened three-fold for easing up on predation). This set of trapping preference is not enough to keep all trappers in business for a too high quitting rate \(d_3\). After reducing the quitting rate to one-tenth of the original (\(d_3:=d_3/10\)), the full dynamics is on a limit cycle, and the catch is right-chiral (negative chirality as shown) because of trapper’s switched preference. We also carried out 100 searches for best-fit starting from 100 randomly chosen parameter sets in a hypercube in the parameter and initial value space that is centered at the changed values with twice the centering value for each parameter’s width for the hypercube. No limit cycles turned up as best-fit, lending another support for the parameter values of Table 2, and the biased preference on lynx pelt by the trapper as a consequence.

We also carried out a similar analysis on the Odum data set. Specifically, we restricted it to the same period as the Leigh data for 1845–1903 for comparison purposes. As it is shown in Fig. 3a, the pattern of oscillation for the later period from 1904 to 1935 is quite regular, fitting well to the classical theory, i.e. the lynx cycle lagged behind the hare cycle by about 2 years. This can be explained by the hypothesis that a strict quota system for trapping was well established and enforced by that time (Gibbard 1967). As a result the annual return in pelts is expected to be proportional to field populations survey which is always right-chiral. In another words, the role of trappers can be effectively eliminated from the HLCT model.

Contrary to the later period, Fig. 8a shows the chirality for the early period was mixed but biassed toward right-chirality. We carried out best-fits for the period of 1874–1903. Specifically, we used the same parameter values of Table 2 but with no trapping preference on either hare or lynx. That is, we used the average values of \(u_1\) and \(u_2\) for the new \(u_1\) and \(u_2\), and similarly for \(v_1,v_2,r_1,r_2\). We then carried out 400 searches starting randomly from a hypercube centered at the neutrality point with twice the value for each parameter and initial value’s width for the hypercube. Table 3 lists the best-fit which is of a mixed-chirality, a right-chirality, a left-chirality, and an as-is fit by the same best-fit parameter value for the 1875–1903 Leigh data. The left-chiral fit is better than the other two in terms of having a smaller fit error. More interestingly, the as-is fit which is automatically left-chiral is also better than the mixed and right chirality fits. As one can see from the table, for the mixed-chirality, the parameter values for \(u_1,u_2\) are comparable. For the right-chirality, \(u_1\gg u_2, v_1\gg v_2, r_1\gg r_2\), and for the left-chirality, \(u_1\ll u_2,v_1\ll v_2, r_1\ll r_2\). Figure 8b–d show the retro-fit time series to the lynx pelt data for the longer period of time from 1847 to 1903 and the chiralities for the \(H_TL_T\)-oscillations. We note that unlike the two left-chiral fits, the mixed and right-chiral fits are both sensitive (not shown) to the intra-interference parameter \(m_3\) for trappers. That is, these two fits lead to opposite conclusion of the left-chiral fits on \(m_3\).

Fig. 8
figure 8

Best-fit to Odum’s data. a The Odum data and its chirality, which is mixed up to 1910 and consistently positive (right-chiral) thereafter. b The mixed-chiral parameters from Table 3 are used to retro-fit the long data from 1847 to 1903. c The same as (b) except for the right-chiral parameters of Table 3. d The same retro-fit but for the parameter values of Table 2

Full size image
Table 3 Best-fit to Odum’s 1875–1903 data
Full size table

We did not best-fit the HLCT model to the later segment of the Odum data between 1904 and 1935. One reason, which was mentioned early, is because the trapper variable T can be effectively eliminated from the model if the pelt returns were largely the result of a quota system. Another considering factor was the immigration of coyotes into the hare-lynx region between 1910 and 1920 (page 1194 of O’Donoghue et al. 1998) that became a key predator of the hares, and a key competitor of the lynx, which in turn should change the parameter values for the alternative predator variable C.

Figure 9 summarizes the result of a comparative study on various provisional models. Among which are the VHL model from Blasius et al. (1999), the HLC model without the trappers, the HLT model without the other predators, and the HLCT1 model with the Holling Type I predation form for the trappers. The last three models are simply subsystems of the HLCT model Eq. (2) setting \(T_0=0, C_0=0\), and \(v_1=v_2=0\), respectively. For the first two models without the trapper, the pelt quantities are set to be proportional to the populations as \(H_T=s_1H, L_T=s_2L\), respectively, with \(s_i\) being the proportion parameters. As shown in the bar plot of Fig. 9, the two models without the trapper do not share the same chirality as the pelt data but all models with the trapper do. Both the VHL model and the HLC model without the trapper are incapable of left-chirality. Notice that even though HLC model has more parameters than VHL, its fit error is not better, disproving the conventional view that more parameters always yield better fits. In fact, no mater how many more parameters are added to either model, for example, adding multiple alternative predators of hares to VHL or to HLC, simply because of the fact the field hare and lynx populations are incapable of HEL oscillation, all proportional catches will always fit worse than trapper-incorporated models. Two-hundred searches for best-fit are carried out for each model. In particular, for the HLC, HLT, HLCT1 models, the initial searching parameter and variable values are randomly chosen from a hypercube centered at the values of Fig. 4 with twice the centering value for the width of each parameter and variable for the hypercube. Even with this help from the best-fit values of the HLCT model, the alternative models incur higher fitting errors. Although the errors for the HLT and HLCT1 models look comparable to that of HLCT’s, their best-fitted dynamics without the trapper stop to be cyclic, a qualitative misfit. The important conclusion is that the HLCT model fits the data the best and hence becomes the benchmark model.

Fig. 9
figure 9

Benchmarking models. The catch dynamics for the VHL model and the HLC model (not shown) are right-chiral and those for the remaining models are left-chiral. It also shows models with the inclusion of T always fit better

Full size image

4 Discussion

Model parameters for a physical system can be estimated by many ways. One of which is by the best-fit process presented here. By this approach the parameter values are forced to give the smallest error between the predicated and the observed. Ideally we like our model’s best-fit to perfectly match with independent observations, or be consistent with them inside a generous range. Such considerations can be used further for parameter selections and model refinement.

It is reported in Rowan and Keith (1956) and Bittner and Rongstad (1982) that a female hare has an average annual reproductive potential of 10.51 leverets with about the equal sex ratio. This translates to a per-capita rate of 5.2 births per year. How many would survive to adult is not clear but the birth rate puts an upper estimate on the rate. Since our model is used to fit pelt data, which corresponds to adult size hares, our model estimate for the per-capita reproductive rate of hares at \(b\approx 2\) (Table 3) is very reasonable. This can be interpreted two ways. One, for every 5.2 births per year per adult hare, about 2 make to the size of a harvest pelt. Alternatively, the 5.2 hares at birth are equivalent to about 2 hares at maturity. We note that as shown in Table 2, these three parameters (\(b,a_1,h_1\)) are among those which are independent of the free parameters \(K_C\) and \(K_T\) and fixed by the best-fit. As a result these parameter values can be replaced by their field estimates in future benchmarking of the models.

On the birth-to-consumption ratio \(b_1\) of the lynx on hare, the estimates from the two left-chiral fits of Table 3 is reasonable because the ratio must not be greater than one if we assume a lynx would have to consume multiple hares to give one birth of offspring. With this constraint, the mixed-chiral fit and the right-chiral fit of the HLCT model to the Odum data are bad fit for violating this mass-conservation limit. Regarding the carrying capacity estimate on \(K_H,\ K_L\) in Table 3, the fit to Leigh’s data is more reasonable than all others because we should expect that as a rule of thumb a prey’s biomass should be of at least two order of magnitude greater than that of its predator (e.g. Deng 2010). In particular, the lynx to hare population in the wild should at least differ by a magnitude of three orders (see Fig. 5 of O’Donoghue et al. 1998). Because of this consideration, the mixed-chiral and the right-chiral fits to Odum’s data are not good. This does not mean there are not better fits with mixed and right chiralities. It simply means we have tried many searches but no better fits have been found yet.

These considerations lead at this moment only to the left-chiral fit to both Leigh and Odum data as a better alternative. Both fits imply that trapper’s intra-competition parameter \(m_3\) can be absent, suggesting, as mentioned before, that trappers were not interfering each other’s business. This was unlikely the case during the earlier time when white settlers emigrated from Europe to colonize North America. In fact, fur trade was the major economical engine that drove the North America expansion because of strong demand of quality furs in Europe. However, by 1820’s the first wild game legislation was enacted in, e.g. Ontario, establishing for example the practice of hunting season which is still used today (Thompson 1967). By 1860, the first trapping line legislation was enacted in Ontario (Gibbard 1967). It gave a trapper the exclusive right to a trapping line on public land that was usually defined by rivers, mountain ridges, and valleys. In return the trapper must maintain the trapping line in good faith, harvest a minimal number of furbearer pelts each year, and file a mandatory catch report each year. It was and still is a criminal offence to steal a trapper’s catch or equipment, or to interfere another trapper’s activity by destroying his equipment, for instance. It was a surprise how well the best-fit of our model to the data had captured this piece of history which was hidden in the data all along. This was probably a good reason why biologists looked at the 1875–1903 period’s pelt data more closely because the earlier period was more unsettling for the trapping practice.

The missing order of magnitude on the carrying capacities on \(K_H,K_L\) between our model estimate and the field study seems to suggest that the hare pelt was under reported. This seems to be consistent with the fact that hares were trapped for their meat and for their fur (Weinstein 1977). If this is the case, then we can simply increase the parameter value of \(s_1\) to fit the elevated hare data without changing any value of the dimensionless parameters. This in turn will raise the hare capacity value \(K_H\) for a better fit to the field result, and change the best-fit parameter values from Table 2 accordingly.

We deliberately left out discrete models (e.g. Stenseth et al. 1997) for benchmarking. This is due to the fact among many other drawbacks (Deng 2009) almost all discrete models in ecology violate the Time Invariance Principle (Deng 2008) without which a model cannot be independently validated by experiments. Our result also supports the One-Life Rule postulation (Deng 2008, 2010) that every organism has a finite life span which is guaranteed by models with carrying capacities for all their species. This in turn is guaranteed by the positivity of all intraspecific competition parameters \(m,m_1,m_2>0\). Curiously this rule does not necessarily apply to the economical–ecological interaction between the trappers and their habitat because our trapper equation does not model the birth and death of the trappers as a species but rather the rise and fall of their trapping business. Our result indeed shows that interferences among trappers can be absent (\(m_3=0\)). That is, a trapper can go out of business and then get back into it again, not obeying the One-Life Rule for organisms. Our result also supports another fundamental theory in ecology—Holling’s theory of predation. Our best-fit shows that all the predation handling times (\(h_i,v_j>0\)) must be non-zero and be sensitive to changes. These results suggest that ecological modeling must move beyond the Rosenzweig–MacArthur producer–consumer model (Rosenzweig and MacArthur 1963) as well as from the Lotka–Volterra model for competitive species.

We have given a numerical demonstration for the phenomenon that the kill rates by a top predator on a predator–prey chain must rotate in opposite direction against the populations of the predator and prey. We believe this anti-chirality property can be proved mathematically for such three-trophic food chains, which we will leave it open for now. We have also tried to solve the inverse problem to fit models to empirical data. However, we have to leave it to future studies on model refinement so that all parameter values fall into their observed ranges. For instance, one can include another trophic level below the hare if the logistic growth model assumption for the hare is inadequate. One can also include alternative preys to the lynx to improve some of the parameter estimates for the lynx which is not strictly a specialist. In conclusion, benchmarking models for the Canadian hare-lynx data is an on-going process, and this paper is only a new start. We expect that ideas and methodologies presented here should prove useful for other problems (e.g. Stenseth et al. 1998; Hanski et al. 2001; Cattadori et al. 2002) in ecology and in biology in general.