Introduction

The Banks grass mite, Oligonychus pratensis (Banks) (Acari: Tetranychidae) was first reported on date palms, Phoenix dactylifera L., in California (USA) by Banks (1914), but is now widely distributed throughout the world, damaging dates, grain crops, and grasses (Negm et al. 2015). Every year, the date growers in the Coachella Valley (Riverside Co., CA) suffer from severe losses due to Banks grass mite infestations. A single early-season application of Savey® (Hexythiazox; Gowan Company, Yuma, AZ, USA) is the main strategy used by the date growers for pest management of Banks grass mites. However, concerns about development of resistance to Savey® encourage a move towards studies on alternative control measures such as biological control. In a search for possible biological control agents of the Banks grass mite in date orchards of the Coachella Valley, we found that Galendromus flumenis (Chant) (Acari: Phytoseiidae) is its key predator occurring on date bunches (Ganjisaffar and Perring 2015a). The predator has a short life cycle (Ganjisaffar and Perring 2015b, 2017), possesses the ability to use alternative foods (Blackwood et al. 2004), and searches efficiently for prey at low densities (Ganjisaffar and Perring 2015a). Therefore, it has been targeted for use in the biological control of the Banks grass mite.

It is important to understand the foraging behavior of G. flumenis and the factors influencing the predator–prey dynamics in an effort to assess its efficacy in the field. Since predator–prey dynamics are influenced by competitive interactions among predators (Skalski and Gilliam 2001; Jensen and Ginzburg 2005; Stephens et al. 2007; Anderson 2010; DeLong and Vasseur 2011; Arditi and Ginzburg 2012; Fryxell 2013) it is relevant to study such interactions. One of the simplest models to study the density-dependent predator–prey dynamics is the Nicholson-Bailey (1935) model. This model defines the area of discovery (a) as the average area searched by a predator per time unit. Therefore, the area of discovery is a measure of a predator’s searching efficiency which is assumed to be independent of prey and predator densities. However, Hassell and Varley (1969) were the first to suggest an inverse relation between the searching efficiency of a predator and its density, and incorporated the effect of predator density into the Nicholson-Bailey model to explain stability of predator–prey interactions. This stabilizing effect was named mutual interference and expressed by the interference constant (m). They showed that the greater the value of m, the greater the tendency for the interaction to become stable since at high predator densities, mutual interference reduces both the prey consumption and the predator’s rate of increase. In fact, as predator density increases, individuals will waste a great portion of their time with encounters of other conspecifics rather than searching for and handling prey (Henne and Johnson 2010). Furthermore, predators that are already feeding may stop when disturbed (Evans 1976). As a result, the number of attacked prey per time unit by the individual predator will decline even though food is in excess (Evans 1976; Eveleigh and Chant 1982; Zhang and Croft 1995; Reis et al. 2003; Kratina et al. 2009). However, Hassel and Varley’s model assumes a linear (Type I) functional response of predators. When the response is not linear, this model leads to biased estimations of searching efficiencies, and consequently underestimates m. Because of this, modified models have been proposed in which a Type II functional response due to the handling time is taken into account (Beddington 1975; DeAngelis et al. 1975; Arditi and Ginzburg 1989; Crowley and Martin 1989; Arditi and Akçakaya 1990, Abrams and Ginzburg 2000; Skalski and Gilliam 2001; Nachman 2006a).

Since G. flumenis displays a type II functional response (Ganjisaffar and Perring 2015a), three models allowing for a non-linear functional response were selected and modified by incorporating an effect of mutual interference. This was done to test the hypothesis that prey density and predator interference in combination impact the foraging efficiency of G. flumenis. We also assessed how predator and prey densities affect the rate at which predators emigrate from an experimental arena. These studies were conducted with the objectives of 1) quantifying the impact of prey and predator densities on the functional response of G. flumenis, and 2) using this information to better understand how G. flumenis might behave under field conditions, thereby guiding us in developing biological control strategies against the Banks grass mite.

Materials and Methods

Mite Colony Maintenance

Colonies of G. flumenis and Banks grass mites have been maintained in our laboratory at 30 ± 1 °C, 60 ± 10% RH, and 16L: 8D photoperiod since they were collected from date bunches in the Coachella Valley in 2012. Every year, the colonies have been supplemented with field-collected mites to insure genetic variability. Banks grass mites were reared on corn plants (Zea mays L., variety 31G71) with 7–8 fully developed leaves, while G. flumenis was reared on a 10 × 10 cm black ceramic tile resting on a water-saturated foam in a stainless steel pan (20 × 20 cm). The edges of the tile were covered with strips of tissue paper immersed in water in the pan to prevent mites from escaping. A microscope cover slip with a few cotton threads underneath was placed in the center of the tile to provide ovipositional site and shelter for the predatory mites (McMurtry and Scriven 1965; Ganjisaffar and Perring 2015a). Three times per week, predators were provided with mixed life stages of Banks grass mite brushed from infested corn leaves using a mite brushing machine (Bioquip Products, Rancho Dominquez, CA, USA).

Experimental Procedure

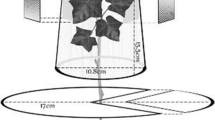
Newly-emerged G. flumenis females and males (the latter of unknown age) were moved from the stock colony to excised corn leaves (4–5 cm in width and 10 cm in length). The excised leaves were placed abaxial side up on a wet cotton wool layer in a Petri dish (14 cm diameter). This Petri dish had a 1-cm-diameter hole drilled in its bottom, and was placed in a pan containing water. Galendromus flumenis females were allowed to mate and feed on a mix of all prey stages for 48 h. Then, these gravid females were moved individually to arenas and were starved for the next 24 h. The arenas consisted of two Petri dishes; a 3-cm-diameter Petri dish with a 5-mm-diameter hole in its bottom was placed in a 5-cm-diameter Petri dish containing water. A cotton layer was placed in the small Petri dish on top of which a corn leaf cut to fit the 3-cm-diameter dish was placed abaxial side up. The leaf margins were covered with a cotton strip to prevent mites from escaping and to maintain freshness of the leaf. The cotton strip was kept saturated by adding water to the larger Petri dish which was absorbed through the hole in the bottom of the smaller Petri dish. A 1-cm-diameter hole was made in the lids of the large Petri dish, and covered with fine mesh for ventilation.

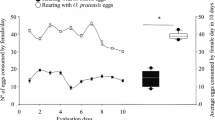
After the 24 h starvation period, the females were moved to experimental corn leaf arenas that were constructed with double Petri dishes in a manner similar to the starvation arenas. Two sizes of experimental arenas were used, small (5 cm diameter) and large (8 cm diameter), each containing 1000 Banks grass mite eggs. To obtain these eggs, 150 Banks grass mite females were transferred to experimental arenas, and allowed to oviposit for 36–48 h. After this time, the spider mite females were removed and the eggs were counted and adjusted so that 1000 eggs were available in each arena. Only eggs were used since our previous studies showed that the egg is the most preferred prey stage for G. flumenis females. 1000 eggs were used because this would insure that the predators had excess food during the experiment (Ganjisaffar and Perring 2015a). The number of starved females placed into each arena varied from 1 to 5, thus, both the prey and predator densities (numbers per unit area) were manipulated.

Predators were allowed to feed 24 h, after which time the number of Banks grass mite eggs consumed and the numbers of predators leaving the arenas were counted. Predator females found alive on the wet cotton surrounding the experimental arenas were considered as “emigrating” individuals. Each G. flumenis density was replicated at least 10 times since the arenas with leaving predators were excluded from the predation analyses. The experiment was conducted in a growth chamber (Percival model 130BLL) at 30 ± 1 °C, a photoperiod of 16L: 8D and a relative humidity of 60 ± 10% RH.

Data Analysis

Holling (1959) and Ivlev (1961) developed mathematical models to describe a Type II functional response of a single predator searching for prey. These models have since been modified by incorporating predator density to account for mutual interference (e.g. Beddington 1975; DeAngelis et al. 1975; Royama 1992; Nachman 2006a, b). In the following we will consider three of such models:

The first model was suggested by Beddington (1975), who added a term to Holling’s disc equation by assuming that predators waste time upon encounters with conspecifics. This leads to

$$N_{a} = \frac{a(N/A)T}{{1 + aT_{h} (N/A) + m((P - 1)/A)}}$$
(1)

where N a is the per capita number of prey killed during time T (24 h), N is the initial number of prey, P is the number of predators, A is the leaf area (19.63 cm2 for the small arena and 50.24 cm2 for the large arena), a is the attack rate, T h is the handling time per killed prey and m is a parameter expressing the intensity of mutual interference.

The second model also is based on Holling’s disc equation, but mutual interference is assumed to reduce the attack rate, yielding

$$N_{a} = \frac{{ae^{ - m((P - 1)/A)} (N/A)T}}{{1 + ae^{ - m((P - 1)/A)} T_{h} (N/A)}}$$
(2)

where a is the attack rate in the absence of mutual interference (i.e., when P = 1 or m = 0). The model assumes that the realized attack rate declines exponentially with predator density.

The third model is based on Ivlev’s (1961) functional response model. It assumes that the upper asymptote of the functional response function declines exponentially with predator density, leading to

$$N_{a} = f_{m} e^{ - m((P - 1)/A)} \left( {1 - e^{ - a(N/A)} } \right)T$$
(3)

where f m is the maximum per capita predation rate, i.e., in the absence of mutual interference and when prey is provided ad libitum, corresponding to N/A → ∞.

It may be seen that all three models, despite differences in underlying assumptions, predict that the per capita predation rate (N a ) will approach 0 with increasing predator density, provided the mutual interference parameter (m) is > 0.

As Eqs. 1 and 2 reduce to Holling’s disc equation and Eq. 3 to Ivlev’s model when P = 1 and/or m = 0, we will use the names Beddington for Eq. 1, Holling for Eq. 2 and Ivlev for Eq. 3, keeping in mind that the three models represent generalizations of the original functional response models.

The expected total predation in absence of prey depletion can be found as N a P, but since the functional response experiments were conducted without prey replacement, N a P may overestimate the observed total predation rate (denoted N e ) and may even exceed the initial number of prey (N). To correct for prey depletion, Rogers (1972) developed the random predator equation from which N e could be obtained by means of iteration (Juliano and Williams 1987), provided that the functional response is described by Holling’s disc equation. More sophisticated approaches, based on either integration or simulation, are provided by Jost and Ellner (2000), Kratina et al. (2009), Clerc et al. (2009), and McCoy et al. (2012). However, we apply a simpler approach to correct for prey depletion by assuming that the likelihood that a prey avoids being eaten during an experiment can be found as the 0-term of the Poisson distribution, i.e., as e −λ, where λ is modelled as \(\lambda = PN_{a} /N\). This yields the expected total predation rate as

$$\hat{N}_{e} = N\left( {1 - e^{{ - PN_{a} /N}} } \right).$$
(4)

Although Eq. 4 was developed to model parasitoids (Hassell 1978) it can be applied to predators provided the parameters determining N a are estimated by fitting \(\hat{N}_{e}\) to observed values of N e , thereby implicitly incorporating the effect of prey depletion. It may be seen that Eq. 4 satisfies the criteria that \(N_{e} \to N_{a} P\) if \(N \to \infty\) and that \(N_{e} \to N\) when \(N_{a} P \to \infty\). Besides, N e  = 0 for N = 0.

PROC NLIN in SAS Enterprise Guide version 7.1 (SAS Institute 2014) was used to fit the three functional response models to observed values of N e . The procedure applies an iterative method to minimize the sum of squared differences between the observed and predicted values of N e by changing the parameter values determining N a until no further improvement can be achieved. The three models were compared by means of the F statistics and the associated P values. As the models have the same number of parameters, the model with the highest F statistics and lowest P value was considered the best. In addition, the observed total predation rates (N e ) were plotted against the predicted values (\(\hat{N}_{e}\)). Data were log transformed to stabilize the variance as the variation in N e tended to increase with \(\hat{N}_{e}\). Thus, \(y = \log N_{e}\) was plotted against \(x = \log \hat{N}_{e}\) and fitted with a straight line given as y = bx + a. The test criterion was that the straight line did not differ significantly from the line given as y = x, i.e., a line with unity slope and zero intercept, characterizing a perfect fit. The slope of the trend line and the \(R_{adj}^{2}\) values were used to test the agreement between observed and predicted values.

For emigration data, the proportion of predators leaving an arena during the experiment was modeled by means of logistic regression using PROC GENMOD in SAS:

$$P_{d} /P = \frac{{e^{y} }}{{1 + e^{y} }}$$
(5)

where P d is the number of predators leaving an arena where P predators were introduced, and y is a linear function of one or more independent (predictor) variables. We modelled y as

$$y = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \beta_{3} x_{1}^{2} + \beta_{4} x_{2}^{2} + \beta_{5} x_{1} x_{2}$$
(6)

where x 1 and x 2 denote the initial densities of prey and predators, respectively, and the βs are the parameters associated with the various terms. The higher order interaction terms were omitted a priori to simplify the model.

As P d /P is assumed to be binomially distributed, we used the logit transformation as the link function in PROC GENMOD. The DSCALE option was used to scale deviance in case of over- or under-dispersion in data which otherwise would bias the P-values. To identify significant terms, we used the Type 3 option, which means that the P value associated with a given variable will be small (P < 0.05) if the variable contributes significantly to improve the model compared with a model where the term is not included. All non-significant terms were omitted from the final model.

Results

All three models described the data very well and yielded non-zero parameter estimates (P < 0.05). However, the Ivlev model gave the best fit to the data (F 3.97 = 596.4, P < 0.0001) (Table 1). The per capita predation rates declined with increasing predator numbers (Fig. 1) even though the density of Banks grass mite eggs within each arena was constant (50.94 eggs/cm2 in the small arena and 19.90 eggs/cm2 in the large arena). Figure 2 shows the observed total predation rates (N e ) plotted against the predicted values (\(\hat{N}_{e}\)) on double logarithmic axes. All three models met the test criterion that the straight line of y = bx + a was not significantly different from the line y = x (Beddington: R 2 adj  = 0.660, F 1.98 = 192.8, P < 0.0001; Holling: R 2 adj  = 0.687, F 1.98 = 207.9, P < 0.0001; Ivlev: R 2 adj  = 0.709, F 1.98 = 241.7, P < 0.0001) (Fig. 2). The line y = x explained 64.9, 67.8 and 69.4% of the total variation in log N e for the Beddington, Holling and Ivlev models, respectively. Thus, although all three models proved to fit the data very well, Ivlev was the one that yielded the best fit to the data. Therefore, it was chosen as the most realistic model to describe the functional response of G. flumenis at different densities of prey eggs and predators.

Table 1 Parameter estimates ± SE of the selected models
Full size table
Fig. 1
figure 1

Three models fit to the observed per capita predation rates (points) of Galendromus flumenis in small and large arenas

Full size image
Fig. 2
figure 2

Relationship between observed and predicted total predation rates of Galendromus flumenis based on three models

Full size image

Based on the predictions of the generalized Ivlev model, the maximum per capita predation rate per day (f m  × 24 h) was predicted as 275.3 (± 34.8) Banks grass mite eggs. The estimated mutual interference constant (m) was significantly greater than 0 (3.634 ± 0.611 cm2) (Table 1), indicating strong interference among predators. The graph of per capita predation rates of G. flumenis at different densities of prey and predator confirms that the mutual interference among adult G. flumenis females is strong and needs to be taken into account even at relatively low predator densities (Fig. 3). The total predation rate (N e ) increases with predator density, but only as long as the predator density remains below 0.28 predators/cm2 (Fig. 4). When the density exceeds this threshold, either because of the predator’s numerical response or as a result of augmentative releases, the total predation rate will decline steeply.

Fig. 3
figure 3

Predicted per capita predation rates of Galendromus flumenis at different densities of prey and predators based on the generalized Ivlev model (Area = 50 cm2)

Full size image
Fig. 4
figure 4

Predicted total predation rates of Galendromus flumenis at different densities of prey and predators based on the generalized Ivlev model (Area = 50 cm2)

Full size image

When emigration data were analyzed by means of logistic regression, only predator density was found to impact emigration probability significantly. The resulting model was: y = −3.6329 (± 0.4350) + 9.3765 (± 2.1485) x 2. As x 2 = P/A, the model shows that higher predator density will increase the emigration rate of G. flumenis significantly (χ 21  = 21.36, P < 0.0001) in an almost exponential way (Fig. 5).

Fig. 5
figure 5

Relationship between predator density and observed (points) and predicted (line) emigration tendency of Galendromus flumenis

Full size image

Discussion

The present study demonstrates that both prey density and predator interference are significant determinants of predation efficiency of G. flumenis. Our results show that the per capita predation rate of G. flumenis is adversely affected by mutual interference effects if the predators aggregate in patches of high densities of Banks grass mite eggs. We applied three different models to identify the best model describing the foraging behavior of G. flumenis. These models reduce to commonly used functional response models when only a single predator searches for prey. Two of the models (Eqs. 1 and 2) are based on Holling’s (1959) disc equation while the third (Eq. 3) is based on Ivlev’s (1961) predation model. Therefore, the attack rate (a) and handling time (T h ), the cumulative time spent on capturing, killing, and digesting the prey (Veeravel and Baskaran 1997), estimated by means of the two former models in the absence of mutual interference (i.e., when P = 1) can be compared with the values reported in our previous work (Ganjisaffar and Perring 2015a). In that study, we conducted functional response experiments with G. flumenis females feeding on 10 different densities of O. pratensis eggs (from 2 through 224 eggs on 19.63 cm2 arenas) exposed to the same environmental conditions as in the present study. We estimated a to be 0.608 ± 0.018 cm2/h and T h to be 0.153 ± 0.001 h. The small standard errors of these estimates are attributed to the fact that we used 10 different prey densities with 15 replicates per density to fit the functional response model. While a is close to the values estimated in the present study and lies inside the 95% confidence intervals, the value of T h estimated previously is significantly higher than the values given in Table 1. This discrepancy is attributed to the fact that previously we offered a maximum of 224 eggs in contrast to 1000 eggs in the present study, which indicates that prey numbers in the former study were insufficient to feed the predators ad libitum. In addition, when 1000 prey eggs were offered to a single predator on the small arenas (corresponding to 50.9 eggs/cm2), the average per capita predation rate based on 10 replicates was 241.0 ± 23.14 eggs/day. This empirically based value is much higher than the maximum predation rate estimated from our previous study’s data as T/T h  = 24/0.153 = 156.9 eggs/day. Furthermore, when the generalized Beddington, Holling and Ivlev models are used to estimate the maximum predation rates (i.e., when N/A → ∞), the values are 11.198, 12.315 and 11.470 eggs/h, respectively, corresponding to 268.8, 295.6 and 275.3 eggs/day. We believe that the generalized models used in the present study provide the most accurate estimates of the handling times and maximum predation rates of G. flumenis on Banks grass mite eggs.

Based on three generalized functional response models, we were able to demonstrate that mutual interference strongly influences predation rates as m in all three models is significantly different from 0 (Fig. 1; Table 1). It should be emphasized that the values of m cannot be compared across models since the models differ with respect to how mutual interference is assumed to affect predation efficiency. The fact that the generalized Ivlev model was found to be the best in terms of R 2 (Fig. 2) does not necessarily imply that the assumptions underlying the two other models are false. Rather, the circumstance that the three models fit the data quite well might indicate that mutual interference simultaneously decreases the time available for hunting and feeding, reduces the attack efficiency and leads to a lower maximum predation rate because the models’ parameters are not independent of each other. Thus, f m in Ivlev’s model and 1/T h in Holling’s model both determine the upper asymptote of the functional response curve when a predator individual has unlimited access to prey. This means that a link between the two models can be established by setting f m  = 1/T h . Consequently, as mutual interference in the generalized Ivlev model is modeled as f m e −m(P−1)/A, it corresponds to 1/(T h e m(P−1)/A), which implies that mutual interference in this model can be interpreted as caused by an exponential increase in handling time.

The disturbing effect of interference on foraging behavior of other phytoseiid predatory mites has also been documented (Zhang and Croft 1995; Nachman 2006b; Farazmand et al. 2012; Khodayari et al. 2016). Aggregation of predators can lead to cannibalism and elimination of potential intraspecific competitors for food, oviposition sites and shelters (Elgar and Crespi 1992; Schausberger 2003). However, we found no cannibalism in the present study. In addition, when predators aggregate in patches of high prey density, they likely will encounter each other, which may result in individuals attempting to leave the area. Kuchlein (1966) showed that increasing densities of the predatory mite, Typhlodromus longipes Nesbitt, led to increased emigration rates from experimental leaf arenas containing prey mites. Schmidt et al. (2014) also demonstrated that patch departure rates by a generalist wolf spider, Pardosa milvina (Hentz), increased in response to increasing conspecific numbers. The same trend was observed in the present study, as the emigration rate from the arenas increased steeply with predator density (Fig. 5).

The findings from the present study are important as they provide fundamental information regarding G. flumenis–O. pratensis interactions; information that is challenging to obtain from field studies because (1) date palms are large trees with many fronds and bunches of fruits, (2) mites are very small and occur in large numbers, and (3) the remains of a consumed prey, especially eggs, are impossible to find and record. Therefore, we assume that a single date fruit is the smallest homogenous spatial unit in the date palm, and that prey and predators on a fruit behave as in experimental leaf arenas. Based on model predictions, G. flumenis has an impressive predation rate of almost 300 Banks grass mite eggs per day which qualifies it as a very effective biological control agent against this pest species. However, the high predation potential of G. flumenis is counteracted by its strong mutual interference. Moreover, it is expected that when predators are less restricted under field conditions, interference will cause a shift in foraging behavior from time allocated for feeding to time spent on dispersing in search of new prey patches.

This study contributes to our growing knowledge in designing strategies for efficient augmentative releases of G. flumenis. Studies on parasitoids have shown that due to the mutual interference effect, higher release rates are less effective or even ineffective compared to lower release rates (Wen and Brower 1994; Hoddle et al. 1997). Our results suggest that at low predator densities, when individuals rarely encounter each other, predation will be high (Fig. 3). Increasing predator density will increase the total predation rate per unit area (N e ), but only up to a threshold density found to be around 0.28 predators per cm2 (Fig. 4). Consequently, adding more predators to the system once this threshold density has been exceeded may lead to a progressively lower predation pressure on the prey, thereby actually producing the opposite outcome of what was attempted. Comparable results have been observed in other studies. For example, Papanikolaou et al. (2016) indicated that the predation rate of an aphidophagous coccinellid, Propylea quatuordecimpunctata (L.), at low prey densities is modified by a critical predator density. In fact, the predation efficiency of the coccinellid predators is adversely affected as the intensity of interference among them increases with their aggregation at low prey densities. Skovgård and Nachman (2015) also showed that increasing densities of a parasitoid wasp, Spalangia cameroni (L.), increased parasitism, but only up to a certain density above which the percentage of parasitized hosts decreased.

Field studies are planned to determine the combined effects of mutual interference and density-induced emigration on the predation efficacy of G. flumenis with the purpose of optimizing release rates of predators in areas infested with Banks grass mite. In this context, the identification of a threshold defining when it is advantageous to add more predators or stop adding predators to the system will be important for the successful outcome of biological control against O. pratensis using G. flumenis.