Science or scientism? On the momentum illusion

Abstract

This study explores the risk of the traditional momentum strategy in terms of its realized variance using various data frequencies. It is shown that momentum risk is infinite regardless of the data frequency, implying that (a) t-statistics for this strategy do not exist, (b) correlation-based metrics such as Sharpe ratios do not exist either, and (c) the momentum premium is not observable in reality. It is further shown that the time-honored lognormal distribution is unable to accurately model extreme events observed at various variance data frequencies. Finally, it is shown that the well-known effect of time aggregation does not work for this investment vehicle. Hence, the study is forced to conclude that momentum stories have no valid foundation for their claims.

1 Introduction

Kelly et al. (2021) introduced their recent study entitled “Understanding momentum and reversal,” published in the well-known Journal of Financial Economics as follows:

Since its introduction by Jegadeesh and Titman (1993), the momentum anomaly has consistently ranked among the most thoroughly researched topics in financial economics. It forms the basis of strategies implemented throughout the asset management industry and underlies a wide range of mutual funds and exchange traded products. Despite its widespread influence on the finance profession, momentum remains a mysterious phenomenon. A variety of positive theories, both behavioral and rational, have been proposed to explain momentum, but none are widely accepted. Momentum also remains one of the few reliable violators of prevailing empirical asset pricing models such as the Fama and French (2015) five-factor model, and research has yet to identify a risk exposure that can explain the cross-sectional return premium associated with recent price performance. Consequently, momentum is often the center piece for debates of market efficiency.

Indeed, the original study by Jegadeesh and Titman (1993) has been cited more than 14,000 times, suggesting that an enormous body of “momentum research” has been produced over the last three decades. A recent literature review by Wiest (2022) summarized the results of 47 out of the 60 momentum studies published in the Journal of Finance, the Review of Financial Studies, and the Journal of Financial Economics—journals often regarded as the three leading finance outlets. As mentioned by Kelly et al. (2021), scholars have proposed many different explanations—which I would like to term “stories”—for rationalizing the existence of the “momentum premium,” postulating that stocks that have performed well recently (i.e., “winner” stocks) tend to generate statistically significant higher returns than stocks that have performed poorly recently (i.e., “loser” stocks). The main sample used in Jegadeesh and Titman’s (1993) original study employed monthly data on United States (US) stocks covering the period from January 1965 to December 1989. Figure 1 plots the compounded returns of the stock-price momentum strategy over the sample used in the original study.¹ We see from Fig. 1 an almost exponential increase in compounded returns over the sample period. It may be not surprising that an investment vehicle generating such impressive performance has attracted a lot of attention from both finance scholars and the finance industry.

Fig. 1

Compounded returns of the momentum strategy from January 1965 to December 1989. I downloaded monthly data for 10 value-weighted portfolios sorted by cumulative past returns from Kenneth French’s data library. The portfolios are constructed daily using NYSE prior (2–12) return decile breakpoints. According to the description provided by Kenneth French’s data library, the portfolios constructed each day include NYSE, AMEX, and NASDAQ stocks with prior return data. Monthly data were obtained from January 1965 to December 1989. The zero-cost momentum portfolio buys the portfolio consisting of stocks with the highest cumulative prior return and sells the portfolio consisting of stocks with the lowest cumulative prior return. The time-series evolution of the compounded return of momentum (CRM)

The momentum effect has been documented not only for equities, but also for global individual stocks, global equity indices, currencies, global government bonds, and commodity futures (Asness et al. 2013). Interestingly, Hou et al. (2020), who implemented a comprehensive replication of 452 cross-sectional asset-pricing anomalies (including momentum), documented that 65% of those anomalies cannot clear the single-test hurdle of $\left|t\right|\ge 1.96$, whereas imposing the higher multiple-test hurdle of 2.78 raises the failure rate to 82%. Whereas the authors argued the biggest casualty of their replication to be the trading frictions literature, they emphasized that “price momentum fares well in our replication” (Hou et al. 2020, p. 2037). Unsurprisingly, Nyberg and Pöyry (2014, pp.1465f) highlighted, “The prevalence and robustness of the momentum effect justify the abundance of theoretical and empirical research that has been directed at uncovering the underlying reasons for the large payoffs from the trading strategy.” It is interesting to note that regardless of the “story” that scholars have told to explain the origin of momentum profits, there is one commonality in their foundations: the scholars have insisted that “the momentum strategy produces, on average, a payoff of about 1% per month with t-statistics indicating statistical significance on at least a 5% level.” Again, this has been even confirmed in Hou et al.’s (2020) scientific replication. Unequivocally, scholars believe in the strategy’s profitability.

Interestingly, Daniel and Moskowitz (2016) documented that the strong positive average returns and Sharpe ratios of momentum strategies are punctuated by occasional crashes manifested in negative returns, which can be pronounced and persistent. To illustrate this issue, Fig. 2 plots the compounded returns of two stock-price momentum strategies over a sample from January 1965 to April 2022. The black curve in Fig. 2 shows the time-series evolution of the compounded returns of the standard momentum strategy, whereas the gray curve in Fig. 2 shows the time-series evolution of the momentum strategy’s compounded returns, where 1% of the sample observations exhibiting the highest level of volatility are excluded.² Unsurprisingly, all those excluded months fall into the ex-post December 1989 period. More interestingly, those 1% of sample observations represent more than 90% of the potential overall compounded return of the momentum strategy—which, paradoxically, seems to be an issue whose theoretical and practical implications have not been further elaborated on in the corresponding momentum literature. This study fills this important gap in the literature.

Fig. 2

Compounded returns of the momentum strategy from January 1965 to April 2022. I downloaded monthly data for 10 value-weighted portfolios sorted by cumulative past returns from Kenneth French’s data library. The portfolios are constructed daily using NYSE prior (2–12) return decile breakpoints. According to the description provided by Kenneth French’s data library, the portfolios constructed each day include NYSE, AMEX, and NASDAQ stocks with prior return data. Monthly data were obtained from January 1965 to April 2022. The zero-cost momentum portfolio buys the portfolio consisting of stocks with the highest cumulative prior return and sells the portfolio consisting of stocks with the lowest cumulative prior return. The black curve in the time-series evolution of the compounded return of momentum (CRM). The gray curve in the time-series evolution of the CRM where the months exhibiting the highest level of volatility were excluded

Hence, the purpose of this study is to examine the realized variance risk of the well-known traditional stock-price momentum strategy implemented among US stocks.³ Perhaps because of its popularity, the standard momentum strategy based on 1-year prior performance and a holding period of 1 month has even been proposed as a risk factor for various asset-pricing models.⁴ In the corresponding finance literature, risk has been typically measured in terms of variance (or volatility, that can also be measured based on standard deviation, i.e., square root of variance of returns). Using daily returns of the momentum portfolio, which is a self-financing investment strategy, I compute realized variances for various time frequencies ranging from weekly to semiannually. Then, I employ log–log regressions to estimate power-law exponents for various variance time frequencies of the momentum strategy. While Mandelbrot (2008) argued that log–log regression lines of different time frequencies with identical slopes is prima facie evidence of power-law behavior, I explicitly perform statistical tests for invariance of realized momentum variances. Additionally, I test whether the estimated power-law exponents are stable over time by splitting variance samples into nonoverlapping subsamples, where the first subsample is used to estimate confidence intervals for hypothesis testing. Furthermore, I test the plausibility of the power-law hypothesis by differentiating the lognormal distribution from power laws. I also implement a more data-driven approach to estimate power-law exponents and test whether those estimates are covered by the confidence intervals derived from the uncertainty of the point estimates from log–log regressions. Finally, I test the effect of time aggregation, which is an important issue, especially in the context of financial risk as studied here.

This study contributes to the existing literature in many important ways. First, while earlier literature has acknowled that the momentum strategy suffers from occasional crashes, as documented by Daniel and Moskowitz (2016) and Barroso and Santa-Clara (2015), among others, the literature has not further quantified the implied risk associated with the momentum strategy. The current study takes a novel perspective by modeling the realized momentum variances as power laws and tests the invariance hypothesis. This methodological approach is in line with Taleb (2020), who argued, “There are a lot of theories on why things should be power laws, as sort of exceptions to the way things work probabilistically. But it seems that the opposite idea is never presented: power laws should be the norm, and the Gaussian a special case …” (p. 91). Recent studies have found evidence for power-law behavior in the unconditional volatility distribution of future markets (Renò and Rizza 2003), realized variances for commodities, exchange rates, cryptocurrencies, and the S&P 500 (Grobys 2021; Grobys et al. 2021). This is the first study testing the power-law hypothesis for realized variances of various time frequencies for a zero-cost investment vehicle such as the popular momentum strategy. The difference between a stock portfolio such as the S&P 500 and the momentum strategy is that the momentum strategy, according to Daniel and Moskowitz (2016), behaves at times like written call options on the market, meaning that momentum risk may exceed the market risk by a substantial margin.⁵

Next, earlier literature has documented that realized asset variances are typically very close to a lognormal distribution (e.g., Andersen et al. 2001a, b). However, Renò and Rizza (2003), who studied the unconditional volatility distribution of the Italian futures market, concluded that the standard assumption of lognormal unconditional volatility has to be rejected and that a much better description is provided by a Pareto distribution. Recent studies have supported Renò and Rizza’s (2003) study by testing the power-law null hypothesis for foreign exchange rate variances, commodity variances, cryptocurrency variances, S&P 500 variances, and volatilities of stable cryptocurrencies, often referred to as “stablecoins” (Grobys 2021; Grobys et al. 2021). To clarify whether Pareto distributions, or power laws, are more appropriate than the lognormal for describing realized momentum variances, we apply Bayes’ rule, as recently proposed by Taleb (2020), to explicitly test the plausibility of the lognormal distribution as opposed to power laws.

In the wake of Mandelbrot’s (1963a) seminal study documenting that the theoretical variance of cotton-price changes is infinite, or undefined, follow-up research neglecting to account for this problem in choosing research methodologies has typically claimed the argument raised by Teichmoeller (1971), among others, who pointed out that the variance stabilizes with increasing sample size because under time aggregation, the overall shape of return distributions gets closer to the normal distribution. Unsurprisingly, this issue was also acknowledged by Mandelbrot (2008): “Likewise with financial data. Scaling works in the broad, macroscopic middle of the spectrum; but at the far ends, in what you might call the quantum and cosmic zones, new laws of economic life apply” (p. 219). On the other hand, Taleb (2020) posited that scholars can’t argue with “Gaussian behavior” if kurtosis is infinite, even when lower moments exist and even for a power-law exponent corresponding to α ≈ 3. Because the central limit operates very slowly, n of the order of 10⁶ is required to become acceptable. As pointed out by Taleb (2020), the problem is that we do not have so much data in the history of financial markets; as a consequence, we are not in a research environment allowing us to use Gaussian methodologies. With earlier studies having focused on financial return processes, the inevitable question arises: When does risk settle down? Adding to this strand of literature, this is the first study that explicitly tests the effect of time aggregation in realized-variance processes of the momentum strategy. Uncovering the risk behavior of the momentum strategy is an important issue, especially because many hedge funds rely on strategies like this, as pointed out by Kelly et al. (2021) and Jegadeesh and Titman (2001), among others.

The results of this study show that realized momentum variance is scaling. Using traditional log–log regressions, the power-law exponents for the variance processes are estimated at $\widehat{\alpha }<2$ regardless of the data frequency. This suggests that the theoretical mean of realized momentum variances is infinite. This result is in line with Mandelbrot (1963a), who was the first to document that the variance for cotton-price changes is infinite. The difference between Mandelbrot’s (1963a) study and the current research is that the current study directly employs realized variances as opposed to simple returns sorted into subsamples of positive and negative returns. Testing for invariances across various variance time frequencies shows that the invariance hypothesis cannot be rejected, meaning that the scaling behavior does not vanish as we move from higher to lower frequented data. This is indeed a novel finding because according to the effect of time aggregation, power-law exponents should be expected to increase in their economic magnitudes as we move from higher to lower frequented data. To explore this issue in more detail, power-law exponents are regressed on the corresponding measured returns, respectively, number of observations used in the vintages of data frequencies. Surprisingly, the regression results rather provide evidence for the opposite effect; that is, as we move from higher to lower frequented data, power-law exponents decrease. This starkly contrasts the literature on the effect of time aggregation and suggests that momentum strategies are even riskier over longer time horizons. Moreover, sample split tests reveal that the invariance hypothesis holds, even over time, because estimated power-law exponents for later subsamples fall into the 95% confidence intervals derived from estimated power-law exponents and their corresponding estimation uncertainty based on earlier subsamples. Again, this result holds regardless of the data frequency examined and suggests that the scaling behavior of momentum risk remains the same over time.

In contrast to Andersen et al. (2001a, b) and others, who argued that realized asset variances follow a lognormal distribution, the results of the current research show that even if we assume the likelihood of the lognormal distribution to be 70%, the odds of the lognormal distribution generating the extreme events observed in the cross-section of variance data frequencies are less than 50%, suggesting that the lognormal distribution can be ruled out as an underlying variance-generating process. While this result contrasts that of Andersen et al. (2001a, b), it aligns with that of Renò and Rizza (2003), who found similar evidence for the volatility process governing the Italian futures market.

Finally, using a more data-driven approach (Lux 2000) as opposed to employing traditional log–log regressions supports the findings that (a) for most time frequencies, the point estimates for power-law exponents are $\widehat{\alpha }<2$ and (b) using a different statistical test, for most time frequencies the power-law null hypothesis cannot be rejected. Because the results of this study show the risk for the momentum strategy to be infinite, there are some inevitable implications for which scholars need to account when referring to “statistical significance.” First, we do not observe the momentum premium, and second, average momentum returns do not have a defined t-statistic, regardless of the time frequency used in the estimation. Another consequence is that Sharpe ratios for the momentum strategy are not defined either. Therefore, the inevitable conclusion of this study is that the momentum literature seems to be subject to “story-telling” rather than documenting scientific results because the common foundation for this literature stays empirically on extremely shaky ground. “Statistically significant average returns to the momentum strategy” are an illusion because in real life we don’t know anything about the profitability of this investment vehicle.

This study is organized as follows. The next section presents the background for this study. The empirical framework is provided in the third section and the last section concludes.

2 Background discussion

Statistical inference based on standard methodologies in finance research, such as ordinary least-squares (OLS) regressions or general autoregressive conditional heteroskedasticity (GARCH) models, are typically derived under Gaussian assumptions. Interestingly, in a Gaussian world, the sum of the largest 1% observations account for only 3.6% of the cumulative total.⁶ The Gaussian model tells us that large deviations have a negligible impact on the cumulative total and that extremely large deviations from the mean are virtually impossible to observe. For instance, the Gaussian model suggests that the odds for observing a 5-sigma event are 1:3,500,000. As we move from 1 to 2 to 2 to 3 standard deviations from the mean, the odds for observing such deviations exponentially decelerate as we move away from the center. In this regard, Taleb (2010, p. 232) argued that the rapid decline in the odds of large standard deviations justifies ignoring outliers. But what does this look like in reality? Mandelbrot (2008) highlighted, “Whatever the stock index, whatever the country, whatever the security, prices only rarely follow the predicted normal pattern. My student, Eugene Fama, investigated this for his doctoral thesis. Rather than examine a broad market index, he looked one-by-one at the thirty blue-chip stocks in the Dow. He found the same, disturbing pattern: Big price changes were far more common than the standard model allowed. Large changes, of more than five standard deviations from the average, happened two thousand times more often than expected. Under Gaussian rules, you should have encountered such drama only once every seven thousand years; in fact, the data showed, it happened once every three or four years” (p. 96).

In his 1963 paper entitled “New methods in statistical economics,” published in the well-known Journal of Political Economy, Benoit Mandelbrot introduced power laws in an effort to address the problem of large standard deviations from the mean, often referred to as “extreme events.”⁷ Indeed, power laws are a distribution class allowing for large standard deviations from the mean despite the remaining rare events. In the same year, Mandelbrot (1963a) published another study proposing the usage of stable Paretian distributions to model the variation of some asset returns. In a review article, Fama (1963) commented on Mandelbrot’s proposition as follows:

… the infinite variance assumption of the stable Paretian model has extreme implications. From a purely statistical standpoint, if the population variance of the distribution of first differences is infinite, the sample variance is probably a meaningless measure of dispersion. Moreover, if the variance is infinite, other statistical tools (e.g., least-squares regression) which are based on the assumption of finite variance will, at best, be considerably weakened and may in fact give very misleading answers. (p. 421)

Paradoxically, despite knowing about the problems associated with financial analysis based on Gaussian frameworks, finance researchers (including Fama whom Mandelbrot supervised) have continued to use techniques such as OLS for the vast majority of scientific studies published in leading finance journals. Yet, another strand of literature has emerged consistent with Mandelbrot’s ideas incorporating power laws in financial research. Often-cited studies in this field are those of Gopikrishna et al. (1998), Jansen and de Vries (1991), Mantegna and Stanley (1995), and Lux (1996), among others. A potential reason why leading finance scholars such as Fama—who was Mandelbrot’s doctoral student and, hence, knew about this issue in detail—have not adopted Mandelbrot’s new methods in financial research could be that more easily applicable alternatives have gained increasing acceptance. For instance, Markowitz’s (1952) modern portfolio theory based on a Gaussian framework has appealed to finance scholars, even though its assumptions do not reflect the reality of financial markets. It is noteworthy that Markowitz’s (1952) study was published a decade before Mandelbrot’s (1963a, b) contributions; incorporating Mandelbrot’s ideas could have had possibly devasting consequences for the finance lobby by nullifying a decade of follow-up research based on Markowitz’s (1952) foundation. Is it possible that the high rate of replication failure for financial studies is a manifestation of researchers’ reliance on Gaussian methodologies, which, in the presence of sample-specific variances, give very misleading results, as noted in Fama’s (1963) early paper?

It is important to note that Lux and Alfarano (2016) argued that power-law exponents for the return-generating processes of most asset classes are greater than 2 and close to 3, thereby rejecting the infinite-variance hypothesis. However, Mandelbrot’s (1963a) infinite-variance hypothesis has been confirmed for the returns on venture capital and research and development (R&D) investments (Lux and Alfarano 2016). On the other hand, Taleb (2020) conjectured that if the fourth moment is unknown, the stability of the second moment is not ensured. This implies that if α < 5, we cannot work with the variance, even if it exists in the theoretical distribution. Whereas the variance is undefined for α < 3, α < 5 implies that the kurtosis is undefined, and hence, the variance is unstable. Further, Taleb (2020, p. 187f) pointed out that for α ≈ 3, the central limit operates very slowly and requires more than 10⁶ observations to become acceptable. As a consequence, α < 3 and α < 5 have qualitatively the same implications because in real life we do not have that much data available in financial markets.

While previous literature has focused on the absolute amount of asset returns when estimating power laws, Grobys et al. (2021) employed realized annualized daily cryptocurrency volatilities based on their intraday quotes for estimating their power-law models. Their approach was supported by Wan and Yang (2009), who documented that.⁸

… realized volatility based on intraday quotes is a consistent and highly efficient estimator of the underlying true volatility … a realized-volatility-based approach is able to uncover volatility features (asymmetric volatility in particular) that the conventional GARCH type models fail to reveal. (p. 600)

Grobys et al. (2021) found that the volatilities of major stablecoins are statistically unstable because α < 3 for the volatility processes implies that the variance of the volatilities is not defined. Another related study by Grobys (2021) computed realized annualized daily financial asset market variances based on intraday quotes for estimating power-law models. For five different markets, the study concluded that the variances of variances do not exist as α < 3. Adopting this new approach, this is the first study that explores the risk of a self-financing investment vehicle such as the popular momentum strategy in terms of its realized variances. Unlike in the works of Grobys et al. (2021) and Grobys (2021), the methodological approach for computing realized variances chosen in this study uses the sum of squared daily returns for various frequencies.⁹

3 Empirical analysis

3.1 Data

I downloaded daily data for 10 value-weighted portfolios sorted by cumulative past returns from Kenneth French’s data library. The portfolios are constructed daily using NYSE prior (2–12) return decile breakpoints. According to the description provided by Kenneth French’s data library, the portfolios constructed each day include NYSE, AMEX, and NASDAQ stocks with prior return data. Daily data were obtained from November 3, 1926 to June 30, 2022 corresponding to 25,171 observations. The zero-cost momentum portfolio buys the portfolio consisting of stocks with the highest cumulative prior return and sells the portfolio consisting of stocks with the lowest cumulative prior return. I compute realized momentum variances (RMVs) for different time frequencies using nonoverlapping squared daily returns:

$$ RMV_{t} = \mathop \sum \limits_{j = 1}^{N} R_{j,t}^{2} , $$

(1)

where ${R}_{j,t}$ denotes the daily return of the momentum portfolio on day j in time unit t and $N\in (5, 20, 60, 90, 125)$. For instance, $N=5$ corresponds to weekly RMV, whereas $N=125$ corresponds to semiannual RMV. Using nonoverlapping observations to compute various RMVs, the range of RMVs is from $t=1,\dots , 200$ for semiannual data to $t=1,\dots , \text{5,033}$ for weekly data . In the appendix in Fig. 4, 5, 6, 7 and 8, the RMVs are plotted for various data frequencies and Table 1 reports the descriptive statistics. As expected, we observe from Table 1 that mean, median, minimum, maximum, and standard deviation increase as we move from higher to lower frequented variance data (viz., as we move from weekly to semi-annually variance data), whereas kurtosis and skewness decrease. Interestingly, we see that the share of the top 20% of the cumulative total of the distribution only slightly decreases as we move from more to less frequent realized-variance data. Specifically, the share of the top 20% of the cumulative total of the distribution is 0.77 for RMV based on five squared daily returns and 0.69 for RMV based on 125 squared daily returns. This is an important issue because it tells us that a small fraction of observations has a large impact. Note that for a normal distribution, the share of the top 20% of the cumulative total of the distribution is only 0.44, whereas this figure is 0.56 for the lognormal distribution. This means that the distributions appear to be closer to the well-known Pareto 80/20 distribution, where the share of the top 20% of the cumulative total of the distribution is 0.80.

Table 1 Descriptive statistics of momentum-realized variances for various time frequencies

3.2 Linear binning and estimation of power-law exponents

A widely used way to quantify an empirical frequency distribution is to bin the observed data using bins of constant linear width, which generates the familiar histogram. Specifically, linear binning entails choosing a bin, i, of constant width, counting the number of observations in each bin, and plotting this count against the average value of realizations in each bin. The traditional approach to estimating the power-law exponent, $\widehat{\alpha }$, is then to fit a linear regression to log-transformed values of both frequency and averaged realization with the slope of the line being the estimates exponent. This approach requires that bins with zero observations are excluded because $\text{ln}(0)$ is undefined. Here, for each time frequency, the variance observations are binned into a series of 10 equal intervals, and then the average variance within each interval is calculated and the number of observations is counted. Denoting the natural logarithm of the number of observations within each interval as ${y}_{i}$ and the natural logarithm of the average realized variance within each interval as ${x}_{i}$, where $i=1,\dots ,N$, we plot the so-called log–log graphs for various time frequencies in Figs. 9, 10, 11, 12 and 13 in the appendix.¹⁰ For each graph, a linear trend line is added. From visual inspection of Figs. 9, 10, 11, 12 and 13, it becomes evident that the dots slope about the same way, which is, according to Mandelbrot (2008, p. 163), prima facie evidence of power-law behavior.

To investigate the scaling behavior of RMVs given various data frequencies, the following power-law model is employed:

$$ p\left( x \right) = Cx^{ - \alpha } $$

(2)

where $x={\text{RMV}}$ and $C={\left(\alpha -1\right)x}_{MIN}^{\alpha -1}$ with $\alpha \in \left\{{\mathbb{R}}_{+}\left|\alpha \right.>1\right\}$, $x\in \left\{{\mathbb{R}}_{+}\left|{x}_{MIN}\le x<\infty \right.\right\}$, ${x}_{MIN}$ is the minimum value of RMV that is governed by the power-law process, and $\alpha$ is the magnitude of the specific tail exponent.¹¹ Regarding $\alpha$, Taleb (2020, p. 34) observed that the tail exponent of a power-law function captures via extrapolation the low-probability deviation not seen in the data, which plays, however, a disproportionately large role in determining the mean. Using this model, it can be shown that the conditional expectation of RMV defined as $E[X{|}X\ge x_{MIN}]$, is given by

$$E[X{|}X\ge x_{MIN}] = \mathop \smallint \limits_{{x_{{{\text{MIN}}}} }}^{\infty } xp\left( x \right)dx = \frac{{\left( {\alpha - 1} \right)}}{{\left( {\alpha - 2} \right)}}x_{{{\text{MIN}}}}, $$

(3)

whereas the conditional second moment, $E[X^{2}{|}X\ge x_{MIN}]$, or the variance of the conditional variance, is defined as

$$E[X^{2}{|}X\ge x_{MIN}] =\mathop \smallint \limits_{{x_{MIN} }}^{\infty } x^{2} p\left( x \right)dx = \frac{{\left( {\alpha - 1} \right)}}{{\left( {\alpha - 3} \right)}}x_{MIN}^{2}. $$

(4)

Conditional higher moments of order $k$ are analogously defined as

$$ E[X^{k}{|}X\ge x_{MIN}] = \frac{{\left( {\alpha - 1} \right)}}{{\left( {\alpha - 1 - k} \right)}}x_{MIN}^{k} .$$

(5)

From Eq. (3), it follows that the mean of the RMV only exists for $\alpha >2$, whereas the variance of RMV only exists for $\alpha >3$. Denoting the natural logarithm of the number of observations within each interval as ${y}_{i}$ and the natural logarithm of the average RMV within each bin as ${x}_{i}$, where $i=1,\dots ,N$, the following regression model is run for each time frequency:

$$ y_{i} = c + \alpha x_{i} + \varepsilon_{i} . $$

(6)

Panel A in Table 2 reports the point estimates for $\alpha$ and $c$, as well as the corresponding t-statistics and the values for the coefficient of determinations for each data frequency. Note that in the regression models, only bins with nonzero entries are accounted for. Further, 95% confidence intervals for $\widehat{\alpha }$ estimates are reported, too. From Panel A in Table 2, we observe that point estimates $\widehat{\alpha }$ are below 2 ($\widehat{\alpha }<2$) for all time frequencies. This suggests (a) prima facie evidence of a power law behavior and (b) that the theoretical means for RMVs are, according to Eq. (3), undefined. Moreover, the values for the coefficients of determination range between 0.94 and 0.99, suggesting an excellent data fit.

Table 2 Estimating power-law exponents using OLS regressions

Next, setting up the power-law model as defined in Eq. (2) requires a value for ${x}_{MIN}$. Hence, the question arises: Which value for ${x}_{MIN}$ should be chosen? The Hill estimator, which coincides with the maximum likelihood estimator (MLE), gives us the corresponding $\widehat{\alpha }$ for each value of $x$ selected for ${x}_{MIN}$, given by

$$ \hat{\alpha } = 1 + T\left( {\mathop \sum \limits_{i = 1}^{T} {\text{ln}}\left( {\frac{{x_{i} }}{{x_{{{\text{MIN}}}} }}} \right)} \right)^{ - 1} $$

(7)

where $\widehat{\alpha }$ denotes the MLE for a given ${x}_{MIN}$, $T$ is the number of observations exceeding ${x}_{MIN}$, and other notations are as before. In the appendix, Figs. 14, 15, 16, 17 and 18 show the Hill plots for various time frequencies, and Panel B in Table 2 shows the value for ${x}_{MIN}$ matched with the corresponding $\widehat{\alpha }$ obtained from OLS regressions. Using these cutoffs, we see from Panel B of Table 2 that the part of the distributions governed by a Paretian tail ranges from 60.20% for the highest data frequency to 99.50% for the lowest data frequency, which is a surprising finding because one might have expected the percentage of observations governed by a power law rather to decrease.

3.3 Can the infinite-variance hypothesis be statistically rejected?

The question arises whether the point estimates from the log–log regression are statistically below the value of 2, which is, obviously, a critical issue. Recall that Fama (1963) reviewed Mandelbrot’s proposition and commented,

From a purely statistical standpoint, if the population variance of the distribution of first differences is infinite, the sample variance is probably a meaningless measure of dispersion. Moreover, if the variance is infinite, other statistical tools (e.g., least-squares regression) which are based on the assumption of finite variance will, at best, be considerably weakened and may in fact give very misleading answers. (p. 421)

Hence, to test the infinite-variance hypothesis, the following hypothesis is tested for each data frequency:

$$ H_{0} : \alpha > 2\;{\text{versus }}\;H_{1} : \alpha \le 2. $$

The one-sided test statistic $\widehat{\lambda }=(2-\widehat{\alpha })$ is distributed as t-distribution with degrees of freedom equal to the number of nonzero bins lowered by 2. For example, for testing the hypothesis for weekly variance data, the t-distribution with five degrees of freedom is used as a reference distribution. The corresponding critical values for each reference distribution and test results are reported in Panel B of Table 2. The results suggest that for the majority of data frequencies (e.g., monthly, quarterly, and semiannually), the null hypothesis is rejected. Hence, the RMVs appear to be governed by power laws with no theoretically defined means. This result supports Mandelbrot’s (1963a) early finding of the infinite variance of cotton-price changes, starting an intense debate in the financial literature.

3.4 Testing for invariance

3.4.1 Testing for invariance across time frequencies

As pointed out by Mandelbrot (2008), the slopes of the log–log regression lines being statistically the same is evidence of power-law behavior. Note that in a time-series context, a process is a fractal, that is, statistical self-similar, if the exponent does not change with increasing or decreasing data frequency. Hence, for each time frequency, a 95% confidence interval is estimated. The confidence interval uses the critical values for a t-distribution with degrees of freedom equal to the number of nonzero bins lowered by 2. For example, a confidence interval for weekly variance data uses the corresponding critical values of the t-distribution with five degrees of freedom multiplied by the standard deviation of the $\widehat{\alpha }$ obtained from the regression model. For instance, the 95% confidence interval for weekly RMV is $\widehat{\alpha }\in$ [1.51, 2.07]. The results for all time frequencies are reported in Panel A of Table 2. Using the confidence interval for weekly RMV as a reference, we observe that point estimates $\widehat{\alpha }$ for other data frequencies (e.g., 1.77, 1.64, 1.60, 1.51) are all inside this interval, regardless which time frequency is considered. Hence, the invariance hypothesis cannot be rejected. In the same manner, the confidence interval for any other time frequency could be used as a reference, too. The results do not change.

3.4.2 Testing for invariance over time: evidence from sample split tests

While the previous section tested the invariance of the power-law exponent across time frequencies, this section addresses the question of whether the estimated power-law exponents are stable over time. The problem with some fractal processes is that it takes a long time to reveal their properties (Taleb 2010). To have at least 200 sample observations available, only RMVs incorporating between 5 and 60 daily squared returns are considered. Specifically, for each time frequency and each subsample, the variance observations are again binned into a series of $N=10$ equal intervals, and then the average realized variance within each interval is calculated and the number of observations is counted. Denoting the natural logarithm of the number of observations within each interval as ${y}_{i}$ and the natural logarithm of the average RMV in each bin as ${x}_{i}$, where $i=1,\dots ,N$, the log–log regression model of Eq. (6) is run for each time frequency and subsample. The results are reported in Table 3. Panel A of Table 3 reports the log–log regression results for the first (e.g., earlier) subsample, and Panel B of Table 3 reports the results for the second (e.g., later) subsample. Note again that only bins with nonzero entries are accounted for in the log–log regressions. Panel A reports 95% confidence intervals for $\widehat{\alpha }$ estimates for the first subsample. The corresponding t-statistic uses the critical values for a t-distribution with degrees of freedom equal to the number of nonzero bins lowered by 2. For instance, weekly RMV (i.e., incorporating five 5-squared daily returns) exhibits a point estimate of $\widehat{\alpha }=1.62$ and a 95% confidence interval of $\widehat{\alpha }\in$ [1.34, 1.90]. The point estimate for the second subsample is $\widehat{\alpha }=1.81$, which clearly is in the confidence interval, implying that the point estimates are statistically not different from each other. The same conclusion is drawn concerning monthly and quarterly RMVs (i.e., incorporating 20 or 60 daily squared returns). Overall, the invariance of the power-law exponents holds, even over time.

Table 3 Estimating power-law exponents using OLS regressions for subsamples

3.5 Robustness checks

3.5.1 Lognormal or power law? Differentiating distributions using Bayes’ rule

So far, the current research has adopted Taleb’s (2020) viewpoint in using power laws for modeling the distribution of RMVs because of the position that “power laws should be the norm.” The informed reader might argue that this approach starkly contrasts with earlier literature documenting that realized asset variances are typically very close to a lognormal distribution (e.g., Andersen et al. 2001a, b). It is interesting to note that Renò and Rizza (2003), who studied the unconditional volatility distribution of the Italian futures market, concluded that the standard assumption of lognormal unconditional volatility has to be rejected and that a much better description is provided by a Pareto distribution. Hence, to clarify whether power laws are indeed more appropriate than the lognormal, Bayes’ rule is applied, as proposed by Taleb (2020), to investigate the plausibility of the lognormal distribution as opposed to power laws.

Table 4 Bayes’ rule

Table 5 Estimating power-law exponents using MLE in association with the KS statistic

Table 6 Block bootstrapped distributions for the estimated power-law exponents

Table 7 Bayes’ rule for discriminating between different power-law functions

Table 8 Two-sample tests

First, in Table 10 in the appendix, extreme events for RMVs across all data frequencies are collected and transformed into so-called sigma events. Doing so requires standardizing each RMV time series and computing the standard deviations of data frequency-specific extreme events. Then, the probabilities are computed for both power-law functions—using the estimates for $\widehat{\alpha }$ and ${x}_{MIN}$ from Table 1—and the lognormal distribution. These probabilities are then used to derive the probabilities of Bayes’ rule, as outlined in detail by Taleb (2020, p. 52), to explore the likeliness of the data-generating processes of RMVs being distributed as lognormal as opposed to power laws, given the low-probability events observed in Table 10. According to Bayes’ rule, the conditional probability that the underlying distribution governing those events follows a lognormal distribution (LGN), conditional on extreme event occurrences, is defined as

$$ P\left( {LGN{|}E} \right) = \frac{{P\left( {{\text{LGN}}} \right)P\left( {E\left| {LGN} \right.} \right)}}{{\left( {1 - P\left( {LGN} \right)} \right)P\left( {E\left| {PL} \right.} \right) + P\left( {LGN} \right)P\left( {E\left| {LGN} \right.} \right)}} $$

(8)

where $P\left(LGN|E\right)$ is the probability that the distribution is lognormal given that the corresponding event occurred, $P(E\left|LGN)\right.$ is the probability of the event given that the distribution is lognormal, and $P(E\left|PL)\right.$ is the probability of the event given that the distribution is governed by a power-law process with $\left(\widehat{\alpha },{\widehat{x}}_{MIN}\right)$. Assuming various probabilities for $P(LGN)$, Table 4 reports the computed conditional probabilities $P\left(LGN|E\right)$. We observe from Table 4 that if it is assumed that the likelihood of the lognormal distribution is 50%—which is “fair”—the probability that the distribution is lognormal given the occurrence of extreme events is less than 30%, regardless which time frequency is considered. Remarkably, even if we assume that the likelihood of the lognormal distribution is 70%—which is rather “unreasonably high” as opposed to “fair”—the probability that the distribution is lognormal given the occurrence of extreme events is still less than 50%, regardless which time frequency is considered. From Table 4, it becomes evident that one needs to assume a likelihood of 90% so that the probability of the distribution being lognormal given the occurrence of the extreme events would exceed 50%—at least for four out of five time frequencies. I regard this as strong evidence in favor of power laws as opposed to the time-honored lognormal distribution.

3.5.2 Time aggregation: does the unconditional distribution converge toward normal?

Concerning time aggregation—that is, as RMV data move from more to less frequent—Segnon and Lux (2013, p. 5f) argued on the one hand that “… the variance stabilizes with increasing sample size and does not explode. Falling into the domain of attraction of the Normal distributions, the overall shape of the return distribution would have to change, i.e. get closer to the Normal under time aggregation. This is indeed the case, as has been demonstrated by Teichmoeller (1971) and many later authors. Hence, the basic finding on the unconditional distribution is that it converges toward the Gaussian, but is distinctly different from it at the daily (and higher) frequencies.” Moreover, the authors mentioned in Footnote 3, “While, in fact, the tail behavior would remain qualitatively the same under time aggregation, the asymptotic power law would apply in a more and more remote tail region only, and would, therefore, become less and less visible for finite data samples under aggregation. There is, thus, both convergence towards the Normal distribution and stability of power-law behavior in the tail under aggregation. While the former governs the complete shape of the distribution, the latter applies further and further out in the tail only and would only be observed with a sufficiently large number of observations.”

On the other hand, Taleb (2020, p. 187f) argued, “In a note ‘What can Taleb learn from Markowitz’ …, Jack L. Treynor, one of the founders of portfolio theory, defended the field with the argument that the data may be fat tailed ‘short term’ but in something called the ‘long term’ things become Gaussian. Sorry, it is not so. (We add the ergodic problem that blurs, if not eliminates, the distinction between long term and short term). The reason is that, simply we cannot possibly talk about ‘Gaussian’ if kurtosis is infinite, even when lower moments exist. Further, for α ≈ 3, Central limit operates very slowly, requires n of the order of 10⁶ to become acceptable, and is not what we have in the history of markets.” It becomes evident that opinions on this issue differ among scholars. So what does the empirical evidence in the current research suggest?

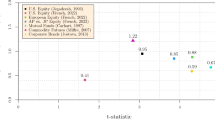
To begin with, the hypothesis tests for finding the invariance of variances, as presented in Sect. 3.3, favor in the first instance Taleb’s (2020) point of view. However, to explore this issue in more detail, I collect the point estimates for $\alpha$ from Table 2 and plot them against the corresponding data frequency, that is, from weekly to semiannual data frequency. The graph is shown in Fig. 3. Note again that here weekly RMV is the highest data frequency incorporating the sum of 5 squared daily returns, whereas semiannual realized momentum variance represents the lowest data frequency incorporating the sum of 125 squared daily returns. Moreover, a linear trend line is added to the graph. Visual inspection reveals that the slope of the trend line decreases as we move from higher to lower data frequency. Fitting an OLS regression shows that the point estimate for the slope parameter is 2.38E–03 with a t-statistic of –15.27, indicating statistical significance on any level.¹² That is, the regression model predicts, for instance, that if we wish to analyze annual RMV, the expected power-law exponent should be, accordingly, $\widehat{\alpha }=1.22$. This suggests, in turn, that as we move from higher to lower RMV data frequency, we would expect rather more extreme events as opposed to a vanishing of extreme events.

Fig. 3

Power-law exponents under time aggregation. The point estimates for α from Table 2 are collected and plotted against the number of observations used in the vintages of data for variance comparisons (‘resolution’), that is, 5, 20, 60, 90, and 125 squared daily returns. Weekly realized momentum variance is the highest resolution incorporating the sum of 5 squared daily returns, whereas semiannual realized momentum variance represents the lowest resolution incorporating the sum of 125 squared daily returns. Moreover, a linear trend line is added to the graph

Finally, from Panel B of Table 1, we observe that the percentage of variance observations governed by a power-law process linearly increases as the data frequency decreases. This starkly contrasts with Segno and Lux’s (2013) aforementioned argument that “the asymptotic power law would apply in a more and more remote tail region only, and would, therefore, become less and less visible for finite data samples under aggregation.” Hence, the overall empirical evidence of the current research suggests that the time aggregation hypothesis appears to be rather an illusion. Note that this result could be a manifestation of the option-like behavior of momentum payoffs—a phenomenon that perhaps results in incomputable riskiness of this investment vehicle.

3.5.3 Alternative maximum likelihood estimation for estimating power-law exponents

From Eq. (7), in association with the Hill plots reported in Figs. 14, 15, 16, 17 and 18, it becomes evident that $\widehat{\alpha }$ depends on the chosen value for the cutoff, that is, ${x}_{MIN}$. Selecting a proper cutoff is, of course, a tricky matter. As an example, in an attempt to replicate a study of Krämer and Runde (1996), who estimated the tail index (e.g., power-law exponent) for the German stock index DAX, as well as 26 individual constitutes over the 1960–1992 sample period, Lux (2000) argued that he couldn’t obtain the same estimates. Further, he pointed out that the enormous discrepancies between his replication attempt and the results documented by Krämer and Runde (1996) are caused by differences in the chosen cutoffs. Moreover, Lux (2000, p. 646) stated, “In view of these problems of implementations, the recent development of methods for data-driven selection of the tail sample constitutes an important advance.” Following Lux’s (2000) argument, this section employs a more recently developed data-driven approach to select $\widehat{\alpha }$, as proposed by the often-cited work of Clauset et al. (2009).

Specifically, Clauset et al. (2009) proposed a goodness-of-fit (GoF) test based on minimizing distance D between the power-law function and the empirical data. First, the Kolmogorov–Smirnov (KS) distance is the maximum distance between the cumulative density functions (CDFs) of the data and the fitted power-law model, as defined by

$$ D = {\text{MAX}}_{{x \ge x_{{{\text{MIN}}}} }} \left| {S\left( x \right) - P\left( x \right)} \right|, $$

(9)

where $S\left(x\right)$ is the CDF of the data for the observation with a value of at least ${x}_{MIN}$, and $P(x)$ is the CDF for the power-law model that best fits the data in the region $x\ge {x}_{MIN}$. Estimate ${\widehat{x}}_{MIN}$ is then the value of ${x}_{MIN}$ that minimizes D. Using the parameter vector $(\widehat{\alpha }, {\widehat{x}}_{MIN})$ that optimizes D, Clauset et al.’s (2009) GoF test generates a p-value that quantifies the plausibility of the power-law null hypothesis. More precisely, this test compares D with distance measurements for comparable synthetic data sets drawn from the hypothesized model. The p-value is then defined as the fraction of synthetic distances that are longer than the empirical distance. If we wish to use a significance level of 5%, the power-law null hypothesis is not rejected for p-values exceeding 5% because the difference between the empirical data and the model can be attributed to statistical fluctuations alone. Implementation of this test is detailed in Clauset et al.’s (2009, p. 675–678) study.

Using Clauset et al.’s (2009) approach to select the cutoffs, the results are reported in Table 5.¹³ From Table 5, we observe that the estimated optimal power-law exponents using Clauset et al.’s (2009) approach vary between 1.93 and 2.24. Specifically, for all data frequencies that have a lower frequency than weekly data, $\widehat{\alpha }<2$, which supports the earlier results based on log–log regressions. Moreover, for all time frequencies with a lower data frequency than monthly data, the GoF test cannot reject the power-law null hypothesis (i.e., p-values > 0.05), which supports the current study’s results documented in Sect. 3.6. Furthermore, for the majority of time frequencies (e.g., 60 days, 90 days, and 125 days), the point estimate for $\widehat{\alpha }$ using Clauset et al.’s (2009) approach falls in the 95% confidence interval for $\widehat{\alpha }$ using traditional log–log regressions, which suggests that—in most cases—Clauset et al.’s (2009) approach selects power-law exponents that are statistically the same as those obtained from log–log regressions. Interestingly, from Table 5 we observe that the percentage of variance observations governed by a power-law process linearly increases as the data frequency decreases which, again, supports the current study’s earlier documented results using log–log regressions.

One could argue that using MLE, the assumption is made that the data are independently distributed.

Hence, the MLE should be acknowledged here to be quasi-MLE (QMLE), as the true MLE would require modeling the dynamics explicitly. Specifically, realized variances (or conditional variances) are typically subject to autocorrelation. To explicitly address this issue, I make use of block bootstraps, as recently proposed by Grobys and Junttila (2021, Sect. 4). The authors pointed out that t-statistics derived from nonparametric block bootstraps are robust to unknown dependency structures in the data. Therefore, for each time frequency, I simulate $B=\text{1,000}$ artificial time series of RMVs using nonparametric block bootstraps with randomly drawn block lengths. For each given data frequency, I choose an expected block length of 10% of the sample length to address the presence of persistent regimes in the RMVs. Following Grobys and Junttila (2021), the randomly drawn block length follows a geometric distribution. For example, for the RMV incorporating five daily data increments, expected block length $E[h]$ corresponds to $E[h]=503$ because the sample length of the data vector is $T=\text{5,033}$. Because the geometric distribution is defined by parameter $p$ and $E\left[h\right]=(1-p)/p$, the distribution of the randomly drawn block length is governed by $GEO\left(p\right)$ with $p=0.0020$. Then, for each $b=1,\dots , B$ artificial RMV time-series vector, I compute the corresponding $\widehat{\alpha }$ using the optimized KS distance as outlined earlier. Then, based on the earlier findings, I test the infinite-theoretical-variance hypothesis

$$ H_{0} : \alpha < 2 \quad vs.\quad H_{1} : \alpha \ge 2, $$

by counting the number of estimated values $\widehat{\alpha }$ for which $\widehat{\alpha }<2$ is satisfied and dividing them by $B$, which corresponds to the empirical p-value.¹⁴ The distributional properties and the corresponding p-values for the statistical tests are reported in Table 6. From Table 6 we observe that even though mean and median are above $\widehat{\alpha }=2$ regardless which frequency is considered, the infinite-theoretical-variance hypothesis cannot be rejected for most data frequencies apart from for the RMV incorporating five daily data increments. This finding strongly supports earlier documented results for log–log regressions.

Finally, one may wonder why this study directly uses realized variances as opposed to returns. The main argument here is that RMVs incorporate aggregated information: whereas monthly returns incorporate information from only two closing prices, monthly RMV incorporates information from (at least) 40 daily closing prices. To illustrate the loss of information, I downloaded monthly data for 10 value-weighted portfolios sorted by cumulative past returns from Kenneth French’s data library covering the period from January 1927 to June 2022. The portfolios are constructed monthly using NYSE prior (2–12) return decile breakpoints. The zero-cost momentum portfolio buys the portfolio consisting of stocks with the highest cumulative prior return and sells the portfolio consisting of stocks with the lowest cumulative prior return. Using the absolute amount of the zero-cost momentum portfolio, I again estimated the power-law exponent using Clauset et al.’s (2009) approach. Interestingly, $\widehat{\alpha }=3.15$ with corresponding ${x}_{MIN}=7.41$, suggesting that both theoretical mean and theoretical variance for (absolute) monthly zero-cost momentum portfolio returns would exist.¹⁵ Recall that using the data frequency-congruent RMV (e.g., 20 daily increments) suggests that the theoretical variance is undefined as $\widehat{\alpha }=1.99$ (Table 5). It is evident that neglecting information content from aggregated information can result in misleading inference.

3.5.4 Data-driven estimation approach or traditional log–log regressions?

Given the slight discrepancy in point estimates, the question arises: Which point estimates should one choose? Taleb (2010, p. 266) pointed out the following issue: “I have learned a few tricks from experience: whichever exponent I try to measure will likely be overestimated (recall that a higher exponent implies a smaller role for large deviations) – what you see is likely to be less Black Swannish than what you don’t see. I call this the masquerade problem. Let’s say I generate a process that has an exponent of 1.7. You do not see what is inside the engine, only the data coming out. If I ask you what the exponent is, odds are that you will compute something like 2.4. You would do so even if you had a million data points. The reason is that it takes a long time for some fractal processes to reveal their properties, and you underestimate the severity of the shock.” Keeping in mind this problematic issue, it appears more reasonable to choose the estimate that delivers the exponent with the lowest economic magnitude.

This would mean in the current study’s context that OLS estimates obtained from employing traditional log–log regressions should be preferred as opposed to Clauset et al.’s (2009) data-driven approach. Recall from Fig. 1 that in the sample used to implement momentum strategies in the original study of Jegadeesh and Titman (1993), there was an absence of evidence for momentum crashes; however, that didn’t mean that there was evidence of absence for momentum crashes. From Table 9 in the appendix, we see that the top 1% of momentum payoffs exhibiting the highest volatility were observed in the ex-post period of the original sample, which underpins the reasonability of Taleb’s (2010) point of view. Indeed, low-probability events that have an extreme impact are not necessarily visible in the data ex-ante simply because these events have, per definition, a low probability of occurrence.

Nevertheless, to explore this issue in more detail, I compute the posterior probabilities using Bayes’ rule, as outlined in Sect. 3.5.1, to assess the likelihood of the data-generating processes of RMVs being governed by power laws with parameters derived from the data-driven approach, as elaborated on in this current section, as opposed to power laws with parameter estimates retrieved from traditional log–log regressions. In Table 11 in the appendix, the corresponding conditional probabilities are reported for the arrival of the observed extreme events given that the underlying distribution is either governed by power laws with parameters derived from the data-driven approach or power laws with parameter estimates derived from traditional log–log regressions. Using Bayes’ rule and those conditional probabilities from Table 11, I report in Table 7 the conditional probabilities that the distributions are governed by power laws with parameters derived from the data-driven approach given that the observed extreme events occurred. We observe from Table 7 that if it is assumed that the likelihood of the power-laws model derived from the data-driven procedure is 50%—which is “fair”—the probability that the distribution is governed by a power law with parameters derived from the data-driven approach given the arrival of the observed extreme events is less than 50%, regardless which time frequency is considered. Strikingly, considering the semiannual frequency, it becomes evident that even if we assume that the likelihood of a power law with parameters derived from the data-driven approach is 70%—which is rather “unreasonably high” as opposed to “fair”—the probability that the distribution is governed by a power law with parameters derived from the data-driven approach is still less than 50%. Overall, given the empirical evidence based on the results reported in Table 7, employing the data-driven approach does not result in superior parametrizations for the power-law functions.

3.5.5 Two-sample tests

Finally, a reader could be concerned about the tests for invariance across time frequencies, as performed in Sects. 3.4.1., because one could argue that testing whether the estimates from one frequency fall into the CI of the other does not have the correct size, as it ignores the estimation error in one sample. To address this issue, I use two-sample tests given by,

$$ z = \frac{{\left( {\hat{\alpha }_{i} - \hat{\alpha }_{j} } \right)}}{{\sqrt {\frac{{\hat{\sigma }_{{\hat{\alpha }_{i} }}^{2} }}{{n_{i} }} + \frac{{\hat{\sigma }_{{\hat{\alpha }_{j} }}^{2} }}{{n_{j} }}} }}, $$

where ${\widehat{\alpha }}_{i}$ (${\widehat{\alpha }}_{j}$) denotes the estimate for $\alpha$ for time frequency i (j), ${\widehat{\sigma }}_{{\widehat{\alpha }}_{i}}^{2}$ (${\widehat{\sigma }}_{{\widehat{\alpha }}_{j}}^{2}$) denotes the corresponding estimated sample variance, and ${n}_{i}$ (${n}_{j}$) denotes the number of observations in relative terms. For each time frequency, I collect the estimates for sample averages (viz., means) for the point estimates as well as the estimates for the corresponding variances − which are simply the squared standard deviations − from Table 6. We then use the highest time frequency (TF) incorporating 5 squared daily return observations as ${\widehat{\alpha }}_{i}$ (viz., ${\widehat{\alpha }}_{i}=2.2368$) in the formula above. The relative sample sizes of observations governed by power laws are collected from Table 5. Then I test whether the estimates for all other time frequencies j are statistically different from the estimate ${\widehat{\alpha }}_{i}$. That is,

$$ H_{0} :\left( {\alpha_{i} - \alpha_{j} } \right) = 0\quad vs.\quad H_{1} :\left( {\alpha_{i} - \alpha_{j} } \right) \ne 0. $$

The results are reported in Table 8. As an example, testing TF 5 against TF 20, the nominator for z is 0.1315. Since 0.1099 of the sample observations are governed by a power law for sample i, whereas 0.4487 of sample observations are governed by a power law for sample j, I obtain $\sqrt{{\widehat{\sigma }}_{{\widehat{\alpha }}_{i}}^{2}/{n}_{i}+{\widehat{\sigma }}_{{\widehat{\alpha }}_{j}}^{2}/{n}_{j}}=\sqrt{0.1967\cdot 0.0241+0.8033\cdot 0.0333}=0.1680$ for the denominator of z. We observe from Table 8 that we cannot reject the invariance hypothesis because the differences ${(\widehat{\alpha }}_{i}-{\widehat{\alpha }}_{j})$ are statistically not different from each other.¹⁶ I infer that the results of this robustness check strongly confirm the results documented in Sect. 3.4.1.

4 Conclusion

This study tests whether RMVs are governed by power laws. In doing, various RMV data frequencies were analyzed. The general findings of this study indicate that regardless of the methodology used to estimate power-law exponents, the power-law null hypothesis cannot be rejected. Testing for invariance shows that power-law behavior is present across all time frequencies. Various sample split tests provide further evidence for the power-law behavior not being subject to any sample specificity because the point estimates for the power-law exponents for the later subsample fall into the 95% confidence interval for the estimated power-law exponents for the first subsample. This result holds regardless of the data frequency analyzed. This implies that the data-generating process is stable across time. This result is contrary to earlier research documenting that realized variances are close to lognormally distributed. To test the lognormal distribution against power laws, this study applies Bayes’ rule. Even if it is assumed that the likelihood of the lognormal distribution is as unreasonably high as 70%, the probability that the RMV distributions are lognormal given the occurrence of observed extreme events is still less than 50%, regardless which time frequency is considered. In this study, this is interpreted as strong evidence in favor of power laws as opposed to the lognormal distribution. Furthermore, the power law behavior does not vanish for less frequent RMVs.

Surprisingly, the empirical outcome documented here suggests rather the opposite; that is, the lower the time frequency, the more extreme events can be expected in the variance processes, which is empirically manifested in a lower economic magnitude of the power-law exponent. Overall, the results of this study show that the risk for the momentum strategy is infinite, which is empirically manifested in power-law exponents of α < 2 which has, in turn, some serious consequences. First, in finite samples, we do not observe the time-honored, pervasive “momentum premium,” which is documented to correspond to 1% per month across various otherwise unrelated asset classes; second, the momentum premium does not have a defined t-statistic regardless of time frequency. The claim raised by many scholars in numerous momentum studies published in leading finance outlets that “the momentum premium exhibits a statistically significant t-statistic” is therefore invalid. Moreover, other metrics incorporating variances or functions of it, such as Sharpe ratios, are not defined either for this investment vehicle. As a result, this study argues that the momentum literature seems to be subject to “story-telling” given the absence of a firm common foundation supporting its fundamental claim. Taleb (2012) pointed out that “… theories come and go; experience stays. Explanations change all the time, and have changed all the time in history (because of casual opacity, the invisibility of causes) with people involved in the incremental development of ideas thinking they had a definite theory; experience remains constant” (p. 350). Keeping this in mind, while this study is empirical in its nature, telling its “story” is left for future studies.

Appendix

See Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18.

Fig. 4

Realized momentum variance based on five squared daily returns. Daily data for 10 value-weighted portfolios sorted by cumulative past returns were retrieved from Kenneth French’s data library. The portfolios are constructed daily using NYSE prior (2–12) return decile breakpoints. The sample is from November 3, 1926 to June 30, 2022. The zero-cost momentum portfolio buys the portfolio consisting of stocks with the highest cumulative prior return and sells the portfolio consisting of stocks with the lowest cumulative prior return. The RMVs uses nonoverlapping squared daily returns:

${RMV}_{t} = \mathop \sum \limits_{j = 1}^{N} R_{j,t}^{2} ,$

where $R_{j,t}$ denotes the daily return of the momentum portfolio on day j in time unit t and $N = 5$. Using nonoverlapping observations to compute the RMV gives us 5,033 realizations. This table plots the time series of the corresponding RMV

Fig. 5

Realized momentum variance based on 20 squared daily returns. Daily data for 10 value-weighted portfolios sorted by cumulative past returns were retrieved from Kenneth French’s data library. The portfolios are constructed daily using NYSE prior (2–12) return decile breakpoints. The sample is from November 3, 1926 to June 30, 2022. The zero-cost momentum portfolio buys the portfolio consisting of stocks with the highest cumulative prior return and sells the portfolio consisting of stocks with the lowest cumulative prior return. The RMVs use nonoverlapping squared daily returns:

${RMV}_{t} = \mathop \sum \limits_{j = 1}^{N} R_{j,t}^{2},$

where $R_{j,t}$ denotes the daily return of the momentum portfolio on day j in time unit t and $N = 20$. Using nonoverlapping observations to compute the RMV gives us 1,255 realizations. This table plots the time series of the corresponding RMV

Fig. 6

Realized momentum variance based on 60 squared daily returns. Daily data for 10 value-weighted portfolios sorted by cumulative past returns were retrieved from Kenneth French’s data library. The portfolios are constructed daily using NYSE prior (2–12) return decile breakpoints. The sample is from November 3, 1926 to June 30, 2022. The zero-cost momentum portfolio buys the portfolio consisting of stocks with the highest cumulative prior return and sells the portfolio consisting of stocks with the lowest cumulative prior return. The RMVs use nonoverlapping squared daily returns:

${RMV}_{t} = \mathop \sum \limits_{j = 1}^{N} R_{j,t}^{2} ,$

where $R_{j,t}$ denotes the daily return of the momentum portfolio on day j in time unit t and $N = 60$. Using nonoverlapping observations to compute the RMV gives us 1,255 realizations. This table plots the time series of the corresponding RMV

Fig. 7

Realized momentum variance based on 90 squared daily returns. Daily data for 10 value-weighted portfolios sorted by cumulative past returns were retrieved from Kenneth French’s data library. The portfolios are constructed daily using NYSE prior (2–12) return decile breakpoints. The sample is from November 3, 1926 to June 30, 2022. The zero-cost momentum portfolio buys the portfolio consisting of stocks with the highest cumulative prior return and sells the portfolio consisting of stocks with the lowest cumulative prior return. The RMVs use nonoverlapping squared daily returns:

${RMV}_{t} = \mathop \sum \limits_{j = 1}^{N} R_{j,t}^{2} ,$

where $R_{j,t}$ denotes the daily return of the momentum portfolio on day j in time unit t and $N = 90$. Using nonoverlapping observations to compute the RMV gives us 278 realizations. This table plots the time series of the corresponding RMV

Fig. 8

Realized momentum variance based on 125 squared daily returns. Daily data for 10 value-weighted portfolios sorted by cumulative past returns were retrieved from Kenneth French’s data library. The portfolios are constructed daily using NYSE prior (2–12) return decile breakpoints. The sample is from November 3, 1926 to June 30, 2022. The zero-cost momentum portfolio buys the portfolio consisting of stocks with the highest cumulative prior return and sells the portfolio consisting of stocks with the lowest cumulative prior return. The RMVs use nonoverlapping squared daily returns:

${RMV}_{t} = \mathop \sum \limits_{j = 1}^{N} R_{j,t}^{2} ,$

where $R_{j,t}$ denotes the daily return of the momentum portfolio on day j in time unit t and $N = 125$. Using nonoverlapping observations to compute the RMV gives us 200 realizations. This table plots the time series of the corresponding RMV

Fig. 9

Log–log graph for realized momentum variance based on five squared daily returns. Variance observations are binned into a series of $N = 10$ equal intervals, and then the average variance within each interval is calculated and the number of observations is counted. Denoting the natural logarithm of the number of observations within each interval as $y_{i}$ and the natural logarithm of the average variance within each interval as $x_{i}$, where $i = 1, \ldots ,N$, this figure shows the log–log graph for realized momentum variance based on five squared daily returns

Fig. 10

Log–log graph for realized momentum variance based on 20 squared daily returns. Variance observations are binned into a series of $N = 10$ equal intervals, and then the average variance within each interval is calculated and the number of observations is counted. Denoting the natural logarithm of the number of observations within each interval as $y_{i}$ and the natural logarithm of the average variance within each interval as $x_{i}$, where $i = 1, \ldots ,N$, this figure shows the log–log graph for realized momentum variance based on 20 squared daily returns

Fig. 11

Log–log graph for realized momentum variance based on 60 squared daily returns. Variance observations are binned into a series of $N = 10$ equal intervals, and then the average variance within each interval is calculated and the number of observations is counted. Denoting the natural logarithm of the number of observations within each interval as $y_{i}$ and the natural logarithm of the average variance within each interval as $x_{i}$, where $i = 1, \ldots ,N$, this figure shows the log–log graph for realized momentum variance based on 60 squared daily returns

Fig. 12

Log–log graph for realized momentum variance based on 90 squared daily returns. Variance observations are binned into a series of $N = 10$ equal intervals, and then the average variance within each interval is calculated and the number of observations is counted. Denoting the natural logarithm of the number of observations within each interval as $y_{i}$ and the natural logarithm of the average variance within each interval as $x_{i}$, where $i = 1, \ldots ,N$, this figure shows the log–log graph for realized momentum variance based on 90 squared daily returns

Fig. 13

Log–log graph for realized momentum variance based on 125 squared daily returns. Variance observations are binned into a series of $N = 10$ equal intervals, and then the average variance within each interval is calculated and the number of observations is counted. Denoting the natural logarithm of the number of observations within each interval as $y_{i}$ and the natural logarithm of the average variance within each interval as $x_{i}$, where $i = 1, \ldots ,N$, this figure shows the log–log graph for realized momentum variance based on 125 squared daily returns

Fig. 14

Hill plot for realized momentum variance based on five squared daily returns. This figure shows the evolution of the Hill estimator, which coincides with the MLE, giving us the corresponding $\hat{\alpha }$ for each value of $x$ selected for $x_{MIN}$ (e.g., variance cutoff):

$\hat{\alpha } = 1 + T\left( {\mathop \sum \limits_{i = 1}^{T} {\text{ln}}\left( {\frac{{x_{i} }}{{x_{MIN} }}} \right)} \right)^{ - 1}$,

where $\hat{\alpha }$ denotes the MLE estimator, or Hill estimator, for a given $x_{MIN}$, and $T$ is the number of observations exceeding $x_{MIN}$

Fig. 15

Hill plot for realized momentum variance based on 20 squared daily returns. This figure shows the evolution of the Hill estimator, which coincides with the MLE, giving us the corresponding $\hat{\alpha }$ for each value of $x$ selected for $x_{MIN}$ (e.g., variance cutoff):

$\hat{\alpha } = 1 + T\left( {\mathop \sum \limits_{i = 1}^{T} {\text{ln}}\left( {\frac{{x_{i} }}{{x_{MIN} }}} \right)} \right)^{ - 1}$,

where $\hat{\alpha }$ denotes the MLE estimator, or Hill estimator, for a given $x_{MIN}$, and $T$ is the number of observations exceeding $x_{MIN}$

Fig. 16

Hill plot for realized momentum variance based on 60 squared daily returns. This figure shows the evolution of the Hill estimator, which coincides with the MLE, giving us the corresponding $\hat{\alpha }$ for each value of $x$ selected for $x_{MIN}$ (e.g., variance cutoff):

$\hat{\alpha } = 1 + T\left( {\mathop \sum \limits_{i = 1}^{T} {\text{ln}}\left( {\frac{{x_{i} }}{{x_{MIN} }}} \right)} \right)^{ - 1}$,

where $\hat{\alpha }$ denotes the MLE estimator, or Hill estimator, for a given $x_{MIN}$, and $T$ is the number of observations exceeding $x_{MIN}$

Fig. 17

Hill plot for realized momentum variance based on 90 squared daily returns. This figure shows the evolution of the Hill estimator, which coincides with the MLE, giving us the corresponding $\hat{\alpha }$ for each value of $x$ selected for $x_{MIN}$ (e.g., variance cutoff):

$\hat{\alpha } = 1 + T\left( {\mathop \sum \limits_{i = 1}^{T} {\text{ln}}\left( {\frac{{x_{i} }}{{x_{MIN} }}} \right)} \right)^{ - 1}$,

where $\hat{\alpha }$ denotes the MLE estimator, or Hill estimator, for a given $x_{MIN}$, and $T$ is the number of observations exceeding $x_{MIN}$

Fig. 18

Hill plot for realized momentum variance based on 125 squared daily returns. This figure shows the evolution of the Hill estimator, which coincides with the MLE, giving us the corresponding $\hat{\alpha }$ for each value of $x$ selected for $x_{MIN}$ (e.g., variance cutoff):

$\hat{\alpha } = 1 + T\left( {\mathop \sum \limits_{i = 1}^{T} {\text{ln}}\left( {\frac{{x_{i} }}{{x_{MIN} }}} \right)} \right)^{ - 1}$,

where $\hat{\alpha }$ denotes the MLE estimator, or Hill estimator, for a given $x_{MIN}$, and $T$ is the number of observations exceeding $x_{MIN}$

See Tables 9, 10 and 11.

Table 9 1% of the highest-volatility months

Table 10 Probabilities of extreme events

Table 11 Probabilities of extreme events for different power-law functions