The value of expected return persistence

Abstract

This work utilizes the fractional Black–Scholes model to estimate the option-implied Hurst exponents, interpreted as forward-looking expectations of return persistence. The focus of the paper is on how corresponding believes enter into factor based asset pricing models. Empirical analyses are carried out for the cross-section of S &P 500 stocks. We make the important observations that (i) stock returns show significant patterns of time-varying persistence and (ii) corresponding believes are reflected within option prices. Incorporating the Hurst exponents allows us to split up CAPM betas into pure market correlation risk (around 70–80%) and into excess persistence believes (about 20–30% of the risk loading). A direct comparison to standard CAPM shows that incorporating persistence believes significantly improves the predictability of future realized returns, and partially releases the beta anomaly. The effects become even stronger the greater the prediction horizon. Hence, the concept of fractal motions enables a deeper understanding of risk structures without the need of additional risk factors.

1 Introduction

It is intuitive to speak of financial markets in terms of ’wild’ and ’mild’ randomness. There are smooth times of recovery and harsh movements of crashes. The fractal approach allows to quantify this behavior via long-range memory (Hurst exponent), recognized as auto-correlation in returns. In this sense, trending price-movements are understood as mild randomness, and highly overreacting ones as wild—a distinction already made by Mandelbrot (1997). Empirical evidence for persistence patterns in returns is broad [e.g., Peters (1989), Kristoufek and Vosvrda (2013)]. This fact rises the important question whether expected—as opposed to historical—persistence has an economic value or not.

Within this work we address this question from a factor-pricing perspective for the cross-section of U.S. stocks. The analytical procedure is to start with the traditional Capital Asset Pricing Model [CAPM; Sharpe (1964), Lintner (1965), Mossin (1966)] and formulate its stochastic equivalent under classic Brownian motion (cBM). In the next step, cBM is generalized to the more flexible fractal Brownian motion (fBM) to allow stock returns to be occasionally auto-correlated. It is then possible to reduce down to a discrete version again, deriving the fractal CAPM. This routine demonstrates the economic value attributed to expected return persistence without the need of inflating the factor zoo. The fractal generalization can be easily extended to multi-factor models. To the best of our knowledge, this work is first to discuss the value of expected long-range memory for the cross-section of returns.

The empirical analysis using S &P 500 data confirms our theoretical presumptions, concluding that persistence in stock returns is economically significant. Stock prices do not only reject cBM at realized returns, but also at investor expectations, which are measured from forward-looking data of option implied volatilities. In realized returns we find the interesting pattern that return persistence was less before the financial crises of 2007/2008, significantly increased during it and then decreased again afterwards. Furthermore, we find that expected return persistence as well as the economic value attributed to it varies largely among stocks. Generally, we can assert that the larger the prediction horizon, the greater the economic value of return persistence. While accounting for return persistence makes sense already for short investment horizons, it is even more beneficial for long-term investments. Comparing prediction quality of expected returns, the fractal CAPM clearly outperforms its cBM based rival. We provide robustness tests for our empirical results by predicting individual stock returns and risks, sorted portfolio analyses and statistical bootstrapping.

Our study extends the existing literature in three ways. First, our main contribution is to demonstrate how fractal Brownian Motion can be introduced into an existing factor-based asset pricing model. Second, we contribute by arguing that persistence believes have an economic value in excess of the market risk premium. And third, our results show that such an economic value empirically exists. Single stocks as well as portfolios with superior ex-ante persistence are found to generate higher absolute and risk-adjusted returns.

The reading is set up as follows. Section 2 discusses the implementation of fractal motions into factor-based models. Section 3 explains the forward-looking measurement of expected return persistence. The empirical analysis is carried out at Sect. 4. Section 5 concludes.

2 Factor pricing under long-range memory

The Capital Asset Pricing Model is one of the most prominent models in finance. It is a discrete time model assuming that equity returns are drawn from a random normal distribution with independent increments,¹ thus implicitly builds on classic Brownian motion. Basically, it states that every stock i’s expected return $\langle r_i\rangle$ is priced relative to the market portfolio m,

$$\begin{aligned} \langle r_i \rangle = \beta _i (\langle r_m \rangle - r_f) + r_f\, \end{aligned}$$

(2.1)

with $r_f$ as the risk-free rate of return and $\beta _i$ as the stock’s risk exposure determined by the covariance to the market,

$$\begin{aligned} \beta _i = \frac{cov(r_i, r_m)}{Var(r_m)} \equiv \frac{cov(R_i, R_m)}{Var(R_m)}. \end{aligned}$$

(2.2)

$R_i, R_m$ are defined below.

Following (Safdari-Vaighani et al. 2020), the basic continuous-time CAPM is now derived as follows. Start with the definition of the process for the market portfolio and the stock,

$$\begin{aligned} \frac{dS_{m,t}}{S_{m,t}} =\mu _m \, dt + \tilde{\sigma }_m \, d\tilde{X}_{m,t}=R_m \qquad {\hbox {and}}\qquad \frac{dS_{i,t}}{S_{i,t}} =\mu _i \, dt + \tilde{\sigma }_i \, d\tilde{X}_{i,t} = R_i \end{aligned}$$

(2.3)

which in excess of the risk free rate writes

$$\begin{aligned} R_m {-} r_f\, dt {=}(\mu _m {-} r_f) \, dt {+} \tilde{\sigma }_m \, d\tilde{X}_{m,t} \qquad {\hbox {and}}\qquad R_i {-} r_f\, dt {=}(\mu _i {-} r_f)\, dt{+} \tilde{\sigma }_i \, d\tilde{X}_{i,t} \end{aligned}$$

(2.4)

Now, $\tilde{X}_{i,t}$ can be split up into systematic plus unsystematic risk $\tilde{X}_{i,u,t}$. Introducing orthogonality between $\tilde{X}_{m,t}$ and $\tilde{X}_{i,u,t}$, the systematic part can be express relative to the market through the beta coefficient of Eq. (2.2). Therefore, setting the excess return of i relative to m, it follows that

$$\begin{aligned} R_i -r_f \, dt&=\beta _i\left( R_m - r_f \, dt\right) +\tilde{\sigma }_i \, d\tilde{X}_{i,u,t} \end{aligned}$$

(2.5)

$$\begin{aligned}&= \beta _i (\mu _m - r_f) \, dt + \beta _i \tilde{\sigma }_m \, d\tilde{X}_{m,t} + \tilde{\sigma }_i \, d\tilde{X}_{i,u,t} \end{aligned}$$

(2.6)

This can now be used in a discrete one-period manner. Consider the investor wants to price i according to Eq. (2.6) for the period $\tau =dt$ ahead. Since expectations of a standard Wiener process are known,

$$\begin{aligned} \forall t: \qquad \langle d\tilde{X}_{m,t}\rangle =\langle d\tilde{X}_{i,u,t}\rangle = 0 \qquad \hbox {and} \qquad \langle dt\rangle = t \end{aligned}$$

(2.7)

hence

$$\begin{aligned} \langle R_m\rangle = \mu _m \, dt \implies \langle r_m\rangle = \mu _m \end{aligned}$$

(2.8)

such that the stock’s expected return evolves as

$$\begin{aligned} \langle R_i \rangle =\left\langle \frac{dS_{i}}{S_{i}}\right\rangle = \beta _i (\mu _m - r_f) \tau + r_f\tau \end{aligned}$$

(2.9)

or in terms of return rates,

$$\begin{aligned} \langle r_i \rangle = \beta _i (\langle r_m \rangle - r_f) + r_f \end{aligned}$$

(2.10)

which is the cBM continuous time equivalent to the original discrete CAPM, meeting that $\beta \equiv \tilde{\beta }$.

We formulate the fractal CAPM as follows. Take Eq. (2.3) and replace $d\tilde{X}_{m,t}/d\tilde{X}_{i,t}$ through the fractal processes $d{X}_{m,t}/d{X}_{i,t}$,

$$\begin{aligned} R_m = \mu _m \, dt + \tilde{\sigma }_m \, d{X}_{m,t} \qquad \hbox {and}\qquad R_i =\mu _i \, dt +\tilde{\sigma }_i \, d{X}_{i,t} = R_i \end{aligned}$$

(2.11)

following the same procedure as above, one will derive

$$\begin{aligned} R_i = \beta _i (\mu _m - r_f) \, dt + \beta _i \tilde{\sigma }_m \, d{X}_{m,t} + \tilde{\sigma }_i \, d{X}_{i,u,t} \end{aligned}$$

(2.12)

By stationarity of fBM, we know that

$$\begin{aligned} \forall t: \qquad \langle d{X}_{m,t}\rangle = \langle d{X}_{i,u,t}\rangle = 0 \end{aligned}$$

(2.13)

such that again Eq. (2.9) will evolve when taking expectations. The variance scaling law of a univariat fractal motion was early discussed by Mandelbrot and Van Ness (1968). As for the multi-variate case, analytical results are presented by Amblard et al. (2012). Using these insights, the difference between classic and fractal CAPM arises from the power-law scaling effects,

$$\begin{aligned} cov(R_i, R_m) = \tilde{\sigma }_i\tilde{\sigma }_m\rho _{im} \tau ^{H_i+H_m} \qquad \hbox {and}\qquad Var(R_m) =\tilde{\sigma }_m^2 \tau ^{2H_m} \end{aligned}$$

(2.14)

in whose context the beta coefficient has now a deeper risk structure,

$$\begin{aligned} \beta _i=\frac{cov(R_i,R_m)}{Var(R_m)^2} = \rho _{im} \frac{\tilde{\sigma }_i}{\tilde{\sigma }_m}\tau ^{H_i-H_m} \end{aligned}$$

(2.15)

hence given fractal markets, $\beta \not \equiv \tilde{\beta }$ rejects classic CAPM to fully describe all risk. Let $\Delta H:=H_i-H_m$, then it gets obvious that the the stock’s risk exposure composes of the cBM risk loading $\tilde{\beta }$ (i.e., correlation risk to the market portfolio) corrected for persistence expectations in excess of the market,

$$\begin{aligned} \beta _i = \underbrace{\tilde{\beta }_i}_{\begin{array}{c} \mathrm{corr.}\\ \textrm{risk} \end{array}}\underbrace{\tau ^{\Delta H}}_{\begin{array}{c} \mathrm{pers.}\\ \textrm{risk} \end{array}} \end{aligned}$$

(2.16)

This enables to formulate the expected return within fractal CAPM as follows:

$$\begin{aligned} \langle r_i \rangle = \tilde{\beta }_i (\langle r_m \rangle - r_f) \tau ^{\Delta H} + r_f \end{aligned}$$

(2.17)

Therefore, given fractal markets, investors do not only require compensation for correlation, but also for persistence risk. From this follows that a stock’s expected persistence has an economic value attributed to it (positive or negative) as soon as $\Delta H \ne 0$. Figure 1 below illustrates fractal CAPM and the value of excess persistence graphically.

Fig. 1

Illustration of expected returns $\langle \mu _i\rangle$ under fractal CAPM, using $r_f=1\%$, $\langle \mu _m\rangle =5\%$, $H_m=0.6$ and $\tau =30$. Different to the classic setting, given fractality there exist two risk sources: correlation risk $\tilde{\beta }$ and persistence risk $\Delta H$. Left plot displays the relation of $\langle \mu _i\rangle$ to $\tilde{\beta }$ for three levels of $\Delta H$. Right plot visualizes the relation of $\langle \mu _i\rangle$ to $\Delta H$ for three levels of $\tilde{\beta }$. In classic CAPM $\Delta H$ would equal 0, indicated as the dashed blue lines in both plots (cBM). As can be seen, classic CAPM will underestimate expected returns if $\Delta H > 0$ and overestimate them if $\Delta H < 0$; due to exponential inter-temporal variance scaling, this effect is not symmetric in $\Delta H$

The first derivative of $\beta$ with respect to $\tau$ seems to uncover some economically interesting relation, that is

$$\begin{aligned} \frac{\partial \beta _i}{\partial \tau }= \Delta H \, \tilde{\beta }_i\tau ^{\Delta H-1} \quad \implies \quad \frac{\partial \langle r_i \rangle }{\partial \tau } = \Delta H \, \tilde{\beta }_i\tau ^{\Delta H-1} (\langle r_m \rangle - r_f) \end{aligned}$$

(2.18)

so ceteris paribus, if $H_i>H_m$, then it is implicitly given that a stock’s expected return rate is believed to increase over the future. Vice versa, for $H_i<H_m$, $r_i$ is believed to decline.² We interpret this phenomenon in the following sense. Consider that H is a determinant of auto-correlation; if investors expect positive auto-correlation for i, then this coerces with a shift in beta which results in an increase in expected return. On the other hand, empirical finance literature frequently refers auto-correlation within realized equity returns to stock momentum. Henceforth, we refer expected values of H to expected momentum:

$$\begin{aligned}&H_i>H_m: \qquad \hbox {pos. auto-corr.} \implies \hbox {pos. beta shift} \implies \hbox {pos. momentum believes} \\&H_i<H_m: \qquad \hbox {neg. auto-corr.} \implies \hbox {neg. beta shift} \implies \hbox {neg. momentum believes} \\&H_i=H_m: \qquad \hbox {no. auto-corr.} \implies \hbox {no. beta shift} \implies \hbox {no. momentum believes} \end{aligned}$$

Respectively, expected stock momentum can be quantified if one is able to evaluate H on an ex-ante basis. And further, it is shown that classic CAPM delivers biased estimates as soon as $H_i\ne H_m$, which we find within the empirical analysis. Fractal CAPM thus allows to correct expected returns for $\Delta H$. But also for ex-post analyzes, it delivers deeper insights into risk structures that would remain hidden under cBM based models. Also, in a fractal market one observes that the expected rate of return is dependent on the horizon $\tau$; the larger $\tau$, the greater the effect of persistence. As mentioned before, in the context of inter-temporal variance scaling effects, Eq. (2.17) now further highlights how cBM’s over/underestimation of risk results in an over/underestimation of expected returns, which fosters the importance of fractal CAPM in terms of asset pricing.

Worth to mention, the one-factor fractal CAPM can be easily extended to include multiple factors [e.g., Carhart (1997) or Fama and French (2015)]. Equation (2.14) comes very handy for such a generalization. Consider one extends basic CAPM by k risk factors, then

$$\begin{aligned} \langle r_i \rangle -r_f = \begin{pmatrix} \beta _{i,m}\\ \vdots \\ \beta _{i,k} \end{pmatrix}' \cdot \begin{pmatrix} \mu _m - r_f\\ \vdots \\ \mu _{k} - r_f \end{pmatrix} = \left[ \begin{pmatrix} \tilde{\beta }_{i,m}\\ \vdots \\ \tilde{\beta }_{i,k} \end{pmatrix} \otimes \begin{pmatrix} \tau ^{H_i-H_m}\\ \vdots \\ \tau ^{H_i-H_{k}} \end{pmatrix}\right] ' \cdot \begin{pmatrix} \mu _m - r_f\\ \vdots \\ \mu _{k} - r_f \end{pmatrix} \end{aligned}$$

(2.19)

Also, the Hurst exponent of a portfolio can be computed as follows. Let p denote the portfolio which’s constituents i are weighted according to $w_p$ and $\forall i \in p: \, \sum w_i=1$, then

$$\begin{aligned} Var(R_p)=\tilde{\sigma }_p^2\tau ^{2H_p}&= \sigma _p^2\tau \end{aligned}$$

(2.20)

$$\begin{aligned} H_p&= 0.5 + \frac{\ln (\sigma _p) - \ln (\tilde{\sigma }_p)}{\ln (\tau )} \end{aligned}$$

(2.21)

where

$$\begin{aligned} \tilde{\sigma }_p^2 = w_p' \tilde{\Sigma } w_p \qquad \hbox {and} \qquad {\sigma }_p^2 = w_p' {\mathcal {T}} \tilde{\Sigma } {\mathcal {T}} w_p, \qquad \tilde{\Sigma } = \tilde{D} \Gamma \tilde{D} \end{aligned}$$

(2.22)

with ${\mathcal {T}}$ capturing individual H’s as a diagonal matrix that takes the form

$$\begin{aligned} diag({\mathcal {T}}) = \begin{pmatrix} \tau ^{H_1-0.5}&\cdots&\tau ^{H_n-0.5} \end{pmatrix} \end{aligned}$$

(2.23)

and $\tilde{D}$ as a diagonal matrix of stock volatilities ($\forall i: \tilde{D}_{ii}=\tilde{\sigma }_i$) and $\Gamma$ as the cross-sectional correlation matrix.

3 Measuring expected persistence

Black and Scholes (1973) were pioneers to develop the first continuous time arbitrage free market model. Consider a financial market of a risk-free asset A and some risky asset S, $dA_t=r_fA_t\,dt$ and $dS_t=\mu S_t \, dt + \hat{\sigma } S_t d\tilde{X}$. Under the assumption that the risky asset S will follow a classic BM (i.e., assuming that $\hat{\sigma } = \tilde{\sigma }$), they derived the closed form solution for a Call option’s price:

$$\begin{aligned} {C}(S_t, K, \tau , r_f, \hat{\sigma })=S_t\phi (\hat{d}_1) -K^{-r_f\tau }\phi (\hat{d}_2) \end{aligned}$$

(3.1)

with

$$\begin{aligned} \hat{d}_1=\frac{ln\left( \frac{S_t}{K}\right) +r_f\tau +\frac{1}{2}\hat{\sigma }^2\tau }{\hat{\sigma }\sqrt{\tau }} \qquad \hbox {and}\qquad \hat{d}_2=\hat{d}_1-\hat{\sigma } \sqrt{\tau } \end{aligned}$$

(3.2)

where $\phi$ denotes the standard normal pdf, C the Call price and K the strike price. Since all parameters except $\hat{\sigma }$ within this equation can be observed from market data, it can be iteratively solved for it, which is commonly known as implied (Black–Scholes) volatility. For some given t, $\hat{\sigma }$ can thus be computed for different strikes and maturities, which spans the three dimensional implied volatility surface. This implied volatility surface would be theoretically flat if all assumptions made in the (Black and Scholes 1973) model would be fulfilled. Empirically, however, this is hardly the case. For the fractal generalization the term-structure of implied volatilities ($\hat{\sigma }$ vs. $\tau$) is of special interest, Fig. 2 visualizes a corresponding example.

Fig. 2

Annualized empirical Black–Scholes implied volatility surface of ATM options of the S &P500 observed on two different dates (30/09/2008 and 29/09/2017). In the standard Black–Scholes model this would be flat, which empirically hardly holds. The problem arises that there is no unique value for the expected volatility such that the true expected risk $\tilde{\sigma }$ of a classic BM will be unknown. From that follows, that certain assumptions made within the model. This motivates to generalize to the more flexible fractal BM

Note that the ATM implied volatility curve reflects (risk-neutral) expected risk of the underlying, as by this 100% moneyness level Put and Call prices are (almost) symmetric. Key within the Black–Scholes market model is that the underlying series is a stationary process with deterministic volatility, hence every price process (taken under the physical ${\mathbb {P}}$ measure) can be transformed into a risk-neutral valuation process (${\mathbb {Q}}$-measured) via the Girsanov theorem in order to incorporate investor preferences (= risk premium).³ Nevertheless, as several assumptions are not met empirically, different approaches exist to release them in order to estimate more realistic option prices. Among other, one of such approaches is to generalize cBM to fBM.

Elliott and Van Der Hoek (2003) and Hu and Øksendal (2003) are first to extend the Black and Scholes (1973) market model in order to allow the risky asset to be driven by a fBM. The setting is similar, except that the risky asset is now driven by a fBM: $dS_t=\mu S_t \,dt + \tilde{\sigma } S_t\, dX_t$. The arbitrage-free proof of Hu and Øksendal (2003) also builds on the Girsanov theorem, which comes handy since fBM is also stationary. Hence, the ${\mathbb {P}}$ to ${\mathbb {Q}}$ transformation is also done via the drift term (i.e., changing $\mu$ to $r_f$ for valuation purposes) such that the price of a fractal Black–Scholes option looks familiar:

$$\begin{aligned} C(S_t, K, \tau , r_f, \sigma , H)=S_t\phi (d_1)-K^{-r_f\tau }\phi (d_2) \end{aligned}$$

(3.3)

with

$$\begin{aligned} {d_1}=\frac{ln\left( \frac{S_t}{K}\right) +r_f\tau +\frac{1}{2}\tilde{\sigma }^2\tau ^{2H}}{\tilde{\sigma }{\tau }^H} \qquad \hbox {and}\qquad {d_2}={d_1}-\tilde{\sigma }\tau ^H. \end{aligned}$$

(3.4)

Different to standard Black–Scholes, in the fractal version one faces two unknown parameters, that is $\tilde{\sigma }$ and H. Since for one underlying there are typically substantially more than one options available, they can be easily estimated by either fitting Eq. (3.3) to Call prices, or in a two-step procedure. The latter is implemented as follows. Consider we are only interested into ATM options that replicate the underlying and let $\hat{\sigma }(\tau )$ be the Black–Scholes point estimate of implied volatility (Eq. 3.1), which, when interpreted as cBM volatility, will be biased with respect to return persistence (see e.g., Eq. 2.20). Note that ${Var(dS/S)}\equiv \hat{\sigma }^2(\tau ){\tau }$ either way but ${Var(dS/S)}\ne \tilde{\sigma }^2(\tau ){\tau }| H\ne 0.5$ contradicts $\hat{\sigma }$ representing cBM volatility. Thus, with respect to the variance scaling effect from before, Black–Scholes implied volatilities actually consist of true cBM volatility and persistence believes,

$$\begin{aligned} \hat{\sigma }(\tau ) = \tilde{\sigma }\tau ^{H-\tfrac{1}{2}} \end{aligned}$$

(3.5)

When taking logarithms and computing $\hat{\sigma }(\tau )$ for at least two levels of $\tau$, implied H and $\tilde{\sigma }$ can be estimated by OLS regression:

$$\begin{aligned} \hat{y}=\hat{\alpha } + \hat{\beta }x + \epsilon : \quad \underbrace{\ln (\hat{\sigma }(\tau ))}_{\hat{y}} = \underbrace{\ln (\tilde{\sigma })}_{\hat{\alpha }} + \underbrace{(H-\tfrac{1}{2})}_{\hat{\beta }} \underbrace{\ln (\tau )}_{x}, \quad \begin{array}{cc} \tilde{\sigma }=\exp (\hat{\alpha })\\ H = \hat{\beta } + 0.5 \end{array}\quad \end{aligned}$$

(3.6)

Back to the example of the S &P500, Fig. 3 displays the log $\hat{\sigma }$ curve with fitted lines according to Eq. (3.6). There we observe that the two-step procedure indeed delivers a proper fit, which supports the fractal decomposition.

Fig. 3

Logarithmic representation of Fig. 2. Applying OLS regression (Eq. 3.6) delivers a good fit of the actual ATM implied volatility surface, which allows to decompose believes into the base level of cBM volatility ($\tilde{\sigma }$) and the correction for expected persistence (H). A high fit is verified by R$^2$ of 0.987 (2008-10-01) and 0.997 (2018-10-01). $H>0.5$ indicates $\partial \hat{\sigma }(\tau )/\partial \tau > 0$ and thus increasing risk expectations over $\tau$ (2018-10-01). Vice versa, risk expected to decline in the long run comes with $H<0.5$ (2008-10-01)

Applying the decomposition upon option data henceforth allows to quantify ex-ante investor expectations of the two risk sources in fractal CAPM.

4 Empirical analysis

The empirical part focuses on three questions, (i) do financial markets show patterns of (anti-)persistent returns, (ii) are persistence expectations observable and (iii) how do such believes relate to future realized return/risk? All three questions together should answer whether expected return persistence has an economic value empirically. The study presented here focuses on the cross-section of the S &P500. All data is derived from Bloomberg L.P. and Thomson Reuters Datastream. Daily return (12/2004 to 09/2018) and monthly option data (12/2007 to 09/2018) is used. For options we have less data available, which is why this data set is smaller. All options used are at-the-money to best replicate the underlying. Analyzes are run for three different target maturities, that is 30, 90 and 180 days ahead. The cross-section is extended such that the analysis corrects for stocks which left or joined the S &P500 during the observation period.

4.1 Persistence patterns of empirically realized returns

Persistence analyzes of realized returns have been already carried out in various other studies [e.g., Peters (1989, 1991, 1994) or Granger and Ding (1995)]. In terms of completeness, however, this topic is also briefly addressed within this work. Since the data set covers a major economic event—the financial crisis of 2008—we believe it is interesting to also analyze time split sub-samples of the original data set. Henceforth, the sub-samples are separated into (a) a pre-crisis set (12/2004 to 06/2007), (b) a crisis set (07/2007 to 07/2009) and (c) a post-crisis set (08/2009 to 09/2018). Due to data availability we are able to start the analysis conducted here earlier than the option based analysis below. To grasp an idea about long-term memory within realized returns, we set up a rescaled range analysis (R/S analysis; Hurst (1956)) to compute empirical Hurst exponents. Details about the method can be found at the appendix.

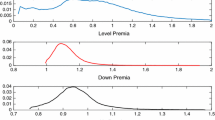
The realized return persistence is now estimated for every stock and (sub-)sample. For the S &P500 index itself, the realized Hurst exponents for the three samples are found to be highly significant with values of 0.507 (a), 0.570 (b), 0.501 (c) and t-statistics of 4.38, 2.29, 2.02. The summarized picture of the cross-section looks similar, Table 1 displays the corresponding estimates which are visualized in Fig. 4.

Table 1 Summary statistics of cross-sectional realized R/S Hurst exponents for three sub-samples and the entire samples: (a) 12/2004 to 06/2007, (b) 07/2007-07/2009, (c) 08/2009-09/2018

Fig. 4

Distribution of cross-section’s realized H for three samples: a before, b during and c after the financial crisis of 2008. This picture shows that persistence in returns seems to inflate during crises times. In terms of risk management, this would mean that long-only investors suffer more as the market down turn is characterized by positively auto-correlated stock returns

If, and only if, all H’s are 0.5, then the financial market is perfectly described by cBM (in terms of fractals). Hence, in case average H’s are different from 0.5, or standard deviation in H distinguishes from 0, then fBM may be more appropriate than cBM. Therefore, to examine whether the equity market is better described by a cBM or by a fBM, we test whether H’s are significantly different from 0.5. Respectively, a one-sample t-tests for all three (sub-)samples is conducted with the null hypothesis H0: $H=0.5$ and the alternative hypothesis H1: $H\ne 0.5$. Further, from Fig. 4 and Table 1 it seems that persistence during (b) is greater than in (a) or (c), which could be interpreted as return persistence increases during crisis times (“if we fall, we will fall together”) and is less during normal times. This hypothesis is tested by two two-sample t-test. The first one is “The Hurst measure is smaller during the financial crisis than before the financial crisis (H0: $H_{(b)}\le H_{(a)}$, H1: $H_{(b)}>H_{(a)}$)” and analogously the second one is “The Hurst measure is smaller during the financial crisis than after the financial crisis (H0: $H_{(b)}\le H_{(c)}$, H1: $H_{(b)}>H_{(c)}$)”. Hence, in sum six t-tests were conducted, which are summarized in Table 2.

Table 2 Summary of t-tests to evaluate whether the equity market is driven by cBM or fBM

All three sub- and the entire sample indicate that empirical H’s are significantly different from 0.5 with very high t-statistics. Hence, we are able to reject the cBM assumption for S &P500 stocks and generalize to fBM. One also recognizes that the mean H in excess of 0.5 is larger (and of higher standard deviation) for the crises sample. The corresponding two-sample t-tests indicate that persistence is indeed significantly greater during the crises time than before or afterwards, from which follows that long-only investors faced additional risk.⁴ Further, also the standard deviation of empirical H’s increased during the crises. So it seems that normal times are a bit closer to follow strict cBM while fractality is stronger pronounced during adverse times.

4.2 Expected persistence

This work emphasizes the forward-looking measurement of investor expectations. A consistent comparison between realized returns and expect risk requires the latter to be evaluated under the physical ${\mathbb {P}}$ probability measure. Option-implied volatilities, however, are by definition risk-neutral (${\mathbb {Q}}$-measured). For this purpose we incorporate a time-varying variance risk premium to transform our input data from ${\mathbb {Q}}$- to ${\mathbb {P}}$-measured expectations. The detailed procedure is described in the appendix.

According to Eq. (3.6) the implied Hurst exponent is computed from ${\mathbb {P}}$-expectations for every stock and month of the cross-sectional data set as well as for the S &P500 index per se. Note that before H’s were computed ex-post from realized data; the focus turns now towards the ex-ante setting. The estimated cross-sectional implied H’s range from 0.013 to 0.987 with a mean of 0.520 and a median of 0.523. Given median and mean do not deviate strongly, the distribution of H is approximately symmetric. Therefore, we apply an one-sample t-test to investigate whether H is significantly different from 0.5 also within the forward looking data. The corresponding t-test delivered a very narrow $95\%$ confidence interval of [0.520, 0.521] at a t-statistic equal to 80.5. Hence, we interpret that investor expectations for return persistence are significantly different from random walk, such that there are indeed believes for long-term memory. From this follows that expectations on the equity market rather fulfill fBM than cBM characteristics. Figure 5 visualizes summaries of the cross-sectional implied H estimates. The graphical interpretation further fosters the presumption of fractals in investor believes, since H’s are broadly scattered over the allowed interval and do not strictly stick to the precise 0.5 level.

Fig. 5

Expected persistence: summary of cross-sectional implied Hurst exponents from option data. Left plot shows the histogram of monthly and cross-sectional H’s, right plot the summary of cross-sectional time series. Under the assumption of classic Brownian motion, all values should equal 0.5 and standard deviation in H should be 0. However, we find that H distributes widely. Hence, the cBM assumption is rejected for investor expectations. The mean ex-ante H is 0.52

Since empirically not only realized returns, but also investor expectations reflect patterns of persistence and anti-persistence, this clearly motivates to investigate the economic value of such. Therefore, the promoted CAPM is used as reference model: Expected stock returns are once evaluated under cBM risk exposures and once under fBM ones. The difference in expected returns between the two predictions then indicates the ex-ante value attributed to expected return persistence. If at the same time prediction quality increases, then expected persistence has an empirical economic value.

4.3 Expected betas, prediction quality, and the value of implied H

While previously it is theoretically argued that expected return persistence should have an economic value, the main purpose of the empirical analysis is to investigate whether it can be verified upon real world data. Therefore, we analyze how cBM and fBM betas differ, decompose risk loadings into correlation and persistence contributions, and investigate which are better in predicting future realized returns.

Computation of market betas requires knowledge about the expected correlation matrix, which is computed following the approach of Skintzi and Refenes (2005). The advantage of this method is that it is purely ex-ante; it finds its application by the Chicago Board Of Exchange (CBOE implied Correlation Index) and can be interpreted as the current view of future stock market diversification [cp. Skintzi and Refenes (2005)]. Driessen et al. (2013) empirically proof that the implied equi-correlation model has significant predictive power. As mentioned in Schadner (2021), for a market of n stocks that are weighted according to w to form the market portfolio m, D the $n\times n$ diagonal matrix of cross-sectional implied volatilities, $\Gamma$ the correlation matrix, E the identity matrix and $\textbf{1}$ the $n\times n$ matrix of ones, computation of the implied equi-correlation matrix can be conducted by

$$\begin{aligned} \sigma _m^2=w'D\Gamma D w&\equiv w'D\bar{\Gamma } D w \qquad \hbox {where}\qquad \bar{\Gamma }=\bar{\rho }(\textbf{1}-E)+E \end{aligned}$$

(4.1)

$$\begin{aligned}&\implies \bar{\rho } = \frac{\sigma _m^2 - w' D^2 w }{w'D(\textbf{1}-E)Dw} \end{aligned}$$

(4.2)

Dependent on which volatilities to use within D, one has to make sure that correlations/volatilities are correctly scaled with respect to Sect. 2. Consistent with the proposed framework, we use $D_{ii}=\tilde{\sigma }_i\tau ^{H_i-0.5},\, \forall i\in \{1,...,n\}$. The $n\times 1$ correlation vector $\bar{\bar{\rho }}_m$ between single stocks and the market portfolio can now be computed by

$$\begin{aligned} \bar{\bar{\rho }}_m=\frac{1}{\sigma _m} \bar{\Gamma } D w \end{aligned}$$

(4.3)

and recap Eq. (2.15), the cross-sectional risk exposure in vector notation is written as

$$\begin{aligned} \beta = \frac{1}{\tilde{\sigma }_m}\bar{\bar{\rho }}_m \tilde{D}{\mathcal {T}} \end{aligned}$$

(4.4)

Summary statistics of expected beta estimates are discussed below.

With point estimates of expected CAPM betas one may be interested into predictability. The prediction quality is evaluated upon three approaches: first, on an individual stock basis. Second, upon sorted portfolios and third, through statistical bootstrapping. In the context of CAPM we believe return predictability is of main interest rather than risk exposure solely. In the subsequent, residuals $\epsilon _{i,t}$ are defined as expected values minus realized ones,

$$\begin{aligned} \epsilon (r)_{i,t} = \langle r_{i,t}\rangle - \vec {r}_{i,t} \qquad \hbox {and}\qquad \epsilon (\beta )_{i,t} = \langle \beta _{i,t}\rangle - \vec {\beta }_{i,t} \end{aligned}$$

(4.5)

Prediction quality is now evaluated whether $\epsilon$’s are centered around zero and by the goodness of fit R$^2$. Following, if it evolves that fractal CAPM efficiently improves prediction quality of future realized returns, then expected return persistence is of considerable value.

Technically, estimates for the expected market risk premium $\langle \mu _m \rangle$ are required, which is an own field of research.⁵ Given the aim of the paper is to analyze the value of risk structures with respect to fractality, predicting the market return may be misleading as it blurs the picture, which we want to analyze in isolation. Hence, to not further inflate model uncertainty, we simplify by setting $\langle \mu _m \rangle = \vec {\mu }_m$.

Individual Stocks Following the described procedure, for every month and every stock within the S &P500 we compute the fractal $\langle \beta _{i,t}\rangle$, the classic BM $\langle \tilde{\beta }_{i,t}\rangle$ as well as the future realized $\vec {\beta }_{i,t}$. Given around 500 stocks for each of the 130 months, this makes about 65,000 beta estimates for each of the three measures, times the three different horizons (1, 3 and 6 months) we derive at around 585,000 beta estimates in total. Table 3 delivers insights into those ex-ante risk estimates and their prediction residuals (Eq. 4.5). Comparing the expected risk estimates, $\langle \beta \rangle$’s seem to be more similar distributed to $\vec {\beta }$’s than $\langle \tilde{\beta }\rangle$’s are since arithmetic averages and standard deviations are more identical. We find that cBM betas are thoroughly higher than the persistence adjusted ones, and that the difference in mean expected betas is less for the short horizon but increases the greater the time-to-maturity (i.e., from 0.41 to 0.70). Also, $\langle \tilde{\beta }\rangle$’s vary over a way larger interval than $\langle {\beta }\rangle$’s do. The average error between $\langle \beta \rangle$ and $\vec {\beta }$ seems to be constant over $\tau$ at 0.05, hence there is a slight overestimation. However, cBM beta’s residuals overshoot future realizations by large, on average between 0.47 and 0.74. Hence interpreting the beta residuals it gets visible that the use of cBM betas seems to cause a considerable overestimation of future risk. Especially the very high maxima of $\langle \tilde{\beta }\rangle$ seem to be very misleading for practical usage. Notably, by construction all ex-ante betas are positive, while realized ones also allow for negative values.

Table 3 Summary statistics over cross-sectional and time-conditional expected as well as future realized CAPM betas

The minor disparity in fBM and cBM betas for the short horizon yields into similar return predictions for $\tau =30$, as both average return residuals are close to zero (0.00/0.01), have almost equal standard deviations (0.07/0.08) and appear at similar intervals. Nevertheless, already at the short return prediction horizon R$^2$’s distinguish remarkably at values of 0.27 in fBM versus 0.17 in cBM. At cBM beta residuals we observe that predictions become more biased the greater $\tau$, which causes mean return residuals to overestimate more the larger the horizon (0.01 at $\tau =30$ vs. 0.05 at $\tau =180$) while the goodness of fit simultaneously declines from 0.17 to 0.14. Following, it seems natural that standard deviations in return residuals grows larger at cBM predictions than under fBM. Hence, with respect to an increasing horizon, cBM loses prediction precision faster than fBM does.

From those patterns on a single stock basis we conclude, that incorporating persistence risk to correlation risk effectively lifts prediction quality. Given the support that fractal CAPM better predicts future realizations than cBM CAPM, the presumption of expected return persistence having economic value finds support. Quantifying the value of H within CAPM, we compute the H-contribution as $\%H=\langle \beta \rangle /\langle \tilde{\beta }\rangle -1$ which is interpreted as by how much excess return predictions are different using cBM or fBM. A histogram of the corresponding values can be found in the Appendix. Here we find that $\%H$ is not only significantly different from zero (t-val.=$-$225.8 for $\tau =30$), but also that it is mainly negative. This allows to draw four conclusions. First, expected return persistence does have an economic value. Second, on average, only 80% of a stock’s market risk exposure is actually attributable to the correlation to the market portfolio, while another 20% come from the side of fractality (in the case of $\tau =30$). Also, this H-contribution can vary largely across stocks. Third, the H-contribution increases the greater the horizon, thus the economic value of persistence is even greater for long-run predictions. And fourth, H-contribution is thoroughly negative, meaning that predictions from cBM CAPM will overestimate future returns. From this conclusions it is not surprising that fractal CAPM delivers substantial better prediction quality than its classic counterpart, which is reflected at closer to zero residuals with lower standard deviation and enhanced R$^2$’s.

Given Eq. (2.16) one can take logs to write the linear decomposition of fractal beta, that is

$$\begin{aligned} \ln (\beta ) = \ln (\tilde{\beta }) + \Delta H \ln (\tau ) \end{aligned}$$

(4.6)

In a market where one could efficiently price assets with CAPM and the cBM assumption, risk exposure and persistence believes should be independent,

$$ \begin{aligned} {\hbox {iff cBM}}\, \& \,{\hbox {CAPM holds}}: \qquad \ln (\tilde{\beta }) \perp \Delta H\qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \,\,\quad \end{aligned}$$

(4.7)

Economically, this statement requires the absence of a beta anomaly, that is, a significant mispricing bias which is proportional to an asset’s beta. The reason why this is the case evolves from Eq. (2.16): if cBM is unbiased with respect to H, then $\tilde{\beta }$’s are identical with true betas and thus, if CAPM fully captures expected risk that will be compensated, Eq. (2.1) will provide unbiased estimates of expected returns. Therefore, validity of cBM and CAPM at the same time implies absence of a beta anomaly, which in turn implies Eq. (4.7) to hold. If Eq. (4.7) is empirically rejected, then either the assumptions of CAPM are not fulfilled (i.e., further risk sources exist) or cBM is not met,

$$ \begin{aligned} {\hbox {iff cBM}} \& {\hbox {CAPM hold}} \implies {\hbox {absence of beta anomaly}} \implies \ln (\tilde{\beta }) \perp \Delta H \end{aligned}$$

hence both cannot exist next to each other as soon as $\ln (\tilde{\beta }) \not \perp \Delta H$. Note that this condition also applies for multi-factor models like (Fama and French 2015). Given this economically interesting question, we analyze the relation between the two parameters for the $\tau =30$ ex-ante data. The output is visualized in Fig. 6 below.

Fig. 6

Decomposing risk: log betas vs. H, both computed ex-ante with $\tau =30$. Left plot shows cBM betas, right plot fBM ones and blue dashed lines indicate linear fits. If cBM and CAPM were valid at the same time, then log cBM betas should be independent of $\Delta H$. This is not the case within empirical data, hence we can reject either one of the two assumptions. The two variables evolve to show a strong negative linear relation, which means that $\tilde{\beta }$’s will significantly overestimate future realized returns when used within CAPM—better known as beta anomaly. When generalizing to fBM, one still observes such a negative relation, however, the link looks way weaker and the slope is essentially flatter. Thus, expected return persistence explains parts of the beta anomaly in CAPM notations

What we observe is that there is a significant negative linear relation between $\Delta H$ and $\ln \tilde{\beta }$ with a correlation of $-$0.761.⁶ This means that using cBM betas together with CAPM (Eq. 2.1) will cause substantial overestimations of future returns the larger a stock’s $\tilde{\beta }$. Hence, while by $\%H$ in Table 3 one did not only observe that $\tilde{\beta }$ overestimates returns on average, now we also see that there is a systematic behind it. With cBM betas one would thus interpret existence of a beta anomaly. However, when generalizing the risk exposure by incorporating persistence believes, large portions of the correlations are removed down from $-$0.761 to $-$0.264 (cp. right panel Fig. 6). Hence, non-surprisingly, in Table 3 it is observed that $\langle \tilde{\beta }\rangle$ ’s overestimate $\vec {\beta }$ notably more than $\langle \beta \rangle$’s. Therefore, already from this brief analysis we are able to claim that return persistence can partially resolve the beta anomaly. But, since still some correlation remains, we also know that the fractal CAPM cannot explain it completely. The picture of the beta anomaly and how fBM partially resolves it gets more clear with a look on beta sorted portfolios within the next section. Anyway, from the single stock analysis we find first support that expected return persistence indeed has notable economic value.

Sorted Portfolios Similar to before, the analysis conducted here compares time-conditional predictions with future realizations. Due to the diversification effect it is obvious that CAPM’s goodness of fit is significantly greater for portfolios than for single firms. Hence, it is useful to evaluate CAPM prediction quality on portfolios. For this purpose we form portfolios based on two sorting criteria, which we believe to be of interest, that is $\tilde{\beta }$ and H. There exists broad literature that documents significant mispricing with respect to market beta [e.g., Schneider et al. (2020)] and the potential of a beta anomaly was also discussed before. Therefore, we briefly investigate this topic using ex-ante cBM betas. Furthermore, since stock momentum [e.g., Carhart (1997)] is also considered to contradict CAPM’s predictions, we also sort on expected H as a proxy for believed auto-correlation. Technically, sorting criteria are clustered into percentiles to generate ten daily return series of monthly re-balanced portfolios; P1 is the portfolio of the lowest criteria’s percentile and P10 of the highest. The focus is set upon the $\tau =30$ ex-ante data, Table 4 delivers the corresponding results of $\tilde{\beta }$ and H sorted portfolios.

Table 4 Portfolios sorted on cBM beta (Panel A) and implied return persistence (Panel B): Analysis of realized returns and (non-/fractal) CAPM predictions

While realized standard deviations are increasing form P1 to P10 at the cBM beta sorted portfolios, mean realized returns are not. Thus, it is not surprising that Sharpe ratios are decreasing the higher the portfolio’s $\tilde{\beta }$. This outcome supports existence of a beta anomaly. Having mentioned this, we observe that cBM prediction errors of returns are moderate for low to mid beta portfolios, but get substantially large for the high beta ones, which results in weaker R$^2$ within P9-P10. As can be seen in mean $\langle \beta \rangle -\vec {\beta }$, this mispricing is largely attributable to the fact that expected cBM betas overestimate future realized returns the greater $\tilde{\beta }$. When switching from cBM to fBM betas, this beta-dependent pricing error is still observable (e.g., by increasing residual means or standard deviations), however, it is substantially less for such. With an focus on P10, R$^2$ improves from 0.24 to 0.79 when accounting in a stock’s H, hence much of the anomaly within large beta portfolios can be reduced by generalizing cBM to the more flexible fBM. Still, as mean residuals are increasing also under fBM, the beta anomaly cannot be completely explained by the fractal approach. Since fBM assumes normally distributed returns, another potential risk source an ex-ante distribution showing heavy tails.⁷ Economically, fat tails on the left side of the probability distribution pushes a firm’s credit risk [cp. Schneider et al. (2020)], thus modeling a fractal process from non-normal probability distributions may further explain the beta related mispricing.

From the observation in Fig. 6 (and the corresponding presumption derived) it is obvious that the H sorted portfolios will show the reverse pattern of the $\tilde{\beta }$-sorted ones: the larger H, the greater the portfolio’s absolute as well as risk adjusted performance. This clearly demonstrates that there is an economic value associated to implied H. The increasing mean return from P1 to P10 confirms the way the fractal CAPM model (Eq. 2.17) is defined. Nonetheless, return residuals still seem to relate to the sorting criteria which also here possibly finds its source in a beta anomaly, as mean $\epsilon (\beta )$ also show such a dependence. But again, we find that this relation between return residuals and sorting criteria is almost half in the fBM than under the cBM predictions. Also here, cBM R$^2$’s get worse for the adverse portfolios (low H).

Hence, while previously suggested that H has economic value on a single stock basis, we further observe that it is not diversified away within portfolios. Actually, on the sorted portfolios the value of H is even stronger visible. Since sorting on some specific criteria may induce a bias with respect to the criteria chosen, we run a third test to confirm robustness.

Statistical Bootstrap The third method to evaluate the validity of fractal CAPM builds on statistical bootstrapping. Different to portfolio sorts above, at the bootstrapping approach stocks are chosen randomly. This removes any systematic bias related to the choice of the sorting criteria. Further, this also allows to generate a substantially higher number of portfolios which in turn provides more predictions that we can compare with realizations. The technical procedure is as follows, for each $\tau \in \{30,90,180\}$ we use a loop algorithm to create 1000 portfolios. The loop pass starts by randomly selecting 50 stocks out of the cross-section that are weighted relative to each other according to $w_{p}$ to form a portfolio. Since the data covers stocks that file bankruptcy during the observation horizon, we re-balance $w_{p,t}$ every month such that $\sum w_{p,t}=1,\;\forall t$ with respect to the initial $w_p$. Note that the number of stocks within a portfolio is sufficiently high to assume that it is well diversified. Having the portfolio weights one is now able to compute rolling portfolio betas, expected returns as well as realized values and complete the loop pass. Repeating the loop passes 1000 times gives 1000 time-series of un-systematically formed portfolios. Table 5 displays the summary results of predicted versus realized returns of fractal CAPM compared to cBM CAPM. For all three horizons, mean $\epsilon (\mu _p)$ is closer to zero under fBM than under cBM predictions, which on the one hand is in line with the conclusion derived from the systematically sorted portfolios, but also further highlights that fractal CAPM has a smaller prediction error. However, we find that both, fBM and cBM, significantly overestimate future realized returns on the 1000 randomly generated portfolios, which clearly supports existence of further, not implemented risk factors. Nonetheless, we see that the mean prediction error is around twice as much under cBM than under fBM, hence the incorporation of expected persistence already accounted in much of CAPM’s inflexibility. Hence, it follows that the prediction quality as measured by R$^2$ is larger under the fractal model. Especially at this measure the long-term effects of persistence get visible: while under fBM R$^2$’s are almost constant for all three horizons, we observe a decline in such given cBM predictions. Keeping in mind the variance scaling effect as discussed previously, this pattern looks logical.

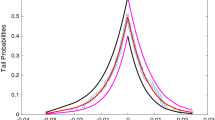
As the bootstrapping allowed to create a large number of portfolios, one can now plot densities of R$^2$’s (see Fig. 7). This picture shows that fBM R$^2$’s are way closer centered to 100% than cBM ones are. So, also the large-scale bootstrapping method favors fBM to have better quality in predicting future risk/returns than cBM CAPM does, confirming that expected persistence empirically matters.

Table 5 Return residuals from bootstrapping: summary statistics of (130) monthly predicted vs. realized returns of 1000 portfolios per $\tau$

Fig. 7

Prediction quality of returns measured by R$^2$: Comparison of cBM vs. fractal CAPM for the horizon $\tau =30$. Residuals are computed from 130 monthly return predictions per 1000 portfolios, R$^2$ are then calculated for each portfolio, thus 1000 R$^2$’s are derived per fBM/cBM. Already in the short time-horizon one sees that fBM R$^2$’s are mainly concentrated to the right end, being larger than cBM ones. Hence the claim that fBM is of greater prediction quality than cBM gets visible. In direct comparison, for each portfolio R$^2$ was larger when using fractal than under cBM CAPM, which comes from the greater flexibility of fBM. Henceforth, this plot confirms that fractals explain portions of future realized returns which would not be captured under cBM market risk exposure

In a nutshell, all three approaches from the empirical analysis indicate that fBM’s flexibility to count in persistence believes via the variance scaling effect could deliver better predictions in future realized risks and returns than basic cBM volatilities/betas. The difference between the two is less for short term-predictions, but gets substantial the longer the prediction horizon. From that follows, that expected return persistence does not only have an economic value within the fractal CAPM model, but also within real world empirical data.

5 Conclusion

Expected persistence in equity returns can be captured by releasing the classic Brownian motion assumption to its more general fractal form. The fractal Brownian motion allows for long-term memory and thus auto-correlation within a process, which can also be interpreted as stock momentum. Through this generalization, factor based asset pricing models such as CAPM can incorporate corresponding believes without the need of adding an additional risk factor, which obviously helps to reduce the factor zoo. Upon a theoretical standpoint, it is found that there should be an economic value attributed to expected return persistence in excess of the market portfolio. On empirical forward-looking data we discuss how expected persistence can be estimated out of option prices and compute them for the cross-section of the S &P500. In direct comparison of standard CAPM versus fractal CAPM, throughout evidence is found that equity markets do not only show significant patterns of persistence in realized returns, but also that respective believes have a significant impact upon return prediction. This allows to decompose the market risk factor beta into pure correlation believes and into the (so far un-noticed) persistence component. Respectively, while CAPM betas should be 100% correlation risk in its classic notation, we find that on average solely 80% of the factor loading is attributable to correlation risk—another 20% are actually sourced by (excess) persistence believes. Further, this division varies largely such that standard CAPM predictions partially lead to very wrong predictions, especially with respect to high beta stocks. Hence, fractal CAPM nominates itself as a candidate to explain the low risk/beta anomaly. All those observations together allow to conclude that expected return persistence has a considerable economic value, both from a theoretical as well as from an empirical perspective.

Appendix

1.1 A1. Expected return and horizon

See Figs. 8 and 9.

Fig. 8

Illustration of the expected rate of return $\langle \mu _i\rangle$ as a function of the time to maturity $\tau$. The setting is as follows: $\langle \mu _m\rangle =5\%$, $r_f=1\%$, $H_m=0.6$ and $\Delta H = \{-0.2, 0, 0.2\}$. Under classic Brownian Motion (i.e., $\Delta H=0$), $\langle \mu _i\rangle$ would be constant and thus independent of $\tau$. With the fractal generalization this independence is removed. As can be seen $\Delta H > 0$ coerces $\langle \mu _i\rangle$ to grow int the future horizon ahead. Differently, with $\Delta H <0$ the stock’s expected rate of return is believed to decline

1.2 A2. H-contribution

Analysis of individual stock’s expected market risk loading decomposed into classic BM correlation and into contribution from expected persistence (H-contribution):

Fig. 9

Histogram of single stock’s H contribution to predicted returns under fractal versus cBM CAPM, $\%H = \beta /\tilde{\beta } - 1$. Three conclusions are worth to mention. First, the contribution varies largely, hence expected persistence cannot be neglected. Second, contributions are mainly negative, which means that most stocks have H below the market portfolio’s H. Third, the negativity of $\%H$ means that cBM CAPM will thoroughly overestimate expected risk compared to fractal CAPM

1.3 A3. R/S analysis

The R/S analysis [cp. Hurst (1956)] is conducted as follows. Say X is the return series of $n_T$ observations for which one wants to compute the Hurst exponent. First, one hast to compute the sample mean $\hbox {m}(X)$ and the excess of mean series $\bar{X}$

$$\begin{aligned} \hbox {m}(X)=\tfrac{1}{n_T}\sum _{i=1}^{n_T}X_i \qquad \hbox {and}\qquad \bar{X}=X-\hbox {m}(X) \end{aligned}$$

(5.1)

by which the computation of the cumulative deviate series Z is straight forward,

$$\begin{aligned} Z_t = \sum _{i=1}^{t}\bar{X}_i \qquad t\in \{1,...,n_T\} \end{aligned}$$

(5.2)

The range R is then defined as the interval length of Z,

$$\begin{aligned} \hbox {R} = max(Z) - min(Z) \end{aligned}$$

(5.3)

and S is simply the sample standard deviation,

$$\begin{aligned} \hbox {S}=\sqrt{\frac{1}{n}\sum _{i=1}^{n}(X_i - \hbox {m}(X))^2} \end{aligned}$$

(5.4)

such that the R/S series is given by

$$\begin{aligned} (\hbox {R}/\hbox {S})_t=\frac{\hbox {R}_t}{\hbox {S}_t} \end{aligned}$$

(5.5)

The Hurst exponent is now defined by

$$\begin{aligned} \left\langle \frac{\hbox {R}}{\hbox {S}} \right\rangle = c\, n_T^H \end{aligned}$$

(5.6)

with c as a constant. Taking logs,

$$\begin{aligned} \log ((\hbox {R}/\hbox {S})_t) = \log (c)+ H \, \log (t) \end{aligned}$$

(5.7)

gives a linear equation that can be fitted to return data by OLS regression, where H corresponds to the regression’s coefficient.

1.4 A4. Expected volatility

As outlined before, option implied volatilities are per construction forward looking proxies of expected risk. Comparing physically realized returns with expected risk requires ${\mathbb {P}}$ implied volatilities—comparing physical returns with risk-neutral risk may delivers biased results. By Black–Scholes market model, volatility is deterministic such that Girsanov theorem applies and the market risk premium is incorporated via the drift term. However, by now the academic consensus agrees that volatility itself is stochastic [e.g., Heston (1993)]. If volatility is stochastic, then it is obvious that fluctuations in it is another source of risk, causing that investors require a premium for it. In the context of implied volatilities, this means that if one uses Black–Scholes formula to compute implied volatilities, the estimates will be derived under the ${\mathbb {Q}}$ measure. Those estimates are likely to be different from ${\mathbb {P}}$ expected volatilities as soon as volatility is stochastic. Just like in standard Black–Scholes there is a premium in the drift term, $\mu \ge r_f$, ($\mu$ is the ${\mathbb {P}}$ expected return, $r_f$ the ${\mathbb {Q}}$ expected one and $\tfrac{\mu - r_f}{\hat{\sigma }}$ is the risk premium), investors require a premium for volatility of volatility such that $\sigma _{{\mathbb {P}}}\le \sigma _{{\mathbb {Q}}}$. Therefore, $\sigma _{{\mathbb {Q}}}$ equals $\sigma _{{\mathbb {P}}}$ plus some variance risk premium [cp. Buss and Vilkov (2012)]. Empirically, this means that on average Black–Scholes implied volatilities slightly over-estimate future realized ones. Figure 10 displays the time-series of future realized volatility in comparison with Black–Scholes’s expected ${\mathbb {Q}}$ volatility

Fig. 10

Time-series of Black–Scholes implied volatility with target maturity of one month vs. future realized volatility of same horizon. On average, risk-neutral implied volatilities ($\sigma _{\mathbb {Q}}$)—as investor expectations—slightly overestimate future realized ones ($\vec {\sigma }$) due to a variance risk premium $\lambda$: in mild times, risk averse investors pay the premium ($\vec {\sigma } < \sigma _{\mathbb {Q}}$); during crises times, realized volatilities overshoot implied ones ($\vec {\sigma } > \sigma _{\mathbb {Q}}$). Investors form believes about future volatility out of historical data and adjust them for the current market outlook. Thus, a slight lag pattern can be observed

Estimation of the expected variance risk premium $\langle \lambda _{v}\rangle$ enjoys its own discussion, for example Bollerslev et al. (2009) or Todorov (2010). Generally it is argued that $\langle \lambda _{v}\rangle$ is driven by the economic cycle and/or market phases. Therefore, we suggest it makes sense to model the variance risk premium relative to the level of $\sigma _{{\mathbb {Q}}}$. Hence, let $\vec {\sigma }(\tau )$ express the future realized volatility of horizon $\tau$, $\langle \lambda _{v}\rangle$ is incorporated by first computing

$$\begin{aligned} \lambda _{v,t}(\tau ) = \frac{\sigma _{{\mathbb {Q}},t}(\tau ) - \vec {\sigma }_{t}(\tau )}{\sigma _{{\mathbb {Q}},t}(\tau )} \qquad \hbox {and}\qquad \bar{\lambda }_v(\tau ) = \frac{1}{n_T} \sum _{t=1}^{n_T}\lambda _{v,t}(\tau )\qquad t\in \{1,...,n_T\} \end{aligned}$$

(5.8)

upon the S &P500 index and then transform ${\mathbb {Q}}$ to ${\mathbb {P}}$ measured expected volatilities by

$$\begin{aligned} \sigma _{{\mathbb {P}}, i, t}(\tau ) = \sigma _{{\mathbb {Q}}, i, t }(\tau ) (1-\bar{\lambda }_v(\tau )) \qquad \begin{array}{r} \forall t\in \{1,...,n_T\}\\ \forall i \in \{1,...,n\} \end{array} \end{aligned}$$

(5.9)

such that the same relative variance risk premium is applied among the cross-section to transform individual risk-neutral $\sigma _{{\mathbb {Q}}}$’s to physically expected $\sigma _{{\mathbb {P}}}$’s while keeping arbitrage-free principles. Estimated ${\lambda }_{v,t}(\tau )$’s are positive with mean values (i.e., $\bar{\lambda }_{v}(\tau )$) of 0.050, 0.075 and 0.100 at t-statistics of 1.39, 1.98, 2.63 ($\tau =30$, 90, and 180 days). For the rest of the analysis we use solely ${\mathbb {P}}$ expected volatilities (if not mentioned differently), hence we drop this subscript for simplification purposes.

To briefly motivate the use of implied volatilities instead of historically realized ones in the context of quantifying expectations, we draw a short comparison between those to future realized ones. The observed output is highlighted in Fig. 11 and Table 6. From the table one sees that for short time-horizons the prediction quality between historical and implied volatilities is almost identical; mean and standard deviations of residuals do not really differ but implied volatilities realize a slightly better goodness of fit (R$^2$’s of 0.60 vs. 0.54).⁸ Hence one could interpret this as option traders use historical volatilities to form their believes for future realizations. However, with an increasing horizon, we clearly observe that implied estimates outperform historical ones, which can be seen upon the R$^2$’s. The fact is while investors typically use historical volatilities to form believes for the future, they also adjust them for example to incorporate the current market situation or the mean reverting behavior of variance. This means that using longer time windows for historical volatilities causes predictions to react to slowly to current situations, hence especially in the aftermath of surprises (like 2009), historical volatilities are bad proxies for future realized risk. Therefore, it seems plausible that historical volatilities realize a very bad R$^2$ at the $\tau =180$ horizon, while implied volatilities—where investors adjust for economic phases and mean reversion—could partially keep its prediction quality. Thus, implied volatilities are not only theoretically, but also empirically better qualified candidates for expected risk.

Fig. 11

S &P500: Residuals of expected minus realized volatility as quantified by historical, ${\mathbb {P}}$ and ${\mathbb {Q}}$ implied volatilities. Both option implied estimates are on average better than the historical one in predicting future realized volatility. This is mainly attributable to the fact that historical volatilities per se are unable to adopt for current market phases: While investors indeed use historical volatilities to grasp an idea about future realizations, they correct them for current market outlooks (e.g. recovery) to adjust their estimates. This is why implied volatilities deliver on average better estimates for future realizations

Table 6 Volatility analysis of the S &P500: Residuals $\epsilon$ of future realized volatility predicted by expected volatilities (historical, ${\mathbb {Q}}$, and ${\mathbb {P}}$)