1 Introduction

Affine short-rate models refer to a class of interest rate models in which the price of any zero-coupon bond can be expressed as the exponential of affine function of the instantaneous short-rate. Well-known affine short-rate models include the Vasicek (Vasicek 1977), Cox–Ingersoll–Ross (CIR) (Cox et al. 2005), Hull–White (Hull and White 1990) and Fong–Vasicek (Fong and Vasicek 1991) models, as well as their multi-factor versions. Such models enjoy wide popularity among practitioners and academics alike because these models are flexible enough to fit the observed yield curve and easy to calibrate, due to the closed-form expression for bond prices, and hence yields.

Despite their widespread use in yield-curve modeling, affine short-rate models are rarely used to price options on bonds or calibrate to the implied volatility surface of bond options. For this task, practitioners assume forward prices of bonds are modeled by a local-stochastic volatility (LSV) model. In particular, the SABR model (Hagan et al. 2002), is often used as a model for forward bond prices because it admits an explicit approximation of implied volatility, which can be used to calibrate to observed implied volatilities.

Yet, if one assumes an affine model for the short-rate, the resulting forward bond prices will not have SABR dynamics. As a result, if a bank uses an affine short-rate model to describe the yield curve, and the SABR model to describe the implied volatility surface of options on bonds, the bank is using two different models for the short-rate. Such a practice clearly introduces arbitrage into the market.

The purpose of this paper is to derive an explicit approximation for the implied volatilities of options on bonds assuming the short-rate is of the affine class. In doing so, we provide a unified framework for calibrating both to observed yields and to observed implied volatilities. To derive the implied volatility approximation, we use the polynomial expansion method that was introduced by Pagliarani and Pascucci (2012) in order to derive approximate prices for options on equity in a scalar setting and later extended in Lorig et al. (2017) in order to obtain approximate implied volatilities in a multi-factor LSV setting. For a comprehensive reference on perturbation methods in finance, see Turfus (221).

The rest of this paper proceeds as follows: in Sect. 2 we introduce the class of affine short-rate models that we will consider in this paper and in Sect. 3 we briefly review how one can compute prices for bonds and options on bonds in the affine short-rate setting. In Sect. 4 we provide an explicit relation between affine short-rate models and classical local-stochastic volatility models. We use this relation in Sects. 5 and 6 to develop explicit approximations for the prices of options on bonds and their corresponding implied volatilities. In Sect. 7, we perform a number of numerical experiments to gauge the accuracy of our implied volatility approximation in four specific affine term-structure models: Vasicek, CIR, two-dimensional CIR and Fong–Vasicek. Some thoughts on future work are offered in Sect. 8.

2 Model and assumptions

Throughout this paper, we will consider a financial market over a time horizon from zero to \({{\overline{T}}} < \infty \) with no arbitrage and no transactions costs. As a starting point, we fix a complete probability space \((\Omega ,{\mathscr {F}},\mathbb {P})\) and a filtration \(\mathbb {F}= ({\mathscr {F}}_t)_{0 \le t \le {{\overline{T}}}}\). The probability measure \(\mathbb {P}\) represents the market’s chosen pricing measure taking the money market account \(M = (M_t)_{0 \le t \le {{\overline{T}}}}\) as numéraire. The filtration \(\mathbb {F}\) represents the history of the market.

We shall assume that money market account M has dynamics of the form

$$\begin{aligned} \text {d}M_t&= R_t M_t \text {d}t , \end{aligned}$$
(2.1)

where \(R = (R_t)_{t \ge 0}\) is the instantaneous short-rate of interest. We further suppose that the short-rate R is given by

$$\begin{aligned} R_t&= r(Y_t) , \end{aligned}$$
(2.2)

for some function \(r : \mathbb {R}^d \rightarrow \mathbb {R}_+\) and some Markov diffusion process \(Y = (Y_t^{(1)}, Y_t^{(2)}, \ldots , Y_t^{(d)})\). Specifically, we suppose that Y is the unique strong solution of a stochastic differential equation (SDE) of the form

$$\begin{aligned} \text {d}Y_t&= \mu (t,Y_t) \text {d}t + \sigma (t,Y_t) \text {d}W_t , \end{aligned}$$
(2.3)

for some functions \(\mu : [0,{{\overline{T}}}] \times \mathbb {R}^d \rightarrow \mathbb {R}^d\) and \(\sigma : [0,{{\overline{T}}}] \times \mathbb {R}^d \rightarrow \mathbb {R}^{d \times d}\), where \(W = (W_t^{(1)}, W_t^{(2)}, \ldots , W_t^{(d)})_{t \ge 0}\) is a d-dimensional \((\mathbb {P},\mathbb {F})\)-Brownian motion. Thus, the ith component of Y is given by

$$\begin{aligned} \text {d}Y_t^{(i)}&= \mu _i(t,Y_t) \text {d}t + \sum _{j=1}^d \sigma _{i,j}(t,Y_t) \text {d}W_t^{(j)} . \end{aligned}$$
(2.4)

Lastly, we shall assume that R is an affine short-rate model, meaning that the functions \((r,\mu ,\sigma )\) satisfy

$$\begin{aligned} \left. \begin{aligned} r(y) = q + \sum _{i=1}^d {\psi _i} y_i ,&\\ \mu (t,y) = b(t) + \sum _{i=1}^d \beta _i(t) y_i ,&\\ \sigma (t,y)\sigma ^\text {Tr}(t,y) = \ell (t) + \sum _{i=1}^d \lambda _i(t) y_i ,&\end{aligned} \right\} \end{aligned}$$
(2.5)

for some constants \(q \in \mathbb {R}\) and \({\psi } \in \mathbb {R}^d\) and some functions \(b, \beta _i : [0,{{\overline{T}}}] \rightarrow {\mathbb {R}}^d\) and \(\ell ,\lambda _i : [0,{{\overline{T}}}] \rightarrow {\mathbb {R}}^{d \times d}\). Note that \(\sigma ^\text {Tr}\) denotes the transpose of \(\sigma \).

3 Bond and option pricing

In this section we review some classical results on bond and option pricing in an affine short-rate setting. Our aim here is not to be rigorous, but rather to present in a concise and formal manner the results that will be needed in subsequent sections. For a rigorous treatment of the formal results presented below, we refer the reader to Filipovic (2009, Chapter 10).

To begin, for any \(T \le {{\overline{T}}}\) and \(\nu \in \mathbb {C}^d\), let us define \(\Gamma ( \,\cdot \,,\,\cdot \,;T,\nu ) : [0,T] \times \mathbb {R}^d \rightarrow \mathbb {C}^d\) by

$$\begin{aligned} \Gamma (t,Y_t;T,\nu ) := \mathbb {E}_t \exp \left( -\int _t^T r(Y_s) \text {d}s + \sum _{i=1}^d \nu _i Y_T^{(i)} \right) , \end{aligned}$$
(3.1)

where we have introduced the short-hand notation \(\mathbb {E}_t( \, \cdot \, ):= \mathbb {E}( \, \cdot \,|{\mathscr {F}}_t )\). The existence of the function \(\Gamma \) follows from the Markov property of Y. Formally, \(\Gamma \) satisfies the Kolmogorov backward partial differential equation (PDE)

$$\begin{aligned} (\partial _t + {\mathscr {A}}(t) - r ) \Gamma (t,\, \cdot \, ; T,\nu )&= 0 ,&\Gamma (T,y;T,\nu )&= \exp \left( \sum _{i=1}^d \nu _i y_i \right) , \end{aligned}$$
(3.2)

where the operator \({\mathscr {A}}\) is the generator of Y under \(\mathbb {P}\). Explicitly, the generator \({\mathscr {A}}\) is given by

$$\begin{aligned} {\mathscr {A}}(t)&= \sum _{i=1}^d \mu _i(t,y) \partial _{y_i} + \frac{1}{2} \sum _{i=1}^d \sum _{j=1}^d \Big ( \sigma (t,y) \sigma ^\text {Tr}(t,y) \Big )_{i,j} \partial _{y_i}\partial _{y_j} , \end{aligned}$$
(3.3)

where \((\sigma \sigma ^\text {Tr})_{i,j}\) denotes its (i, j)-th component of \(\sigma \sigma ^\text {Tr}\). One can verify by direct substitution that the solution to (3.2) is

$$\begin{aligned} \Gamma (t,y;T,\nu )&= \exp \Big ( - F(t;T,\nu ) - \sum _{i=1}^d G_i(t;T,\nu ) y_i \Big ) , \end{aligned}$$
(3.4)

where the functions F and \(G=(G_i)_{i=1,2,\ldots ,d}\) are the solution of the following system of coupled ordinary differential equations (ODEs)

$$\begin{aligned}&\left. \begin{aligned} \partial _t F(t;T,\nu )&= \frac{1}{2}G^{\text {Tr}}(t;T,\nu )\ell (t)G(t;T,\nu ) \\&\quad -b^{\text {Tr}}(t)G(t;T,\nu )-q , \\ F(T;T,\nu )&= 0 , \end{aligned} \right\} \end{aligned}$$
(3.5)
$$\begin{aligned}&\left. \begin{aligned} \partial _t G_i(t;T,\nu )&= \frac{1}{2}G^{\text {Tr}}(t;T,\nu )\lambda _i(t)G(t;T,\nu ) \\&\quad -\beta _i^{\text {Tr}}(t)G(t;T,\nu )-{\psi }_i , \\ G_i(T;T,\nu )&= - \nu _i . \end{aligned} \right\} \end{aligned}$$
(3.6)

Now, for any \(T \le {{\overline{T}}}\), let us denote by \(B^T = (B_t^T)_{0 \le t \le T}\) the value of a zero-coupon bond that pays one unit of currency at time T. In the absence of arbitrage the process \(B^T/M\) must be a \((\mathbb {P},\mathbb {F})\)-martingale. As such, we have

$$\begin{aligned} \frac{B_t^T}{M_t}&= \mathbb {E}_t \left( \frac{B_T^T}{M_T} \right) = \mathbb {E}_t \left( \frac{1}{M_T} \right) , \end{aligned}$$
(3.7)

where we have used \(B_T^T = 1\). Solving for \(B_t^T\), we obtain

$$\begin{aligned} B_t^T&= \mathbb {E}_t \left( \frac{M_t}{M_T} \right) = \mathbb {E}_t \Big ( \text {e}^{- \int _t^T r(Y_s) \text {d}s} \Big ) = \Gamma (t,Y_t;T,0) \end{aligned}$$
(3.8)
$$\begin{aligned}&= \exp \Big ( - F(t;T,0) - \sum _{i=1}^d G_i(t;T,0) Y_t^{(i)} \Big ), \end{aligned}$$
(3.9)

where the third equality follows from (3.1) and the fourth equality follows from (3.4).

Next, let \(V = (V_t)_{0 \le t \le T}\) denote the value of a European option that pays \(\varphi ( \log B_T^{{\overline{T}}} )\) at time T for some function \(\varphi : \mathbb {R}_- \rightarrow \mathbb {R}\). With the aim of finding \(V_t\), let \({\widehat{\varphi }}:\mathbb {C}\rightarrow \mathbb {C}\) denote the generalized Fourier transform of \(\varphi \), which is defined as follows

$$\begin{aligned} {\widehat{\varphi }}(\omega )&:= \int _{-\infty }^{\infty } \text {d}x \, \text {e}^{-\mathtt {i}\omega x} \varphi (x) ,&\omega&= \omega _r + \mathtt {i}\omega _i ,&\omega _r, \omega _i&\in \mathbb {R}. \end{aligned}$$
(3.10)

We can recover \(\varphi \) from \({\widehat{\varphi }}\) using the inverse Fourier transform

$$\begin{aligned} \varphi (x)&:= \frac{1}{2\pi } \int _{-\infty }^{\infty } \text {d}\omega _r \, \text {e}^{\mathtt {i}\omega x} {\widehat{\varphi }}(\omega ) . \end{aligned}$$
(3.11)

Noting that, in the absence of arbitrage, the process V/M must be a \((\mathbb {P},\mathbb {F})\)-martingale, we have

$$\begin{aligned} \frac{V_t}{M_t}&= \mathbb {E}_t \left( \frac{V_T}{M_T} \right) = \mathbb {E}_t \left( \frac{\varphi \left( \log B_T^{{\overline{T}}}\right) }{M_T} \right) . \end{aligned}$$
(3.12)

Solving for \(V_t\), we have that

$$\begin{aligned} V_t&= \mathbb {E}_t \exp \left( -\int _t^T r(Y_s) \text {d}s \right) \varphi ( \log B_T^{{\overline{T}}} ) \end{aligned}$$
(3.13)
$$\begin{aligned}&= \frac{1}{2\pi } \int _{-\infty }^{\infty } \text {d}\omega _r \, {\widehat{\varphi }}(\omega ) \mathbb {E}_t \exp \left( -\int _t^T r(Y_s) \text {d}s \right) \exp ( \mathtt {i}\omega \log B_T^{{\overline{T}}} ) \end{aligned}$$
(3.14)
$$\begin{aligned}&= \frac{1}{2\pi } \int _{-\infty }^{\infty } \text {d}\omega _r \, {\widehat{\varphi }}(\omega ) \mathbb {E}_t \exp \left( -\int _t^T r(Y_s) \text {d}s \right) \mathbb {E}_T \exp ( \mathtt {i}\omega \log B_T^{{\overline{T}}} ) \end{aligned}$$
(3.15)
$$\begin{aligned}&= \frac{1}{2\pi } \int _{-\infty }^{\infty } \text {d}\omega _r \, {\widehat{\varphi }}(\omega ) \exp \left( - \mathtt {i}\omega F(T;{{\overline{T}}},0) \right) \end{aligned}$$
(3.16)
$$\begin{aligned}&\quad \times \mathbb {E}_t \exp \left( -\int _t^T r(Y_s) \text {d}s - \sum _{i=1}^d \mathtt {i}\omega G_i(T;{{\overline{T}}},0) Y_T^{(i)} \right) \end{aligned}$$
(3.17)
$$\begin{aligned}&= \frac{1}{2\pi } \int _{-\infty }^{\infty } \text {d}\omega _r \, {\widehat{\varphi }}(\omega ) \exp \left( - \mathtt {i}\omega F(T;{{\overline{T}}},0) \right) \Gamma (t,Y_t;T,-\mathtt {i}\omega G(T;{{\overline{T}}},0)) \end{aligned}$$
(3.18)
$$\begin{aligned}&\quad =: u(t,Y_t;T,{{\overline{T}}}) , \end{aligned}$$
(3.19)

where the second equality follows from (3.7), the fourth follows from (3.9) and the fifth follows from (3.1). For the particular case of a T-maturity European Call option written on \(B^{{\overline{T}}}\) we have

$$\begin{aligned} \varphi (x)&= ( \text {e}^x - \text {e}^k )^+ ,&{\widehat{\varphi }}(\omega )&= \frac{-\text {e}^{k- \mathtt {i}k \omega }}{\omega ^2 + \mathtt {i}\omega } ,&\omega _i&< -1 , \end{aligned}$$
(3.20)

where k is the \(\log \) of the strike.

4 Relation to local-stochastic volatility models

While (3.19) in conjunction with (3.20) can be used to compute T-maturity Call prices on \(B^{{\overline{T}}}\), the resulting expression tells us very little about the corresponding implied volatilities. In this section, we will establish a precise relation between affine short-rate models and local-stochastic volatility models. This relation will be used in subsequent sections to find an explicit approximation for Call option implied volatilities.

We begin deriving the dynamics of \(B^T/M\). Using (2.1) and (3.9), we have by Itô’s Lemma that

$$\begin{aligned} \text {d}\left( \frac{B_t^T}{M_t} \right)&= \left( \frac{B_t^T}{M_t} \right) \sum _{j=1}^d \gamma _j(t,Y_t;T) \text {d}W_t^{(j)} , \end{aligned}$$
(4.1)

where we have introduced

$$\begin{aligned} \gamma _j(t,Y_t;T)&:= \sum _{i=1}^d \sigma _{i,j}(t,Y_t) \partial _{y_i} \log \Gamma (t,Y_t;T,0), \end{aligned}$$
(4.2)
$$\begin{aligned}&= - \sum _{i=1}^d \sigma _{i,j}(t,Y_t) G_i(t;T,0) . \end{aligned}$$
(4.3)

Observe that \(B^T/M\) is a \((\mathbb {P},\mathbb {F})\)-martingale, as it must be.

It will be helpful at this point to introduce the T-forward probability measure \({\widetilde{\mathbb {P}}}\), whose relation to \(\mathbb {P}\) is given by the following Radon-Nikodym derivative

$$\begin{aligned} \frac{\text {d}{\widetilde{\mathbb {P}}}}{\text {d}\mathbb {P}}&:= \frac{M_0 B_T^T}{B_0^T M_T} \end{aligned}$$
(4.4)
$$\begin{aligned}&= \exp \left( - \frac{1}{2} \sum _{j=1}^d \int _0^T \gamma _j^2(t,Y_t;T) \text {d}t + \sum _{j=1}^d \int _0^T \gamma _j(t,Y_t;T) \text {d}W_t^{(j)} \right) . \end{aligned}$$
(4.5)

Note that the the last equality follows from (4.1). The following lemma will be useful.

Lemma 1

Let \(\Pi = (\Pi _t)_{0 \le t \le {{\overline{T}}}}\) denote the value of a self-financing portfolio and let \(\Pi ^T = (\Pi _t^T)_{0 \le t \le T}\), defined by \(\Pi _t^T := \Pi _t/B_t^T\), be the T-forward price of \(\Pi \). Then the process \(\Pi ^T\) is a \(({\widetilde{\mathbb {P}}},\mathbb {F})\)-martingale.

Proof

Define the Radon-Nikodym derivative process \(Z = (Z_t)_{0 \le t \le T}\) by \(Z_t := \mathbb {E}_t (\text {d}{\widetilde{\mathbb {P}}}/ \text {d}\mathbb {P})\). Using the fact that \(\Pi /M\) is a \((\mathbb {P},\mathbb {F})\)-martingale as well as Shreve (2004, Lemma 5.2.2) we have for any \(0 \le t \le s \le T\) that

$$\begin{aligned} \frac{\Pi _t}{M_t}&= \mathbb {E}_t \left( \frac{\Pi _s}{M_s} \right) = Z_t {\widetilde{\mathbb {E}}}_t \left( \frac{1}{Z_s} \frac{\Pi _s}{M_s} \right) = \frac{B_t^T}{M_t} {\widetilde{\mathbb {E}}}_t \left( \frac{M_s}{B_s^T} \frac{\Pi _s}{M_s} \right) , \end{aligned}$$
(4.6)

where \({\widetilde{\mathbb {E}}}\) denotes an expectation under \({\widetilde{\mathbb {P}}}\). Dividing both sides of Eq. (4.6) by \(B_t^T\) and canceling common factors of \(M_t\) and \(M_s\), we obtain

$$\begin{aligned} \Pi _t^T&= \frac{\Pi _t}{B_t^T} = {\widetilde{\mathbb {E}}}_t \frac{\Pi _s}{B_s^T} = {\widetilde{\mathbb {E}}}_t \Pi _s^T , \end{aligned}$$
(4.7)

which establishes that \(\Pi ^T\) is a \(({\widetilde{\mathbb {P}}},\mathbb {F})\)-martingale, as claimed. \(\square \)

Now, let us denote by \(X = (X_t)_{0 \le t \le T}\) the \(\log \) of the T-forward price of a \({{\overline{T}}}\)-maturity bond \(B^{{\overline{T}}}\). We have

$$\begin{aligned} X_t&:= \log \left( \frac{B_t^{{\overline{T}}}}{B_t^T} \right) \end{aligned}$$
(4.8)
$$\begin{aligned}&= F(t;T,0) - F(t;{{\overline{T}}},0) + \sum _{i=1}^d \big ( G_i(t;T,0) - G_i(t;{{\overline{T}}},0) \big ) Y_t^{(i)} , \end{aligned}$$
(4.9)

where the second equality follows from (3.9). It follows from the explicit relationship (4.9) between X and Y that the process

$$\begin{aligned} (X,{\widetilde{Y}}) := (X_t,Y_t^{(2)},\ldots ,Y_t^{(d)})_{0 \le t \le T} \end{aligned}$$

is a d-dimensional Markov process. We are now in a position to state the main result of this section.

Proposition 2

Let \(V^T = V/B^T\) denote the T-forward price of an option that pays \(\varphi ( \log B_T^{{\overline{T}}})\) at time T. Then there exists a function \(v(\,\cdot \,,\,\cdot \,,\,\cdot \,;T,{{\overline{T}}}): [0,T] \times \mathbb {R}_- \times \mathbb {R}^{d-1} \rightarrow \mathbb {R}\) such that

$$\begin{aligned} V_t^T&= v(t,X_t,{\widetilde{Y}}_t;T,{{\overline{T}}}) . \end{aligned}$$
(4.10)

Moreover, the function v satisfies the following PDE

$$\begin{aligned} (\partial _t + {\widetilde{{\mathscr {A}}}}(t)) v(t,\,\cdot \,,\,\cdot \,;T,{{\overline{T}}})&= 0 ,&{v(T,x,{\widetilde{y}};T,{{\overline{T}}})}&= \varphi (x) , \end{aligned}$$
(4.11)

where \({\widetilde{{\mathscr {A}}}}\) is the generator of \((X,{\widetilde{Y}})\) under \({\widetilde{\mathbb {P}}}\). Explicitly, \({\widetilde{{\mathscr {A}}}}\) is given by

$$\begin{aligned}&{\widetilde{{\mathscr {A}}}}(t) = \frac{1}{2} \sum _{i=1}^d \sum _{j=1}^d \Big ( {\widetilde{\sigma }}(t,x,{\widetilde{y}};T,{{\overline{T}}}) {\widetilde{\sigma }}^\text {Tr}(t,x,{\widetilde{y}};T,{{\overline{T}}}) \Big )_{i,j} \end{aligned}$$
(4.12)
$$\begin{aligned}&\quad \times \Big ( G_i(t;T,0) - G_i(t;{{\overline{T}}},0) \Big ) \Big ( G_j(t;T,0) - G_j(t;{{\overline{T}}},0) \Big ) (\partial _x^2-\partial _x) \end{aligned}$$
(4.13)
$$\begin{aligned}&\quad +\sum _{i=2}^d \Big ( {\widetilde{\mu }}_i(t,x,{\widetilde{y}};T,{{\overline{T}}}) - \sum _{j=1}^d \Big ( {\widetilde{\sigma }}(t,x,{\widetilde{y}};T,{{\overline{T}}}) {\widetilde{\sigma }}^\text {Tr}(t,x,{\widetilde{y}};T,{{\overline{T}}}) \Big )_{i,j} G_j(t;T,0) \Big ) \partial _{y_i} \end{aligned}$$
(4.14)
$$\begin{aligned}&\quad + \frac{1}{2} \sum _{i=2}^d \sum _{j=2}^d \Big ( {\widetilde{\sigma }}(t,x,{\widetilde{y}};T,{{\overline{T}}}) {\widetilde{\sigma }}^\text {Tr}(t,x,{\widetilde{y}};T,{{\overline{T}}}) \Big )_{i,j} \partial _{y_i}\partial _{y_j} \end{aligned}$$
(4.15)
$$\begin{aligned}&\quad + \sum _{i=2}^d \sum _{j=1}^d \Big ( {\widetilde{\sigma }}(t,x,{\widetilde{y}};T,{{\overline{T}}}) {\widetilde{\sigma }}^\text {Tr}(t,x,{\widetilde{y}};T,{{\overline{T}}}) \Big )_{i,j} \end{aligned}$$
(4.16)
$$\begin{aligned}&\quad \times \Big ( G_j(t;T,0) - G_j(t;{{\overline{T}}},0) \Big ) \partial _x \partial _{y_i} , \end{aligned}$$
(4.17)

where the functions \({\widetilde{\mu }}(\,\cdot \,,\,\cdot \,,\,\cdot \,;T,{{\overline{T}}}) : [0,T] \times \mathbb {R}_- \times \mathbb {R}^{d-1} \rightarrow \mathbb {R}^d\) and \({\widetilde{\sigma }}(\,\cdot \,,\,\cdot \,,\,\cdot \,;T,{{\overline{T}}}) : [0,T] \times \mathbb {R}_- \times \mathbb {R}^{d-1} \rightarrow \mathbb {R}^{d \times d}\) are given by

$$\begin{aligned} \left. \begin{aligned} {\widetilde{\mu }}(t,x,{\widetilde{y}};T,{{\overline{T}}})&:= \mu (t,\eta (t,x,{\widetilde{y}};T,{{\overline{T}}}),{\widetilde{y}}) , \\ {\widetilde{\sigma }}(t,x,{\widetilde{y}};T,{{\overline{T}}})&:= \sigma (t,\eta (t,x,{\widetilde{y}};T,{{\overline{T}}}),{\widetilde{y}}) , \end{aligned} \right\} \end{aligned}$$
(4.18)

the function \(\eta (\,\cdot \,,\,\cdot \,,\,\cdot \,;T,{{\overline{T}}}) : [0,T] \times \mathbb {R}_- \times \mathbb {R}^{d-1} \rightarrow \mathbb {R}\) is defined as follows

$$\begin{aligned}&\eta (t,x,{\widetilde{y}};T,{{\overline{T}}}) = \frac{1}{G_1(t;{{\overline{T}}},0)-G_1(t;T,0)}\Big (F(t;T,0) - F(t;{{\overline{T}}},0) - x \Big ) \end{aligned}$$
(4.19)
$$\begin{aligned}&\quad + \frac{1}{G_1(t;{{\overline{T}}},0)-G_1(t;T,0)} \left( \sum _{i=2}^d (G_i(t;T,0) - G_i(t;{{\overline{T}}},0) ) y_i \right) , \end{aligned}$$
(4.20)

and the functions F and \(G_i\) satisfy the system of coupled ODEs (3.5) and (3.6).

Proof

Noting that \(V^T\) is a \(({\widetilde{\mathbb {P}}},\mathbb {F})\)-martingale, we have

$$\begin{aligned} V_t^T&= \frac{V_t}{B_t^T} = {\widetilde{\mathbb {E}}}_t \left( \frac{V_T}{B_T^T} \right) = {\widetilde{\mathbb {E}}}_t\varphi \left( \log B_T^{{\overline{T}}}\right) = {\widetilde{\mathbb {E}}}_t\varphi (X_T) =: v(t,X_t{,{\widetilde{Y}}_t};T,{{\overline{T}}}) , \end{aligned}$$
(4.21)

where the existence of the function v follows from the Markov property of \((X,{\widetilde{Y}})\). The function v satisfies the Kolmogorov backward PDE (4.11) where \({\widetilde{{\mathscr {A}}}}\) denotes the generator of \((X,{\widetilde{Y}})\) under \({\widetilde{\mathbb {P}}}\). To derive the expression (4.17) for \({\widetilde{{\mathscr {A}}}}\), we note that, by Girsanov’s theorem and (4.5), the process \({\widetilde{W}}:= ({\widetilde{W}}_t^{(1)}, {\widetilde{W}}_t^{(2)}, \ldots , {\widetilde{W}}_t^{(d)})_{0 \le t \le T}\), defined as follows

$$\begin{aligned} {\widetilde{W}}_t^{(j)}&:= - \int _0^t \gamma _j(s,Y_s;T) \text {d}s + W_t^{(j)} , \end{aligned}$$
(4.22)

is a d-dimensional \(({\widetilde{\mathbb {P}}},\mathbb {F})\)-Brownian motion. Thus, we have from equations (2.4), (4.3) and (4.22) that

$$\begin{aligned}&\text {d}Y_t^{(i)} = \Big ( \mu _i(t,Y_t) - \sum _{j=1}^d \Big ( \sigma (t,Y_t) \sigma ^\text {Tr}(t,Y_t) \Big )_{i,j} G_j(t;T,0) \Big ) \text {d}t + \sum _{j=1}^d \sigma _{i,j}(t,Y_t)\text {d}{\widetilde{W}}_t^{(j)} \end{aligned}$$
(4.23)
$$\begin{aligned}&= \Big ( {\widetilde{\mu }}_i(t,X_t,{{\widetilde{Y}}_t};T,{{\overline{T}}}) - \sum _{j=1}^d \Big ( {{\widetilde{\sigma }}(t,X_t,{\widetilde{Y}}_t;T,{{\overline{T}}})} {\widetilde{\sigma }}^\text {Tr}(t,X_t,{{\widetilde{Y}}_t};T,{{\overline{T}}}) \Big )_{i,j} G_j(t;T,0) \Big ) \text {d}t \end{aligned}$$
(4.24)
$$\begin{aligned}&+ \sum _{j=1}^d {\widetilde{\sigma }}_{i,j}(t,X_t,{{\widetilde{Y}}_t};T,{{\overline{T}}})\text {d}{\widetilde{W}}_t^{(j)} , \end{aligned}$$
(4.25)

where, in the the second equality, we have used \(Y_t^{(1)} = \eta (t,X_t,{\widetilde{Y}}_t;T,{{\overline{T}}})\), which follows from from (4.9). Similarly, using (4.1) and (4.8), we find using Itô’s Lemma that

$$\begin{aligned} \text {d}X_t&= -\frac{1}{2} \sum _{i=1}^d \sum _{j=1}^d \Big ( \sigma (t,Y_t) \sigma ^\text {Tr}(t,Y_t) \Big )_{i,j} \end{aligned}$$
(4.26)
$$\begin{aligned}&\quad \times \Big ( G_i(t;T,0) - G_i(t;{{\overline{T}}},0) \Big ) \Big ( G_j(t;T,0) - G_j(t;{{\overline{T}}},0) \Big ) \text {d}t \end{aligned}$$
(4.27)
$$\begin{aligned}&\quad + \sum _{i=1}^d \sum _{j=1}^d \sigma _{i,j}(t,Y_t) \Big ( G_i(t;T,0) - G_i(t;{{\overline{T}}},0) \Big ) \text {d}{\widetilde{W}}_t^{(j)} \end{aligned}$$
(4.28)
$$\begin{aligned}&= -\frac{1}{2} \sum _{i=1}^d \sum _{j=1}^d \Big ( {\widetilde{\sigma }}(t,X_t,{{\widetilde{Y}}_t};T,{{\overline{T}}}) {\widetilde{\sigma }}^\text {Tr}(t,X_t,{{\widetilde{Y}}_t};T,{{\overline{T}}}) \Big )_{i,j} \end{aligned}$$
(4.29)
$$\begin{aligned}&\quad \times \Big ( G_i(t;T,0) - G_i(t;{{\overline{T}}},0) \Big ) \Big ( G_j(t;T,0) - G_j(t;{{\overline{T}}},0) \Big ) \text {d}t \end{aligned}$$
(4.30)
$$\begin{aligned}&\quad + \sum _{i=1}^d \sum _{j=1}^d {\widetilde{\sigma }}_{i,j}(t,X_t,{{\widetilde{Y}}_t};T,{{\overline{T}}}) \Big ( G_i(t;T,0) - G_i(t;{{\overline{T}}},0) \Big ) \text {d}{\widetilde{W}}_t^{(j)} . \end{aligned}$$
(4.31)

The explicit expression (4.17) for the generator \({\widetilde{{\mathscr {A}}}}\) follows from (4.25) and (4.31). \(\square \)

Observe that \(\text {e}^X = B^{{\overline{T}}}/B^T\) is a strictly positive \(({\widetilde{\mathbb {P}}},\mathbb {F})\)-martingale. Thus, the process \((X,{\widetilde{Y}})\) has the same form as a local-stochastic volatility model where X represents the \(\log \) of the T-forward price of an risky asset (e.g., stock, index, etc.) and \({\widetilde{Y}}\) represents \((d-1)\) non-local factors of volatility.

Example 1

Consider a one-factor affine short-rate model (\(d = 1\)). Then X has the form of a (pure) local volatility model with generator

$$\begin{aligned} {\widetilde{{\mathscr {A}}}}(t)&= c(t,x) (\partial _x^2 - \partial _x ) ,&\end{aligned}$$
(4.32)
$$\begin{aligned} c(t,x)&:= \frac{1}{2} {\widetilde{\sigma }}^2(t,x;T,{{\overline{T}}}) {\Big ( G(t;T,0) - G(t;{{\overline{T}}},0) \Big )}^2, \end{aligned}$$
(4.33)

where we have omitted the argument \({\widetilde{y}}\) as it plays no role.

Example 2

Consider a two-factor affine short-rate model (\(d=2\)). Then the process \((X,Y^{(2)})\) has the form of a local-stochastic volatility model with a single non-local factor of volatility. The generator in this case, is given by

$$\begin{aligned} {\widetilde{{\mathscr {A}}}}(t)&= c(t,x,y_2) (\partial _x^2 - \partial _x ) + f(t,x,y_2) \partial _{y_2} + g(t,x,y_2) \partial _{y_2}^2 \end{aligned}$$
(4.34)
$$\begin{aligned}&\quad + h(t,x,y_2) \partial _x \partial _{y_2}, \end{aligned}$$
(4.35)

where the functions c, f, g and h are given by

$$\begin{aligned} c(t,x,y_2)&:= \frac{1}{2}\Big ({\widetilde{\sigma }}^2_{1,1}(t,x,y_2;T,{{\overline{T}}})+{\widetilde{\sigma }}^2_{1,2}(t,x,y_2;T,{{\overline{T}}})\Big ) \end{aligned}$$
(4.36)
$$\begin{aligned}&\quad \times \Big ( G_1(t;T,0) - G_1(t;{{\overline{T}}},0)\Big )^2 \end{aligned}$$
(4.37)
$$\begin{aligned}&\quad + \Big ( {\widetilde{\sigma }}_{1,1}(t,x,y_2;T,{{\overline{T}}}){\widetilde{\sigma }}_{2,1}(t,x,y_2;T,{{\overline{T}}}) \end{aligned}$$
(4.38)
$$\begin{aligned}&\quad +{\widetilde{\sigma }}_{1,2}(t,x,y_2;T,{{\overline{T}}}){\widetilde{\sigma }}_{2,2}(t,x,y_2;T,{{\overline{T}}})\Big ) \end{aligned}$$
(4.39)
$$\begin{aligned}&\quad \times \Big (G_1(t;T,0) - G_1(t;{{\overline{T}}},0)\Big )\Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0)\Big ) \end{aligned}$$
(4.40)
$$\begin{aligned}&\quad + {\frac{1}{2}}\Big ({\widetilde{\sigma }}^2_{2,1}(t,x,y_2;T,{{\overline{T}}})+{\widetilde{\sigma }}^2_{2,2}(t,x,y_2;T,{{\overline{T}}})\Big ) \end{aligned}$$
(4.41)
$$\begin{aligned}&\quad \times \Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0)\Big )^2, \end{aligned}$$
(4.42)
$$\begin{aligned} f(t,x,y_2)&:= {\widetilde{\mu }}_2(t,x,y_2;T,{{\overline{T}}}) \end{aligned}$$
(4.43)
$$\begin{aligned}&\quad -\Big ({\widetilde{\sigma }}^2_{2,1}(t,x,y_2;T,{{\overline{T}}})+{\widetilde{\sigma }}^2_{2,2}(t,x,y_2;T,{{\overline{T}}})\Big )G_2(t;T,0) \end{aligned}$$
(4.44)
$$\begin{aligned}&\quad - \Big ({\widetilde{\sigma }}_{1,1}(t,x,y_2;T,{{\overline{T}}}){\widetilde{\sigma }}_{2,1}(t,x,y_2;T,{{\overline{T}}}) \end{aligned}$$
(4.45)
$$\begin{aligned}&\quad + {\widetilde{\sigma }}_{1,2}(t,x,y_2;T,{{\overline{T}}}){\widetilde{\sigma }}_{2,2}(t,x,y_2;T,{{\overline{T}}})\Big )G_1(t;T,0), \end{aligned}$$
(4.46)
$$\begin{aligned} g(t,x,y_2)&:= \frac{1}{2}\Big ({\widetilde{\sigma }}^2_{2,1}(t,x,y_2;T,{{\overline{T}}}) + {\widetilde{\sigma }}^2_{2,2}(t,x,y_2;T,{{\overline{T}}})\Big ), \end{aligned}$$
(4.47)
$$\begin{aligned} h(t,x,y_2)&:= \Big ({\widetilde{\sigma }}^2_{2,1}(t,x,y_2;T,{{\overline{T}}})+{\widetilde{\sigma }}^2_{2,2}(t,x,y_2;T,{{\overline{T}}})\Big )\nonumber \\&\quad \qquad \Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0)\Big ) \end{aligned}$$
(4.48)
$$\begin{aligned}&\quad + \Big ({\widetilde{\sigma }}_{1,1}(t,x,y_2;T,{{\overline{T}}}){\widetilde{\sigma }}_{2,1}(t,x,y_2;T,{{\overline{T}}}) \end{aligned}$$
(4.49)
$$\begin{aligned}&\quad + {\widetilde{\sigma }}_{1,2}(t,x,y_2;T,{{\overline{T}}}){\widetilde{\sigma }}_{2,2}(t,x,y_2;T,{{\overline{T}}})\Big ) \Big (G_1(t;T,0) - G_1(t;{{\overline{T}}},0)\Big ). \end{aligned}$$
(4.50)

5 Option price asymptotics

We have from (4.11) that v satisfies a parabolic PDE of the form

$$\begin{aligned} ( \partial _t + {\widetilde{{\mathscr {A}}}}(t) ) v(t, \,\cdot \,)&= 0 ,&{\widetilde{{\mathscr {A}}}}(t)&= \sum _{|\alpha |\le 2} a_\alpha (t,z) \partial _z^\alpha ,&v(T, \, \cdot \,)&= \varphi , \end{aligned}$$
(5.1)

where \(z := (x, y_2, \ldots , y_d)\). Note that, for brevity, we have omitted the dependence on T and \({{\overline{T}}}\) and we have introduced standard multi-index notation

$$\begin{aligned} \alpha&= (\alpha _1, \alpha _2, \dots , \alpha _d) ,&\partial _z^\alpha&= \prod _{i=1}^d \partial _{z_i}^{\alpha _i} , z^\alpha&= \prod _{i=1}^d {z_i}^{\alpha _i} , \end{aligned}$$
(5.2)
$$\begin{aligned} |\alpha |&= \sum _{i=1}^d \alpha _i ,&\alpha !&= \prod _{i=1}^d \alpha _i! . \end{aligned}$$
(5.3)

In general there is no explicit solution to PDEs of the form (5.1). In this section, we will show in a formal manner how an explicit approximation of v can be obtained by using a simple Taylor series expansion of the coefficients \(a_\alpha \) of \({\widetilde{{\mathscr {A}}}}\). The method described below was introduced for scalar diffusions in Pagliarani and Pascucci (2012) and subsequently extended to d-dimensional diffusions in Lorig et al. (2017) and Lorig et al. (2015).

To begin, for any \(\varepsilon \in [0,1]\) and \({\bar{z}}: [0,T] \rightarrow \mathbb {R}^d\), let \(v^\varepsilon \) be the unique classical solution to

$$\begin{aligned} 0&= ( \partial _t + {\widetilde{{\mathscr {A}}}}^\varepsilon (t) ) v^\varepsilon (t, \,\cdot \,) ,&v^\varepsilon (T, \, \cdot \,)&= \varphi , \end{aligned}$$
(5.4)

where the operator \({\widetilde{{\mathscr {A}}}}^\varepsilon \) is defined as follows

$$\begin{aligned} {\widetilde{{\mathscr {A}}}}^\varepsilon (t)&:= \sum _{|\alpha |\le 2} a_\alpha ^\varepsilon (t,z) \partial _z^\alpha ,&\text {with}&a_\alpha ^\varepsilon&:= a_\alpha (t,{\bar{z}}(t) + \varepsilon (z - {\bar{z}}(t))) , \end{aligned}$$
(5.5)

Observe that \({\widetilde{{\mathscr {A}}}}^\varepsilon |_{\varepsilon = 1} = {\widetilde{{\mathscr {A}}}}\) and thus \(v^\varepsilon |_{\varepsilon =1} = v\). We will seek an approximate solution of (5.4) by expanding \(v^\varepsilon \) and \({\widetilde{{\mathscr {A}}}}^\varepsilon \) in powers of \(\varepsilon \). Our approximation for v will be obtained by setting \(\varepsilon = 1\) in our approximation for \(v^\varepsilon \). We have

$$\begin{aligned} v^\varepsilon&= \sum _{n=0}^\infty \varepsilon ^n v_n ,&{\widetilde{{\mathscr {A}}}}^\varepsilon (t)&= \sum _{n=0}^\infty \varepsilon ^n {\widetilde{{\mathscr {A}}}}_n(t) , \end{aligned}$$
(5.6)

where the functions \((v_n)\) are, at the moment, unknown, and the operators \(({\widetilde{{\mathscr {A}}}}_n)\) are given by

$$\begin{aligned} {\widetilde{{\mathscr {A}}}}_n(t)&= \frac{\text {d}^n }{\text {d}\varepsilon ^n} {\widetilde{{\mathscr {A}}}}^\varepsilon |_{\varepsilon =0} = \sum _{|\alpha |\le 2} a_{\alpha ,n}(t,z) \partial _z^\alpha ,&\end{aligned}$$
(5.7)
$$\begin{aligned} a_{\alpha ,n}&= \sum _{|\beta |=n} \frac{1}{\beta !} (z - {\bar{z}}(t))^\beta \partial _z^\beta a_\alpha (t,{\bar{z}}(t)) . \end{aligned}$$
(5.8)

Note that \(a_{\alpha ,n}(t, \, \cdot \,)\) is the sum of the nth order terms in the Taylor series expansion of \(a_\alpha (t,\,\cdot \,)\) about the point \({\bar{z}}(t)\). Inserting the expansions from (5.6) for \(v^\varepsilon \) and \({\widetilde{{\mathscr {A}}}}^\varepsilon \) into PDE (5.4) and collecting terms of like order in \(\varepsilon \) we obtain

$$\begin{aligned} {\mathscr {O}}(\varepsilon ^0):\,&\begin{aligned} ( \partial _t + {\widetilde{{\mathscr {A}}}}_0(t) ) v_0(t, \,\cdot \,)&= 0, \\ v_0(T, \, \cdot \,)&= \varphi , \end{aligned} \end{aligned}$$
(5.9)
$$\begin{aligned} {\mathscr {O}}(\varepsilon ^n):\,&\begin{aligned} ( \partial _t + {\widetilde{{\mathscr {A}}}}_0(t) ) v_n(t, \,\cdot \,) + \sum _{k=1}^n {\widetilde{{\mathscr {A}}}}_k(t) v_{n-k}(t,\,\cdot \,)&= 0 , \\ v_n(T, \, \cdot \,)&= 0 . \end{aligned} \end{aligned}$$
(5.10)

Now, observe that the coefficients \((a_{\alpha ,0})\) of \({\widetilde{{\mathscr {A}}}}_0\) do not depend on z. Thus, \({\widetilde{{\mathscr {A}}}}_0\) is the generator of a d-dimensional Brownian motion with a time-dependent drift vector and covariance matrix. As such, \(v_0\) is given by

$$\begin{aligned} v_0(t,z)&= {\mathscr {P}}_0(t,T)\varphi (z) = \int _{\mathbb {R}^d} \text {d}z' \, p_0(t,z;T,z') \varphi (z') . \end{aligned}$$
(5.11)

where \({\mathscr {P}}_0\) is the semigroup generated by \({\widetilde{{\mathscr {A}}}}_0\) and \(p_0\) is the associated transition density (i.e., the solution to (5.9) with \(\varphi = \delta _{z'}\)). Explicitly, we have

$$\begin{aligned} p_0(t,z;T,z')&= \frac{1}{\sqrt{(2\pi )^d|{\mathbf {C}}(t,T)|}} \end{aligned}$$
(5.12)
$$\begin{aligned}&\quad \times {\exp \left( -\frac{1}{2} (z'-z-{\mathbf {m}}(t,T))^\text {Tr} {\mathbf {C}}^{-1}(t,T) (z'-z-{\mathbf {m}}(t,T)) \right) } , \end{aligned}$$
(5.13)

where \({\mathbf {m}}\) and \({\mathbf {C}}\) are given by

$$\begin{aligned} {\mathbf {m}}(t,T)&:= \int _t^T \text {d}s \, m(s) ,&{\mathbf {C}}(t,T)&:= \int _t^T \text {d}s \, A(s) , \end{aligned}$$
(5.14)

and m and A are, respectively, the instantaneous drift vector and covariance matrix

$$\begin{aligned} m(s)&:= \begin{pmatrix} a_{(1,0,\cdots ,0),0}(s) \\ a_{(0,1,\cdots ,0),0}(s) \\ \vdots \\ a_{(0,0,\cdots ,1),0}(s) \end{pmatrix} ,&\end{aligned}$$
(5.15)
$$\begin{aligned} A(s)&:= \begin{pmatrix} 2a_{(2,0,\cdots ,0),0}(s) &{} a_{(1,1,\cdots ,0),0}(s) &{} \ldots &{} {a_{(1,0,\cdots ,1),0}(s)} \\ a_{(1,1,\cdots ,0),0}(s) &{} 2a_{(0,2,\cdots ,0),0}(s) &{} \ldots &{} a_{(0,1,\cdots ,1),0}(s) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ a_{(1,0,\cdots ,1),0}(s) &{} a_{(0,1,\cdots ,1),0}(s) &{} \ldots &{} 2 a_{(0,0,\cdots ,2),0}(s) \\ \end{pmatrix} . \end{aligned}$$
(5.16)

By Duhamel’s principle, the solution \(v_n\) of (5.10) is

$$\begin{aligned}&v_n(t,z) = \sum _{k=1}^n \int _t^T \text {d}t_1 \, {\mathscr {P}}_0(t,t_1) {\widetilde{{\mathscr {A}}}}_k(t_1) v_{n-k}(t_1,z) \end{aligned}$$
(5.17)
$$\begin{aligned}&= \sum _{k=1}^n \sum _{i \in I_{n,k}} \int _{t}^T \text {d}t_1 \int _{t_1}^T \text {d}t_2 \cdots \int _{t_{k-1}}^T \text {d}t_k \Big ( {\mathscr {P}}_0(t,t_1) {\mathscr {A}}_{i_1}(t_1) {\mathscr {P}}_0(t_1,t_2) {\mathscr {A}}_{i_2}(t_2) \end{aligned}$$
(5.18)
$$\begin{aligned}&\cdots {\mathscr {P}}_0(t_{k-1},t_k) {\mathscr {A}}_{i_k}(t_k) {\mathscr {P}}_0(t_k,T)\varphi (z) \Big ) , \end{aligned}$$
(5.19)
$$\begin{aligned}&I_{n,k} = \{ i = (i_1, i_2, \cdots , i_k ) \in \mathbb {N}^k : i_1 + i_2 + \cdots + i_k = n \} . \end{aligned}$$
(5.20)

While the expression (5.19) for \(v_n\) is explicit, it is not easy to compute as operating on a function with \({\mathscr {P}}_0\) requires performing a d-dimensional integral. The following proposition establishes that \(v_n\) can be expressed as a differential operator acting on \(v_0\).

Proposition 3

The solution \(v_n\) of PDE (5.10) is given by

$$\begin{aligned} v_n(t,z)&= {\mathscr {L}}_n(t,T) v_0(t,z) , \end{aligned}$$
(5.21)

where \({\mathscr {L}}\) is a linear differential operator, which is given by

$$\begin{aligned} {\mathscr {L}}_n(t,T)&= \sum _{k=1}^n \sum _{i \in I_{n,k}} \int _{t}^T \mathrm{d} t_1 \int _{t_1}^T \mathrm{d} t_2 \cdots \int _{t_{k-1}}^T \mathrm{d} t_k {\mathscr {G}}_{i_1}(t,t_1) {\mathscr {G}}_{i_2}(t,t_2) \cdots {\mathscr {G}}_{i_k}(t,t_k) , \end{aligned}$$
(5.22)

the index set \(I_{n,k}\) as defined in (5.20) and the operator \({\mathscr {G}}_i\) is given by

$$\begin{aligned} \left. \begin{aligned} {\mathscr {G}}_i(t,t_k)&:= \sum _{|\alpha |\le 2} a_{\alpha ,i}(t_k,{\mathscr {Z}}(t,t_k)) \partial _z^\alpha , \\ {\mathscr {Z}}(t,t_k)&:= z + {\mathbf {m}}(t,t_k) + {\mathbf {C}}(t,t_k) \nabla _z . \end{aligned} \right\} \end{aligned}$$
(5.23)

Proof

The proof, which is given in Lorig et al. (2017, Theorem 2.6), relies on the fact that, for any \(0 \le t \le t_k < \infty \) the operator \({\mathscr {G}}_i\) in (5.23) satisfies

$$\begin{aligned} {\mathscr {P}}_0(t,t_k) {\mathscr {A}}_{i}(t_k)&= {\mathscr {G}}_i(t,t_k) {\mathscr {P}}_0(t,t_k) . \end{aligned}$$
(5.24)

Using (5.24), as well as the semigroup property \({{\mathscr {P}}_0}(t_1,t_2) {{\mathscr {P}}_0}(t_2,t_3) = {{\mathscr {P}}_0}(t_1,{t_3})\), we have that

$$\begin{aligned}&{\mathscr {P}}_0(t,t_1) {\mathscr {A}}_{i_1}(t_1) {\mathscr {P}}_0(t_1,t_2) {\mathscr {A}}_{i_2}(t_2) \cdots {\mathscr {P}}_0(t_{k-1},t_k) {\mathscr {A}}_{i_k}(t_k) {\mathscr {P}}_0(t_k,T) \varphi (z) \end{aligned}$$
(5.25)
$$\begin{aligned}&= {\mathscr {G}}_{i_1}(t,t_1) {\mathscr {G}}_{i_2}(t,t_2) \cdots {\mathscr {G}}_{i_k}(t,t_k) {\mathscr {P}}_0(t,t_1) {\mathscr {P}}_0(t_1,t_2) \cdots {\mathscr {P}}_0(t_{k-1},t_k) {\mathscr {P}}_0(t_k,T) \varphi \end{aligned}$$
(5.26)
$$\begin{aligned}&= {\mathscr {G}}_{i_1}(t,t_1) {\mathscr {G}}_{i_2}(t,t_2) \cdots {\mathscr {G}}_{i_k}(t,t_k) {\mathscr {P}}_0(t,T) \varphi \end{aligned}$$
(5.27)
$$\begin{aligned}&= {\mathscr {G}}_{i_1}(t,t_1) {\mathscr {G}}_{i_2}(t,t_2) \cdots {\mathscr {G}}_{i_k}(t,t_k) v_0(t,\,\cdot \,) , \end{aligned}$$
(5.28)

where, in the last equality we have used \({\mathscr {P}}_0(t,T) \varphi = v_0(t,\,\cdot \,)\). Inserting (5.28) into (5.19) yields (5.21). \(\square \)

Having obtained explicit expressions for the functions \((v_n)\), we define \({\bar{v}}\), the nth order approximation of v, as follows

$$\begin{aligned} {\bar{v}}_n := \sum _{k=0}^n {v_k} . \end{aligned}$$
(5.29)

Note that \({\bar{v}}_n\) depends on the choice of \({\bar{z}}\). In general, if one is interested in the value of v(t, z) a good choice for \({\bar{z}}\) is \({\bar{z}}(t) = z\). Indeed, when one chooses \({\bar{z}}(t) = z\), we have from [Lorig et al. (2015), Theorem 3.10] that

$$\begin{aligned} |v(t,z) - {\bar{v}}_n(t,z)|&= {\mathscr {O}}\left( (T-t)^{(n+k+2)/2} \right)&\hbox { as}\ T-t \rightarrow 0 , \end{aligned}$$
(5.30)

when the terminal data \(\varphi \) is a bounded function with globally Lipschitz continuous derivatives of order less than or equal to k.

6 Implied volatility asymptotics

The goal of this section is to find an explicit approximation for the implied volatility corresponding to the T-forward Call price \(v(t,x,{\widetilde{y}};T,{{\overline{T}}},k)\) where we have included now the dependence on the \(\log \) strike k. For brevity, in what follows, we will omit the dependence on \((t,x,{\widetilde{y}};T,{{\overline{T}}},k)\).

To begin, we remind the reader that, in the Black–Scholes setting, the T-forward price of a risky asset S has dynamics of the form

$$\begin{aligned} \text {d}\left( \frac{S_t}{B_t^T} \right)&= \Sigma \left( \frac{S_t}{B_t^T} \right) \text {d}{\widetilde{W}}_t , \end{aligned}$$
(6.1)

where \(\Sigma > 0\) is the Black–Scholes volatility and \({\widetilde{W}}\) is a one-dimensional Brownian motion under \({\widetilde{\mathbb {P}}}\). Given that \(\log (S_t/B_T^T) = x\), the T-forward Black–Scholes Call price with volatility \(\Sigma > 0\) is given by

$$\begin{aligned} v^\text {BS}(\Sigma )&:= \text {e}^x \Phi (d_+) - \text {e}^k \Phi (d_-) , \end{aligned}$$
(6.2)
$$\begin{aligned} d_\pm&= \frac{1}{\Sigma {\sqrt{T-t}}} \left( x - k \pm \frac{\Sigma ^2 (T-t)}{2} \right) , \end{aligned}$$
(6.3)
$$\begin{aligned} \Phi (d)&= \int _{-\infty }^d \text {d}x \, \frac{1}{\sqrt{2\pi }} \text {e}^{-x^2/2} . \end{aligned}$$
(6.4)

From this, one defines the implied volatility corresponding to the T-forward Call price v as the unique positive solution \(\Sigma \) to

$$\begin{aligned} v^\text {BS}(\Sigma )&= v . \end{aligned}$$
(6.5)

As in the previous section, we will seek an approximation of the implied volatility \(\Sigma ^\varepsilon \) corresponding to \(v^\varepsilon \) by expanding \(\Sigma ^\varepsilon \) in power of \(\varepsilon \). Our approximation of \(\Sigma \) will then be obtained by setting \(\varepsilon = 1\). We have

$$\begin{aligned} \Sigma ^\varepsilon&= \Sigma _0 + \delta \Sigma ^\varepsilon ,&\delta \Sigma ^\varepsilon&= \sum _{n=1}^\infty \varepsilon ^n \Sigma _n . \end{aligned}$$
(6.6)

Next, expanding \(v^\text {BS}(\Sigma ^\varepsilon )\) in powers of \(\varepsilon \) we obtain

$$\begin{aligned} v^\text {BS}(\Sigma ^\varepsilon )&= v^\text {BS}(\Sigma _0 + \delta \Sigma ^\varepsilon ) \end{aligned}$$
(6.7)
$$\begin{aligned}&= \sum _{k=0}^\infty \frac{1}{k!}(\delta \Sigma ^\varepsilon \partial _\Sigma )^k v^\text {BS}(\Sigma _0) \end{aligned}$$
(6.8)
$$\begin{aligned}&= v^\text {BS}(\Sigma _0) + \sum _{k=1}^\infty \frac{1}{k!} \sum _{n=1}^\infty \varepsilon ^n \sum _{I_{n,k}} \Big ( \prod _{j=1}^k \Sigma _{i_j} \Big ) \partial _\Sigma ^k v^\text {BS}(\Sigma _0) \end{aligned}$$
(6.9)
$$\begin{aligned}&= v^\text {BS}(\Sigma _0) + \sum _{n=1}^\infty \varepsilon ^n \sum _{k=1}^\infty \frac{1}{k!} \sum _{ I_{n,k}} \Big ( \prod _{j=1}^k \Sigma _{i_j} \Big ) \partial _\Sigma ^k v^\text {BS}(\Sigma _0) \end{aligned}$$
(6.10)
$$\begin{aligned}&= v^\text {BS}(\Sigma _0) + \sum _{n=1}^\infty \varepsilon ^n \bigg ( \Sigma _n \partial _\Sigma + \sum _{k=2}^\infty \frac{1}{k!} \sum _{ I_{n,k}} \left( \prod _{j=1}^k \Sigma _{i_j} \right) \partial _\Sigma ^k \bigg ) v^\text {BS}(\Sigma _0) , \end{aligned}$$
(6.11)

where \(I_{n,k}\) is given by (5.20). Inserting the expansions for \(v^\varepsilon \) and \(v^\text {BS}(\Sigma ^\varepsilon )\) into \(v^\varepsilon = v^\text {BS}(\Sigma ^\varepsilon )\) and collecting terms of like order in \(\varepsilon \) we obtain

$$\begin{aligned}&{\mathscr {O}}(\varepsilon ^0)&v_0&= v^\text {BS}(\Sigma _0) , \end{aligned}$$
(6.12)
$$\begin{aligned}&{\mathscr {O}}(\varepsilon ^n)&v_n&= \left( \Sigma _n \partial _\Sigma + \sum _{k=2}^\infty \frac{1}{k!} \sum _{ I_{n,k}} \left( \prod _{j=1}^k \Sigma _{i_j} \right) \partial _\Sigma ^k \right) v^\text {BS}(\Sigma _0) . \end{aligned}$$
(6.13)

Now, from (5.11) we have

$$\begin{aligned} v_0 = v^\text {BS}\left( {\sqrt{ {\mathbf {C}}_{1,1}(t,T)/(T-t) }} \right) , \end{aligned}$$
(6.14)

where \({\mathbf {C}}\) is defined in (5.14). Thus, it follows from (6.12) that

$$\begin{aligned} \Sigma _0&= {\sqrt{ {\mathbf {C}}_{1,1}(t,T)/(T-t) }} . \end{aligned}$$
(6.15)

Having identified \(\Sigma _0\), we can use (6.13) to obtain \(\Sigma _n\) recursively for every \(n \ge 1\). We have

$$\begin{aligned} \Sigma _n&= \frac{1}{\partial _\Sigma v^\text {BS}(\Sigma _0)} \left( v_n - \sum _{k=2}^\infty \frac{1}{k!} \sum _{ I_{n,k}} \left( \prod _{j=1}^k \Sigma _{i_j} \right) \partial _\Sigma ^k v^\text {BS}(\Sigma _0) \right) . \end{aligned}$$
(6.16)

Using the expression given in (5.21) for \(v_n\), one can show that \(\Sigma _n\) is an nth order polynomial in \(\log \)-moneyness \(k-x\) with coefficients that depend on (t, T); see Lorig et al. (2017, Section 3) for details. We provide explicit expressions for \(\Sigma _0\), \(\Sigma _1\), and \(\Sigma _2\) for the cases \(d=\{1,2\}\) in “Appendix A”.

Having obtained expressions for \((\Sigma _n)\), we define \({\bar{\Sigma }}\), the nth order approximation of \(\Sigma \), as follows

$$\begin{aligned} {\bar{\Sigma }}_n&:= \sum _{k=0}^n \Sigma _k . \end{aligned}$$
(6.17)

Note that \({\bar{\Sigma }}_n\) depends on the choice of \({\bar{z}}\). In general, the best choice for \({\bar{z}}\) is \({\bar{z}}(t) = (x,{\widetilde{y}})\). In this case, we have under mild conditions on the generator \({\widetilde{{\mathscr {A}}}}\) that

$$\begin{aligned} |\Sigma (t,x,{\widetilde{y}};T,{{\overline{T}}},k)-{\bar{\Sigma }}_n(t,x,{\widetilde{y}};T,{{\overline{T}}},k)|&= {\mathscr {O}}((T-t)^{(n+1)/2}), \end{aligned}$$
(6.18)
$$\begin{aligned} \text {as } |k-x|&= {\mathscr {O}}( {\sqrt{T-t}}). \end{aligned}$$
(6.19)

by Pagliarani and Pascucci (2017, Theorem 5.1).

7 Examples

In this section we use the results from Sect. 6 to compute approximate implied volatilities for T-forward Call prices written on \(B^{{\overline{T}}}\) for the following four affine short-rate models:

  • Section 7.1: Vasicek model,

  • Section 7.2: Cox–Ingersoll–Ross model,

  • Section 7.3: Two-factor Cox–Ingersoll–Ross model,

  • Section 7.4: Fong–Vasicek model.

Note that, given \((X_t,{\widetilde{Y}}_t) = (x,{\widetilde{y}})\), exact T-forward Call prices can be computed using

$$\begin{aligned} v(t,x,{\widetilde{y}};T,{{\overline{T}}}) = \frac{u(t,y;T,{{\overline{T}}})}{\Gamma (t,y;T,0)} ,&\quad y_1&= \eta (t,x,{\widetilde{y}};T,{{\overline{T}}}) , \end{aligned}$$
(7.1)

where \(\Gamma \), u and \(\eta \) are given in (3.4), (3.19)–(3.20) and (4.20), respectively. The corresponding “exact” implied volatilities can be obtained by inserting (7.1) into (6.5) and solving for \(\Sigma \) numerically. We will use this in what follows below in order to gauge the numerical accuracy of our implied volatility approximation \({\bar{\Sigma }}_n\).

7.1 Vasicek

In the short-rate model developed in Vasicek (1977), the dynamics of \(R=r(Y)\) are given by

$$\begin{aligned} \text {d}Y_t&= \kappa ( \theta - Y_t) \text {d}t + \delta \text {d}W_t ,&R_t&= Y_t . \end{aligned}$$
(7.2)

Comparing (7.2) with (2.2) and (2.4), we see that the functions r, \(\mu \), and \(\sigma \) are given by

$$\begin{aligned} r(y)&= y ,&\mu (t,y)&= \kappa ( \theta - y) ,&\sigma (t,y)&= \delta , \end{aligned}$$
(7.3)

and comparing (7.3) with (2.5) we identify

$$\begin{aligned} q&= 0 ,&\psi&= 1 ,&b(t)&= \kappa \theta ,&\beta (t)&= - \kappa ,&\ell (t)&= \delta ^2,&\lambda (t)&= 0 , \end{aligned}$$
(7.4)

where we have dropped the subscripts from \(\psi \), \(\beta \) and \(\lambda \) as \(d=1\). With the above parameters, the solution G of ODE (3.6) is

$$\begin{aligned} G(t;T,\nu )&= - \text {e}^{-\kappa (T-t)}\nu + \frac{1-\text {e}^{-\kappa (T-t)}}{\kappa } . \end{aligned}$$
(7.5)

While the solution F of ODE (3.5) is needed to compute exact Call option prices, we shall see that it is not needed to compute implied volatilities in the Vasicek setting. As such, we do not provide a formula for F here. From (4.18), (4.20), and (7.3), we have

$$\begin{aligned} {\widetilde{\sigma }}(t,x;T,{{\overline{T}}})&:= \delta . \end{aligned}$$
(7.6)

And thus, using (4.32), (7.5) and (7.6), the generator \({\widetilde{{\mathscr {A}}}}\) is given by

$$\begin{aligned} {\widetilde{{\mathscr {A}}}}(t)&= c(t,x) (\partial _x^2 - \partial _x ) ,&c(t,x)&= \frac{1}{2} \delta ^2 \left( \frac{1-\text {e}^{-\kappa (T-t)}}{\kappa } - \frac{1-\text {e}^{-\kappa ({{\overline{T}}} - t)}}{\kappa } \right) ^2 . \end{aligned}$$
(7.7)

The explicit implied volatility approximation \({\bar{\Sigma }}_n\) up to order \(n=2\) can now be computed using the formulas in “Appendix A”. Because the coefficient c does not depend on x in the Vasicek setting, the zeroth order implied volatility approximation is exact

$$\begin{aligned} \Sigma = \Sigma _0&= {\sqrt{ \frac{1}{T-t} \int _t^T \text {d}s \, \delta ^2 \Big ( \frac{1-\text {e}^{-\kappa (T-s)}}{\kappa } - \frac{1-\text {e}^{-\kappa ({{\overline{T}}} - s)}}{\kappa } \Big )^2 }} \end{aligned}$$
(7.8)
$$\begin{aligned}&=\frac{\delta }{\kappa ^{3/2}}{\sqrt{\frac{\text {e}^{2 \kappa T}-\text {e}^{2 \kappa t}}{2 (T - t)}}} \left( \text {e}^{-\kappa T}-\text {e}^{-\kappa {{\overline{T}}}}\right) . \end{aligned}$$
(7.9)

From the above, it is easy to identify the following limits

$$\begin{aligned} \lim _{t \rightarrow T} \Sigma&= {\frac{\delta }{\kappa } \left( 1 - \text {e}^{- \kappa \left( {{\overline{T}}} - T \right) }\right) } ,&\lim _{T \rightarrow {{\overline{T}}}} \Sigma&= 0 ,&\end{aligned}$$
(7.10)
$$\begin{aligned} \lim _{{{\overline{T}}} \rightarrow \infty } \Sigma&= {\frac{\delta }{\kappa ^{3/2}}{\sqrt{\frac{1-\text {e}^{-2 \kappa (T-t)}}{2(T-t)}}}},&\lim _{t \rightarrow T,{{\overline{T}}} \rightarrow \infty }\Sigma&= \frac{\delta }{\kappa }. \end{aligned}$$
(7.11)

In Fig. 1 we plot \(\Sigma \) as a function of t for various valued of \({{\overline{T}}}\) with T fixed.

Fig. 1
figure 1

For the Vasicek short-rate model described in Sect. 7.1, we plot implied volatility \(\Sigma \) as a function of t with the maturity date of the options fixed at \(T = 0.5\) and with the maturity date of the underlying bond taking the following values \({{\overline{T}}} = \{1, 3, 5, 10\}\), which correspond to the blue, orange, green, and red curves, respectively. The following model parameters remained fixed: \(\kappa = 0.9\), \(\delta = \sqrt{0.033}\), and \(\theta = \frac{0.08}{0.9}\)

Full size image

7.2 Cox–Ingersoll–Ross

In the Cox–Ingersoll–Ross (CIR) short-rate model developed in Cox et al. (2005), the dynamics of \(R=r(Y)\) are given by

$$\begin{aligned} \text {d}Y_t&= \kappa ( \theta - Y_t) \text {d}t + \delta {\sqrt{Y_t}}\text {d}W_t ,&R_t&= Y_t . \end{aligned}$$
(7.12)

Comparing (7.12) with (2.2) and (2.4), we see that the functions r, \(\mu \), and \(\sigma \) are given by

$$\begin{aligned} r(y)&= y ,&\mu (t,y)&= \kappa ( \theta - y) ,&\sigma (t,y)&= \delta {\sqrt{y}} , \end{aligned}$$
(7.13)

and comparing (7.13) with (2.5) we identify

$$\begin{aligned} q&= 0 ,&\psi&= 1 ,&b(t)&= \kappa \theta ,&\beta (t)&= - \kappa ,&\ell (t)&= 0,&\lambda (t)&= \delta ^2 , \end{aligned}$$
(7.14)

where we have dropped the subscripts from \(\psi \), \(\beta \) and \(\lambda \) as \(d=1\). With the above parameters, the solutions F and G of coupled ODEs (3.5) and (3.6) are

$$\begin{aligned} F(t;T,\nu )&= -\frac{2\kappa \theta }{\delta ^2}\bigg (\log \Big (2\Lambda \exp \big ((\Lambda +\kappa )\tau /2\big ) \end{aligned}$$
(7.15)
$$\begin{aligned}&\quad -\log \Big (-\delta ^2\nu (\exp (\Lambda \tau )-1)+\Lambda (\exp (\Lambda \tau )+1) \end{aligned}$$
(7.16)
$$\begin{aligned}&\quad +\kappa (\exp (\Lambda \tau )-1) \Big ) \bigg ) , \end{aligned}$$
(7.17)
$$\begin{aligned} G(t;T,\nu )&=\frac{2(\exp (\Lambda \tau )-1)-\big (\Lambda (\exp (\Lambda \tau )+1)-\kappa (\exp (\Lambda \tau )-1)\big )\nu }{-\delta ^2\nu \big (\exp (\Lambda \tau )-1\big )+\Lambda (\exp (\Lambda \tau )+1)+\kappa (\exp (\Lambda \tau )-1)},&\end{aligned}$$
(7.18)
$$\begin{aligned} \tau&:= T-t,&\end{aligned}$$
(7.19)
$$\begin{aligned} \Lambda&:= {\sqrt{\kappa ^2+2\delta ^2}}. \end{aligned}$$
(7.20)

From (4.18), (4.20), and (7.13), we have

$$\begin{aligned} {\widetilde{\sigma }}(t,x;T,{{\overline{T}}})&= \delta {\sqrt{\frac{F(t;T,0) - F(t;{{\overline{T}}},0) - x }{G(t;{{\overline{T}}},0)-G(t;T,0)}}} , \end{aligned}$$
(7.21)

And thus, using (4.32) and (7.21), the generator \({\widetilde{{\mathscr {A}}}}\) is given by

$$\begin{aligned} {\widetilde{{\mathscr {A}}}}(t)&= c(t,x) (\partial _x^2 - \partial _x ) , \end{aligned}$$
(7.22)
$$\begin{aligned} c(t,x)&= \frac{\delta ^2}{2}\Big (F(t;T,0) - F(t;{{\overline{T}}},0)-x\Big )\Big (G(t;{{\overline{T}}},0) - G(t;T,0)\Big ). \end{aligned}$$
(7.23)

Introducing the short-hand notation \(c_j(t,x) := \partial _x^j c(t,x) / j!\), we have

$$\begin{aligned} c_{0}(t,x)= & {} \frac{\delta ^2}{2}\Big (F(t;T,0) - F(t;{{\overline{T}}},0)-x\Big )\Big (G(t;{{\overline{T}}},0) - G(t;T,0)\Big ) , \end{aligned}$$
(7.24)
$$\begin{aligned} c_{1}(t,x)\equiv & {} c_1(t) = -\frac{\delta ^2}{2}\Big (G(t;{{\overline{T}}},0) - G(t;T,0)\Big ) , \end{aligned}$$
(7.25)
$$\begin{aligned} c_n(t,x)= & {} 0 ,\quad n \ge 2 . \end{aligned}$$
(7.26)

The explicit implied volatility approximation \({\bar{\Sigma }}_n\) can now be computed up to order \(n=2\) using the formulas in “Appendix A”. We have

$$\begin{aligned} \Sigma _0&= {\sqrt{\frac{2}{\tau }\int _{t}^T \text {d}s \, c_0(s,x)}} , \end{aligned}$$
(7.27)
$$\begin{aligned} \Sigma _1&={\frac{2(k-x)}{\Sigma ^3_0\tau ^2}\int _{t}^T\text {d}s \, c_1(s,x)\int _{t}^s \text {d}q \, c_0(q,x)} , \end{aligned}$$
(7.28)
$$\begin{aligned} \Sigma _2&= \frac{6(k-x)^2}{\Sigma _0^7 \tau ^4}\bigg ( -2 \Bigg (\int _t^T \text {d}s \, c_1(s) \int _{t}^s \text {d}q \, c_0(q,x) \Bigg ){}^2 \end{aligned}$$
(7.29)
$$\begin{aligned}&\quad + \Sigma _0^2 \tau \int _t^T \text {d}s_1 \, \int _{s_1}^T \text {d}s_2 \, c_1(s_1) c_1(s_2) \int _{t}^{s_1}\text {d}q \, c_0(q,x) \bigg ) \end{aligned}$$
(7.30)
$$\begin{aligned}&\quad +\frac{(\Sigma _0^2 \tau +12)}{{2 \Sigma _0^5 \tau ^3}}\bigg (\Bigg (\int _t^T\text {d}s \, c_1(s) \int _{t}^s \text {d}q \, c_0(q,x) \Bigg ){}^2 \end{aligned}$$
(7.31)
$$\begin{aligned}&\quad -\Sigma _0^2 \tau \int _t^T \text {d}s_1 \, \int _{s_1}^T \text {d}s_2 \, c_1(s_1) c_1(s_2) \int _{t}^{s_1}\text {d}q \, c_0(q,x)\bigg ) . \end{aligned}$$
(7.32)
Fig. 2
figure 2

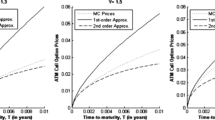
For the CIR short-rate model described in Sect. 7.2, we plot exact implied volatility \(\Sigma \) and approximate implied volatility \({\bar{\Sigma }}_n\) up to order \(n=2\) as a function of \(\log \)-moneyness \(k-x\) with the maturity date of the bond fixed at \({{\overline{T}}} = 2\) and with the maturity of the option taking the following values \(T = \{\frac{1}{12}, \frac{1}{4}, \frac{1}{2}, \frac{3}{4}\}\). The zeroth, first, and second order approximate implied volatilities correspond to the orange, green and red curves, respectively, and the blue curve correspond to the exact implied volatility. The following parameters, which were taken from Filipovic (2009, Example 10.3.2.2), remained fixed \(t = 0\), \(\kappa = 0.9\), \(\delta = \sqrt{0.033}\), \(\theta = \frac{0.08}{0.9}\), \(y = 0.08\)

Full size image

In Fig. 2 we plot our explicit approximation of implied volatility \({\bar{\Sigma }}_n\) up to order \(n=2\) as a function of \(\log \)-moneyness \(k-x\) with \(t=0\) and \({{\overline{T}}} = 2\) fixed and with option maturities ranging over \(T = \{\frac{1}{12},\frac{1}{4},\frac{1}{2},\frac{3}{4}\}\). For comparison, we also plot the exact implied volatility \(\Sigma \). We observe that the second order approximation \({\bar{\Sigma }}_2\) accurately matches the level, slope, and convexity of the exact implied volatility \(\Sigma \) near-the-money for all four option maturity dates. In Fig. 3 we plot the absolute value of the relative error of our second order approximation \(|{\bar{\Sigma }}_2-\Sigma |/\Sigma \) as a function of \(\log \)-moneyness \(k-x\) and option maturity T. We observe that the error decreases as we approach the origin in both directions of \(k-x\) and T and the best approximation region is within \(0.2 \%\) of the exact implied volatility.

7.3 Two-factor Cox–Ingersoll–Ross

In the Two-factor Cox–Ingersoll–Ross (2-D CIR) short-rate model developed in Cox et al. (2005), the dynamics of \(R=r(Y)\) are given by

$$\begin{aligned} \text {d}Y^{(1)}_t&= \kappa _1 ( \theta _1 - Y^{(1)}_t) \text {d}t + \delta _1 {\sqrt{Y^{(1)}_t}}\text {d}W^{(1)}_t ,&\end{aligned}$$
(7.33)
$$\begin{aligned} \text {d}Y^{(2)}_t&= \kappa _2 ( \theta _2 - Y^{(2)}_t) \text {d}t + \delta _2 {\sqrt{Y^{(2)}_t}}\text {d}W^{(2)}_t ,&\end{aligned}$$
(7.34)
$$\begin{aligned} R_t&= Y^{(1)}_t + Y^{(2)}_t . \end{aligned}$$
(7.35)

Comparing (7.35) with (2.2) and (2.4), we see that the functions r, \(\mu \), and \(\sigma \) are given by

$$\begin{aligned} \left. \begin{aligned} r(y_1,y_2) = y_1+y_2 ,&\\ \mu (t,y_1,y_2) = \begin{pmatrix}\kappa _1 ( \theta _1 - y_1) &{}\\ \kappa _2 ( \theta _2 - y_2) \end{pmatrix} , \\ \sigma (t,y_1,y_2) = \begin{pmatrix}\delta _1 {\sqrt{y_1}} &{} 0 &{}\\ 0 &{} \delta _2 {\sqrt{y_2}} \end{pmatrix} , \end{aligned} \right\} \end{aligned}$$
(7.36)

and comparing (7.36) with (2.5) we identify

$$\begin{aligned} q&= 0 ,&\psi&= \begin{pmatrix}1 \\ 1 \end{pmatrix} ,&b(t)&= \begin{pmatrix}\kappa _1 \theta _1 \\ \kappa _2 \theta _2 \end{pmatrix} ,&\beta _1(t)&= - \begin{pmatrix}\kappa _1 \\ 0 \end{pmatrix} ,&\end{aligned}$$
(7.37)
$$\begin{aligned} \beta _2(t)&= - \begin{pmatrix} 0 \\ \kappa _2 \end{pmatrix} ,&\ell (t)&= 0,&\lambda _1(t)&= \begin{pmatrix}\delta ^2_1 &{} 0 \\ 0 &{} 0 \end{pmatrix} ,&\lambda _2(t)&= \begin{pmatrix} 0 &{} 0 \\ 0 &{} \delta ^2_2 \end{pmatrix} . \end{aligned}$$
(7.38)

With the above parameters, the solutions F and \(G = (G_1,G_2)\) of coupled ODEs (3.5) and (3.6) are, for \(i =\{1,2\}\),

$$\begin{aligned} F(t;T,\nu )&=-\sum _{i=1}^2 \frac{2\kappa _i \theta _i}{\delta _i^2} \bigg ( \log \Big (2\Lambda _i\exp \big ((\Lambda _i+\kappa _i)\tau /2\big )\Big ) \end{aligned}$$
(7.39)
$$\begin{aligned}&\quad -\log \Big (-\delta _i^2\nu _i\big (\exp (\Lambda _i \tau )-1\big )+\Lambda _i(\exp (\Lambda _i \tau )+1) \end{aligned}$$
(7.40)
$$\begin{aligned}&\quad +\kappa _i(\exp (\Lambda _i \tau )-1)\Big ) \bigg ), \end{aligned}$$
(7.41)
$$\begin{aligned} G_i(t;T,\nu )&= \frac{2(\exp (\Lambda _i \tau )-1)-\big (\Lambda _i(\exp (\Lambda _i \tau )+1)-\kappa _i(\exp (\Lambda _i \tau )-1)\big )\nu _i}{-\delta _i^2\nu _i\big (\exp (\Lambda _i \tau )-1\big )+\Lambda _i(\exp (\Lambda _i \tau )+1)+\kappa _i(\exp (\Lambda _i \tau )-1)}, \end{aligned}$$
(7.42)
$$\begin{aligned} \Lambda _i&:= {\sqrt{\kappa _i^2+2\delta _i^2}}. \end{aligned}$$
(7.43)

From (4.18), (4.20), and (7.36), we have

$$\begin{aligned} \eta (t,x,y_2;T,{{\overline{T}}})&= \frac{1}{G_1(t;{{\overline{T}}},0)-G_1(t;T,0)}\bigg (F(t;T,0) - F(t;{{\overline{T}}},0) - x \end{aligned}$$
(7.44)
$$\begin{aligned}&\quad + \Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0) \Big ) y_2\bigg ), \end{aligned}$$
(7.45)
$$\begin{aligned} {\widetilde{\sigma }}(t,x,y_2;T,{{\overline{T}}})&= \begin{pmatrix} \delta _1{\sqrt{\eta (t,x,y_2;T,{{\overline{T}}})}} &{} 0 \\ 0 &{} \delta _2 {\sqrt{y_2}} \end{pmatrix} , \end{aligned}$$
(7.46)

and thus, using (4.35) and (7.3), the generator \({\widetilde{{\mathscr {A}}}}\) is given by

$$\begin{aligned} {\widetilde{{\mathscr {A}}}}(t)&= c(t,x,y_2) (\partial _x^2 - \partial _x ) + f(t,x,y_2) \partial _{y_2} + g(t,x,y_2) \partial _{y_2}^2 + h(t,x,y_2) \partial _x \partial _{y_2}, \end{aligned}$$
(7.47)

where the functions c, f, g and h are given by

$$\begin{aligned} c(t,x,y_2)&= \frac{1}{2}\delta ^2_1 \bigg (F(t;T,0) - F(t;{{\overline{T}}},0) - x \end{aligned}$$
(7.48)
$$\begin{aligned}&\quad + \Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0) \Big ) y_2\bigg ) \end{aligned}$$
(7.49)
$$\begin{aligned}&\quad \times \Big (G_1(t;{{\overline{T}}},0)-G_1(t;T,0)\Big ) \end{aligned}$$
(7.50)
$$\begin{aligned}&\quad + \frac{1}{2} \delta ^2_2 \Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0)\Big )^2 y_2 , \end{aligned}$$
(7.51)
$$\begin{aligned} f(t,x,y_2)&= \kappa _2(\theta _2-y_2) -\delta ^2_2 y_2 G_2(t;T,0), \end{aligned}$$
(7.52)
$$\begin{aligned} g(t,x,y_2)&= \frac{1}{2}\delta ^2_2 y_2, \end{aligned}$$
(7.53)
$$\begin{aligned} h(t,x,y_2)&=\delta ^2_2 y_2 \Big ( G_2(t;T,0) - G_2(t;{{\overline{T}}},0) \Big ). \end{aligned}$$
(7.54)

Introducing the notation \(\chi _{i,j}(t,x,y_2) := \partial _x^i \partial _{y_2}^j \chi (t,x,y_2)/ (i! j!)\) where \( \chi \in \{c,f,g,h\}\), we compute

$$\begin{aligned} \chi _{0,0}(t,x,y_2)&= \chi (t,x,y_2), \end{aligned}$$
(7.55)
$$\begin{aligned} c_{1,0}(t,x,y_2)&= -\frac{1}{2}\delta ^2_1 \Big (G_1(t;{{\overline{T}}},0)-G_1(t;T,0) \Big ), \end{aligned}$$
(7.56)
$$\begin{aligned} c_{0,1}(t,x,y_2)&= \frac{1}{2} \delta ^2_1 \Big ( G_2(t;T,0) - G_2(t;{{\overline{T}}},0) \Big ) \Big ( G_1(t;{{\overline{T}}},0)-G_1(t;T,0) \Big ) \end{aligned}$$
(7.57)
$$\begin{aligned}&\quad + \frac{1}{2} \delta ^2_2 \Big ( G_2(t;T,0) - G_2(t;{{\overline{T}}},0) \Big )^2 , \end{aligned}$$
(7.58)
$$\begin{aligned} f_{0,1}(t,x,y_2)&= -\left( \kappa _2 +\delta ^2_2\right) G_2(t;T,0), \end{aligned}$$
(7.59)
$$\begin{aligned} g_{0,1}(t,x,y_2)&= \frac{1}{2}\delta ^2_2, \end{aligned}$$
(7.60)
$$\begin{aligned} h_{0,1}(t,x,y_2)&= \delta ^2_2 \Big ( G_2(t;T,0) - G_2(t;{{\overline{T}}},0) \Big ) , \end{aligned}$$
(7.61)

and \(\chi _{i,j}(t,x,y_2) = 0\), for any term not given above. The explicit implied volatility approximation \({\bar{\Sigma }}_n\) can now be computed up to order \(n=2\) using the formulas in “Appendix A”. We have

$$\begin{aligned} \Sigma _0&= {\sqrt{\frac{2}{\tau }\int _{t}^T \text {d}s \, c_{0,0}(s,x,y_2)}}, \end{aligned}$$
(7.62)
$$\begin{aligned} \Sigma _1&= \frac{(k-x)}{\tau ^2\Sigma ^3_0}\Big (2\int _{t}^T\text {d}s \, c_{1,0}(s,x,y_2)\int _{t}^s \text {d}q \, c_{0,0}(q,x,y_2) \end{aligned}$$
(7.63)
$$\begin{aligned}&\quad + \int _{t}^T \text {d}s \, c_{0,1}(s,x,y_2)\int _{t}^s \text {d}q \, h_{0,0}(q,x,y_2)\Big ) \end{aligned}$$
(7.64)
$$\begin{aligned}&\quad + \frac{1}{2\tau \Sigma _0}\int _{t}^T \text {d}s \, c_{0,1}(s,x,y_2)\Bigg (2\int _{t}^s \text {d}q \, f_{0,0}(q,x,y_2)+ \int _{t}^s \text {d}q \, h_{0,0}(q,x,y_2)\Bigg ) , \end{aligned}$$
(7.65)

where we have omitted the 2nd order term \(\Sigma _2\) due to its considerable length.

Fig. 3
figure 3

For the CIR short-rate model described in Sect. 7.2, we plot the absolute value of the relative error of our second order implied volatility approximation \(|{\bar{\Sigma }}_2 - \Sigma |/\Sigma \) as a function of log-moneyness \((k-x)\) and option maturity T. The horizontal axis represents log-moneyness \((k -x)\) and the vertical axis represents option maturity T. Ranging from darkest to lightest, the regions above represent relative errors in increments of \(0.2 \%\) from \(< 0.2 \%\) to \(>1.4 \%\). The maturity date of the bond is fixed at \({{\overline{T}}} = 2\). The following parameters, which were taken from Filipovic (2009, Example 10.3.2.2), remained fixed \(t = 0\), \(\kappa = 0.9\), \(\delta = \sqrt{0.033}\), \(\theta = \frac{0.08}{0.9}\), \(y = 0.08\)

Full size image
Fig. 4
figure 4

For the 2-D CIR short-rate model described in Sect. 7.3, we plot exact implied volatility \(\Sigma \) and approximate implied volatility \({\bar{\Sigma }}_n\) up to order \(n=2\) as a function of \(\log \)-moneyness \(k-x\) with the maturity date of the bond fixed at \({{\overline{T}}} = 2\) and with the maturity of the option taking the following values \(T = \{\frac{1}{12}, \frac{1}{4}, \frac{1}{2}, \frac{3}{4}\}\). The zeroth, first, and second order approximate implied volatilities correspond to the orange, green and red curves, respectively, and the blue curve correspond to the exact implied volatility. The following parameters remained fixed \(t = 0\), \(\kappa _1 = \kappa _2 = 0.9\), \(\delta _1 = \delta _2 = \sqrt{0.033}\), \(\theta _1 = \theta _2 = \frac{0.08}{0.9}\), \(y_1 = y_2 = 0.04\)

Full size image
Fig. 5
figure 5

For the 2-D CIR short-rate model described in Sect. 7.3, we plot the absolute value of the relative error of our second order implied volatility approximation \(|{\bar{\Sigma }}_2 - \Sigma |/\Sigma \) as a function of log-moneyness \((k-x)\) and option maturity T. The horizontal axis represents log-moneyness \((k -x)\) and the vertical axis represents option maturity T. Ranging from darkest to lightest, the regions above represent relative errors in increments of \(0.1 \%\) from \(< 0.1 \%\) to \(>0.8 \%\). The maturity date of the bond is fixed at \({{\overline{T}}} = 2\). The following parameters remained fixed \(t = 0\), \(\kappa _1 = \kappa _2 = 0.9\), \(\delta _1 = \delta _2 = \sqrt{0.033}\), \(\theta _1 = \theta _2 = \frac{0.08}{0.9}\), \(y_1 = y_2 = 0.04\)

Full size image

In Fig. 4 we plot our explicit approximation of implied volatility \({\bar{\Sigma }}_n\) up to order \(n=2\) as a function of \(\log \)-moneyness \(k-x\) with \(t=0\) and \({{\overline{T}}} = 2\) fixed and with option maturities ranging over \(T = \{\frac{1}{12},\frac{1}{4},\frac{1}{2},\frac{3}{4}\}\). For comparison, we also plot the the exact implied volatility \(\Sigma \). As is the case with the (1-D) CIR model, we observe in the 2-D CIR model that the second order approximation \({\bar{\Sigma }}_2\) accurately matches the level, slope, and convexity of the exact implied volatility \(\Sigma \) near-the-money for all four option maturity dates. In Fig. 5 we plot the absolute value of the relative error of our second order approximation \(|{\bar{\Sigma }}_2-\Sigma |/\Sigma \) as a function of \(\log \)-moneyness \(k-x\) and option maturity T. We observe that the error decreases as we approach the origin in both directions of \(k-x\) and T and the best approximation region is within \(0.1 \%\) of the exact implied volatility.

7.4 Fong–Vasicek

In the Fong–Vasicek short-rate model developed in Fong and Vasicek (1991), the dynamics of \(R=r(Y)\) are given by

$$\begin{aligned} \text {d}Y^{(1)}_t&= \kappa _1 \left( \theta _1 - Y^{(1)}_t\right) \text {d}t + {\sqrt{Y^{(2)}_t}}\text {d}W^{(1)}_t ,&\end{aligned}$$
(7.66)
$$\begin{aligned} \text {d}Y^{(2)}_t&= \kappa _2 \left( \theta _2 - Y^{(2)}_t\right) \text {d}t + \delta _2 \rho {\sqrt{Y^{(2)}_t}} \text {d}W^{(1)}_t + \delta _2 {\bar{\rho }}{\sqrt{Y^{(2)}_t}} \text {d}W^{(2)}_t ,&{\bar{\rho }}= {\sqrt{1-\rho ^2}} \end{aligned}$$
(7.67)
$$\begin{aligned} R_t&= Y^{(1)}_t. \end{aligned}$$
(7.68)

Comparing (7.68) with (2.2) and (2.4), we see that the functions r, \(\mu \), and \(\sigma \) are given by

$$\begin{aligned} \left. \begin{aligned} r(y_1,y_2) = y_1 ,&\\ \mu (t,y_1,y_2) = \begin{pmatrix}\kappa _1 ( \theta _1 - y_1) \\ \kappa _2 ( \theta _2 - y_2) \end{pmatrix} ,&\\ \sigma (t,y_1,y_2) = \begin{pmatrix} \sqrt{y_2} &{} 0 \\ \delta _2 \rho \sqrt{y_2} &{} \delta _2 {\bar{\rho }}\sqrt{y_2} \end{pmatrix} ,&\end{aligned} \right\} \end{aligned}$$
(7.69)

and comparing (7.69) with (2.5) we identify

$$\begin{aligned} q&= 0 ,&\psi&= \begin{pmatrix}1 \\ 0 \end{pmatrix} ,&b(t)&= \begin{pmatrix}\kappa _1 \theta _1 \\ \kappa _2 \theta _2 \end{pmatrix} ,&\beta _1(t)&= - \begin{pmatrix}\kappa _1 \\ 0 \end{pmatrix} ,&\end{aligned}$$
(7.70)
$$\begin{aligned} \beta _2(t)&= - \begin{pmatrix} 0 \\ \kappa _2 \end{pmatrix} ,&\ell (t)&= 0,&\lambda _1(t)&= \begin{pmatrix}0 &{} 0 \\ 0 &{} 0 \end{pmatrix} ,&\lambda _2(t)&= \begin{pmatrix} 1 &{} \delta _2\rho \\ \delta _2\rho &{} \delta ^2_2 \end{pmatrix} . \end{aligned}$$
(7.71)

With the above parameters, we find using (3.5) and (3.6) that the ODEs satisfied by F and \(G = (G_1, G_2)\) are

$$\begin{aligned}&\begin{aligned} \partial _t F(t;T,\nu )&= -\kappa _1\theta _1 G_1(t;T,\nu )-\kappa _2\theta _2 G_2(t;T,\nu ) , \\ F(T;T,\nu )&= 0 , \end{aligned} \end{aligned}$$
(7.72)
$$\begin{aligned}&\begin{aligned} \partial _t G_1(t;T,\nu )&= \kappa _1 G_1(t;T,\nu )-1 , \\ G_1(T;T,\nu )&= - \nu _1 , \end{aligned} \end{aligned}$$
(7.73)
$$\begin{aligned}&\begin{aligned} \partial _t G_2(t;T,\nu )&= \frac{1}{2}\delta ^2_2 G^2_2(t;T,\nu ) + \Big (\delta _2\rho G_1(t;T,\nu ) + \kappa _2 \Big ) G_2(t;T,\nu ) \\&\quad + \frac{1}{2}G^2_1(t;T,\nu ) , \\ G_2(T;T,\nu )&= - \nu _2 . \end{aligned} \end{aligned}$$
(7.74)

Although one can obtain explicit expressions for \(F(t;T,\nu )\), \(G_1(t;T,\nu )\) and \(G_2(t;T,\nu )\), these expressions are given in terms of confluent hypergeometric fuctions (CHFs). As numerical evaluation of CHFs is time-consuming, computing explicit Call prices using (7.1) is not practical because it involves integrals with respect to \(\nu \). By contrast, in order to compute our explicit approximation of implied volatility \({\bar{\Sigma }}_n\), we need only expressions for F(t; T, 0), \(G_1(t;T,0)\) and \(G_2(t;T,0)\), which we provide in “Appendix B”.

From (4.18), (4.20), and (7.69), we have

$$\begin{aligned} \eta (t,x,y_2;T,{{\overline{T}}})&= \frac{1}{G_1(t;{{\overline{T}}},0)-G_1(t;T,0)}\bigg ( F(t;T,0) - F(t;{{\overline{T}}},0) - x \end{aligned}$$
(7.75)
$$\begin{aligned}&\quad + \Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0)\Big ) y_2 \bigg ), \end{aligned}$$
(7.76)
$$\begin{aligned} {\widetilde{\sigma }}(t,x,y_2;T,{{\overline{T}}})&= \begin{pmatrix} \sqrt{y_2} &{} 0 \\ \delta _2 \rho \sqrt{y_2} &{} \delta _2 {\bar{\rho }}\sqrt{y_2} \end{pmatrix} , \end{aligned}$$
(7.77)

And thus, using (4.35) and (7.77), the generator \({\widetilde{{\mathscr {A}}}}\) is given by

$$\begin{aligned} {\widetilde{{\mathscr {A}}}}(t)&= c(t,x,y_2) (\partial _x^2 - \partial _x ) + f(t,x,y_2) \partial _{y_2} + g(t,x,y_2) \partial _{y_2}^2 + h(t,x,y_2) \partial _x \partial _{y_2}, \end{aligned}$$
(7.78)

where the functions c, f, g and h are given by

$$\begin{aligned} c(t,x,y_2)&= \frac{1}{2}y_2 \Big (G_1(t;T,0) - G_1(t;{{\overline{T}}},0)\Big )^2 \end{aligned}$$
(7.79)
$$\begin{aligned}&\quad + \rho \delta _2 y_2 \Big (G_1(t;T,0) - G_1(t;{{\overline{T}}},0)\Big ) \end{aligned}$$
(7.80)
$$\begin{aligned}&\quad \times \Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0)\Big ) \end{aligned}$$
(7.81)
$$\begin{aligned}&\quad + \frac{1}{2}\delta ^2_2 y_2 \Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0)\Big )^2, \end{aligned}$$
(7.82)
$$\begin{aligned} f(t,x,y_2)&= \kappa _2(\theta _2-y_2) -\delta ^2_2 y_2 G_2(t;T,0) - \rho \delta _2 y_2 G_1(t;T,0), \end{aligned}$$
(7.83)
$$\begin{aligned} g(t,x,y_2)&= \frac{1}{2}\delta ^2_2 y_2, \end{aligned}$$
(7.84)
$$\begin{aligned} h(t,x,y_2)&= \delta ^2_2 y_2 \Big ( G_2(t;T,0) - G_2(t;{{\overline{T}}},0)\Big ) \end{aligned}$$
(7.85)
$$\begin{aligned}&\quad + \rho \delta _2 y_2 \Big (G_1(t;T,0) - G_1(t;{{\overline{T}}},0)\Big ). \end{aligned}$$
(7.86)

Once again using the short-hand notation \(\chi _{i,j}(t,x,y_2) := \partial _x^i \partial _{y_2}^j \chi (t,x,y_2)/ (i! j!)\) where \(\chi \in \{c,f,g,h\}\), we compute

$$\begin{aligned} \chi _{0,0}(t,x,y_2)&= \chi (t,x,y_2), \end{aligned}$$
(7.87)
$$\begin{aligned} c_{0,1}(t,x,y_2)&= \frac{1}{2} \Big (G_1(t;T,0) - G_1(t;{{\overline{T}}},0)\Big )^2 \end{aligned}$$
(7.88)
$$\begin{aligned}&\quad + \rho \delta _2 \Big (G_1(t;T,0) - G_1(t;{{\overline{T}}},0)\Big ) \Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0) \Big ) \end{aligned}$$
(7.89)
$$\begin{aligned}&\quad + \frac{1}{2}\delta ^2_2 \Big (G_2(t;T,0) - G_2(t;{{\overline{T}}},0) \Big )^2, \end{aligned}$$
(7.90)
$$\begin{aligned} f_{0,1}(t,x,y_2)&= -\kappa _2 -\delta ^2_2 G_2(t;T,0) - \rho \delta _2 G_1(t;T,0), \end{aligned}$$
(7.91)
$$\begin{aligned} g_{0,1}(t,x,y_2)&= \frac{1}{2}\delta ^2_2, \end{aligned}$$
(7.92)
$$\begin{aligned} h_{0,1}(t,x,y_2)&= \delta ^2_2 \Big ( G_2(t;T,0) - G_2(t;{{\overline{T}}},0) \Big ) \end{aligned}$$
(7.93)
$$\begin{aligned}&\quad + \rho \delta _2 \Big ( G_1(t;T,0) - G_1(t;{{\overline{T}}},0) \Big ) , \end{aligned}$$
(7.94)

where \(\chi _{i,j}(t,x,y_2) = 0\) for any term not given above. The explicit implied volatility approximation \({\bar{\Sigma }}_n\) can now be computed up to order \(n=2\) using the formulas in “Appendix A”. We have

$$\begin{aligned} \Sigma _0&= \sqrt{\frac{2}{\tau }\int _{t}^T \text {d}s \, c_{0,0}(s,x,y_2)}, \end{aligned}$$
(7.95)
$$\begin{aligned} \Sigma _1&= \frac{k-x}{\tau ^2\Sigma ^3_0}\Bigg (\int _{t}^T \text {d}s \, c_{0,1}(s,x,y_2)\int _{t}^s \text {d}q \, h_{0,0}(q,x,y_2)\Bigg ) \end{aligned}$$
(7.96)
$$\begin{aligned}&\quad + \frac{1}{2\tau \Sigma _0}\int _{t}^T \text {d}s \, c_{0,1}(s,x,y_2)\Bigg (2\int _{t}^s \text {d}q \, f_{0,0}(q,x,y_2)+ \int _{t}^s \text {d}q \, h_{0,0}(q,x,y_2)\Bigg ). \end{aligned}$$
(7.97)

where we have omitted the second order term \(\Sigma _2\) due to its considerable length.

In Fig. 6 we plot our second order approximation of implied volatility \({\bar{\Sigma }}_2\) as a function of \(\log \)-moneyness \(k-x\) with the maturity date of the bond fixed at \({{\overline{T}}} = 2\), the maturity date of the option taking the following values \(T = \{\frac{1}{12}, \frac{1}{4}, \frac{1}{2}, \frac{3}{4}\}\) and the correlation parameter taking the following values \(\rho = \{-0.7,-0.3,0.3,0.7\}\). We can see the convexity near-the-money changes from concave to convex as we increase \(\rho \). From the expression of \(\Sigma _1\) in (7.97) we observe that the slope of \(\Sigma _1\) with respect to \(k-x\) is controlled by the sign of \(c_{0,1}\) and \(h_{0,0}\). As G(t; T, 0) is an increasing function in T, the expression \(G_i(t;T,0)-G_i(t;{{\overline{T}}},0)\) is negative, which means that, fixing all other parameters, \(\rho \) controls the sign of \(c_{0,1}\) and \(h_{0,0}\). As a result, as we change \(\rho \) from \(-1\) to 1 the slope of \(\Sigma _1\) changes accordingly. A similar analysis can be done on the sign of coefficients of \((k-x)^2\) of \(\Sigma _2\) to show that \(\rho \) controls the convexity of \(\Sigma _2\) with respect to \(k-x\). This is in contrast to the CIR and 2-D CIR models, where the implied volatility curve near-the-money is concave.

Fig. 6
figure 6

For the Fong–Vasicek short-rate model described in Sect. 7.4, we plot the approximate implied volatility \({\bar{\Sigma }}_2\) as a function of \(\log \)-moneyness \(k-x\) with the maturity date of the bond fixed at \({{\overline{T}}} = 2\), with the maturity of the option taking the following values \(T = \{\frac{1}{12}, \frac{1}{4}, \frac{1}{2}, \frac{3}{4}\}\) and with the correlation parameter taking values \(\rho = \{-0.7,-0.3,0.3,0.7\}\) corresponding to the blue, orange, green and red curves respectively. The following model parameters remained fixed in all four plots \(t=0\), \(\kappa _1 = \kappa _2 = 0.9\), \(\delta _2 = \sqrt{0.08}\), \(\theta _1 = \theta _2 =0.08\), \(y_2 = 0.08\)

Full size image

8 Conclusion

In this paper, we have provided an explicit asymptotic approximation for the implied volatility of Call options on bonds assuming the short-rate is given by an affine term-structure model. In future work, we plan to extend our results by providing explicit implied volatility approximations for other short-rate derivatives including caps and floors.