1 Introduction

Capital adequacy is a priority which banking supervision authorities have addressed on an ongoing basis since 1988 (the first Basel Accord, initially drafted by the central banks of 13 members of the Organisation for Economic Development). Regulatory capital requirements defined by the Basel Committee on Banking Supervision (BCBS) have changed substantially from the first release. Over the last decades, according to the European Parliament (2016, p. 1), the regulatory frameworks for capital adequacy “have shifted from simplicity to risk-sensitivity, probably at the expense of transparency and comparability of capital positions across banks”.

Since the crisis period, banks are simultaneously facing times of tight capital ratios, unfavourable market conditions, and an extensive use of accounting discretionFootnote 1 (e.g. the use of Internal Rating Based models). In order to restore confidence in the banking system and to create a safer global economic system (Morkoetter et al. 2014; Alexander et al. 2014) spawned by the financial meltdown, the BCBS has updated the existing capital adequacy regulatory framework, introducing liquidity regulation and a non-risk-weighted leverage ratio (that is computed as the ratio between capital and assets), designed to supplement risk-based capital requirements. The experiences from the banking crises in several countries during the last decades have made regulators, authorities, and banks more aware of the importance of maintaining a sufficient capital ratio (capital requirement) (Lindquist 2004; Dermine 2013). With respect to capital requirements, the regulatory effort involves enhancing both the quantity and the quality of capital buffers. Indeed, banks are required to maintain a minimum Total Capital Ratio, which incorporates a minimum Common Equity Tier 1 (CET1) capital ratio,Footnote 2,Footnote 3 and a minimum capital conservation buffer ratio.Footnote 4

The literature that investigates the impact of the regulation is wide and constantly growing (Chiaramonte and Casu 2017). Focusing on capital adequacy, several studies suggest that better capitalised banks were better protected during the global financial crisis. Demirgüç-Kunt et al. (2013), Beltratti and Stultz (2012), Brogi and Lagasio (2016) find that banks with higher capital ratios, performed better during the financial crisis. As concerns the leverage ratio—which is a non-risk-weighted capital measure—Mayes and Stremmel (2014) and Beltratti and Stultz (2012) find that it is more useful in explaining bank distress and failures than capital requirements.

Concerning the association between the new regulatory framework and bank distress, a strand of recent studies has focused on the new Basel III liquidity measures: Net Stable Funding Ratio and Liquidity Coverage Ratio. Investigating the association between liquidity and leverage, Vazquez and Federico (2015), for example, report that distressed banks were characterized by lower structural liquidity and higher leverage ratios. Conversely, Hong et al. (2014) find weak significance for the association between new Basel III liquidity measures and bank failures.

Despite the actions put in place by BCBS to restore confidence in the global banking system, regulators need to monitor the system in order to prevent bank financial distress. In November 2013, the European Central Bank and the European Banking Authority agreed on new parameters for the European Banking Union analysing the leading banks balance sheets in the Eurozone. The first step for the implementation of the European banking project was the Asset Quality Review. The European Central Bank’s objective was to evaluate the soundness and quality of financial balance sheets of 130 lenders. It was a European transparency initiative whose main goal is to restore the confidence of international investors in the soundness of the European Union’s financial system. The Asset Quality Review included a general risk assessment of the banks and a stress test in order to check the resilience in case of unfavourable market conditions.

In this context, recent developments in capital stress testing have shaped the view of academics and practitioners regarding bank capital. In particular, Acharya and Steffen (2015) report that Eurozone bank risks during 2007–2013 can best be characterised as carry trade behaviour. They find a positive correlation between stock returns of banks and a peripheral country (Greece, Italy, Ireland, Portugal, Spain, or GIIPS) bond returns and a negative correlation with German bund returns, which generated carry until the deteriorating GIIPS bond returns adversely affected bank balance sheets.

Acharya et al. (2014) also investigate the importance of risk weights, comparing the capital shortfall measured by regulatory stress tests to that of a benchmark methodology (the so-called “V-Lab stress test”) that employs only publicly available market data. They find that when capital shortfalls are measured relative to risk-weighted assets, the ranking of financial institutions is very different from the V-Lab stress test, whereas when measured relative to total assets, the results are quite similar. They also report that the risk measures used in risk-weighted assets are cross-sectionally uncorrelated with market measures of risk.

In this paper, we propose a novel and simple early-warning system model for the minimum regulatory requirements of financial institutions classified by the Financial Stability Board and BCBS as Global Systemically Important Financial Institutions (GSIFIs). More specifically, we study the ability of both balance sheet items and market data to predict bank distress. To do so we apply the model proposed by Merton (1974).

Our model estimates the probability of breaching the CET1 capital requirements on a time horizon of one-year for banking institutions subject to Basel III. The approach adopted to perform the analysis is a particular application of the Merton model. We calibrate the Merton model using balance sheet data and market data in order to match the probability of default implied by the model with the probability of default implied in the market quotations for credit default swaps (CDSs). Then, assuming the minimum requirement for the CET1 ratio as a threshold for the Merton model, the calibrated Merton model is used to estimate the probability of breaching the capital requirements as a function of capitalization level and probability of default implied in CDS quotes.

The model we propose is related to the model proposed by De Spiegeleer et al. (2016). Under this framework, in order to treat contingent convertibles (CoCo) bonds as derivative instruments contingent on the CET1 level, the authors introduce the notion of implied CET1 volatility. They then model the CET1 ratio as a continuous geometric Brownian motion in the absence of any drift. However, in contrast to the model proposed by De Spiegeleer et al. (2016), our model focusses on asset modelling where a classical geometric Brownian motion is adopted to establish a theoretical framework and to estimate asset implied volatility.

We calculate the probability of breaching the CET1 capital requirements from 2005 to 2015 and compare it with respect to the evolution of the CET1 ratio for 24 banks selected among the GSIFIs.Footnote 5 However, we are aware that the minimum CET1 ratio level may change due to the evolution of the prudential rules. For instance, Bevilacqua et al. (2019) and the ECB (2019) state that it may increase in the future. Nonetheless, such CET1 changes can be factorized under the proposed model by simply imposing a different minimum level of required CET1 ratio, as in Liberadzki and Liberadzki (2019).

We find that the probability of breaching the capital requirements estimated under the proposed model is a useful metric because it can synthetize the information available in terms of balance sheet items (i.e. CET1 ratio) and market data (i.e. CDS). The major findings are threefold. First, banks with the same CET1 ratio may have a different probability of breaching the capital requirements. This means that banks with the same CET1 ratio may have a different volatility for their capital position and, consequently, a different level of resilience in preserving the capital buffer under stressed conditions. Second, banks with a different CET1 ratio may have a similar probability of breaching the capital requirements. This means that banks with a different CET1 ratio may have a similar volatility for their capital position and, consequently, a similar level of resilience to face adverse scenarios. Finally, we find that the asset volatility calibrated according to the proposed model appears as a good an estimator of the risk-weighted asset density. At the same time, this means that the risk-weighted asset density could be used as a good proxy to estimate the asset’s volatility.

The organization of the paper is as follows. In Sect. 2, we present the theoretical framework for the proposed model. Section 3 describes the model’s calibration methodology while Sect. 4 illustrates the approach adopted for estimating the probability of breaching the capital requirements. The empirical results are presented in Sect. 5 and the conclusions are provided in Sect. 6.

2 The theoretical framework

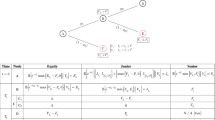
Since the publication of Merton’s (1974) paper on the valuation of corporate debt securities, the structural model of default he proposed has become the workhorse for gaining insights about how firms choose their capital structure. Being the first structural model, it has served as the cornerstone for all other structural models. The Merton model employs option pricing theory in corporate debt valuation, where the underlying firm value is random with some distribution. If the value of assets should happen to decline such that this value is less than the value of the firm’s liabilities, which we refer to as the default threshold, then it will be impossible for the firm to satisfy its obligations and it will thus default.

The Merton model assumes that there is a simple debt structure and that the total value \( A\left( t \right) \) of a firm’s assets follows a geometric Brownian motion under the risk-neutral measure,

$$ dA\left( t \right) = rA\left( t \right)dt + \sigma A\left( t \right)dW\left( t \right) $$

where \( A\left( t \right) > 0 \), \( r \) is the (constant) risk-free rate, \( \sigma \) is the asset volatility, and \( dW\left( t \right) \) is a standard Brownian motion. There are two further assumptions for the Merton model: (1) there are no bankruptcy charges, meaning the liquidation value equals the firm value and (2) the debt and equity are frictionless tradeable assets.

The Merton model assumes firms, at time \( t \), are funded by equity, denoted by \( E\left( t \right) \), and debt, denoted by \( \bar{P}\left( {t,T} \right) \). Debt consists of a single outstanding bond with face value \( K \) and maturity \( T \). At maturity, if the total value of the assets is greater than the debt, the latter is paid in full and the remainder is distributed among shareholders. However, if \( A\left( t \right) < K \) then default is deemed to occur: the bondholders exercise a debt covenant giving them the right to liquidate the firm and receive the liquidation value in lieu of the debt while shareholders receive nothing in this case.

From these simple observations, we see that shareholders have a cash flow at time \( T \) equal to \( \left[ {A\left( T \right) - K} \right]^{ + } \) and so equity can be viewed as a European call option on the firm’s assets. Applying the standard Black–Scholes–Merton call option formula,Footnote 6 we have that

$$ E\left( t \right) = A\left( t \right)\Phi \left( {d_{1} } \right) - P\left( {t,T} \right)K\Phi \left( {d_{2} } \right) $$

where \( \Phi \) denotes the cumulative distribution function of the standard Gaussian distribution and \( P\left( {t,T} \right) \) is the price of a risk-free zero-coupon bond valued at time \( t \) with maturity at time \( T > t \). Moreover, we have that,

$$ d_{1} = \frac{{log\left[ {\frac{A\left( t \right)}{K}} \right] + \left( {r + \frac{{\sigma^{2} }}{2}} \right)\left( {T - t} \right)}}{{\sigma \sqrt {\left( {T - t} \right)} }} $$
$$ d_{2} = \frac{{log\left[ {\frac{A\left( t \right)}{K}} \right] + \left( {r - \frac{{\sigma^{2} }}{2}} \right)\left( {T - t} \right)}}{{\sigma \sqrt {\left( {T - t} \right)} }} $$

On the other hand, the bondholder receives

$$ min\left[ {A\left( T \right),K} \right] = A\left( T \right) - \left[ {A\left( T \right) - K} \right]^{ + } = K - \left[ {K - A\left( T \right)} \right]^{ + } $$

Consequently, the fundamental identity of accounting holds,

$$ A\left( t \right) = E\left( t \right) + \bar{P}\left( {t,T} \right) $$

and the pricing of the debt is such that:

$$ \bar{P}\left( {t,T} \right) = P\left( {t,T} \right) - \left[ {P\left( {t,T} \right)K\Phi \left( { - d_{2} } \right) - A\left( t \right)\Phi \left( { - d_{1} } \right)} \right] $$

An important result under the Merton model is that the probability of default of the firm (\( PD) \), fixed at time \( t \) for the maturity \( T \), is such that

$$ PD\left( {t,T} \right) =\Phi \left( { - d_{2} } \right) $$

Therefore, under the Merton model, it is possible to estimate a firm’s probability of default by looking at the asset’s volatility and balance sheet items.

3 Model’s calibration approach

In order to calculate the probability of breaching of the capital requirements under the Merton model, a specific calibration approach is adopted.

Structural models such as Merton’s model depend on the unobserved volatility of the assets. For this reason, the Merton model must be calibrated in the sense that asset volatility has to be estimated using other information sources such as the quotes on traded instruments. For publicly traded companies, the share price (and hence total equity) is observed in the market. The usual “ad-hoc” approach to obtaining an estimate for the firm’s asset volatility involves calibrating the model using the information related to equity volatility.Footnote 7

In contrast to the usual calibration approach, we propose a calibration approach using CDS quotes. Market data are collected for the risk-free rate and CDS quotes. Risk-free rates are needed as input into the Black–Scholes–Merton formula, while CDS quotes are used to derive the probability of default implied by the market. In particular, given CDS for a reference name (i.e. bank), the CDS premium for the appropriate time horizon is transformed into the market implied probability of default (\( PD^{M} ) \) using the following approximated relation,

$$ PD^{M} \left( {t,T} \right) \cong 1 - exp\left( { - \frac{{CDS\left( {t,T} \right)}}{LGD}\left( {T - t} \right)} \right) $$

where \( CDS\left( {t,T} \right) \) is the premium of a CDS quoted at time \( t \), with maturity \( T \), while \( LGD \) is the loss given default.

Senior or subordinated CDSs quotes can be used for model calibration. However, for the scope of the calculation of the probability of breaching capital requirements, we consider that is more appropriate using senior CDS quotes because we are interested in estimating the issuer’s probability of default and not the probability of default related to a specific security issued.Footnote 8

Once that \( PD^{M} \) is derived from the market in relation to a reference name, asset volatility \( \sigma \) for the single name can be derived by performing an optimization/numerical procedure. The procedure involves choosing the values of \( \sigma \) (\( \hat{\sigma } \)) in such a way that the probability of default implied by the market matches the probability of default implied by the theoretical model.

In performing the optimization procedure to derive asset volatility, the threshold \( K \) is assumed as follows,

$$ K = A\left( t \right) - CET1_{AV} $$

where \( CET1_{AV} \) is the amount of available capital corresponding to the CET1 ratio (\( CET1\% \)) such that

$$ CET1_{AV} = CET1\%_{AV} \times RWA $$

The quantity \( RWA \) represents the amount of the risk-weighted assets quantified according to the Basel III requirements.

It is important to note that the model calibration is performed under a risk-neutral framework. In fact, model parameters (i.e. asset volatility) are calibrated using financial instruments quoted in the market where CDSs are used to infer the probability of default. This approach is consistent as both quantities, the probability of default implied in market quotations (also replicated by the model) and the probability of breaching capital requirement, are calculated under a risk-neutral setting.

4 Estimating the probability of breaching capital requirements

Once asset volatility is quantified following the procedure described in Sect. 3, the probability of breaching the capital requirements can be estimated. In calculating the probability of breaching the capital requirements in a coherent manner with the time horizon \( T \), the new threshold, denoted by \( K^{*} \), is such that,

$$ K^{*} = A\left( t \right) - CET1_{AV} + CET1_{MIN} $$

where \( CET1_{MIN} \) is the amount of minimum capital corresponding to the CET1 ratio (\( CET1\% \)) such that,

$$ CET1_{MIN} = CET1\%_{MIN} \times RWA $$

Finally, the probability of breaching the CET1 capital requirements is calculated as

$$ PB\left( {t,T} \right) =\Phi \left( { - d_{2}^{*} } \right) $$

where

$$ d_{2}^{*} = \frac{{log\left[ {\frac{A\left( t \right)}{{K^{*} }}} \right] + \left( {r - \frac{{\hat{\sigma }^{2} }}{2}} \right)\left( {T - t} \right)}}{{\hat{\sigma }\sqrt {\left( {T - t} \right)} }} $$

Summarizing, our approach involves the following: (1) estimating asset volatility replacing equity with the CET1 (in this case \( K \) is used for the calibration of the PD) and (2) keeping asset volatility unchanged and using threshold \( K^{*} \) for the calculation of the \( PB \).

5 Numerical results

In this section, we discuss the results obtained using the proposed model in order to estimate the probability of breaching the CET1 capital requirements under Basel III for 24 banks selected classified as GSIFIs.

The scope in analyzing different banking institutions is to highlight the cases in which banks with similar CET1 may have a different probability of breaching the capital requirements. In other cases, banks with a similar probability of breaching the minimum CET1 ratio have a different level of capitalization. In order to perform the empirical analysis, for each bank we collected several balance sheet items. The list of these variables is shown in Table 1. We also have considered the amount of minimum capital corresponding to the CET1 ratio (CET1%). The minimum CET1 ratio levels \( (CET1\%_{MIN} ) \) were considered for the different years as follows: 4.5% for 2015, 4%, and 3.5% for 2013 and prior to that year.

Table 1 List of variables considered in the empirical analysis
Full size table

In addition, we collected the following financial market data: (1) the term structure of interest rates derived from traded instruments quoted in the cash, forward rate agreement/futures, and swap marketsFootnote 9 and (2) CDSs on a single name having as their underlying the banks studied in this paper.Footnote 10 A flat LGD equal to 60% was assumed for all the banks to perform all the calculations.

Using these two inputs, the market implied default probability was derived from the CDS quotes. Consequently, asset volatility was calibrated on the basis of the approach described in Sect. 3, and the probability of breaching of the CET1 requirements was estimated for the considered cases. Table 2 reports the results of the analysis as of year-end 2015. From the table, it is important to note that the probability of breaching of CET1 (denoted by \( PB \)) is greater than the probability of default (\( PD \)) for the same one-year time horizon. For our proposed model, this is true by definition because if the value of the asset decreases, the bank is not able to comply with the capital requirements and it can also fail. The results of the analysis for year-end 2014 and 2013 are shown in Tables 3 and 4 respectively.

Table 2 Results as of year-end 2015 (data in USD/bln)
Full size table
Table 3 Results as of year-end 2014 (data in USD/bln)
Full size table
Table 4 Results as of year-end 2013 (data in USD/bln)
Full size table

Analyzing the data reported in Tables 2, 3 and 4, the first relevant aspect to be considered is the meaning of the information contained in the asset volatility calibrated according to the proposed model. Asset volatility estimated under the proposed model is a useful metric as it is able to synthetize the information available in terms of balance sheet items under Basel III (i.e. CET1 ratio) and market data (i.e. CDS).

It is interesting to note how the dynamic of the asset volatility is similar to the dynamic of the risk-weighted assets (RWA) density across the banks analyzed at a point in time. For example, the three panels in Fig. 1 compare asset volatility and RWA density for all the banks examined as of year-end 2013, 2014 and 2015.

Fig. 1
figure 1

Asset’s volatility and density

Full size image

There are two main takeaways from Fig. 1. First, the two variable results are highly correlated where asset volatility, estimated using the proposed approach, appears to be a good proxy for the RWA density. This finding is confirmed by the high correlation coefficients we have estimated using data across the three years. In fact, the estimated coefficients are 79%, 85%, and 83% respectively for year-end 2013, 2014, and 2015. Furthermore, we have performed a linear regression analysis using all available data across the 3 years where asset volatility has been treated as an independent variable while density has been assumed to be the dependent variable. This analysis shows significant results from a statistical point of view with a \( R^{2} \) equal to 65%. Second, comparing banks with a similar CET1 ratio, there are cases in which a different probability of breaching of CET1 arise under the proposed model.

To better analyze these findings, we compared banks with a similar CET1 ratio (around 17%) as of 2015. These results are reported in Table 5a. Notice that despite banks shown in Table 5a having more or less the same CET1 ratio, they have a different probability of breaching the CET1. This is because the probability of breaching is a function of both the capitalization level and CDS quotes. Consequently, \( PB \) is able to synthetize the information contained in the bank’s balance sheet with the information implied by the market for that bank. For example, Banco Santander SA has a CET1 ratio aligned with the other banks but the CDS level, equal to 137 bps, is higher than the CDS levels of the other three banks. The higher CDS level justifies the higher probability of breaching of the CET1 for Banco Santander SA with respect to the other three banks taken into consideration.

Table 5 Banks with similar CET1 and PB as of year-end 2015
Full size table

Table 5b shows that for a similar analysis for two banks (BNP Paribas and JP Morgan), there is a similar probability of breaching the CET1 taking into consideration the key risk indicators as of 2015. The two banks have substantially the same \( PB \) but a different CET1. Moreover, in this case the CDS level is the same. However, it is important to highlight that the RWA density is very different in the two cases: 31.6% for BNP Paribas and 62.3% for JP Morgan. As a result, this difference is reflected in the estimation of the asset volatility that is higher for JP Morgan. Consequently, despite JP Morgan being better capitalized than BNP Paribas, we can argue that in reality the two banks have the same probability of breaching the CET1 capital requirements because JP Morgan’s assets are riskier.

In addition, we calibrated our model using balance sheet and market data observed for 11 years, from year-end 2005 up to year-end 2015. Taking into consideration different historical dates allow us to appreciate how the key risk parameters (i.e. \( CET1 \), \( PD \), \( PB \), …) change over time. In order to evaluate how the key risk indicators for the banks in our study evolved over time, we provided a further analysis where we derive the probability of breaching capital requirements from 2005 to 2015. For each bank and for each year, we derived the probability of breaching the CET1 for a one-year time horizon. Furthermore, in Fig. 2 we compared the \( PB \) with the CDS quote and with the CET1 level. From the figure, it is possible to see how the \( PB \) is able to synthetize and combine the balance sheet information related to the CET1 ratio to the market implied information related to the CDS quotes.

Fig. 2
figure 2

Key risk indicators for four banks

Full size image

In Fig. 2 we plotted the evolution of the risk indicators for the Banco Santander SA, Bank of America Corporation, Bank of China, and Royal Bank of Scotland. From the figure, it can be seen that after the credit crisis of 2008–2009, the CDS spread for Banco Santander SA increased, reflecting an implicit increase for the probability of default discounted by the market. At the same time, the CET1 increases more or less regularly from 2005 to 2015 and it does not seem to be impacted by the increased CDS spread. In this context, the probability of breaching the CET1 is able to capture the increase in the level of the CDS and, at the same time, it reflects the dynamic of the CET1 ratio. In fact, during the period 2009-2012, PB increased, while after 2013 it decreased in a coherent manner with the increased level of CET1 in the last three years (2013–2015). Similar results can be observed for the Bank of America and Bank of China.

6 Conclusions

In this paper, we propose and empirically investigate a Merton-type model for estimating the probability of breaching the capital requirements under the Basel III rules. More specifically, we define a model to estimate the probability of breaching the CET1 capital requirements for a one-year time horizon for 24 banking institutions classified as GSIFIs.

The proposed approach is a particular application of the Merton model where balance sheet data and market data are used to match the probability of default implied by the model with the probability of default implied in the market quotations of CDS instruments. Then, assuming the minimum requirement for the CET1 ratio as the threshold for the Merton model, we estimate the probability of breaching the CET1 capital requirements as a function of the bank’s capitalization level and probability of default implied by CDS quotes. We find that the probability of breaching the capital requirements estimated under the proposed model is a useful metric because it is able to synthetize the information available in terms of balance sheet items (i.e. CET1 ratio) and market data (i.e. CDS quotes).

One of the main findings is that banks with the same CET1 ratio may have a different probability of breaching capital requirements. Analyzing banks with a similar CET1 ratio, there are cases in which, even if the CET1 ratio is the same, a different probability of breaching the CET1 can arise based on the proposed model. This means that banks with the same CET1 ratio may have a different volatility for its capital position and, consequently, a different ability to be resilient in order to preserve the capital buffer under stressed conditions. Likewise, banks with a different CET1 ratio may have a similar probability of breaching the capital requirements; some banks exhibit a very similar probability of breaching the capital requirement but a different CET1 ratio. In this case, the CDS level is the same but the risk-weighted asset density is very different. This means that banks with a different CET1 ratio may have a similar volatility for its capital position and, consequently, a similar ability to be resilient when facing adverse scenarios.

Finally, we focus on the meaning of the information contained in the asset volatility calibrated according to the proposed model. We find that asset volatility calibrated according to the proposed model appears to be a good estimator of the risk-weighted asset density. At the same time, this means that the risk-weighted asset density could be used as a good proxy to estimate the asset’s volatility.