When enough is not enough: bank capital and the Too-Big-To-Fail subsidy

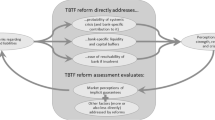
Abstract

This paper takes a unique approach to study the relationship between bank capital and Too-Big-To-Fail (TBTF) during the Financial Crisis. A structural credit risk model is used to compute implied market value capital ratios which, when compared to traditional risk-based capital, illustrates the capital deficiency of large BHCs. As these BHCs’ implied capital deteriorated, their default probabilities spiked. The model is then used to solve for the amount of capital needed to reduce default probabilities. This amount is compared to the TARP capital infusions to quantify the TBTF subsidy which is associated with size and reliance on short-term volatile funding.

1 Introduction

Despite what we hear about the credit crisis and the problems facing banks, the fact is that the bulk of the U.S. banking industry is healthy and remains well-capitalized.

FDIC Chairman, Sheila Bair, October 14, 2008¹

A common refrain from regulators and bank executives at the start of the Financial Crisis was that financial institutions were “well-capitalized”. Nonetheless, the debate about how much capital banks should have—especially large, systemically important banks—is still ongoing years later. This paper provides a unique look at bank capital during the Financial Crisis through the lens of a structural credit risk model. The model uses stock price and volatility along with detailed data on bank liabilities to solve for a market-implied measure of bank capital. The market value capital ratio is highly sensitive to default probabilities, which not necessarily a weakness of the analysis and, in fact, may be viewed as a strength in that it provides a dynamic and time-varying measure of bank capital. When market conditions deteriorate and the bank is faced with a challenging liability structure, default probabilities will rise and the market value capital ratio will fall suggesting that the bank needs to de-leverage and recapitalize; however, when market conditions improve and/or the de-leveraging and recapitalization process stabilizes, market value capital ratios will rise indicating that the bank is in a better condition.

The first empirical evidence presented is that the largest bank holding companies (BHCs) in the United States were well capitalized by regulatory standards. This is consistent with the claims of regulators and bankers, however in market value terms most of them were severely undercapitalized. The fall in market value capital ratios occurred in tandem with the rise in short-term default probabilities. In fact, in the third quarter of 2008 when short-term default probabilities spiked, market value capital ratios converged with the risk-based regulatory capital ratios.²

The data shows that risk-based capital ratios do not change much over time, and can be misleading about the true condition of a distressed bank or the financial system in times of crisis. Any indications of trouble often appear too late, leaving regulators and bank managers with limited alternatives. This can be attributed to the fact that traditional measures of bank capital adequacy are static in nature and are the result of historical analysis of the institution’s balance sheet and operations. Furthermore, they only account for asset risk. More recently, global policymakers have worked to address this in new regulatory standards such as Basel III which takes into account the financing side of bank risk with new metrics such as the Liquidity Coverage Ratio (LCR) and Net Stable Funding Ratio (NSF).³ However, when it comes to capital it seems that risk-weighted assets and Value-at-Risk (VaR) still play a central role which remains a source of contention (see, e.g., Jarrow 2013; Admati 2016). Another debate that is relevant to the analysis presented in this paper deals with mark-to-market versus book value accounting. Essentially the regulatory capital measures are using book values (albeit weighted by somewhat arbitrary risk classes), so whether an analytical method such as the one proposed in this paper are embraced depends on how regulators and risk managers view the current state of mark-to-market practices and the reliability of market data rather than book value accounting reports. To the extent that asset and liability valuations do not reflect deteriorating conditions during a financial crisis, regulators and risk managers will not see an accurate representation of the bank’s capital position and likely will be forced to act in a reactionary rather than proactive manner. The other side of this argument is that market data can be noisy so there may be concern about how regulators and risk managers address dramatic fluctuations in capital ratios in the face of rapid changes. This debate has played out in the finance, economics, and accounting literature in the years immediately following Lehman Brothers’ failure; see, e.g., Allen and Carletti (2008), Plantin et al. (2008), Heaton et al. (2010). Finally, one further complication to the bank capital conundrum is the call to require differential capital treatment for larger banks that are systemically more important so as to minimize the perverse incentives associated with Too-Big-To-Fail (TBTF).⁴

A main contribution of the paper is that it makes use of the structural credit risk model’s endogenous default, which is the point at which the bank will no longer be able to raise capital in a perfect market. Therefore, the model can be used to solve for the amount of capital that is needed to increase the “distance-to-default” and reduce default probabilities below a specified level. This is referred to as the Ex-Post Implied Capital Shortfall of the bank or $\text{ EPICS }$. Using the model, $\text{ EPICS }$ is estimated for the ten largest BHCs in the U.S. at the first quarter of 2009.

This provides an interesting natural experiment since by this time the federal government was injecting hundreds of billion dollars into the financial system and these ten banks were among the first to receive the support through the Troubled Asset Relief Program (TARP). Each $\text{ EPICS }$ value is then compared to the amount of TARP funds that the particular bank received under the Capital Purchase Program (CPP) and the Targeted Investment Program (TIP).⁵ It turns out that all ten of BHCs needed more capital than they actually received; however, none of the banks failed and their default probabilities did indeed fall. A plausible explanation lies in the belief of market participants that similar “bailouts” would occur in the future and the government would not allow those banks to fail. Therefore, the amount by which the $\text{ EPICS }$ exceeds the TARP funds received represents a way to quantify the TBTF subsidy that was priced in at the time.

To summarize, this paper makes several contributions with important insights and clear policy implications. First, capital ratios should be dynamic and capital requirements should be time-varying. Second, bigger banks should be required to hold disproportionately more capital to reduce the perverse incentives associated with TBTF. Additionally, the model developed in the paper provides a way to determine how much more capital these large banks should have by using market information to quantify the negative externality, the TBTF subsidy, which can then be internalized by requiring that the bank have at least that much capital. From an empirical standpoint, this paper provides a direct link between the amount of capital the largest banks had versus how much they needed during the crisis and quantifies the extent to which these same banks relied on the support of the government to survive. Lastly, the analysis shows that short-term volatile sources of funding exacerbate the TBTF problem. Therefore, there is a positive relationship between bank size, the TBTF subsidy, and the reliance on short-term volatile sources of funding. Thus, perhaps additional capital should be required for those banks who excessively rely on those funding channels.

The remainder of the paper is structured as follows. Section 2, reviews the relevant extant literature. Section 3 proposes a structural model of the banking firm, derives the default probabilities, presents the application to capital requirements and introduces the $\text{ EPICS }$ measure. Section 4 discusses the data and methodology. The empirical results are presented in Sect. 5. Section 6 concludes.

2 Literature review

Structural credit risk models, based on the seminal work of Black and Scholes (1973) and Merton (1974), model corporate securities as contingent claims on the firm’s assets, where equity is viewed as a call option on the firm’s assets. Option pricing techniques can be used to compute default probabilities as the likelihood that that the call option is not exercised but rather allowed to expire worthless, i.e. the debt holders take control of the firm. The application of option-theoretical models to bank capital is not a new idea; many papers were published in the late 1970’s into the 1980’s within the context of risk-based deposit insurance.⁶

After the turn of the century the focus has shifted to risk-based capital requirements. Two papers that have successfully used a structural model of capital adequacy are Flannery (2014) and Flannery and Giacomini (2015). These papers use a Merton-type model to evaluate the capital adequacy for U.S. bank holding companies and European banks, respectively.⁷ The analysis presented here is similar, but differs in that it uses a structural credit risk model with a tiered liability structure and endogenous default.

Structural credit risk models have also recently been used to determine how distressed financial institutions should recapitalize. It is well-known in the corporate finance literature that distressed firms encounter severe agency problems when trying to raise new equity (see Myers 1977). These problems are even more pronounced for financial institutions (see Flannery 1994). Kashyap et al. (2008) advocate a capital insurance system that would payout to participating banks in distressed states, thereby providing a capital infusion without the negative externalities and agency problems of issuing new equity. The state-contingent nature of the capital insurance scheme is similar in theme to the use of Contingent Capital Certificates (CCC) as proposed by Flannery (2016). CCCs are debt securities that pay coupons like any other bond, but are junior to subordinated notes and debentures. In the event of some downturn, represented by the so-called “trigger” the CCCs automatically convert into equity, thereby replenishing the capital cushion on the bank’s balance sheet. The downside of CCCs is that there is no new cash infusion into the bank. Therefore, the CCCs must be used in prudential, a priori planning for risk management and capital structure solutions.

Contingent-capital-like securities have received a lot of attention from both policymakers and academics alike and are often referred to as “contingent-convertible” bonds or co-co bonds. The Squam Lake Working Group (2009a) recommends the use of “regulatory hybrid securities” in bank recapitalization. In the years following the Financial Crisis, there were quite a few articles that examined contingent capital from many different perspectives including the pricing, design, and regulatory considerations of such securities (see Glasserman and Nouri 2012; McDonald 2013; Pennacchi et al. 2014; Albul et al. 2015; Sundaresan and Wang 2015; Pennacchi and Tchistyi 2019a, b). At the center of every discussion is determining what the trigger should be for these securities. Contingent capital securities with a market-based trigger represent a way of integrating market discipline into bank capital adequacy standards. In fact, one could potentially use the model in this paper and its endogenous default point to solve for an optimal trigger for a co-co type of hybrid capital security.⁸ It is left as a topic for future research.

The $\text{ EPICS }$ measure developed in this paper is similar to the capital shortfall ($\text{ CS }$) and marginal expected shortfall ($\text{ MES }$) put forth in Acharya et al. (2012, 2017), respectively.

By comparing the $\text{ EPICS }$ measure to TARP funds received, this paper provides a novel way to quantify the TBTF subsidy at the time of the crisis. One of the first papers to rigorously examine the implications and quantify the costs of the TARP was Veronesi and Zingales (2010). They provide some very unique insights into the dynamics and values associated with the largest financial bailout in history, utilizing a variety of data sources. Particularly relevant to the present paper is their examination of the government’s capital infusion into the first nine banks to receive funds through the TARP and the impact on the banks’ claims, both debt and equity. Their analysis illustrates an increase in the banks’ enterprise value of almost $130 billion. A structural credit risk model—essentially an extension to the original Black–Scholes–Merton—is employed in both the computation of the cost of the federal guarantee on bank debt as well as in quantifying the ex-ante effects of the capital infusion. The structural credit risk model employed in the present paper is a bit more sophisticated, incorporating multiple classes of liabilities and an endogenous default point. It will be shown later in the paper the additional insights this provides when evaluating the capital adequacy of a financial institution. While such an evaluation can also be performed in an ex-ante capacity, the analysis in the present paper is on quantifying the ex-post effects of being Too-Big-To-Fail during the crisis.⁹

A similar analysis was performed by Glasserman and Wang (2011) with respect to the subsequent Capital Assistance Program (CAP). The CAP was instituted after TARP, when the well-known stress tests were conducted to determine the ex-ante capital needs of the largest financial institutions in the event the crisis worsened. Santos (2014) provides empirical evidence that the largest banks were borrowing at lower costs, confirming the existence of TBTF during the crisis. Over a long sample period that includes the Financial Crisis, Santos (2014) finds that if a bank was in the top five in terms of asset size, then it traded at a discount of on average more than 40 basis points.

Another approach is provided by Kelly et al. (2016) which documents the presence of a sector-wide guarantee for financial firms implied by option prices. Their analysis established that, during the crisis, the government cut off downside tail risk for the entire financial sector, effectively eliminating the need for sector-wide crash insurance via index put options. The backstop that was in place during this time essentially served as “free insurance” for bank stockholders. The authors quantify the value of this benefit accrued by bank shareholders in the wake of the crisis was about $282 billion.

The recent literature establishes that during the crisis TBTF was very real with both implicit and explicit governmental guarantees supporting the financial system. Furthermore, the evidence in these papers shows that the guarantees were priced into bank stocks, bonds, options, and CDS contracts. While equity holders and debt holders appear to have benefited from the backstop that was put in place and the bailouts that were provided, very few economists would agree that this is a good thing because of the distortive effects and negative externalities associated with TBTF.¹⁰ This paper provides additional evidence for the extent to which TBTF played a role, and was priced, during the crisis; additionally there are some prescriptive implications for addressing TBTF through bank capital requirements.

3 A structural model of bank default

3.1 Structural credit risk models and the banking firm

The basic Black–Scholes–Merton (BSM) model provides an efficient, analytical method for calculating risky debt prices, credit spreads, and comparative statics, thereby taking the economics of credit risk to another level. Since the 1970s many extensions have been developed, in response to some of the restrictive and unrealistic assumptions behind the basic BSM model. One class of extensions are the “barrier” structural models where default can occur at any time and is the result of the asset value process hitting a barrier. Many of these models assume an exogenous default barrier (Black and Cox 1976; Longstaff and Schwartz 1995; Collin-Dufresne and Goldstein 2001) although the Leland (1994) and Leland and Toft (1996) models include an endogenous default barrier. Another structural credit risk model with endogenous default is the compound option model of Geske (1977). The model used in this paper takes the Geske compound option structural credit risk model and applies it in a dynamic context.

Structural credit risk models are commonly used to compute default probabilities. Within the original BSM framework, the probability that the call option is not exercised at time T is the probability that the firm defaults; that is because if the market value of the firm’s assets is not greater than the face value of the debt, then shareholders will let their option expire and leave the assets to the debt holders. The extensions that include a continuous default barrier compute default probabilities by the first passage density. The compound option structural model actually computes default probabilities at every discrete cash flow time which gives rise to a term structure of default probabilities.

Despite relatively good success in using structural credit risk models for computing default probabilities and predicting corporate default, empirical studies typically exclude financial institutions.¹¹ Leland (2009) discusses some of the difficulties in applying structural credit risk models to financial institutions. Two of the biggest issues are the high degree of leverage and the disproportionate use of short-term debt, including repurchase agreements.

A structural credit risk model that is widely used in practice is the KMV model (see Crosbie and Bohn 2003). However, as with many other structural credit risk models, the KMV model has found little success in the application to financial institutions. This is perhaps attributable to exogenous default condition where the entire liability structure is simplified to a linear combination of short-term and long-term debt, not taking into account seniority. In addition to endogenous default, the model in this paper exploits the steeply tiered liability structure that is characteristic of most financial institutions.

The Leland and Toft (1996) model has endogenous default and is attractive for several reasons. First, there is a closed-form solution for the values of debt and equity, default probabilities, and the default barrier. Furthermore, it is assumed that all debt is rolled-over which, in normal market conditions, is in line with the practices of financial institutions. However, the Leland and Toft (1996) model does not capture all of the features of a bank because it assumes that there is only one class of debt with a fixed maturity.¹²

Gorton and Santomero (1990) use a modified version of the Black and Cox (1976) structural credit risk model, which has an exogenous default barrier, adapted for a banking firm with the intention of understanding the role that subordinated debt has in enforcing market discipline. One of the modifications to Black and Cox (1976) and adaptations to banking firms is that there are two different classes of debt: senior insured, such as deposits, and junior unsecured, such as subordinated debt. Both classes of debt have the same maturity date. The model is able to capture the nonlinear relationship between the value of a bank’s liabilities and risk. The authors are able to show that the structural credit risk model, which uses market information, is better able to capture the effects of market discipline than accounting measures of bank risk.

The compound option structural credit risk model of Geske (1977) has endogenous default and allows for multiple classes of debt. In this model, default can occur whenever a cash flow is due rather than the two extremes of defaulting at maturity, as with European options and the original BSM model, or defaulting anytime between now and maturity, as with barrier models. This can then be used to model coupon-paying debt, where default can occur if it is not economically feasible to make an interest and/or principal payment; or it can be used to model a complex seniority or maturity structure where debt holders are to be paid sequentially. This is a practical way to capture the realistic feature of cross-default provisions in debt contracts.

When there are just two cash flows, the model can be solved analytically as shown by Geske (1979). Geske and Johnson (1984) amend the earlier versions of the model (Geske 1977, 1979) to more appropriately specify the default conditions when there are two distinct classes of debt, which leads to the correct closed-form expression for the intertemporal values of equity and junior debt. Geske (1979) also illustrated that there is an explicit leverage effect that causes the volatility to change with the value of the underlying assets.

This compound option structural model provides a consistent and intuitive framework for valuing corporate securities and quantifying credit risk. Furthermore, the model captures the complex and important capital structure of a bank rather nicely. The model is simple enough where it can be computed analytically, but still has the information regarding the seniority structure of debts and the inherent compound-optionality in the decision to default.¹³

The drawback of the compound option structural model is that it assumes all debt obligations are satisfied by issuing new equity. This implies that the firm being analyzed will have a leverage ratio that decreases systematically over time and it will ultimately become an all-equity firm. There are very few firms that practice such extreme de-leveraging, especially in the banking industry.¹⁴ However, in the face of severe financial distress and potential bank failure, the proposed model’s intended purpose of determining the endogenous point at which the banks would need to raise capital and then solving for the necessary capital infusion makes both the de-leveraging and compound-optionality that much more relevant. The de-leveraging reflects the idea that banks must raise equity to reduce risk of failure in the face of distress, consistent with what was observed in 2008-2009 during the crisis. The compound-optionality reflects the fact that when the capital backstop is provided by a lender of last resort, as it was in both the Global Financial Crisis in 2008-2009 and the European Crisis in 2011-2012, quite often this capital comes with either the explicit or implicit promise of further contingent capital infusions which may be priced by the market in a way similar to a compound option.¹⁵

The model that is used in this paper is based on the Geske compound option structural credit risk model, but is used in a more dynamic capacity. When used in this manner, the compound option structural model has the interpretation that, as long as default probabilities are sufficiently low approaching the first cash flow (i.e. payment to short-term senior creditors), it will continue as a going concern and therefore will refinance some or all of its debt in a manner that is consistent with its existing financial policy. The model can then be re-run using updated values for the short-term and long-term debt outstanding. In the model, default is endogenous and is triggered when the value of the bank’s assets is too low to justify the sale of any new equity. The inability to raise fresh capital can be thought of as the driving force of bank distress, especially during the recent financial crisis. Therefore, the endogenous default condition given by the model is crucial to understand the events that unfolded during the crisis and solving for the ex-post capital needs of the banks.

3.2 Assumptions and model setup

First, it should be noted that the structural credit risk model developed in this paper assumes that financial institutions exist in a world with no market frictions. Specifically, it is assumed that there are no taxes, no distress costs, no transaction costs, and perfect liquidity. The model highlights the fact that static measures of capital adequacy, such as a fixed percentage of assets, are arbitrary and do not capture the true health of a financial institution. Rather, a dynamic approach that is forward-looking and tied to market conditions is more appropriate for determining the capital needs. One implication is that capital requirements may be time-varying and conditional upon the health of the particular bank and the financial system as a whole. The model provides a quantitative and objective method for determining how much capital a financial institution needs in good times and bad. All of this can be demonstrated without the presence of market frictions.

Although default is determined endogenously, the bank’s initial capital structure is not.¹⁶ The exogenous capital structure means that default probabilities are computed given the bank’s current liability structure and equity value. In addition to the fact that the bank’s capital structure is exogenous, no claim is made regarding the optimality of contracts in the model.

To set up the model, several additional assumptions have to be made. First, assume that the market value of the bank’s portfolio of assets (i.e. loans, investment securities, etc.) evolves according to a Geometric Brownian Motion. That is, at time t the asset value process is given by the stochastic differential equation

$$\begin{aligned} d{{V}_{t}}={{r}_{t}}\ {{V}_{t}}\ dt+{{\sigma }_{V}}\ {{V}_{t}}\ dW\, \end{aligned}$$

(1)

where $d{{W}_{t}}$ represents a standard Brownian increment under the risk-neutral probability measure.¹⁷ In Eq. (1) $r_{t}$ represents the risk-free interest rate at time t and ${{\sigma }_{V}}$ is the asset volatility. Also assume that neither the interest rates nor asset volatility are stochastic.

For the liabilities, it is assumed that there are two general classes of debt: short-term senior debt with face value $F_{1}$ maturing at time $T_{1}$ and long-term junior debt with face value $F_{2}$ maturing at time $T_{2}$, where ${{T}_{1}}<{{T}_{2}}$. This follows the assumptions in the Geske compound option setup that short-term debt is senior to long-term debt.¹⁸ The short-term senior debt can be time deposits, repurchase agreements, federal funds purchased, and/or other similar claims. While many of these claims are secured, they need not be; the key feature is that they are expected to be repaid by time $T_{1}$ or have priority in the event of a liquidation. The long-term junior debt can be thought of as subordinated debentures, which are issued by many financial institutions and featured prominently in the market discipline literature. The subordinated debentures lie just above equity in terms of seniority, but since they are unsecured, have longer maturities, and have lower priority, they bear more risk than the senior debt.

This two-tiered liability structure lends itself nicely to the idea that the bank’s equity is a compound call option on the bank’s assets. First, short-term senior creditors must be paid; then, the junior long-term debt is paid; and, finally, whatever is left goes to the shareholders, the residual claimants. Note that the balance sheet equality must hold in market value terms: ${{V}_{t}}={{S}_{t}}+{{J}_{t}}+{{E}_{t}}$, where $S_{t}$ is the market value of the short-term senior debt at time t, $J_{t}$ is the market value of the long-term junior debt at time t, and $E_{t}$ is the market value of the equity at time t. This quantity, $E_{t}$, is the only readily observable market value which means solving the model depends on solving an inverse problem.¹⁹ In the model, the market value of equity is computed using the compound call option formula as a function of the market value of the bank’s assets, the asset volatility, and the face value of the liabilities, which serve as the strike prices for the compound option. Thus, the outputs, equity value and equity volatility, are observed given the unobservable inputs, asset value and asset volatility. An iterative procedure is used to solve for the two unknown inputs given the known and observed outputs.

3.3 Default dynamics

Although the compound option structural credit risk model is a based on an absolutely continuous stochastic process and therefore relies on continuous-time financial mathematics, since the cash flows occur at discrete times it is helpful to visualize the default process as a binomial tree. In Fig. 1 the solid nodes (A, B, and D) represent survival states and the dashed nodes (C and E) represent default states. The accompanying table shows the value of the corporate securities (equity, junior debt, and senior debt) at each node as expected values; solving the expectations at node A gives rise to the closed-form valuation equations in Appendix A.

Fig. 1

Source Author’s unpublished dissertation

Figure shows a simple two-period binomial lattice to illustrate the intuition behind the compound option structural credit risk model. The accompanying table shows each of the corporate securities’ payoffs (equity, junior debt, and senior debt) at times $T_1$ and $T_2$ as well as the expected value at time $t=0$.

Moving from node A to node B means that the bank survives to time $T_{1}$ and the senior debt holders will be paid. Survival at the first cash flow time, $T_{1}$, depends on the asset value relative to the default barrier, ${\bar{V}}$, which is endogenously determined (see Sect. 3.4). Since, at node B, the asset value is greater than the default barrier, the first cash flow obligation, $F_{1}$ is satisfied in full and all that remains are the junior debt and equity claims. The probability of getting to node B, or equivalently the probability that ${{V}_{{{T}_{1}}}}>{\bar{V}}$, is the short-term survival probability, denoted as $p_{1}$ in Fig. 1.

On the other hand, if the value of the bank’s assets are less than or equal to the default barrier, then the bank will hit the default state at node C. Node C is actually further broken down into two states, $C_{1}$ and $C_{2}$, which represent partial versus total default, respectively. $C_{1}$ is referred to as partial default, because senior debt holders are paid in full but the asset value is not high enough to pay junior debt holders so the latter receives only the residual payment. In and near this distressed state, equity has no value and the bank’s subordinated debentures will behave more like equity than debt. $C_{2}$, on the other hand, represents total default where neither equity holders nor junior debt holders are paid, and the senior debt holders will receive whatever value the assets are worth at default time.

In the static compound option framework if the firm makes it to node B, then new equity is issued at the current market price and used to finance the payment to the senior creditors. Thus, once the short-term senior debt holders are paid at node B the leverage of the firm is reduced by $F_{1}$ and only long-term junior debt remains outstanding. The model then reduces to the standard BSM setup. If the value of the assets at time $T_{2}$ is greater than the face value of the junior debt (${{V}_{{{T}_{2}}}}>{{F}_{2}}$) then the bank will end up in the terminal survival state, represented by node D in the lattice. The assets are liquidated, junior creditors are repaid what they are owed, and shareholders receive the residual value ${{V}_{{{T}_{2}}}}-{{F}_{2}}$ . However, if the value of the assets is less than or equal to the face value of the junior debt (${{V}_{{{T}_{2}}}}\le {{F}_{2}}$) then the bank will end up in the terminal default state, represented by node E, with conditional probability of $1-{{p}_{2}}$. This is the conditional default probability because it is depends on the bank’s survival to time $T_{1}$.

From the perspective at node A, at time $t=0$, the model gives a forward-looking measure of the likelihood that the bank will be able to meet all of its financial obligations, both those that are due at time $T_{1}$ (short-term senior) and those that are due at time $T_{2}$ (long-term junior). In fact, the endogenous default barrier intuitively reflects the expectation that the level of the bank’s capital is sufficiently high to justify the payments of both classes of debt in expectation.

3.4 Endogenous default and default probabilities

In the compound option structural model the default condition arises from the fact that the firm must have access to capital in order to survive. At time $T_{1}$, when the short-term senior debt is due, the firm must be able to raise enough capital to satisfy the pending obligations. Given the assumption that capital is raised in a frictionless market, equity can always be issued at the current market prices. As the market value of equity approaches zero, the firm will find itself under increasing pressure to raise the funds needed to service the outstanding debt. Recall that equity, in turn, is a function of the value of the firm’s assets. Thus, there must be some breakeven asset value such that the market value of equity is high enough that a new issuance will just satisfy the next cash flow, leaving nothing for the residual claimants. In other words, the default condition maintains that equity must have positive value for survival.²⁰ Mathematically, the default boundary is the asset value, ${{V}_{{{T}_{1}}}}={\bar{V}}$, that is the internal solution to the integral equation

$$\begin{aligned} E\left( {{\bar{V}}} \right) -{{F}_{1}}=0 . \end{aligned}$$

(2)

It follows from Eq. (2) and the market value balance sheet identity that

$$\begin{aligned} {\bar{V}}={{F}_{1}}+{{J}_{{{T}_{1}}}} \end{aligned}$$

(3)

where ${{J}_{{{T}_{1}}}}$ is the market value of the long-term junior debt at the time the senior debt holders are paid. In order to find the default boundary, Eq. (2) can be solved so that

$$\begin{aligned} {{F}_{1}}=E\left( {{\bar{V}}} \right) ={\bar{V}}\,N\left( d_{+}^{*} \right) -{{F}_{2}}\,{{e}^{-r\left( {{T}_{2}}-{{T}_{1}} \right) }}\,N\left( d_{-}^{*} \right) \end{aligned}$$

(4)

where ${{d}_{+}^{*}}=\frac{\ln \left( \frac{{{\bar{V}}}}{{{F}_{2}}} \right) +\left( r + \frac{{{\sigma }^{2}}}{2} \right) \left( {{T}_{2}}-{{T}_{1}} \right) }{\sigma \sqrt{{{T}_{2}}-{{T}_{1}}}}$ and ${{d}_{-}^{*}}=\frac{\ln \left( \frac{{{\bar{V}}}}{{{F}_{2}}} \right) +\left( r - \frac{{{\sigma }^{2}}}{2} \right) \left( {{T}_{2}}-{{T}_{1}} \right) }{\sigma \sqrt{{{T}_{2}}-{{T}_{1}}}}$.

Solving for ${\bar{V}}$ in Eq. (4) gives the endogenous default boundary. If the asset value at time $T_{1}$ is less than this amount, then the firm will not be able to raise capital and will default. Once the default boundary has been found, the default probabilities can be specified in closed-form.²¹

The short-term survival probability, or the probability that the bank survives until time $T_{1}$, is:

$$\begin{aligned} Q\left( T_{1} \right) =\Pr \left\{ {V}_{{T}_{1}}>{\bar{V}} \right\} =N\left( h_{1}^{-} \right) \end{aligned}$$

(5)

where $Q\left( \cdot \right)$ denotes the survival probability under the risk-neutral measure and $N\left( h_{1}^{-} \right)$ similar to what is found in the BSM model. The expression for $h_{1}^{-}$ is defined in Eq. 10, below.

At time $T_{1}$, either the bank pays the senior creditors, and survives, or it defaults. Therefore, the short-term default probability is:

$$\begin{aligned} DP\left( {{T}_{1}} \right) =\Pr \left\{ {{V}_{{{T}_{1}}}}\le {\bar{V}} \right\} =1-\Pr \left\{ {{V}_{{{T}_{1}}}}>{\bar{V}} \right\} = 1-N\left( h_{1}^{-} \right) = N\left( -h_{1}^{-} \right) \end{aligned}$$

(6)

which follows directly from Eq. (5) and the laws of probability for mutually exclusive events.

The total survival probability, or the joint probability of the bank surviving to both $T_{1}$ and $T_{2}$, is:

$$\begin{aligned} Q\left( T_{2} \right) = \Pr \left\{ \left( {V}_{{{T}_{1}}}>{\overline{V}} \right) \; \& \; \left( {V}_{{{T}_{2}}}>{{F}_{2}} \right) \right\} = {{N}_{2}}\left( h_{1}^{-},h_{2}^{-};\rho \right) \end{aligned}$$

(7)

where, again, $Q\left( \cdot \right)$ denotes the survival probability under the risk-neutral measure and ${{N}_{2}}\left( h_{1}^{-},h_{2}^{-};\rho \right)$ is the cumulative bivariate standard normal distribution for two jointly distributed standard normal random variables with correlation $\rho$. This comes from the assumption that the underlying stochastic process is a Geometric Brownian Motion which ensures that the solution is a function of the bivariate normal distribution in $h_{1}^{-}$ and $h_{2}^{-}$.

Since the bank cannot default at time $T_{2}$ without first having survived to time $T_{1}$ only the conditional forward default probability exists. That is, the probability that the bank defaults at time $T_{2}$ given that the bank defaulted in $T_{1}$ is undefined. In other words, short-term default is an absorbing state; the bank cannot emerge from bankruptcy. Thus, the forward default probability can be computed once the short-term survival probability and the total survival probability are known simply by applying Bayes’ Theorem. The forward default probability is defined as the probability that the long-term debt obligations will not be satisfied given that the short-term debt obligations have been satisfied, or $\Pr \left\{ {{V}_{{{T}_{2}}}}\le {{F}_{2}}|{{V}_{{{T}_{1}}}}>{\bar{V}} \right\}$. This is equal to one minus the conditional survival probability, or $1-\Pr \left\{ {{V}_{{{T}_{2}}}}>{{F}_{2}}|{{V}_{{{T}_{1}}}}>{\bar{V}} \right\}$:

$$\begin{aligned} DP\left( {{T}_{2}} \right)= & {} \Pr \left\{ {{V}_{{{T}_{2}}}}\le {{F}_{2}}|{{V}_{{{T}_{1}}}}>{\bar{V}} \right\} \nonumber \\= & {} 1-\Pr \left\{ {{V}_{{{T}_{2}}}}>{{F}_{2}}|{{V}_{{{T}_{1}}}}>{\bar{V}} \right\} = 1-\frac{\Pr \left\{ \left( {{V}_{{{T}_{2}}}}>{{F}_{2}} \right) \; \& \; \left( {{V}_{{{T}_{1}}}}>{\bar{V}} \right) \right\} }{\Pr \left\{ {{V}_{{{T}_{1}}}}>{\bar{V}} \right\} } \nonumber \\= & {} 1-\frac{{{N}_{2}}\left( h_{1}^{-},h_{2}^{-};\rho \right) }{N\left( h_{1}^{-} \right) } \end{aligned}$$

(8)

where, it has already been established that the short-term and total survival probabilities, are $N\left( h_{1}^{-} \right)$ and ${{N}_{2}}\left( h_{1}^{-},h_{2}^{-};\rho \right)$, respectively. Bayes’ Theorem gives the conditional survival probability as $\frac{{{N}_{2}}\left( h_{1}^{-},h_{2}^{-};\rho \right) }{N\left( h_{1}^{-} \right) }$ and the conditional default probability then follows from mutual exclusivity; i.e. the bank cannot both survive and fail at $T_{2}$.

Proposition

The capital needs of the bank should be a function of the short-term default probability, defined in Eq. (6).

While critics may contend that this is a myopic approach, it is quite the contrary. Since it is a function of the default boundary, ${\bar{V}}$, $DP\left( {{T}_{1}} \right)$ contains all relevant information including asset risk, endogenous default, and the complete liability structure—not only the short-term debt but also the expectation of the bank’s ability to pay its long-term debt in the future.

The forward default probability, on the other hand, does not capture all of this information and is much less relevant for the analysis of financial institutions. To see why, recall the key assumption for the compound option structural model: when debt is due, new equity is issued and the proceeds are used to finance the debt payment. In the case where there are just two classes of debt the degree of leverage in the firm’s capital structure will fall immediately after the first payment is made, since the first class of debt will be replaced entirely with equity.²² This may be problematic for financial institutions for two reasons. First, financial institutions tend to have a lot of short-term senior debt, so assuming that it will all be paid off by issuing new equity results in a large drop in leverage for a firm that is typically characterized by high leverage. Second, as mentioned earlier, financial institutions tend to roll-over short-term debt. This means that the true forward default probability should not only use the junior long-term debt in creating the forward default boundary but also some portion of the short-term debts that had been rolled-over.

As a result, the forward default probabilities calculated with Eq. (8) are biased downward. The implicit de-leveraging that is built into the compound model creates the unrealistic impression that bank default risk declines over time. It is worth noting here that Chen et al. (2014) develop a structural credit risk model that extends the Geske compound option approach to allow for optional rollover of maturing short-term debts and argue that changes in the forward default probabilities could potentially serve as an early warning signal for regulators to identify financial institutions that are likely to encounter distress in the future. However, their model does not have an analytical solution and is solved numerically using a lattice approach.

In contrast, in this paper the compound option model may be recalibrated each time it is used, with new inputs for volatility, liabilities, interest rates, etc. This introduces a “dynamic” component to it and ensures that the financial institution being analyzed never actually gets past time $T_{1}$ where the mechanical de-leveraging takes place. The short-term default probability, or $DP\left( {{T}_{1}} \right)$ as given by Eq. (6), still represents a valid measure of the financial institution’s default risk since it takes the entire liability structure into account, but is also updated to reflect any short-term debt that may have been rolled-over since the last time the model was run. Furthermore, because it relies on the endogenous default boundary this is an internally consistent metric for determining the capital needs for a financial institution. In the next subsection the computation and treatment of equity capital is covered.

3.5 Equity and bank capital

Recall, from Fig. 1, that the market value of the bank’s equity at time $t=0$ is given by the conditional expectation

$$\begin{aligned} \mathop {{\mathbb {E}}}\left[ {{e}^{-r{{\tau }_{1}}}}\,\max \left\{ {{E}_{{{T}_{1}}}}-{{F}_{1}},0 \right\} \left| {{V}_{t}} \right. \right] , \end{aligned}$$

(9)

where ${{E}_{{{T}_{1}}}}$ is equal to the value of a European call option at time ${T}_{1}$, which is not known at time t. Let ${{\tau }_{1}}=\left( {{T}_{1}}-t \right)$ be the time between t and the short-term senior debt maturity $T_{1}$ and${{\tau }_{2}}=\left( {{T}_{2}}-t \right)$ be the time between t and the long-term junior debt maturity $T_{2}$. The expectation given in Eq. (A.1) is equal to:²³

$$\begin{aligned} {{E}_{t}}={{V}_{t}}\,{{N}_{2}}\left( h_{1}^{+},h_{2}^{+};\rho \right) -{{F}_{2}}{{e}^{-r{{\tau }_{2}}}}\,{{N}_{2}}\left( h_{1}^{-},h_{2}^{-};\rho \right) -{{F}_{1}}{{e}^{-r{{\tau }_{1}}}}N\left( h_{1}^{-} \right) \end{aligned}$$

(10)

where $h_{1}^{+}=\frac{\ln \left( \frac{{{V}_{t}}}{{{\bar{V}}}} \right) +\left( r+\frac{{{\sigma }^{2}}}{2} \right) {{\tau }_{1}}}{\sigma \sqrt{{{\tau }_{1}}}}$,

$h_{1}^{-}=\frac{\ln \left( \frac{{{V}_{t}}}{{{\bar{V}}}} \right) +\left( r-\frac{{{\sigma }^{2}}}{2} \right) {{\tau }_{1}}}{\sigma \sqrt{{{\tau }_{1}}}}=h_{1}^{+}-\sigma \sqrt{{{\tau }_{1}}}$,

$h_{2}^{+}=\frac{\ln \left( \frac{{{V}_{t}}}{{{F}_{2}}} \right) +\left( r+\frac{{{\sigma }^{2}}}{2} \right) {{\tau }_{2}}}{\sigma \sqrt{{{\tau }_{2}}}}$,

$h_{2}^{-}=\frac{\ln \left( \frac{{{V}_{t}}}{{{F}_{2}}} \right) +\left( r-\frac{{{\sigma }^{2}}}{2} \right) {{\tau }_{2}}}{\sigma \sqrt{{{\tau }_{2}}}}=h_{2}^{+}-\sigma \sqrt{{{\tau }_{2}}}$,

$N\left( \centerdot \right)$ denotes the cumulative standard normal distribution,

${{N}_{2}}\left( \centerdot \right)$ denotes the cumulative bivariate standard normal distribution,

and correlation $\rho =\sqrt{{\frac{\tau _1}{\tau _2}}}$which follows from the properties of Brownian Motion.

${\bar{V}}$ is the endogenous default boundary, from Sect. 3.4.

Note, as discussed above, the default probabilities are explicitly a function of the endogenous default boundary which takes both the short-term senior debt, due at time $T_{1}$, and the long-term junior debt, due at time $T_{2}$, into account.

Therefore, if one knows the market value and volatility of the bank’s assets, then the model can be used to solve for the short-term default probability, $N\left( -h_{1}^{-} \right)$ [see Eq. (6)] which, in this analysis, is the primary indicator for bank insolvency and and is used in the calculation of EPICS. Since market values are being used in the calculation of the short-term default probability and the determination of bank capital needs via EPICS, the argument could be made that these values are riddled with noise. However, it will be shown below in the empirical analysis, that the risk-based capital (RBC) ratios are perhaps too steady to be trusted. The fluctuations in market value capital (MVC) ratios can allow regulators and risk managers real-time information for evaluating capital adequacy; furthermore, the case is made below that the MVC not be used in lieu of RBC ratios but in conjunction with one another. In the empirical analysis, the MVC ratio is calculated as the market value of equity divided by the book value of assets since the market value of assets is unobservable.²⁴

In practical implementation of the model, however, one encounters an inverse problem where the outputs are observed—equity value and equity volatility—given the unobservable inputs, asset value and asset volatility. Since equity is a compound call option in the model, the implied market value of the bank’s assets can be extracted from market information. The market information specifically being used are the market value of equity and equity volatility. Using an iterative procedure, the market value of the bank’s assets and the asset volatility can be computed as two equations in two unknowns.

Although asset volatility is assumed to be constant, equity volatility is a function of asset value and other parameters in the model. This was first shown by Geske (1979). Equity, being a compound option on the underlying asset, has its own stochastic dynamics which can be specified using Ito’s Lemma. From the Ito expansion, the volatility term for equity is

$$\begin{aligned} {{\sigma }_{E}}=\frac{\partial E}{\partial V}\,\frac{V}{E}{{\sigma }_{V}}. \end{aligned}$$

(11)

The partial derivative $\frac{\partial E}{\partial V}$ can be found by differentiating Eq. (10) with respect to asset value and is known as the “equity delta”:

$$\begin{aligned} \frac{\partial E}{\partial V}={{N}_{2}}\left( h_{1}^{+},h_{2}^{+};\rho \right) . \end{aligned}$$

(12)

The equity delta shows the sensitivity of the market value of the bank’s equity capital to changes in the market value of the underlying asset portfolio.

Substituting Eq. (12) into Eq. (11) gives

$$\begin{aligned} {{\sigma }_{E}}={{N}_{2}}\left( h_{1}^{+},h_{2}^{+};\rho \right) \,\frac{V}{E}{{\sigma }_{V}}. \end{aligned}$$

(13)

Thus, holding everything else constant, as more leverage is introduced the equity volatility becomes greater than the asset volatility. This leverage effect is consistent with standard corporate finance theory which says that leverage increases the riskiness of a firm’s equity as financial risk is compounded on top of the inherent total business risk (as proxied by ${{\sigma }_{V}}$).

There is a clear logical, mathematical, and economic link between the short-term default probability, the endogenous default boundary—which takes into consideration both long-term and short-term liabilities—with the MVC ratio. When the market value of a bank’s assets begin to approach the endogenous default boundary, $({\bar{V}})$, then default probabilities will rise and the MVC ratio will drop suggesting that the institution is undercapitalized, based on the market’s expectations and the nonlinear relationship between leverage and risk. When default probabilities rise above a certain level, the model can be used in an ex-post capacity to solve for how much capital the distressed financial institution would need to reduce the default probability to more acceptable levels. This is the Ex-Post Implied Capital Shortfall, or $\text{ EPICS }$, which represents the cash infusion needed to bring short-term default probability below the specified $\alpha$-level, where $\alpha$ is the highest acceptable short-term default probability. To isolate the effect that a cash infusion has on the default probability, first assume that V and ${{\sigma }_{V}}$ are the only parameters that change. The solvency condition as specified by the regulator is that $D{{P}_{{{T}_{1}}}}\left( V,{{\sigma }_{V}} \right) \le \alpha$.

Further assumptions underlying $\text{ EPICS }$ are that there are no transaction costs associated with raising the additional capital nor is any claim made about how the capital is raised; rather assume it comes entirely from some exogenous source. Finally, it is assumed that this fresh capital is held in cash on the bank’s balance sheet.

Let C denote the amount of fresh capital raised; after the capital infusion the bank has total assets valued at:

$$\begin{aligned} {{V}^{*}}=V+C. \end{aligned}$$

(14)

Since cash has no volatility and is completely uncorrelated with the risky assets in the bank’s portfolio, the new asset volatility can be computed as a weighted average:

$$\begin{aligned} {{\sigma }_{{{V}^{*}}}}=\left( \frac{V}{{{V}^{*}}} \right) {{\sigma }_{V}}+\left( \frac{C}{{{V}^{*}}} \right) 0=\left( \frac{V}{{{V}^{*}}} \right) {{\sigma }_{V}} . \end{aligned}$$

(15)

The cash assumption allows the capital infusion to simultaneously achieve two objectives: on the one hand, it increases the market value of the bank’s assets by an amount $\varDelta V=C$; at the same time it reduces the total risk of the bank’s portfolio. Both of these, in isolation, will result in lower default probabilities. The combination of increased asset value along with decreased asset risk gives a proverbial “one-two punch” in combating bank distress.

$\text{ EPICS }$ is therefore the solution to the following nonlinear optimization problem:

$$\begin{aligned} EPICS=\inf \left\{ C\,:\,D{{P}_{{{T}_{1}}}}\left( {{V}^{*}}, {{\sigma }_{{{V}^{*}}}}\right) \le \alpha \right\} \end{aligned}$$

(16)

subject to the constraints in Eqs. (14) and (15). That is, find the smallest C such that the short-term default probability is below the specified level, $\alpha$. This can be done numerically and, in fact, a simple search algorithm was used to perform the empirical analysis in Sect. 5.

The reason that an infimum is used in Eq. (16) is because the conventional wisdom is that banks prefer to have as little equity capital as possible. The existence of minimum capital requirements is a testament to this idea. It has traditionally been argued that capital is the more expensive financing choice and that banks can keep their cost of capital lower by using more debt in the capital structure. However, there is recent evidence against this argument (see Admati et al. (2010)). An alternative explanation is that too much equity capital runs counter to the essential roles of the bank as an asset transformer and liquidity provider. Regardless, it is understood that banks must maintain some specified level of capital to serve as a buffer against distress. For some acceptable level of default probability, the model provides a technique to determine how much additional capital is needed for controlling bank risk and maintaining solvency without being excessively deleterious to the bank’s core functions.

Lastly, one may make the objection that a bank holding excessive amounts of cash on the balance sheet for an extended period of time would be counterproductive. First, in practice it need not be tied up in cash but could be used to purchase Treasury securities or other very low risk, highly liquid instruments. Furthermore, it is important to remember that at this point the model is just being proposed in an abstract manner without the presence of market frictions including transaction costs. With that being said, once the bank’s default risk falls back down to acceptable levels that same cash can be used to purchase risky assets or make new loans. This allows the bank to grow its balance sheet in a safe and measured manner.

4 Data and methodology

4.1 Sample construction and data collection

The empirical study looks at the top 10 American bank holding companies (BHCs) in terms of assets. The sample is examined cross-sectionally, over time from 2005:Q1 to 2009:Q4. The sample of BHCs along with their year-end consolidated assets for 2009 are reported in Table 1. Not only were these the 10 largest BHCs at the time, but they were also among the first recipients and biggest beneficiaries of TARP funds which allows for the computation of the TBTF subsidy later in the analysis. Despite all being “large” there is some degree of variation, and almost separation into two cohorts, with the bottom six being smaller big banks and the top four being the largest big banks. The top four BHCs all have balance sheets in excess of $1 trillion, with the largest two—Bank of America and JP Morgan Chase,respectively—having over $2 trillion in assets; the bottom six in the sample average a little over $208 billion, which is far from small by any account, but perhaps in a different league from the top four banks.

Table 1 Table shows the ten Bank Holding Companies (BHCs) that are included in the study

Most of the data for this study comes from the FR Y-9C reports, which are submitted quarterly to the Federal Reserve by BHCs with consolidated assets of $500 million or more. The FR Y-9C reports contain very detailed information about the income and condition of BHCs, and are intended to parallel the Call Reports, which are submitted to the FDIC by commercial banks. The difference is that the Call Reports are at the individual commercial bank level rather than the holding company level; as such, there can be multiple entities that roll up into the BHC. The two reports do not reconcile even when aggregated due to non-commercial bank subsidiaries that are included in the consolidated figures for the BHCs. Since this study deals with BHCs, the FR Y-9C reports are the most appropriate source for the bank-specific data needed. The FR Y-9C data is accessed through the Bank Holding Company Database (BHCDB) in WRDS by RSSD ID number. Table 2 shows all of the data items that were used in the analysis. The table lists the data items, the source, and the variable code. In addition to the BHCDB, CRSP and Compustat were used to obtain market data and some supplementary financial statement data for the banks in the sample.

Table 2 Table shows the data items that were collected and used in the empirical analysis

Table 2 can be used to show how the model inputs and other relevant values were created from the BHCDB downloads. The sum of Item 1 through Item 4 gives the Total Deposits. Adding Total Deposits with Federal Funds Purchased (Item 5), Repurchase Agreements (Item 6), Commercial Paper (Item 7), and Other Borrowed Money with remaining maturity of 1 year or less (Item 8) gives the face value of the short-term senior debt, or $F_{1}$ in the model. The face value of the long-term junior debt is taken to be the sum of Item 9 and Item 10, Subordinated Notes and Debentures and Trust Preferred Securities, respectively; this is $F_{2}$ in the model. Another important quantity computed from the BHCDB download is the Risk-Based-Regulatory Capital ratio (RBC ratio), which will be compared to the Market Value Capital ratio (MVC ratio) which, as described earlier, is calculated as the market value of equity divided by the book value of assets. The RBC ratio is Tier 1 Capital (Item 11) divided by the Total Risk-Weighted Assets (Item 12). The market value of the bank’s equity is obtained from CRSP and is Stock Price (Item 13) multiplied by Shares Outstanding (Item 14).

The market value of equity and equity volatility are the two primary market inputs. Implied volatility, when available, is obtained from the Thomson Reuters Eikon system. This is preferable because option-implied volatility is forward looking and consistent with the objective of the structural credit risk model to quantify forward looking estimates of bank risk. Specifically, the 30 day at-the-money put option implied volatility is used, although the results are robust to other implied volatilities.²⁵ As for data availability, unfortunately the implied volatility can only be obtained from September 2007 through the end of the sample period. For the earlier part of the sample period, that is from January 2005 through the summer of 2007, volatility is computed as the three-month rolling standard deviation of daily log-price-relatives times the square root of 252.²⁶ Obviously, this is less desirable since by definition the historical volatility is backward-looking. However, prior to the Financial Crisis there was not a substantial difference between ex-post realized volatility and option implied volatility.²⁷

Finally, the risk-free rate data is from the Federal Reserve Bank of St. Louis FRED database. The one year Constant Maturity Treasury (CMT) yield was retrieved for every month over the sample period; the data point for the last day of each quarter was then used to proxy for the risk-free rate in the model. Monthly yields were downloaded from the FRED database and then matched to the FR Y-9C reports by date.

4.2 Methodology

The model in this paper uses both market information and the liability structure of the bank in question. At this point only equity market information is considered because every public BHC has traded equity with market information readily available and accessible. Specifically, the market information that is used as inputs into the model are the market value of the bank’s equity $\left( E_{t}\right)$ and the equity volatility $\left( {{\sigma }_{E}}\right)$. Recall that $E_{t}$ is the value of the compound call option on the bank’s assets, which is known in closed-form as a function of the bank’s asset value and asset volatility. The fact that the market value of equity and equity volatility are observable, while the true market value of the bank’s assets and asset volatility are unobservable gives rise to the inverse problem discussed above. Fortunately, the model allows for this problem to be solved rather easily and the solution yields the implied market value of the bank’s assets at any given time. The other required inputs to the model are from the bank’s liability structure. First, the face value of the short-term senior debt that is outstanding at a particular point in time, $F_{1}$, which serves as the first strike price in the compound option model. Next, the face value of the long-term junior debt, $F_{2}$, which is the sum of the outstanding subordinated notes and debentures and trust preferred securities, serving as the second strike price in the compound option model. The endogenous default boundary is, in fact, explicitly a function of the values of these inputs $F_{1}$ and $F_{2}$. The model also requires as inputs the average maturities of the outstanding short-term senior debt and the long-term junior debt; $T_{1}$ and $T_{2}$, respectively. Due to unavailability of this data it will be assumed that ${{T}_{1}}=1$ and ${{T}_{2}}=20$, which implies that the average maturity of the short-term senior debt is one year and the average maturity of the long-term junior debt is 20 years.²⁸ The last input is the risk-free rate.²⁹ In the empirical implementation of the model the risk-free rate is set equal to the one year CMT yield at the same point in time as the FR Y-9C report (i.e. 04-01-2005 for the end of 2005:Q1).

Once the inputs are obtained, the model must be calibrated because the closed-form solution gives the value of an observable market value (equity) but all of the outputs are in terms of an unobservable quantity: the market value of the bank’s assets. At any given time t, the observable equity value and equity volatility, $E_{t}$ and $\sigma _{E}$ , are related to the unobservable asset value and asset volatility, $V_{t}$ and $\sigma _{E}$, through the relationships given in Appendix A. Let $E\left( {{V}_{t}},{{\sigma }_{V}} \right)$ refer to the closed-form expression in Eq. (10).³⁰Also let ${{\sigma }_{E}}\left( {{V}_{t}},{{\sigma }_{V}},{{E}_{t}} \right)$ refer to the expression relating equity volatility to asset volatility given in Eq. (A.9). The goal is to simultaneously solve for $V_{t}$ and $\sigma _{V}$ in the following set of equations:

$$\begin{aligned}&E\left( {{V}_{t}},{{\sigma }_{V}} \right) =Equity \end{aligned}$$

(17)

$$\begin{aligned}&{{\sigma }_{E}}\left( {{V}_{t}},{{\sigma }_{V}},{{E}_{t}} \right) =Volatility \end{aligned}$$

(18)

where Equity is the market value of equity and Volatility is the calculated or measured equity volatility (using one of the two methods discussed above). For each quarter in the sample period there are 10 values of Equity and Volatility corresponding to each of the BHCs in the sample. The iterative procedure to solve for $V_{t}$ and $\sigma _{V}$ is therefore run for each of the 200 observations (10 BHCs times 20 quarters) to calibrate the model to the market data.

For each BHC-quarter the iterative procedure is defined as follows. First, the initial values are set as ${{V}_{0}}=Assets$ and ${{\sigma }_{{{V}_{0}}}}=Volatility*\left( \frac{Liabilities}{Assets} \right)$, where Assets and Liabilities are the book values of total assets and total liabilities, respectively, from the bank’s balance sheet; Volatility is the contemporaneous value for equity volatility from the market data. Then, $V_{t}$ is numerically solved so that Eq. (17) is satisfied. Although the compound call value computed by Eq. (10) will equal the current market value of the bank’s equity, the value of $\sigma _{E}$ will change as per Eq. (A.9). Consequently, $\sigma _{V}$ must then be numerically solved so that Eq. (18) is satisfied. This causes the compound call as a function of the asset value and new asset volatility to deviate from the market value of equity, so the procedure must be repeated until the results converge.

Once the conditions given by Eqs. (17) and (18) are satisfied for all 200 of the BHC-quarters, the model outputs can be used for analysis. While there are many outputs from the model, only two outputs are of particular interest for this study. The first is the short-term default probability which is computed in closed-form and given by Eq. (6). Since the short-term default probability takes the entire liability structure into account and is a function of the endogenous default boundary (${\bar{V}}$), this is the key output and metric that should be used in evaluating the bank’s capital needs. Recall, the exercise will be to find the minimum amount of capital infusion to ensure that the bank will be able to fund and pay the pending debt obligations, considering the size and timing of all future promised payments to creditors. It is, therefore, of utmost importance to know the likelihood that the most imminent obligations will be satisfied. Then, if the short-term default probability is high, the model can be used to solve for how much capital should be added to reduce the probability to a more comfortable level.

Some may argue that using market values in the management of bank capital will introduce too much noise into the process. It should be noted that the MVC ratios are not necessarily proposed to be used in lieu of RBC ratios but rather in conjunction with the existing measures of bank capital. When both the MVC ratio and the RBC ratio are analyzed with respect to one another there are many interesting patterns that can be identified. Furthermore, the MVC ratios are not as prone to manipulation or regulatory arbitrage and they provide a way to integrate market discipline into the management and oversight of bank capital.

5 Empirical results and analysis

After the model was run for all 10 BHCs over the 20 quarter sample period, resulting in 200 data points for each output, the results were averaged cross-sectionally and can be seen plotted in Figs. 2, 3, and 4. These aggregated results illustrate that, for the entire sample of BHCs, existing regulatory measures fell short precisely when conditions began to really deteriorate in the financial system.

Fig. 2

Figure shows the short-term default probabilities computed by the model for the 10 BHCs in the sample. The plot is of the cross-sectional average of the default probabilities and illustrates the evolution of the average market-implied default probabilities for the largest BHCs in America over the sample period

Fig. 3

Figure shows the cross-sectional average of the ratio of equity to equity volatility (blue solid line, left vertical axis) and the equity volatility (green dashed line, right vertical axis) for the 10 BHCs in the sample

Fig. 4

Figure shows the Risk-Based Capital (RBC) ratios and Market Value Capital (MVC) ratios over the sample period. The plot shows the cross-sectional average of these ratios for the 10 BHCs in the sample

The starting point in analyzing the results is the short-term default probabilities since they are, by construct, forward-looking and take the entire liability structure into account. Hence, they provide an objective, quantitative measure of the solvency of the financial institution using the most recent and relevant information. Taking the cross-sectional average across the 10 BHCs in the sample gives rise to a time-series of default probabilities. Figure 2 plots this time-series of average short-term default probabilities over the sample period. It is interesting to see that short-term default probabilities for the 10 largest BHCs were essentially zero up until the latter half of 2007 when the infamous subprime crisis began to incite the first wave of losses and fear throughout the financial system.³¹ Default probabilities show an initial rise in the first quarter of 2008, but by the summer of 2008 fears seem to have temporarily been subdued. However, in the third and fourth quarter of 2008 default probabilities began their dramatic ascent, peaking in the first quarter of 2009 when they almost reached 50%. The fact that short-term default probabilities come back down throughout the rest of 2009 is an indication that the stabilizing effects of TARP began to take hold. This peak in Q1:2009 is one reason why it is chosen as the point for the natural experiment to compare the market-implied capital needs with the TARP capital infusions to quantify the TBTF subsidy.

A plot of the market value of equity to assets and equity volatility tell a similar story and add further justification for Q1:2009 as an appropriate time to calculate $\text{ EPICS }$ and quantify the TBTF subsidy. Examining Fig. 3, it can be seen that the cross-sectional average of market value equity as a multiple of book value of assets (solid line, left vertical axis) reaches its highest point in Q4:2006 when equity volatility levels were still relatively low, although starting to rise. In fact the plot of equity volatility (dashed line, right vertical axis) appears almost as a mirror image of the equity value plot with the two lines crossing one another in the third quarter of 2007. The cross sectional average of equity volatility reaches its highest level in Q1:2009 at 128.37%. These opposing forces of dropping equity values and rising equity volatility are precisely the conditions in which the financial system as a whole needs to recapitalize. And the fact that they are opposing forces should not come as much of a surprise given the well-known leverage effect documented in the literature. This point is returned to later in the section, where it is noted that the compound option model does a particularly nice job at capturing the leverage effect as well as the high nonlinearities in these relationships.

Figure 4 shows the trajectories of the cross-sectional average MVC capital ratio along with the average RBC ratio, which is Tier 1 Capital divided by Total Risk-Weighted Assets (RWA) often referred to as the “core capital ratio”. On average the MVC ratios of the BHCs declined for most of the sample period while the RBC ratios stayed fairly constant over the sample period and even show a small increase at the end of 2008. The MVC and RBC ratios actually cross one another between the third and fourth quarters of 2008 and by the end of the sample period they converge. Convergence in the MVC and RBC ratios, can be viewed as a signal of bank distress to the extent that it stems from the MVC levels falling dramatically or potential evidence of window dressing and regulatory arbitrage on the part of the bank’s management to the extent that the convergence is driven by the RBC levels rising. Here it appears that both may be going on, although the former forces seem to be stronger than the latter. This pattern is similar to Figure 2 in Flannery (2014), where it is shown that book-value equity ratios rose slightly from 2004 to 2009, while two market solvency indicators—market-value equity ratios and CDS spreads—deteriorate after 2007, with the former dropping and the latter spiking.

The idea is that a bank’s MVC ratio falling to level at or below the RBC ratio is analogous to a firm’s book-to-market ratio going above 1 being indicative of distress (Fama and French 1995; Griffin and Lemmon 2002). Since the RBC ratio is essentially the book value of equity divided by a re-weighted asset value, then the implication is that the condition of the bank in question has deteriorated so severely that the market value of its common equity has fallen to levels such that it is in line with the book value of core capital. This should be concerning for bank managers, shareholders, and regulators. From the data, it can be seen that the MVC ratio declined from a maximum of 20.55% in the forth quarter of 2006, falling gradually at first but then dropping sharply to 12% in second quarter of 2008 and then further to 5.7% in the first quarter of 2009. As for the average RBC ratio rising from about 9% to over 11% in the fourth quarter of 2008, it could be reflective of one or more of the three following situations. First, it could be an indication of banks window dressing their true risk and leverage by moving risky assets off balance sheet and reclassifying assets as less risky to reduce the denominator of the ratio. This practice of “regulatory arbitrage” has been documented in the literature (Gordy 2003; Herring 2004; Calomiris and Mason 2004). An alternative explanation is that the elevation in RBC reflects the capital infusions from the initial TARP distributions. Lastly, it is also possible that the subtle increase in RBC ratios reflects the initial attempts of the banks to de-leverage after the failure of Lehman Brothers.

This is clear evidence that, as measured by the RBC ratios, the largest BHCs in the U.S. were by regulatory standards indeed “well-capitalized”; however, the MVC ratios tell a different story as they fell to less than one-third of their maximum values at the depth of the crisis. While both equity values and implied asset values were falling during this time, volatility was rising making this a complex nonlinear relationship. Fortunately, the compound option model sheds light on the dynamics of what was going on and provides some valuable insight into the benefit of using market information to supplement the existing regulatory tools. Equity—as a compound call option—is a convex function on the bank’s assets.³² This means that although both equity values and asset values were falling, they were not doing so at the same rate. In fact, because of the convexity, the dollar amount the equity decline will necessarily be less than the dollar amount of the asset decline. However, because of leverage, equity may be orders of magnitude less than assets so in relative changes equity drops by much more thereby eroding the bank’s buffer in market value terms. The higher the leverage, the more extreme is the effect. The compound option model captures this dynamic very well, whereas looking at static regulatory capital measures gave no indications that this was happening.

Increasing volatility during this time also added to the complex and highly nonlinear effect, which is not reflected by regulatory ratios. When volatility rises, option theory is clear that the value of both call and put options increase. The bank’s equity, being modeled as a compound call option, therefore would increase in value when volatility rises which seems a bit counterintuitive. However, as noted in Geske (1979) the compound option model is one of the only structural credit risk models that explicitly takes into account the well-known “leverage effect”, or the phenomenon that stock prices and stock volatility move in opposite directions.³³ Precisely how this is captured by the compound option structural model has only recently been examined more closely empirically within the compound option model (see Geske et al. 2016). This helps to further explain what was happening to the largest banks as the financial crisis began to unfold. When equity volatility rises, as was observed in the third and fourth quarters of 2008, then the MVC falls. Simply rearranging Eq. (11) shows the inverse relationship between equity volatility and the MVC:

$$\begin{aligned} {{\sigma }_{E}}=\frac{\partial E}{\partial V}\,\frac{1}{MVC}{{\sigma }_{V}}. \end{aligned}$$

(19)

Thus, another way in which the structural credit risk model adds value to the static regulatory models is in its incorporation of market risk in real-time, capturing the complex and highly nonlinear relationships. In theory, increasing risk on the banks’ balance sheets should have found their way into the weighting scheme for computing RWA, but there were neither the controls nor incentives to make sure this was done and, even if they were, they would not be explicitly connected to a market determined parameter such as volatility.

The MVC ratio and short-term default probabilities exhibit a fairly strong negative correlation. Looking at Figs. 2 and 4 together, one can see that the average MVC ratio falls to its lowest level in the first quarter of 2009, while the average short-term default probability peaks at this same time. Consistent with the inference drawn from the cross-sectional average, this is actually the period where all but one of the 10 BHCs reached their maximum default probability. The individual risk-neutral short-term default probabilities for Q1:2009 are given in Table 3; the only BHC that was off from its maximum was Bank of New York Mellon, though not by much. Bank of New York Mellon’s risk-neutral short-term default probability was at its maximum of 25.94% in the forth quarter of 2008 whereas the model returns a risk-neutral short-term default probability of 21.5% in the first quarter of 2009. These short-term default probabilities may appear to be exorbitantly high, but it illustrates two important features of the analysis. First, when there is a positive risk premium, the risk-neutral default probability (RNDP) will be greater than the actual or physical default probability. In fact, Giesecke et al. (2011) show empirically that the RNDP tends to be about twice the actual default frequency. Therefore, a rough rule of thumb, without having to perform a change of measure or estimate the risk premium, is to divide the RNDP by two. The second point is that the extraordinarily high market-implied default probabilities is precisely what makes this point in time ideal for quantifying the TBTF subsidy.

Table 3 Table shows the risk-neutral short-term default probabilities, denoted $DP\left( T_1\right)$, for each of the ten BHCs at the end of the first quarter of 2009

The model suggests that in March 2009 the market was still pricing failure of these banks at very high levels, ranging from 21.5% (Bank of New York Mellon) to 84.7% (Citigroup). But within six months all but one BHC had risk-neutral default probabilities below 5.5% (the one exception was Citigroup with a short-term default probability that was below 19.5%, which was still a reduction to 77% of its maximum value). So one conclusion could be that the market finally absorbed the effects of TARP by the end of 2009. Therefore, the cumulative amount of the capital infusions received by each BHC would have been enough to prevent failure. So the experiment here is to compare how much capital each BHC would have needed in the absence of government support to stay solvent with total amount that each one did receive to stave off failure. The former is computed using the structural credit risk model and is precisely the $\text{ EPICS }$ measure described in Sect. 3.5. The latter is the sum of all TARP distributions paid to each of the ten BHCs, through either the CPP or TIP. The TBTF subsidy is then defined as the difference between how much the bank should have received and how much they did receive.

For this empirical analysis and experimentation the $\alpha$-level was set to 5%. Recall that $\alpha$ represents the default probability that serves as a trigger for capital infusion, that is the level above which the bank would need additional capital to bring default probabilities back down to more “reasonable” levels (the assumption being that $DP_{T_{1}} \le 5\%$ is “reasonable” and can be thought of within the context of a one-year 95% VaR analysis). The nonlinear optimization problem specified by Eq. (16) was solved numerically. The results, in billions of dollars and as a percentage of total assets, are presented in Table 4. It is not surprising that in dollar amounts the four largest BHCs—Bank of America, Citigroup, JPMorgan Chase, and Wells Fargo—required the most capital to restore stability and calm the market. When viewed as a percentage of their respective Total Assets in that quarter, their results are not much different than the other BHCs in the sample. Together the model suggests that all 10 BHCs would have required a combined capital infusion of almost $1.3 trillion. This reinforces the argument that has been made throughout the paper that these financial institutions were dramatically undercapitalized in market value terms. For perspective, the combined assets of these 10 BHCs at the end of the first quarter of 2009 was over $8.7 trillion.

Table 4 Table shows the $\text{ EPICS }$ value calculated in the first quarter of 2009 in billions of dollars and as a percentage of Total Assets for each BHC in the sample the $\text{ EPICS }$ is the minimum capital infusion that would have been needed, given market conditions at the time, to reduce default probabilities below 5%

By May 2009 the U.S. government had invested almost $240 billion into the banking sector (this does not include more than $40 billion of TARP funds to AIG during this same period of time);³⁴ the 10 BHCs in the sample accounted for $171.6 billion. The TARP distributions and repayments as of September 2010 are shown in Table 5.

Table 5 Table  shows the TARP payments made to the ten BHCs in the sample, both how much and when, as well as repayments. An asterisk next to the amount indicates that the distribution was part of the Targeted Investment Program (TIP); the rest are part of the more familiar Capital Purchase Program (CPP).

One interesting point is that based on the $\text{ EPICS }$ measure even the most distressed bank, Citigroup, only requires a capital infusion of roughly 20% of its asset value. Considering the post-crisis era calls from critics to increase bank capital levels up to 30% (see, for example, Admati (2014)) this does not seem too unreasonable. The other astonishing feature is how much less the total TARP distributions were as a percentage of asset value. They range from 1.2% for JP Morgan Chase (at this time they are the second biggest BHC in the sample behind only Bank of America) to 2.71% for SunTrust. The difference between the two amounts—$\text{ EPICS }$ minus TARP—is the TBTF subsidy.

Figure 5 shows the breakdown of $\text{ EPICS }$ (dotted light bar), TARP (solid dark bar), and the TBTF subsidy (the difference between the two). The BHCs are ordered along the horizontal axis from largest to smallest, by assets. Looking at Fig. 5, there is not a clear monotonic relationship between the TBTF subsidy and bank size. Surely, it stands out that Bank of America, Citigroup, and Wells Fargo, three of the four largest BHCs in the sample, received much less capital than the model indicates; but so does State Street Bank, which is the smallest BHC in the sample. There is one other element that needs to be considered in the analysis and that is the extent to which the BHCs rely on short-term volatile funding.

Fig. 5

Figure shows the capital needs for each of the 10 BHCs in the sample as of the first quarter of 2009. The light bar shows the Ex-Post Implied Capital Shortfall, or $\text{ EPICS }$, which is solved for using the structural credit risk model. This represents the amount of additional capital that the model suggests each bank would have needed in the first quarter of 2009 to reduce its default probabilities below the 5% level. This is compared to the amount of capital that was received in reality through TARP (shown as the dark bar). The difference between how much of a capital infusion that was implied by market prices at the time—$\text{ EPICS }$—and the amount of capital that was received—TARP—is interpreted as the Too-Big-To-Fail Subsidy as discussed in the paper

Banks’ reliance on short-term volatile funding has been identified as a source of risk in the Financial Crisis and that banks financing their operations with a greater proportion of short-term debt should be required to set aside more capital.³⁵ Figure 6 shows a bubble plot of the TBTF subsidy against the average amount of short-term volatile funding employed by each BHC over the sample period. The short-term volatile funding (STVF) is constructed in the same way as $F_1$ in the model. This is consistent with similar measures in the literature (e.g. Bassett et al. (2015)). Another feature of this bubble plot is that the diameter of each bubble is proportional to the average Total Assets for the respective BHC over the sample period. Because, naturally, larger banks are going to employ dollar-for-dollar more leverage, the STVF measurement is going to be skewed. Therefore, both axes are given in logarithmic scale. Also, superimposed over the plot are the median values for the TBTF subsidy ($26.4 billion), as a horizontal dashed line, and STVF ($184 billion), as a vertical dashed line.

Figure 6 shows that there is a positive relationship between STVF and the TBTF subsidy. The fact that the four largest BHCs in the sample are in the upper right quadrant should not come as much surprise: these four banks are the biggest in terms of assets, but also employ the most short-term leverage, and were associated with some of the largest TBTF subsidies. However, there is another interesting pattern that emerges from this plot occuring just at the margin between the biggest large BHCs (BAC, C, JPM, and WFC) and the smaller large BHCs. The top five BHCs in the sample in terms of STVF, which are not necessarily the largest in terms of assets as US Bank is about $20 billion smaller than PNC bank, are also the top five BHCs in terms of their TBTF subsidy. The remaining five BHCs, including the fifth largest by assets PNC, are clearly in the bottom 50th percentile of the sample for both STVF and the TBTF subsidy. Also interesting is that State Street is the smallest bank in the sample by assets, but yet has more STVF and a higher TBTF subsidy than SunTrust and Capital One Financial which are just above it in terms of asset ranking. All of this evidence combined supports the case for increased capital requirements not only for the biggest banks, but also for the banks that rely more heavily on these short-term volatile sources of funding.

Fig. 6

Figure shows a bubble plot of the TBTF Subsidy as a function of the amount of Short-Term Volatile Funding (STVF) that each BHC relied on at the time as well as the size of each BHC in terms of Total Assets. There is a positive relationship between the size of the bank and the TBTF subsidy, represented by the bubble diameter increasing as they get higher in the coordinate plane. There is also a clear separation between the three largest BHCs which have an estimated TBTF subsidy of more than $100 billion. Another interesting pattern that emerges is that there is also a positive relationship between the amount of STVF (defined in the paper) and the TBTF subsidy, which has important policy and regulatory implications. For instance, big banks that rely more heavily on these volatile sources of funding should be required to hold more capital to avert a crisis

6 Conclusion

This paper proposed the use of a structural credit risk model to analyze the capital position of banks during the Financial Crisis and understand capital needs within the context of the TBTF problem. The approach has many features that make it attractive relative to the existing methods for determining the amount of capital needed by financial institutions during both crisis and non-crisis times. First, the structural credit risk model takes both the asset risk and the liability structure into account. Second, the model uses market information and, by definition, is forward-looking. This is in contrast to the existing static measures that use historical data. Third, the model has endogenous default which is a critical feature in determining the amount of capital needed by a financial institution.

The model yields several useful metrics for evaluating the solvency and capital adequacy of financial institutions including the Market Value Capital (MVC) ratio. It was also shown that the driving force behind the capital analysis for financial institutions is the short-term default probability. Although this may seem like a myopic approach for risk management of banks it is quite the opposite. The short-term default probability computed by the model contains all relevant information including asset risk, endogenous default, and the complete liability structure—i.e. it is a function of not only the amount of debt in the capital structure, but the mix of short-term versus long-term debt in funding the bank’s operations.

The model gives rise to many interesting insights about financial institutions, both theoretically and empirically, during the Financial Crisis. The model captures the complex, nonlinear relationship among volatility, default probabilities, and bank capital. The Market Value Capital (MVC) ratios can be compared with the Risk-Based Capital (RBC) ratios to identify patterns indicating that a bank might be on the verge of distress and can also identify distress in the entire banking system. Additionally, the model can be used to compute the $\text{ EPICS }$, which is the amount of capital needed to bring short-term default probabilities below a specified acceptable level. Lastly, by comparing the $\text{ EPICS }$ to the TARP capital infusions in 2008–2009, the model provides a novel way to quantify the TBTF subsidy during the Financial Crisis. It was shown that the TBTF subsidy varies not only with bank size but also with the reliance on short-term volatile funding (STVF). These findings suggest some powerful prescriptive policy recommendations including time-varying capital ratios tied to market values which may be used in conjunction with or in addition to RBC ratios, as well as differential capital requirements for larger banks and banks that rely more heavily on STVF. This could provide an effective mechanism for internalizing the negative externalities associate with TBTF.

The model does not allow for asset sales, which could be one additional tool that a distressed bank could use when undercapitalized and in the midst of a crisis. However, the risk of fire sales and liquidity spirals arise which are beyond the scope of the current model. The model could potentially be expanded to incorporate market frictions such as liquidity, explicit distress costs, and asymmetric information. However, the inclusion of any one of these market frictions would be extremely nontrivial and it was shown that, even in this primitive form, the model provides significant insight into the management and analysis of bank capital and risk.

Appendix: Valuation of corporate securities in the compound option model

To value the securities within the compound option framework it is helpful to visualize the default process as a binomial tree. In Fig. 1 the solid nodes represent survival states, whereas the dashed nodes represent default states. The accompanying table shows the value of the corporate securities (equity, junior debt, and senior debt) at each node. Solving the expectations at node A results in the closed-form valuation equations below.

The value of the securities can be determined at node A (time $t=0$) by taking the discounted expected value of the future cash flows at each of the subsequent nodes. For equity and junior debt this results in nested expectations. Consequently, the assumption that Geometric Brownian Motion is the underlying stochastic process ensures that the solution is a function of the bivariate normal distribution, which is very manageable.

Now, for any time t, $0\le t<{{T}_{1}}$, evaluating the expectations at t gives the closed-form expressions for valuing all of the bank’s claims. Equity is a compound call on the bank’s assets in that shareholders have a claim to

$$\begin{aligned} \mathop {{\mathbb {E}}}\left[ {{e}^{-r{{\tau }_{1}}}}\,\max \left\{ {{E}_{{{T}_{1}}}}-{{F}_{1}},0 \right\} \left| {{V}_{t}} \right. \right] , \end{aligned}$$

(A.1)

where ${{E}_{{{T}_{1}}}}$ is equal to the value of a European call option at time ${T}_{1}$, which is not known at time t. Let ${{\tau }_{1}}=\left( {{T}_{1}}-t \right)$ be the time between t and the short-term senior debt maturity $T_{1}$ and${{\tau }_{2}}=\left( {{T}_{2}}-t \right)$ be the time between t and the long-term junior debt maturity $T_{2}$. The expectation given in Eq. (A.1) is equal to:³⁶

$$\begin{aligned} {{E}_{t}}={{V}_{t}}\,{{N}_{2}}\left( h_{1}^{+},h_{2}^{+};\,\rho \right) -{{F}_{2}}{{e}^{-r{{\tau }_{2}}}}\,{{N}_{2}}\left( h_{1}^{-},h_{2}^{-};\,\rho \right) -{{F}_{1}}{{e}^{-r{{\tau }_{1}}}}N\left( h_{1}^{-} \right) \end{aligned}$$

(A.2)

where $h_{1}^{+}=\frac{\ln \left( \frac{{{V}_{t}}}{{{\bar{V}}}} \right) +\left( r+\frac{{{\sigma }^{2}}}{2} \right) {{\tau }_{1}}}{\sigma \sqrt{{{\tau }_{1}}}}$,

$h_{1}^{-}=\frac{\ln \left( \frac{{{V}_{t}}}{{{\bar{V}}}} \right) +\left( r-\frac{{{\sigma }^{2}}}{2} \right) {{\tau }_{1}}}{\sigma \sqrt{{{\tau }_{1}}}}=h_{1}^{+}-\sigma \sqrt{{{\tau }_{1}}}$,

$h_{2}^{+}=\frac{\ln \left( \frac{{{V}_{t}}}{{{F}_{2}}} \right) +\left( r+\frac{{{\sigma }^{2}}}{2} \right) {{\tau }_{2}}}{\sigma \sqrt{{{\tau }_{2}}}}$,

$h_{2}^{-}=\frac{\ln \left( \frac{{{V}_{t}}}{{{F}_{2}}} \right) +\left( r-\frac{{{\sigma }^{2}}}{2} \right) {{\tau }_{2}}}{\sigma \sqrt{{{\tau }_{2}}}}=h_{2}^{+}-\sigma \sqrt{{{\tau }_{2}}}$, $N\left( \centerdot \right)$ denotes the cumulative standard normal distribution,

${{N}_{2}}\left( \centerdot \right)$ denotes the cumulative bivariate standard normal distribution, and correlation $\rho =\sqrt{{}^{{{\tau }_{1}}}\!\!\diagup \!\!{}_{{{\tau }_{2}}}\;}$which follows from the properties of Brownian Motion.

${\bar{V}}$ is the endogenous default boundary, derived in Sect. 3.4.

The senior debt is to be paid at time $T_{1}$. If the market value of the assets at that time is greater than ${\bar{V}}$, then senior debt holders will be paid the amount $F_{1}$ in full. However, if the market value of the assets is less than or equal to ${\bar{V}}$ and less than the face value of the senior debt, then there is [total] default at time $T_{1}$. In this case, the assets will be liquidated and senior debt holders will only recover a portion of what they are owed; specifically they will recover the market value of the assets at the time of default, $T_{1}$. Thus, the value of the short-term senior debt at time t is given by the expectation

$$\begin{aligned} \mathop {{\mathbb {E}}}\left[ {{e}^{-r{{\tau }_{1}}}}\,\,\min \left\{ {{V}_{{{T}_{1}}}},{{F}_{1}} \right\} \left| {{V}_{t}} \right. \right] . \end{aligned}$$

(A.3)

It is relatively straightforward to show that the expectation given in Eq. (A.3) is equal to

$$\begin{aligned} {{S}_{t}}={{V}_{t}}\left[ 1-N\left( {{k}^{+}} \right) \right] +{{F}_{1}}\,{{e}^{-r{{\tau }_{1}}}}N\left( {{k}^{-}} \right) , \end{aligned}$$

(A.4)

where ${{k}^{+}}=\frac{\ln \left( \frac{{{V}_{t}}}{{{F}_{1}}} \right) +\left( r+\frac{{{\sigma }^{2}}}{2} \right) {{\tau }_{1}}}{\sigma \sqrt{{{\tau }_{1}}}}$ and ${{k}^{-}}=\frac{\ln \left( \frac{{{V}_{t}}}{{{F}_{1}}} \right) +\left( r-\frac{{{\sigma }^{2}}}{2} \right) {{\tau }_{1}}}{\sigma \sqrt{{{\tau }_{1}}}}={{k}^{+}}-\sigma \sqrt{{{\tau }_{1}}}$.

Then, finally, there is the bank’s junior debt which has the interesting property that when asset values are well above the default boundary they are a fixed claim and their prices behave like debt, but in times of distress they are a residual claim and their prices behave like equity. The model captures this characteristic of bank subordinated debentures well. The value of the long-term junior debt at time t is given by the expectation:

$$\begin{aligned} {\mathbb {E}}\left[ {{e}^{-r{{\tau }_{1}}}}\left( \left( {J}_{{T}_{1}}\,\cdot {\mathbb {I}}_{\left\{ {V}_{{T}_{1}}>{\bar{V}} \right\} } \right) +\left( \max \left\{ {V}_{{T}_{1}}-{{F}_{1}},0 \right\} \cdot {\mathbb {I}}_{\left\{ {V}_{{T}_{1}}\le {\bar{V}} \right\} } \right) \right) \left| {V}_{t} \right. \right] \end{aligned}$$

(A.5)

where ${\mathbb {I}}_{\left\{ V>{\bar{V}} \right\} }$ is the indicator function that equals 1 if $V>{\bar{V}}$ and 0 otherwise.

To obtain the closed-form solution for the long-term junior debt the expectation given in Eq. (A.5) can be evaluated directly or, since the expectation for short-term senior debt is considerably more straightforward, the fact that ${{V}_{t}}={{E}_{t}}+{{J}_{t}}+{{S}_{t}}$ can be used to solve for ${{J}_{t}}={{V}_{t}}-{{E}_{t}}-{{S}_{t}}$. Subtracting Eqs. (A.2) and (A.4) from $V_{t}$ gives:

$$\begin{aligned} {{J}_{t}}={{V}_{t}}\left[ N\left( {{k}^{+}}\right) -{{N}_{2}}\left( h_{1}^{+},\,h_{2}^{+};\,\rho \right) \right] +{{F}_{1}}{{e}^{-r{{\tau }_{1}}}}\left[ N\left( h_{1}^{-}\right) N\left( {{k}^{-}}\right) \right] +{{F}_{2}}{{e}^{-r{{\tau }_{2}}}}{{N}_{2}}\left( h_{1}^{-},h_{2}^{-};\,\rho \right) \end{aligned}$$

(A.6)

where all of the terms are as previously defined in Eqs. (A.2) and (A.4).

Although asset volatility is assumed to be constant, equity volatility is not constant but rather changes as a function of asset value and other parameters in the model. This was first shown by geske-1979. Equity, being a compound option on the underlying asset, has its own stochastic dynamics which can be specified using Ito’s Lemma. From the Ito expansion, the volatility term for equity is

$$\begin{aligned} {{\sigma }_{E}}=\frac{\partial E}{\partial V}\,\frac{V}{E}{{\sigma }_{V}}. \end{aligned}$$

(A.7)

The partial derivative $\frac{\partial E}{\partial V}$ can be found by differentiating Eq. (A.2) with respect to asset value and is known as the “equity delta”:

$$\begin{aligned} \frac{\partial E}{\partial V}={{N}_{2}}\left( h_{1}^{+},h_{2}^{+};\,\rho \right) . \end{aligned}$$

(A.8)

Plugging Eq. (A.8) into Eq. (A.7) gives

$$\begin{aligned} {{\sigma }_{E}}={{N}_{2}}\left( h_{1}^{+},h_{2}^{+};\,\rho \right) \,\frac{V}{E}{{\sigma }_{V}}. \end{aligned}$$

(A.9)

This equation says that, holding everything else constant, as more leverage is introduced the equity volatility becomes greater than the asset volatility. This leverage effect is consistent with standard corporate finance theory which says that leverage increases the riskiness of a firm’s equity as financial risk is compounded on top of the inherent total business risk (as proxied by ${{\sigma }_{V}}$).