The mechanisms and properties of inertial microfluidics: from fundamental models to biomedical applications

Abstract

With continuous efforts of researchers all over the world, the field of inertial microfluidics is constantly growing, to cater to the requirements of diverse areas like healthcare, biological and chemical analysis, materials synthesis, etc. The scale, automation, or unique physics of these systems has been expanding their scope of applications. In this review article, we have provided insights into the fundamental mechanisms of inertial microfluidics, the forces involved, the interactions and effects of different applied forces on the suspended particles, the underlying physics of these systems, and the description of numerical studies, which are the prime factors that govern designing of effective and practical devices.. Further, we describe how various forces lead to the migration and focusing of suspended particles at equilibrium positions in channels with different cross-sections and also review various factors affecting the same. We also focus on the effect of suspended particles on the flow of fluids within these systems. Furthermore, we discuss how Dean flows are created in a curved channel and how different structures affect the creation of secondary flows, and their application to mixing, manipulating, and focusing particles as fluid. Finally, we describe various applications of microfluidics for diagnostic and other clinical purposes, and discuss the challenges and advancements in this field. We anticipate that this manuscript will elucidate the basics and quantitative aspects of inertial fluid dynamic effects for application in biomedicines, materials synthesis, chemical process control, and beyond.

Graphical abstract

1 Introduction

Until recently, there was a widespread belief that all useful and practically achievable flows in the microfluidic systems operate not only within the laminar flow regime but also in the Stokes flow regime ($\mathrm{Re}<1$) (Squires and Quake 2005) The Stokes flow assumption is made where the channel dimension, H, is very small. However, for water ($\rho$ = 1000 kg/m³, $\mu$ = 0.001 Pa.s) in a channel having the diameter of 100 mm, the Reynolds number approaches 1 for a low mean flow velocity of 0.01 m/s (Di Carlo 2009) Neglecting inertia while using the Stokes flow approximation for this reasonably common situation can result in incorrect results. Due to this assumption, the inertia of the fluid is never taken into consideration in the Navier–Stokes equation, which can lead to linear and time-reversible equations of motions for the Newtonian fluid. However, the significance of intermediate flow, for $1 \sim <\mathrm{Re}<\sim 100$ has been recently highlighted, wherein nonlinear and irreversible motions of fluids and particles within microchannels are observed (Di Carlo et al. 2007). This regime, having finite inertia and viscosity of the fluid, still lies in the laminar flow region ($\mathrm{Re}$ < < 2300), which offers a definite nature. Thus, both fluid and particles within the microfluidic channel can be controlled. The velocity gradient across the particle or the obstacle length scale is very important to generate inertial effects because it directly influences the inertial lift force by the magnitude of lift coefficient or secondary flow magnitude, respectively, which will be discussed in further sections of this manuscript (Amini et al. 2014).

Segre and Silberberg were the first to observe the inertial migration or tubular pinch effect. They observed that the spherical particles migrated to an annulus located at 0.6 times the radius of a cylindrical channel between the center line and wall (Segré and Silberberg 1961, 1962). Thereafter, many scientists have worked hard to understand the physics behind this phenomenon through experimental studies, theoretical analyses, and numerical simulations. For example, Saffman (1965) and (McLaughlin (1991) studied the lift force acting on a small sphere in an unbounded linear shear flow. Cox and Hsu (1977) using the theory developed by Cox and Brenner (1968) obtained the analytical expressions for the migration velocity of a particle settling parallel to a vertical wall. Jeffrey and Pearson (1965), Eichhorn and Small (1964) conducted experiments on the inertial movement of non-neutrally buoyant particles within a vertical channel flow. They demonstrated that when a particle leads an undisturbed flow, it migrates toward the channel walls, whereas when its velocity is low, it migrates in the opposing direction. Ho and Leal (1974) investigated the movement of a neutrally buoyant sphere in a planar flow confined by two flat walls. The laser-Doppler technique was used to understand the interaction between the particles and the wall, in a bounded flow, which was demonstrated with the help of microspheres and platelets (Uijttewaal et al. 1994). The regular perturbation method was used by Vasseur and Cox (1976) and Cox and Hsu (1977) to evaluate the lift in a linear and parabolic wall-bounded flow. Feng et al. (1994) simulated the behavior of a two-dimensional circular particle in Couette and Poiseuille flows numerically. Patankar et al. (2001) and Joseph and Ocando (2002) modeled the motion of a two-dimensional circular particle in Newtonian and viscoelastic fluids in plane Poiseuille flows perpendicular to gravity. They demonstrated that particles with intermediate densities have numerous equilibrium states, which can be stable or unstable. Di Carlo et al. (2009) studied the focusing of particles in square channels by varying Reynolds numbers between 20 and 80 and the ratio of particle size to channel size between 0.05 and 0.2. In contrast to circular pipes, which focus particles to an annulus, they discovered that square channels focused particles to four symmetrically organized positions.

We have reviewed the work done by these scientists and researchers in this manuscript. The manuscript describes the various forces that act on particles, causing them to migrate and focus at their equilibrium positions. It also discusses the various mechanisms that can be used to induce lateral migration and particle control due to fluid inertia, fluid viscoelasticity, particle shape, and particle deformability within straight microchannels. Also reviewed are the inter-particle interactions and how particles can be used to manipulate the fluid in straight microchannels. An overview has then been presented of how the channels could be modified to control both, particles and fluids, by adding microstructures such as micropillars, creating microgrooves, or creating curved channels, which may facilitate the creation of net secondary flow. We have also presented an overview of the numerical methods to simulate particle motion in Newtonian and Non-Newtonian fluids. This review presents an in-depth study of the fundamentals and the recent developments in the field, pertaining to the numerical simulation and its challenges, thus giving a good mix of references from the initial mechanisms given by the old researchers to the improvements made by the newest ones. Finally, the manuscript also presents a summary on how the concept of inertial microfluidics and its employment for microfluidic device design may be applied in the biomedical field, like for diagnosis of infectious diseases and for studying the migration of cancer cells.

2 The fundamental mechanism in inertial microfluidics

During a practical application of inertial microfluidics, suspended particles are introduced into the microfluidic channels. Several forces act on the suspended particles within the fluid domain, which are used to determine the motion of the suspended particles along the axial and lateral directions of the microfluidic channel, as depicted in Fig. 1. Among the applied forces, a major force is the viscous drag force which acts along the mainstream of the flow direction. As the particle moves in a fluid, it pushes the fluid in front of it and creates a region of higher pressure in front of the particle which creates a drag force, opposing the motion of particle. Besides, several other lift forces act in the lateral direction. The fluid above the fluid flows with a higher velocity, while the lower one has a low velocity, thus a pressure gradient is created, according to Bernoulli’s principle, giving an upward lift force i.e., rotational lift force, slip-induced lift force, shear gradient lift force, secondary flow drag force (Ho and Leal 1974; Martel and Toner 2014). During practical application of microfluidics system, some of these forces, which are dependent on the property of the working fluid medium, the shapes of the particles as well as the structure of the microchannels, are neglected. The different forces applied on suspended particles in the fluid domain have been discussed in this section.

Fig. 1

Mainstream (drag) and lateral (lift) forces on a particle in a fluid

2.1 Viscous drag force

Drag force is mainly formed due to the relative motion between suspended particles and fluid particle elements. In addition, drag force also arises due to some of the following reasons:

• 1. Wall shear stress It acts in a tangential direction over the suspended particle surface and is caused by the frictional forces that arise due to the suspended particle's viscosity, which is also dubbed as skin or friction drag. The shear stress, in general is defined as, the component of a stress that is co-planar with a material cross-section. It arises from the shear force, the component of force vector parallel to the material cross- section.

• 2. Pressure stresses These stresses basically act perpendicular to the suspended particle’s surface and are formed by how pressure, caused by the movement of the fluid particle elements, is distributed around the particle. These stresses are also defined in terms of form drag.

In other words, the skin drag is more significant for a larger body surface area aligned with the mainstream fluid flow direction. So, the viscous drag force related to the moving suspended spherical particles within the fluid domain can be expressed as stated in Eq. (1) as,

$$F_{{{\text{drag}}}} = S \times f_{{{\text{drag}}}} = \frac{{\pi a^{2} f_{{{\text{drag}}}} }}{4},$$

(1)

where, ${F}_{\mathrm{drag}}$ is the viscous drag force on the suspended particle (N); S is the cross-sectional area of the suspended particle (m²); ${f}_{\mathrm{drag}}$ is the viscous drag coefficient; a is the diameter of the suspended particle within the fluid domain (m), respectively.

The expression of the viscous drag coefficient has different mathematical expressions depending upon the range and value of the Reynolds number of the operating particle. But the viscous drag coefficient is most widely used in the Stokes drag equation (Richardson et al. 2002) when the relative velocity between the fluid particle elements and the suspended particles is very low (Richardson et al. 2002; Michaelides 2006). The viscous drag coefficient and drag force are defined in Eqs. (2–3):

$$f_{{{\text{drag}}}} = \frac{{12\mu v_{t} }}{a},$$

(2)

and

$$F_{{{\text{drag}}}} = 3\pi \mu v_{t} a,$$

(3)

where, $\mu$ is the dynamic viscosity of fluid (Pa.s); ${v}_{t}$ is the relative velocity of fluid particle elements to suspended particles (m/s).

In the context of applications of inertial microfluidics, the drag force has the following two major components, namely,

• 1. Mainstream fluid flow direction-based drag force: It is formed due to the axial velocity difference between the surrounding fluid particle elements and the suspended particles

• 2. Lateral fluid flow direction-based drag force: It arises due to the secondary flow induced by the curvature of the microchannel channel or the flow disturbance structure.

2.2 Description of lift forces acting on the suspended particles

In addition to the drag force, lift forces act on a suspended particles within a microfluidic channel, in a direction perpendicular to the direction of the flow. Typically, the final lateral positions of the suspended particles are determined by four different lift forces, namely Magnus force (a rotation-induced lift force acting on a particle rotating in the fluid domain), Saffman force (caused due to the interaction of slip velocity and shear force), the wall lift force, which creates the velocity gradient in the fluid flow, and the shear gradient lift force, that arises from the curvature of the fluid’s velocity profile. In the subsequent sections, we have elaborately discussed the physical insights underlying these forces and the essential equations that govern them.

2.2.1 Magnus force: rotation-induced lift force

To understand the physical behavior of rotationally induced lift force, we consider a stationary cylinder that is rotating within the viscous fluid flow medium with a uniform velocity $\overrightarrow {{U_{{\text{f}}} }}$. Here, the proposed system moves with constant angular velocity, $\vec{\Omega }$. The velocity at the top of the cylinder is higher than that at the bottom surface of the cylinder. Further, we assume a no-slip boundary condition (no-slip boundary condition means that the velocity of the fluid relative to a solid boundary is zero. In general, the slip boundary condition assumes that there is a relative motion between the fluid and the solid boundary, that is there is a “slip”) of the fluid to understand the respective force. Thus, based on Bernoulli's principle, the pressure exerted at the bottom of the cylinder is higher than that at the top. This results in a lift force, that helps to lift the cylinder. This lift force, $\overrightarrow {{F_{{{\text{LR}}}} }}$, acting on the surface of the cylinder has been stated in Eq. (4) (Michaelides 2006)

$$\overrightarrow {{F_{{{\text{LR}}}} }} = \pi \rho_{{\text{f}}}^{2} a\overrightarrow {{U_{{\text{f}}} }} \times \vec{\Omega },$$

(4)

where, $\overrightarrow {{F_{{{\text{LR}}}} }}$ is the rotation induced lift force (N); $\rho_{{\text{f}}}$ is the density of the fluid (kg/m³); a is the diameter of cylinder in fluid i.e., the suspended particle (m); $\overrightarrow {{U_{{\text{f}}} }}$ is the average velocity of the fluid (m/s).

In a similar way, in the context of rigid sphere, rotating with angular velocity $\vec{\Omega },$. a lateral lift force is formed due to the transverse pressure difference. This lateral ft force is also called Magnus force, as has been stated in Eq. (5) (Rubinow and Keller 1961)

$$\overrightarrow {{F_{{{\text{LR}}}} }} = \frac{1}{8} \pi \rho_{{\text{f}}} a^{3} \overrightarrow {{U_{{\text{f}}} }} \times \overrightarrow {{\Omega^{\prime}}} ,$$

(5)

where, a is the diameter of the sphere (the suspended particle (m)), $\overrightarrow {{{\Omega }{\prime} }}$ is the relative rotation between the fluid and the sphere (rad/s) $\left( {\overrightarrow {{{\Omega }{\prime} }} = \vec{\Omega } - 0.5\nabla \times \overrightarrow {{U_{{\text{f}}} }} } \right)$

If the spherical particles are not stationary within the fluid domain and move through the fluid with a velocity  $\overrightarrow {{U_{{\text{p}}} }}$, we replace fluid velocity vector in Eq. (5)$, \;{\text{that is}}\; \overrightarrow {{U_{{\text{f}}} }}$, with the relative velocity $(\overrightarrow {{U_{{\text{f}}} }} - \overrightarrow {{U_{{\text{p}}} }}$). The direction of the Magnus force is perpendicular to the plane of the vectors where the relative velocity and the axis of rotation are considered. Thus, as a result of the rotation of the particle, a velocity difference is created between the upper and lower parts due to the asymmetry of streamlines, leading to a difference in pressures, which is the cause of the Magnus lift force. All the aforementioned equations are valid for low operating Reynolds numbers. This kind of lift force is formed due to the rotation of the body, and it is strongly interlinked with the inertial flow (Matas et al. 2004b; Michaelides 2006).

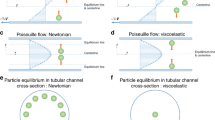
2.2.2 Saffman force: slip-shear-induced lift force

When a particle moves through the fluid domain (considering no particle rotation), it may either be led or lagged by the fluid flow. Saffman force is caused due to the interaction of slip velocity and shear and is generally a magnitude higher as compared to the Magnus force. In case of the Couette flow behavior, the particle leads the flow, and the relative velocity between the surrounding fluid and the particles would be higher as compared to the velocity of the particles. As a result, high pressure is developed above the surface of the particle, pushing it toward the stagnant wall, which is depicted in Fig. 2c (Jebakumar et al. 2016). On the other hand, when the particle lags the fluid flow, the Saffman force acts directly on the moving wall of the particles and its direction is always toward the side with maximum relative velocity, as in Fig. 2d. Furthermore, in case of flow-through channel or the Poiseuille flow, the lift force acts at the centerline of the proposed channel, when the particle lags the flow. In other words, the lift force acts towards the wall of the channel, when the particles lead the flow for non-neutrally buoyant particles (Kim and Yoo 2009; Amini et al. 2014).

Fig. 2

a Schematic illustration of the relative velocity of a particle in a parabolic velocity profile; Large slip velocity, ${v}_{\mathrm{s}}$. Adapted from Jebakumar et al. (2016). b Schematic illustration of the relative velocity of a particle in a parabolic velocity profile; Small slip velocity, ${v}_{\mathrm{s}}$. Adapted from Jebakumar et al. (2016). c Saffman force on a sphere in a simple shear flow. V_t > 0 indicates that the particle moves faster than the corresponding fluid element, leading the flow. Adapted from Zhang et al. (2017). d Saffman force on a sphere in a simple shear flow. V_t < 0 means that the particle moves slower than the fluid element, lagging the flow. Adapted from Zhang et al. (2017). e Forces on particle when boundary (wall) is present on only one side. Adapted from Zhang et al. (2017). f Forces on particle when boundary (wall) is present on both the sides. g Shear gradient lift force F_LS on a particle in a Poiseuille flow. Adapted from Zhang et al. (2017). h Balance of shear gradient lift force and wall lift force. Reproduced from Zhang et al. (2017). i The net lift coefficient is a function of immersed lateral particle position, x, and channel Reynolds number, $\mathrm{Re}$. Reproduced from Matas et al. (2004a)

For a larger slip velocity, (as shown in Fig. 2a), the relative velocity of the particles towards the wall is lower compared to the relative velocity to the center plane. The particle is pushed away from the wall as a result of the increased static pressure created between the particle and the wall. The relative velocity between the particle and the wall, as opposed to the particle and the center plane, is higher when the slip velocity of the suspended particles is low (Fig. 2b). As a result, there is an increase in static pressure between the particle and the center plane, pushing the particle in the direction of the wall. The Saffman lift can, therefore, push a particle in a channel flow in either direction, i.e., towards to the wall or the center plane (Jebakumar et al. 2016).

The magnitude of this Saffman lift force F_S, calculated by using the matched asymptotic expansion method, is defined by Eq. (6) as,

$$F_{{\text{s}}} = \frac{{KV_{t} a^{2} \left( {\gamma \upsilon^{ - 1} } \right)^{\frac{1}{2}} }}{4},$$

(6)

where, K is the numerical constant (K $\sim$ 81.2); γ is the shear rate (1/s); υ is the kinematic viscosity (m²/s); a is the diameter of sphere i.e., the suspended particle (m), $V_{t}$ is the relative velocity between the fluid and particles at a streamline through center of the particle (m/s).

2.2.3 Wall lift force

A velocity gradient of fluid flow is formed due to the walls of the channels, where fluid particles move. This velocity gradient is also responsible for creating a rotational movement under the influence of the shear force. Thus, the Magnus force, which acts in a transverse direction, and Saffman force may act on the immersed particles to migrate them in lateral direction. Retarding the motion of the particles in both perpendicular and parallel directions and exerting transverse migration motion are some of the effects of the channel wall on the motion of immersed particles.

Primarily, two main types of interactions are considered between immersed particles and the walls of the channel,

• 1. The particle's motion is affected only by a single wall on one side of the object. This decelerates the particle and drives it away from the wall by force, called the wall lift force, F_LW. In this case, any other wall is too far from the particle to affect its motion significantly. This condition is valid when the size of the particle is very small as compared to the dimensions of the channel (Vasseur and Cox 1977), as shown in Fig. 2e. Ellipsoid particles are depicted as cell mimics in Fig. 2.

• 2. The particle is affected by walls on both sides, which decelerates the motion of the immersed particles significantly and pushes it towards the centerline. In this condition, the dimensions of the particles are of the same order as the dimensions of the flow channel, as depicted in Fig. 2f (Michaelides 2006). This force increases inversely with the distance of the immersed particles from the wall (Martel and Toner 2014).

2.2.4 Shear gradient lift force

Because of the wall, the particle lags by the flow behavior. If there is no curvature to the velocity profile undisturbed by the particle motion, it becomes a simple shear flow, with the pressure being high towards the left wall (as shown in Fig. 2g). Thus, the immersed particles are pushed to the center of the channel. In addition, the relative velocity of the fluid to particles in Poiseuille flow is much higher towards the left side of the particle due to the parabolic nature of the velocity profile. Thus, according to Bernoulli's principle, a low-pressure zone is created towards the wall, and thus the particle is pushed near the wall in absence of the wall lift force repelling it. The shear gradient lift force F_LS acts opposite to the wall lift force F_LW (Feng et al. 1994; Matas et al. 2004b).

2.2.5 Net inertial lift force

Amongst the four lateral lift forces described above, the shear gradient lift force is an order of magnitude higher than the Saffman force and around three orders of magnitude higher than the Magnus force(Ho and Leal 1974; Amini et al. 2014; Martel and Toner 2014). Thus, the wall lift force and shear gradient lift force are the only dominant forces in a microfluidic channel with flow near the wl and in a highly viscous fluid, for a small particle size (Amini et al. 2014) A balance between the shear gradient lift force, F_LS, and the wall lift force, F_LW, lead to several equilibrium positions near the center of the channel, which have been already explained by Segre and Silberberg (Fig. 2(h)) (Segré and Silberberg 1961, 1962).

Using the method of matched asymptotic expansions (Asmolov 1999), Asmolov derived an analytical expression in order to understand the net inertial lift force acting on a small sphere, viz. a/H <  <  < 1, where a is the diameter of the particles and H is the hydraulic diameter of the channel $\left(H=\frac{4\times \mathrm{area \, of \, cross-section}}{\mathrm{wetted \, perimeter}}\right)$ in a Poiseuille flow, which can be written as stated in Eq. (7), as,

$$F_{{\text{L}}} = f_{{\text{L}}} \rho_{{\text{f}}} \gamma^{2} a^{4} .$$

(7)

The net inertial lift force can be further simplified as stated in Eq. (8),

$$F_{{\text{L}}} = \frac{{f_{{\text{L}}} \rho_{{\text{f}}} U_{{\text{f}}}^{2} a^{4} }}{{H^{2} }},$$

(8)

where, $F_{{\text{L}}}$ is the net inertial lift force (N); $f_{{\text{L}}}$ is the non-dimensional lift coefficient.

H can be defined as H = D for a circular channel (m). D is the diameter of the circular cross-section or $H=\frac{2wh}{w+h}$ for a rectangular cross-section (w = width, h = height of the rectangular cross-section, respectively). The lift coefficient, ${f}_{\mathrm{L}}$, is a function of the Reynolds number (based on the channel dimension), $Re$, and lateral position of the particles, which is denoted as $x$ as shown in Fig. 2i (Asmolov 1999; Bhagat et al. 2009). The lateral position ${x}_{eq}$, where ${f}_{\mathrm{L}}$ = 0 corresponds to the initial equilibrium position. The immersed particles are not in a stable position when the immersed particles are placed on the center line, $x = 0$, since even a little deflection from the centerline will never return the particles back. Additionally, it has been discovered that ${f}_{L}$ decreases when $\mathrm{Re}$ (or $\overrightarrow{{U}_{\mathrm{f}}}$) increases, indicating that the scale of the inertial lift force is lower than $\overrightarrow{{U}_{\mathrm{f}}^{2}}$ (di Carlo 2009; Zhou and Papautsky 2013).

Recent research revealed that the particle size affects the inertial particle migration. The flow in the main channel is disturbed by the aspect ratio of the immersed particles, with a finite size of $0.05\le a/H\le 0.2$, where a/H is defined as the aspect ratio of the immersed particles/ particle blockage ratio. The lift force is defined as ${F}_{\mathrm{L}} \alpha \frac{{\rho }_{\mathrm{f}}\overrightarrow{{U}_{\mathrm{f}}^{2}}{a}^{2}}{{H}^{4}}$ near the channel center, when the wall effects are not strongly dominant. In other words, it can also be scaled as ${F}_{\mathrm{L}} \alpha \frac{{\rho }_{f}\overrightarrow{{U}_{\mathrm{f}}^{2}}{a}^{6}}{{H}^{4}}$ when the particles are close to the channel wall, in which case the wall effects predominate (Di Carlo et al. 2009).

3 Inertial migration and focusing

The drag and the lift forces mentioned in the previous section play an important role in displacing the particles to their equilibrium positions along the channel cross section, which is termed as inertial migration and focusing. Segré and Silberberg (1961, 1962) first discovered the inertial migration of the suspended particles in cylindrical pipes by observing particles having diameter of 1 mm. These suspended particles moved within the annulus of the cylindrical pipe having the diameter of 1 cm. This behavior was also observed with different shapes of microchannels (Matas et al. 2004a, b; Choi and Lee 2010). The behavior was also examined by other researchers who investigated the motion of single rigid spheres in the laminar flow, within a vertical duct, and made similar observations. (Repetti and Leonard 1964). As mentioned earlier, the particles suspended in different microfluidics channels experience both, shear and normal stresses that act over the surface of the particles. These stresses yield two dominant forces, i.e., the viscous drag force (${F}_{\mathrm{drag}}$), which acts on the particles along the streamlines, and the inertial lift force (${F}_{\mathrm{L}}$), which acts on the suspended particles along the transverse direction of the flow streamlines. The two components of the inertial lift forces are defined in terms of the wall-induced lift force (${F}_{\mathrm{LW}}$) and the shear-induced lift force (${F}_{\mathrm{LS}}$), respectively (Matas et al. 2004a, b; Di Carlo et al. 2009). The directions of these forces are shown in the Fig. 3. These forces act up the velocity gradient of the suspended particles, towards the channel centerline, and act down the velocity gradient of the particles, towards the channel walls, respectively. The balance between the drag force and the net inertial lift force is responsible for the migration of the suspended particles to an annulus of approximately 0.2 times the diameter, away from the wall (Zhou and Papautsky 2013). A certain length, referred as the minimum length, is required for the suspended particles to attain the equilibrium positions, after entering into the channel, which has been depicted in Fig. 3.

Fig. 3

The lateral migration speed, U_L, and minimum channel length for particle focusing ${L}_{\mathrm{min}}$ (${F}_{\mathrm{LS}}$= shear gradient lift force, ${F}_{\mathrm{LW}}$=wall lift force, ${X}_{\mathrm{eq}}$= initial equilibrium position). Adapted from Bhagat et al. (2009), Zhang et al. (2016)

Both shear and normal stresses act on suspended particles in a flow which yields drag and lift forces in parallel and perpendicular directions, over the fluid flow streamlines, respectively. Theoretically, it has also been proved that lift force depends upon the cross-sectional position within a microchannel system and also the channel operating Reynolds number (Schonberg and Hinch 1989; Asmolov 1999; Matas et al. 2004a), as reflected from Eq. (9).

$$F_{{\text{L}}} = \frac{{f_{{\text{L}}} \left( {{\text{ Re}},\frac{x}{h}} \right)\rho U_{{\text{f}}}^{2} a^{4} }}{{H^{2} }},$$

(9)

where, ${f}_{\mathrm{L}}$ is the non-dimensional lift coefficient that is a function of operating channel Reynolds number, and the normalized cross-sectional position, $\left(\frac{x}{h}\right)$; ${U}_{\mathrm{f}}$ is the average fluid velocity (m/s). ${f}_{\mathrm{L}}$ decreases with the increase in operating Reynolds number, $Re$ or ${U}_{f}$; thus, lift scales slightly less strongly than with ${U}_{\mathrm{f}}^{2}$.

3.1 Particle motion in Newtonian fluid system

Newtonian fluids are the ones whose dynamic viscosity remains constant, irrespective of the shear force applied, at a constant temperature. The behavior of the Newtonian fluid shows a linear relationship between the shear stress and strain rate, and the constant of proportionality is defined in terms of the dynamic viscosity of the fluid. Some examples of Newtonian fluids include here as water, light crude oil, organic and inorganic liquids, gases, etc. In this section, we provide the physical insights about how suspended particles are moving within the microchannels with the various types of geometries (i.e., circular, square, and rectangular cross-sections), under the influence of Newtonian fluid flow behavior.

3.1.1 Inertial particle focusing in straight tubes and square channels

Only inertial migration affects particle focusing when particles flow in a linear type/straight channel, at an intermediate Reynolds number. In other words, under the influence of shear gradient-induced lift force and wall-induced lift force perpendicular to the mainline, the particles migrate laterally to the sites of dynamic equilibrium. The cross-section of the microchannel determines the number and location of the particles' eventual equilibrium locations (Tang et al. 2020). For a circular cross-section in a straight microchannel, the particles are directed radially inwards under the influence of the flow-induced elastic lift force, thus focusing the particles along the centerline (Karnis et al. 1963; Karnis and Mason 1966). In a straight microchannel, inertial equilibrium positions are placed within the narrow annulus at about 0.6 times the channel radii from the axis (Segré and Silberberg 1961), as shown in Fig. 4a. For a square channel, wherein the aspect ratio (height/width) AR = 1, the particles facing the center of each wall migrate to four equilibrium positions, as shown in Fig. 4b (Chun and Ladd 2006; Di Carlo et al. 2007; Bhagat et al. 2008a, 2009). In other words, for a straight microchannel, a balance between the Stokes drag and net inertial lift forces provides a relationship in terms of the lateral migration velocity $\left({U}_{L}\right)$ and the minimum straight channel length, L_min, which governs migration of particles on to their inertial equilibrium positions, and is represented by Eqs. (10–12) (Bhagat et al. 2009).

$$F_{{{\text{stokes}}}} = 3\pi \mu U_{{\text{L}}} a$$

(10)

$$F_{{\text{L}}} = \frac{{f_{{\text{L}}} \rho_{{\text{f}}} U_{{\text{f}}}^{2} a^{4} }}{{H^{2} }}$$

(11)

$$U_{{\text{L}}} = \frac{{F_{{\text{L}}} }}{3\pi \mu a} = \frac{{f_{{\text{L}}} \rho_{{\text{f}}} U_{{\text{f}}}^{2} a^{3} }}{{3\pi \mu H^{2} }},$$

(12)

where, $f_{{\text{L}}}$ is the lift coefficient, a = radius of suspended particle (m), H is the hydraulic diameter of the channel (m), $U_{{\text{F}}}$ is the average velocity of the particle (m/s), $\mu$ is the dynamic viscosity of the fluid (Pa.s), $\rho_{{\text{f}}}$ is the density of the fluid (kg/m³), H is the hydraulic diameter of the microchannel (m), $U_{L}$= lateral migration velocity (m/s).

Fig. 4

a Focusing of particles in a cylindrical microchannel. b Focusing on particles in a square microchannel. Adapted from Di Carlo (2009)

Two non-dimensional numbers can be used to characterize the lateral migration velocity of the suspended particles in a straight channel, namely, (1) the channel Reynolds number,${\text{Re}}$_, explaining the ratio between inertial and viscous forces and (2) the particle Reynolds number, ${\text{Re}}_{{\text{p}}}$ which additionally considers the size ratio of particle (a) to the hydraulic diameter of the microchannel (H), represented by Eq. (13), as Di Carlo et al. (2007)

$${\text{Re}}_{{\text{p}}} = {\text{ Re}}\frac{{a^{2} }}{{H^{2} }}.$$

(13)

The neutrally and non-neutrally buoyant motion of the suspended particles in 2D horizontal Couette and Poiseuille flows was considered, followed by studying in three dimensions (Feng et al. 1994; Patankar et al. 2001). Arbitrary Lagrangian–Eulerian (ALE) method was used for simulation and the evidence for the fact that the density difference between fluid and suspended particles plays an important role in focusing was given using numerical studies. The motion of particle in a tube was also investigated at different operating Reynolds number, $\mathrm{Re}$. It was reported that as the Re increased, the particle focusing position shifted from the Segre Silberberg center to the inner radius of the tube. This critical Re depended upon the particle size and the distance between each particle in the flow (Shao et al. 2008; Razavi Bazaz et al. 2020).

3.1.2 Particle focusing in rectangular microchannels

The situation of focusing of particles becomes even more complex for a straight channel having a rectangular cross-sectional area, which is the most widely used structure due to the limitations of the microfabrication techniques. For an even lower aspect ratio of 0.5, for a rectangular cross-section of the microchannel systems, the number of favored dynamic equilibrium positions decreases from four to two as shown in Fig. 5a (Lee et al. 2011a; Zhou and Papautsky 2013; Chung et al. 2013a). In this case, the suspended particles within the rectangular microchannel are focused along the midpoints of the wider face of the channels. Irrespective of the aspect ratio of the microchannel systems, the particles migrate towards the wider faces, towards four equilibrium positions. However, for a rectangular cross-section, the equilibrium positions on the shorter faces of the channels are unstable (Gossett et al. 2012a). In a rectangular channel, the particles experience a shear solid gradient lift force along the transverse direction, causing them to move away from the centerline of the microchannel. In such a cross-section area, shear gradient lift force acts significantly away from the walls. This force is strong, as a function of the z direction of the fluid flow streams, but much weaker as a function of the transverse direction (Di Carlo et al. 2009; Gossett et al. 2012a).

Fig. 5

a Focusing of particles in rectangular channels. Adapted from Gossett et al. (2012a). b Effect of Reynolds number on focusing in square and rectangular channels. Adapted from Zhang et al. (2017)

In this study, the flow at specific particle position (FSPP) method was used to study the migration of particles in a straight microchannel with rectangular cross-section (Liu et al. 2015; Mashhadian and Shamloo 2019). The particles entered into the microchannel randomly and then arranged themselves along the walls. The particles then slowly moved to reach their equilibrium positions, under the influence of the lift and drag forces. Experimental results of various studies provided different results at the output of the microchannel. As a result, the researchers conducted numerical experiments to investigate the lift force at various positions across the channel cross-section (Razavi Bazaz et al. 2020). The lift force acting on the particles was plotted against the distance from the center to the inner wall. At the point where the lift force value became zero, with a negative slope, a stable equilibrium position was achieved for that wall (Di Carlo et al. 2009).

3.1.3 Particle focusing in non-straight non-planar microchannels

For all practical purposes, mostly non-straight microchannels like serpentine or spiral channels are utilized. The most common shape that results in both inertial effects and also decreases the channel length and the overall device footprint is the spiral channel, with a curvature along a single constant direction. The inertial lift force and the Dean drag force act on a particle in superposition as it moves along the spiral channel. The Dean drag force tends to entrain particles down the streamline of symmetrically cycling vortices, whereas the inertial lift forces stabilize particles at specified equilibrium locations within the cross-section of the channel. (Tang et al. 2020) The distribution of lift force across the channel cross-section in such microchannels is also studied using the FSPP method. Here, the particle trajectories are obtained using the point particle model, by combining the applied force with other existing forces. These trajectories of the suspended particles in non-straight, non-planer microchannel systems have an explicit formula as shown in Eq. (14) (Liu et al. 2015; Razavi Bazaz et al. 2020)

$$\frac{{m_{{\text{p}}} {\text{d}}^{2} x_{{\text{p}}} }}{{{\text{d}}t^{2} }} = F_{{\text{Inertial force}}} + F_{{{\text{Drag}}}} + F_{{\text{Virtual mass}}} ,$$

(14)

where, ${m}_{\mathrm{p}}$ is the mass of the particle, $\frac{{\mathrm{d}}^{2}{x}_{p}}{\mathrm{d}{t}^{2}}$ gives the acceleration of the particle and F represents the force on the particle.

The drag and inertial lift forces play a significant role in case of serpentine microchannel channels systems for particle focusing (Shamloo and Mashhadian 2018). If a particle's velocity exceeds a certain threshold, the particle is focused along the long walls of the microchannel (Liu et al. 2016). Similarly, in spiral microchannel systems, if the size of the suspended particle is less than the threshold value $(a < 0.07H)$, the drag forces dominate as compared to the inertial lift forces and the particles are trapped in the laminar vortices of the flow(Razavi Bazaz et al. 2020).

3.2 Lateral migration of particles in a non-Newtonian fluid system

Lateral migration is observed in a laminar duct flow for a low operating Reynolds number limit. This mechanism arises in the presence of the dispersed phase of suspended particles that migrate across the flow streamlines and reach the characteristic equilibrium position (Asmolov 1999). In the context of the pressure-driven channel flow, the suspended particles migrate toward the center or the wall in a proposed microfluidic channel. This migration of the suspended particles is also affected by the rheological properties of the working fluid systems, known as the shear thickening or thinning fluid systems, and the particle blockage ratio ($\alpha =\frac{a}{H}$), where, $a$ = diameter of the particles and H is the hydraulic diameter of the microchannel (Gao and Hartnett 1993; Matas et al. 2004b). Ho and Leal studied non-uniform, normal stress distribution in a second order fluid where stresses do not vary linearly with shear rate, leading to lateral migration of particles. The fluids that change their flow behavior in terms of flow behavior index and consistency index, under the influence of applied shear stress, are defined as non-Newtonian fluid systems. Unlike, Newtonian fluids, they do not follow the Newton’s law of viscosity i.e., the shear stress is not directly proportional to strain rate. The viscosity of non-Newtonian fluids can either increase (i.e., shear-thickening behavior) or decrease (i.e., shear-thinning behavior) under the applied shear stress. This fluid flow behavior typically includes both, the biological fluids as well as chemicals such as blood, plasma, polymers, thermoplastics, paints, etc. This study considers the viscoelastic type of non-Newtonian fluids, which have both the elastic and viscous nature, thus behaving as a viscous fluid in certain circumstances and elastic solid in others (Denn 2004). The viscoelasticity nature of viscoelastic fluids generally decreases as a function of the shear rate due to the macromolecular nature of viscoelastic fluid (Phan-Thein 2012). This phenomenon is called as shear thinning behavior of the working fluid system, which causes outward migration of particles in viscoelastic flow (Jefri and Zahed 1989; Huang and Joseph 2000).

On the other hand, the elastic behavior, is due to the generation of normal stresses due to the orientation and the alignment of macromolecules along the direction of flow (Shaw 2012). The difference between these normal stresses gives rise to particle cross-stream migration in the viscoelastic flow. Three normal stress components give rise to two independent normal stress differences. The first is the difference between the stress along the flow direction and the stress acting perpendicular to the flow direction, i.e., ${N}_{1}={\sigma }_{xx}-{\sigma }_{yy}$ (Phan-Thein 2012; Shaw 2012). While this difference is zero in Newtonian fluids as the normal stresses are equal in all directions, they are responsible for particle migration in viscoelastic flows (Leshansky et al. 2007). The second difference is between the normal stresses, ${N}_{2}={\sigma }_{yy}-{\sigma }_{zz}$, which is the measure of the relative stretching of the macromolecules in the transverse y direction versus the z direction (Shaw 2012).

Due to an imbalance in the normal stresses, the particles suspended in the viscoelastic fluid migrate across the streamlines. As against the Newtonian fluid, the particles near the center in a non-Newtonian fluid migrate towards the closest wall, which has been proven both, by experiments and numerical simulations (Halow and Wills 1970; Ho and Leal 1974; D’Avino et al. 2012). In case of migration of particles in a microfluidics channel with viscoelastic fluid, the fluid inertia vs. elasticity, migration induced by ${N}_{1}$ vs. the secondary flow induced by ${N}_{2}$ and elasticity vs. the shear thinning effect mainly govern the particle migration and positioning (Zhou and Papautsky 2020). For an elasto-inertial migration, i.e., when both Re and Wi have a definite value, the inertial and elastic forces along with the effects of shear thinning and microchannel geometry act on the particles leading to their lateral migration. In square microchannel systems, for Re between 0.01 and 10, the otherwise stable positions (for $\mathrm{Re} << 1$) at the corners of the square become unstable. This is owing to the wall-induced lift force and the elastic forces, respectively, pushing the particle away from the wall and dragging it towards the centerline, making the center of the square microchannel the only stable position. The combined effect of these two applied forces $(0.01< \mathrm{Re} < 10)$ is more dominant as compared to the opposing force provided by the shear induced lift force which pushes the particle towards the inner wall of the microchannel system (Zhou and Papautsky 2020). In rectangular microchannel system having low aspect ratio, when the particles are away from the wall, the shear induced lift force competes with the elastic force in the horizontal direction, giving rise to two different focusing positions near the walls but at the centerline. The two positions come closer to each other as the elastic force is increased and eventually merge to form a single focusing position (Yang et al. 2017). When both, elastic and wall induced lift forces are comparable, where elasticity number,$\mathrm{El} \sim 1$, the elasticity of the fluid dominates and determines the migration dynamics of particles. 2D simulations indicated that Wi should be at last two orders of magnitude smaller than Re for the inertial forces to be competitive (Lim et al. 2014; Trofa et al. 2015).

To obtain the flow field for non-Newtonian fluids, continuity and momentum conservation equations. as stated in Eqs. (15) and (16), need to be solved just as for the Newtonian fluids. However, an extra stress tensor term $\tau$ is added to the total stress tensor, $\sigma$, to take the effect of viscoelasticity into consideration (Beris et al. 1992):

$$\nabla {\varvec{u}} = 0$$

(15)

$$\rho_{f} \left( {\frac{{\partial {\varvec{u}}}}{\partial t} + \left( {{\varvec{u}}.\nabla } \right){\varvec{u}}} \right) = \nabla .\sigma$$

(16)

$${\varvec{\sigma}} = - pI + 2\mu e\left( {\varvec{u}} \right) + {\varvec{\tau}}\user2{.}$$

(17)

Here, $u$ is the velocity field, $t$ is the time, $p$ is the acting pressure and ${\varvec{\sigma}}$ is the deviatoric stress tensor, respectively. To obtain numerical solution of these equations (Eqs. 15 and 16), constitutive relation is defined as; Larson (1988), D’Avino and Maffettone (2015).

$${\varvec{\tau}} + \lambda \left( {\frac{{\delta {\varvec{\tau}}}}{\delta t} + u.\nabla {\varvec{\tau}} - \nabla u^{T} .{\varvec{\tau}} - {\varvec{\tau}}.\nabla u + \frac{\alpha }{{\eta_{p} }}\left( {{\varvec{\tau}}.{\varvec{\tau}}} \right)} \right) = \eta_{p} \left( {\nabla {\varvec{u}} + \left( {\nabla {\varvec{u}}} \right)^{T} } \right),$$

(18)

where $\lambda$ is the fluid relaxation time (s) and ${\eta }_{p}$ is the polymer viscosity (Pa.s). If the mobility factor $\alpha$ becomes zero, the Giesekus Eq. (18) reduces to the Oldroyd-B equation.

For numerical modeling in case of a staggered grid approach, the Distributed Lagrange multiplier (DLM) method inside the framework of the finite volume method was applied to study the effects of fluid elasticity, fluid inertia, and shear-thinning viscosity. It was found that the particles in Oldroyd-B fluid are focused at the center of the channel, while in case of Giesekus fluid, the equilibrium position is away from the center. Numerical simulations also proved that increase in the channel corner angle causes the elastic force to push the particles more efficiently towards the center of the cross-section (Razavi Bazaz et al. 2020).

The motion of particles in a microfluidic channel within the non-Newtonian fluid system is governed by some dimensionless numbers, such as the operating channel Reynolds number, Weissenberg number, etc. (Amini et al. 2014). The channel operating Reynolds number, $Re$, and particle operating Reynolds number ${Re}_{p}$ are characterized by the influence of the inertial effects on the fluid and the suspended particles, both of which compare in terms of the ratio between the inertial force and the viscous force. In addition, the non-dimensional Weissenberg number, $Wi$, is defined in terms of the applied shear rate $\left(\gamma \right)$ (1/s) and fluid relaxation time, $\lambda$, (s), respectively. It is used to characterize the viscoelasticity of the working fluid system. In the context of the rectangular microchannel system, the Weissenberg number can be expressed by Eq. (19), as

$${\text{Wi}} = \lambda \gamma = \lambda \frac{{2U_{{\text{f}}} }}{H},$$

(19)

Weissenberg number is the ratio of the elastic to viscous forces. Considering steady simple shear flow, the dominant elastic force is the difference between the normal stresses ${\tau }_{xx}-{\tau }_{yy}$, and the viscous force is the shear stress ${\tau }_{xy}$. According to Maxwell and Oldroyd model, ${\sigma }_{xx}-{\sigma }_{yy}$ can be written as $2\lambda \mu {\gamma }^{2}$ and ${\sigma }_{xy}=\mu \gamma$. Thus, the ratio of ${\tau }_{xx}-{\tau }_{yy}$ and ${\tau }_{xy}$ gives Wi, and the factor 2 comes from the elastic forces (Poole 2012).

To understand the viscoelastic property in non-Newtonian fluid systems, another non-dimensional number, known as the Deborah number, is considered. In this study, the non-dimensional number Deborah number, D, is defined as the ratio of fluid relaxation time $\left(\lambda \right)$ to the characteristic time of an experimental observation, ${t}_{\mathrm{p}}$, (D’Avino and Maffettone 2015; D’Avino et al. 2017), as stated in Eq. (20).

$$D = \frac{\lambda }{{t_{{\text{p}}} }}.$$

(20)

The Deborah number is a dimensionless number that measures the rate of change of flow conditions, which is related to the unsteady state of the flow. Thus, in slowly changing or steady flows, in which the characteristic time for deformation is infinite, the Deborah number is zero. In such cases, it becomes essential to use the Weissenberg number. However, in complex geometries, the flow is never steady. Thus, the Deborah and Weissenberg numbers coincide, when the hydraulic diameter of a geometry is equal to its length, for example, a square cavity. In such a case, the residence time (t) of the fluid would be the length of the cavity (L) divided by the fluid velocity $\left(t=\frac{L}{{U}_{f}}\right)$ and the shear rate can be defined as $\left(\gamma =\frac{{U}_{f}}{H}\right)$. For H = L and if the residence time is equal to the characteristic time, Deborah and Weissenberg numbers can be related as: $\mathrm{Wi}=D=\frac{\lambda {U}_{\mathrm{f}}}{L}$, for square cavity. However, for any other cavity shape, both these numbers can be related by a geometric factor. In general, if two length scales are required to determine the dynamics of flow, D and Wi can be related through a geometric factor (Poole 2012).

Based on these above-mentioned non-dimensional numbers, we can introduce another non-dimensional number, the Elasticity number, $\mathrm{El}$, which may be used to define the viscoelastic effect of the working fluid systems. It is explained in terms of the ratio between the Weissenberg number or Deborah number to the operating channel Reynolds number, and indicates the relative strength of elastic forces to inertial effects, as expressed by Eq. (21),

$${\text{El}} = \frac{{{\text{Wi}}}}{{{\text{Re}}}} = \frac{{2\lambda U_{{\text{f}}} }}{{\rho H^{2} }}.$$

(21)

A viscoelastic fluid flowing around suspended particles exerts a force on it due to the shear stress and pressure acting on the surface of the particles. These forces can be classified in terms of the drag and lift forces, respectively. Furthermore, the lift force also consists of two components, inertial lift force (${F}_{iL}$) and elastic lift force (${F}_{\mathrm{eL}}$). The inertial lift force consists of the wall-induced lift force and the shear gradient lift force, which act as dominant forces on the suspended particle movements. On the other hand, the elastic lift force, ${F}_{eL}$_, is formed due to the non-uniform normal stress distributions in the viscoelastic fluid flows.

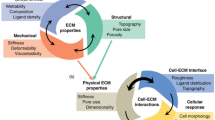
Introducing geometrical features like curvatures or disturbance structures may amplify and promote particle separation using different lateral forces. In other words, the behavior of the secondary flow depends on different structures of microchannels as well as inertial lift force, which is responsible for particle size, shape, and deformability. Therefore, we can conclude that the number and location of final equilibrium position of the particles is strongly affected by the structure of the microchannels. The characteristics of the applied forces on the particles in case of different microstructures have been summarized in Table 1.

Table 1 Various applied forces in microchannels with different microstructures (Martel and Toner 2014; Zhang et al. 2016)

3.3 Factors affecting the focusing of particles in different channels

The focusing and migration of particles in a microchannel are affected by various factors including the microchannel geometry and particle Reynolds number, the particle blockage ratio and the particle concentrations, respectively. For example, a neutrally buoyant particle migrates to midplane between the channel wall and center, while a lighter particle goes near the walls of the channel and a heavier one migrates to the channel axis. All these factors that are related to the focusing of the particles within the microchannels are correlated. For instance, it was observed for migration of spherical particles in square microchannels, that if both the measurement distance from the inlet and the aspect ratio of the suspended particles, $\frac{a}{H}$ ratio are large then, particle migration can take place even at small operating Reynolds number, $\mathrm{Re}.$ In order to apply the mechanisms of focusing to real life systems, it becomes important to understand the influence of all these factors.

3.3.1 Effect of channel Reynolds number on focusing of particles

In a channel with a square or rectangular cross-section, the particles tend to shift away from the center and towards the wall at a higher operating channel Reynolds number, i.e., up to $\mathrm{Re}$ = 150. This phenomenon can also be described in terms of the two competing lift forces, i.e., wall lift force and shear gradient lift force, respectively. It is noticed that the magnitude of both the wall lift force and shear gradient lift force increases with the increase in the operating channel Reynolds number. However, the increase in shear gradient lift is larger than that in wall lift force for a given Reynolds number (Asmolov 1999; Gossett et al. 2012a). Thus, the shear lift dominates and the particle is pushed slightly toward the wall, which has been depicted in Fig. 5b. Similarly, in a rectangular channel, the wall effect becomes less dominant in directing the particles away along the long face, which increases the equilibrium position to four (Hur et al. 2010; Ciftlik et al. 2013).

3.3.2 Effect of $\frac{{\varvec{a}}}{{\varvec{H}}}$ on focusing positions

The size of particles is another important factor affecting the equilibrium position of the suspended particles. The focusing position approaches $x\sim 0.6\left(\frac{H}{2}\right)$ when $\frac{a}{H}\ll 1$. While if $\frac{a}{H}$ approaches 1, the particles are geometrically forced to pass through the microchannels along the centerline due to increasing steric effects (Di Carlo et al. 2009; Hur et al. 2010; Mao and Alexeev 2011). In general, a large particle size to channel width ratio, accelerates the lateral migration while hardly any migration is seen in case of small $\frac{a}{H}$ ratio.

3.3.3 Effect of particle concentrations on focusing positions

The number of focusing positions and their location is also dependent upon the number of particles per unit along the length of the channel. For high-length fractions, which are defined in terms of the fraction of particle diameters per channel length, i.e., $\phi >\approx 75\%$, multiple streams are formed across the channel (Humphry et al. 2010).Thus, if particles are to occupy two to four streams in such a condition, the hydrodynamic interactions between the particles increase. Thus, a few particles move out of the stream and form new focusing streams nearby. These particle–particle interactions act as a limiting condition to achieve the precision focusing of all suspended particles along the streamlines of the channels (Amini et al. 2014).

3.3.4 Effect of particle Reynolds number on focusing positions

In straight tube and square channels, when the particle Reynolds number, ${\mathrm{Re}}_{\mathrm{p}} \ll 1$, viscous forces dominate to direct the particle movements along the streamlines. When ${\mathrm{Re}}_{\mathrm{p}} \gg 1$, lateral migration of particles starts due to the dominance of the inertial lift forces. On the other hand, in rectangular channels, two equilibrium positions are observed for a value of ${\mathrm{Re}}_{\mathrm{p}}\ge 1$. However, when the ${\mathrm{Re}}_{\mathrm{p}}>\approx 4.7$, the particles are again focused at four positions, like in square channels (Hur et al. 2010). Also, in a rectangular channel, the degree of focusing increases with the particle Reynolds number for a given length of the channel (Di Carlo et al. 2007).

4 Secondary flow in microchannels

Secondary flow occurs due to the difference in velocity between the fluid near the wall and the center, while the fluid flows through curved channels (Dean flow) or channels having disturbances like grooves or pillars. It might be obtained in curved and straight microchannels systems due to the geometrical features of the proposed system causing disturbances in the flow of the fluid. Secondary flow has an influence on the manipulation of the suspended particle, their mixing and dispersion within the microchannels, and thus it becomes important to comprehend it in microfluidics. Secondary flows can be precisely controlled to enable accurate fluid handling and to improve the functionality of lab-on-a-chip devices, microreactors, and bioassays etc. This leads to improvements in microscale chemical analyses, drug delivery, and medical diagnostics, ultimately enhancing the reliability and efficacy of microfluidic systems.

4.1 Effect of microstructure on flow and particles

In this section, we have discussed how change in geometries of the microchannel can induce a secondary flow in it, which in turn can help in controlling the fluid flow and the motion of the suspended particles. There are many ways to impose deviations from a straight channel, including channel curvature, grooves on the channel walls, and obstructions inside the channel. In the context of fluid flow behavior related to the secondary flow, analytical solutions of the Navier stoke equation becomes difficult as the boundary conditions become more complex owing to the changes in the microchannel geometry. Thus, we have tried to understand the physical insight underlying these systems and have tried to solve their problems in the subsequent sections.

4.1.1 Curving channels: Dean flow

The generation of secondary flow in curved channels like spiral or serpentine channels is obtained due to the difference in velocity between the fluid in the center and the fluid near the wall in the downstream direction. Due to the higher inertia of the fluid elements near the central line of the channel, they tend to flow outward around a curve, under the influence of the centrifugal effect, thus creating a pressure gradient in the radial direction within the channel. Due to this pressure gradient under the influence of the centrifugal effect and to conserve mass, the fluid near the wall recirculates inwards, forming two symmetric circulating vortices due to the enclosed channel, called the Dean vortices (Di Carlo 2009), as shown in Fig. 6a, d. Usually, two vortices rotating in opposite directions are formed in spiral channels, but multiple might exist at high operating channel Reynolds number, $\mathrm{Re}$. The magnitude of this flow is determined by a dimensionless number, known as the Dean number (De), which is represented as shown in Eq. (22) (Berger et al. 1983).

$${\text{De}} = {\text{Re}}\sqrt{\frac{H}{2R}} ,$$

(22)

where, R is the radius of curvature of the proposed system (m). The distribution and strength of secondary flow are also influenced by the channel Reynolds number, ${\text{Re}}$, the aspect ratio of the channel (height/width) and the shape of cross-section of the channel. The dependence of secondary flow velocity on Dean number, ${\text{De}}$, is defined as stated in Eq. (23),

$$U_{{\text{D}}} { }\sim \frac{{{\text{De}}^{2} \mu_{{\text{f}}} }}{{\rho_{{\text{f}}} H}}.$$

(23)

Fig. 6

a Dean flow creation in the curving channel due to velocity mismatch (Martel and Toner 2012). b Spiraling channels. Reproduced from Martel and Toner (2012), with permission of AIP Publishing. c Alternating asymmetric curving channels (Di Carlo et al. 2007; Di Carlo 2009) Copyright (2007) National Academy of Sciences, U.S.A. d Dean flow in the curved channel. Reproduced from Di Carlo (2009)

Furthermore, the magnitude of secondary flow velocity, $U_{{\text{D}}}$, can be approximated as shown in Eq. (24) (Bhagat et al. 2010; Kemna et al. 2012)

$$U_{{\text{D}}} = 1.8 \times 10^{ - 4} \times {\text{ De}}^{1.63} .$$

(24)

An increase in Dean Number not only provides a measurement of the Dean flow velocity but also affects the secondary flow's shape, with the centers of the symmetric vortices migrating towards the outer wall and the formation of hydrodynamic boundary layers and additional vortices with the increasing in Dean Number.

Besides, there are spiral channels with a single direction of curvature, as shown in Fig. 6b (Kuntaegowdanahalli et al. 2009; Russom et al. 2009; Lee et al. 2011b; Kemna et al. 2012; Sun et al. 2012b; Martel and Toner 2012; Seo et al. 2012; Hou et al. 2013; Xiang et al. 2013; Guan et al. 2013) and sigmoidal curving channels having alternating curvatures, as depicted in Fig. 6(c) (Di Carlo et al. 2007; Gossett and Carlo 2009; Gossett et al. 2012b) which enhance inertial focusing under the influence of induced secondary flow. In case of spiral microchannel, a transition regime in the focusing behavior of the suspended particles is obtained, and it is developed with an increase in the channel curvature ratio for a specific operating Reynolds number, $\mathrm{Re}$ ($\mathrm{Re}$ = 400). In addition, it has been noted that the microchannel width goes on increasing with the increase in Dean drag force, which acts on the suspended particles as a function of mainstream flow direction. Thus, Dean drag force plays a significant role at some critical channel widths for the lateral migration of particles. With respect to focusing, the larger particles are typically focused near the inner wall while smaller particles are focused near the center after flowing through a spiral channel, followed by a branched outlet to collect the concentrated, focused particles due to the synergistic effect of inertial migration and secondary flow. However, the highest particle concentration factor that can be attained utilizing a single outlet system's splitting effect is quite constrained (Tang et al. 2020). To get over this limitation, six waste channels that extend from the spiral channel's outermost ring were created, revealing a 14 times concentration rise and a recovery rate of almost 100% for the human breast cancer cells (MCF-7 cells) injected into whole blood (Burke et al. 2014). In contrast to the spiral channel, which has curvature in a single, constant path, Dean flow is introduced into sigmoidal/serpentine channels by joining alternating curvatures in sequence. The sigmoidal channel has been drawing more attention for particle inertial manipulation due to the promising potential of the linear structure in parallelization. However, because the direction and strength of the generated Dean flow change along the channel, the behavior of particles travelling in a sinusoidal channel becomes confusing and unpredictable (Tang et al. 2020). Moreover, unlike spiral channels, the secondary flow in sigmoidal channels does not approach steady-state Dean flow and leads to even complex inertial focusing behavior of particles as a function of operating channel Reynolds number (Gossett and Carlo 2009; Martel and Toner 2012). The opposing channel segments must be asymmetric so that the curvature-induced secondary flows are not considered against each other and reduce the net action force (Amini et al. 2014).

4.1.2 Microgrooves on channel walls

Secondary flows can also be developed by adding grooves on the inner walls of the microchannels and thus disturbing the flow (Stroock et al. 2002), as shown in Fig. 7a. Numerical studies have shown that the arc-grooves can help in inducing secondary flow in a microchannel and the randomly distributed particles migrate to new equilibrium positions wherein the larger particles are pushed to the corners and the smaller particles concentrate at the center of the microchannel (Zhao et al. 2017). These secondary flows, as a replacement for the Dean flow, can be used to modify the inertial focusing behavior of the suspended particles (Mao and Alexeev 2011). But, most of such systems have been operated in low-$Re$ flow regime, wherein the inertia force is negligible. Thus, for this phenomenon to be effective in Stokes flow, the grooves must not have lengthwise symmetry or there will be no net deformation of the fluid. Using numerical simulations, it has been proved that these systems can be used to sort the suspended particles based on their effective sizes, in combination with the inertial forces. These structures are also utilized to develop hydrodynamically focused sheath flow to perform flow cytometry operations, as depicted in Fig. 7b (Howell Jr et al. 2008; Golden et al. 2009) This is performed by initially focusing the suspended particles near the top and bottom walls of a microchannel having a low aspect ratio. The smaller particles are found to take the equilibrium positions closer to the channel walls, thus giving a size-based separation. Two symmetrical secondary flows are generated by the periodical ridges on the top and bottom walls of the channel. Due to the different initial positions of the larger and smaller particles due to inertial focusing, they move in different directions leading to different lateral locations. But this proposed technique, like other secondary flow-inducing techniques, is largely employed to achieve faster mixing of fluids (Stroock et al. 2002; Williams et al. 2008).

Fig. 7

a Creation of hydrodynamic sheath (Howell Jr et al. 2008). b Manipulation of particles to increase interaction and capture cells on surfaces. Reproduced from Stott et al. (2010)

4.1.3 Micro pillars arrays or expansion–contraction arrays

The introduction of disturbance obstacles in a straight microchannel can also help in the generation of secondary flow, similar to other curved channels (Lee et al. 2009a). In a contraction–expansion pattern on a single side of a straight channel, as shown in Fig. 8d, a three-dimensional single-stream particle can be focused in a sheath flow along with a series of particle separations in the expansion–contraction array (Lee et al. 2009b). Expansion–contraction arrays lead to Dean-like secondary rotating flows due to sudden change in cross-section, acting on the suspended particles along with the inertial lift forces. This pattern can also be made on both sides of the channels (multi-orifice microchannel), which does not require sheath flow (Park et al. 2009), as depicted in Fig. 8e. The particles are focused at the center or at the sides, depending upon the particle Reynolds number. A lateral drift in the equilibrium position is induced due to the trajectory difference between the particles and the fluid element in the expansion–contraction region. This lateral drift varies as a function of different particle sizes and flow rate and alignment of the particles, which depends upon their effective size, for a particular range of channel Reynolds number$,\mathrm{Re}$, thus giving a size-based separation. When a fluid stream enters the contraction area in these microchannel systems, the streamlines from the wider part upstream gain acceleration and follow a curved path, causing a Dean-like effect as in a curved microchannel system. On the other hand, the fluid decelerates in the expansion region resulting in disappearance of the Dean flow vortices. Furthermore, the centrifugal forces become dominant in the contraction region, producing Dean Vortices for laminar flow conditions. This is the passive microfluidics method utilized for particle filtration, mixing of two liquids, etc. (Lee et al. 2009a; Zhang et al. 2022). However, there is a complete reversal of secondary flow when this varying cross-section returns to its original shape downstream (Fig. 8a).

Fig. 8

a Deformation of fluids and creation of secondary flows due to centrally located micropillar. Reproduced from Amini et al. (2013). b Four dominant modes of operation for the secondary flow. Reproduced from Amini et al. (2013). c Dependence of lateral position of secondary flow on secondary particles. Reproduced from Amini et al. (2013). d Inertial separation of particles by expansion contraction array on one side of the channel. Reproduced from Lee et al. (2011a). e Inertial separation of particles by expansion contraction array on both sides of the channel. Reproduced from Park et al. (2009), Park and Jung (2009). f Contraction–expansion microchannels for cell manipulation. Reproduced from Jiang et al. (2021), with permission of AIP Publishing

A micropillar in a microfluidic channel also helps in generating irreversible twisted flows by deforming the fluids around the micropillars at a finite inertial flow. A double-spiral inertial microfluidic device with herringbone grooves and sawtooth walls was proposed to capture and enrich bacteria from gaseous media. Herringbones were sporadically arranged throughout the spiral to create turbulence and improve the effectiveness of bacteria sample, and sawtooth wave-shaped walls were used to better accept aerosol particles. Periodic and localized microstructures may be developed and added to the spiral channels to deterministically control the secondary flow. For instance, to increase the particle focusing in time and space, a sequence of micro-bars were meticulously arranged along the inner wall of a spiral channel with an extremely low aspect ratio (Tang et al. 2020). A demonstration based on numerical simulations and experiments proved that the pressure gradient created by the presence of these pillars leads to Dean-like flow by irreversibly pushing the fluid parcels laterally (Lauga et al. 2004). The presence of a circular pillar, giving a finite inertia symmetric change in channel geometry, can be used to result in net deformation of fluid (Amini et al. 2013) and the fluid does not return to the original position downstream. Also, the shape and position of the net circulating flows across the channel can be tuned by the lateral position of micropillars. Like the expansion–contraction array, the locally induced secondary flows caused by the sequenced micropillars could be helpful in modifying the inertial migration process. However, unlike Dean flow which gives a relatively steady-state behavior along the curvature of microchannels, this proposed phenomenon leads to net motion with added complexities.

Also, the direction of secondary flow is dependent upon flow conditions and geometry of microchannels. Furthermore, four important dominant modes have been quantified for this phenomenon, which have been represented in Fig. 8b. For instance, Mode 1 is observed for channels having a low aspect ratio and operating channel Reynolds number of $\mathrm{Re} \sim <40$. In this case, the fluid near the center of the proposed microchannel deforms, while due to the conservation of mass, the fluid parcel near the top and bottom of the microchannel moves to the center, giving rise to a symmetric set of net flow deformations within the channel, as shown in Fig. 8a. In case of micropillar with a circular cross-section, located at the center of the channel, three non-dimensional numbers are required to understand the system based on their dimensional analysis. These are $\frac{D}{w},\frac{h}{w},$ and $\mathrm{Re}$, where D is the diameter, h is the height, and w is the width of the micropillars. The magnitude of inertial flow deformation increases significantly with an increase in channel operating Reynolds number, $\mathrm{Re}$ and $\frac{D}{w}$, provided the micropillar diameter is comparable to the microchannel width. Four different combinations of these non-dimensional groups have been classified based on the number of net secondary flows. They give rise to a quadrant of the channel and the directions of these flows are responsible for four dominant modes of operation. The location of net secondary flows can be tuned by simply positioning the micropillars at different locations across the microchannel. For example, as shown in Fig. 8c, there is a shift of half-width in the net secondary flows when two half-micropillars are present on the sides of microchannels, which results in the total flow being opposite to that observed in the situation when there is only one pillar in the middle of the microchannel (Amini et al. 2013).

This geometry is also employed for biomedical applications. Inertial microfluidics in a straight microchannel system is insufficient to deliver high efficiency and good performance in case of cell/particle separation as represented in Fig. 8f. Thus, a contraction–expansion channel with inertial microfluidics, secondary flow, and vortex in the chamber is being widely used. The contraction–expansion channels are one of the most versatile systems as they come in different chamber sizes and shapes. Also, to multiply the throughput and enhance the sorting purification, they can be easily double graded (Wang et al. 2016) and given a parallel design (Mach et al. 2011). It is also possible to combine the contraction expansion channels with other microchannel patterns like curved (Shamloo et al. 2019), spiral and serpentine (Nasiri et al. 2020) patterns to improve the manipulation performance. Additionally, viscoelastic fluid is another potential buffer solution used in the contraction–expansion channel to improve sorting effectiveness, raise particle recovery rates, and lower flow rates to safeguard delicate cells during separation procedures (Lu et al. 2017) The smaller particles are focused more effectively due to elastic effects (Lim et al. 2014) Inertial lift force, vortex flow, Dean flow, and other secondary flows are all included in the microfluidics of contraction–expansion array (CEA) microchannel system, rendering them as a multi-purpose tool for particle manipulation. The processing time and channel length may be drastically decreased by the concept of dean flow in the contraction–expansion microchannels. Different particle sizes are more easily detected by the elastic force. In future, more accurate and effective microfluidic chip designs may be based on a combination of contraction–expansion microchannels and viscoelastic flow (Jiang et al. 2021).

4.2 Effect of particles on fluid flow

The particle–particle interaction within the secondary fluid flow stream is an important concept. The fluid around the suspended particles is disturbed in various ways i.e., reversing streamlines, creation of secondary flows. Thus, the particles cannot be considered as passive components of the proposed microchannel systems.

4.2.1 Reversing streamlines

The term reversing streamlines refers to the fluid that moves towards the particle in its reference frame and then moves away again. It is one of the distinguishing features of the flow field around a freely rotating particle in a shear flow with a finite operating Reynolds number. It is expected that the fluid would get diverted by the rigid particles' motion and then continue flowing in a similar direction post returning to a similar location, as shown in Fig. 9a. These reversing streamlines may lead to repulsive particle–particle interactions (Zurita-Gotor et al. 2007; Kulkarni and Morris 2008; Lee et al. 2010), as depicted in Fig. 9f. For example, the flow streamlines around a suspended cylindrical particle, in context of simple two-dimensional shear flow, differ from that for inertial and Stokes flow, where the operating Reynolds number, $\mathrm{Re}\ll 1$ (Kossack and Acrivos 1974) Due to the concept of fluid inertia, the region of closed streamlines gets smaller and smaller and the flow is reversed due to the increase in the operating Reynolds number, as shown in Fig. 9a, b (Poe and Acrivos 1975).

Fig. 9

a Non-reversing streamlines around unbounded particles under Stokes flow conditions. Reproduced from Subramanian and Koch (2006b), with permission of AIP Publishing. b Creation of reversing streams and saddle points near the unbounded particle on the addition of fluid inertia. Reproduced from Subramanian and Koch (2006b), with permission of AIP Publishing. c Creation of reversing streamlines due to channel confinement in the absence of fluid inertia (Lee et al. 2010). Copyright (2006) National Academy of Sciences, U.S.A. d Real systems with confinement and fluid inertia (Lee et al. 2010). Copyright (2006) National Academy of Sciences, U.S.A. e Formation of reversing streamlines for low as well as finite Re values (Lee et al. 2010). Copyright (2006) National Academy of Sciences, U.S.A. f Reversing streamlines leads to the inertial ordering of the particles by generating repulsion between particles (Lee et al. 2010). Copyright (2006) National Academy of Sciences, U.S.A. g Inertially focused particles create strong net secondary flows as they rotate and flow downstream. Reproduced from Amini et al. (2012). h Particle-induced convection for fluid mixing. Reproduced from Amini et al. (2012). i Dependence of secondary flow on the lateral position of the particle. Reproduced from Amini et al. (2012)

Reversing streamlines are also observed for finite operating Reynolds number (Mikulencak and Morris 2004; Subramanian and Koch 2006a, b; Kulkarni and Morris 2008) This fluid inertia not only leads to reversing of flow streamlines but also results in the breaking down of closed streamlines. As a result, the suspended fluid particles move spirally in the outward direction to improve the heat and mass transfer of the proposed process (Subramanian and Koch 2006b).

Numerical studies in a bounded geometrical structure have proved that the presence of a wall near a particle may also contribute to reversing of the flow by breaking off closed streamlines and generating open and reversing streamlines (Amini et al. 2014). A microfluidic channel contains both fluid inertia and confining walls, thus giving rise to reverse streamlines (Lee et al. 2010). The reverse streamlines are almost similar to those present in a simple shear flow, except that the symmetry in the vertical direction is broken due to the parabolic base flow, as shown in Fig. 9c, d. Numerical simulations and experiments have confirmed the formation of reversing streamlines at both finite-Reynolds number and zero operating Reynolds number ($Re\to 0$) in a microfluidic channel, as depicted in Fig. 9c–e. Repulsive particle–particle interactions are formed during the entire process in case of inertial ordering by the reversing streamlines. There is self-assembly of ordered structures by the particle-induced reversing streamlines, which pushes the particles in the transverse direction, and the particle centers are directed onto the streamlines with opposite flow directions.

4.2.2 Particle-induced convection

Reversing streamlines is not the only consequence of the particles flowing in a fluid, but these particles also lead to net secondary flow in the channel cross-section. This is described as the phenomenon of "particle induced-convection", which induces net flows spanning across the channel from the focused particle and recirculating around the top and bottom of the channel, following conservation of mass (Amini et al. 2012) as depicted in the Fig. 9e. This kind of secondary flow is formed by the flow differences of the upstream suspended particles for the inertial flow.

The strength of this convective flow is a strong function of the particle size $(\sim {a}^{3})$. It shows an inertial scaling with convective flow velocity ($\sim {U}^{2})$ and scales linearly with the working fluid density. For a physically bound system, numerical studies suggest that both rotational and translational components of the motion of suspended particles influences the magnitude of net secondary flow (Amini et al. 2014).The net flow increases with the increase in the drag force (mainstream force) of the suspended particles i.e., for increasing the slip velocity of the suspended particle as compared to the fluid velocity. The increase in drag force dominates with a decrease in torque.

For the operating Reynolds number of the particle, ${\mathrm{Re}}_{\mathrm{p}}>\sim 2$, the particle-induced convection can significantly influence the flow field streams. The magnitude and direction of the flow is largely dependent upon the fluid inertia and the location of the particle in the microchannel. In other words, a small change in the lateral position of the suspended particles can change the secondary flow to a large extent, as shown in Fig. 9i. When the particle is near the center of the proposed microchannel system, the weakest secondary flow and reverse streamlines are observed since the local velocity difference across the particle is the minimum. The results of the experiments show that uniform flows between particles in inertial focusing equilibrium positions individually serve as a dynamic site for mass convection while moving downstream and combine constructively to efficiently transport fluid through channels (as depicted in Fig. 9h). As a result, a high particle concentration in the channel, implying a greater number of convection sites can support the dominance of the effect.. It has also been found that the particles in a channel remain focused in their equilibrium positions and are not influenced by the secondary flow (Amini et al. 2012). Each particle acts as a site for mass convection and thus higher concentrations of particles increase the convection sites, leading to dominant secondary flow. Therefore, a strongly directed secondary flow is formed owing to the unique lateral positioning of the suspended particles, due to the inertial focusing (Fig. 9g). Hence, for, ${\mathrm{Re}}_{\mathrm{p }}>\sim 2$, the particle-induced convection dominates over diffusive transport for lateral fluid transport, especially at higher particle concentrations (Amini et al. 2014).

5 Applications of secondary flow in microfluidic systems

Secondary flow has been extensively applied for fluid and particle manipulation, such as mixing, trapping, focusing, and separation. The ability to control the fluid streams using Dean flow has been employed for three-dimensional hydrodynamic focusing, as depicted in Fig. 10b, and the creation of variable inertially modulated focal length scales, as shown in Fig. 10c (Mao et al. 2007a, b). Out of these, mixing of fluids is most widely used in the application of secondary flow. Many conventional techniques, for example the use of wavy walls, slanted wells, ridges, and grooves, focus on increasing the interfacial area between the two fluid streams so that diffusive mixing can occur.

Fig. 10

Applications of secondary flow in curved channels. a Increasing interfacial area for diffusive mixing (Sudarsan and Ugaz 2006) Copyright (2006) National Academy of Sciences, U.S.A. b 3-D hydrodynamic focusing of fluid streams Reproduced from Mao et al. (2007a). c Creation of variable focal length. Reproduced from Mao et al. (2007b). d Separation of particles since larger particles intersect different regions of the secondary flow velocity field. Reproduced from Yoon et al. (2009)

Secondary flows in curved microfluidic channel systems have been proven helpful to increase the interfacial area for diffusive mixing. For example, three-dimensional twisted microchannels are analogous to the macroscale systems that take advantage of the chaotic advection, wherein the fluid interfaces are stretched and folded to increase the interfacial area to an extreme level, as depicted in Fig. 10a (Liu et al. 2000). Using this method related to twisted microchannel systems, complete mixing was obtained even for operating Reynolds number of the working fluid streams, $\mathrm{Re}<25$ as against a planar serpentine channel, wherein the Dean flow stretched the interfaces symmetrically back and forth with each turn failing to give chaotic advection (di Carlo 2009). The aspect ratio of the proposed microchannel systems is also important while mixing of two fluids takes place. A high aspect ratio (> 1) in a spiral microchannel system provides relatively higher mixing as compared to a low aspect ratio of about 0.5. A few advantages of using secondary flow for mixing in curved channels include the relatively simple design and operation, enhanced mixing with increasing flow rate as opposed to diffusive mixing, and the possibility of its application to various fluids having different viscosities, densities, and conductivities.

These Dean vortices have also been employed for particle sorting and separation. Particles having a density higher than the fluid can be separated because larger particles hinder different secondary flow velocity fields than the smaller ones, thus giving differential movement, which is depicted in the Fig. 10b (Yoon et al. 2009).

6 Numerical modeling of inertial microfluidics

Till date, numerous research groups have attempted to develop a numerical solution for better understanding of the fundamental elements of particle focusing inside inertial microfluidic devices. These resulting numerical solutions can be divided into three categories. First, asymptotic analysis of fluid equations predicts inertial forces acting on a particle within a micro channel. It has also been reported that the phenomena depicted by this numerical solution are far from the real situation due to oversimplified assumptions and limitations. Secondly, scientists have used Navier–Stokes-based solutions for inertial microfluidics, where all the concerns of particle size or particle effects on fluid streamline in asymptotic solutions were addressed. However, Navier–Stokes-based techniques present challenges while tracking the solid–fluid interface and calculating equations. Finally, for inertial flow modelling, researchers have employed the Lattice Boltzmann method (LBM). The relative ease of algorithm parallelization, the addition of new physics, and the strength of LBM in the intermediate Re regime have all contributed to its considerable application in inertial microfluidics during the previous decade. Accordingly, the primary aim of this section is to provide researchers with the latest updates regarding computational solutions of inertial particle motion within a microfluidic device.

In order to obtain the evidence for the observation made by Segre and Silberberg (1961), asymptotic solutions were taken into consideration for predicting the migration of particles in confined and non-confined flows. The semi-analytical and asymptotic solutions were based on perturbation theories, providing explicit formula for the forces acting on a particle and thus explaining the physics of motion of particles (Rubinow and Keller 1961; Saffman 1965). However, these proposed methods failed to explain details like the interaction between the particles and the surrounding fluid medium, the perturbed fluid velocity profiles around the suspended particles, and the application to a complex 3D domain. Thus, numerical methods were needed to understand the particle dynamics for a wide range of sizes and Reynolds number. We have discussed some of the most common methods for inertial particulate flows which use direct numerical simulation (DNS) method for simulating particle motion. DNS can be considered as an alternative and robust method, in which forces acting on a particle are calculated from the interaction between the fluid and the particle. In the context of Navier–Stokes based solutions, the DNS technique was adopted to simulate the particulate motion as briefly explained in the subsequent sections.

6.1 Flow at specific particle position (FSPP) method

This involves studying the steady-state flow around the particles and the inertial forces acting at a specific point on the suspended particle. Thus, it avoids the problems such as remeshing at each time step for calculation of transient particle motion. In order to calculate the steady-state flow conditions around a particle at a specific position (y, z) of the channel cross-section, a part of the channel length is considered, and then the particle is located at the center of this part at a specific position (y, z) and appropriate boundary conditions are implemented. The particle is considered at rest initially, followed by the calculation of pressure and velocity fields around the particle using Eqs. (25) and (26).

$${\text{Continuity \, equation}}:\nabla \vec{u} = 0$$

(25)

$${\text{Momentum}} \, {\text{equation}}:\rho \left( {\frac{{\partial \vec{u}}}{\partial t} + \left( {\vec{u} .\nabla } \right)\vec{u} } \right) = - \nabla p + \mu \nabla^{2} \vec{u} .$$

(26)

Following this, the values of forces and torques are calculated. The translational and angular velocities of the particle are calculated using the following Eqs. (27) and (28),

$$m_{{\text{p}}} \frac{{{\text{d}}\overrightarrow {{u_{p} }} }}{{{\text{d}}t}} = \oint\limits_{{\partial V_{{\text{P}}} }} {\left[ { - pI + \mu \left( {\nabla \vec{u} + \nabla \overrightarrow {{u^{T} }} } \right)} \right].\hat{n}{\text{d}}S{\prime} }$$

(27)

$$I_{{\text{p}}} \frac{{{\text{d}}\vec{\Omega }}}{{{\text{d}}t}} = \oint\limits_{{\partial V_{{\text{P}}} }} {\vec{r} \times \left\{ {\left[ { - pI + \mu \left( {\nabla \vec{u} + \nabla \overrightarrow {{u^{T} }} } \right)} \right].\hat{n}} \right\}{\text{d}}S{\prime} }$$

(28)

where ${\partial V}_{P}$ and n represent the particle domain and outward unit normal vector; ${m}_{p}, { u}_{p}, \Omega , r, {I}_{p}, I$ are the mass of the particle, linear velocity vector, angular velocity vector, position vector, moment of inertia of the particle and identity tensor, respectively, and $S{\prime}$ represents the surface area of the particle. The iterations are continued and the boundary conditions are updated in every time step. The iterations are stopped when the momenta in the y and z directions and the force per surface area become smaller as compared to the specified value. Finally, the components of inertial lift force acting on the particle in the y–z plane at point $({y}_{1},{z}_{1})$ are calculated. The distribution of inertial forces in the cross section of the channel can be derived by repeating this process for different places of the channel cross-section Thus, we see that, the FSPP method is a Lagrangian method which focuses on individual suspended particles and estimating the trajectory of each particle separately. However, FSPP has certain limitations when dealing with complex geometries or moving boundary conditions. Next we see the arbitrary Lagrangian–Eulerian method, which is incorporates the strengths of both between the Lagrangian and Eulerian methods, employing the Lagrangian approach for modelling the microstructure fluid flow behavior based on Eulerian approach.

6.2 Arbitrary Lagrangian–Eulerian (ALE) method

This method focuses on rigid particles suspended in an incompressible fluid. The surface velocity of particles is defined as: $u={u}_{p}+\Omega \times (x-{x}_{p})$ where, ${u}_{p}$, $\Omega$, and ${x}_{p}$ are particle’s center velocity, angular velocity, and center position, respectively. The Navier–Stokes equation and the incompressible continuity equation are used to solve the fluid flow. A finite element scheme is often used to solve for the flow behavior. This characteristic approach converts the non-linear Navier–Stokes equation into a linear Stokes-like solution. The Stokes-like equation is resolved using the finite element approach. For example, the pressure is calculated using piecewise linear finite element functions. The solution from the reference domain is converted back to the original moving domain once more via a change in variables (Duarte et al. 2004). Particle positions, orientations, and the velocities are updated in every time step by integrating the total stress on the surface of each particle and the Newton’s second law using Eqs. (27) & (28). Numerical simulations have suggested that the ALE approach largely eliminates the requirement to re-mesh the domain for each time step, while maintaining the interface conditions. Before continuing with the numerical simulation, the domain can be re-meshed if the quality of the triangle mesh deteriorates. By doing this, the needed mesh distortions can be kept under control long enough for the problem to be solved successfully. This enables to prevent projection errors and conserve computational time (Duarte et al. 2004). Also, if the density of the particle is less than that of fluid this method gives unstable results. This instability can be overcome by separating part of the drag force, which contributes to the acceleration of fluid around the particles from the total drag force. For more information about the arbitrary Eulerian–Lagrangian method and methods for stabilizing its numerical solutions, readers can refer to previously published articles in this area (Prosperetti and Tryggvason 2007). To eliminate re-meshing entirely, another group of methods, called the fictitious domain methods, can be adapted, wherein a force is applied to a particle’s domain to ensure that it obeys the rigid body motion.

6.3 Fictitious domain methods

As stated in the ALE method, the computational domain is re-meshed after certain intervals to simulate the flow of particles in this method. In this method, Navier–Stokes equation is used to solve the flow field for the entire computational domain. It is ensured that the fluid inside each particle obeys rigid body motion by applying a force to its domain. According to the application of this force on the suspended particles, the fictitious domain methods are classified as immersed boundary method (IBM), where force is applied on the surface of the particle and the immersed body method in which the force is applied to the body of the particle, respectively. Distributed Lagrange multiplier (DLM) method, which is a subset of immersed body method is being widely used. Here, one fixed mesh for pressure field and one finer mesh for fluid velocity are required to solve the fluid flow problem. Particles domain are discretized with additional meshes, which move with their corresponding particles. The size of the fluid mesh is smaller as compared to the particle mesh to avoid the overestimation of the proposed system. The flow field is solved within the computational domain, including the particles’ interior. With the consideration of rigid body motion, a distribution of Lagrange multipliers acts as body force densities, which are utilized to force the flow into particles. For more details on this method, the readers can refer to the work by Prosperetti and Tryggvason (2007).

In case of the IBM method, two computational meshes are considered. The first one is for the fluid motion which is defined as fix staggered Cartesian grid and it is also refereed as the Eulerian grid. The second one is defined by a set of markers which distribute evenly over the surface of the suspended particles. In case of boundary conditions, no-slip boundary condition is not explicitly imposed at the surface of the suspended particles. A force should be explained on the particle surface and added to the Navier–Stokes equation in order to maintain the constrained rigid motion of the particle. Finally, force is added to the Navier–Stokes equation to calculate the flow field and the motion of the particles, by employing the Newton’s second law of motion (Peskin 2002; Mittal and Iaccarino 2005).

7 Applications of inertial microfluidics in biomedical investigations

The conventional cell sorting techniques like the fluorescence- activated cell sorting (FACS), magnetic sorting, filtration, centrifugation and others need significant processing times, have complex preparation procedures, require larger spaces for their apparatuses, may lead to loss of cell viability, introduce contaminants in the sample and give low yields (Liao et al. 2016; Rahmanian et al. 2017; Bankó et al. 2019; Syal 2021; Farahinia et al. 2021; Xue et al. 2021; Li et al. 2021) For techniques involving PCR (polymerase chain reaction), various factors like the poor specificity of the primers, presence of PCR inhibitors in blood serum and DNA contamination from nucleated blood cells can affect the accuracy and precision of the results (Hänscheid and Grobusch 2002; Makanjuola and Taylor-Robinson 2020; Bosco et al. 2020) Thus, the novel field of microfluidics is being explored mainly due to low sample consumption, high efficiency, multifunction integration and a small device footprint. The separation of WBCs (White Blood Corpuscles) from whole blood was accomplished using a spiral inertial microfluidic channel, which had a U-shaped cross-section (Mehran et al. 2021). A microfluidic device having an aptamer-affinity was recently developed for the isolation of exosomes (Zhou et al. 2022). Microfluidics has also proven helpful for drug delivery and drug release. An asymmetric microfluidic/chitosan device giving controlled drug release was developed, which ensured preventing infections and guided bone regeneration (Shi et al. 2022). Table 2 presents an overview of the applications explored in the area of inertial microfluidics, the general achievements and shortcomings for the same.

Table 2 General overview of inertial microfluidics in terms of applications, achievements and limitations for biomedical applications

Here we have discussed the applications of inertial microfluidics in cancer cell migration, malaria diagnosis, separation of bacterial cells from RBCs, sustained drug release for guided bone regeneration (GBR) applications and the fractionation of blood.

7.1 Migration of cancer cells from blood samples using inertial microfluidics

The circulating tumor cell (CTC) test is a widely used test to assess the development or curing of breast cancers. It provides information about cancer by counting the number of cancer cells in a peripheral blood sample (Tanaka et al. 2012). Thus, a good separation technique is required to make this test accurate. Microfluidic systems that separate rigid particles or cells using hydrodynamic forces have proven useful for this application. Large hematocrit blood samples are preferred for cancer cell isolation to reduce the total separation time. However, for high hematocrit blood, the mixing effect is dominant due to the interactions between RBCs (Red Blood Corpuscles), which may result in inertial migration of cancer cells (Lima et al. 2008a; Saadatmand et al. 2011).

The migration of cancer cells from blood samples using an inertial microfluidics device was conducted in an experimental setup consisting of an inverted microscope and a high-speed camera as shown in Fig. 11a. Here, authors used two types of microchannels as depicted in Fig. 11b, Tanaka et al. (2012) which comprised of type A for rigid microspheres or cancer cells in dilute suspensions and type B, with three outlets, for high-hematocrit samples and were placed on the stage (Tanaka et al. 2012). The particles flowing in the restricted test portion, where the particle Reynolds number was high, were subjected to a strong inertial force. The microchannels were fabricated by using soft lithography (Lima et al. 2008b). The migration of cancer cells in PBS (phosphate buffer solution) and RBC suspension showed that the particle Reynolds number, $R{e}_{p}$, and the channel length/migration length, L played an important role in achieving the strong migration of the suspended particles. However, when rigid particles were tested for migration in PBS, they displayed better migration and they required shorter microchannel length as compared to the cancer cells, mainly due to the deformability of cancer cells and variation in their sizes. In case of the RBC suspension, when channel B was used (Fig. 11b), Tanaka et al. (2012) it resulted in a lower amount of sample in the second outlet stream as compared to the outlet streams 1 and 3. This indicated that the particles migrated to the inertial positions, even in presence of RBCs. Also, the migration became small as the concentration of RBCs increased i.e., when the RBC-RBC interactions increased (Tanaka et al. 2012). A high resolution microfluidic device with square concave obstacle was developed for the separation of particles with different sizes and the cancer cells (Cha et al. 2023).

Fig. 11

Experimental setup. a Schematic representation of the experimental setup (where, cancer cell migration takes place). b Geometries of two types of PDMS microchannel system. Adapted from Tanaka et al. (2012)

Tumor cell isolation and enrichment from peripheral blood samples has been actively pursued using microfluidic techniques, as an efficient tool for cell manipulation and detection (Pamme 2007; Tsutsui and Ho 2009; Ai et al. 2009; Wang et al. 2011; Chen et al. 2011; Zhu and Xuan 2011; Sun et al. 2012a). Since most CTCs are epithelial tumor cells larger than the surrounding blood cells and measuring between 13 and 25 µm in diameter, cell size is the frequently utilized metric for CTC enrichment (Bhagat et al. 2011). To obtain an efficient downstream detection, the pre-separation of rare CTC cells from the blood cells has become a prerequisite (Zhu et al. 2020a, b). For effective tumor cell separation without labeling and external force fields, hydrodynamic-based microfluidic cell separation approaches that only rely on the manipulation of fluids on a small length scale have been used. Tumor or blood cell separation was accomplished by producing hydrodynamic effects inside the specific micro-geometries, such as curved serpentine or spiral structures, whereby the trajectories and equilibrium positions of cells were size dependent (Hur et al. 2011). Utilizing the hydrodynamic forces inside the curved shape, a double spiral microfluidic device could quickly separate particles or cells without the use of labels. Such devices separated the tumor and blood cells based on size differences, with a throughput that was comparable to the conventional techniques. The geometry of the channel, the flow circumstances, and the characteristics of the suspending liquid medium were some of the variables that affected the operation of these microfluidic particle/cell sorting systems (Sun et al. 2013). Recently, a hybrid device combining the passive spiral inertial microfluidics with active surface acoustic waves was also numerically simulated for the separation of CTCs from the RBCs and WBCs (Altay et al. 2022).

7.2 Malaria detection using inertial microfluidics

Polymerase chain reaction (PCR), a molecular method, can detect low levels of parasites due to its high sensitivity and ability to recognize different malarial species and strains (Makler et al. 1998). However, the accuracy of this PCR technique may be affected due to various factors like less specific primers, the presence of PCR inhibitors in the blood serum and the contamination of DNA from nucleated blood cells (Hänscheid and Grobusch 2002). Label-free shear modulated inertial microfluidic system has been used to enrich the malaria parasites from the blood and increase the accuracy of PCR-based malaria detection. Cell-focusing behaviors based on the aspect ratio of the microchannel system and pinched flow dynamics were employed to separate the malaria parasites from lysed blood containing white blood cells (WBCs). This technique also used a rectangular microchannel system, having a high aspect ratio, with expansion–contraction arrays and three outlets, viz. two peripheral and one central outlet. The general procedure for the malaria diagnosis has been represented in Fig. 12a. A reduction in the particle size as compared to the diameter of the microchannel, resulted in disturbance in the balance between the shear-modulated lift force and wall-induced lift force, causing a change in the lateral equilibrium position of the suspended particles. Thus WBCs, having sizes comparable to the microchannel dimensions, experienced strong inertial lift forces and moved to the peripheral outlets, while most of the malarial parasites moved to the central outlet, since they were not focused (Fig. 12b). A cascaded method was created to execute 2-cycle enrichments in order to increase parasite enrichment while decreasing WBC contamination as shown in Fig. 12c (Warkiani et al. 2015).

Fig. 12

Reproduced from the reference (Warkiani et al. 2015) with permission from the Royal Society of Chemistry

a Steps in sample processing. b Schematic of the configurational and operational mechanism of the microfluidic chip. c Optical pictures of the actual cascaded device for enriching the malarial parasite.

7.3 Separation of bacteria from human blood cells using soft inertial microfluidics

Separation of bacteria from human cells, in small sample volumes for omics applications, is met with numerous challenges. Firstly, care has to be taken that the mRNA or protein expression profiles do not change; thus, high throughput is required to separate the cells quickly. Also, the method must be efficient enough to work for small sample volumes consisting of low bacterial cell densities. Lastly, the method must be able to separate a heterogenous bacterial population, alive, and if possible, from a heterogeneous mixture of human epithelial and blood cells (Wang et al. 2005). In particular, the RBCs are difficult to separate from bacteria because they have a size close to that of bacteria, in one dimension (2–3 µm), due to their disc shape. This decreases the effective size difference between the two cell types. When the particle Reynolds number is large enough, the particles have enough momentum to escape the trajectory of flow, when the flow experiences a sudden change. Figure 13a illustrates a sample flow carrying the particle joining a stronger acting flow, and both are introduced into a small channel at the same time. Due to the mismatch between the convective velocity, the particle flow is focused and accelerated near the entrance. A sheath flow of a very low flow rate is also provided to avoid direct interaction of the wall and the particle. During its flow, the particle loses momentum several times, and thus the mismatch leads to its separation from the original fluid axis (Wu et al. 2009a).

There is a substantial difference between the sizes of the RBCs (6—8 µm) and the bacterial cells (1–2 µm), thus increasing the separation efficiency. The larger particles (green dots, as shown in Fig. 13b, particle Reynolds number, ${\mathrm{Re}}_{\mathrm{P}}$ is high) get deflected from the original carrier flow, while the smaller ones (green dots, as depicted in Fig. 13b, ${\mathrm{Re}}_{\mathrm{P}}$ is small) are held inside the fluid. Thus, the two differently sized particles are separated into two subgroups (Wu et al. 2009b) (see Fig. 13)

Fig. 13

a Schematics of the formation of the curved and focused sample flow segment and particle momentum loss induced inertial force on the fluid element. b Schematics of the particle separation in the device. The right corner shows an example of the larger particles deflecting from the ordinal sample flow at the expanded outlet and c schematic diagram of the device design. Reproduced from Wu et al. 2009a)

The device design includes curved and focused sample flow segment formation and a mechanism for particle collection. The device schematics have been shown in Fig. 11c. It consists of three inlets, including sample fluid, protecting and acting sheath flow converge in the major channels. There are three collectors for small particles, large particles, and waste which are then connected to the major channel downstream section. There is a control channel designed between the inlets and collectors, which is controlled separately with an extra pump. A control channel that is situated between the inlets and collectors and is operated by an additional pump helped to ease the tuning of cell separation and responded to fabrication-related differences. The spreading inside the major channel could be changed by adding or removing fluid, which allowed the particle delivery to be adjusted according to appropriate collectors (Wu et al. 2008, 2009a).

7.4 Microfluidic device for sustained drug release

In this section we have discussed how a microfluidic device can enable guided bone regeneration (GBR) by a controlled drug release. The GBR technique traditionally uses a membrane which covers the bone defect area and prevents the migration of epithelial cells and the fibroblasts from hindering the bone formation. A large number of GBR membranes, having antibacterial properties have been developed till date (He et al. 2018). Chitosan has been used as an antimicrobial barrier membrane for GBR and guided tissue regeneration (GTR) (Xu et al. 2012; Husain et al. 2017). The microfluidic device prevents the fibroblasts from entering the defective region of the bones by employing dense polylactic acid (PLA) substrates along with a continuous drug release from the embedded reservoir at the gingival region., as shown in Fig. 14a, b. In therapeutic usage, the reservoir might be initially filled with drug-loaded nanoparticles and then topped off with specialized solutions. At the site of the bone defect, the chitosan side promotes osteoblast adhesion and growth. The device consists of three PLA layers, porous chitosan discs, a sealing film and a chitosan layer (Fig. 14c), respectively. The PLA film was used to cut the top and bottom of the PLA layers. To investigate the in vitro drug release characteristics under various drug-loaded techniques, minocycline was employed in this study. The device was loaded with minocycline and nanoparticles and subjected to specified experimental conditions, followed by calculating the concentration of minocycline at regular intervals, to calculate the cumulative release. The proliferation of Escherichia coli and Streptococcus mutans were also analyzed to assess the microfluidic/chitosan device in terms of antibacterial effectiveness (Shi et al. 2022). Using L929 fibroblasts and MC3T3-E1 osteoblasts, respectively, the microfluidic/chitosan device's fibrogenic and osteogenic properties were further investigated. Normal cell counting kit-8 (CCK-8) assay was utilized for this purpose (Yu et al. 2014). Minocycline was released due to molecular diffusion, and the release amount Q (mol) was calculated as;

$$Q=JAt$$

(29)

where, J is the molecular diffusion flux ($mol/{m}^{2}s)$, A is the exposed surface area (${\mathrm{m}}^{2})$, and t is the time scale (s). The diffusion flux can be estimated using the Fick’s first law of diffusion. The porosity of chitosan film was varied in order to control the release velocity of minocycline and fine tune the results. The chitosan discs (formulated from the chitosan films and placed in the microfluidic devices) adjusted the contact area between the embedded reservoir and the external microfluidic environment. Furthermore, the antibacterial properties of the device were also evaluated by using the optical density (OD) values of the test bacteria (Shi et al. 2022)

Fig. 14

a Microfluidic device between the gingival region and the bone defect region. b The working principle of the device. c Structure of the microfluidic device. Reproduced from Shi et al. (2022)

7.5 Blood fractionation using inertial microfluidics

Blood tests are the most sought after procedures to diagnose a disease. But the complex composition of the blood cells, can often hinder accurate analysis. Thus, a point-of-care diagnosis techniques are recommended as they utilize label-free microfluidic technologies, solely depending upon the inherent cellular properties of the blood cells, for separation and disease detection, without any need for antibody binding. The label-free microfluidic technologies for cell separation and detection have the advantage of being economic and giving rapid results. Inertial microfluidics has become increasingly popular for label-free separation of bio-fluids like blood, urine and semen. In the designing of inertial cell separators, it is important to make provisions for both, the target and the non-target cells, the cell sizes, their concentrations and volume, etc. (Lu et al. 2023). A zig-zag microchannel was designed for separation of the circulating tumor cells (CTCs) from whole blood. The zigzag structure helped in size-based particle migration and stabilized the focused particles and the larger CTCs $(>10 \mu m)$ to the channel center (Abdulla et al. 2020). Another type of channel structure employed is a spiral microchannel. Due to the larger channel dimensions, the clogging issues in these channels were minimized (Zhu et al. 2020b). A new inertial microfluidic cube was integrated with four spiral channels and stacked together to separate WBCs from whole blood under 2 min, with an efficiency of 88.1%. In order to separate smaller particles, a non-equilibrium cell-focusing approach was adapted, wherein a spiral microchannel with a diameter comparable to the particle diameter was employed to separate submicron bacteria and nanoparticles (Tay et al. 2017), which was further used to isolate extracellular vesicles (EVs) (Tay et al. 2021) (as shown in Fig. 15). Another passive microfluidic technique for cell sorting employed a viscoelastic fluid for focusing of particles. Due to the non-uniform distribution of the normal stress between the centerline and the walls of the microchannel, the elasticity of diluted polymer solutions leads single particles to migrate laterally and concentrate towards the channel center (Kim et al. 2021). It was recently reported that a sheath-less focusing device using viscoelastic fluid could isolate platelet-derived micro-particles (PDMPs $\sim 0.3-2 \mu m$) from RBCs in 2 min with a 4.8-fold higher yield than centrifugation (Nam et al. 2020).

Fig. 15

Reproduced from the reference with permission from the reference Tay et al. (2021) Royal Society of Chemistry

Spiral shaped single and multiplexed ExoDFF device for isolation of circulating EVs.

8 Conclusion and discussion

In this review, we discussed some crucial aspects of inertial microfluidics, like the forces involved, factors affecting the particle focusing, applications, along with the numerical simulations for inertial microfluidic devices. We concluded that several forces act on a particle in a fluid, including the viscous drag forces and the inertial lift forces. The viscous drag force acts in the direction parallel to the flow, while the lift forces act perpendicular to the flow. Magnus force is a rotation-induced lift force acting on a particle rotating in the fluid domain, while Saffman force is caused due to the interaction of slip velocity and shear. The wall lift forces create a velocity gradient in the fluid flow, and the shear gradient lift force makes the particle lag behind the fluid. We went on to describe the ways in which the wall lift forces and the shear gradient lift forces are of more significance than the other two, under the conditions of flow near the wall and in a highly viscous fluid. Under the influence of these inertial lift and drag forces, the particles migrate within the microfluidic channel. All these lift forces work towards focusing the particles to the equilibrium positions in a microfluidic channel after the particles have covered a certain length of the channel. For a non-Newtonian fluid, the motion of particles in the system can be understood in terms of non-dimensional numbers like the particle and channel Reynolds number and the Weissenberg number, while the Deborah number can help in understanding the viscoelastic properties of non-Newtonian fluid systems. We have also discussed about the ways in which focusing of particles occurs in channels with different cross-sections, namely the circular, square, and rectangular channels.

Various effects of particles on the fluid flow and the utility of secondary flow in the microfluidic channels were also discussed. The particles in the fluid are responsible for disturbing the flow of the fluid that is moving towards them, which may lead to repulsive interactions between the particles. The presence of a wall near a particle adds to the breaking of the closed streamlines and creating open and reversing streamlines. The creation of secondary flows in the channel cross-section is another effect of the particles in a fluid system, also known as particle-induced convection. This may result in small flows across the channel, originating from the focused particles and recirculating around the top and bottom of the channel due to conservation of mass. The particle size, flow velocity, and fluid density strongly affect this secondary flow. These secondary flows are the results of the local velocity difference around the particle and hence the weakest flows are obtained around the particle, near the center of the channel. Various modifications in a straight channel can help in the easier generation of these secondary flows. These include the curved microchannels (secondary flows generated is known as Dean flow), creating microgrooves in the channel, and introducing micropillars, which gives expansion–contraction structure to the channel. Major applications of these secondary flows depend on mixing the fluid and creating chaos, but due to their inevitable nature in laminar flow, these techniques can be used to induce order into a random system, with the use of flows transverse to downstream fluid streamlines, as a powerful tool for positioning fluid particles in the microchannels in a controlled manner.

The microfluidic devices can be used for various clinical applications like the separation of cancer cells, diagnosis of malaria, and much more. Micro and nanodevices have become increasingly popular because they give faster responses, can handle small fluid volumes and can control flows and pattern substrates on small length scales (Stone and Kim 2001). There are many more emerging applications of microfluidics, especially in the fields of biomedicine, industrial filtration, and beyond. One of the examples is the mechanophenotyping platform developed at UCLA, commercialized by CytoVale, which uses inertial focusing along with deformability cytometry to produce a new class of biomarkers (Tse et al. 2013). Another case is that of Clearbridge BioMedics, from the National University of Singapore, which is also making use of inertial microfluidics within spiral microchannels to segregate larger cancer cells from other components of blood in their ClearCell FX system (Hou et al. 2013).

Despite various advancements in the field of inertial microfluidics, right from the understanding of the underlying physics to the progress in the application to the biomedical sector, there are still a number of questions that are unanswered, especially pertaining to the numerical simulation. Inertial microfluidics can sometimes fail to separate smaller particles as they experience less inertial forces or require very large channel lengths for proper focusing. The areas that are least explored are that of the non-straight channels, deformable particles, and the viscoelastic fluids, solely for the reason that these studies are time consuming and complex. The non-spherical particles require a smaller time step, thus the amount of time required for numerical simulation is increased. The simulations of channels with no periodic pattern, for example, spiral channels, are difficult. It is challenging to conduct numerical simulations of viscoelastic fluids with high Wi. Commonly known as the high Weissenberg number problem (HWNP), which affects the numerical convergence for fluids with high Wi, this a well-known issue. This issue arises because conformation fields might have steep boundary layers that cannot be accurately represented by low-order polynomial interpolation algorithms. (Razavi Bazaz et al. 2020) In inertial microfluidic chips, there’s often a trade-off between the efficient particle manipulation and precise control over the particle behavior within microchannels owing to various reasons like the complex flow dynamics, microchannel geometry, and interparticle interaction. Furthermore, universal design rules need to be developed, which can be applied to a broad range of microfluidic devices (Xiang and Ni 2022).. A high sample throughput requires a high flow rate, which again increases the complexity of flow through the microchannels, thus hindering precise control. Also, automation in the microfluidic devices is an important goal that needs to be achieved.

Artificial intelligence can also prove helpful for design of inertial microfluidics devices. Machine learning, for instance, has been used to speed up the prediction of inertial lift in inertial microfluidic channels. This information can then be incorporated into the Lagrangian tracking method to precisely predict the particle focusing in spiral channels and channels with various cross-sectional shapes (Su et al. 2021). Additionally, machine learning with failure trials might be used to swiftly control the separation of a desired sample, making it feasible to automatically discover the best separation parameters when switching the samples. The different channels used for inertial microfluidics applications, including straight, spiral and serpentine channels, need to be optimized and modified and redeveloped considering the actual physical mechanisms of the system (Fukada and Seyama 2022).

Inertial microfluidics devices often show low specificity due to various reasons like the variability of sample, non-uniform flow rates, and the dominance of diffusion. Integration of inertial microfluidics should be performed with active microfluidics in order to increase the efficiency, throughput and the purity. For example, a hybrid microfluidic device was recently fabricated which consisted of two chips, the PDMS chip which was serpentine in shape (inertial/passive microfluidics) connected to the trifugal-shaped acoustofluidic chip (active microfluidics—acoustophoretic). The serpentine chip can pre-focus the particle in two rows, followed by the acoustofluidic chip to separate the particles based on size by the acoustic radiation force (Kim et al. 2022). Dielectric technology was integrated with an arcuate channel and in-situ mRNA extraction platform was accomplished measure the marker-gene expression of the target cells (Li et al. 2017). A novel external dielectrophoretic force field coupled with inertial forces was introduced to provide a hybrid DEP-inertial microfluidic platform for particle adjustable separation (Zhang et al. 2018). In this technology, the electrical voltage could be changed without changing the channel structure or the dimensions to change the size of the target particle mixture. Viscoelasticity based microfluidic system was created to directly separate the exosomes from the cell culture, with high purity and recovery (Liu et al. 2017). 3D printing can be used to fabricate complex microfluidic structures for mixing applications. 3D printing allows provides freedom for designing complex novel structures which cannot be obtained with the traditional methods like planar micromachining techniques (Nielsen et al. 2020). The most advanced method that can be considered for use in biomedical and pharmaceutical applications is microfluidic cell culturing. Applications requiring high throughput will continue to adopt continuous-flow microfluidics. Continuous-flow microfluidics are less suited to applications requiring small sample sizes due to the issue of bulky external liquid delivery and the requirement for optical microscopy for characterization. The issue of bulky external systems and the comparatively large sample volume is resolved by digital microfluidics using droplets and liquid marbles (Nguyen et al. 2017). Thus, inertial microfluidics holds great potential, but this still being a novel field, a fundamental and in-depth study of various systems is required to incorporate them into more valuable, advanced and realistic platforms.