1 Introduction

The focusing and enrichment processes for rarefied samples are important for increasing diagnostic sensitivity in numerous biological and chemical research fields. Several microfluidic devices have been developed to increase diagnostic sensitivity. However, the use of conventional methods, such as membrane filtration, gave rise to clogging problems and high maintenance costs. Several membrane-less techniques that operate in continuous-flow modes and are free from the aforementioned problems have recently been developed (Bhagat et al. 2008; Di Carlo 2009; Jaggi et al. 2007; Kim and Yoo 2012; Wickramasinghe et al. 2001; Yang et al. 2006). These devices usually focus the particles into a tight stream by using hydrodynamic lateral forces that induce inertial migration. A particle that is subjected to shear flow migrates across the streamline because of inertia. Segre and Silberberg (1961) observed that a spherical particle in a pipe flow moves outward from the center and inward from the wall to a specific equilibrium position. Kim and Yoo (2009a, b) demonstrated the same phenomena by using charged particles and an electric field. Choi and Lee (2010) investigated the inertial migration of neutrally buoyant spherical particles, which were suspended in a microscale pipe flow at a Reynolds number range of 1.6 ≤ Re ≤ 77.4 by using a digital holography technique. Particles in straight rectangular microchannels are focused at two or four symmetric equilibrium positions depending on the cross-sectional shape of the channel (Chun and Ladd 2006).

Kim and Yoo (2008) experimentally investigated the inertial migration of particles inside a square microchannel in the range of 0.06 ≤ Re ≤ 58.65. Di Carlo et al. (2009) conducted experimental and numerical studies to account for the finite size of the suspended particles in a square channel. The three-dimensional (3D) positions of neutrally buoyant spherical particles inside a square microchannel were measured by using the digital holographic microscopy technique (Choi et al. 2011). In a theoretical study, Schonberg and Hinch (1989) calculated the inertial migration of a small sphere in a two-dimensional (2D) Poiseuille flow by using the matched asymptotic expansion method. They found that the equilibrium position moves toward the wall as Re increases. Matas et al. (2004, 2009) investigated the inertial migration of particles at high Re ranges for a planar channel flow and a pipe flow in experimental and theoretical studies. Shao et al. (2008) investigated the inertial migration of spheres in a pipe flow in the range of Re ≤ 2,200. They observed the inner equilibrium positions as Re exceeded a critical value. Chun and Ladd (2006) numerically simulated the inertial migration of particles inside a square duct in the range of 100 ≤ Re ≤ 1,000.

The secondary Dean flow can be combined with the effect of inertial migration to reduce the number of equilibrium positions further. For example, curved or spiral microchannels have been demonstrated to create a single focused particle stream by inducing the interaction between the inertial lift and the Dean drag. Ookawara et al. (2006) numerically examined the development of particle concentration profiles over cross-sectional planes through a series of angular positions in a curved microchannel, which is the functional part of a microseparator. Studies by Bhagat et al. (2008) and Kuntaegowdanahalli et al. (2009) suggest an inertial microfluidic device that achieves continuous particle separation by using the principle of Dean-coupled inertial migration in spiral microchannels. However, in practice, curved or spiral microchannels have high costs because of their complex fabrication processes as well as the limited accessibility to expensive facilities. In addition, little is known about the Dean-coupled inertial migration of a particle. Thus, instead of using microchannels, we employed a flexible microtube, which is relatively inexpensive, for the basic study on the particle behavior and the purpose of simple sample focusing and enrichment.

The secondary Dean flows in a curved tube originate from the centrifugal hydrodynamic pressure imbalance in the main flow, which can be weighed by using the Dean number (De). The pressure imbalance generates fluid inertia that is directed toward the outward walls. The flow inertia is larger in the central region than in the near-wall regions because of flow velocity. The symmetric tube geometry induced the dual recirculation of the flow at the top and bottom halves of the tube cross-section to satisfy continuity, as shown in Fig. 1a. De, which describes the magnitude of the secondary flow, is defined as follows: \( De = Re\sqrt \delta \), where δ is the ratio of the tube radius (D/2) to the radius of curvature (R c), that is, \( \delta = D/(2R_{\text{c}} ) \) (Berger et al. 1983; Dean 1928; Kim and Lee 2009). The characteristic secondary flow velocity can then be scaled as \( U_{D} \sim (De)^{2} (\nu /D) \), where ν is the kinematic viscosity (Dean 1928). The Dean vortex flow in a curved pipe flow as well as its effect on the mass transfer through the liquid–liquid interface of two fluids is well studied numerically (Gelfgat et al. 2003).

Fig. 1
figure 1

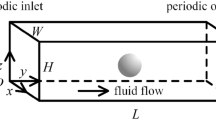
a Configuration of the curved microtube with an inner diameter of 350 μm. The positional information of particles was measured at θ of 0°, 90°, and 180°. The Dean flow in a curved channel has two counter-rotating vortices that are perpendicular to the direction of the main flow. Suspended particles are subjected to Dean drag and inertial lift forces. The focusing positions of particles in curved channels are determined through the superposition of these two forces. b Schematic diagram of the experimental setup for digital holography

Full size image

The particles in the curved microtube exhibited both the inertial lift force (F L) from the main streamwise flow and the Dean drag force (F D) from the secondary flow. The particles tended to be positioned in the force-free region, where F L and F D are balanced. The technique of matched asymptotic expansions proved to be one of the most useful methods in determining dominant lateral forces on particles: \( F_{\text{D}} = f_{\text{L}} \rho U_{m}^{2} d^{4} /D^{2} \), where f L is a non-dimensional lift coefficient, U m is the streamwise mean flow velocity, and d is the particle diameter (Asmolov 1999; Matas et al. 2004; Schonberg and Hinch 1989). F D can be estimated by using the Stokes drag given by \( F_{\text{D}} = 3\pi \rho \nu dU_{D} = k\rho dU_{m}^{2} D^{2} /R \), where k is a constant (Berger et al. 1983). The inertial equilibrium positions can be modified to a specific position where F L and F D are balanced, that is, F L ≈ F D. However, given that f L and the secondary flow velocity U D strongly depend on the flow condition, the particle and channel dimensions, and on the spatial position of the particle, the conditions required for the exact force balance are difficult to define clearly.

Although a number of experimental techniques have been employed in previous studies, most of these techniques are based on the point-wise scanning of the measurement area or on the 2D imaging of the mid-plane of a channel or pipe. An accurate measurement of particle motion in a circular pipe is especially difficult to achieve because of the curved surface of the pipe. Chun and Ladd (2006) have recently mentioned that the inertial migration of particles in a narrow channel is a fully 3D phenomenon. Therefore, a 3D measurement technique is ultimately required to measure the complex flow phenomena directly. In our previous study (Choi and Lee 2010), the lateral migration and tubular pinch effect of particles in a straight microtube were investigated at a certain Reynolds number (Re). In the present study, we obtained the 3D measurement of spherical particles transported through a curved microscale pipe flow by utilizing a digital holography technique for the basic study of particle motions as well as for simple particle focusing. We focused on Dean-coupled inertial migration and on the transient agglomeration of particles at the curved section of the tube. In addition, we experimentally investigated the effects of Re and De on the said phenomena.

2 Experimental conditions

The microtube in this study had a diameter D of 350 μm and was made of fluorinated ethylene propylene (FEP), which has a similar refractive index as that of water. The optical distortion attributed to refraction was prevented by immersing the tube in a water bath. The tube was bent at an angle of 180°, 30 cm downstream from the entrance. The 30 cm length ensured the fully developed state of radial migration under the experimental conditions. The radii of curvature (R C) at the bending region were 2.5, 5.0, and 7.5 mm, and the corresponding ratios of the tube to the radius of curvature δ were 0.07, 0.035, and 0.023, respectively. Polystyrene microspheres with mean diameters d of 7, 15, and 30 μm were used as test particles. The particles were suspended in purified water with concentrations below 0.5 % in the volume fraction to disregard the particle–particle interactions. The density of water was then by using dissolved sodium chloride to achieve neutral particle buoyancy (ρ = 1.05 g/cm3). Flow rates were adjusted by using a syringe pump, such that the value of Re was in the range of 6.4–129, and the corresponding value of De was in the range of 1.69–34.1. The experimental conditions are summarized in Table 1.

Table 1 Summary of experimental conditions
Full size table

3 Digital holography

3.1 Digital holographic microscopy

In this study, the particle positions in the cross-sectional plane of a microtube are measured by using digital inline holographic microscopy (DIHM) (Choi and Lee 2010; Choi et al. 2011; Sheng et al. 2006). The DIHM method measures the 3D positional information of particles. Figure 1b shows a schematic diagram of the DIHM setup that comprises a continuous Nd:YAG laser (CrystaLaser, USA), a water-immersion objective lens (20×, NA = 0.50, Nikon, Japan), and a digital high-speed camera (Ultima-APX, Photron, Japan).

3.2 Numerical reconstruction of hologram

Prior to hologram reconstruction, the time-averaged background image is subtracted from the original raw holograms to eliminate the noises caused by optical components and misalignment. The background-subtracted hologram image is then numerically reconstructed to analyze the 3D positional information of the particles by employing the following Fresnel–Kirchhoff diffraction formula, which consists of the convolution between the hologram function h(x, y) and the diffraction kernel g(x, y) at each reconstruction plane:

$$ \Upgamma (\xi ,\eta ) = \frac{i}{\lambda }\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {E_{R} (x,y)h(x,y)} } \frac{{\exp \left( { - i\frac{2\pi }{\lambda }\rho } \right)}}{\rho }{\text{d}}x{\text{d}}y $$
(1)
$$ \rho = \sqrt {d^{2} + \left( {\xi - x} \right)^{2} + (\eta - y)^{2} } . $$
(2)

where \( \rho \) is the distance between a point in the hologram plane and a point in the reconstruction plane. The coordinate system of the numerical reconstruction is described in Fig. 2. Eq. 1 calculates the complex amplitude of the reconstructed wave field at a distance d from the hologram plane. To reconstruct the volume information of the object field, reconstruction should be performed through the whole volume with varying the reconstruction distance d.The Fresnel–Kirchhoff integral of Eq. 1 can be interpreted as a convolution of the hologram function h(x, y) and of diffraction kernel g(x, y):

$$ \Upgamma \left( {\xi ,\eta } \right) = \left\{ {h(x,y) \otimes g(x,y)} \right\}\left( {\xi ,\eta } \right) $$
(3)
$$ g(x,y) = \frac{i}{\lambda }\frac{{\exp \left( { - i\frac{2\pi }{\lambda }\sqrt {d^{2} + x^{2} + y^{2} } } \right)}}{{\sqrt {d^{2} + x^{2} + y^{2} } }}. $$
(4)

From the convolution theorem, the integral can be efficiently calculated by using the 2D fast Fourier transforms (FFTs) as follows:

$$ \Upgamma \left( {\xi ,\eta } \right) = \Im^{ - 1} \left[ {\Im \left\{ {h\left( {x,y} \right)} \right\}\Im \left\{ {g\left( {x,y} \right)} \right\}} \right] $$
(5)

where \( \Im \) and \( \Im^{ - 1} \) denote the FFT and inverse-FFT, respectively. The intensity field of the reconstructed images can be obtained by taking the absolute \( \left| {\Upgamma (\xi ,\eta )} \right| \).

Fig. 2
figure 2

Coordinate systems for the numerical reconstruction

Full size image

3.3 Determination of 3D particle position

After numerical reconstruction, the 3D positional information of the particles is determined. To identify the in-plane (x, y) positions of each particle, the center position of the particles that have higher intensity values than the background is investigated by using a local-peak-searching algorithm.

After identifying the in-plane position of each particle, a rectangular section that encloses each particle is generated through particle segmentation. The size of each segment is determined to hold the neighboring pixels that exceed 80 % of the particle center intensity in the projection image. Each reconstructed particle image is then cropped along the rectangular section, and the corresponding focus value of each section is calculated by adopting an autofocus function (Choi and Lee 2009). This process generates a list of focus values for each particle throughout the depth direction. Thus, the z-position of the particle can be determined as the peak position of each focus value profile. We used LAP as a focus function, which accounts for the variation in the intensity gradient defined as follows:

$$ {\text{LAP}}(z) = \sum\limits_{x,y} {\{ \nabla^{2} I(x,y;z)\}^{2} } , $$
(6)

where I(x, y, z) is the discrete intensity distribution of the segmented reconstruction image. A typical example of the focus value profiles that are obtained from reconstructed particle images is shown in Fig. 3.

Fig. 3
figure 3

Typical hologram image of 15 μm particles and the corresponding reconstructed images at different depthwise positions. Each particle is optimally focused at a certain z-position, where the corresponding focus value becomes the maximum. The particle surrounded by a square box is located 134 μm away from the focal plane, which corresponds with the result obtained from the focus value profile

Full size image

4 Inertial migration in straight pipe flow

The inertial migration of the suspended particles at the entrance of the curved section (θ = 0°) is initially investigated by adjusting the particle size and the value of Re. Figure 4a shows the spatial distribution of the 15-μm particles (D/d = 23) at θ = 0°. The particles accumulate around the central region of the tube at approximately r/R < 0.6 at the lowest Re of 6.4 because the hydrodynamic particle–wall interaction pushes the particles away from the wall. On the other hand, the particles in the central region migrate toward the wall when the value of Re increases because of the increased shear gradient force. The so-called tubular pinch effect consequently becomes distinct. Figure 5a shows the variations in the radial equilibrium position (r eq), in which the particles are pinched, as a function of the Re and of the particle size ratio D/d. Under the present experimental conditions, r eq /R varies from 0.55 to 0.73, where R is the radius of the tube (R = D/2). The r eq /R value increases with increasing Re because of the increase in the outward F L. The outward lift force is proportional to U 2 m , whereas the wall repulsion is proportional to U m . With fixed Re, the r eq /R decreases with increasing particle size because of the decrease in the gap between the particle and the tube wall, which significantly increases the hydrodynamic wall-repulsion force arising at the gap.

Fig. 4
figure 4

Cross-sectional views of particle distributions (D/d = 23) flowing in a curved pipe (δ = 0.07) at a θ = 0°, b θ = 90°, and c θ = 180°

Full size image
Fig. 5
figure 5

a Variations in equilibrium positions (r eq) according to the value of Re. b Variations in F C with respect to the value of Re and of the particle distribution (D/d) at the entrance of the curved channel (θ = 0). The inertial migration effect was fully developed when F C was over 100

Full size image

The specific condition under which the “tubular pinch effect” is fully developed by the inertial lift force is evaluated at the entrance of the curved region (θ = 0°). In our previous study (Choi et al. 2011), we suggested a dimensionless parameter called “Focusing number” (F c) that determines the flow condition for inertial focusing by balancing the inertial lift and the Stokes drag as follows: \( f_{\text{L}} \rho U_{m}^{2} d^{4} /D^{2} = 3\pi U_{\text{Dean}} d \). In addition, Di Carlo et al. (2009) reported that the product of the inertial lift coefficient f L and of the particle size ratio d/D can be fitted into a single curve as \( f_{\text{L}} \times (d/D) = C_{\text{L}} \), in which C L varies in the range of 0–0.04. By simply relating these two expressions, a ratio between the streamwise and lateral velocity components of a migrating particle can be deduced and the resultant traveling distances of the particle can be estimated directly as follows:

$$ \frac{{L_{x} }}{{L_{l} }} \approx \frac{{U_{\text{m}} }}{{U_{l} }} = \frac{3\pi }{{C_{\text{L}} {Re}_{\text{C}} (d/D)^{2} }} $$
(7)

Given that the particle equilibrium position exists around 0.6–0.7 times half width of a channel, the appropriate lateral migration distance L l should be approximately 3/D. Furthermore, the required L E needs to be designed longer than the streamwise sweeping distance L x . Thus, a dimensionless parameter F C, which determines the inertial focusing flow condition, can be obtained by substituting these values into Eq. (6) as follows:

$$ F_{\text{C}} \equiv {{Re}}_{\text{C}} \left( \frac{d}{D} \right)^{2} \frac{{L_{\text{E}} }}{D} > \frac{\pi }{{C_{\text{L}} }}, $$
(8)

where Re c is the channel Reynolds number at maximum flow velocity, L E is the entrance length. The particles in a square channel are obviously fully focused on the lateral direction when F c exceeds a certain critical value of π/0.02. Moreover, the cross-lateral focusing of particles on the four equilibrium positions of each surface of a square channel occurs when F C exceeds a higher value of π/0.01 (Choi et al. 2011). Several F C values are obtained from various Re, which is in the range of 6.4–129, and from various particle size ratios as shown in Fig. 5b. From the experimental observations, we verify that the tubular pinch effect is fully developed in a straight pipe flow over 100 of F c, where C L corresponds to 0.03.

5 Inertial migration combined with secondary flow effects

Experimentally, we tested a wide range of flow rates, 1.67 < De < 34, by using a U-shaped, single-turned microscale pipe flow, where we systematically varied the radius of curvature (R C) and particle size (d). The flow information and velocity field of secondary flow were investigated before studying the interaction between particles and flow. Figure 6 shows a typical velocity field of the secondary flow as well as the velocities of the main and secondary flows. Two large counter-rotating vortices that are perpendicular to the main flow are clearly observed. The fast-moving fluid along the horizontal midline of the tube cross-section is directed outwards, whereas the slow-moving fluid along the top and bottom walls of the tube is directed inwards, as shown in Fig. 6a.

Fig. 6
figure 6

Numerical analysis was conducted to investigate the secondary flow in a curved pipe by using the same numerical model with experiments. We conducted 3D, finite-element simulations that solve the steady-state Navier–Stokes equations in software (COMSOL Multiphysics). a Typical velocity field of secondary flow. The Dean number is 17.1, which corresponds to a Reynolds number of 64.7 in the tube (θ = 90°) with a diameter (D) of 350 μm and a radius of curvature (R C) of 2.5 mm. b Instantaneous iso-velocity contours of the secondary flow at θ = 90°, where the tube diameter (D) is 300 μm (Kim and Lee 2009). c Variation of the mean streamwise velocity and the maximum velocity of secondary flow in a curved circular tube (D = 350 μm) as a function of the Reynolds number, the ratio of tube diameter to radius of curvature (δ) and θ

Full size image

In our previous study (Kim and Lee 2009), Dean flow in a curved microtube (D = 300 μm) was measured using digital holographic particle tracking velocimetry (DHPTV) technique in the range of 5 ≤ De ≤ 100. For the case of De = 50, the center of the large-scale counter-rotating vortex is located close to the center of the half-region of the microtube, as shown in Fig. 6b. As the Dean number increases, the center of the large-scale vortex moves toward the outer bend and the iso-velocity contours of the secondary flow in the central region of the microtube are bent upward. With increasing De, additional small-scale vortex structures are developed. Gelfgat et al. (2003) found a similar structure of the transverse flow (Dean vortices) numerically by using finite volume method. In the present study, the interaction between the secondary flow and particles was investigated in the range of 1 < De < 34, corresponding to the case of low De in the previous study. Therefore, the flow conditions of the present study can be regarded as a steady-state, two large-scale counter-rotating vortices called as classical Dean flow.

The drag force exerted on a particle in the orthogonal direction relative to the mainstream can be obtained by assuming the Stokes drag as follows: \( F_{\text{D}} = 3\pi U_{\text{Dean}} d \). Therefore, the rate of particle transportation across the main flow is directly proportional to the local velocity of the secondary flow.

The secondary flow deforms the particle trajectories when the tubular-pinched particles pass through the curved section of the tube. The deformation of the circular particle annulus depends on the measurement location (θ) and on the value of De. The particle annuli, which are initially circular, were observed to change, and the unique agglomeration patterns of the particles appeared. Figure 4b, c shows the cross-sectional position of the particles at two cross-sections with θ of 90° and 180°, respectively, and with varying values of De. Initially, the particles (d = 15 μm, D/d = 23) located near the inner bend (left side) start to migrate toward the outer bend (right side) along the horizontal midline of the tube cross-section at De = 8.55, as shown in Fig. 4b. The particles that are positioned near the outer bend are swept along the top and bottom walls of the tube, and outward migration along the midline is further developed as De increases (Fig. 4). The cross-lateral migration of particles across the main flow is further developed at θ = 180° compared with those at θ = 90°, as shown in Fig. 4c. The particle migration exhibits diverse distribution patterns according to De and θ.

The local particle distribution was evaluated by using the probability density function (PDF). Figure 7 represents the PDF distributions, where the locally concentrated regions are prominently colored red. The particles tend to agglomerate at a narrow cross-sectional region near the outer bend when θ = 90° and when De is in the range of 25–34. The particles exhibit gradual migration with various agglomeration patterns as they are transported downstream of the curved region and as De increases. Although the local concentrations at θ = 180° are not extremely high, the particles focus around the inner bend or the center region when the value of De is properly controlled in the range of 17–34, as shown in Fig. 7b.

Fig. 7
figure 7

Normalized particle distributions in a curved tube (D/d = 23, δ = 0.07) at the cross-sections of a θ = 90° and b θ = 180°

Full size image

Under the critical value of F C for the condition of the fully developed tubular pinch effect, the agglomeration patterns do not appear in the curved region, and the particles are affected mainly by the Dean drag force compared with the inertial lift force (F D ≫ F L). Such a phenomenon can be attributed to low Re, insufficient entry length, and small particle size compared with channel dimension; for instance, the inertial lift force exerted on a particle is insufficient because of small particle size and low Re (d = 7 μm, F C = 22–88). Thus, the agglomeration patterns do not appear clearly, as shown in Fig. 9a. At a high De value, the inertial lift force can be disregarded versus the Dean drag force (F D ≫ F L). Therefore, the mixing process attributed to secondary flow is dominant, and particle agglomeration is destroyed. These observations imply that transient particle focusing can occur at a moderate range of flow conditions (F D ≈ F L).

Figure 8 shows the top view (general 2D observation) of the PDFs of the particles along the lateral axis of the tube with θ of 90° and 180°, respectively. D nor represents the lateral position normalized by the tube diameter. The PDF distributions show the accumulation of particles at certain lateral positions. When θ = 90° and the value of De is in the range of 25–34, most particles accumulate in the region near the outer wall of the tube (D nor of 0.7–0.8). In addition, the particles accumulate near the inner bend (D nor of 0.25) when θ = 180° and De is 25.7.

Fig. 8
figure 8

Lateral PDF distributions of the particles across the microtube at a θ = 90° and b θ = 180°

Full size image

The effects of particle size (d) and the radius of curvature (R c) were investigated by using spherical particles with d of 7, 15, and 30 μm and curved tubes with R c of 2.5, 5, and 7.5 mm, respectively. Figures 9 and 10 show the spatial distributions of particles for the aforementioned cases. As shown in Fig. 9a, in the case of small particles (d = 7 μm), the focusing patterns of the particles are not evident because the inertial lift force is insufficient to establish a fully developed particle annulus at the entrance of the curved section. On the other hand, in the case of a sufficiently large particle size, similar agglomeration patterns of the particles are clearly observed under the same Re conditions (Fig. 9b, c) because the lift force exerted on a particle is proportional to the particle size. Interestingly, the similar focusing patterns of the particles are observed at the different radii of curvatures and ratios between a particle and tube diameter under modulate flow conditions.

Fig. 9
figure 9

Effects of particle size on the particle migration flowing in a curved circular microtube. Cross-sectional distributions of stationary particles a D/d = 50, b D/d = 23, c D/d = 12 in a curved tube at θ = 180°, δ = 0.035. In the case of (a) a small particle (d = 7 μm) and a low Reynolds number, particle migration is not fully developed because of insufficient inertial lift force. Despite the different ratios of particles and of the channel diameter, the migration pattern is similar under the same flow conditions

Full size image
Fig. 10
figure 10

Effects of the ratio of channel diameter to radius of curvature (δ) on the particles (D/d = 23) migrating in a curved circular tube. Cross-sectional distributions of stationary particles a δ = 0.07, b δ = 0.035, and c δ = 0.023 in a curved tube at θ = 180°

Full size image

We demonstrate the obtainment of a single particle stream by using a U-turned curved tube with an R C of 5 mm (δ = 0.035) and sphere particles with d of 15, 30, 50 μm at the tube outlet (θ = 180°). The flow condition can be controlled to obtain similar cross-sectional particle distributions for De = 25.7–34.1 for a single particle stream near the outer wall of the tube outlet, as shown in Fig. 7a. Figure 11 represents the trajectories of particles (d = 30 μm) passing through the curved pipe flow at Re = 51.2, where the corresponding De value is 9.6. Most particles pass through the half plane near the outer wall in the cross-section at the outlet of the curved section. To get more detailed statistical information on the particle focusing at the tube outlet, the histogram of the normalized number of particle across the tube outlet was extracted, as shown in Fig. 12. The values 0 and 1 of D nor represent the inner and outer walls, respectively. The lateral positions of particles over 1,000 are measured for each case. The three different sizes of particles are well focused at D nor values from 0.6 to 0.8. Particularly, in the case of d = 50 μm, particles are focused at a narrow stream near the outer wall, where more than 80 % of particles are focused at D nor = 0.7 ± 0.04.

Fig. 11
figure 11

Trajectories of particles (d = 30 μm) at Re = 51.2 and De = 9.6. Most particles pass through the half plane near the outer wall in the cross-section at the outlet of curved section

Full size image
Fig. 12
figure 12

Histograms illustrating the normalized number of particles across the tube outlet at Re = 51.2 and De = 9.6

Full size image

6 Conclusions

In this study, we experimentally investigated the Dean-coupled inertial migration and transient focusing of particles in curved microscale pipe flows by using a 3D imaging technique under varying flow conditions. The randomly suspended particles formed a circular annulus in the straight entrance section of the tube and were subsequently deformed by the secondary flow in the curved section. The particles were focused in a narrow cross-sectional position under a specific flow condition. The particle focusing position can be controlled and adjusted by properly tailoring the curve and flow conditions. We demonstrated particle focusing on a narrow stream at the exit of the curved pipe flow. This phenomenon can be used as a simple method for particle focusing to make sample diagnoses in microfluidic devices easier.