1 Introduction

Recently, there has been a rapid development of microfluidic technologies. The design of microfluidic laboratories on chips is one of the interesting directions of using such technologies for detecting macromolecules in human biological liquids for needs of chemical diagnostics [1]. For example, there are already known examples of developing cheap devices for determining high-density lipoprotein cholesterol and low-density lipoprotein cholesterol in plasma of human blood [2], developing of a microfluidic concentrator to assist trapping miRNA [3], and creating a microfluidic device for irreversible dissociation and quantification of miRNA from ribonucleoproteins [4]. All the devices are based on the ion-selective materials and the effect of the concentration polarization that occurs near such surfaces. Using flat geometry for design simplifies the manufacture of such devices but limits their functionality. Three-dimensional geometry, even in a relatively simple, spherical configuration, allows to combine a micro-pump, a micromixer and a micro-concentrator in one device. In the paper of S.-C. Wang [5], an ion-selective microgranule was used, creating concentration polarization due to the occurrence of an electroosmosis of the 2nd kind [6, 7], which, having a quadratic dependence on the field strength, at large values gives the effect of concentration of ions, which could not be observed near a conventional dielectric microsphere. The same device can work as a micromixer [8, 9]. Moreover, the variety of regimes that were predicted theoretically in the electrophoresis of ion-selective microparticles [10] indicate the need for a detailed analysis of potential devices and, perhaps, in the future will inspire researchers on the development of new technologies using ion-selective microparticles.

The paper will present a theoretical study of the concentration effect in a spherical configuration close to that presented in [5] and [8]. As our studies have shown [9], this configuration can be used not only to concentrate ions, but also to generate a concentration jet, which can be useful for solving the separation of the fluid flow problem, as it happens, for example, during electrodialysis [11]. Laboratories on a chip are usually designed in theory with micron and even submicron channels in which the influence of gravity can be neglected, and the entire transport of liquids is carried out by electroosmosis. Nevertheless, when it comes to experiments [3, 5] and even more to constructing prototypes [4], the dimensions of the channels become the size up to a millimeter, and the whole device can easily reach several centimeters. On such a scale, the influence of classical convection can indeed be neglected in most cases [12], but the tubes and channels filled with liquid leading to the device will inevitably create additional pressure, which will create an additional flow of liquid in the device other than the electroosmotic one. That is why we paid special attention to this phenomenon in our work. Since such experimental devices are quite expensive to produce, numerical and theoretical studies are an inexpensive way to develop prototypes and study configurations of new devices.

2 Statement

2.1 Geometric characteristics

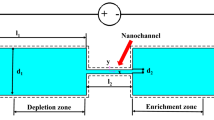
The proposed device design (Fig. 1) consists of a spherical chamber with an ion-selective microgranule placed in its center. The chamber has an inlet and outlet for the fluid flow. A constant electric field is created using electrodes at the inlet and the outlet, this field creates an electroosmotic flow in the chamber. Besides, when the device is positioned vertically, there is a pressure difference between the inlet and outlet, which is another fluid control mechanism. The pressure difference depends on the height of the water column in the supply channel. The problem is assumed to be axisymmetric. A liquid is an electrolyte solution consisting of two types of ions. At the inlet, a homogeneous, electroneutral flow of electrolyte is assumed. It is assumed that the ion-selective microgranule has ideal selectivity, that is, the flow of coions through it is completely absent. For the sake of certainty, we will assume that an ion-selective particle is a cation exchange.

Fig. 1
figure 1

A diagram of the device with the designation of the main areas near the ion-selective microgranule. The concentration of ions is highlighted in color on the background

Full size image

2.2 Dimension statement

The behavior of the electrolyte is described by the system of Nernst–Planck–Poisson–Stokes equations, thus,

$$\begin{aligned}{} & {} \frac{\partial \tilde{C}^\pm }{\partial \tilde{t}} +\tilde{\bar{U}} \cdot \nabla \tilde{C}^\pm = \frac{z^\pm \tilde{D}^\pm \tilde{F}}{\tilde{R}\tilde{T}}\nabla \cdot \left( \tilde{C}^\pm \nabla \tilde{\Phi }\right) +\tilde{D}^\pm \nabla ^2\tilde{C}^\pm , \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \tilde{\varepsilon }\nabla ^2\tilde{\Phi }= -\tilde{F}\left( z^+\tilde{C}^++z^-\tilde{C}^-\right) , \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \tilde{\nabla }\Pi -\tilde{\mu }\nabla ^2\tilde{\bar{U}} = -\tilde{F}\left( z^+\tilde{C}^++z^-\tilde{C}^-\right) \nabla \tilde{\Phi }, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \nabla \cdot \tilde{\bar{U}} = 0. \end{aligned}$$
(4)

The unknowns are the molar density of the concentration of positively and negatively charged ions, \(\tilde{C}^\pm \), the electric potential, \(\tilde{\Phi }\), the pressure, \(\tilde{\Pi }\), and the velocity field, \(\tilde{\bar{U}}\). Here \(\tilde{F}\) is the Faraday number, \(\tilde{R}\) is the universal gas constant, and \(\tilde{T}\) is the absolute temperature. The tilde sign (\(\tilde{f}\)) will be used for dimensional variables. For dimensionless variables, in contrast, the tilde (f) will not be used. The liquid is assumed to be symmetric (valence, \(z^+ = -z^-=1\)), the binary electrolyte is assumed to have the same diffusion coefficient for cations and anions \(\tilde{D}^+=\tilde{D}^- =\tilde{D}\), dynamic viscosity, \(\tilde{\mu }\), electrical permeability, \(\tilde{\varepsilon }\). The system of equations is solved in a spherical axisymmetric formulation.

On the surface of the outer dielectric sphere, \(\tilde{r}= \tilde{r}_1\), \(\theta _0< \theta < \pi - \theta _0\), the ion impermeability condition is accepted,

$$\begin{aligned} \frac{\partial \tilde{C}^\pm }{\partial \tilde{r}} \pm \frac{\tilde{F}}{\tilde{R}\tilde{T}} \tilde{C}^\pm \frac{\partial \tilde{\Phi }}{\partial \tilde{r}} = 0, \end{aligned}$$
(5)

where \(\tilde{r}\) is the direction along the radius centered in the middle of the ion-selective microgranule, and \(\theta \) is the angle (Fig. 1).

A charge is assumed to be present on the surface of the outer sphere, which makes it possible to establish a boundary condition for the electric potential \(\tilde{\Phi }\),

$$\begin{aligned} \tilde{\varepsilon }\frac{\partial \tilde{\Phi }}{\partial \tilde{r}} = -\tilde{s}. \end{aligned}$$
(6)

The no-slip condition applies to the outer sphere,

$$\begin{aligned} \tilde{\bar{U}} \equiv 0. \end{aligned}$$
(7)

The boundary conditions of the reservoir for the molar ionic concentration are given together with the boundary conditions for pressure and electric potential on the outlet is \(\tilde{r} = \tilde{r}_1\), \(0< \theta < \theta _0\) (see Fig. 1),

$$\begin{aligned} \frac{\partial \tilde{C}^\pm }{\partial \tilde{r}} = 0,\quad \tilde{\Pi }= 0,\quad \tilde{\Phi }= \Delta \tilde{V}/2. \end{aligned}$$
(8)

At the inlet, \(\tilde{r} = \tilde{r}_1\), \(\pi - \theta _0< \theta < \pi \), salt concentration, pressure and electric potential values are fixed,

$$\begin{aligned} \tilde{C}^++\tilde{C}^- = 2\tilde{C}_{\infty }, \quad \tilde{C}^+-\tilde{C}^-=0,\quad \tilde{\Pi }= \Delta \tilde{\Pi }, \quad \tilde{\Phi }= -\Delta \tilde{V}/2. \end{aligned}$$
(9)

The driving force for moving the liquid through the chamber is created by the pressure and the potential drops between the inlet and outlet, \(\Delta \tilde{\Pi }\) and \(\Delta \tilde{V}\). The following boundary conditions are set on the surface of an ion-selective microgranule \(\tilde{r} = \tilde{r}_0\),

$$\begin{aligned} \frac{\partial \tilde{C}^-}{\partial \tilde{r}} - \frac{\tilde{F}}{\tilde{R}\tilde{T}} \tilde{C}^-\frac{\partial \tilde{\Phi }}{\partial \tilde{r}} = 0, \quad \tilde{C}^+ = \tilde{p}, \quad \tilde{\Phi }=0, \quad \tilde{\bar{U}} \equiv 0. \end{aligned}$$
(10)

The first boundary condition corresponds to the absence of anion flow through an ideal cation exchange membrane. The condition that the concentration of cations on the membrane surface is equal to a constant is shown by Rubinstein and Shtilman [13], and its validity has been verified in many works (see [14,15,16]). For a better understanding of this condition, consider the structure of the membrane. A cation exchange membrane is an organic polymer consisting of matrices and pores. In the matrix, the anions (\(\tilde{C}_a\)) are fixed and immobile, which creates a fixed charge of the membrane \(\tilde{p}\) (\(\tilde{C}_a = \tilde{p}\)). When the membrane is placed in an electrolyte without the influence of an electric field, its pores are filled with electrolyte and ions of the opposite sign (\(\tilde{C}^+\)) accumulate in them. Moreover, their number is almost equal to the charge of the membrane (\(\tilde{C}^+ = \tilde{p}\)); thus, the membrane as a whole is shielded from the inside. If the charge of the membrane is large enough (\(\tilde{p}\gg \tilde{C}_\infty \)), then it becomes more difficult for external forces to change the number of cations inside the membrane, that is, we can accept \(\tilde{C}^+ = \tilde{p}\) inside the membrane and on the surface. Studies of flat membranes show that for limiting and over-limiting modes, the solution is practically independent of the values of \(\tilde{p}\) for \(\tilde{p}\gg \tilde{C}_\infty \). For a spherical ion-selective granule with a sufficiently strong external electric field, the solution does not depend on \(\tilde{p}\) [10, 17, 18]. The third condition means that the membrane is a conductor and the potential on the membrane is a constant. Without loss of generality, this constant can be assumed to be zero. The last condition indicates that the velocity components on a solid surface are zero.

2.3 Dimensionless statement

In order to make the simulation results more general, we will make the mathematical model dimensionless with a choice of characteristic quantities. The value of the dimensional characteristics may vary, but the dimensionless distributions of functions remain the same and can be used to recalculate the dimensional characteristics for specific devices.

To render Eqs. (1)–(10) dimensionless, the following characteristic quantities are used:

\(\displaystyle \tilde{r}_0\):

The ion-selective granule radius is taken as a characteristic length;

\(\displaystyle {\tilde{r}_0^2}/{\tilde{D}}\):

The characteristic time;

\(\displaystyle {\tilde{D}}/{\tilde{r}_0}\):

The characteristic velocity;

\(\displaystyle \tilde{\mu }\):

The liquid viscosity is taken as the characteristic dynamic value;

\(\displaystyle {\tilde{\mu } \tilde{D}}/{\tilde{r}_0^2}\):

The characteristic stress;

\(\displaystyle \tilde{\Phi }_0 = {\tilde{R}\tilde{T}}/{\tilde{F}}\):

The thermal potential is taken as the characteristic voltage;

\(\displaystyle \tilde{C}_{\infty }\):

The concentration of ions in the reservoir on the outside of the inlet;

\(\displaystyle {\tilde{D} \tilde{F}\tilde{C}_{\infty }}/{\tilde{r}_0}\):

The characteristic electric current.

The characteristic radius of a microgranule \(\tilde{r}_0\) varies from 10 \(\mu \)m to 500 \(\mu \)m [5]. The typical electrolyte is a sodium solution (e.g., KCl or NaCl), but sometimes more complex liquids, like Tris [5] are used. We will consider simple KCl solution and diffusion coefficients \(\tilde{D}\) for ions K\(^+\) and Cl\(^-\) are about, \(\tilde{D} \sim 2\times 10^{-9}\) m\(^2\)/s. Diluted solutions are considered, so the characteristic density of ion concentration varies in the range from \(\tilde{C}_\infty = 5\) \(\mu \)M to \(\tilde{C}_\infty = 500\) \(\mu \)M.

The thermal potential at \(\tilde{T} =300\) K is approximately \(\tilde{\Phi }_0 = 25\) mV. In accordance with the idea of laboratories on a chip, it can be assumed that their power supply will be carried out using small batteries with an electric potential drop of the order of several volts. If so, we can assume electric field about 10 V/cm. Nevertheless, researchers [5] consider electric field up to 100 V/cm, which can be achieved by increase electric source or by decrease space between electrodes. Our model supposed that electrodes placed at the inlet and outlet, so for the biggest microparticle with a diameter of 1 mm placed in a chamber with 6 mm diameter with 6 V potential drop we can achieve electric field 10 V/cm, and 6 V corresponds to 240\(\tilde{\Phi }_0.\)

It is assumed that the pressure is created by a column of liquid, so we assume \(\Delta \tilde{\Pi }\) is up to 10 P, with corresponds the pressure of 1 mm column of water.

We consider aqueous solutions of highly diluted electrolytes, therefore, the parameters of the dynamic viscosity and the permittivity were chosen for pure water, \(\tilde{\mu }= 9\times 10^{-4}\) P s, \(\tilde{\varepsilon }= 7\times 10^{-10}\) C/V m.

The above equations in the dimensionless form and in the polar spherical coordinates are as follows. Equation (1) for the ion transport turns into,

$$ \begin{gathered} \frac{{\partial C^{ + } }}{{\partial t}} + U\frac{1}{r}\frac{{\partial C^{ + } }}{{\partial \theta }} + V\frac{{\partial C^{ + } }}{{\partial r}} = \left[ {\frac{1}{{r^{2} \sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta C^{ + } \frac{{\partial \Phi }}{{\partial \theta }}} \right)} \right.\left. { + \frac{1}{{r^{2} }}\frac{\partial }{{\partial r}}\left( {r^{2} C^{ + } \frac{{\partial \Phi }}{{\partial r}}} \right)} \right]\quad \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left[ {\frac{1}{{r^{2} \sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{{\partial C^{ + } }}{{\partial \theta }}} \right)} \right.\left. { + \frac{1}{{r^{2} }}\frac{\partial }{{\partial r}}\left( {r^{2} \frac{{\partial C^{ + } }}{{\partial r}}} \right)} \right], \hfill \\ \end{gathered} $$
(11)
$$ \begin{gathered} \frac{{\partial C^{ - } }}{{\partial t}} + U\frac{1}{r}\frac{{\partial C^{ - } }}{{\partial \theta }} + V\frac{{\partial C^{ - } }}{{\partial r}} = - \left[ {\frac{1}{{r^{2} \sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta C^{ - } \frac{{\partial \Phi }}{{\partial \theta }}} \right)} \right.\left. { + \frac{1}{{r^{2} }}\frac{\partial }{{\partial r}}\left( {r^{2} C^{ - } \frac{{\partial \Phi }}{{\partial r}}} \right)} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left[ {\frac{1}{{r^{2} \sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{{\partial C^{ - } }}{{\partial \theta }}} \right)} \right.\left. { + \frac{1}{{r^{2} }}\frac{\partial }{{\partial r}}\left( {r^{2} \frac{{\partial C^{ - } }}{{\partial r}}} \right)} \right], \hfill \\ \end{gathered} $$
(12)

the Poisson Eq. (2) is now presented by the following equation:

$$\begin{aligned} \frac{\nu ^2}{r^2}\left[ \frac{\partial }{\partial r} \left( r^2 \frac{\partial \Phi }{\partial r} \right) + \frac{1}{ \sin \theta } \frac{\partial }{\partial \theta } \left( \sin \theta \frac{\partial \Phi }{\partial \theta } \right) \right] = C^- - C^+ \equiv - \rho ; \end{aligned}$$
(13)

and the Stokes Eqs. (3)-(4) for creeping flow turn into the following ones:

$$\begin{aligned}{} & {} -\frac{1}{r} \frac{\partial \Pi }{\partial \theta } + \frac{\partial ^2 U}{\partial r^2} + \frac{2}{r}\frac{\partial U}{\partial r} + \frac{1}{r^2}\frac{\partial ^2 U}{\partial \theta ^2} + \frac{\cot \theta }{r^2} \frac{\partial U}{\partial \theta }\nonumber \\{} & {} - \frac{U}{r^2 \sin ^2 \theta }+\frac{2}{r^2}\frac{\partial V}{\partial \theta } = \rho \frac{1}{r} \frac{\kappa }{\nu ^2} \frac{\partial \Phi }{\partial \theta }; \end{aligned}$$
(14)
$$\begin{aligned}{} & {} -\frac{\partial \Pi }{\partial r}+\frac{\partial ^2 V}{\partial r^2}+\frac{2}{r}\frac{\partial V}{\partial r} + \frac{1}{r^2}\frac{\partial ^2 V}{\partial \theta ^2} - \frac{2 V}{r^2} + \frac{\cot \theta }{r^2}\frac{\partial V}{\partial \theta }\nonumber \\{} & {} - \frac{2 U}{r^2}\cot \theta - \frac{2}{r^2}\frac{\partial U}{\partial \theta } = \rho \frac{1}{r} \frac{\kappa }{\nu ^2} \frac{\partial \Phi }{\partial r}. \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \frac{\partial }{\partial \theta } \left( \sin \theta \, r\, U \right) +\frac{\partial }{\partial r} \left( \sin \theta \, r^2\, V \right) = 0. \end{aligned}$$
(16)

Here, (U, V) are the velocity components. The dimensionless parameter \(\nu \) is the Debye number, which is the ratio of the Debye length \(\tilde{\lambda }_D\) to the microgranule radius \(\tilde{r}_0 \) ( \(\nu \ll 1\) is a small parameter of the problem, a thin electric double layer (EDL) is considered),

$$\begin{aligned} \nu = \frac{\tilde{\lambda }_D}{\tilde{r}_0}, \qquad \tilde{\lambda }_D = \left( \frac{\tilde{\varepsilon } \tilde{\Phi }_0}{\tilde{F}\tilde{C}_{\infty }}\right) ^{\frac{1}{2}}, \end{aligned}$$

and \(\kappa \) is a coupling coefficient between the hydrodynamics and electrostatics,

$$\begin{aligned} \kappa = \frac{\tilde{\varepsilon }\tilde{\Phi }_0^2}{\tilde{\mu }\tilde{D}}. \end{aligned}$$

This quantity characterizes the physical properties of the electrolyte solution and is fixed for a given liquid and electrolyte. The value of \(\nu \) depends on two main factors. The first one is \(\tilde{r}_0\), \(\nu \) decrease with increasing of characteristic length \(\tilde{r}_0\). The second one is \(\tilde{C}_\infty \), \(\nu \) decrease with increasing of characteristic concentration \(\tilde{C}_\infty \). It means that \(\nu \) is different for highly diluted and moderately diluted electrolytes. For example, the Debye number varies from \(\nu = 10^{-4}\) to \(\nu = 0.05\) according the assumptions in the begin of the section. Despite wide range of the Debye number the behavior of the electrolyte weakly depends on \(\nu \), only assumption \(\nu \ll 1\) is important, so the Debye number is fixed \(\nu =0.01\) in the paper.

The conditions on the outer dielectric sphere, \( r = R=\tilde{r}_1/\tilde{r}_0\), \(\theta _0< \theta < \pi - \theta _0\), Eqs. (5)-(7), turn into

$$\begin{aligned}{} & {} \frac{\partial C^\pm }{\partial \tilde{r}} \pm C^\pm \frac{\partial \Phi }{\partial r} = 0, \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \nu \frac{\partial \Phi }{\partial r} = -s, \end{aligned}$$
(18)
$$\begin{aligned}{} & {} {\bar{U}} \equiv 0. \end{aligned}$$
(19)

where \(s = \tilde{s} \tilde{\lambda }_D/\tilde{\varepsilon }\tilde{\Phi }_0\) is the dimensionless surface charge.

At the outlet boundary \( r = R\), \(0< \theta < \theta _0\) conditions (8) now are rewritten in dimensionless form,

$$\begin{aligned} \frac{\partial C^\pm }{\partial r} = 0,\quad \Pi = 0,\quad \Phi = \Delta V/2, \end{aligned}$$
(20)

where \(\Delta V/2\) in the dimensionless potential at the outlet.

At the inlet \( r = R\), \(\pi - \theta _0< \theta < \pi \) the salt concentration distribution along the hole, the electroneutrality condition, the pressure and the electric potential are given,

$$\begin{aligned} C^++ C^- = 2, \quad C^+- C^-=0,\quad \Pi = \Delta \Pi , \quad \Phi = -\Delta V/2. \end{aligned}$$
(21)

These conditions are the dimensional forms of Eqs. (9). The voltage \(\Delta V= \Delta \tilde{V}/\tilde{\Phi }_0\) and the pressure drop \(\Delta \Pi = \Delta \tilde{\Pi }\tilde{r}_0^2/\tilde{\mu }\tilde{D}\) can have different signs, they can be either co- or counter- directed. The direction depends on a vertical orientation of the device. They give rise to the electroosmotic or the pressure driven flow, respectively.

On the surface of the ion-selective granule, at \(r=1\), BC’s (10) have their dimensionless form,

$$\begin{aligned} \frac{\partial C^-}{\partial r} - C^-\frac{\partial \Phi }{\partial r} = 0, \quad C^+ = p, \quad \Phi =0, \quad { U} = 0, \quad V=0. \end{aligned}$$
(22)

Thus, the system has two geometric dimensionless parameters, \(R =\tilde{r}_1 /\tilde{r}_0 \) and \(\theta _0\). The first parameter characterizes the channel width, and the second parameter characterizes the size of the inlet and outlet holes.

The dimensional voltage was varied from 0 to \(\Delta \tilde{V} = 6.25\) V and the drop of pressure from 0 to \(\Delta \tilde{\Pi }= 10\) P or approximate 1 mm of water; the corresponding range of the dimensionless parameters are \(0<\Delta V \le 250\) and \(0<\Delta \Pi \le 1000\). In most calculations, the value of \(\Delta \Pi = 1000\) is fixed, and \(\Delta V\) changes. The surface charge density for different types of glass-quartz is between \(\tilde{s} = 10^{-4}\) C/m\(^2\) to \(\tilde{s} = 10^{-3}\) C/m\(^2\). The dimensionless surface charge was fixed, \(s = 1\); our calculations show that its influence on the processes is weak. The radius of the outer sphere and the angle of the entrance section were fixed, \(R=3\) and \(\theta _0 = 30^\circ \). The parameters \(\kappa \) was fixed, \(\kappa =0.2\) corresponds to potassium chloride solution.

2.4 Numerical method

The system of Eqs. (11)–(22) has a small parameter, the Debye number, at the highest derivatives. As a result, there is a thin charge region with a rapid change of the unknowns function near the surface. This causes significant difficulties for numerical solution of the problem. These difficulties are compounded by the complexity of the chaotic regime when the flow contains a wide range of different scales. There are two approaches to overcome these difficulties. The first one is semi-analytical, when the solution in the Debye layer is sought analytically as the inner expansion but numerically in the diffusion region that is treated as the outer expansion, with a proper matching of the inner and outer expansions. This method was systematically applied for charged dielectric particles by Yariv’s group (see, for example [19]) and for ion-selective granules in [17, 18]. The second approach solves the entire system of Nernst–Planck– Poisson–Stokes equations numerically, without any simplification.

The problem was solved numerically using the finite-difference method on a nonuniform grid for discretization in spatial variables r and \(\theta \). Time integration was carried out using a semi-implicit method. Details of the numerical simulation method can be found in the papers [10, 17]. The only difference is that for the present problem we do not need to use the force balance to obtain the granule speed, because the granule is fixed in space and its velocity is zero.

3 Results

Two criteria were chosen to evaluate the efficiency of the device: 1. The maximum concentration value in the electrolyte is \(K_{max}\). Due to the specific behavior of the electrolyte near the ion-selective microgranule, this maximum value is reached at the edge of the particle near the outlet \(r=1, \theta =0\). This criterion reflects the maximum possible local concentration of ions. 2. The standard deviation of the concentration profile at the outlet from the average value, taking into account the spherical geometry:

$$\begin{aligned} \sigma ^2 = \frac{1}{1-cos(\theta _1)} \int _0^{\theta _1} (K - \bar{K})^2 \sin \theta d\theta , \end{aligned}$$
(23)

for \(r=R\), where \(\bar{K}=\frac{1}{1-cos(\theta _1)} \int _0^{\theta _1} K\sin \theta d\theta \). This criterion reflects the degree of flow stratification at the outlet and reflects the intensity of the formed concentration jet at the outlet.

Fig. 2
figure 2

The dependences of the maximum concentration (a) and the standard deviation of the concentration profile at the outlet from the electrical potential drop (b) for \(\Delta \Pi =0\). The solid line is a stationary value and averaged over time, the dotted line is the maximum value for the entire calculation time

Full size image

3.1 Case \(\Delta \Pi = 0\)

First, the case of the absence of an external pressure drop will be considered. In this case, the fluid flow is created by electroosmosis near the ion-selective microgranule. At low values of the electric field strength, the rate of electroosmosis linearly depends on \(\Delta V\) (electroosmosis of the first kind), and with increasing intensity it can reach a quadratic dependence (electroosmosis of the second kind [6]). In Fig. 2, the dependences of the studied criteria on the difference of electrical potentials are presented. The maximum concentration value monotonically increases with increasing \(\Delta V\), however, this dependence has features that allow us to distinguish three zones. I is the zone of the presence of a steady state regime, the maximum values of the criteria of which are achieved in the stationary case, II is the zone of the presence of a steady state solution, but the corresponding maximum values of the criteria are achieved in the transition time (dotted line) before the stationary regime (solid line) and III is the area of the non-stationary regime. In region I, the transition regime from the initial distribution to the stationary one is carried out monotonically (curve 1 in Fig. 3) in time. This behavior indicates that electrostatic phenomena develop more slowly than hydrodynamic ones and electroconvective instability does not have time to develop, since it is suppressed by the viscosity of the liquid. In zone II, the regime is characterized by the fact that electrostatic phenomena manifest themselves faster than hydrodynamic ones, which leads to a short-term occurrence of maximum values of criteria greater than stationary ones, however, over time, the disturbances decrease and a stationary regime arises (curve 2 in Fig. 3). In zone III, the disturbances of the transition regime no longer decrease, since electroconvective instability prevails over viscous forces and an unsteady flow regime arises. For small subcritical values of \(\Delta V\), this mode is periodic (curve 3 in Fig. 3), but for sufficiently uncritical it becomes stochastic.

Fig. 3
figure 3

The dependence of the maximum concentration (a) and the standard deviation (b) on the time for \(\Delta V=200\) (1), \(\Delta V=300\) (2) and \(\Delta V=500\) (3)

Full size image

Regime III has a bad effect on the concentration process. For the maximum concentration value, a slowdown in growth is noticeable with an increase in \(\Delta V\) (Fig. 2a), and for the standard deviation, there is no monotony at all (Fig. 2b). This phenomenon is due to the fact that the presence of electroconvective instability leads to excessive vortex formation and additional mixing of the concentration trace behind the particle. Thus, it can be judged that for the operation of the simulated device there is an optimal range of \(\Delta V\) in which the best concentration can be achieved for a given type of electrolyte.

3.2 Case of presence of pressure drop \(\Delta \Pi \ne 0\)

Adding an external pressure drop to the system leads to some changes in the flow. If the additional pressure driven flow is co-directional with the electromotic flow (\(\Delta \Pi >0\)), then it leads to stabilization, and an increase in fluid flow reduces the maximum concentration and standard deviation criteria, since they lead to a more intensive salt outflows from the enriched zone into the outlet. The case of \(\Delta \Pi <0\) is more interesting, since in this case the external pressure drop slows down the electroosmotic flow and destabilizes the flow. It is important to note that due to the increase in \(\Vert \Delta \Pi \Vert \), it is not possible to completely stop the electroosmotic flow and achieve a stationary regime with zero flow rate, since electroosmosis occurs due to surface forces near the particle, and the pressure driven flow has a volumetric character, therefore, in different places of the computational domain, its own mechanism of fluid movement prevails, and the resulting vortex formation leads to instability of the main flow. In this case, with a decrease in \(\Delta \Pi \), there is a shift of regions II and III to smaller values of \(\Delta V\). Data for \(\Delta V=200\) present in Fig. 4. The figure shows that even for a slight decrease in \(\Delta \Pi \), the features of region II appear, when the maximum of the criteria is reached during the transition time. Decreasing the main flow leads to an increase in both the maximum concentration and the standard deviation. However, excessive decreasing of \(\Delta \Pi \) leads to the opposite effect. This is due to the fact that the convective vortices formed, caused by the competition between the two mechanisms of fluid flow, destroy the electrokinetic zones of desalination and concentration and mix them inside the chamber.

Fig. 4
figure 4

The dependence of the maximum concentration (a) and the standard deviation (b) vs the pressure drop. Solid line is a stationary value, dotted line is a maximum value for the entire calculation time

Full size image

Thus, it can be concluded that due to the pressure drop the concentration process can be additionally controlled. Due to two-parameter optimization of the parameters \(\Delta \Pi \) and \(\Delta V\) at the same time, even better concentration or separation can be achieved than in the case of \(\Delta \Pi =0\).

4 Conclusion

The paper presents a theoretical study of the concentration of ions in an electrolyte near an ion-selective microparticle under the action of an external electric field. Numerical simulation of the concentration device, the geometric configuration of which was previously presented in the experimental work of other authors, has been carried out. The device is a spherical chamber that is embedded in a circular microchannel. In the middle of the chamber there is an ion-selective microparticle. Due to the external electric field, ions are concentrated from the side of the outlet, a concentration jet is formed, which goes into the outlet channel. Calculations have shown that with an increase in the intensity of the external electric field, an increase in the concentration of ions occurs, however, starting from a certain critical value of the electric potential drop, there is a loss of flow stability, which leads to vortex formation and deterioration of concentration. The addition pressure drop allows to additionally control the degree of concentration. It has been shown that due to two-parameter optimization of the electric potential drop and the pressure drop, it is possible to achieve better concentration for given electrolytes and suspended particles.