1 Introduction

The development of microfluidic technologies such as lab-on-chip systems requires miniaturization of components, i.e., valves, mixers, and pumps. Especially for the latter, the use of electroosmotic actuation is an attractive strategy, due to small size and avoidance of complicated designs with moving parts.

The majority of studies on electroosmotic pumping concern liquid flow though porous materials or dense multiparticle systems (Rathore and Horvath 1997; Colon et al. 2000; Stol et al. 2001; Zeng et al. 2001; Yao et al. 2003; Reichmuth et al. 2003; Tallarek et al. 2005; Holtzel and Tallarek 2007; Nischang et al. 2007; Suss et al. 2011), where the flow–voltage relation is linear or the deviation from linearity is relatively low. However, depending on the used voltage and the shape of charged interfaces, the liquid velocity may not only be a linear function of the electric field strength E (classical or standard electroosmosis), but can also show nonlinear relationships due to polarization effects. For example, the flow velocity has been reported to scale with E 3/2 (Dukhin and Mishchuk 1988b; Mishchuk and Dukhin 1989, 2002a) for non-conductive particles and with E 2 (Mishchuk and Takhistov 1995; Mishchuk and Dukhin 2002b; Mishchuk 2006) for conducting ones.

The phenomenon of concentration polarization can be observed for systems of various geometries and physical properties of solid and liquid, including membranes (Rubinstein and Shtilman 1979; Listovnichij 1991; Zabolotskii and Nikonenko 1996a, b; Rubinstein et al. 1997; Zaltzman and Rubinstein 2007), densely packed or monolith ion-exchange materials (Leinweber and Tallarek 2005; Tallarek et al. 2005; Wang et al. 2006; Nischang et al. 2006, 2008; Strickland et al. 2010; Kivanc and Litster 2011), non-conducting (Dukhin and Mishchuk 1988b; Mishchuk and Dukhin 1989, 2002a) and conducting spherical and elongated (Dukhin et al. 1987; Mishchuk and Takhistov 1995; Mishchuk and Dukhin 2002b; Mishchuk 2006) particles. In many cases, the induced charge resulting from concentration polarization is small compared to the classical electrical double layer charge and nonlinear electroosmosis can be neglected. For specific geometries and solid/liquid properties, the deviation from linearity becomes large and the linear flow described by Smolouchowsky’s expression is only small part of the total electroosmotic transport.

In recent years, several studies have been made on nonlinear electrokinetic effects for various systems (Ajdari 2000; Roberts and Chang 2000; Mpholo et al. 2003; Studer et al. 2004; Ramos et al. 2005). One of the promising directions of research is the use of the phenomenon named “electroosmosis of the second kind” or “EO2” (Mishchuk and Takhistov 1995; Mishchuk and Dukhin 2002b; Mishchuk 2006). EO2 was theoretically predicted and demonstrated experimentally more than 20 years ago for particles of ion exchangers, metals, and semiconductors (Dukhin and Mishchuk 1988a; Mishchuk et al. 1998; Mishchuk and Dukhin 2002b; Mishchuk 2006) and also near surfaces of ion-exchange membranes (Rubinstein and Maletzki 1991; Rubinstein et al. 1997; Mishchuk 1998a, b; Belova et al. 2006). The name was introduced to stress how EO2 differs from classical electroosmosis: While linear electroosmosis is caused by a charge of the ordinary (primary) electrical double layer, the new phenomenon is caused by the secondary electrical double layer, arising in strong electric fields outside the primary one. Since, the velocity of EO2 is the squared function of electric field strength and frequently exceeds the velocity of classical EO by a factor 10–100, the phenomenon is attractive for microfluidic applications, where a small electrode distance can result in high electric field strengths and, correspondingly, in high flow rates even at low AC or DC voltages.

EO2 can be exploited to create micromixers (Takhistov et al. 2003; Lastochkin et al. 2004; Hu and Li 2007; Eckstein et al. 2009), which is important for express analyses, as well for microsized pumps (Mishchuk et al. 2009), intended, e.g., for the creation of compact analysis devices (Debesset et al. 2004), intensification of electrodialysis (Dukhin and Mishchuk 1993; Mishchuk 1998a, b; Mishchuk et al. 2001), etc.

This study is concerned with the theoretical and experimental aspects of EO2 near ordered assemblies of ion-exchange microspheres, and its application to directed fluid pumping in microchannels. The effect of bead size and arrangement, applied voltage and pulse frequency on the developed liquid flow is investigated. The nonlinear dependences of liquid velocity and obtained pressure on applied voltage are analyzed.

2 Theory

2.1 General notion about electroosmosis of the second kind

According to the theoretical prediction (Mishchuk and Dukhin 2002b; Mishchuk 2006), the polarized spherical particle is surrounded by a convective-diffusion layer with changed concentration of electrolyte. The higher the electric field strength is, the stronger is the change of electrolyte concentration in the convective-diffusion layer and the larger the induced charge, which for a permselective ion-exchange particle is located on the side where counterions enter the particle from the liquid (Fig. 1).

Fig. 1
figure 1

The convective-diffusion layer (δ) and the region of induced charge (S 0) near a spherical ion-exchange bead submerged in an electrolyte and subjected to an electric field. The arrows indicate electroosmotic flow

Full size image

In general, this phenomenon can occur near both nonconductive and conductive particles (Mishchuk 2010). However, the largest induced charge is obtained for conductive materials with high selectivity of current carriers (positive or negative ions for ion exchangers, electrons for metals, or holes for semi-conductors). Taking into account that the passage of current through metals and semiconductors is accompanied by red-ox reactions involving voltage drops, larger electroosmotic velocities can be obtained with ion-exchange materials for a given voltage (Mishchuk and Dukhin 2002b).

The velocity of EO2 becomes larger than the classical one when the averaged electric field strength E in experimental cell fulfills the criterion

$$ E \gg E_{\text{cr}} , $$
(1)

where \( E_{\text{cr}} = \Upphi_{\text{cr}} /2a, \) \( \Upphi_{\text{cr}} \) is the potential drop over one characteristic distance equalling the dimension of the spherical or elongated particle measured in parallel to the electric field 2a. Under this condition, the potential drop over a convective-diffusion layer near a particle surface becomes larger than its electrokinetic potential, meaning that the interface polarization becomes strong enough for nonlinear electroosmosis to appear (Mishchuk and Dukhin 2002b; Mishchuk 2010). The value of the critical potential drop \( \Upphi_{\text{cr}} \) for ion-exchange materials is typically equal to 100–150 mV. In the case of metals and semiconductors its value reaches 1.3–1.5 V, since part of the potential drop is spent on oxidation/reduction reactions.

When this requirement is satisfied, the density of induced charge C s and the thickness on the induced charge region S 0 near the surface of ion-exchange bead can be expressed as:

$$ C_{\text{s}} = C_{0} \frac{\sqrt 2 }{{\kappa \sqrt {\delta S_{0} } }} $$
(2)

and

$$ S_{0} = \left( {\frac{3}{2}\frac{FEa}{RT}} \right)^{2/3} \delta^{1/3} \kappa^{ - 2/3} , $$
(3)

where C 0 is liquid electrolyte concentration, κ −1 is the thickness of a classical electrical double layer, F is Faraday’s constant, R is the gas constant, and T is the absolute temperature. Further

$$ \delta = a/\sqrt {Pe} $$
(4)

is the thickness of a convective-diffusion layer defined by the Peclet number (Pe), which depends on the radius of the particle a, the velocity of electroosmosis U eo, and the ion diffusion coefficient in the electrolyte, D

$$ Pe = aU_{\text{eo}} /D. $$
(5)

From Eqs. (3) and (4), one can see that the increase of an external electric field leads to extension of the induced charge region and to the increase of its density. In turn the growth of charge provides the increase of the electroosmotic velocity (Mishchuk and Takhistov 1995; Mishchuk and Dukhin 2002b; Mishchuk 2006).

Near the single ion-exchange bead the velocity of EO2 at the outer boundary of a convective-diffusion layer for moderate field strengths can be presented as (Mishchuk and Dukhin 2002b; Mishchuk 2010)

$$ V_{{{\text{eo}},2}} \approx \frac{5\varepsilon }{4\eta }\zeta_{\text{ef}} E\sin 2\theta , $$
(6)

where ɛ is the dielectric permittivity of the liquid, η is the liquid’s dynamic viscosity, \( \zeta_{\text{ef}} = 2aE \) is the effective electrokinetic potential of EO2, and θ is the angle counted from the direction of an external electric field facing the bead where counter ions move toward its surface.

In the general case, the angular distribution of the electric field around the polarized bead is more complicated than reflected by Eq. (6), therefore it should be assumed valid at angles \( \theta < 70 \div 80^{ \circ } . \) At larger angles, the velocity of electroosmosis gradually decreases, approaching the velocity of classical electroosmosis (Mishchuk 1996; Mishchuk and Dukhin 2002b; Mishchuk and Barinova 2005, Barinova and Mishchuk 2008).

The expression (6) demonstrates the maximum possible velocity at \( \theta = 45^{ \circ } \) (see Eq. (6)), however, the actual velocity can be lower due to a number of factors. Too large pore size leads to decreased permselectivity of the ion exchanger, with resulting weaker concentration polarization and reduced EO velocities. The application of too strong electric fields can lead to so-called tangential drift of the induced charge (Mishchuk and Takhistov 1995; Mishchuk and Dukhin 2002b), also reducing the velocity compared to Eq. (6). Furthermore, the electroosmotic velocity depends on electrolyte concentration. If it is too low (deionized water), the water splitting affects the concentration polarization weakening the EO2 flow (Mishchuk 1999; Mishchuk and Dukhin 2002b). At too high concentrations (centimolar and higher) the conductivity of ion-exchange materials approaches the conductivity of liquid (Gnusin and Grebenyuk 1972), diminishing the polarization and, correspondingly, the EO2 velocity (Mishchuk and Dukhin 2002b).

Since effective electrokinetic potential \( \zeta_{\text{ef}} \) is proportional to the bead size a and electric field strength E, one can accelerate the liquid flow by increasing the values of both. However, the electroosmotic flow pattern near an assembly of beads strongly depends on its detailed configuration. As can be seen in Fig. 1, near a single bead electroomosis of the second kind only produces closed vortices (Mishchuk 1996; Mishchuk and Takhistov 1995; Ben and Chang 2002). To obtain directed electroosmotic flow, the beads should be oriented in rows parallel to an external electric field and with a relatively low inter-particle spacing (Fig. 2, see also Mishchuk and Barinova 2005; Barinova and Mishchuk 2008).

Fig. 2
figure 2

EO flow patterns around row of beads oriented perpendicularly to the electric field

Full size image

The characteristics of EO2 flow around or between beads depends on the distance between them (Mishchuk and Barinova 2005). If the beads are placed at large distances, the liquid flows around them do not affect one another. Therefore, similarly to the case of a single bead (Fig. 1), the continuity of the liquid flow is provided by the formation of closed electroosmotic vortices. On the other hand, when the space becomes smaller than the bead radii, closed vortices no longer form and the liquid moves through the gap. However, if the space near the extreme beads is not limited by the walls, vortices may still be created around those (Fig. 2).

As has been shown earlier (Mishchuk et al. 2009) the flow velocity between a pair of beads can be obtained on the basis of expression (6) as

$$ \tilde{V}_{{{\text{eo}},2}} \approx \frac{5}{14}\frac{\varepsilon }{\eta }\zeta_{\text{ef}} E, $$
(7)

where \( E = \varphi /L \) is averaged electric field strength between electrodes with distance L, and \( \varphi \) is the corresponding voltage drop.

It can be seen that the average theoretical velocity of electroosmosis of the second kind is \( 5\zeta_{\text{ef}} /14\zeta = 5Ea/7\zeta \) times larger than the velocity of classical electroosmosis and 2/7 times smaller than the maximum local velocity of EO2. To obtain a significantly larger velocity than for linear electroosmosis at a given field strength E (for example, in five times) the latter should satisfy the condition

$$ E \ge \frac{7\zeta }{a} $$
(8)

Thus, the necessary electric field strength, for example, for \( a = 50\;\mu {\text{m}} \) and \( \zeta = 50\;{\text{mV,}} \) will be about 20 V/mm.

Using an assembly of ion-exchange beads adds to the complication. As it was shown earlier (Barinova and Mishchuk 2008; Mishchuk 2010) beads placed in close vicinity of each other do not polarize independently. This is also illustrated by the study of electroosmosis at monolithic polarisable structures (Nischang et al. 2006), where flow velocities are far below those expected for a developed space charge along the wetted surfaces.

The so-called limiting current phenomenon (plateau in the current voltage curve) has been studied extensively for ion-exchange membranes (Rubinstein and Shtilman 1979). A similar phenomenon is present for ion-exchange beads, where the current density through a single polarized bead will be smaller than the value in its absence (Dukhin and Mishchuk 1988a). This lower current is compensated by an increase in current around the bead, provided by the local redistribution of the electric field.

As was shown by Mishchuk and Barinova (2005), the velocity of electroosmosis of the second kind for a pair of beads placed perpendicularly to an external electric field is close to the velocity near the surface of a single bead and reaches its maximum value at the point of closest proximity. However, if more than one pair or rows of beads are placed after another along the electric field, the measured velocity diminishes with decreasing distances between the rows (Barinova and Mishchuk 2008). With small distances between neighboring beads (in the direction of the external electric field) the polarization of one bead affects the polarization of the next one, decreasing both the density of current through the next successive particle and the value of the induced charge created near its surface.

In the case of a chain of beads arranged along the electric field at relatively small distances, the ion fluxes, after rounding first bead, cannot fully restore their initial density before entering the next bead. For this reason, every subsequent bead is polarized at a lower current density, leading to weaker polarization and lower electroosmotic velocity. In the limiting case of direct contact of adjacent beads in the direction of the electric field the current will mostly go through the highly conductive beads, with the resulting decrease in the tangential electric field component bringing both classical electroosmosis and EO2 almost to zero.

On the other hand, if the bead distance along the field reaches the size of one bead diameter or more, the distribution of ion fluxes and current at the incoming side of each bead becomes homogeneous, and the polarization of each subsequent bead becomes independent. As a result, the local velocity in the gaps between the different pairs remains the same along whole chain (Barinova and Mishchuk 2008).

We also must take into account that electroosmotic pumps generally consist of an active part over which an electric field is applied, and a passive fluidic network providing flow resistance (Fig. 3).

Fig. 3
figure 3

The general scheme of the micropump based on electroosmosis of the second kind

Full size image

A correction factor for calculating velocities in such systems consisting of active and passive segments both consisting of cylindrical capillaries was presented as (Tikhomolova 1993)

$$ K = \frac{{\beta_{\text{p}} R_{\text{p}}^{2} l_{\text{a}} }}{{\beta_{\text{p}} R_{\text{p}}^{2} l_{\text{a}} + \beta_{\text{a}} R_{\text{a}}^{2} l_{\text{p}} }} $$
(9)

Here, βa,p, l a,p, R a,p are the porosities, thickness, and pore radii in the active (a) and passive (p) parts of the diaphragm, respectively. Thus, if the passive part is structurally identical to the active, it will result in a velocity reduction of 50%.

Although Eq. (9) cannot be assumed to be very accurate for the geometries of the EO2 pump, the main regularities should be retained, i.e., a larger active section with smaller pore size should generate higher pressures and flow rates.

2.2 Electroosmosis in the AC regime

Electroosmotic pumping is further complicated by electrochemical reactions at the electrodes. The function of an electroosmotic pump in the direct current (DC) regime is complicated by electrolysis of water at the electrodes with concomitant pH changes and bubble formation resulting in electrode screening and possibly blocking of the channel.

One strategy has been to place the electrodes in open reservoirs separated from the pump section with ion-exchange membranes. Due to leakage and larger size, this method is not particularly suited for applications like compact lab-on-chip systems.

Another way to inhibit the electrode reactions is by using an alternating driving voltage.

With sufficiently high frequency, ions generated will not have time to combine and form molecules leading to bubble formation. As was discussed by Mishchuk et al. (2009), a necessary condition for the avoidance of gas formation is

$$ I_{1} = - I_{2} , $$
(10)

where I 1,2 are the currents during opposite pulses.

In the case of linear electroosmosis this condition means that not only the currents, but also the liquid flows in opposite directions compensate each other. Thus, directed pumping cannot be obtained using a symmetric AC signal. However, the nonlinearity of EO2 can be exploited to obtain unidirectional pumping using an asymmetric AC signal fulfilling the condition (10), which can also be written as

$$ E_{1} t_{1} = E_{2} t_{2} \quad {\text{or}}\quad \varphi_{1} t_{1} = \varphi_{2} t_{2} , $$
(11)

where E 1,2 are the electric field strength during the strong and weak pulses, t 1,2 are their durations, \( \varphi_{1,2} \) are the voltages applied to the electrodes.

For example, a square pulse signal with offset and duty cycles could be used, with a strong pulse creating significant EO2 flows followed by a weaker longer pulse (Mishchuk et al. 2009). It was suggested to use an aperiodical signal to measure velocity of electrophoresis (Minor et al. 1997; Oddy and Santiago 2004) and its nonlinear components (Mishchuk and Dukhin 2002a) or to separate macromolecules (Dukhin and Dukhin 2005). This method was since justified theoretically (Mishchuk and Gonzalez-Caballero 2006a, b) and confirmed experimentally (Mishchuk et al. 2007).

The average linear component becomes small if the liquid movement during the every pulse reaches a quasi-stationary profile, as is the case when the frequency ω satisfies the condition (Minor et al. 1997; Mishchuk et al. 2007; Bhattacharyya et al. 2003; Yang et al. 2003)

$$ \omega = \frac{1}{{t_{1} + t_{2} }} \ll \frac{1}{\tau }, $$
(12)

where \( \tau = \rho h^{2} /\eta \) is the characteristic time of transition to quasi-stationary flow in the given channel with its characteristic width h and ρ and η are the density and dynamic viscosity of the liquid, respectively. For example, for a channel width 100 μm, one obtain τ = 0.01 s or a maximum frequency of 100 Hz.

According to the theoretical analysis of non-stationary processes (Mishchuk et al. 2009), the averaged electroosmotic velocity for a pulse regime V AC should equal

$$ V_{\text{AC}} = - \frac{{\varepsilon }}{\eta }\Updelta\zeta\;E_{2} \frac{{t_{2} }}{{t_{1} + t_{2} }}, $$
(13)

where \( \Updelta \zeta \) is the polarization component of the electrokinetic potential, \( E_{2} = \varphi_{2} /L,\;\varphi_{2} \) is the voltage during the stronger pulse, and L is the electrode distance.

Since at a sufficiently strong electric fields the nonlinear component is totally dominating, Eq. (13) can be rewritten as

$$ V_{\text{AC}} \approx V_{{{\text{eo}},2}} (E_{2} )\frac{{t_{2} }}{{t_{1} + t_{2} }} = K_{1} V_{{{\text{eo}},2}} (E_{2} ), $$
(14)

where \( V_{{{\text{eo}},2}} (E_{2} ) \) is defined by Eq. (7) at E = E 2 and K 1 is the correction factor \( K_{1} = {t_{2}}/({{t_{1} + t_{2} }}) \) accounting for the lower velocity in the AC regime.

In expression (14), the electric field strength during the weak pulse \( \varphi_{1} \) is assumed not to be strong enough for bead polarization. However, if the applied electric field E 1 during a weak pulse satisfies the condition E 1 > E cr (see Eq. (1)), polarization and corresponding EO2 will take place also during this pulse. In this case, the resulting electroosmotic velocity can be expressed through two nonlinear velocities as

$$ V_{\text{AC}}^{*} \approx \frac{{V_{\text{eo,2}} (E_{2} )t_{2} - V_{\text{eo,2}} (E_{1} )t_{1} }}{{t_{1} + t_{2} }} = K_{2} V_{\text{eo,2}} (E_{2} ) $$
(15)

with the new correction factor \( K_{2}=K_{1} ({{t_{1} - t_{2} }})/{{t_{2} }} . \) Since K 2 < K 1, the resulting velocity of electroosmosis V *AC is smaller than its value V AC defined by expression (14).

3 Experimental investigations of liquid velocity in pumps based on electroosmosis of the second kind

3.1 Microfluidic device fabrication

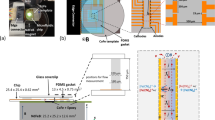
The experimental investigations were performed using microfluidic chip presented in Fig. 4.

Fig. 4
figure 4

Micropump on a chip

Full size image

The pump consists of N polarizable beads with diameter 50 or 90 μm and three-dimensional gold electrodes and is situated in a 2,000 μm long and 750 μm wide channel compartment. The channel height was 50 or 90 μm, correspondingly to the size of the used beads. On each side, the channel narrows down to 375 μm and extends 1,000 μm on each side to reach the two liquid reservoirs. The beads were placed in five rows with 8 (90 μm) (see Fig. 4) and 12 (50 μm) beads in every row (pumps 1 and 2, correspondingly). To make comparison possible a smaller pump where the beads were placed in five rows with three beads in every row was also developed (pump 3).

The microfluidic chips were made of glass and PDMS. PDMS chips were cast onto Silicon masters produced using deep reactive ion etching (DRIE). The PDMS chip was sealed onto a glass plate containing electroformed three-dimensional gold electrodes (height from 30 to 50 μm). The electrode distances in the liquid flow direction and perpendicular to this were 1,200 and 107 μm. The pump section of the PDMS chip was supplied with five rows of eight small holes used to fix sulfonated polystyrene cross-linked with divinylbenzene (PS-DVB) beads (from Finex OY, Finland). In order to obtain closed loop pumping (eliminating static pressure effects during flow measurements), a liquid bridge was provided on top of the chip connecting the two reservoirs.

To select electrode shapes and configurations giving a homogeneous electric field distribution in the active pump section numerical solution of the Laplace equation was performed for various electrode geometries. The resulting electrode configuration is shown with field distribution in Fig. 5.

Fig. 5
figure 5

Numerical simulation of an electric field distribution between the microfabricated electrodes

Full size image

3.2 Flow generation, visualization, and measurements

The power supply consisted of an Agilent 33120 A arbitrary signal generator (CA, USA) connected to a custom built DC coupled amplifier based on two Apex PA12A (Cirrus Logic Inc., TX, USA) operational amplifiers and powered by a Xantrex XKV 150-7 power supply (Xantrex Technology USA Inc.). This equipment allows for creating arbitrary AC and DC signals with amplitudes up to 100 V peak-to-peak.

The small electrode distance allows for high electric field strength at low applied voltage. For example, using a potential difference of 50 V, one obtains an electric field strength about 420 V/cm. This is high enough for obtaining electroosmosis of the second kind for the selected bead diameters.

Liquid flow velocity was measured by introducing fluorescent ink or particles in one of the reservoirs and observing through an inverted microscope (Zeiss Axiovert 200 m) at magnification 5, 10, and 20. 514 nm Flouresbrite latex particles in 1 or 2% solution was diluted 500 times in DI water or alcohol, and approximately 1 μl of the solution introduced to the reservoir near the channel entrance. Alternatively, 1 μl of Bodipy D6141 fluorescent ink in concentration 5 mg/ml (Polysciences, Germany) was used in some experiments.

All flow measurements were taken when pumping in a closed loop. The measurements were performed in the narrow part of the microchannel. To verify the symmetry of the system, important for the AC regime, the measurements under the DC regime were also performed with the electric field pointing in both directions.

In order to measure the pumping pressure, the tip of a graded syringe was inserted into one of the liquid reservoirs on the PDMS chip, creating a vertical extension of the fluidic channel (Fig. 6).

Fig. 6
figure 6

Experimental setup for pressure measurements

Full size image

After filling the horizontal part of the channel, the vertical syringe was filled to a certain level while applying a voltage to the EO pump, making it pump against the pressure created by the water column. The initial water level was set high enough for the water to flow in the direction opposite to that of EO pumping. After a period of several seconds the flow would cease, at which point the pressure generated by the water column would equal that generated by the EO pump. The pump pressure was then calculated from the actual liquid level in the syringe. Measurements were taken for different voltages applied to the EO pump.

4 Results and discussion

Experimental flow and pressure data are presented in Figs. 7, 8, and 9. The average flow rates through the channel cross-section were measured experimentally and calculated using standard expressions for hydrodynamic flow in rectangular channels.

Fig. 7
figure 7

The liquid flow velocity under DC regime as a function of an electric field strength E. The points and the dashed lines show the experimental data and the trends lines, respectively (curve 1—pump 1, curve 2—pump 2, curve 3—pump 1, without second and fourth rows). The solid lines show the results from numerical calculations for pump 1: curve 0—the averaged velocity of electroosmosis of the second kind (Eq. (7)), curve 1′—the averaged velocity with the channel hydrodynamic resistance taken into account, curve 1″—the sum of electroosmosis of the second kind and classical electroosmosis on the channel walls. Curve 4 shows the sum of classical electroosmosis on the channel walls and the beads

Full size image
Fig. 8
figure 8

The velocity of a liquid flow through five rows of 50 μm beads as a function of an electric field strength E 2 at the strong pulse amplitude (asymmetric square pulse signal with 20% duty cycle and an offset resulting in zero average DC component, t 1/t 2 = 5). The points and the dashed lines show the experimental data and the trend lines: ω = 20 (1, 2), 50 (3), 100 Hz (4), where curve 1 corresponds to pump 1 and curves 2–4 to pump 3. The solid lines 1′ and 1″ show the results from numerical calculations for experimental data, presented in curve 1, with correction factors K 1 and K 2 (see Eq. (15)), correspondingly

Full size image
Fig. 9
figure 9

The pressure created by microfluidic pumps at deionized water (curve 1) and methanol (curve 2) as a function of the electric field strength. The points and the dashed line show the experimental data and the trend line, respectively

Full size image

The averaged velocity \( \bar{v} \) and its distribution across the flat channel v(x, y) at a pressure drop Δp and channel length L can be presented (Lojtsjanskij 1973) as

$$ \bar{v} = \frac{{\frac{\Updelta p}{4\eta L}\frac{{h_{1} }}{{h_{3} }}\left( {\frac{{h_{1} }}{2}} \right)^{4} \left( {\frac{16}{3} - \frac{1024}{{\pi^{5} }}\frac{{h_{3} }}{{h_{1} }}} \right)\left( {\tanh \frac{{\pi h_{1} }}{{2h_{3} }} + \frac{1}{{3^{3} }}\tanh \frac{{3\pi h_{1} }}{{2h_{3} }} + \ldots } \right)}}{{4h_{1} h_{3} }} $$
(16)
$$ v(x,y) = \frac{16}{{\pi^{3} }}\left( {\frac{{h_{1} }}{{h_{3} }}} \right)^{2} \frac{{h_{1}^{2} \Updelta p}}{\eta L}\sum\limits_{n = 0}^{\infty } {\frac{{( - 1)^{n} }}{{(2n + 1)^{3} }}} \left[ {1 - \frac{{\cosh \left( {\frac{2n + 1}{2}\frac{{\pi h_{3} }}{{h_{1} }}y} \right)}}{{\cosh \left( {\frac{2n + 1}{2}\frac{{\pi h_{3} }}{{h_{1} }}} \right)}}} \right]\cos \left( {\frac{2n + 1}{2}\frac{{\pi h_{3} }}{{h_{1} }}x} \right), $$
(17)

where h 1,3 are the half of width (1) and the half of the height (3) of the channel and x, y are the distances from the center of the channel.

The calculated ratio between the maximum velocity (as measured in the channel center) and average velocity, \( \bar{v}/v, \) is approximately 0.695. This factor was used when comparing with experimental velocities measured in the channel center (see Figs. 7, 8).

The experimental velocity can be seen to be considerably higher than for classical electroosmosis (see the model values in Fig. 7, curve 4). It is approximately proportional to the squared electric field strength (Fig. 7, curves 1–3), as predicted by theory (Eqs. (6, 7)) and to the size of the beads (Fig. 7, curves 1, 2). However, the absolute values are considerably lower than the values calculated for a single bead (see curve 0 in Fig. 7) and the velocities measured in the gap between two isolated ion-exchange beads (Mishchuk and Barinova 2005; Barinova and Mishchuk 2008).

The difference between experimental and theoretical velocities (curves 0 and 1) cannot be explained by the rows influencing one another, given the relatively large distance between rows (86 μm) (Barinova and Mishchuk 2008). Instead, a plausible explanation is the hydrodynamic resistance in the cell. The join solution of Naviers–Stokes equation for active and passive parts of channel with the detailed geometry taken into account, boundary conditions and flow continuity equations (Mishchuk et al. 2009) showed that the flow velocity is reduced approximately by a factor of 70 by the hydrodynamic resistance of the passive part of cell (or 35 times, taking into account that the flow is measured in the narrow part of the channel). These calculations lead to the curve 1′, presented in Fig. 7. Taking this into account, one obtains a good agreement between experimental and theoretical values.

Also, supporting this conclusion is the fact that velocity was significantly lower in pumps with three instead of five rows of beads (Fig. 7, curve 3).

A zeta potential \( \zeta = 50\;{\text{mV}} \) was obtained experimentally for the channel walls from measurements in a system without microbeads. Adding the corresponding classical electroosmotic flow to the calculated EO2 flow yields curve 1″, Fig. 7, which is again in good agreement with experimental data.

Contrary to for the DC regime, experimental flow rates using AC is considerably lower than the theoretical values (Fig. 8). A possible explanation is that the field strength might be strong enough to cause nonlinear flow in the weak pulse, but still not strong enough for fully developed EO2 flow in the strong pulse. The closer the flow is to linear, the smaller the net flow.

Another reason for the velocity decrease could be related with the complicated geometrical characteristics and inhomogeneous resistance of the micropump, which at AC conditions lead to temporary swirls of water in transition from the wide to narrower spaces between the beads. As a result, the transition time to quasi-stationary liquid movement during every pulse is longer than according to Eq. (12) and therefore the resulting velocity at the AC regime is lower than its possible maximum value. This is aggravated by the relatively small active part of the pump. When the surface area where EO flows are generated is very small compared to the passive part of the channel, the pressure gradient, which tries to push the liquid, is also small and cannot quickly overcome the opposite liquid flow during previous pulse. That is why the transition period from the nonstationary swirls at the beginning of every pulse to laminar flow is quite long and leads to lower velocity of liquid flow. The proof of this idea is the decrease of liquid velocity at transition from the pump 1 (Fig. 8, curve 1) to the pump 3 (curves 2–4) and with the frequency increase, when the role of inertia increases (see condition (12)).

Many practical applications require not only a high flow, but also significant pressure, especially when the liquid should be pumped through materials with higher hydrodynamic resistance than the pump.

The electroosmotic pressure was measured in the DC regime using the setup presented in Figs. 4 and 6. The obtained data for pure water and methanol are presented in the Fig. 9.

One can see that the obtained pressure reflects the dependence of EO2 on the applied voltage, i.e., is the approximately squared function of electric field strength.

Since the electroosmotic velocity and pressure should be proportional to the dielectric permittivity, the obtained data should reflect this factor. In reality, a somewhat bigger difference is obtained between the two liquids. Probably, this can be ascribed differences in the behavior of the beads with regards to swelling and surface charge of beads in the two liquids.

5 Conclusions

A micropump based on electroosmosis of the second kind was developed and successfully tested using AC and DC signals. The experiments showed an approximately second order dependence of flow velocity and pressure on applied voltage, as predicted from the theory of electroosmosis of the second kind.

The possibility of directed pumping using AC signals was confirmed also in agreement with the theory. Although, the application of AC current results in lower liquid velocities compared to DC, it brings important advantages such as inhibiting electrolytic bubble formation and pH changes, which is important to obtain reliable operation and minimum changes to the liquids and solutions to be pumped.

Since the active part of pump was considerably smaller than its passive part, and also the pore size of the active part was several μm, there is a great potential for increasing the liquid velocity and pump pressure by increasing the active part length and surface area.