Investigation of MHD effects on micropolar–Newtonian fluid flow through composite porous channel

Abstract

The present study investigates the influence of uniform magnetic field on the flow of a Newtonian fluid sandwiched between two micropolar fluid layers through a rectangular (horizontal) porous channel. Fluid flow in the every region is steady, incompressible and the fluids are immiscible. Uniform magnetic field is applied in a direction perpendicular to the direction of fluid motion. The governing equations of micropolar fluid are expressed in Eringen’s approach and further modified by Nowacki’s approach. For respective porous channels, expressions for linear velocity, microrotations, stresses (shear and couple) are obtained analytically. Continuity of velocities, continuity of microrotations and continuity of stresses are employed at the porous interfaces; conditions of no slip and no spin are applied at the impervious boundaries of the composite channel. Numerical values of flow rate, wall shear stresses and couple stresses at the porous interfaces are evaluated by MATHEMATICA and listed in tables. Graphs of flow rate and fluid velocity are plotted and their behaviors discussed.

1 Introduction

Micropolar fluids respond to micro-rotational motions and spin inertia which can support stress moments (i.e. couple stresses) and body moments (i.e. body couples) (Lukaszewicz 1999). Motion of micropolar fluids can represent the various effects that are not possible in non-polar Stokesian fluids, given in the book by Stokes (1984). Eringen (1966) reported the fundamental concepts on micropolar fluids consisting of the effects of couple stresses and microstructure. An explicit dependence on components of deformation tensors was reported by Nowacki (1970). In the presence of magnetic field, an incompressible and electrically conducting micropolar fluid flow through a rectangular channel with suction and injection was reported by Murthy et al. (2011). Srinivasacharya et al. (2001) observed the unsteady incompressible micropolar fluid motion between two porous plates with a periodic injection/suction. Yadav et al. (2018) formulated a mathematical model for the flow of two immiscible fluids through a porous horizontal channel and obtained its analytical solution using direct method. Yadav et al. (2018) reported steady and incompressible fluid flow of an Eringen fluid sandwiched between two Newtonian fluid layers flowing through a porous channel. Perturbation solutions were obtained for a diverging channel filled with conducting micropolar fluid by Srinivasacharya and Shiferaw (2009). Jaiswal and Yadav (2020) investigated the effect of width of the layers on the micropolar–Newtonian fluid flow through the porous layered rectangular channel by sandwiching of non-Newtonian fluid between the Newtonian fluid layers. Sherief et al. (2014) reported the quasi-steady micropolar fluid flow between two coaxial cylinders by considering two types of flow problems: one is flow parallel to axes of cylinders and other is the flow perpendicular to axes of cylinders. Lok et al. (2018) reported flow of a micropolar fluid over a extensible surface on applying the slip condition. Deo et al. (2020) investigated the Stokesian flow of a micropolar fluid through a cylindrical tube enclosing an impermeable core coated with porous layer in the presence of external magnetic field. Deo et al. (2021) reported the magnetic effects on hydrodynamic permeability of biporous membrane relative to the flow of micropolar liquid using four known cell models. In addition, Maurya et al. (2021) investigated the Stokes flow of non-Newtonian fluid flow through a porous cylinder and compared the flow patterns for two types of BVPs.

Krishna et al. (2019) considered the unsteady magnetohydrodynamic convection flow of an incompressible, viscous and heat-absorbing fluid over a flat plate. Asia et al. (2016) investigated the flow and heat transfer characteristics of an electrically conducting micropolar fluid using different methods. Krishna et al. (2020) studied the effects of Hall and ion slip on MHD rotating flow of ciliary propulsion and mixed convective flow past an infinite porous plate. Krishna et al. (2019) studied the Soret and Joule effects of magnetohydrodynamic flow of an incompressible and electrically conducting viscous fluid past an infinite vertical porous plate. Krishna and Chamkha (2022) investigated the hall and ion slip effects on the flow of micropolar and elastico-viscous fluid between two porous surfaces.

Porosity of a porous medium is fraction of the total volume of medium that is occupied by void space (Nield and Bejan 2006). Brinkman (1947) improved the Darcy’s law for porous medium with an appropriate combination of the usual Darcy term analogous to the Laplacian terms. Deo and Maurya (2019) obtained the generalized stream function solution of the Brinkman equation in the cylindrical polar coordinates. Recently, Maurya and Deo (2020) reported the analytical solution of Brinkman and Stokes equations in the parabolic cylindrical coordinates. On using cell model techniques, hydrodynamic permeability of biporous medium composed by porous cylindrical particles which is located in another porous medium was investigated  by Yadav et al. (2013). In the porous channel, fully developed flow of an incompressible, electrically conducting viscous fluid through a porous medium of variable permeability in the presence of transverse magnetic field was studied in Srivastava and Deo (2013). Umavathi et al. (2010) reported the analytical concept of Couette flow and heat transfer in a composite channel. Recently, Maurya and Deo (2022) investigated the MHD effects on micropolar–Newtonian fluid flows through coaxial cylindrical shells.

In this research work, the magnetohydrodynamic effects on Newtonian fluid flowing through a porous channel, sandwiched between two rectangular porous channels filled with micropolar fluids have been investigated. The direction of fluid flow is taken along $x^*$-axis and the uniform magnetic field is applied in a direction perpendicular to the direction of fluid flow. For the corresponding fluid flow regions, velocity profiles, shear stresses, couple stresses and flow rate are obtained. Numerical values of the shear wall stresses and couple wall stresses at the porous interfaces are also tabulated. The volumetric flow rate and fluid velocity are plotted and discussed for different values of flow parameters.

2 Flow assumptions

• Fluid is flowing through the porous channels with constant pressure gradient.

• It is supposed that both outer boundaries of the composite channel are impervious and fluids are electrically conducting.

• Assume that induced magnetic field is very small in the comparison of the external magnetic field (${\textbf {B}}^*$).

• Fluids are immiscible and flow in each porous channel is steady, laminar and fully developed.

• The applied fluid pressure ${p}^{*}$ is same for both the micropolar and Newtonian fluids.

• Assume that the magnetic Reynolds number is very small and external electric field (${\textbf {E}}^*$) is absent so that the induced electric current can be neglected.

3 Mathematical formulation

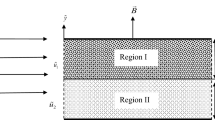
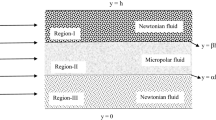
The mathematical model of the present investigation is based on the sandwiching of Newtonian fluid between two non-Newtonian fluid layers through a horizontal porous channel. The horizontal composite porous channel is divided into three porous layers of equal width $h^*$. The external magnetic field is of uniform strength, applied in a direction perpendicular to the flow. Here, modified Brinkman’s model for momentum equation is used to investigate the Newtonian fluid, and the governing equations for micropolar fluid proposed by Nowacki, are applied.

Assuming that the electrically conducting immiscible fluids are flowing with characteristic velocity $U^*$ along the $x^*$-axis in the presence of uniform magnetic field $B^{*}$. The lower porous channel ($0 \le y^* \le h^*$) and the upper porous channel $(2 h^* \le y^* \le 3 h^*)$ are filled with micropolar fluids having permeability ${k_1}^*$ and ${k_3}^*$, respectively. The sandwiched porous channel i.e. middle channel $(h^* \le y^* \le 2 h^*)$ is filled with Newtonian fluid having permeability ${k_2}^*$ (Fig. 1).

In the Eringen approach (Eringen 1966), governing equations of an incompressible steady micropolar fluid flow, in the absence of magnetic field, body forces and body couples, are given by

$$\begin{aligned}&\nabla ^{*} \cdot {\textbf {v}}^{*}=0, \end{aligned}$$

(3.1)

$$\begin{aligned}&\quad \left( \frac{\mu _e^{*}+\kappa _e^{*}}{k^{*}}\right) {\textbf {v}}^{*}+\nabla ^*{p}^{*}-\frac{\kappa _e^{*}}{2}\ \nabla ^*\times {\textbf {w}}^{*}\nonumber \\&\quad +(\mu _e^{*}+\kappa _e^{*})\ \nabla ^*\times \nabla ^*\times {\textbf {v}}^{*}={\textbf {0}}, \end{aligned}$$

(3.2)

$$\begin{aligned}&\quad -2 \kappa _e^{*}{} {\textbf {w}}^{*}+\kappa _e^{*} \nabla ^*\times {\textbf {v}}^{*}-\gamma _e^{*}\nabla ^*\times \nabla ^*\times {\textbf {w}}^{*}\nonumber \\&\quad +(\alpha _e^{*}+\beta _e^{*}) \nabla ^* (\nabla ^* \cdot \ {\textbf {w}}^*)={\textbf {0}}, \end{aligned}$$

(3.3)

where $k^{*}$ is the permeability of the porous medium, ${\textbf {v}}^{*},{} {\textbf {w}}^{*}$ and ${p}^{*}$ are representing the fluid velocity vector, microrotation vector and fluid pressure at any point of the fluid region, respectively. The material’s constants $(\mu _e^{*}, \kappa _e^{*})$ are viscosity coefficients and $(\alpha _e^{*}, \beta _e^{*}, \gamma _e^{*})$ are angular-viscosity coefficients of the micropolar fluid.

Stokes (1984) suggested to redefine viscosity coefficients using simple replacement $\mu _e^*=\mu ^*-\kappa ^*$ and $\kappa _e^*=2\kappa ^*$. Nowacki (1970) proposed to choose angular-viscosity coefficients as $\gamma _e^*=\delta ^*+\tau ^*$, $\beta _e^*=\delta ^*-\tau ^*$ and $\alpha _e^*=\alpha ^*$. In the presence of uniform magnetic field $B^*$, governing equations (Yadav et al. 2018) of an incompressible steady micropolar fluid flow through the porous channels ($0 \le y^* \le h^*$) and $(2h^* \le y^* \le 3 h^*)$, in the absence of body forces and body couples, are given by

$$\begin{aligned}&\nabla ^{*} . {\textbf {v}}^{*}_{i}=0, \end{aligned}$$

(3.4)

$$\begin{aligned}&\quad \left( \frac{\mu ^{*}+\kappa ^{*}}{{k_i}^{*}}\right) {\textbf {v}}^{*}_{i}+\nabla ^*{p}^{*}-\kappa ^{*}\nabla ^*\times {\textbf {w}}^{*}_{i}\nonumber \\&\quad +(\mu ^{*}+\kappa ^{*})\nabla ^*\times \nabla ^*\times {\textbf {v}}^{*}_{i}-{\textbf {J}}^{*}_{i} \times {\textbf {B}}^{*}={\textbf {0}}, \end{aligned}$$

(3.5)

$$\begin{aligned}&\quad -2 \kappa ^{*}{} {\textbf {w}}^{*}_{i}+\kappa ^{*} \nabla ^*\times {\textbf {v}}^{*}_{i}-(\delta ^*+\tau ^*)\nabla ^*\times \nabla ^*\times {\textbf {w}}^{*}_{i}+(\alpha ^{*}\nonumber \\&\quad +\delta ^*-\tau ^*) \nabla ^* (\nabla ^* \cdot \ {\textbf {w}}^*_{i})={\textbf {0}}, \end{aligned}$$

(3.6)

where ${\textbf {v}}^{*}_{i},{} {\textbf {w}}^{*}_{i}$ are representing the velocity vectors and microrotation vectors of micropolar fluid for lower porous channel $(i=1)$ and upper porous channel $(i=3)$, at any point ($x^*, y^*, z^*$), respectively.

The governing equations (Brinkman 1947) for Newtonian fluid through the porous channel $(h^* \le y^* \le 2h^*)$, in the presence of uniform magnetic field and in the absence of body forces, are given by

$$\begin{aligned}&\nabla ^* \cdot {\textbf {v}}_2^{*}=0\ , \end{aligned}$$

(3.7)

$$\begin{aligned}&\quad -\nabla ^*{p}^{*}- \frac{{{\mu }_2}^{*}}{{k_2}^{*}} \ {\textbf {v}}^{*}_2-{{\mu }_2}^*\ {\nabla }^* \times {\nabla }^* \times {\textbf {v}}^*_2\nonumber + {\textbf {J}}^{*}_2 \times {\textbf {B}}^{*} ={\textbf {0}}, \end{aligned}$$

(3.8)

where velocity and dynamic viscosity of the Newtonian fluid are represented by ${\textbf {v}}^*_2$ and $\mu _2^{*}$, respectively. The material’s constants $(\mu ^{*}, \kappa ^{*})$ are viscosity coefficients and $(\alpha ^{*}, \delta ^{*}, \tau ^{*})$ are gyro-viscosity coefficients. These viscosity coefficients are related by inequalities:

$$\begin{aligned}&\mu ^{*}\ge 0,\ \kappa ^{*} \ge 0,\ \delta ^{*}\ge 0, \ \delta ^{*} +\tau ^{*}\ge 0,\ 3\alpha ^{*}+2\delta ^{*} \ge 0,\\&\quad -(\delta ^{*}+\tau ^{*})\le (\delta ^{*}-\tau ^{*})\le (\delta ^{*}+\tau ^{*}). \end{aligned}$$

By Ohm’s law, ${\textbf {J}}^*_i = \sigma ^*_{i} ({\textbf {E}}^*+{\textbf {v}}^*_i \times {\textbf {B}}^*)$, where $\sigma ^*_i (\textit{i}=1,2,3)$ and ${\textbf {E}}^*$ stand for electrical conductivity of micropolar fluid and electric field, respectively. Therefore,

$$\begin{aligned} {\textbf {J}}^*_i\times {\textbf {B}}^*=-{\sigma ^*_i} {B^*}^2\ {\textbf {v}}^*_i, \end{aligned}$$

(3.9)

where $B^*=|{\textbf {B}}^*|.$ To treat governing equations of the micropolar fluid flow problem into dimensionless form, some non-dimensionalizing variables are introduced:

$$\begin{aligned}&{\textbf {v}}_{i}=\frac{{{\textbf {v}}{^{*}_{i}}}}{U^*},\\&\quad {\textbf {w}}_{i}=\frac{{h^{*}{} {\textbf {w}}{^{*}_{i}}}}{U^*},\\&\quad y=\frac{y^*}{h^*}, \\&\quad p=\frac{h^* p^{*}}{\mu ^*U^*},{{\eta }_i}^2=\frac{h^{*2}}{{k_i}^*},\\&\quad \Lambda _1=\frac{\sigma ^*_2}{\sigma ^*_1},\Lambda _3=\frac{\sigma ^*_2}{\sigma ^*_3},\\&\quad \phi =\frac{\mu ^*_2}{\mu ^*}, {H}= B^*h^*\sqrt{\frac{\sigma ^{*}_{2}}{\mu ^*}},\\&\quad H_1=\frac{H}{\sqrt{\Lambda _1}}, H_3=\frac{H}{\sqrt{\Lambda _3}},\\&\quad M^2=\frac{\kappa ^*}{\mu ^*+\kappa ^*},\\&\quad L^2=\frac{\delta ^*+\tau ^*}{2\mu ^* h^{*2}},\\&\quad W^2=\frac{\alpha ^{*}+\delta ^*-\tau ^*}{2\mu ^* h^{*2}}. \end{aligned}$$

Fig. 1

Geometry of the problem

Here, H is the Hartmann number $(0\le H< \infty )$, M is micropolar parameter ($0\le M<1$) and L is couple stress parameter $(0\le L< \infty )$. The non-dimensional form of the governing equations (3.4)–(3.6) for $i=1,3$, are

$$\begin{aligned}&\nabla \cdot {\textbf {v}}_{i}=0, \end{aligned}$$

(3.10)

$$\begin{aligned}&\quad \nabla {p}+\left( \frac{{{\eta }_i}^2}{1-M^2}+{{H}_{i}}^2\right) {\textbf {v}}_{i}-\frac{M^2}{1-M^2}\ \nabla \times {\textbf {w}}_{i}\nonumber \\&\quad +\frac{1}{1-M^2}\ \nabla \times \nabla \times {\textbf {v}}_{i}={\textbf {0}}, \end{aligned}$$

(3.11)

$$\begin{aligned}&\quad {\textbf {w}}_{i}-\frac{1}{2}\ \nabla \times {\textbf {v}}_{i}+ \frac{L^2 (1-M^2)}{M^2}\ \nabla \times \nabla \nonumber \\&\quad \times {\textbf {w}}_{i}-\frac{W^2 (1-M^2)}{M^2}\ \nabla (\nabla \cdot {\textbf {w}}_{i})={\textbf {0}}. \end{aligned}$$

(3.12)

Similarly, the field equations (3.7) and (3.8) for middle channel are

$$\begin{aligned}&\nabla . {\textbf {v}}_2=0, \end{aligned}$$

(3.13)

$$\begin{aligned}&\quad \nabla {p}=-\phi \ \eta _2^2\ {\textbf {v}}_2+\phi \ \nabla ^2 {\textbf {v}}_2 -{{H}}^2\ {\textbf {v}}_2. \end{aligned}$$

(3.14)

For micropolar fluid, the non-dimensional form of tangential stresses ($T_{yx(i)}$) and couple stresses ($m_{yz(i)}$) for $i=1,3$ are

$$\begin{aligned}&T_{yx(i)}=\bigg [\frac{1}{1-M^2}\ \left( \frac{du_i}{dy} \right) + \left( \frac{M^2}{1-M^2} \right) \ w_i \bigg ]\nonumber \\&\quad \hbox {and} \,m_{yz(i)}=\bigg [\frac{dw_i}{dy}\bigg ]. \end{aligned}$$

(3.15)

For Newtonian fluid, the non-dimensional form of tangential stress ($T_{yx(2)}$) will be

$$\begin{aligned} T_{yx(2)}=\phi \ \frac{du_2}{dy}. \end{aligned}$$

(3.16)

4 Analytical solution

4.1 For lower and upper channels

The fluid velocities ${\textbf {v}}_{i}$ and microrotation vectors ${\textbf {w}}_{i}$ for plane Poiseuille flow of micropolar fluid along the x-axis of lower ($i=1$) and upper ($i=3$) porous channels are ${\textbf {v}}_{i} =(u_i (y),\ 0,\ 0)$ and ${\textbf {w}}_{i} =(0,\ 0, w_{i}(y))$, respectively. Therefore, governing equations (3.10)–(3.12) will assume the form

$$\begin{aligned} (D^2-s_i ^2)(D^2-\varepsilon _i^2) u_i=- \frac{P M^2}{L^2}, \end{aligned}$$

(4.1)

where

$$\begin{aligned}&s_i^2+\varepsilon _i^2=\frac{(-2+M^2)M^2}{2L^2(-1+M^2)}+\eta _i^2- (-1+M^2){H_1}^2,\\&\quad s_i^2\varepsilon _i^2=\frac{M^2}{L^2(-1+M^2)} [(-1+M^2){H_1}^2-\eta _i ^2], \end{aligned}$$

and pressure gradient $P=$ $\frac{dp}{dx}$  is taken constant.

The general solution of Eq. (4.1) represents velocity of the micropolar fluid and it comes out as

$$\begin{aligned}&u_i(y)=A_i\ e^{s_i y}+B_i\ e^{-s_i y}+C_i\ e^{\varepsilon _i y}\nonumber \\&\quad +D_i e^{-\varepsilon _i y}-\frac{P M^2}{s_i ^2 \varepsilon _i ^2 L^2}, \end{aligned}$$

(4.2)

where $A_i, B_i, C_i$, and $D_i\ (i=1,3)$ are arbitrary parameters.

The microrotation component can be computed using following expression:

$$\begin{aligned}&w_i=\left( -\frac{1}{2}+ \frac{L^2(1-M^2)}{M^4}\left( \eta _i^2+(1-M^2){H_i}^2\right) \right) \nonumber \\&\quad \frac{d u_i}{dy}-\frac{L^2(1-M^2)}{M^4}\frac{d^3 u_i}{dy^3}. \end{aligned}$$

(4.3)

Therefore, we have

$$\begin{aligned}&w_i=\left( \frac{L^2 \left( M^2-1\right) \left( H_i^2 \left( M^2-1\right) -\eta _i^2\right) }{M^4}-\frac{1}{2}\right) \nonumber \\&\quad \left( A_i s_i e^{s_i y}-B_i s_i e^{-s_i y}+\epsilon _i e^{-y \epsilon _i} \left( C_i e^{2 y \epsilon _i}-D_i\right) \right) \nonumber \\&\quad -\frac{L^2 \left( 1-M^2\right) }{M^4} \left( A_i s_i^3 e^{s_i y}-B_i s_i^3 e^{-s_i y}+\epsilon _i^3 e^{-y \epsilon _i} \left( C_i e^{2 y \epsilon _i}-D_i\right) \right) . \end{aligned}$$

(4.4)

The tangential stresses for corresponding micropolar fluid regions are

$$\begin{aligned}&T_{yx(i)}=\frac{1}{2 M^2 \left( 1-M^2\right) }\nonumber \\&\quad \left[ A_i s_i e^{s_i y} \left( 2 L^2 \left( M^2-1\right) \left( -\eta _i^2+H_i^2 \left( M^2-1\right) +s_i^2\right) \right. \right. \nonumber \\&\quad \left. -M^2 \left( M^2-2\right) \right) \nonumber \\&\quad +e^{-y \left( s_i+\epsilon _i\right) } \left( \epsilon _i e^{s_i y} \left( C_i e^{2 y \epsilon _i}-D_i\right) \left( 2 L^2 \left( M^2-1\right) \right. \right. \nonumber \\&\quad \left( -\eta _i^2+H_i^2 \left( M^2-1\right) +\epsilon _i^2\right) \nonumber \\&\quad -M^2 \left( M^2-2\right) )-B_i s_i e^{y \epsilon _i} (2 L^2 \left( M^2-1\right) \left( -\eta _i^2+H_i^2 \left( M^2-1\right) +s_i^2\right) \nonumber \\&\quad -M^2 \left( M^2-2\right) ))]. \end{aligned}$$

(4.5)

Couple stresses for corresponding micropolar fluid regions are

$$\begin{aligned}&m_{yz(i)}=\left( \frac{L^2 \left( M^2-1\right) \left( H_i^2 \left( M^2-1\right) -\eta _i^2\right) }{M^4}-\frac{1}{2}\right) \nonumber \\&\quad (A_i s_i^2 e^{s_i y}+B_i s_i^2 e^{-s_iy}\nonumber \\&\quad +\epsilon _i^2 e^{-y \epsilon _i} \left( C_i e^{2 y \epsilon _i}+D_i\right) )\nonumber \\&\quad +\frac{L^2 \left( M^2-1\right) }{M^4} [e^{-y \left( s_i+\epsilon _i\right) }(A_i s_i^4 e^{y \left( 2 s_i+\epsilon _i\right) }\nonumber \\&\quad +B_i s_i^4 e^{y \epsilon _i}+\epsilon _i^4 e^{s_i y} \left( C_i e^{2 y \epsilon _i}+D_i\right) )]. \end{aligned}$$

(4.6)

4.2 For middle channel

The fluid velocity ${\textbf {v}}_2$ for plane Poiseuille flow along the x-axis of the middle porous channel filled by Newtonian fluid is ${\textbf {v}}_2 =(u_2(y),\ 0,\ 0)$. Therefore, Eqs. (3.13) and (3.14) will reduce to

$$\begin{aligned} \frac{d^2 u_2}{dy^2}-\lambda ^2 u_2=\frac{P}{\phi }, \end{aligned}$$

(4.7)

where $\lambda ^2=\eta _2^2+\left( \frac{H^2}{\phi }\right) .$

Therefore, the analytical form of velocity vector of Newtonian fluid will be

$$\begin{aligned} u_2(y)=A_2\ e^{\lambda y}+B_2\ e^{-\lambda y}-\frac{P}{\lambda ^2 \phi }, \end{aligned}$$

(4.8)

where $A_2$ and $B_2$ are arbitrary parameters.

Tangential stress for Newtonian fluid is

$$\begin{aligned} T_{yx(2)}=\lambda \phi e^{-\lambda y} \left( A_2\ e^{2 \lambda y}-B_2\right) . \end{aligned}$$

(4.9)

5 Determination of arbitrary parameters

To determine ten parameters $A_1, B_1, C_1, D_1, A_2, B_2,A_3, B_3, C_3, D_3$, we will apply the following boundary conditions (Yadav et al. 2018) that are physically realistic and mathematically valid:

• (i) no slip condition at $y=0$ implies that

  $$\begin{aligned} u_1=0. \end{aligned}$$

  (5.1)

• (ii) no spin condition at $y=0$ implies that

  $$\begin{aligned} w_1=0. \end{aligned}$$

  (5.2)

• (iii) continuity of the velocity at $y=1$ implies that

  $$\begin{aligned} u_1=u_2. \end{aligned}$$

  (5.3)

• (iv) continuity of tangential stress at $y=1$ implies that

  $$\begin{aligned} T_{yx (1)}=T_{yx(2)}. \end{aligned}$$

  (5.4)

• (v) no couple stress at $y=1$ implies that

  $$\begin{aligned} m_{yz (1)}=0. \end{aligned}$$

  (5.5)

• (vi) continuity of the velocity at $y=2$ implies that

  $$\begin{aligned} u_2=u_3. \end{aligned}$$

  (5.6)

• (vii) continuity of tangential stress at $y=2$ implies that

  $$\begin{aligned} T_{yx(2)}=T_{yx(3)}. \end{aligned}$$

  (5.7)

• (viii) no couple stress at $y=2$ implies that

  $$\begin{aligned} m_{yz (3)}=0. \end{aligned}$$

  (5.8)

• (ix) no slip condition at $y=3$ implies that

  $$\begin{aligned} u_3=0. \end{aligned}$$

  (5.9)

• (x) no spin condition at $y=3$ implies that

  $$\begin{aligned} w_3=0. \end{aligned}$$

  (5.10)

Substituting the boundary conditions (BCs) from Eqs. (5.1) to (5.10), we will obtain a system of linear equations for the arbitrary parameters appearing in the solution of the velocities $u_1,\ u_2,\ u_3$. The system of linear equations can be expressed in matrix form in the following way:

$$\begin{aligned} N X=Z, \end{aligned}$$

(5.11)

where matrices N, X and Z are

$$\begin{aligned} N= & {} \begin{bmatrix} 1&{}\xi _1 &{}e^{s_1} &{}-e^{s_1} \xi _2&{}s_1 e^{s_1} \xi _1&{}0&{}0&{}0&{}0&{}0\\ 1&{}-\xi _1 &{}e^{-s_1} &{}e^{-s_1}\xi _2&{}s_1 e^{-s_1} \xi _1 &{}0&{}0&{}0&{}0&{}0\\ 1&{}\zeta _1 &{}e^{\varepsilon _1} &{}-e^{\varepsilon _1} \zeta _2 &{}\varepsilon _1 e^{\varepsilon _1} \zeta _1 &{}0&{}0&{}0&{}0&{}0\\ 1&{}-\zeta _1 &{}e^{-\varepsilon _1} &{}e^{-\varepsilon _1} \zeta _2 &{}\varepsilon _1 e^{-\varepsilon _1} \zeta _1 &{}0&{}0&{}0&{}0&{}0\\ 0&{}0 &{}-e^\lambda &{}0 &{}0 &{}e^{2\lambda }&{}-e^{2\lambda }\Omega &{}0&{}0&{}0\\ 0&{}0 &{}-e^{-\lambda }&{}0 &{}0 &{}e^{-2\lambda }&{}e^{2\lambda }\Omega &{}0&{}0&{}0\\ 0&{}0 &{}0&{}0 &{}0 &{}-e^{2s_3}&{}- e^{2s_3}\xi _4 &{}s_3e^{2s_3}\xi _3&{}e^{3s_3}&{}e^{3s_3}\\ 0&{}0 &{}0&{}0 &{}0 &{}-e^{-2s_3}&{}e^{-2s_3}\xi _4&{}s_3e^{-2s_3}\xi _3&{}e^{-3s_3}&{}-e^{-3s_3}\xi _3\\ 0&{}0 &{}0&{}- e^{\lambda }\Omega &{}0 &{}-e^{2\varepsilon _3}&{}-e^{2\varepsilon _3} \zeta _4&{}\varepsilon _3 e^{2\varepsilon _3} \zeta _3&{}e^{3\varepsilon _3}&{}e^{3\varepsilon _3}\zeta _3\\ 0&{}0 &{}0&{}e^{-\lambda } \Omega &{}0 &{}-e^{-2\varepsilon _3}&{}e^{-2\varepsilon _3}\zeta _4&{}\varepsilon _3 e^{-2\varepsilon _3} \zeta _3&{}e^{-3\varepsilon _3}&{}-e^{-3\varepsilon _3}\zeta _3\\ \end{bmatrix},\\ X= & {} \begin{bmatrix} A_1&B_1&C_1&D_1&A_2&B_2&A_3&B_3&C_3&D_3 \end{bmatrix}^T,\\ \text{ and }~~~~Z= & {} \begin{bmatrix} \frac{M^2 P}{L^2 s_1^2 \varepsilon _1^2}&0&(\frac{M^2 P}{L^2 s_1^2 \varepsilon _1^2}-\frac{P}{\lambda ^2 \phi })&0&0&-(\frac{M^2 P}{L^2 s_3^2 \varepsilon _3^2}-\frac{P}{\lambda ^2 \phi })&0&0&\frac{M^2 P}{L^2 s_3^2 \varepsilon _3^2}&0 \end{bmatrix}^T, \end{aligned}$$

where $\xi _1= s_1[-\frac{1}{2}+\frac{L^2(-1+M^2)}{M^4}((-1+M^2)H_1^2-\eta _1^2)+\frac{s_1^2 L^2(-1+M^2)}{M^4}]$,

$\zeta _1= \varepsilon _1[-\frac{1}{2}+\frac{L^2(-1+M^2)}{M^4}((-1+M^2)H_1^2-\eta _1^2)+\frac{\varepsilon _1^2 L^2(-1+M^2)}{M^4}]$,

$\xi _2=s_1[M^2(-2+M^2)-2L^2(-1+M^2)((-1+M^2)H_1^2+s_1^2-\eta _1^2)]$,

$\zeta _2= \varepsilon _1[M^2(-2+M^2)-2L^2(-1+M^2)((-1+M^2)H_1^2+\varepsilon _1^2-\eta _1^2)]$,

$\xi _3= s_3[-\frac{1}{2}+\frac{L^2(-1+M^2)}{M^4}((-1+M^2)H_3^2-\eta _3^2)+\frac{s_3^2 L^2(-1+M^2)}{M^4}]$,

$\zeta _3= \varepsilon _3[-\frac{1}{2}+\frac{L^2(-1+M^2)}{M^4}((-1+M^2)H_3^2-\eta _3^2)+\frac{\varepsilon _3^2 L^2(-1+M^2)}{M^4}]$,

$\xi _4=s_3[M^2(-2+M^2)-2L^2(-1+M^2)((-1+M^2)H_3^2+s_3^2-\eta _3^2)]$,

$\zeta _4= \varepsilon _3[M^2(-2+M^2)-2L^2(-1+M^2)((-1+M^2)H_3^2+\varepsilon _3^2-\eta _3^2)]$,

$\Omega =2M^2 \lambda \phi (1-M^2)$.

Using MATHEMATICA, all parameters (i.e. $A_1, B_1, C_1, D_1, A_2,B_2, A_3, B_3, C_3, D_3$) have been evaluated uniquely. Due to cumbersome expressions of these parameters, we refrain the values of these parameters from the text of manuscript.

6 Evaluation of flow rate and stresses

6.1 Flow rate

The flow rate through channels $(0<y<3)$ can be evaluated using the formula:

$$\begin{aligned} Q=\int _{0}^{1} u_1\ dy+\int _{1}^{2} u_2\ dy+ \int _{2}^{3} u_3\ dy. \end{aligned}$$

(6.1)

Substituting expressions of velocities from Eqs. (4.2) and (4.8) in Eq. (6.1), we are able to find the analytical expression for the volumetric flow rate of Newtonian-micropolar fluid flow. Therefore, the analytical expression of the flow rate will be

$$\begin{aligned}&Q=\frac{e^{-2 \lambda } \left( e^{\lambda }-1\right) \lambda \left( A_2 e^{3 \lambda }+B_2\right) -\frac{P}{\phi }}{\lambda ^2}+\frac{A_1 \left( e^{s_1}-1\right) }{s_1}\nonumber \\&\quad +\frac{A_3 e^{2 s_3} \left( e^{s_3}-1\right) }{s_3}\nonumber \\&\quad +\frac{B_1 \left( 1-e^{-s_1}\right) }{s_1}+\frac{B_3 e^{-3 s_3} \left( e^{s_3}-1\right) }{s_3}\nonumber \\&\quad +\frac{e^{-\epsilon _1} \left( e^{\epsilon _1}-1\right) \epsilon _1 \left( C_1 e^{\epsilon _1}+D_1\right) -\frac{M^2 P}{L^2 s_1^2}}{\epsilon _1^2}\nonumber \\&\quad +\frac{e^{-3 \epsilon _3} \left( e^{\epsilon _3}-1\right) \epsilon _3 \left( C_3 e^{5 \epsilon _3}+D_3\right) -\frac{M^2 P}{L^2 s_3^2}}{\epsilon _3^2}. \end{aligned}$$

(6.2)

6.2 Tangential and couple stresses at the interfaces

6.3 At porous interface ${\textbf {y=1}}$:

The non-dimensional form of the tangential stress ($T_{yx(1)}$) and couple stress ($m_{yz (1)}$) at lower interface ($y=1$) of the porous layers are denoted by $T^{(1)}_{yx}$ and $m^{(1)}_{yz}$, respectively. Mathematically,

$$\begin{aligned}&T^{(1)}_{yx}=\bigg [\frac{1}{1-M^2}\ \left( \frac{du_1}{dy} \right) + \left( \frac{M^2}{1-M^2} \right) \ w_1 \bigg ]_{y=1}\\&\quad \text{ and } m^{(1)}_{yz}=\bigg [\frac{dw_1}{dy}\bigg ]_{y=1}. \end{aligned}$$

Therefore,

$$\begin{aligned}&T^{(1)}_{yx}= \frac{1}{2 M^2 \left( 1-M^2\right) }\nonumber \\&\quad \left[ A_1 e^{s_1} s_1 \left( 2 L^2 \left( M^2-1\right) \left( -\eta _1^2+H_1^2 \left( M^2-1\right) +s_1^2\right) \right. \right. \nonumber \\&\left. \quad -M^2 \left( M^2-2\right) \right) \nonumber \\&\quad +B_1 e^{-s_1} s_1 \left( M^2 \left( M^2-2\right) -2 L^2 \left( M^2-1\right) \right. \nonumber \\&\quad \left. \left( -\eta _1^2+H_1^2 \left( M^2-1\right) +s_1^2\right) \right) \nonumber \\&\quad +e^{-\epsilon _1} \epsilon _1 \left( C_1 e^{2 \epsilon _1}-D_1\right) \left( 2 L^2 \left( M^2-1\right) \right. \nonumber \\&\quad \left. \left( -\eta _1^2+H_1^2 \left( M^2-1\right) +\epsilon _1^2\right) -M^2 \left( M^2-2\right) \right) ]. \end{aligned}$$

(6.3)

and

$$\begin{aligned}&m^{(1)}_{yz}= \left( \frac{L^2 \left( M^2-1\right) \left( H_1^2 \left( M^2-1\right) -\eta _1^2\right) }{M^4}-\frac{1}{2}\right) \nonumber \\&\quad \left( A_1 e^{s_1} s_1^2+B_1 e^{-s_1} s_1^2+e^{-\epsilon _1} \epsilon _1^2 \left( C_1 e^{2 \epsilon _1}+D_1\right) \right) \nonumber \\&\quad +\frac{L^2 \left( M^2-1\right) }{M^4} \nonumber \\&\quad \left[ e^{-s_1-\epsilon _1} \left( A_1 s_1^4 e^{2 s_1+\epsilon _1}+B_1 s_1^4 e^{\epsilon _1}+e^{s_1} \epsilon _1^4 \left( C_1 e^{2 \epsilon _1}+D_1\right) \right) \right] . \end{aligned}$$

(6.4)

6.4 At porous interface ${\textbf {y=2}}$

The non-dimensional form of the tangential stress ($T_{yx(3)}$) and couple stress ($m_{yz (3)}$) at upper interface ($y=2$) of the porous layers are denoted by $T^{(3)}_{yx}$ and $m^{(3)}_{yz}$, respectively. Mathematically,

$$\begin{aligned}&T^{(3)}_{yx}=\bigg [\frac{1}{1-M^2}\ \left( \frac{du_3}{dy} \right) + \left( \frac{M^2}{1-M^2} \right) \ w_3 \bigg ]_{y=2}\\&\quad \hbox {and} m^{(3)}_{yz}=\bigg [\frac{dw_3}{dy}\bigg ]_{y=2}. \end{aligned}$$

Therefore,

$$\begin{aligned}&T^{(3)}_{yx}=\frac{1}{2 M^2 \left( 1-M^2\right) }\nonumber \\&\quad [A_3 e^{2 s_3} s_3 (2 L^2 \left( M^2-1\right) \left( -\eta _3^2+H_3^2 \left( M^2-1\right) +s_3^2\right) \nonumber \\&\quad -M^2 \left( M^2-2\right) )+e^{-2 \left( s_3+\epsilon _3\right) } (e^{2 s_3} \epsilon _3 \left( C_3 e^{4 \epsilon _3}-D_3\right) \nonumber \\&\quad (2 L^2 \left( M^2-1\right) \nonumber \\&\quad \left( -\eta _3^2+H_3^2 \left( M^2-1\right) +\epsilon _3^2\right) -M^2 \left( M^2-2\right) )-B_3 s_3 e^{2 \epsilon _3}\nonumber \\&\quad (2 L^2 \left( M^2-1\right) \left( -\eta _3^2+H_3^2 \left( M^2-1\right) +s_3^2\right) -M^2 \left( M^2-2\right) ))], \end{aligned}$$

(6.5)

and

$$\begin{aligned}&m^{(3)}_{yz}=\left( \frac{L^2 \left( M^2-1\right) \left( H_3^2 \left( M^2-1\right) -\eta _3^2\right) }{M^4}-\frac{1}{2}\right) \nonumber \\&\quad \left( A_3 s_3^2 e^{s_3 y}+B_3 s_3^2 e^{-s_3y}\right. \nonumber \\&\quad \left. +\epsilon _3^2 e^{-y \epsilon _3} \left( C_3 e^{2 y \epsilon _3}+D_3\right) \right) +\frac{L^2 \left( M^2-1\right) }{M^4}\nonumber \\&\quad \left[ e^{-y \left( s_3+\epsilon _3\right) } \left( A_3 s_3^4 e^{y \left( 2 s_3+\epsilon _3\right) }\right. \right. \nonumber \\&\quad \left. \left. +B_3 s_3^4 e^{y \epsilon _3}+\epsilon _3^4 e^{s_3 y} \left( C_3 e^{2 y \epsilon _3}+D_3\right) \right) \right] . \end{aligned}$$

(6.6)

7 Discussion of flow rate

In this section, we will discuss the variation of the flow rate with respect to permeability parameter ($\eta _2$) on micropolar parameter (M), couple stress parameter (L), viscosity ratio ($\phi$), Hartmann number (H), permeability parameters $(\eta _1, \eta _3)$ and conductivity ratio parameters ($\Lambda _1, \Lambda _3$). Numerical values of flow rate, wall shear stresses and couple stresses at the porous interfaces are mentioned in Tables (1)–(8). To plot graphs of flow rate, pressure gradient ($P=-0.2$) and permeability parameter ($\eta _2=0\ \text{ to }\ 5$) are used.

7.1 Effect of micropolar parameter M

Figure 2 shows the effect of micropolar parameter $(M=0.25,\ 0.5,\ 0.75)$ on the flow rate of the fluid flow in the three respective porous regions when couple stress parameter $(L=0.2)$, viscosity ratio parameter ($\phi =1$), Hartmann number $(H=1)$, permeability parameters $(\eta _1=1.2,\ \eta _3=1.3)$ and conductivity ratio parameters ($\Lambda _1=1,\ \Lambda _3=2$). As the parameter M grows, the volumetric flow rate decreases in all respective porous channels. The behavior of volumetric flow rate is almost similar for very small values of M. Along the variation of permeability parameter $\eta _2$, we observed that the flow rate is rapidly decreasing for very small variation in $\eta _2$ and for the large values of $\eta _2$, flow rate decreases very slowly. Numerical values of flow rate (Q), shear stresses ($T_{yx (1)}, T_{yx(3)}$) and couple stresses $(m_{yz(1)}, m_{yz(3)})$ at the porous interfaces ($y=1\ \hbox {and}\ y=2$), (i.e. named earlier as $T^{(1)}_{yx}, T^{(3)}_{yx}, m^{(1)}_{yz}, m^{(3)}_{yz}$ in (6.2) and (6.2)), are mentioned in the Table 1.

Table 1 Numerical values of flow rate, shear stresses and couple stresses at porous interfaces for micropolar parameter M when: $P=-0.2,\ L=0.2,\ \phi =1,\ H=1,\ \Lambda _1=1,\ \Lambda _3=2,\ \eta _1=1.2,\ \eta _2=0.2,\ \eta _3=1.3$

7.2 Effect of couple parameter L

Effect of couple stress parameter $(L=0.02,\ 0.2,\ 2)$ on the flow rate of the fluid flow in the three respective porous regions are reported using Fig. 3 when micropolar parameter $(M=0.25)$, viscosity ratio $\phi =1$, Hartmann number $(H=1)$, permeability parameter $(\eta _1=1.2,\ \eta _3=1.3)$ and conductivity ratio parameters ($\Lambda _1=1,\ \Lambda _3=2$). As the couple stress parameter increases, the volumetric flow rate (Q) decreases in all respective porous regions. Behavior of the flow rate is almost similar for large values of this stress parameter. For $\eta _2>3$, the behavior of the graph of flow rate is almost same for every value of micropolar parameter. Along the variation of parameter $\eta _2$, we found that the flow rate is decreasing rapidly for the small variation of the permeability parameter $\eta _2$ and for the large values of this permeability parameter, the flow rate decays smoothly. Numerical values of flow rate, shear stresses and couple stresses at the porous interfaces are given in Table 2.

Table 2 Numerical values of flow rate, wall shear stresses and couple stresses for couple stress parameter L when: $P=-0.2,\ M=0.25,\ \phi =1,\ H=1,\ \Lambda _1=1,\ \Lambda _3=2,\ \eta _1=1.2,\ \eta _2=0.2,\ \eta _3=1.3$

7.3 Effect of viscosity ratio parameter $\phi$

Figure 4 represents the effect of viscosity parameter $(\phi )$ on the flow rate of the fluid flow in the three respective porous regions when micropolar parameter $(M=0.25)$, couple stress parameter $(L=2)$, Hartmann number $(H=1.1)$, permeability parameter $(\eta _1=1.2,\ \eta _3=1.3)$ and conductivity ratio parameters $(\Lambda _1=1, \Lambda _3=2)$ are substituted. As the viscosity parameter $(\phi )$ increases, the volumetric flow rate decreases in all respective porous regions. Along the variation of parameter ($\eta _2$), we observed that the flow rate is decreasing rapidly for the small variation of permeability parameter and for the large values of this ratio parameter, the flow rate is decreasing slowly. Numerical values of flow rate, wall shear stresses and couple stresses at the porous interfaces are given in Table 3.

Table 3 Numerical values of flow rate, wall shear stresses and couple stresses for viscosity ratio parameter $\phi$ when: $P=-0.2,\ M=0.25,\ L=2,\ H=1,\ \Lambda _1=1,\ \Lambda _3=2,\ \eta _1=1.2,\ \eta _2=0.2,\ \eta _3=1.3$

7.4 Effect of Hartmann number H

Effect of magnetic parameter (H) on the flow rate is described in the three respective fluid flow regions when micropolar parameter $(M=0.25)$, couple stress parameter $(L=2)$, viscosity ratio parameter ($\phi =1$), conductivity ratio parameter ($\Lambda _1=1, \Lambda _3=2$), and permeability parameter $(\eta _1=1.2,\ \eta _3=1.3)$ (Fig. 5). As the Hartmann number (H) increases, the volumetric flow rate decreases in all regions whenever permeability parameter $\eta _2<2.5$. Now, for $\eta _2>2.5$, the flow rate is increasing with the increment in the Hartmann number H. Along with the small variation of this ratio parameter $(\eta _2)$, we see that the flow rate is decreasing rapidly and for $\eta _2>2.5$, flow rate is almost coincided. Numerical values of flow rate (Q), wall shear stresses $(T^{(1)}_{yx}, T^{(3)}_{yx})$ and couple stresses $(m^{(1)}_{yz}, m^{(3)}_{yz})$ are mentioned in Table 4.

Table 4 Numerical values of flow rate, wall shear stresses and couple stresses for Hartmann number H when: $P=-0.2,\ M=0.25,\ L=2,\ \phi =1,\ \Lambda _1=1,\ \Lambda _3=2,\ \eta _1=1.2,\ \eta _2=0.2,\ \eta _3=1.3$

7.5 Effect of conductivity ratio parameter $\Lambda _1$

Effect of conductivity ratio parameter $(\Lambda _1)$ on the flow rate in the three respective porous regions (Fig. 6) when micropolar parameter $(M=0.25)$, couple stress parameter $(L=0.2)$, viscosity ratio parameter ($\phi =1$), Hartmann number ($H=1$), conductivity ratio parameter ($\Lambda _3=2$), and permeability parameters ($\eta _1=1.2,\ \eta _3=1.3$) is discussed. The flow rate decreases in all porous regions with the increment in the values of the parameter $(\Lambda _1)$. For the large value of conductivity ratio parameter $\Lambda _1$, the behavior of flow rate is similar. In addition, the flow rate is decaying rapidly whenever $\eta _2<3$ and for $\eta _2>3$, the similar variations in the flow rate are found for every values of $\Lambda _1$. For the porous interfaces ($y=1\ \text{ and }\ y=2$), numerical values of flow rate (Q), wall shear stresses $(T_{yx(1)}, T_{yx(3)})$ and couple stresses $(m_{yz(1)}, m_{yz(3)})$ are written in Table 5.

Table 5 Numerical values of flow rate, wall shear stresses and couple stresses for $\Lambda _1$ when: $P=-0.2,\ M=0.25,\ L=0.2,\ \phi =1,\ H=1,\ \Lambda _3=2,\ \eta _1=1.2,\ \eta _2=0.2,\ \eta _3=1.3$

7.6 Effect of conductivity ratio parameter $\Lambda _3$

Effect of conductivity ratio parameter $(\Lambda _3)$ on the flow rate in the three respective porous regions (Fig. 7) when micropolar parameter $(M=0.25)$, couple stress parameter $(L=2)$, viscosity ratio parameter ($\phi =1$), Hartmann number ($H=1$), conductivity ratio parameter ($\Lambda _1=1$), and permeability parameters ($\eta _1=1.2,\ \eta _3=1.3$) is discussed. For all value of conductivity ratio parameter $\Lambda _3$, the flow rate is almost same for all the values of $\eta _2$. The volumetric flow rate decreases in respective porous regions as the values of the parameter $(\Lambda _1)$ increases. In addition, the flow rate is decaying rapidly whenever $\eta _2<4$ and for $\eta _2>4$, decreases very slowly for every values of $\Lambda _3$. At the porous interfaces ($y=1\ \text{ and }\ y=2$), numerical values of flow rate (Q), wall shear stresses $(T_{yx(1)}, T_{yx(3)})$ and couple stresses $(m_{yz(1)}, m_{yz(3)})$ are given in Table 6.

Table 6 Numerical values of flow rate, wall shear stresses and couple stresses for $\Lambda _3$ when: $P=-0.2,\ M=0.25,\ L=2,\ \phi =1,\ H=1,\ \Lambda _1=1,\ \eta _1=1.2,\ \eta _2=0.2,\ \eta _3=1.3$

7.7 Effect of permeability parameter $\eta _1$

Effects of permeability parameter $(\eta _1)$ on the flow rate in the three respective porous regions are discussed when $M=0.25,\ L=0.2,\ \phi =1,\ H=1,\ \Lambda _1=1,\ \Lambda _3=2,\ \eta _3=1.3$ (Fig. 8). Volumetric flow rate decreases in all respective porous regions whenever the parameter $(\eta _1)$ increases. In addition, we observed that for a fixed value of $\eta _1$, the flow rate is decreasing rapidly for the small variation of the permeability parameter $(\eta _2)$ and for the large values of $\eta _2$, the flow rate decreases slowly. In addition, for the large variation in $\eta _2$, flow rate is converging therefore, streamlines become very close to each other. Numerical values of flow rate (Q), wall shear stresses $(T^{(1)}_{yx}, T^{(3)}_{yx})$ and couple stresses $(m^{(1)}_{yz}, m^{(3)}_{yz})$ are mentioned in Table 7.

Table 7 Numerical values of flow rate, wall shear stresses and couple stresses for permeability parameter $\eta _1$ when: $P=-0.2,\ M=0.25,\ L=0.2,\ \phi =1,\ H=1,\ \Lambda _1=1,\ \Lambda _3=2,\ \eta _2=0.2,\ \eta _3=1.3$

7.8 Effect of permeability parameter $\eta _3$

Effects of permeability parameter $(\eta _3)$ on the flow rate of the fluid flow in the three respective porous regions are explained by Fig. 9 when values of micropolar parameter, couple stress parameter, viscosity ratio parameter, Hartmann number, conductivity ratio parameters, and permeability parameter are taken as $\ M=0.25,\ L=0.2,\ \phi =1,\ H=1,\ \Lambda _1=1,\ \Lambda _3=2,\ \eta _1=1.2$, respectively. As the permeability parameter $\eta _3$ increases, the volumetric flow rate decreases in all respective porous regions. Graphs of flow rate are looking similar for every values of $\eta _2$ whenever, the parameter $\eta _3$ decreases. Flow rate is decaying rapidly for small variation of permeability parameter $\eta _2$ and the streamlines passing through a cross-section coincide to each other for the large values of $\eta _2$. Numerical values of flow rate, wall shear stresses and couple stresses at the porous interfaces are mentioned in Table 8.

Table 8 Numerical values of flow rate, wall shear stresses and couple stresses for permeability parameter $\eta _3$ when: $P=-0.2,\ M=0.25,\ L=0.2,\ \phi =1,\ H=1,\ \Lambda _1=1,\ \Lambda _3=2,\ \eta _1=1.2,\ \eta _2=0.2$

Fig. 2

Variation of the flow rate: $(1)\ M=0.25,(2)\ M=0.5,(3)\ M=0.75$

Fig. 3

Variation of the flow rate: $(1)\ L=0.02,\ (2)\ L=0.2,\ (3)\ L=2$

Fig. 4

Variation of the flow rate: $(1)\ \phi =0.5,\ (2)\ \phi =1,\ (3)\ \phi =1.5$

8 Discussion of the fluid velocity

In this section, we will discuss the graphical behavior of the fluid velocity along with the variation of width of channel y in which pressure gradient $P=-0.2$ is kept fixed for the following parameters: (i) effect of micropolar parameter (M), (ii) effect of couple stress parameter (L), (iii) effect of viscosity ratio parameter ($\phi$), (iv) effect of Hartmann number (H), (v) effect of conductivity ratio parameter ($\Lambda _1$), (vi) effect of conductivity ratio parameter ($\Lambda _3$), (vii) effect of permeability parameter ($\eta _1$), (viii) effect of permeability parameter ($\eta _2$), and (ix) effect of permeability parameter ($\eta _3$).

Fig. 5

Variation of the flow rate: $(1)\ H=0.01, (2)\ H=0.5, \ (3)\ H=1$

Fig. 6

Variation of the flow rate: $(1)\ \Lambda _1=0.75, \ (2)\ \Lambda _1=1.5, \ (3)\ \Lambda _1=5$

Fig. 7

Variation of the flow rate: $(1)\ \Lambda _3=0.6, \ (2)\ \Lambda _3=1, \ (3)\ \Lambda _3=3$

8.1 Effect of micropolar parameter M

Effects of micropolar parameter $(M=0.4,\ 0.5,\ 0.6)$ on the fluid velocity in the three respective porous regions are discussed when couple stress parameter $(L=0.2)$, viscosity ratio parameter ($\phi =1$), Hartmann number ($H=1$), conductivity ratio parameters ($\Lambda _1=1,\ \Lambda _3=2$), and permeability parameters: $\eta _1=1.1,\ \eta _2=1.2,\ \eta _3=1.3$ (Fig. 10). The velocity of fluid flow through channels decreases whenever the parameter M increases and streamlines are parabolic. In addition, we observed that the velocity profile on the width of the channel y varies up to a maximum values whenever $y<1$, almost constant for $1<y<2$ and decreases smoothly for $y>2$. Near the walls (both lower and upper), velocity vanishes due to presence of no slip conditions at walls (i.e. $y=0\ \text{ and }\ y=3$).

Fig. 8

Variation of the flow rate: $(1)\ \eta _1=1,\ (2)\ \eta _1=1.5,\ (3)\ \eta _1=2$

Fig. 9

Variation of the flow rate: $(1)\ \eta _3=0.75,\ (2)\ \eta _3=1,\ (3)\ \eta _3=1.5$

8.2 Effect of couple stress parameter L

Effects of couple stress parameter $(L=0.01,\ 0.1,\ 1)$ on the fluid velocity in the all porous regions when micropolar parameter $(M=0.25)$, viscosity ratio parameter ($\phi =1$), Hartmann number ($H=1$), conductivity ratio parameters ($\Lambda _1=1,\ \Lambda _3=2$), and permeability parameters ($\eta _1=1.1,\ \eta _2=1.2,\ \eta _3=1.3$) are discussed (Fig. 11). Velocity of fluid flow through channels decreases whenever the couple stress parameter L increases and the streamlines are parabolic. In addition, we observed that the velocity profile on the width of the channel y varies up to a maximum value whenever $y<1$, varies constantly for $1<y<2$ and decays smoothly for $y>2$.

8.3 Effect of viscosity ratio parameter $\phi$

Figure 12 represents the effect of viscosity ratio parameter $(\phi =1,\ 2,\ 3)$ on the fluid velocity in the three respective porous regions when micropolar parameter $(M=0.25)$, couple stress parameter ($L=0.2$), Hartmann number ($H=1$), conductivity ratio parameters ($\Lambda _1=1,\ \Lambda _3=2$), and permeability parameters ($\eta _1=1.1,\ \eta _2=1.2,\ \eta _3=1.3$) are used. Velocity of fluid flow through porous channels decreases as parameter $\phi$ increases. In addition, it is seen that the velocity profile on the width of the channel y varies up to a maximum value whenever $y<1$, varies constantly for $1<y<2$ and decays smoothly for $y>2$. Streamlines are fluctuating in the middle porous region which is filled by the Newtonian fluid.

8.4 Effect of Hartmann number H

Effects of the Hartmann number $(H=0.75,\ 1,\ 1.25)$ on the fluid velocity in three respective porous regions are explained when micropolar parameter $(M=0.25)$, couple stress parameter ($L=0.2$), viscosity ratio ($\phi =1$), conductivity ratio parameters ($\Lambda _1=1,\ \Lambda _3=2$), and permeability parameters: $\eta _1=1.1,\ \eta _2=1.2,\ \eta _3=1.3$ (Fig. 13). When the values of width of channel $y<1$, the velocity of fluid flow through porous channels increases as parameter H increases and for middle channel ($1<y<2$), it decreases as H increases. For $y>2$, velocity profiles are found almost same for all values of H. Streamlines are parabolic and the velocity profile for width of the channel y varies whenever $y<1$. In addition, the velocity decays slowly within the region ($1<y<2$) and rapidly for $y>2$.

8.5 Effect of conductivity ratio parameter $\Lambda _1$

Effects of conductivity ratio parameter $(\Lambda _1=0.5,1,1.5)$ on the fluid velocity in the three respective porous regions are discussed using Fig. 14 when micropolar parameter $(M=0.25)$, couple stress parameter ($L=0.2$), viscosity ratio ($\phi =1$), Hartmann number ($H=1$), conductivity ratio parameter ($\Lambda _3=2$), and permeability parameters ($\eta _1=1.1,\ \eta _2=1.2,\ \eta _3=1.3$) are used. The velocity of fluid flow through porous channels decreases as parameter $\Lambda _1$ increases in all fluid regions. For large values of y, velocity profiles are same for all values of $\Lambda _1$. The nature of streamlines are looking as parabolic.

Fig. 10

Variation of the fluid velocity: $(1)\ M=0.4,\ (2)\ M=0.5,\ (3)\ M=0.6$

Fig. 11

Variation of the fluid velocity: $(1)\ L=0.01,\ (2)\ L=0.1,\ (3)\ L=1$

8.6 Effect of conductivity ratio parameter $\Lambda _3$

Effects of conductivity ratio parameter $(\Lambda _3=0.2,0.4,0.8)$ on the fluid velocity in the three respective porous regions are described (Fig. 15) when micropolar parameter $(M=0.25)$, couple stress parameter ($L=0.2$), viscosity ratio ($\phi =1$), Hartmann number ($H=1$), conductivity ratio parameter ($\Lambda _1=1$), and permeability parameters ($\eta _1=1.1,\ \eta _2=1.2,\ \eta _3=1.3$. Velocity of fluid flow through porous channels decreases as parameter $\Lambda _3$ increases in all fluid regions. For very small values of y, velocity profiles are same for all values of $\Lambda _3$ and for large values of y, different graphs are obtained. In addition, in fluid velocity, more fluctuations can be seen in the region ($2<y<3$) for small values of $\Lambda _3$.

Fig. 12

Variation of the fluid velocity: $(1)\ \phi =1,\ (2)\ \phi =2,\ (3)\ \phi =3$

Fig. 13

Variation of the fluid velocity: $(1)\ H=0.75,\ (2)\ H=1,\ (3)\ H=1.25$

8.7 Effect of permeability parameter $\eta _1$

Figure 16 shows the effect of permeability parameter $(\eta _1=0.5,1,1.5)$ on the fluid velocity in the three respective porous regions when value of micropolar parameter $(M=0.25)$, couple stress parameter ($L=0.2$), viscosity ratio ($\phi =1$), Hartmann number ($H=1$), conductivity ratio parameters ($\Lambda _1=1, \ \Lambda _3=2$), and permeability parameters ($\eta _2=1.2,\ \eta _3=1.3$) are taken. As the permeability parameter $\eta _1$ increases, fluid velocity through porous channels decreases. For $y>2.5$, similar velocity profiles are obtained for all values of $\eta _1$. Behavior of streamlines are of parabolic. For the small values of y, different graphs are obtained.

8.8 Effect of permeability parameter $\eta _2$

Effects of permeability parameter $(\eta _2=0.5,1,1.5)$ on the fluid velocity (Fig. 17) in the three respective porous regions when micropolar parameter $(M=0.25)$, couple stress parameter ($L=0.2$), viscosity ratio ($\phi =1$), Hartmann number ($H=1$), conductivity ratio parameters ($\Lambda _1=1, \ \Lambda _3=2$), and permeability parameters ($\eta _1=1.2,\ \eta _3=1.3$) are discussed. As the permeability parameter $\eta _2$ increases, the fluid velocity through porous channels decreases. For the regions $y<0.5$ and $y>2.5$, velocity profiles are similar for all values of $\eta _2$. Behavior of streamlines are of parabolic. In addition, for the region $0.5<y<2.5$, different graphs are obtained for every value of $\eta _2$. In addition, for a fixed value of $\eta _2$, we found that velocity increases up to a maximum value when $y=1.5$.

Fig. 14

Variation of the fluid velocity: $(1)\ \Lambda _1=0.5,\ (2)\ \Lambda _1=1,\ (3)\ \Lambda _1=1.5$

Fig. 15

Variation of the fluid velocity: $(1)\ \Lambda _3=0.2,\ (2)\ \Lambda _3=0.4,\ (3)\ \Lambda _3=0.8$

8.9 Effect of permeability parameter $\eta _3$

Effect of permeability parameter $(\eta _3=1,1.5,2)$ on the fluid velocity in the three respective porous regions are described with the help of Fig. 18 when micropolar parameter $(M=0.25)$, couple stress parameter ($L=0.2$), viscosity ratio ($\phi =1$), Hartmann number ($H=1$), conductivity ratio parameters ($\Lambda _1=1, \ \Lambda _3=2$), and permeability parameters ($\eta _1=1.3,\ \eta _2=1.2$) are substituted. As the permeability parameter $\eta _3$ increases, the fluid velocity through porous channels decreases. For the region $0<y<1$, almost similar variations are obtained and variations of streamlines for region $1<y<3$ are different.

Fig. 16

Variation of the fluid velocity: $(1) {\eta }_{1}=0.5, (2) {\eta }_{1}=1, (3) {\eta }_{1}=1.5$

Fig. 17

Variation of the fluid velocity: $(1)\ {\eta }_2=0.5,\ (2)\ {\eta }_2=1,\ (3)\ {\eta }_2=1.5$

Fig. 18

Variation of the fluid velocity: $(1)\ {\eta }_3=1,\ (2)\ {\eta }_3=1.5,\ (3)\ {\eta }_3=2$

9 Conclusion

In this research work, we have investigated the micropolar–Newtonian flow through composite porous channels in the presence of magnetic field. The volumetric flow rate and fluid velocity are plotted for different values of various parameters and these parameters are such as micropolar parameter (M), couple stress parameter (L), viscosity ratio parameter ($\phi$), Hartmann number (H), conductivity ratio parameters ($\Lambda _1,\ \Lambda _3$), and permeability parameters ($\eta _1,\ \eta _2,\ \eta _3$). Numerical values of flow rate, tangential stresses and couple stresses at both porous interfaces (i.e. $y=1$ and $y=2$) are calculated by MATHEMATICA and listed in tables. Investigating the effect of these parameters, following conclusions are made:

• The fluid flow rate through the cross-section of channels, decreases in each case when either M increases or L increases or $\phi$ increases or H increases or $\Lambda _1$ increases or $\Lambda _3$ increases or $\eta _1$ increases or $\eta _2$ increases or $\eta _3$ increases.

• The fluid velocity passing through respective porous channels, decreases in each case when either M increases or L increases or $\phi$ increases or H increases or $\Lambda _1$ increases or $\Lambda _3$ increases or $\eta _1$ increases or $\eta _2$ increases or $\eta _3$ increases. The velocity profile is looking approximately parabolic in each case.

• The obtained results can be utilized for investigating the industrial problems associated with the filtration and purification of contaminated groundwater, oil recovery process through non-homogeneous reservoir, circulation of blood flow through veins of human body, etc. These results can also be used for solving the problem of cooling and heating process of refrigerator (air conditioned), problem of sedimentation, etc.