Lateral migration of deformable particles in microfluidic channel flow of Newtonian and viscoelastic media: a computational study

Abstract

The dynamics of an initially spherical elastic particle in pressure-driven flow of Newtonian and viscoelastic fluids in a square-cross-section microfluidic channel is studied in 3D by the finite element method. Two viscoelastic constitutive equations are considered, i.e., the Oldroyd-B and Giesekus models. The dependence of particle deformation and cross-stream migration on geometric confinement, particle deformability, and fluid rheology is investigated. If its initial position is not on the center line of the channel, the bead attains an asymmetric shape and migrates transversally to the stream direction. In an inertialess Newtonian liquid, the migration is always directed towards the channel center line and its velocity depends on geometric confinement and particle deformability, whereas, in a viscoelastic liquid, the migration direction and velocity depend on the complex interplay among geometric confinement, particle deformability, fluid elasticity, shear-thinning, and secondary flows.

1 Introduction

Many operations of interest in fields such as material processing and biological diagnostics require the capability of controlling the trajectories of particles suspended in flowing liquid carriers. In the last two decades, microfluidics has turned out to be suitable for this purpose (see, e.g., Whitesides 2006). In particular, the the so-called ‘3D-focusing’, namely, the generation of a single row of particles, can be important in many applications, such as counting, detection (Toner and Irimia 2005), and separation (Villone et al. 2017). Numerous microfluidic techniques for particle focusing are reported in the literature (as a reference, the reviews by Bhagat et al. 2008 and Xuan et al. 2010 can be seen). In the recent years, the normal stresses arising in viscoelastic suspending media have been exploited to induce the lateral motion of rigid particles in the absence of inertia and externally-imposed forces, such as acoustic, electrical, or magnetic fields. Experimental and numerical studies have demonstrated that viscoelasticity-induced inertialess focusing is an effective method for particle alignment in microchannels with a variety of geometries (see, for example, the very recent review by Stoecklein and Di Carlo 2018 and the references therein). While the literature on lateral migration of rigid particles in microfluidics is vast, the study of the behavior of suspensions of deformable particles is more an open issue, whose comprehension would be of interest for applications involving, for example, biological cells (Galaev and Mattiasson 2007b). Recently, Villone et al. (2016) studied through direct numerical simulations the deformation and cross-streamline migration of an initially spherical elastic bead in microfluidic pipe flow of Newtonian and viscoelastic fluids, showing that, unlike rigid particles, elastic particles migrate orthogonally to the flow direction even in inertialess flows of Newtonian fluids, as it happens also to red blood cells (see the review by Geislinger and Franke 2014 and the references therein), vesicles, and capsules (see the review by Barthès-Biesel 2016 and the references therein). In a Newtonian liquid, cross-streamline migration is always directed towards the channel axis, in agreement to what Tam and Hyman (1973) had derived by a perturbative analysis for a Hookean elastic particle, whereas the scenario qualitatively changes if a viscoelastic suspending medium is considered. In this case, the direction of lateral migration can be twofold, with the particle going towards the channel center or wall depending on its initial radial position. The parameters have competing effects on the phenomenon, because increasing particle deformability or geometrical confinement promotes migration towards the axis, while increasing liquid elasticity and, above all, shear-thinning can promote migration towards the wall.

In this paper, we study by means of three-dimensional Arbitrary Lagrangian Eulerian (ALE) Finite Element Method (FEM) numerical simulations the dynamics of an initially spherical elastic particle suspended in Newtonian and viscoelastic liquids subjected to inertialess pressure-driven flow in a square-cross-section microfluidic channel. Two viscoelastic constitutive equations are considered, i.e., the constant-viscosity Oldroyd-B model and the shear-thinning Giesekus model. Due to the applied flow, the bead deforms and migrates orthogonally to the flow direction of the suspending medium. The effects of the geometrical and physical parameters on deformation and migration of the soft particle are investigated. In the case of dilute systems at negligible inertia (like the one considered here), our ALE FEM combines accuracy and computational efficiency in calculating the velocity, pressure and stress fields in both the deformable solid and the liquid phase and in tracking the interface between them. Its use in the solution of problems dealing with suspensions carrying deformable inclusions is consolidated in the literature (see, e.g., Gao and Hu 2009; Villone et al. 2014a, b, 2016, 2017). Other techniques that have been employed in the literature to simulate the flow behavior of suspensions of deformable solid particles include the FEM with level set (see, e.g., Liu and Walkington 2001), the Immersed Boundary (IB) FEM (Saadat et al. 2018), the IB Finite Volume Method (FVM) (Mendez et al. 2014), and the Finite Difference Method (FDM) with level set (Rosti et al. 2018; Rosti and Brandt 2018). Studies on problems somehow analogous to the one investigated here, yet involving elastic capsules at non-negligible inertia, can be instead found in Kilimnik et al. (2011) and Raffiee et al. (2017a, b).

2 Mathematical model

Fig. 1

Geometry of an initially spherical elastic particle suspended in a fluid under pressure-driven flow in a square-cross-section channel

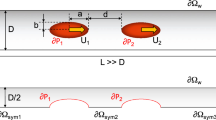
In Fig. 1, a schematic drawing of the system is displayed: a square-cross-section channel of length L and height H is considered. A Cartesian system of coordinates is set with the origin at the center of the channel, the x-axis parallel to the channel length, and the y- and z-axes parallel to the channel cross-section. A single, non-Brownian, neutrally buoyant, initially spherical elastic particle is suspended in a fluid subjected to pressure-driven flow in the positive x-direction. The particle has an initial diameter $D_{\mathrm{p}}$ and we define the confinement ratio $\beta$ as the ratio between the particle diameter and channel height, i.e., $\beta = D_{\mathrm{p}}/H$. We assume that both the solid and the liquid are incompressible and that inertia can be neglected. Typical flow conditions in microfluidic devices indeed justify the latter assumption (Squires and Quake 2005), whereas considering a single particle makes our results applicable to the case of dilute suspensions.

Given the aforementioned assumptions, the mass and momentum balance for both the particle and the suspending matrix read

$$\begin{aligned} {\varvec{\nabla }}\cdot \varvec{u}& = 0, \end{aligned}$$

(1)

$$\begin{aligned} {\varvec{\nabla }}\cdot {\varvec{T}}&= \varvec{0}, \end{aligned}$$

(2)

where $\varvec{u}$ is the velocity vector and $\varvec{T}$ is the stress tensor, which, in turn, can be expressed as $\varvec{T} = -p\varvec{I} + \varvec{\sigma }$, with p the pressure, $\varvec{I}$ the identity tensor, and ${\varvec{\sigma }}$ the deviatoric contribution to the stress tensor. For a Newtonian fluid, the constitutive equation for $\varvec{\sigma }$ is

$$\begin{aligned} \varvec{\sigma } = 2\eta \varvec{D}, \end{aligned}$$

(3)

with $\eta$ the viscosity and $\varvec{D} = (\nabla \varvec{u} + \nabla \varvec{u}^{\text {T}})/2$ the symmetric part of the velocity gradient tensor $\nabla \varvec{u}$. For a viscoelastic liquid, instead, we write

$$\begin{aligned} \varvec{\sigma } = 2\eta _{\mathrm{s}}\varvec{D} + \varvec{\tau }, \end{aligned}$$

(4)

with $\eta _{\mathrm{s}}$ the ‘solvent’ viscosity and $\varvec{\tau }$ the viscoelastic contribution to the deviatoric part of the stress tensor. The Giesekus constitutive equation for $\varvec{\tau }$ reads

$$\begin{aligned} \lambda \overset{\scriptscriptstyle \bigtriangledown }{\varvec{\tau }} + \varvec{\tau }+ \frac{\lambda \alpha }{\eta _{\mathrm{m}}} {\varvec{\tau }}^{2} = 2\eta _{\mathrm{m}} \varvec{D}, \end{aligned}$$

(5)

with $\lambda$ the relaxation time, $\eta _{\mathrm{m}}$ the ‘polymer’ viscosity, $\alpha$ the so-called ‘mobility parameter’, and the symbol $^{\nabla}$ denoting the upper-convected time derivative (for more details, see Larson 1988). Notice that the overall zero-shear viscosity of a Giesekus liquid is $\eta _{0} = \eta _{\mathrm{s}} + \eta _{\mathrm{m}}$. The attributes ‘solvent’ and ‘polymer’ denoting the two contributions to the viscosity of a Giesekus fluid come from its typical use in modeling the rheological behavior of polymeric solutions. The Giesekus model predicts shear-thinning, namely, a decrease of the viscosity at increasing shear rate, and the mobility parameter $\alpha$ modulates such effect: the larger $\alpha$, the more shear-thinning the fluid. On the other hand, when $\alpha$ goes to zero, the fluid has a constant viscosity and the Giesekus constitutive equation degenerates into the Oldroyd-B model (Larson 1988)

$$\begin{aligned} \lambda \overset{\scriptscriptstyle \bigtriangledown }{\varvec{\tau }} + \varvec{\tau }= 2\eta _{\mathrm{m}} \varvec{D} . \end{aligned}$$

(6)

For what concerns the solid particle, we model its elastic constitutive behavior by the neo-Hookean model. In its velocity-based formulation, it reads

$$\begin{aligned} \overset{\scriptscriptstyle \bigtriangledown }{\varvec{\tau }} = 2G\varvec{D} . \end{aligned}$$

(7)

In this paper, we choose to model viscoelastic suspending liquids by the Giesekus and Oldroyd-B constitutive equations because these models can suitably describe the behavior of many polymeric solutions of interest in microfluidics (see, for example, Leshansky et al. 2007; Yang et al. 2011; D’Avino et al. 2012; Del Giudice et al. 2013; Seo et al. 2014), while the neo-Hookean constitutive equation chosen for the solid can adequately describe the behavior of many microgel beads and biological particles, e.g., white blood cells, when they do not undergo ‘extreme’ deformations (see Gao et al. 2011, 2012).

The model equations for the system shown in Fig. 1 are solved with the following boundary conditions:

$$\begin{aligned} \varvec{u}|_{{\partial \varOmega }_{\mathrm{w}}}&= \varvec{0}, \end{aligned}$$

(8)

$$\begin{aligned} \varvec{u}|_{{\partial \varOmega }_{\mathrm{in}}}&= \varvec{u}|_{{\partial \varOmega }_{\mathrm{out}}}, \end{aligned}$$

(9)

$$\begin{aligned} -(\varvec{\sigma }\cdot \varvec{m})|_{{\partial \varOmega }_{\mathrm{in}}}& = (\varvec{\sigma }\cdot \varvec{m})|_{{\partial \varOmega }_{\mathrm{out}}} - \varDelta p \varvec{m}|_{{\partial \varOmega }_{\mathrm{out}}}. \end{aligned}$$

(10)

Equation (8) is the no-slip and no-penetration condition for the liquid velocity on the channel wall $\partial \varOmega _{\mathrm{w}}$. Equations (9) and (10) express the periodicity of velocity and traction in the matrix fluid along the flow direction between the channel inlet $\partial \varOmega _{\mathrm{in}}$ and the outlet $\partial \varOmega _{\mathrm{out}}$, with $\varDelta p$ the pressure drop between $\partial \varOmega _{\mathrm{in}}$ and $\partial \varOmega _{\mathrm{out}}$ (to be computed) and $\varvec{m}$ the outwardly directed unit vector normal to the boundary. At the channel inlet, the flow rate Q of the suspending liquid is imposed as

$$\begin{aligned} -\int _{{\partial \varOmega }_{\mathrm{in}}} \varvec{u} \cdot \varvec{m}\,dS= Q, \end{aligned}$$

(11)

while the boundary conditions on the particle - liquid interface $\partial \varOmega _{\mathrm{p}}$ are

$$\begin{aligned} \varvec{u}|_{\mathrm{f}} = \varvec{u}|_{\mathrm{p}}, \end{aligned}$$

(12)

i.e, the no-slip and no-penetration condition between the fluid (f) and the particle (p), and

$$\begin{aligned} ({\varvec{\sigma }}\cdot \varvec{n})|_{\mathrm{f}} = ({\varvec{\sigma }}\cdot \varvec{n})|_{\mathrm{p}}, \end{aligned}$$

(13)

i.e., the continuity of traction across the fluid-particle interface, where $\varvec{n}$ is a unit vector normal to the particle interface and directed towards the suspending fluid. The flow rate in Eq. (11) is implemented through a constraint whose Lagrange multiplier is the pressure difference $\varDelta p$, which is itself computed within the solution procedure (see Bogaerds et al. 2004).

Since both the particle and the suspending medium are inertialess, no initial condition for the velocity is needed, whereas an initial condition for the extra-stress tensor is necessary. We assume that the particle (and the matrix, when viscoelastic) is initially stress-free, thus

$$\begin{aligned} {\varvec{\tau }}|_{t=0} = \varvec{0}. \end{aligned}$$

(14)

The mathematical model of the system is made dimensionless by choosing the channel height H as the characteristic length, the average velocity of the fluid $\bar{u} = Q/H^2$ as the characteristic velocity, the ratio of the characteristic length and the characteristic velocity $H/\bar{u}$ as the characteristic time, $\eta \bar{u}/H$ (or $\eta _{0}\bar{u}/H$) as the characteristic stress in the matrix, and the shear modulus of the elastic material G as the characteristic stress in the particle. All the variables appearing in the following are dimensionless. With the aforementioned choices, the elastic capillary number $\text {Ca}_{\mathrm{e}} = \eta \bar{u}/(HG)$ (or $\text {Ca}_{\mathrm{e}} = \eta _{0}\bar{u}/(HG)$) will appear in Eq. (13). $\text {Ca}_{\mathrm{e}}$ is the ratio of the matrix viscous stress to the particle elastic stress. In case a viscoelastic matrix is considered, the Deborah number $\text {De} = \lambda \bar{u}/H$ will also appear in the momentum balance equation and the viscoelastic constitutive equation, which is the ratio between the relaxation time of the viscoelastic fluid and the characteristic time of the flow.

3 Numerical technique

An ALE FEM-based numerical code implementing well-known stabilization techniques, i.e., SUPG, DEVSS, and log-conformation, is used to solve the equations presented in Sect. 2. To track the fluid-particle interface, a FEM with second-order time discretization is defined on it, where the normal component of the mesh velocity equals the normal component of the physical velocity, whereas the tangential velocity of the nodes is such that the distribution of the elements on the interface is kept uniform. This approach lets the mesh get rid of any ‘tank-treading’ motion of the elastic material, so largely reducing the distortion of the ALE volume mesh. To stabilize the interface, the SUPG method is used. A detailed description of the numerical method, and, in particular, of the approach used to treat the interface, with several validation cases, is given in Villone et al. (2014b).

The fluid domain $\varOmega _{\mathrm{f}}$ and the solid domain $\varOmega _{\mathrm{p}}$ are discretized by a mesh of quadratic tetrahedra. The fluid-particle interface mesh aligns with element faces (quadratic triangles), which are the same on both the matrix and the particle side (conforming geometry). In our formulation, we use an ALE grid that rigidly moves along the flow direction with the particle x-velocity, namely, the x-component of the velocity computed in the center of volume of the particle. In this way, the only motion allowed is in the yz-plane, i.e., particle lateral migration. Adoption of a co-moving grid drastically reduces the mesh distortion.

Convergence tests have been performed, thus mesh resolution and time-step for the numerical solution of the problem depicted in Sect. 2 have been chosen so as to ensure invariance of the results upon further refinements. For the simulations presented in this paper, meshes with a number of tetrahedra in the order of $2.5-3.5\times 10^{4}$ and time-steps in the order of $10^{-3}-10^{-4} \times \bar{u}/H$ have been found to be adequate. The mesh elements on the surface of the particle are approximately twice finer than the ones on the boundaries of the channel. A detailed description of the convergence procedures for problems analogous to that of interest here is given in Villone et al. (2014b). Finally, since periodicity is imposed in the flow direction, in all the simulations it has been verified that the x-dimension of the domain L is sufficiently large so that the particle does not feel the influence of its periodic images along the flow direction. With a channel long 10 times the particle diameter, this condition is verified for all the cases presented in the following. As an example, we display in Fig. 2 the convergence test on the y-coordinate of the particle center of volume $y_{\mathrm{p}}$ for the migration of a particle in a Newtonian fluid starting from $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.1,0.1)$ on the diagonal of the channel cross-section at $\beta = 0.3$ and $\text {Ca}_{\mathrm{e}} = 0.1$ (the dynamics of $z_{\mathrm{p}}$ being the same due to symmetry). In this case, a number of elements on the equator of the sphere # = 30, a time-step $\varDelta t = 0.002 \times \bar{u}/H$, and a channel length $L = 10 D_{\mathrm{p}}$ ensure mesh-, time-step-, and domain-size-independency of the results.

Fig. 2

Convergence test on the y-coordinate of the particle center of volume $y_{\mathrm{p}}$ for the migration of a particle in a Newtonian fluid starting from $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.1,0.1)$ at $\beta = 0.3$ and $\text {Ca}_{\mathrm{e}} = 0.1$

A validation of the numerical method used in this paper for the simulation of the behavior of elastic particles in channel flow is given in Figs. 2 and 3 in Villone et al. (2016) through comparison with theoretical predictions from Murata (1981).

The simulations have been run on blades with two hexacore processors Intel Xeon E5649@2.53GHz and 48 Gb of RAM, with a computational time ranging from 2–3 days for a Newtonian suspending liquid to 2–3 months for viscoelastic matrices.

4 Results

An initially spherical neo-Hookean elastic particle is suspended in a fluid subjected to Poiseuille flow, i.e., pressure-driven flow, in a square-cross-section microfluidic channel. When the particle initial position is out of the center line of the channel, the bead migrates transversally to the suspending fluid streamlines. Due to the channel geometry, the particle is confined in both the y- and the z-direction, thus the hydrodynamic interactions with the side walls in both these directions contribute to its lateral motion. The simulations are performed by considering the whole channel as the computational domain, but we can limit the particle initial yz-positions considered in the simulations to a half-quadrant of the channel cross-section, the trajectories of particles starting in the rest of the channel cross-section being reproducible by symmetry.

4.1 Migration of a neo-Hookean particle in a Newtonian liquid

Fig. 3

yz-projections of particle trajectories in a Newtonian fluid for different particle initial positions. For symmetry, only the the upper-right quadrant of the channel cross-section is reported. Top row: $\beta =0.1$, $\text {Ca}_{\mathrm{e}}=0.001$ (a), 0.01 (b), 0.1 (c). Bottom row: $\beta =0.3$, $\text {Ca}_{\mathrm{e}}=0.001$ (d), 0.01 (e), 0.1 (f). The black dashed lines delimit the region accessible to the center of volume of the particle (considered as a sphere). The gray dashed line is the cross-section diagonal. The black circles identify the particle starting positions. In (a)–(e), empty circles are reported on the trajectories every 5 time units; in (f), empty squares are reported on the trajectories every time unit

The behavior of a neo-Hookean particle in a Newtonian fluid is first investigated. In Fig. 3, the projections of particle trajectories on the upper-right quadrant of the channel cross-section are shown for a low confinement ($\beta = 0.1$, top row) and a medium confinement ($\beta = 0.3$, bottom row). For each, three orders of magnitude of the elastic capillary number are considered, i.e., $\text {Ca}_{\mathrm{e}} = 0.001$ (left column), 0.01 (central column), and 0.1 (right column). In Fig. 3 and in the diagrams below reporting analogous information for other fluids, the black circles represent the particle initial positions considered in the simulations, whereas information on migration time, thus on migration velocity, is given through the open symbols on the trajectories. In particular, the open circles in panels (a)–(e) mark a time of 5, whereas the squares in panel (f) mark a time of 1. Therefore, Fig. 3 can be regarded as a phase portrait.

It emerges from Fig. 3 that a neo-Hookean particle suspended in a Newtonian fluid migrates towards the center line of the channel from whatever initial position. In other words, the center of the channel cross-section is the only attractor for particle dynamics. Such result agrees with what is known for elastic particles in inertialess pressure-driven flow in a cylindrical pipe (see Villone et al. 2016). As expected, when the starting position is on the diagonal of the channel cross-section, the particle trajectory stays on the diagonal due to symmetry. Neither changing the confinement ratio $\beta$ nor the elastic capillary number $\text {Ca}_{\mathrm{e}}$ has a qualitative effect on the direction of particle migration. From the quantitative point of view, given an initial position, both increasing $\beta$ and $\text {Ca}_{\mathrm{e}}$ speeds up the migration, as it is apparent by comparing the spacings of the time markers on the trajectories. In addition, it can be observed that, given $\beta$ and $\text {Ca}_{\mathrm{e}}$, the migration is faster when the particle is closer to the channel wall. All these effects can be explained by considering that, in an inertialess Newtonian fluid, the driving force for the migration of an elastic particle is linked to its shear-induced deformation (see Villone et al. 2014a, 2016). Both increasing $\beta$ and $\text {Ca}_{\mathrm{e}}$ enhances such deformation, thus speeding up particle migration. Given $\beta$ and $\text {Ca}_{\mathrm{e}}$, the migration velocity spatially varies within the cross-section of the channel, namely, the yz-plane. This is due to the fact that the shear stress making the particle deform (and consequently migrate) depends on the fluid shear rate and, in square-channel Poiseuille flow, the shear rate is maximum at the wall and goes to zero at the center line.

Fig. 4

3D views of the deformed shapes attained by a neo-Hookean particle starting from $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.28,0.28)$ in a Newtonian fluid at $\beta = 0.3$ and $\text {Ca}_{\mathrm{e}} = 0.1$. Yellow: $t=0$, red: $t=0.1$, green: $t=0.2$, blue: $t=0.3$, orange: $t=0.4$, violet: $t=0.5$, cyan: $t=0.6$, purple: $t=10$. a xy-view from the positive z-axis. b xy-view from the negative z-axis

In Fig. 4, we show a temporal sequence of 3D views of the shape of a particle starting from a position $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.28,0.28)$, i.e., on the channel cross-section diagonal in the region with high shear rate, at $\beta = 0.3$ and $\text {Ca}_{\mathrm{e}} = 0.1$. It can be observed that the characteristic times of deformation and migration are very different: the particle reaches its maximum deformation very fast (within about 0.6 time units), but almost no cross-stream migration occurs in such time (translation in the flow direction is subtracted in Fig. 4), then, as migration goes on, the shape of the particle evolves through a quasi-static process (indeed, at $t=10$, an appreciable migration has occurred with respect to $t=0.6$, but the shape of the particle has changed very little).

In Fig. 5, we show the 3D views of the shape of a particle starting from a position $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.15,0.28)$, i.e., in the region with high shear rate, at $\beta = 0.3$ and $\text {Ca}_{\mathrm{e}} = 0.001$ (a), 0.01(b), 0.1(c). In all cases, the snapshot is taken at a short time after particle release such that its deformation has reached the maximum (but almost no migration has occurred). Moving along the panels in Fig. 5, namely, increasing $\text {Ca}_{\mathrm{e}}$, the particle deformed shape goes from one hardly distinguishable from a sphere to an almost spheroidal one and, finally, to a slipper-like one, thus confirming that higher migration velocities arise from larger deformations.

Fig. 5

3D views of the deformed shape of a neo-Hookean particle starting from $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.15,0.28)$ in a Newtonian fluid at $\beta = 0.3$ and $\text {Ca}_{\mathrm{e}} = 0.001$ (a), 0.01 (b), 0.1 (c)

Finally, it is worth mentioning that, in Fig. 3a, no appreciable lateral migration is observed over the simulated time. Since in such plot $\beta$ is equal to 0.1 and $\text {Ca}_{\mathrm{e}}$ to 0.001, it can be inferred that, at such low values of the confinement ratio and the elastic capillary number, the particle practically does not deform at all. Hence, it behaves like a rigid bead, for which it is known that no cross-stream migration occurs in an inertialess Newtonian fluid due to the time-reversibility of Stokes equations.

Fig. 6

Effect of the confinement ratio $\beta$ and of the elastic capillary number $\text {Ca}_{\mathrm{e}}$ on the inverse magnitude of the migration velocity $-\sqrt{v_{\mathrm{py}}^2 + v_{\mathrm{pz}}^2}$ of a neo-Hookean particle lying on the diagonal of the square cross-section of a microfluidic channel filled with a Newtonian fluid under pressure-driven flow

The simulation results show that a ‘master surface’ exists for both the components $v_{\mathrm{py}}$ and $v_{\mathrm{pz}}$ of the particle migration velocity. In other words, there are two universal functions $v_{\mathrm{py}}(y_{\mathrm{p}},z_{\mathrm{p}})$ and $v_{\mathrm{pz}}(y_{\mathrm{p}},z_{\mathrm{p}})$ (parametric in $\beta$ and $\text {Ca}_{\mathrm{e}}$) that yield the particle migration velocity depending on its position in the channel cross-section. We report in Fig. 6 the inverse of the magnitude of the migration velocity $-\sqrt{v_{\mathrm{py}}^2 + v_{\mathrm{pz}}^2}$ as a function of particle ‘pseudo-radial’ position on the diagonal of the channel cross-section $\sqrt{y^2_{\mathrm{p}} + z^2_{\mathrm{p}}}/\sqrt{2}$. (The negative sign of the migration velocity accounts for the direction of lateral migration.) It can be observed that, along the diagonal, the magnitude of the migration velocity decreases going from the cross-section corner to the center line, where it must be zero due to symmetry. From the quantitative point of view, at any fixed position, the magnitude of the migration velocity increases with both $\beta$ and $\text {Ca}_{\mathrm{e}}$, as already discussed above in commenting Fig. 3. Given $\beta$ and $\text {Ca}_{\mathrm{e}}$, the time needed by a particle starting at a certain position on the diagonal to reach the center line of the channel can be readily derived from the time integration of $\sqrt{v_{\mathrm{py}}^2 + v_{\mathrm{pz}}^2}\large (\sqrt{y^2_{\mathrm{p}} + z^2_{\mathrm{p}}}/\sqrt{2}\large ) = d/dt \large (\sqrt{y^2_{\mathrm{p}} + z^2_{\mathrm{p}}}/\sqrt{2}\large )$. Then, from the knowledge of the profile of the particle x-velocity in the channel cross-section $v_{\mathrm{px}}(y_{\mathrm{p}},z_{\mathrm{p}})$, the longitudinal distance covered by the particle in such time can be estimated. Therefore, a design equation can be written for a square-cross-section microfluidic device aimed at focusing elastic particles in a Newtonian fluid. By defining the focusing length $L_{\mathrm{focus}}$ as the device length needed by a particle whose center of volume initially lies on the cross-section diagonal at 90% of the available distance from the center to reach a position at 1% of the available distance, the following project equation, parametric in $\beta$ and $\text {Ca}_{\mathrm{e}}$, arises:

$$\begin{aligned} L_{\mathrm{focus}} \simeq \frac{0.29}{\beta ^{3}\text {Ca}_{\mathrm{e}}}. \end{aligned}$$

(15)

It is then apparent from Eq. (15) that the 3D focusing of elastic particles in a Newtonian fluid is easy for medium confinement and non-vanishing elastic capillary number. For example, given a device with $H = 100\,\upmu \hbox {m}$, a focusing length of approximately 1 cm would be needed at $\beta = 0.3$ and $\text {Ca}_{\mathrm{e}} = 0.1$, which would become ten times larger, i.e., of 10 cm, thus still feasible, at $\text {Ca}_{\mathrm{e}} = 0.01$. On the other hand, at $\beta = 0.1$ and $\text {Ca}_{\mathrm{e}} = 0.001$, a focusing length of about 29 m would be necessary, which is unfeasible.

4.2 Migration of a neo-Hookean particle in a viscoelastic liquid

In this Section, the dynamics of a neo-Hookean particle suspended in a viscoelastic liquid is examined. Since we want to investigate independently the effects of particle deformability and fluid elasticity on cross-stream migration, we imagine to fix the geometry of the system and the fluid flow rate Q, and to tune the elastic capillary number $\text {Ca}_{\mathrm{e}}$ by changing G and the Deborah number De by changing $\lambda$.

4.2.1 Oldroyd-B liquid

Let us start our analysis from the case of the constant-viscosity Oldroyd-B liquid defined by Eq. (6). We choose the ‘viscosity ratio’ of the fluid $\eta _{\mathrm{s}}/\eta _{0}$ equal to 0.09.

Fig. 7

yz-projections of particle trajectories in an Oldroyd-B fluid with $\eta _{\mathrm{s}}/\eta _{0} = 0.09$ for different particle initial positions. For symmetry, only the the upper-right quadrant of the channel cross-section is reported. Top row: $\beta =0.1$, $\hbox {De} = 0.1$, $\text {Ca}_{\mathrm{e}}=0.001$ (a), 0.01 (b), 0.1 (c). Central row: $\beta =0.3$, $\hbox {De} = 0.1$, $\text {Ca}_{\mathrm{e}}=0.001$ (d), 0.01 (e), 0.1 (f). Bottom row: $\beta =0.3$, $\hbox {De} = 5.0$, $\text {Ca}_{\mathrm{e}}=0.001$ (g), 0.01 (h), 0.1 (i). The black dashed lines delimit the region accessible to the center of volume of the particle (considered as a sphere). The gray dashed line is the cross-section diagonal. The black circles identify the particle starting positions. In (a)–(e), empty circles are reported on the trajectories every 5 time units; in (f)–(i), empty squares are reported on the trajectories every time unit

In Fig. 7, the projections of particle trajectories on the upper-right quadrant of the channel cross-section are shown for a low and a medium confinement ($\beta = 0.1$ and 0.3), a low and a high value of the Deborah number ($\hbox {De} = 0.1$ and 5.0), and three orders of magnitude of the elastic capillary number ($\text {Ca}_{\mathrm{e}} = 0.001$, 0.01, and 0.1). (For each panel, the values of the parameters are written in the legend and the caption.)

First of all, it can be observed that, unlike in a Newtonian liquid, in an Oldroyd-B liquid a particle with $\beta = 0.1$ and $\text {Ca}_{\mathrm{e}} = 0.001$ appreciably migrates in the time-window considered (see Fig. 7a). Even if at $\beta = 0.1$ and $\text {Ca}_{\mathrm{e}} = 0.001$ the particle practically does not deform, thus no deformation-induced migration occurs, the phenomenon can be ascribed to the appearance of the migration force due to the elasticity of the suspending medium, as reported in Villone et al. (2013), Del Giudice et al. (2013) for rigid particles. It is also apparent from Fig. 7 that in an Oldroyd-B fluid there are some parameter combinations for which the particle migrates towards the channel center line or the corner of the channel cross-section depending on its initial position. Indeed, for $\beta = 0.1$, $\hbox {De} = 0.1$, and $\text {Ca}_{\mathrm{e}} = 0.001$ and 0.01 (see Figs. 7a, b, respectively), a bead starting on the diagonal of the channel cross-section at $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.35,0.35)$ migrates towards the upper-right corner. (It is worth remarking that the fact that the trajectory does not lie exactly on the diagonal is due to slight numerical errors, for example caused by slight asymmetry of the mesh with respect to the diagonal, since there is no physical reason for the particle to detach from such symmetry line.) Hence, a separatrix exists that divides the channel cross-section in two zones, with the particle being attracted towards the center line if its initial position is between the center line and the separatrix and towards the corner if its initial position is between the separatrix and the walls. In this sense, the separatrix can be regarded as a locus of unstable equilibrium positions from which no lateral motion occurs and we can identify five stable equilibrium points, i.e., the channel center line and the four corners of the channel cross-section. Bi-stability had been already found by Villone et al. (2016) for neo-Hookean particles in viscoelastic fluids under Poiseuille flow in cylindrical pipes.

Changing the geometrical and physical parameters has both qualitative and quantitative effects on particle migration. Given $\beta = 0.1$ and $\hbox {De} = 0.1$, increasing $\text {Ca}_{\mathrm{e}}$ to 0.1 (Fig. 7c) makes the corner-attracted migration disappear and also speeds us the migration dynamics. This is consistent with the fact that increasing $\text {Ca}_{\mathrm{e}}$ enhances particle deformation, and the more deformed the particle the faster it migrates towardss the center line. Coherently, by comparing the first two rows in Fig. 7, it emerges that, at $\hbox {De} = 0.1$ and for each $\text {Ca}_{\mathrm{e}}$, the migration towards the center is accelerated when going from $\beta = 0.1$ to 0.3, since also increasing the geometrical confinement enhances bead deformation. In the bottom row of Fig. 7, De is increased to 5.0 at $\beta = 0.3$. By comparing the time markers on the trajectories at high De and low $\text {Ca}_{\mathrm{e}} = 0.001$ in Fig. 7g with the ones at low De (and same $\beta$ and $\text {Ca}_{\mathrm{e}}$) in Fig. 7d, it is apparent that, when the particle is very little deformable, a higher fluid elasticity speeds up its migration, as it enhances the migration force connected to the normal stresses in the suspending medium (as reported for rigid particles in Villone et al. 2013; Del Giudice et al. 2013, 2017). However, a greater fluid elasticity in turn hinders particle deformation (see Villone et al. 2016), thus, at high $\text {Ca}_{\mathrm{e}}$, there is a twofold effect: on one hand, the contribution to the migration force due to fluid elasticity is promoted; on the other hand, the contribution that would come from particle deformation due to high $\text {Ca}_{\mathrm{e}}$ is suppressed. For this reason, by comparing the second and the third row in Fig. 7, it can be observed that, given $\beta$, increasing De from 0.1 to 5.0 accelerates migration at $\text {Ca}_{\mathrm{e}} = 0.001$, but it slows it down at $\text {Ca}_{\mathrm{e}} = 0.01$ and 0.1.

Finally, a feature of the migration dynamics at high De that is interesting to remark is that, at $\beta = 0.3$, $\hbox {De} = 5.0$, and $\text {Ca}_{\mathrm{e}} = 0.001$, 0.01, when starting from $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.35,0.35)$, the particle displaces towards the channel cross-section corner at short times, than the migration direction inverts and its long-term tendency is towards the center line (see the blue lines in Fig. 7g, h) This behavior can be due to the build-up of viscoelastic stresses in the suspending liquid.

4.2.2 Giesekus liquid

Let us now investigate the case of a neo-Hookean particle suspended in a Giesekus liquid. As in Sect. 4.2.1, we set $\eta _{\mathrm{s}}/\eta _{0}$ to 0.09. One constitutive difference between an Oldroyd-B and a Giesekus fluid is that the latter exhibits shear-thinning. Here, the shear-thinning parameter $\alpha$ appearing in Eq. (5) is chosen equal to 0.2. In addition, differently from Oldroyd-B constitutive equation, Giesekus model predicts a non-zero second normal stress difference, which, for the channel geometry considered in this work, yields non-zero components of the fluid velocity orthogonally to the flow direction, known as ‘secondary flows’. In Fig. 8, the secondary flows for a Giesekus fluid without particles are plotted by grey arrows on the background pf each panel. Given $\eta _{\mathrm{s}}/\eta _{0}$ and $\alpha$, the pattern of the secondary flows is a function of the geometry of the channel cross-section, whereas their intensity is a function of the Deborah number. For visualization reasons, the arrows in Fig. 8 are not to scale, as the ones in the third row should have been $50^4$ times longer than those in the first two rows (Yue et al. 2008).

Fig. 8

yz-projections of particle trajectories in a Giesekus fluid with $\eta _{\mathrm{s}}/\eta _{0} = 0.09$ and $\alpha = 0.2$ for different particle initial positions. For symmetry, only the upper-right quadrant of the channel cross-section is reported. Top row: $\beta =0.1$, $\hbox {De} = 0.1$, $\text {Ca}_{\mathrm{e}}=0.001$ (a), 0.01 (b), 0.1 (c). Central row: $\beta =0.3$, $\hbox {De} = 0.1$, $\text {Ca}_{\mathrm{e}}=0.001$ (d), 0.01 (e), 0.1 (f). Bottom row: $\beta =0.3$, $\hbox {De} = 5.0$, $\text {Ca}_{\mathrm{e}}=0.001$ (g), 0.01 (h), 0.1 (i). The black dashed lines delimit the region accessible to the center of volume of the particle (considered as a sphere). The gray dashed line is the cross-section diagonal. The black circles identify the particle starting positions. In (a)–(b), empty triangles are reported on the trajectories every 5 time units; in (c)–(e) and (g)–(i), empty circles are reported on the trajectories every 5 time units; in (f), empty squares are reported on the trajectories every time unit. The (not-to-scale) grey arrows represent the secondary flows of a Giesekus fluid without particles

In Fig. 8, the projections of particle trajectories on the upper-right quadrant of the channel cross-section are shown for $\beta = 0.1$, 0.3, $\hbox {De} = 0.1$, 5.0, and $\text {Ca}_{\mathrm{e}} = 0.001$, 0.01, and 0.1. (For each panel, the values of the parameters are written in the legend and the caption.) Like in the Oldroyd-B medium, fluid-elasticity-induced cross-stream migration is found for little confined and little deformable particles (see panel a). Analogously to the Oldroyd-B case, for $\beta = 0.1$, $\hbox {De} = 0.1$, and $\text {Ca}_{\mathrm{e}} = 0.001$, 0.01 (Fig. 7a, b), a bead starting on the diagonal of the channel cross-section at $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.35,0.35)$ migrates towards the upper-right corner, thus bi-stability exists even for the Giesekus liquid. Increasing $\text {Ca}_{\mathrm{e}}$ to 0.1 (Fig. 7c) makes the corner-attracted migration disappear and speeds us the migration dynamics due to the increased weight of the contribution of the deformability-induced migration towards the center. In addition, it can be observed that more deformable particles ‘feel’ less the effect of the secondary flows, as their trajectories go ‘straighter’ towards the attractor, whereas the trajectories of less deformable particles are more influenced by the in-plane components of the fluid velocity (see, e.g., the orange, blue and purple curves in Fig. 7a). If De is kept to 0.1, thus the secondary flows are the same as above, and the confinement is increased from 0.1 to 0.3, the corresponding increase in bead deformation suppresses the migration towards the corner of the channel cross-section and hinders the effects of the secondary flows on particle trajectories. Of course, the greater $\text {Ca}_{\mathrm{e}}$ the faster the migration (see the central row in Fig. 7). In the bottom row of Fig. 8, De is increased to 5.0 at $\beta = 0.3$. In this case, particle migration is slower than at $\hbox {De} = 0.1$ for every $\text {Ca}_{\mathrm{e}}$. Several factors have to be taken into account here, namely: (i) the contribution to particle migration force due to fluid elasticity is increased (for rigid particles, this scales proportionally to $\text {De}^2$, as reported in Villone et al. (2013)), (ii) the flow-disturbance caused to the particle by the secondary flows is much more increased (as reported above, the intensity of the secondary flows scale proportionally to $\text {De}^4$), (iii) the contribution to particle migration towards the center due to shear-induced deformation is hindered by both fluid elasticity and shear-thinning, which lowers the fluid viscosity, thus the shear stress making the particle deform, in the region of the channel at high shear rate, i.e., near the wall. In addition, it can be observed that migration towards the cross-section corner is always present in a Giesekus fluid at $\hbox {De} = 5.0$, rather the attraction basin of such equilibrium position is quite large at low $\text {Ca}_{\mathrm{e}}$. This is indeed consistent with the results reported in Villone et al. (2013) for rigid particles.

Some further comments on the trajectories shown and discussed above. When particle migration is directed towards the channel center line, such equilibrium position is asymptotic, thus, strictly speaking, it will be only reached by the particle after an infinite time. In addition, the closer the particle to the axis, the lower the migration velocity, so an unaffordable computational time would be needed to see the particle get much closer to the channel center line than shown. On the other hand, given that the employed numerical technique considers two different material domains and a sharp interface between them, it is impossible to simulate migration until the particle touches the walls of the channel, because the mesh in the fluid domain would crash. Hence, the simulations are carried out until computationally feasible, which, in some cases, corresponds to a situation in which the particle has actually almost reached the wall (see, for example, the trajectories in Fig. 8a).

Fig. 9

Maps of the trace of the conformation tensor $\text {tr}(\varvec{c})$ in the cross-section of the channel passing through the center of volume of a particle migrating in a Giesekus fluid at $\beta = 0.3$ and starting position $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.15,0.28)$. The fluid has $\eta _{\mathrm{s}}/\eta _{0} = 0.09$ and $\alpha = 0.2$. Top row: $\hbox {De} = 0.1$, $\text {Ca}_{\mathrm{e}}=0.001$ (a), 0.01 (b), 0.1 (c). Bottom row: $\hbox {De} = 5.0$, $\text {Ca}_{\mathrm{e}}=0.001$ (d), 0.01 (e), 0.1 (f)

To visualize simultaneously particle deformation and the perturbation the bead provides to the fluid stress field, we display in Fig. 9 the distribution of the trace of the conformation tensor $\varvec{c} = \lambda \varvec{\tau }/\eta _{\mathrm{p}} + \varvec{I}$ in the cross-section of the channel passing through the center of volume of a particle migrating in a Giesekus fluid at $\beta = 0.3$ and starting position $(z_{\mathrm{p}},y_{\mathrm{p}}) = (0.15,0.28)$. Two De-values are considered, i.e., 0.1 and 5.0, and, for each, $\text {Ca}_{\mathrm{e}} = 0.001$, 0.01, 0.1. For each parameter-set, a snapshot is reported at a time value for which the deformation initial dynamics is over and quasi-steady migration is ongoing. First, it can be observed that, given $\text {Ca}_{\mathrm{e}}$, increasing fluid elasticity, i.e., De, hinders particle deformation, thus the deformation-induced contribution to its migration. At the same time, the trace of the conformation tensor $\text {tr}(\varvec{c})$ is a measure of fluid elastic energy (Larson 1988) and it can be seen that such energy has a minimum at the channel center line and the four corners of the cross-section. For rigid particles, Villone et al. (2013) have conjectured that the migration tends to follow the steepest gradient of $\text {tr}(\varvec{c})$ towardss a minimum. Here, depending on the cases, this phenomenon combines or competes with deformation-induced migration, which is always towards the center line of the channel.

5 Conclusions

In this paper, the cross-streamline migration of an initially spherical neo-Hookean elastic particle suspended in inertialess pressure-driven flow of Newtonian and viscoelastic fluids in a square-cross-section microfluidic channel is studied by means of three-dimensional finite element numerical simulations. Two viscoelastic constitutive equations are considered, namely, the Oldroyd-B and Giesekus models. The first one predicts a constant viscosity and no second normal stress difference, whereas the second one predicts shear-thinning and a non-zero second normal stress difference, giving rise to secondary flows orthogonal to the main flow direction.

When suspended in a Newtonian fluid, the particle migrates transversally to the flow direction towards the center line of the channel. The migration velocity depends on particle geometrical confinement and on the ratio between shear stress and particle deformability. In dimensionless terms, these effects are measured by the confinement ratio $\beta$ and the elastic capillary number $\text {Ca}_{\mathrm{e}}$. In this paper, a low and a medium value of the confinement ratio ($\beta = 0.1$, 0.3) and three orders of magnitude of the elastic capillary number ($\text {Ca}_{\mathrm{e}} = 0.001$, 0.01, 0.1) are considered. When both the confinement and the capillary number are little, the bead practically behaves like a rigid particle. Hence, given the absence of inertia, it almost does not migrate. Both increasing $\beta$ and $\text {Ca}_{\mathrm{e}}$ enhance particle deformation, thus deformation-driven particle migration towards the center. A design equation for a square-cross-section microfluidic device aimed at focusing elastic particles on its center line is proposed on the basis of the numerical results.

When the particle is suspended in a viscoelastic medium, also fluid elasticity comes into play and affects particle migration. In dimensionless terms, the weight of fluid elasticity with respect to the flow characteristic time is measured by the Deborah number De. In this paper, a low and a high value of such parameter are considered ($\hbox {De} = 0.1$, 5.0). In general terms, $\beta$- and $\text {Ca}_{\mathrm{e}}$-increases always promote faster migration towards the center, while the effect of fluid elasticity is complex.

In an Oldroyd-B liquid, for low confinement and particle deformability (i.e., at low $\beta$ and $\text {Ca}_{\mathrm{e}}$), increasing De speeds up lateral migration (as it was already known for rigid particles, see, e.g., Villone et al. 2013), but it has the opposite effect at high $\beta$ and $\text {Ca}_{\mathrm{e}}$, since it hinders particle deformation, thus suppressing the deformation-driven contribution to migration. In addition, for certain combinations of the parameter values, cross-stream migration can be also directed towards the corners of the channel cross-section depending on particle initial position.

In a Giesekus liquid, shear-thinning and secondary flows give rise to even more complex behaviors, especially at high De (the intensity of secondary flows is proportional to $\text {De}^4$). In this case, the secondary flows can strongly influence particle trajectories, thus making lateral migration much slower. Moreover, the presence of shear-thinning can enhance migration towards the walls of the channel cross-section, thus hindering flow-focusing.