1 Introduction

Electrokinetic technique has been widely used to manipulate fluids and samples (ranging from dissolved ionic species to suspended micro/nanoparticles) for various microfluidic and nanofluidic applications (Kang and Li 2009; Zhao and Yang 2012; Chang et al. 2012). It transports fluids via electroosmosis and samples (if charged) via electrophoresis through the use of a direct-current (DC) electric field (Li 2004). Both motions, together termed electrokinetic flow (for fluids) or electrokinetic motion (for particles), are associated with the electric double layer formed at the liquid/solid (i.e., fluid/channel and fluid/particle) interface (Masliyah and Bhattacharjee 2006). Electrokinetic flow has multiple advantages over the traditional pressure-driven pumping such as free of moving parts, simple control and ease of integration etc. (Chang and Yeo 2009). Moreover, it has a favored plug-like velocity profile in microchannels (Whitesides and Stroock 2001), leading to a more precise control of samples with a reduced dispersion (Ghosal 2006). This feature, however, breaks down if the surface charge (or equivalently zeta potential) of the microchannel walls or the electric properties of the fluid (e.g., conductivity and permittivity) becomes non-uniform. The former variation of wall surface property may occur due to heterogeneous patterning (Stroock et al. 2000; Biddiss et al. 2004), field effect control (Lee et al. 2004; Wu and Liu 2005) or induced charge effect (Thamida and Chang 2002; Yossifon et al. 2006; Eckstein et al. 2009; Zehavi et al. 2016; Prabhakaran et al. 2017b), each of which has been reported to produce local fluid circulations for enhanced sample mixing or trapping in electrokinetic flows (Chang and Yang 2007; Chen and Yang 2008; Lee et al. 2011; Zehavi and Yossifon 2014; Harrison et al. 2015; Ren et al. 2018).

The variation of fluid properties is automatically induced by the ubiquitous Joule heating phenomenon in electrokinetic flows that causes temperature gradients in both the fluid and the entire system (Xuan 2008). Such effects become significant if there exists a non-uniform heating in the fluid, which has been reported to cause strong electrothermal circulations in insulator-based dielectrophoretic microdevices (Hawkins and Kirby 2010; Sridharan et al. 2011; Prabhakaran et al. 2017a; Wang et al. 2017). The variation of fluid properties in electrokinetic flows can also be inherently formed at the interface of two fluids that are either displacing (Ren et al. 2001) or co-flowing with (Nguyen and Wu 2005) each other. The former action takes place in the current monitoring method (for measuring the electroosmotic flow rate and wall zeta potential) (Saucedo-Espinosa and Lapizco-Encinas 2016), field amplified sample stacking (Goet et al. 2011), and isoelectric focusing (Herr et al. 2003), etc. The co-flow of two or more fluids with dissimilar electric properties is a common setting in electrokinetic mixing (Chang and Yang 2007) and separation (Kawamata et al. 2008; Sajeesh and Sen 2014; Lu et al. 2015), etc. It has been reported to become unstable with periodic (Lin et al. 2004) or even chaotic (Posner et al. 2012) instabilities formed at the fluid interface due to the coupling of electric field with conductivity gradients. Such electrokinetic instabilities in microchannel fluid flows with conductivity gradients, which are found in a linear stability analysis to be controlled by an electric Raleigh number (Chen et al. 2005), have been extensively studied both experimentally and numerically (Storey et al. 2005; Oddy and Santiago 2005; Park et al. 2005; Posner and Santiago 2006; Kang et al. 2006; Lin et al. 2008; Lin 2009; Luo 2009; Li et al. 2016; Dubey et al. 2017).

Electrokinetic instabilities have also been studied in co-flowing fluids with both conductivity and permittivity gradients due to the addition of non-dilute colloids into one of them (Navaneetham and Posner 2009). A similar idea was later employed by our group to investigate the electrokinetic co-flow of ferrofluid and water solutions in a T-shaped microchannel (Kumar et al. 2015). We found that the measured threshold electric field, at which electrokinetic instabilities are induced at the ferrofluid/water interface, along with the dynamic interfacial behaviors can be closely predicted by a depth-averaged numerical model (Song et al. 2017). Such an electric field-driven mixing has the advantage of simplicity as compared to the magnetic field-driven mixing of ferrofluid and water (Mao and Koser 2007; Wen et al. 2009, 2011; Zhu and Nguyen 2012a, b). It is because the applied DC electric field can not only pump (via electroosmosis) but also mix (via electrokinetic instabilities) the two solutions without the need of an additional hydrodynamic pumping. Moreover, an AC electric field can potentially be combined to the DC field to induce an extra magnetic force for enhanced mixing (Mao and Koser 2007; Wen et al. 2009, 2011). Built upon these earlier papers (Kumar et al. 2015; Song et al. 2017), we perform in this work a combined experimental and numerical study on the electrokinetic co-flow of ferrofluid and buffer solutions with matched electric conductivities. The objective is to examine if electrokinetic instabilities can still be generated in the absence of apparent conductivity gradients and what the role of permittivity gradients is.

2 Experiment

2.1 Materials

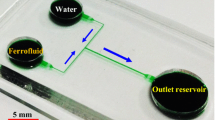
The T-shaped microchannel with two symmetric inlets and one outlet was fabricated using polydimethylsiloxane (PDMS) with the standard soft lithography technique. The detailed fabrication procedure can be referred to our earlier paper (Kumar et al. 2015). Each side-branch of the channel is 8 mm long and 100 µm wide, while the length and width of the main-branch are 10 mm and 200 µm, respectively. The channel is uniformly 45 µm deep, and its top-view picture is shown in Fig. 1. EMG 408 ferrofluid (Ferrotec Corp., the original concentration of magnetic nanoparticles is 1.2% vol.) was diluted with DI water (Fisher Scientific) to three different concentrations (in volume fraction), 0.1 × , 0.2 × and 0.3 ×. The electric conductivities of these ferrofluid solutions were measured using a portable conductivity meter (accumet AP85, Fisher Scientific). They were each matched (with at most ± 5% errors) to the electric conductivity of a phosphate buffer solution whose concentration (the original value in store is 50 mM) was adjusted with DI water. Table 1 summarizes the electric conductivity of each of these ferrofluid solutions and the corresponding concentration of the matching buffer solution.

Fig. 1
figure 1

Top-view picture of the T-shaped microchannel (filled with green food dye for clarity) used in experiments. The two “+” symbols represent an equal positive electric voltage imposed to each of the two inlet reservoirs (i.e., the two circular wells on the left) for the ferrofluid and buffer solutions, respectively. The symbol in the circular well on the right represents a grounded outlet reservoir. The block arrows indicate the flow directions

Full size image
Table 1 Electric conductivities and concentrations of the matching ferrofluid and buffer solutions
Full size table

2.2 Methods

Prior to experiment, the microchannel was flushed with DI water to remove any debris that may be generated during the fabrication. Next, an equal volume of ferrofluid and buffer solutions with a matching electric conductivity were filled into the two inlet reservoirs each. The outlet reservoir was filled with the buffer solution, whose liquid level was adjusted to balance out any hydrostatic pressure difference between the inlet and outlet reservoirs. Three platinum electrodes were then inserted into the three reservoirs each, where the two at the inlets were connected to the power source (Glassman High Voltage Inc.) in parallel while that at the outlet was grounded. The co-flowing ferrofluid and buffer solutions in the main-branch of the microchannel were each driven from one inlet to the outlet using an equal DC electric field. The applied DC voltage at the inlets started with a low value (to form a clear ferrofluid and buffer interface) and was then increased gradually to find the threshold voltage under which the electrokinetic flow became unstable. The dynamic behavior at the interface of the two solutions near the T-junction was visualized and recorded using an inverted microscope (Nikon Eclipse TE2000U, Nikon Instruments) with a CCD camera (Nikon DS-Qi1Mc) at a rate of 15 frames per second. The obtained digital images were post-processed using the Nikon imaging software (NIS-Elements AR 2.30).

3 Simulation

3.1 Governing equations

We developed a 2D numerical model for a preliminary understanding of the experimentally observed electrokinetic instability in co-flowing ferrofluid and buffer solutions with matched electric conductivities. This model was built upon those in previous studies for electrokinetic microchannel flows with either conductivity (Lin et al. 2004; Chen et al. 2005; Kang et al. 2006; Luo 2009; Li et al. 2016; Dubey et al. 2017) or conductivity/permittivity (Navaneetham and Posner 2009; Kumar et al. 2015) gradients. As we will demonstrate in the results Sect. 4.2, the permittivity gradient alone is unable to cause any electrokinetic instability in our simulation even under a very high electric field. We, therefore, propose to use the diffusion-induced conductivity gradients formed at the ferrofluid/buffer interface to explain our experimental observations. Specifically, as the magnetic nanoparticles in the ferrofluid solution have a smaller diffusivity than the electrolyte ions in the buffer solution, the electric conductivity of the former increases during the process of (diffusive) mixing while that of the buffer solution decreases. This is because the drop of magnetic nanoparticle concentration in the ferrofluid solution is slower than the rise of buffer ion concentration therein. The opposite phenomenon takes place in the buffer solution.

Our model considers the conservation of charge, mass, momentum, and (two) species for the electric potential, fluid flow and concentration fields, respectively. The associated governing equations are presented below, and more details are referred to the work of Lin et al. (2004) and Chen et al. (2005),

$$\nabla \cdot (\sigma {\mathbf{E}})=0$$
(1)
$$\nabla \cdot {\mathbf{u}}=0$$
(2)
$$\rho \left( {\frac{{\partial {\mathbf{u}}}}{{\partial t}}+{\mathbf{u}} \cdot \nabla {\mathbf{u}}} \right)= - \nabla p+\nabla \cdot (\mu \nabla {\mathbf{u}})+{\rho _{\text{e}}}{\mathbf{E}} - \frac{1}{2}({\mathbf{E}} \cdot {\mathbf{E}})\nabla ({\varepsilon _0}{\varepsilon _{\text{r}}})$$
(3)
$$\frac{{\partial {c_f}}}{{\partial t}}+\nabla \cdot ({\mathbf{u}}{c_{\text{f}}})={D_{\text{f}}}{\nabla ^2}{c_{\text{f}}}$$
(4)
$$\frac{{\partial {c_b}}}{{\partial t}}+\nabla \cdot ({\mathbf{u}}{c_{\text{b}}})={D_{\text{b}}}{\nabla ^2}{c_{\text{b}}}.$$
(5)

In the above, Eq. (1) is the electric field equation obtained from the Maxwell’s equation, where \(\sigma\) is the electric conductivity of the fluid, and \({\mathbf{E}}= - \nabla \phi\) is the electric field with \(\phi\) being the electric potential. Equations (2) and (3) are the continuity and momentum equations for the flow field, where \({\mathbf{u}}={\mathbf{u}}(x,y)\) is the velocity vector in the horizontal plane of the microchannel, \(\rho\) is the fluid density, \(t\) is the time, \(p\) is the pressure, \(\mu\) is the fluid viscosity, \({\rho _{\text{e}}}=\nabla \cdot ({\varepsilon _0}{\varepsilon _{\text{r}}}{\mathbf{E}})\) is the free charge density from Poisson’s equation, \({\varepsilon _0}\) is the vacuum permittivity, and \({\varepsilon _{\text{r}}}\) is the relative permittivity of the fluid. The last two terms in Eq. (3) represent the Coulomb and dielectric forces, respectively (Melcher and Taylor 1969). Equations (4) and (5) are the convection–diffusion equations for the transport of ferrofluid nanoparticles and buffer ions, where \(c\) is the species concentration normalized by the initial concentration, \({c_0}\) (see the values in Table 1), \(D\) is the species diffusivity, and the subscripts \({\text{f}}\) and \({\text{b}}\) represent the properties of ferrofluid and buffer, respectively. It should be noted that the electrophoretic motion of species is not considered in Eq. (4) or (5). The electrophoresis of ferrofluid nanoparticles has been numerically demonstrated in our earlier study (Kumar et al. 2015) to have an insignificant impact on electrokinetic instabilities in co-flowing ferrofluid and water solutions with strong conductivity gradients. Its influence on the electrokinetic flow of conductivity-matched ferrofluid and buffer solutions in the current work will be discussed in Sect. 4.

3.2 Model setup

Figure 2 shows the computational domain used in our model, where the lengths of both the main- and side-branches of the microchannel are cropped to save the computational time. Important boundary and initial conditions are also highlighted in Fig. 2: for the electric field in Eq. (1), the two inlets are imposed with an equal electric potential (\(\phi ={\phi _{{\text{in}}}}\)), the outlet is grounded (\(\phi =0\)), and all channel sidewalls are electrically insulated (\(\nabla \phi \cdot {\mathbf{n}}=0\) with \({\mathbf{n}}\) denoting the unit normal vector); for the flow field in Eqs. (2) and (3), the channel sidewalls are imposed with the Helmholtz–Smoluchowski slip velocity (\({\mathbf{u}} \cdot {\mathbf{t}}={U_{{\text{slip}}}}= - \ {\varepsilon _0}{\varepsilon _{\text{r}}}\zeta {\mathbf{E}} \cdot {\mathbf{t}}/\mu\) with t being the unit tangential vector and \(\zeta\) the wall zeta potential) that is valid under the limit of thin electric double layers (Li 2004; Chang and Yeo 2009), and the inlets/outlet are imposed with an equal pressure (\(p=0\)); for the concentration field in Eqs. (4) and (5), the ferrofluid inlet is imposed with \({c_{\text{f}}}=1\) and \({c_{\text{b}}}=0\), the buffer inlet is imposed with \({c_{\text{f}}}=0\) and \({c_{\text{b}}}=1\), the channel sidewalls and outlet are imposed with a non-penetrating condition and a fully developed condition, respectively (both are \(\nabla {c_{\text{f}}} \cdot {\mathbf{n}}=\nabla {c_{\text{b}}} \cdot {\mathbf{n}}=0\)). At the initial state, the ferrofluid and buffer solutions are assumed stationary with a uniform concentration of unity in each half of the computation domain in Fig. 2.

Fig. 2
figure 2

The computational domain (drawn to scale) and the important boundary conditions of the 2D model in the horizontal plane of the T-shaped microchannel. The gray and white areas represent the ferrofluid and buffer solutions, respectively, at the initial state. The block arrows indicate the flow directions

Full size image

As the density (\({\rho _{\text{f}}} \approx 1.01\) g/cm3) and viscosity (\({\mu _{\text{f}}} \approx 1.04\) mPa⋅s) (Zhu et al. 2011; Liang et al. 2011) of our diluted ferrofluid (0.2 × EMG 408) are each fairly close to that of the buffer solution (\({\rho _{\text{b}}}=1.0\) g/cm3 and \({\mu _{\text{b}}}=1.0\) mPa s), we assumed a uniform and constant fluid density and viscosity in our model. We also assumed a uniform and constant fluid (relative) permittivity, \({\varepsilon _{\text{r}}}=80\) (equal to that of water) because the nanoparticle concentration of the diluted ferrofluid (i.e., 0.24% for 0.2 × EMG 408) and the ionic concentration of the buffer solution (see Table 1) were each kept low (Navaneetham and Posner 2009; Posner 2009). The effect of permittivity gradient on electrokinetic instability will be discussed in the “Results” section (see Sect. 4.2). The fluid conductivity was assumed to be the summation of the electric conductivities of the ferrofluid and buffer solutions, which are each a linear function of the species concentration (each normalized by the initial species concentration, i.e., \({c_{{\text{f0}}}}\) or \({c_{{\text{b0}}}}\), in Table 1),

$$\sigma ={\sigma _{{\text{f0}}}}{c_{\text{f}}}+{\sigma _{{\text{b0}}}}{c_{\text{b}}}.$$
(6)

The electric conductivity values of the ferrofluid and buffer solutions in the inlet reservoirs, \({\sigma _{{\text{f0}}}}\) and \({\sigma _{{\text{b0}}}}\), are presented in Table 1. In addition, following the approach used in our earlier studies (Kumar et al. 2015; Song et al. 2017), we assumed an equal and constant zeta potential for the channel sidewalls that are in contact with the ferrofluid and buffer, respectively. However, the value of the wall zeta potential (in the unit of mV) was considered to vary with the initial buffer concentration, \({c_{{\text{b0}}}}\) (in the unit of M, see Table 1) via the following empirical relationship (Kirby and Hasselbrink 2004):

$$\zeta = - \;6.75+29.75\log ({c_{{\text{b0}}}}).$$
(7)

This consideration was used in the “Results” section (see Sect. 4.3) to explain the effect of ferrofluid concentration (and in turn the buffer concentration for a matching conductivity) on electrokinetic instability. The diffusivity of buffer ions was assumed to be \({D_{\text{b}}}=1 \times {10^{ - 9}}\) m2/s. The diffusivity of ferrofluid nanoparticles was calculated as \({D_{\text{f}}}=4.39 \times {10^{ - 11}}\) m2/s from the Stokes–Einstein equation (Zhu and Nguyen 2012a, b). It was, however, set to \({D_{\text{f}}}={D_{\text{b}}}/5=2 \times {10^{ - 10}}\) m2/s in our model to minimize the numerical dispersion and reduce the computational cost (Wen et al. 2011; Zhu and Nguyen 2012a, b).

3.3 Numerical implementation

Our model was developed in COMSOL® 5.2. The governing equations for the electric potential, fluid flow, and (two) species concentration fields were solved in “Electric Currents”, “Laminar Flow”, and “Transport of Diluted Species” modules, respectively. The computational domain was meshed using mapped rectangular elements that are symmetric about the centerline of the main-branch (Fig. 3). As the elements near the channel center and walls are especially important, their sizes were made smaller than those in the other regions of the domain. This was implemented by setting the largest ratio of the element size in the channel width direction to 4. We performed a grid-independence study, where the number of elements in the channel width direction and the element size in the channel length direction were each adjusted. Figure 4a shows a comparison of the time-averaged velocity profiles for the co-flow of conductivity-matched 0.2 × ferrofluid and buffer solutions at a cross-section 2.5 mm downstream from the T-junction (similar results were also observed at other cross-sections) under an electric field of 179 V/cm. We, therefore, chose a fixed 6 µm element size in the channel length direction along with 25 elements in the channel half-width. We also performed a time step-independence study based on this mesh setting. The plot of time-averaged velocity profiles under different time-step values in Fig. 4b indicates that a time step of 2 ms is sufficient for our 2D simulation.

Fig. 3
figure 3

Illustration of the meshed computational domain with mapped rectangular elements (note that the main-branch of the microchannel in the model is not completely displayed here due to the space limitation). The inset is a close-up view of the highlighted region at the T-junction

Full size image
Fig. 4
figure 4

Grid-size (a) and time-step (b) independence studies of the 2D numerical model via the comparison of the time-averaged velocity profiles in the co-flow of conductivity-matched 0.2 × ferrofluid and buffer solutions under an electric field of 179 V/cm at the cross-section 2.5 mm downstream from the T-junction (see the computational domain in Fig. 2). The three quantities in each legend represent the element size in the channel length direction, number of elements in the channel half-width, and time step from left to right

Full size image

4 Results and discussion

4.1 Effect of electric field magnitude

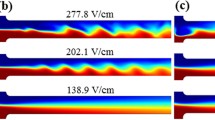
Figure 5 shows the experimentally observed interfacial behaviors in the electrokinetic co-flow of conductivity-matched 0.2 × ferrofluid and buffer solutions at the T-junction of the microchannel. Under a DC electric field of 389 V/cm (estimated from a 700 V voltage drop across the overall 1.8 cm channel length), no apparent mixing occurs between the two solutions due to the essentially slow diffusion of either species. Increasing the electric field to 428 V/cm (correspond to a 770 V voltage drop) leads to the formation of periodic waves at the ferrofluid and water interface. This field, which is defined as the experimental threshold electric field, is more than twice the threshold value (around 175 V/cm) for the 0.2 × ferrofluid/water co-flow (i.e., without the electric conductivity matching) through an identical microchannel in our previous studies (Kumar et al. 2015; Song et al. 2017). However, the observed instability waves in Fig. 5 are weaker than those in the latter. Moreover, they are not apparently inclined downstream or upstream, which is inconsistent with the upstream inclination of instability waves in non-matched ferrofluid/water co-flows (Kumar et al. 2015; Song et al. 2017). Further increasing the electric field to 500 V/cm does not seem to have a significant impact on the amplitude or frequency of the instability waves (see the bottom image in Fig. 5). This observation is different from the strongly enhanced electrokinetic instabilities (which can even become chaotic) in ferrofluid/water co-flows with the increase of electric field magnitude (Kumar et al. 2015; Song et al. 2017).

Fig. 5
figure 5

Experimentally captured top-view images (taken at 16 s after the electric field was imposed) for the electrokinetic co-flow of 0.2 × ferrofluid (dark) and buffer (bright) solutions with a matched electric conductivity at the channel T-junction under varying DC electric fields. The arrow indicates the flow direction in the main-branch of the channel, and the scale bar represents 200 µm

Full size image

Figure 6 shows the numerically obtained concentration field of ferrofluid nanoparticles, \({c_{\text{f}}}\), which can be compared against the darkness level of the ferrofluid stream on the experimental images in Fig. 5. No electrokinetic instabilities are predicted to occur until the electric field is increased to 188 V/cm. This value, which is defined as the numerical threshold electric field, is, however, significantly smaller than the experimental threshold value (428 V/cm) in Fig. 5. Moreover, the onset of the predicted concentration waves, which are slightly inclined towards the T-junction in Fig. 6, is pushed further downstream as compared to the experimental observation. Under an electric field greater than the numerical threshold value, the predicted electrokinetic instability in Fig. 6 is apparently enhanced. This is distinctly different from the experimental result in Fig. 5, which, along with the other discrepancies between experiment and simulation as stated above, may be a consequence of the neglected stabilizing effects of the top and bottom channel walls that have been proved strong in our previous study (Song et al. 2017). As noted in the simulation section (see Sect. 3.2) above, we used a greater diffusivity value for ferrofluid nanoparticles than that calculated from the Stokes–Einstein equation. This treatment reduces the diffusivity gradient between the ferrofluid and buffer solutions in the model, and hence leads to an over-prediction of the numerical threshold electric field (i.e., deviating further away from the experimental threshold value).

Fig. 6
figure 6

Numerically predicted contours of ferrofluid concentration (obtained at 16 s after the electric field was imposed) for the electrokinetic co-flow of conductivity-matched 0.2 × ferrofluid and buffer solutions at the channel T-junction under varying DC electric fields

Full size image

We also estimated the influence of electrophoresis of ferrofluid nanoparticles by replacing the fluid velocity, \({\mathbf{u}}\), in Eq. (4) with \({\mathbf{u}}+{\varepsilon _0}{\varepsilon _r}{\zeta _p}{\mathbf{E}}/\mu\), where \({\zeta _p}= - \;30\) mV was the assumed particle zeta potential. It was found that the resulting decrease in nanoparticle velocity (because the nanoparticle electrophoresis is against the fluid electroosmosis in our experiment and model) reduces the numerical threshold electric field to 167 V/cm (about 10% less than that in the absence of electrophoresis). This happens because of the increasing role of nanoparticle diffusion (and hence the diffusion-induced conductivity gradients) when ferrofluid nanoparticles move slower. In other words, the assumption of a positive nanoparticle zeta potential should increase the numerical threshold electric field. However, such an effect is unlikely to be strong enough to explain the huge discrepancy between the experimental (Fig. 5) and numerical (Fig. 6) threshold electric fields.

4.2 Numerical understanding of the instability mechanism

Figure 7 shows the numerical images of other property fields from the 2D model under the numerical threshold electric field (188 V/cm). For a better comparison, the concentration field of ferrofluid nanoparticles, \({c_{\text{f}}}\), is included in Fig. 7a (the same as the middle image in Fig. 6). The predicted concentration field of buffer ions, \({c_{\text{b}}}\), in Fig. 7b shows an opposite distribution to that of ferrofluid nanoparticles due to the interfacial mixing between the two fluids. Moreover, the mixing zone (i.e., the region with non-zero or non-unity concentration) of buffer ions in Fig. 7b is obviously wider than that of ferrofluid nanoparticles in Fig. 7a due to the latter’s smaller diffusivity. The combination of the distributions of \({c_{\text{f}}}\) and \({c_{\text{b}}}\) leads to local gradients in the fluid conductivity, \(\sigma\), within the mixing zone. As demonstrated in Fig. 7c, the electric conductivity in the ferrofluid half (around 0.13 S/m at maximum) becomes greater than that in the buffer half (around 0.09 S/m at minimum) like what we have explained in Sect. 3.1 (note the initial conductivity of either fluid is 0.108 S/m in Table 1). While it is not large enough to produce significant distortions to the electric field lines in Fig. 7d, such diffusion-induced fluid conductivity gradients cause the formation of free charge density, \({\rho _{\text{e}}}= - \;({\varepsilon _0}{\varepsilon _r} /\sigma )({\mathbf{E}} \cdot \nabla \sigma )\), in between the two fluids in Fig. 7e. This in turn produces an electric body force, \({{\mathbf{F}}_{\text{e}}}={\rho _{\text{e}}}{\mathbf{E}}\), in Fig. 7f that deforms the ferrofluid/buffer interface and causes the instability wave in Fig. 7g.

Fig. 7
figure 7

Numerically predicted property fields for the electrokinetic co-flow of conductivity-matched 0.2 × ferrofluid and buffer solutions under the numerical threshold electric field of 188 V/cm: a concentration contour of ferrofluid nanoparticles, \({c_{\text{f}}}\); b concentration contour of buffer ions, \({c_{\text{b}}}\); c fluid electric conductivity, \(\sigma\); d electric field lines, \({\mathbf{E}}\); e free charge density, \({\rho _{\text{e}}}\); f electric body force vectors, \({{\mathbf{F}}_{\text{e}}}\); g fluid streamlines and velocity contour, \({\mathbf{u}}\). The background curving lines in e, f are the contour lines of ferrofluid concentration in a, which can be viewed as an approximate indication of the ferrofluid/buffer mixing zone

Full size image

We further tested numerically if the mismatch of ferrofluid and buffer permittivity can cause the electrokinetic instability in Fig. 5. The diffusivity value was set to \({D_{\text{f}}}={D_{\text{b}}}=1 \times {10^{ - 9}}\) m2/s for both ferrofluid nanoparticles and buffer ions to remove the diffusion-induced conductivity gradients in Fig. 7c. The relative permittivity of 0.2 × ferrofluid was assumed to be \({\varepsilon _{{\text{f0}}}}=96\) (corresponding to a relative permittivity of 160 for 1 × EMG 408 ferrofluid that has only 1.2% w/w nanoparticles!) while that of the buffer solution was still kept equal to water at \({\varepsilon _{{\text{b0}}}}=80\). Moreover, the relative permittivity of the fluid in the model was assumed to vary linearly with the concentration of ferrofluid nanoparticles, i.e. \({\varepsilon _{\text{r}}}={\varepsilon _{{\text{b0}}}}+({\varepsilon _{{\text{f0}}}} - {\varepsilon _{{\text{b0}}}}){c_{\text{f}}}\). All other conditions remained the same as those used in Figs. 6 and 7. We found that the electrokinetic co-flow remained stable even under an electric field triple the experimental threshold value in Fig. 5 (or more than 6 times the numerical threshold electric field in Fig. 6). We, therefore, propose that the fluid permittivity mismatch between the ferrofluid and buffer solutions should not be the primary cause of the observed electrokinetic instability in Fig. 5. The role of permittivity gradients was found in our model with the diffusivity mismatch to increase the numerical threshold electric field by only 8% even for \({\varepsilon _{{\text{f0}}}}=112\) [or equivalently a relative permittivity of 240 for 1 × EMG 408 ferrofluid, which does not seem practical (Navaneetham and Posner 2009; Posner 2009)]. We, therefore, have chosen to ignore the influence of permittivity variation in our model as noted in Sect. 3.

4.3 Effect of ferrofluid concentration

Figure 8 shows the effect of ferrofluid concentration on the electrokinetic co-flow of conductivity-matched ferrofluid and buffer solutions under the threshold electric field. The increase of ferrofluid concentration from 0.1 × to 0.3 × causes a nearly 20% decrease in the experimental threshold electric field (specifically, from 483 V/cm in 0.1 × ferrofluid to 389 V/cm in 0.3 ×). It, however, does not seem to strongly affect the amplitude or frequency of the instability waves in Fig. 8a. Considering that the variation of ferrofluid viscosity (around 1.02 and 1.06 mPa s for 0.1 × and 0.3 × ferrofluids, respectively) is less than 5% in the same range of concentrations, the diffusivity of ferrofluid nanoparticles does not change significantly. Moreover, the inclusion of permittivity gradients into the model should cause an increase in the numerical threshold electric field at a higher ferrofluid concentration because of their opposing effects to diffusion-induced conductivity gradients (Navaneetham and Posner 2009; Kumar et al. 2015). We, therefore, attribute the decrease in the experimental threshold electric field to the smaller wall zeta potential in a higher-concentration ferrofluid/buffer co-flow. This variation was considered using Eq. (7) in our model, and the simulation results in Fig. 8b indicate a 12% decrease (from 203 to 179 V/cm) in the numerical threshold electric field when the ferrofluid concentration is increased from 0.1 × to 0.3 ×. These threshold values are all much lower than the experimental threshold electric fields (see the plot in Fig. 8c for a quantitative comparison), which may be related to the neglected stabilizing effects of the top and bottom channel walls in a 2D model (Song et al. 2017).

Fig. 8
figure 8

Ferrofluid concentration effect on the electrokinetic instability of conductivity-matched ferrofluid/buffer co-flows: a experimental images (dark for ferrofluid and bright for buffer, where the arrow indicates the flow direction in the main-branch of the microchannel and the scale bar represents 200 µm) under the experimental threshold electric fields; b numerical images of ferrofluid concentration field under the numerical threshold electric fields; c comparison of the experimental and numerical threshold electric fields

Full size image

5 Conclusion

We have studied the electrokinetic co-flow of ferrofluid and buffer solutions with matched electric conductivities. Periodic waves are observed to form at the interface of the two streams when the applied electric field reaches a threshold value. However, unlike those reported in previous studies (e.g., Lin et al. 2004; Chen et al. 2005; Navaneetham and Posner 2009; Posner et al. 2012; Kumar et al. 2015; Song et al. 2017), our observed electrokinetic instabilities do not appear to be significantly enhanced at electric fields higher than the threshold value. We have also developed a 2D numerical model for a preliminary understanding of the underlying mechanism. Our model indicates that the permittivity difference between the ferrofluid and buffer solutions plays an insignificant role in the observed electrokinetic instability. We propose the instability phenomenon is a result of the electric body force that acts on the diffusion-induced conductivity gradients formed at the ferrofluid and buffer interface because of the mismatching diffusivities of ferrofluid nanoparticles and buffer ions. While it is able to qualitatively capture the dynamic interfacial behaviors, our model significantly under-predicts the threshold electric field because the top and bottom channel walls’ stabilizing effects are ignored.