1 Introduction

In conventional flow cytometry, hydrodynamic spreading and focusing have been used for detection and sorting of particles. Hydrodynamic focusing was also used to improve mixing in microchannels by reducing the mixing path. Hydrodynamic focusing utilizes the flow rate ratio and the viscosity ratio between two sheath flows and a core flow to adjust the width of the core [1]. The flows are driven by either pressure or electro-osmosis or the combination of both. For sorting applications, the focused stream is switched by increasing the flow rate of one sheath stream or applying a voltage to this stream.

A magnetic fluid consists of a carrier fluid and a suspension of magnetic particles. If the magnetic particles are smaller than about 10 nm, the thermal energy dominates over the magnetic energy induced by an external magnetic field. Thus, the particles can disperse well in the carrier fluid. The whole fluid behaves as a paramagnetic liquid and is called ferrofluid. If the magnetic particles are large enough, ranging from 10 nm to 10 μm, they interact and react to the external magnetic field changing the viscosity of the fluid [2]. In a uniform magnetic field, the paramagnetic particles become magnetic dipoles. Pankhurst et al. [3] reviewed the underlying physics of magnetic nanoparticles under an external magnetic field. Magnetic nanoparticles have been extensively used in medical and biomedical assays. Magnetic particles isolated from magnetotactic bacteria were used for enzyme immobilization [4]. The detection and enumeration of genetic variations for DNA molecules were realized by using fluorescent magnetic particles [5]. In molecular biology and biochemistry, magnetic particles were used for separation and extraction of cells and DNAs [6]. Microfluidic mixing and assaying were achieved by using magnetic beads under a local alternating magnetic field [7]. Effective mixing with efficiency in the order of 95 % was achieved by tuning the magnitude and the frequency of the field. Furthermore, the capability for a single-step immunoassay could be achieved by investigating the changes in Brownian rotation dynamics of magnetic particles [8]. Shinkai reviewed the medical application of magnetic particles including separation, immunoassay, magnetic resonance imaging (MRI), drug delivery and hyperthermia enhancement [9]. By filling nanotubes with paramagnetic nanoparticles, magnetic tubes can be realized with numerous potential applications [10].

Recently, the field of micro-magnetofluidics concerning the interactions between magnetism and fluid flow on the microscale was reviewed by Nguyen [11]. On the one hand, microfluidics allows the investigation of magnetically induced phenomena which is not possible on the large scale. On the other hand, magnetism provides a convenient and wireless way for control and manipulation of fluid flow on the microscale. Investigation of magnetofluidic phenomena in a microfluidic device has the advantage of a well-defined experimental condition. The small dimension of microchannels allows the generation of a large shear stress. The small device size also allows the simple implementation of a precisely controllable and uniform magnetic field. The low Reynolds number involved in microchannel allows experiments with negligible inertial force, simplifying the experimental conditions.

The use of ferrofluid for sorting has been reported recently. Size-dependent manipulation of diamagnetic particles can be realized with ferrofluid as the carrier medium. Under a magnetic field gradient, the non-magnetic particles experience a magnetic buoyancy force which is proportional to the volume of the particles. Both two-dimensional (2D) and three-dimensional (3D) simulation as well as experimental investigation were carried out and reported by Zhu et al. [12–14]. A ferrohydrodynamic cell sorting device was developed for separating Escherichia coli and Saccharomyces cerevisiae with a sorting efficiency close to 100 % [15]. Kose et al. [16] reported size-dependent separation with 99 % efficiency within 1 min, as well as shape-dependent separation of live red blood cells from sickle cells and bacteria. To facilitate the application in flow cytometry and particle sorting, a main task is the focusing of particles into a narrow stream. Negative magnetophoresis is used for deflection of non-magnetic particles suspended in the ferrofluid. The particles were confined with a diamagnetic stream at the interface of the two streams. Experiments were carried out to examine the effect of ferrofluid flow rate and particle volume [17]. Since the diamagnetic particles are collected at the interface between the magnetic and non-magnetic fluids, controlling the position of this interface would allow active sorting of these particles.

Extensive efforts have been dedicated to study the transport phenomena of magnetic colloids in a magnetic field. Most of the studies focused on magnetic particles in a nonuniform field. The magnetic force is one of the parameters that are affected by the field gradient. In addition to a magnetic volume force in the Navier–Stokes equation, the motion of particles are also affected by the magnetic force acting on each particle. The volume concentration of the particles is governed by a drift–diffusion equation. Blums [18] reported a numerical study on the mass transport of ferrosuspensions and ferrofluids. In the case of micromixing driven by magnetic particles, a numerical simulation was carried out and agreed well with experimental results [19]. The three-dimensional (3D) problem was solved using spray module of the commercial software CFD-ACE+. For the similar purpose of magnetically induced mixing, the finite volume method (FVM) was used by Le et al. [20] for solving the flow and concentration field with an implicit scheme. A finite volume-based code was also developed and utilized for investigating the effect of a magnetic field on the concentration field of magnetic nanoparticles [21]. In a recent work, the drift–diffusion equation was numerically solved, while the magnetic field and force were obtained from an analytical model [22]. A microseparator based on forces induced by magnetic particles was proposed and numerically investigated [23]. Chaotic mixing of magnetic particles inside the microfluidic separator was numerically studied using the commercial multiphysics finite element package Comsol [24].

The present paper reports the investigation of the spreading phenomena of ferrofluid in a uniform magnetic field. The magnetization of magnetic nanoparticles results in magnetic force acting on each particle, affecting the corresponding particle concentration distribution. The experimental setup and the results are presented and discussed in detail. The uniform magnetic field was generated by a custom-made electromagnet. The experiments were carried out with two miscible fluids: mineral oil and an oil-based ferrofluid. The flow rate ratio was varied to test the spreading performance. In addition, a numerical simulation was carried out to verify the experimental data. The mass, momentum and diffusion equations are solved by the finite volume method.

2 Materials and experimental method

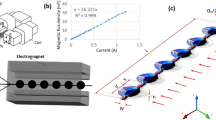
The flow system consists of two liquids: a ferrofluid and a mineral oil. The ferrofluid (APG 2134, FerroTec) consists of superparamagnetic nanoparticles suspended in an oil-based carrier fluid. The ferrofluid has a saturation magnetization of 22 mT and a density of \(\rho_{\rm FF}=1.07\times 10^3\) kg/m3. As tested by FerroTec, the ferrofluid is only slightly shear dependent with the viscosity decreasing from 984 to 967 mPa s for a shear rate ranging from 46 to 196 s−1. The maximum increase in viscosity due to magnetoviscous effect is only about 2 % [25]. The mineral oil (Sigma-Aldrich, Cat No. 330779) has a viscosity of \(\eta_{\rm O}=23.6\) mPa s and a density of \(\rho_{\rm O}=0.838\times 10^{3}\) kg/m3. The zero-shear viscosity was given by the manufacturer as \(\eta_{\rm FF0}=1,000\) mPa s. We modified a transformer to make the electromagnet (Fig. 1a). An air gap of 5.5 mm was cut through the ferromagnetic core of the transformer to accommodate the microfluidic device. The length of the test section is 11 mm. Varying the supply current up to 1.8 A can generate a magnetic flux density up to 50 mT in the air gap.

Fig. 1
figure 1

Experiment setup for magnetofluidic spreading in microchanels: a electromagnet for generation of a uniform magnetic field; b magnetofluidic spreading with ferrofluid core; c magnetofluidic spreading with ferrofluid cladding

Full size image

The microfluidic device was made of polydimethylsiloxane (PDMS) by soft lithography. The test channel has three inlets and two exits. The test channel has a depth of H = 50 μm, a width of W = 200 μm and a length of L = 2,500 μm, Fig. 1b, c. The whole setup was placed on an inverted microscope (TE2000, Nikon) equipped with a high-speed camera (APX RS, Photron). The length of the test channel is less than 1/4 of the width of the section in the air gap. Thus, a uniform magnetic field perpendicular to the microchannel can be assumed. With a size of magnetic particles of about \(d_{\rm p}=10\) nm and a temperature of T = 300 K, the diffusion coefficient of the particles into the mineral oil is estimated according to Einstein’s model as \(D=k_{\rm B}T/3\pi\eta_{\rm O}d_{\rm p}=1.86\times 10^{-12}\) m2/s where \(k_{\rm B}\) is the Boltzmann constant.

In the spreading experiment with ferrofluid core (Fig. 1b), the ferrofluid is delivered into the middle inlet at a constant flow rate of 0.05 ml/h. The flow rate of the two sheath streams varies from 0.2 to 0.6 ml/h. Using the properties of the mineral oil, the Reynolds number \(\text{Re}=\rho_{\rm O}UD_{\rm h}/\eta_{\rm O}\) ranges between 1.97 × 10−2 to 5.13 × 10−2. Using the estimated diffusion coefficient of the magnetic particles in mineral oil, the Peclet number \({\rm Pe}=WU/D\) ranges between 7.45 × 105 and 1.94 × 106. In the experiment with ferrofluid cladding (Fig. 1c), mineral oil is delivered into the middle inlet with a flow rate ranging from 0.2 to 0.6 ml/h, while the flow rate of ferrofluid in the two sheath streams is fixed at 0.05 ml/h. In this case, the corresponding range for the Reynolds number and the Peclet number are the same as in the case of ferrofluid core. The above conditions imply that the flow in the experiments is laminar, and diffusive mixing between the streams is negligible [26].

3 Numerical description

The numerical simulation was carried out with a 3D model to obtain qualitative insights into the physics of the phenomenon. All dimensions of the channel follow those of the fabricated device used in the experiment. At the inlet, the core flow and sheath flows are taken to be fully developed with an average velocity of

$$ \bar u = \frac{Q}{{WH}} $$
(1)

where Q is the volumetric flow rate of each inlet stream. No-slip condition was enforced at the walls. No flux condition was employed at the walls for solving the concentration distribution. Outflow condition was used at the outlet.

For a unsteady, viscous and incompressible system, the governing equations are expressed as

$$ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho {\varvec{{\rm u}}}} \right) = 0 $$
(2)
$$ \frac{\partial }{{\partial t}}\left( {\rho {\varvec{{\rm u}}}} \right) + \nabla \cdot \left( {\rho {\varvec{{\rm u}}}{\varvec{{\rm u}}}} \right){} = - \nabla P + \nabla \cdot \left[ {\eta \left( {\nabla {\varvec{{\rm u}}} + \nabla {{{\varvec{{\rm u}}}}^{\rm T}}} \right)} \right] + {\varvec{{\rm F}}} $$
(3)
$$ \frac{{\partial C}}{{\partial t}} + \left( {{\varvec{{\rm u}}}_{p} \cdot \nabla } \right)C = D{\nabla ^2}C $$
(4)

where ρ is the density of the liquid, u is the velocity vector, and P represents the pressure. The ferrofluid diffusion related to a mass transfer of magnetic particles is governed by Eq. (4) with C representing the non-dimensional volume concentration and \({\varvec{{\rm u}}}_{p}\) indicating the velocity of the magnetic particles. The action of the magnetic field results in rotation of magnetic particles suspended in the ferrofluid. It is reported that the hindrance of the rotation leads to flow resistance and exhibits magnetoviscous effect [27]. As a result, the angular term is omitted in the momentum conservation equation for the ferrofluid which is only slightly shear dependent. In addition to the hydrodynamic flow field, the velocity of a particle due to magnetic force is given by Stokes drag law. Through balancing the hydrodynamic force and magnetic force on each particle, the velocity can be expressed as:

$$ {\varvec{{\rm u}}}_{\rm p}={\varvec{{\rm u}}}+{\varvec{{\rm u}}}_{\rm mag} $$
(5)

where \({\varvec{{\rm u}}}_{\rm mag}={\varvec{{\rm F}}}_{\rm mag}/6\pi \mu r_{\rm p}\) with r p representing the radius of the magnetic particles. The magnetic force on a single particle \({\varvec{{\rm F}}}_{\rm mag}\) can be expressed as

$$ {\varvec{{\rm F}}}_{\rm mag}=\frac{1}{2} V_{\rm p} \mu_{0} \nabla {\chi} {{\varvec{{\rm H}}}}^2 $$
(6)

where V p is the volume of a single particle, χ is the susceptibility of the mixed fluid, μ0 is the peameability of free space which has a constant value of 4π × 10− 7 NA− 2 and \({\varvec{{\rm H}}}\) is the strength of the applied magnetic field. In the concentration equation, the diffusion coefficient would be affected by magnetic force according to the reports by Blums [28, 29]. Compared with the value at zero field strength, the diffusion coefficient would be increased by two times by a field strength of 200 kA/m. The increase of diffusion coefficient was omitted in this work as the field strengths in our experiments are much lower than that reported by Blums. It is worth noting that there is a false numerical diffusion in the simulation even if the second-order upwind scheme was employed for coupling advection and diffusion. As a result, the magnitude of the magnetic force in the simulation is much smaller than the value in the experiment because of the lower concentration gradient caused by numerical diffusion. In the present work, the magnetic force is compensated by a correction factor to fit the simulation results with the experimental data. The correction factor is 1000 for ferrofluid core and 100 for ferrofluid-cladding case. Thus, the numerical results reported in this paper only provide a qualitative understanding of the underlying physics of magnetofludic spreading.

The forces acting on the fluid in magnetofluidic spreading \({\varvec{{\rm F}}}\) consist of gravitational force \({\varvec{{\rm F}}}_{\rm g}, \) interfacial force \({\varvec{{\rm F}}}_{\rm s}\) and magnetic force \({\varvec{{\rm F}}}_{\rm m}. \) In the numerical simulation, the gravitational force is negligible due to the small scale involved. In addition, interfacial force does not exist as the system consists of two miscible fluids. The magnetic force can be calculated by introducing the magnetic scalar potential ψ in the form of \({\varvec{{\rm H}}}=-\nabla\psi. \) For the numerical implementation with miscible fluids, the susceptibility is a function of the concentration of the magnetic particles \(\chi = \chi(C)\) [29]. A linear dependence of susceptibility on the concentration was assumed. According to a recent work by Wen et al., the magnetic potential equation can be expressed as:

$$ \nabla \cdot \left[ {\left( {1 + {\chi }} \right)\nabla \psi } \right] = 0. $$
(7)

The corresponding magnetic force in a uniform field is calculated by:

$$ {{\varvec{{\rm F}}}_{\rm m}} = - \frac{1}{2}{\mu _0}{\left| {{\varvec{{\rm H}}}} \right|^2}C_{\rm V}\nabla {\chi } $$
(8)

where C V is the volume concentration of the particles which can be represented by C V = C V0 C with the initial value of C V0 = 0.04. The non-dimensional volume concentration C is determined by Eq. (4). The boundary condition for the magnetic field is:

$$ {\varvec{{\rm H}}} \cdot \hat n = - \frac{{\partial \psi }}{{\partial n}},\qquad\forall {\varvec{{\rm x}}} \in \partial \Upomega .$$
(9)

The variation of density and viscosity as function of concentration C is determined as [30]:

$$ \rho = C\rho_{\rm m} + \left( {1 - C} \right){\rho_0} $$
(10)
$$ \eta = \eta_{\rm m}{{\rm e}^{R( {1 - C})}} $$
(11)

where \(\rho _{\rm m}\) and \(\rho_{\rm o}\) are the densities of ferrofluid and mineral oil, respectively. The viscosity parameter R can be expressed as \(R = \ln \left( {{\eta_{\rm o}}/{\eta_{\rm m}}} \right)\) with \(\eta_{\rm m}\) and \(\eta_{\rm o}\) representing the viscosities of ferrofluid and mineral oil, respectively.

The governing equations listed above are solved using finite volume method (FVM) on a Cartesian staggered grid. The SIMPLER algorithm was employed for coupling between the pressure and the velocity fields to improve convergent efficiency of the calculation [31]. The second-order upwind scheme with superbee limiter function is used for formulating the discretization equation involving convection and diffusion. The time integration is achieved by using the fully implicit scheme.

4 Results and discussions

In conventional hydrodynamic focusing, the relative width of the middle stream can be estimated as w = (1 + βκ)−1 with the viscosity ratio \(\beta=\eta_{\rm sheath}/\eta_{\rm core}\) and the flow rate ratio \(\kappa=Q_{\rm sheath}/Q_{\rm core}\) [32]. In the spreading experiment with ferrofluid core shown in Fig. 1b, the core width will increase under an applied uniform magnetic field, because of the pulling force (8) and the migration of magnetic particles due to the gradient in susceptibility between the ferrofluid and the mineral oil. In the spreading experiment with ferrofluid cladding shown in Fig. 1c, the core width decreases because of the spreading of the ferrofluid-cladding streams.

Figure 2a, b show the typical images of the fluid system at different applied magnetic flux densities for the two spreading cases. The results clearly show an entrance effect. Without an applied magnetic field, the core stream is focused to a constant width which is established at about two channel widths downstream from the entrance. To investigate the effect of magnetic field on the interface between the ferrofluid and the mineral oil, we used a customized image-processing program written in MATLAB to detect and plot the overlapping interfaces at different flux densities for both hydrodynamic (Fig. 2c) and magnetofluidic cases (Fig. 2d).

Fig. 2
figure 2

Magnetofluidic spreading in a microchannel. The flow rates of ferrofluid and mineral oil are fixed at 0.05 and 0.2 ml/h, respectively. a Ferrofluid core. b Ferrofluid cladding. c Overlapped interfaces of hydrodynamic spreading. d Overlapped interfaces of magnetofluidic spreading

Full size image

Without a magnetic field, the width of the core stream can be adjusted by hydrodynamic means such as the flow rate ratio or viscosity ratio. Figure 2c shows that as expected for low-Reynolds-number flow, the entrance is short and the width achieves a constant value near the channel inlet. The spreading of the liquid/liquid interface occurs along the entire flow system.

With a moderate magnetic field, the interface at the entrance remains unchanged (Fig. 2d). The width gradually changes along the flow direction to reach a constant value. The entrance is significantly longer than that of purely hydrodynamic spreading.

Figure 3a, b shows the experimental results for the spreading case. The spreading effects were characterized by the width fraction of the ferrofluid-core stream. As shown in Fig. 3a, the spreading effect is more apparent under larger magnetic flux value. Upon reaching a critical value of magnetic flux, instability occurred. As mentioned above, the experiments were carried out with fixed \({Q_{\rm FF}}\) and various \(Q_{\rm o}. \) The flow rate ratio is defined as the ratio of \(Q_{\rm o}\) to \(Q_{\rm FF}. \) For the spreading case, a larger magnetic flux is required to achieve spreading at a flow rate ratio. To characterize the spreading effect with flow rate ratio and applied magnetic flux, a contour map was provided for the normalized width of the core stream, Fig. 3b. The contour diagram can work as an operating map of magnetofluidic spreading assisting the design of applications such as sorting.

Fig. 3
figure 3

Magnetofludic spreading with ferrofluid core. a Normalized width of the core stream as function of flux density; b contour map of normalized width

Full size image

Experiments were also carried out to investigate the spreading phenomena with ferrofluid cladding. Similarly, the spreading effects were illustrated in terms of the width fraction of the mineral oil core stream. However, the width of the core stream decreases under a larger magnetic flux value as the magnetic nanoparticles diffuse toward the diamagnetic core stream. For increasing magnetic flux, the two cladding ferrofluid steams spread until they overlap. Figure 4a, b shows the experimental results for the ferrofluid-cladding case. The flow rate ratio was set to be the same as the ferrofluid-core case.

Fig. 4
figure 4

Magnetofludic spreading with ferrofluid cladding: a Normalized width of the core stream as function of flux density; b contour map of normalized width

Full size image

The numerical study focuses on the spreading phenomenon under an external magnetic field. We first investigated the concentration distribution inside the channel without the magnetic field. Neglecting gravitational force and interfacial tension force, the flow is thoroughly determined by flow rate and viscosity ratio between the two phases when the field strength is zero. The calculation was implemented with the flow rate ratio fixed at Q o/Q FF = 4. The typical simulation results of the velocity field and the corresponding scalar potential ψ of the magnetic field under a flux density of 2.87 mT are shown in Figs. 5 and 6 for the ferrofluid-core case and the cladding case, respectively. Part (a) of the figures shows the results of the middle plane, while part (b) depicts the results of the cross section at the end of the channel. The results show that under a relatively weak magnetic field, the flow is laminar and stable. The velocity flow field of the cross section clearly shows the existence of a secondary flow field that promotes advective mixing at the interface between the ferrofluid and the mineral oil.

Fig. 5
figure 5

Velocity field and scalar potential of spreading with ferrofluid core at 2.87 mT, Q o/Q FF = 4 (the magnitudes of the velocity vectors are not to scale, and the magnitude of velocity components in x–y plane is about two orders of magnitude higher than those of y–z plane): a x–y plane; b y–z plane

Full size image
Fig. 6
figure 6

Velocity field and scalar potential of spreading with ferrofluid cladding with 2.87 mT, Q o/Q FF = 4 (the magnitudes of the velocity vectors are not to scale, and the magnitude of velocity components in x–y plane is about two orders of magnitude higher than those of y–z plane): a x–y plane; b y–z plane

Full size image

The simulation was carried out with an external magnetic field ranging from 1.74 to 4.93 mT. The typical results of the depth-averaged concentration of magnetic particles are presented in Fig. 7a, b, respectively. Due to the secondary flow, the concentration distribution of the magnetic particles is not uniform along the channel depth. Since ferrofluid appears in the recorded images as a dark area with almost no gray scales, the simulated concentration needs to be averaged along the channel depth to achieve a realistic comparison with the experimental data.

The spreading effect can clearly be observed in the ferrofluid-core case (Fig. 7a). The additional drift of particles caused by magnetic force leads to an increase in apparent diffusion coefficient. At a higher flux density, the bulk magnetic force caused by the susceptibility gradient is large enough to induce instability or secondary flow at the interface of the ferrofluid and the oil. The concentration profile shows a typical broad base caused by the secondary flow (Fig. 7a). This secondary flow will be dominant at a higher flux density leading to complete mixing in the microchannel. A similar spreading behavior can be observed in the ferrofluid-cladding case (Fig. 7b). A stronger broadening at the interface at high flux density can also be observed. However, due to the dominant hydrodynamic transport at the center of the channel, the effect of the secondary flow in the ferrofluid-cladding case is not as strong as in the ferrofluid-core case.

Fig. 7
figure 7

Depth-averaged concentration across the channel width at different field strengths (Q o/Q FF = 4): a Magnetofluidic spreading with ferrofluid core; b magnetofluidic spreading with ferrofluid cladding

Full size image

Experimental and numerical results were compared based on the normalized width of the core stream at the corresponding field strength. Based on the depth-averaged concentration, the width of the core stream can be determined from the simulation. In the computational domain, the width of the core stream is evaluated at the end of the channel. Figure 8 compares the simulation results with the experimental results. Without an external magnetic field, the core flow is focused to a constant value as observed in the experiments. In the presence of the magnetic field, the drift of magnetic particles leading to improved apparent diffusion and mixing at the interface leads to the expansion of the ferrofluid core. The core width increases with increasing field strength. The same phenomenon was observed in both experimental and numerical simulation. The normalized width of the core stream in both experimental and numerical simulation are compared for the ferrofluid-core case and the ferrofluid-cladding case in Fig. 8a, b, respectively. Both experimentalal and numerical results show a similar trend in the relationship between the normalized width and the magnetic flux density. The simulation gives good insights into the underlying physics of the observed spreading phenomena. However, more effort is required for a quantitative description of magnetofluidic spreading, especially overcoming the problem of numerical diffusion.

Fig. 8
figure 8

Comparison between experimental and numerical results with Q o/Q FF = 4: a Magnetofluidic spreading with ferrofluid core; b magnetofluidic spreading with ferrofluid cladding

Full size image

5 Conclusions

The present paper investigates experimentally and numerically the phenomenon of magnetofluidic spreading of ferrofluid as core and cladding in a three-stream low system. The magnetofluidic spreading effect is investigated in the presence of an external uniform magnetic field. In the case of ferrofluid cladding, the width of the core stream was evaluated as a function of the applied magnetic flux density. As the field strength is increased, a stronger spreading effect can be observed. Due to the secondary flow, the ferrofluid-core configuration is more sensitive to the applied magnetic field. The numerical simulation shows that magnetofluidic spreading is caused by increased apparent diffusion due to drift of magnetic particles and secondary flow at the ferrofluid/oil interface. Both phenomena are caused by a susceptibility gradient or the concentration gradient of magnetic particles in the ferrofluid. Both experiment and simulation show a similar behavior of the flow system. However, the current numerical model can only provide a qualitative investigation of the phenomenon. Computational schemes to overcome numerical diffusion need to be considered to have qualitative results, because the interaction between magnetic field and the flow field is extremely sensitive to the gradient of particle concentration.