1 Introduction

Time-dependent fully developed rarefied gas flows driven by harmonically oscillating boundaries have attracted considerable attention mainly due to their applicability in a variety of microelectromechanical systems (MEMS) and particularly in resonating filters, sensors and actuators (Ho and Tai 1998; Veijola and Turowski 2001; Kandlikar 2006; Frangi et al. 2007). The research work includes shear driven flows and sound propagation in half space (Sharipov and Kalempa 2007), between parallel plates (Park et al. 2004; Hadjiconstantinou 2005; Sharipov and Kalempa 2008; Kalempa and Sharipov 2009; Manela and Pogorelyuk 2014) and in rectangular cavities (Wu et al. 2014), as well as in nonplanar geometries (Emerson et al. 2007). The accurate computation of the damping forces in the narrow gaps between moving microstructures is of major importance in order to control the resolution and sensitivity of the signal and to enhance the acoustic transduction or even to achieve “acoustic cloaking” (Manela and Pogorelyuk 2014).

The flow parameters characterizing oscillatory rarefied gas flows include the level of gas rarefaction and the oscillation frequency. To have reliable solutions in the whole range of gas rarefaction with arbitrary oscillation frequencies, a kinetic type approach must be applied (Cercignani 1988). Since the direct solution of the Boltzmann equation (BE) is computationally expensive, the flow is modeled stochastically via the direct simulation Monte Carlo (DSMC) method (Bird 1994) or deterministically by introducing kinetic model equations (Βhatnagar et al. 1954; Holway 1966; Shakhov 1968), which are numerically solved in an efficient and accurate manner (Sharipov 2016). Both approaches have been successfully applied. More specifically, the DSMC approach is applied in (Park et al. 2004; Hadjiconstantinou 2005; Manela and Pogorelyuk 2014; Emerson et al. 2007) and the linearized Bhatnagar–Gross–Krook (BGK) model in (Frangi et al. 2007; Sharipov and Kalempa 2007; Sharipov and Kalempa 2008; Kalempa and Sharipov 2009) (in (Wu et al. 2014), the linearized BE is solved). In the latter approach, the velocity amplitude of the oscillating plate is assumed to be adequately small so that the governing equations can be linearized. No restriction is applied to the oscillation frequency which may be arbitrary. Also, in most cases first- and second-order slip results are reported validating the kinetic solutions at the hydrodynamic limit.

The corresponding time-dependent fully developed rarefied gas flow driven by harmonically oscillating or pulsating pressure, which may be realized by a periodically moving piston or membrane, has received much less attention. The available work is very limited, and simulations have been presented only in the slip regime in an effort to model pneumatic actuators for pressure sensors (Caen and Colin 1992; Colin et al. 1998) and boundary layer flow controllers in order to improve vehicle stability (Batikh et al. 2008; Wang et al. 2014). This Poiseuille-type oscillatory flow may be also introduced in other applications related to fluidic resonators and oscillators including microcooling, measuring devices, microseparators and micropropulsion.

Of course, in the hydrodynamic limit, this is a classical problem and may be analytically solved by applying the unsteady Stokes equation subject to no-slip boundary conditions (oscillatory Poiseuille flow in channels and pipes) (Schlichting and Gersten 2017; White 1974; Zamir 2000). In spite of its simplicity however, interesting findings for the velocity field in terms of the oscillation speed have been reported. For small oscillation frequencies, the velocity distribution has the same phase as the pressure gradient, while for large oscillation frequencies the velocity lags the pressure gradient by 90°. Furthermore, in the latter case the flow consists of the inviscid piston flow core layer and the viscous Stokes wall layer. In addition, the time average of the velocity square exhibits its maximum within the Stokes layer and not, as expected, in the center of the core, which is well known as the “Richardson annular effect” (Schlichting and Gersten 2017; White 1974; Zamir 2000). Oscillating and pulsating pressure gradient flows, due to their theoretical and technological interest, remain an active area of research even in the hydrodynamic regime using continuum-based flow models (Tsangaris and Vlachakis 2003; Majdalani 2008; Blythman et al. 2016). However, it is clear that the continuum approach is valid under the provisions that both the mean free path and time are much smaller than the distance between the plates and the reference oscillating time, respectively. If either of these restrictions is violated, the problem must be tackled via kinetic theory [e.g., in low-pressure chemical vapor deposition, the Richardson annular effect may cause anomalous solid formation (Abreu et al. 1994)].

In this context, the present work is devoted to the kinetic solution of the rarefied gas flow in a circular tube due to harmonically oscillating pressure gradient imposed in the longitudinal direction. The periodic flow is investigated by numerically solving the time-dependent linearized Bhatnagar–Gross–Krook (BGK) kinetic equation subject to diffuse boundary conditions. Detailed results of the amplitude and the phase of the bulk velocity and the flow rate are provided in terms of the reference gas rarefaction parameter and the ratio of the intermolecular collision frequency over the externally imposed oscillation frequency of the pressure gradient. The time evolution of the macroscopic quantities over an oscillation period is presented. The limiting solutions in the free molecular and hydrodynamic limits for very low and high oscillation frequencies are also discussed.

2 Flow configuration

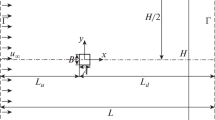
Consider the isothermal flow of a monatomic rarefied gas through an infinite long circular tube of radius \(R\). Let \(z^{\prime}\) be the coordinate along the tube axis and \(r^{\prime} \in \left[ {0,R} \right]\) the radial distance from the center. The flow is caused by an externally imposed oscillatory pressure gradient of the form

$$\frac{{{\text{d}}\tilde{P}\left( {z^{\prime},t^{\prime}} \right)}}{{{\text{d}}z^{\prime}}} = \frac{{{\text{d}}P\left( {z^{\prime}} \right)}}{{{\text{d}}z^{\prime}}}\cos \left( {\omega t^{\prime}} \right) = {\mathbb{R}}\left[ {\frac{{{\text{d}}P\left( {z^{\prime}} \right)}}{{{\text{d}}z^{\prime}}}\exp \left( { - i\omega t^{\prime}} \right)} \right],$$
(1)

where \({\mathbb{R}}\) denotes the real part of a complex expression, \(i = \sqrt { - 1}\), \(t^{\prime}\) is the time independent variable, \({\text{d}}P\left( {z^{\prime}} \right)/{\text{d}}z^{\prime}\) is the amplitude of the oscillating pressure gradient and \(\omega\) is the oscillation (cyclic) frequency. The flow is assumed fully developed, and therefore, the pressure distribution \(\tilde{P}\left( {z^{\prime},t^{\prime}} \right)\) is independent of \(r^{\prime}\), i.e., spatially varies only in the flow direction. The oscillatory pressure gradient yields an unsteady gas flow in the \(z^{\prime} -\) direction, which depends harmonically on time, and it is characterized by its bulk velocity given by

$$\tilde{U}\left( {t^{\prime},r^{\prime}} \right) = {\mathbb{R}}\left[ {U\left( {r^{\prime}} \right)\exp \left( { - i\omega t^{\prime}} \right)} \right],$$
(2)

where \(U\left( {r^{\prime}} \right)\) is a complex function completely determining the oscillatory pressure driven flow. For \(\omega = 0\), the well-known stationary cylindrical Poiseuille flow is deduced. It is clear from Eqs. (1) and (2) that in general the pressure gradient and velocity are not in phase with each other.

The flow parameters defining the problem are the gas rarefaction parameter \(\delta\) and the dimensionless oscillation frequency \(\theta\) (Sharipov and Kalempa 2008). The first one is the same as in steady-state configurations, and it is given by

$$\delta = \frac{PR}{\mu \upsilon },$$
(3)

where \(\mu\) is the gas viscosity at some reference temperature \(T\) and \(\upsilon = \sqrt {2R_{\text{g}} T}\) is the most probable molecular speed (\(R_{\text{g}} = k_{\text{B}} /m\), with \(k_{\text{B}}\) denoting the Boltzmann constant and \(m\) the molecular mass, is the gas constant). The rarefaction parameter is proportional to the inverse Knudsen number. The second one is the ratio of the intermolecular collision frequency \(\nu = P/\mu\), over the oscillation frequency \(\omega\):

$$\theta = \frac{P}{\mu \omega }.$$
(4)

Hence, small and large values of \(\theta\) correspond to high- and low-pressure gradient oscillation, respectively. The two parameters are independent of each other.

At this point, it may be useful to point out that the Strouhal number (also known as the ballistic Stokes number), which is commonly applied in oscillatory flows, is related to the \(\delta\) and \(\theta\) parameters as follows: \({\text{St}} = \left( {\omega R} \right)/\upsilon = \delta /\theta\). Also, it is readily found that the Stokes number \(\beta\) (or the kinetic Reynolds number \(\beta^{2}\)), which is a measure of viscous versus unsteady effects in oscillatory flow, may be written as \(\beta = R\sqrt {\omega \rho /\mu } = \delta /\sqrt {2\theta }\). For the purposes of the present work however, it is more convenient parametrizing the problem in terms of \(\delta\) and \(\theta\), instead of replacing both of them with one of these classical fluid mechanics numbers, because it is easier to uncouple and separately investigate the effects due to gas rarefaction and oscillation frequencies. Also, the limiting solutions are identified more clearly.

Here, the flow is solved in the whole range of the two parameters, which may vary from zero to infinity. The flow is in the hydrodynamic and slip regimes when both \(\delta \gg 1\) and \(\theta \gg 1\), i.e., when both the equivalent mean free path is small compared to the tube radius \(R\) and the collision frequency is much higher than the oscillation frequency \(\omega\) (Sharipov and Kalempa 2008). In these regimes, the solution is based on the unsteady Stokes equation with either no-slip or slip boundary conditions. In all other cases including the limiting regimes for \(\delta \ll 1\) (free molecular regime) and \(\theta \ll 1\) (high-speed oscillation regime), the solution is based on the linearized BGK kinetic model equation.

Next, it is convenient to introduce the dimensionless independent variables

$$x = x^{\prime}/R,z = z^{\prime}/R\,{\text{and}}\,t = t^{\prime}\omega ,$$
(5)

as well as the dimensionless amplitude of the local pressure gradient defined as

$$X_{\text{P}} = \frac{R}{P}\frac{{{\text{d}}P}}{{{\text{d}}z^{\prime}}}$$
(6)

with the assumption of \(X_{\text{P}} < < 1\). This assumption is typical in fully developed flows (also in steady-state setups), in order to permit the linearization of the governing kinetic equation (Sharipov 2016).

The dimensionless complex velocity distribution

$$u\left( r \right) = \frac{{U\left( {r^{\prime}} \right)}}{{X_{\text{P}} \upsilon }} = u_{Re} \left( r \right) + iu_{\text{Im}} \left( r \right) = u_{A} \exp \left( {iu_{P} } \right)$$
(7)

is also introduced. The subscripts Re and \(\text{Im}\) denote the real and imaginary parts, while the subscripts \(A\) and \(P\) denote the amplitude and the phase of the complex velocity. Then, the dimensionless time-dependent velocity distribution is accordingly defined as

$$\begin{aligned} \tilde{u}\left( {r,t} \right) & = \frac{{\tilde{U}\left( {r^{\prime},t^{\prime}} \right)}}{{X_{P} \upsilon }} = {\mathbb{R}}\left[ {u\left( r \right)\exp \left( { - it} \right)} \right] \\ & = {\mathbb{R}}\left[ {u_{A} \left( r \right)\exp \left[ {i\left( {u_{P} \left( r \right) - t} \right)} \right]} \right] = u_{A} \left( r \right)\cos \left[ {t - u_{P} \left( r \right)} \right] \\ \end{aligned}$$
(8)

It is evident that both \(u_{A} \left( r \right)\) and \(u_{P} \left( r \right)\) are of main importance in determining the flow behavior and they will be computed in terms of the two main parameters, \(\delta\) and \(\theta\), fully defining the flow.

In addition, the mass flow rate is also of major practical importance. It is defined as

$$\tilde{\dot{M}}\left( {t^{\prime}} \right) = {\mathbb{R}}\left[ {\dot{M}\exp \left( { - i\omega t^{\prime}} \right)} \right]$$
(9)

where

$$\dot{M} = 2\pi \rho \int\limits_{0}^{R} {U\left( {r^{\prime}} \right)r^{\prime}{\text{d}}r^{\prime}}$$
(10)

with \(\rho\) denoting the mass density. Introducing the dimensionless quantities defined in Eqs. (6–8) in Eq. (10) and implementing the equation of state \(P = \rho \upsilon^{2} /2\) result in \(\dot{M} = \pi R^{2} PX_{\text{P}} G/\upsilon\), where

$$G = 4\int\limits_{0}^{1} {u\left( r \right)r\,{\text{d}}r} .$$
(11)

The dimensionless flow rate \(G\) may be written in complex notation as

$$G\left( {\delta ,\theta } \right) = G_{Re} \left( {\delta ,\theta } \right) + iG_{\text{Im}} \left( {\delta ,\theta } \right) = G_{A} \left( {\delta ,\theta } \right)\exp \left[ {iG_{\text{P}} \left( {\delta ,\theta } \right)} \right],$$
(12)

where its real \(G_{Re}\) and imaginary \(G_{\text{Im}}\) parts, as well as its amplitude \(G_{\text{A}}\) and phase \(G_{\text{P}}\), may be computed by integrating the corresponding velocity distributions in Eq. (7). The time-dependent form of the dimensionless flow rate is given by

$$\tilde{G}\left( {t,\delta ,\theta } \right) = {\mathbb{R}}\left[ {G\exp \left( { - it} \right)} \right] = {\mathbb{R}}\left[ {G_{\text{A}} \exp \left[ {i\left( {G_{P} - t} \right)} \right]} \right] = G_{\text{A}} \left( {\delta ,\theta } \right)\cos \left[ {t - G_{\text{P}} \left( {\delta ,\theta } \right)} \right].$$
(13)

It is expected that as \(\omega \to 0\) (or \(\theta \to \infty\)), the imaginary parts of the macroscopic quantities are gradually diminishing and the solution tends toward the steady-state one.

3 Kinetic formulation and numerical scheme

For arbitrary values of the parameters \(\delta\) and \(\theta\), the flow may be simulated at the kinetic level by the time-dependent BGK kinetic model equation (Bird 1994; Sharipov 2016), which for the present axisymmetric \(\left( {r^{\prime},z^{\prime}} \right)\) setup may be written as (Sharipov 2016; Pantazis and Valougeorgis 2013)

$$\frac{{\partial \tilde{f}}}{{\partial t^{\prime}}} + \xi_{r} \frac{{\partial \tilde{f}}}{{\partial r^{\prime}}} - \frac{{\xi_{\varphi } }}{{r^{\prime}}}\frac{{\partial \tilde{f}}}{\partial \varphi } + \xi_{z} \frac{{\partial \tilde{f}}}{{\partial z^{\prime}}} = \frac{P}{\mu }\left( {f^{M} - \tilde{f}} \right).$$
(14)

Here, \(\tilde{f} = \tilde{f}\left( {t^{\prime},r^{\prime},{\varvec{\upxi}}} \right)\) is the unknown distribution function, \({\varvec{\upxi}} = \left( {\xi_{r} ,\xi_{\varphi } ,\xi_{z} } \right)\) is the molecular velocity vector, \(\varphi \in \left( {0,2\pi } \right)\) is the corresponding angle in the \(r^{\prime} - \varphi\) plane, \(P/\mu\) is the collision frequency, and

$$f^{M} = n\left( {\frac{m}{2\pi kT}} \right)^{3/2} \exp \left[ { - {{m\left[ {{\varvec{\upxi}} - \tilde{U}\left( {t^{\prime},r^{\prime}} \right)} \right]^{2} } \mathord{\left/ {\vphantom {{m\left[ {{\varvec{\upxi}} - \tilde{U}\left( {t^{\prime},r^{\prime}} \right)} \right]^{2} } {\left( {2kT} \right)}}} \right. \kern-0pt} {\left( {2kT} \right)}}} \right]$$
(15)

is the local Maxwellian distribution. Due to the assumption of isothermal fully developed flow, the temperature \(T\) is constant and the number density \(n\) varies only in \(z^{\prime} -\) direction. Also, the macroscopic velocity \(\tilde{U}\left( {t^{\prime},r^{\prime}} \right)\) is defined by Eq. (2) and may be obtained by the first moment of the distribution function according to

$$\tilde{U}\left( {t^{\prime},r^{\prime}} \right) = \frac{1}{n}\int {\xi_{z} } \tilde{f}\left( {t^{\prime},r^{\prime},{\varvec{\upxi}}} \right){\text{d}}{\varvec{\upxi}}.$$
(16)

Due to the condition of very small local pressure gradient (\(X_{P} \ll 1\)), the unknown distribution function is linearized as

$$\tilde{f}\left( {t^{\prime},r^{\prime},{\varvec{\upxi}}} \right) = f_{0} \left[ {1 + X_{\text{P}} \tilde{h}\left( {t,r,\varvec{c}} \right) + X_{\text{P}} z\exp \left( { - {\text{it}}} \right)} \right] ,$$
(17)

where \({\mathbf{c}} = {\varvec{\upxi}}/\upsilon ,f_{0} = \frac{n}{{\pi^{3/2} \upsilon^{3} }}\exp \left[ { - c^{2} } \right]\) is the absolute Maxwellian and \(\tilde{h}\left( {t,r,\varvec{c}} \right)\) is unknown perturbed distribution function. Substituting expression (17) into Eq. (14) and introducing the dimensionless variables as defined in Eqs. (5) and (6) yields the time-dependent linearized BGK kinetic model equation

$$\frac{\delta }{\theta }\frac{{\partial \tilde{h}}}{\partial t} + c_{r} \frac{{\partial \tilde{h}}}{\partial r} - \frac{{c_{\varphi } }}{r}\frac{{\partial \tilde{h}}}{\partial \varphi } + c_{z} e^{{ - {\text{it}}}} = \delta \left( {2c_{z} {\mathbb{R}}\left( {\tilde{u}} \right) - \tilde{h}} \right).$$
(18)

Here, \(\delta\) and \(\theta\) are defined by Eqs. (3) and (4), respectively, while \(\tilde{u}\left( {r,t} \right)\) is the dimensionless time-dependent velocity distribution given in Eq. (8).

Next, it is convenient to introduce the complex distribution function \(h\left( {r,\varvec{c}} \right)\) so that

$$\tilde{h}\left( {t,r,\varvec{c}} \right) = {\mathbb{R}}\left[ {h\left( {r,\varvec{c}} \right)\exp \left( { - {\text{it}}} \right)} \right].$$
(19)

Also, the molecular velocity vector \({\mathbf{c}} = \left( {c_{r} ,c_{\varphi } ,c_{z} } \right)\) is transformed as \({\mathbf{c}} = \left( {\zeta ,\varphi ,c_{z} } \right)\), where \(c_{r} = \zeta \cos \varphi\) and \(c_{\varphi } = \zeta \sin \varphi\). Then, Eq. (18) is rewritten in terms of \(h\) as

$$\zeta \cos \varphi \frac{\partial h}{\partial r} - \frac{\zeta \sin \varphi }{r}\frac{\partial h}{\partial \varphi } + h\left( {\delta - \frac{\delta }{\theta }i} \right) + c_{z} = 2\delta c_{z} u ,$$
(20)

where the macroscopic velocity is given by

$$u\left( r \right) = \frac{1}{\pi }\int\limits_{ - \infty }^{\infty } {\int\limits_{0}^{2\pi } {\int\limits_{0}^{\infty } {c_{z} he^{{ - c^{2} }} } } } {\text{d}}\zeta {\text{d}}\varphi {\text{d}}c_{z} .$$
(21)

At this stage, the \(z -\) component of the molecular velocity vector may be eliminated by applying the so-called projection procedure and introducing the reduced distribution function

$$Y\left( {r,\zeta ,\varphi } \right) = \frac{1}{\pi }\int\limits_{ - \infty }^{\infty } {h\left( {r,\zeta ,\varphi ,c_{\text{z}} } \right)\exp \left[ { - c_{\text{z}}^{2} } \right]{\text{d}}c_{z} } .$$
(22)

Equation (20) is multiplied by \(c_{\text{z}} \exp \left( { - c_{\text{z}}^{2} } \right)/\sqrt \pi\), and the resulting equation is integrated over \(c_{\text{z}}\) to deduce

$$\zeta \cos \varphi \frac{\partial Y}{\partial r} - \frac{\zeta \sin \varphi }{r}\frac{\partial Y}{\partial \varphi } + \left( {\delta - i\frac{\delta }{\theta }} \right)Y = \delta u + \frac{1}{2} ,$$
(23)

where \(u\left( r \right)\) is defined by Eq. (7) and it is computed from the reduced distribution function according to

$$u\left( r \right) = \frac{1}{\pi }\int\limits_{0}^{2\pi } {\int\limits_{0}^{\infty } Y } e^{{ - \zeta^{2} }} \zeta {\text{d}}\zeta {\text{d}}\varphi .$$
(24)

It is noted that \(Y = Y_{Re} + iY_{\text{Im}}\) is complex and obviously and the same applies for \(u\) (see Eq. (7)). Equation (23) is the governing kinetic equation, and it is valid in the whole range of \(\delta\) and \(\theta\).

Turning now to the boundary conditions, it is noted that purely diffuse scattering is assumed at the wall, i.e., \(f^{ + } = f_{w}^{M}\), where the superscript \(\left( + \right)\) denotes particles departing from the wall and \(f_{w}^{M}\) is the Maxwellian distribution defined by the wall conditions. Based on the above and following the linearization and projection procedures, it is readily deduced that the wall boundary (\(r = 1\)) is given by

$$Y\left( {1,\zeta ,\varphi } \right) = 0,\pi /2 < \varphi < 3\pi /2.$$
(25)

At the symmetry axis (\(r = 0\)), molecules are reflected specularly, i.e.,

$$Y\left( {0,\zeta ,\varphi } \right) = Y\left( {0,\zeta ,\varphi - \pi } \right),0 < \varphi < \pi /2,3\pi /2 < \varphi < 2\pi .$$
(26)

The flow setup is now properly defined by Eq. (23) with the associated condition (24) subject to boundary conditions (25) and (26). For each pair of input parameters \(\delta\) and \(\theta\), the complex velocity \(u\left( r \right)\) and the corresponding complex flow rate \(G\), given by Eq. (11), are computed.

The numerical solution is deterministic. The discretization in the molecular velocity space is performed using the discrete velocity method. The continuum spectrum \(\zeta \in \left[ {0,\infty } \right)\) is substituted by a discrete set \(\zeta_{m} ,m = 1,2, \ldots ,M\), which is taken to be the roots of the Legendre polynomial of order \(M\), accordingly mapped from \(\left[ { - 1,1} \right]\) to \(\left[ {0,\infty } \right)\). Also, a set of discrete angles \(\varphi_{n} ,n = 1,2, \ldots ,N\), equally spaced in \(\left[ {0,2\pi } \right]\), is defined. The discretization in the physical space is based on a second-order central difference scheme by dividing the distance \(r \in \left[ {0,1} \right]\) into \(L\) segments. The discretized equations are solved in an iterative manner. The iteration map is concluded when the following criteria are fulfilled:

$$\left| {u_{Re,i}^{{\left( {k + 1} \right)}} - u_{Re,i}^{\left( k \right)} } \right| < \varepsilon \,{\text{and}}\,\left| {u_{{\text{Im} ,i}}^{{\left( {k + 1} \right)}} - u_{{\text{Im} ,i}}^{\left( k \right)} } \right| < \varepsilon ,\quad i = 1,2, \ldots ,L + 1.$$
(27)

Here, the superscript \(k\) denotes the iteration index, \(u_{Re,i}\) and \(u_{{\text{Im} ,i}}\) are the real and imaginary part of macroscopic velocity, respectively, at each node \(i\), and \(\varepsilon\) is the tolerance parameter. This numerical scheme has been extensively applied in steady-state and time-dependent flow configurations with considerable success (Pantazis and Valougeorgis 2013; Lihnaropoulos and Valougeorgis 2011; Buchina and Valougeorgis 2012). In general, the number of iterations required for convergence is increased as either \(\theta\) or \(\delta\) are increased. The most computationally intensive cases are when both flow parameters are large and the flow is in the slip and hydrodynamic regimes. The numerical parameters have been gradually refined to ensure grid independent results up to at least three significant figures.

Closing this section, it is interesting to comment on the behavior of Eq. (23) at limiting values of \(\theta\) or \(\delta\). As \(\theta \to \infty\) (\(\omega = 0\)) and \(\delta < < \theta\) (finite values of \(\delta\)), Eq. (23) is reduced to the one describing the steady-state cylindrical Poiseuille rarefied gas flow at the corresponding \(\delta\). In the specific case of \(\delta = 0\) with \(\theta > 0\), the kinetic equation for steady-state flow at the free molecular limit is recovered. At the other end, as \(\theta \to 0\) (\(\omega \to \infty\)), Eq. (23) yields \(Y \to 0\), i.e., the solution tends to vanish at very high frequencies due to fluid inertia. It is expected this behavior at the limiting conditions to be also present in the numerical solution.

4 Hydrodynamic and slip regimes

At the hydrodynamic and slip regimes, the oscillatory fully developed flow is defined by the \(z -\) momentum equation (White 1974; Zamir 2000)

$$\rho \frac{{\partial \tilde{U}^{\left( j \right)} }}{{\partial t^{'} }} = - \frac{{{\text{d}}\tilde{P}}}{{{\text{d}}z^{'} }} + \mu \left( {\frac{{\partial^{2} \tilde{U}^{\left( j \right)} }}{{\partial r^{'2} }} + \frac{1}{{r^{'} }}\frac{{\partial \tilde{U}^{\left( j \right)} }}{{\partial r^{'} }}} \right),$$
(28)

where the pressure gradient \({\text{d}}\tilde{P}\left( {z^{\prime},t^{\prime}} \right)/{\text{d}}z^{\prime}\) is defined by Eq. (1) and the bulk velocity \(\tilde{U}^{\left( j \right)} \left( {t^{\prime},r^{\prime}} \right)\), with \(j = H,S\), denoting the hydrodynamic and slip solutions, is defined by Eq. (2).

Introducing the dimensionless quantities (5–8), along with the definitions (3) and (4), Eq. (28) is rewritten in dimensionless form in terms of the present notation as

$$\frac{{\partial^{2} u^{\left( j \right)} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u^{\left( j \right)} }}{\partial r} + 2i\frac{{\delta^{2} }}{\theta }u^{\left( j \right)} = - \delta .$$
(29)

Here, \(u^{\left( j \right)} = u^{\left( j \right)} \left( r \right)\) is the complex hydrodynamic or slip velocity, and it may be written in the form of Eq. (7), as \(u^{\left( j \right)} \left( r \right) = u_{Re}^{\left( j \right)} \left( r \right) + iu_{\text{Im}}^{\left( j \right)} \left( r \right) = u_{\text{A}}^{\left( j \right)} \left( r \right)\exp \left[ {iu_{\text{P}}^{\left( j \right)} \left( r \right)} \right]\), \(j = H,S\). Then, integrating the velocity distribution over the cross section, according to Eq. (11), the complex flow rate, \(G^{\left( j \right)} = G_{\text{Re}}^{\left( j \right)} + iG_{\text{Im}}^{\left( j \right)} = G_{A}^{\left( j \right)} \exp \left( {iG_{P}^{\left( j \right)} } \right)\), \(j = H,S\), is recovered. Equation (29) is valid in the hydrodynamic and slip regimes, and in practice, it may be applied for large values of \(\delta\) and \(\theta\).

In the hydrodynamic regime (\(j = H\)), the associated boundary conditions include the axi-symmetry condition at \(r^{\prime} = 0\) and the no-slip condition at \(r^{\prime} = R\), written as

$$\left. {\frac{{{\text{d}}u^{\left( H \right)} \left( r \right)}}{{{\text{d}}r}}} \right|_{r = 0} = 0,\quad u\left( 1 \right) = 0.$$
(30)

Equation (29) subject to boundary conditions (30) is analytically solved to yield the velocity distribution and the flow rate in the hydrodynamic regime (White 1974; Zamir 2000):

$$u^{\left( H \right)} (r) = i\frac{\theta }{2\delta }\left[ {1 - \frac{{J_{0} \left( {r\sqrt {2i} \delta /\sqrt \theta } \right)}}{{J_{0} \left( {\sqrt {2i} \delta /\sqrt \theta } \right)}}} \right],$$
(31)
$$G^{\left( H \right)} = i\frac{\theta }{\delta }\left[ {1 - 2\frac{\sqrt \theta }{{\sqrt {2i} \delta }}\frac{{J_{1} \left( {\sqrt {2i} \delta /\sqrt \theta } \right)}}{{J_{0} \left( {\sqrt {2i} \delta /\sqrt \theta } \right)}}} \right].$$
(32)

Here, \(J_{0}\) and \(J_{1}\) are the Bessel functions of the first kind of zero and first order, respectively.

In the slip regime (\(j = S\)), the axi-symmetry boundary condition at \(r^{\prime} = 0\) remains the same, while at the wall the slip boundary condition is introduced (Sharipov 2016):

$$\left. {\frac{{{\text{d}}u^{\left( S \right)} \left( r \right)}}{{{\text{d}}r}}} \right|_{r = 0} = 0,\quad u^{\left( S \right)} \left( 1 \right) = - \frac{{\sigma_{\text{P}} }}{\delta }\left. {\frac{{{\text{d}}u^{\left( S \right)} }}{{{\text{d}}r}}} \right|_{r = 1} .$$
(33)

The viscous slip coefficient \(\sigma_{P} = 1.016\) is known, and it is computed by solving the corresponding half-space viscous slip flow setup (or Kramers problem) based on the linearized BGK model equation (Sharipov 2016). Equation (29) subject to boundary conditions (33) is analytically solved to yield the velocity distribution and flow rate in the slip regime:

$$u^{\left( S \right)} \left( r \right) = i\frac{\theta }{2\delta }\left[ {1 - \frac{{J_{0} \left( {\sqrt {2i} \frac{\delta }{\sqrt \theta }r} \right)}}{{J_{0} \left( {\sqrt {2i} \frac{\delta }{\sqrt \theta }} \right) - \sqrt {2i} \frac{{\sigma_{P} }}{\sqrt \theta }J_{1} \left( {\sqrt {2i} \frac{\delta }{\sqrt \theta }} \right)}}} \right],$$
(34)
$$G^{\left( S \right)} = i\frac{\theta }{\delta }\left[ {1 - 2\frac{\sqrt \theta }{{\sqrt {2i} \delta }}\frac{{J_{1} \left( {\sqrt {2i} \frac{\delta }{\sqrt \theta }} \right)}}{{J_{0} \left( {\sqrt {2i} \frac{\delta }{\sqrt \theta }} \right) - \sqrt {2i} \frac{{\sigma_{P} }}{\sqrt \theta }J_{1} \left( {\sqrt {2i} \frac{\delta }{\sqrt \theta }} \right)}}} \right].$$
(35)

These analytical solutions are implemented to check the accuracy of the numerical scheme at large values of \(\delta\) and \(\theta\).

In both the hydrodynamic and slip regimes, two limiting solutions may be considered based on the quantity \(\delta /\sqrt \theta\), which is proportional to the ballistic Stokes number and measures viscous versus unsteady effects in oscillatory flows. The analysis is applied only in the flow rate expressions. First, assuming \(1 \ll \delta \ll \sqrt \theta\), i.e., that the oscillation frequency is very slow (\(\omega \to 0\) or \(\theta \to \infty\)), Eqs. (32) and (35) are manipulated by expanding the Bessel functions for small arguments \(\delta /\sqrt \theta \ll 1\). By keeping only the main terms, the well-known flow rates of the stationary cylindrical Poiseuille flow subject to constant pressure gradient are recovered in the hydrodynamic and slip regimes (Sharipov 2016):

$$G^{\left( H \right)} = \frac{\delta }{4},G^{\left( S \right)} = \frac{\delta }{4} + \sigma_{\text{P}} .$$
(36)

Secondly, assuming \(\delta \gg \sqrt \theta \gg 1\), the Bessel functions in Eqs. (32) and (35) are now expanded for large arguments \(\delta /\sqrt \theta > > 1\) and, following some manipulation, the following expressions are obtained:

$$G^{\left( H \right)} = \frac{{\theta^{3/2} }}{{\delta^{2} }} + i\frac{\theta }{\delta }\left( {1 - \frac{\sqrt \theta }{\delta }} \right),$$
(37)
$$G^{\left( S \right)} = \frac{{\theta^{3/2} }}{{\delta^{2} }} + i\frac{\theta }{\delta }\left[ {1 - \frac{\sqrt \theta }{\delta }\left( {1 + \frac{{2\sigma_{P} }}{\sqrt \theta }} \right)^{ - 1} } \right].$$
(38)

The closed-form expressions (36–38) are also applied to examine the accuracy of the kinetic solutions at these limits provided that the corresponding restrictions in terms of \(\delta\) and \(\theta\) are fulfilled.

5 Results and discussion

The fully developed rarefied gas flow in a cylindrical tube due to an imposed oscillatory pressure gradient has been simulated in a wide range of the gas rarefaction and oscillation parameters. The computed dimensionless complex velocity distributions and flow rates are based on the kinetic formulation, while some complimentary analytical results in the slip regime are also reported. The results include the amplitude and the phase angle, as well as the periodic time evolution of the macroscopic quantities.

In Table 1, the flow rate amplitude \(G_{A} \left( {\delta ,\theta } \right)\) is presented in terms of the gas rarefaction \(\delta \in \left[ {10^{ - 4} ,10^{2} } \right]\) and the oscillation parameter \(\theta = \left[ {0.1,1,10,50,10^{2} } \right]\). In addition, the flow rate amplitude in the slip regime \(G_{A}^{\left( S \right)} \left( {\delta ,\theta } \right)\), based on the analytical expression (35), is provided in the seventh and eighth column of Table 1 for \(\theta = 50\) and \(\theta = 10^{2}\), respectively, and for \(\delta \ge 1\). In the last column of Table 1, the well-known flow rates of the steady-state cylindrical Poiseuille flow with constant pressure gradient (\(\theta \to \infty\)), denoted by \(G_{SS} \left( \delta \right)\), for \(\delta \le 10\) are also included (Sharipov 2016).

Table 1 Flow rate amplitude \(G_{\text{A}} \left( {\delta ,\theta } \right)\) in terms of gas rarefaction parameter \(\delta\) and oscillation parameter \(\theta\)
Full size table

By comparing \(G_{A} \left( {\delta ,\theta } \right)\) with the corresponding \(G_{A}^{\left( S \right)} \left( {\delta ,\theta } \right)\), it is readily seen that the agreement is, in general, good and more important that it is improved as both \(\delta\) and \(\theta\) are increased. On the contrary, even for these two relatively large values of \(\theta\), the discrepancies are gradually increased as \(\delta\) is decreased. This comparison demonstrates the efficiency of the kinetic results to properly recover the analytical slip solution, as well as the range of validity of the slip solution depending on the required accuracy. Next, the values \(G_{A} \left( {\delta ,\theta } \right)\) for the large oscillation parameter \(\theta = 10^{2}\) (or very small oscillation frequency \(\omega\)) are compared to the corresponding steady-state flow rates \(G_{\text{SS}} \left( \delta \right)\). It is seen that the agreement is very good in small and intermediate values of \(\delta\) (free molecular and part of transition regimes), and then, as \(\delta\) is further increased, the discrepancies also increase. It is evident that in order to recover the steady-state solution, it requires: a) the oscillation parameter to be large (which it is, since \(\theta = 10^{2}\)) and b) \(\delta < < \theta\) (which is not, when \(\delta > 10\)). This is in agreement with the reported behavior of kinetic Eq. (33) as \(\theta \to \infty\) approaching the stationary solution (last paragraph in Sect. 3), as well as with the analytical results in the hydrodynamic and slip regimes, where it has been shown that the steady-state solution is recovered as \(\theta \to \infty\), with \(\delta \ll \sqrt \theta\) (Sect. 4). In general, steady-state conditions may be reached faster as the flow becomes more rarefied (or as \(\delta\) is decreased) provided of course that the oscillation parameter is adequately large (\(\omega\) adequately small).

The discussion in Table 1 is continued by analyzing the behavior of the flow rate amplitude \(G_{\text{A}} \left( {\delta ,\theta } \right)\) in the whole range of \(\delta\) and \(\theta\). For any given \(\delta\), \(G_{\text{A}} \left( {\delta ,\theta } \right)\) is monotonically increased as \(\theta\) is increased, with \(G_{\text{A}} \left( {\delta ,\theta } \right)\) being always less than the corresponding stationary solution \(G_{\text{SS}} \left( \delta \right)\). The dependency of \(G_{\text{A}} \left( {\delta ,\theta } \right)\) on \(\delta\) is more complex. For \(\theta \le 1\), as \(\delta\) is increased, \(G_{\text{A}} \left( {\delta ,\theta } \right)\) is monotonically decreased, while for \(\theta \ge 10\) it is initially decreased until \(\delta = 0.5\), where a local minimum is observed, then it is increased up to some \(\delta\), which depends on \(\theta\), and finally as \(\delta\) is further increased, it is again decreased. It is noted that for all \(\theta\), as \(\delta \to 0\), the well-known analytical steady-state free molecular flow rate equal to \(8/\left( {3\sqrt \pi } \right) = 1.504\) (Sharipov 2016) is properly recovered. Also, for small values of \(\theta\) and adequately dense atmosphere (large values of \(\delta\)), \(G_{\text{A}} \left( {\delta ,\theta } \right)\) tends to diminish. This behavior, which appears in high oscillation frequencies (small \(\theta\)), is due to inertia forces (the fluid has great difficulty to reach a peak flow) and will be further analyzed, later on, by examining the velocity distributions.

In Table 2, the dimensionless flow rate phase \(G_{\text{P}} \left( {\delta ,\theta } \right)\) is presented in terms of the same parameters as in Table 1. The phase angles vary between zero and \(\pi /2 = 1.571\), which correspond to no phase and maximum phase difference, respectively, between the flow rate and the pressure gradient. The dimensionless flow rate phase in the slip regime \(G_{\text{P}}^{\left( S \right)} \left( {\delta ,\theta } \right)\), based on the analytical expression (35), is also provided in the last two columns of Table 2 for \(\theta = 50\) and \(\theta = 10^{2}\) with \(\delta \ge 1\). The comparison between the corresponding \(G_{\text{P}} \left( {\delta ,\theta } \right)\) and \(G_{\text{A}}^{\left( S \right)} \left( {\delta ,\theta } \right)\) supports all remarks previously made for the flow rate amplitudes and also establishes more confidence to the kinetic solution, which is in very good agreement with the slip analytical solution, provided that the oscillatory flow is in the slip regime.

Table 2 Flow rate phase \(G_{P} \left( {\delta ,\theta } \right)\) (rad) in terms of gas rarefaction parameter \(\delta\) and oscillation parameter \(\theta\)
Full size table

Furthermore, it is seen from Table 2 that, as expected, for any given \(\delta\), the phase difference \(G_{\text{P}} \left( {\delta ,\theta } \right)\) is increased as \(\theta\) is decreased, i.e., as the oscillation frequency is increased. Taking into consideration the corresponding values of \(G_{\text{A}} \left( {\delta ,\theta } \right)\) in Table 1, it is concluded that as the oscillation frequency is increased, the flow rate amplitude is decreased, while the phase shift is increased. At very high frequencies and adequately large \(\delta\), this may result to almost zero amplitude with \(\pi /2\) phase difference. Also, for any given \(\theta\), \(G_{\text{P}} \left( {\delta ,\theta } \right)\) is monotonically increased with \(\delta\), i.e., the phase difference is almost zero in the free molecular regime, and then, it is increased as the oscillatory flow becomes less rarefied, reaching the maximum phase angle lag in the hydrodynamic limit.

A view, in graphical form, of the flow rate amplitude \(G_{\text{A}} \left( {\delta ,\theta } \right)\) and phase \(G_{\text{P}} \left( {\delta ,\theta } \right)\) is provided in Fig. 1, where these quantities are plotted versus \(\delta /\theta\) for \(\theta = \left[ {0.1,1,10,50,10^{2} } \right]\). The behavior of \(G_{A} \left( {\delta ,\theta } \right)\) in terms of the ratio \(\delta /\theta\) is qualitatively similar to the one observed in Table 1 in terms of \(\delta\). Three regimes may be identified in terms of \(\delta /\theta\): the first one for \(\delta /\theta \le 10^{ - 2}\), the second one for \(10^{ - 2} < \delta /\theta < 1\) and the third one for \(\delta /\theta \ge 1\). In the first and third regimes, the results of \(G_{\text{A}} \left( {\delta ,\theta } \right)\) depend only on the ratio \(\delta /\theta\) and they almost coincide for all \(\theta\), while in the second regime they depend on \(\delta /\theta\) and \(\theta\). Furthermore, for \(\theta = \left[ {0.1,1} \right]\), \(G_{\text{A}} \left( {\delta ,\theta } \right)\) is monotonically reduced, while for \(\theta = \left[ {10,50,10^{2} } \right]\) it is initially slightly decreased; then, it is increased up to some \(\delta /\theta \in \left[ {0.1,1} \right]\), and finally, it is decreased. This behavior is justified by the fact that when the oscillation frequency is adequately high (\(\theta = \left[ {0.1,1} \right]\)), \(G_{\text{A}} \left( {\delta ,\theta } \right)\) is significantly affected and it is monotonically reduced, while when the oscillation frequency is not high enough \(\left( {\theta = \left[ {10,50,10^{2} } \right]} \right)\), \(G_{\text{A}} \left( {\delta ,\theta } \right)\) has some resemblance with the steady-state flow rate profile including the Knudsen minimum, as long as \(\delta /\theta\) is sufficiently small to ensure \(\delta < < \theta\) (as reported above steady-state conditions are reached as \(\theta \to \infty\), with \(\delta < < \theta\)). Then, as \(\delta /\theta\) is further increased, the inequality condition does not hold and \(G_{\text{A}} \left( {\delta ,\theta } \right)\) is decreased. Next, with regard to the phase difference, \(G_{\text{P}} \left( {\delta ,\theta } \right)\) is monotonically increased with \(\delta /\theta\). At very small values of \(\delta /\theta\) (free molecular regime), it is almost zero; then at moderate values of \(\delta /\theta\) (transition regime), it is rapidly increased, and finally at large values of \(\delta /\theta\) (slip and hydrodynamic regimes), it is asymptotically increased reaching the limiting value of \(\pi /2\). An interesting and useful outcome of Fig. 1 may be the determination of the optimal gas rarefaction level for a given oscillation frequency to induce the maximum flow rate amplitude \(G_{\text{A}} \left( {\delta ,\theta } \right)\).

Fig. 1
figure 1

Flow rate amplitude \(G_{\text{A}} \left( {\delta ,\theta } \right)\) and phase \(G_{\text{P}} \left( {\delta ,\theta } \right)\) (rad) in terms of the ratio of the gas rarefaction parameter \(\delta\) over the oscillation parameter \(\theta\), with \(\theta = \left[ {0.1,1,10,50,10^{2} } \right]\)

Full size image

In Fig. 2, the time evolution of the dimensionless flow rate, defined in Eq. (13) as \(\tilde{G}\left( {t,\delta ,\theta } \right) = G_{\text{A}} \cos \left( {t - G_{\text{P}} } \right)\), is plotted over one period of oscillation \(t \in \left[ {0,2\pi } \right]\) for typical values of \(\delta\) and \(\theta\). The time evolution of the dimensionless pressure gradient is equal to \(\cos t\), and it is also plotted to facilitate the phase shift observation between pressure gradient and dimensionless flow rate. It is seen that \(\tilde{G}\left( {t,\delta ,\theta } \right)\) depends heavily on both the gas rarefaction parameter and the oscillation frequency. When \(\delta = 0.1\), the \(\tilde{G}\left( {t,\delta ,\theta } \right)\) profiles for \(\theta = \left[ {1,10,10^{2} } \right]\) (low and moderate oscillation frequencies) are very close to each and in phase with the pressure gradient, while for \(\theta = 0.1\) (high oscillation frequency) \(\tilde{G}\left( {t,\delta ,\theta } \right)\) has a significantly smaller amplitude and a lagging phase angle. As \(\delta\) is increased, the effect of \(\theta\) becomes more dominant. At \(\delta = 1\), the \(\tilde{G}\left( {t,\delta ,\theta } \right)\) profiles only for \(\theta = \left[ {10,10^{2} } \right]\) are close to each other and in phase, while for \(\theta = \left[ {0.1,1} \right]\) the amplitude is reduced and the phase lag is increased. Actually now, for \(\theta = 0.1\) the amplitude is very small and the phase lag is almost \(\pi /2\). This behavior is further enhanced at \(\delta = 10\), where the effect of the oscillation frequency is very significant for \(\theta = \left[ {0.1,1,10} \right]\) and remains not important only for \(\theta = 10^{2}\). As expected, these results are in very good agreement with the remarks made in Tables 1 and 2. It is also concluded that the peak of the flow rate amplitude always falls short of reaching the corresponding flow rate of the steady-state Poiseuille flow with constant pressure gradient. This is clearly contributed to the inertia of the fluid, which must be accelerated in each cycle, and therefore, this effect is intensified as the flow becomes more viscous and the oscillation frequency is increased.

Fig. 2
figure 2

Time evolution of flow rate \(\tilde{G}\left( {t,\delta ,\theta } \right)\) over one period of oscillation for \(\delta = \left[ {0.1,1,10} \right]\) and \(\theta = \left[ {0.1,1,10,10^{2} } \right]\); the time evolution of the dimensionless pressure gradient equal to \(\cos t\) is also included

Full size image

Next, the behavior of the velocity distributions in terms of \(\delta\) and \(\theta\) is investigated. In Fig. 3, the amplitude \(u_{\text{A}} \left( r \right)\) and the phase angle \(u_{\text{P}} \left( r \right)\) of the velocity distribution are plotted for \(\delta = \left[ {0.1,1,10} \right]\) and \(\theta = \left[ {10^{ - 2} ,10^{ - 1} ,1,10} \right]\) covering a wide range of the flow parameters. As the oscillation parameter is decreased, i.e., the oscillation frequency is increased, the amplitude is reduced and the phase angle lag is increased. This behavior is expected, and it is in accordance with the flow rate results studied above. Here, it is more interesting to focus on the radial variation of the velocity amplitude and phase angle with regard to \(\delta\) and \(\theta\). Starting with \(u_{\text{A}} \left( r \right)\), it is seen that for some \(\delta\) and \(\theta\) (e.g., \(\delta = 0.1\) and \(\theta \ge 0.1\)) the velocity amplitudes have the expected shape with their maximum at \(r = 0\), while the corresponding phase angles are small and almost constant in the radial direction. However, as \(\delta\) is increased and \(\theta\) is reduced, \(u_{A} \left( r \right)\) remains constant from the center of the tube until close to the wall, where it rapidly changes. In these cases (e.g., \(\delta = 1\) and \(\theta \le 0.1\) or \(\delta = 10\) and \(\theta \le 1\)) near the wall, there is a region where the velocity amplitude is higher than in the center of the flow. The corresponding values of \(u_{P} \left( r \right)\) are large, resulting in phase lags up to \(90^{0}\) with regard to the pressure gradient, and also, they are constant from the center of the tube until this region close to the wall, where they change significantly in an oscillatory manner. The thickness of this region is decreased as \(\delta\) is increased and \(\theta\) is reduced. Therefore, in high or even moderate frequencies (it depends on \(\delta\)), the flow consists of two layers: the inviscid piston flow in the core, dominated by inertia forces, and the frictional Stokes wall layer dominated by viscous forces. This flow description, including the velocity overshoot, which is known as “annular effect” or “Richardson effect,” is well known in classical hydrodynamics (Schlichting and Gersten 2017; White 1974; Zamir 2000). It is interesting, however, to see that these effects are also present in oscillatory rarefied flows. Of course as the gas rarefaction is increased, higher oscillation frequencies are needed to trigger these flow patterns.

Fig. 3
figure 3

Velocity distribution amplitude \(u_{\text{A}} \left( r \right)\) and phase angle \(u_{\text{P}} \left( r \right)\) versus radial distance \(r\) for \(\delta = \left[ {0.1,1,10} \right]\) and \(\theta = \left[ {10^{ - 2} ,10^{ - 1} ,1,10} \right]\)

Full size image

In Fig. 4, the time evolution of the dimensionless velocity distribution, defined in Eq. (8) as \(\tilde{u}\left( {r,t} \right) = u_{\text{A}} \cos \left( {t - u_{\text{P}} } \right)\), is plotted versus the radial distance \(r\) at certain times \(t \in \left[ {0,2\pi } \right]\) covering one period of oscillation for \(\delta = 1\) with \(\theta = \left[ {10^{ - 2} ,10^{ - 1} ,1,10} \right]\). The observed radial variation of the velocity distribution at these timeframes is the typical one expected, as the oscillation parameter is increased, i.e., as the oscillation frequency is decreased. The two layers flow pattern with the core oscillating in a plug-flow mode and the velocity maximum (or minimum) inside the thin Stokes layer plus the small amplitude and large phase lag are all clear at \(\theta = 10^{ - 2}\), and then, as \(\theta\) is increased, these effects are reduced, and finally, they are diminishing at \(\theta = 10\), where the velocity profile has an amplitude close to the corresponding steady-state one and the phase lag with the pressure gradient is small. Furthermore, it is interesting to note that at high frequencies (\(\theta = 10^{ - 2} ,0.1\)) and at times \(t = 0\) and \(t = \pi\) the velocity distribution along the radial direction changes sign and may be either positive or negative. This velocity reversal does not show up at low frequencies (large \(\theta\)). In addition, the position of the maximum or the minimum of the velocity distribution is moving with time in the radial direction inside the Stokes layer. This is clearly shown in the case of \(\theta = 0.1\) where the overshoot is carried away from the wall (Panton 1996). Although this motion is due to viscous diffusion, it does have some resemblance with transverse decaying waves from the boundary toward the centerline of the pipe.

Fig. 4
figure 4

Time evolution of velocity distribution \(\tilde{u}\left( {r,t} \right)\) versus radial distance \(r\) at certain times \(t \in \left[ {0,2\pi } \right]\) over one period of oscillation for \(\delta = 1\) with \(\theta = \left[ {10^{ - 2} ,10^{ - 1} ,1,10} \right]\) (dashed lines refer to \(t \in \left[ {0,\pi } \right)\) and solid lines to \(t \in \left( {\pi ,2\pi } \right]\))

Full size image

Closing this section, a remark with regard to the Strouhal number, defined as \(St = \delta /\theta\), is made. In Fig. 5, \(\tilde{u}\left( {r,t} \right)\) is plotted versus the radial distance \(r\) at certain times \(t \in \left[ {0,2\pi } \right]\) covering one period of oscillation for \(\delta = \theta = 0.1\) and \(\delta = \theta = 10\). In both setups, \(St = 1\). It is readily seen that the radial variation of \(\tilde{u}\left( {r,t} \right)\) in the two setups at the same time steps, although the Strouhal number is the same, is completely different. This is a clear indication that the \({\text{St}}\) number is not adequate, only by itself, to characterize the flow. Furthermore, according to previous observations, for \(\delta = 0.1\) the flow is highly rarefied, and even with \(\theta = 0.1\), it behaves like a low oscillation flow, while for \(\delta = 10\), the flow is dense enough, and even with \(\theta = 10\), it starts to behave like a moderate- to high-frequency flow. In this latter case, the Stokes layer is thick and affects the whole velocity profile. The corresponding time-dependent flow rates obtained by integrating the velocity profiles presented in Figs. 4 and 5 may be found, in most cases, in Fig. 3.

Fig. 5
figure 5

Time evolution of velocity distribution \(\tilde{u}\left( {r,t} \right)\) versus radial distance \(r\) at certain times \(t \in \left[ {0,2\pi } \right]\) over one period of oscillation for \(\delta = \theta = 0.1\) (left) and \(\delta = \theta = 10\) (right); the Strouhal number in both cases is equal to 1 (dashed lines refer to \(t \in \left[ {0,\pi } \right)\) and solid lines to \(t \in \left( {\pi ,2\pi } \right]\))

Full size image

6 Concluding remarks

The time-dependent isothermal fully developed rarefied gas flow in a cylindrical tube driven by harmonically oscillating pressure gradient is investigated based on the linearized unsteady BGK kinetic model equation. The two parameters characterizing the flow are the gas rarefaction and the oscillation parameters. The former is proportional to the inverse Knudsen number, and the latter one is defined as the ratio of the collision over the oscillation frequency. Computational results for the amplitude and the phase angle of the flow rates and the velocity distributions have been provided in a wide range of these two parameters in tabulated and graphical form. In addition, the time evolution of the macroscopic quantities over a cycle is also reported. The limiting flow rates in the slip and free molecular regimes for very low and high speed oscillations are properly recovered by the kinetic solution, and very good agreement with analytical solutions in these regimes has been obtained.

The flow rate amplitude is decreased as the oscillation frequency is increased. However, in terms of the gas rarefaction the dependency is not monotonic and it is found that for a given oscillation parameter, there is an optimum gas rarefaction level to obtain the maximum flow rate amplitude. The phase shift of the flow rate is monotonically increased as the oscillation frequency is increased and the gas rarefaction is decreased. At low oscillation frequencies, the flow rate and velocity distribution are in phase with the pressure gradient, while as the frequency is increased the amplitude of the macroscopic quantities is decreased and the phase angle lag is increased. At high frequencies, the flow consists of the core oscillating in a plug-flow mode and the Stokes layer with a velocity overshoot. These effects, which are well known in classical hydrodynamics, are also present in oscillatory rarefied flows. Of course as the gas rarefaction is increased, it is more difficult for energy to be transferred from the initial oscillation to the bulk flow, and therefore, higher oscillation frequencies are needed to observe these phenomena.

Overall, it is hoped that the present work may be useful in experimental work related to oscillatory microflows as well to support the design of microfluidic devices (sensors, controllers, resonators). Future work area may include pulsatile flows in long orthogonal microchannels and short microtubes.