1 Introduction

Electroosmosis has become important in transporting or mixing fluids in MEMS, micro-fluidics and biosensors. The electrolyte can be efficiently driven by applying a steady or time-varying voltage due to the existence of electric double layer (EDL) developed on the wall. The present study is aimed to obtain analytical solutions for EO flow in ducts of some basic shapes, which were not obtained in the literature. Analytic solutions for EO flows are important because not only they reveal properties of basic micro-duct geometries, but also they serve as accuracy standards for approximate solutions, whether numerical or asymptotic. The few analytic solutions for steady EO flows are as follows. The steady EO flow in a parallel plate duct has long been known. Rice and Whitehead (1965) first obtained the closed-form solution to the circular duct and Yang and Li (1998) the series solution to the rectangular duct. The solution to the annular duct was found by Tsao (2000), the semicircular duct by Wang et al. (2008) and the sector duct by Chang and Wang (2009), and the polygonal duct by Wang and Chang (2011). Unsteady electroosmosis in micro-ducts includes starting flow when an axial electric field is suddenly applied, and the oscillatory flow due to an AC field. The previous literature on starting EO flows includes Soderman and Jonsson (1996) and Keh and Tseng (2001) who found exact solutions to the flow in the parallel plate channel and the circular tube. Gillespie et al. (2002) developed a one-dimensional model of coupling Poisson–Nernst–Planck (PNP) and density functional theory (DFT) to calculate ion flux. The starting EO flow in an annulus and a rectangular duct was studied by Chang and Wang (2008) and the sector duct by Chang and Wang (2009). On the other hand, the EO flow due to an AC oscillating applied axial field was considered by Bhattacharyya et al. (2003) for the circular tube, Campisi et al. (2005) for the rectangular duct, Jian et al. (2010) and Moghadam (2014) for the annular duct. Recently, an analytical approach was presented by Moghadam (2016) to explore the EOF and associated heat transfer in a semi-annular micro-capillary. Another research related to the unsteady flow of fluid through a parallel rotating micro-channel was carried out by Gheshlaghi et al. (2016). Gillespie (2015) examined several different continuum models (i.e., Poisson–Boltzmann) that attempt to include ion size, ion concentrations and surface charges. In addition, with regard to the possible interactions of electroosmotic slip and Navier slip conditions, Goswami and Chakraborty (2011) first derived a general semi-analytical formalism for the implications of electroosmotic flows in the presence of Navier slip, corresponding to micro-channel geometries with complex cross-sectional shapes (elliptic, polygonal, point star-shaped, and annular micro-channel).

All the references mentioned above used the Debye–Hückel approximation for low electric potential. Since the equations are linear, superposition methods such as separation of variables, Laplace transform, Green’s functions can be used. Also, the cross-sectional geometries must be described by separable coordinates. We mention that for unsteady EO flow using the nonlinear Poisson–Boltzmann equation, it often requires fully numerical means (Zhang et al. 2006; Kamali and Eslami 2008), patching approximations (Kang et al. 2002) or perturbation method (Chang et al. 2011).

This paper describes an eigenfunction superposition method to solve linear unsteady EO flows in ducts. The only requirement is that for the same cross-sectional geometry there exist a complete set of eigenfunctions for the Helmholtz equation. The process is somewhat similar to the method of Green’s functions (Morse and Feshbach 1953; Riley et al. 2006), except that Green’s function itself is not needed. Previous reference using such a method include Wakasugi (1961a, b) who studied the buckling of simply supported triangular plates, and Aggarwala and Iqbal (1969) who investigated the heat convection in some triangular ducts. The unsteady oscillatory flow in a right isosceles duct was solved by Tsangaris and Vlachakis (2003). As a matter of fact, flow in a pipe of various geometries is of fundamental interest in viscous flow; see, e.g., Landau and Lifshitz (1987, Sec. 17).

In this study, we consider a parallel EO flow. The longitudinal velocity w′ is governed by (see, e.g., Bruus 2008, p. 158)

$$ \rho \frac{{\partial w^{{\prime}}}}{{\partial t^{{\prime}}}} = \mu \nabla^{{{\prime}2}} w^{{\prime}} + \rho_{e} E(t^{{\prime}}) $$
(1)

Here \( t^{{\prime}} \) is the time, E is the longitudinal applied electric field, \( \rho_{e} \) is the charge density, ρ and μ are the fluid density and viscosity, respectively. The fluid flow on the wall is required to satisfy the no-slip condition.

On the other hand, we make the Debye–Hückel approximation; namely, the potential for the electric double layer \( \psi^{{\prime}} \) is related to ρ e by

$$ \rho_{e} = - \varepsilon \nabla^{{{\prime}2}} \psi^{{\prime}} = \frac{{- 2z^{2} e^{2} n_{0}}}{{k_{b} T}}\psi^{{\prime}} $$
(2)

where z is the valence, e is the electron charge, n 0 is the bulk electrolyte concentration, k b is the Boltzmann constant and T is the absolute temperature. In particular, we assume a constant permittivity ɛ throughout the entire micro-duct. The EDL potential \( \psi^{{\prime}} \) is assumed to have a constant zeta potential ψ 0 on the wall (Stern layer). It is noted that the Debye–Hückel approximation is valid for dilute solution (say, n 0 < 10−3 M) of point-like ions when the zeta potential ψ 0 (or the applied voltage across the EDL) is much less than the thermal voltage k b T/e (see, e.g., Storey et al. 2008). Moreover, due to low solid–liquid interactions, the zeta potential is somewhat smaller for slip flow (Papadopoulos et al. 2012), and thus, one may expect that the Debye–Hückel approximation is valid for most hydrophobic micro-ducts.

Let ψ 0 be the constant potential on the wall, E 0 be the magnitude of the unsteady applied potential and L be a characteristic cross-sectional length. Normalize the variables as follows

$$ \psi = \frac{{\psi^{{\prime}}}}{{\psi_{0}}},\quad w = \frac{{w^{{\prime}}}}{{- E_{0} \varepsilon \psi_{0}/\mu}},\quad t = \frac{{t^{{\prime}}}}{{\rho L^{2}/\mu}},\quad F(t) = \frac{{E(t^{{\prime}})}}{{E_{0}}} $$
(3)

Equations (1, 2) become

$$ w_{t} = \nabla^{2} w + K^{2} \psi F(t) $$
(4)
$$ \nabla^{2} \psi = K^{2} \psi $$
(5)

with the boundary conditions on the wall

$$ \psi = 1,w = 0 $$
(6)

where

$$ K = L/\lambda_{D} = zeL\sqrt {\frac{{2n_{0}}}{{\varepsilon k_{b} T}}}, $$
(7)

is the important non-dimensional electrokinetic width with \( \lambda_{\text{D}} \) the Debye length of the electric double layer (EDL) for the potential.

It is worth mentioning the typical values of the important parameters in the range of practical applications. For example, n 0 = 10−4 M, T = 288 K (15 °C), the thermal voltage is k b T/e = 0.0248 V (k b = 8.62 × 10−5 eV K−1), ɛ = 7 × 10−10 C2 J−1 m−1, and λ D is around 3 nm. The potential value of 25 mV (either positive or negative) can be taken as a useful reference that separates low-charged surfaces from high-charged surfaces. Therefore, the zeta potential \( \psi_{0} \) = 2.50 mV which is within 10 % tolerance of the thermal voltage can be considered a valid case for the Debye–Hückel approximation. On the other hand, it is apparent from the definition that a large value of K denotes a relatively thin electric double layer and vice versa. The capillary electrophoresis applications usually have K at the orders of about 103–105 with the Debye lengths (\( \lambda_{\text{D}} \)) in the range of about 1–10 nm in a micro-fluidic channel (with characteristic widths: 10–100 μm). A smaller K (with overlapped EDLs) can be produced by fabricating a smaller cross section or decreasing the bulk electrolyte concentration (low n 0). However, for small K, the polarization of water dipoles in the vicinity would also severely alter the permittivity close to the wall. One may also refer to some recent studies for the practical ranges of the dimensional parameters involved (see, e.g., He et al. 2009; Bandopadhyay and Chakraborty 2011, 2013; Kilic and Bazant 2007a, b; Peng and Li 2015; Iglic et al. 2010; Bandopadhyay et al. 2015).

2 General formulation for steady and unsteady electroosmotic flow

An important application of the Helmholtz equation is the vibration of elastic membranes. Existing exact solutions for various membrane shapes have been compiled in the book by Wang and Wang (2014), where the exact eigenvalues and eigenfunctions of isosceles right triangle, equilateral triangle and 30°–60°–90° triangle are given. These solutions will be utilized for our EO flow problems.

We shall first briefly formulate the method for general duct cross sections. Let (\( \lambda_{j},\phi_{j} \)) be an eigenpair of the two-dimensional Helmholtz equation,

$$ \nabla^{2} \phi_{j} + \lambda_{j} \phi_{j} = 0 $$
(8)

with the homogeneous boundary condition on the wall,

$$ \phi_{j} = 0 $$
(9)

Namely, \( \lambda_{j} \) denotes the (positive)jth eigenvalue and \( \phi_{j} \) the corresponding eigenfunction. The eigenvalues are arranged in the ascending order of their magnitudes: \( 0 \le \lambda_{1} \le \lambda_{2} \le \cdots \), (each counted with its algebraic multiplicity). It can be shown that the set of eigenfunctions is complete, and any pair of eigenfunctions corresponding to distinct eigenvalues is mutually orthogonal to each other (Morse and Feshbach 1953).

2.1 Steady flow

Let \( \bar{w} \) be the velocity for steady EO flow. Equations (4, 5) reduce to

$$ \nabla^{2} \bar{w} + K^{2} \psi = \nabla^{2} (\bar{w} + \psi) = 0 $$
(10)

The conditions in (6) gives \( \bar{w} + \psi = 1 \) on the wall, which must also be satisfied in the entire duct owing to the maximum principle for the Laplace equation (Strauss 2007, p. 154). In other words, we have the identity, \( \psi = 1 - \bar{w} \) in the entire duct, and thus,

$$ - \nabla^{2} \bar{w} + K^{2} \bar{w} = K^{2} $$
(11)

with \( \bar{w} = 0 \) on the boundary. Note that Eq. (11), even the homogeneous part, is not the Helmholtz equation. A good advantage of using the eigenfunctions of the Helmholtz equation is that the operator \( - \nabla^{2} + K^{2} \) on the LHS of Eq. (11) is fully positive definite. Namely, it is assured that one may invert the operator to obtain the solution for the EO flow w.

First of all, we expand unity in terms of the Helmholtz eigenfunctions

$$ 1 = \sum\limits_{j = 1}^{\infty} {a_{j} \varphi_{j}} $$
(12)

Using the orthogonality property, inversion gives the coefficient a j

$$ a_{j} = \frac{{C_{j}}}{{D_{j}}},\quad C_{j} = \iint {\varphi_{j} {\text{d}}A},\quad D_{j} = \iint {\varphi_{j}^{2} {\text{d}}A} $$
(13)

where the double integrations are over the cross-sectional area. Next, we express also the steady velocity in terms of the eigenfunctions which satisfy the zero boundary conditions

$$ \bar{w} = \sum\limits_{j = 1}^{\infty} {A_{j} \varphi_{j}} $$
(14)

Equations (11, 12, 14) yield the coefficients

$$ A_{j} = \frac{{K^{2} a_{j}}}{{\lambda_{j} + K^{2}}} $$
(15)

where \( \lambda_{j} + K^{2} \)(>0) is called the signature of the EO flow differential operator \( - \nabla^{2} + K^{2} \) [cf. Eq. (11)] associated with the eigenfunction \( \phi_{j} \). The steady flow rate is

$$ \bar{Q} = \iint {\bar{w}{\text{d}}A} = \sum\limits_{j = 1}^{\infty} {\frac{{K^{2} C_{j}^{2}}}{{D_{j} (\lambda_{j} + K^{2})}}} $$
(16)

It is known that for large K (or thin EDL) the velocity in the interior is almost unity and there exists a boundary layer near the wall. If η is the distance pointing inward from the wall, Eq. (11) can be approximated by

$$ \bar{w}_{\eta \eta} - K^{2} \bar{w} = - K^{2} $$
(17)

with the solution

$$ \bar{w} = 1 - e^{- K\eta} $$
(18)

Thus, the velocity deficiency per lateral length due to the boundary layer is, asymptotically

$$ \int\limits_{0}^{\infty} {e^{- K\eta} {\text{d}}\eta = \frac{1}{K}} $$
(19)

The approximation of the flow rate for large K is thus

$$ \bar{Q} = A - \frac{P}{K} $$
(20)

where A is the cross-sectional area and P is the perimeter length.

2.2 Starting flow

Consider a suddenly applied constant axial electric field,

$$ F(t) = H(t) $$
(21)

where H(t) is the unit step function. Let

$$ w = \bar{w}(x,y) - \tilde{w}(x,y,t) $$
(22)

that is, the transient solution w is written as the difference between the steady-state solution \( {\kern 1pt} \bar{w}(x,y){\kern 1pt} \) and the unsteady part \( {\kern 1pt} \tilde{w}(x,y,t) \). The unsteady part, thus defined, can be considered as the “deficit” away from the steady-state solution. The unsteady part of Eq. (4) is therefore simply governed by

$$ \tilde{w}_{t} = \nabla^{2} \tilde{w} $$
(23)

with the initial condition

$$ \tilde{w}\left| {_{t = 0}} \right. = \bar{w} $$
(24)

Apparently the unsteady part in (22) is defined such that it decays as time evolves. By Eqs. (8, 14, 23, 24), the transient solution is

$$ \tilde{w} = \sum\limits_{j = 1}^{\infty} {A_{j} \varphi_{j} e^{{- \lambda_{j} t}}} $$
(25)

The analytic solution in terms of the Helmholtz eigenfunctions is then

$$ w = \sum\limits_{j = 1}^{\infty} {\frac{{K^{2} C_{j}}}{{D_{j} (\lambda_{j} + K^{2})}}\varphi_{j} \left({1 - e^{{- \lambda_{j} t}}} \right)} $$
(26)

The instantaneous flow rate is

$$ Q = \iint {w{\text{d}}A} = \sum\limits_{j = 1}^{\infty} {\frac{{K^{2} C_{j}^{2}}}{{D_{j} (\lambda_{j} + K^{2})}}\left({1 - e^{{- \lambda_{j} t}}} \right)} $$
(27)

The first eigenvalue λ 1 governs the rate of the EO flow approaching the steady state. For example, to find the time to approach 1 % of the steady state, we set \( \lambda_{1} t = 5 \), or

$$ t \approx \frac{5}{{\lambda_{1}}} $$
(28)

2.3 Oscillatory flow

Next we consider an oscillatory applied electric field \( E_{0} \cos (\varOmega t^{{\prime}}) \), where Ω is the frequency. Equation (4) then yields, preferably in complex form,

$$ w_{t} = \nabla^{2} w + K^{2} \psi e^{ist} $$
(29)

where \( i = \sqrt {- 1} \), \( s = \varOmega L^{2}/\nu \) is the normalized frequency. Let

$$ w = \sum\limits_{j = 1}^{\infty} {B_{j} \varphi_{j} e^{ist}} $$
(30)

Using \( \psi = 1 - \bar{w} \) and Eqs. (14, 29, 30), after some algebra, we obtain the coefficients

$$ B_{j} = \frac{{K^{2} a_{j} \lambda_{j}}}{{(\lambda_{j} + K^{2})(\lambda_{j} + is)}} $$
(31)

Thus, the induced oscillatory velocity is

$$ w = \text{Re} \left[{\frac{{K^{2} C_{j} \lambda_{j}}}{{D_{j} (\lambda_{j} + K^{2})(\lambda_{j} + is)}}\varphi_{j} e^{ist}} \right] $$
(32)

The flow rate is

$$ \begin{aligned} Q & = \iint {wdA} = \text{Re} \sum {\frac{{K^{2} C_{j}^{2} \lambda_{j}}}{{D_{j} (\lambda_{j} + K^{2})(\lambda_{j} + is)}}e^{ist}} \\ & = G_{1} \cos (st) + G_{2} \sin (st) \\ \end{aligned} $$
(33)

where

$$ \begin{aligned} G_{1} & = \sum {\frac{{K^{2} C_{j}^{2} \lambda_{j}^{2}}}{{D_{j} (\lambda_{j} + K^{2})(\lambda_{j}^{2} + s^{2})}}} \\ G_{2} & = \sum {\frac{{K^{2} C_{j}^{2} \lambda_{j} s}}{{D_{j} (\lambda_{j} + K^{2})(\lambda_{j}^{2} + s^{2})}}} \\ \end{aligned} $$
(34)

The amplitude of the oscillatory flow rate is

$$ M = \sqrt {G_{1}^{2} + G_{2}^{2}} $$
(35)

The phase lag is

$$ \beta = \tan^{- 1} (G_{2}/G_{1}) $$
(36)

The results for the steady EO flow in (16), transient flow in (27) and oscillatory flow in (33)–(36) are the general formulas, and can be explicitly evaluated as long as the eigenpairs \( \lambda_{j},\phi_{j} \) of the Helmholtz equation for a given shape of duct are known.

2.4 Discussion of the solution of the general formulation

It is conceivable that the key roles of the present method are played by the eigenpairs \( \lambda_{j},\phi_{j} \) of the Helmholtz equation. Associated with each eigenpair, the differential operator \( - \nabla^{2} + K^{2} \) [cf. Eq. (11)] of the EO flow has the signatures \( \lambda_{j} + K^{2} (>0) \). And thus \( 1/(\lambda_{j} + K^{2}) \) is the system response to the component of the unit input in \( \phi_{j} \), i.e.,. \( a_{j} = C_{j}/D_{j} \), whence yielding the result in (15) for the steady flow [note that the input of Eq. (11) is K 2]. In the cases of transient flow, the system simply responds by an additional factor \( 1 - e^{{- \lambda_{j} t}} \) in each eigencomponent [cf. Eq. (26)]; hence, the first eigenvalue λ 1 of the Helmholtz equation governs the rate of EO flow approaching the steady state. On the other hand, the oscillatory flow responds with a different factor \( \frac{{\lambda_{j}}}{{\lambda_{j} + is}} \) [cf. Eq. (32)] in each eigencomponent, which contributes to the changes in the magnitude as well in the phase change in response to the external forcing \( e^{ist} \). The resultant phase lag is complicated although each \( \frac{{\lambda_{j}}}{{\lambda_{j} + is}} \) is simply coupling between λ j and s.

The analytical solutions enable us to ascertain several salient features of the flow rates. It must be noted that λ j , C j , D j and \( \phi_{j} \) as well are all shape factors; they are determined once the geometry of the duct is specified. Given a duct, the steady EO flow rate \( \bar{Q} = \iint {\bar{w}dA} = \sum\nolimits_{j = 1}^{\infty} {\frac{{K^{2} C_{j}^{2}}}{{D_{j} (\lambda_{j} + K^{2})}}} \) [Eq. (16)] may only vary with changing the electrokinetic width K. In the limit of small K, all each summand behaves like \( \frac{{C_{j}^{2}}}{{D_{j} \lambda_{j}}}K^{2} \), and thus, the flow rate is small of order K 2. In the limit of large K, the first few summands are approximately \( \frac{{C_{j}^{2}}}{{D_{j} \lambda_{j}}} \), which are simply combinations of the geometric factors, and thus, the flow is expected to approach its maximum at very large K. In the intermediate range of K, we expect that the steady flow rate \( \bar{Q} \) increases monotonically with increase in K, for there are more and more terms turning from the behavior of \( \frac{{C_{j}^{2}}}{{D_{j} \lambda_{j}}}K^{2} \) to that of \( \frac{{C_{j}^{2}}}{{D_{j} \lambda_{j}}}. \) Next we examine the transient flow rate \( Q = \iint {wdA} = \sum\nolimits_{j = 1}^{\infty} {\frac{{K^{2} C_{j}^{2}}}{{D_{j} (\lambda_{j} + K^{2})}}\left({1 - e^{{- \lambda_{j} t}}} \right)} \) [Eq. (27)]. It is noted that everything said about the steady flow rate applies to the transient flow rate except that each summand is multiplied by the shape determined transient factor \( 1 - e^{{- \lambda_{j} t}} \). The larger the first eigenvalue \( \lambda_{1} \) is, the faster the flow approaches the steady state. Finally, we examine the oscillatory flow, which has the EO flow rate [Eq. (33)],

$$ \begin{aligned} Q & = \iint {wdA} = \text{Re} \sum {\frac{{K^{2} C_{j}^{2} \lambda_{j}}}{{D_{j} (\lambda_{j} + K^{2})(\lambda_{j} + is)}}e^{ist}} \\ & = G_{1} \cos (st) + G_{2} \sin (st) \\ \end{aligned} $$

The facts about the non-shape factor K said above still apply, yet the additional non-shape parameter s reduces the flow rate through all the summands, especially for the modes with \( \lambda_{j} < s. \) Thus, we may conclude that the magnitude of the EO flow rate decreases with increase in the external frequency s. The phase lag \( \beta = \tan^{- 1} (G_{2}/G_{1}) \) with G 1, G 2 given in (34) is complicated by all the shape and non-shape parameters. But as s is a common factor to all summands in G 2 (not in G 1), we expect that the phase lag increases with increase in s.

3 Validation of Helmholtz eigenfunction method

The present method is validated by computing the EO flow rates for the circular duct. For this cross section, the solutions were found previously by the method of separation of variables.

3.1 Steady flow

The steady EO flow was found by Rice and Whitehead (1965). The velocity and the flow rate are

$$ \bar{w} = 1 - \frac{{I_{0} (Kr)}}{{I_{0} (K)}} $$
(37)
$$ \bar{Q} = 2\pi \left[{\frac{1}{2} - \frac{{I_{1} (K)}}{{KI_{0} (K)}}} \right] $$
(38)

Here the I’s denote the modified Bessel functions.

For the circle, our Helmholtz equation gives

$$ \lambda_{j} = k_{j}^{2} $$
(39)

where k j is the \( j{\text{th}} \) root of

$$ J_{0} (k_{j}) = 0 $$
(40)

i.e., {k j } = 2.40483, 5.52008, 8.65373, 11.7915. The third and higher eigenvalues are well represented by (Abramowitz and Stegun 1970)

$$ k_{j} = \alpha_{j} + \frac{1}{{8\alpha_{j}}} - \frac{124}{{3(8\alpha_{j})^{3}}} + \cdots, \quad \alpha_{j} = (j - 1/4)\pi $$
(41)

The eigenfunctions are

$$ \varphi_{j} = J_{0} (k_{j} r) $$
(42)

Equation (13) gives

$$ C_{j} = \frac{{2\pi J_{1} (k_{j})}}{{k_{j}}},\quad D_{j} = \pi J_{1}^{2} (k_{j}) $$
(43)

From Eq. (16), the steady flow rate is

$$ \bar{Q} = 4\pi K^{2} \sum\limits_{1}^{\infty} {\frac{1}{{k_{j}^{2} (K^{2} + k_{j}^{2})}}} $$
(44)

Now the question is: Does Eq. (44) give the same results as Eq. (38)?

Let us first consider some limiting cases. When \( K \to 0 \), a series expansion for Eq. (38) gives the leading term

$$ \bar{Q} = \frac{{\pi K^{2}}}{8} $$
(45)

On the other hand, Eq. (44) yields

$$ \bar{Q} = 4\pi K^{2} \sum\limits_{1}^{\infty} {\frac{1}{{k_{j}^{4}}}} $$
(46)

But Sneddon (1960), on the zeros of Bessel functions, showed

$$ \sum\limits_{1}^{\infty} {\frac{1}{{k_{j}^{4}}} = \frac{1}{32}} $$
(47)

Thus, the results given by Eqs. (38) and (44) are identical when \( K \to 0 \).When \( K \to \infty \), Eq. (38) gives

$$ \bar{Q} = \pi $$
(48)

which is the same as Eq. (44) for large K when we use another Sneddon (1960) identity

$$ \sum\limits_{1}^{\infty} {\frac{1}{{k_{j}^{2}}} = \frac{1}{4}} $$
(49)

For general values of K, we show numerically the two solutions are equivalent in Table 1.

Table 1 Steady EO flow rate for the circular duct
Full size table

3.2 Starting flow

The starting flow was solved by Keh and Tseng (2001) using the method of separation of variables. In brief, Eqs. (22–24) are used to obtain

$$ \tilde{w} = \sum\limits_{1}^{\infty} {A_{j} J_{0} (k_{j} r)e^{{- k_{j}^{2} t}}} $$
(50)
$$ \tilde{w}\left| {_{t = 0}} \right. = 1 - \frac{{I_{0} (Kr)}}{{I_{0} (K)}} $$
(51)

Inversion gives

$$ A_{j} = \frac{{2K^{2}}}{{J_{1} (k_{j})(K^{2} + k_{j}^{2})}} $$
(52)

The transient flow rate is integrated

$$ \tilde{Q} = 4\pi K^{2} \sum\limits_{1}^{\infty} {\frac{1}{{k_{j}^{2} (K^{2} + k_{j}^{2})}}e^{{- k_{j}^{2} t}}} $$
(53)

This is exactly the transient part of our Eq. (27), i.e.,

$$ Q = 4\pi K^{2} \sum\limits_{1}^{\infty} {\frac{1}{{k_{j}^{2} (K^{2} + k_{j}^{2})}}} \left({1 - e^{{- k_{j}^{2} t}}} \right) $$
(54)

Thus, the two methods are completely equivalent.

3.3 Oscillatory flow

The oscillatory EO flow was previously studied by Bhattacharyya et al. (2003), but we shall derive a simpler form. Let

$$ w = u(r)e^{ist} $$
(55)

Equation (29) yields

$$ u^{{\prime \prime}} (r) + u^{{\prime}}/r - isu = - K^{2} \psi $$
(56)

where

$$ \psi = 1 - \bar{w} = \frac{{I_{0} (Kr)}}{{I_{0} (K)}} $$
(57)

Since \( u(1) = 0 \), the solution to Eq. (56) is

$$ u = \frac{{K^{2}}}{{(K^{2} - is)}}\left[{\frac{{I_{0} (\sqrt {is} r)}}{{I_{0} (\sqrt {is})}} - \frac{{I_{0} (Kr)}}{{I_{0} (K)}}} \right] $$
(58)

It follows

$$ \begin{aligned} Q & = 2\pi \int\limits_{0}^{1} {wrdr} = 2\pi \int\limits_{0}^{1} {\text{Re} [ue^{ist}]rdr} \\ & = G_{1} \cos (st) + G_{2} \sin (st) \\ \end{aligned} $$
(59)

where we have

$$ \begin{aligned} G_{1} & = 2\pi \int\limits_{0}^{1} {\text{Re} [u]r{\text{d}}r} \\ G_{2} & = - 2\pi \int\limits_{0}^{1} {\text{Im} [u]r{\text{d}}r} \\ \end{aligned} $$
(60)

It is quite tedious to handle the integrals in (60) analytically. Instead, we use numerical integration to evaluate the amplitude and phase

$$ M = \sqrt {G_{1}^{2} + G_{2}^{2}},\quad \beta = \tan^{- 1} (G_{2}/G_{1}) $$
(61)

On the other hand, Eq. (34) gives

$$ \begin{aligned} G_{1} & = 4\pi K^{2} \sum\limits_{1}^{\infty} {\frac{{k_{j}^{2}}}{{(K^{2} + k_{j}^{2})(s^{2} + k_{j}^{2})}}} \\ G_{2} & = 4\pi K^{2} \sum\limits_{1}^{\infty} {\frac{s}{{(K^{2} + k_{j}^{2})(s^{2} + k_{j}^{2})}}} \\ \end{aligned} $$
(62)

The amplitude and phase are then evaluated by Eq. (25). Table 2 shows a comparison of Eq. (60) form separation of variables and Eq. (62) from the Helmholtz eigenfunctions. We see that except for small numerical errors in the fifth digit, the values are identical.

Table 2 Amplitude M and phase β
Full size table

In conclusion, the two methods show identical results. For the steady EO flow, the separation of variables method is more convenient than the Helmholtz eigenfunction method. For oscillatory EO flow, the Helmholtz eigenfunction method is more convenient. For starting EO flow, both methods are equivalent.

However, we emphasize that for the three triangular ducts studied in this paper, the separation of variables method fails, and only the Helmholtz eigenvalue method is successful.

4 Examples: three triangular ducts

4.1 The isosceles right triangular duct

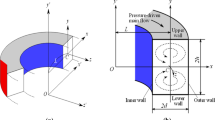
Figure 1a shows the cross section of the isosceles right triangular duct which has a short side as the length scale. The eigenvalues and eigenfunctions are

$$ \begin{aligned} \lambda_{mn} & = \pi^{2} (m^{2} + n^{2}) \\ \varphi_{mn} & = \sin (n\pi x)\sin (m\pi y) - \sin (m\pi x)\sin (n\pi y) \\ \end{aligned} $$
(63)

where m, n are non-equal, positive integers. Since \( \lambda_{mn}^{{}} \) are distinct, m > n > 0. Notice the solution Eq. (63) is equivalent, but somewhat simpler, than the form given by Tsangaris and Vlachakis (2003). Equation (13) gives

$$ C_{mn} = \frac{4}{{(m^{2} - n^{2})\pi^{2}}}\left\{{\begin{array}{*{20}l} {m/n,} \hfill & \quad{m\,even,n\,odd} \hfill \\ {n/m,} \hfill & \quad{m\,odd,n\,even} \hfill \\ {0,} \hfill & \quad{m + n = even} \hfill \\ \end{array}} \right. $$
(64)
$$ D_{mn} = \frac{1}{4} $$
(65)
Fig. 1
figure 1

Three triangular cross sections: a Isosceles right triangular duct, b equilateral triangular duct, c 30°–60°–90° duct. Locations of Cartesian axes are shown

Full size image

The steady-state velocity distribution solution is given by Eq. (14). Figure 2 shows that the velocity profile is rounded for low K (thick EDL) but turns into a plateau for large K (thin EDL). The flow rate is shown in Fig. 3. Since the steady EO flow for this triangular duct is derived for the first time, numerical values are given in Table 3 as benchmarks. Here, we use 16 terms to achieve excellent convergence in the series expansion (16). We see the boundary layer approximation Eq. (20), which is valid for large K, compares very well with our exact solution for high K. For less than 1 % error, K should be larger than 40.

Fig. 2
figure 2

Steady velocity distribution for the isosceles triangular duct: a K = 1 velocity from outside: 0, 0.005, 0.01, 0.015, 0.02, 0.025 max 0.026, b K = 30 velocity from outside: 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 max 0.999

Full size image
Fig. 3
figure 3

Steady flow rate \( \bar{Q} \) versus K for the isosceles triangular duct

Full size image
Table 3 Steady-state EO flow rate for the isosceles right triangular duct
Full size table

The solution to starting flow is given by Eqs. (26, 27). The velocity distribution for low K is quasi-steady, rounded as shown in Fig. 2a. Figure 4 shows typical instantaneous velocity distributions for a high K, where we see, at small times, the EDL near the boundary first induces the flow forward, and the interior velocity catches up only later. Figure 5 shows the unsteady flow rate for starting EO flow. From Eq. (63), the first (lowest) eigenvalue is 5π 2, and Eq. (28) shows the time to reach steady state is about 0.1, which is indeed the case.

Fig. 4
figure 4

Velocity distribution for starting flow in an isosceles triangular duct, K = 20. a t = 0.01, velocity from outside = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, max near sharp corner 0.610, depression near center 0.263, b t = 0.1, max velocity near center 0.979, c t = 1, max velocity near center 0.992

Full size image
Fig. 5
figure 5

Unsteady flow rate Q versus time t for the isosceles triangular duct. From top, K = 40, 20, 10, 5, 1

Full size image

The velocity profiles for low frequency are almost in phase with the external applied potential. Figure 6 shows the velocity profiles for large frequency, while Fig. 7 shows the magnitudes and phase lags for various frequencies. Not only there is a phase lag, but also the maximum velocity is in the boundary layer near the walls (Fig. 6 at st = 0 and 3π/4), which is equivalent to the “annular effect” for viscous flow in circular ducts (Schlichting 1979).

Fig. 6
figure 6

Instantaneous velocity profiles for the isosceles right triangular duct. K = 20, s = 20. a st = 0, instantaneous velocity from outside = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.81, max near corner 0.83, b \( st = 0. 5\pi \), instantaneous velocity from outside = 0, 0.1, 0.2, 0.3, 0.4, max near center 0.457, c st = π, instantaneous velocity from outside = 0, −0.1,−0.2, −0.3, −0.4, −0.5, −0.6, −0.7, −0.81, min near corner—0.83, local max near center—0.791

Full size image
Fig. 7
figure 7

Oscillatory flow rate for EO flow in an isosceles right triangular duct. a Magnitude versus frequency s. From top K = 50, 20, 10, 5, 1. b Phase lag versus frequency. From top K = 1, 5, 10, 20, 50

Full size image

4.2 The equilateral triangular duct

Figure 1b shows the cross section of the equilateral triangular duct where the length scale is one third of the triangle height. Let us place the origin of the Cartesian coordinates at the centroid. The boundaries are at

$$ x = 1,y = \pm (x + 2)/\sqrt 3 $$
(66)

Schelkunoff (1943) gave the eigenfunctions for the Helmholtz equation inside the equilateral triangular region, which in our variables is

$$ \begin{aligned} \varphi_{mn} & = \cos \left[{\frac{(m + 2n)\pi y}{3\sqrt 3}} \right]\sin \left[{\frac{m\pi (2 + x)}{3}} \right] \\ & \quad - \cos \left[{\frac{(m - n)\pi y}{3\sqrt 3}} \right]\sin \left[{\frac{(m + n)\pi (2 + x)}{3}} \right] \\ & \quad + \cos \left[{\frac{(2m + n)\pi y}{3\sqrt 3}} \right]\sin \left[{\frac{n\pi (2 + x)}{3}} \right] \\ \end{aligned} $$
(67)

with the eigenvalues

$$ \lambda_{mn}^{{}} = \frac{{4\pi^{2}}}{27}\left({m^{2} + mn + n^{2}} \right) $$
(68)

Here m and n are integers which are nonzero, and do not add up to zero. Schelkunoff’s solution is symmetric about the x-axis. The solution for fluid flow is more restricted, that it must also have threefold rotational symmetry. A rotation of 120° about the origin is given by the transform

$$ \bar{x} = - x/2 - \sqrt 3 y/2,\bar{y} = \sqrt 3 x/2 - y/2 $$
(69)

We require

$$ \varphi_{mn} (x,y) = \varphi_{mn} (\bar{x},\bar{y}) $$
(70)

This yields the restriction

$$ m\cos \left({\frac{2m\pi}{3}} \right) - (m + n)\cos \left({\frac{2(m + n)\pi}{3}} \right) + n\cos \left({\frac{2n\pi}{3}} \right) = 0 $$
(71)

We also found, for \( m \ne n \),

$$ \iint\limits_{{}} {\varphi_{mn} dA = 0} $$
(72)

Thus, the only admissible integers are m = n = 1, 2, 3,…, from which we find

$$ C_{nn} = \frac{9\sqrt 3}{n\pi},\quad D_{nn} = \frac{9\sqrt 3}{2} $$
(73)

Let \( \varphi_{j} = \varphi_{jj} \), the eigenfunctions and eigenvalues are simplified to

$$ \phi_{j} = 2\cos \left({\frac{j\pi y}{\sqrt 3}} \right)\sin \left({\frac{j\pi (2 + x)}{3}} \right) - \sin \left({\frac{2j\pi (2 + x)}{3}} \right) $$
(74)
$$ \lambda_{j}^{{}} = \frac{{4j^{2} \pi^{2}}}{9} $$
(75)

The steady-state velocity is simplified to

$$ \bar{w} = \sum\limits_{j = 1}^{\infty} {\frac{{2K^{2}}}{{j\pi (\lambda_{j} + K^{2})}}} \varphi_{j} $$
(76)

Typical profiles are similar to those shown in Fig. 2. The steady flow rate, from Eq. (16), is

$$ \bar{Q} = \frac{{162\sqrt 3K^{2}}}{{\pi^{2}}}\sum\limits_{j = 1}^{\infty} {\frac{1}{{j^{2} (4\pi^{2} j^{2} + 9K^{2})}}} $$
(77)

We are fortunate that Eq. (77) can be summed into closed form (e.g., Jolly 1961)

$$ \bar{Q} = \frac{\sqrt 3}{{K^{2}}}\left[{4 + 3K^{2} - 6K\coth \left({\frac{3K}{2}} \right)} \right] $$
(78)

Equation (78) is shown in Fig. 8. Table 4 shows a comparison of this exact result with those of Wang and Chang (2011) who used a semi-numerical point match method. Here, again we use 16 terms to achieve excellent convergence in the series expansion (78).

Fig. 8
figure 8

Steady flow rate versus K for the equilateral triangular duct

Full size image
Table 4 Steady-state EO flow rate for the equilateral triangular duct
Full size table

The steady flow rate for K = ∞ is the cross-sectional area \( 3\sqrt 3 \).

The solution to starting flow is given by Eqs. (26, 27). Typical velocity profiles are similar to those of the isosceles right triangular duct and are not presented in this paper. Figure 9 shows the flow rate for starting EO flow. Since the lowest eigenvalue is λ 1 = 4π 2/9, the time to approach steady state is approximately 1.1 which is indeed reflected in the figure. For oscillatory flow, the amplitude and phase lag, as given by Eqs. (35, 36) are shown in Fig. 10.

Fig. 9
figure 9

Flow rate for starting EO flow in an equilateral triangular duct. From top K = 40, 20, 10, 5, 2, 1

Full size image
Fig. 10
figure 10

Oscillatory flow rate for EO flow in an equilateral triangular duct. a Magnitude versus frequency s. From top K = 50, 10, 5, 2, 1. b Phase lag versus frequency. From top K = 1, 2, 5, 10, 50

Full size image

4.3 The 30°–60°–90° triangular duct

Figure 1c shows the cross section. The length scale used is the short side. The solution to the corresponding Helmholtz equation was found by Seth (1947), which in our formulation the eigenfunctions are

$$ \begin{aligned} \varphi_{mn} & = \cos \left[{\frac{(3 + 2m + 4n)\pi}{6}(3 + 2x)} \right]\cos \left[{\frac{(1 + 2m)\pi}{2}\left({1 + \frac{2y}{\sqrt 3}} \right)} \right] \\ & \quad - \cos \left[{\frac{(3 + 2n + 4m)\pi}{6}(3 + 2x)} \right]\cos \left[{\frac{(1 + 2n)\pi}{2}\left({1 + \frac{2y}{\sqrt 3}} \right)} \right] \\ & \quad + \sin \left[{\frac{(m - n)\pi}{3}\left({3 + 2x} \right)} \right]\sin \left[{(1 + m + n)\pi \left({1 + \frac{2y}{\sqrt 3}} \right)} \right] \\ \end{aligned} $$
(79)

The eigenvalues are

$$ \lambda_{mn} = \frac{{4\pi^{2}}}{9}[4(m^{2} + mn + n^{2}) + 6(m + n) + 3] $$
(80)

Here m > 0, \( m \ne n \), and \( m \ge \left| n \right| \). In terms of increasing eigenvalues (increasing j), the (m, n) pairs are (1, −1), (1, 0), (2, −2), (2, −1), (2, 0), (3, −2), (3, −3), (3, −1), (2, 1), (3, 0), (4, −3), (4, −2), (4, −4), (4, −1), (3, 1), (4, 0), etc.

We find

$$ C_{mn} = \frac{3\sqrt 3}{{\pi^{2}}}\left\{\begin{array}{l} \frac{{1 + (- 1)^{n} \cos [(2m + n)\pi/3]}}{(1 + 2n)(3 + 4m + 2n)} - \frac{{1 - (- 1)^{m + n} \cos [(m - n)\pi/3]}}{4(m - n)(1 + m + n)} \hfill \\ \quad -\, \frac{{1 + (- 1)^{m} \cos [(m + 2n)\pi/3]}}{(1 + 2m)(3 + 2m + 4n)} \hfill \\ \quad +\, \frac{{(3 + 2m + 4n)\left\langle {1 - \cos [2(m + 2n)\pi/3]} \right\rangle}}{8(1 + 2m)(m - n)(3 + 4m + 2n)} \hfill \\ \quad +\, \frac{{(3 + 4m + 2n)\left\langle {1 + \cos [(3 + 4m + 2n)\pi/3]} \right\rangle}}{8(1 + 2n)(m - n)(3 + 2m + 4n)} \hfill \\ \quad -\, \frac{1 - \cos [2(n - m)\pi/3]}{8(1 + m + n)(3 + 2m + 4n)} + \frac{1 + \sin [(9 - 4m + 4n)\pi/6]}{8(1 + m + n)(3 + 4m + 2n)} \hfill \\ \end{array} \right\} $$
(81)
$$ D_{j} = \iint\limits_{\varOmega} {\varphi_{j}^{2} {\text{d}}\varOmega = \frac{3\sqrt 3}{8}} $$
(82)

The steady-state solution flow rate, given by Eq. (16), is shown in Fig. 11. Table 5 gives the numerical values. Here we also use 16 terms to achieve excellent convergence in the series expansion (16). The K = ∞ limit is the area \( \sqrt 3/2 \).

Fig. 11
figure 11

Steady-state flow rate versus K for the 30°–60°–90° duct

Full size image
Table 5 Steady-state EO flow rate for the 30°–60°–90° triangular duct
Full size table

Figure 12 shows the starting EO flow rate versus time. Since the lowest eigenvalue is λ 1 = 28π 2/9, the time to approach steady state is approximately 5/λ 1 ≈ 0.16, which is reflected in Fig. 12. For oscillatory EO flow, the magnitude and the phase lag are shown in Fig. 13.

Fig. 12
figure 12

Transient flow rate versus time t for the 30°–60°–90° duct. From top K = 50, 20, 10, 5, 3, 1

Full size image
Fig. 13
figure 13

Oscillatory flow rate for EO flow in a 30°–60°–90° triangular duct. a Magnitude versus frequency s. From top K = 50, 20, 10, 5, 1. b Phase lag versus frequency. From top K = 1, 5, 10, 20, 50

Full size image

5 Concluding remarks

In this study, we have presented a general procedure of using eigenpairs of the Helmholtz equation for solving EO flow in micro-ducts. The solutions are exact series solutions (some of which are in closed form) under the Debye–Hückel approximation. The method has only the requirement that the eigenvalues and eigenfunctions of the Helmholtz equation can be found for the duct.

The ducts to which the present method of solution is applicable include a variety of shapes whose boundaries are given in separable coordinates. However, the EO flows for these shapes (rectangle, sector, annulus, etc.) are more easily obtained by the method of separation of variables. Thus, the method of using the Helmholtz eigenfunctions is most suitable for cross sections which are not describable in separable coordinates. The three examples of triangular shapes discussed in this paper have these properties. Nonetheless, the method of using Helmholtz eigenfunctions is first validated for the EO flow in a circular duct.

The solution in the general formulation enables us to identify general behaviors of the flow rates before proceeding with detailed examples. It is the definite signature of the differential operator of EO flow that explains the success of the Helmholtz eigenfunction method in obtaining convergent series solutions. The EO flow is characterized by the eigenfunctions of the Helmholtz equations, the electrokinetic width K as well as the external forcing frequency s (only for the oscillatory flow). For obvious reasons, the eigenfunctions are shape factors, while K and s are non-shape physical factors. Given the geometry of the duct, the trend of the steady flow rate is determined by the relative importance of λ j and K 2. For the transient flow, the rate with which the EO flow approaches the steady state is governed by the first eigenvalue of the Helmholtz equation. For the oscillatory flow, the magnitude of the EO flow rate decreases with increasing the external frequency s, while the phase lag β is complicated by all the geometric and physical factors. In general, β increases with increasing s. At large external frequency s, not only there is a phase lag, but also the maximum velocity in the boundary layer is closer to the walls.

The three examples of triangular shapes, besides their technical contents, not only concretely add to new analytical solutions for EO flow in ducts, but also testify all the salient features revealed from the analytical solutions in the general formulation. The general formulation applies to cases whether the eigenfunctions can be obtained analytically (say, by numeric methods) or not. Nevertheless, the geometries of triangular ducts considered here are not readily amenable to the current fabrication techniques. The present work stands from a completely theoretical point of view that the choice of test cases (for other numerical or experimental methods) can be justified.

As a final remark, in a wider range of applications with the ratio \( \lambda = ze\psi_{0}/k_{b} T \) being not small but close to 1, the DHA is no longer valid and one may resort to the analysis of the Poisson–Boltzmann equation. Nevertheless, in the line of our previous approach (Chang et al. 2011), the present DHA solution provides the base for extension of analysis to the Poisson–Boltzmann equation, or the more general Poisson–Nernst–Planck equations. In other realistic applications, one may need more accurate model to account for the physics and chemistry.