1 Introduction

Fluid-conveying pipes/beams are not only the indispensable part of industrial setups such as oil and gas installations, pump discharge lines, heat exchangers, but also are of great importance in MEMS, NEMS applications. Being the simplest form of fluid structure interaction problems, dynamic analysis of fluid-conveying pipe has attracted a significant deal of attention from researchers due to the rich and interesting properties observed in their dynamic behavior. Numerous studies have been carried out on the stability of a pipe/beam conveying fluid. Dynamics of a system of articulated pipes conveying fluid was first studied by Benjamin (1961a, b) theoretically and experimentally, which was followed by Gregory and Paidoussis (1966a, b), who thoroughly investigated the flutter of tubular cantilevers conveying fluid theoretically and experimentally. Olson and Jamison (1997) introduced a general-purpose finite element program to simulate the dynamics of elastic pipes conveying fluid with different boundary conditions. Sinha et al. (2001) investigated the dynamic behavior of an open-ended cantilever-type pipe conveying fluid and found that the additional mass of fluid should be considered in the analysis. The dynamics of fluid-conveying cantilevered pipe consisting of two segments made of different materials focusing on the effects induced by different length ratios between the two segments was studied by Dai et al. (2013). The nonlinear transverse vibrations of highly tensioned pipes with vanishing flexural stiffness and conveying fluid with variable velocity were investigated by OzÖz (2001). Bou-Rabee et al. (2002) examined the stability of a tubular cantilever conveying fluid in a multi-parameter space based on nonlinear beam theory. Taking into account the nonlinear coupling between the longitudinal and transverse vibrations, Lee and Chung (2002) studied the stability of a double-clamped pipe conveying fluid. Ryu et al. (2002) thoroughly investigated the transference of eigenvalue curves and the corresponding unstable modes of cantilevered pipes conveying fluid. Reddy and Wang (2004) derived equations of motion governing the deformation of fluid-conveying beams employing Euler–Bernoulli and Timoshenko beam theories based on von K´arm´an principle. They have presented finite element models of the resulting nonlinear equations of motion. Kuiper and Metrikine (2004) proved analytically the stability of a riser conveying oil from seabed to a floating platform as a pipe conveying fluid surrounded by an external fluid. Taking into account the low fluid velocity, they employed a D-decomposition method for stability analysis. Stationary bifurcations in several nonlinear models of pipes conveying fluids fixed at both ends have analyzed with the use of Lyapunov–Schmidt reduction and singularity theory by Nikolić and Rajković (2006). Qian et al. (2009) studied the effects of thermal loads on the instability of simply supported pipes conveying fluid. Utilizing generalized differential quadrature (GDQ) method, Tornabene et al. (2010) extracted the critical flow velocity of straight pipes conveying fluids for various fluid densities.

Due to the recent technological evolutions in micro/nano-structures, they have employed to transmit fluids in many micro- and nano-fluidic devices. Micro- and nano-pipe conveying fluids have potential applications in nano-pipettes, fluid filtration devices, and targeted drug delivery devices. Consequently, increasing attention has been devoted to the vibrations of pipe conveying fluids in micro/nanoscales. Based on nonlocal elasticity theory, stability of tubular micro- and nano-beams conveying fluid was studied by Wang (2009). In an another work, he developed a new theoretical model based on the modified couple stress theory for the vibration analysis of fluid-conveying micro-tubes by introducing one internal material length scale parameter (Wang, 2010). Ahangar et al. (2011) studied the instability of a cantilever and clamped–clamped microbeam conveying fluid based on modified couple stress theory (MCST) and compared the results with those derived based on classical beam theory. They showed that the material length scale parameter affects the natural frequencies and critical flow velocities. Based on the strain gradient theory, Yin et al. (2011) presented a microstructure-dependent Bernoulli–Euler model to analyze the vibration and stability of microscale pipes conveying fluid. Analyzing in-plane and out-of-plane flexural vibrations of microscale pipes conveying fluid by including size effects of micro-flow and microstructure into the classical equations of motion is the subject of a recent research by Wang et al.(2013). Recently, Setoodeh and Afrahim (2014) presented an analytical solution based on strain gradient theory for the size-dependent nonlinear vibrational behavior of micro-pipes conveying fluid made of functionally graded materials (FGMs).

The applications of the smart materials such as piezoelectric materials in engineering structures have drawn serious attention recently. The piezoelectric materials are light and able to provide rapid response through electromechanical coupling. Such materials generate an electric field when subjected to strain fields and undergo deformation when an electric field is applied. However, in the knowledge of the authors, there has not been any discussion regarding piezoelectrically actuated microbeams conveying fluid.

The objective of this paper is to investigate the effect of applying piezoelectric layers on stability of the fluid-conveying micro-pipes. The equation of motion is derived via variational principle. The effect of piezoelectric voltage on frequencies and critical flow velocities is discussed thoroughly using eigenfrequency branches. For cantilever micro-pipes, applying positive/negative voltages on the piezoelectric layers generates compressive/tensile forces which are inherently nonconservative. This alters the stiffness properties of the system which in turn can change the stability situation of the structure. In addition, effects of the intermediate support on stability of the system are examined and it is shown that for some particular range of the system configuration, the instability type may change from flutter to divergence.

2 Model description and governing equations

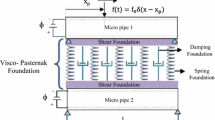
Figure 1 shows the system under consideration, which is a cantilever micro-pipe of length L, width b, thickness h, density ρ, Young’s modulus E, sandwiched with piezoelectric layers with thickness \(h_{p}\), density \(\rho_{p}\), Young’s modulus \(E_{p}\) which are attached to the free end of the micro-pipe. Parameters U and m are introduced as the average velocity and mass per unit length of the fluid flowing axially through the micro-pipe. The structure may also be modified to include an intermediate support as shown in the figure.

Fig. 1
figure 1

Schematic views of the piezoelectrically actuated micro-pipe conveying fluid with intermediate simply support

Full size image

Denoting the transverse displacement of the micro-pipe as w(x, t), the bending strain energy U b and the kinetic energy T b of the micro-pipe can be expressed as:

$$U_{b} = \frac{1}{2}\mathop \int \limits_{0}^{L} {\text{EI}}\left( {\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}} \right)^{2} {\text{d}}x$$
(1)
$$T_{b} = \frac{1}{2}\rho A\mathop \int \limits_{0}^{L} \left( {\frac{\partial w(x,t)}{\partial t}} \right)^{2} {\text{d}}x$$
(2)

where EI is the flexural rigidity, ρ is the mass density, and A is the cross-sectional area of the micro-pipe. The potential and the kinetic energy of the operating fluid can be written, respectively, as (Paidoussis 1998):

$$U_{f} = \frac{1}{2}\left( {m + \rho A} \right)g\mathop \int \limits_{0}^{L} \left( {L - x} \right)\frac{\partial w}{\partial x}{\text{d}}x$$
(3)
$$T_{f} = \frac{1}{2}m\mathop \int \limits_{0}^{L} \left( {U^{2} + \left( {\frac{\partial w(x,t)}{\partial t} + U\frac{\partial w(x,t)}{\partial x}} \right)^{2} } \right){\text{d}}x$$
(4)

Applying a voltage V p on the piezoelectric layers located on the micro-pipe surfaces, the resulted compressive or tensile follower force is expressed as (Azizi et al. 2012):

$$F_{p} = 2\frac{{b\bar{e}_{31} V_{p} {\text{AE}}}}{{2A_{p} E_{p} + {\text{AE}}}}$$
(5)

in which \(\bar{e}_{31}\) denotes the equivalent piezoelectric coefficient, A p and E p refer to the cross-section area and Young’s modulus of the piezoelectric layers, respectively. Moreover, the potential energy related to the piezoelectric layers can be written as:

$$U_{p} = \frac{1}{2}\mathop \int \limits_{0}^{L} \left( {F_{p} } \right)\left( {\frac{\partial w(x,t)}{\partial x}} \right)^{2} {\text{d}}x$$
(6)

The Lagrangian of the coupled system, accounting for the kinetic and potential energies, is written as:

$${\mathcal{L}}\left( t \right) = T_{b} + T_{f} - U_{b} - U_{f} - U_{p}$$
(7)

Now, referring to the principle of variation, time integral of variation of Lagrangian vanishes in any desired time interval as

$$\delta \mathop \int \limits_{{t_{0} }}^{{t_{1} }} {\mathcal{L}}(t){\text{d}}t = 0$$
(8)

Now the equation of motion for the micro-pipe in lateral vibration will be

$${\text{EI}}\frac{{\partial^{4} w}}{{\partial x^{4} }} + mU^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2mU\frac{{\partial^{2} w}}{\partial x\partial t} + \left( {m + \rho A} \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} = F_{p} \frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(9)

where the potential energy of the operating fluid due to gravitation is ignored (U f  = 0). The first term in the above equation stems from the elastic flexural restoring force, and the second term corresponds to the centrifugal force of the fluid flowing with constant speed U. Third term is recognized as being associated with the Coriolis acceleration, and the last term represents inertial effects of both pipe and fluid. In order to ease the calculations, following dimensionless parameters are defined

$$\eta = \frac{w}{L} ; \xi = \frac{x}{L} ; \tau = \left[ {\frac{\text{EI}}{{\left( {\rho A + m} \right)}}} \right]^{\frac{1}{2}} \frac{t}{{L^{2} }} ; \beta = \frac{m}{{\left( {\rho A + m} \right)}}$$
(10)

Substituting these parameters into Eq. (9) results in the following dimensionless equation of motion:

$$\frac{{\partial^{4} \eta }}{{\partial \xi^{4} }} + u^{2} \frac{{\partial^{2} \eta }}{{\partial \xi^{2} }} + 2\beta^{1/2} u\frac{{\partial^{2} \eta }}{\partial \xi \partial \tau } + \frac{{\partial^{2} \eta }}{{\partial \tau^{2} }} = \hat{F}_{p} \frac{{\partial^{2} \eta }}{{\partial \xi^{2} }}$$
(11)

where u and \(\hat{F}_{p}\) are the nondimensional flow velocity and piezoelectric force, respectively, defined as:

$$u = \left[ {\frac{m}{\text{EI}}} \right]^{\frac{1}{2}} {\text{UL}} ; \hat{F}_{p} = \frac{{F_{p} L^{2} }}{\text{EI}}$$
(12)

The corresponding boundary conditions for the cantilever and clamped–clamped micro-pipes are given by Eqs. (13a) and (13b), respectively:

$$\eta \left( {0,\tau } \right) = \frac{\partial \eta (0,\tau )}{\partial \xi } = \frac{{\partial^{2} \eta (1,\tau )}}{{\partial \xi^{2} }} = \frac{{\partial^{3} \eta (1,\tau )}}{{\partial \xi^{3} }} = 0$$
(13a)
$$\eta \left( {0,\tau } \right) = \frac{\partial \eta (0,\tau )}{\partial \xi } = \eta \left( {1,\tau } \right) = \frac{\partial \eta (1,\tau )}{\partial \xi } = 0$$
(13b)

In the case of a micro-pipe with intermediate simply support, the micro-pipe is divided into two parts with two different coordinate systems. The lateral deflection of the left and right parts is denoted by η 1 and η 2, respectively. At the intermediate support, compatibility equations between the left and right parts will be

$$\begin{aligned} \eta_{1} \left( {\xi_{1} = e,\tau } \right) = \eta_{2} \left( {\xi_{2} = 0,\tau } \right) = 0 \hfill \\ \frac{{\partial \eta_{1} (\xi_{1} = e,\tau )}}{{\partial \xi_{1} }} = \frac{{\partial \eta_{2} (\xi_{2} = 0,\tau )}}{{\partial \xi_{2} }} \hfill \\ \frac{{\partial \eta_{1}^{2} (\xi_{1} = e,\tau )}}{{\partial \xi_{1}^{2} }} = \frac{{\partial \eta_{2}^{2} (\xi_{2} = 0,\tau )}}{{\partial \xi_{2}^{2} }} \hfill \\ \end{aligned}$$
(14)

where ξ 1 and ξ 2 are the spatial coordinates in left and right parts, respectively. In order to discretize Eq. (11), Galerkin projection method is used by approximating η(ξ, τ) as:

$$\eta \left( {\xi ,\tau } \right) = \mathop \sum \limits_{j = 1}^{N} q_{j} \left( \tau \right)\varphi_{j} (\xi )$$
(15)

in which q j (τ) denotes the unknown generalized coordinates, and φ j (ξ) represents the j th natural mode shapes of a cantilever microbeam. Substituting Eq. (15) into Eq. (11) and multiplying by φ i (ξ) as a weight function and integrating the outcome over\(0 \le \xi \le 1\), results in:

$$\mathop \sum \limits_{j = 1}^{N} M_{ij} \textit{\"{q}}_{j} (\tau ) + \mathop \sum \limits_{j = 1}^{N} B_{ij} \dot{q}_{j} (\tau ) + \mathop \sum \limits_{j = 1}^{N} \left( {K_{ij}^{m} - K_{ij}^{p} + K_{ij}^{f} } \right)q_{j} (\tau ) = 0$$
(16)

where

$$M_{ij} = \mathop \int \limits_{0}^{1} \varphi_{i} \varphi_{j} d\xi ; B_{ij} = 2\beta^{1/2} u\mathop \int \limits_{0}^{1} \varphi_{i} \varphi^{\prime}_{j} d\xi ; K_{ij}^{m} = \mathop \int \limits_{0}^{1} \varphi_{i} \varphi_{j}^{iv} d\xi$$
$$K_{ij}^{p} = \widehat{T}_{p} \mathop \int \limits_{0}^{1} \varphi_{i} \varphi^{\prime}_{j} d\xi ; K_{ij}^{f} = u^{2} \mathop \int \limits_{0}^{1} \varphi_{i} \varphi^{\prime\prime}_{j} d\xi$$
(17)

For stability analysis, the solution of Eq. (16) can be written in the following form:

$$q_{j} \left( \tau \right) = \bar{q}_{j} e^{s\tau }$$
(18)

where \(\bar{q}_{j}\) are unknown functions of vibration amplitude, and s denotes the complex eigenvalues of the system where imaginary part of s ‘Im(s)’ is the natural frequency of micro-pipe conveying fluid. The pipe is unstable if at least one of the eigenvalues has a positive real part. Substituting Eqs. (18) into (16), one obtains a homogeneous equation, which corresponds to the generalized eigenvalue problem

$$\left( {s^{2} \left[ M \right] + s\left[ B \right] + \left[ {K^{m} } \right] - \left[ {K^{p} } \right] + \left[ {K^{f} } \right]} \right)\left\{ {\bar{q}_{j} } \right\} = \left\{ 0 \right\}$$
(19)

To obtain a nontrivial solution of Eq. (19), it is required that the determinant of the coefficient matrix vanishes, namely:

$$\det \left( {s^{2} \left[ M \right] + s\left[ B \right] + \left[ {K^{m} } \right] - \left[ {K^{p} } \right] + \left[ {K^{f} } \right]} \right) = 0$$
(20)

In general, roots or eigenvalues of the characteristic Eq. (20) for pipe conveying fluid cannot be expressed in simple explicit form in terms of u, V, and β. There are different numerical techniques to derive the eigenvalues. The most commonly used methods are straightforward numerical method (Païdoussis 2004), Galerkin method and Argand diagram (Dai et al. 2014), and D-composition method. In this paper, employing MATLAB software, the straightforward numerical method is used to obtain the eigenfrequencies.

3 Numerical results and discussion

In this section, the vibrational properties and stability of the micro-pipe for different values of fluid velocity as well as the applied voltage to piezoelectric layers are investigated. Moreover, effects of the intermediate support on the stability are studied. The fluid density used in the simulations is 1000 kg/m3, and the geometrical and material properties of the micro-pipe and the piezoelectric layers are listed in Table 1.

Table 1 Geometrical and material properties of the microbeam, piezoelectric layers, and fluid
Full size table

It should be noted that the centrifugal fluid force acts as a compressive load, and the piezoelectric layers are subject to compressive or tensile loads depending on the sign of the imposed voltage. Therefore beyond a critical fluid velocity u cr, the micro-pipe loses its stability by divergence (Pitchfork) or flutter (Hopf bifurcation) types. Figure 2 presents the variations of the nondimensional critical velocity of the fluid for the cantilever micro-pipe versus the mass ratio β for various applied voltages to the piezoelectric layers. Beyond this critical velocity, flutter instability occurs and vibration of the micro-pipe becomes amplified. The results show that increasing the value of mass ratio increases the critical fluid velocity and consequently extends the practical range of the micro-pipe. On the other hand, applying a positive/negative voltage to the piezoelectric layers softens/stiffens the micro-pipe and consequently reduces/enhances the critical velocity of fluid.

Fig. 2
figure 2

Nondimensional critical velocity of the fluid versus mass ratio for different voltages for cantilever micro-pipe

Full size image

Effects of the intermediate simply support on the critical fluid velocity are shown in Fig. 3. Assuming the support in different locations along the micro-pipe, the variations of the critical velocity versus the mass ratio for different piezoelectric voltages are depicted in the figure. It is revealed that moving the support toward the free end increases the stiffness of the micro-pipe and consequently boosts the critical velocity. Figure 3c shows that for a specific range of the support location (e > 0.4L), the critical velocity will not change by the mass ratio and it only depends on the piezoelectric voltage level.

Fig. 3
figure 3

Nondimensional critical velocity of the fluid versus mass ratio for different location of the intermediate support and various imposed voltages, a e = 0.2L, b e = 0.3L, c e = 0.4L

Full size image

It is shown when the support is placed at the end of the cantilever micro-pipe (e = L) irrespective of the mass ratio, the critical velocity is a specific value. This is depicted in Fig. 4 where the critical velocity for double-clamped micro-pipe is also shown for comparison. It is revealed that due to its higher stiffness, double-clamped micro-pipe has a larger critical velocity compared to clamped-pinned pipe.

Fig. 4
figure 4

Nondimensional critical fluid velocity versus mass ratio for different voltages for fixed–fixed and clamped-pinned micro-pipes

Full size image

It should be noted that a cantilever micro-pipe conveying fluid is a nonconservative system, and for a specific value of the flow velocity, it may lose its stability by flutter. However, imposing intermediate support can change the critical velocity as well as the type of instability. Taking into account different voltages of the piezoelectric layers and various locations of the intermediate support, imaginary and real parts of the nondimensional three lowest eigenfrequencies are plotted versus the flow velocity. The system is unstable if the real part of the any of the eigenfrequencies becomes positive.

Ignoring the intermediate support and assuming the mass ratio β = 0.5, Fig. 5 shows the effect of piezoelectric voltage on the critical velocity. It is revealed as the flow velocity increases, real part of the eigenvalue vanishes and the corresponding imaginary part still has a nonzero value; this point corresponds to flutter instability. Moreover, it is inferred that the positive and negative voltages of the piezoelectric layers do not change type of the instability. However, the negative voltages stiffen the structure and extend the stable ranges. In Fig. 5, dimensionless critical flow velocities of 10.7, 9.47, and 8.05 correspond to dimensional values of 97.03, 85.87, and 73 m/s, respectively.

Fig. 5
figure 5

Imaginary and real parts of the first three eigenfrequencies of the cantilever micro-pipe versus nondimensional flow velocity for different piezoelectric voltages as the mass ratio is set β = 0.5, a V = −0.5 v, b V = 0 v, c V = 0.5 v

Full size image

In Figs. 6 through 8, effects of the intermediate support on the form of the instability are studied. Assuming the support position as e = 0.2L and V = 0, variations of the real and imaginary parts of the eigenfrequencies versus the flow velocity for two mass ratios are presented in Fig. 6. It can be seen that the real part of one of the modes becomes zero for u = 11.17 where its imaginary parts are nonzero. This physically implies that the system becomes unstable by the flutter instability. Comparison of Fig. 6a, b shows that raising the mass ratio is responsible for increasing the critical flow velocity.

Fig. 6
figure 6

Imaginary and real parts of the lowest three eigenfrequencies versus the nondimensional flow velocity for the cantilever micro-pipe with intermediate support (e = 0.2L, V = 0 v) with different mass ratios, a β = 0.5, b β = 0.9

Full size image

Moving the intermediate support to new position e = 0.4L, the diagrams for the evolution of the real and imaginary parts of the eigenvalues as a function of the flow velocity are plotted in Fig. 7. It is shown for β = 0.2, the flutter type instability takes place at u = 8.4 (Fig. 7a). Figure 7b shows the variations of the real and imaginary parts for β = 0.8. It is shown the critical velocity increases as the mass ratio increases (u cr = 10.67). However, at the instability point, the imaginary part of the eigenvalue becomes zero and its real part becomes positive value. This physically denotes the divergence instability. Comparison of Figs. 3 and 7 reveals that imposing intermediate support beyond 0.4L in addition to the magnitude of the critical velocity, the form of the instability also changes from flutter to divergence type for some ranges of the mass ratio (β > 0.33).

Fig. 7
figure 7

Imaginary and real parts of the lowest three eigenfrequencies versus the nondimensional flow velocity for the cantilever micro-pipe with intermediate support (e = 0.4L, V = 0 v) at different mass ratios, a β = 0.2, b β = 0.8

Full size image

Finally, the evolution of the eigenfrequencies of clamped–clamped micro-pipe conveying fluid with increasing flow velocity is shown in Fig. 8. In this figure, it is assumed that the mass ratio β and voltage of the piezoelectric layers are fixed at 0.5 and 0 v, respectively. It is clear that the real and imaginary parts of the first nondimensional eigenvalue become zero when the flow velocity is 6.25. Therefore the divergence instability is taking place.

Fig. 8
figure 8

Real and Imaginary parts of the first three eigenfrequencies of the clamped–clamped micro-pipe conveying fluid versus nondimensional velocity for β = 0.5 and V = 0 v

Full size image

4 Conclusion

This paper introduces a novel system to enhance the dynamic behavior of a micro-pipe conveying fluids. To extend the stable margins, the micro-pipe was axially loaded with a pair of piezoelectric layers located at its top and bottom surfaces. It was shown that imposing negative voltage to the piezoelectric layers stiffens the micro-pipe and increases the critical fluid velocity. Effects of mass ratio (defined as the ratio of unit mass of operating fluid to the unit mass of micro-pipe) on the critical velocity were studied extensively. It was revealed that increasing the mass ratio increases the critical velocity and could also change the instability type from flutter to divergence. In addition, imposing an intermediate simply support, it was shown that the stability margins of the system can be improved effectively. It is found that placing the support at about 40 % of the beam length from clamped support changes instability type from flutter to divergence. The proposed mechanism can be employed in the applications where the high fluid velocity is required.