1 Introduction

Instabilities can occur in single or co-flowing fluids with non-uniform fluid properties, which is an important area in both fundamental and applied research of fluid dynamics (Darrigol 2002; Rahman 2005; Theofilis 2011). A wide range of flow instabilities have been identified and investigated, among which Rayleigh–Benard instabilities in fluids heated from below (Bodenschatz et al. 2000) and Rayleigh–Taylor instabilities in density stratified shear flows (Kull 1991) are readily seen in our day-to-day life. Flows in microfluidic devices are often characterized by low Reynolds numbers with a stable transport of fluids because of the dominant viscous damping (Knight 2002; Li 2004). However, fluid instabilities can also occur in microscale flows wherein fluid property gradients exist due to, for example, a non-uniform heating (Castellanos et al. 2003; Sridharan et al. 2011; Kale et al. 2013) or a mismatch of co-flowing fluids (Chang and Yang 2007; Lin 2009). The latter situation appears in numerous microfluidic applications such as particle/cell sorting and micro-mixing, where in the former case fluid instabilities must be suppressed in order for a precise control of particles and cells (Watarai 2013; Sajeesh and Sen 2014). In contrast, microfluidic mixing requires promoting the instabilities at the interface of co-flowing fluids because otherwise the samples therein are only exchanged through a slow molecular diffusion process (Nguyen and Wu 2005; Lee et al. 2011).

Ferrofluids are opaque suspensions of superparamagnetic nanoparticles (made of magnetite, Fe3O4, with an average diameter of 10 nm) that are coated with surfactants to prevent agglomerations for a uniform dispersion in either pure water or organic oil (Rosensweig 1985). They become strongly magnetized in the presence of a magnetic field. In the past decade, ferrofluids have been increasingly used for diamagnetic particle and cell manipulations such as focusing (Liang and Xuan 2012a; Zeng et al. 2012a; Zhu et al. 2011), trapping (Erb and Yellen 2008; Zeng et al. 2012b; Wilbanks et al. 2014), self-assembling (Feinstein and Prentiss 2006; Erb et al. 2009; Li and Yellen 2010), and sorting (Kose et al. 2009; Kose and Koser 2012; Liang and Xuan 2012b; Liang et al. 2013; Zeng et al. 2013; Zhu et al. 2010, 2012, 2014) in microfluidic devices via negative magnetophoresis (Liang et al. 2011; Cheng et al. 2014). They have also been recently exploited to achieve a fast microfluidic mixing through magnetic field-induced flow instabilities at the ferrofluid/water interface (Mao and Koser 2007; Wen et al. 2009, 2011; Zhu and Nguyen 2012b). This happens because of a magnetic body force acting on the ferrofluid (Zhu and Nguyen 2012a) that causes the ferrofluid to expand toward the water.

In the current work, we demonstrate for the first time that the application of a DC electric field can not only pump ferrofluids through a microchannel via electroosmosis, but also produce strong instabilities and even chaotic flows at the ferrofluid/water interface. These fluid instabilities arise from the interaction of the applied electric field and the induced free charge at the interface due to the electrical conductivity mismatch in the two fluids. Similar electrokinetic instabilities have been reported for electrolyte solutions with spatial conductivity gradients under the application of an electric field (Hoburg and Melcher 1976; El Moctar et al. 2003; Lin et al. 2004; Chen et al. 2005; Park et al. 2005; Shin et al. 2005; Posner and Santiago 2006). Chaotic (Posner et al. 2012) and even turbulent (Wang et al. 2014) flows were observed at the interface of two co-flowing electrolytes with significantly different electrical conductivities though the Reynolds number is only on the order of 1. Both theoretical (Baygents and Baldessari 1998; Storey et al. 2005; Oddy and Santiago 2005; Lin et al. 2008) and numerical (Lin et al. 2004; Kang et al. 2006; Vasudevan 2009) models have been developed to understand the physics involved and simulate directly the observed flow instabilities. Recently, electrokinetic instabilities have also been observed in non-dilute colloidal suspensions (Navaneetham and Posner 2009) whose electrical properties (e.g., conductivity and permittivity) are altered by the addition of charged colloidal particles (Posner 2009).

We perform in this work a combined experimental and numerical study of the electroosmotic ferrofluid/water co-flow through a T-shaped microchannel. The effects of electric field magnitude on the flow instabilities are studied by visualizing the dynamic behavior of the ferrofluid/water interface at the T-junction. The values of threshold electric field for the onset of flow instabilities are measured for ferrofluids of different concentrations. We also develop a 2D numerical model to solve the charge, fluid and mass transport equations in the horizontal plane of the microchannel. The numerically predicted ferrofluid concentration distributions are compared with the experimental images for different electric fields. Moreover, the predicted threshold electric fields are compared with the experimentally measured data for different ferrofluid concentrations.

2 Experimentation

2.1 Microchannel fabrication

The microchannel used for experiments was a T-shaped channel with two inlets and one outlet. Its fabrication was performed by the standard soft lithography technique using liquid polydimethylsiloxane (PDMS). The channel geometry was drawn in AutoCAD®, which was printed onto a transparent thin film at a resolution of 10,000 dpi (CAD/Art Services, Inc.) to make the photomask. SU-8-25 Photoresist (MicroChem) was spin-coated (WS-400B-6NPP/LITE, Laurell Technologies) onto a clean glass slide, which started at 500 rpm for 10 s and ramped by 300 rpm/s to the terminal spin speed of 1,000 rpm with a dwelling of 28.3 s, yielding a nominal thickness of 40 µm. After that, the slide was soft-baked on a hotplate (HP30A, Torrey Pines Scientific) in two steps, 65 °C for 5 min and 95 °C for 15 min. Next, the photoresist film was exposed to 365 nm UV light (ABM Inc.) through the negative photomask for 30 s and then subjected to another two-step hard bake (65 °C for 1 min and 95 °C for 4 min). It was subsequently developed in SU-8 developer solution (MicroChem) for 10 min, leaving a positive replica of the microchannel on the glass slide. The slide was subjected to another two-step post-bake (65 °C for 1 min and 95 °C for 5 min) after being briefly rinsed with isopropyl alcohol (Fisher Scientific). The patterned photoresist on the slide, called a master, was then ready to be used as the mold of the T-shaped microchannel.

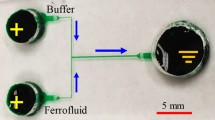
Liquid PDMS was prepared by mixing Sylgard 184 and the curing agent at a 10:1 weight ratio. It was filled onto the channel mold positioned in a Petri dish and then degassed for 15 min in an isotemp vacuum oven (13-262-280A, Fisher Scientific). Following a curing in a gravity convection oven (13-246-506GA, Fisher Scientific) for 3 h at 70 °C, the portion of the PDMS covering the complete microchannel was removed from the mold using a scalpel. Next, two holes for the inlets and one hole for the outlet, which served as reservoirs in experiments, were made using a metal punch. Subsequently, the channel surface of the PDMS and a clean glass slide were plasma-treated (PDC-32G, Harrick Scientific) for 1 min before being bonded to each other to form the microchannel. Once sealed, DI water was dispensed into the channel by capillary action to wet the channel and preserve the walls’ hydrophilicity. Figure 1 shows a picture of the fabricated T-shaped microchannel used for the experiment. Each side-branch is 8 mm long and 100 µm wide, whereas the main branch has a length of 10 mm with a width of 200 µm. The depth of the channel is 40 µm throughout.

Fig. 1
figure 1

Picture of a fabricated T-shaped microchannel (filled with green food dye for clarity) where the block arrows indicate the flow directions during the experiment

Full size image

2.2 Experimental technique

The electrokinetic instability in ferrofluid microflows was studied using three different concentrations of ferrofluid, namely 0.1×, 0.2× and 0.3× by volume of the original EMG 408 ferrofluid (Ferrotec). A total of 100 µL of each concentration was prepared by mixing 10, 20 and 30 µL of the original ferrofluid with 90, 80 and 70 µL of DI water (Thermo Scientific), respectively, using a fixed-speed vortex mixer (Fisher Scientific). Prior to experiment, all reservoirs were emptied. DI water (appears transparent) and ferrofluid (appears dark) of equal volume were dispensed separately into the two inlet reservoirs of the T-shaped microchannel in Fig. 1. They flowed through the main branch to the outlet reservoir, making an interface along the centerline. This pressure-driven motion was carefully eliminated by gradually adding DI water into the outlet reservoir to match the liquid level in the inlet reservoirs. The electric field in the fluid was generated by imposing an equal magnitude of DC voltage (Glassman High Voltage Inc.) to the inlet reservoirs, while grounding the outlet reservoir. The evolution of interfacial instability between the ferrofluid and water flows at the T-junction of the microchannel was visualized using an inverted microscope (Nikon Eclipse TE2000U, Nikon Instruments). Digital videos were recorded through a CCD camera (Nikon DS-Qi1Mc) at a rate of 15 frames per second and post-processed using the Nikon imaging software (NIS-Elements AR 2.30). The experiment in every tested case was carried out with a continuously increasing electric field (started at a low magnitude) to find the threshold value at which the interfacial instability was visually observed at the T-junction.

3 Simulation

3.1 Governing equations

The variation of electrical properties between ferrofluid and DI water induces electrical body forces on their interface in the presence of an electric field (Stratton 2007), when strong enough can alter the flow behaviors in the two fluids and result in instabilities as we will demonstrate in the Sect. 4 (cf., Fig. 6 from experiments and Fig. 7 from simulations). To capture the physics of this phenomenon, the transport equations for electrical charge, fluid flow and mass species need to be solved. As the magnetic effects are negligible (see our analysis in the Supplementary Material), the equations that govern the electric field are obtained from the Maxwell’s equations as follows (Melcher 1981; Saville 1997),

$$ {\nabla } \cdot \left( {\varepsilon {\mathbf{E}}} \right) = \rho_{e} $$
(1)
$$ \frac{{\partial \rho_{e} }}{\partial t} + \nabla \cdot {\mathbf{i}} = 0 $$
(2)

where \( {\mathbf{E}} = - \nabla \emptyset \) is the electric field vector with \( \emptyset \) being the electrostatic potential, \( \rho_{e} \) is the free charge density, \( \varepsilon \) is the dielectric permittivity of the fluid, t is the time and i is the electric current density. As the diffusional and convectional currents are insignificant compared to the conduction current in our system, the current density can be expressed as (Melcher 1981; Castellanos et al. 2003),

$$ {\mathbf{i}} = - \sigma {\nabla }\emptyset $$
(3)

where \( \sigma \) represents the electrical conductivity of the fluid. Combining Eqs. (1)–(3) gives,

$$ \nabla \cdot \left[ {(\sigma + i\omega \varepsilon )\nabla \emptyset } \right] = 0 $$
(4)

where \( \omega \) is the angular frequency of the applied electric field. Since only DC electric fields (i.e., \( \omega = 0 \)) are used in our experiments, the electrostatic potential satisfies,

$$ \nabla \cdot (\sigma \nabla \emptyset ) = 0 $$
(5)

The flow field is governed by the continuity and momentum equations,

$$ \nabla \cdot {\mathbf{u}} = 0 $$
(6)
$$ \rho \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} + {\mathbf{u}} \cdot \nabla {\mathbf{u}}} \right) = - \nabla p + \mu \nabla^{2} {\mathbf{u}} + \rho_{e} {\mathbf{E}} - \frac{1}{2}{\mathbf{E}}^{2} \nabla \varepsilon $$
(7)

where \( \rho \) is the fluid density, u is the velocity vector, p is the pressure and \( \mu \) is the fluid dynamic viscosity. The last two terms in the momentum equation represent the Coulomb and dielectric forces (Melcher and Taylor 1969), respectively. Since there is no chemical reaction and species generation, the conservation of mass species (i.e., magnetic nanoparticles in the ferrofluid) yields,

$$ \frac{\partial c}{\partial t} + {\mathbf{u}} \cdot \nabla c = D\nabla^{2} c $$
(8)

where D is the diffusivity and c is the ferrofluid concentration. Note that the effect from the electrophoretic motion of magnetic nanoparticles is small (see our analysis in the Supplementary Material) and has been neglected in Eq. (8).

3.2 Model setup

Ferrofluid comes in direct contact with DI water only in the main branch of the T-shaped microchannel (see Fig. 1), and hence the T-junction is our primary area of focus. A two-dimensional domain chosen for the study is shown in Fig. 2, where only a length of 2,000 µm in the main branch and a length of 350 µm in each side-branch are considered to reduce the computational cost. The following boundary conditions are prescribed,

Fig. 2
figure 2

Illustration of the two-dimensional domain (i.e., in the horizontal plane of the T-shaped microchannel in Fig. 1, drawn to scale) used in the numerical simulation with important dimensions being indicated

Full size image

Water inlet: \( \emptyset = \emptyset_{\text{in}} ;\;p = 0; \;c = 0 \);

Ferrofluid inlet: \( \emptyset = \emptyset_{\text{in}} ; \;p = 0; \;c = c_{0} \);

Outlet: \( \emptyset = 0; \;p = 0;\; \nabla c \cdot {\mathbf{n}} = 0 \);

Walls: \( \nabla \emptyset \cdot {\mathbf{n}} = 0;\; {\mathbf{u}} \cdot {\mathbf{n}} = 0;\; {\mathbf{u}} \cdot {\mathbf{t}} = U_{\text{HS}} = {{ - \varepsilon \zeta {\mathbf{E}} \cdot {\mathbf{t}}} \mathord{\left/ {\vphantom {{ - \varepsilon \zeta {\mathbf{E}} \cdot {\mathbf{t}}} \mu }} \right. \kern-0pt} \mu };\; \nabla c \cdot {\mathbf{n}} = 0 \).

In the above, \( c_{0} \) is the ferrofluid concentration in the inlet reservoirs (specifically, the volume fraction of the original EMG 408 ferrofluid, e.g., 0.2× denotes a concentration of 0.2 with no unit), n and t represent the unit normal and tangential vectors, respectively, of a surface, \( \zeta \) is the zeta potential of the channel wall, and \( U_{\text{HS}} \) is the so-called Helmholtz–Smoluchowski velocity (Probstein 1994) that is a frequently used boundary condition in electroosmotic flows (Li 2004; Chang and Yeo 2009). Such a slip condition is valid under the assumption of a thin electrical double layer, which is fulfilled in our system because the smallest channel dimension (i.e., 40 µm depth) is more than two orders of magnitude greater than the double layer thickness in water (about 300 nm if the ionic concentration is treated as 1 nM). In addition, the initial conditions are as follows, At t = 0: \( \emptyset = 0;\;p = u = v = 0;\;c = 0 {\text{ for }}y > 0\,({\text{water}});\;c = c_{0} \;{\text{for}}\; y < 0\,({\text{ferrofluid}}) \).

Equations (1) and (5)–(8) are coupled through the concentration dependence of ferrofluid properties including density \( \rho \), viscosity \( \mu \), electrical conductivity \( \sigma \), and possibly dielectric permittivity \( \varepsilon \). The former two properties were considered in our model using the same formulae as those in Wen et al. (2011) and Zhu and Nguyen (2012a, b),

$$ \rho = c\rho_{\text{f}} + (1 - c)\rho_{\text{w}} $$
(9)
$$ \mu = \mu_{\text{f}} e^{{\ln \left( {\mu_{\text{w}} /\mu_{\text{f}} } \right)\left( {1 - c} \right)}} $$
(10)

where the subscripts f and w indicate the properties of the original EMG 408 ferrofluid and water, respectively. The electrical conductivities of ferrofluids in a range of concentrations were measured using Accumet AP85 pH/conductivity meter (Fisher Scientific), which were found to vary linearly with concentration as shown in Fig. 3,

$$ \sigma = c\sigma_{\text{f}} + (1 - c)\sigma_{\text{w}} $$
(11)

Since there are no established permittivity data for ferrofluids in the literature, we assumed an equal value to that of water in our model. The potential influence of the permittivity gradients is discussed later. The property values involved in Eqs. (9)–(11) are listed in Table 1.

Fig. 3
figure 3

Measured values (symbols) and the linear fit (line with the equation and R-squared value indicated) of electrical conductivity for EMG 408 ferrofluid at the range of concentrations from 0.01× to 0.3× (volume fraction)

Full size image
Table 1 Physicochemical properties of the tested ferrofluid–water microchannel system
Full size table

The average wall zeta potential of the PDMS/glass channel filled with ferrofluid was determined indirectly from the measurement of electroosmotic mobility via the electric current method (Li 2004). It was found to vary insignificantly with the ferrofluid concentration in the tested range from 0.1× to 0.3× if the ferrofluid permittivity was assumed constant as noted above. Moreover, the obtained value was found to be slightly lower than that of water reported in the literature (Kirby and Hasselbrink 2004). Therefore, we simply chose −100 mV for both ferrofluid and water in the model (see Table 1). The diffusion coefficient of ferrofluid can be calculated from the Stokes–Einstein equation (Zhu and Nguyen 2012a, b) by assuming a 10 nm diameter for the suspended magnetic nanoparticles (Rosensweig 1985). The obtained diffusivity of 4.39 × 10−11 m2/s is very small, which makes the computation of concentration field in Eq. (8) very expensive in order to render the numerical dispersion effects small. We therefore chose the same value, D = 1.0 × 10−9 m2/s (see Table 1), as in the paper from Wen et al. (2011) to reduce the computational cost.

3.3 Numerical implementation

The set of transport equations, i.e., Eqs. (1) and (5)–(8), were solved numerically in a finite element-based commercial solver, COMSOL® 4.3b, over the two-dimensional domain shown in Fig. 2 using the parameters listed in Table 1. As illustrated in Fig. 4, the main body of the computational domain was meshed with square elements, while the fillet regions at the T-junction (see the inset) were meshed with triangular elements. An automatic time stepping method available in COMSOL® was employed for the simulation. We performed a grid-independence study for selecting a mesh size that is small enough to capture the physics of flow instability, while big enough to run the simulation efficiently. Since the governing equations are coupled and highly nonlinear, comparing the results at a particular instance for different mesh sizes turns out to be difficult. To overcome this difficulty, time-averaged fluid velocity profiles along various cross sections of the main branch were compared for different sizes of square meshes. For example, Fig. 5 shows such a comparison for the 0.1 × ferrofluid/water co-flow at a cross section 1,200 µm downstream from the T-junction under an electric field of 96 V/cm in the main branch. The plot shows no significant difference between the profiles with a mesh size of 4 µm and 2 µm, respectively, which was also observed for other cross sections of the main branch. Hence, a mesh size of 4 µm was chosen in our model.

Fig. 4
figure 4

Illustration of the 2D computational domain (see Fig. 2) meshed with structured square elements. The inset shows a close-up view of the highlighted fillet region at the T-junction that is meshed with triangular elements. Note that the elements (there are actually 50 elements in the channel width direction) are not clearly displayed due to the limited resolution of the plot

Full size image
Fig. 5
figure 5

Grid-independence study of structured square meshes in the 2D computational domain (see Fig. 4) via the comparison of velocity profiles of 0.1× ferrofluid/water co-flow at a cross section 1,200 µm downstream from the T-junction. The applied DC electric field is 96 V/cm in the main branch of the microchannel. This plot was generated in COMSOL® directly

Full size image

4 Results and discussion

4.1 Experimental results

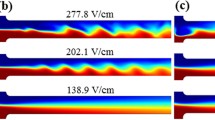
Experiments were carried out for three concentrations of ferrofluids, namely 0.1×, 0.2× and 0.3×, co-flowing with DI water in the T-shaped microchannel. Figure 6 shows the snapshot images captured at the T-junction at different time instances for the 0.2× ferrofluid (dark)/water co-flow under different DC electric fields. The experimental values of electric field were determined by simply dividing the DC voltage imposed to the inlet reservoir with the overall channel length from the inlet to the outlet reservoirs (which is 18 mm for our channel in Fig. 1). They were found to be slightly larger (less than 7 %) than the values obtained from a 2D full-scale numerical model (i.e., the entire T-shaped microchannel was considered) by solving Eq. (5) with a uniform fluid (which then reduces to Laplace’s equation). Note that the contrast in the original colors of ferrofluid (black, non-transparent) and water (transparent) has been utilized to visualize the interface, and so the images in Fig. 6 are all in grayscale.

Fig. 6
figure 6

Snapshot images of the 0.2× ferrofluid (dark, non-transparent)/water (transparent) co-flow captured at the T-junction of the microchannel at different time instances under the application of various DC electric fields. The scale bar on the top-most image in (a) represents 200 µm. The flow direction is from left to right in all images

Full size image

No signs of flow instability were observed under an electric field of up to 172.2 V/cm (corresponding to an applied DC voltage of 310 V), where just pure diffusion happened between the ferrofluid and water as seen from Fig. 6a. At 175.0 V/cm, intermittent instability waves occurred at the ferrofluid/water interface but could not be maintained as demonstrated in Fig. 6b. The system is at a transition state at this electric field, and even a small disturbance due to debris was found to generate temporary instability waves at the ferrofluid/water interface. When the electric field was increased to 177.8 V/cm, consistent periodic instability waves were generated near the T-junction and convected downstream in Fig. 6c. This value is thus designated as the threshold electric field, which signifies the minimum electric field at which sustainable flow instabilities can be visually identified. Further increases in the electric field generated rich dynamic instability features, which may even exhibit a chaotic behavior (Posner et al. 2012) as viewed from Fig. 6d under the electric field of 555.6 V/cm. Similar trend of flow instabilities with the increase in electric field was also observed in 0.1× and 0.3× ferrofluid/water co-flows (images not shown due to the space limit). However, the threshold electric fields were found to be 213.8 V/cm and 169.4 V/cm, respectively, for the 0.1× and 0.3× ferrofluids, which apparently decreases with the increase in ferrofluid concentration.

4.2 Numerical results

The time evolution of numerically predicted ferrofluid (essentially magnetic nanoparticles) concentration in the 0.2× ferrofluid/water co-flow at the T-junction is shown in Fig. 7 for different electric fields. The listed values of electric field were all obtained in the middle of the main branch directly from the numerical simulation. Under low electric fields such as 22.0 V/cm, pure diffusion happens quickly at the ferrofluid/water interface in Fig. 7a due to the weak electroosmotic flow and hence a small Peclet number (defined as \( Pe = U_{\text{HS}} d/D \approx 10 \) with d the hydraulic diameter of the microchannel) therein. At an increased electric field of 70.5 V/cm in Fig. 7b, instability waves are generated in the initial short period but soon dampened out as time progresses. Moreover, the diffusion at later times in Fig. 7b happens at an apparently slower rate than in Fig. 7a due to the increased Peclet number. This predicted concentration development is qualitatively similar to the experimental observation in Fig. 6b, the latter of which was, however, obtained at a much greater electric field. When the applied field is further increased to 81.1 V/cm in Fig. 7c, stronger flow instabilities occur at the ferrofluid/water interface and exhibit a dynamic pattern in the initial 4 s. They are subsequently stabilized and appear as sustainable periodic waves, which agree qualitatively with the experimental observations in Fig. 6c. However, this numerically predicted threshold electric field for the onset of stable flow instabilities is less than one half of the experimentally obtained value. Moreover, the predicted waves in Fig. 7c are inclined downstream, while those experimental ones in Fig. 6c seem to be inclined more toward the upstream. This may be due to the over-prediction of electroosmotic velocity in the ferrofluid flow. Further increase in electric field leads to an increased amplitude of instability waves and can even produce chaotic flows as shown in Fig. 7d. This again is qualitatively similar to the experiment result in Fig. 6d.

Fig. 7
figure 7

Time evolution of numerically predicted ferrofluid concentration (more accurately, the magnetic nanoparticle concentration) in the 0.2× ferrofluid/water co-flow at the T-junction under various DC electric fields

Full size image

Figure 8 shows the plots for numerically predicted quantities of the 0.2× ferrofluid/water co-flow at the T-junction under the threshold electric field. These plots are associated with the concentration contour at 20 s in Fig. 7c that is also included in the top panel of Fig. 8 for an easy reference. Figure 8a shows the electric field lines (blue) that become nearly straight quickly after the T-junction, i.e., parallel to the length direction in the main branch of the microchannel. However, the electric field lines coming from the side-branch for water flow (cf., Figs. 2 and 6) are squeezed toward the top sidewall in the main branch. In contrast, the electric field lines coming from the side-branch for ferrofluid flow are expanded to cover nearly the entire width of the main branch. This is attributed to the much lower electrical conductivity of water compared to that of ferrofluid. The iso-concentration lines (black) are included in Fig. 8a and also retained in Fig. 8b–d for relating each parameter illustrated therein to the position of instability waves. Figure 8b presents the contour of free charge density, i.e., \( \rho_{e} \) in Eqs. (1) and (7), which is negative above the centerline and positive below the centerline in the diffusion zone that immediately follows the T-junction. This imparts an anticlockwise force and deforms the ferrofluid/water interface, leading to the formation of instability waves downstream. Moreover, the free charge density changes sign at the fore and rear of each wave, thereby stretching the wave as illustrated by the vector plot of electrical body force, \( \rho_{e} {\mathbf{E}} \), in Fig. 8c. Consequently the flow velocity decreases and increases alternatively in the fore and rear regions of each wave as demonstrated by the velocity magnitude in Fig. 8d.

Fig. 8
figure 8

Numerical predictions of electric field lines (a), free charge density (b, contour), electrical body force (c, vector plot) and fluid velocity magnitude (d, contour) of the 0.2× ferrofluid/water co-flow at the T-junction. All plots are associated with the concentration contour at 20 s in Fig. 7c (also included in the top panel of this figure for easy references) under the threshold electric field

Full size image

Similar simulations were also carried out for both 0.1× and 0.3× ferrofluids. The predicted threshold electric fields for observing stable flow instabilities at the ferrofluid/water interface are compared with the experimentally obtained values in Fig. 9. It is evident that the numerical model significantly under-predicts the threshold electric fields obtained from experiments. However, the experimentally observed decrease in threshold electric field with increasing ferrofluid concentration is correctly predicted. The current model assumes ferrofluid as a continuous fluid where the electrophoretic and magnetophoretic motions of magnetic nanoparticles are not taken into account. We have investigated each of these parameters and found that their effects on the threshold electric field are insignificant as presented in the Supplementary Material. It is speculated that the following factors may be (partially) responsible for the under-estimation of the threshold electric field: (1) the top and bottom wall effects in the microchannel are not considered in our model, which have been demonstrated by Storey et al. (2005) to stabilize the electroosmotic flow; (2) a much larger ferrofluid diffusivity than the real value (e.g., calculated via the Stokes–Einstein equation) is used in the current model, which has been demonstrated by Kang et al. (2006) to delay the onset of flow instability between co-flowing electrolytes of dissimilar electrical conductivities; (3) the mismatch of the ferrofluid and water permittivity values is neglected in this model, which, if ferrofluid has a greater permittivity than water, can generate a dielectric force, \( - \frac{1}{2}{\mathbf{E}}^{2} \nabla \varepsilon \), acting in the opposite direction to the Coulomb force, \( \rho_{e} {\mathbf{E}} \), in Eq. (7) (Navaneetham and Posner 2009), and hence stabilize the flow.

Fig. 9
figure 9

Comparison of the experimentally observed and numerically predicted threshold electric fields for the onset of stable flow instabilities in ferrofluids of different concentrations

Full size image

5 Conclusions

We have demonstrated for the first time the electric field-induced electrokinetic instabilities in ferrofluid/water co-flows through a T-shaped microchannel. Instability waves and even chaotic flows are experimentally observed with the increase in the applied DC electric field. These flow instabilities arise from the significant mismatch of electrical conductivity between the two fluids, which happen in a similar pattern to those reported in the literature for co-flowing electrolytes of dissimilar concentrations (and hence different conductivities) (e.g., El Moctar et al. 2003; Lin et al. 2004; Park et al. 2005; Posner and Santiago 2006; Posner et al. 2012; Wang et al. 2014). The threshold electric field, at which the instability waves can be sustained, is found to decrease with the increase in ferrofluid concentration. We have also developed a 2D numerical model that is similar to those in the literature (Kang et al. 2006; Vasudevan 2009) and capable of simulating the electrokinetic instability due to the conductivity difference between ferrofluid and water. It is found that the dynamic behaviors at the ferrofluid/water interface at various electric fields can be qualitatively simulated by the computed ferrofluid (essentially the magnetic nanoparticles therein) concentration field. However, the numerical model substantially under-predicts the threshold electric field for all three tested concentrations of ferrofluids. Moreover, we have carried out brief studies (see the Supplementary Material) on the effects of electrophoretic and magnetophoretic motions of nanoparticles in ferrofluids on the threshold electric field, which are both found to be insignificant. It is speculated that the significant discrepancy between the experimentally and numerically obtained threshold electric fields may be (partially) due to the neglect of the top/bottom channel walls’ stabilizing effects, the inappropriate use of a greater ferrofluid diffusivity than real, and the omission of the permittivity difference between ferrofluid and water.