1 Introduction

The flow of a salt-containing liquid driven by an applied electric field, known as electroosmosis, is widely adopted in separation technology, micro-pump (Jacobsa et al. 2012; Lee et al. 2013), lab-on-chip, ionic current rectification (Kutter 2000; Mei et al. 2008; White and Bund 2008; Wang et al. 2009; Karenga and El Rassi 2010; Yusko et al. 2010; Pevarnik et al. 2012; Yan et al. 2013), and single-molecule biosensors (So et al. 2005; Sorgenfrei et al. 2011; Choi et al. 2013). Recent advances in fabrication technology (Gasparac et al. 2004; Dekker 2007; Lam et al. 2012; Wang et al. 2012; Xia et al. 2012) further extend its application to nanoscaled devices. As the linear size of a channel down to submicron or even nanosize, the characteristics of the flow inside can no longer easily measured by those used in larger sized channels such as volumetric flow rate. In this case, the ionic current (or conductance), which can be measured accurately on the order of pico ampere (pA) (Storm et al. 2005), is an appropriate choice. In practice, ionic current can be generated without too much difficulty through applying electrical field to a nanochannel (Stein et al. 2004; van der Heyden et al. 2007; Xu et al. 2010; Li et al. 2013). Choi and Kim (2009) showed that the current induced by the electroosmotic flow (advection current) in a silica nanoslit can be important, and impose several impacts on the total current.

The analyses on the ionic current in a nanochannel are usually based on the frame of either a Poisson Boltzmann (PB) model (Huang and Yang 2007; Wang and Revil 2010) or a Nernst–Planck (NP) model (Daiguji et al. 2004; Park et al. 2007; Yaroshchuk 2012; Zhao and Yang 2012). Although the later is more rigorous, the former is sufficiently accurate if a channel is sufficiently long so that concentration polarization is unimportant, or the salt concentration is sufficiently high so that double-layer overlapping is insignificant.

For simplicity, previous analyses often assumed that the surface of a channel is maintained either at a constant surface potential (Rice and Whitehead 1965; Shugai and Carnie 1999) or at a constant charge density (Qian et al. 2006; Ai et al. 2010). In practice, because the charge on a channel surface usually comes from the dissociation/association of its functional groups (Holland et al. 1999; Xia et al. 2000; Tseng et al. 2013a), the corresponding charged conditions are somewhere between those two limiting cases, and vary with solution properties (Wall 2010). For example, when immersed in an aqueous medium, the surface of metal oxide such as SiO2 reacts as \({\text{MOH}} \Leftrightarrow {\text{MO}}^{ - } + {\text{H}}^{ + }\) and \({\text{MOH}} + {\text{H}}^{ + } \Leftrightarrow {\text{MOH}}_{2}^{ + }\). Apparently, the charged conditions in this case depend highly on solution pH. This also implies that the presence of ionic species other than those coming from background salt can be significant. For example, if pH deviates appreciably from 7, the concentrations of H+ and OH− might exceed those of the background salt. This factor is usually overlooked in previous studies (Hsu et al. 2000; Yu et al. 2004; Wang et al. 2010). In a study of the electrophoresis of a charge-regulated particle, Hsu and Tai (2010) and Hsu et al. (2011) concluded that considering the ionic species coming from background salt only might yield appreciable deviation in particle mobility. Because the behavior of electroosmotic flow depends highly on the thickness of double layer, which varies with ionic strength, taking account of all the ionic species with an appreciable concentration is necessary.

Recently, Tseng et al. (2013b) modeled the flow of an aqueous salt solution in a charge-regulated cylindrical nanochannel. Because this study focused on characterizing the flow behavior only, the results obtained are inconvenient for future applications. It is desirable and necessary to extend that analysis to consider the behavior of a more readily measurable quantity such as ionic current. This is done in the present study, along with a detailed discussion on the mechanisms involved in ionic transport under various conditions by varying the pH, the density of surface functional groups, and the background salt concentration. For illustration, the flow of an aqueous NaCl solution in a SiO2 nanochannel with pH adjusted by HCl and NaOH in a pH-regulated nanochannel is considered.

2 Theory

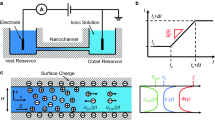
As illustrated schematically in Fig. 1, we consider the electroosmotic flow of an incompressible Newtonian fluid along its axis of a cylindrical nanochannel of radius R driven by an applied uniform electrical field E. r and z are, respectively, the radial and the axial distances of the cylindrical coordinates adopted with the origin on the nanochannel axis. ΩW and ΩE are the lateral surface and the inlet and outlet surfaces of the nanochannel, respectively.

Fig. 1
figure 1

Electroosmosis in a cylindrical nanochannel of radius R subject to an applied uniform electrical field E in the z direction; r and z are, respectively, the radial and the axial distances of the cylindrical coordinates adopted with the origin on the nanochannel axis; ΩW and ΩE are the lateral surface and the inlet and outlet surfaces of the nanochannel, respectively

Full size image

We assume that the liquid phase contains N kinds of ionic species, the flow field is in the creeping flow regime, and the system under consideration is at a pseudo-steady state. In addition, E is weak compared with the electrical field established by the nanochannel, and it is sufficiently long so that the effect of concentration polarization (Kim et al. 2007; Zangle et al. 2010) and that of the reservoirs at the ends of the nanochannel (Yeh et al. 2013) are insignificant. Furthermore, we assume that the ionic concentration is sufficiently high (>10−4 M) so that the double layer is sufficiently thin (<30 nm), and the overlapping of electric double layer (EDL) is insignificant if the channel radius is large (e.g., 50 nm). Under these conditions, a Boltzmann distribution can be assumed for the ionic species. Similar to the treatments of O’Brien and White (1978) and Ohshima (1995, 2006), the original problem is partitioned into an equilibrium problem and a perturbed one. In this approach, the dependent variables (electrical potential, ionic concentration, charge density, and fluid velocity) are partitioned into an equilibrium term and a perturbed term; the former is the value of that variable when E is not applied, and the latter is that coming from E. Because no pressure gradient is applied and the equilibrium term of the fluid velocity vanishes, the equations governing the present problem are

$$\nabla^{2} \phi_{\text{e}} = - \frac{{\rho_{\text{e}} }}{\varepsilon } = - \sum\limits_{j = 1}^{N} {\frac{{z_{j} en_{{j{\text{e}}}} }}{\varepsilon }} = - \sum\limits_{j = 1}^{N} {\frac{{z_{j} en_{j0} }}{\varepsilon }} \exp \left( { - \frac{{z_{j} e}}{{k_{\text{B}} T}}\phi_{\text{e}} } \right)$$
(1)
$$\nabla^{2} \delta \phi = 0$$
(2)
$$\eta \nabla^{2} \delta {\mathbf{v}} + \nabla^{2} \phi_{\text{e}} \nabla \delta \phi = {\mathbf{0}}$$
(3)
$$\nabla \cdot \delta {\mathbf{v}} = 0$$
(4)
$$n_{{j{\text{e}}}} = n_{j0} \exp \left( { - \frac{{z_{j} e}}{{k_{\text{B}} T}}\phi_{\text{e}} } \right),\quad j = 1,2, \ldots ,N$$
(5)

In these expressions, the subscript e and the prefix δ denote the equilibrium and the perturbed properties, respectively. ε, η, ρ, e, k B, T, ϕ, and v are the permittivity and the viscosity of the liquid phase, the space-charge density, the elementary charge, Boltzmann constant, the absolute temperature, the electrical potential, and the fluid velocity, respectively. z j , n j , and n j0 are the valence, the number concentration, and the bulk ionic concentration of ionic species j, respectively, j = 1,2,…,N. Equation 2 implies that concentration polarization is neglected (i.e., δn j  = 0).

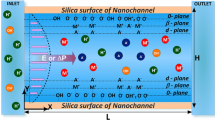
Suppose that the nanochannel surface has functional groups AH with associated reactions (Binner and Zhang 2011):

$${\text{AH}} \Leftrightarrow {\text{A}}^{ - } + {\text{H}}^{ + }$$
(6)
$${\text{AH}} + {\text{H}}^{ + } \Leftrightarrow {\text{AH}}_{2}^{ + }$$
(7)

Let \(K_{a} = N_{\text{A}} - \left[ {{\text{H}}^{ + } } \right]/N_{\text{AH}}\) and \(K_{b} = N_{{{\text{AH}}_{2}^{ + } }} /N_{\text{AH}} \left[ {{\text{H}}^{ + } } \right]\) be the corresponding equilibrium constants with \(N_{{{\text{A}}^{ - } }}\), \(N_{{{\text{AH}}_{2}^{ + } }}\), N AH, and [H+] being the surface densities (mol/m2) of A−, AH2 +, AH, and the concentration of H+, respectively. The total density of AH on the nanochannel surface, N total, can be expressed as \(N_{\text{total}} = N_{{{\text{A}}^{ - } }} + N_{\text{AH}} + N_{{{\text{AH}}_{2}^{ + } }}\). If we let [H+]0 and F be the bulk concentration of H+ and Faraday constant, respectively, it can be shown that the surface charge density, σ s, is

$$\sigma_{\text{s}} = - FN_{\text{total}} \left( {\frac{{K_{\text{a}} - K_{\text{b}} ([{\text{H}}^{ + } ]_{0} \exp ( - e\phi_{\text{e}} /k_{\text{B}} T))^{2} }}{{K_{\text{b}} ([{\text{H}}^{ + } ]_{0} \exp ( - e\phi_{\text{e}} /k_{\text{B}} T))^{2} + [{\text{H}}^{ + } ]_{0} \exp ( - e\phi_{\text{e}} /k_{\text{B}} T) + K_{\text{a}} }}} \right)$$
(8)

The surface potential can be obtained from this expression by applying Gauss’s law.

We assume that the nanochannel surface is non-conductive and non-slip, the equilibrium potential is z independent, and the flow field is fully developed. These yield the following boundary conditions:

$${\mathbf{n}} \cdot (\varepsilon \nabla \phi_{\text{e}} ) = - \sigma_{\text{s}} \;{\text{on}}\;\varOmega_{\text{W}}$$
(9)
$${\mathbf{n}} \cdot \nabla \delta \phi = 0\;{\text{on}}\;\varOmega_{\text{W}}$$
(10)
$${\mathbf{n}} \cdot \nabla \phi_{\text{e}} = 0\;{\text{on}}\;\varOmega_{\text{E}}$$
(11)
$${\mathbf{n}} \cdot \nabla \delta \phi = - E_{z} \;{\text{on}}\;\varOmega_{\text{E}}$$
(12)
$$\delta {\mathbf{v = 0}}\;{\text{on}}\;\varOmega_{\text{W}}$$
(13)
$${\mathbf{n}} \cdot \nabla \delta {\mathbf{v}} = {\mathbf{0}}\;{\text{on}}\;\varOmega_{\text{E}}$$
(14)

E z is the strength of the applied electrical field; n is the unit outer normal vector on a surface, except that it is in the z direction on ΩE; v r and v z are the r and z components of v, respectively. Because we assume that the nanochannel is sufficiently long, v r is far less important than v z.

The flux of ion species j, J j , can be described by Nernst–Planck equation (Liu et al. 2007; Ai and Qian 2011),

$${\mathbf{J}}_{j} = - D_{j} \left( {\nabla n_{j} + \frac{{z_{j} e}}{{k_{\text{B}} T}}n_{j} \nabla \phi } \right) + n_{j} {\mathbf{v}},$$
(15)

where D j is the diffusivity of ionic species j. According to this expression, J j is driven by three mechanisms: concentration gradient, electrical potential gradient, and flow field. Because the perturbed concentration is neglected, so is the contribution from the concentration gradient. For convenience, we define the ionic flux coming solely from the electroosmotic flow, J Aj , as

$${\mathbf{J}}_{Aj} = n_{j} {\mathbf{v}}$$
(16)

The ionic current, I, and the ionic current contributed solely by electroosmotic flow, I A , can be evaluated, respectively, by

$$I = \iint\limits_{\varOmega } {\sum\limits_{i = 1}^{N} {z_{j} e({\mathbf{n}} \cdot {\mathbf{J}}_{j} ){\text{d}}\varOmega } }$$
(17)
$$I_{A} = \iint\limits_{\varOmega } {\sum\limits_{i = 1}^{N} {z_{j} e({\mathbf{n}} \cdot {\mathbf{J}}_{Aj} ){\text{d}}\varOmega } ,}$$
(18)

where Ω is the cross-section area of the nanochannel.

The governing equations and the associated boundary conditions are solved numerically by FlexPDE (2000), and the results obtained are substituting into Eqs. (17) and (18) to calculate I and I A , respectively.

3 Results and discussion

3.1 Model verification

Our model is first applied to the experimental data of Karnik et al. (2005), where the electroosmosis of an aqueous KCl solution was conducted in a silanol-coated nanochannel. To fit their data, we assume pKa = 7, pKb = 2, and D +K =1.96 × 10−9 m2 s−1. Figure 2 shows the variation of the conductance, I/V, where V is the applied electrical voltage difference, with C KCl; both the experimental data and the present results at several values of N total are presented. This figure shows that the conductance (or ionic current) increases with increasing C KCl, as expected. The conductance is seen to depend on the value of N total. In general, our model is capable of describing successfully the behavior of the experimental data. The estimated value of N total is ca. 10−5 mol/m2, which is typical to a fused silica surface (Kirby and Hasselbrink 2004; Dolnik 2004).

Fig. 2
figure 2

Variations of the conductance with KCl concentration C KCl for various values of N total at R = 25 nm and pH 7. Discrete symbols: experiment data of Karnik et al. (2005); curve present result

Full size image

3.2 Numerical simulation

To examine the behavior of the system under various conditions, numerical simulation is conducted by varying pH, bulk salt concentration, and N total. For illustration, we consider an aqueous NaCl solution with pH adjusted by HCl and NaOH, implying the presence of Na+, Cl−, H+, and OH−. The diffusivities of these ions are 1.33 × 10−9, 2 × 10−9, 9.38 × 10−9, and 5.29 × 10−9 m2 s−1, respectively. Other parameters assumed are E z  = 10 kV/m, R = 50 nm, pKa = 7, and pKb = 2. Note that the following relationships need be satisfied: if pH < pKw/2, [H+]0 = 10−pH, [Na+]0 = C NaCl, \([{\text{Cl}}^{ - } ]_{0} = C_{\text{NaCl}} + 10^{{ - {\text{pH}}}} - 10^{{ - ({\text{pK}}_{\text{w}} - {\text{pH}})}}\), and \([{\text{OH}}^{ - } ]_{0} = 10^{{ - ({\text{pK}}_{\text{w}} - {\text{pH}})}}\); if \({\text{pH}} \ge {\text{pK}}_{\text{W}} /2\), [H+]0 = 10−pH, \([{\text{Na}}^{ + } ]_{0} = C_{\text{NaCl}} + 10^{{ - ({\text{pK}}_{\text{w}} - {\text{pH}})}} - 10^{{ - {\text{pH}}}}\), [Cl−]0 = C NaCl, and \([{\text{OH}}^{ - } ]_{0} = 10^{{ - ({\text{pK}}_{\text{w}} - {\text{pH}})}}\). We assume that C NaCl > 10−5 M so that EDL overlapping is insignificant.

3.3 Electrical potential in the channel

Figure 3 summarizes the radial distributions of the electrical potential ϕ at various values of pH. As can be seen in Fig. 3a, if pH is low, neglecting the presence of H+ and OH− can yield an appreciable deviation in ϕ, with the maximum percentage of 95 % occurring at pH 3 and r/R = 0.6. This is because the presence of H+ is important at a low level of pH. As pH approaches 7, because both [H+] and [OH−] are far below C NaCl, neglecting their presence yields negligible deviation. Note that for the level of C NaCl considered, ϕ(r/R = 0) does not vanish. This is because the thickness of EDL is comparable to the nanochannel radius in this case and, therefore, it fills essentially the whole cross-section of the nanochannel. As shown in Fig. 3b, if C NaCl is raised to ca. 10−2 M, the presence of H+ and OH− is unimportant for the levels of pH considered. |ϕ| is seen to decrease with increasing C NaCl, which is consistent with the nature of a charge-regulated surface (Wang and Revil 2010).

Fig. 3
figure 3

Radial distributions of electrical potential for various values of pH at N total = 10−5 mol/m2 and C NaCl = 10−4 M (a), and C NaCl = 10−2 M (b). Solid curve H+, OH−, Na+, and Cl− are all considered; dashed curve only Na+ and Cl− are considered

Full size image

Figure 4 illustrates the influence of N total on the radial distribution of ϕ. Because the larger the N total the greater the number of functional groups on the nanochannel surface, yielding a higher |ϕ|. As in the case of Fig. 3, considering all four kinds of ionic species is necessary at a low pH.

Fig. 4
figure 4

Radial distributions of electrical potential for various values of N total at C NaCl = 10−3 M, and pH 3 (a), and pH 7 (b). Solid curve H+, OH−, Na+, and Cl− are all considered; dashed curve only Na+ and Cl− are considered

Full size image

3.4 Electroosmotic velocity distribution

Fluid velocity is one of the important factors affecting ionic current. Figure 5 shows that if C NaCl is sufficiently high, the z component of the fluid velocity v z becomes roughly constant at a point sufficiently far from the nanochannel surface. This is expected because the EDL thickness is roughly inversely proportional to \(\sqrt {C_{\text{NaCl}} }\). Note that depending upon the levels of pH and C NaCl, neglecting the presence of H+ and OH− may either overestimate or underestimate v z. A comparison between Fig. 5a and b suggests that the thicker the EDL (lower C NaCl) the faster the v z(r/R = 0), in general.

Fig. 5
figure 5

Radial distributions of v z for the case of Fig. 3 at C NaCl = 10−4 M (a) and C NaCl = 10−2 M (b). Solid curve H+, OH−, Na+, and Cl− are all considered; dashed curve only Na+ and Cl− are considered

Full size image

Figure 6 illustrates the radial distribution of the z component of the fluid velocity v z for the case of Fig. 4. This figure indicates that an increase in N total yields a larger v z, which is expected because the larger the N total the higher the surface potential. As can be seen in Fig. 6a that if pH is low (e.g., 3) and N total is not large, neglecting the presence of H+ and OH− will overestimate v z. However, if N total is sufficiently large (e.g., 10−3 mol/m2), that will overestimate (underestimate) v z for r/R smaller (larger) than ca. 0.5. This results from the competition between the effect of surface potential and that of EDL thickness. However, this competition is significant only if N total is sufficiently large (e.g., 10−3 mol/m2) so that the surface potential is high enough to attract counterions closely (Hsu and Chen 2007). Figure 6b reveals that the contribution of H+ and OH− to v z at pH 7 is negligible because their concentrations are much lower than C NaCl.

Fig. 6
figure 6

Radial distributions of v z for the case of Fig. 4 at pH 3 (a) and pH 7 (b). Solid curve H+, OH−, Na+, and Cl− are all considered; dashed curve only Na+ and Cl− are considered

Full size image

3.5 Dependence of ionic current on pH and salt concentration

Figure 7 illustrates the variations in the ionic current I and the ratio (I A /I) with C NaCl for the case of Fig. 3. As can be seen in this figure, neglecting the presence of H+ and OH− yields appreciable deviation in both I and (I A /I) when pH is low, and that deviation becomes negligible at pH 7. Apparently, I will be underestimated when fewer kinds of ionic species are considered, and the lower the C NaCl the more significant is the deviation in I. However, if C NaCl exceeds ca. 0.1 M, only Na+ and Cl− need be taken into account. As seen in Fig. 3, the higher the pH the higher the absolute value of the nanochannel surface potential, implying a stronger EOF, and therefore, I(pH 7) > I(pH 5) > I(pH 3). Figure 7b shows that I A increases with increasing pH, which is expected. However, if the presence of H+ and OH− is also considered, I(pH 5) is smaller than both I(pH 3) and I(pH 7), as seen in Fig. 7a. This is because the bulk ionic concentration at pH 5 is lower than that at pH 3, and the electroosmotic effect at pH 7 is more significant than that at pH 5. It is interesting to observe that I(pH 7) > I(pH 3) if C NaCl exceeds ca. 2 × 10−3 M, and this trend in reversed if C NaCl is lower than that level. This is because if C NaCl is high, the total amount of ionic species remains roughly the same as pH varies. In this case, the contribution of ionic current coming from EOF is important. On the other hand, if C NaCl is low, the total amount of ionic species varies appreciably with pH, so that I(pH 3) > I(pH 7). Figure 7b reveals that I A increases with decreasing C NaCl. This is because the lower the C NaCl the thicker the EDL, yielding a higher surface potential and therefore a stronger EOF. Figure 7a also shows that I decreases with decreasing C NaCl, and approaches a constant value when C NaCl is sufficiently low. This behavior is enhanced at low pH because the contribution of H+ to I is significant in that case.

Fig. 7
figure 7

Variations of the ionic current I (a), and the ratio (I A /I) (b), with C NaCl for the case of Fig. 3. Solid curve H+, OH−, Na+, and Cl− are all considered; dashed curve only Na+ and Cl− are considered

Full size image

The variations of the ionic current I and the ratio (I A /I) with pH for the case of Fig. 4 are illustrated in Fig. 8. It is interesting to see in Fig. 8a that the competition between the ionic migration and EOF yields a local minimum in I, which is clearer when all the ionic species are considered. This phenomenon was not observed in the experiment (Stein et al. 2004), presumably due to insufficient data or conductance saturation. Note that ionic migration dominates when C NaCl is high. If pH is low (<3), I is dominated by H+, with I decreases with decreasing pH, that is, the influence of N total is insignificant. This is consistent with the result shown in Fig. 8b, where I A contributes less than 2.5 % to I for the range of N total examined. The influence of N total is important, however, if pH is high, as can be verified by that I A becomes appreciable. In this case, I increases with increasing pH and N total, which is consistent with the results presented in Figs. 4 and 7. If only Na+ and Cl− are considered, because the influence of H+ is ignored, the behavior of I is governed by I A, implying that the effect of ionic migration is negligible. Figure 8a indicates that if H+ and OH− are not considered, I has a local minimum at pH 2.5, the point of zero charge (PZC), if N total is sufficiently large. This is because the contribution of I A vanishes at PZC. If pH <2.5, although the direction of EOF is reversed, so are the sign of the counterions in EDL, and therefore, I A does not change its sign. In this case, I increases with decreasing pH.

Fig. 8
figure 8

Variations of the ionic current I (a) and the ratio (I A /I) (b), with pH for the case of Fig. 4. Solid curve H+, OH−, Na+, and Cl− are all considered; dashed curve only Na+ and Cl− are considered

Full size image

3.6 Estimation of critical nanochannel radius

The flow properties such as the volumetric flow in a larger-scaled channel are usually proportional to its cross-section area. In the present case, because the double layer plays an important role, that rule can be violated. To examine the difference between the nature of the present nanochannel and that of a larger-scaled one, a critical radius R c is defined (Tseng et al. 2013b) by that \(I \propto \varOmega^{n}\) for R c  < R with n = 1 ± 0.02, that is, I is roughly proportional to its cross-section area in that region. Figure 9 reveals that R c decreases with increasing C NaCl. This is because the higher the C NaCl the thinner the EDL and, therefore, the larger the portion of the nanochannel in which the velocity profile is uniform. Note that R c  ≅ 50 nm at C NaCl = 10−2 M, that is, the whole cross-section of the nanochannel is occupied by EDL. Figure 9 suggests that the behavior of I in a nanoscaled channel is more complicated than that in a larger-scaled one (e.g., microchannel), where I is essentially proportional to its cross-section area (Chen et al. 2005).

Fig. 9
figure 9

Variation of the critical radius R c with C NaCl at pH 7 and N total = 10−5 mol/m2

Full size image

4 Conclusions

We evaluated the ionic current and the associated mechanisms in a pH-regulated nanochannel under conditions that are closer to reality than those in previous analyses. Adopting an aqueous NaCl solution with pH adjusted by HCl and NaOH as an example, the electrical potential, velocity distribution, and ionic current are examined by varying the pH, the background salt concentration C NaCl, and the density of surface functional groups. The results of numerical simulation can be summarized as following. (1) Neglecting the presence of H+ and OH− overestimates the electrical potential because the thickness of EDL is overestimated. The deviation in the electric potential is insignificant if pH is closer to the point of zero charge (PZC) and/or C NaCl is high. (2) The higher the functional groups density on the nanochannel surface N total the higher the surface potential, and therefore, a stronger electroosmotic flow (EOF). (3) Neglecting the presence of H+ and OH− overestimates the fluid velocity. However, due to the competition between the effect of EDL thickness and that of the surface potential, the fluid velocity when Na+, H+, Cl−, and OH− are all considered is faster than that when only Na+ and Cl− are considered if EDL thickness is comparable to the nanochannel radius. This phenomenon is more significant at high N total (=10−3 mol/m2) and low pH (=3). (4) If only Na+ and Cl− are considered, the ionic current I at various levels of pH ranks as I(pH 7) > I(pH 5) > I(pH 3). However, if Na+, H+, Cl−, and OH− are all considered, the competition of the ionic migration driven by the applied electrical field and EOF makes I(pH 5) the smallest. In addition, the relative magnitudes of I(pH 3) and I(pH 7) depend upon the level of C NaCl. (5) At PZC, EOF does not contribute to I, and a decrease in pH from PZC does not alter the direction of I because both the sign and the flow direction of counterions in EDL reverse. In addition, if pH is sufficiently low, I increases with decreasing pH, and it is unaffected by N total. (6) The main difference between the I of the present nanoscaled channel and that of a larger (e.g., micron) scaled channel is reflected by the portion of the cross-section of a channel where I is linearly proportional to its area. Because the nanochannel radius is comparable to the EDL thickness, the presence of EDL plays the key role; the higher the C NaCl the thinner the EDL and the larger that portion is.