Current monitoring in nanochannels

Abstract

Current monitoring (CM) is an indirect experimental method for characterizing surface zeta potentials in confined channels. Although this method has been successfully used in microchannels, its validity in nanofluidic devices has remained elusive due to non-negligible effects from relatively thick electrical double layers and large surface conduction. In this work, we numerically investigated current monitoring and its accuracy in nanochannels filled with the monovalent binary salt solution under various conditions, including different ionic concentrations, ion diffusivities, surface charge densities, and channel heights. Our results show that the zeta potential measured by current monitoring deviates from the actual value as the electrical double layer becomes thick, reaching zero when the Debye length is more than 15% of the half channel height. However, for cases with a smaller Debye length, the magnitude of deviation can be precisely predicted by a simple expression, which is only related to the ratio of the Debye length to the nanochannel height and the average ion diffusivity even when the surface conduction is in the moderate range. Our observations can be explained by the deionization shock wave effect, and this new expression provides guidelines for accurately measuring zeta potentials in nanochannels using current monitoring, which would lead to better control of electrokinetic flows for various nanofluidic applications.

1 Introduction

Nanofluidic devices, such as slit-shaped nanochannel and cylindrical nanotube devices, have been used in various applications, including chemical analysis, biomolecular separation, preconcentration, label-free sensing, as well as nanofluidic diodes and transistors (Han et al. 2008; Sparreboom et al. 2009; Escobedo et al. 2012). These devices benefit from strong electrostatic interactions between nanoscale conduit surfaces and aqueous solutions, and the associated unique electrokinetic behaviors in nanoscale confinements. As surface zeta potential is one of the most important parameters that determine the surface-liquid electrostatic interactions (Kirby 2010; Berg 2010), it is crucial to measure this property inside the nanofluidic devices to understand transport behaviors further and to develop new applications.

However, unlike zeta potential measurement of open surface or colloidal suspensions in open solutions, the confined space in microscale and nanoscale conduits prevents direct probing at the inner channel walls. One strategy to overcome this challenge is to measure zeta potential in an indirect manner (Kirby and Hasselbrink 2004; Huang et al. 1988). Current monitoring (CM) has been a popular indirect experimental method to measure zeta potentials inside microfluidic channels filled with ionic solutions (Sze et al. 2003). In this method, the electroosmotic flow (EOF) velocity is first measured by recording the transient current change along the channel in response to the change of ionic concentration inside the channel. Zeta potential is then reversely calculated from the measured EOF velocity based on the Helmholtz–Smoluchowski equation.

Recently, this method has been used to characterize EOF and/or surface zeta potential in nanofluidic devices. Chou et al. (2018) demonstrated that CM could be used to observe a change in both surface charge and zeta potential as different electrolytes are introduced into nanochannels. Peng and Li (2016) used CM to measure the EOF velocity in nanoscale PDMS conduits and showed a reduced velocity for shallower channels filled with more dilute solutions, attributing their findings to more dominant effects from the electrical double layer (EDL). The argument receives support from previous results found by Haywood et al. (2014), and Pennathur and Santiago (2005a, 2005b), using methods other than CM. Despite these attempts, several critical questions have remained: How accurately can CM measure EOF velocities inside nanochannels/nanotubes? How to correlate CM measurements with the actual zeta potentials in such cases?

It is well known that the success of CM in measuring zeta potential in microfluidic devices is based on the fact that the Debye Screening length $\lambda _D$, a characteristic length that defines the thickness of EDL and thus the penetration depth of electrostatic interactions into the solution, is negligible compared to the characteristic channel dimension (e.g., half of the channel height for a slit-shaped nanochannel). In such a scenario, the transverse EOF velocity profile is uniform across the channel height direction, and the changing rate of the electrical current reflects the EOF velocity. Consequently, zeta potential can be accurately extracted based on its linear correlation with the EOF velocity. However, it is different in nanochannels as the EDLs can occupy a significant portion of the channels or even overlap between opposite channel walls. It has been discussed that thicker EDLs with non-uniform ion distributions in a nanochannel would produce a non-linear velocity profile in the height direction (Pennathur and Santiago 2005a). This would result in a breakdown of the linear proportionality between the zeta potential and the measured EOF velocity, invalidating assumptions for CM. McCallum and Pennathur (2016) used both numerical and experimental methods in a previous study (Sze et al. 2003) to investigate CM and its application in nanochannels filled with diluted solutions. They reported an empirical expression that can account for the reduction of electroosmotic velocity due to thicker EDLs and can convert the measured zeta potentials to the correct values. However, their conclusion was based on a limited set of nanofluidic systems with fixed ionic mobilities and diffusivities. The physical origin of the empirical expression is not well understood, and a universal expression with a clear physical origin for all cases where CM is valid is still missing.

On the other hand, it is worth noting that the CM method in microchannels also assumes that surface conduction over charged channel surface is negligible and thus will not affect the EOF velocity. However, it is well known that surface conduction will promote ion depletion (Mani et al. 2009; Mani and Bazant 2011; Huang and Yang 2008), and a recent study (Babar et al. 2020) further shows that such ion depletion could form a concentration shock wave in the reversed direction to the EOF flow. This deionization shock wave actually can lead to a significant decrease in the apparent electroosmotic velocity, even in the microchannels. Furthermore, the effect of such surface-conduction-induced deionization shock wave will become more prominent as the Dukhin number (the ratio of surface conduction over bulk conduction) increases. They derived an analytical model that accounts for the deionization shock wave based on previous studies (Mani et al. 2009; Zangle et al. 2009; Mani and Bazant 2011; Bahga et al. 2016) and validated the model by experiments in the microchannels. Although this model can well predict the decrease of electroosmotic velocity in microchannels with a wide range of Dukhin number conditions, it is still built based on the “negligibly thin EDL” assumption. In nanochannels where the EDLs can easily occupy a significant portion of the channels, the validity of this model remains unknown.

In this work, we systematically investigated the validity of CM in determining zeta potentials for two-dimensional slit-shaped nanochannels via numerical simulation. We simulated the time-dependent current change along the nanochannel using the Poisson–Nernst–Planck model coupled with the Navier–Stokes equation and compared the zeta potentials “measured” by CM with the actual zeta potentials at the nanochannel walls. We studied various factors that could affect the CM measurements, such as surface charge density, channel height, ionic concentration, and ion diffusivity of monovalent salt solution. For commonly used salt solution, KCl, for instance, in the nanochannel with a typical surface charge density range, our results indicate that a simple and universal analytical expression that is only a function of the ratio of the Debye length to the nanochannel height and the average ion diffusivity can be used to correct the “measured” zeta potentials into actual values. This work provides a convenient means to employ CM for correct zeta potential measurement in nanochannels, allowing us to characterize ion and particle transport with greater accuracy in nanofluidic conduits and better control electrokinetic flow in various nanofluidic applications.

2 Modeling current monitoring

2.1 Current monitoring overview

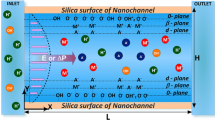
The current monitoring technique investigated in the nanofluidic system is derived from the original method employed in microchannels with minimal alteration. It is simulated following the steps defined in prior research (Sze et al. 2003). A simplified model for the virtual experiment is shown in Fig. 1, in which two reservoirs are connected to the inlet and outlet of a slit-shaped nanochannel with height H, length L, and width W. The channel is regarded as a two-dimensional structure containing two infinite parallel plates because of its substantial width-to-height ratio. Both reservoirs are initially filled with identical electrolyte solutions at the same bulk concentration $c_0$. Each wall of the channel is treated as a solid surface that obtains a net negative surface charge density $\sigma$ (Jensen et al. 2011; Behrens and Grier 2001). Dissolved cations are attracted toward the wall by electrostatic forces, whereas anions are repelled from the surface, partially screening the negative charge and forming the EDL at each wall.

Fig. 1

Schematics of current monitoring (CM): a Experimental setup for CM in a nanochannel connecting two reservoirs with Ag/AgCl electrodes immersed in solution adjacent to the inlet and the outlet of the nanochannel. b Idealized I(t) plot generated from CM. c Physical behaviors of ions in the channel. Cations and anions are driven by the electrophoretic flow (EPF) and the electroosmotic flow (EOF) to generate electrical currents. Ion concentration is distributed along the channel height direction according to the electrostatic potential profile

To initiate the CM process, a voltage, $V_{app}$, is applied across the nanochannel length direction using the electrodes in each reservoir. An ammeter is also connected in series with the external source for current measurement. The resulting electric field drives the unbalanced net charge in the EDLs to move in one direction, dragging the confined liquid to induce EOF. Cations and anions, in general, also move in opposite directions under the applied electric field due to Coulomb forces in the phenomenon referred to as electrophoretic flow (EPF). A constant ionic current through the channel, arising from both EOF and EPF, is recorded as $I_0$. At the time $t_0$, the solution in the inlet reservoir is instantaneously traded for one with a slightly higher ionic concentration $c_1$. The EOF continuously pumps the new solution into the nanochannel for transient solution displacement, spurring an increase in channel conductance and a subsequent increase in measured current over time. A final current $I_1$ is reached when the more concentrated solution fully fills the channel. By tracing the current change from the I(t) diagram, the velocity of EOF flow $u_{EOF}$, is revealed by knowing the length of the channel and the time taken for the full displacement ${\Delta }t$.

As shown in Fig. 1c, the measured electrical current I along the nanochannel consists of two components from EPF and EOF as $I=I_{EOF}+I_{EPF}$. The EPF current $I_{EPF}$ can be written as

$$\begin{aligned} I_{EPF}=W\int _{-H/2}^{H/2}\sum _{i=1} {u_{EP,i}z_ic_i(y)F}dy \end{aligned}$$

(1)

where F is the Faraday constant, $u_{EP,i}$, $z_i$ and $c_i\left( y\right)$ are the EPF velocity, the charge and the concentration profile for ion species i, respectively. The EPF velocity for a given ionic species is proportional to the applied electric field from the external voltage source $E=V_{app}/L$, with a proportionality constant known as the ion’s electrophoretic mobility $\mu _{EP,i}$. The EPF mobility is related to the ion diffusivity by the Nernst–Einstein relation ($\mu _{EP,i}=\frac{z_ieD_i}{k_BT}$, e is the charge of an electron, $D_i$ is the diffusivity of ion i, $k_B$ is the Boltzmann’s constant and T is the temperature). The concentration profile in the channel height direction follows the prediction by the Boltzmann distribution,

$$\begin{aligned} c_i\left( y\right) =c_0\exp {\left[ -\frac{z_ie\varphi \left( y\right) }{k_BT}\right] } \end{aligned}$$

(2)

where $c_0$ is the ionic concentration in the bulk phase solution in reservoirs and $\varphi \left( y\right)$ is the electrical potential related to the surface charge density and the corresponding EDL (Pennathur and Santiago 2005a).

The general form of the EOF current can be expressed as

$$\begin{aligned} I_{EOF}=W\int _{-H/2\ }^{H/2}{\sum _{i}{u_{EOF}z_ic_i\left( y\right) F}dy} \end{aligned}$$

(3)

In this equation, the EOF velocity profile for the confined fluid is given by the Helmholtz–Smoluchowski equation,

$$\begin{aligned} u_{EOF}\left( y\right) =-\frac{\varepsilon _r\varepsilon _0\zeta E}{\eta }\left[ 1-\frac{\varphi \left( y\right) }{\zeta }\right] \end{aligned}$$

(4)

in which $\varepsilon _0$ is the permittivity of free space, $\varepsilon _r$ is the relative permittivity of water, $\eta$ is the viscosity of water, and $\zeta$ is the zeta potential of the channel wall. The first term in this $u_{EOF}$ expression represents the max EOF velocity, that is, $u_{EOF,max}=-\frac{\varepsilon _r\varepsilon _0\zeta E}{\eta }$.

It is worth noting that the diffusive flux of ions due to the concentration gradient along the channel also contributes to the ionic current. However, for typical CM measurements, the current induced by the diffusive flux is negligible compared to those from the convective flux since the concentration change $\Delta c=c_1-c_0$ is minimal (10% of $c_1$ or even less) and the electric field is set as such that the characteristic timescale for diffusion is much greater than for convective flow.

In cases where the EDL is negligibly thin compared to the characteristic channel dimension $(2\lambda _D/H\approx 0$), as commonly encountered in a microchannel, the electrostatic interactions between the surface charge and the solution are insignificant in most regimes along the height direction [$\varphi (y)\approx 0$, except near wall]. The concentration profile is thus uniform at the bulk phase concentration for essentially the entire channel, and the EPF current can be simplified to

$$\begin{aligned} I_{EPF}=WHF\sum _{i}{u_{EP,i}z_ic_i} \end{aligned}$$

(5)

Meanwhile, given that cations and anions both possess the same $u_{EOF}$ and exist in roughly equal quantities, the resulting ionic fluxes due to EOF are equal in magnitude but opposite in directions. Therefore, it is valid to consider the net flux $I_{EOF}$ negligible. As a result, the total change of current during a transient CM process is equivalent to the change in $I_{EPF}$, where $\Delta I\approx \Delta I_{EPF}$.

To simplify the model, a binary monovalent electrolyte salt, such as KCl with the valency of $z_{+}=+1$ and $z_{-}=-1$, is utilized. The electrophoretic mobilities for the cations and anions are defined as $\mu _{EP,+}$ and $\mu _{EP,-}$, respectively. The change in total current can be rewritten as

$$\begin{aligned} \Delta I\approx \ WHFE\Delta c\left( \mu _{EP,+}-\mu _{EP,-}\right) \end{aligned}$$

(6)

Since ion distribution is relatively uniform, $u_{EOF}(y)$ profile is in a plug-shape and ${\bar{u}}_{EOF}\approx u_{EOF,max}$. As a result, the concentrated solution will be uniformly pumped across the channel, resulting in a linear change in current I(t) over time with a slope $k=\Delta I/\Delta t$. The duration time for the concentration front to propagate from inlet to outlet can be given by $\Delta t=L/\bar{u}_{EOF}$. It is then possible to directly relate the slope of I(t) and EOF velocity as $k=\Delta I{\bar{u}}_{EOF}/L$. Combining with Eq. (4), we reach the final equation correlating the measured zeta potential $\zeta _{CM}$ to known system parameters and values obtained from the I(t) graph:

$$\begin{aligned} \zeta _{CM}=\frac{-kL\eta }{\varepsilon _r\varepsilon _0E\Delta I} \end{aligned}$$

(7)

The $\zeta _{CM}$ in the above equation is accurately equal to the actual $\zeta$ of channels as long as certain conditions are satisfied in the system: The EDL is thin enough to claim bulk concentration and plug-shape velocity profile in the channel; $\mu _{EP,+}$ and $\mu _{EP,-}$ are constant and do not change with concentration or applied voltage; The change in bulk phase concentration is small; Hydraulic pressure gradients are not formed during transient current change; The Joule heating effect can be ignored (Kirby and Hasselbrink 2004). Since the CM estimation based on Eq. (7) does not require any prior knowledge regarding the channel height or the surface charge density, it has been considered a very useful method for characterizing zeta potentials in microchannels.

2.2 Numerical simulation of CM in nanochannels

When applying CM in nanochannels, since the criteria for Eq. (7) can quickly fail — especially the thin EDL approximation and the time-dependent nature of $c\left( y\right)$ and $\varphi \left( y\right)$ in an actual experiment, it is necessary to utilize numerical simulation to profile the ionic current change. In this work, COMSOL Multiphysics v5.2 is used to simulate the time-dependent ionic current change. The Poisson–Nernst–Planck Equation and the Navier–Stokes Equation (neglecting inertial terms) are coupled to simulate ion transport, electrostatic fields, and laminar flow. The governing equations are as follows:

$$\begin{aligned}&\frac{\partial c_i}{\partial t}=\nabla \cdot \left( D_i\nabla c_i+z_i\mu _{EP,i}Fc_i\nabla V\right) -\mathbf {u}\cdot \nabla c_i \end{aligned}$$

(8)

$$\begin{aligned}&\varepsilon _r\varepsilon _0\ \nabla ^2V=-\sum _{i}{z_ic_iF} \end{aligned}$$

(9)

$$\begin{aligned}&\rho \frac{\partial \mathbf{u}}{\partial t}=-\nabla p+\eta \nabla ^2\mathbf{u}+\sum _{i} \mathbf{f}_i \end{aligned}$$

(10)

where V is electrostatic potential, $\mathbf {u}$ is the fluid’s velocity field, $\rho$ is the fluid’s density, and $\mathbf {f_i}$ is the body force of electrolyte solution, where $\mathbf {f_i}=z_ic_iF\mathbf {E}$.

Fig. 2

Simulation models and example I(t): a Rectangular half-channel domain. b An example of simulated I(t) plot where the current rises linearly before reaching the final equilibrium current

To simplify the simulation conditions, the system is chosen to be an asymmetric two-dimensional channel, as shown in Fig. 2a. Our studies consider a conduit with $H = 30\mathrm {-}100 ~\mathrm {nm}$, $L= 50 ~\mathrm {\mu m}$ and $W= 5 ~\mathrm {\mu m}$. The model represents only a half-channel of the height in an effort to reduce computation load, as the physical behavior is symmetric about the system’s center line. The wall is set to be a non-slip boundary for fluid flow with no orthogonal fluid flux and ionic flux, and it also retains a constant surface charge density of $\sigma$. In all of our simulations, $\sigma$ is set as a fixed value, given that the small change in concentration during the CM process would limit the possible change of $\sigma$. We define a coordinate system with its origin at the intersection between the axial center line and the inlet as in Fig. 2a.

A constant electrical potential difference is applied across the nanochannel to create an axial electric field along the length direction, with $V_{app}$ at the inlet and with the outlet grounded. $V_{app}$ is selected to be 40 V for all trials such that strong and sufficient convection along the length direction dominates over any contributions from ionic diffusion. We have also run simulations using different values of $V_{app}$ or using different channel lengths and found that these parameters would not affect CM performance as long as the electric field is sufficiently high. No external pressure difference is applied between the inlet and the outlet. An aqueous solution containing the binary electrolyte KCl is used as the working fluid. Experiments are performed under isotherm conditions at a temperature of $T=293.15$ K with $\mu _{EP,K^+}=7.76\times {10}^{-8}~\mathrm {m^2 V^{-1} s^{-1}}$ and $\mu _{EP,Cl^-}=-8.04\times {10}^{-8}~\mathrm {m^2 V^{-1} s^{-1}}$ ($D_{K^+}=1.96\times {10}^{-9}~\mathrm {m^2/s}$ and $D_{Cl^-}=2.03\times {10}^{-9}~\mathrm {m^2/s}$).

An initial steady-state solution is computed prior to each virtual CM experiment. Both the inlet and the outlet are set to have the same initial concentration $c_0$. Such settings are identical to real experimental conditions. Afterward, starting from the equilibrium solution of the initial condition, the transient CM process is then “performed” by manually increasing the inlet concentration to a higher concentration of $c_1$ while holding the outlet at the original $c_0$, where $c_0=0.9c_1$ is used in all simulations. The simulation progresses until the introduced solution has entirely displaced the initial solution in the channel, mimicking the change in the final state expected in the real CM procedure.

The total ionic current $I=I_{EOF}+I_{EPF}$ is acquired by integrating cross-sectional ionic fluxes using Eq. (1) and Eq. (3). It is then graphed as a set of discrete points as Fig. 2b. The resulting I(t) plot shows a gradual increase in the current until the function reaches a plateau denoting a final equilibrium state. Both the overall current change and the slope are taken from the plot. With these “measured” values and the given system constants like the channel dimensions and the fluid properties, Eq. (7) is used to derive the measured zeta potential $\zeta _{CM}$. At the same time, the actual zeta potential $\zeta _{actual}$, is found directly in simulation as the electrical potential at the channel wall. A correction factor, $\alpha =\zeta _{CM}/\zeta _{actual}$, is finally defined to represent the extent to which $\zeta _{CM}$ deviates from $\zeta _{actual}$. When $\alpha$ shifts from unity, CM begins to produce inaccurate estimations of the actual zeta potential.

3 Results and discussion

3.1 Measured zeta potential and bulk concentration

To gain preliminary insight into how CM performs in nanochannels where non-negligible EDLs may influence the EOF profile, initial simulations first consider systems with different concentrations for a fixed channel geometry and surface charge density ($H=100 ~\mathrm {nm}$, $\sigma =-5 ~\mathrm {mC/m^2}$). The I(t) graphs are normalized for easier comparison based on ideal behavior under the thin EDL approximation. Time is normalized by a time constant as $t^*=t\varepsilon _r\varepsilon _0E\zeta _{actual}/\eta L$; and the current is normalized by the final equilibrium current as $I^*=I/(I_0+\Delta I)$. Since the concentration change is designed as 10% of the final concentration ($\Delta c=10\%c_1$), the normalized current change $\Delta I^*$ should also be 10% such that the normalized slope for an ideal case should be $k^*=\Delta I^*/\Delta t^*=0.1$ if $\alpha =100\%$. Figure 3a shows a set of simulated results, where $I^*(t^*)$ curves are presented as solid lines, compared with ideal cases drawn as the dashed lines.

Fig. 3

Results for the nanochannel with $H=100~\mathrm {nm}$ and $\sigma =-5 ~\mathrm {mC/m^2}$ at different concentration $c_1$: a Normalized $I^*(t^*)$ plot and velocity profiles $u^*(y)$ (on the basis of the maximum velocity) corresponding to Cases A, B, and C. In the $I^*(t^*)$ diagrams, solid lines represent simulated transient current; dashed lines represent current change with ideal slope $k^*=0.1$ when $\alpha =100\%$. b Comparison between actual zeta potential based on Poisson–Boltzmann distribution from simulation results $\zeta _{actual}$, and the value generated from the I(t) plot $\zeta _{CM}$. c Comparison between the simulated average velocity $\bar{u}_{EOF}$, and the value derived from the I(t) plot $\bar{u}_{EOF,CM}$

From the observation, we find that the reported conditions correspond to three typical cases for the behavior of CM: (A) the $I^*(t^*)$ curve and its slope closely follow the dashed line, namely, the I(t) is almost the same as the ideal case; (B) the $I^*(t^*)$ plot remains linear, but with a slope less than the ideal slope; and (C) the plot deviates significantly from the ideal case and shows an almost constant current. Such three different cases are also evident when comparing the simulated and measured zeta potentials as in Fig. 3b. It is obvious from the graph that the difference between $\zeta _{CM}$ and $\zeta _{actual}$, which is valued by $\alpha$, varies at different bulk phase concentrations $c_1$ and behaves differently in these three regimes. At high concentrations (Case A, when $c_1$ is roughly above 0.5 M for the investigated conditions), CM measured zeta potentials are very close to the actual values ($\zeta _{CM}\approx \zeta _{actual}$ and $\alpha \approx 100\%$). In such a case, the nanochannel resembles a system with thin EDLs, and the EOF velocity profile is in a plug shape, as shown in Fig. 3a. Consequently, the CM method produces a reliable measurement for zeta potential in this regime. In contrast, at sufficiently low concentration (Case C, when $c_1$ is roughly below 2 mM), the CM measured zeta potential is zero, indicating an inevitable failure for the CM technique in this regime ($\zeta _{CM}\approx 0 mV$ and $\alpha \approx 0\%$). To some extent, this is also not surprising and expected as the thicker EDLs near the two opposite walls overlap and occupy the entire nanochannel. The concentration distribution along the y-axis is thus mainly determined by the charged surface and is insensitive to the bulk concentration in the inlet and the outlet. As a result, the current and the conductivity remain almost unchanged over time despite the introduction of a new solution, and the EOF velocity profile shows a non-linear shape. This case is also known as the surface charge governed regime (Stein et al. 2004). It is worth noting that the Case C scenario exists even when high ionic concentration (i.e., 0.1 M) is filled in smaller nanochannels (i.e., 10 nm). In such conditions, the EDLs’ thickness can still be comparable to nanochannels’ heights and the EDLs can occupy significant portions of the nanochannels that prevent ion concentration change.

Different from case C, at intermediate concentrations (Case B), where EDLs occupy noticeable portions of the nanochannels, the CM method leads to certain non-zero values of the zeta potentials. However, those CM measured a value are smaller than the actual value, and the difference becomes significant as ionic concentration decreases. In the meantime, the EOF velocity profile only partially deviates from the plug shape. Therefore, we may conclude that the CM method partially works in this case but would underestimate the actual zeta potential. If the underestimation can be quantitatively predicted in advance, it is still possible to use the CM method to measure the zeta potential for this regime.

One possible explanation for such underestimation of the zeta potential is that the thicker EDLs at lower ionic concentrations causes notable variations in the EOF velocity profiles, and the average EOF velocity $\bar{u}_{EOF}$ becomes lower than the maximum EOF velocity $u_{EOF,max}$, whose value is assumed to represent the entire plug-form velocity profile in Case A. If this explanation is correct, the velocity calculated from the $I-t$ diagram of the CM measurement ($\bar{u}_{EOF,CM}=L/\Delta t$) should be the same as the true average EOF velocity $\bar{u}_{EOF}$ of fluid flow. However, as shown in Fig. 3c, we found that this is not true - $\bar{u}_{EOF,CM}$ actually also underestimates $\bar{u}_{EOF}$ and the difference becomes more significant as the concentration decreases. Therefore, the deviation of the CM measured zeta potential cannot be fully explained by the velocity change induced by thick EDLs. This also indicates that the CM method cannot directly measure the average EOF velocity in Case B.

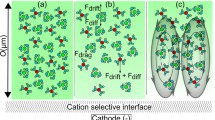
Another explanation for the underestimation might be the reduced EOF velocity caused by the deionization shock wave. Babar et al. (2020) pointed out that surface conduction due to extra counter ions in the electrical double layer can lead to ion polarization. In the application of CM, such ion polarization can promote a self-sharping concentration shock wave in the reverse direction of EOF, slowing down the propagation of the concentration front caused by the introduction of a high concentration solution (Babar et al. 2020; Mani et al. 2009; Zangle et al. 2009; Mani and Bazant 2011; Bahga et al. 2016). As the result of this effect, the EOF velocity reflected by the $I-t$ diagram ($\bar{u}_{EOF,CM}$) can have a smaller magnitude compared to the actual value ($\bar{u}_{EOF}$).

To investigate these two effects on the deviation of $\zeta$, we rewrite $\alpha$ in the following form to compare the contributions from the reductions of EOF velocity.

$$\begin{aligned} \alpha =\frac{\zeta _{CM}}{\zeta _{actual}}=\frac{-\frac{\varepsilon _r\varepsilon _0E \zeta _{CM}}{\eta }}{-\frac{\varepsilon _r\varepsilon _0E\zeta _{actual}}{\eta }}=\delta \beta \end{aligned}$$

(11)

where $\delta =\bar{u}_{EOF,CM}/\bar{u}_{EOF}$ compares the mismatch between the average EOF velocity taken from the I(t) plot ($\bar{u}_{EOF,CM}$) and the actual value directly generated by the simulation model ($\bar{u}_{EOF}$); while $\beta =\bar{u}_{EOF}/u_{EOF,max}$ describes the difference between the simulated average EOF velocity versus the max EOF velocity ($u_{EOF,max}$) in the EOF velocity profile.

To accurately predict $\alpha$, it is thus necessary to know how the operating conditions, channel geometry, and channel surface properties affect both $\beta$ and $\delta$. We first investigate the effect of ionic concentrations on these two factors. Figure 4a shows $\alpha$, $\beta$ and $\delta$ as a function of $c_1$ for two different nanochannels ($H=30~\mathrm {nm}$ and $100~\mathrm {nm}$). While these parameters show different concentration dependence for different nanochannel heights, they all reside between 0% and 100%, and all reduce as concentration decreases. Furthermore, for most of the conditions, $\beta$ and $\delta$ always have values higher than the corresponding $\alpha$, suggesting that neither $\beta$ nor $\delta$ can solely determine $\alpha$.

Fig. 4

Parametric study on EDLs dominance in nanochannels. $\alpha$,$\ \beta$ and $\delta$ are plotted with respect to (a) ionic concentration $c_1$ and (b) $2\lambda _D/H$ for nanochannel with $H=30$ and $100~\mathrm {nm}$, $\sigma =-5~\mathrm {mC/m^2}$. In (b), the blue dashed line corresponds to analytically predicted $\beta$ by Eq. (12); the green dashed line is the linear fitting of $\delta$ with a slope of $-K$

It is well known that $\beta$ has an analytical solution when the Debye–Huckel approximation is used to solve the electrical potential in the Poisson–Boltzmann equation (Kirby 2010), which can be written as

$$\begin{aligned} \beta =1-\frac{2\lambda _D}{H} \tanh \frac{H}{2\lambda _D}. \end{aligned}$$

(12)

Since this expression is only a function of the ratio between the Debye length (determined by the final concentration $c_1$) and characteristic confinement of the nanochannel (H/2), we also directly plot $\alpha$, $\beta$ and $\delta$ as a function of the ratio $2\lambda _D/H$ in Fig. 4b and compare $\beta$ calculated from the simulation with the analytical expression of Eq. (12), as plotted in blue dashed line. It can be observed that for conditions included in Case A and B (high concentration and low $2\lambda _D/H$), the analytical expression can well predict the value of $\beta$. Both the analytical prediction and simulation results show that $\beta$ is almost linearly proportional to $2\lambda _D/H$ and has a value of 100% when $2\lambda _D/H$ reaches zero.

This is expected as the term $\tanh (H/2\lambda _D)$ approaches unity when $2\lambda _D/H$ is small in Eq. (12). Interestingly, we find that in addition to $\beta$, both $\alpha$ and $\delta$ also show a linear dependence on $2\lambda _D/H$, and all of them reach the value of 1 when $2\lambda _D/H$ reaches zero. What’s more, the curves of $\alpha$, $\beta$, and $\delta$ for different channel heights now collapse into single curves, respectively. Consequently, it is safe to assume that for these simulated cases, $\delta$ also has the form of $1-K(2\lambda _D/H)$ where K is a constant, and thus $\alpha$ can be expressed as

$$\begin{aligned} \alpha =\delta \beta = \left( 1-K\frac{2\lambda _D}{H}\right) \left( 1-\frac{2\lambda _D}{H} \tanh \frac{H}{2\lambda _D}\right) \end{aligned}$$

(13)

When $2\lambda _D/H$ is small ($<30\%$), expanding Eq. (13) gives rise to $\alpha \approx 1-(2\lambda _D/H)[K+\tanh (2\lambda _D/H)]$. As a result, $\alpha$ is almost linearly dependent on $2\lambda _D/H$, which is consistent with the observation in Fig.4b. At this point, the $\alpha$ expression in Eq. (13) has only one unknown variable K. We will investigate the dependence of other factors on this variable in the following sections to study whether this is consistent with the deionization shock wave theory.

It is worth noting that Eq. (13) is only suitable for conditions corresponding to Case A and B. In Case C, as concentration decreases or the zeta potential becomes more significant, the Debye-Huckel approximation fails, and Eq. (12) does not apply anymore. Moreover, CM does not work in the surface charge governed regime since the transient current change cannot generate an available slope, as aforementioned. Therefore, Eq. (13) cannot serve its purpose to predict $\alpha$. Since Eq. (13) is clearly related to the ratio $2\lambda _D/H$, it is reasonable to conclude the boundaries that separate three regimes using the value of $2\lambda _D/H$. Based on our observations: Case A ($\alpha \approx 100\%$) corresponds to where $2\lambda _D/H<2.5\%$; Case B (non-zero $\alpha$ exits and $\alpha <100\%$) corresponds to regimes where $2.5\%<2\lambda _D/H<15\%$; when $2\lambda _D/H>15\%$, Case C is reached and CM fails ($\alpha \approx 0\%$).

3.2 The effect of surface charge density

The surface charge density $\sigma$ on a channel wall determines how intense the electrostatic interactions with the fluid are and, therefore, how great the zeta potential is. The origin of the surface charge should be traced back to the interactions between the solid surface and the aqueous solution, including ion adsorption, pronation, and deprotonation of the surface functional groups. For example, the silica surface can possess negatively charged silanol groups in an aqueous solution with neutral pH, and its surface charge density is generally affected by confinement, pH, ionic concentration, and solution composition (Karnik et al. 2007; Jensen et al. 2011; Behrens and Grier 2001; Ma et al. 2015; van der Heyden et al. 2005). The presence of surface charge gives rise to net charge transport in the electrical double layer, which would lead to ion polarization whenever there is a bulk concentration change or geometry change in the micro/nano-confinement. In fact, as explained in the previous sections, in the application of CM, such ion polarization can lead to a self-sharpening concentration shock wave in the reverse direction of EOF, decreasing the apparent EOF velocity ($\bar{u}_{EOF,CM}$) (Babar et al. 2020). In the microchannel with negligible thin EDL, Barbar et al. further derived an analytical formula for the time-dependent ionic current, indicating the decrease of the apparent EOF velocity (i.e., $\delta$ in our definition) should clearly depend on the dominance of surface charge density. This dominance of surface charge can be characterized by the Dukhin number, $Du=-\sigma /{c_1 H F}$, which indicates the ratio between surface conduction over bulk conduction (Mani and Bazant 2011). In their model, when Du is at the scale of $0.1-1$, the shock wave effect must not be ignored. Therefore, for our studies in the nanochannel, it is important to study how the deviation ($\alpha$ and $\delta$) respond to different surface charge densities or different Du.

Fig. 5

Parametric study on surface charge density in nanochannels: (a) and (b) $\zeta _{actual}$ and $\zeta _{CM}$ for nanochannel of $H=100~\mathrm {nm}$ with different $\sigma$. c $\alpha$ is plotted in respect to $c_1$ for varying $\sigma$ and H. Inset in (c) illustrates a magnified view of the plot (c)

In this simulation, we use three different but typical surface charge densities that have been utilized in previous studies, $\sigma =-2, -5, -10 ~\mathrm {mC/m^2}$ and investigate the change of $\zeta$, $\alpha$ and K under different concentrations and heights. The corresponding Du ranges from 0.002 to 0.5. Figure 5a and b illustrate that an increase in charge density leads to a corresponding rise in the magnitude of both $\zeta _{actual}$ and $\zeta _{CM}$ as expected. Those quantities, however, change in almost identical proportions with any changes in the surface charge density according to the correlation between $\alpha$ and $\sigma$ shown in Fig. 5c. In fact, for a fixed nanochannel height, the $\alpha$ v.s. $c_1$ curves for three different $\sigma$ collapse into almost the same curve, and the difference of $\alpha$ between different $\sigma$ is less than 1%. These results show that neither $\alpha$ nor K are dependent on $\sigma$ for the range of typical values studied.

Our finding suggests that, at the range of $\sigma$ as discussed in this work, if CM is applied in nanochannels that are fabricated from different materials yet have identical geometries, there should not be a difference in the measured $\alpha$ if the same experimental conditions are used, regardless of the exact value of $\sigma$. This finding is thus different from the previous study in microchannels and would offer great advantages for applying CM to characterize zeta potential in the nanochannel because $\sigma$ cannot be accurately measured inside the nanochannel at such high ionic concentrations in real experiments (Daiguji et al. 2004).

3.3 The effect of diffusivity

Besides the surface charge density, another factor that may affect K, and therefore $\alpha$, is the ion diffusivity $D_i$. This is because the change in $I_{EPF}$ dominates the change in the total measured current, and $I_{EPF}$ is linearly proportional to $D_i$ through $\mu _{EP,i}$, as shown in Eq. (5). In real applications, the ion diffusivity also differs when using different salts or performing CM at different temperatures. Therefore, it is important to study the dependence of K and $\alpha$ on ion diffusivity. For simplicity, we use the average ion diffusivity D to characterize the effect, where $D=(z_+-z_-)D_+D_-/(D_+ z_+-D_- z_- )$ (Lide and Haynes 2009). For monovalent salt as studied in this report, such as KCl, $D=2 D_+D_-/(D_++D_-)=1.99\times {10}^{-9}~\mathrm {m^2/s}$.

To study the effect of D, four sets of trials with different $c_1$ ($c_1=0.1, 0.333, 0.01, 0.00333$ M) are simulated, all of which possess identical channel geometries ($H=100~\mathrm {nm}$) and surface charge densities ($\sigma =-10~\mathrm {mC/m^2}$). D is varied for each trial between 20% and 150% of the aforementioned KCl diffusion coefficient. Figure 6a show the $\zeta _{actual}$ and $\zeta _{CM}$ for these conditions. While the $\zeta _{actual}$ does not change with the change of D (which is expected as zeta potential is majorly determined by the surface property), the $\zeta _{CM}$ significantly changed. The simulated $\delta$ as a function of D in Fig. 6b displays four negative linear relationships, each with unique slopes that only differ in ionic concentration and thus $2\lambda _D/H$. Given the fact that $\delta$ is expressed as $1-K(2\lambda _D/H)$, those linear relationships indicate that K has to be related to D. From Fig. 6b, we also find that the slope of each linear fitting is proportional to D. As a consequence, K must be in the form of BD, in which B is a constant with the unit of $\mathrm {s^2m^{-1}}$. This is also confirmed by plotting $\delta$ as a function of $D\times 2\lambda _D/H$ in Fig. 6c, in which a linear line can well fit all data points and we can further extract $B=2.5050 \times 10^9~\mathrm {s^2m^{-1}}$.

Fig. 6

Parametric study on ion diffusivity in nanochannels. a $\zeta _{CM}$ and $\zeta _{actual}$ are plotted with respect to average ion diffusivity D for varying conditions ($H=100~\mathrm {nm}$, $\sigma =-10~\mathrm {mCm^2}$ at varying $c_1$). b Linear relationship between $\delta$ and D for (a). c Linear relationship between $\delta$ and $D\times 2\lambda _D/H$ for conditions in (a)

Considering the quadratic term in Eq. (13) is negligible, the simplified form of this equation for $\alpha$ can thus be rewritten as

$$\begin{aligned} \alpha =1-\frac{2\lambda _D}{H}\left( BD+\tanh {\frac{H}{2\lambda _D}}\right) \end{aligned}$$

(14)

Altogether, Eq. (14) provides an analytical expression of the deviation when applying the CM technique in the nanochannels for Case A and B (when $2\lambda _D/H$ is less than 15%).

This expression contains two major terms that represent distinct mechanisms contributing to the deviation between measured $\bar{u}_{EOF,CM}$ and the actual value $\bar{u}_{EOF}$. While the hyperbolic tangent term considers the expected decrease in $\bar{u}_{EOF}$ as a result of the increase of EDLs’ thickness in the nanochannel confinement, the other term ($2\lambda _D BD/H$), which is proportional to the product of average diffusivity and the ratio of Debye screening length to the channel height, is somewhat surprising and not straightforward to understand.

We find that this term still results from the surface-charge-induced shock wave and can be derived analytically by adopting the 1-D transport analysis as discussed in the previous work (Karnik et al. 2007). In this analysis, we assume that both concentration and fluid velocity profiles remain uniform in the channel height direction. Assuming concentration in the nanochannel is uniform across the nanochannel length direction, when surface conduction to bulk conduction is small (i.e., Du is small), the cation and anion concentration inside the nanochannels for a monovalent salt can be approximated

$$\begin{aligned}&c_+=-\frac{\sigma }{HF}+\sqrt{\frac{\sigma ^2}{H^2F^2}+c_0^2} \end{aligned}$$

(15)

$$\begin{aligned} c_-=\frac{\sigma }{HF}+\sqrt{\frac{\sigma ^2}{H^2F^2}+c_0^2} \end{aligned}$$

(16)

where $c_0$ is the concentration of the salt at the bulk phase, and $c_{+}$ and $c_{-}$ are the concentrations of the cation and anion, respectively.

Fig. 7

Prediction from the 1-D analysis. a Schematics of ion depletion at the reservoir-nanochannel interface. b, c Comparison of $\delta$ and $\alpha$ from 2-D simulation results, fitting results using Eqs. (13) and (14), and prediction from 1-D analysis Eqs. (25) and (26) for KCl solution in the $H=100$ nm nanochannel

Figure 7a shows the schematics of depletion fluxes of ions at the interface. Assuming the electrical field across the interface between the reservoir and nanochannel is $E_1$ and $E_2$, respectively, one can write the cation ion flux leaving the interface as

$$\begin{aligned} J_{+,leave}=c_+ \mu _{EP,+} E_2+ c_{+} \bar{u}_{EOF} \end{aligned}$$

(17)

The first term in the above equation represents the contribution from the electrophoretic flow and the second term represents the contribution from the electroosmotic flow.

On the other hand, the cation flux entering the interface can be written as

$$\begin{aligned} J_{+,enter}=c_0\mu _{EP,+}E_1+c_0{\bar{u}}_{EOF} \end{aligned}$$

(18)

The net depletion flux for the cation at the interface is thus the difference between $J_{+,enter}$ and $J_{+,leave}$, which can be written as

$$\begin{aligned} J_{+,depletion}=J_{+,enter}-J_{+,leave} \end{aligned}$$

(19)

Similarly, the depletion flux for the anions at the interface can be expressed as

$$\begin{aligned} J_{-,depletion}=J_{-,enter}-J_{-,leave} \end{aligned}$$

(20)

Since the combination of depletion fluxes for the cation and anion have to be zero to ensure electroneutrality in the reservoir ($J_{+,depletion}+J_{-,depletion}=0$), we can rewrite the depletion flux only as a function of $E_2$ by eliminating $E_1$ from Eqs. (19) and (20).

$$\begin{aligned} \begin{aligned} J_{+,depletion} =&\frac{2\sigma }{HF}\frac{\mu _{EP,+}\mu _{EP,-}E_2}{\left( \mu _{EP,-}-\mu _{EP,+}\right) } \\&+\frac{\sigma }{HF}{\bar{u}}_{EOF}\frac{\left( \mu _{EP,+}+\mu _{EP,-}\right) }{\left( \mu _{EP,-}-\mu _{EP,+}\right) }\\&-\left( \sqrt{\frac{\sigma ^2}{H^2F^2}+c_0^2}-c_0\right) {\bar{u}}_{EOF} \end{aligned} \end{aligned}$$

(21)

As this depletion flux is in the opposite direction of the electroosmotic flow, which is supposed to replace the low concentration with the high concentration, it behaves as a shock wave, and the apparent electroosmotic total charge flux can be written as

$$\begin{aligned} \begin{aligned} J_{EO,apparent}&= \left( c_+{\bar{u}}_{EOF}+J_{+,depletion}\right) \\&-\left( {-c_-{\bar{u}}_{EOF}+J}_{-,depletion}\right) \end{aligned} \end{aligned}$$

(22)

It is worth noting that $J_{EO,apparent}$ here is not the net charge flux carried by the apparent electroosmotic flux, but instead is the total charge flux, corresponding to the total number of ions which would all contribute to the dominant current term $I_{EPF}$ in Eq. (5) that the apparent electroosmotic flow carries to the nanochannel.

Consequently, the ratio between $J_{EO,apparent}$ and $J_{EO}=c_+{\bar{u}}_{EOF}+c_-{\bar{u}}_{EOF}$, which is essentially $\delta = J_{EO,apparrent}/J_{EO}$ in this work, can be derived as below

$$\delta = 1 + \frac{{\frac{{2\sigma }}{{HF}}\frac{{\mu _{{EP, + }} \mu _{{EP, - }} }}{{\left( {\mu _{{EP, - }} - \mu _{{EP, + }} } \right)\mu _{{EO}} }}}}{{\sqrt {\frac{{\sigma ^{2} }}{{H^{2} F^{2} }} + c_{0}^{2} } }} + \frac{{\frac{\sigma }{{HF}}\frac{{\left( {\mu _{{EP, + }} + \mu _{{EP, - }} } \right)}}{{\left( {\mu _{{EP, - }} - \mu _{{EP, + }} } \right)}}}}{{\sqrt {\frac{{\sigma ^{2} }}{{H^{2} F^{2} }} + c_{0}^{2} } }} - \frac{{\left( {\sqrt {\frac{{\sigma ^{2} }}{{H^{2} F^{2} }} + c_{0}^{2} } - c_{0} } \right)}}{{\sqrt {\frac{{\sigma ^{2} }}{{H^{2} F^{2} }} + c_{0}^{2} } }}$$

(23)

Note that the above equation’s third and fourth terms correlate to the difference between cation and anion mobilities (or diffusivities), concentration (or bulk conductivity), nanochannel height, and surface charge density. For relatively small Du using a monovalent salt solution like KCl as our simulation conditions, in which diffusivities of cation and anion are close, these two terms are typically below 1%, which is negligible compared to the first two terms. Therefore, using the facts that $\lambda _D^2=\frac{\varepsilon _0\varepsilon _rk_BT}{eFc_0z_+\left( z_+-z_-\right) }$, ${\bar{u}}_{EOF}=\beta u_{EOF,max}\approx -\frac{\sigma \lambda _D\beta }{\eta }{E_2}$ and $\mu _{EP,i}=\frac{{eD}_iz_i}{k_BT}$, for monovalent salt, we can simplify the above equation as

$$\begin{aligned} \delta \approx 1+\frac{\left( \frac{2\eta }{HF\lambda _D\beta }\right) \left( \frac{\mu _{EP,+}\mu _{EP,-}}{\mu _{EP,+}-\mu _{EP,-}}\right) }{\sqrt{\frac{\sigma ^2}{H^2F^2}+c_0^2}} \end{aligned}$$

(24)

The denominator in this equation is the concentration of conducting charges in the entire nanochannel, where $c_0$ scales with the bulk solution conductivity and $\sigma /{HF}$ scales with the surface conductivity. For relatively small Du case as discussed in this report, $\sqrt{\frac{\sigma ^2}{H^2F^2}+c_0^2}\approx c_0$. Therefore, the above equation can be further simplified as

$$\begin{aligned} \delta \approx 1+\frac{\left( \frac{2\eta }{HF\lambda _D\beta }\right) \left( \frac{\mu _{EP,+}\mu _{EP,-}}{\mu _{EP,+}-\mu _{EP,-}}\right) }{c_0} \end{aligned}$$

(25)

From the aforementioned analysis, $\alpha$ can be readily derived using Eq. (25) and $\alpha =\beta \delta$ as

$$\begin{aligned} \alpha =1-\left( \frac{2\lambda _D}{H}\right) \tanh \left( \frac{H}{2\lambda _D}\right) -\left( \frac{2\lambda _D}{H}\right) \frac{e^2\eta D}{\varepsilon _0\varepsilon _rk_B^2T^2} \end{aligned}$$

(26)

The analytical expressions shown in Eqs. (25) and  (26) are very similar to the expressions in Eq. (14) derived from simulation results. This confirms that thick electrical double layer and surface charge induced shock wave are the two major sources of the deviation of the electroosmotic velocity and zeta potential measured in the CM. Furthermore, these two analytical expressions derived based on the 1-D analysis are independent of surface charge, which is also consistent with the simulation results.

To quantitatively compare the results, we plot $\delta$ and $\alpha$ calculated from Eq. (25) and Eq. (26) at several different surface charge densities for $H=100$ nm nanochannel in Fig. 7b and c, along with those from our 2-D simulation model. It is clear that 1-D analytical expression of Eq. (25) can well describe the simulation results, almost as same as the fitting line described by Eq. (14) using fitted $B=2.5050 \times 10^9~\mathrm {s^2m^{-1}}$.

The consistency not only shows that the assumptions used in the 1-D analysis do not affect the CM result, but also proves that surface-charge induced shock wave can cause a significant decrease of $\delta$ and $\alpha$, even when the contribution of surface conduction is not significant (or when Du is not large).

Note that in previous studies discussing the shock wave effects in the microchannel (Babar et al. 2020; Bahga et al. 2016), a similar analytical expression for $\delta$ was also derived to characterize the reduced apparent EOF velocity that was generated by $I-t$ curve. To be more specific, $\delta$ value, or the ratio between $I-t$ curved derived $\bar{u}_{EOF,CM}$ and the actual $\bar{u}_{EOF}$, can be readily derived as

$$\begin{aligned} \delta =\frac{{\bar{u}}_{EOF,CM}}{{\bar{u}}_{EOF}}=1+\frac{k}{\sigma _B+k}\ \frac{\mu _{EP,-}}{\mu _{EO}} \end{aligned}$$

(27)

where $\sigma _B=\left( \mu _{EP,+}-\mu _{EP,-}\right) c_0F$ is the conductivity of solution in bulk phase (in reservoir) and $k=-2\mu _{EP,+}\sigma /H$ is the EDLs conductivity induced by surface charge. The above equation can be rearranged as below, indicating that the ratio between surface conductivity and total conductivity in the channel can be used to characterize how much reduction of apparent EOF velocity caused by the shock wave.

$$\begin{aligned} {\bar{u}}_{EOF,CM}={\bar{u}}_{EOF}+\frac{k}{\sigma _B+k}\mu _{EP,-}E \end{aligned}$$

(28)

Similarly, we can also rearrange Eq. (24) in this form as

$$\begin{aligned} {\bar{u}}_{EOF,CM}={\bar{u}}_{EOF}+\frac{k}{\sigma _T}\mu _{EP,-}E \end{aligned}$$

(29)

where $\sigma _T=\left( \mu _{EP,+}-\mu _{EP,-}\right) F\sqrt{\frac{\sigma ^2}{h^2F^2}+c_0^2}$ is the total conductivity of solution in the channel. To compare with the above two equations, the difference lies in the estimation of the total conductivity. In fact, $\sigma _T$ in Eq. (29) is more accurate than $\sigma _B+k$ in Eq. (28), especially when Du number is at moderate level (when $Du \sim 0.1$ or larger). This is because the derivation of Eq. (28) assumes that the thickness of the EDLs is negligible compared to the channel height, and the surface conduction contribution does not affect the bulk contribution (Mani et al. 2009). Although this simplification helped to derive an analytical expression for the original non-linear equations, it can inevitably introduce inaccuracy and incorrect surface charge dependence (although $k/\bar{u}_{EOF}$ is independent of $\sigma$, $\sigma _B+k$ is a function for $\sigma$ even when Du is small), especially in the cases discussed in this work. The Eq. (29), however, has a more accurate estimation of the total ion concentration in the nanochannel, which leads to a more correct estimation of $\bar{u}_{EOF,CM}$ and the surface charge insensitive $\alpha$ and $\delta$ ($k/\bar{u}_{EOF}$ is independent of $\sigma$ and $\sigma _T$ is much less dependent on $\sigma$ when Du is smaller than 1). In Fig. 8, we selected some of our simulated results and compare with the prediction from Eqs. (23),  (25) and  (27). Note that although the Eq. (25) is the simplified version of Eq. (23), it still shows better accuracy compared with Eq. (27), especially when $2\lambda _D/H$ or Du becomes larger. Since the Eq. (25) does not requires the quantitative knowledge of $\sigma$, it should be more valuable compared with Eq. (23).

Fig. 8

Comparison of $\delta$ calculated by different equations for simulation results in a $H=100$ nm, $\sigma =-5~\mathrm {mC/m^2}$ and b $H=30$ nm, $\sigma =-10~\mathrm {mC/m^2}$

In short, our findings in Eqs. (25) and (26) provide a more convenient and reliable estimation of the shock wave induced reduced EOF flow, which can be used to translate the CM measure transient current change into the zeta potential of the nanochannel. For small Du cases, these expressions show an improved accuracy in characterizing the effect of the shock wave in CM application in nanochannels and do not require the knowledge of the surface charge density of the nanochannel in the estimation. We can bridge the gap between previous microchannel studies and the current nanochannel conditions with these simple forms.

3.4 Final validation of the expression

The simulation results in the previous sections suggest that $\alpha$, the deviation of zeta potential, is only affected by D and $2\lambda _D/H$, and an analytical expression exists. The 1-D analysis not only further confirms this conclusion but also suggests that the derived analytical expression for $\alpha$, i.e., Eq. (26) should be a more universal analytical expression for all monovalent electrolytes in Case B. In Fig. 9, we use Eq. (26) to map the $\alpha$ as the function of both D and $2\lambda _D/H$ for monovalent salt (whose $z_+z_-=-1$). The equation can provide a convenient estimation of $\alpha$ for the CM process to evaluate $\zeta$ in a 2-D nanochannel with known geometry and filled solution composition.

To further validate the expression of $\alpha$, we simulated additional sets of conditions and compared them with the Eq. (26). We selected two conditions with random values of H, $c_1$, and $\sigma$ for the KCl solution, and compared their simulated $\alpha$ with the prediction. We also considered different monovalent electrolyte solutions with more distinct diffusivities between cations and anions (NaCl and LiCl, for example) to testify our analytical expression in more broad applications. The results are listed in Table 1. These conditions are also labeled in Fig. 9. These results show good agreement between simulated value and predicted value regardless of the change of monovalent electrolyte type, H, $c_1$, and $\sigma$. These results confirm that the final expression is suitable for a broader range of conditions.

Table 1 Tested conditions

Fig. 9

Validation of analytical expression of Eq. (26). Color scale indicates the value of $\alpha$ as the function of $2\lambda _D/H$ and D for monovalent salt. Circles represent simulation results as presented in previous figures; Stars represent results from test conditions in Table 1 for different D. All results can be well predicted by the Eq. (26)

The results in Fig. 9 show that during the CM process, although the I(t) plot cannot present the actual $\bar{u}_{EOF}$ for thicker EDL conditions ($2\lambda _D/H <15\%$), it is still possible to use $\alpha$ to transform the information from the transient current reading to the true $\zeta$ of the nanochannel with the following correlation:

$$\begin{aligned} \zeta =\frac{-kL\eta }{\varepsilon _r\varepsilon _0E\Delta I\alpha } \end{aligned}$$

(30)

where, $\alpha$ can be calculated by the simple analytical expression of Eq. (26). As long as the nanochannel geometry and bulk phase solution properties are known, the above equation can be used alongside CM measurement to evaluate the zeta potential in the system. It is worth noting that our simulation and analysis only focus on monovalent ionic solutions. For more complex ionic solutions (i.e., multivalent ionic solutions), through our simulation and analysis, we have found that the expressions for $\alpha$ and $\delta$ are much more complicated and appear to be strong functions of the surface charge density. Therefore, it would be challenging to use those expressions to measure surface zeta potentials without knowing the surface charge density.

4 Conclusion

In this work, numerical simulation is used to examine the utility of current monitoring in measuring the zeta potentials of nanochannels filled with the monovalent salt solution. Although this technique is intended for thin electric double layer conditions, in which higher ionic concentrations negate much of the field emanating from the surface charge, we found that it can still be used in nanochannels when the ratio of the Debye length over the channel characteristic confinement $2\lambda _D/H$ is less than 15%. A correction factor, $\alpha$, is introduced to account for the underestimated electroosmotic velocity and zeta potential derived from the transient current change. Its value is found to be only determined by the normalized double layer thickness, $2\lambda _D/H$, and the average ion diffusivity of the electrolyte solution, D. There was no observed correlation between surface charge density on the nanochannel walls and $\alpha$ even when the Dukhin number is up to 0.5. The 1-D analysis further confirmed this finding, and a universal analytical expression that works for all binary electrolytes was derived.

Our results show that as long as the characteristic confinement of the channel and bulk solution properties (including ion diffusivities and ionic concentration) are known, $\alpha$ can be easily predicted by Eq. (26). Consequently, zeta potential can be accurately derived by executing the current monitoring experiment. This study provides an improved solution for applying the current monitoring method in nanoscale conduits for estimating accurate zeta potentials, which paves the way to better predict and control electrokinetic flow in various applications.