1 Introduction

Despite the rapid development of microengineering and lab-on-a-chip devices in the last two decades, our scientific knowledge of the physical phenomena occurring in these scales is not yet well established. Particularly, with regard to microfluidics, which is the fundamental engine of the lab-on-a-chip devices, microreactors and microelectronic cooling systems, extrapolation of our knowledge and engineering concepts from conventional scales to microscales is still questionable (Sobhan and Garimella 2001; Hetsroni et al. 2005). Therefore, comprehensive studies focused on dynamics of flows in such scales are crucial for future developments in this field.

Furthermore, recent advances in microfabrication have given rise to a new generation of complicated fluid circuits which often comprise multiple functional flow components to deliberately guide and/or control the flow of interest. In order to predict the overall performance of such complex systems, their elements should be first studied individually. This requires development of new measurement techniques which can both overcome the experimental challenges associated with the small dimensions of such devices and be applied non-intrusively in a large array of studies in the vicinity of geometrical complexities (Aubin et al. 2010).

Sudden expansions are examples of such functional components commonly used in a variety of microdevices, such as droplet generators, microchannel cold plates, valves, chemical mixers and injectors. Moreover, cardiovascular stenoses, heart valves and venous valves are all examples of the occurrence of sudden expansions in bio-systems and blood-wetted medical devices (Karino et al. 1979; Varghese et al. 2007; Zhao et al. 2008). Therefore, knowledge of their dynamics is important for modeling and designing a large group of applied systems. Such flows have been also of great fundamental and theoretical interest since they display a rich variety of features, namely flow separation and reattachment, a range of different types of flow instabilities, turbulence and mixing dynamics. As a result of their importance, there are a number of previous studies looking into hydrodynamics of such flows in larger geometries, but micro sudden expansion flows, especially at lower Reynolds numbers, have been overlooked so far.

While most of the studies on circular sudden expansions in macroscales were focused on transitions, instabilities and turbulent regimes, flows found in microgeometries are often laminar. In fact, flows at Re ∼ O(1), which were hardly investigated before, are the most common regimes used in microfluidic devices. At low Reynolds numbers Re d < 200, the flow downstream of a sudden expansion in a circular channel typically forms an axisymmetric annular vortex trapped between the jetlike core flow and the downstream channel walls, see the schematic in Fig. 1, which then develops axially until relaxing into a fully developed Poiseuille flow (Macagno and Hung 1967). The dimensionless length of the annular recirculation region formed just downstream of the expansion \({L}_{\rm r} = \frac{{x}_{\rm r}}{d}\) has been found to be a function of inlet flow Reynolds number \({Re}_{\rm d} = \frac{{\overline{U}}_{\rm d}\,d}{\nu}\), expansion ratio e = D/d and the inlet velocity profile. In particular, in macroscale geometries, L r was found to increase linearly with increasing Re d for moderate Reynolds numbers (Macagno and Hung 1967; Hammad et al. 1999; Cantwell et al. 2010; Sanmiguel-Rojas et al. 2010). The slope of this linear curve \({\alpha}_{\rm r} = \frac{\partial {L}_{\rm r}}{\partial {Re}_{\rm d}}\) was shown to be a function of expansion ratio e and inlet velocity profile (Scott et al. 1986; Badekas and Knight 1992; Dagtekin and Ünsel 2012, Latornell and Pollard 1986). In the present study, the effects of expansion ratio e and Reynolds numbers Re d on micro sudden expansion flows with fully developed inlet velocity profiles will be investigated.

Fig. 1
figure 1

Schematic of flow downstream of a sudden expansion: x c and r c correspond to the vortex center coordinates. x r and x d are the recirculation and redevelopment lengths, respectively. The dashed green line defines the limits of the control volume bounded between planes 1 and 2, and the downstream tube wall as used in the pressure drop calculations, see Sect. 3.2

Full size image

Due to the sudden enlargement of the channel cross-sectional area and energy dissipation at the walls and flow recirculating zones, sudden expansions lead to head losses in the flow. In order to estimate such losses, the common approach in engineering applications is to add an extra sudden expansion local pressure loss term \({\Updelta P}_{\rm{SE}}\) to the fully developed channel frictional pressure loss \({\Updelta P}_{\rm FD}\) to estimate the total pressure drop \({\Updelta P}_{\rm total}\) in sudden expansion flows (Idelchik 2008). While \({\Updelta P}_{\rm FD}\) can be calculated knowing the geometry and the flow Reynolds number, no analytical solution is available for accurate estimation of \({\Updelta P}_{\rm SE}\). Therefore, empirical and simplified theoretical models are often used for prediction of this parameter. The simplified theory, as discussed in White (1999), results in a relation which defines the sudden expansion excessive pressure drop coefficient K SE as a simple function of the area ratio \(\sigma = \frac{A_{\rm d}}{A_{\rm D}} = {(\frac{1}{e})}^{2}\):

$${K}_{\rm SE} = \frac{{\Updelta P}_{\rm SE}}{ \frac{1}{2} \rho \overline{U}_{\rm d}^{2}} = {(1-\sigma)}^{2}$$
(1)

This relationship is widely used to predict the pressure drop in turbulent sudden expansion flows where the inlet and outlet velocity profiles can be approximated to be uniform and the size of the recirculation region shrinks significantly creating a confined jet which fills the entire downstream channel cross-sectional area shortly after the expansion. However, in the laminar regime, where the inlet and outlet velocity profiles are very close to the fully developed parabolic prediction and the recirculating vortex can highly modify the wall and internal pressure distributions, the validity of this relationship is arguable.

The only empirical correlation for low Reynolds number sudden expansion flows was suggested in the revised edition of Idelchik (2008) only for uniform inlet velocity profiles which is usually far from the real inlet boundary condition for flows of a viscous liquid:

$${K}_{\rm SE} \simeq \frac{30}{{Re}_{\rm d}}$$
(2)

This relation was proposed for Re d < 10 with no dependency on the expansion ratio, while a very complex empirical correlation was suggested by the same authors for 10 < Re d < 500. Oliveira and Pinho (1997) and Oliveira et al. (1998) studied the problem of pressure drop in laminar sudden expansion flows numerically and showed that the corresponding pressure drop coefficient is not only a function of area expansion ratio σ but is also a strong function of inlet Reynolds number Re d, especially for relatively low Reynolds numbers, namely Re d < 50. They also discussed the reasons why the simplified theory fails to predict the pressure drop in the laminar regime. In the present study, we will thus experimentally investigate the complex nonlinear trend that Oliveira and Pinho (1997) and Oliveira et al. (1998) observed in their pressure drop results and relate them to the flow dynamics at the corresponding Reynolds numbers.

Based on a literature survey, no experimental measurement of pressure drops in flows through micro sudden expansions at low Reynolds numbers has been previously reported. This is mainly due to the following technical problems: (1) mounting pressure transducers, regardless of their type, generates significant perturbations in the microflows and thus result in erroneous measurements, (2) the excessive pressure drop caused by the sudden expansion needs to be back calculated from the total pressure drop measurements, which involves several simplifying assumptions, and (3) the inlet Reynolds number is also expected to have an effect on the pressure drop in addition to the expansion ratio in this regime. This latter point implies that the measurements should also be carried out for a large range of Reynolds numbers.

The main aim of this work is to simultaneously study the hydrodynamics and pressure distribution of flows through circular micro sudden expansions for a large range of inlet Reynolds numbers: 1 < Re d < 120. Moreover, the validity of the trends and relations proposed for conventional channels and their extrapolations to smaller scales will be investigated. To do this, an optical non-intrusive micro particle shadow velocimetry μPSV technique (Khodaparast et al. 2013) is applied to obtain full velocity field. Results of these measurements will then be used to determine the recirculation and redevelopment lengths of the flow at different Reynolds numbers. Such accurate high resolution measurements not only provide a comprehensive insight into the flow dynamics but also allow us to subsequently calculate other important flow parameters, such as the pressure drop caused by the expansion. Although applied to axisymmetric flows through circular sudden expansions here, the present technique can also be adapted to study other complex microscale geometries for simultaneous measurement of flow dynamics and pressure drop. A similar approach was followed previously by Fujisawa et al. (2006) to calculate the pressure drop coefficient for flows through micro-T-junctions using the velocimetry results obtained by fluorescent μPIV. The optical configuration and the post-processing procedure used in the present study are, however, simpler and more affordable.

Circular geometries were chosen over rectangular channels in the present study because the microfabricated planar microchannels are often trapezoidal rather than rectangular in cross-section. Moreover, non-circular channels are usually fabricated as open ducts which are then bonded to a cover plate, usually of a different material, resulting in a non-uniform surface condition on the channel walls. Therefore, the experimental measurements in microrectangular channels cannot be directly compared to analytical solutions or available numerical simulation results. On the other hand, besides their common appearance in bio-fluidic passages and medical devices which are among the most interesting applications of such flows, microcircular channels are more likely to have the same shape factor as those in macroscales and numerical models which makes the comparison of results more reliable.

The following sections explain the experimental technique used in this work and illustrate the obtained quantitative measurements. The experimental facility including the fluid loop and the optical setup is described in Sect. 2. Following that measurement techniques and processing methods performed in this study are presented in Sect. 3. Flow dynamics and pressure drop measurements are presented in Sect. 4 for two different expansion ratios, where comparisons with the available numerical and experimental results from the previous studies are provided wherever possible. Finally, the main achievements and conclusions of the present study are summarized in the last section of the paper.

2 Experimental setup

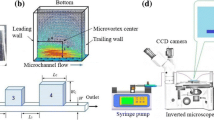
Experiments were carried out in a horizontal 100-mm-long fluorinated ethylene propylene (FEP) tube submerged in a water bath to remove the optical distortions due to the tube wall curvature (Budwig 1994), see the schematic shown in Fig. 2. Demineralized water was used as the working fluid. This ensured a fully refractive-index-matched media with respect to FEP and allowed accurate optical measurement of the tube diameters before and after the expansion. The sudden expansion was created by inserting a 20-mm-long blunt headed hypodermic tube whose outer diameter was slightly smaller than the inner diameter of the FEP tube allowing it to slide inside. Since the inlet velocity profile at the expansion plane has a significant effect on the characteristics of flow downstream of the enlargement (Latornell and Pollard 1986 and Oliveira and Pinho 1997), a sufficiently long hypodermic tube with a dimensionless length to diameter ratio of L/d = 80 was used to ensure fully developed flow at the sudden expansion plane. According to the widely accepted relation for the development length (Schlichting 1997), L/d > 8 is required for the highest Re studied here to achieve this goal. Two different hypodermic and FEP tube diameters, and thus two distinct expansion ratios, were tested in this study, see Table 1. Since even very small geometrical imperfections can lead to asymmetries in the flow downstream of the expansion, great care was taken in selecting a hypodermic tube with a very uniform wall thickness which did not deform the polymer tube when it was inserted.

Fig. 2
figure 2

Schematic of the experimental setup

Full size image
Table 1 The tested expansion ratios and the corresponding upstream and downstream tube diameters
Full size table

Demineralized water containing 2 μm diameter spherical polystyrene particles was pumped into the FEP tube using a non-oscillating pressure pump. The volumetric flow rate was roughly determined, with 5 % accuracy, using a microflow meter, while 1 % accurate flow rate measurements were obtained by a weighing technique using a digital balance at the outlet of the fluid circuit. The fluid temperature was measured at the inlet and outlet of the test section, and the fluid properties were determined at each step at the average of these temperatures. Since the large volume of liquid in the inlet tank of the pressure pump prevented any temperature increase due to the increase in the pumping pressure at higher flow rates, all the tests were performed close to the room temperature, namely T = 24 °C, which minimized possible heat transfer to the ambient. Tests were performed by increasing the flow rate with small steps of \({\Updelta Re_{\text{d}}} < 5\) over the range of 1 < Re d < 120. These steps were proved to be small enough so that the results were independent of the step size. Between each step and after stabilization of the pressure in the pump tank, enough time was taken to ensure that steady state was attained in the circuit.

Velocities were measured downstream of the expansion using the micro particle shadow velocimetry μPSV technique. A comprehensive introduction to the concepts and basic elements of an optimized μPSV system was presented in Khodaparast et al. (2013) for the first time. μPSV was proved to provide advantageous achievements compared to μPIV especially when optical access to the test section is not restricted. The technique is based on back-lit volume illumination of the region of interest in the flow and imaging the shadow of the tracer particles, here spherical polystyrene microbeads, using an objective with thin focal depth and a high-speed camera. In the present study, the field of view was backlit with a volume illuminating green LED focused on the region of interest using the microscope’s condenser. A Nikon 10X objective with numerical aperture of 0.3 was used for isolating the center plane of the tube where the measurements took place. The estimated depth of field using the relation proposed by Inoué and Spring (1997) was calculated to be around 10 μm. Images of microparticles shadows, produced by the high contrast between the background illumination and forward scattering of the microparticles, were taken using a high-speed camera at frame rates and shutter speeds of up to 2,400 fps and 1/75,000 s, respectively. Each pixel on the imaging array corresponds to 2.5 × 2.5 μm2 in the actual plane within the frame size of 256 × 900 pixels. For more details on different aspects of μPSV, such as the appropriate choice of the seeding particles, accuracy of the technique and its advantages compared to μPIV, please refer to Khodaparast et al. (2013).

Using the low-intensity LED as the light source in the present study ensured no localized heating of the test section, which can lead to undesirable secondary flows and consequently induce asymmetries in the flow. Moreover, back-lit illumination of the fully refractive-index-matched test section by a non-coherent light source allowed precise identification of tube wall location, which is of critical importance in accurately determining velocity gradients and thus calculating pressure gradients along the channel wall.

3 Measurement techniques

3.1 Visualization and velocimetry technique

The particle streaklines were obtained by calculating the standard deviation of a sequence of 1000 raw particle shadow images at each flow rate, as can be seen in Fig. 3. Recirculation length and quantitative vortex shape measurements, which will be presented in the next section, are achieved using these visualizations. Such results also provide valuable qualitative information on flow symmetry and stability in time. Once the flow was found to be steady in time at the Reynolds number of interest, the velocity vectors were calculated using the open source PIV software package JPIV (JPIV 2012). The volumetric concentration of the particles in the working liquid was kept below 10−4 to ensure no undesired disturbance in the flow. However, the ensemble cross-correlation technique suggested by Meinhart et al. (2000) was applied to maximize the signal-to-noise ratio of the results and minimize the Brownian motion effects arising especially at low Reynolds numbers and compensate for the low particle seeding densities (Williams et al. 2010). Rectangular interrogation windows elongated in the flow direction were then used for cross-correlation in the central part of the downstream channel since the axial velocity vectors are larger than those in the radial direction in this region. This resulted in vector spacings of 16 and 8 pixels in the axial and radial directions, respectively. Close to the channel walls, where the velocities are relatively lower, the axial spacing was reduced to 8 pixels in order to increase the spatial resolution of pressure gradient calculations. Such settings were observed to result in less than 2 % relative errors in velocities when experimental measurements were compared with the analytical Poiseille profile in the fully developed region of the downstream channel.

Fig. 3
figure 3

Particle streak image of flow downstream of the sudden expansion of e = 1.96 at Re = 50.9

Full size image

3.2 Pressure loss calculation

In order to estimate the pressure drop for sudden expansion flows, two different approaches can be followed. Firstly, experimental velocimetry results can be used to numerically calculate the pressure distribution in the flow field of interest in a post-processing step. To do this, the pressure gradients on the flow boundaries are calculated by simply inserting the measured velocities into the Navier-Stokes momentum equation. Then, these results are used as the Neumann boundary conditions for solving the Poisson equation for pressure. The difference between the calculated inlet and outlet pressure values then provides the total pressure drop from which the excessive sudden expansion pressure drop can be derived. This is a non-intrusive technique for precise estimation of the pressure field in cases where mounting pressure probes can disturb the flow and lead to erroneous measurements (Bauer and Koengeter 1999; Fujisawa et al. 2005; Gurka et al. 1999; van Oudheusden et al. 2007). More particularly in smaller scales, where not only the size of the measurement sensor is an issue but also the sensitivity of the differential sensor should be down to few Pascals per unit length of interest, this technique is a promising solution for accurate high resolution measurements of the pressure (Fujisawa et al. 2006). In the second approach, which is followed in the present study, only the pressure gradients on the walls surrounding a control volume, which contain the region of interest, have to be calculated. The region of interest contains the downstream channel until the point where the flow redevelops back to the Poiseuille profile (Oliveira et al. 1998). Such a control volume is bounded by plane 1, plane 2 and the downstream tube wall, as depicted in Fig. 1 by the dashed lines. Cross-sectional plane 1 is situated at the expansion plane, while plane 2 is located at the axial position where the flow regains its fully developed Poiseille profile at x d. The pressure drop is then calculated by inserting these measurements in the momentum and energy balance for the corresponding control volume. Since the focus of this work is to attain only the excessive pressure drop caused by the sudden expansion, the latter procedure can fulfill our goal while demanding fewer numerical calculations.

Applying the second solution discussed above, for the control volume bounded by the dashed lines in Fig. 1, the momentum balance is:

$${P}_{1}{A}_{\rm d} + ({P}_{1} + {\overline{\Updelta P}}_{\rm s}) ({A}_{\rm D} - {A}_{\rm d}) + {\Upphi_m}_{\rm d} = {P}_{2}{A}_{\rm D} + {\Upphi_m}_{\rm D} + {\Updelta P}_{w}{A}_{w}$$
(3)

where P 1 and P 2 represent the pressure at the inlet and outlet cross-sectional areas namely A d and A D. The pressure on the expansion step of plane 1 was estimated by \({P}_{1} + {\overline{\Updelta P}}_{\rm s}\), where \({\overline{\Updelta P}}_{\rm s}\) is the average pressure drop on the expansion wall and can be calculated by averaging the integrated radial pressure gradient on the expansion step using the experimental velocity results as follows:

$${\overline{\Updelta P}}_{\rm s} = \frac{1}{({A}_{\rm D} - {A}_{\rm d})} \int\limits_{{A}_{\rm D}-{A}_{\rm d}} \left( \frac{\partial P}{\partial r}\hbox{d} r\right)\hbox{d} A = \frac{1}{({A}_{\rm D} - {A}_{\rm d})} \int\limits_{{A}_{\rm D}-{A}_{\rm d}} \mu \left[ \left(\frac{{\partial}^{2} {U}_{\rm r}}{\partial {x}^{2}}\right)\hbox{d} r \right]\hbox{d} A$$
(4)

The last term in Eq. 3 corresponds to the total frictional pressure drop \({\Updelta P}_{w}\) on the downstream channel wall surface A w while \({\Upphi_{\rm m}}_{\rm d}\) and \({\Upphi_{\rm m}}_{\rm D}\) refer to the inlet and outlet flow momentum across the corresponding cross-sectional areas A d and A D, respectively, and are defined as follows:

$${\Upphi_{\rm m}} = \int\limits_{A} \rho {U}^{2}\hbox{d} A$$
(5)

where U is the local axial velocity at the corresponding cross-section. After simple manipulation of Eq. 3 and normalizing all the terms with the inlet dynamic pressure, the total pressure drop coefficient is then calculated as follows:

$${C}_{\rm total} = \frac{{P}_{1} - {P}_{2}}{ \frac{1}{2} \rho \overline{U}_{\rm d}^{2}} = \frac{{\Upphi_m}_{\rm D} - {\Upphi_m}_{\rm d}}{\frac{1}{2}\rho {A}_{\rm D} \overline{U}_{\rm d}^{2}} - \frac{{\overline{\Updelta P}}_{\rm s} (1 - \sigma)}{\frac{1}{2}\rho \overline{U}_{\rm d}^{2}} + \frac{{\Updelta P}_{w}}{\frac{1}{2}\rho \overline{U}_{\rm d}^{2}}\left(\frac{4 {x}_{\rm d}}{D}\right)$$
(6)

where \(\overline{U}_{\rm d}\) is the mean velocity in the upstream channel and σ is the area ratio \(\frac{{A}_{\rm d}}{{A}_{\rm D}}\).

For the same control volume, the conservation of energy yields:

$${P}_{1} + {\Upphi_{\rm e}}_{\rm d} = {P}_{2} + {\Upphi_{\rm e}}_{\rm D} + {\Updelta P}_{fd} + {\Updelta P}_{I}$$
(7)

The pressure loss in the control volume is divided into two terms: the fully developed frictional term \({\Updelta P}_{fd}\) and the additional irreversible term appearing due to the sudden expansion in the flow \({\Updelta P}_{I}\). \({\Upphi_{\rm e}}_{\rm d}\) and \({\Upphi_{\rm e}}_{\rm D}\) in Eq.7, respectively, refer to the kinetic energy per unit volume of the inlet and outlet flows across A d and A D and are defined as follows:

$${\Upphi_{\rm e}} = \frac{ \int_{A} \frac{1}{2} \rho {U}^{3}\hbox{d} A}{\overline{U} A}$$
(8)

The normalized energy balance equation also results in a relation defining the total pressure drop coefficient:

$${C}_{\rm {total}} = \frac{{P}_{1} - {P}_{2}}{ \frac{1}{2} \rho \overline{U}_{\rm d}^{2}} = \frac{{\Upphi_e}_{\rm D} - {\Upphi_e}_{\rm d}}{\frac{1}{2}\rho \overline{U}_{\rm d}^{2}} + \frac{{\Updelta P}_{fd}}{\frac{1}{2}\rho \overline{U}_{\rm d}^{2}} + \frac{{\Updelta P}_{I}}{\frac{1}{2}\rho \overline{U}_{\rm d}^{2}}$$
(9)

The total pressure difference is therefore due to the gain in the reversible dynamic pressure and the irreversible loss in the pressure due to the internal energy dissipation and friction at the boundaries.

Comparing Eq. 9 to Eq. 6, the excessive sudden expansion irreversible pressure loss coefficient, C I , can be derived as follows:

$${C}_{I} = \frac{{\Updelta P}_{I}}{\frac{1}{2}\rho U_{\rm d}^{2}} = \frac{{\Upphi_m}_{\rm D} - {\Upphi_m}_{\rm d}}{\frac{1}{2}\rho {A}_{\rm D} \overline{U}_{\rm d}^{2}} - \frac{{\Upphi_e}_{\rm D} - {\Upphi_e}_{\rm d}}{\frac{1}{2}\rho \overline{U}_{\rm d}^{2}} - {C}_{\rm s}(1 - \sigma) + {C}_{w}\left(\frac{4 {x}_{\rm d}}{D}\right) - {C}_{fd}$$
(10)

where C s is the frictional pressure drop coefficient on the expansion step, C w is the actual frictional pressure drop coefficient on the downstream channel wall in the developing region and C fd is the frictional pressure drop coefficient assuming fully developed Poiseuille flow in the same region:

$${C}_{\rm s} = \frac{{\overline{\Updelta P}}_{\rm s}}{\frac{1}{2}\rho \overline{U}_{\rm d}^{2}}$$
(11)
$${C}_{\rm w} = \frac{1}{\frac{1}{2}\rho \overline{U}_{\rm d}^{2}} \int\limits_0^{{x}_{\rm d}} \! \frac{\partial P}{\partial x}\hbox{d} x = \frac{1}{\frac{1}{2}\rho \overline{U}_{\rm d}^{2}} \int\limits_0^{{x}_{\rm d}} \! \mu \left[\frac{1}{r}\frac{\partial}{\partial r}\left ( r \frac{\partial {U}_{x} }{\partial r} \right) \right]\hbox{d} x$$
(12)
$${C}_{\rm fd} = \frac{1}{\frac{1}{2} \rho \overline{U}_{\rm d}^{2}} f \frac{{x}_{\rm d}}{D} \frac{\rho \overline{U}_{\rm D}^{2}}{2} = {\sigma}^{2} {f} \frac{{x}_{\rm d}}{D}$$
(13)

In the equations above, the liquid density ρ and viscosity μ are calculated at the measured average flow temperature at each Reynolds number. The average pressure drop on the expansion step \({\overline{\Updelta P}}_{\rm s}\) and the total pressure drop downstream channel walls \({\Updelta P}_{\rm w}\), which appear in Eq. 4 and Eq. 12, are formulated assuming axisymmetric flow with a no-slip boundary condition at the walls in the axial and radial Navier-Stokes equations, respectively. The validity of the no-slip assumption at the tube walls was controlled by extrapolating the experimental velocity values to the wall locations. Velocity gradients in these equations were then calculated by fitting quadratic polynomial curves in the least square sense to the velocity data points close to the channel walls. Therefore, the spatial resolution and the accuracy of the pressure gradient calculations are directly dependent on those achieved in the experimental velocimetry technique, the spatial calibration accuracy and also on the errors in specifying the wall location in the images. Moreover, experimentally measured velocities at the inlet and outlet of the control volume of interest were used in Eq. 5 and Eq. 8 to estimate the momentum and kinetic energy terms.

It should be noted that the sudden expansion pressure drop coefficient K SE , which is commonly used in text books (White 1999), is derived considering uniform inlet and outlet velocity profiles which is a fair assumption in turbulent flows. As the result, the momentum and energy terms across a certain surface A are simply as follows:

$${\Upphi_{\rm m}} = \rho A {\overline{U}}^{2}$$
(14)
$${\Upphi_{\rm e}} = \frac{1}{2} \rho {\overline{U}}^{2}$$
(15)

Therefore, K SE is equal to (1 − σ)2 if the difference between the actual and the fully developed pressure drop on the downstream tube wall and the pressure drop on the expansion plane are neglected.

4 Results and discussion

4.1 Flow characteristics

Previous experimental investigations on sudden expansion flows were all performed in tubes diameters of 10 mm or larger and were mainly dedicated to flows at Re d  > 20. However, the present study is focused on flows in sub-millimeter dimensions in which flows at Re d  < 20 are of great practical importance. Currently, the linear trends in flow dynamics at higher Reynolds numbers are often simply extrapolated to predict the flows as \({Re}_{\rm d} \rightarrow 0\). A very common example is the linear prediction curve for the dimensionless recirculation length L r  = x r /d which has always been used as a benchmark in both numerical and experimental studies of flows through sudden expansions. However, at lower Reynolds numbers Re d  < Re tr , a clear nonlinear trend was observed in the growth rate of the recirculation length in the present study for both expansion ratios, see Fig. 6. This observation is in agreement with the conclusions of the studies focused on creeping sudden expansion flows by Monnet et al. (1982) and Macagno and Hung (1967) in larger tubes, d > 20 mm. In order to ensure that the tracer particles, used for visualization, have no disturbing effect in this regime, experimental tests were also performed with 1 μm diameter particles for e = 1.96 in the range of 0 < Re d  < 50. A Nikon 20X objective with numerical aperture of 0.45 was used for magnifying the region of interest in these experiments. Results of such measurements, as presented in Fig. 7, show identical asymptotic trends when \({Re}_{\rm d} \rightarrow 0\) for the two sets of experiments. Therefore, such flow characteristics are believed not to be related to the length scale of the system nor to the size of the tracer particles used for visualizations. It can be seen in Fig. 6 that L r approximately asymptotes to L r ≃ 0.28 at lower Reynolds numbers for e = 1.96, while it reaches L r ≃ 0.15 for e = 1.51. These measurements agree favorably with the results of Monnet et al. (1982) and Macagno and Hung (1967) for e = 2.26 and e = 2 who reported asymptotic values of \({L}_{\rm r} \rightarrow 0.3\) and \({L}_{\rm r} \rightarrow 0.27\) at very low Reynolds numbers, respectively. The following correlations were found to predict L r at Re d  < Re tr with less than 5 % error:

$$L_{\rm r} = 0.165\,{e}^{0.04 Re_{\rm d}}\,\hbox{for}\,e =1.51\,\rm{at}\,Re_{\rm d} < 30$$
(16)
$$L_{\rm r} = 0.278\,{e}^{0.05 Re_{\rm d}}\,\hbox{for}\,e =1.96\,\rm{at}\,Re_{\rm d} < 20$$
(17)

The flow characteristics in this regime were also investigated by quantifying the shape of the recirculation zone developed around the confined jet. As can be seen in Fig. 4, at least two distinct flow patterns were observed in the laminar sudden expansion flows: for Re d  < Re tr , the angle between the separation streamline and the vertical expansion step β increases from values close to 0 to π/2 when increasing the flow Reynolds number. This observation is in excellent agreement with numerical streamlines presented by Macagno and Hung (1967) at the corresponding Reynolds numbers. The trapped vortex grows in both radial and axial directions in this regime, while the dimensionless coordinates of its center, R c and L c , follow nonlinear trends, see Fig. 5. Increasing the flow velocity and passing the transition Reynolds number Re tr , the flow enters a new regime in which the vortex fills the expansion step, while the separation angle value remains constant at β = π/2, see Fig. 5. At Re d  > Re tr , the vortex center proceeds downstream in a linear manner while remaining at the same radial coordinate. The transition Reynolds number Re tr , which can be considered as the threshold for the onset of the linear trends in laminar sudden expansion flows, was observed to increase when decreasing the expansion ratio. Although not covered in this study, it is worth mentioning that Monnet et al. (1982) observed another distinct flow pattern at even lower Reynolds numbers Re d  < 1 in which the inlet jet does not detach from the wall at the expansion but instead follows the step, resulting in the separation angle of β = 0.

Fig. 4
figure 4

Distinct flow configurations at low Reynolds numbers for expansion ratio e = 1.96 at: a Re = 12.0 and b Re = 50.9

Full size image
Fig. 5
figure 5

Evolution of vortex center coordinates and separation angle: a e = 1.51 and b e = 1.96

Full size image

Unlike the nonlinear regime, the circular sudden expansion flow characteristics at relatively larger Reynolds numbers are well understood and quantified. As suggested by the previous studies, linear curves were fitted to the present experimental measurements of recirculation length, but only for the range Re d  > Re tr , see Fig. 6. The gradients of the linear curves fitted to the measurements α r are then compared to those reported previously in the literature in Table 2. It should be noted that results are compared to the closest expansion ratios available in the numerical and experimental works, namely e = 2 and e = 1.5. It can be seen that despite the different techniques and tube diameters, the reported values for the slope of the linear fit are in very good agreement, suggesting that no length-scale effects are present for the range of Reynolds numbers and tube diameters studied here. The small differences are believed to stem from: experimental uncertainties, possible slight differences in the exact values of expansion ratios, deviation of the inlet velocity profile from the fully developed flow in reality, which is not considered in some of the numerical results, and including the data in the nonlinear range in the linear curve fitting procedure (Fig. 6).

Fig. 6
figure 6

Dimensionless recirculation length versus inlet Reynolds number

Full size image
Fig. 7
figure 7

Effect of the tracer particles diameter on the flow characteristics for expansion ratio e = 1.96 at low Reynolds numbers

Full size image
Table 2 Comparison of the reported slopes for the linear curve fitted to the dimensionless recirculation length results
Full size table

Numerical studies by Scott et al. (1986) and Dagtekin and Ünsal (2010) on axisymmetric sudden expansion flows showed that the gradient of this linear fit α r grows linearly with increasing expansion ratio e. The experimentally measured recirculation length in this study suggests the following relationship between α r and e:

$${\alpha}_{\rm r} = 0.062 \; e - 0.083$$
(18)

Although obtained for expansion ratios up to around 2 in this study, this correlation predicts the values of α r calculated numerically by Scott et al. (1986), Dagtekin and Ünsel (2010) and Oliveira et al. (1998) with less than 5 % error for higher expansion ratios up to e = 8.

As the flow proceeds downstream of the enlargement, the effect of the expansion gradually diminishes and the flow redevelops back to the fully developed parabolic Poiseuille profile. From the practical point of view, having a prediction correlation for redevelopment length is very important especially in pressure drop measurements where the sensors should be mounted in the fully developed region and not before, thus accounting for the total excessive pressure drop caused by the expansion. Moreover, in complex microfluidic circuits, the interactions between the individual geometrical components cannot be neglected if their affected zones overlap. The downstream channel length affected by the sudden expansion was characterized by the dimensionless redevelopment length L d  = x d /d, where x d is defined as the axial distance from the expansion plane at which the relative difference between two successive velocity vectors becomes less than 1 % for the first time, see Fig. 8. The dimensionless redevelopment length L d was found to grow linearly when increasing the Reynolds number for Re d  > Re tr , see Fig. 9. For lower Reynolds numbers, the following empirical fits were found to predict the measurements with less than 3 % error:

$$L_{\rm d} = 1.095\,{e}^{0.014 Re_{\rm d}}\,\hbox{for} \,e =1.51\, \rm{at} \,Re_{\rm d}<30$$
(19)
Fig. 8
figure 8

Evolution of dimensionless centerline axial velocity along the tube axis for expansion ratio e = 1.96 at Re = 50.9: after a rapid decrease immediately downstream of the expansion, the centerline axial velocity then decreases asymptotically until it reaches the fully developed value

Full size image
Fig. 9
figure 9

Dimensionless redevelopment length versus inlet Reynolds number

Full size image
$$L_{\rm d} = 1.134\,{e}^{0.034 Re_{\rm d}}\,\hbox{for}\,e =1.96\,\rm{at}\,Re_{\rm d}<20$$
(20)

Measurements of this parameter for e = 1.96 compare favorably with those reported by Hammad et al. (1999) for e = 2, while the differences are believed to be due to the slight difference in the expansion ratios and the different definitions used for development length in the two studies.

4.2 Pressure drop

As discussed previously, the conventional simplified theories and empirical correlations are not expected to estimate the pressure drop in sudden expansion flows at very low Reynolds numbers effectively. Oliveira et al. (1997) showed that one of the main reasons behind this is that the simplified theory does not include the modification of frictional pressure drop on the downstream wall. Fortunately, the approach followed in the present study allowed for accurate estimation of the local axial pressure gradient every 20 μm along the channel wall. It can be clearly seen in Fig. 10 that the pressure gradient trend is far from the predicted constant value in the presence of fully developed flow in the channel. The axial pressure gradient on the wall has negative values close to the expansion plane owing to the backward flow direction and consequently pressure recovery in the flow in this zone. Its value then increases until reaching a constant value, showing the redevelopment of the flow, farther downstream. These results not only show the high spatial resolution provided by the present technique for pressure gradient measurements but also demonstrate the capacity of the technique to capture very small pressure gradient values. As mentioned before, the spatial resolution of the pressure drop measurements in this study is directly dependent on the corresponding velocity vector spacing set in the cross-correlation step.

Fig. 10
figure 10

Evolution of dimensionless static pressure gradient on the tube wall for expansion ratio e = 1.96 at Re = 50.9

Full size image

Assuming that the asymptotic value of the pressure gradient achieved downstream of the expansion is due to the redevelopment of the flow, these constant pressure gradient values at x > x d, are expected to agree with that predicted by the analytical solution for fully developed steady-state laminar Poiseille flow in a circular channel. The experimental fully developed friction factor is calculated using the asymptotic pressure gradient value in the following relationship:

$$f = \left({\frac{\partial P}{\partial x}}\right)\left({ \frac{D}{\frac{1}{2} \rho \overline{U}_{\rm d}^{2}}}\right)$$
(21)

The calculated results are compared with the analytical solution for Poiseuille flow in a circular channel, namely f = 64/Re D in Fig. 11. Re D is calculated based on the downstream channel diameter and bulk velocity. It can be seen that the experimental measurements are in very good agreement with the theoretical prediction, and the relative errors in determination of the local frictional pressure drop coefficient are smaller than 5 %. This also confirms that the flow at the outlet of the channel is fully developed and showing no microscale effects present in the range of tube diameters and Reynolds numbers tested in this work.

Fig. 11
figure 11

Fully developed frictional pressure drop coefficient downstream of the sudden expansion

Full size image

In order to calculate the irreversible pressure drop coefficient C I , as was derived in Sect. 3.2, different terms of Eq. 10 were calculated at each Reynolds number using the experimental velocity measurements. Considering the relative errors in determination of the tubes’ diameters, flow velocities and frictional pressure drop coefficients to be about 0.5, 2 and 5 % accordingly, the experimental measurements of C I contain up to around 11 % of relative errors. The results of the calculations in this study were compared to those achieved by Oliveira et al. (1998) numerically, see Fig. 12. The differences between the experimental and numerical results are believed to be due to the experimental uncertainties, the differences in the expansion ratios and simplifications in estimation of the pressure on the expansion plane. It can be clearly observed that the irreversible pressure loss coefficient is a strong function of Reynolds number for lower flow rates while its value is nearly constant for Re d > 30 with e = 1.51 and Re d > 20 with e = 1.96. These two distinct trends in the pressure drop measurements are in good agreement with the transitions observed in the flow dynamics at lower Reynolds numbers.

Fig. 12
figure 12

Irreversible pressure drop coefficient caused by the sudden expansion

Full size image

The asymptotic irreversible pressure drop coefficient, which was observed at Re d > Re tr, increases from around 0.50 for e = 1.51 to 0.95 for e = 1.96, implying that higher expansion ratios result in higher irreversible pressure drops. These measurements are in excellent agreement with the prediction method suggested by Oliveira et al. (1998) for Re d  > 50. Moreover, the complex general correlation proposed by Oliveira et al. (1998), illustrated in Fig. 10, predicts the experimental results of this study for expansion ratios of 1.96 and 1.51 with average errors of 12 and 10 % and maximum relative errors of 30 and 20 %, respectively. The same correlation predicted their own numerical results with a maximum relative error of 7 %. Empirical correlations were found in this study by least square curve fitting to the experimental measurements for the two tested expansion ratios, see Eq. 22 and Eq. 23 below. These two correlations were able to predict our experimental irreversible pressure loss coefficient with an accuracy better than 5 % for Re d < 10 and Re d  > 50 and an error of 8 % in the intermediate range close to the transition Reynolds number Re tr . Accuracy of these correlations was also investigated upon the numerical results of Oliveira et al. (1998), which were claimed to contain less than 0.8 % of error. As the result, their numerical results could be predicted with an average relative error of less than 15 % for Re d > 1.

$${{C}_{I}}_{(e=1.51)} = 0.509 + 5.143 {e}^{-0.185 {Re}_{\rm d}}$$
(22)
$${{C}_{I}}_{(e=1.96)} = 0.986 + 8.124 {e}^{-0.214 {Re}_{\rm d}}$$
(23)

The prediction method suggested in the revised edition of Idelchik (2008) for laminar flows is also depicted in Fig. 10 for the two expansion ratios. However, it should be noted that this correlation was proposed for uniform inlet velocity profiles only. For Re d  < 10, no expansion ratio effect is considered in the suggested correlation, see Eq. 2. Moreover, at higher Reynolds numbers Re d  > 10, the proposed correlations were observed not to follow the trend observed in this study or that of Oliveira et al. (1998), especially close to the transition regime.

5 Conclusions

Flow dynamics and pressure drop were studied downstream of a microcircular sudden expansion. High quality experimental measurements were conducted using a non-oscillating pressure pump, calibrating the flow rate measuring equipment accurately and taking temperature measurements at multiple locations. Moreover, special care was taken in matching the refractive indices of the working fluid, tube wall and the tube exterior medium in order to avoid the possible optical distortions due to the curved walls of the tube. As a result, the tube walls were located accurately in the images and errors in measurement of tube diameter and locating velocity vectors calculated by the velocimetry technique were minimized.

Velocimetry was carried out downstream of sudden expansions with ratios of e = 1.51 and e = 1.96. The μPSV technique was chosen for measuring the velocity field, which enabled tracking the tracer particles up to relatively high velocities without using a high-power laser light source and therefore reducing the possible undesired heating effects. The recirculation and redevelopment lengths of the flow were measured using visualization and velocimetry results for Re d  < 120. These results were in very good agreement with the numerical and experimental observations reported for macro circular sudden expansions, thus proving no length scale dependency in the flow of interest in the range of tube diameters and Reynolds numbers studied. As reported previously for much larger channels, a linear trend was observed in the growth of both the recirculation and redevelopment lengths with increasing Reynolds number for Re d  > Re tr . However, below a certain transition Reynolds number Re tr , the trend was observed to be nonlinear. Quantitative detailed study of the confined vortex shape is performed in this range. Although such flow characteristics are not believed to be exclusive to microscales, they have been overlooked in macroscales since flows at very low Reynolds numbers were not of particular interest.

The pressure drop caused by the sudden expansion was also calculated using the velocimetry results in the energy and momentum balance equations for the control volume containing the flow downstream of the sudden expansion plane. The pressure gradient far downstream of the expansion accurately followed the analytical solution for the fully developed steady-state laminar Poiseuille flow in circular channels, while the calculated irreversible pressure drop coefficient was in good agreement with the numerical results reported by Oliveira et al. (1998). The irreversible pressure drop coefficient was found to be a strong function of Reynolds number for Re d  < Re tr with a decreasing trend toward an asymptotic value for higher Reynolds numbers. This conclusion shows that extrapolation of the commonly used prediction methods in larger scales to microfluidics should be only performed after careful investigation of the validity of the fundamental assumptions considered in deriving the models.

Finally, this study can be considered as the first experimental attempt to accurately measure the excessive pressure drop caused by a sudden expansion in a circular tube and to validate the available numerical predictions in the laminar regime. The proposed correlations for prediction of the pressure drop in sudden expansion flows in the present study can be useful in the future design of more performant microfluidics devices. Moreover, the present technique provides a powerful and accurate method to non-intrusively measure pressure drops with high spatiotemporal resolutions, especially in complicated small or microscale geometries where often common pressure measurement techniques are either not feasible, too intrusive to implement or lack sensitivity. Namely, we were able to measure the pressure gradients along the channel wall with a spatial resolution of 20 μm and a sensitivity of around 15 Pa/m, to an accuracy of 5 %.