Dynamics of isolated confined air bubbles in liquid flows through circular microchannels: an experimental and numerical study

Abstract

Experimental and numerical studies are performed to characterise the dynamics of isolated confined air bubbles in laminar fully developed liquid flows within channels of diameters d = 0.5 mm and d = 1 mm. Water and glycerol are used as the continuous liquid phase, and therefore, a large range of flow capillary numbers 10⁻⁴ < Ca < 10⁻¹ and Reynolds numbers 10⁻³ < Re < 10³ are covered. An extensive investigation is performed on the effect of bubble size and flow capillary number on different flow parameters, such as the shape and velocity of bubbles, thickness of the liquid film formed between the bubbles and the channel wall, and the development lengths in front and at the back of the bubbles. The micro-particle shadow velocimetry technique (μPSV) is employed in the experimental measurements allowing simultaneous quantification of important flow parameters using a single sequence of high-speed greyscale images recorded at each test condition. Bubble volume and flow rate of the continuous liquid phase are precisely determined in the post-processing stage using the μPSV images. These parameters are then used as initial and boundary conditions to set up CFD simulations reproducing the corresponding two-phase flow. Simulations based on the volume of fluid technique with the aim of capturing the interface dynamics are performed with both ANSYS Fluent v. 14.5, here augmented by implementing self-defined functions to improve the accuracy of the surface tension force estimation, and ESI OpenFOAM v. 2.1.1. The present approach not only results in valuable findings on the underlying physics involved in the problem of interest but also allows us to directly compare and validate results that are currently obtained by the experimental and computational methods. It is believed that similar methodology can be employed to rigorously investigate more complex two-phase flow regimes in micro-geometries.

1 Introduction

Fundamental investigations of micro-scale two-phase flow dynamics are of great interest to a large variety of applications ranging from micro-evaporators to micro-biochemical reactors (Kreutzer et al. 2005; Waelchli and Rohr 2006; Kashid and Agar 2007; Teh et al. 2008; Tung et al. 2009; Theberge et al. 2010; Abiev and Lavretsov 2012; Seemann et al. 2012). One of the most commonly observed regimes in micro-scale two-phase flows concerns transfer of confined bubbles/droplets separated intermittently by a liquid phase, which is often referred to as slug or Taylor flow (Triplett et al. 1999). The high rate of heat and mass transfer, even at low Reynolds numbers, and the minimum amount of working liquid used in the micro-scale, has established this flow regime as an optimal operating condition for micro-heat exchangers and chemical reactors (Baten and Krishna 2004; Ribatski et al. 2006; Wegmann and Rohr 2006; Kashid et al. 2011).

Micro-scale slug flows often exhibit complex spatiotemporal features and interfacial phenomena which render them as challenging problems to both numerical and experimental approaches. Despite the great scientific efforts made in the recent decades for characterising this problem, reports on systematic experimental measurements are still very limited in the literature. Therefore, direct comparison of such measurements with numerical simulations and analytical studies, and thus their validation, is often not possible due to several main reasons: (1) Experimental measurements are usually performed for trains of bubbles separated by liquid slugs. Dynamics of such flows are strongly dependent on the characteristics of the two-phase flow mixer and flow rates of the two fluid phases involved (Gu et al. 2011). These measurements naturally lack precise identification of the flow boundary conditions in the carrier liquid phase, which are essential for reproducing the problem numerically and creating reliable mechanistic models. Moreover, the available analytical models are only valid in the presence of well-defined fully developed boundary conditions far behind and in front of the bubbles, which is usually not investigated in such experimental measurements; (2) most of the previous experimental studies were dedicated to the measurements of individual flow parameters, such as liquid film thickness and/or bubble velocity (Taylor 1961; Chen 1986; Han and Shikazono 2009). In fact, parametric experimental studies providing simultaneous measurements of other important flow parameters, such as bubble volume, shape of the phase interface, velocity field in the liquid phase and development lengths, are largely missing in the literature, mainly due to the limitations of the available experimental techniques. Therefore, there exists no experimental data for validating results of the corresponding numerical simulations for some of these flow parameters; (3) experimental measurements are usually performed in rectangular micro-channels, whose cross sections might considerably vary from a perfect rectangle with sharp 90° corners depending on the micro-fabrication process used for their manufacturing (Qu et al. 2000; Gunnasegaran et al. 2010). Moreover, the relative surface roughness in micro-channels can potentially modify the flow characteristics, especially for flow regimes where the thickness of the liquid film decreases significantly and becomes of the same order of magnitude (Chen 1986). Such effects eventually cause notable discrepancies when comparing experimental measurements to the results of numerical simulations in perfectly smooth rectangular micro-channels; and (4) in order to cover a large range of flow parameters in micro-scale slug flows, high spatial and temporal resolutions are required. As an example, the liquid film thickness surrounding the bubbles at the channel walls can decrease down to hundreds of nanometres at very low velocities, while the frequency of the waves on the bubble interface can reach up to few kilohertz at high velocities. These features have largely limited the range of available numerical and experimental data in the literature at such extreme flow conditions. In this light, more comprehensive and well-designed experiments are essential, not only for understanding of this particular flow regime, but also to provide accurate and reliable databases for validating the available analytical models and numerical simulation results.

Reliable and accurate experimental measurements in micro-scale two-phase flows demand highly sensitive instruments to quantify the relatively small quantities of interest in the flow in a non-invasive manner. This has largely motivated the application of high resolution non-intrusive optical techniques for such measurements in the last decade (Aubin et al. 2010; Williams et al. 2010; Khodaparast et al. 2014). Although quantitative optical methods can potentially be employed to achieve a wealth of knowledge on the dynamics of the flow of interest, they have rarely been used in the past for parametric studies in two-phase flows. This is mostly due to the fact that quantification of multiple flow parameters has often been equated with adding complex and expensive instrumentation to the experimental facility in the past. Unlike the experimental studies, numerical simulations are more likely to provide simultaneous quantification of important flow parameters in two-phase flows. In the last decade, the advances made by Eulerian techniques for tracking the interface between two immiscible fluids on a fixed computational mesh made the numerical simulation of flows characterised by large interface deformations possible. This allowed the computational investigation of many micro-channel two-phase flow features, such as bubble formation at co-current (Chen et al. 2009) and T-junction (Qian and Lawal 2006) injection arrangements, heat transfer in non-evaporating segmented flows (Lakehal et al. 2008; He et al. 2010), bubble and fluid dynamics under flow boiling conditions (Mukherjee et al. 2011; Li et al. 2007). A comprehensive review of numerical methods and applications for multiphase flows in micro-fluidics was presented by Wörner (2012). However, results of such studies are mainly dependent on mathematical models, which are still to be validated against reliable and accurate experimental measurements with well-defined necessary initial and boundary conditions, especially in complex two-phase flows.

This work reports the results of systematic experimental measurements and numerical simulations aimed to characterise the dynamics of isolated confined air bubbles in laminar fully developed liquid flows within smooth circular channels of diameters d = 0.5 mm and d = 1 mm. Water and glycerol are used as the continuous liquid phase, and therefore, a large range of flow capillary numbers 10⁻⁴ < Ca < 10⁻¹ and Reynolds numbers 10⁻³ < Re < 10³ are presently covered. The non-intrusive micro-particle shadow velocimetry technique (μPSV) is employed to simultaneously resolve the phase interface and the flow dynamics. All experimental quantifications are derived from a single sequence of high-speed greyscale images captured using a rather simple and affordable optical set-up (Khodaparast et al. 2014). Alongside the experimental measurements, CFD simulations based on the volume of fluid (VOF) (Hirt and Nichols 1981) interface capturing method are performed by means of the commercial software ANSYS Fluent v. 14.5, here augmented by implementing self-defined functions to improve the accuracy of the surface tension force estimation, and the InterFOAM solver included in the open-source package ESI OpenFOAM v. 2.1.1. Precise experimental measurements of the flow rate in the continuous liquid phase and volume of the bubble are used as inputs to numerically simulate the flow. While ANSYS Fluent has been extensively utilised for the simulation of two-phase flows in narrow channels (Gupta et al. 2009; Mehdizadeh et al. 2011; Gregorc and Zun 2013; Qian and Lawal 2006; Talimi et al. 2012), the literature concerning the use of OpenFOAM is still limited (Hoang et al. 2013; Pattamatta et al. 2014; Ghaini et al. 2011). Hence, simulations were presently run by employing both the solvers with the aim of comparing their performances and providing further validation to OpenFOAM. The combination of the computational and experimental approaches used in the present study allows us to fully compare the final results obtained on liquid velocity, interface shape and dynamics, bubble velocity and volume, liquid film thickness and development length and highlight the advantages and shortcomings of the different applied methods.

The present paper is organised as follows: a brief introduction to the physics of confined bubble flows in micro-channels and a review of the state of the art is included in Sect. 2; descriptions of the current experimental and numerical methods are provided in Sects. 3 and 4, respectively; analysis and comparison of the corresponding results are presented for a large range of flow parameters for confined air bubbles in both low and high viscous liquid flows in Sect. 5; finally, the concluding remarks and research findings are summarised in the last section of the paper.

Supplementary data processed from the experimental measurements, which may be useful to benchmark computational codes aimed to simulate two-phase flows in narrow channels, are provided in tabular form in Appendix 1.

2 State of the art

Motion of elongated confined bubbles transferred by fully developed Poiseuille liquid flows, as shown schematically in Fig. 1, has for a long time been the topic of experimental, analytical and numerical studies (Fairbrother and Stubbs 1935; Bretherton 1961; Hyman and Skalak 1972). In the absence of significant buoyancy and inertial effects ($We \ll 1$ and $Re \ll 1$), dynamics of such flows is mainly ruled by the result of the competition between the viscous and surface tension forces. The ratio of these forces defines the most important dimensionless number in the so-called visco-capillary regime, namely the capillary number:

$$\begin{aligned} Ca = \frac{\mu _c U_d}{\sigma } \end{aligned}$$

(1)

where μ _c is the viscosity of the continuous liquid phase, U _d is the velocity of the dispersed phase, here the bubble, and σ is the surface tension.

Fig. 1

Schematic of an isolated confined bubble transferred by axisymmetric fully developed Poiseuille flow

At very low capillary numbers, surface tension is naturally expected to play the dominant role in defining the flow characteristics. Therefore, bubbles with both a spherical nose and rear are expected to fill almost the entire cross section of the channel. The liquid film surrounding the bubbles at such flow conditions is very thin, and the bubble velocity is very close to the mean velocity in the continuous liquid phase $U_d\,\simeq \,\overline{U_c}$. However, as the flow capillary number increases, the liquid film becomes thicker and the ratio of the bubble to mean liquid flow velocity ${U_d}^{*} = \frac{U_d}{\overline{U_c}}$ increases.

Studies by Taylor (1961) and Bretherton (1961) can be considered as two of the most classic investigations performed on the creeping motion of elongated confined bubbles in horizontal channels of small diameters. Based on the assumption that the thin liquid film surrounding the bubble is stagnant in the visco-capillary regime, Taylor related his experimental measurements of ${U_d}^{*}$, for nearly inviscid bubbles, to the prediction of the dimensionless liquid film thickness δ*, using the following relationship (Goldsmith and Mason 1963):

$$\begin{aligned} {\delta }^{*} = \frac{\delta }{d} = 0.5 \left( 1- \frac{1}{\sqrt{\frac{{U}_{d}}{\overline{U}_{c}}}}\right) \end{aligned}$$

(2)

where d is the tube diameter.

More recently, an empirical correlation was fitted to Taylor’s experimental measurements by Aussillous and Quéré (2000), which has since been referred to as Taylor’s law and has been used for benchmarking experimental and numerical results:

$$\begin{aligned} {\delta }^{*} = \frac{0.67\, {Ca}^{2/3}}{1 + 3.35\,{Ca}^{2/3}} \end{aligned}$$

(3)

Bretherton (1961) applied lubrication theory to the creeping flow in the liquid film surrounding a long inviscid bubble in small tubes, in the absence of gravitational and inertial forces. As a result, he found the following simplified relationship for the prediction of the liquid film thickness at low capillary numbers Ca < 5 × 10⁻³:

$$\begin{aligned} {\delta }^{*} = 0.67\,{Ca}^{2/3} \end{aligned}$$

(4)

More recently, the effect of inertia on the motion of confined elongated bubbles was investigated in a few numerical and experimental studies (Aussillous and Quéré 2000; Heil 2001; Ryck 2002; Kreutzer et al. 2005; Han and Shikazono 2009). In general, this effect was found to increase the thickness of the liquid film around the gas bubbles. Aussillous and Quéré (2000) observed that above a threshold capillary number Ca _tr , the thickness of the low viscous liquid film is significantly higher than the value predicted by Taylor’s law. Furthermore, inertial effects were observed to modify the shape of the bubbles: increasing the flow Reynolds number at a constant capillary number was found to elongate the bubble nose, while flattening the tail of the bubble. In the same context, Ryck (2002) derived a correction term for Bretherton’s problem to compensate for the thickening effect of inertia on the liquid film, which was observed in low viscous liquids, by introducing a new dimensionless parameter $F = \frac{Re}{Ca} = \frac{\rho _c \sigma R}{{\mu _c}^2}$. This correction term was found to be negligible for highly viscous liquids, such as glycerol with low values of F number, while it could explain the deviation from the Taylor’s law observed in the experimental results of Aussillous and Quéré (2000) at high Re and F numbers (Re ~ 1000, F > 10,000). Similarly, it was shown by Heil (2001) that inertia effects become more significant in Bretherton’s problem at higher Reynolds numbers and lower capillary numbers, which are typical in low viscous liquid flows.

Despite the large number of numerical and experimental studies dedicated to the hydrodynamics of elongated bubbles, most of these investigations were only focused on quantifying the bubble to mean flow velocity ratio and the film thickness, while other aspects of the flow such as the shape of the bubbles, the development length in front and at the back of the bubbles, and the onset of the transitions to non-axisymmetric and time-dependent flows were usually overlooked in the literature, especially in the experimental studies due to the limitations in the measurement techniques.

Moreover, effect of the bubble size on flow dynamics in small channels has been rarely investigated before and most of the results reported in the literature are dedicated to the dynamics of confined elongated bubbles whose volume-equivalent diameter is larger than 1.5 times the tube diameter ${d_{eq}} > 1.5 d$. The volume-equivalent diameter of the bubble d _eq is defined as the diameter of a sphere whose volume is equal to that of the non-spherical bubble V _d :

$$\begin{aligned} {d}_{eq} = \left( {6{V_d}/\pi }\right) ^{1/3} \end{aligned}$$

(5)

However, liquid flows containing small particles, liquid droplets or gas bubbles in small channels are relevant to numerous engineering applications. Furthermore, motion of deformable bubbles and drops has been often used to model the flow of blood cells in small capillaries (Hyman and Skalak 1972; Hsu and Secomb 1989; Pozrikidis 2005).

Hyman and Skalak (1972) numerically studied the flow of equally spaced spherical droplets along the tube centreline in creeping liquid flows ($Re \ll 1$) for the range of $0.1< {{d}_{eq}}^{*} < 0.8$, where ${{d}_{eq}}^{*}$ is the dimensionless volume-equivalent diameter of the bubble with respect to channel diameter. The measurements performed by Ho and Leal (1975) on the motion of small neutrally buoyant droplets in creeping liquid flows within circular channels still remains as one of the only experimental studies directly relevant to the present problem of interest. The effect of flow viscosity and droplet size on flow characteristics were investigated in this study; however, dispersed-to-continuous phase viscosity ratios $\lambda = \frac{\mu _d}{\mu _c}$ below 0.19, which is typical of gas-liquid flows, and bubble diameters ${{d}_{eq}}$ smaller than 0.7d, were not covered in their measurements. They observed that the dimensionless velocity of the droplets ${U_d}^*$ in the range $0.7 < {{d}_{eq}}^{*} < 1.1$ decreased as the droplet diameter increased. Increasing the flow rate of the continuous phase was also shown to increase the dimensionless velocity of the droplets. Acceptable agreement was achieved between their experimental measurements and the numerical results of Hyman and Skalak (1972), although the latter seemed to slightly over-predict the experimental results. This study was later continued by Olbricht and Leal (1982), who investigated the buoyancy effects on droplets of $0.5 < {{d}_{eq}}^{*} < 0.85$ in creeping liquid flows. The dimensionless velocity of the droplet in the presence of gravitational effects was observed to increase when decreasing the droplet size only until around ${{d}_{eq}}^{*} = 0.6-0.7$. A descending trend was then observed in the velocity of the bubble as ${{d}_{eq}}^{*}$ was further reduced. This resulted in the appearance of a maximum in the evolution of ${U_d}^*$ versus ${{d}_{eq}}^{*}$, which was found to be more noticeable at lower flow rates.

More recently, numerical studies performed by Martinez and Udell (1990), Lac and Sherwood (2009) and Feng (2010) have focused on the dynamics of deformable neutrally buoyant droplets along the axis of a circular channel. The effect of the droplet size was investigated by Martinez and Udell (1990) for relatively high viscosity ratios λ > 0.1 and capillary numbers Ca > 0.05. In general, the following conclusions were obtained: the dimensionless velocity of the droplet decreased as its size increased until reaching an asymptotic value; the droplet shape and velocity were observed to be independent of the droplet size for ${{d}_{eq}}^{*} > 1.1$, and droplets of ${{d}_{eq}}^{*} < 0.5$ were found to not be sensitive to the viscosity ratio. Finally, good agreement was obtained versus the measurements of Ho and Leal (1975), although the numerical simulations slightly over-predicted the experimental results. As can be observed, there are not sufficient reports in the literature for experimental investigations probing the impact of bubble size on the flow dynamics. Moreover, dynamics of small, low viscous bubbles was not the topic of studies even in the numerical investigations.

In view of the lack of such information for characterising the flows of interest here, a systematic investigation of different flow parameters characterising the dynamics of nearly inviscid small and elongated air bubbles in low and high viscous liquids is performed in the present study. For each flow parameter, the effects of bubble size and capillary number (for elongated bubbles) are determined and analysed.

3 Experimental technique

3.1 Experimental facility

Fig. 2

Schematic of the experimental facility used in the current study

A relatively simple experimental facility is used for the current measurements, see Fig. 2. Tests were performed in 10-cm-long circular transparent tubes submerged in a liquid bath. Experiments were designed carefully so that the refractive indices of the tube wall material, the liquid in the medium surrounding the tube and the working liquid were approximately identical. Therefore, no optical distortion was present in the final images since the tube was observed through the flat surface of the fully transparent liquid bath. Physical properties of the working fluids at the region of interest (ROI) were determined at the average of the temperatures measured at the inlet and outlet of this test section. Detailed properties of the working fluids and specifications of the tubes used in the present experiments are reported in Table 1. Tube diameters were measured using a pre-calibrated 40× microscope objective.

Table 1 Specifications of the tubes and the working fluids used in the experiments. n and μ represent refractive index and fluid viscosity, respectively

A pressure pump was used for generating non-oscillating flow of liquid into the tube, while single air bubbles were injected through a T-junction located 15 cm upstream of the tube inlet to ensure fully developed flow at the region of interest. This assumption was further investigated in the post-processing step by examining the spatial and temporal stability in the velocity of both the continuous and the dispersed phases. A micro-flow meter and a digital balance, collecting the liquid from the channel outlet, were employed for estimating the bulk flow rate of the continuous phase (Fig. 2). However, more accurate and reliable local flow rate measurements were performed by integrating the experimental velocimetry results over the tube cross section; see Khodaparast et al. (2014) for more details.

3.2 Optical set-up

The micro-particle shadow velocimetry μPSV technique (Khodaparast et al. 2013) was applied here for simultaneous interface detection and velocimetry. To this end, the liquid phase was seeded with colourless spherical polystyrene particles of 1.5 μm diameter. The fully transparent test section described before was set above a low-power LED light source of wavelength 530 nm and maximum power 475 mW. In order to enhance the light efficiency of the optical set-up, the LED light source was collimated and then passed through the microscope condenser which focused the light with the appropriate conical angle onto the ROI (Khodaparast et al. 2013). The plane of interest, here centre-plane of the tube, was isolated in the illuminated volume of the fluid by a Nikon 20×, NA = 0.45 objective, facing the test section from the top. As will be discussed later, for air–water flows at very low capillary numbers, higher optical magnifications were achieved using the Nikon 40×, NA = 0.6 objective in order to obtain an acceptable resolution within the very thin liquid film forming around the air bubbles. The magnified images of the flow of interest on the centre-plane of the tube were finally recorded by a Photron FASTCAM SA3 high-speed camera which possesses a 1024 × 1024 sensitive array of 17 × 17 μm² pixels. Frame rates up to 10 kHz and exposure times down to 5 μs were set for the experimental tests according to the flow velocity, such that the illumination power was always kept at the minimum necessary value.

3.3 Post-processing and velocimetry methods

Simultaneous quantification of important flow parameters, namely the flow rates of the continuous and the dispersed phases, shape and volume of the bubble, thickness and dynamics of the liquid film surrounding the bubble, and the development lengths in front and at the back of the bubble, was achieved applying the following post-processing methods:

• Phase interface The significant difference between the refractive indices of the continuous and the dispersed phase, here liquid and gas, respectively, results in a high contrast gradient level at the phase interface in the shadowgraphy images. Thanks to this feature, a Canny edge detector (Canny 1986) was applied to the raw μPSV images recorded presently in order to detect the phase interface. In this context, the local gradients were calculated, the non-maximum gradient values were filtered out, and the final results were thresholded.

• Bubble volume This parameter was determined by calculating the volume created by rotating the detected bubble interface around the centreline of the tube, considering the axisymmetric flow assumption. Considering one pixel error in defining the bubble interface, the relative error in measurements of bubble volume ranged from 3 to 1 % for small spherical and elongated bubbles, respectively.

• Velocities The velocity of the bubble is measured using the time strip method by plotting the evolution of the greyscale image intensity in time, on the tube centreline, and relating the slope of this strip to the bubble velocity. This resulted in less than 0.5 % error in the corresponding results. The velocity field in the continuous liquid phase seeded with tracer particles is measured by applying the well-known cross-correlation technique using the free PIV software package JPIV (JPIV 2013). Less than 2 % of relative error was obtained when comparing the result of the cross-correlated μPSV images with known velocity fields (Khodaparast et al. 2013).

• Development length In order to quantify this parameter, the local velocity in the liquid phase is measured continuously using the cross-correlation technique at a fixed point located on the tube centreline. If this point is located adequately far from the bubbles nose, it can be observed that the fully developed local velocity at the tube centreline is modified as the bubble gets sufficiently close to the measurement point. Once the bubble leaves this point and its tail gradually gets far enough from the measurement location, the magnitude of this local velocity changes back to the fully developed value at the corresponding flow rate. Presently, the distance between the bubble tip (or the rear end) and the location where the relative difference between two successive liquid velocity vectors becomes less than 5 %, is considered as the development length in front X _n (or at the back X _t ) of the bubble. The uncertainty in defining this parameter from the experimental measurements can be up to 30 %, especially at higher liquid-phase velocities.

• Flow rate For the axisymmetric steady-state laminar liquid phase, the volumetric flow rate was calculated by integrating the fully developed experimentally measured centre-plane velocity profile across the circular cross section of the tube (Khodaparast et al. 2013). This resulted in reliable instantaneous flow rate measurements with better than 5 % of accuracy.

• Film thickness Film thickness measurements were performed based on the information obtained on the exact location of the tube wall and the phase interface in the previous steps. The optical magnification in the experimental tests was chosen carefully so that the relative errors in measurement of this parameter never exceeded 10 %.

For more detailed presentation of the current flow loop, optical set-up and the post-processing methods, and their application to a similar two-phase flow regime, please refer to Khodaparast et al. (2014).

4 Numerical method

4.1 Governing equations

The VOF algorithm belongs to the class of the single-fluid multiphase methods, as the phases are treated as a single fluid whose properties change abruptly across the interface. A unique velocity and pressure field are shared among the phases, such that a single set of flow equations is written and solved throughout the flow domain. A colour function is defined to identify each phase on a discretised domain: the volume fraction α. It represents the ratio of the cell volume occupied by the primary phase, and therefore, it is 1 if the cell is filled with the primary phase, 0 if filled with the secondary phase and 0 < α < 1 for an interfacial cell with both phases inside. Every fluid property is mapped on the computational mesh as the average of the primary and secondary phases’ specific properties, weighted by the local volume fraction value, e.g. density ρ and viscosity μ:

$$\begin{aligned} \rho&= \rho _2+(\rho _1-\rho _2)\alpha \end{aligned}$$

(6)

$$\begin{aligned} \mu&= \mu _2+(\mu _1-\mu _2)\alpha \end{aligned}$$

(7)

where α denotes the volume fraction value in the cell, and the subscripts 1 and 2 refer to the primary and secondary phases.

Different methodologies for updating the volume fraction field are adopted within ANSYS Fluent and the InterFOAM solver of OpenFOAM, a brief description is provided in Sect. 4.2. The single-fluid continuity and momentum equations for an incompressible flow and Newtonian fluid take the following form:

$$\begin{aligned} \nabla \cdot \varvec{u}&= 0 \end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial (\rho \varvec{u})}{\partial t}+\nabla \cdot (\rho \varvec{u} \cdot \varvec{u})&= -\nabla p + \nabla \cdot \biggl [ \mu \biggl ( \nabla \varvec{u}+\nabla \varvec{u}^T \biggr ) \biggr ] + \rho \varvec{g}+ \varvec{F}_{\sigma } \end{aligned}$$

(9)

where u is the fluid velocity vector, p is the pressure, g indicates the gravity acceleration vector, and $\varvec{F}_{\sigma }$ is the surface tension force. The latter is formulated as a body force by means of the continuum surface force (CSF) method proposed by Brackbill et al. (1992):

$$\begin{aligned} \varvec{F}_{\sigma }=\frac{\rho }{\hat{\rho }}\sigma \kappa \nabla \alpha \end{aligned}$$

(10)

where the surface tension coefficient σ is considered constant here, and κ is the local interface curvature. The density correction term $\rho /\hat{\rho }$, with $\hat{\rho }=(\rho _1+\rho _2)/2$, biases the force toward the fluid with higher density to prevent unphysical accelerations in the region occupied by the lighter fluid. The interface curvature is not available explicitly in interface capturing frameworks such as the VOF algorithm, but it has to be reconstructed according to the local values of the volume fraction in proximity of the interface. The different methodologies presently adopted are described in Sect. 4.3.

4.2 The volume fraction equation

Within the VOF method, the volume fraction field is transported as a passive scalar by the flow field, and hence, the interface location is in principle evolved by solving the following conservation equation:

$$\begin{aligned} \frac{\partial \alpha }{\partial t}+\nabla \cdot ( \alpha \varvec{u})=0 \end{aligned}$$

(11)

When integrated in a finite-volume discretisation framework, the convective term of Eq. 11 involves the interpolation of the volume fraction on the computational cell faces. A suitable interpolation scheme needs to preserve the fundamental properties of the volume fraction, i.e. boundedness (between 0 and 1) and sharpness. However, low-order upwind schemes preserve boundedness but tend to smear the interface as the simulation evolves with time, while high-order schemes are less diffusive but generate unbounded oscillations of the volume fraction field.

A classical remedy to this issue has been to interpret the convective term of Eq. 11 as a balance of the primary phase volume fluxes across the faces of the computational cell and hence to geometrically compute these fluxes after an approximation of the local interface profile has been reconstructed. To this purpose, ANSYS Fluent implements the Youngs (1982) Piecewise Linear Interface Calculation (PLIC) algorithm which is the solver option presently used.

A different approach was studied by Weller (2008) and consists of manipulating the volume fraction equation by adding an artificial compressive term to counteract the effect of numerical diffusion. This methodology is implemented within the presently used InterFOAM solver for OpenFOAM under the name of Multidimensional Universal Limiter with Explicit Solution (MULES) algorithm. The VOF equation is modified as follows:

$$\begin{aligned} \frac{\partial \alpha }{\partial t}+\nabla \cdot (\alpha \varvec{u})+\nabla \cdot (\alpha (1-\alpha )\varvec{U}_{r})=0 \end{aligned}$$

(12)

where the second term is the standard convective term while the third one operates the interface compression. The compressive term is built in such a way that, due to the presence of the multiplying factor $\alpha (1-\alpha )$, it is nonzero only for cells cut by the interface. The artificial compression velocity $\varvec{U}_{r}$ is given by:

$$\begin{aligned} \varvec{U}_{r}= {\rm min} \biggl [ C_{\gamma } \frac{|\phi |}{|\varvec{S}|}, \biggl ( \frac{|\phi |}{|\varvec{S}|} \biggr )_{{\rm max}} \biggr ] \cdot \varvec{n} \end{aligned}$$

(13)

where S is the cell boundary face normal vector and $\phi =\varvec{u} \cdot \varvec{S}$ is the volume flux across the cell face. $C_{\gamma }$ is the coefficient that tunes the interface compression. A value of 0 defines no compression, while higher values ensure a sharp interface. However, high values for $C_{\gamma }$ are discouraged because, as the volume fraction field becomes steeper, the computation of the interface topology becomes less accurate. The results of validation benchmarks conducted by Deshpande et al. (2012) and Hoang et al. (2013) suggested the value of 1 to be the best trade-off solution and is thus adopted to perform the simulations presented in this paper.

4.3 Curvature calculation algorithm

By default, ANSYS Fluent (version 14 and earlier) and OpenFOAM evaluate the interface unit normal vector and curvature by differentiating volume fractions, according to the following formulation originally proposed by Brackbill et al. (1992):

$$\begin{aligned} \varvec{n}=\frac{\nabla \alpha }{|\nabla \alpha |} \,\,\,\,\, \hbox{and} \,\,\,\,\, \kappa =-\nabla \cdot \varvec{n} = -\nabla \cdot \frac{\nabla \alpha }{|\nabla \alpha |} \end{aligned}$$

(14)

However, such an approach is known to have poor accuracy because the volume fraction changes abruptly across the interface, and standard finite-difference schemes do not converge when applied to highly discontinuous functions. The consequence is the generation and growth of unphysical velocities, known as spurious velocities or parasitic currents (Lafaurie et al. 1994), especially in low capillary number flows, such as those which are of concern in this work.

To overcome this issue, a Height Function (HF) algorithm (Cummins et al. 2005) and a Laplacian Filter technique (Lafaurie et al. 1994) were introduced here within ANSYS Fluent by means of self-defined external functions. The HF algorithm is based on the local integration of the volume fraction field to obtain a discrete field of local heights of the interface above a reference axis. First- and second-order derivatives of the heights are discretised by means of central finite-difference schemes, which ensure a computed curvature that exhibits a second-order convergence rate with respect to the mesh refinement. Details of the present implementation and the results of several validation benchmarks are illustrated in Magnini et al. (2013) and Magnini (2012). However, the use of the HF algorithm is restricted to uniform computational grids. Therefore, its application is presently limited to flows characterised by liquid film thicknesses down to about 0.025d in order to adequately solve the flow within the liquid film surrounding the confined bubble without making the computational run prohibitively costly.

For thinner films, non-uniform grids with local refinement at the channel wall were utilised, in order to capture the film dynamics with a reasonable computational cost. With this mesh configuration, the interface topology is reconstructed by differentiating a smoothed version of the volume fraction field, which can be promptly obtained by using the following Laplacian filter:

$$\begin{aligned} \widetilde{\alpha }=\frac{\sum _{i=1}^{N_f} \alpha _f S_f}{\sum _{i=1}^{N_f} S_f} \end{aligned}$$

(15)

where N _f is the number of boundary faces of the computational cell, S _f is the area of the cell face and α _f is the value of the volume fraction interpolated at the face centre. The application of this filter can be repeated as many times as desired to get a smoother field, although Lafaurie et al. (1994) and Hoang et al. (2013) did not detect any significant improvement in curvature calculation for using more than two cycles. Then, the interface normal vector and the curvature are calculated by applying Eq. 14 to the smoothed volume fraction field. A preliminary benchmark test, consisting of a transient simulation of a two-dimensional inviscid static droplet in the absence of external forces, showed that the present implementation of the Laplacian filter technique reduced the maximum magnitude of the spurious velocities by a factor of 2 with respect to ANSYS Fluent’s default method based on unsmoothed volume fractions.

4.4 Numerical set-up

Both ANSYS Fluent and OpenFOAM discretise the governing equations based on a finite-volume discretisation in a co-located grid arrangement. Table 2 presents a list of the chosen solvers options adopted for the discretisation of the various terms appearing in the flow equations. The Pressure Implicit Splitting of Operators (PISO) algorithm, based on the work of Issa (1985), was chosen for ANSYS Fluent since it converged faster than the other options available, while it is the only option available for time-dependent two-phase flow simulations in OpenFOAM. The default number of corrector steps for the PISO algorithm was maintained for both solvers. Within ANSYS Fluent, the PRESTO (PRessure STaggering Option) option, which solves the pressure correction equation for a staggered control volume, was adopted as it exhibited a lower magnitude of the spurious velocity fields compared with the other choices available. A variable time step was chosen for the time-marching of the solution, and its value is calculated by the solver according to a maximum Courant number of Co = 0.25. OpenFOAM includes several solution algorithms which can be selected independently for each equation. A much faster convergence of the pressure equation was observed when the Geometric–Algebraic Multigrid (GAMG) preconditioner was employed for the solution, and by selecting to perform two grid coarsening/refining levels at a time. The convergence criterion is based on the values of the absolute normalised residuals of the flow equations solution, and the threshold values are indicated in Table 2.

The flow domain of the numerical simulations is a horizontal circular channel which is modelled as a 2D axisymmetric domain, and thus, gravity effects are not included in the momentum equation. Structured orthogonal uniform and non-uniform computational meshes are employed to discretise the flow domain as presented in Sect. 4.5. As initial condition, a gas bubble is patched at the upstream of the channel. A fully developed parabolic velocity profile with a liquid-only flow and a zero-gradient condition for the pressure are imposed at the channel inlet. At the channel wall, a no-slip boundary condition is specified. At the channel outlet, a zero-gradient velocity condition along with a constant value for the pressure is set. Bubble initial volume and liquid inlet flow rate for each simulation run are obtained from the experimental measurements.

Table 2 Details of the discretisation schemes adopted to set up the numerical solvers

4.5 Computational mesh

Structured orthogonal uniform computational grids comprised of square cells are used to discretise the flow domain when modelling working conditions characterised by δ/d > 0.025, with δ being the thickness of the liquid film trapped between the bubble and the channel wall as measured in the experiments. The sizes of the mesh elements range from d/60 to d/200 so that at least five grid cells exist in the liquid film in the radial direction for all the flow conditions, as suggested by Gupta et al. (2009).

Table 3 Parameters characterising the non-uniform computational meshes studied to model flows with a thin liquid film surrounding the bubble

A computational grid with a uniform coarse mesh in the core of the domain and a radially refined mesh in the near-wall region is used when $\delta /d<0.025$. Gupta et al. (2009) and Hoang et al. (2013) modelled confined bubble flows in micro-channels by adopting computational grids which included a near-wall refined region overlapping with the lubricating film. However, in the present study, such a configuration would lead to computationally expensive grids due to the very thin liquid films occurring under the working conditions investigated in this work, with δ down to less than d/100. Therefore, mesh grids with the graded mesh region extended beyond the zone occupied by the lubricating film were also taken into consideration.

A grid convergence analysis was performed to select the optimal computational mesh. This involved the simulation of the confined flow of an air bubble within a d = 514 μm channel, with a water inflow characterised by an average velocity of 0.242 m/s. These working conditions were tested experimentally and yielded a terminal velocity of the bubble of 0.261 m/s, corresponding to Ca = 0.0029 and Re = 150, and a liquid film thickness of $\delta /d=0.0138.$ Many different grids were tested against this benchmark case. Table 3 reports the main parameters identifying four representative mesh configurations, where $h_{ref}$ defines the thickness of the refined grid region near the wall, N _{cells, R} identifies the number of cells discretising the flow domain in the radial direction (core − near-wall regions) and $AR_{max}$ represents the maximum aspect ratio of the cells. As the mesh elements are gradually refined, while approaching the channel wall, the maximum aspect ratio is achieved for the computational cell next to the channel wall. $E_{vol}$ defines the error in the initial volume of the bubble, computed as $(V_{CFD}-V_{exp})/V_{exp}$, while N _{cells, lf} indicates the minimum number of cells discretising the liquid film in the radial direction when the flow is steady state. Mesh grids 1–3 present the same thickness of the refined grid region near the wall, which extends beyond the flow domain occupied by the lubricating film and the bubble interface, and a similar cell maximum aspect ratio, but different levels of mesh refinement. Grid 4 is made of square mesh cells of size d/200, while the layer of cells next to the wall, where the liquid film is expected to be located, is divided into six gradually refined smaller cells similar to the grid arrangement adopted by Hoang et al. (2013). All the mesh grids tested here gave approximately the same terminal bubble shape, velocity and thickness of the liquid film. No relevant differences were observed between the results obtained by OpenFOAM and ANSYS Fluent. In particular, the deviations between experimental and numerical bubble velocity and liquid film thickness were within the error bands of the present experimental measurements. However, grid 1 was discarded because it was not sufficient to solve the flow in the liquid film for the lowest capillary numbers tested in this work, and because of the relatively large error in the numerical initialisation of the bubble volume. As grids 3 and 4 did not improve significantly the results obtained with the coarser grid 2, the latter was the computational mesh presently selected to model flows characterised by thin liquid films ($\delta /d<0.025$).

5 Results and discussion

Quantitative findings of the present experimental measurements and numerical simulations for confined isolated air bubbles in liquid flows are presented in this section for both air–water and air–glycerol flows. The high viscosity of glycerol allows achieving relatively high capillary numbers at very low Reynolds numbers ($Re \ll 1$), while for air–water flows even at low capillary numbers (Ca ~ 10⁻²), impact of significant inertia could be observed and investigated in the flow. The bubble shape, buoyancy effects, bubble velocity, liquid film thickness and flow development length in front of the nose and behind the tail of the bubble are quantified and analysed separately for each case. For each parameter, results of two different analyses are presented: (1) For small bubbles (${d_{eq}} < d$), effect of the volume-equivalent diameter of the bubble d _eq on the quantity of interest is investigated at constant capillary numbers. (2) For elongated bubbles (${d_{eq}} > 1.5 d$), where d _eq has no significant effect on the flow dynamics, the effect of capillary number on the flow characteristics is quantified and discussed.

For air–water flows, results are presented at relatively low capillary numbers Ca < 0.025 mainly due to the fact that the axisymmetric and steady-state assumptions were no longer valid at higher capillary numbers. However, steady-state axisymmetric air–glycerol flows were investigated up to Ca ≃ 0.2.

The flow direction in all the results presented in this section is from left to right. The flow capillary number Ca is based on the velocity of the elongated confined bubbles. For small bubbles, Ca is based on the velocity of an elongated bubble transferred by the continuous liquid phase flowing at an identical flow rate.

The flow parameters characterising the flow conditions and results for 22 selected experimental runs are reported in tabular form in Appendix 1.

5.1 Bubble shape

5.1.1 Effect of bubble size

The restricting walls of the channels are known to modify the interface of a deformable bubble and modify the drag coefficient, when compared to the motion of deformable bubbles in unconfined uniform liquid flows (Clift et al. 1978). In the absence of inertial effects, the deformation of gas bubbles in liquid flows is a function of the flow capillary number Ca and the volume-equivalent diameter of the bubble d _eq (Martinez and Udell 1990). However, at very low capillary numbers, bubble dynamics is mainly dominated by surface tension, and thus, only small deviations from spherical shape are expected even for relatively large bubbles, ${d_{eq}}^{*} \simeq 1$; that is, the bubble size is expected to have no significant effect on the shape of the phase interface in this flow regime. On the contrary, at higher capillary numbers, even very small bubbles experience notable deformations due to the effect of viscous forces.

Fig. 3

Experimental influence of bubble size on the dimensionless diameter of the fitted circular curve to the nose and the back of the bubbles: a for air–glycerol flow in the d = 494 μm tube, and b for air–water flow in the d = 514 μm tube

The effect of bubble volume on its shape was studied quantitatively for the present experimental results by measuring the diameter of the fitted circular curve to the front and the back of the image of the bubble on the centre-plane of the tube. For gas bubbles in motion in fully developed Poiseuille flows, the curvature at the nose of the bubble is expected to be higher than that at the back of bubble (Martinez and Udell 1990). This effect is confirmed by Fig. 3a, which plots the dimensionless bubble nose and rear diameters, ${d_{\rm nose}}^{*} = \frac{d_{\rm nose}}{d}$ and ${d_{\rm tail}}^{*} = \frac{d_{\rm tail}}{d}$, as a function of the bubble volume-equivalent diameter for air–glycerol flows. As can be seen, bubbles are no longer spherical for ${d_{eq}}^{*} > 0.5$, and this effect is amplified at larger capillary numbers. A similar trend is observed for air–water flows at $Ca\sim 10^{-3}$, where small but noticeable deformations are already observed at about ${d_{eq}}^{*} > 0.7$, see Fig. 3b. However, as the flow capillary number is further reduced (on the order of $Ca\sim 10^{-4}$), viscous effects on the bubble profile become negligible and thus bubbles tend to maintain their spherical shape even up until their equivalent diameters approach the channel diameter.

For ${d_{eq}}^{*} > 1.5$, no significant change in the curvatures of the nose and the tail of the bubbles was observed for the range of parameters studied here. In general, larger capillary numbers make the bubble nose more slender and the bubble tail flatter, and this will be investigated in more details in the following section. It is worth mentioning that at ${d_{eq}}^{*} \simeq 1$ an interesting pattern can be seen in all the presented results, especially at lower capillary numbers: the diameter of bubble nose and tail reaches a maximum before dropping to a constant asymptotic value in the confined elongated bubble regime. This corresponds to a minimum value of the bubble velocity as will be shown later in Sect. 5.3. Such an effect, reported here experimentally for the first time, was also observed in the results of the numerical simulations performed by Martinez and Udell (1990) and Lac and Sherwood (2009).

Fig. 4

Time-dependent flow patterns observed experimentally for small air bubbles in water flows in the d = 514 μm tube at a Ca = 0.011 and Re = 527, and b Ca = 0.023 and Re = 1065. Images from top to bottom for both cases are 2 × 10⁻⁴ s apart in time. The flow Reynolds number is based on the bubble velocity and tube diameter

For air–water flows with higher bubble velocities, Ca > 0.01 and Re = 500, inertial effects were observed to be no longer negligible. Such effects resulted in distinct non-axisymmetric and time-dependent flow patterns, which are shown in Fig. 4. Although precise quantification of the curvatures at the nose and tail of the bubbles was not possible at these flow conditions due the transient effects, bubbles’ interfaces were found to form a bell-shape profile with their nose more elongated in the direction of the flow, when compared to creeping flows of small bubbles at similar capillary numbers.

Fig. 5

Comparison of the experimental (blue, top) and numerical (red, bottom) results for a air–glycerol flow in the d = 494 μm tube at Ca = 0.05: ${{d}_{eq}}^{*}$ = 0.354, 0.513, 0.677, 0.747, 0.813, 1.047 and 1.189, and b air–water flows in the d = 514 μm tube at Ca = 0.0007: ${{d}_{eq}}^{*} = 0.789$, 0.852, 0.946, 1.016 and 1.386. The bubble profile given by the numerical simulations is depicted as the α = 0.5 iso-contour (colour figure online)

Furthermore, the detected interfaces by the present experimental and numerical approaches are directly compared in Fig. 5. The excellent agreement achieved for these measurements not only demonstrates the reliability of the numerical framework adopted here, but also proves that the experimental method is reasonably non-invasive and adequately accurate. The interfaces achieved by the numerical simulations performed by OpenFOAM are not included in Fig. 5 since the results were very close to those obtained via ANSYS Fluent. As can be seen, noticeable deformations on the phase interface were observed in air–glycerol flows at Ca = 0.05 as the bubble volume increases, while the curvature at the nose and the tail of the air bubbles in water flows remains almost unchanged as the bubble grows in size. Numerical results for small air bubbles of ${d_{eq}}^{*} < 0.8$ in water flows are not presented here due to the severe effects of numerical errors. As a matter of fact, such small capillary numbers (on the order of 10⁻⁴) represent a limit for interface capturing numerical methods due to the appearance of strong unphysical flows at the gas–liquid interface (so-called spurious velocities as introduced in Sect. 4.3), especially when decreasing the bubble size for a given computational mesh.

5.1.2 Effect of capillary number

Fig. 6

Effect of capillary number on the dimensionless diameter of the fitted circular curve to the nose and the tail of the bubbles: a for air–glycerol flows in the d = 494 μm tube, b for air–water flows in the d = 514 μm tube

For elongated bubbles at very low capillary numbers, due to the dominating effect of surface tension, the nose and the tail of the bubbles resemble closely hemispheres with diameters close to that of the tube. Therefore, the dimensionless diameter of the fitted spheres to the nose and the tail of the bubble, ${d_{\rm nose}}^{*}$ and ${d_{\rm tail}}^{*}$, are very close to unity. As observed in the previous section, the curvature at the nose of the bubble is expected to be higher than that at the back due to the streamwise pressure gradient, and thus as the flow velocity and this pressure gradient increase, this difference is expected to be enhanced, consequently making the bubble nose more elongated and the bubble tail flatter (Martinez and Udell 1990). The diameter of the fitted circular curve to the nose and tail of confined elongated bubbles was measured in the present study for air–water and air–glycerol flows for ${d_{eq}}^{*} > 1.5$, and the results are compared to those achieved numerically by Martinez and Udell (1989) and Giavedoni and Saita (1999) for creeping flows. As can be seen in Fig. 6a, measurements in air–glycerol flows agree favourably with those obtained in the axisymmetric numerical studies by Martinez and Udell (1989) and Giavedoni and Saita (1999) for creeping flow conditions. However, the non-negligible effects of inertia in air–water flows were noted to significantly modify the shape of the bubbles and consequently leading to discrepancies in the reported results. This is to say that the curvature at the nose of the bubble is higher and the tail of the bubble is flatter compared to the creeping flow at the same capillary number when inertia effects are not negligible, see Fig. 6b.

Fig. 7

Effect of inertia on the bubble shape and the interface dynamics: a air–glycerol flow in the d = 494 μm tube at Ca = 0.024, Re = 0.0027, and b air–water flow in the d = 514 μm tube at Ca = 0.023, Re = 1065

Fig. 8

Transient effects at the rear end of the air bubble moving in the d = 514 μm diameter capillary filled with water at Ca = 0.023 and Re = 1065. Images from left to right are 10⁻⁴ s apart in time. Re number is based on the bubble velocity

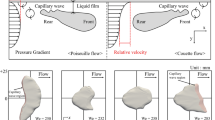
It should be noted that precise determination of the curvature at the nose and the tail of the air bubbles in water flows at Ca > 0.015 was not possible due to the onset of non-axisymmetric and transient effects in the flow. Non-axisymmetric patterns are identified as oblique capillary waves appearing at the bubble interface in proximity of its tail and a bubble nose which is shifted with respect to the tube centreline, as can be observed in Fig. 7; instead, time-dependent effects appear as the flapping of the bubble tail as it is evident in Fig. 8 for air–water flows.

Fig. 9

Comparison of the experimental (blue) and numerical (red: ANSYS Fluent, green: OpenFOAM) interfaces for air–glycerol flows in the d = 494 μm tube: a Ca = 0.008, b Ca = 0.052, c Ca = 0.075, d Ca = 0.098, and e Ca = 0.163 (colour figure online)

Fig. 10

Comparison of the experimental (blue) and numerical (red: ANSYS Fluent, green: OpenFOAM) interfaces for air–water flows in the d = 514 μm tube: a Ca = 0.003, b Ca = 0.008, c Ca = 0.0098, d Ca = 0.015 and e Ca = 0.023 (colour figure online)

Comparison of the interfaces captured by the current experimental and numerical approaches for elongated air bubbles in glycerol and water flows at different capillary numbers is presented in Figs. 9 and 10, respectively. Excellent agreement was achieved for air–glycerol flows which remained axisymmetric and steady state for the entire range of capillary numbers studied here, especially between the experimental and numerical results obtained by ANSYS Fluent, see Fig. 9. For air–water flows, experimental measurements and axisymmetric numerical simulation results agree approvingly at low capillary numbers, while slight discrepancies were observed for flows at Ca > 0.01 (Figs. 10d, e), due to the following reasons: (1) Time-dependent features appear at the interface, especially at the back of the bubbles in this regime, and therefore, it is no longer straightforward to obtain experimental and numerical interfaces which correspond to the exact same position of the bubble back, see Figs. 10d, e; (2) relatively large errors occur in calculating the bubble volume from experimental visualisation by assuming an axisymmetric interface profile in this flow regime, since the rear end of the bubble and the interface exhibit oscillations and non-axisymmetric profiles; (3) the non-axisymmetric flow features which were observed in the experimental visualisation results are not modelled in the numerical simulations. Besides these sources of errors, it can be observed that in general, the numerical simulations performed by OpenFOAM resulted in narrower bubbles compared to the results of ANSYS Fluent simulations and the experimental measurements. This can be ascribed to larger errors in the surface tension force calculation, as no improved methodology for the calculation of the interface curvature was presently implemented in OpenFOAM.

5.2 Buoyancy effect

Fig. 11

Bubble shapes under negligible gravity effects for air–glycerol flows in the d = 494 μm tube at Ca = 0.05 for different dimensionless volume-equivalent diameters, ${d_{eq}}^{*}$: a 0.06, b 0.21, c 0.35, d 0.46, e 0.51, f 0.67, g 0.76, h 0.81, i 0.96, j 1.04, k 1.18

Fig. 12

Bubble shapes under gravity effects for air–water flows in the d = 514 μm at Ca = 0.007 for different dimensionless volume-equivalent diameters, ${d_{eq}}^{*}$: a 0.07, b 0.21, c 0.33, d 0.46, e 0.58, f 0.65, g 0.74, h 0.82, i 0.91, j 1.03, k 1.13

The focal plane of the microscope objective in the present experimental measurements was always fixed on the centre-plane of the tube. Therefore, as long as the axes of symmetry of the bubbles of interest were aligned with the tube centreline, their widest horizontal sections appeared in-focus in the captured shadowgraphy images. This created a sharp phase interface in the final images for such bubbles, see Fig. 11. However, in the presence of non-negligible buoyancy effects, the bubbles are elevated with respect to the focal plane of the microscope objective, here the tube centre-plane, and therefore the widest horizontal sections of such bubbles appeared as out-of-focus shadow patterns in the images, see Fig. 12. This effect was used in the present study to distinguish the flow regimes in which buoyancy effects was relatively significant. It should be noted that such effects were not investigated in the present axisymmetric numerical simulations.

Fig. 13

Particle shadow images of large spherical polystyrene particles of diameters: a 90 μm, b 45 μm. The images were taken at identical illumination power with the 20× objective from particles resting on a microscope slide submerged in water. z represents the distance between the focal plane of the objective and the particle centres in micrometres

Bubble images presented in Figs. 11 and 12 were captured by the 20× objective with numerical aperture NA = 0.45, whose focal depth was estimated to be around 5 μm by the correlation proposed by Inoue and Spring (1997). This estimation was currently further verified by imaging large spherical particles of diameters 90 and 45 μm using the same objective. As can be seen in Fig. 13, clear out-of-focus patterns were observed for particles centred farther than 6 μm from the focal plane of the objective. Moreover, the visibility depth of the 20× objective was investigated for such large particles that fairly resemble the small bubbles studied in this section. It was found that large particles elevated even up to 0.2d with respect to the focal plane of the objective could be clearly captured in the images. Obviously, the largest horizontal sections of such particles were no longer in-focus, but still the diameter of its out-of-focus shadow corresponding to this section was observed to be sufficiently close to that of the actual particle diameter. This optical feature allowed us not only to distinguish the regimes with significant buoyancy effect, but also to estimate the volume of the elevated bubbles in such flows.

In air–glycerol flows, due to the relatively large viscous forces, the role of the gravitational force was observed to be fairly negligible for the range of flow parameters studied here. Sample shadowgraphy images of air bubbles in glycerol flows at Ca = 0.05 are presented in Fig. 11, where a very sharp and clear interface between the phases can be detected. It should be noted that such bubbles could still be slightly elevated with respect to the centre-plane of the tube, within the finite focal depth of the microscope objective. Gravitational effects were, however, found to be more significant in air–water flows, where clear out-of focus effects were noticed for relatively small bubbles, especially at lower velocities, as can be observed in Fig. 12. For the same bubble size, the ratio of buoyancy-to-viscous forces is around 500 times larger in air–water flows due to the smaller viscosity of the carrier liquid. Buoyancy effects were found to significantly influence the bubble to mean flow velocity ratio for ${d_{eq}} < d$, which will be addressed in Sect. 5.3.

5.3 Bubble velocity

Effect of bubble size on its velocity is discussed in this section. Considering a fully developed Poiseuille velocity profile in the circular channel of interest, under no-slip and no-through boundary conditions, the velocity of the liquid phase increases from zero at the tube wall to a maximum value on the tube centreline that is two times of the mean velocity of the liquid $\overline{U_c}$. In such a flow condition, confined elongated bubbles are expected to be transported at velocities close to the mean velocity of the continuous phase $\overline{U_c}$. This assumption is, however, not entirely valid, especially at higher velocities, where a considerably thick annular liquid film is formed around the bubbles, causing the bubbles to move at slightly higher velocities than $\overline{U_c}$. As the volume of the bubble decreases and its volume-equivalent diameter $d_{eq}$ becomes smaller than the tube diameter, the velocity of the bubbles $U_d$ is expected to increase, compared to that of the confined elongated bubble regime, provided that gravity effects are negligible. This is obviously due to the fact that smaller bubbles are transferred by the central stream of the liquid in the tube, which moves at higher velocities (Martinez and Udell 1990). However, in the presence of non-negligible gravity effects, such bubbles are elevated with respect to the centreline of the tube. As a consequence, their velocity is lower compared to that of a similar bubble moving in axisymmetric flow conditions because the local velocity of the carrier liquid is lower. This effect is expected to become relatively less notable when the bubble volume is significantly reduced, ${d_{eq}}^{*} \simeq 0.2$, and buoyancy effects are not significant anymore. In fact, very small bubbles are expected to behave very similar to small non-deformable solid particles in that they stay spherical and follow the local velocity of the liquid (Hetsroni et al. 1970; Hyman and Skalak 1972). Considering that gravity effects can be neglected due the small volumes of such bubbles, they are expected to be centred on the tube centreline, and therefore reaching the maximum velocity ($2\overline{U_c}$) in the fully developed Poiseuille profile in a circular channel. Effect of the dimensionless volume-equivalent diameter of the bubble ${d_{eq}}^{*}$ on the bubble velocity was investigated both experimentally and numerically in the present study. Direct comparison of the present measurements with the reported results in the literature is not possible since deformable bubbles with low gas-to-liquid viscosity ratio (λ ~ 0) were not covered in previous studies, see Ho and Leal (1975); Martinez and Udell (1990); Lac and Sherwood (2009).

Fig. 14

Effect of bubble size on the dimensionless velocity of the bubble in air–glycerol flows in the d = 494 μm tube at Ca = 0.05. The capillary number is calculated based on the velocity of the elongated bubbles

For air–glycerol flows, experimental measurements as well as numerical results obtained with ANSYS Fluent and OpenFOAM suggest that the bubble velocity is independent of its size when ${d_{eq}}^{*} > 1.1$, see Fig. 14. In such a condition, the bubble velocity predicted by both numerical solvers is within the error band of the value measured in the experiments. As was predicted before, a minimum in the dimensionless bubble velocity ${{U}_{d}}^*$ was found around ${d_{eq}}^{*} \simeq 1$, in both the experimental and numerical data. This is believed to be associated with the evolution of the bubble shape, where a maximum in the bubble nose diameter was found at around ${d_{eq}}^{*} \simeq 1$, see Fig. 3. For ${d_{eq}} < d$, the bubble velocity increases as its diameter is reduced for the reason mentioned earlier. However, the numerical model predicts a steeper rise in the velocity with respect to what was found experimentally. The largest deviation between the numerical and experimental results, although less than 10 %, occurs within the range $0.2 < {d_{eq}}^{*} < 0.7$. This discrepancy is ascribed to small but nonzero gravity effects present in the experimental measurements. It is worth mentioning that gravity effects not only shift the bubble upward with respect to the channel axis, thus motivating its lower velocity than that given by the axisymmetric model, but they also increase experimental errors in the measurement of bubble volume-equivalent diameter. As a reference, Fig. 14 also includes the analytical solution for the bubble velocity obtained by Hyman and Skalak (1972) for the axisymmetric creeping flow of spherical bubbles with very low and high viscosity ratios (λ = 0 and 1).

Fig. 15

Effect of bubble size on the dimensionless velocity of the bubble in air–water flows: a d = 514 μm, Ca = 7 × 10⁻⁴, b d = 962 μm, Ca = 9 × 10⁻⁴

Similar to air–glycerol flows, both experiments and simulations indicate that the bubble velocity is independent of its size when ${d_{eq}}^{*} > 1.1$ for air–water flows. In this flow regime characterised by elongated bubbles, the predictions of the bubble velocity given by the CFD results are in excellent agreement with the experiments for both ANSYS Fluent and OpenFOAM, see Fig. 15. A local minimum in the bubble velocity trend is still detected at about ${d_{eq}}^{*} \simeq 1$. For ${d_{eq}}^{*} < 1$, the bubble velocity increases with respect to the value attained for elongated bubbles as expected. However, for ${d_{eq}}^{*} < 0.9,$ the numerical and experimental trends differ substantially due to the relatively more significant gravitational effects present in air–water flows than those observed for air–glycerol flows, resulting from the relatively smaller viscous forces. In the experimental measurements, the bubble velocity reaches a maximum and then drops as the bubbles are reduced in size, down to values which are less than the mean velocity of the liquid phase $\overline{U_c}$ when ${d_{eq}}^{*} < 0.6$. This observation confirms the predictions associated with the significant buoyancy effects and elevation of the small bubbles with respect to the tube centreline. Moreover, this finding is in excellent agreement with experimental measurements of Olbricht and Leal (1982). The axisymmetric model presently used in numerical simulations cannot capture this trend, and therefore, the predicted bubble velocity shows a monotonic trend as the bubble diameter is decreased.

Figure 15 presents the comparison of the experimental and numerical bubble velocity results for air–water flows in tubes of diameters d = 514  and 962 μm. The tube diameter was found to have a negligible effect on the results provided that the capillary number is constant. This is not surprising because the capillary number of the flow is still small enough (Ca ~ 10⁻⁴–10⁻³) such that viscous and surface tension effects alone dominate this flow regime. However, bubbles’ velocities are dropping slightly more rapidly in the presence of significant gravitational effects for ${d_{eq}}^{*} < 0.9$ in the d = 962 μm tube confirming that buoyancy effects are more enhanced in the wider channel.

Fig. 16

Effect of bubble size on the dimensionless bubble velocity in air–water flows at different capillary numbers: a d = 514 μm, b d = 962 μm. Capillary numbers are calculated based on the velocity of the elongated bubbles

In addition, the effect of bubble size on the velocity of the bubbles at different capillary numbers was experimentally studied for tubes of diameters d = 514 and 962 μm and air–water flows, with the results presented in Fig. 16. The dimensionless bubble volume-equivalent diameter of ${d_{eq}}^{*} \approx 1.1$ still represents the threshold beyond which the bubble velocity becomes independent of its size. In this elongated bubble regime, the bubble velocity increases while increasing the capillary number, in agreement with the Bretherton’s law (Bretherton 1961). The magnitude of the maximum bubble velocity, detected at about ${d_{eq}}^{*} \sim 0.9$ for all the cases considered here, increases with the capillary number. This is due to the fact that gravity effects are relatively less significant at higher capillary numbers. For air–water flows in the d = 514 μm tube at Ca = 0.007, where very small bubbles could also be captured in the experimental tests, it was observed that for ${d_{eq}}^{*} < 0.4$, the gravity effect becomes once again less noticeable due to the small volume of the bubbles, see Fig. 16a. Eventually, bubbles of ${d_{eq}}^{*} < 0.2$ experience only negligible gravitational effects and thus were found to follow closely the local velocity of the liquid on the tube centreline.

With regard to the effect of flow capillary number on the velocity of elongated bubbles, Fig. 16 suggests that the dimensionless bubble velocity ${U_d}^{*}$ increases with Ca. However, since the velocity ratio in this regime is tightly linked to the liquid film thickness, a more thorough analysis of the effects of the flow capillary number on the bubble dimensionless velocity and the film thickness is outlined in the following section.

5.4 Film thickness

The thickness of the liquid film surrounding the confined elongated bubbles at the tube wall δ is quantified and analysed in this section. The range of the fluid and flow parameters covered in the present measurements of air–glycerol flows are very well in accordance with the conditions defining the visco-capillary regime: (1) the viscosity of the carrier liquid is relatively high so that moderate capillary numbers are achieved at very low flow velocities, and therefore, inertial effects are negligible ($Re, We \ll 1$); (2) the viscosity ratio between the phases is very low $\lambda = \frac{{\mu }_{d}}{{\mu }_{c}} = 3 \times {10}^{-5}$ and, (3) the tube diameter is small, d = 494 μm, and thus gravitational effects can be neglected for confined elongated bubbles. Therefore, the film thickness is expected to depend only on the flow capillary number.

Fig. 17

Dimensionless thickness of the liquid film at the wall versus the capillary number for confined elongated air bubbles moving within: a glycerol flows in the d = 494 μm capillary tube, and b water flows in the d = 962 μm tube at Ca < 10⁻³, and in the d = 514 μm tube at Ca > 10⁻³

The experimental measurements of film thickness for air–glycerol flows were performed using the Nikon 20× objective resulting in less than 10 % error in the measurements at the lowest capillary number Ca = 8 × 10⁻³. Figure 17a presents the comparison between the present experimental and numerical film thickness measurements for air–glycerol flows. Results of both approaches were found to follow precisely Taylor’s law. Furthermore, the validity of the stagnant liquid film assumption used in experimental measurements of Fairbrother and Stubbs (1935) and Taylor (1961) was investigated using the measurements of the film thickness and bubble to mean flow velocity ratio. As was discussed earlier, it was assumed in these studies that the liquid in the film surrounding the bubble is nearly stationary, and thus, bubble to mean flow velocity ratio alone can be used to predict the dimensionless film thickness using Eq. 2. In the present study, the difference between the direct measurement of the glycerol film thickness by means of interface detection and those achieved using Eq. 2 were always less than 1.5 μm for the experimental measurements, which is negligible considering the smallest resolvable length in these experiments to be 1.28 μm, and including also the errors in determination of the bubble and the mean flow velocities. This assumption was further verified directly using the results of the current numerical simulations, where the local velocity of the liquid within the film was found to be always less than 100 times smaller than that of the bubble, at the highest capillary number presented in Fig. 17a. Therefore, the stagnant liquid film assumption is concluded to be valid for air–glycerol flows in the range of capillary numbers presented here.

For air–water flows, at very low capillary numbers Ca < 10⁻³, even the highest available optical magnification in our experimental set-up (using the 40× microscope objective), which provided a spatial resolution of 0.65 μm per pixel on the image plane, was not sufficient to capture precisely the film thickness in the 514 μm diameter tube. Therefore, experiments for this range were performed in a 962 μm diameter tube to achieve a more acceptable relative accuracy in the measurements. Even so, for the extreme cases presented in Fig. 17b (Ca < 3 × 10⁻³), the errors in the experimental measurements can be up to 30 %, while for higher capillary numbers, in the 514 μm diameter tube, the measurements accuracy was always better than 10 %. It should be noted that direct experimental measurements of film thickness for this range of flow capillary numbers have not been reported in the literature previously. For Ca < 0.01, good agreement was achieved between the results of both numerical simulations and the experimental measurements, and the previously reported results based on the creeping flow condition and stagnant liquid film assumption. However, at higher capillary numbers, the present measurements in air–water flows showed systematic deviation from Taylor’s law at around Ca > 9 × 10⁻³. Above this threshold in the capillary number ${Ca}_{tr} \simeq 9\times {10}^{-3}$, the water film in the current experimental and numerical measurements was observed to be thicker compared to the conventional predictions, see Fig. 17b. The reason behind this phenomenon is that inertial effects are significant in gas–liquid flows with a low viscous liquid phase even at relatively low capillary numbers. In fact, for air–water flows at Ca > 0.01, the Reynolds and Weber numbers of the flow are larger than unity: $We = \frac{\rho {U_d}^2 d}{\sigma } > 5$ and $Re = \frac{{U_c} d}{\nu } > 500$. Therefore, bubble shape, liquid film thickness and interface dynamics are expected to differ significantly compared to the air–glycerol flows at the same capillary numbers, as was presented in Fig. 7. For this range of flow capillary numbers Ca > 0.01, present experimental measurements and numerical simulation results of ANSYS Fluent were in excellent quantitative agreement with the experimental results of Han and Shikazono (2009) for air–water flows in a d = 0.5 mm tube, while the film thickness calculated numerically using OpenFOAM was relatively larger. Although clear non-axisymmetric patterns were observed in the present experimental results at Ca > 0.015, the axisymmetric numerical studies were found to qualitatively capture the wave dynamics on the interface. The dimensionless number introduced by Aussillous and Quéré (2000) and Ryck (2002), $F = \frac{Re}{Ca} = \frac{\rho \sigma R}{{{\mu }_{c}}^2}$, was calculated to be around 45500 for the present air–water flows in the d = 514 μm capillary tube. Therefore, the existence of a threshold capillary number observed in our study is in agreement with their conclusion claiming that for low viscous liquids and high F numbers, significant inertial effects and subsequent deviation from the Taylor’s law are expected. Furthermore, according to the study of Aussillous and Quéré (2000), for air–water flows in the d = 514 μm capillary tube, the threshold capillary number is predicted to be approximately ${Ca}_{tr} = 0.015$, which is close to the threshold capillary number ${Ca}_{tr} \simeq 9\times {10}^{-3}$ found in the present study.

It is worth mentioning that even for bubbles three times longer than the tube diameter, identification of a region along the interface with uniform film thickness was not possible at the largest capillary numbers in air–water flows. Therefore, determination of a single value for the film thickness becomes a subjective task which leads to discrepancies when comparing the results at high capillary numbers. The same observation was also reported before by Edvinsson and Irandoust (1996). In this study, the film thickness presented in Fig. 17b is defined as an average value in the region far from the nose of the bubble for both numerical and experimental results. In these flow conditions, the noses of the air bubbles were observed to be more elongated, and the water film thickness was found to decrease gradually from the nose to the tail of the bubble until it reached the wavy section close to the rear end of the bubble. To the aim of investigating whether a flat region between the nose and the wavy zone at the tail of the bubble would be achieved above a certain threshold in the bubble length, a series of numerical simulations were presently performed using ANSYS Fluent for air bubbles of different lengths in water flows at Ca = 0.015. The results of these tests showed that a flat liquid film region was found for bubbles at least five times longer than the tube diameter. Moreover, comparing the interfaces of very long air bubbles in water and glycerol flows at the same capillary number Ca = 0.015, it was observed that the film thickness was larger in water even at the back of the bubble, where a region with a minimum thickness was found.

Fig. 18

Comparison between the direct film thickness measurements obtained from interface detection in simulations (ANSYS Fluent) and the indirect determination of film thickness using Eq. 2 for air–water flows in the d = 514 μm tube

The range of applicability of Eq. 2 in defining the film thickness in air–water flows and the stagnant liquid film assumption was investigated for air–water flow, using numerical results obtained with ANSYS Fluent. Experimental measurements were not used for this test, since the velocity in the continuous liquid phase was beyond the limitations of our velocimetry technique and thus could not be resolved accurately. As presented in Fig. 18, above a certain capillary number, the results of the film thickness measurements from interface detection do not follow those obtained using the bubble to mean flow velocity ratio in Eq. 2. In accordance with the observations reported above, it can be seen that for Ca > 0.01, the relative bubble velocity alone is no longer sufficient to determine the film thickness, thus suggesting that the stagnant liquid film assumption is no longer valid. More precisely, the results of the present numerical simulations for air–water flows above the threshold Ca _tr not only show non-negligible axial velocities in the liquid film, but also reveal relatively more significant velocity magnitudes in the radial direction. As an example, at Ca = 0.013, the maximum axial and radial velocity magnitudes in the liquid film reach about 0.07 and 0.01 of the bubble velocity, respectively.

5.5 Development lengths before and after bubbles

5.5.1 Effect of bubble size

Fig. 19

Effect of bubble size on the development length in front and at the back of the bubbles for air–glycerol flows in the d = 494 μm tube at Ca = 0.05

In this section, the length of the regions in the liquid phase influenced by the presence of the air bubbles is quantified using the procedure described in Khodaparast et al. (2014). As a result, the effect of bubble size on the development lengths in front ${X_n}^{*}$ and at the back ${X_t}^{*}$ of the bubbles is quantified at a constant liquid-phase flow rate. Figure 19 displays the experimental and numerical results for air–glycerol flows. For the sake of clarity, only ANSYS Fluent results are presented for all results on development lengths. The threshold for defining the development length, as described in Sect. 3.3, was reduced to 2 % to increase the sensitivity of the measurements to the size of the bubbles, especially for very small bubbles. It can be seen that the development lengths are independent of the bubble size when ${d_{eq}}^{*} > 1$. As the bubble diameter is reduced in the small bubble flow regime, the length of the region where the flow is influenced by the motion of the bubble decreases and approaches zero for very small bubbles, as expected. As a general trend, the development length in front of the bubbles was slightly shorter than that obtained at the back of the bubbles. For the entire range of bubble diameters studied here, the development length was observed to be always shorter than half of the tube diameter, thus suggesting that only very short gaps between bubbles will promote mutual interactions (multiple bubbles were, however, not studied here). Good agreement was achieved when comparing the numerical and experimental trends and magnitude, also considering the large error affecting these measurements, especially in the experimental approach. The spatial resolution in defining the development length in the present experimental study is directly dependent on the size of the interrogation windows used in the velocimetry step, which can reach up to 10 % of relative error with respect to the tube diameter.

For air water flows, the relatively high-velocity magnitudes at very low capillary numbers resulted in large uncertainty in the determination of the development length relative to the bubble size. Therefore, due to a considerable scattering in the numerical and experimental data, a clear meaningful trend could not be captured for ${X_n}^*$ and ${X_t}^*$ versus ${d_{eq}}^{*}$ and thus these results are not reported here. However, it was found that the development length was always less than 0.7d in air–water flows for the range of flow parameters investigated here.

5.5.2 Effect of capillary number

The effect of flow capillary number on the development lengths in front ${X_n}^{*}$ and at the back ${X_t}^{*}$ of confined elongated air bubbles in glycerol flows is shown in Fig. 20a. A monotonic decreasing trend was observed in ${X_n}^{*}$ when increasing the flow capillary number, while the development length (or the length of the wake region) behind the bubble tail ${X_t}^{*}$ was observed to decrease very slowly as the capillary number increased until Ca ≃ 0.05, and then, its magnitude remained almost unchanged at higher capillary numbers. Similarly, as reported in Sect. 5.1.2, the capillary number was found to affect the curvature at the nose of the bubbles more than the rear end of the bubbles in air–glycerol flows. Hence, the trend of ${X}^{*}$ versus Ca is possibly related to the change in the curvature of the nose and the tail of the bubble; as a matter of fact, a slender bubble nose is expected to influence less the liquid flow in front of it than a more spherical one. As a general trend, the development length in front of the bubble was always shorter than the development length behind the bubble tail, and the relative difference between these two parameters was found to increase at higher capillary numbers. The length of these developing regions did not exceed 0.32 times of the tube diameter, and the relative difference between the experimental and numerical results was always less than 7 %.

Fig. 20

Dimensionless development length in front of the bubble nose ${X_n}^{*}$ and behind the bubble tail ${X_t}^{*}$ versus capillary number for confined elongated air bubbles in: a laminar creeping glycerol flows in the d = 494 μm tube, b water flows in the d = 514 μm tube

Figure 20b presents the experimental and numerical results obtained for air–water flows. Due to the relatively high velocity of the water phase for Ca > 0.01, precise experimental determination of the development lengths was not possible, and hence, experimental results in this range are omitted from Fig. 20b. In general, the developing region in air–water flows was found to be relatively longer than what was observed in air–glycerol flows, up to 0.7 times of the tube diameter measured in front of the bubble at the lowest capillary numbers tested. Unlike air–glycerol flows, the length of the developing region of the flow in the front of the bubble nose was longer than the one measured behind the tail of the bubble. In spite of the different range of capillary numbers, air–water and air–glycerol flows present similar magnitudes of the development lengths behind the rear end of the bubbles. However, the development length in front of the bubble is substantially longer in air–water flows, especially at very low capillary numbers. This difference can be ascribed to the larger diameter of the fitted sphere to the nose of the bubbles in air–water flows at low capillary numbers (above ${d_{eq}}^{*}=0.9$) with respect to the values measured in the air–glycerol flows, such that the nose of the bubble is expected to influence the liquid flow field in front of it to a greater extent. A descending trend was observed for both ${X_n}^{*}$ and ${X_t}^{*}$ in air–water flows as the flow capillary number was increased up to Ca = 0.005, although the experimental data for the development length behind the bubble tail show some scattering. At higher capillary numbers, however, the development lengths in front and at the back of the bubbles were observed to increase as the flow capillary number was increased.

6 Conclusions

Experimental measurements and numerical simulations were performed in the present study in order to investigate the dynamics of air bubbles in liquid flows through circular channels of diameters $d = 0.5\,\hbox {mm}$ and $d = 1\,\hbox {mm}$. Water and glycerol were used as the continuous phase so that a large range of flow capillary numbers $10^{-4} < Ca < 10^{-1}$ and Reynolds numbers ${10}^{-3} < Re < {10}^{3}$ could be covered. Measurements were reported for several flow parameters, such as the shape, velocity and size of the bubbles, velocity of the continuous phase, thickness of the liquid film surrounding the bubbles at the wall and the development lengths in front of the bubble nose and behind the bubble tail. For each parameter, the effects of bubble size and flow capillary number were quantified.

For small confined bubbles ${d_{eq}} < d$, the nose and the back of the bubbles remained spherical at very low capillary numbers Ca < 10⁻³, while the curvature at the nose was higher than the one at the back for higher capillary numbers when ${d_{eq}} > 0.5d$. For ${d_{eq}} > 1.5d$, bubble size was found to have no significant effect on the bubble shape. For such bubbles, the curvature at the nose increased, while the back of the bubble became flatter as the flow capillary number was increased. Inertial effects were found to be no longer negligible in air–water flows at Ca > 0.01. Such effects resulted in non-axisymmetric time-dependent features at the phase interface and the back of the bubble.

In the absence of buoyancy effects in air–glycerol flows, in the range of ${d_{eq}} < d$ decreasing the bubble size increased the bubble velocity, while for ${d_{eq}} > 1.1d$ an asymptotic value of the bubble velocity was achieved. Air bubbles with volume-equivalent diameters of ${d_{eq}} < 0.2d$ were found not to significantly disturb the glycerol flow and to nearly follow the localised liquid velocity on the tube centre line. Buoyancy effects were, however, found to be more significant in air–water flows, especially for $0.2d < {d_{eq}} < 0.8d$.

For air–glycerol flows, where the velocity in the liquid film was found to be always less than 1 % of the bubble velocity and the flow Reynolds number was always well below unity, the thickness of the liquid film was observed to agree favourably with the well-known Taylor’s law. However, Taylor’s law was observed to under-predict the film thickness measurements in air–water flows, especially at Ca > 0.01 due to the presence of significant inertial effects.

In general, the development lengths in air–water flows were longer than those measured in air–glycerol flows. For the range of parameters and both liquids presently studied, the development lengths in front and at the back of the bubbles were found to be always smaller than the tube diameter.

The numerical results obtained with both ANSYS Fluent and OpenFOAM agreed well with the experimental measurement, with except of a few cases characterised by very small capillary numbers ($Ca \sim {10}^{-4}$) and small bubbles ($d_{eq}<0.8d$) due to spurious velocity fields related to insufficient accuracy in the surface tension discretisation. ANSYS Fluent, here enhanced with self-implemented algorithms for surface tension estimation, performed slightly better than OpenFOAM in reproducing the dynamics of the liquid film for air–water flows at the largest capillary numbers presently tested.

In summary, the dynamics of two-phase flows in micro-geometries still remains a challenging problem in fluid mechanics; however, the present methodology, based on non-intrusive experimental measurements in conjunction with CFD simulations with interface capturing techniques, proves to be a promising approach toward acquiring more reliable and accurate fundamental knowledge in the field.

Appendix 1: Selected experimental data

This appendix reports, in a tabular form, the flow parameters characterising the flow conditions (fluids, channel diameter d, dispersed phase volume $V_d$, and mean liquid flow velocity $\overline{U}_{c}$) and results (dispersed phase velocity ${U}_{d}$, dimensionless liquid film thickness δ*, dimensionless diameter of the fitted sphere to the bubble nose ${d_{\rm nose}}^{*}$ and tail ${d_{\rm tail}}^{*}$) for 22 selected experimental runs, whose corresponding bubbles shape are displayed in Figs. 5a, b, 9 and 10 of the present paper. These data are useful for benchmarking computational codes aimed to simulate the confined small and elongated bubbles in liquid flows within narrow channels.

The experimental test conditions are the following:

• Temperature: 25 °C.

• Density: water 997 kg/m³, glycerol solution 1250 kg/m³, air 1.204 kg/m³.

• Viscosity: water 0.88 mPa·s, glycerol solution 550 mPa·s, air 0.019 mPa·s.

• Surface tension: air–water 72.8 mN/m, air–glycerol 63.4 mN/m.

Case	Fluids	d (μm)	$V_d$ [μl]	$\overline{U}_{c}$ [m/s]	${U}_{d}$ [m/s]	δ* [–]	${d_{\rm nose}}^{*}$ [–]	${d_{\rm tail}}^{*}$ [–]
1. Figure 5a, ${{d}_{eq}}^{*}=0.354$	Air–glycerol	494	0.0028	0.00553	0.01033	–	0.35	0.36
2. Figure 5a, ${{d}_{eq}}^{*}=0.513$	Air–glycerol	494	0.0085	0.00454	0.00777	–	0.50	0.54
3. Figure 5a, ${{d}_{eq}}^{*}=0.677$	Air–glycerol	494	0.0196	0.00360	0.00599	–	0.62	0.74
4. Figure 5a, ${{d}_{eq}}^{*}=0.747$	Air–glycerol	494	0.0263	0.00451	0.00713	–	0.67	0.81
5. Figure 5a, ${{d}_{eq}}^{*}=0.813$	Air–glycerol	494	0.0339	0.00463	0.00708	–	0.69	0.92
6. Figure 5a, ${{d}_{eq}}^{*}=1.047$	Air–glycerol	494	0.0724	0.00435	0.00568	–	0.72	1.06
7. Figure 5a, ${{d}_{eq}}^{*}=1.189$	Air–glycerol	494	0.1061	0.00454	0.00599	0.065	0.68	1.07
8. Figure 5b, ${{d}_{eq}}^{*}=0.789$	Air–water	514	0.0349	0.0454	0.0533	–	0.79	0.79
9. Figure 5b, ${{d}_{eq}}^{*}=0.852$	Air–water	514	0.0439	0.0593	0.0697	–	0.85	0.85
10. Figure 5b, ${{d}_{eq}}^{*}=0.946$	Air–water	514	0.0602	0.0557	0.0607	–	0.95	0.97
11. Figure 5b, ${{d}_{eq}}^{*}=1.016$	Air–water	514	0.0745	0.0534	0.0550	–	0.94	0.99
12. Figure 5b, ${{d}_{eq}}^{*}=1.386$	Air–water	514	0.1893	0.0543	0.0554	0.006	0.94	0.99
13. Figure 9a, Ca = 0.008	Air–glycerol	494	0.1970	0.00084	0.00095	0.026	0.85	1.00
14. Figure 9b, Ca = 0.052	Air–glycerol	494	0.1061	0.00450	0.00600	0.062	0.69	1.05
15. Figure 9c, Ca = 0.075	Air–glycerol	494	0.1086	0.00618	0.00871	0.075	0.64	1.11
16. Figure 9d, Ca = 0.098	Air–glycerol	494	0.1231	0.00777	0.01137	0.083	0.61	1.14
17. Figure 9e, Ca = 0.163	Air–glycerol	494	0.0780	0.01145	0.01888	0.099	0.60	1.05
18. Figure 10a, Ca = 0.003	Air–water	514	0.1751	0.242	0.261	0.013	0.89	0.96
19. Figure 10b, Ca = 0.008	Air–water	514	0.1715	0.666	0.704	0.023	0.82	1.03
20. Figure 10c, Ca = 0.0098	Air–water	514	0.2208	0.757	0.815	0.025	0.78	1.05
21. Figure 10d, Ca = 0.015	Air–water	514	0.1882	1.118	1.293	0.039	0.72	1.23
22. Figure 10e, Ca = 0.023	Air–water	514	0.2179	1.580	1.944	0.054	0.64	–