1 Introduction

Characterizing the flow behavior of liquids at high shear rates is of importance to many industrial applications where the system length scale L is relatively small. Examples include flow through porous media as well as lubricating, coating, and extruding processes. Recently, there have been many proposed methods to measure the rheological properties of liquids in microsystems that rely on particle velocimetry (Nordstrom et al. 2010; Schultz and Furst 2011; Gisler and Weitz 1998; Gittes et al. 1997; Mason and Weitz 1995), measuring pressure drops in flows through capillaries and slit geometry (Pipe et al. 2008; Kang et al. 2005; Laun 1983), and diffusing wave spectroscopy (Kim and Pak 2010; Palmer et al. 1999). Despite such advances, there are still many challenges in making such devices user friendly. On the other hand, obtaining reliable rheological data for liquids at high shear rates (>103 s−1) in conventional, commercially available macroscopic rheological instruments is not an easy task due to the development of hydrodynamic instabilities at high Reynolds number (Larson et al. 1990; Larson 1999; Pipe et al. 2008). The Reynolds number (Re) describes the relative importance of inertial to viscous forces and is usually defined as Re = ρ UL/μ, where ρ is the fluid density, U is the mean fluid velocity, L is a characteristic length scale, and μ is the fluid viscosity. Due to its inherent small length scale L, microfluidics is an attractive system to investigate the rheological properties of liquids at low Re and high shear rates (U/L) (Schultz and Furst 2011; Gisler and Weitz 1998; Gittes et al. 1997; Mason and Weitz 1995; Pipe et al. 2008; Kang et al. 2005; Laun 1983; Kim and Pak 2010; Palmer et al. 1999). Here, we present such system that relies on in situ pressure sensors to measure the fluid wall shear stresses flowing through a long and straight microchannel.

In recent years, PDMS-based microfluidic devices have been widely used for MEMS due to their low cost, ease of fabrication, and well-characterized mechanical properties (Quake and Scherer 2000; Wu et al. 2011; Li et al. 2010; Orth et al. 2011). Moreover, the conductivity of the well-known PDMS elastomer can be tuned by adding conductive fillers to it, such as metallic powder, carbon black, and carbon nanotubes (Niu et al. 2007; Abyaneh and Kulkarni 2008; Lipomi et al. 2011). This PDMS composite shows piezoresistive property that is mainly determined by the electron tunnelling between isolated filler particles in the polymer matrix (Strumpler and Glatz-Reichenbach 1999; Toker et al. 2003). This PDMS composite has become an attractive material for fabricating pressure sensing devices (Liu 2007; Chuang and Wereley 2009; Wang et al. 2009; Lipomi et al. 2011) due to its capability to measure a wide range of pressure with high sensitivity achieved by simply changing the type and concentration of filler materials, as well as the polymer film thickness.

In this work, we present a PDMS-based microfluidic rheometer that uses in situ pressure signals to measure the shear viscosity of liquids. This PDMS-based microfluidic device can be fabricated in laboratory without sophisticated cleanroom facilities. The working principles of the device are tested using both Newtonian and non-Newtonian (i.e., shear thinning) fluids. The flow of both Newtonian and non-Newtonian fluids in the device is characterized using particle tracking velocimetry and numerical simulations. The fluid rheological properties such as viscosity and shear stress are measured as a function of shear rate up to 104 s−1. Due to the device small length scale, L = 100 μm, the flow of all fluids remains in the low Re regime to avoid hydrodynamic instabilities that usually complicate data analysis. Finally, viscosity data obtained with the microfluidic device are compared to data obtained using a commercially available macroscopic rheometer.

2 Experimental method

2.1 Experimental design

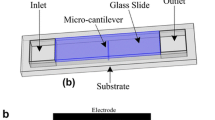
The integrated microfluidic device consists of two PDMS layers that are the sensing membrane and channel layer, as well as a glass substrate layer, as shown schematically in Fig. 1a. The microfluidic channel layer is comparatively thick (∼2 mm), while the sensing membrane is very thin (120 μm). Different channel geometries can be utilized due to the simple bonding method between the channel and sensing layer; here we focus on a simple straight channel that is 100 μm deep and 100 μm wide. Figure 1b shows a schematic drawing of the micro-channel along with multiple pressure sensors. Each sensing element consists of a sensing bar (length: 1,000 μm, width: 30 μm, height: 100 μm) and two square electrode pads for wire bonding as shown in Fig. 1b. These sensors are placed along the length of the microchannel in order to measure the deformation of the channel wall that results from the fluid shear stress at different locations along the channel. The distance between two adjacent sensors is 5,000 μm so that under small deformation the coupling between adjacent sensors is negligible. Channel wall deformations captured by the piezoresistive sensors are transformed into voltage signals which are read by an oscilloscope. These signals are then used to estimate the viscosity of various liquids.

Fig. 1
figure 1

a Schematic illustration of the PDMS-based microfluidic device (not to scale). Top layer is the PDMS sensing membrane, middle layer is a thick PDMS layer with channel geometry, and the bottom is the glass substrate layer. The sensing elements are connected to measurement circuits via the electrical wires. b The design of the sensing piezoresistive layer with a channel. c Image of a fabricated microfluidic-based rheometer

Full size image

2.2 Sensor material

Pressure sensors are made by mixing conductive particles with an elastomer (PDMS) matrix. The conductive (filler) particles are a mixture of silver particles (1–3 μm in diameter, Strem Chemicals Inc.) and carbon black particles (42 nm in diameter, Strem Chemicals Inc.). These particles are thoroughly mixed and introduced into an elastomer (PDMS, Sylgard) matrix. The mass fraction of silver and carbon-black particles is chosen such that the final composite is conductive and possesses appropriate material properties. For example, we find that the final composite breaks very easily if the concentration of silver particles is too high (>90 % by weight). On the other hand, the final composite does not conduct well if the concentration of silver particles is too low (<80 % by weight). Hence, we add carbon black particles to silver particles in order to achieve good conductivity while keeping the material from becoming brittle. We find that, for our purposes, the optimal total mixture composition (by weight) is 82 wt% silver particles, 10 wt% carbon black, and 8 wt% PDMS.

The PDMS-metal composites are obtained by first cleaning the conductive particles (silver and carbon-black) using acetone, ethanol and deionized water, respectively. Next, the filler particles are thoroughly mixed in methanol to completely wet the particles and then mixed with the silicone (PDMS) elastomer. The mixture is then heated to 85 °C and kept at that temperature for 30 min so that methanol and other remaining solvents can completely evaporate. The PDMS cross-linking reagent is then added to the sample after it has been cooled to room temperature. We then stir the PDMS-filler mixture thoroughly and degas it for 20 min. Finally, we plaster the PDMS-filler composite into a mold.

2.3 Fabrication

In this section, we describe an accessible fabrication process for a microfluidic-based rheometer (Fig. 2). First, a 100 μm thick negative photoresist (SU-8) is spin-coated on a bare silicon wafer, and patterned with the sensing structure using the standard photolithography method (step a). Then, a 120 μm thick PDMS is spin-coated on the sample and baked at 85 °C for 30 min (step b). After cooling the sample down to room temperature, we immerse it in isopropanol (IPA) for 15 min in order to ease the peeling-off of the thin PDMS layer. At the same time, a channel layer is fabricated using the standard soft-lithography method with desired channel geometry (Xia and Whitesides 1998; McDonald and Whitesides 2002; Sia and Whitesides 2003). Here, we use a long (3 cm) straight channel with a square (100 μm wide and 100 μm deep) cross-section.

Fig. 2
figure 2

Fabrication process of the integrated microfluidic device: a photolithography of 100 μm thick SU-8 on silicon wafer, b spin coating of 120 μm thick PDMS, c bonding of the thin PDMS membrane with the channel layer, d plastering the conductive composites into the mold, e cleaning up the extra conductive composites, f bonding of the two bonded PDMS layers with a glass cover slip

Full size image

Alignment of the sensing structure with the channel geometry is required before the bonding of these two layers and it is important to the device performance. Therefore, after taking the samples out of the plasma machine, we dip the treated surfaces into methanol thoroughly for protection and align them under microscope. Next we evaporate the remaining methanol between the two layers by heating the sample on a hotplate at 120 °C. Note that after the methanol is evaporated, the two treated surfaces become hydrophilic again and can thus be bonded together (step c). We then plaster the prepared conductive composites into the sensing structure mold (step d). Next we clean up the extra conductive material using a razor blade (step e) and bake the sample on a hotplate at 120 °C for 2 h so that the conductive composites solidify and bond with the mold. Note that we plaster the composites after the bonding of all the PDMS layers to reduce the surface damage. Both the inlet and outlet are made by punching a hole in PDMS. These holes are very small (0.75 mm in diameter) and it is where the inlet and outlet tubes are placed. Finally, a glass cover slip is bonded below the channel layer to seal the microfluidic device and to increase the stiffness of the whole device as well (step f). For each bonding procedure, the surfaces are cleaned with a diluted HCl solution (HCl:DI water = 1:5 by volume) in order to increase the bonding strength for enabling high shear-stress experiments (Jo et al. 2000; Eddings et al. 2008). The electrode pads are bonded with 30 AWG electric wires using silver paste. Finally, the fabricated microfluidic device is connected to an electric circuit board (Fig. 1c) which is used only to connect the device to the oscilloscope and power supply.

When fabricating the sensing membrane, it is important to take into account the PDMS thickness since the sensitivity caused by membrane deformation is inversely proportional to the cubic power of its thickness. That is, if the membrane is too thick, then the response time is relatively short due to the high stiffness of the membrane, but the sensitivity to shear stresses is comparatively low. By contrast, a thin membrane shows good sensitivity but much longer response time. We find that a PDMS membrane of 120 μm was optimal for our purposes. This membrane is fabricated by first spin-coating PDMS on a silicon wafer at the initial speed (500 rpm) for 5 s so that it spreads uniformly. Then this evenly coated PDMS layer is spin-coated at 1,400 rpm for 10 s to obtain the desired thickness.

2.4 Working fluids

Several liquids are used to demonstrate the working principles of this microfluidic-base rheometer. The apparatus is calibrated using a fluid of known viscosity μ = 1,018 mPa s, namely silicon oil (Cannon Instrument, Silicone oil RT1000). The performance of the apparatus is tested using both Newtonian and non-Newtonian fluids. The Newtonian fluids are pure glycerol, a 90 % aqueous glycerol solution, and a 65 % aqueous glycerol solution. The non-Newtonian fluid is made by adding 5,000 ppm (by weight) of high molecular weight, stiff polymer Xanthan Gum (XG, M W = 2 × 106) to water. This XG solution is known to possess shear rate-dependent viscosity behavior (Arratia et al. 2005).

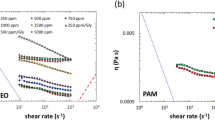
In Fig. 3, we show viscosity data as a function of shear rate for all fluids. Viscosity measurements are obtained using a stress-controlled cone-plate rheometer (Bohlin Gemini). The measured viscosity values of the calibration oil, pure glycerol, 90 % glycerol and 65 % glycerol solutions are 1,037, 994, 179, and 17.1 mPa s, respectively. As expected, the viscosity of such fluids is independent of shear rate. On the other hand, the viscosity of the XG solution shows distinct shear-thinning behavior with a power law exponent n of approximately 0.16, according to Eq. (1). The shear viscosity of the XG solution can be fitted quite well by the Bird–Carreau–Yasuda model (Larson 1999; Macosko 1994)

$$ \frac{\mu-{\mu}_\infty}{{\mu}_0-{\mu}_\infty}={\left[ 1+{\left( \lambda\dot{\gamma}\right)}^2 \right]}^\frac{n-1}{2} $$
(1)

where \(\mu_\infty\) = 0.001 Pa s is the infinite shear viscosity, μ0 = 21 Pa s is the zero shear viscosity, λ = 10 s is a time scale which characterizes the transition from Newtonian to shear-thinning behavior, and n = 0.16 is the power-law index. Figure 3 shows that shear viscosity computed using Bird–Carreau–Yasuda model fits well with the XG viscosity data. We note that no appreciable first normal stress difference was observed for the XG solution (data not shown) which indicates that fluid elastic effects are negligible.

Fig. 3
figure 3

Fluid rheological characterization using a commercially available macroscopic rheometer (Bohlin). Viscosity data for both Newtonian and non-Newtonian fluids measured using a cone-plate, stress-controlled rheometer. The non-Newtonian fluid is a Xanthan Gum (XG) aqueous solution that possess shear-thinning viscosity. The solid line represents the best fit to the XG viscosity data using Bird–Carreau–Yasuda model (see text)

Full size image

2.5 Working principles

In this section, we briefly discuss the main operating principle for the microfluidic-based rheometer; for more information, please see Supplemental Material. The main goal is to estimate the fluid viscosity by measuring the pressure drop along a channel at low Re using in situ pressure sensors. The Reynolds number can be re-written in terms of the fluid flow rate Q such that Re = ρ Q/wμ, where w is the channel width. Using a simple force balance between the pressure force acting on the cross-section of the channel and the viscous shear stress acting on the wall (see Supplementary Material), the shear stress can be written as

$$ \tau_{\hbox{w}} = \frac{w}{4l} \left( \Updelta P \right). $$
(2)

For a squared channel, the above equation is simply \({\Updelta}P= 4l\tau_{\hbox{w}}/w.\) In our experiments, both the width and depth of the channel are 100 μm, and l is the length from the pressure sensor to the outlet of channel (l = 2 cm). We now must find a way to relate the fluid viscosity μ to the shear rate at the wall \(\dot{\gamma}_{\hbox{w}}\) and the pressure drop \(\Updelta P.\)

Newtonian fluids—For Newtonian fluids, the shear stress is linearly proportional to the shear rate \({\dot{\gamma}}\) such that \(\mathbf{\bar{\bar{\tau}}}=\mu(\nabla\mathbf{u}+ {\nabla\mathbf{u}}^{T}0)=\mu{\bar{\bar{\dot{\gamma}}}}.\) Using the relationship between flow rate and pressure drop (Eq. SM 1.5), the wall shear rate \({\dot{\gamma}}_{\hbox{w}}\) can be related to the volumetric flow rate Q as (Eq. SM 1.9)

$${\dot{\gamma}_{w}}{\approx}\frac{7Q}{w^3}. $$
(3)

Therefore, the viscosity of Newtonian fluids in square channels at low Re can be expressed as

$${\mu}=\frac{w}{4l}\frac{{\Updelta}P}{\dot{\gamma_{\hbox{w}}}}. $$
(4)

Hence, one can measure the viscosity of Newtonian liquids flowing in a square microchannel by measuring the pressure drop along the channel. Here, the pressure drop is measured using in situ piezoresistive membranes that deflect under an applied pressure; the resultant strain from the deflected membrane changes the resistance value of the sensing piezoresistors. This piezoresistive effect results in a linear relationship between the change of resistances \(\Updelta R\) and the pressure drop \(\Updelta P\) for small strain. Thus, fluid viscosity can be obtained from the measured resistance signals at different shear rates.

Non-Newtonian fluids—The wall shear rate \(\dot{\gamma_{\hbox{w}}}\) for liquids that possess shear rate-dependent viscosity such as the XG solution cannot be obtained by using Eq. 3 which is valid only for Newtonian fluids. To estimate the values of \(\dot{\gamma_{\hbox{w}}}\) for the shear-thinning XG fluid, we performed numerical simulations using a three-dimensional, finite element model in COMSOL Multiphysics. The goal is to find the values of the wall shear rate for the shear-thinning XG fluid flowing in a square microchannel.

The steady, incompressible flow of both Newtonian and non-Newtonian (shear thinning) fluids in a square microchannel is investigated by solving the steady-state Navier–Stokes equation in the low Re regime. Under such condition, the convective derivatives vanish and the governing equations are

$$ \nabla\cdot{\mathbf u} = 0, $$
(5)
$$ \nabla P=\nabla\cdot{\mathbf{\bar{\bar{\tau}}}}. $$
(6)

Simulations are performed by simultaneously solving the above equations with an appropriate fluid constitutive equation and no-slip boundary conditions. For Newtonian fluids, the stress is linearly proportional to the strain rate such that \(\mathbf{\bar{\bar{\tau}}}=\mu{\bar{\bar{\dot{\gamma}}}}.\) Here, simulations are performed for the calibration oil of viscosity μ = 1,018 mPa s. For shear-thinning fluids, we use the well-known Bird–Carreau–Yasuda model (see Eq. 1) because it adequately describes the XG solution rheological data (Fig. 3).

The simulated geometry is a long, straight channel of L = 1 mm with a square cross-section of 100 × 100 μm 2. The governing equations are solved along with the no-slip boundary condition (u = 0) at the channel solid walls and with additional conditions at the channel inlet and outlets. The flow at the channel inlet is set by a constant mass flow rate or an inflow velocity U 0 while the channel outlet is set to be open to the atmosphere p 0 p 0 = 1.01 × 105 Pa).

By simultaneously solving Eqs. 5 and 6, along with the appropriate constitutive equations, we obtain the velocity and shear strain-rate fields for both Newtonian and non-Newtonian fluids. In Fig. 4a, we show the velocity profiles obtained using numerical simulations for the Newtonian fluid (oil) and the XG solution. Note that the viscosity function of the XG fluid is described by the Bird–Carreau–Yasuda as discussed above. The Newtonian fluid displays the typical parabolic-like velocity profile, while the XG fluid shows a blunt profile expected for shear-thinning fluids flowing in capillaries (Larson 1999). Figure 4b, c shows the shear strain-rate fields obtained using numerical simulations across the channel for both Newtonian fluid and XG solution. It becomes clear that the wall shear rates are different for both cases. Hence, we cannot use Eq. 3 to estimate the wall shear rate of the XG fluid.

Fig. 4
figure 4

Fluid flow characterization: experiments and numerical simulations. a Spanwise velocity profiles of both Newtonian and shear-thinning fluids where solid and dash lines indicate simulations and symbols indicate experiments. Newtonian velocity profiles show characteristic parabolic-type profile while shear-thinning features the expected blunt profile. Simulation seems to agree well with experiments. b and c Cross-sectional (100 × 100 μm2) view of the shear strain-rate fields obtained using numerical simulations for the b Newtonian and c XG fluids. The unit for scale bar is s−1

Full size image

Next, we compare the numerical simulation data to experiments under the same flow conditions. This is necessary in order to validate the simulation results. The experimental velocity profiles for both Newtonian fluid and XG solution are obtained using particle tracking velocimetry (PTV) methods (Arratia et al. 2005, 2006; Shen and Arratia 2011; Crocker and Grier 1996) and a fast camera due to the high velocity gradients. The flow is seeded with small fluorescent particles (0.86 μm in diameter) that are tracked using a CMOS camera and an epi-fluorescent microscope. The images are taken at a frame rate of 4,000 frames per second to ensure that one particle could be tracked for a certain period of time with a displacement smaller than the distance between two adjacent particles. The particle tracks are measured at a mid-plane between the top and bottom walls of the channel in order to minimize the effects of out-of-plane velocity gradients; the thickness of the measuring plane is approximately 2 μm. The measured particle tracks are then used to compute the velocity profiles.

The experimental velocity profiles for both the oil fluid and the XG solution are shown in Fig. 4a. We find that the experimental profiles are very similar to the numerical profiles. Note that, under steady state, the (experimental) velocity profiles shown in Fig. 4a are the mean velocity profiles that are averaged over 50,000 images to ensure the precision and accuracy. The agreement, of course, is not perfect. The discrepancy between numerical u sim and experimental velocity profiles u exp can be quantified using the root-mean-square (RMS) deviation:

$$ {\hbox{RMS}}\,=\,\frac{{\left[\frac{1}{i}\sum_1^i(u_{\hbox{sim}}-u_{\hbox{exp}})^2 \right]}^{1/2}}{{\left[\frac{1}{i}\sum_1^i(u_{\hbox{exp}})^2 \right]}^{1/2}} $$
(7)

where i is the number of points in the velocity field. The RMS values are 3.50 and 4.94 % for Newtonian fluid (oil) and XG solution, respectively. The main source of error is next to the walls where the presence of solid walls and high velocity gradients produce spurious results. Nevertheless, the experimental velocity profiles are consistent with the numerical predictions (Fig. 4a), which indicates that the simulations are able to faithfully capture the main features of the flow of both Newtonian fluid and XG solution in a square microchannel. Therefore, we use the simulation results to calculate the non-Newtonian (XG) fluid wall shear rate at each flow rate Q.

3 Results and discussion

3.1 Electrical characterization

The sensor resistance stability and current–voltage relationship are important features in designing piezoresistive devices. Long-term stability tests of sensor resistance are performed under steady water pressure conditions for different sensors as shown in Fig. 5a. We find that the resistance of the sensors is very stable up to 400 min with a maximum noise level about 1 %. Note that the resistance values are different for each sensor due to variations in sensor fabrication. However, this difference can be accounted for during the calibration procedure as discussed below.

Fig. 5
figure 5

a Long-term stability test of the sensor resistance showing the pressure sensors are stable up to 400 min. b Current–voltage (I–V) curve of the resistance suggests a linear, ohmic behavior of the piezoresistive sensor

Full size image

Next, the current–voltage (I–V curve) characteristics of different sensors resistance are measured using a USB data acquisition module (Measurement Computing). We find that the resistors show a linear, ohmic relationship (Fig. 5b) which indicates that the sensor piezoresistivity mainly relates to the strain-induced shape deformation of the sensing membrane. The inverse of the slope of the curve represents the resistance of the sensor in Fig. 5b. As discussed above, this means that each sensor must be independently calibrated. But this is a simple procedure once the value of the slope (resistance) is known since this is a linear, ohmic relationship.

In Fig. 6, we show the voltage signals as a function of flow rate (or shear stress) for a single sensor (sensor 2 from Fig. 5). A voltage signal is produced as the sensor deforms due to the flowing fluid wall shear stresses and to the piezoresistive effect of the sensing material. This results in a linear relationship between the change of resistance and the pressure drop for low strain (Fig. 7). We observe that the sensor response to the applied pressure drop decreases as the pressure drop (flow rate) increases (Fig. 6). For the lowest flow rate, the sensor time response is approximately 20 s. This is certainly not an issue for measuring steady-state shear viscosity, but it is certainly the limiting factor if oscillatory measurements are to be performed. Here, we only report steady-state measurements and measurements are performed at time-scales well above the initial sensor transient.

Fig. 6
figure 6

Voltage signal as a function of time measured by oscilloscope under different shear stresses in the channel

Full size image
Fig. 7
figure 7

Calibration curve for the microfluidic-based rheometer based on the known viscosity of calibration oil (1,037 mPa s) at an ambient temperature of approximately 23.5 °C

Full size image

3.2 Shear-stress calibration procedure

We calibrate the microfluidic rheometer using silicone oil with known (Newtonian) viscosity of 1,018 mPa s. Note that the wall shear rate \(\dot{\gamma}_{w}\) can be computed for different values of flow rates (Q) using Eq. 3. Since the viscosity of the calibration is known, the wall shear stress can be calculated as a function of each flow rate using the equation below:

$$ {\tau_{\hbox{w}}(Q)}={\mu}{\dot{\gamma_{\hbox{w}}}(Q)}. $$
(8)

Once the calibration fluid begins to flow in the channel, the shear stresses at the channel walls lead to a certain deformation of the sensing membrane which results in a change in resistance of the pressure sensor. This resistance is measured using an oscilloscope (Tektronix TDS 2004C) for different values of wall shear stresses (or flow rate) under steady-state conditions as shown in Fig. 7. In other words, the wall shear stress \({\tau_{\hbox{w}}}\) is calculated for each flow-rate Q value using Eq. 8, and the sensor change in resistance \(\Updelta R\) is measured for each value of Q or wall shear stress. Then, we construct a calibration curve of wall shear stress as a function of \(\Updelta R,\) as shown in Fig. 7. Note that data is shown for a single sensor (sensor 2 from Fig. 5) and for the calibration fluid; the linear trend shown in Fig. 7 is similar for all the other sensors. Next, we fit the data to a linear equation of the type:

$$ {\Updelta}{R}={a_1}{\dot{\gamma}_{{\hbox{w}}}}+{a_2} $$
(9)

where a 1 and a 2 are constants. For calibration oil, the viscosity is known and constant at ambient temperature. Therefore, Eq. 9 can be written as

$$ {\Updelta}{R}={a_1}\frac{\tau_{\hbox{w}}}{\mu}+a_2 $$
(10)

Therefore, a general expression for wall shear stress and change of resistance can be written as

$$ {\tau_{\hbox{w}}}={c_1}({\Updelta}{R})+c_2 $$
(11)

where c 1 and c 2 are constants. These constants must be determined independently for each sensor due to variations in sensor to sensor resistance. We proceed with data for a single sensor (sensor 2). As discussed before, for small deformations, the change of resistance \(\Updelta R\) is linearly proportional to the wall shear stress \( {\tau_{\hbox{w}}},\) as shown in Fig. 7. For sensor 2, the calibration curve is

$${\tau_{w}}=34.2({\Updelta}R)-381.0 $$
(12)

where the units of shear stress \( {\tau_{\hbox{w}}},\) and change of resistance (\(\Updelta R\)) are Pa and k\(\Upomega,\) respectively. From Eq. 2 and 11, we can also find a linear relationship between the pressure drop \(\Updelta P\) and change of resistance \(\Updelta R\)

$$ {\Updelta}{P}={b_1}({\Updelta}{R})+b_2 $$
(13)

where b 1 and b 2 are constants determined in the calibration process. For the sensor shown here, b 1 and b 2 are equal to 27.4 and −304.8, respectively.

We can now compare the values of wall shear stress obtained from experiments to (1) the analytical solution valid for the Newtonian fluid (pure glycerol) only and (2) to simulation results for XG solution at different flow rates, as shown in Fig. 8a, b, respectively. Overall, we find a reasonably good agreement between experiments and the analytical solution for Newtonian fluid and simulation values for XG solution. Deviations become more pronounced at higher flow rates (or shear stresses) where small deformation assumption and the linear relationship between the change in resistance and shear stress begin to fail.

Fig. 8
figure 8

Comparison of wall shear stress from a experimental and analytical results for Newtonian fluid (pure glycerol) and b experimental and simulation results for XG solution as a function of flow rates

Full size image

Using the procedure discussed above, we can now calculate the wall shear stress using Eq. 12 for different working fluids in order to obtain the fluid viscosity as a function of shear rate. In the following section, we measure the viscosity of Newtonian and non-Newtonian liquids in the microfluidic device and compare the data to a commercially available macroscopic rheometer.

3.3 Viscosity results

We test the feasibility of measuring the viscosity of liquids using the microfluidic-based rheometer using the Newtonian fluids mentioned in Sect. 2.4 The change of resistances in a piezoresistive sensor placed on the walls of microchannel (width w = 100 μm, depth d = 100 μm) is measured to obtain the wall shear stress and consequently calculate fluid viscosity. Figure 9 shows viscosity data obtained both with the commercially available macroscopic rheometer Bohlin (solid gray symbols in Fig. 9) and the proposed microfluidic rheometer (open color symbols in Fig. 9). The microfluidic data shows, as expected, that the viscosity values of all Newtonian fluids are independent of shear rate. In addition, shear viscosities measured by both commercially available macroscopic rheometer (Bohlin) and microfluidic-based device are compared with expected viscosity values (see Table 1). We note that there are some discrepancies in measured viscosity data for both macroscopic and microfluidic rheometers compared to the expected viscosity values. These discrepancies are most likely caused by the variations in temperature since the viscosity of glycerol is known to be highly temperature-dependent.

Fig. 9
figure 9

Rheometry: data obtained from both commercially available macroscopic rheometer (Bohlin) and microfluidic device. Shear viscosity measured using the microfluidic-based rheometer at an ambient temperature of 23.5 °C for both Newtonian and non-Newtonian fluids. The solid gray symbols represent data obtained using the commercially available macroscopic rheometer (Bohlin), while the open color symbols represent results using the microfluidic-based rheometer. The Newtonian fluids show a constant viscosity even at high shear rates, while the non-Newtonian fluid shows a shear-thinning behavior

Full size image
Table 1 Shear viscosity measured by macroscopic rheometer and microfluidic-based rheometer
Full size table

We note that significant viscous heating and inertial effects (Re ∼10) are observed for viscous fluid being tested in the commercial rheometer. Viscous heating effects are minimized in the microfluidic rheometer because it operates under continuous flow rather than in batch mode; the microfluidic pressure sensors only probe fresh fluid. Also, the flow is purely viscous (low Re) even at high shear rates due to the system inherent small length scales (L = 100 μm). The microfluidic device investigated here can perform at shear rates up to 104 s−1 while maintaining a nominal Re below 1, which simplifies the analysis of rheological data and avoids undesirable hydrodynamic instabilities.

Next, we test the microfluidic rheometer using the shear-thinning XG solution. As discussed in Sect. 2.5, the fluid viscosity of shear-thinning fluids can only be obtained by adequately estimating the values of the wall shear rate \(\dot{\gamma}_{\hbox{w}}\) using numerical simulation results along with the wall shear stress \( {\tau_{\hbox{w}}},\) values measured using the pressure sensor. We find that the shear-dependent viscosity values of the XG fluid are in good agreement with the values obtained using a commercial rheometer, as shown in Fig. 9. In addition to viscosity values, we compare the shear-stress values obtained using (1) microfluidic rheometer, (2) numerical simulations, and (3) macroscopic (commercial) rheometer. Figure 10 shows shear-stress data as a function of shear rate, and we find good agreement among all the above-mentioned cases.

The measurement capability/sensitivity of this microfluidic rheometer is set by the signal to noise ratio in measuring the wall shear stress which is limited by the bonding strength of the device (Eddings et al. 2008). In our experiments, the average bonding strength is approximately 200–500 kPa. On the other hand, experiments must be performed in the small-displacement regime so that linearity between the change in resistance and pressure drop can be ensured (Eq. 8). Given these two limiting regimes, the dynamical range in measuring shear stresses in this microfluidic rheometer ranges from 1 to 350 Pa; the resolution is approximately 0.1 k\(\Upomega\) for the resistance measurement, which implies a sensitivity of 1 Pa for the shear stress measurement. This resolution also sets the lower end of measurement capacity of the device. The dynamical range and sensitivity can be vastly increased by improving the membrane fabrication by using different materials and relaxing the linearity limit.

Fig. 10
figure 10

Shear stress of non-Newtonian fluid (5,000 ppm XG) measured using the microfluidic-based rheometer and macroscopic rheometer Bohlin, and computed using COMSOL

Full size image

4 Conclusions

In this paper, we demonstrate a PDMS-based microfluidic rheometer that uses in situ pressure sensors to calculate the viscosity of viscous fluids. We present results for both Newtonian and non-Newtonian (i.e. shear thinning) fluids for shear rates up to 104 s−1. The microfluidic device consists mainly of a channel layer and a sensing membrane integrated with piezoresistive pressure sensors via plasma surface treatment. The micro-pressure sensors are fabricated using conductive particles/PDMS composites and embedded in a 120 μm thick membrane that can be bonded with different channel geometries. The fluid wall shear stresses are calculated by measuring the change of resistances of the sensor in order to estimate the fluid viscosity. Corrected values of the shear stress for non-Newtonian fluids are obtained using numerical simulations. Experimental validation of this microfluidic-based rheometer is performed using calibration oil of known viscosity as well as the macroscopic rheometric data, both of which achieved good consistency. Importantly, for all the experiments shown here in the microfluidic device, the Reynolds numbers is below 1. In fact, the value of Re for the lowest viscosity fluid at the highest shear rate is approximately 0.86. Viscous heating, a problem usually encountered in macroscopic devices for high-viscosity fluids at high shear rates is minimized in the microfluidic device. This can be quantified using the Nahme number usually defined as Na = α T v 2μ/k, where α T is the temperature coefficient of viscosity, v is the velocity, and k is the thermal conductivity. In all our experiments, Na is smaller than 10−4 which indicates that viscous dissipation is negligible. The mode of operation, continuous flow versus batch, is also an important difference between the continuous flow-operated microfluidic device and the batch-operated conventional rheometer. The use of fresh fluid minimizes viscous heating and fluid degradation during measurement. In summary, the simple design, easy fabrication, low cost, and biocompatibility make this microfluidic rheometer easy to integrate with other systems.