High shear rate viscometry

Abstract

We investigate the use of two distinct and complementary approaches in measuring the viscometric properties of low viscosity complex fluids at high shear rates up to 80,000 s⁻¹. Firstly, we adapt commercial controlled-stress and controlled-rate rheometers to access elevated shear rates by using parallel-plate fixtures with very small gap settings (down to 30 μm). The resulting apparent viscosities are gap dependent and systematically in error, but the data can be corrected—at least for Newtonian fluids—via a simple linear gap correction originally presented by Connelly and Greener, J. Rheol, 29(2):209–226, 1985). Secondly, we use a microfabricated rheometer-on-a-chip to measure the steady flow curve in rectangular microchannels. The Weissenberg–Rabinowitsch–Mooney analysis is used to convert measurements of the pressure-drop/flow-rate relationship into the true wall-shear rate and the corresponding rate-dependent viscosity. Microchannel measurements are presented for a range of Newtonian calibration oils, a weakly shear-thinning dilute solution of poly(ethylene oxide), a strongly shear-thinning concentrated solution of xanthan gum, and a wormlike micelle solution that exhibits shear banding at a critical stress. Excellent agreement between the two approaches is obtained for the Newtonian calibration oils, and the relative benefits of each technique are compared and contrasted by considering the physical processes and instrumental limitations that bound the operating spaces for each device.

Introduction

The behavior of complex liquids at large deformation rates is relevant in many processes involving coating, spraying, lubrication, and injection molding. Although both shear and extensional deformations can be important in complex flows, in this study, we concentrate on the rheological behavior in steady shearing flow. From dimensional analysis, we expect $\dot{\gamma}\sim U/L$, where U is a characteristic velocity difference acting over a characteristic distance L, indicating that, to attain high shear rates, it is necessary to either (a) increase U or (b) decrease L. Large velocities can lead to high Reynolds numbers Re=ρU L/ η, where ρ is the density and η the dynamic viscosity of the fluid, and loss of viscometric flow. Thus, it is usual to strive to minimize L, and the limiting factor in accessing high shear rates is the accuracy with which flow devices or rheological test fixtures can be manufactured and aligned so that geometric perturbations remain small (δL/L<1), even when L is reduced.

Various experimental configurations have been proposed for measuring viscosity at high shear rates, including cylindrical Couette flow with narrow gaps (Merrill 1954), torsional flow between rotating parallel plates (Connelly and Greener 1985; Dontula et al. 1999; Kramer et al. 1987), flow through capillaries (Duda et al. 1988; Talbot 1974) and slits (Erickson et al. 2002; Laun 1983; Lodge and de Vargas 1983), and impact flow between a rotating ball and plate (O’Neill and Stachowiak 1996).

Measurements using narrow gap Couette flows between concentric cylinders and between parallel-plate fixtures have been used to measure the viscosity of Newtonian and shear-thinning liquids up to $\dot{\gamma}\sim10^{6}~{\rm s^{-1}}$ (Connelly and Greener 1985; Davies and Stokes 2005; Dontula et al. 1999; Kulicke and Porter 1981; Merrill 1954; Mriziq et al. 2004) using gaps $0.5~\upmu\textrm{m}\le H \le50~\upmu\textrm{m}$. Suggestions that Newtonian fluids might show a decrease in viscosity at shear rates $\dot{\gamma} \approx 5\times10^{4}~{\rm s^{-1}}$ presented by (Ram 1961) have been reexamined by (Dontula et al. 1999), who argue that the fall in viscosity of a glycerin–water solution at high shear rates may well be due to non-viscometric flow phenomena such as viscous heating or hydrodynamic instabilities, rather than arising from a true rate-dependent material property.

Flows through capillaries and slit channels have also been widely used to study rheology at high shear rates (Duda et al. 1988; Erickson et al. 2002; Kang et al. 2005; Laun 1983; Lodge and de Vargas 1983; Talbot 1974), and capillary viscometry can be an extremely simple and reliable technique for measuring shear viscosities. However, to minimize the importance of non-viscometric flow at the entrance and exit of the capillary, it is usual to use long capillaries that can lead to long residence times for fluid elements in the shearing flow. Furthermore, at high shear rates, an evolving thermal boundary layer resulting from viscous heating must be accounted for (Duda et al. 1988).

Beyond the realm of classical rheometry, custom microfabricated devices have also been used to measure the rheological response of complex fluids on length scales of 1–$10~\upmu{\rm m}$ (Clasen and McKinley 2004; Dhinojwala and Granick 1997; Mukhopadhyay and Granick 2001). With advances in micro- and nano-fabrication techniques (Marrian and Tennant 2003; Xia and Whitesides 1998) enabling the routine and reliable manufacture of flow devices with geometric features $<~100\ \upmu {\rm m}$, there has been a significant increase in studies exploiting microfluidic flow geometries for rheological characterization (Degré et al. 2006; Guillot et al. 2006; Hudson et al. 2004; Zimmerman et al. 2006), although none of these studies have addressed the response at high shear rates.

As the characteristic length scale of the geometry is decreased to $O(1~\upmu{\rm m})$, it becomes increasingly important to separate the bulk rheological response of a sample from effects due to the confining surfaces (McKenna 2006). The issue of wall slip has been shown to be significant, as very small length scales are probed, but nearly all experimental evidence suggests that slip, if present, occurs over length scales 0–50 nm (Granick et al. 2003; Lauga et al. 2007) and is therefore usually negligible for most homogeneous fluids on the micron scale. However, apparent wall slip, caused by depletion or adhesion layers at the walls, can be detected when testing heterogeneous liquids that have distinct microstructural elements even in flows with length scales $\sim10~\upmu\rm m$ (Clasen et al. 2006; Degré et al. 2006).

Studies of strongly inertial flows through channels with characteristic depths $O(100~\upmu{\rm m})$ are reviewed by Obot (2002) who finds that, despite some reports that the transition to turbulent flow in smooth-walled microchannels can occur at Reynolds numbers as low as Re≈200 (e.g., Peng et al. 1994), the experimental evidence so far does not support a significant decrease below the usual value for macroscale flows Re≤2,000.

In the present study, we compare and contrast the efficacy of two devices, a conventional rotational parallel-plate rheometer using sample gaps in the range 10–500 $\upmu {\rm m}$, and two microfluidic slit channels with depths of 24.6 and $50.7~\upmu {\rm m}$, to characterize shear-dependent viscosities at deformation rates up to 10⁵ s⁻¹. We show that the viscometric response at high rates for fluids ranging from constant viscosity mineral oils to strongly shear-thinning polymer solutions and shear-banding micellar solutions can all be determined using these techniques. We compare the results from each device to illustrate the experimental difficulties that can be encountered in each geometry and the level of reproducibility that can be obtained. We first present an overview of the fluids used in this work as well as the relevant analytical framework for the parallel-plates geometry and the microfluidic channels. We then investigate the use of conventional rotational rheometers to access high deformation rates and identify errors in zeroing the gap as a primary source of discrepancy between measured values of apparent viscosity and the true viscosity. Using Newtonian calibration oils, we then implement a calibration procedure originally presented by Connelly and Greener (1985) to evaluate the gap errors. We use the resulting gap corrections to obtain true shear rates and true viscosities from the apparent values provided by the rheometer software. In addition, we investigate two additional phenomena that can affect the viscous response at high shear rates; centrifugal stresses and viscous heating. We then proceed to investigate the viscometric response of Newtonian fluids using microfluidic slit channels equipped with flush-mounted pressure sensors. Subsequently we investigate the response in both types of device due to highly shear-thinning liquids. Finally, we compare and contrast the results from each device to illustrate the principal experimental difficulties associated with each geometry and the level of reproducibility that can be obtained. The material and instrumental parameters constraining the application of each device are then combined to produce operating space diagrams that can guide the effective use of each approach.

Experimental techniques

Test fluids

Liquids exhibiting a range of viscometric behaviors, from Newtonian to strongly shear-thinning, were investigated experimentally. Mineral oils S60 and N1000 supplied by Cannon Instrument (Pennsylvania, USA) and marketed as constant viscosity calibration fluids for viscometers as well as a Silicone oil (DMS T25) from Gelest (Pennsylvania, USA) were used to test the response of Newtonian fluids with nominally constant viscosity. Henceforth, these fluids will be referred to by the labels N1, N3, and N2, respectively, as indicated in Table 1. We also study a weakly shear-thinning solution of 0.1% poly(ethylene oxide) (PEO) in a mixture of 55% glycerol–44.9% distilled water (supplied by Sigma Aldrich, MO, USA). The PEO was polydisperse with viscosity—averaged molecular weight $M_{v}=2\times10^{6}$ g/mol, and the solution was prepared with gentle mixing and rolling to avoid degradation of the polymer. The aqueous PEO solution was then gently mixed with the glycerol for 5 min and left to stand for a further 24 h. More complex viscometric responses were explored using a strongly shear-thinning aqueous solution of 0.3% xanthan gum (Milas et al. 1990) supplied by CP Kelco (Georgia, USA) as well as a wormlike micellar solution of 3.2 wt%/0.76 wt% cetylpyridinium chloride/sodium salicylate in 0.56 wt% sodium chloride brine (Pipe et al., in preparation), which exhibits shear-banding behavior above a certain critical shear rate $\dot{\gamma} \approx 1\ {\rm s}^{-1}$.

Table 1 Overview of test fluids used in the present study and relevant physical parameters at 20°C

Parallel-plate apparatus and gap error correction

The rheological response of the Newtonian and non-Newtonian fluids were measured using parallel-plate fixtures on an advanced rheometric expansion system (ARES) strain controlled rheometer (TA Instruments, New Castle DE, USA) and an AR-G2 stress-controlled rheometer (TA Instruments). In Fig. 1a, we show the typical idealized arrangement assumed to exist with a parallel-plate geometry. The arrangement consists of two plates of radius R, separated by a constant and uniform gap height H. In the ARES, the top plate is fixed and attached to a torque transducer, while the bottom plate rotates with an imposed angular velocity Ω. In the AR-G2 the bottom plate is fixed and the top plate rotates under the action of an imposed torque ${\mathcal T}$. The radii of the plates on the ARES and AR-G2 devices were 50 and 40 mm, respectively. The gap separations used in our experiments span the range from 500 mm to $10~\upmu{\rm m}$ . In each case, the temperature control is provided through the Peltier plate system, which is accurate to within ±0.1°C. In all experiments, the fluid was carefully loaded between the two plates to avoid air bubbles and the excess fluid removed to ensure a smooth cylindrical interface.

Fig. 1

Schematic diagram of a conventional rotational rheometer; two plates of radius R, at gap height H. The top or the bottom plate rotates with an angular velocity Ω. a Ideal situation in a parallel-plate rheometer, the plates are perfectly parallel. b Sources of error during gap zeroing; a slight parallax (exaggerated in the figure) causes the plates to touch when not parallel, thus introducing a gap error of size ε. c Profile of the fluid sample when placed between nonparallel plates

To accurately measure the true viscosity in rotational rheometers at narrow gaps and high shear rates, precise alignment of the parallel plates is crucial (Connelly and Greener 1985; Kramer et al. 1987). At very small gaps ($H \le 10\ \upmu {\rm m}$), even the viscosity of air in the narrow gap between the plates while zeroing the gap has been noted as a possible source of error (Davies and Stokes 2005). In this paper, we use a calibration procedure based on the work of Connelly and Greener (Connelly and Greener 1985) to estimate the total effective error associated with ‘zeroing the gap’. Figure 1b shows the principal source of error in the alignment of plates associated with axial ‘run-out’ of the shaft and the resulting non-orthogonality between the plate and rotation axis. In a modern rotational rheometer using ‘auto-gap zeroing’ based on electrical conductivity or friction detection, the gap is considered to be ‘zeroed’ when any point of the top plate touches the bottom plate. A parallax in the alignment of the plates can cause the situation shown in Fig. 1b, in which the gap is considered to be zero, but in reality, different parts of the upper fixture are at different distances from the bottom plate. The maximum distance between the top fixture and the bottom plate sets a scale for the error incurred in zeroing the gap. This error is denoted the ‘gap error’ (ε). For large gap separations (H>>ε), this error is expected to be negligible but it is of increasing importance for small gaps. The final configuration with fluid filled between the plates is shown in Fig. 1c, where the gap is small enough (H ~ε) that the effect of plate misalignment is noticeable in the fluid sample confined within the plates. The analogous problem has been considered analytically for the cone-and-plate rheometer by Dudgeon and Wedgewood (1994) using a domain perturbation approach. Because the measured rheological quantities of interest such as shear rate and viscosity are dependent on the gap height, the gap error introduces a systematic error in measured quantities, in addition to the intrinsic instrument accuracy.

Torque, displacement, and normal force are the fundamental quantities measured by the rheometer. These raw measurements are then used to calculate stress, strain, shear rate, viscosity, and normal stress difference. To eliminate the systematic discrepancies associated with the gap error ε and to obtain accurate values of the calculated quantities from the measured variables, it is necessary to determine the error in gap heights via calibration, and the apparent values of measured quantities then have to be corrected for this gap error.

There are several published procedures for assessing the gap error for the parallel-plate geometry (Connelly and Greener 1985; Kramer et al. 1987). We follow this method with a slightly modified analysis, which is presented below. The procedure consists of single point tests of a Newtonian fluid of known viscosity under steady simple shear flow at different gaps. In the steady shear single point test on a strain controlled rheometer, for example, a shear rate and the duration for which the specified shear rate is to be applied is specified by the user, and the viscosity is measured after the specified equilibration time. We have used shear rates from 10 to $100\ {\rm s}^{-1}$ for different fluids. The specific shear rates used were chosen such that the measured torque was well above the minimum measurable torque. At the beginning of the experiment, the gap is zeroed to obtain a reference datum for all subsequent measured gap heights. The fluid is then loaded, and the upper plate is lowered to a specified gap height H and left undisturbed for 120 s to equilibrate at the specified temperature. An ‘apparent shear rate’ $\dot{\gamma}_{\rm a}$ and the duration of measurement are then specified in the rheometer software. The duration for which the shear rate is applied was 30 s. At the end of one single point measurement, an ‘apparent viscosity’ η _a is reported by the software. The fluid is then removed, a new sample is loaded, and the procedure is repeated at a different gap height H. The range of specified gap heights was decreased steadily from 500 to 10 µm.

For a given plate of radius R, specified gap height H, and angular velocity Ω, the apparent shear rate $\dot{\gamma}_{\rm a}$ at the rim of the rotating parallel-plate fixture is given by:

$$\dot{\gamma}_{\rm a} = \frac{\Omega\ R}{H}.$$

(1)

The apparent viscosity η _a reported by the software is computed from the definition:

$$\eta_{\rm a} = \frac{<\tau>}{\dot{\gamma}_{\rm a}},$$

(2)

where <τ> is the expected shear stress at the rim calculated from the measured torque, ${\mathcal T}$, assuming an ideal torsional shear flow, and is given by:

$$<\tau>\,\equiv \frac{ 2\,{\mathcal T}}{\pi\, R^{3}} = \eta_{\rm true}\, \dot{\gamma}_{\rm true},$$

(3)

where $\dot{\gamma}_{\rm true}$ and η _true are the true shear rate at the rim and the true viscosity, respectively. Combining Eqs. 1, 2, and 3, we have,

$$\eta_{\rm a} = \frac{\eta_{\rm true}\, \dot{\gamma}_{\rm true}}{{\Omega\, R/H}}.$$

(4)

As discussed previously, in practice, there is always some error in zeroing the gap between the plates. For errors of the form sketched in Fig. 1, the gap is always biased toward larger values than the commanded value. The simplest form of correction is to postulate (Connelly and Greener 1985) that H →(H+ε) so that the true shear rate at the rim is

$$\dot{\gamma}_{\rm true} = \frac{\Omega\, R}{\left(H + \epsilon \right)}.$$

(5)

Combining Eqs. 4 and 5, we can write (Kramer et al. 1987):

$$\frac{1}{\eta_{\rm a}} = \frac{1}{\eta_{\rm true}} \left\{ 1 + \frac{\epsilon}{H} \right\}.$$

(6)

Equation 6 suggests that, for a constant gap error ε, the reciprocal of the ‘apparent’ or reported viscosity 1/η _a should increase linearly with 1/H. A linear regression of the apparent viscosity η _a for various gap heights H provides us with two relevant quantities: the intercept of the line gives 1/η _true and the slope gives ε/η _true, enabling us to calculate the gap error ε. The analysis for a stress-controlled rheometer is analogous, with the same resulting relation between the true viscosity and the commanded gap. We utilize this analysis in conjunction with gap calibration experiments on the ARES and AR-G2 rheometers to obtain typical values of the gap errors for both instruments, when using parallel-plate geometries. We use the values of gap errors and Eqs. 1–6 to obtain true shear rates and true viscosities from the apparent values reported by the software.

For non-Newtonian fluids in a parallel-plate geometry, we note that the correction to the viscosity resulting from shear thinning leads to (Bird et al. 1987):

$$\eta_{\rm a} = \frac{(\mathcal{T}/2 \pi R^{3})}{\dot{\gamma}_{\rm a}}\left[ 3 + \frac{d \ln (\mathcal{T}/2 \pi R^{3})}{d \ln \dot{\gamma}_{\rm a}}\right].$$

(7)

Equation 7 gives the correction to viscosity due to inhomogeneity of the shear rate in a torsional flow between parallel plates. For Newtonian liquids, the logarithmic derivative term has a value of unity, thus simplifying to Eq. 2. However, for non-Newtonian fluids, the logarithmic gradient term can be substantially less than one, and this can change the value of measured viscosity by up to 25%. In the section entitled “Parallel-plates geometry: Newtonian fluids,” we present calibration experiments using Newtonian mineral oils, implement the gap error correction analysis outlined above, and compare the results with independent measurements obtained using the microfluidic viscometer described in the next section. We also present a similar analysis for non-Newtonian fluids, making use of Eq. 6 to determine gap errors and Eq. 7 to calculate rate-dependent corrections to measured values of the apparent viscosities.

When the fluid sample confined between two parallel plates is sheared, the free surface may deviate from a purely cylindrical shape. This perturbation of the free surface arises due to the additional viscous stresses that act at the interface and has been considered in detail by Olagunju (1994) for Newtonian and Oldroyd-B fluids. According to this analysis, for coaxial parallel plates of radii R and separation H, rotating with angular velocity Ω, the correction to the measured viscosity is of the form:

$$\eta_{\rm a} = \frac{2 \mathcal{T}}{\pi R^{3} \dot{\gamma}_{\rm a}}\left[1 + O\left(\frac{H^{4}}{R^{4}}\right)\right].$$

(8)

Equation 8 shows that the effect of any free surface perturbations on the measured viscosity is $O \left(\frac{H}{R}\right)^{4}$. For the configurations considered in the present paper, the aspect ratios for the plates of 25-mm radii range from H/R=0.04 for a 1-mm gap height to H/R=0.002 for a gap height of 50 µm. Edge effects on the measured viscosity are therefore negligibly small.

Microfluidic slit rheometer

The microchannels were fabricated by RheoSense (VROC^TM, San Ramon CA, USA) and are made from Pyrex mounted on a gold-coated silicon base containing three flush mounted microelectromechanical systems (MEMS) pressure sensors. Figure 2 indicates the fundamental configuration of the microchannels. Values of the channel depth d, slit width w, aspect ratio  = d/w, hydraulic diameter $d_{h}={4\times\textrm{area}}/{\textrm{circumference}}$, and volume $\mathcal{V}=L\times w\times d$, for the two devices used in this work, are given in Table 2. For both slits, the total channel length L from inlet to outlet is 12.65 mm, and the distance between the inlet and the first pressure sensor is 2.025 mm. This latter distance is equivalent to 42d _h and 20d _h for channels A and B, respectively, and, for all flows considered in the present study, is significantly larger than the entrance length needed for fully developed flow: For low Reynolds numbers Re=ρQ d _h / w d η, the entrance length is L _e =d _h (0.6/(1+0.035Re)+0.056Re), and for larger Reynolds numbers before the transition to turbulence at Re≈2,000, L _e =d _h (0.5+0.05Re) (Nguyen and Wereley 2002). The center-to-center distances between the first and second pressure sensors and between the second and third sensors are 2.5 and 3.8 mm, respectively, resulting in pressure measurements over a total streamwise distance L=6.3 mm. The MEMS pressure sensors, each measuring $800\times800~\upmu$m², are located along the centerline of the channel and were manufactured using similar techniques to those presented in Baek and Magda (2003). The maximum absolute measurable pressure P _max of the devices used in the present work are given in Table 2; clearly, the maximum available pressure drop across the sensor array ΔP _max is less than the value P _max in Table 2, as the latter value must also allow for additional pressure losses due to viscous stresses for the rest of the slit downstream of the final sensor before the flow exits the VROC channel at atmospheric pressure. The wet-etching process used to make the flow channels leads to eroded interior corners that are undercut with a radius of curvature similar to the channel depth; for channel aspect ratios  $\ll$ 1, this deviation from a rectangular cross-section is negligible. The cross sectional profile of the device was measured across the channel width using a mechanical surface profiler (Alpha Step IQ, KLA-Tencor, San Jose, CA, USA) accurate to ±50 nm. Away from the undercut regions at each sidewall, deviations in the channel height were found to be less than 1% of the total height, which is typical for this fabrication technique. During experiments, the temperature is monitored to an accuracy of ±0.25°C using a temperature sensor located below the silicon membrane at the center of the channel.

Fig. 2

Sketch of RheoSense VROC slit micro-rheometer; the dimensions are given in the text

Table 2 Properties of VROC microchannels used in the present study (quantities are defined in the text)

The volume flow rate Q in the channel was controlled using a PHD4400 Syringe Pump supplied by Harvard Apparatus (Holliston, MA, USA) in conjunction with Hamilton Gastight glass syringes (Reno, NV, USA) with volumes from 50 μl to 2.5 ml. Two types of tubing of varying modulus, perfluoro alkoxy alkane (PFA; E=0.035 GPa) and polyetheretherketone (PEEK; E=3.6 GPa), were used to connect the syringe to the VROC, and no reactions were observed between the tubing and the test fluids.

Before starting the experiments, the microchannel was filled with the test fluid by syringe and then left to relax so that all transients had decayed and steady-state baseline pressure readings were achieved with no flow. It should be noted that, for the strongly shear-thinning fluids, the time necessary for pressure transients associated with the filling process to decay can be O(1,000 s) because even small transient flow rates give rise to large viscous stresses as a result of the large zero shear viscosities of the fluids. At the beginning of each experiment, before starting the syringe pump, the pressure sensors are zeroed in the software. During experimental runs, the pressure measured by each of the sensors was monitored at 67 Hz using LabView software, and each flow rate was maintained for at least 60 s to ensure that a steady state was achieved. The total volume of test fluid necessary for experiments depends greatly on the viscosity and also the duration of the transient viscoelastic response. A Newtonian liquid with viscosity O(1 Pa s) requires as little as 100 μl to fill the system (syringe, tubing, and channel) and perform measurements over the accessible range of flow rates, whereas liquids with viscosity O(0.001 Pa s) need up to 15 ml as a result of the higher volumetric flow rates needed to achieve suitable shear rates and viscous pressure drops. We note that fluids exhibiting a non-Newtonian viscosity can necessitate more measurements and, thus, a greater sample volume to accurately capture the viscous response.

To find the equilibrium flow curve connecting the imposed flow rate and the measured pressure difference and, hence, evaluate the shear rate-dependent viscosity of a solution, the steady flow in the microchannel is considered to be a fully developed two-dimensional (2-D) flow, which is a good approximation for  $\ll$ 1. The pressure drop ΔP necessary to drive the flow a streamwise distance l ₀ is related to the wall shear stress τ _w by:

$$wd\,\Delta P = 2l_{0}(w+d)\tau_{\rm w}.$$

(9)

which represents a force balance between the pressure acting across the cross-sectional area of the channel and the viscous shear stresses present at the walls. For incompressible 2-D flow of a constant viscosity liquid in a rectangular channel, the wall shear rate $\dot{\gamma}_{\rm w}$ is a linear function of the flow rate Q:

$$\dot{\gamma}_{\rm w} = \frac{6Q}{wd^{2}}.$$

(10)

For incompressible fully developed 2-D flows of liquids with a rate-dependent viscosity, the calculation of $\dot{\gamma}_{\rm w}$ is more complex because the velocity profile is no longer parabolic. Using Eq. 10 thus results in an apparent shear rate $\dot{\gamma}_{\rm a}={6Q}/(wd^{2})$ analogous to Eq. 1 obtained from the rheometer. However, because the channel dimensions are known precisely and the flow is steady and two dimensional, the true wall shear rate can be found using the Weissenberg–Rabinowitsch–Mooney equation (e.g., Macosko 1994):

$$\dot{\gamma}_{\rm w, true} = \frac{\dot{\gamma}_{\rm a}}{3}\left[2 + \frac{{\rm d}(\ln\dot{\gamma}_{\rm a})}{{\rm d}(\ln\tau_{\rm w})}\right],$$

(11)

where τ _w is calculated from Eq. 9. The true viscosity function is then computed as

$$\eta(\dot{\gamma}_{\rm w, true}) \equiv \frac{\tau_{\rm w}}{\dot{\gamma}_{\rm w, true}} = \frac{w d\Delta P}{2l_{0}(w + d)}\ \frac{1}{\dot{\gamma}_{\rm w, true}}.$$

(12)

It should be noted that, although Eq. 11 is sometimes called a ‘correction’, it is an exact solution of the steady linear momentum equation for a generalized Newtonian fluid with a rate-dependent viscosity. To evaluate the derivative in Eq. 11, fitting the variation of $\ln\dot{\gamma}_{\rm a}{(\ln\tau_{\rm w})}$ with a first or second order polynomial is generally sufficient; for the wormlike micellar solution discussed below, it is necessary to fit polynomials piecewise over specific ranges to capture the extreme shear-thinning behavior observed at a critical shear rate.

Results and discussion

Parallel-plates geometry: Newtonian fluids

Gap error calibration

We first calibrate the rheometers to quantify the gap error. It was demonstrated above that the simplest gap correction model leads to a linear variation between 1/η _a and 1/H (Eq. 6). In Figs. 3 and 4, we show the gap calibration for ARES and AR-G2, respectively, for three Newtonian liquids N1, N2, and N3 (with properties given in Table 1). Each fluid was subjected to steady shear for 30 s, at gap heights varying from 10 to $400\ \upmu{\rm m}$, and the apparent viscosity η _a was calculated from the measured torque. Gap settings from 10 to $100\ \upmu{\rm m}$ were varied in steps of $10 \upmu{\rm m}$ and then from 100 to $500\ \upmu{\rm m}$ in steps of $100\ \upmu{\rm m}$. Each data point on the plot represents the steady-state value of apparent viscosity at a specific gap height. Temperatures T and apparent shear rates $\dot{\gamma}_{\rm a}$ used for each fluid in the data shown are given in Table 3. The solid symbols are experimental data points, and the dashed lines are fits to the data using Eq. 6, using 1/η _true and ε as fitting parameters.

Fig. 3

Gap error calibration data for three Newtonian fluids N1, N2, and N3 for the strain-controlled ARES rheometer. The plot shows the inverse of the apparent viscosity plotted against inverse of the gap height. The solid symbols are the experimental data, and the dashed lines show the fits of Eq. 6 to the data. The experimental parameters, and the results of the fit, the true viscosities η _true, and the gap errors ε are given in Table 3

Fig. 4

Gap error calibration data for three Newtonian fluids N1, N2, and N3 for the stress-controlled AR-G2 rheometer. The plot shows the inverse of the apparent viscosity plotted against inverse of the gap height. The solid symbols are the experimental data, and the dashed lines show the fits of Eq. 6 to the data. The experimental parameters, and the results of the fit, the true viscosities η _true, and the gap error ε are given in Table 3

Table 3 Results of gap error calibration for the three Newtonian fluids

It can be seen from the figures that all three liquids closely follow the simple linear relationship given in Eq. 6. The intercept of the straight line fit gives 1/η _true, and the slope gives ε/η _true. Combining the two, we calculate the measured true viscosity η _true and the size of the gap error ε. For example, for the fluid N3, fitting Eq. 6 to the data for ARES, we find:

$$\begin{array}{l}{\rm intercept:}~\frac{1}{\eta_{\rm true}} = 0.369 \pm 0.008\ {\rm Pa}^{-1}{\rm s}^{-1}\\ {\rm gradient\ :}~\frac{\epsilon}{\eta_{\rm true}} = 8.93 \pm 0.22\ {\rm m}\,{\rm Pa}^{-1}{\rm s}^{-1} \end{array}$$

which gives η _true=2.704±0.060 Pa s, and $\epsilon = 24 \pm 1~\upmu{\rm m}$, where we have propagated uncertainties in both the slope and the intercept to obtain uncertainties in the true viscosity and the gap error. The gap error obtained in this manner is a quantitative measure of the errors introduced in zeroing the gap between two plates. The results are tabulated in Table 3, where the manufacturer’s stated viscosity, η ₀, is compared with that found from the intercept of the straight line fit to the data using Eq. 6. Also shown are the gap errors obtained for each case.

For the two fluids N2 and N3, the discrepancy in the stated viscosities η ₀ and measured true viscosities η _true are 8% and 6%, respectively, using the ARES, and 6% and 1% on AR-G2, respectively. In addition, the effective gap errors obtained on both rheometers have values between 25–$30\ \upmu {\rm m}$. For the lowest viscosity liquid N1, the discrepancy between the stated viscosity and measured true viscosity is the largest, 21% on the ARES and 18% on the AR-G2. The gap errors obtained are also the largest, $54 \pm1~\upmu$m on ARES and $49 \pm 2 \upmu$m on AR-G2. This indicates that, for low viscosity fluids, there are additional sources of errors possibly due to secondary flows induced between the fixtures, which cannot be captured by a simple analysis of the form given above. The discrepancy between the value η _true determined experimentally and the nominal reported value η ₀ of the calibration oils provides an estimate of the accuracy of the measurements after the gap correction has been applied to the apparent viscosity η _a.

The principal contribution to this effective gap error is the intrinsic misalignment between the rotating fixture and the stationary lower plate or base. We measured this gap error directly in the absence of any fluid using plastic shim stock of precise thicknesses. The fixture spacing was set to a nominally zero gap using the rheometer software, and strips of shim stock of increasing thickness (13, 19, and $25\, \upmu{\rm m}$) were then inserted in the clearance between the top and the bottom plates to determine the residual gap between the plates. For the ARES rheometer, the physical gap clearance was determined to be at least $19\, \upmu{\rm m}$, and for the AR-G2 rheometer, the corresponding gap error was at least $13\, \upmu{\rm m}$.

Another important source of potential error is the concentricity of the parallel plates. We addressed this issue by measuring the eccentricity of the rotating bottom plate and comparing it to the eccentricity of the top plate using a swivel-head dial indicator with a resolution of $2.5\, \upmu{\rm m}$. The two plates were determined to be concentric to within $17~\upmu {\rm m}$, which is well within the manufacturer’s stated tolerances for the motor alignment.

The apparent viscosity reported by the rheometer software is a function of both the commanded gap height H and the magnitude of the gap error ε intrinsic to the instrument and is thus systematically in error. On rearranging Eq. 6, we find that the relative error in η _a with respect to its stated value η _true is given by:

$$\frac{\eta_{\rm true} - \eta_{\rm a}}{\eta_{\rm a}} = \frac{\epsilon}{H}$$

(13)

Table 4 shows the percentage error in the true viscosity and the measured or apparent viscosity at different gap settings. It can be seen from the table that the relative percent errors increase significantly as one goes to smaller gaps; for example, assuming a representative value for the gap error to be $30\,\upmu{\rm m}$, at 2-mm gap height, the apparent viscosity is systematically in error by 1.5%, but at 30-μm gap height, the discrepancy is 100%. Although the fractional error between measured values of the apparent viscosity and the true viscosity can be very large at small gaps, the gap-corrected values of true viscosity using Eq. 6 fall within 10% of the stated viscosity for moderate viscosity fluids.

Table 4 Relative percent error in apparent viscosity and true viscosity at different gap heights H, assuming a representative gap error $\epsilon = 30\, \upmu {\rm m}$

Ultimately, the gap error determined using this approach is a composite property of the instrument and the geometry used. Using the procedures outlined above, we can estimate the size of the gap error for each instrument and the geometric fixture used. These errors in the gap setting are, of course, not limited to Newtonian fluids, as we will demonstrate in later sections, in which we apply the same procedure for non-Newtonian fluids. The highest shear rate achievable in the instrument, $\dot{\gamma}_{\max} \sim \Omega_{\max} R/H$, is inversely dependent to the gap height. In any experiment, there is thus a trade-off between minimizing the errors due to imperfect zeroing of the gap and achieving as high a shear rate as possible. Therefore, at high shear rates and small gaps, corrections due to the systematic gap error become essential in obtaining accurate viscometric measurements of both Newtonian and complex fluids as we now proceed to demonstrate.

High shear rate measurements

In this section, we describe the behavior of Newtonian and weakly shear-thinning fluids at very high shear rates. Even for Newtonian fluids, the issue of ‘apparent shear-thinning behavior’ at high shear rates is important (Dontula et al. 1999). Do some ‘Newtonian’ liquids become shear thinning at high enough shear rates, or is the apparent shear-thinning behavior explained by some other mechanism such as viscous heating? For the non-Newtonian case, particularly, for wormlike micellar solutions, the high shear rate behavior of the solution beyond the plateau in the flow curve remains unclear (Radulescu et al. 2003).

We begin by describing results for Newtonian fluids. The three Newtonian fluids N1, N2, and N3 were subjected to a steady shear ramp test on the ARES rheometer using a plate–plate geometry with a plate diameter of 50 mm. The fluids were subjected to shear rates from 1 to $60,\!000\ {\rm s}^{-1}$, in logarithmic steps with five points per decade. Each shear step was maintained for 20 s. The commanded gap height was set to $50~\upmu{\rm m}$, and the temperature at the lower plate was held fixed at 25°C.

Figure 5 shows the plot of true viscosity with shear rate for the three nominally-Newtonian fluids. The true viscosity and the true shear rate were obtained from the apparent values reported by the software, by correcting for the gap error, as described above. The gap error ε for the ARES rheometer was found as described in “Gap error calibration.” Once the gap error was known, Eq. 5 was used to calculate true shear rate and the gap-adjusted true viscosity using Eq. 6 in the form

$$\eta_{\rm true} = \eta_{\rm a} \Biggl( \frac{H + \epsilon}{H}\Biggr)$$

(14)

The solid symbols in the plot show the experimental data points. The two dashed lines running diagonally across the plot represent the minimum and the maximum limiting values of the measurable torque. The minimum and maximum torque values, for the force transducer used, are ${\mathcal T}_{\rm min} = 1.96 \times 10^{-4}\ {\rm N\ m}$ and ${\mathcal T}_{\rm max} = 0.196\ {\rm N\ m}$, respectively. These torque limits correspond to minimum and maximum stress values $\tau_{\min} = 7.989\ {\rm Pa}$ and $\tau_{\max} = 7,\!989\ {\rm Pa}$, respectively, for the 50-mm diameter plate (Eq. 3). Having determined the minimum and maximum shear stresses, the range of viscosities and shear rates accessible are related by the expressions:

$$\eta_{\rm min} = \frac{\tau_{\rm min}}{\dot{\gamma}_{\rm true}}$$

(15)

$$\eta_{\rm max} = \frac{\tau_{\rm max}}{\dot{\gamma}_{\rm true}}$$

(16)

where the true shear rate is given by incorporating the gap error via Eq. 5.

Fig. 5

High shear rate behavior of Newtonian fluids N1, N2, and N3 in the ARES rheometer, using a 50-mm diameter parallel-plate geometry at 25°C. The solid symbols are the gap-corrected or ‘true’ experimental data points, and the dashed lines show the limiting curves of slope −1 given by Eq. 16, based on the minimum and the maximum measurable torque values

The viscosity of each Newtonian fluid is constant for more than three decades in shear rate, up to $\dot{\gamma} \approx 10^{4}~{\rm s}^{-1}$. For the fluid N2 with viscosity η ₀=0.485 Pa s, there is a visible drop in viscosity beyond shear rates of 20,000 s ⁻¹. We investigate this case of apparent shear thinning in further detail below.

At very high shear rates, there are several additional factors such as inertial effects and viscous heating that impact rheometric measurements (Bird et al. 1987; Macosko 1994). At high rotation rates, centrifugal stresses may become sufficiently large to overcome the surface tension stresses that hold the liquid between the plates resulting in liquid being thrown out of the gap; a phenomenon termed euphemistically the ‘radial migration effect’ (Connelly and Greener 1985). Once the confined fluid is partially ejected, the subsequent measurements are made with less fluid within the plates, which results in a drop in measured torque and, hence, in the viscosity. In particular, for a fluid with density ρ and surface tension σ in a parallel-plate geometry with plate radius R, rotating with angular velocity Ω, and gap height H, the centrifugal stresses overcome the surface tension stresses when (Connelly and Greener 1985; Tanner and Keentok 1983),

$$\frac{3}{20}\ \rho\ (\Omega^{2} R{^2}) > \frac{\sigma}{H}.$$

(17)

The critical apparent shear rate at which the fluid begins to migrate outward is given by rearranging Eq. 17:

$$\dot{\gamma}_{\rm app, c} = \Biggl(\frac{\Omega R}{H}\Biggr)_{c} = \sqrt{\frac{20 \sigma}{3 \rho H^{3}}}.$$

(18)

In addition, incorporating the gap error correction, we get:

$$\dot{\gamma}_{\rm c} = \sqrt{\frac{20 \sigma}{3 \rho (H + \epsilon)^{3}}}.$$

(19)

Equation 19 shows that the critical shear rate for radial migration to occur decreases as gap height increases ($\dot{\gamma}_{\rm c} \sim {\rm H}^{-3/2}$). Thus, the radial migration effect can be reduced by going to very small gap heights. Furthermore, it is clear that a gap error results in a critical shear rate that is lower than the predicted critical shear rate without correcting for the gap errors. For the fluid N2 (η ₀=0.485 Pa s), the estimated critical shear rates at which the radial migration occurs at different gap heights (assuming a gap error of $30\ \upmu {\rm m}$) are found to be $\dot{\gamma}_{\rm c} = 8,\!096\ {\rm s}^{-1}$ for $H = 100\ \upmu {\rm m}$, $\dot{\gamma}_{\rm c} = 16,\!770\ {\rm s}^{-1}$ for $H = 50\ \upmu {\rm m}$, and $\dot{\gamma}_{\rm c} = 29,\!419\ {\rm s}^{-1}$ for $H = 25\ \upmu {\rm m}$. It is noteworthy that these critical rates are within the range of shear rates imposed in our experiments and of the same order as the shear rates at which the viscosity shows a noticeable drop.

Many experimental and theoretical studies have shown that viscous heating can also significantly affect the flow properties of Newtonian fluids (Bird and Turian 1962; Connelly and Greener 1985; Dontula et al. 1999; Kramer et al. 1987; Olagunju et al. 2002; Rothstein and McKinley 2001). In a previous study (Ram 1961), a drop in viscosity of water/glycerol solutions was reported and described as a shear-thinning transition in an apparent Newtonian fluid at high shear rates. We reexamine this issue with fluid N2, which shows a similar drop in viscosity at high shear rates. In addition to the radial migration effect discussed above, it is possible that, at very high shear rates, there is sufficient viscous heating to lower the viscosity of some fluids.

The effects of viscous heating can be characterized by the Nahme number, which is a dimensionless ratio of the time scales for thermal diffusion to viscous heating:

$${Na} = \frac{\eta_0 \beta H^2 \dot{\gamma}_{\rm true}^{2}}{ k T},$$

(20)

where η ₀ is the zero-shear viscosity, H is the true gap separation, $\dot{\gamma}_{\rm true}$ is the true shear rate, k is the thermal conductivity, T is the temperature, and β is the logarithmic derivative of viscosity with temperature or “thermal sensitivity” and is given by:

$$\beta = \frac{T}{\eta_0} \Biggl| \frac{d\eta}{dT}\Biggr|_{T=T_0}.$$

(21)

At low shear rates, the Nahme number is very small (Na ~10⁻⁹). However, as the shear rate increases, the Nahme number and, hence, the magnitude of viscous heating increase quadratically with shear rate and the gap height. This means that viscous heating effects become significant at lower shear rates, as the gap size increases. Therefore, repeating the steady shear rate step test with different gap separations should result in noticeable differences in the viscosity/shear rate curve if viscous heating is important. As fluid N2 shows the most noticeable decrease in viscosity at high shear rates, we perform additional tests using this fluid at gap heights of 25, 50, and $100\ \upmu {\rm m}$ and rotation rates corresponding to shear rates 1–$60,\!000\ {\rm s}^{-1}$. This range in shear rate was spanned in logarithmically spaced steps, with five points per decade, and each shear rate was maintained for a duration of 30 s. Table 5 shows the critical shear rates for the onset of radial migration effect as well as the minimum and maximum Nahme numbers for fluid N2 at three different gap heights: The use of small gaps is clearly advantageous in trying to reduce the Nahme number experienced at high shear rates and thus minimize the effects of viscous heating.

Table 5 Critical shear rates for the onset of radial migration effect and minimum and maximum Nahme numbers at different gap heights H for the fluid N2

Figure 6 shows the data for the apparent viscosity versus shear rate for N2; for convenience, apparent viscosities are plotted here instead of the corrected or true viscosities, as these would collapse vertically onto each other at low rates and obscure the onset of viscous heating. The data clearly show that the onset of apparent shear-thinning occurs at different shear rates for different gap sizes, as indicated by the dashed vertical lines. Quantitatively, the shear rates at which the apparent shear-thinning begins, for $100\ \upmu {\rm m}$, and 50-$\upmu$m gap sizes are $\dot{\gamma} \approx 10^4~\rm s^{-1}$ and $\dot{\gamma} \approx 2 \times 10^{4}~\rm s^{-1}$, respectively. At the smallest gap of $25\ \upmu {\rm m}$, viscous heating effects are negligible up to the maximum shear rate $\dot{\gamma} \approx 3.5 \times 10^4~{\rm s}^{-1}$. This is consistent with the argument based on the scaling ${Na} \sim (H \dot{\gamma})^{2}$: If the gap height is halved, the shear rate necessary for the fluid to experience the same Nahme number doubles.

Fig. 6

High shear behavior of Newtonian fluid N2, at three different gap sizes, $H = 25\ \upmu {\rm m}$, $H = 50\ \upmu {\rm m}$, and $H = 100\ \upmu {\rm m}$. The filled symbols are the experimental data from steady shear step tests, and the lines are the a priori predictions of the modified Bird–Turian analysis (Eq. 22). The vertical dashed lines show the shear rates for the onset of apparent shear-thinning. The minimum and the maximum Nahme numbers Na _min and Na _max corresponding to the minimum and maximum shear rates are given in Table 5

The first effects of viscous heating in the cone-and-plate geometry have been considered asymptotically by Bird and Turian (Bird et al. 1987; Bird and Turian 1962), and the analysis has been extended more recently by Olagunju (2003) for parallel-plate fixtures of finite radius R with walls held at a constant temperature. The measured torque on the rotating plate is given by:

$${\mathcal T} = \frac{\pi\ {R}^{3}\ \dot{\gamma}_{a}\ \eta_0}{2}\left[1 + A\,{Na} +{O}({Na}^{2}) \right],$$

(22)

where $\dot{\gamma}_{\rm a} = \Omega R/ H$ and A=−1/18+0.104 (H/R)+O[(H/R)²]. Detailed computational analysis shows that this asymptotic result is accurate for a wide range of aspect ratios up to Na≈1 (Zhang and Olagunju 2005). By combining Eqs. 20–22, we can calculate the shear stress and apparent viscosity at each shear rate. In Fig. 6, we show the predictions of the asymptotic theory (solid lines) and the data. The general trends are similar; however, the decrease in viscosity observed experimentally is larger than the asymptotic theory predicts at very high shear rates. The reasons for this may include several factors, such as edge effects, the thermal variation of the thermal sensitivity β(T), or most importantly the radial migration effect discussed above. For gap heights of 50 and $100\ \upmu {\rm m}$, beyond a shear rate of $\dot{\gamma} \sim 10^{4}\ {\rm s}^{-1}$, both viscous heating and radial migration contribute synergistically to the drop in viscosity.

To confirm the presence of viscous heating and isolate its effects from those of radial migration effect, we perform thixotropic loop tests on fluid N2, at a gap height of $50\ \upmu {\rm m}$ following the protocol of Connelly and Greener (1985). In this test, fluid N2 was subjected to a continuous shear ramp from 1,000 to $20,\!000\ {\rm s}^{-1}$ and then brought back down to $1,\!000\ {\rm s}^{-1}$ in the same manner. The duration of the thixotropic loop, t _L , was varied from 4 to 40 s. The maximum shear rate was chosen using Eq. 18 and Table 5 such that no significant radial migration occurs. In a thixotropic loop test, viscous heating is manifested in the form of hysteresis in the stress–strain rate curve. If the area between the ‘up’ and ‘down’ sweeps increases with loop time, it signifies greater viscous heating due to a longer duration of shearing. In Fig. 7, stress—shear rate data for four different loop times, t _L = 4, 10, 20, and 40 s, are shown. For clarity, the stress values for t _L = 10 s, t _L = 20 s, and t _L = 40 s are shifted vertically by 500, 1,000, and 2,000 Pa, respectively. In agreement with Connelly and Greener (1985), we observe that, as the loop time is reduced, the hysteresis decreases. For the smallest loop time of 4 s, viscous heating is negligible, even for a maximum imposed shear rate $\dot{\gamma} = 20,\!000\ {\rm s}^{-1}$.

Fig. 7

Thixotropic loops showing variation of stress with shear rate at four different loop times, t _L =4 s, t _L =10 s, t _L =20 s, and t _L =40 s. The latter three curves are shifted vertically by 500, 1,000, and 2,000 Pa for clarity of presentation only

The relevant timescales in these thixotropic loop experiments are the thermal timescale, the viscous heating timescale, and the loop time. The thermal diffusion timescale $t_{\rm{diff}} = H^2/\cal{D}_{T}$ (based on the gap height H and the thermal diffusivity of the fluid ${\cal{D}}_{T} =k/ \rho C_{p}$) is a measure of the time over which thermal energy diffuses to the boundaries. The viscous heating timescale is a measure of the rate at which the fluid rheology changes due to viscous heating and is given by $t_{\rm{visc}} = \rho C_p T_0/(\beta \eta_0 \dot{\gamma}) = t_{\rm{diff}}/{Na}$. This timescale decreases rapidly with increasing shear rate; hence, the need to perform rapid thixotropic loops in which the total time that the sample is held at very high shear rates is minimized. The question then arises as to whether the test sample is in local thermal equilibrium. A thixotropic loop enables us to probe the steady shear viscosity of a fluid provided $t_{{{\text{diff}}}} \ll t_{L}$. In our case, for fluid N2 with thermal diffusivity ${\cal D}_{T} = 1.1\times 10^{-7}\,{\rm m^{2}\ s^{-1}}$, at a gap of $50\, \upmu {\rm m}$, between plates of radii R=25 mm, the thermal diffusion timescale is t _diff=23 ms. For a continuous shear rate ramp, the ratio of the thermal diffusion time and the smallest loop time (t _L =4 s) is $t_{\rm diff}/t_{L} = \rho C_p H^{2}/ k t_{L} = 0.0058$. Thus the flow is quasi-steady at every intermediate shear rate with a fully developed temperature profile across the gap.

To conclude, we have shown that modern rotational rheometers are capable of measuring accurate viscometric properties at high shear rates up to $\dot{\gamma} \sim 5 \times 10^{4}\ {\rm s}^{-1}$ provided the gap heights are kept small. Using the gap correction procedure outlined in “Parallel-plate apparatus and gap error correction,” accurate measurements of viscosity can be obtained, at least for constant viscosity Newtonian fluids. We have also shown that the effects of viscous heating and centrifugal stresses can both be appreciable at high shear rates and can manifest themselves as apparent shear-thinning behavior for nominally Newtonian fluids. In view of this, we now turn to the use of microchannel devices, which are not susceptible to the effects of either viscous heating or centrifugal stresses.

Rectilinear flow of Newtonian fluids in microchannels

Fundamentally, the VROC microchannel device allows us to measure the pressure P(x,t) at various streamwise locations along the center of a straight channel for an imposed flow rate Q. The steady-state pressure as a function of streamwise location x for fluid N1 is shown in Fig. 8 at three different flow rates $10 < Q \le 50\ \upmu {\rm l\,min}^{-1}$. The pressure readings are sampled at $67\ {\rm Hz}$ and averaged for more than 10 s to show the steady-state pressure for each flow rate. Fitting a first order polynomial shows that, as one expects, for a given flow rate, the streamwise pressure gradient dP/dx is constant for a straight channel of uniform cross-section.

Fig. 8

Fluid S60 in channel B, steady state pressure P(x) measured at each pressure sensor for 10 s at three flow rates Q. The lines are a least-squares fit of a first order polynomial

The transient pressure response to a step change in flow rate is illustrated clearly in Fig. 9: In these tests, the fluid is initially at rest, and then, the syringe pump is started impulsively at time t=0 s; thereafter, the commanded flow rate is reduced every 60 s. The pressure is sampled at 67 Hz, and the data output from the sensor software is treated with a moving average filter applied over 25 consecutive samples. The pressure drop ΔP over the array of pressure sensors as a function of time is shown for two different types of tubing, PFA (elastic modulus E≈0.035 GPa) and PEEK (E≈3.6 GPa) tubing. The residual noise of the pressure sensor is approximately ± 0.25% full scale of the sensor, corresponding to ±150 Pa for channel B, and limiting the lowest practical working pressure drop to approximately 300 Pa (by averaging over a large number of samples). However, much greater noise in the measured pressure can be caused by periodic fluctuations in the flow rate from the syringe pump: At $50~\upmu{\rm l\, min}^{-1}$, the error is ±5% for the two sets of data with no bubble in the syringe. Fluctuations in flow rate can be damped significantly by introducing a compliant air bubble into the syringe, and, in this case, the error is ±1%. Hence, it is important to average over a large number of samples to account for periodicity in the flow rate from the syringe pump.

Fig. 9

Fluid S60 in channel B, pressure drop ΔP as a function of time at several flow rates Q

The transient response in the pressure difference to a step change of Q is clear, and it is important to wait for the signal to attain a steady state to calculate the equilibrium values of the pressure difference ΔP. This transient response is highly dependent on any air bubbles in the system as well as the viscosity of the fluid. For fluid N1 shown in Fig. 9, the transient pressure drop with an air bubble present is well fitted by a decaying exponential with a time constant of 3 s, while with no bubbles in the system, the time constant is <1 s. Therefore, to avoid long transient flows, it is important to ensure that the syringe and tubing are free of bubbles. This is critical for the shear-thinning viscoelastic liquids discussed in the following section where the time needed to reach a steady state may be O(1,000 s) depending on the flow rate.

In Fig. 10, we show that the pressure difference ΔP for the three constant viscosity liquids N1, N2, and N3 is a linear function of flow rate Q passing through the origin as expected. At the highest flow rate shown in Fig. 10, $Q= 80~\upmu$l/min, the Reynolds number based on the hydraulic diameter of the channel is ${Re} = \rho Qd_{h}/(\eta wd) = 8\times10^{-3}$, indicating that the flow is dominated by viscous stresses and far from the onset of any inertial effects or turbulence. The Nahme number (Eq. 20) describes the importance of viscous heating, and using the properties listed in Fig. 1, we find for all flow rates Na<10⁻⁴ for fluids N1–3 indicating that viscous heating is insignificant even at the largest flow rates used in this work. Thus, we consider Eqs. 9 and 10 for the wall shear rate and wall shear stress to provide an accurate description of the flow curve.

Fig. 10

Pressure drop ΔP as a function of flow rate Q in VROC channel B for Newtonian fluids N1, N2, and N3; experimental data (symbols) and linear fit (solid line)

Viscosity data from VROC channel B for four constant viscosity fluids are shown in Fig. 11. The scatter in the measured value of $\eta(\dot{\gamma})$ is less than 5%, and the measured viscosity is independent of shear rate as expected. As we show in Table 1, the data are in good agreement with the gap-corrected measurements from the parallel-plate fixture using a standard rheometer. The upper and lower sensing limits of the VROC channel B are indicated by the dashed lines in Fig. 11: In the parameter space of viscosity and shear rate, a specified pressure drop ΔP _min corresponds to a fixed minimum wall shear stress $(\eta\dot{\gamma})_{\min} = \tau_{\min} = wd \Delta P_{\min} /(2L(w+d))$ from Eq. 9. This corresponds to a slope of −1 on a log–log plot of viscosity versus shear rate. A similar analysis of course also applies for the maximum pressure drop, and thus, for fluids with a lower viscosity, higher shear rates can be attained.

Fig. 11

Measured viscosity as a function of shear rate for the three viscous Newtonian calibration fluids N1, N2, N3, and water. Solid symbols are for data from the VROC microchannel obtained using channel A, and hollow symbols are for data obtained using plate–plate geometry on ARES. The dashed lines show the minimum and maximum operating pressures for the microchannel

On the same figure, we show data for water; here, we can clearly see the advantage the VROC offers for low viscosity fluids, allowing shear rates $10^{3} \le \dot{\gamma} \le10^{5}\ {\rm s}^{-1}$ to be obtained for shear viscosities η~1 mPa s. For these measurements, the Reynolds number is in the range 1<Re<100, which is still significantly below the onset of turbulent flow in a channel Re=2,000. At the maximum shear rate of $\dot{\gamma} = 8\times10^4~{\rm s^{-1}}$, the Nahme number Na<10⁻³ and viscous heating are negligible even at these high shear rates.

We now proceed to investigate the viscosity of a weakly shear-thinning PEO–water–glycerol solution. In Fig. 12, we show data for the viscosity as a function of shear rate obtained using VROC channel A. Complementary measurements with a 60-mm diameter cone-and-plate fixture on an AR-G2 shear rheometer show that the PEO solution has a zero shear viscosity η ₀=0.015 Pa s at 22.5°C. With the cone-and-plate fixture, shear rates of up to 1,000 s⁻¹ can be attained, and the fluid exhibits slight shear thinning for $\dot{\gamma}\gtrsim100~{\rm s}^{-1}$. Agreement between the viscosity measured using the cone-and-plate fixture and the microchannel is excellent, and using the VROC, we are able to extend the shear rate range over which we can probe the viscous response to $\dot{\gamma}=10,\!000~{\rm s^{-1}}$. We also indicate by the error bars the magnitude of the fluctuations in the pressure signal. At low flow rates, the viscous stresses fall below the stated resolution of the VROC, and there is considerable noise in the data; for example, at ΔP _min =55 Pa, we measure τ _min =0.12 ±0.11 Pa.

Fig. 12

Viscosity as a function of shear rate for a shear-thinning PEO solution (55% glycerol, 44.9% water, and 0.1% PEO). Data from measurements performed using VROC channel A

The PEO solution is only weakly shear thinning, and in Eq. 11, the derivative term ${\rm d}(\ln\dot{\gamma}_{\rm a})/{\rm d}(\ln\tau_{\rm w})=1.06$, resulting in only 2% difference between $\dot{\gamma}_{\rm a}$ and $\dot{\gamma}_{\rm w}$. This error is of the same order as other experimental errors that we would expect due to fluctuations in temperature, imposed flow rate and the precision and accuracy of the pressure transducers, and it is sufficiently accurate to process the measurements for such a weakly shear-thinning fluid in the same way for a Newtonian liquid.

In summary, we have seen how streamwise pressure measurements along a straight microfluidic channel allow us to calculate the viscosity for several Newtonian liquids and weakly shear-thinning liquids over a wide range of shear rates. The measurements agree extremely well with data from a narrow gap parallel-plate geometry and have the additional advantage that no fluid is ejected from the device due to large rotation rates, and the flow remains in a low Reynolds number and low Nahme number regime.

Measurements of fluids with a rate-dependent viscosity using parallel plates and microchannels

In the two sections above, we have demonstrated two complementary techniques for accurately measuring the shear viscosities of Newtonian liquids at large shear rates by reducing the characteristic length scale of the device to l ~ 30–50$\ \upmu{\rm m}$. For weakly shear-thinning fluids, the small rate-dependent change in viscosity allows the same analysis as for a constant viscosity liquid, to within experimental error. We now extend the analysis to complex liquids with a strongly rate-dependent viscosity. To investigate the possibilities and limitations of the two techniques, we present results for an aqueous xanthan gum and a CPyCl/NaSal micellar solution, which are both known a priori to have shear viscosities that change by several orders of magnitude over certain shear rate ranges. The xanthan gum solution is a strongly shear-thinning liquid (Milas et al. 1990), while the micellar solution shows a yield-like behavior at a critical shear stress that is associated with the onset of shear-banding flow (Rehage and Hoffmann 1991; Pipe et al., in preparation).

We first consider gap correction of measurements in a parallel-plate fixture with narrow gaps from 500 to 10 µm. The method for determining the gap error and the resulting analysis to obtain true shear rates and viscosities remain the same, as described in “Parallel-plate apparatus and gap error correction.” In Fig. 13, we show gap error calibration using aqueous xanthan gum and for the CPyCl/NaSal micellar solution using the AR-G2. Both fluids were subjected to steady shear for a duration of 60 s, at constant apparent shear rates of $\dot{\gamma}_{\rm a} = 1\ {\rm s}^{-1}$ and $\dot{\gamma}_{\rm a} = 0.006\ {\rm s}^{-1}$ for CPyCl/NaSal micellar solution and xanthan gum, respectively. The shear rates were chosen such that the viscometric response is expected to remain in the zero shear rate plateau, even though the actual shear rates in the sample for small gaps may be substantially larger than the nominal values (see Table 4). The solid symbols in the plot are the experimental data, and the solid lines are linear regression fits to the data using Eq. 14, with true viscosity 1/η _true and size of the gap error ε as fitting parameters. The results of the fitting show that, for xanthan gum, η _true=17.7 ±0.6 Pa s, and $\epsilon = 31 \pm 1\ \upmu {\rm m}$. For the micellar solution, η _true=19.1 ±0.4 Pa s, and $\epsilon = 53 \pm 1\ \upmu {\rm m}$. These calculated values of the viscosity at low shear rates are slightly higher but in good agreement with the zero shear rate viscosities given in Table 1. Although the analysis presented in “Parallel-plate apparatus and gap error correction” is only valid for Newtonian fluids, it also appears to apply, at least empirically, to the data in Fig. 13. However, interpretation of the gap error correction is complicated by the fact that it is now fluid dependent. The value of the gap error obtained with CPyCl/NaSal is much larger than the value obtained with xanthan gum solution, which is similar to that obtained for Newtonian fluids N2 and N3. Furthermore, the ‘gap-correction’ is found to be dependent on the imposed shear rate $\dot{\gamma}_{\rm a}$ when higher deformation rates beyond values corresponding to the zero shear rate plateau are employed.

Fig. 13

Gap error calibration data for two non-Newtonian fluids (CpyCl/NASal and xanthan gum) on the AR-G2 rheometer. The gap separations range from 10 to $500\ \upmu {\rm m}$. For CPyCl/NaSal the apparent shear rate was held constant at $\dot{\gamma}_{\rm a} = 1\ {\rm s}^{-1}$, and for xanthan gum, $\dot{\gamma}_{\rm a} = 0.006\ {\rm s}^{-1}$. The lines are fits of Eq. 6 to the data, and the errors in the least-squares linear fit are reported in the text

In particular, for the aqueous xanthan gum solution, the apparent shear rate chosen was selected to be at the edge of the constant viscosity plateau; therefore, the ‘true viscosity’ obtained may not correspond to the zero shear rate viscosity. The range of applicable shear rates in the case of xanthan gum is limited by the minimum measurable torque on AR-G2, which, in practice, is ${\mathcal T}_{min} = 1.0\,\upmu{\rm Nm}$, and the true shear rate at which shear-thinning behavior begins, which is at $\dot{\gamma}_{\rm true} = 0.1\,{\rm s}^{-1}$. If the gap-corrected true shear rate is greater than the shear rate at which shear-thinning occurs, the analysis for gap correction needs further modification. Instead of the simple linear model for the gap error correction, corrections to the calculated viscosity due to inhomogeneity of shear rate must also be included. Thus, Eq. 6 should be modified to include variations in the shear rate given by Eq. 7. Details of the resulting nonlinear modification to the simple linear model of gap error correction are given in the Appendix. For the shear rates used here (close to the zero shear rate plateau), the additional correction is less than 5%, which is within the precision of the measured data. We, therefore, retain the simpler linear analysis of Eq. 6.

In Fig. 14, the measured pressure drop ΔP in the microfluidic channel shown as a function of flow rate Q for the CPyCl/ NaSal and xanthan gum solutions. For both fluids, d(ln ΔP)/d(ln Q)≠1, indicating that the viscometric response is non-Newtonian over the range of flow rates studied. As with a constant viscosity liquid, we can still use conservation of linear momentum (Eq. 9) to relate the measured pressure drop to the wall shear stress τ _w, but to find the true shear rate at the wall $(\dot{\gamma}_{\rm w})$, we use Eqs. 10 and 11. To determine the gradient term in Eq. 11, the values of $\ln\dot{\gamma}_{\rm a} = g(Q)$ evaluated from Eq. 10 are plotted as a function of ln τ _w as shown in Fig. 15. Polynomial functions can be fitted to this data, which can then easily be differentiated. For the strongly shear-thinning xanthan gum solution, a single, second-order polynomial is sufficient, but the highly nonlinear response of the micellar solution necessitates fitting polynomials piecewise to the data. At flow rates where shear banding occurs in the CPyCl/NaSal solutions, the gradient becomes very large; that is, the system “spurts” (Méndez-Sánchez et al. 2003). Fitting a polynomial in this region leads to a large uncertainty, which is reflected in subsequent calculations. However, the Newtonian-like regime at low shear rates, the onset of shear-thinning, as well as the high shear rate regime observed after the shear-banding regime is over are well described by the respective polynomial fits. It should be noted that the value of ${\rm d}(\ln\dot{\gamma}_{\rm a})/{\rm d}(\ln\tau_{\rm w})$ is significantly different to unity for the CPyCl/NaSal and xanthan gum solutions and is therefore essential in calculating the true shear rate at the wall ($\dot{\gamma}_{\rm w}$) using Eq. 11.

Fig. 14

Pressure drop ΔP versus flow rate Q for the CPyCl/NaSal micellar fluid and the xanthan gum solution measured using VROC channel A

Fig. 15

$g(Q) = \ln\dot{\gamma}_{\rm a}$ versus ln τ _w for CPyCl/NaSal and xanthan gum solution (measured using VROC channel A). The polynomial functions fitted are given next to the data

In Fig. 16, we show the composite steady-state flow curve for the CPyCl/NaSal solution. The measured shear stress as a function of shear rate from both microchannels is in excellent agreement with the data measured using an ARES-controlled rate rheometer. The plate–plate data from the ARES, for gap heights of 500 and $50~\upmu {\rm m}$, were first corrected for the gap error using Eq. 5 and subsequently corrected for the inhomogeneous shear rate using Eq. 7. At low shear rates, the Newtonian-like (constant viscosity) response and the onset of shear thinning are captured accurately. In the steady-state stress plateau regime, the error in determining the imposed shear rate, indicated by the error bars, is large as explained above because d(ln Q)/d(ln ΔP) diverges. The stress increases slowly once more after the stress plateau, and data are shown up to $\dot{\gamma} = 3,\!000~{\rm s^{-1}}$ for channel A and $\dot{\gamma} = 10,\!000~{\rm s^{-1}}$ for channel B. Cone-and-plate geometries that are frequently used to characterize the behavior of micellar solutions can cause the sample to foam at high shear rates above the stress plateau due to the large viscoelastic stresses acting at the free surface. However, the microchannels do not have a free surface in the measurement section of the channel, and this allows significantly higher deformation rates to be imposed without causing foaming or incorporation of air. In this high rate region of the flow curve, the measured stress as a function of the shear rate is in good agreement between the two microchannels; however, the results are systematically lower than the data from the plate–plate geometry. The difference between the two techniques could be due to foaming or different wetting conditions; the flow after the shear stress plateau is highly nonlinear (Pipe et al., in preparation), and the interaction of velocity fluctuations and interfacial tension may play a role in determining the flow established in this regime.

Fig. 16

Flow curve for CPyCl/NaSal. The error bars for the VROC data in the stress plateau are discussed in the text

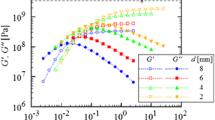
The strong monotonic shear-thinning behavior of the xanthan gum solution is clearly illustrated in Fig. 17. Using a 60-mm cone-and-plate geometry with the controlled stress rheometer (AR-G2), the zero shear viscosity and the onset of shear-thinning behavior are readily documented. Measurements with a 40-mm plate–plate geometry also show very similar behavior. The plate–plate data were corrected for the gap as well as for the shear rate inhomogeneity using Eqs. 6 and 7. Measurements performed with VROC channel A are also able to quantify the viscosity in the shear-thinning region and capture the viscosity out to shear rates $\dot{\gamma}=25,\!000~{\rm s^{-1}}$. In this study, the shear-thinning behavior begins to decrease in severity, and the viscosity tends toward an infinite shear rate limit η _∞; however, as noted by Kulicke and Porter (1981), shear rates in excess of 10⁶ s⁻¹ would be required to accurately determine η _∞. The microfluidic channel provides nearly an extra two decades of information on the shear viscosity of the xanthan gum solution compared to using a classical cone-and-plate geometry and nearly an extra decade compared to the narrow gap parallel-plate technique. This is of considerable interest for industrial processes such as coating and spraying for which deformation rates may often approach $\dot{\gamma}\sim O(10^{4}~{\rm s^{-1}})$. A Carreau–Yasuda model (Bird et al. 1987) can be fitted to the complete set of cone-and-plate and microchannel data and describes the rate-dependent viscosity well over seven decades of shear rate.

Fig. 17

Viscosity as a function of shear rate for aqueous xanthan gum solution from $10^{-3} < \dot{\gamma} < 3 \times 10^{4}\ {\rm s}^{-1}$

It should be noted that the good agreement between the cone-and-plate and VROC measurements at high rates strongly suggests that there is no apparent wall slip present in the VROC for the aqueous xanthan gum solutions. As discussed by Degré et al. (2006), apparent wall slip due to depletion layers is dependent on the surface chemistry of the system as well as the ratio between the solvent and solution viscosity, and here, we conclude that the hydrophilic xanthan gum polymer is not significantly repelled by the glass or gold surfaces of the microfluidic channel.

Conclusions

In this paper, we have demonstrated methodologies for exploring the steady-state viscous response of Newtonian and non-Newtonian fluids at high shear rates using conventional controlled stress and controlled rate rheometers as well as a new microfluidic channel-based device. For both types of device, the key to accessing high shear rates involves minimizing the length scale over which shearing occurs.

Using the conventional rotational rheometers, it is important to accurately calibrate the errors incurred in zeroing the gap when narrow gaps ($H\lesssim250~\upmu$m) are employed. We have demonstrated that the simple linear approach proposed by Connelly and Greener can be used to evaluate gap errors and correct the apparent viscosities obtained at different gaps to obtain true viscosities. We have implemented this approach for both Newtonian and non-Newtonian fluids and demonstrated that the method works surprisingly well for both. We observe that, for moderate viscosity Newtonian fluids N2 and N3, the true viscosities calculated via gap calibration (Eq. 6) are within 7% of the stated zero-shear viscosities. The systematic gap offset errors obtained with these two fluids are $\epsilon\approx30\ \upmu {\rm m}$ for both rheometers used. The lowest viscosity Newtonian fluid N1 shows significant deviation from these values. This may be due, at least partially, to larger levels of noise in the data at the lower torque limits of the instrument, but it serves to remind us that this approximate gap correction approach involves both the geometry and the test fluid. In the case of non-Newtonian fluids, we have demonstrated that the same linear approximate correction works, although not uniformly well. The gap error calibration approach for the viscous aqueous xanthan gum yields values for the gap error consistent with the two Newtonian fluids N2 and N3, but the gap error obtained with a strongly shear-thinning micellar solution yields higher values similar to those measured for the low viscosity Newtonian fluid N1. Thus, the approach is valid for both Newtonian and non-Newtonian fluids, but with differing (and a priori) unknown accuracy.

We also studied the high shear rate behavior of Newtonian and non-Newtonian fluids. To achieve high shear rates using conventional rheometers, very small gap heights ($H<100~\upmu$m) must be used, leading to increased differences between the apparent viscosities and true viscosities (see Table 4), and it is essential to correct for gap errors. Using such protocols may lead to apparent shear-thinning behavior even in Newtonian calibration oils. We identified two key systematic sources of error that could account for these observations, radial migration and viscous heating. Relevant dimensionless scalings show that both effects become important in the vicinity of shear rates 10⁴–$10^5\ {\rm s}^{-1}$.

We have also investigated the viscous response of Newtonian and non-Newtonian fluids in straight microfluidic channels. For constant viscosity liquids, we are able to measure η ₀ over two and a half decades of shear rate, with the attainable range of shear rates dependent on the viscosity of the fluid. For any given fluid, there are resolution limits associated with the resolution of the pressure sensor, at the highest shear rates, the percentage error is O(±0.25%); whereas the error at the very lowest shear rates is O(±50%), although this can be reduced by sampling over longer times to determine an appropriate mean value. Additional errors in the measured steady-state viscosity can be introduced by the syringe/syringe pump setup. To ensure that these errors are small (< 5%), it is important to select a combination of syringe/syringe pump that can provide a steady and constant flow at the desired flow rate. In our experimental setup, this constraint limits measurements of high zero shear rate viscosity liquids at low shear rates due to the difficulty in imposing very low flow rates with sufficient accuracy. Step changes in applied flow rate lead to transient pressure drops in the microchannel, and we associate this with the stiffness of the tubing between the channel and the syringe and also at the channel exit. It is especially important to reduce flow transients when using highly shear-thinning viscoelastic liquids, and we show that a transient pressure response with a time constant <1 s can be obtained by using stiff PEEK tubing.

At moderate shear rates O(100 s⁻¹), the measured viscosities of Newtonian calibration oils N1–3 are in excellent agreement with those obtained from conventional rheometers. Shear rates O(10⁴ s⁻¹) can be obtained using lower zero shear-viscosity liquids, and the viscosity of water was measured up to a shear rate of 8×10⁴ s⁻¹. The viscosities of two highly shear-thinning fluids calculated using the Weissenburg–Rabinowitsch–Mooney equation (Eq. 11) were also found to be in good agreement with results from cone-and-plate measurements, and the effective shear rate range that can be accessed is significantly increased due to the decrease in viscosity associated with increasing shear rate. Thus, we were able to characterize the viscosity of an aqueous xanthan gum solution up to $\dot{\gamma}=30,\!000~{\rm s}^{-1}$ and capture the approach to the infinite shear rate viscosity. Furthermore, for a shear-banding worm-like micellar liquid, we have been able to explore the steady-state flow curve up to $\dot{\gamma}=10,\!000~{\rm s}^{-1}$, charting the viscous response at shear rates significantly beyond the end of the plateau in the steady shear stress.

The results presented here show that both conventional rheometry and microchannel rheometry have their specific domains of applicability. To access high shear rates, both viscometric approaches can be used, but each has particular strengths and weaknesses. In rotational rheometers, the effects of centrifugal stresses and viscous heating can be significant. Viscous heating effects can be substantially reduced by applying shear ramps in a very short interval of time. Radial migration effects can be mitigated by moving to very small gaps, but the resulting systematic gap error grows. In addition, the magnitude of the gap correction that must be applied to the measured data appears to be dependent on the viscosity of the fluids under investigation.

Microfluidic-based rheometry offers several distinct advantages over conventional rheometry. We have demonstrated that high shear rates can be achieved using the microchannels while still minimizing inertial and viscous heating effects, avoiding the need for an ad hoc correction. On the other hand, the dynamic range of the pressure transducers mounted on the microchannels constrains the range of fluid viscosities that can be effectively studied. For constant viscosity fluids with a zero shear rate viscosity beyond 1 Pa s, the applicability of the technique is also limited by the range of flow rates that can be reached by the syringe/syringe pump setup.

Important questions thus arise with regard to the optimal choice of rheometer for investigating the high shear rate viscometry of a given fluid. To assess which approach is more suitable, it is helpful to have a picture of the operating space in terms of the fluid viscosities and the range of shear rates achievable for each class of device and compare and contrast them. In Fig. 18, we show the relevant operating spaces in terms of viscosity and shear rate for a microfluidic channel (Fig. 18a) and a controlled strain device (ARES) with typical fixture settings (Fig. 18b). The lines 1 and 2 in Fig. 18a represent the lower and upper bounds for the VROC channel B based on the minimum and maximum measurable pressure differences, ΔP. According to Eq. 9, the measured pressure difference is directly related to the wall stress, and the apparent shear rate is directly related to the volume flow rate by Eq. 10. Thus, for the limiting values of minimum and maximum measurable pressure differences, we get:

$$ \tau_{\rm w, \min} = \frac{ w d \Delta P_{\min}}{2 l_0 (w + d)},\ \ \tau_{\rm w, \max} = \frac{ w d \Delta P_{\max}}{2 l_0 (w + d)}.\\ $$

(23)

Combining Eq. 23 with the relation $\tau = \eta\dot{\gamma}$ gives two limiting curves of the form:

$$ \eta_{\min} = \frac{\tau_{\rm w, \min}}{\dot{\gamma}_{\rm w}} $$

(24)

$$ \eta_{\max} = \frac{\tau_{\rm w, \max}}{\dot{\gamma}_{\rm w}}. $$

(25)

These lines are power laws of slope −1 on a log–log plot. For the VROC channel B with the minimum and maximum pressure differences given in Table 2, we find τ _min =0.8 Pa and τ _max =160.0 Pa. Another important limiting case arises when the flow rate in the slit is so large that the Reynolds number for the fully developed viscous flow in the channel exceeds Re≡ρQd _h /(ηwd)=2,000. In this limit, the onset of turbulence results in non-viscometric flow, although it should be noted that some studies in microfluidic channels (Peng et al. 1994) suggest that the turbulent transition may happen considerably earlier at Re≈200. Using Eq. 10, we can cast the expression for the critical Reynolds number in terms of the shear rate and viscosity relation at which Re=2,000:

$$ 2,\!000 = \frac{\rho\, d_{h}\, d\, \dot{\gamma}_{\rm w}}{6\eta} $$

(26)

which gives:

$$ (\dot{\gamma}_{\rm w})_{\rm{crit}} = \frac{12,\!000\, \eta}{\rho\, d_{h}\, d}. $$

(27)

At the other extreme, a minimum attainable flow rate limited by the choice of syringe and the syringe pump sets a lower cutoff for the shear rate based on Eq. 10, which, in this case, is $\dot{\gamma}_{\min} = 0.014\ {\rm s}^{-1}$, for the minimum flow rate of $Q_{\min}= 1 \times 10^{-3}\ \upmu {\rm l}/{\min}$.

Fig. 18

Operating region in the viscosity/shear rate space for a microfluidic rheometer (VROC) and a strain-controlled rheometer (ARES). a The operating region for VROC channel B. The lines labeled 1 and 2 of slope −1 are the limiting curves based on the minimum and the maximum measurable pressure differences ΔP (Eqs. 9 and 10). Line 3 is based on the shear rate viscosity cutoff at which the flow approaches a Reynolds number Re=2,000 and can become turbulent. The vertical line 4 is a low shear rate cutoff ($\dot{\gamma} = 0.0132\ {\rm s}^{-1}$) based on the minimum flow rate achievable. b Equivalent operating space for a strain-controlled rheometer (ARES). The lines 1 and 2 are the limiting curves based on the minimum and the maximum measurable torques (Eq. 16). The vertical line 3 is the high shear rate cutoff ($\dot{\gamma} = 2\times 10^4\ {\rm s}^{-1}$) for the onset of radial migration and viscous heating at a typical gap setting ($H = 50\ \upmu {\rm m}$). The vertical line 4 is the low shear rate cutoff ($\dot{\gamma} = 0.002\ {\rm s}^{-1}$) based on the minimum controllable rotation rate of the fixture

Analogously, we obtain the limiting curves and, hence, operating space for a conventional rheometer such as the ARES as shown in Fig. 18b. Lines 1 and 2 represent the limit curves based on the minimum and maximum measurable torques of the transducer. These limiting curves are the same as those given by Eq. 16 and are of the form $\eta_{\min} = \tau_{\min}/\dot{\gamma}$ and $\eta_{\max} = \tau_{\max}/\dot{\gamma}$. Based on the minimum and maximum torques ${\mathcal T}_{\min} = 1.96\times 10^{-4}\enspace {\rm N\,m}$ and ${\mathcal T}_{\max} = 0.196 \enspace {\rm N\,m}$, the values of the minimum and maximum shear stresses are $\tau_{\min} = 7.989\ {\rm Pa}$ and $\tau_{\max} = 7989\ {\rm Pa}$ for a parallel-plate fixture of radius R=25 mm. Again, these are power laws with a slope of −1. The vertical line 3 is the high shear rate cutoff at $\dot{\gamma} = 2 \times 10^4\ {\rm s}^{-1}$, based on the onset of radial migration (Eq. 18) and viscous heating (Eq. 20) for a typical gap height of $50\ \upmu {\rm m}$. As the gap spacing is increased, this limit shifts to lower shear rates (see Eq. 19). The vertical line 4 is a low shear rate cutoff constrained by the minimum achievable rotation rate of the plate. The minimum rotation rate of the ARES motor is $\Omega = 2\times 10^{-6}\ {\rm rad\,s}^{-1}$, and the minimum achievable shear rate is given by $\dot{\gamma}_{\min} = R \Omega_{\min} /H$, which for a plate of radius R=25 mm, and a typical gap height $H = 50\ \upmu {\rm m}$, gives $\dot{\gamma}_{\rm min} = 0.001\ {\rm s}^{-1}$.

These operating space diagrams show the range of shear rates that can be accessed for Newtonian fluids and shear-thinning fluids of differing viscosities. For the VROC, the viscosity scale spans 7 orders of magnitude from η=10⁻⁵ Pa s (providing the low Knudsen number limit Kn=λ/d<0.001 is respected, where λ is the mean free path of molecules in a gas) to η=10² Pa s; whereas for the ARES, the viscosity scale spans 9 orders of magnitude, but from η=10⁻³ Pa s to η=10⁶ Pa s. This points to one important difference between the two approaches: For high viscosity liquids, a conventional modern rheometer typically offers a broader dynamic range compared to the solid state pressure sensors in the microfluidic channel. For example, if the fluid has a zero shear viscosity of 10 Pa s, for the VROC, the minimum and maximum shear rates applicable are $\dot{\gamma}_{\min} = 0.1~ {\rm s}^{-1}$ and $\dot{\gamma}_{\max} = 20~{\rm s}^{-1}$, respectively, whereas using the ARES with a plate–plate fixture of radius R=25 mm and gap height $H=50~\upmu$m, the minimum and the maximum shear rates are $\dot{\gamma}_{\min} = 1~ {\rm s}^{-1}$ and $\dot{\gamma}_{\rm min} = 1,\!000~{\rm s}^{-1}$, respectively. On the other hand, inertial effects are significant for low viscosity fluids using the ARES rheometer, severely constraining the useful range at high shear rates, while the lowest measurable torque limit curtails the accessible shear rates at the low shear rate end. For a fluid with zero shear viscosity of 0.001 Pa s (1 cPs), the dynamic range of shear rates for the microfluidic device VROC is from $\dot{\gamma}_{\min} = 1,\!000\ {\rm s}^{-1}$ to $\dot{\gamma}_{\max} = 200,\!000\ {\rm s}^{-1}$, whereas for the ARES, the effective range with a gap of $50~\upmu\rm m$ is from $\dot{\gamma}_{\min} = 8,\!000\ {\rm s}^{-1}$ to $\dot{\gamma}_{\max} = 20,000\ {\rm s}^{-1}$.

Furthermore, it should be noted that the Weissenberg–Rabinowitsch–Mooney equation (Eq. 11) can be applied robustly to any pressure–flow rate relationship obtained in the microfluidic device. By contrast, the simple linear gap correction applied to the narrow gap results for the parallel-plate device is strictly applicable only to Newtonian fluid data. Our measurements suggest that a simple gap error calibration can be applied to measurements with more complex shear-thinning fluids; however, the gap offset correction ε is both gap and fluid dependent. Ideally, to confirm the applicability of the simple linear gap correction algorithm for a given fluid, it is necessary to compare the gap-corrected data with a direct measure of the true shear rate-dependent material functions obtained, for example, using the microfluidic channel.

The flexibility of microfluidic fabrication technologies also enables a wide range of different flow channel configurations to be considered. Having demonstrated the efficacy of a simple rectilinear slit device to determine flow curves for a range of complex fluids up to shear rates of 10⁵ s⁻¹, we hope in the future to use this robust pressure-sensing technology to also measure entrance pressure drops and planar elongational viscosities using other rheometer-on-a-chip designs.

Appendix

In this appendix, we outline the difficulties in adapting the expression for the rate-dependent viscosity measured using a parallel plate device (Eq. 7):

$$ \eta_{\rm true}(\dot{\gamma}_{\rm true}) = \frac{\mathcal{T}/2 \pi R^3}{\dot{\gamma}_{\rm true}}\left[3+\frac{{\rm d} (\ln \mathcal{T}/2 \pi R^3)}{{\rm d}(\ln\dot{\gamma}_{\rm true})}\right], $$

(28)

to include the linear gap error analysis of Connelly and Greener. We start by noting that the analysis can follow two distinct approaches: one, to find the gap error ε where the apparent shear rate $\dot{\gamma}_{\rm a}$ is held constant and the gap height H is altered and, the other, to find the true rate-dependent viscosity where the gap height H is held constant and the shear rate or rotation rate is altered.

Where possible the analysis to find the gap height error ε should be performed in the zero shear rate region so that the fluid viscosity is not a function of applied shear rate. However, for fluids that start shear thinning at very low shear rates, this can result in shear stresses below the resolution of the rheometer torque transducer, and it is not possible to access this region. In this case, we expect the apparent viscosity to be a function of both the true shear rate and the gap setting, and we want to find the gap error ε as a function of the apparent shear rate $\dot{\gamma}_{\rm a} = {\Omega R}/{H}$, which can be commanded in the software. We start from the expression for the true shear rate $\dot{\gamma}_{\rm true} = {\Omega R}/(H + \epsilon)$:

$$ {\dot{\gamma}_{\rm true}} = {\dot{\gamma}_{\rm a}}\left(\frac{H}{H + \epsilon}\right), $$

(29)

and, differentiating using the chain rule, we find:

$$ \left.\frac{{\rm{d}}\dot{\gamma}_{\rm true}}{{\rm{d}}\dot{\gamma}_{\rm a}}\right|_{\Omega} = \left(\frac{\partial\dot{\gamma}_{\rm true}}{\partial H}\right)_{\Omega}\frac{{\rm d}H}{{\rm d}\dot{\gamma}_{\rm a}}=\left(\frac{H}{H + \epsilon}\right)^2. $$

(30)

Thus, we can rewrite Eq. 28 in terms of the apparent shear rate:

$$ \begin{array}{*{20}l} \eta_{\rm true} &=& \frac{\mathcal{T}/2 \pi R^3}{\dot{\gamma}_{\rm a}} \left(\!\frac{H + \epsilon}{H}\!\right)\times\\ &&\times\left[3\!+\!\left(\!\frac{H}{H+\epsilon}\!\right)\left.\frac{{\rm d} (\ln \mathcal{T}/2 \pi R^3)}{{\rm d}(\ln\dot{\gamma}_{\rm a})}\right|_{\Omega}\right]. \end{array}$$

(31)

To solve for the gap error ε, we cast Eq. 31 in terms of the apparent viscosity η _a (c.f. Eq. 6):

$$ \begin{array}{*{20}l} \frac{1}{\eta_{\rm a}} &=& \frac{1}{\eta_{\rm true}} \left(\!1+\frac{\epsilon}{H}\!\right)\frac{1}{4}\times \\ &&\times\left[3\!+\!\left(\!\frac{1}{1+\epsilon/H}\!\right)\left.\frac{{\rm d} (\ln \mathcal{T}/2 \pi R^3)}{{\rm d}(\ln\dot{\gamma}_{\rm a})}\right|_{\Omega}\right], \end{array}$$

(32)

and we note that, for a complex liquid outside the zero shear-viscosity regime, 1/η _a is a nonlinear function of 1/H. For a Newtonian viscous response in which $\tau\sim\dot{\gamma}_{\rm a}$, we recover Eq. 6, and 1/η _a varies linearly with 1/H.

We now turn to the case where we wish to determine the rate-dependent viscosity as a function of the apparent shear rate for a fixed gap height and known gap error. In this instance:

$$ \left.\frac{{\rm{d}}\dot{\gamma}_{\rm true}}{{\rm{d}}\dot{\gamma}_{\rm a}}\right|_{H} = \left(\frac{\partial\dot{\gamma}_{\rm true}}{{\partial}\Omega}\right)_{H}\frac{{\rm d}\Omega}{{\rm{d}}\dot{\gamma}_{\rm a}}=\left(\frac{H}{H + \epsilon}\right), $$

(33)

and, for measurements performed over a range of rotation rates at a fixed gap height, Eq. 28 becomes (cf. Eq. 7):

$$ \eta_{\rm true}(\dot{\gamma}_{\rm true}) = \eta_{\rm a}\left(1+\frac{\epsilon}{H}\right)\frac{1}{4}\left[3+\left.\frac{{\rm d} (\ln \mathcal{T}/2 \pi R^3)}{{\rm d}(\ln\dot{\gamma}_{\rm a})}\right|_{H}\right]. $$

(34)

It is therefore clear that, for shear-thinning fluids, slightly different results can be obtained depending on whether measurements are performed at constant gap (varying rotation rate) or constant rotation rate (and varying the shear rate by changing the gap). It is instructive to compare the magnitude of the leading order correction due to (a) the error in gap height ε and (b) the derivative of the logarithmic term due to a rate-dependent viscosity. At small gaps, $H\sim50~\upmu{\rm m}$, $\epsilon\sim30~\upmu{\rm m}$, and the correction provided by the gap correction term in Eq. 34 can be O(100%). On the other hand, the corrections associated with the shear-thinning term in square brackets are much smaller. At low apparent shear rates, a ratio of Eq. 32 or 34 with the linear form of Eq. 6 in the text shows that the results in Eqs. 32 and 34 differ by at most [3+(1+ε/H)⁻¹]/4. In the case of an extremely shear-thinning fluid in which

$$ \frac{{\rm d} (\ln \mathcal{T}/2 \pi R^3)}{{\rm d}(\ln\dot{\gamma}_{\rm a})}\rightarrow0, $$

both Eqs. 32 and 34 approach the same limit and the additional correction to the viscosity is only 25%. Given that the majority of fluids do not shear thin this strongly, the additional error due to a shear-rate-dependent viscosity in many cases will be less than 10% of that due to gap error. Thus, we conclude that, in the majority of experiments, applying the gap error analysis alone will provide a good estimate of the shear-rate-dependent viscosity.