Erlangen pipe flow: the concept and DNS results for microflow control of near-wall turbulence

Abstract

The concept of a micropatterned surface morphology capable of producing self-stabilization of turbulence in wall-bounded flows is considered in pipes of non-circular cross-sections which act to restructure fluctuations towards the limiting state where these must be entirely suppressed. Direct numerical simulations of turbulence in pipes of polygon-shaped cross-sections with straight and profiled sides were performed at a Reynolds number $Re_\tau \simeq {\mathrm 300}$ based on the wall shear velocity and the hydraulic diameter. Using the lattice Boltzmann numerical algorithm, turbulence was resolved with up to ${\mathrm 540\times 10^6}$ grid points (${\mathrm 8,192\times 257 \times 256}$ in the x ₁, x ₂ and x ₃ directions). The DNS results show a decrease in the viscous drag around corners, resulting in a reduction of the skin-friction coefficient compared with expectations based on the well-established concept of hydraulic diameter and the use of the Blasius correlation. These findings support the conjecture that turbulence might be completely suppressed if the pipe cross-section is a polygon consisting of a sufficient number of profiled sides of the same length which intersect at right angles at the corners.

1 Introduction

In previous studies carried out by the authors and associates (Frohnapfel et al. 2007; Jovanović and Hillerbrand 2005; Jovanović et al. 2005), the unified theory of skin-friction reduction in turbulent wall-bounded flows was proposed along with the results of its validity using available databases of direct numerical simulations. The starting point in reasoning about the main mechanism involved in turbulent drag reduction in fully developed channel and pipe flows by high polymers, surfactant additives, rigid fibers, and riblets including the closely related phenomena observed in strongly accelerated and supersonic flows, relied on the role played by the average total energy dissipation $\overline{\Upphi}:$

$$ \overline{\Upphi}= \frac{1}{V}\int_V \underbrace { \nu \left(\frac{\partial\overline{U}_i}{\partial x_j}+ \frac{\partial\overline{U}_j}{\partial x_i}\right)\frac{\partial\overline{U}_i}{\partial x_j}} _{\rm I}{\rm d}V+ \frac{1}{V}\int_V \underbrace{\nu \overline{\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right) \frac{\partial u_i}{\partial x_j}}} _{\rm II, \textstyle{\varepsilon}}{\rm d}V =\frac{A_{\rm w} \tau_{\rm w} U_{\rm B}}{\rho V}. $$

(1)

The two terms in Eq. 1 correspond to direct (I) and turbulent dissipation (II) and their overall contribution to $\overline{\Upphi}$ can be evaluated from the work done against the wall shear stress, τ_w, per unit mass of the working fluid, ρ V, where A _w is the wetted surface area and U _B is the bulk velocity. The analysis involving an order of magnitude estimation of the terms in Eq. 1 shows that, in turbulent flows at large Reynolds numbers, the largest contribution to $\overline{\Upphi}$ is due to turbulent dissipation, $\varepsilon,$ which reaches a maximum at the wall and decays away from the wall region. This evidence leads to the conclusion that a large turbulent drag reduction can be expected if the turbulent dissipation at the wall is minimized, leading to minimization of $\overline{\Upphi}.$

By projecting the dynamics of turbulence from the real space into the functional space formed by two scalar invariants, ${\mathrm II_a}=a_{ij}a_{ji}$ and ${\mathrm III_a}=a_{ij}a_{jk}a_{ki},$ of the anisotropy tensor, $a_{ij}=\overline{u_i u_j}/q^2-1/3\delta_{ij}$ ($\overline{u_i u_j}$ and q ² denote the Reynolds stress tensor and its trace, respectively), it was shown (Jovanović and Hillerbrand 2005) that the turbulent dissipation rate must vanish at the wall, $\varepsilon_{\mathrm wall}\rightarrow 0$ as $x_2 \rightarrow 0,$ if the velocity fluctuations in the near-wall region satisfy local axisymmetry with invariance to rotation about the axis (say x ₁) aligned with the mean flow direction so that the streamwise intensity, $\overline{u_1^2},$ is much larger than in the other two directions along which the intensities are same, $\overline{u_2^2}=\overline{u_3^2},$ and the wall location corresponds to the one-component state. Owing to the invariances $\overline{(\partial u_1/\partial x_2)^2}=\overline{(\partial u_1/\partial x_3)^2}, \overline{(\partial u_2/\partial x_2)^2}=\overline{(\partial u_3/\partial x_3)^2}$ and $\overline{(\partial u_2/\partial x_3)^2}=\overline{(\partial u_3/\partial x_2)^2},$ which must be satisfied in this special state of wall turbulence leading to $\varepsilon_{\rm wall}\rightarrow 0,$ kinetic energy k, which grows as $k=1/2(\varepsilon_{\rm wall}/\nu){x_2}^2$ as $x_2\rightarrow 0,$ cannot be amplified and therefore turbulence must decay, leading to flow relaminarization (for details see Jovanović and Hillerbrand 2005 and Jovanović et al. 2005). These conclusions are in close agreement with results of direct numerical simulations with forced boundary conditions which display a high drag reduction when turbulence in the viscous sublayer is manipulated to tend towards the one-component limit in an axisymmetric fashion (Frohnapfel et al. 2007; Lee and Kim 2002; Satake and Kasagi 1996).

We may support this fundamental deduction more clearly by examination of the Reynolds equations for the mean flow:

$$ \frac{\partial \overline{U}_i}{\partial t} +\overline{U}_k \frac{\partial \overline{U}_i}{\partial x_k}= -\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_i}+ \frac{\partial}{\partial x_k}[\nu \frac{\partial \overline{U}_i}{\partial x_k}-\overline{u_i u_k}],\quad i,k=1,2,3, $$

(2)

in simple parallel wall-bounded flows, considered in Sect. 4, by demanding statistical axisymmetry in the turbulent stress tensor $\overline{u_i u_j}=A\delta_{ij}+B k_i k_j,$ where A and B are the scalar functions and k _i is the unit vector defined in such way that $\overline{u_i u_j}$ is invariant under rotation about the axis defined by its scalar arguments say k _i  = (1, 0, 0). It is straightforward to show that for such a stress configuration Eq. 2 transforms from the unclosed to the closed form:

$$ \frac{\partial \overline{U}_i}{\partial t} +\overline{U}_k \frac{\partial \overline{U}_i}{\partial x_k}= -\frac{1}{\rho}\frac{\partial}{\partial x_i}\underbrace{(\overline{P}+\frac{1}{3}\rho q^2+\frac{2}{3}\rho B)}_{{\rm modified\;\; pressure\;\;} P^*}+ \nu \frac{\partial^2 \overline{U}_i}{\partial x_k \partial x_k},\quad i,k=1,2,3, $$

(3)

and obviously lead to solutions which coincide with corresponding solutions for laminar flows. Following a similar analytical path, constraints were derived in Rotta (1972) which insure persistence of the secondary flows and the self-maintenance of turbulence in pipes of non-circular cross-sections. From these results, it also appears that statistical axisymmetry, as discussed above, in the turbulent stresses leads to flow relaminarization and therefore to a large viscous drag reduction effect.

Based on the considerations summarized above, we may attempt to devise a microflow control technique, in the form tentatively proposed in Fig. 1, with the aim of producing a large viscous drag reduction in wall-bounded flows. The outstanding question is whether and how this can be accomplished rationally by simple means such as modification of the surface morphology in order to force the velocity fluctuations in the near-wall region to tend towards the statistically axisymmetric state and reach the one-component limit at the wall.

Fig. 1

Enlarged cross-sectional view of the micropattern surface morphology manufactured in a thin plastic foil for producing a large viscous drag reduction effect. The flow direction is perpendicular to the plane of the figure. The surface pattern design follow the analysis presented in this study. It is expected that turbulence will reach the statistically axisymmetric state in and around the region occupied by the cavity and that this state will prevail over the surrounding almost flat region leading to flow relaminarization. The minimum attainable dimensions are restricted by the production process and correspond to the pattern width period b of 100 μm and the recession depth h of 25 μm (see Fig. 2e′)

2 The cross-sectional geometry

In order to elucidate the surface morphology which promotes a large viscous drag reduction, we shall first examine the statistical features of turbulence in a fully developed flow through a straight duct of square cross-section as shown in Fig. 2 (center). It is well known (Schlichting 1968) that secondary flows appear near duct corners known as Prandtl’s vortices of the second kind, which cannot develop if the flow assumes the laminar state. These counter-rotating vortices are formed due to interaction of the high-speed fluid, originating from the core region, as it is transported towards the duct corners where it is forced to split sideways along both walls.

Fig. 2

The structure of turbulence in a square duct flow (center) and in pipes of non-circular cross-sections (left and right). a Along wall-normal bisectors, the turbulence structure has the form common for wall-bounded flows. b Along corner bisectors, turbulence approaches the ideal trajectory in the anisotropy-invariant map, resulting in a significant reduction in the dissipation ($\varepsilon$) and spectral transfer with formation of quasi-deterministic highly elongated streaks induced by secondary motions. c, d Close to corners, reduced spectral transfer results in a noticeable reduction in the wall shear stress. e–h′ Possible, polygonal or similar, flow configurations of pipe cross-sections with a finite number of corner bisectors: in such configurations, turbulence might be self-suppressed whenever secondary motions start to appear

The flow development along the wall normal bisector shown in Fig. 2 (center-bottom-right) is weakly influenced by side walls and the turbulence statistics resemble trends observed in the plane channel flow. The trajectory in the anisotropy-invariant map shows that the data corresponding to the region of the viscous sublayer lie along the two-component state (2C) mid-way between the two-component isotropic state (2C-iso) and the one-component state (1C). Away from the wall region, the trajectory shows a pronounced tendency for turbulence to approach the axisymmetric state, which is reached at the duct centerline. In the viscous sublayer, the velocity fluctuations normal to the wall are suppressed, u ₂ ≈ 0, so that fluid motions are constrained to planes parallel to it (x ₁, x ₃) having only streamwise, u ₁, and spanwise, u ₃, velocity components. Such a flow structure allows the development of turbulent dissipation which reaches a maximum at the wall and decays away from it following the local equilibrium between the turbulence production and turbulence dissipation. As a consequence of spatial variation of turbulence statistics, the mean velocity profile is almost uniform in the core region and exhibits a steep gradient at the wall (see Fig. 2, center-top-left).

The evolution of turbulence along corner bisectors shown in Fig. 2 (center-top-right) is strongly influenced by side walls forcing normal and spanwise velocity components to develop in the same fashion. Both of these velocity components are suppressed near walls and the trajectory in the anisotropy-invariant map shows that turbulence is axisymmetric along the entire corner bisector starting from the wall at the one-component limit (1C) up to the duct centerline where turbulence is almost isotropic. The structure of the viscous sublayer is altered in such a way that turbulent dissipation cannot develop at the wall and is reduced significantly away from it compared with the corresponding distribution along the wall normal bisector. As a result of such spatial development of turbulence, the mean velocity profile shows a tendency for flow relaminarization with a significant reduction in the slope at the wall (see Fig. 2, center-top-left). The distribution of the wall shear stress (reproduced from the study of Gavrilakis 1992) shown in Fig. 2 (center-bottom-left) reflects these trends and displays consequential changes in the turbulence structure along various cross-sections of the duct.

The variation of turbulence statistics along two different bisectors of the duct flow provides useful hints on how turbulence anisotropy, dissipation rate, mean flow and the wall shear stress can be altered rationally. This immediately suggests that if we intend to achieve a large viscous drag reduction, the cross-sectional geometry has to be composed of a large number of corner bisectors in order to ensure that axisymmetry in turbulence prevails not only near the wall but also across the entire flow domain.

As an initial guess, polygon-shaped cross-sections, shown in Fig. 2 (left), consisting of a large number of straight sides between corners, might be considered. For a large number of corners, such configurations asymptotically approach the circle and we may argue, in the context of the previous discussion, that the mechanism responsible for the remarkable stability of circular pipe flows at very large Reynolds numbers is due to increased anisotropy in the disturbances induced by the surface curvature. Some supporting evidence may be added with respect to the above issue: (1) examination of the transport equations for the Reynolds stresses and anisotropy-invariant mapping of turbulence in circular pipe flows using DNS databases reveal higher anisotropy in the viscous sublayer compared with plane channel flows (Pashtrapanska 2004); (2) experiments performed in circular pipes confirmed an increase in the transition Reynolds number with increasing surface curvature, e.g., decreasing the pipe diameter (Haddad 2009); (3) analysis of the experimental and numerical data shows that the turbulent Reynolds number, R _λ  = qλ/ν based on Taylor’s micro-scale λ which is related to $\varepsilon$ by $\varepsilon \simeq 5\nu q^2/\nu,$ in pipe flows (R _λ ≈ 1.996 Re ^1/2_τ  + 0.108) is lower than in plane channel flows (R _λ ≈ 2.971 Re ^1/2_τ  − 6.618), which implies a reduction in the spectral separation L/η _K due to the surface curvature effect (Jovanović and Pashtrapanska 2004). The spectral separation L/η _K measures the strength of turbulence and represents the ratio between the large, L, and smallest scale, η _K , of turbulent motion defined in terms of Kolmogorov’s length scale $\eta_K=(\nu^3/\varepsilon)^{1/4}.$

For a finite number of corner bisectors, simple polygon configurations with straight sides between corners are not appropriate since these configurations do not ensure axisymmetry of turbulence near the wall (as will be shown in Sect. 4.2). In order to force axisymmetry, polygons with profiled side walls intercepting at right-angles are suggested, as shown in Fig. 2 (right), as the simplest means to obtain the desired turbulence structure which promotes high drag reduction. The preferred cross-sectional geometry can be conveniently characterized in terms of the corner recession depth, h, and the distance between neighboring corners, b. These two parameters should logically scale with flow quantities available at the wall such as the wall shear velocity, u _τ, and the fluid viscosity, ν. Following the discussion presented in Sect. 1, we may suggest that h has to be of the order of the sublayer thickness, h ⁺ = h u _τ/ν ≤ 5, and b is expected to scale with the width of low-speed streamwise streaks observed in the viscous sublayer of fully developed wall turbulence, b ⁺ = bu _τ/ν ≈ 20–25 (Kline et al. 1967).

3 Computational domain and numerical method

3.1 Computational domain

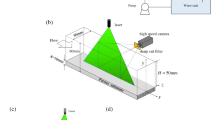
The simulated flow configurations and the coordinate system employed are shown in Fig. 3. For wall-bounded flows the velocity scale u _τ is related to the streamwise pressure gradient ${\partial\overline {P}/\partial x_{1}}$ through the mean momentum equation $u_{\tau} = [0.25({D_h}/{\rho})({\partial\overline{ P}}/{\partial x_{1}})]^{1/2},$ where D _h is the hydraulic diameter defined in terms of the cross-sectional area, A, and the wetted perimeter, O, as D _h  = 4A/O. Following common practice, all variables are normalized using inner scales (u _τ and ν) and this is identified in the text by the superscript +, e.g., x ⁺ = x u _τ/ν.

Fig. 3

Computational domain with coordinate system (a) and simulated cross-section configurations (b)

There are two possibilities for performing numerical simulations of a turbulent pipe flow: either to fix the flow rate through the pipe or to prescribe the axial pressure gradient and therefore u _τ. For our simulations, we chose the latter option and thereby the Reynolds number Re _τ, based on u _τ and the hydraulic diameter D _h , was fixed, for the flow simulations described in Sect. 4, to the value Re _τ = D _h u _τ/ν = D ⁺ _h ≃ 300.

For the geometries shown in Fig. 3, the flow is homogeneous in the streamwise direction so that periodic boundary conditions were used in this direction. Using an equidistant cartesian grid with 4,096 × 129 × 129 points in the x ₁, x ₂ and x ₃ directions for a pipe of square cross-section considered in Sect. 4.1 and ${\mathrm 8{,}192\times257\times256}$ points for pipes with octagonal cross-sections presented in Sect. 4.2, the non-dimensional grid spacings were $\Updelta x_i^+={\mathrm 2.32}$ and $\Updelta x_i^+={\mathrm 1.17,}$ respectively. The estimated value of the Kolmogorov length scale, η ⁺ _K  = (0.25 Re _τ u _τ / U _B)^1/4, obtained from the average dissipation rate across the entire flow domain per unit mass of the working fluid, was $\eta^{+}_{K}\approx {\mathrm 1.5}.$ The grid resolutions $\Updelta x_i^+\simeq 1.54 \eta_{K}^+$ and $\Updelta x_i^+\simeq 0.78 \eta_{K}^+$ were therefore fine enough to resolve almost all dissipation and obtain reliable results for first- and second-order turbulence statistics.

3.2 Numerical method

The choice of the numerical method was motivated by the demand for an algorithm with small computing costs per grid point and time step. In this respect, the lattice Boltzmann method (LBM) was a logical and attractive choice and will be briefly described.

The LBM utilizes the fact that information on the velocity U and the pressure p of a viscous fluid can be obtained by solving a kinetic equation for a one-particle distribution function f instead of Navier–Stokes equations directly. The function $\tilde{f}=\tilde{f}({\xi},{\mathbf r},t)$ depends on the molecular velocity ξ, the position in space r and the time $\tilde{t}.$ The hydrodynamic quantities are obtained from the moments of the distribution function.

A very popular kinetic model is described by the Boltzmann equation together with the so-called Bhatnagar–Gross–Krook (BGK) ansatz (Bhatnagar et al. 1954) for the collision operator

$$ \big( \partial_{\tilde{t}} + \xi \cdot \nabla_{r} + {{\fancyscript{F}}} \cdot \nabla_{\xi} \big) \tilde{f}({\xi},{\mathbf r},\tilde{t}) = - \frac{\tilde{f} ({\xi} ,{\mathbf r},\tilde{t}) - \tilde{f}^{\rm eq} ({\xi},{\mathbf r},\tilde{t})} {\lambda}, $$

(4)

where ${{\fancyscript{F}}}$ is the external force. The function $\tilde{f}^{\rm eq}$ corresponds to the equilibrium (Maxwell–Boltzmann) distribution and λ is a relaxation time. This equation is discretized in time and space. Additionally, a finite set of velocities ${\mathbf c}_i$ for ξ has to be defined. As a result of discretization, the following non-dimensional equation is obtained:

$$ f_{i}({\mathbf x} +{\mathbf c}_{i}, t + 1) - f_{i}({\mathbf x}, t) = - \omega ( f_{i}({\mathbf x} , t) - f_{i}^{\rm eq}(\rho,{\mathbf U}+\textstyle\frac{{\fancyscript E}}{2\rho},{\mathbf x}, t) + 3 t_p \frac{2-\omega}{2} {\mathbf c}_i \cdot {\fancyscript E}, $$

(5)

where f _i is the distribution function of the velocity ${\mathbf c}_i.$ A detailed derivation of how the lattice Boltzmann equation recovers the Navier–Stokes equation can be found in Hou et al. (1995) and especially for Eq. 5 in Buick and Greated (2000).

Equation 5 appears to be a first-order scheme but is in fact second order in time (He and Luo 1997). Without loss of generality, we may choose δt = 1 for the time step and ρ = 1 for the density. The force density ${\fancyscript{E}}$ is given by the pressure gradient according to ${{\fancyscript{E}} = {\nabla} p, }$ whereby ${{\fancyscript{E}}_1}$ is the only remaining component in our case. The macroscopic behavior of Eq. 5 is obtained by a Chapman–Enskog procedure (Chapman and Cowling 1999) together with a Taylor expansion of the Maxwell–Boltzmann equilibrium distribution for small velocity (small Mach number). For this equilibrium distribution

$$ f^{\rm eq}_i = t_{p} \rho \left\{ 1 + \frac{ c_{i_{\alpha}} U_{\alpha} }{ c_s^2 } + \frac{ U_{\alpha} U_{\beta} }{ 2 c_s^2 } \left( \frac{ c_{i_{\alpha}} c_{i_{\beta}} }{c_s^2} - \delta_{\alpha \beta} \right) \right\} $$

(6)

it can be shown that the Mach number must be |u/c _s | ≪1 in order to satisfy the incompressible Navier–Stokes equations. The parameters t _p and $p=\|{\mathbf c}_i\|^2$ depend on the discretization of the molecular velocity space. Various models can be found in (Qian et al. 1992). For the present simulations, a three-dimensional model with 19 velocities ${\mathbf c}_i,\;i=0,\ldots,18$ (D3Q19) was employed. The D3Q19 model has the parameters t ₀ = 1/3, t ₁ = 1/18 and t ₂ = 1/36. A sketch of ${\mathbf c}_i$ is given in Fig. 4.

Fig. 4

Employed lattice arrangement and the velocity vectors ${\mathbf c}_i$ for three-dimensional 19-velocity D3Q19 model

The most commonly used condition to implement solid walls into the LBM is the so-called bounce-back rule sketched in Fig. 5. This rule forces the populations leaving the computational domain to return to the node of departure with the opposite velocity. This rule is very simple and enforces mass conservation. Here it is implemented in such a way that the solid boundaries are placed half way between two nodes. This is referred to in the literature as a bounce-back on the link (BBL). It has been shown that the BBL scheme gives second-order accurate results for plane boundaries (He et al. 1997) but the same cannot be claimed for curved boundaries. In combination with the marker-and-cell approach, even geometries much more complex than plane walls can be matched to the grid. The bounce-back rule is used for treatment of the flow close to the solid boundaries in the present simulations.

Fig. 5

The bounce-back rule and its implementation into LBM for the treatment of the wall boundaries in numerical simulations of turbulence

For all simulations reported in this paper, an initial field was generated by a superposition of the universal velocity distribution ${\mathbf u}^{ +}_0$ and perturbation produced by a periodic array of eddies according to

$$ \begin{aligned} {\mathbf v}^{+}_{0} = {\mathbf u}^{+}_{0} + \underbrace{A^+ \left(\begin{array}{l} \;\;\;\;\;0\;\;\;\;\;\\ x_{3_{1}}^{c\;+} - x_{3}^{+}\\ x_{2}^{+} - x_{2_{1}}^{c\;+} \end{array}\right) \exp \left[\frac{-\left((x_{2}^{+} - x_{2_{1}}^{c})^{2} + (x_{3}^{+} - x_{3_{1}}^{c})^2\right)}{(R^{+})^{2}} \right]}_{\hbox{streamwise}}\\ + \underbrace{B^+ \sum_{i=2}^{N_{c}+1} \left(\begin{array}{l} \;\;x_{2_{i}}^{c\;+} - x_{2}^{+}\\ x_{1}^{+} - x_{1_{i}}^{c\;+}\\ 0 \end{array} \right) \left[\frac{-\left((x_{1}^+ - x_{1_{i}}^c)^2 + (x_{2}^+ - x_{2_{1}}^c)^2\right)}{(R^{+})^2} \right]} _{\hbox{spanwise}}. \end{aligned} $$

(7)

Although the exponential functions violate the incompressibility condition, they served to damp the amplitude of the eddies near the wall and avoid stability problems during the initial phase of the simulation. In the present simulation, the constants in the universal velocity distribution

$$ \frac{\overline{U}_1}{u_\tau}=\frac{1}{\kappa} {\text{ln}}\frac{x_2 u_\tau}{\nu} +C, $$

(8)

were chosen as $\kappa={\mathrm 0.4}$ and $C={\mathrm 5.2}.$ The other parameters involved in Eq. 7 were set to $A^+=B^+ \simeq {\mathrm 0.001}$ and N _c  = 8. The initial velocity field corresponds to a finite array of periodic spanwise eddies with centers along a line parallel to the x ₁ axis and one streamwise eddy centering in the middle of the x ₂–x ₃ plane. The center of the first spanwise eddy was located at $x_{1_{i}}^c={\mathrm D_{h}^{+}/2}$ from the inflow boundary and the rest of the eddies were separated at regular intervals of about ${\mathrm 2D_{h}^{+}}.$

Our implementation of LBM, shown in Fig. 6, was validated against the well-resolved pseudo-spectral simulation of a plane channel flow at Re _τ ≈ 180. Results of the lattice Boltzmann simulation reported previously (Lammers 2004; Lammers et al. 2006; Lammers et al. 2011) confirm that profiles of the mean velocity, root-mean-square velocity fluctuations, turbulent shear stress and the balance of the turbulence kinetic energy equation agree closely with the published results (Kim et al. 1987).

Fig. 6

Flowchart of the LBM and the computer code BEST employed for direct numerical simulations of turbulence in wall-bounded flows reported in Sect. 4 and various levels of algorithm implementation for high-performance computing on different computer architectures (Lammers 2004)

The computations presented in the following section were performed on the NEC SX-8 of the High Performance Computing Center in Stuttgart.

4 DNS results

4.1 Turbulent flow through a pipe of square cross-section

In order to produce the desired componentality of the velocity fluctuations by cross-sectional geometry which leads to the realization of axisymmetric turbulence in the near-wall region, we first performed a simulation of turbulence in a pipe of square cross-section. It is expected that in such a configuration turbulence will reach the axisymmetric state along corner bisectors and tend towards the one-component state at the wall. By evaluating the turbulence statistics in the region between the wall normal and corner bisectors, it is possible to confirm the results of the theoretical considerations outlined in Fig. 2 and show that the axisymmetric state of wall turbulence leads to a large reduction in the wall shear stress. Starting from the initial field, governing equations were integrated for about 30 turnover times D _h /u _τ before the flow reached a statistically steady state. This state could be identified by monitoring running averages of the turbulence statistics, which were found to differ marginally along four half-parts of corner bisectors as shown in Fig. 7.

Fig. 7

The mean velocity in the flow direction (top) and turbulence intensity components (bottom) across four corner bisectors denoted by I, II, III and IV of a pipe with square cross-section

Figure 8 shows distributions of the mean flow, all components of the Reynolds stress tensor and the turbulence anisotropy across one of the eight octants of a square cross-section. These results provide a demonstration of desired modifications of turbulence induced by the presence of the side walls which intersect at right-angles. Distributions of the Reynolds stresses reveal that turbulence reaches the axisymmetric state in the close vicinity of the corners with invariance to rotation for 90° about the axis aligned with the mean flow direction. At corners, turbulent stresses satisfy the relations which hold for such a form of axisymmetric turbulence: $\overline{u_1^2}> \overline{u_2^2}=\overline{u_3^2}$ and $\mid\overline{u_1 u_2}\mid{=}\mid\overline{u_1 u_3}\mid.$ Trajectories in the anisotropy-invariant map reflect these trends and confirm that anisotropy increases as corners are approached so that turbulence along the corner bisector follows the right-hand boundary of the anisotropy map which represents axisymmetric turbulence with the one-component state located at the wall.

Fig. 8

The turbulence statistics in a pipe flow of square cross-section at Re _m  = D _h U _B/ν≃ 4,362. The profiles of the mean velocity, Reynolds stresses and turbulence anisotropy in the region between the normal (a), and corner bisectors (d). Arrows indicate the maximum value of turbulence anisotropy. These data are non-dimensionalized by the wall friction velocity calculated from the pressure gradient along the pipe and plotted versus the normalized distance starting from the pipe centerline up to the wall, s ⁺ = s u _τ/ν

Following trends in the turbulence statistics between the profiles shown in Fig. 8a, d, it can be concluded that the tendency towards axisymmetry is accompanied by a reduction in the turbulent shear stresses, decrease in the intensity components and suppression of the pressure fluctuations. Above corners, peaks in turbulence intensity and pressure fluctuations are reduced by more than 30 % in comparison with sections which lie along normal bisectors. Approaching corners, slopes of the turbulent stresses and of the mean flow continuously decrease at the wall. This trend supports the expectation that a decrease in the turbulent dissipation rate at the wall, $\varepsilon_{\mathrm wall},$ leads to a lower value of the integral (Eq. 1) and therefore a decrease in the wall shear stress, $\tau_{\mathrm w}.$

4.2 Turbulent flow through pipes of polygon cross-sections

In reasoning about the cross-sectional configurations which would notably increase the anisotropy of turbulence along the entire wetted perimeter, which would then prevail across the whole flow domain, we suggested in Sect. 2 polygon cross-sectional geometries composed of profiled sides intersecting at right-angles at the corners. For such configurations with estimated values for h and b, simulation is, however, very demanding owing to the fine resolution needed to capture the evolution of the flow structures near corners. These structures are expected to have a significant impact on the viscous drag.

Using the very efficient lattice Boltzmann algorithm which currently operates extremely well exclusively on the equidistant grids, cross-sectional configurations with only a few corners can be simulated with reasonable effort. Therefore, an attempt was made to obtain results by conducting two simulations of turbulence development in pipes with octagonal cross-sections having straight and profiled sides. By studying differences in the flow development through such pipes, it is possible to extract effects expected to prevail for a large number of corners.

The simulated cross-sectional geometries are shown in Fig. 9. Owing to uniform discretization of the flow domain using equidistant cartesian grids, the wall boundaries are smooth within the grid resolution, $\Updelta x_i^+={\rm 1.17},$ and symmetry between various orthants of the octagon cross-sections is preserved within an equivalent degree of approximation.

Fig. 9

Discretisized cross-sectional geometries of turbulent pipe flow: octagon with straight sides (left) and octagon with profiled sides (right)

Comparisons of the flow development in pipes of octagonal cross-sections with straight and profiled sides are shown in Fig. 10. These results display essential differences in the flow development in the region around corners which are expected to play a major role in turbulent drag reduction and potentially also in self-stabilization of the laminar boundary layer development at large Reynolds numbers.

Fig. 10

The structure of turbulence in pipes with octagonal-shaped cross-sections. Comparisons of trajectories in the anisotropy-invariant maps and profiles of mean velocity in the region between the wall normal bisector and the corner bisector for an octagon with straight sides against an octagon with profiled sides. Arrows indicate the maximum level of the turbulence anisotropy

The computed trajectories in the anisotropy-invariant maps in Fig. 10 (right) reveal that anisotropy increases along the profiled sides of the octagonal cross-section and reaches at the corners almost the one-component limit. This trend in turbulence anisotropy is reflected in distributions of the mean velocity which display a continuous reduction of the wall shear stress as corners are approached. These results correspond to a Reynolds number of Re _m  = D _h U _B/ν ≃ 4,386 and a skin-friction coefficient of c _f  = τ_w/(0.5U ²_ρb ) = 2(Re _τ/Re _m )² = 9.35 × 10⁻³. This value of c _f is 3.9 % lower than the prediction based on the well-known Blasius correlation c _f  = 0.0791Re ^−1/4 _m (Schlichting 1968).

Across the octagonal cross-section with straight sides, there is no noticeable increase in anisotropy as observed in the cross-section with profiled sides and consequently no trend in reduction of the wall shear stress at and near corners, as can be concluded from Fig. 10 (left). These results correspond to a Reynolds number of Re _m ≃ 4,277 and a skin-friction coefficient of c _f ≃ 9.838 × 10⁻³. For this cross-sectional configuration, the value of c _f obtained is slightly higher than that deduced from the Blasius correlation.

5 Conclusions

An attempt was made, on purely theoretical grounds, to derive the cross-sectional geometry of a fully developed pipe flow which forces near-wall turbulence to approach the limiting state where it must be completely suppressed. Following invariant analysis of turbulence, a cross-sectional geometry was suggested in the form of polygon with profiled sides intersecting at right-angles at the corners. A description is provided of the manner in which the proposed geometry alters near-wall turbulence leading to a significant turbulent drag reduction.

In order to support the proposed concept of microflow control, direct numerical simulations of turbulence in pipes of non-circular cross-sections were performed using the lattice Boltzmann numerical method. Simulation results confirmed that the main mechanism responsible for the turbulent drag reduction is related to the ability of the profiled surface to increase the anisotropy in the velocity fluctuations very close to the wall. It is hoped that further simulation work following the concept outlined in this paper will bring additional evidence in closer accord with the theoretical expectations.