1 Introduction

Non-slip boundary condition has been commonly accepted and adopted in fluid dynamics at conventional scale. However, when the dimensions shrink to be extremely small, e.g., sub-micro or nano-scales, the continuum assumption breaks down (Gad-el-Hak 1999). For liquid channel flow, the slippage has been experimentally observed at the flow boundary on a hydrophobic wall surface (Brigo et al. 2008; Byun et al. 2008). Molecular dynamics simulation (MDS) has demonstrated that slip, non-slip and locking boundary conditions (corresponding to positive, zero and negative slippages) could all exist and the degree of slippage depends on interfacial parameters such as liquid–solid bonding strength, interfacial thermal roughness, commensurability of solid and liquid densities (Thompson and Troian 1997). The non-slip boundary condition only occurs in situations where all the factors lead to zero slippage. Similar slippage also exists for temperature, which is often called the temperature jump. The thermal boundary resistance, or the Kapitza resistance, was experimentally observed between liquid helium and solids (Swartz and Pohl 1989). The acoustic mismatch model (AMM) was used to explain the phenomenon. The MDS study has shown that the liquid–solid bonding strength, which is directly related to the wettability of the fluid to the wall surface, plays a crucial role in determining the Kapizta resistance. The Kapitza length exhibits exponential and power functions of the liquid–solid bonding strength for non-wetting and wetting liquids (Xue et al. 2003). Further studies have revealed that the liquid–solid bonding strength greatly affects density, velocity, temperature and pressure profiles (Nagayama and Cheng 2004; Voronov et al. 2006, 2007, 2008; Kim et al. 2008b).

With rapid development in micro/nanoscale machining and processing, microstructures can now be fabricated on wall surfaces for MEMS (Byun et al. 2008; Hao et al. 2009; Woolford et al. 2009). Studies on micro/nanoflows over rough surfaces have shown their importance in the design of micro-devices. Cao et al. (2006) found that the surface nanostructure has dual effect on the surface wettability and the hydrodynamic disturbance. More recent work has revealed that the atom localization inside the rectangular cavities results in reductions of velocity values and slip length and the reductions are affected by the size of the cavities (Sofos et al. 2009).

Recent investigations have demonstrated that MDS is a powerful tool for interfacial studies because of its capability of capturing the interfacial phenomena. Yet huge computational load has greatly restricted the simulation size within tens of nanometers. On the other hand, traditional CFD becomes invalid to deal with the slippages at velocity and temperature boundaries. Therefore, the hybrid simulation method, having advantages of both MDS and CFD, emerges as a feasible solution (Hu and Li 2007) and has shown promise in multi-scale and trans-scale studies in the last decade (Mohamed and Mohamad 2010). Since the pioneering work by O’Connell and Thompson (1995), the MD–continuum hybrid simulation method has been applied to solve various fluid flow and heat transfer problems (Flekkoy et al. 2000; Wagner et al. 2002; Delgado-Buscalioni and Coveney 2003; Nie et al. 2004a, b, 2006; Delgado-Buscalioni et al. 2005a, b; Liu et al. 2007; Wang and He 2007; Xu and Li 2007; Yen et al. 2007; Li and He 2009; Sun et al. 2009, 2010, 2011b). Nie et al. (2004a) verified the feasibility of using the hybrid simulation method to study the micro/nanoflows in rough channels and showed the distinctive advantage of acquiring quantities at multi-scales. Coupling schemes were proposed and developed previously by Sun et al. (2010) and the effects of relative roughening element height on the velocity and temperature boundary conditions were investigated by Sun et al. (2011b). The present study focuses on the effects of the liquid–solid bonding, surface nanostructure and channel height.

2 Simulation method

2.1 Domain decomposition

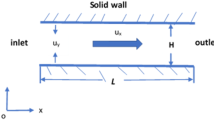
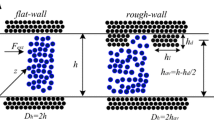
Figure 1 shows the hybrid computational model. Liquid flows in the 2D micro/nanochannels (formed by parallel surfaces with micro/nano spacing) with five different shapes of roughening element, namely half-circular, rectangular, forward triangular, backward triangular and isosceles triangular. l x , l y and l z are the overall dimensions in x-, y- and z-directions. H is the height of the channel. h, w and p are the height, length and pitch of the periodic roughening element in x-direction, respectively. Values of these quantities can be found in Table 1. Owing to symmetry, the lower half of the channel (see the dashed box in Fig. 1) is taken to be the simulation domain. The domain is decomposed into three regions, namely particle (P) region, overlap (O) region and continuum (C) region. Molecular dynamics and fluid dynamics are used to describe the mass, momentum and energy transports in P and C regions, while a set of customized coupling schemes for momentum and energy are used in O region in order to ensure the consistency between P and C regions. During each run, quantities are exchanged iteratively between P and C regions until the convergent results are obtained. The numerical methods used in each region are described below. More details are given in Sun et al. (2010, 2011b).

Fig. 1
figure 1

Schematics of the hybrid computational model. The dashed box shows the simulation domain. The shapes of the roughening elements are: a half-circular, b rectangular, c forward triangular, d backward triangular and e isosceles triangular

Full size image
Table 1 Simulation conditions
Full size table

2.2 Molecular dynamics simulation

The classical 3D MDS serves as P solver. The settings remain the same as those used by Sun et al. (2010) and (2011b). The modified Lennard-Jones (L-J) potential function proposed by Stoddard and Ford (1973) is used to describe the interaction between liquid molecules:

$$ \varphi (r) = 4\varepsilon \left\{ {\left[ {\left( {\frac{\sigma }{r}} \right)^{12} - \left( {\frac{\sigma }{r}} \right)^{6} } \right] + \left[ {6\left( {\frac{\sigma }{{r_{\text{c}} }}} \right)^{12} - 3\left( {\frac{\sigma }{{r_{\text{c}} }}} \right)^{6} } \right]\left( {\frac{r}{{r_{\text{c}} }}} \right)^{2} - \left[ {7\left( {\frac{\sigma }{{r_{\text{c}} }}} \right)^{12} - 4\left( {\frac{\sigma }{{r_{\text{c}} }}} \right)^{6} } \right]} \right\} $$
(1)

where σ and ɛ are the length and energy characteristic parameters, respectively. The cut-off radius is taken to be r c = 2.5σ. When r increases to r c, both φ and dφ/dr continuously go to zero, therefore no discontinuous forces will appear. Molecules outside the r c range can be treated as free molecules. The interaction between a liquid molecule and a solid atom is also described by Eq. 1 but with different length and energy characteristic parameters of σ ls = 0.91σ and ɛ ls = βɛ. Here β is a factor adjusting the liquid–solid bonding strength.

The solid wall is represented by 13 layers of atoms in FCC (111) pattern at the bottom of simulation domain (see Fig. 1) with the number of atoms N s = 2,620–6,460 and the lattice constant σ s = 0.814σ. Hookean springs with the constant k = 3,249.1ɛσ −2 (Yi et al. 2002) are set between neighboring atoms. To keep the wall temperature constant at T w = 1.1ɛk −1B , two extra layers of “phantom atoms” are set below this configuration (Maruyama and Kimura 1999; Maruyama 2000; Sun et al. 2009). The lower layer is stationary as a frame while the upper layer is controlled with the Langevin method, where the random force vectors to excite phantom atoms are sampled from the Gaussian distribution with mean μ = 0 and standard deviation \( \sigma = \sqrt {2\alpha k_{\text{B}} T_{\text{w}} /\delta t^{\text{P}} } \) (α = 168.3τ −1 is the damping constant, δt P = 0.005τ is the time step for P region).

The size of P region is l P x  × l P y  × l P z  = (28.5σ–83.0σ) × 7.0σ × 23.1σ including the thickness of the solid wall. Periodic boundary conditions are used in x- and y-directions. The upper boundary is a part of O region, which will be discussed in Sect. 2.4.

For initialization, all the space above the solid wall in P region is uniformly occupied by liquid molecules with the number of molecules N l = 2,192–9,216 and the density ρ = 0.81 mσ −3 (m is the mass of a molecule). When the simulation starts, the initial period of 250τ allows the solid and liquid to reach a thermal equilibrium state at T = 1.1ɛk −1B (only P region operates in this period). The following period of 5,000τ is used to let the whole system (P, C and O regions operate) to reach the steady state when the coupling between P and C regions is executed. An extra period of 2,500τ is used to obtain the profiles of quantities by averaging. For integrating of equations of motion, the leapfrog scheme is used. For higher computational efficiency, the cell subdivision technique (Allen and Tildesley 1987; Rapaport 2004) is employed.

2.3 Finite volume method

For the 2D incompressible fluid flow, the governing equations are written as:

continuity equation:

$$ \nabla \cdot {\mathbf{u}} = 0 $$
(2)

momentum equation:

$$ \frac{{\partial {\mathbf{u}}}}{\partial t} + {\mathbf{u}} \cdot \nabla {\mathbf{u}} = \frac{\mu }{\rho }\nabla^{2} {\mathbf{u}} - \frac{1}{\rho }\nabla p $$
(3)

energy equation:

$$ \frac{\partial T}{\partial t} + {\mathbf{u}} \cdot \nabla T = \frac{\lambda }{{\rho c_{v} }}\nabla^{2} T + \frac{\mu }{{\rho c_{v} }}\left[ {2\left( {\frac{\partial u}{\partial x}} \right)^{2} + 2\left( {\frac{\partial w}{\partial z}} \right)^{2} + \left( {\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}} \right)^{2} } \right] $$
(4)

where u and w are the x- and z- components of the velocity vector u. μ = 2.18ɛτσ −3, λ = 6.92k B σ −1 τ −1 and c v  = 2.40k B m −1 (NIST 2005) are the dynamic viscosity, thermal conductivity and isochoric specific heat capacity, respectively, corresponding to the liquid state of T = 1.25ɛk −1B and ρ = 0.81 mσ −3. The unsteady term is retained for compatibility with MDS in time evolution. Periodic conditions are used for the inlet and outlet while a symmetric condition is used at the top boundary. The flow is assumed to be fully developed so that u, w and T are uniform along the x-direction at the bottom boundary and will be provided by P region during the simulation.

The finite volume method (FVM) is chosen and the semi-implicit method for pressure linked equations consistent (SIMPLEC) algorithm is used as C solver (Versteeg and Malalasekera 1995). The size of C region is l C x  × l C z  = (170.8σ–497.9σ) × (20.4σ–235.0σ) and is uniformly divided with the mesh number of n C x  × n C z  = 6 × 6–6 × 69. The simulation conditions for different cases are listed in Table 1. It should be noted that l C x  = n C x l P x is ensured to guarantee the compatibility between P and C regions in size and l C z /n C z is kept constant to save the computational time in the way of enlarging the channel by merely increasing C mesh numbers. The time step for C region is determined as δt C = 100δt P = 0.5τ by trial and error.

2.4 Coupling method

Liquid flow in rough channels is considered to be 2D fully developed. MDS is 3D in principle to reproduce the realistic micro-structure of the materials such as the crystalline structure. The accuracy of the information provided by P region is crucial to the performance of the hybrid solver and this can be improved by adding more molecules benefitting the extra dimension. Therefore, the O region, bridging between 3D MDS and 2D FVM, is of the key importance for the hybrid simulation method. In the present work, the O region contains three basic functional layers, i.e., the C-P, relaxation and P-C layers from the top to bottom (see Fig. 2). In C-P layer the node information is transferred to the molecules within this layer and in P-C layer the molecular dynamic information is obtained by averaging over the molecules within this layer and transferred to corresponding C nodes. Relaxation layer serves as a buffer.

Fig. 2
figure 2

Schematic of configuration in overlap region (dot node, circle u-velocity, cross w-velocity)

Full size image

In the C-P layer, the coupling schemes of momentum and energy are required for correct information transfer from the part with low degree of freedom to that with much higher degree of freedom. O’Connell and Thompson (1995) proposed a coupling scheme, primarily based on constraint dynamics, for momentum. Yen et al. (2007) improved the scheme by replacing the instant terms with time-averaging ones in order to achieve relatively higher signal-to-noise ratio and better convergent characteristics. Wang and He (2007) made a further improvement to determine the coupling parameter during computation rather than using an empirical value. Sun et al. (2010) made further modifications by introducing locally linearized constraint as well as a QUICK-type extrapolation for better coupling performance in C-P layer. Their coupling scheme for x-momentum, as an example, is given by Eq. 5:

$$ \ddot{r}_{x,i} \left( {z,t} \right) = {\text{f}}_{c} \left( t \right) + 2\left[ {{\text{f}}_{4} \left( t \right) - {\text{f}}_{c} \left( t \right)} \right]\left( {z - z_{c} } \right)/\Updelta z^{\text{C}} + \left[ {\frac{{f_{x,i} \left( t \right)}}{m} - \left\langle {\frac{1}{{N^{\text{C - P}} }}\sum\limits_{j = 1}^{{N^{\text{C - P}} }} {\frac{{f_{x,j} \left( t \right)}}{m}} } \right\rangle_{{p\delta t^{\text{P}} }} } \right] $$
(5)

where \( {\text{f}}_{c} \left( t \right) = \frac{1}{{\left( {p/2 + 1} \right)\delta t^{\text{P}} }}\left[ {u_{c} \left( {t + \delta t^{\text{P}} } \right) - \left\langle {\frac{1}{{N^{c} }}\sum\limits_{j = 1}^{{N^{c} }} {\dot{r}_{x,j} \left( t \right)} } \right\rangle_{{p\delta t^{\text{P}} }} } \right] \) is the constraint at face c and \( {\text{f}}_{4} \left( t \right) = \frac{1}{{\left( {p/2 + 1} \right)\delta t^{\text{P}} }}\left[ {u_{4} \left( {t + \delta t^{\text{P}} } \right) - \left\langle {\frac{1}{{N^{4} }}\sum\limits_{j = 1}^{{N^{4} }} {\dot{r}_{x,j} \left( t \right)} } \right\rangle_{{p\delta t^{\text{P}} }} } \right] \) is the constraint at node 4 (see Fig. 2). The QUICK-type extrapolation is used to obtain the quantity at face c:

$$ u_{c} \left( {t + \delta t^{\text{P}} } \right) = \frac{6}{8}u_{3} \left( {t + \delta t^{\text{P}} } \right) + \frac{3}{8}u_{4} \left( {t + \delta t^{\text{P}} } \right) - \frac{1}{8}u_{2} \left( {t + \delta t^{\text{P}} } \right) $$
(6)

The coupling scheme for momentum in the z-direction is similar with slight geometric differences due to the staggered mesh (Versteeg and Malalasekera 1995). Based on the same concept of local linearization, Sun et al. (2010) also proposed the modified constraint equations for energy.

In P-C layer, the velocity and temperature at node 1 (see Fig. 2) are obtained by a spatial averaging within P-C layer and a temporal averaging over a period of \( p\delta t^{\text{P}} \) for velocity:

$$ {\mathbf{u}}_{1}^{{}} = \left\langle {\frac{1}{{N^{{{\text{P}} - {\text{C}}}} }}\sum\limits_{j = 1}^{{N^{{{\text{P}} - {\text{C}}}} }} {{\dot{\mathbf{r}}}_{j} } } \right\rangle_{{p\delta t^{\text{P}} }} $$
(7)

and for temperature:

$$ T_{1}^{{}} = \frac{m}{{3k_{\text{B}} }}\left\langle {\frac{1}{{N^{{{\text{P}} - {\text{C}}}} }}\sum\limits_{j = 1}^{{N^{\text{P - C}} }} {\left( {{\dot{\mathbf{r}}}_{j} - {\mathbf{u}}_{1} } \right)^{2} } } \right\rangle_{{p\delta t^{\text{P}} }} $$
(8)

Since the flow is driven by pressure difference, the pressure gradient −dp/dx obtained from C region should also be transferred to P region and exerted on all the molecules as an external driving force:

$$ f_{\text{e}} = - \frac{m}{\rho }\left( {\frac{{{\text{d}}p}}{{{\text{d}}x}}} \right) $$
(9)

An extra depressing force f d is exerted on the molecules in C-P layer to avoid molecules drifting away (Nie et al. 2004a; Yen et al. 2007):

$$ f_{\text{d}} \left( z \right) = - p_{0} \sigma \frac{{z - z_{e} }}{{1 - \left( {z - z_{e} } \right)/\Updelta z}} $$
(10)

where p 0 is the average pressure in P region.

3 Results and discussion

Fifty cases were simulated. They are labeled as ‘shape_β_p/w_H’ for short, featuring different shapes of roughening element (cir: half-circular, rec: rectangular, tri1: forward triangular, tri2: backward triangular and tri3: isosceles triangular), liquid–solid bonding strengths (β = 0.1, 1, 10, 50), ratios of pitch to length of roughening element (p/w = 1, 1.5, 2, 3) and channel heights (H = 61σ, 122σ, 245σ, 490σ). Table 1 summarizes the simulation conditions. For all the cases, the maximum velocity at the center of the channel is fixed constant at U = 1στ −1 as the uniform standard so that the present simulation results can be compared with those in Sun et al. (2010).

3.1 Velocity and temperature profiles and flow and density fields

Figure 3 shows the hybrid velocity and temperature profiles as functions of z/H. Previous results for smooth channels (Sun et al. 2010) showed significant slip with the relative velocity slip (u s/U) of about 20–2% for H = 60σ–408σ. However, in Fig. 3 the velocity boundary condition shifts from significant slip to locking because the liquid molecules are blocked by the roughening elements. The locking range and temperature jump both decrease apparently with increasing H. When the channel height is large enough (H = 490σ), the slippages become negligible and non-slip boundary conditions seem acceptable. As seen in the previous results (Sun et al. 2010, 2011b), all the profiles eventually converge to the analytical solution with non-slip boundary condition when H is large enough, irrespective of the types of the boundaries at microscale (see Fig. 3a, c, e, g). Therefore, the cases with the smallest channel height (H = 61σ), where the differences can be clearly seen, were conducted. The rectangular case of H = 61σ seems to have the most blocking influence, giving the thickest blocking region and smallest temperature jump.

Fig. 3
figure 3

Hybrid velocity and temperature profiles with different shapes of roughening element at: a, b H = 61σ; c, d H = 122σ; e, f H = 245σ and g, h H = 490σ

Full size image

Figures 4 and 5 show the flow and density fields and the snapshots in the vicinity of the wall for the cases of H = 61σ and H = 490σ. The layering can be seen clearly in the density fields and the snapshots within the range of several molecular diameters from the wall surface. This interfacial layering phenomenon has been theoretically and numerically investigated in terms of liquid–solid molecular interaction (Curtin 1987; Sikkenk et al. 1987), and optically verified (Magnussen et al. 1995; Regan et al. 1995; Huisman et al. 1997). Xue et al. (2004) found that the layering structure is the representation of liquid–solid molecular bonding strength. Stronger bonding leads to a larger range and magnitude of density oscillation. The layering structure influences the Kapitza resistance and the interfacial energy transport efficiency. The stronger bonding gives more efficient heat transfer across the liquid–solid interface. However, the layering structure itself has been proved to give no enhancement in heat transfer (Xue et al. 2004). From Figs. 4 and 5, smooth streamlines and steady vortices are seen for small channel cases while distorted streamlines and very small eddies are seen for larger channel cases. From Fig. 5, the eddies exist mainly in the area covered by the density layering, especially in the corners. This suggests that the molecules forming the eddies are influenced by the balance of shear stress of the bulk flow, which tends to drive the molecules to flow away, and the liquid–solid bonding from the wall surface, which tends to lock the adjacent molecules. Since the maximum velocity is fixed, larger channel case gives smaller shear stress and the molecules are inclined to be trapped forming random eddies. The geometric blocking is noticeable because more eddies can be found in the cases with larger blocking influence (rec and tri2 cases). Moreover, more and clearer peaks and troughs in density can be found in the concaves, especially in the corners. In the rectangular case, for example, at least five peaks and troughs can be clearly seen in the concave while only one or two on the convex is identifiable. This may be due to the fact that the molecules in the concaves are less active due to local geometric confinement, as seen in the previous study on condensation (Sun et al. 2011a).

Fig. 4
figure 4

Flow and density fields (left) and snapshots (right) near wall surface with different shapes of roughening element (β = 1, p/w = 2, H = 61σ and snapshots are taken at t = 7,750τ)

Full size image
Fig. 5
figure 5

Flow and density fields (left) and snapshots (right) near wall surface with different shapes of roughening element (β = 1, p/w = 2, H = 490σ and snapshots are taken at t = 7,750τ)

Full size image

The hybrid velocity and temperature profiles for different p/w are shown in Fig. 6. The blocking influence becomes weaker with increasing p/w. For the cases of p/w = 1, the velocity value within the roughening element height is restrained at zero, while the blocking influence is so weak for the cases of p/w = 3 that even small slips are noticeable. It should be noted that the rectangular case always shows the most apparent confinement except the case of p/w = 1, where the surface becomes smooth. The geometric variation also slightly influences the temperature boundary condition. The temperature jump starts from around \( 0.1\varepsilon k_{\text{B}}^{ - 1} \) and then gradually increases to roughly \( 0.15\varepsilon k_{\text{B}}^{ - 1} \) with increasing p/w. However, the maximum temperature does not change much. More details can be found by comparing Fig. 7 with Fig. 8 that the eddies emerge in the concaves when p/w = 1 and totally disappear when p/w = 3. This indicates that the geometric confinement of the roughening elements is dependent more on p/w than the shape.

Fig. 6
figure 6

Hybrid velocity and temperature profiles with different shapes of roughening element at: a, b p/w = 1; c, d p/w = 1.5; e, f p/w = 2 and g, h p/w = 3 (H = 61σ)

Full size image
Fig. 7
figure 7

Flow and density fields (left) and snapshots (right) near wall surface with different shapes of roughening element (β = 1, p/w = 1, H = 61σ and snapshots are taken at t = 7,750τ)

Full size image
Fig. 8
figure 8

Flow and density fields (left) and snapshots (right) near wall surface with different shapes of roughening element (β = 1, p/w = 3, H = 61σ and snapshots are taken at t = 7,750τ)

Full size image

It is apparent from Fig. 9 that the variation of β has significant influence on the velocity and temperature boundary conditions. The liquid–solid bonding strength determines the efficiency of the interfacial energy transport. Larger β means more efficient heat transfer, which causes the whole temperature profile to drop. This variation becomes more obvious for smooth cases from considerable velocity slip for small β to multi-layer locking for large β. It should be noted that when β = 10 the boundary temperatures for smooth and rough cases are almost identical and very close to T w while when β = 50, this temperature for rough cases drops even a bit lower than T w with severe local oscillation. It is probably due to the fact that the molecules are confined so firmly that even their vibrational motions are restricted to some extent. This is supported by Figs. 10 and 11, where it is clearly shown that weak confinement on the molecules adjacent to the wall (β = 0.1) gives smooth streamlines over surface without any eddies while strong confinement (β = 50) causes significant peaks and troughs in density contour and apparent layering in the snapshots, and many small eddies and distorted streamlines in flow field. It should be mentioned that the locally linear temperature gradient observed in previous work (Sun et al. 2011b) is also found in Fig. 9f, h but is not apparent in other cases. The reason for this is probably that larger β gives an equivalent strong confinement as the compact arrangement of the square roughening elements did in previous work (Sun et al. 2011b). In principle, a linear gradient should exist when liquid molecules are tightly restricted due to either interactive condition or geometric condition or both because only pure thermal conduction is then permitted.

Fig. 9
figure 9

Hybrid velocity and temperature profiles with different shapes of roughening element at: a, b β = 0.1; c, d β = 1; e, f β = 10 and g, h β = 50 (H = 61σ). Data for the smooth (smt) cases are from Sun et al. (2010)

Full size image
Fig. 10
figure 10

Flow and density fields (left) and snapshots (right) near wall surface with different shapes of roughening element (β = 0.1, p/w = 2, H = 61σ and snapshots are taken at t = 7,750τ)

Full size image
Fig. 11
figure 11

Flow and density fields (left) and snapshots (right) near wall surface with different shapes of roughening element (β = 50, p/w = 2, H = 61σ and snapshots are taken at t = 7,750τ)

Full size image

3.2 Slip length and Kapitza length

The slip length (L s) is widely used to quantitatively measure the velocity slip and is defined (Gad-el-Hak 1999) as:

$$ L_{\text{s}} = {{u_{\text{s}} } \mathord{\left/ {\vphantom {{u_{\text{s}} } {\left. {\frac{\partial u}{\partial n}} \right|_{\text{w}} }}} \right. \kern-\nulldelimiterspace} {\left. {\frac{\partial u}{\partial n}} \right|_{\text{w}} }} $$
(11)

where u s is the velocity slip. Figure 12 shows the schematic for slip, non-slip and locking velocity boundary conditions by curves a, b and c. Based on the definition by Eq. 11, the values of slip length are positive (L s,a ), zero and negative (L s,c ), respectively. Similarly, the Kapitza length (L K) is used to measure the degree of temperature jump quantitatively and is defined (Kim et al. 2008a) as:

$$ L_{\text{K}} = {{T_{\text{j}} } \mathord{\left/ {\vphantom {{T_{\text{j}} } {\left. {\frac{\partial T}{\partial n}} \right|_{\text{w}} }}} \right. \kern-\nulldelimiterspace} {\left. {\frac{\partial T}{\partial n}} \right|_{\text{w}} }} $$
(12)

where T j is the temperature jump.

Fig. 12
figure 12

Schematic of slip, non-slip and locking velocity boundary conditions

Full size image

The variations of relative slip length (L s/H) and relative Kapitza length (L K/H) versus H, p/w and β are shown in Figs. 13 and 14. In all the cases, different shapes of roughening element give very similar variation. L s/H increases sharply for small H and slightly for large H. L s/H generally increases linearly with increasing p/w. L s/H decreases sharply for small β and slightly for large β. L K/H decreases sharply for small H and slightly for large H. L K/H generally increases with increasing p/w but the rate decreases. L K/H decreases sharply for small β and slightly for large β. By curve-fitting, it is found that both L s/H and L K/H versus H still follow the power law (Sun et al. 2010; Sun et al. 2011b):

$$ \frac{{L_{\text{s}} }}{H}{\text{ or }}\frac{{L_{\text{K}} }}{H} = a\left( {\frac{H}{\sigma }} \right)^{b} $$
(13)
Fig. 13
figure 13

Variation of relative slip length (L s/H) versus a channel height (H), b pitch ratio (p/w) and c liquid–solid bonding factor (β) with different shapes of roughening element. Data for the smooth (smt) cases are from Sun et al. (2010). The solid line is a guide for the eye

Full size image
Fig. 14
figure 14

Variation of relative Kapitza length (L K/H) versus a channel height (H), b pitch ratio (p/w) and c liquid–solid bonding factor (β) with different shapes of roughening element. Data for the smooth (smt) cases are from Sun et al. (2010). The solid line is a guide for the eye

Full size image

The variations of L s/H versus β seem similar for both smooth and rough cases. They decrease rapidly when β < 5 and then decrease slightly when β > 5. The differences are small, 0.31 to −0.029 for smooth channel cases and −0.068 to −0.11 for rough channel cases. This suggests that negative slip likely occurs in rough channels while positive, zero and negative velocity slips occur in smooth channels based on different liquid–solid bonding strengths. L K/H decreases rapidly with increasing β when β < 10 for both smooth and rough channels. However, the difference emerges when β > 10, where L K/H for rough cases starts to increase (see Fig. 14c). Similar phenomenon has been found for T j of smooth cases in the previous work (Sun et al. 2010). This characteristic is apparently related to very strong liquid–solid bonding but further studies are still needed for the insight into the mechanism and regulation. Besides, it is worth mentioning that the apparent values of u s and T j to calculate L s and L K are obtained based on fitting curves despite the local characteristics near boundaries like curve c in Fig. 12.

3.3 Flow resistance

Figure 15 shows the minus pressure gradients (−dp/dx) against H, p/w and β for all cases simulated. As in the smooth channel case (see Sun et al. (2010)), −dp/dx versus H, irrespective of the shape of roughening element, can be well fitted by the power function:

$$ - \frac{{\sigma^{4} {\text{d}}p}}{{\varepsilon {\text{d}}x}} = a\left( {\frac{H}{\sigma }} \right)^{b} $$
(14)

where a and b are constants determined by curve-fitting as a = 84.84 and b = −2.289. This indicates that the shape of roughening element almost shows no influence on the variation of −dp/dx versus H in the present simulation range. It can be seen from Fig. 15a that the effect of surface topology on −dp/dx is negligible when H is great than about 150σ whereas −dp/dx for rough channels are significantly higher than those for smooth channels when H is less than about 150σ. −dp/dx generally decreases linearly with increasing p/w and increases sharply for small β and slightly for large β. The value of −dp/dx at β = 50 for the rectangular case is relatively low. This may be due to the very strong liquid–solid bonding and relatively larger contact surface area. Further investigation into the interfacial mechanism is needed.

Fig. 15
figure 15

Variation of pressure gradient (−dp/dx) versus a channel height (H), b pitch ratio (p/w) and c liquid–solid bonding factor (β) with different shapes of roughening element. Data for the smooth (smt) cases are from Sun et al. (2010). The solid line is a guide for the eye

Full size image

4 Conclusions

A parametric study is carried out using a molecular dynamics–continuum hybrid simulation method to examine the effects of liquid–solid bonding strength and surface topology on the velocity and temperature boundary conditions for liquid flow in micro/nanochannels. The conclusions are as follows:

  1. 1.

    The velocity boundary condition shifts from significant slip to locking due to the blocking of the roughening element. The locking range and temperature jump both apparently decrease with increasing H and eventually collapse to analytical solutions (with non-slip boundary conditions). The blocking influence becomes weaker with increasing p/w and becomes more appreciable with increasing β. Distorted streamlines, small eddies and appreciable density oscillation are observed in the vicinity of the wall in the flow and density fields for small p/w and large β. On the other hand, smooth streamlines and weak oscillation are observed for large p/w and small β.

  2. 2.

    The results indicate that L s/H, L K/H and −dp/dx versus H clearly follow the power laws as found in the previous work (Sun et al. 2011b). The variations of L s/H and −dp/dx versus p/w seem nearly linear while L K/H increases with increasing p/w but the rate decreases. The data for the very strong bonding cases (β > 10) seem changing unexpectedly from others, which demands further studies.

  3. 3.

    The effect of the shape of roughening element on the velocity and temperature boundary conditions is much less significant compared with the other factors studied.

The present work has revealed that when the channel size is small, the flow condition (shear rate), interactive condition (liquid–solid bonding) and geometric condition (surface topology) can considerably influence the velocity and temperature boundary conditions and friction. The present work is of value for potential use of adjusting or controlling velocity, temperature and friction by surface micro-machining.