Enhanced thermal conductivity of nanofluids: a state-of-the-art review

Abstract

Adding small particles into a fluid in cooling and heating processes is one of the methods to increase the rate of heat transfer by convection between the fluid and the surface. In the past decade, a new class of fluids called nanofluids, in which particles of size 1–100 nm with high thermal conductivity are suspended in a conventional heat transfer base fluid, have been developed. It has been shown that nanofluids containing a small amount of metallic or nonmetallic particles, such as Al₂O₃, CuO, Cu, SiO₂, TiO₂, have increased thermal conductivity compared with the thermal conductivity of the base fluid. In this work, effective thermal conductivity models of nanofluids are reviewed and comparisons between experimental findings and theoretical predictions are made. The results show that there exist significant discrepancies among the experimental data available and between the experimental findings and the theoretical model predictions.

1 Introduction

Heat transfer plays an important role in many fields such as power generation, air conditioning, transportation, and microelectronics due to the heating and cooling processes involved. It is desirable to increase the efficiency of heat transfer devices used in these fields, since in case of such an improvement, it becomes possible to reduce the size of the devices and decrease the operating costs of the associated processes. Therefore, various attempts have been made in order to enhance heat transfer in these devices.

One of the major parameters in heat transfer is the thermal conductivity of the working fluid. Commonly used fluids in heat transfer applications; such as water, ethylene glycol, and engine oil have low thermal conductivities, when compared to thermal conductivities of solids, especially metals. As a consequence, researchers have tried to find a way of improving thermal conductivity of these commonly used fluids. One of the methods to achieve this objective is to create mixtures by adding solid particles into the fluid. Since solid materials have thermal conductivities much higher than fluids, such an attempt obviously results in a thermal conductivity enhancement. Unfortunately, when the particle sizes are on the order of millimeters or micrometers, there exist severe problems in the usage of these mixtures in practice (Keblinski et al. 2002; Wang et al. 2003). Two of the problems are that the mixtures are unstable, therefore, sedimentation occurs and solid particles may erode the channel walls. In addition to these, presence of solid particles increases the pressure drop significantly, which increases the required pumping power and associated operating cost. Due to these significant drawbacks, usage of solid particles has not become practically feasible.

Recent improvements in nanotechnology made it possible to produce solid particles with diameters smaller than 100 nm. As a result, an innovative idea of preparing liquid suspensions by dispersing these nanoparticles instead of millimeter- or micrometer-sized particles in a base fluid and utilizing them for heat transfer enhancement was proposed (Masuda et al. 1993; Choi 1995). These liquid suspensions are called nanofluids. An important feature of nanofluids is that since nanoparticles are very small, they behave like fluid molecules and this solves the problem of clogging of small passages in case of the usage of larger particles. It is even possible to use nanofluids in microchannels (Chein and Chuang 2007; Lee and Mudawar 2007). It was also shown that by the use of proper activators and dispersants, it is possible to obtain stable suspensions.

In the last decade, a significant amount of experimental and theoretical research was made to investigate the thermophysical behavior of nanofluids. In these studies, it was observed that a high thermal conductivity enhancement could be obtained with nanofluids, even in the case of very small particle volume fractions. Furthermore, most of the experimental work showed that the thermal conductivity enhancement obtained by using nanoparticle suspensions was much higher than that obtained by using conventional suspensions with particles that are millimeter- or micrometer-sized. Many researchers proposed theoretical models to explain and predict those anomalous thermal conductivity ratios, defined as effective thermal conductivity of the nanofluid (k _eff) divided by the thermal conductivity of the base fluid (k _f).

In this article, experimental studies on thermal conductivity enhancement with nanofluids are reviewed. Theoretical attempts made to explain the associated thermal conductivity enhancement mechanisms are also outlined. In addition to these, theoretical models proposed for the determination of thermal conductivity of nanofluids are summarized, predictions of the models are compared with experimental findings, and significant discrepancies are indicated.

There are many reviews available in the literature about nanofluid research (Wang and Mujumdar 2007; Murshed et al. 2008a; Yu et al. 2008; Chandrasekar and Suresh 2009; Choi 2009; Wen et al. 2009). In all of the nanofluid thermal conductivity reviews, both theoretical models and experimental results are discussed. However, most of the time, a detailed comparison between theoretical models and experimental results is not provided. In this article, a systematic comparison between recent theoretical models especially developed for nanofluids and experimental results is provided, for the first time in the literature. It is thought that such an analysis provides important information about the validity of the proposed models and the associated thermal conductivity enhancement mechanisms.

2 Experimental studies of thermal conductivity

In thermal conductivity measurements of nanofluids, the transient hot-wire technique is the most commonly used method (Hong et al. 2005; Ding et al. 2006; Zhu et al. 2007; Beck et al. 2009). A modified transient hot-wire method is required in the measurements, since nanofluids conduct electricity. The modification is made by insulating the wire. Some other methods such as steady-state parallel-plate technique, temperature oscillation technique, microhot strip method, and optical beam deflection technique have also been utilized by some researchers (Wang et al. 1999; Czarnetzki and Roetzel 1995; Ju et al. 2008; Putnam et al. 2006).

Experimental studies show that thermal conductivity of nanofluids depends on many factors such as particle volume fraction, particle material, particle size, particle shape, base fluid material, and temperature. Amount and types of additives and the acidity of the nanofluid were also shown to be effective in the thermal conductivity enhancement.

In this part, experimental studies about the thermal conductivity of nanofluids are summarized. In each section, a specific parameter that is effective on thermal conductivity is discussed.

2.1 Effect of particle volume fraction

There are many studies in the literature about the effect of particle volume fraction on the thermal conductivity of nanofluids. Masuda et al. (1993) measured the thermal conductivity of nanofluids containing Al₂O₃ (13 nm), SiO₂ (12 nm), and TiO₂ (27 nm) nanoparticles (values in parentheses indicate the average particle diameter). This is the first experimental study regarding the thermal conductivity of nanofluids. Water was used as the base fluid and a two-step method was utilized for the preparation of nanofluids. An enhancement as high as 32.4% was observed for the effective thermal conductivity of 4.3 vol.% Al₂O₃/water nanofluid at 31.85 °C (all percentage enhancement values are indicated according to the expression 100(k _eff − k _f)/k _f throughout the article). It was found that thermal conductivity enhancement linearly increases with particle volume fraction. Lee et al. (1999) studied the room temperature thermal conductivity of nanofluids by dispersing Al₂O₃ (38.5 nm) and CuO (23.6 nm) nanoparticles, which were produced by gas condensation method, in water and ethylene glycol. Similar to the study of Masuda et al. (1993), a linear relationship was observed between thermal conductivity and particle volume fraction (thermal conductivity increases with particle volume fraction). Highest enhancement was 20%, which was observed for 4 vol.% CuO/ethylene glycol nanofluid. A similar study was performed by Wang et al. (1999), who examined the thermal conductivity performance of nanofluids with Al₂O₃ (28 nm) and CuO (23 nm) nanoparticles. For the case of 8 vol.% Al₂O₃/water nanofluid, thermal conductivity enhancement as high as 40% was achieved. For water- and ethylene glycol-based nanofluids, thermal conductivity ratio showed a linear relationship with particle volume fraction and the lines representing this relation were found to be coincident.

Particle volume fraction is a parameter that is investigated in almost all of the experimental studies and the results are usually in agreement qualitatively. Most of the researchers report increasing thermal conductivity with increasing particle volume fraction and the relation found is usually linear. However, there are also some studies, which indicate nonlinear behavior. An example is the study made by Murshed et al. (2005). They measured the thermal conductivity of TiO₂/deionized water nanofluid at room temperature by using transient hot-wire method. Volume fraction of nanoparticles was varied between 0.5 and 5%. A nonlinear relationship was observed between thermal conductivity ratio and particle volume fraction, especially at low volume fractions. The authors noted that the nonlinear behavior might be due to the cetyltrimethyl ammonium bromide (CTAB) surfactant, application of sonication for a long time, or hydrophobic surface forces involved. Choi et al. (2001) investigated the thermal conductivity of nanofluids prepared by dispersing multiwalled carbon nanotubes (MWCNT) in oil. They also found a nonlinear relation between thermal conductivity ratio and particle volume fraction. According to the authors, such a nonlinear relation is an indication of interactions between particles. It was concluded that despite the fact that particle volume fraction is very small, nanotubes interact with each other due to the very high particle concentration (10¹¹ particles/cm³).

2.2 Effect of particle material

Most of the studies show that particle material is an important parameter that affects the thermal conductivity of nanofluids. At first glance, it might be thought that the difference in the thermal conductivities of particle materials is the main reason of this effect. However, studies show that particle type may affect the thermal conductivity of nanofluids in other ways. For example, Lee et al. (1999) considered the thermal conductivity of nanofluids with Al₂O₃ and CuO nanoparticles as mentioned in the previous section and they found that nanofluids with CuO nanoparticles showed better enhancement when compared to the nanofluids, which are prepared by using Al₂O₃ nanoparticles. It should be noted that Al₂O₃, as a material, has higher thermal conductivity than CuO. Therefore, thermal conductivity of particle material may not be the dominant parameter that determines the thermal conductivity of the nanofluid. According to the authors, the key factor is the fact that Al₂O₃ nanoparticles formed relatively larger clusters when compared to CuO nanoparticles. That might be an explanation if the main mechanism of thermal conductivity enhancement is accepted to be the Brownian motion of nanoparticles, since the effect of Brownian motion diminishes with increasing particle size. However, it should also be noted that there are some studies that consider the clustering of nanoparticles as a thermal conductivity enhancement mechanism. Another study that considers the effect of nanoparticle type was made by Chopkar et al. (2008). They dispersed Al₂Cu and Ag₂Al nanoparticles into water and ethylene glycol. 1 vol.% oleic acid was added as the surfactant. Measurements were made at room temperature. It was found that Ag₂Al nanoparticles enhanced thermal conductivity slightly more when compared to Al₂Cu nanoparticles. According to the authors, this is due to the fact that the thermal conductivity of Ag₂Al is higher when compared to Al₂Cu.

Effect of particle material is much more pronounced when carbon nanotubes are used for the preparation of nanofluids. Choi et al. (2001) studied the thermal conductivity enhancement of oil based nanofluids containing MWCNT with a mean diameter of around 25 nm and length around 50 μm. The base fluid used was synthetic poly (α-olefin) oil. Measurements were conducted at room temperature. 160% enhancement (a thermal conductivity ratio of 2.6) was observed for 1 vol.% MWCNT/oil nanofluid. Authors noted that such an anomalous enhancement might be due to the liquid nanolayers forming around the nanotubes. On the other hand, the fact that heat is transported ballistically inside the nanotubes improves the conduction of heat in the tubes, but the effect of this factor is not dominant according to the authors. It should also be noted that the shape of nanotubes might also be effective in the anomalous enhancement values. The length of the nanotubes is on the order of micrometers, and this enables rapid heat conduction across relatively large distances, which is not possible for spherical nanoparticles as long as there is no clustering. Another study about nanofluids with carbon nanotubes was made by Assael et al. (2005). They compared the nanofluids containing double-walled CNT (DWCNT) and MWCNT. For DWCNT, average outer diameter was 5 nm and average inner diameter was larger than 2.5 nm. It was noted that MWCNT also exist in the samples with DWCNT. For MWCNT, length was larger than 10 µm and average outer diameter was 130 nm. Thickness of the walls was determined to be around 90 graphitic layers (about 30 nm) with interlayer distance around 0.34 nm. CTAB and Nanosperse AQ were added to the nanofluids and ultrasonic vibration was applied in order to obtain proper dispersion. Transient hot-wire method was used in the measurements. A thermal conductivity enhancement as high as 34% was achieved for the 0.6 vol.% MWCNT/water nanofluid, whereas the 0.75 vol.% DWCNT/water nanofluid showed only 3% enhancement. Authors noted that the reason of such low enhancement was that the size of the DWCNT reached the order of micrometers due to clustering effects.

It should also be noted that the mean-free path of phonons in nanoparticles may be smaller than the size of the nanoparticles. In such a condition, heat transfer mechanism inside the particles is not diffusion but heat is transported ballistically. When this fact is considered, relating the superior enhancement characteristics of a specific nanoparticle material to its high bulk thermal conductivity is not reasonable.

2.3 Effect of base fluid

According to the conventional thermal conductivity models such as the Maxwell (1873) model, as the base fluid thermal conductivity of a mixture decreases, the thermal conductivity ratio (thermal conductivity of nanofluid divided by the thermal conductivity of base fluid) increases. When it comes to nanofluids, the situation is more complicated due to the fact that the viscosity of the base fluid affects the Brownian motion of nanoparticles and that in turn affects the thermal conductivity of the nanofluid (Xuan et al. 2003). Moreover, Lee (2007) examined the effect of electric double layer forming around nanoparticles on the thermal conductivity of nanofluids and showed that the thermal conductivity and thickness of the layer depends on the base fluid. It is difficult to determine the quantitative effects of these factors completely. Therefore, systematic experiments are required that will show the effect of base fluid on the thermal conductivity of nanofluids. Some experimental studies made in this area are summarized below.

In the previously mentioned study of Wang et al. (1999), Al₂O₃ and CuO nanoparticles were used to prepare nanofluids with several base fluids; water, ethylene glycol, vacuum pump fluid, and engine oil. With Al₂O₃ nanoparticles, the highest thermal conductivity ratio was observed when ethylene glycol was used as the base fluid. Engine oil showed somewhat lower thermal conductivity ratios than ethylene glycol. Water and pump fluid showed even smaller ratios, respectively. With CuO nanoparticles, only ethylene glycol- and water-based nanofluids were prepared and it is interesting to note that they showed exactly the same thermal conductivity ratios for the same particle volume fraction. The effect of the base fluid on the thermal conductivity of nanofluids was also analyzed by Xie et al. (2002b). Nanofluids with Al₂O₃ nanoparticles were prepared by using different base fluids; deionized water, glycerol, ethylene glycol, and pump oil. In addition, ethylene glycol–water and glycerol–water mixtures with different volume fractions were also used as base fluids and the variation of the thermal conductivity ratio with thermal conductivity of the base fluid mixture was examined. It was seen that, thermal conductivity ratio decreased with increasing thermal conductivity of the base fluid. Results were compared with a theoretical analysis made by Hasselman and Johnson (1987). Theoretical results were found to be nearly independent of the thermal conductivity of the base fluid, being contrary to the experimental data. However, it should be noted that these experimental results are in agreement with the Maxwell (1873) model qualitatively. Chopkar et al. (2008) also analyzed the effect of base fluid by comparing water and ethylene glycol. Al₂Cu and Ag₂Al nanoparticles were used in the study and it was found that water-based nanofluids showed a higher thermal conductivity ratio. It should be noted that more than 100% enhancement was obtained for the 2.0 vol.% Ag₂Al (30 nm)/water nanofluid.

Base fluid effect was also investigated with MWCNT nanofluids. Ethylene glycol and synthetic engine oil were used as base fluids in the experiments conducted by Liu et al. (2005). Thermal conductivity of nanofluids were measured by a transient hot-wire method. 1 vol.% MWCNT/ethylene glycol nanofluid showed 12.4% thermal conductivity enhancement, whereas for 2 vol.% MWCNT/synthetic engine oil nanofluid, enhancement was 30%. It was observed that higher enhancements were achieved with synthetic engine oil as the base fluid, in general.

2.4 Effect of particle size

Particle size is another important parameter of thermal conductivity of nanofluids. It is possible to produce nanoparticles of various sizes, generally ranging between 5 and 100 nm. Eastman et al. (2001) studied Cu nanoparticles, with ethylene glycol as the base fluid. By using a one-step production method, suspensions with Cu nanoparticles smaller than 10 nm were obtained. Thioglycolic acid less than 1 vol.% was added to some of the samples for stabilizing purposes and those samples showed much better enhancement when compared to samples without thioglycolic acid. A 40% increase in thermal conductivity was observed at a particle volume fraction of 0.3% (with thioglycolic acid). To make a comparison, it should be noted that in the study of Lee et al. (1999), researchers obtained 20% enhancement with 4 vol.% CuO (23.6 nm)/ethylene glycol nanofluid. As a result of the anomalous enhancements obtained, Eastman et al. concluded that the size of the nanoparticles is an important factor that affects the thermal conductivity enhancement, which is contrary to the predictions of conventional models such as Hamilton and Crosser (1962) model, which does not take the effect of particle size on thermal conductivity into account. Chopkar et al. (2006) prepared nanofluids by dispersing Al₇₀Cu₃₀ nanoparticles into ethylene glycol. Nanoparticles were obtained by mechanical alloying. By transmission electron microscopy, they illustrated the fact that there is no significant clustering in the samples. They varied the particle size between 9 and 83 nm and they showed that thermal conductivity enhancement decreases with increasing particle size. For 0.5 vol.% nanofluid, thermal conductivity enhancement decreased from 38 to 3% by increasing the particle size from 9 to 83 nm. In another study, Chopkar et al. (2008) investigated the effect of particle size on the thermal conductivity of water- and ethylene glycol-based nanofluids with Al₂Cu and Ag₂Al nanoparticles. Nanoparticles with sizes varying between 30 and 120 nm were used in the study. For all four types of nanofluids, it was observed that thermal conductivity enhancement increases with decreasing particle size.

Another systematic particle size dependence study for the thermal conductivity of nanofluids was made by Beck et al. (2009) for Al₂O₃/water and Al₂O₃/ethylene glycol nanofluids. Particle size was varied between 8 and 282 nm. HCl was added to the nanofluids to adjust the pH value to 4. Conductivity measurements were carried out by a transient hot-wire method at room temperature. It was observed that for the same particle volume fraction, thermal conductivity ratio decreases with decreasing particle size. This effect is more pronounced for nanofluids with particles smaller than 50 nm. As a result of the experimental findings, it was concluded that nanoparticle thermal conductivity decrease with decreasing particle size is responsible for the observed size dependence of the thermal conductivity of nanofluids. It should be noted that these results are not in agreement with the aforementioned studies. The results also contradict with the effect of Brownian motion, since the effect of Brownian motion decreases with increasing particle size, which decreases the associated thermal conductivity enhancement. Mintsa et al. (2009) measured the thermal conductivity of Al₂O₃/water nanofluids. Two different sizes of Al₂O₃ nanoparticles were used in the experiment (36 and 47 nm). Particle volume fraction was varied between 0 and 18% and temperature was varied between 20 and 50 °C. It was observed that the thermal conductivity enhancements were nearly the same for the two different particle sizes of Al₂O₃ nanoparticles at room temperature. However, at higher temperatures, Al₂O₃/water nanofluid with smaller particles showed higher enhancement. The experimental results were compared with theoretical models and it was concluded that the model proposed by Chon et al. (2005) predicted their experimental data well. On the contrary, when the temperature dependent thermal conductivity data of Al₂O₃/water nanofluid provided by Murshed et al. (2008b), Das et al. (2003), and Chon and Kihm (2005) is compared, it is seen that the thermal conductivity ratio is not much different from each other for significantly different particle sizes (80, 38.4, and 47 nm, respectively).

The general trend in the experimental data is that the thermal conductivity of nanofluids increases with decreasing particle size. This trend is theoretically supported by two mechanisms of thermal conductivity enhancement; Brownian motion of nanoparticles and liquid layering around nanoparticles. However, there is also significant amount of contradictory data in the literature that indicate decreasing thermal conductivity with decreasing particle size. In fact, for the case of nanofluids with Al₂O₃ nanoparticles, such results are more common than the results showing increasing thermal conductivity with decreasing particle size. The associated data for Al₂O₃/water nanofluids is illustrated in Sect. 4.2. It is thought that the data indicating decreasing thermal conductivity with decreasing particle size may be the result of severe clustering of nanoparticles in the associated samples. Although clustering at a certain level may improve thermal conductivity enhancement, excessive clustering creates an opposite effect due to associated sedimentation (Prasher et al. 2006). At this point, it is important to note that Feng et al. (2007) showed that clustering effects are more pronounced in nanofluid samples with smaller particles. This may explain the results in which nanofluids with smaller particles show lower enhancement.

2.5 Effect of particle shape

There are mainly two particle shapes used in nanofluid research; spherical particles and cylindrical particles. Cylindrical particles usually have a large length-to-diameter ratio. The thermal conductivity of SiC/distilled water and SiC/ethylene glycol nanofluids were investigated by Xie et al. (2002a). Two types of nanoparticles were used for the preparation of nanofluids; spherical particles with 26 nm average diameter and cylindrical particles with 600 nm average diameter. It was found that 4.2 vol.% water-based nanofluid with spherical particles had a thermal conductivity enhancement of 15.8%, whereas 4 vol.% nanofluid with cylindrical particles had a thermal conductivity enhancement of 22.9%. Authors compared the results with the Hamilton and Crosser (1962) model. It was noted that Hamilton and Crosser model was successful in predicting the enhancement in cylindrical particles, whereas it underestimated the values associated with nanofluids with spherical particles. Another study related to the particle shape was made by Murshed et al. (2005). They measured the thermal conductivity of TiO₂/deionized water nanofluid. Two types of nanoparticles were used, spherical particles (15 nm) and rod-shaped particles (10 nm in diameter and 40 nm in length). Stability and dispersion of nanoparticles were improved by using oleic acid and CTAB surfactants. For nanofluids with spherical particles, a maximum enhancement of 29.7% was obtained at 5 vol.%. At the same volume fraction, rod-shaped nanoparticles showed an enhancement of 32.8%.

In addition to these experimental results, the fact that nanofluids with carbon nanotubes (which are cylindrical in shape) generally show greater thermal conductivity enhancement than nanofluids with spherical particles should also be considered. As a result, one can conclude that cylindrical nanoparticles provide higher thermal conductivity enhancement than spherical particles. One of the possible reasons of this is the rapid heat transport along relatively larger distances in cylindrical particles since cylindrical particles usually have lengths on the order of micrometers. However, it should be noted that nanofluids with cylindrical particles usually have much larger viscosities than those with spherical nanoparticles (Timofeeva et al. 2009). As a result, the associated increase in pumping power is large and this reduces the feasibility of usage of nanofluids with cylindrical particles.

2.6 Effect of temperature

In conventional suspensions of solid particles (with sizes on the order of millimeters or micrometers) in liquids, thermal conductivity of the mixture depends on temperature only due to the dependence of thermal conductivity of base liquid and solid particles on temperature. However, in case of nanofluids, change of temperature affects the Brownian motion of nanoparticles and clustering of nanoparticles (Li et al. 2008a), which results in dramatic changes of thermal conductivity of nanofluids with temperature. Masuda et al. (1993) measured the thermal conductivity of water-based nanofluids containing Al₂O₃, SiO₂, and TiO₂ nanoparticles at different temperatures. Thermal conductivity ratio decreased with increasing temperature, which is contradictory to many findings in the literature. The temperature dependence of the thermal conductivity of Al₂O₃ (38.4 nm)/water and CuO (28.6 nm)/water nanofluids was studied by Das et al. (2003). Thermal diffusivity was measured by using a temperature oscillation technique and then thermal conductivity was calculated. Several measurements were made at different temperatures varying between 21 and 51 °C. It was seen that for 1 vol.% Al₂O₃/water nanofluid, thermal conductivity enhancement increased from 2% at 21 °C to 10.8% at 51 °C. Temperature dependence of 4 vol.% Al₂O₃ nanofluid was much more significant. From 21 to 51 °C, enhancement increased from 9.4 to 24.3%. A linear relationship between thermal conductivity ratio and temperature was observed at both 1 and 4 vol.% cases. Li and Peterson (2006) also investigated the effect of temperature on thermal conductivity of CuO (29 nm)/water and Al₂O₃ (36 nm)/water nanofluids. For both nanofluid types, it was observed that at a constant particle volume fraction thermal conductivity ratio increased with temperature. In addition, it was noted that for Al₂O₃/water nanofluid, the dependence of thermal conductivity ratio on particle volume fraction became more pronounced with increasing temperature. A regression analysis based on the experimental data showed that particle volume fraction dependence of thermal conductivity is much higher than the temperature dependence. For the Al₂O₃/water nanofluid and CuO/water nanofluid, two correlations were proposed for the determination of the thermal conductivity. Another study regarding the temperature dependence of thermal conductivity was made by Turgut et al. (2009). They measured the thermal conductivity of TiO₂ (21 nm)/deionized water nanofluid. Nanofluids used in the experiment were prepared by a two-step method and ultrasonic vibration was applied to the samples. 3ω method was used in the measurements. Measurements were made at different temperatures; 13, 23, 40, and 55 °C. Particle volume fraction of the sample nanofluids were varied between 0.2 and 3 vol.%. It was noted that the results of the analysis can be well predicted by conventional theoretical models such as Hamilton and Crosser (1962) model. It was also observed that thermal conductivity ratio does not vary with temperature significantly. This observation is contradictory with the aforementioned studies. The results can be considered as an indication of the importance of the usage of surfactants in nanofluids, because no surfactant was used in this study.

Temperature dependence of thermal conductivity of nanofluids was also investigated for the case of nanofluids with carbon nanotubes. Ding et al. (2006) measured the thermal conductivity of MWCNT/water nanofluid. Ultrasonic vibration was applied to samples. First Gum Arabic was added to the samples in order to obtain better dispersion and to adjust the pH value, then the nanofluid was homogenized with a high shear homogenizer. Transient hot-wire method was applied for thermal conductivity measurements. No information was given about the size of MWCNT but from the provided scanning electron microscopy images, a very rough estimation of nanotube diameter could be made as 40 nm. Measurements were made at three different temperatures; 20, 25, and 30 °C. Particle weight fraction was varied between 0.1 and 1%. It was found that thermal conductivity ratio increases with both particle volume fraction and temperature. However, at 20 and 25 °C, increase of thermal conductivity ratio with particle volume fraction stopped after 0.5 wt%. On the other hand, at 30 °C, thermal conductivity ratio continued to increase after 0.5 wt%. A maximum enhancement of 80% was achieved at 30 °C for 1 wt% of MWCNT/water nanofluid. At 20 °C, the associated enhancement decreased to 10%.

Thermal conductivity research of nanofluids in terms of temperature dependence is not limited to the aforementioned studies. Other research efforts about the dependence of thermal conductivity on temperature for various nanofluids exists (Zhang et al. 2006a, b; Roy et al. 2006; Murshed et al. 2008b).

2.7 Effect of clustering

Clustering effect is always present in nanofluids and it is an effective parameter in thermal conductivity. Hong et al. (2006) investigated this effect for Fe (10 nm)/ethylene glycol nanofluids. The thermal conductivity of nanofluids were determined as a function of the duration of the application of the ultrasonic vibration, which was varied between 0 min, that is, no vibration applied, and 70 min. It was seen that thermal conductivity ratio increased with increasing vibration time and the rate of this increase became smaller for longer vibration time. Furthermore, the variation of thermal conductivity of nanofluid with time after the application of vibration was investigated and it was found that thermal conductivity decreases as time progressed. Variation of average size of clusters was also determined as a function of time after the application of vibration and it was noted that cluster size increases with time. As a result of these observations, it was concluded that the size of the clusters formed by the nanoparticles had a major influence on the thermal conductivity. In addition, the variation of thermal conductivity ratio of the Fe/ethylene glycol nanofluid with particle volume fraction was found to be nonlinear. It was stated that this behavior is due to the fact that nanoparticles in the nanofluids with high volume fractions formed clusters at a higher rate. It should be noted that Zhu et al. (2006) also examined the effect of nanoparticle clustering, on the thermal conductivity of Fe₃O₄/water nanofluid and noted that clustering and nanoparticle alignment were mainly responsible for the anomalous thermal conductivity enhancement.

Theoretical aspects of clustering of nanoparticles are discussed in Sect. 3.2.

2.8 Effect of pH

The number of studies regarding the pH value of nanofluids is limited when compared to the studies regarding the other parameters. Xie et al. (2002c) measured the thermal conductivity of nanofluids, which are prepared by dispersing Al₂O₃ nanoparticles into water, ethylene glycol, and pump oil. They reported significant decrease in thermal conductivity ratio with increasing pH values. It was also observed that the rate of change of thermal conductivity with particle volume fraction was dependent on pH value. Thermal conductivity enhancement of 5 vol.% Al₂O₃/water nanofluid is 23% when pH is equal to 2.0 and it becomes 19% when pH is equal to 11.5. Authors related the dependence of thermal conductivity on pH to the fact that as the difference between the isoelectric point of Al₂O₃ nanoparticles and pH value of the solution increases, mobility of nanoparticles increases, which improve the micro-convection effect. Wang et al. (2009) also investigated the effect of pH on the thermal conductivity of nanofluids. They considered Cu/water and Al₂O₃/water nanofluids. As the dispersant, sodium dodecylbenzene sulfonate was added to the samples. They obtained optimum values of pH (approximately 8.0 for Al₂O₃/water and 9.5 for Cu/water nanofluids) for maximum thermal conductivity enhancement. It should also be noted that the thermal conductivity of base fluid does not change significantly with pH. Authors related the observed phenomenon to the fact that at the optimum value of pH, surface charge of nanoparticles increases, which creates repulsive forces between nanoparticles. As a result of this effect, severe clustering of nanoparticles is prevented (excessive clustering may result in sedimentation, which decreases thermal conductivity enhancement). Another study regarding the pH of nanofluids was presented by Murshed et al. (2008c). They investigated the thermal conductivity of TiO₂/water nanofluid and observed a decrease in the thermal conductivity with increasing pH value. However, this decrease is not significant, only 2% change was observed when pH value was increased from 3.4 to 9.

Although the exact quantitative values are not known, it was shown that pH value affects the thermal conductivity of nanofluids. This is mainly due to the associated change in the surface charge of nanoparticles. In most of the nanofluids research, some additives are used in the samples for obtaining proper dispersion characteristics, which also alters the pH values of the nanofluids. Unfortunately, most of the researchers do not report detailed information about the pH values of the samples they utilized in the measurements. As a consequence, it is thought that the effect of pH value of nanofluid might be one of the main reasons of discrepancy in thermal conductivity data.

Yu et al. (2008) systematically analyze the effects of most of these parameters by comparing various experimental data and tabulate the significant results. Partially based on the tables provided by Yu et al. (2008), we summarize aforementioned experimental studies on thermal conductivity of nanofluids in Table 1. When Table 1 is observed, it is seen that there exists significant discrepancy in experimental data. An important issue regarding this discrepancy in experimental data is the debate about the measurement techniques. Li et al. (2008b) compared the transient hot-wire method and steady-state cut-bar method and showed that the results of thermal conductivity measurements conducted at room temperature do not differ in these two measurement techniques. However, the authors noted that there is significant discrepancy in the data when measurements are conducted at higher temperatures. The authors explained this discrepancy by the fact that natural convection effect in the transient hot-wire method starts to deviate the results in a sense that higher values are measured by the method. At this point, the study of Ju et al. (2008) should also be mentioned. They showed that transient hot-wire method can give erroneous results if the measurements are carried out just after the sonication since sonication results in an increase in the temperature of the sample. In their study, the effect of this temperature increase lasted for 50 min. In addition to this, they noted that the measurements made successively (in order to prevent random errors) can also create erroneous results if the interval between heating pulses is around 5 s. Therefore, although Li et al. (2008b) found nearly the same thermal conductivity values in their measurements, there might still be some erroneous results in the literature due to the abovementioned factors noted by Ju et al. (2008).

Table 1 Summary of experimental studies of thermal conductivity enhancement

Consequently, to improve the accuracy of predicting the effective thermal conductivity of nanofluids and to improve their potential benefits in heat transfer enhancement, more experimental investigation and data sets are needed for the verification of the models used.

3 Theoretical studies of thermal conductivity

More than a century ago, Maxwell derived an equation for calculating the effective thermal conductivity of a solid–liquid mixture consisting of spherical particles (Maxwell 1873):

$$ k_{\text{eff}} = {\frac{{k_{\text{p}} + 2k_{\text{f}} + 2(k_{\text{p}} - k_{\text{f}} )\phi }}{{k_{\text{p}} + 2k_{\text{f}} - (k_{\text{p}} - k_{\text{f}} )\phi }}}k_{\text{f}} , $$

(1)

where k _eff, k _p, and k _f are the thermal conductivity of the nanofluid, nanoparticles and base fluid, respectively. ϕ is the volume fraction of particles in the mixture. As seen from the expression, the effect of the size and shape of the particles was not included in the analysis. It should be noted that the interaction between the particles was also neglected in the derivation.

Hamilton and Crosser (1962) extended the Maxwell model in order to take the effect of the shape of the solid particles into account, in addition to the thermal conductivities of solid and liquid phases and particle volume fraction. The model is as follows:

$$ k_{\text{eff}} = {\frac{{k_{\text{p}} + (n - 1)k_{\text{f}} - (n - 1)\phi (k_{\text{f}} - k_{\text{p}} )}}{{k_{\text{p}} + (n - 1)k_{\text{l}} + \phi (k_{\text{f}} - k_{\text{p}} )}}}k_{\text{f}} , $$

(2)

where n is the empirical shape factor and it is defined as:

$$ n = {\frac{3}{\psi }}, $$

(3)

where ψ is the sphericity. Sphericity is the ratio of the surface area of a sphere with a volume equal to that of the particle to the surface area of the particle. Therefore, n = 3 for a sphere and in that case the Hamilton and Crosser model becomes identical to the Maxwell (1873) model.

Both Maxwell and Hamilton and Crosser models were originally derived for relatively larger solid particles that have diameters on the order of millimeters or micrometers. Therefore, it is questionable whether these models are able to predict the effective thermal conductivity of nanofluids. Nevertheless, these models are utilized frequently due to their simplicity in the study of nanofluids to have a comparison between theoretical and experimental findings.

Recently, many theoretical studies were made and several mechanisms were proposed in order to explain the anomalous thermal conductivity enhancement obtained with nanofluids. In the following sections, proposed mechanisms of thermal conductivity enhancement in nanofluids are discussed and thermal conductivity models based on those mechanisms are summarized.

3.1 Brownian motion of nanoparticles

Brownian motion is the random motion of particles suspended in a fluid. When nanofluids are considered, this random motion transports energy directly by nanoparticles. In addition, a micro-convection effect, which is due to the fluid mixing around nanoparticles, is also proposed to be important. There are many studies in the literature regarding the effect of Brownian motion on the thermal conductivity of nanofluids. Bhattacharya et al. (2004) used Brownian dynamics simulation to determine the effective thermal conductivity of nanofluids, by considering the Brownian motion of the nanoparticles. Effective thermal conductivity of the nanofluid was defined as:

$$ k_{\text{eff}} = \phi k_{\text{p}} + (1 - \phi )k_{\text{f}} , $$

(4)

where k _p is not simply the bulk thermal conductivity of the nanoparticles, but it also includes the effect of the Brownian motion of the nanoparticles on the thermal conductivity. A method called the Brownian dynamics simulation was developed, the expressions were provided to calculate k _p, then the effective thermal conductivity of Cu/ethylene glycol and Al₂O₃/ethylene glycol nanofluids were calculated for different particle volume fractions. The results were compared with previous experimental data (Eastman et al. 2001; Xie et al. 2002c) and they were found to be in agreement. The prediction of the Hamilton and Crosser (1962) model for these two nanofluids was also included in the comparison. It was found that conduction-based Hamilton and Crosser model underpredicted the effective thermal conductivity of the nanofluid, since it does not take into account the Brownian motion of the particles within the base fluid. Prasher et al. (2005) compared the effect of translational Brownian motion and convection induced by Brownian motion. They also considered the existence of an interparticle potential. By making an order-of-magnitude analysis, authors concluded that convection in the liquid induced by Brownian motion of nanoparticles was mainly responsible for the anomalous thermal conductivity enhancement of nanofluids. It should be noted that in their work, the authors did not analyze the effect of clustering of nanoparticles.

There are also some studies, which propose that Brownian motion is not very effective in thermal conductivity enhancement. For example, Evans et al. (2006) theoretically showed that the thermal conductivity enhancement due to Brownian motion is a very small fraction of the thermal conductivity of the base fluid. This fact was also verified by molecular dynamics simulations. As a result, it was concluded that Brownian motion of nanoparticles could not be the main cause of anomalous thermal conductivity enhancement with nanofluids. Another study was made by Li and Peterson (2007) who investigated the effect of mixing due to the Brownian motion of nanoparticles on the effective thermal conductivity of nanofluids numerically. Velocity, pressure, and temperature distribution around the nanoparticles were investigated for a single nanoparticle, for two nanoparticles, and for numerous nanoparticles. It was seen that improvement in thermal conduction capability of the nanofluid induced by two nanoparticles that were close to each other was more than twice the improvement observed for a single nanoparticle. A similar behavior was also observed for the simulation of several nanoparticles. As a result, it was concluded that the mixing effect created by the Brownian motion of the nanoparticles is an important reason of the large thermal conductivity enhancement of nanofluids. It should be noted that in this study, the flow around the nanoparticles was solved as if the nanoparticles are macroscale objects. Slip boundary condition and wettability of particles were not considered.

Many models were developed for the determination of thermal conductivity of nanofluids based on the Brownian motion of nanoparticles. Three of these models are explained below. Additionally, an empirical model is also discussed which provides information about the effect of Brownian motion on thermal conductivity of nanofluids.

Jang and Choi (2004) modeled the thermal conductivity of nanofluids by considering the effect of Brownian motion of nanoparticles. The proposed model is a function of not only thermal conductivities of the base fluid and nanoparticles, but it also depends on the temperature and size of the nanoparticles. Energy transport in nanofluids was considered to consist of four modes; heat conduction in the base fluid, heat conduction in nanoparticles, collisions between nanoparticles (due to Brownian motion), and micro-convection caused by the random motion of the nanoparticles. Among these, the collisions between nanoparticles were found to be negligible when compared to other modes. As a result of the consideration of the three remaining modes, the following expression was presented:

$$ k_{\text{eff}} = k_{\text{f}} (1 - \phi ) + k_{\text{p}}^{*} \phi + 3C_{\text{l}} {\frac{{d_{\text{f}} }}{{d_{\text{p}} }}}k_{\text{f}} {Re}_{\text{d}}^{2} Pr_{\text{f}} \phi , $$

(5)

where C _l is a proportionality constant, d _f the diameter of the fluid molecules, d _p the diameter of the nanoparticles, Pr _f Prandtl number of base fluid, and k ^*_p is defined so that it also includes the effect of the Kapitza resistance,

$$ k_{\text{p}}^{*} = \beta k_{\text{p}} , $$

(6)

where β is a constant. Reynolds number is defined as:

$$ {Re}_{\text{d}} = {\frac{{\bar{C}_{{{\text{R}}.{\text{M}}.}} d_{\text{p}} }}{{\nu_{\text{f}} }}}, $$

(7)

where $\bar{C}_{{{\text{R}} . {\text{M}} .}}$ is the random motion velocity of the nanoparticles and ν _f is the kinematic viscosity of the base fluid. $\bar{C}_{{{\text{R}} . {\text{M}} .}}$ can be determined by using

$$ \bar{C}_{{{\text{R}} . {\text{M}} .}} = {\frac{{D_{\text{o}} }}{{\lambda_{\text{f}} }}}, $$

(8)

where λ _f is the mean-free path of the base fluid molecules. D _o is nanoparticle diffusion coefficient and it can be calculated by using the following expression (Einstein 1956):

$$ D_{\text{o}} = {\frac{{k_{\text{B}} T}}{{3\pi \mu_{\text{f}} d_{\text{p}} }}} $$

(9)

k _B is the Boltzmann constant, T the temperature in K, and µ_f the dynamic viscosity of base fluid. When the model’s dependence on nanoparticle size is considered, it is seen that nanofluid thermal conductivity increases with decreasing particle size, since decreasing particle size increases the effect of Brownian motion. In the derivation of this model, thickness of the thermal boundary layer around the nanoparticles was taken to be equal to 3d _f/Pr, where d _f is the diameter of the base fluid molecule. Furthermore, the volume fraction of the liquid layer around nanoparticles was assumed to be equal to the nanoparticle volume fraction. These assumptions and some others were criticized by Prasher et al. (2006) since they were not verified by any means.

Koo and Kleinstreuer (2004) considered the thermal conductivity of nanofluids to be composed of two parts:

$$ k_{\text{eff}} = k_{\text{static}} + k_{\text{Brownian}} , $$

(10)

where k _static represents the thermal conductivity enhancement due to the higher thermal conductivity of the nanoparticles and k _Brownian takes the effect of Brownian motion into account. For the static part, classical Maxwell (1873) model was proposed:

$$ {\frac{{k_{\text{eff}} }}{{k_{\text{f}} }}} = {\frac{{k_{\text{p}} + 2k_{\text{f}} + 2(k_{\text{p}} - k_{\text{f}} )\phi }}{{k_{\text{p}} + 2k_{\text{f}} - (k_{\text{p}} - k_{\text{f}} )\phi }}}. $$

(11)

For k _Brownian, Brownian motion of particles was considered together with the effect of fluid particles moving with nanoparticles around them. As a result, the following expression was proposed:

$$ k_{\text{Brownian}} = 5 \times 10^{4} \beta \phi \rho_{\text{f}} c_{{{\text{p}},{\text{f}}}} \sqrt {{\frac{{k_{\text{B}} T}}{{\rho_{\text{p}} d_{\text{p}} }}}} f, $$

(12)

where ρ_p and ρ_f are the density of nanoparticles and base fluid, respectively, and T the temperature in K. c _p,f is specific heat capacity of base fluid. In the analysis, the interactions between nanoparticles and fluid volumes moving around them were not considered and an additional term, β, was introduced in order to take that effect into account. Koo and Kleinstreuer indicated that this term becomes more effective with increasing volume fraction. Another parameter, f, was introduced to the model in order to increase the temperature dependency of the model. Both f and β were determined by utilizing available experimental data:

$$ f = ( - 134.63 + 1722.3\phi ) + (0.4705 - 6.04\phi )T, $$

(13)

which is obtained by using the results of the study of Das et al. (2003) for CuO nanofluids. For other nanofluids, f can be taken as 1 due to lack of experimental data. Associated β values are listed in Table 2. It is difficult to determine theoretical expressions for f and β due to the complexities involved and this can be considered as a drawback of the model.

Table 2 β values for different nanoparticles to be used in Eq. 12 (Koo and Kleinstreuer 2004)

Xu et al. (2006) proposed another thermal conductivity model for nanofluids, based on the Brownian motion of nanoparticles. Thermal conductivity was modeled to be composed of a static and a dynamic part, similar to the aforementioned study of Koo and Kleinstreuer (2004):

$$ k_{\text{eff}} = k_{\text{static}} + k_{\text{dynamic}} . $$

(14)

The static part can be determined from the Hamilton and Crosser (1962) model (Eqs. 2, 3). The dynamic part was modeled by considering the flow over the nanoparticles and taking the fractal distribution of the nanoparticle sizes into account:

$$ k_{\text{dynamic}} = k_{\text{f}} c{\frac{{Nu \cdot d_{\text{f}} }}{Pr}}{\frac{{(2 - D_{\text{f}} )D_{\text{f}} }}{{(1 - D_{\text{f}} )^{2} }}}{\frac{{\left[ {\left( {{\frac{{d_{{{\text{p}},\max }} }}{{d_{{{\text{p}},\min }} }}}} \right)^{{1 - D_{\text{f}} }} - 1} \right]^{2} }}{{\left( {{\frac{{d_{{{\text{p}},\max }} }}{{d_{{{\text{p}},\min }} }}}} \right)^{{2 - D_{\text{f}} }} - 1}}}{\frac{1}{{\bar{d}_{\text{p}} }}}, $$

(15)

where

$$ D_{\text{f}} = 2 - {\frac{\ln \phi }{{\ln \left( {{\frac{{d_{{{\text{p}},\min }} }}{{d_{{{\text{p}},\max }} }}}} \right)}}}. $$

(16)

Here, c is an empirical constant, $\bar{d}_{\text{p}}$ is the average diameter of nanoparticles, and d _p,min and d _p,max are the minimum and maximum diameters of nanoparticles. It was noted that d _p,min /d _p,max can be taken as 0.001. Nusselt number for liquid flow over a sphere is (Tomotika et al. 1953)

$$ Nu = 2.0 + 0.5{Re} {Pr} + {\text{O}}({Re}^{2} {Pr}^{2} ), $$

(17)

where

$$ Pr = {\frac{{\mu_{\text{f}} c_{{{\text{p}},{\text{f}}}} }}{{k_{\text{f}} }}} $$

(18)

and

$$ Re = {\frac{{d_{\text{p}} u_{\text{p}} }}{{\upsilon_{\text{f}} }}}, $$

(19)

where u _p is the velocity of nanoparticles. Since Re < < 1 and Pr is of the order of 1, Nu ≈ 2. Constant c comes from the fact that the thermal boundary layer around the nanoparticle due to the Brownian motion of the particle is not known. The proposed model was compared with experimental data and it was shown that c is a function of the type of base fluid and it does not depend on the type of nanoparticles. c is found to be 85.0 for deionized water and 280.0 for ethylene glycol. Thermal conductivity enhancement predicted by the model decreases with increasing particle size. It was noted that this is due to the fact that the effect of Brownian motion diminishes with increasing particle size. It should also be noted that the expression used for the Nusselt number is for macroscale flows and it does not consider microscale effects such as slip flow at the surface of the nanoparticles.

Chon et al. (2005) investigated the thermal conductivity of Al₂O₃/water nanofluid experimentally and proposed a correlation for the determination of the thermal conductivity of Al₂O₃ nanofluids based on the experimental data. Three different nanopowders were used in the experiments with nominal diameters of 11, 47, and 150 nm. Experimental data showed that thermal conductivity increases with increasing temperature and decreasing particle size. Dependence on temperature becomes more pronounced at higher temperatures.

The correlation provided is

$$ {\frac{{k_{\text{eff}} }}{{k_{\text{f}} }}} = 1 + 64.7\phi^{0.7460} \left( {{\frac{{d_{\text{f}} }}{{d_{\text{p}} }}}} \right)^{0.3690} \left( {{\frac{{k_{\text{p}} }}{{k_{\text{f}} }}}} \right)^{0.7476} {Pr}^{0.9955} {Re}^{1.2321} , $$

(20)

where Prandtl number and Reynolds number are defined as:

$$ Pr = {\frac{{\mu_{\text{f}} }}{{\rho_{\text{f}} \alpha_{\text{f}} }}} $$

(21)

and

$$ Re = {\frac{{\rho_{\text{f}} V_{\text{Br}} d_{\text{p}} }}{{\mu_{\text{f}} }}} = {\frac{{\rho_{\text{f}} k_{\text{B}} T}}{{3\pi \mu_{\text{f}}^{2} \lambda_{\text{f}} }}}. $$

(22)

α_f is the thermal diffusivity of the base fluid. The dynamic viscosity of the base fluid is

$$ \mu_{\text{f}} = A \cdot 10^{B/(T - C)} , $$

(23)

where A, B, and C are constants, which are equal to 2.414 × 10⁻⁵, 247.8, and 140, respectively, for water. T is in K. V _Br is the Brownian velocity of nanoparticles (Einstein 1956),

$$ V_{\text{Br}} = {\frac{{k_{\text{B}} T}}{{3\pi \mu d_{\text{p}} \lambda_{\text{f}} }}} = {\frac{{k_{\text{B}} }}{{3\pi d_{\text{p}} \lambda_{\text{f}} }}} \cdot {\frac{T}{{A \cdot 10^{B/(T - C)} }}}, $$

(24)

where λ _f is the mean-free path and it was taken as 0.17 nm for water.

In the correlation provided, effects of the base fluid thermal conductivity, Prandtl number, and Reynolds number were investigated and it was seen that Reynolds number, which is a measure of the mobility of particles, is the dominant factor in determining the amount of thermal conductivity enhancement. Then, it was concluded that Brownian motion is mainly responsible for the anomalous enhancement in thermal conductivity. Brownian velocity of nanoparticles were also examined through the expression given for V _Br and it was stressed that temperature increases the Brownian motion, whereas increasing particle size slows down the particles dramatically. The correlation provided is valid for nanoparticle sizes ranging between 11 and 150 nm. For temperature, the associated validity range is 21–71 °C.

3.2 Clustering of nanoparticles

Nanoparticles are known to form clusters (Prasher et al. 2006; He et al. 2007). These clusters can be handled by using fractal theory (Wang et al. 2003). Evans et al. (2008) proposed that clustering can result in fast transport of heat along relatively large distances since heat can be conducted much faster by solid particles when compared to liquid matrix. They investigated the dependence of thermal conductivity of nanofluids on clustering and interfacial thermal resistance. Effect of clusters was analyzed in three steps by using Bruggeman model (Prasher et al. 2006), the model by Nan et al. (1997), and Maxwell–Garnett (M–G) model (Prasher et al. 2006; Wang et al. 2003). The resulting thermal conductivity ratio expression is

$$ {\frac{{k_{\text{eff}} }}{{k_{\text{f}} }}} = {\frac{{(k_{\text{cl}} + 2k_{\text{f}} ) + 2\phi_{\text{cl}} (k_{\text{cl}} - k_{\text{f}} )}}{{(k_{\text{cl}} + 2k_{\text{f}} ) - \phi_{\text{cl}} (k_{\text{cl}} - k_{\text{f}} )}}}, $$

(25)

where k _cl is the thermal conductivity of the cluster and ϕ_cl is the particle volume fraction of the clusters, which are defined in the study and the related expressions are also given therein to calculate effective thermal conductivity theoretically. In addition to the theoretical work, Evans et al. (2008) also determined the effective thermal conductivity of the nanofluid by utilizing a Monte Carlo simulation. The results of the theoretical approach and the computer simulation were compared and they were found to be in good agreement. It was shown that the effective thermal conductivity increased with increasing cluster size. However, as particle volume fraction increased, the nanofluid with clusters showed relatively smaller thermal conductivity enhancement. When it comes to interfacial resistance, it was found that interfacial resistance decreases the enhancement in thermal conductivity, but this decrease diminishes for nanofluids with large clusters. Another conclusion was that fiber shaped nanoparticles are more effective in thermal conductivity enhancement when compared to spherical particles. However, it was also noted that such fiber shaped particles or clusters increase the viscosity of the nanofluids significantly. At this point, it should be noted that excessive clustering of nanoparticles may result in sedimentation, which adversely affects the thermal conductivity (Prasher et al. 2006). Therefore, there should be an optimum level of clustering for maximum thermal conductivity enhancement.

Another study that proposes the clustering effect as the main reason of thermal conductivity enhancement was made by Keblinski et al. (2008). They analyzed the experimental data for thermal conductivity of nanofluids and examined the potential mechanisms of anomalous enhancement. Enhancement mechanisms such as micro-convection created by Brownian motion of nanoparticles, nanolayer formation around particles, and near field radiation were concluded not to be the major cause of the enhancement. It was noted that effective medium theories can predict the experimental data well when the effect of clustering is taken into account. Feng et al. (2007) modeled the effect of clustering by taking the effect of particle size into account. It was found that clustering improves thermal conductivity enhancement and formation of clusters is more pronounced in nanofluids with smaller nanoparticles since distances between nanoparticles are smaller in those nanofluids, which increases the importance of van der Waals forces attracting particles to each other.

Following paragraphs explain two theoretical models that are based on the clustering of nanoparticles (first model also considers the effect of Brownian motion).

Xuan et al. (2003) studied the thermal conductivity of nanofluids by considering Brownian motion and clustering of nanoparticles. An equation was proposed to predict the thermal conductivity of nanofluids:

$$ {\frac{{k_{\text{eff}} }}{{k_{\text{f}} }}} = {\frac{{k_{\text{p}} + 2k_{\text{f}} - 2\phi (k_{\text{f}} - k_{\text{p}} )}}{{k_{\text{p}} + 2k_{\text{f}} + \phi (k_{\text{f}} - k_{\text{p}} )}}} + {\frac{{\rho_{\text{p}} \phi c_{{{\text{p}},{\text{p}}}} }}{{2k_{\text{f}} }}}\sqrt {{\frac{{k_{\text{B}} T}}{{3\pi r_{\text{cl}} \mu_{\text{f}} }}}} . $$

(26)

Here, r _cl is the apparent radius of the nanoparticle clusters, which should be determined by experiment. T is temperature in K. µ_f is the dynamic viscosity of the base fluid and it can be calculated from the study of Li and Xuan (2000). The first term on the right-hand side of Eq. 26 is the Maxwell (1873) model for thermal conductivity of suspensions of solid particles in fluids. The second term on the right-hand side of Eq. 26 adds the effect of the random motion of the nanoparticles into account. For the contribution of this term, the following values were presented for Cu (50 nm)/water nanofluid: For ϕ = 0.03%, contribution of the second term is 11% when clustering occurs and 17% when clustering does not occur. For ϕ = 0.04%, contribution of the second term is 14% when clustering occurs and 24% when clustering does not occur. It was indicated that Brownian motion of nanoparticles becomes more effective with increasing temperature. On the other hand, as nanoparticles (or clusters) become larger, their random motion becomes slower and this decreases the enhancement in thermal conductivity. It should be noted that the second term on the right-hand side of the equation is not nondimensional, which is an indication of a mistake in the analysis.

Chen et al. (2009) measured the viscosity of TiO₂/water and TiO₂/ethylene glycol nanofluids and proposed a way of calculating the thermal conductivity of nanofluids by using the data. Two types of nanoparticles were used; spherical particles (25 nm) and cylindrical particles (10 nm in diameter and 100 nm in length). A model for the determination of the viscosity of the suspensions given by Krieger and Dougherty (1959) was modified in order to take the effect of clustering into account. The modified model became a function of cluster radius, and cluster radius values of the sample nanofluids were determined by matching the predictions of the modified model with experimental data. Then, the determined cluster radius values were used in the thermal conductivity model proposed, which is a modification of Hamilton and Crosser (1962) model (Eqs. 2, 3):

$$ {\frac{{k_{\text{eff}} }}{{k_{\text{f}} }}} = {\frac{{k_{\text{cl}} + (n - 1)k_{\text{f}} - (n - 1)\phi_{\text{cl}} (k_{\text{f}} - k_{\text{cl}} )}}{{k_{\text{cl}} + (n - 1)k_{\text{f}} + \phi_{\text{cl}} (k_{\text{f}} - k_{\text{cl}} )}}}, $$

(27)

where k _cl and ϕ_cl are the thermal conductivity and volume fraction of the clusters, respectively. n was taken as 3 for the spheres and 5 for the cylinders in this work.

$$ \phi_{\text{cl}} = \phi (r_{\text{cl}} /r_{\text{p}} )^{3 - D} $$

(28)

where r _cl and r _p are the radii of the clusters and nanoparticles, respectively. D is the fractal index, which was taken as 1.8 in the viscosity model and the same value might be used here. r _cl /r _p values are equal to 2.75 and 3.34, for TiO₂/water (spherical) and TiO₂/ethylene glycol (spherical) nanofluids, respectively. For the estimation of k _cl, the following expression was proposed for spherical particles (Bruggeman 1935):

$$ {\frac{{k_{\text{cl}} }}{{k_{\text{f}} }}} = {\frac{1}{4}}\left\{ \begin{gathered} (3\phi_{\text{in}} - 1){\frac{{k_{\text{p}} }}{{k_{\text{f}} }}} + (3(1 - \phi_{\text{in}} ) - 1) \hfill \\ + \left[ {((3\phi_{\text{in}} - 1){\frac{{k_{\text{p}} }}{{k_{\text{f}} }}} + (3(1 - \phi_{\text{in}} ) - 1))^{2} + 8{\frac{{k_{\text{p}} }}{{k_{\text{f}} }}}} \right]^{1/2} \hfill \\ \end{gathered} \right\}, $$

(29)

where ϕ_in is the solid volume fraction of clusters and it is defined as

$$ \phi_{\text{in}} = \phi (r_{\text{cl}} /r_{\text{p}} )^{D - 3} . $$

(30)

For the estimation of k _cl, the following expression was proposed for nanotubes (Nan et al. 2003).

$$ {\frac{{k_{\text{cl}} }}{{k_{\text{f}} }}} = {\frac{{3 + \phi_{\text{in}} [2\beta_{x} (1 - L_{x} ) + \beta_{z} (1 - L_{z} )]}}{{3 - \phi_{\text{in}} [2\beta_{x} L_{x} + \beta_{z} L_{z} ]}}}, $$

(31)

where

$$ \beta_{x} = (k_{x} - k_{\text{f}} )/[k_{\text{f}} + L_{x} (k_{\text{t}} - k_{\text{f}} )], $$

(32)

and

$$ \beta_{z} = (k_{z} - k_{\text{f}} )/[k_{\text{f}} + L_{z} (k_{\text{t}} - k_{\text{f}} )]. $$

(33)

k _x and k _z are the thermal conductivity of nanotubes along transverse and longitudinal directions, respectively. k _t is the isotropic thermal conductivity of the nanotube. k _x , k _z and k _t can be taken to be equal to k _p as an approximation. L _x and L _z are defined as:

$$ L_{x} = {\frac{{p^{2} }}{{2(p^{2} - 1)}}} - {\frac{p}{{2(p^{2} - 1)^{3/2} }}}\cosh^{ - 1} (p) $$

(34)

and

$$ L_{z} = 1 - 2L_{x} . $$

(35)

r _cl /r _p values are equal to 5.40 and 12.98 for TiO₂/ethylene glycol (nanotube) and TiO₂/water (nanotube) nanofluids, respectively. p is the aspect ratio of the nanotubes defined as length of nanotube divided by diameter of nanotube. The modified Hamilton and Crosser (1962) model was compared with experimental data for both spherical particles and nanotubes, and a good agreement was observed.

3.3 Liquid layering around nanoparticles

A recent study showed that liquid molecules form layered structures around solid surfaces (Yu et al. 1999) and it is expected that those nanolayers have a larger effective thermal conductivity than the liquid matrix (Yu and Choi 2003). As a result of this observation, the layered structures that form around nanoparticles are proposed to be responsible for the thermal conductivity enhancement of nanofluids (Yu and Choi 2003).

The fact that there is no experimental data regarding the thickness and thermal conductivity of these nanolayers is an important drawback of the proposed mechanism. Some researchers develop a theoretical model by considering liquid layering around nanoparticles and illustrate the predictions of their model by just assuming some values for the thermal conductivity and thickness of the nanolayer (Yu and Choi 2003). Some others model the thermal conductivity of the nanolayer so that it linearly varies across the radial direction (Xie et al. 2005) and there are also some researchers that take the temperature dependence of the thermal conductivity of these layers into account (Sitprasert et al. 2009). By choosing the parameters of the nanolayer accordingly, it is possible to produce results, which are consistent with experimental data but this does not prove the validity of the proposed mechanism.

Recently, Lee (2007) proposed a way of calculating the thickness and thermal conductivity of the nanolayer by considering the formation of electric double layer around the nanoparticles. According to the study, thickness of nanolayer depends on the dielectric constant, ionic strength, and temperature of the nanofluid. When it comes to the thermal conductivity of the nanolayer, the parameters are total charged surface density, ion density in the electric double layer, pH value of the nanofluid, and thermal conductivities of base fluid and nanoparticles. Another theoretical way to calculate the thickness and thermal conductivity of the nanolayer is proposed by Tillman and Hill (2007). They used the classical heat conduction equation together with proper boundary conditions to obtain a relation between the radial distribution of thermal conductivity in the nanolayer and nanolayer thickness. The relation requires an initial guess about the function that defines radial variation of thermal conductivity inside the nanolayer. According to the guess, it is possible to determine the thickness of the nanolayer and check the validity of the associated assumption. There are also some investigations, which show that nanolayers are not the main cause of thermal conductivity enhancement with nanofluids. Among those studies, Xue et al. (2004) examined the effect of nanolayer by molecular dynamics simulations and showed that nanolayers have no effect on the thermal transport. In the simulations, a simple monoatomic liquid was considered and authors noted that in case of water, results might be different.

There are many theoretical models that take the effect of liquid layering around nanoparticles into account. Six of them are explained below. Some models discussed below also take the effect of Brownian motion and clustering into account.

Yu and Choi (2003) presented a model for the determination of the effective thermal conductivity of nanofluids by modifying the Maxwell (1873) model. In the modification, the effect of the liquid nanolayers formed around nanoparticles was taken into account. The nanoparticle and the layer around it were considered as a single particle and the thermal conductivity of this particle was determined by using effective medium theory (Schwartz et al. 1995). The result was substituted into the Maxwell model and the following expression was obtained.

$$ k_{\text{eff}} = {\frac{{k_{\text{pe}} + 2k_{\text{f}} + 2(k_{\text{pe}} - k_{\text{f}} )(1 + \beta )^{3} \phi }}{{k_{\text{pe}} + 2k_{\text{f}} - (k_{\text{pe}} - k_{\text{f}} )(1 + \beta )^{3} \phi }}}k_{\text{f}} , $$

(36)

where k _pe is the thermal conductivity of the equivalent nanoparticle;

$$ k_{\text{pe}} = {\frac{{[2(1 - \gamma ) + (1 + \beta )^{3} (1 + 2\gamma )]\gamma }}{{ - (1 - \gamma ) + (1 + \beta )^{3} (1 + 2\gamma )}}}k_{\text{p}} , $$

(37)

where

$$ \gamma = {\frac{{k_{l} }}{{k_{p} }}}, $$

(38)

and k _l is thermal conductivity of the nanolayer. β is defined as:

$$ \beta = {\frac{t}{{r_{\text{p}} }}}, $$

(39)

where t is nanolayer thickness and r _p the nanoparticle radius.

Yu and Choi later applied the same idea to the Hamilton and Crosser (1962) model and proposed a model for non-spherical particles (Yu and Choi 2004). Another model that considers non-spherical particles was developed by Xue (2003).

Wang et al. (2003) proposed an equation for the determination of the thermal conductivity of nanofluids by considering the effect of nanoparticle clustering and surface adsorption. Bruggeman (1935) model and fractal theory were utilized in the analysis. The resulting thermal conductivity ratio expression is:

$$ {\frac{{k_{\text{eff}} }}{{k_{\text{f}} }}} = {\frac{{(1 - \phi ) + 3\phi \int\limits_{0}^{\infty } {{\frac{{k_{\text{cl}} (r)n(r)}}{{k_{\text{cl}} (r) + 2k_{\text{f}} }}}{\text{d}}r} }}{{(1 - \phi ) + 3\phi \int\limits_{0}^{\infty } {{\frac{{k_{\text{f}} n(r)}}{{k_{\text{cl}} (r) + 2k_{\text{f}} }}}{\text{d}}r} }}}. $$

(40)

k _cl is the equivalent thermal conductivity of the cluster determined by the Bruggeman model,

$$ k_{\text{cl}} = (3\phi^{*} - 1)k_{\text{p}} + \left[ {3(1 - \phi^{*} ) - 1} \right]k_{\text{f}} + \sqrt \Updelta , $$

(41)

where

$$ \Updelta = (3\phi^{*} - 1)^{2} k_{\text{p}}^{2} + \left[ {3(1 - \phi^{*} ) - 1} \right]^{2} k_{\text{f}}^{2} + 2\left[ {2 + 9\phi^{*} (1 - \phi^{*} )} \right]k_{\text{p}} k_{\text{f}} , $$

(42)

and for ϕ*, following expression should be substituted.

$$ \phi^{*} = (r_{\text{cl}} /r_{\text{p}} )^{{D_{{{\text{f}}1}} - 3}} , $$

(43)

where r _cl is the radius of nanoparticle clusters, r _p the radius of a single nanoparticle, and D _f1 the fractal dimension. D _f1 was determined as 1.66 for 6.5 wt% SiO₂ (25 nm)/ethanol nanofluid, 1.73 for 0.13 vol.% CuO/water nanofluid, 1.76 for 0.25 vol.% CuO/water nanofluid, and 1.81 for 0.38 vol.% CuO/water nanofluid. CuO particles were 50 nm in size. n(r) is defined as

$$ n(r) = {\frac{1}{{r_{\text{cl}} \sqrt {2\pi } \ln \sigma }}}\exp \left\{ { - \left[ {{\frac{{\ln (r_{\text{cl}} /\bar{r}_{\text{cl}} )}}{{\sqrt {2\pi } \ln \sigma }}}} \right]^{2} } \right\}, $$

(44)

where $\bar{r}_{\text{cl}}$ is the geometric mean radius of nanoparticle clusters (which was recommended to be replaced by average particle radius) and σ is the standard deviation, which can be taken as 1.5. Surface adsorption was also considered and it was proposed that the thickness of the adsorption layer can be found by using the formula

$$ t = {\frac{1}{\sqrt 3 }}\left( {{\frac{{4M_{\text{f}} }}{{\rho_{\text{f}} N_{\text{A}} }}}} \right)^{1/3} , $$

(45)

where M _f and ρ _f are the molecular weight and density of base liquid, respectively, and N _A the Avogadro constant (6.023 × 10²³/mol). Then, thermal conductivity of nanoparticles, by taking surface adsorption into account, can be written as

$$ k_{\text{cp}} = k_{\text{l}} {\frac{{(k_{\text{p}} + 2k_{\text{l}} ) + 2A^{3} (k_{\text{p}} - k_{\text{l}} )}}{{(k_{\text{p}} + 2k_{\text{l}} ) - A^{3} (k_{\text{p}} - k_{\text{l}} )}}}, $$

(46)

where A = 1 − t/(t + r _p) and k _l the effective thermal conductivity of the adsorption layer. It should be noted that in Eqs. 40–43, 46; (r _p + t), [(r _p + t)/r _p]³ϕ and k _cp should be substituted for r _p, ϕ, and k _p, respectively, when surface adsorption is taken into account. Since k _l is difficult to predict, this model can be used as an upper bound for the determination of effective thermal conductivity by letting k _l = k _p.

The validity of the model was checked with the results of a previous experimental study (Zhou and Wang 2002) of CuO/water nanofluids. D _f values were determined by using transmission electron microscopy (TEM) photos of CuO/water nanofluids of different particle volume fraction. It was seen that the model predicts the thermal conductivity well as long as the effect of adsorption is taken into account. Smaller values were calculated when adsorption was neglected.

Xie et al. (2005) also studied the effect of the interfacial nanolayer on the enhancement of thermal conductivity with nanofluids. A nanolayer was modeled as a spherical shell with thickness t around the nanoparticle. This is similar to the approach made by Yu and Choi (2003), but Yu and Choi assumed the nanolayer thermal conductivity to be a constant, whereas here the thermal conductivity was assumed to change linearly across the radial direction, so that it is equal to thermal conductivity of base liquid at the nanolayer–liquid interface and equal to thermal conductivity of the nanoparticle at the nanolayer–nanoparticle interface. The associated expression for the determination of the thermal conductivity of nanofluid was given as

$$ {\frac{{k_{\text{eff}} - k_{\text{f}} }}{{k_{\text{f}} }}} = 3\Uptheta \phi_{\text{T}} + {\frac{{3\Uptheta^{2} \phi_{\text{T}}^{2} }}{{1 - \Uptheta \phi_{\text{T}} }}}, $$

(47)

where

$$ \Uptheta = {\frac{{\beta_{\text{lf}} \left[ {(1 + \gamma )^{3} - {\frac{{\beta_{\text{pl}} }}{{\beta_{\text{fl}} }}}} \right]}}{{(1 + \gamma )^{3} + 2\beta_{\text{lf}} \beta_{\text{pl}} }}}, $$

(48)

and

$$ \beta_{\text{lf}} = {\frac{{k_{\text{l}} - k_{\text{f}} }}{{k_{\text{l}} + 2k_{\text{f}} }}}, $$

(49)

$$ \beta_{\text{pl}} = {\frac{{k_{\text{p}} - k_{\text{l}} }}{{k_{\text{p}} + 2k_{\text{l}} }}},\, $$

(50)

$$ \beta_{\text{fl}} = {\frac{{k_{\text{f}} - k_{\text{l}} }}{{k_{\text{f}} + 2k_{\text{l}} }}}, $$

(51)

where ϕ_T is the total volume fraction of nanoparticles and nanolayers. k _l is the thermal conductivity of the nanolayer. ϕ_T can be determined using

$$ \phi_{\text{T}} = \phi (1 + \gamma )^{3} , $$

(52)

where

$$ \gamma = t/r_{\text{p}} . $$

(53)

k _l was defined as:

$$ k_{\text{l}} = {\frac{{k_{\text{f}} M^{2} }}{(M - \gamma )\ln (1 + M) + \gamma M}}, $$

(54)

where

$$ M = \varepsilon_{\text{p}} (1 + \gamma ) - 1 $$

(55)

$$ \varepsilon_{\text{p}} = k_{\text{p}} /k_{\text{f}} . $$

(56)

When the thermal conductivity of the nanolayer is taken as a constant, this model gives the same results as Yu and Choi (2003) model. It was shown that for a chosen nanolayer thickness, the model is in agreement only with some of the experimental data. As a result, it was concluded that liquid layering around nanoparticles is not the only mechanism that affects the thermal conductivity of nanofluids.

Xue and Xu (2005) presented another theoretical study for the effective thermal conductivity of nanofluids. In their derivation, nanoparticles were assumed to have a liquid layer around them with a specific thermal conductivity. First, an expression for the effective thermal conductivity of the “complex particle,” which was defined as the combination of the nanoparticle and nanolayer, was determined. Then, by using Bruggeman’s (1935) effective media theory, the effective thermal conductivity of the nanofluid was determined. The resulting implicit expression for thermal conductivity of nanofluids is

$$ \left( {1 - {\frac{\phi }{\alpha }}} \right){\frac{{k_{\text{eff}} - k_{\text{f}} }}{{2k_{\text{eff}} + k_{\text{f}} }}} + {\frac{\phi }{\alpha }}{\frac{{(k_{\text{eff}} - k_{\text{l}} )(2k_{\text{l}} + k_{\text{p}} ) - \alpha (k_{\text{p}} - k_{\text{l}} )(2k_{\text{l}} + k_{\text{eff}} )}}{{(2k_{\text{eff}} + k_{\text{l}} )(2k_{\text{l}} + k_{\text{p}} ) + 2\alpha (k_{\text{p}} - k_{\text{l}} )(k_{\text{l}} - k_{\text{eff}} )}}} = 0, $$

(57)

where subscript l refers to nanolayer. α is defined as

$$ \alpha = \left( {{\frac{{r_{\text{p}} }}{{r_{\text{p}} + t}}}} \right)^{3} , $$

(58)

where t is the thickness of the nanolayer.

Li et al. (2008a) considered the effect of Brownian motion, liquid layering around nanoparticles, and clustering together. The effect of temperature on average cluster size, Brownian motion, and nanoparticle thermal conductivity was taken into account. Nanoparticle thermal conductivity is calculated by using the following expression (Chen 1996):

$$ k_{\text{p}} = {\frac{{3r^{*} /4}}{{3r^{*} /4 + 1}}}k_{\text{b}} . $$

(59)

Here, k _b is thermal conductivity of the bulk material and r* = r _p/λ, where λ is the mean-free path of phonons. Mean-free path of phonons can be calculated according to the following expression:

$$ \lambda = {\frac{{10aT_{\text{m}} }}{\gamma T}} $$

(60)

Here, a is crystal lattice constant of the solid, γ Gruneisen constant, T temperature, and T _m the melting point (in K). Thickness of nanolayer around nanoparticles is calculated according to Eq. 45. It is assumed that thermal conductivity of the nanolayer is equal to the thermal conductivity of nanoparticles. As a result, particle volume fraction is modified according to the expression:

$$ \phi_{\text{eff}} = (1 + t/r_{\text{p}} )^{3} \phi . $$

(61)

r _p is particle radius in this equation. The expressions presented above are substituted into the Xuan et al. (2003) model (Eq. 26) to obtain:

$$ {\frac{{k_{\text{eff}} }}{{k_{\text{f}} }}} = {\frac{{k_{\text{p}} + 2k_{\text{f}} - 2\phi (k_{\text{f}} - k_{\text{p}} )}}{{k_{\text{p}} + 2k_{\text{f}} + \phi (k_{\text{f}} - k_{\text{p}} )}}} + {\frac{{\rho_{\text{p}} \phi c_{{{\text{p}},{\text{p}}}} }}{{2k_{\text{f}} }}}\sqrt {{\frac{{k_{\text{B}} T}}{{3\pi r_{\text{cl}} \mu_{\text{f}} }}}} . $$

(62)

Here, r _cl is the apparent radius of the nanoparticle clusters, which should be determined by experiment. Authors introduced the effect of temperature on clustering according to the fact that decreasing temperature results in a decrease in particle surface energy, which decreases the severity of clustering. As a result, the average cluster size was proposed to be calculated by:

$$ r_{\text{cl}} = r_{{{\text{cl}}0}} (1 + b\Updelta T). $$

(63)

Here, r _cl0 is the average cluster size at the reference temperature and ΔT is defined as the difference between the nanofluid temperature and reference temperature. b is a negative constant. Finally, nanofluid viscosity is calculated according to the expression proposed by Einstein (1906):

$$ \mu_{\text{eff}} = (1 + 2.5\phi )\mu_{\text{f}} . $$

(64)

Another study regarding the effect of nanolayers was made by Sitprasert et al. (2009). They modified the model proposed by Leong et al. (2006) by taking the effect of temperature on the thermal conductivity and thickness of nanolayer into account. Leong et al.’s static model is as follows:

$$ k_{\text{eff}} = {\frac{{(k_{\text{p}} - k_{\text{l}} )\phi k_{\text{l}} [2\beta_{1}^{3} - \beta^{3} + 1] + (k_{\text{p}} + 2k_{\text{l}} )\beta_{1}^{3} [\phi \beta^{3} (k_{\text{l}} - k_{\text{f}} ) + k_{\text{f}} ]}}{{\beta_{1}^{3} (k_{\text{p}} + 2k_{\text{l}} ) - (k_{\text{p}} - k_{\text{l}} )\phi [\beta_{1}^{3} + \beta^{3} - 1]}}}. $$

(65)

Here, subscript l refers to nanolayer. β and β₁ are defined as:

$$ \beta = 1 + {\frac{t}{{r_{\text{p}} }}} $$

(66)

$$ \beta_{1} = 1 + {\frac{t}{{2r_{\text{p}} }}} $$

(67)

t is the thickness of the nanolayer and r _p is the radius of the nanoparticles. This model was modified by providing the following relation for the determination of nanolayer thickness:

$$ t = 0.01(T - 273)r_{\text{p}}^{0.35} , $$

(68)

where T is temperature in K and r _p the particle radius in nanometers. After the determination of nanolayer thickness, thermal conductivity of the nanolayer should be found according to the expression:

$$ k_{\text{l}} = C{\frac{t}{{r_{\text{p}} }}}k_{\text{f}} , $$

(69)

where C is 30 and 110 for Al₂O₃ and CuO nanoparticles, respectively. It should be noted that the above expressions provided for the determination of the thickness and thermal conductivity of the nanolayer were determined by using experimental data (which is known to have great discrepancies and uncertainties) and no explanation was made regarding the physics of the problem.

When the theoretical models based on nanolayer formation around nanoparticles are considered, it is seen that the main challenge is finding the thermal conductivity and thickness of the nanolayer. Therefore, the future studies should focus on that aspect of the problem.

3.4 Ballistic phonon transport in nanoparticles

In solids, diffusive heat transport is valid if the mean-free path of phonons is smaller than the characteristic size of the particle in consideration. Keblinski et al. (2002) estimated the phonon mean-free path of Al₂O₃ nanoparticles at room temperature according to the theory developed by Debye (Geiger and Poirier 1973) as 35 nm. In a particle with a diameter smaller than 35 nm, the heat transport is not diffusive, but heat is transported ballistically. Although this fact prevents the application of conventional theories for the modeling of thermal conductivity of nanofluids, Keblinski et al. noted that ballistic heat transport still cannot explain the anomalous thermal conductivity enhancements, because temperature inside the nanoparticles is nearly constant and this fact does not depend on whether heat is transported by diffusion or ballistically. Therefore, the boundary conditions for the base fluid are the same in both cases, and this results in identical thermal conductivity values for the nanofluid. On the other hand, Keblinski et al. indicated that ballistic heat transport can create a significant effect on thermal conductivity of nanofluids if it enables efficient heat transport between nanoparticles. This is only possible if the nanoparticles are very close to each other (a few nanometers separated) and they note that this is the case for nanofluids with very small nanoparticles. Furthermore, the authors stress on the fact that the particles may become closer to each other due to the Brownian motion.

Another study regarding this subject was made by Nie et al. (2008). They investigated the possibility of a change in the phonon mean-free path of the liquid phase of nanofluids due to the presence of nanoparticles theoretically. The authors found that the layering structure, in which there is significant change in phonon mean-free path, is confined to a distance around 1 nm. As a result, it was concluded that such a highly localized effect cannot be responsible for the anomalous thermal conductivity enhancement with nanofluids. Furthermore, change of phonon transport speed in the liquid phase due to the presence of nanoparticles was also investigated and the associated effect was found to be negligible.

3.5 Near field radiation

Domingues et al. (2005) studied the effect of near field radiation on the heat transport between two nanoparticles. They analyzed the problem by utilizing molecular dynamics simulation and found that when the distance between the nanoparticles is smaller than the diameter of the particles, the heat conductance is two to three orders of magnitudes higher than the heat conductance between two particles that are in contact. This finding can be considered as a heat transfer enhancement mechanism for nanofluids since the separation between nanoparticles can be very small in nanofluids with nanoparticles smaller than 10 nm. Furthermore, Brownian motion of nanoparticles can also improve that mechanism since the distance between nanoparticles changes rapidly due to the random motion. An important study regarding this subject was made by Ben-Abdallah (2006). In that study, near field interactions between nanoparticles were analyzed numerically for the case of Cu/ethylene glycol nanofluid, and it was shown that the near field interactions between nanoparticles do not significantly affect the thermal conductivity of the nanofluid. It was noted that the results are valid also for other nanoparticle types; metals, metal oxides, and polar particles.

4 Comparison of thermal conductivity models with experimental data

4.1 Effect of particle volume fraction

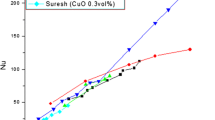
Predictions of some of the aforementioned thermal conductivity models are compared with the experimental data of four research groups for Al₂O₃/water nanofluid in Figs. 1 and 2. Al₂O₃/water nanofluid is selected, since it is one of the most commonly used nanofluids in thermal conductivity research. All of the experimental data were obtained around room temperature. Average particle diameter is taken as 40 nm in the models since the particle sizes in the experiments are close to that value, as indicated in the figures. Nanoparticle size varies in the study of Wen and Ding (2004), but its average value is 41.5 nm. Thermal conductivities of nanoparticles are calculated by using Eq. 59. That expression is valid for nonmetallic substances. For metallic nanoparticles, the following equation can be used when the relaxation times of electrons and phonons are comparable (Nimtz et al. 1990):

Fig. 1

Comparison of the experimental results of the thermal conductivity ratio for Al₂O₃/water nanofluid with theoretical models as a function of particle volume fraction at a particle size around 40 nm

Fig. 2

Comparison of the experimental results of the thermal conductivity ratio for Al₂O₃/water nanofluid with theoretical models as a function of particle volume fraction at a particle size around 40 nm

$$ k_{\text{p}} = \left( {{\frac{{2r_{\text{p}} }}{{5 \times 10^{ - 6} }}}} \right)^{3} k_{\text{b}} . $$

(70)

As seen in the figures, there exists significant discrepancy between experimental data. This discrepancy can be explained by the fact that parameters such as pH of the nanofluid, severity of clustering, and method of production of nanofluids usually differ in each experiment. Experimental results of Wen and Ding (2004) are relatively higher than the results of other research groups and they are predicted best by the model of Koo and Kleinstreuer (2004). However, since the size distribution of particles is not known in detail, it is difficult to reach a conclusion about the validity of the models. Dependency of the data of Lee et al. (1999) on particle volume fraction is somewhat low and none of the models have such a small slope in the figures. Hamilton and Crosser (1962) model is relatively closer to the experimental data of Lee et al. (1999) and Das et al. (2003). It was noted that clusters as large as 100 nm were observed in the study of Lee et al. (1999). Therefore, it may be suggested that those samples are closer to the validity range of the Hamilton and Crosser model. However, Das et al. (2003) also considered the effect of temperature in their study and indicated that this agreement is just a coincidence.

It should also be noted that all of the experimental results presented here show nearly linear variation of thermal conductivity with particle volume fraction and theoretical models are in agreement with experimental results in that aspect.

4.2 Effect of particle size

Dependence of theoretical models on particle size is compared with experimental data in Figs. 3, 4, 5, and 6 for Al₂O₃/water nanofluids. Experimental data are around room temperature, and room temperature is substituted for model calculations. Linear interpolation was applied to some of the experimental data for determining thermal conductivity ratio at integer values of particle volume fraction. Since a nearly linear relationship exists between thermal conductivity ratio and particle volume fraction, associated errors are not expected to be large.

Fig. 3

Comparison of the experimental results of the thermal conductivity ratio for Al₂O₃/water nanofluid with Hamilton and Crosser (1962) model as a function of the particle size at various values of the particle volume fraction

Fig. 4

Comparison of the experimental results of the thermal conductivity ratio for Al₂O₃/water nanofluid with Xue and Xu (2005) model as a function of the particle size at various values of the particle volume fraction

Fig. 5

Comparison of the experimental results of the thermal conductivity ratio for 1 vol.% Al₂O₃/water nanofluid with theoretical models as a function of particle size

Fig. 6

Comparison of the experimental results of the thermal conductivity ratio for 3 vol.% Al₂O₃/water nanofluid with theoretical models as a function of particle size

In Figs. 3 and 4, an experimental data set prepared by combining the results of five different research groups is compared with the predictions of two theoretical models. As seen from the figures, there is significant discrepancy in experimental data. Nevertheless, the general trend is increasing thermal conductivity with increasing particle size. As mentioned in Sect. 2.4, although this trend is the case for nanofluids with Al₂O₃ nanoparticles, when overall trend is considered for different types of nanofluids, it is seen that thermal conductivity generally increases with decreasing particle size. At this point, it should be noted that thermal conductivity increases with decreasing particle size when Brownian motion is considered as the main mechanism of thermal conductivity enhancement, because the effect of Brownian motion increases with decreasing particle size, which improves micro-convection around nanoparticles. Same is true for the formation of liquid layers around nanoparticles as an enhancement mechanism, because the enhancement effect of nanolayers increases with increasing specific surface area of nanoparticles. Since specific surface area of nanoparticles is higher in case of smaller particles, decreasing particle size increases the thermal conductivity enhancement according to the models, which are based on liquid layering. It is thought that the contradictory trend in the results of nanofluids with Al₂O₃ nanoparticles might be due to the uncontrolled clustering of nanoparticles and such trends do not prove that these proposed mechanisms of thermal conductivity enhancement are incorrect.

When Fig. 3 is observed, it is seen that Hamilton and Crosser (1962) model predicts increasing thermal conductivity with increasing particle size. The Hamilton and Crosser model does not take the effect of particle size on thermal conductivity into account, but it becomes slightly dependent on particle size due to the fact that particle thermal conductivity increases with increasing particle size according to Eq. 59. However, the model still fails to predict experimental data for particle sizes larger than 40 nm since particle size dependence diminishes with increasing particle size.

Predictions of six other models, which are analyzed in the previous section, are also examined and it was seen that all of them predict increasing thermal conductivity with decreasing particle size. Since the associated plots are very similar to each other qualitatively, only the model of Xue and Xu (2005) is presented in Fig. 4. This trend of increasing thermal conductivity with decreasing particle size is due to the fact that these models are either based on Brownian motion (Koo and Kleinstreuer (2004) and Jang and Choi (2004) models) or based on liquid layering around nanoparticles (Yu and Choi (2003), Xie et al. (2005), Xue and Xu (2005), and Sitprasert et al. (2009) models).

Although the general trend for Al₂O₃/water nanofluids is as presented in Figs. 3 and 4, there is also experimental data for Al₂O₃/water nanofluids, which shows increasing thermal conductivity with decreasing particle size. In Figs. 5 and 6, those experimental results are combined in order to provide some meaningful comparison with theoretical models. Due to the limited data, results are only plotted for 1 and 3 vol.% nanofluids. When the experimental results are observed, it is seen that the discrepancy in the data is somewhat larger for the 3 vol.% case. This might be due to the fact that at higher particle volume fractions, clustering of particles is more pronounced, which affects the thermal conductivity of nanofluids. It should be noted that clustering may increase or decrease the thermal conductivity enhancement. If a network of nanoparticles is formed as a result of clustering, this may enable fast heat transport along nanoparticles. On the other hand, excessive clustering may result in sedimentation, which decreases the effective particle volume fraction of the nanofluid.

When the predictions of the models are compared (Figs. 5, 6), it is seen that Yu and Choi (2003) model, Jang and Choi (2004) model, and Xue and Xu (2005) model provide very close results. All of these three models generally predict the experimental data well, and it is interesting to note that two of these models are based on nanolayer formation around nanoparticles (Yu and Choi (2003) and Xue and Xu (2005) models), whereas Jang and Choi (2004) model is based on Brownian motion. Therefore, it is possible to obtain similar results by considering different mechanisms of thermal conductivity enhancement and more systematic experimental data sets are required in order to differentiate these models. For example, it is known that the effect of Brownian motion diminishes with increasing viscosity of base fluid. By preparing different nanofluids by using two base fluids with significantly different viscosities and measuring the thermal conductivities, Tsai et al. (2008) showed that Brownian motion has a significant effect on thermal conductivity enhancement especially for nanofluids with low viscosity base fluids.

It is also seen that Sitprasert et al. (2009) model underpredicts the experimental data for large nanoparticles. In that model, the relation between the nanolayer thickness and particle size was found empirically by utilizing experimental data. There is not much data in the literature that considers spherical particles larger than 100 nm and this might be the reason behind such a result. On the other hand, Koo and Kleinstreuer (2004) model overpredicts the experimental data for large nanoparticles. It should be noted that Koo and Kleinstreuer model includes an empirical term (f), which is a function of temperature and particle volume fraction. It is taken as 1 since authors did not provide an expression for nanofluids with Al₂O₃ nanoparticles. By choosing a proper function for that term accordingly, it might be possible to prevent the associated overprediction. However, since that term is not a function of particle size, a modification in f will also affect the results for smaller particle sizes. Finally, when the results of Xie et al. (2005) model is considered, it is seen that the model does not predict significant increase in thermal conductivity enhancement with decreasing particle size up to 20 nm. It is thought that this is mainly due to the fact that the thermal conductivity of nanolayer is modeled to vary linearly in radial direction which diminishes the associated effect of nanolayer.

4.3 Effect of temperature

In this section, dependence of the theoretical models on temperature is compared with experimental data (Figs. 7, 8, 9). It should be noted that the presented data of Li and Peterson (2006) is obtained by using the line fit provided by the authors since data points create ambiguity due to fluctuations. In determining the thermal conductivity ratio, thermal conductivity of the nanofluid is divided by the thermal conductivity of water at that temperature. In the models, particle size is selected as 40 nm since most of the experimental data is close to that value, as explained in the previous sections.

Fig. 7

Comparison of the experimental results of the thermal conductivity ratio for Al₂O₃/water nanofluid with Koo and Kleinstreuer model (2004) as a function temperature at various values of particle volume fraction

Fig. 8

Comparison of the experimental results of the thermal conductivity ratio for Al₂O₃/water nanofluid with Jang and Choi model (2004) as a function temperature at various values of particle volume fraction

Fig. 9

Comparison of the experimental results of the thermal conductivity ratio for Al₂O₃/water nanofluid with Sitprasert et al. model (2009) as a function temperature at various values of particle volume fraction

Although there is no agreement in the quantitative values, experimental results generally suggest that thermal conductivity ratio increases with temperature. It is seen that the temperature dependence of the data of Li and Peterson (2006) is much higher than the results of other two research groups. On the other hand, the results of Chon et al. (2005) show somewhat weaker temperature dependence. This might be explained by the fact that the average size of nanoparticles in that study is larger when compared to others, since increasing particle size decreases the effect of both Brownian motion and nanolayer formation. It should also be noted that dependence on particle volume fraction becomes more pronounced with increasing temperature in all of the experimental studies.

When it comes to theoretical models, predictions of Hamilton and Crosser (1962) model, Yu and Choi (2003) model, Xue and Xu (2005) model, and Xie et al. (2005) model do not depend on temperature except a very slight decrease in thermal conductivity ratio with temperature due to the increase in the thermal conductivity of water with temperature. Therefore, these models fail to predict the aforementioned trends of experimental data. Since the predictions of these four models with respect to temperature do not provide any additional information; associated plots are not shown here.

The model proposed by Koo and Kleinstreuer (2004) considers the effect of Brownian motion on the thermal conductivity and the predictions of this model are presented in Fig. 7. In the model, temperature dependence of thermal conductivity is taken into account by an empirical factor f, which is a function of particle volume fraction and temperature. Authors did not provide the associated function for nanofluids with Al₂O₃ nanoparticles. Because of this, the function provided for nanofluids with CuO nanoparticles is used in the calculations (Eq. 13). A multiplicative constant is introduced into the associated expression in order to match experimental data. As seen from Fig. 7, model of Koo and Kleinstreuer generally predicts the trend in the experimental data correctly. Since f is a function of both particle volume fraction and temperature, one can make further adjustments in the associated parameters to predict a specific data set with high accuracy. It is interesting to note that, the relation between particle volume fraction and thermal conductivity ratio is not linear at high temperatures. This is mainly due to the second term on the right-hand side of Eq. 13, which creates a reduction in the effect of particle volume fraction with increasing temperature. By using a different function for f and finding the associated constants, it is possible to eliminate such effects.

In Fig. 8, results of Jang and Choi (2004) model is presented. It is important to note that this model predicts nonlinear temperature dependence of thermal conductivity, whereas other two models predict linear behavior. Experimental results of Das et al. (2003) and Li and Peterson (2006) show nearly linear variation of thermal conductivity ratio with temperature, which is contradictory with the model. On the other hand, result of Chon et al. (2005) suggests nonlinear variation and the associated trend is somewhat in agreement with the model of Jang and Choi.

Predictions of Sitprasert et al. (2009) model is shown in Fig. 9. The model predicts linear variation of thermal conductivity ratio with increasing temperature. It should be noted that the effect of particle volume fraction dramatically increases with temperature and starts to overpredict the rate of thermal conductivity increase with particle volume fraction. Since the temperature dependence of thermal conductivity is introduced to the model empirically, it is possible to modify the associated expression in order to predict experimental data better.

5 The effect of thermal conductivity on heat transfer

The main objective in finding the right values of the effective thermal conductivity of nanofluids for industrial applications is to find the heat transfer coefficient for cooling and heating processes. If one considers the Graetz solution for parabolic velocity profile with constant surface temperature and constant wall heat flux boundary conditions, the following expressions are obtained for the Nusselt number, respectively (Kakaç and Yener 1994):

$$ Nu_{x} = {\frac{{h_{x} d}}{{k_{\text{eff}} }}} = {\frac{{\sum\limits_{n = 0}^{\infty } {A_{n} e^{{ - \lambda_{n}^{2} \xi }} } }}{{2\sum\limits_{n = 0}^{\infty } {{\frac{{A_{n} }}{{\lambda_{n}^{2} }}}e^{{ - \lambda_{n}^{2} \xi }} } }}},\;{\text{for}}\,{\text{constant}}\,{\text{wall}}\,{\text{temperature}}, $$

(71)

$$ Nu_{x} = {\frac{{h_{x} d}}{{k_{\text{eff}} }}} = \left[ {{\frac{11}{48}} - {\frac{1}{2}}\sum\limits_{n = 1}^{\infty } {{\frac{{e^{{ - \beta_{n}^{2} \xi }} }}{{A_{n} \beta_{n}^{4} }}}} } \right]^{ - 1} ,\;{\text{for}}\,{\text{constant}}\,{\text{wall}}\,{\text{heat}}\,{\text{flux}}. $$

(72)

These expressions are valid for the thermal entrance region of a circular pipe with hydrodynamically fully developed laminar nanofluid flow. Eigenvalues and coefficients are given in Kakaç and Yener (1994).

Under the fully developed conditions, Nusselt number becomes:

$$ Nu_{\infty } = {\frac{{\lambda_{0}^{2} }}{2}} = {\frac{{(2.7043644)^{2} }}{2}} = 3.657,\;{\text{for}}\,{\text{constant}}\,{\text{wall}}\,{\text{temperature}}, $$

(73)

$$ Nu_{\infty } = 4.364,\,{\text{for}}\,{\text{constant}}\,{\text{wall}}\,{\text{heat}}\,{\text{flux}}. $$

(74)

In order to stress the importance of the accurate determination of the effective thermal conductivity of nanofluids, convective heat transfer coefficient of the laminar flow of Al₂O₃/water nanofluid inside a circular tube is investigated by using the abovementioned asymptotic values of Nusselt number. Spherical particles are assumed and particle size is selected as 38.4 nm. Two different temperatures are used in the analysis; room temperature and 50 °C. Flow is assumed to be both hydrodynamically and thermally fully developed. Tube diameter is selected as 1 cm.

For the determination of the thermal conductivity of the nanofluids at room temperature, Hamilton and Crosser (1962) model is utilized. As a result, fully developed convective heat transfer coefficients are determined. In Table 3, results of 1 and 4 vol.% Al₂O₃/water nanofluids are compared with pure water. As seen from the table, due to the definition of the Nusselt number (Nu = h·d/k), the enhancement in thermal conductivity by the use of nanofluids directly results in the enhancement in convective heat transfer coefficient.

Table 3 Thermal conductivity and heat transfer coefficient values for pure water and Al₂O₃/water nanofluid, room temperature

At 50 °C, thermal conductivity of the nanofluids is determined by using the model of Jang and Choi (2004). Additionally, experimental thermal conductivity data provided by Das et al. (2003) is also included for comparison. The experimental data is also for Al₂O₃/water nanofluid with a particle size of 38.4 nm (spherical) at 50 °C. In Table 4, results of 1 and 4 vol.% Al₂O₃/water nanofluids are compared with pure water. As seen in this table, there exists significant difference between the experimental and theoretical thermal conductivity data especially for the 1 vol.% case. This difference directly causes a discrepancy in the associated convective heat transfer coefficient values. When the thermal conductivity data of Murshed et al. (2008b) is considered, it is seen that at 60 °C, 1 vol.% Al₂O₃ (80 nm)/water nanofluid has a thermal conductivity enhancement around 12%. When the particle size of 80 nm is substituted to the Jang and Choi (2004) model, a thermal conductivity enhancement of 4.8% is obtained. As a result, using this data would cause an even larger discrepancy in the convective heat transfer coefficient values. On the other hand, Mintsa et al. (2009) measured the thermal conductivity of 4 vol.% Al₂O₃ (47 nm)/water nanofluid at 48 °C and reported an 18% thermal conductivity enhancement (corresponding prediction of Jang and Choi model is 19.8%). Therefore, care must be taken when using the theoretical models of thermal conductivity in heat transfer calculations.

Table 4 Thermal conductivity and heat transfer coefficient values for pure water and Al₂O₃/water nanofluid, T = 50 °C

A more detailed convective heat transfer performance analysis, together with two additional cases (slug flow case and linear wall temperature boundary condition case) is provided by Kakaç and Pramuanjaroenkij (2009).

Many experimental and numerical investigations have been made about the determination of convective heat transfer with nanofluids. Wang and Mujumdar (2007) and Murshed et al. (2008a) provide a comprehensive review of such studies. These reviews also discuss the experimental and theoretical aspects of thermal conductivity of nanofluids.

6 Conclusions and future work

This paper summarizes the research in nanofluid thermal conductivity. Both experimental and theoretical investigations are reviewed and theoretical models are compared with the experimental findings.

Results show that there exists significant discrepancy in the experimental data. Effect of particle size on the thermal conductivity of nanofluids has not been completely understood yet. It is expected that Brownian motion of nanoparticles results in higher thermal conductivity enhancement with smaller particle size. However, some of the experiments show that the thermal conductivity decreases with decreasing particle size. This contradiction might be due to the uncontrolled clustering of nanoparticles resulting in larger particles. Particle size distribution of nanoparticles is another important factor and it is suggested that average particle size is not sufficient to characterize a nanofluid due to the nonlinear relations involved between particle size and thermal transport. It is also known that particle shape is effective on the thermal conductivity. Since cylindrical and rod-shaped particles offer higher enhancement when compared to spherical particles, more research should be made for the investigation of the performance of such particles when compared to spherical particles.

An important reason of discrepancy in experimental data is clustering of nanoparticles. Although there are no universally accepted quantitative values, it is known that the level of clustering affects the thermal conductivity of nanofluids (Hong et al. 2006). The level of clustering depends on many parameters. It was shown that adding some surfactants and adjusting the pH value of the nanofluid provide better dispersion and prevents clustering to some extent (Wang et al. 2009). Therefore, when examining experimental results, one should also consider the type and amount of additives used in the samples and pH value of the samples. Two nanofluid samples with all of the parameters being the same can lead to completely different experimental results if their surfactant parameters and pH values are not the same. Therefore, researchers providing experimental results should give detailed information about the additives utilized and pH values of the samples.

A commonly utilized way of obtaining good dispersion and breaking the clusters is to apply ultrasonic vibration to the samples. It is obvious that the duration and the intensity of the vibration affect the dispersion characteristics. Moreover, immediately after the application of vibration, clusters start to form again and size of the clusters increases as time progresses (Hong et al. 2006). Therefore, by using exactly the same samples, one can obtain different results just by varying the time between the sonication and measurement of thermal conductivity. In order to prevent further complication about the experimental results, researchers should clearly specify the procedures associated with the application of sonication. In addition to examining the effects of some apparent parameters such as particle size, base fluid, and particle volume fraction, researchers should also investigate the effects of parameters associated with additives, pH value, and ultrasonic vibration.

Temperature dependence is also an important parameter in the thermal conductivity of nanofluids. Limited study has been done about this aspect of the thermal conductivity of nanofluids up to now. Investigation of the thermal performance of nanofluids at high temperatures may widen the possible application areas of nanofluids.

When the application of nanofluids is considered, two important issues are erosion and settling. Before commercialization of nanofluids, possible problems associated with these issues should be investigated and solved. It should also be noted that, increase in viscosity by the use nanofluids is an important drawback due to the associated increase in pumping power. Therefore, further experimental research is required in that area in order to determine the feasibility of nanofluids.

In order to predict the thermal conductivity of nanofluids, many theoretical models have been developed recently. However, there is still controversy about the underlying mechanisms of the thermal conductivity enhancement of nanofluids. As a result of this, none of the theoretical models is able to completely explain the thermal conductivity enhancement in nanofluids. On the other hand, some researchers report experimental data of thermal conductivity that is consistent with the predictions of the classical models (such as Hamilton and Crosser (1962) model). Consequently, further work is required in theoretical modeling of heat transport in nanofluids as well.