Introduction

In the development of efficient heat transfer equipment, the thermal conductivity of the heat transfer fluids plays a vital role. Traditional heat transfer fluids such as water, oil and ethylene glycol mixture are inherently poor heat transfer fluids. Therefore, the metallic nanoparticles are added into traditional fluids in order to increase the heat transfer efficiency. These mixtures are called nanofluids. The heat transfer efficiency of nanofluids is increased because the thermal conductivity of the metallic nanoparticles is higher than that of the traditional fluids.

Previously, the enhancement in the thermal conductivity of nanofluids was assumed to depend mainly on the volume fraction of nanoparticles (Masuda et al. 1993; Eastman et al. 1997; Pak and Cho 1998; Lee et al. 1999; Eastman et al. 2001; Xie et al. 2002; Kwak and Kim 2005). A thermal conductivity model that was based on the above assumption was called a stationary model (e.g. Maxwell’s model 1873; Hamilton and Crosser’s model 1962). However, later works showed that the increase in temperature also enhanced the thermal conductivity of nanofluids (Das et al. 2003; Chon et al. 2005; Li and Peterson 2006). A dynamic model was therefore developed based on the stationary model with the inclusion of the thermal dispersion effect due to the Brownian motion of nanoparticles (Khanafer et al. 2003; Koo and Kleinstreuer 2004; Chon et al. 2005). Although the temperature-dependent effect could be predicted by the dynamic model, the volume-fraction-dependent effect was not satisfactorily predicted.

Recently, the thermal conductivity of the interfacial layer of the nanoparticles has been shown to have an effect on the thermal conductivity of nanofluids (Patal et al. 2003; Wang et al. 2003; Yu and Choi 2003; Yu and Choi 2004; Xue et al. 2004; Leong et al. 2006). Leong et al. (2006) have proposed a stationary model that includes the interfacial layer effect. Their model has been shown to have higher accuracy in predicting the volume-fraction-dependent effect than the other stationary models. Nevertheless, the Leong et al.’s stationary model has not been able to predict the temperature-dependent effect.

The current work therefore first modifies the Leong et al.’s stationary model by including the thermal dispersion effect due to the Brownian motion of nanoparticles (Amiri and Vafai 1994; Khanafer et al. 2003; Koo and Kleinstreuer 2004). This modified model is called the ‘Leong et al.’s dynamic model’ in this article (Section “Leong et al.’s stationary model (2006)”). It is shown in “Results and discusion” section that the Leong et al.’s dynamic model gives good prediction for the non-flowing fluid. This is because the Brownian motion of nanoparticles is dominant in the non-flowing fluid. However, the Leong et al.’s dynamic model gives poor prediction for the flowing fluid. This is because the Brownian motion of nanoparticles in the flowing fluid is negligibly small compared to the velocity of the main flow. Hence, for the flowing fluid, the velocity of the main flow is used instead and this leads to the overprediction of the thermal conductivity of nanofluids by all dynamic models. This accords with the Keblinski et al. (2002) and Buongiorno (2006), who have suggested that the role of the Brownian motion is not important for the flowing fluid. Therefore, the enhancement in the thermal conductivity of the flowing nanofluids due to the increase in temperature does not come from the thermal dispersion effect due to the Brownian motion of nanoparticles. It is more likely that the enhancement in heat transfer of the flowing nanofluids comes from the temperature-dependent interfacial layer effect.

It can be seen from the literature that there is still no thermal conductivity model for nanofluids that includes the effect of the temperature-dependent interfacial layer. Therefore, the stationary model of Leong et al. (2006) is again modified in the present work to include the effect of the temperature variation on the thermal conductivity of the interfacial layer. The model constants for Al2O3 and CuO nanoparticles are also evaluated. This thermal conductivity model for nanofluids that includes the effect of the temperature-dependent interfacial layer is called the ‘present model’. The performance of the present model is assessed by comparison with the thermal conductivity models of Maxwell (1873), Chon et al. (2005) and Leong et al. (2006) for the non-flowing fluid using the experimental data of Masuda et al. (1993), Eastman et al. (1997), Pak and Cho (1998), Lee et al. (1999), Das et al. (2003), Chon et al. (2005) and Li and Peterson (2006) for Al2O3 and CuO nanoparticles. Then, the present model is evaluated for the flowing fluid using the turbulent convective heat transfer problem in nanofluids along a uniformly heated tube using the experimental data of Pak and Cho (1998) and the simulation by Maïga et al. (2004).

Thermal conductivity models

Leong et al.’s stationary model (2006)

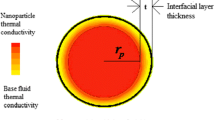
The interfacial layer is a solid–liquid interface which has different thermo-physical properties from base liquid and solid particle. The thermal conductivity of the interfacial layer is less or equals to that of the solid particle, but it is greater or equals to that of the base liquid (Leong et al. 2006). It is important to consider the interfacial layer as a separate component in the solid (particle)–liquid mixture in order to determine its effect on the mixture (nanofluids). A sketch of a single particle with an interfacial layer in a liquid medium is shown in Fig. 1.

Fig. 1
figure 1

Single spherical particle with an interfacial layer in a liquid medium (Leong et al. 2006)

Full size image

The Leong et al.’s stationary model for the effective thermal conductivity of nanofluids is derived from the determination of the temperature field and gradients of nanoparticles by including effect of the interfacial layer. The Leong et al.’s stationary model can be written as follows:

$$ k_{\text{eff}} = k_{\text{static}} = \frac{{\left( {k_{\text{p}} - k_{\text{lr}} } \right)\phi k_{\text{lr}} \left[ {2\beta_{1}^{3} - \beta^{3} + 1} \right] + \left( {k_{\text{p}} + 2k_{\text{lr}} } \right)\beta_{1}^{3} \left[ {\phi \beta^{3} \left( {k_{\text{lr}} - k_{\text{f}} } \right) + k_{\text{f}} } \right]}}{{\beta_{1}^{3} \left( {k_{\text{p}} + 2k_{\text{lr}} } \right) - \left( {k_{\text{p}} - k_{\text{lr}} } \right)\phi \left[ {\beta_{1}^{3} + \beta^{3} - 1} \right]}} $$
(1)

where\( \beta = 1 + \frac{h}{a}, \) \( \beta_{1} = 1 + \frac{h}{2a}, \) h is the interfacial layer thickness, a is the particle radius, k is the thermal conductivity, ϕ is the volume fraction of nanoparticles. The thickness and the thermal conductivity of the interfacial layer in Leong et al.’s stationary model are assumed to be 1 nm and 1–5 times of base fluid, respectively.

Leong et al.’s dynamic model

The effective thermal conductivity of the dynamic models for nanofluids can be generally written as

$$ k_{\text{eff}} = k_{\text{static}} + k_{\text{V}} $$
(2)

where the static part k static is from the Leong et al.’s stationary model (Eq. 1) and the dynamic part k V is modified from Khanafer et al.’s model (2003) and Koo and Kleinstreuer’s model (2004) as follows:

$$ k_{\text{v}} = C\left( {\rho c} \right)_{\text{nf}} \left| {\bar{V}} \right|\phi d_{\text{p}} $$
(3)

where \( \left| {\bar{V}} \right| = \sqrt {\frac{{18k_{\text{b}} T}}{{\pi \rho_{\text{p}} d_{\text{p}}^{3} }}} \) for the non-flowing fluid (Koo and Kleinstreuer 2004), \( \left| {\bar{V}} \right| = \sqrt {u^{2} + v^{2} + w^{2} } \) for the flowing fluid (Amiri and Vafai 1994; Khanafer et al. 2003), c and ρ stand for specific heat and density of nanofluids. The C is an unknown parameter which can be determined by calibrating with the experimental data (Das et al. 2003; Chon et al. 2005). Also, the parameter C combines the probability for a particle to travel along any direction with the function of temperature and volume fraction. The parameter C is given in this work as:

$$ C = \frac{0.1}{{\left( {\phi + 0.04} \right)}}\left( {T - 298} \right){\text{For}}\,{{{\text{Al}}_{2} {\text{O}}_{3} } \mathord{\left/ {\vphantom {{{\text{Al}}_{2} {\text{O}}_{3} } {\text{Water}}}} \right. \kern-\nulldelimiterspace} {\text{Water}}} $$
$$ C = \frac{0.1}{{\left( {\phi + 0.001} \right)}}\left( {T - 298} \right)\,{\text{For}}\,{{\text{Cuo}} \mathord{\left/ {\vphantom {{\text{Cuo}} {\text{Water}}}} \right. \kern-\nulldelimiterspace} {\text{Water}}} $$

It should be noted that the experiments on thermal conductivity were mostly done at room temperature, assumed to be 298 K. The stationary models were originally developed using data collected at room temperature. Thus, when including the thermal dispersion effect into the stationary models, the value of 298 K should be deleted from the function of temperature because the stationary models are already able to predict the effective thermal conductivity satisfactory at room temperature.

The Leong et al.’s dynamic model can be written using Eqs. 1–3 as:

$$ k_{\text{eff}} = \frac{{\left( {k_{\text{p}} - k_{\text{lr}} } \right)\phi k_{\text{lr}} \left[ {2\beta_{1}^{3} - \beta^{3} + 1} \right] + \left( {k_{\text{p}} + 2k_{\text{lr}} } \right)\beta_{1}^{3} \left[ {\phi \beta^{3} \left( {k_{\text{lr}} - k_{\text{f}} } \right) + k_{\text{f}} } \right]}}{{\beta_{1}^{3} \left( {k_{\text{p}} + 2k_{\text{lr}} } \right) - \left( {k_{\text{p}} - k_{\text{lr}} } \right)\phi \left[ {\beta_{1}^{3} + \beta^{3} - 1} \right]}} + C\left( {\rho c} \right)_{\text{nf}} \left| {\bar{V}} \right|\phi d_{\text{p}} $$
(4)

Present model

The value of the interfacial layer thickness is negligibly small on a macroscopic scale. However, on the scale of a nanoparticle, the interfacial layer thickness can play an important role in the thermal conductivity of nanofluids. Moreover, the value of the interfacial layer thickness depends on temperature (Eastman et al. 2004).

The Leong et al.’s stationary model (2006) has already included the interfacial layer effect in their model. However, their model cannot predict the dependence of the thermal conductivity of nanofluids on temperature. In this section, the Leong et al.’s stationary model is modified to include the effects of the temperature and the nanoparticle size variations on the thickness and consequently on the thermal conductivity of the interfacial layer. The thickness and the thermal conductivity of the interfacial layer are assumed to be as h = f(T, a) and k lr  = f(h, a), respectively.

The expression for the interfacial layer thickness h can be found using the available experimental data (Masuda et al. 1993; Eastman et al. 1997; Pak and Cho 1998; Lee et al. 1999; Das et al. 2003; Chon et al. 2005; Li and Peterson 2006) as follows:

$$ h = 0.01\left( {T - 273} \right)a^{0.35} $$
(5)

where the interfacial layer thickness range for various nanoparticle sizes and temperatures accords with Xue et al.’s model (2004) and Leong et al.’s stationary model (2006) [See “Results and discusion” section].

Also, the expression for the thermal conductivity of the interfacial layer, k lr is found using the same experimental data as for the expression for the interfacial layer thickness as follows:

$$ k_{\text{lr}} = C\frac{h}{a}k_{\text{f}} $$
(6)

where the constants C = 30 and 110 for Al2O3 and CuO nanoparticles, respectively. Therefore, the present model can be written as Eqs. 1, 5 and 6.

Convective transport in nanofluids

The approaches used so far for the convective transport in nanofluids are homogeneous approach, dispersion approach and species transport approach. In homogeneous approach, the conventional transport equations for pure fluids are directly extended to nanofluids. This means that all traditional heat transfer correlations can be used also for nanofluids, provided that the nanofluid’s thermo-physical properties are used in calculations. Therefore, the enhancement in heat transfer is assumed to come only from the higher thermal conductivity of nanofluids. The approach was used by Maïga et al. (2004) and it was found by Buongiorno (2006) that the nanofluid heat transfer coefficient was under-predicted. This was because the thermal conductivity model used in Maïga et al. did not depend on temperature.

The dispersion approach is based on the assumption that the convective heat transfer enhancement in nanofluids comes from two factors, the higher thermal conductivity and the dispersion of the nanoparticles. This approach was first proposed for nanofluids by Xuan and Roetzel (2000). The effect of the nanoparticle/base fluid relative velocity is treated as a perturbation of the energy equation and an empirical dispersion coefficient is introduced to describe the heat transfer enhancement. Nevertheless, Buongiorno’s work (2006) on the energy equation using dimensional analysis showed that the heat transfer enhancement from the nanoparticle dispersion can be negligible in nanofluids.

Buongiorno also suggested that the species transport equation of nanoparticles should be solved for convective transport in nanofluids. However, it is still not clear which approach should be used. In this work, the homogenous approach and the species transport approach are employed in order to find the suitable approach to describe the convective transport in nanofluids.

Numerical method

The computational fluid dynamics software FLUENT (version 6.2) is used to solve the transport equations for the turbulent flow in a uniformly heated tube of 1 m in length and 1 cm in diameter with the constant heat flux of 500,000 W/m 2 and Re = 50,000. The continuity, momentum, energy and species transport equations with the standard k-ε turbulence model are solved using the finite volume method with the QUICK scheme. The grid-independent study is made. The thermal conductivity models for nanofluids are implemented separately in FLUENT using the user-defined functions.

Results and discussion

The performances of the Leong et al.’s dynamic model and the present model for the non-flowing fluid are assessed by making the comparison with the Maxwell’s stationary model (1873), the Leong et al.’s stationary model (2006) and the Chon et al.’s dynamic model (2005). All models are also evaluated by using the available experimental data of thermal conductivity for nanofluids (Masuda et al. 1993; Eastman et al. 1997; Pak and Cho 1998; Lee et al. 1999; Das et al. 2003; Chon et al. 2005; Li and Peterson 2006).

The dependence of the thermal conductivity on volume fraction for various sizes of Al2O3 nanoparticles (particle diameters = 13 nm, 33 nm and 38.4 nm) in water at room temperature is shown in Figs. 2, 3 and 4. Figure 5 shows this dependence for 35 nm CuO nanoparticles in water at room temperature. The thermal conductivity dependence on temperature is shown in Figs. 6, 7, 8, 9 and 10 at a range of 290–350 K, for different sizes of Al2O3 nanoparticles (particle diameters = 11 nm, 38.4 nm, 47 nm and 150 nm) in water at volume fractions of 1% and 4%. Figures 11 and 12 show this dependence for 29 nm CuO nanoparticles in water at volume fractions of 4% and 6%.

Fig. 2
figure 2

Thermal conductivity models for Al2O3 nanoparticles in water base fluid at room temperature (particle diameter = 13 nm)—Particle volume-fraction dependent (Non-flowing fluid)

Full size image
Fig. 3
figure 3

Thermal conductivity models for Al2O3 nanoparticles in water base fluid at room temperature (particle diameter = 33 nm)—Particle volume-fraction dependent (Non-flowing fluid)

Full size image
Fig. 4
figure 4

Thermal conductivity models for Al2O3 nanoparticles in water base fluid at room temperature (particle diameter = 38.4 nm)—Particle volume-fraction dependent (Non-flowing fluid)

Full size image
Fig. 5
figure 5

Thermal conductivity models for CuO nanoparticles in water base fluid at room temperature (particle diameter = 35 nm)—Particle volume-fraction dependent (Non-flowing fluid)

Full size image
Fig. 6
figure 6

Thermal conductivity models for Al2O3 nanoparticles in water base fluid (particle diameter = 11 nm, particle volume fraction = 1%)—Temperature dependent (Non-flowing fluid)

Full size image
Fig. 7
figure 7

Thermal conductivity models for Al2O3 nanoparticles in water base fluid (particle diameter = 47 nm, particle volume fraction = 1%)—Temperature dependent (Non-flowing fluid)

Full size image
Fig. 8
figure 8

Thermal conductivity models for Al2O3 nanoparticles in water base fluid (particle diameter = 150 nm, particle volume fraction = 1%)—Temperature dependent (Non-flowing fluid)

Full size image
Fig. 9
figure 9

Thermal conductivity models for Al2O3 nanoparticles in water base fluid (particle diameter = 38.4 nm, particle volume fraction = 4%)—Temperature dependent (Non-flowing fluid)

Full size image
Fig. 10
figure 10

Thermal conductivity models for Al2O3 nanoparticles in water base fluid (particle diameter = 47 nm, particle volume fraction = 4%)—Temperature dependent (Non-flowing fluid)

Full size image
Fig. 11
figure 11

Thermal conductivity models for CuO nanoparticles in water base fluid (particle diameter = 29 nm, particle volume fraction = 4%)—Temperature dependent (Non-flowing fluid)

Full size image
Fig. 12
figure 12

Thermal conductivity models for CuO nanoparticles in water base fluid (particle diameter = 29 nm, particle volume fraction = 6%)—Temperature dependent (Non-flowing fluid)

Full size image

The predictions of the Maxwell’s stationary model (1873) for the dependence of the thermal conductivity on volume fraction are lower than values produced by the experimental data of 13 nm and 33 nm Al2O3 nanoparticles and 35 nm CuO nanoparticles in water-based fluid as shown in Figs. 2, 3 and 5. Also, Fig 4 shows that the Maxwell’s model over-predicts the thermal conductivity of 38.4 nm Al2O3 nanoparticles. The Maxwell’s model cannot predict the dependence of the thermal conductivity on temperature for all nanoparticle sizes and types and this is shown in Figs. 6, 7, 8, 9 and 12.

The Leong et al.’s stationary model (2006) predicts the volume-fraction-dependent thermal conductivity of nanofluids accurately for different sizes of nanoparticles when assessed by using the experimental data of 13 nm, 33 nm and 38.4 nm Al2O3 nanoparticles and 35 nm CuO nanoparticles in water-based fluid. This is shown in Figs. 2, 3, 4 and 5. However, the Leong et al.’s stationary model cannot predict the dependence of the thermal conductivity on temperature for all nanoparticle sizes and types as shown in Figs. 6, 7, 8, 9 and 12.

For the dependence of the thermal conductivity on volume fraction, the predictions of the Leong et al.’s dynamic model coincide with those of the Leong et al.’s stationary model as shown in Figs. 2, 3, 4 and 5. However, the Leong et al.’s dynamic model gives good prediction for the dependence of thermal conductivity on temperature for all nanoparticle sizes and types which is shown in Figs. 6, 7, 8, 9 and 12.

The accuracy of the Chon et al.’s dynamic model (2005) in predicting the dependence of thermal conductivity on volume fraction is low when assessed by using the experimental data of 13 nm, 33 nm and 38.4 nm Al2O3 nanoparticles and 35 nm CuO nanoparticles in water-based fluid. This is shown in Figs. 2, 3, 4 and 5. The Chon et al.’s model gives reasonable prediction for the dependence of thermal conductivity on temperature for all nanoparticle sizes and types which is shown in Figs. 6, 7, 8, 9 and 12.

The capability of the present model in predicting the volume-fraction-dependent thermal conductivity of nanofluids for different sizes of nanoparticles is shown to be satisfactory when assessed against the experimental data of 13 nm, 33 nm and 38.4 nm Al2O3 nanoparticles (Figs. 2, 3 and 4) and 35 nm CuO nanoparticles (Fig. 5) in water-based fluid. The present model also gives good prediction for the dependence of thermal conductivity on temperature for all nanoparticle sizes and types which is shown in Figs. 6, 7, 8, 9 and 12.

The interfacial layer thickness in the present model ranges between 0.5 and 3 nm for various nanoparticle sizes and temperatures which accords with Xue et al.’s model (2004) and Leong et al.’s stationary model (2006) that assume 3 nm and 1 nm for the interfacial layer thickness, respectively.

The present model gives a reasonable account of thermal conductivity of nanofluid in the case of the flowing fluid along a uniformly heated tube. Although the Leong et al.’s dynamic model gives better prediction in the case of the non-flowing fluid, it over-predicts the thermal conductivity of nanofluids in the case of the flowing fluid as shown in Table 1 for the averaged thermal conductivity of nanofluids for the turbulent convective heat transfer in nanofluids along a uniformly heated tube of Pak and Cho (1998).

Table 1 Averaged thermal conductivity of nanofluid for the turbulent convective heat transfer in nanofluid of Pak and Cho (1998)
Full size table

The present model also gives good prediction for the ratio of averaged heat transfer coefficients (h nf/h nf) in the case of the flowing fluid when assessed against the experimental data of Pak and Cho (1998) as shown in Fig. 13. The Maxwell’s model, the Leong et al.’s stationary model and the simulation by Maïga et al. (2004) under-predict the results.

Fig. 13
figure 13

Effect of particle volume fraction on the ratio of averaged heat transfer coefficients for water/Al2O3 nanoparticle with particle diameter = 13 nm (Flowing fluid)

Full size image

Furthermore, solving the species transport equation of nanoparticles for the convective transport in nanofluids, gives values close to the homogenous approach as can be seen in Table 2. Hence, it can be concluded that the convective heat transfer of nanofluids can be solved by the homogenous approach because the convective heat transfer of nanofluids mostly depends on the properties of the nanofluids. However, the thermal conductivity of nanofluids strongly depends on the volume fraction and temperature. Therefore, it is very important that the thermal conductivity models have to include both volume fraction and temperature dependences. The present model including effect of the temperature-dependent interfacial layer covers both dependences.

Table 2 Ratio of averaged heat transfer coefficients using the homogeneous approach and species transport approach for the turbulent convective heat transfer in nanofluid along a uniformly heated tube
Full size table

Conclusions

The inclusion of the effect of the temperature variation on the thermal conductivity of the interfacial layer for different sizes of nanoparticles in the present model is proved to be necessary for the accurate prediction of the thermal conductivity of nanofluids. The present model including effect of the temperature-dependent interfacial layer makes good predictions for volume-fraction- and temperature-dependent thermal conductivity of nanofluids for both non-flowing and flowing fluids.