1 Introduction

The microfluidic community is keen on looking for an optimized patterned surface that can give rise to as large boundary slip as achievable. Recent works on flow in microfluidic devices have reported that slip lengths as large as 200 μm can be achieved on a properly micro-engineered superhydrophobic surface (e.g. Choi et al. 2006; Lee et al. 2008). The slip length (Navier 1823), which is defined as the depth at which the velocity would become zero by extrapolation of the velocity profile into the envelope of a surface, is a standard measure of the velocity slip on a surface. It is also equal in magnitude to the slip velocity per unit shear rate of flow near a boundary surface.

The boundary slip has been reviewed from an experimental perspective by Neto et al. (2005) and Lauga et al. (2007), while superhydrophobic surfaces have been reviewed from a material perspective by Zhang et al. (2008). The body of work in this area has been fast growing in recent years. While the main thrust is to develop experimental methods and to make observations in the laboratory (e.g. Zhu and Granick 2001, 2002; Cottin-Bizonne et al. 2002; Tretheway and Meinhart 2002; Choi et al. 2003, 2006; Ou and Rothstein 2005; Joseph et al. 2006), numerical simulations and theoretical modeling have also been conducted using continuum or discrete-element approaches (e.g. Lauga and Stone 2003; Cottin-Bizonne et al. 2003, 2004; Zhang and Kwok 2004; Priezjev et al. 2005; Hendy et al. 2005; Priezjev and Troian 2006; Davies et al. 2006; Sbragaglia and Prosperetti 2007a, b; Hendy and Lund 2007; Ng and Wang 2009).

The boundary slip as observed on the macroscale is an apparent or asymptotic behavior in the far field, arising from a composite surface of mixed boundary conditions on the microscale. A surface can be engineered to feature micro- or nanopatterns, such as grates, posts, cones, turf, or holes. If the surface is made of hydrophobic (i.e. nonwetting) material, the interstitial pores will not be filled with liquid until the capillary pressure is exceeded. In this so-called Cassie (fakir) state, the liquid flow is restricted to the top of the microstructure, and the micropores are filled with gas or vapor which offers little resistance to the flow. Hence, the liquid experiences mixed boundary conditions on approaching the surface: no-slip (or partial slip if the solid is chemically treated) on the solid part, and no-shear on the void part of the surface. It is a spatial average of these micro-effects that will lead to the apparent or effective slip on the macroscale.

As remarked by Ybert et al. (2007), the hydrodynamic problem of flow over a surface with mixed boundary conditions is not easy to solve, and analytical results are available only for some simple one-dimensional patterns. A mathematical model that can help predict slippage on more complex geometries is still much wanting. Most of the above-mentioned theoretical modeling studies are for two-dimensional flows over a structure like grates or grooves. The existing literature lacks in particular theoretical work on flow over a three-dimensional structure like posts or holes.

Motivated by the need for characterizing different geometries, Ybert et al. (2007) have proposed some predictive scaling laws for the amounts of slippage achievable on stripes, posts, and holes as functions of the solid fraction. They have also proposed interpolation relationships to account for effects due to intrinsic or micro-slip, vapor dissipation and curvature of the meniscus.

This paper aims to examine in some further detail the problem of shear flow over bidimensional patterns, such as posts and holes, based on the scaling laws put forward by Ybert et al. (2007). Our basic formulation, namely Stokes flow over a heterogeneous surface, is the same as the one considered by them. Our solution method is, however, different from theirs. Ybert et al. (2007) have resorted to two approaches on numerically calculating the slip length. The first approach is the mathematical model previously used by Cottin-Bizonne et al. (2004), and the second approach is a 3D finite-element analysis implemented on a commercial package. In the model developed by Cottin-Bizonne et al. (2004), the problem is to solve numerically the Fourier-transformed components of the vorticity in the Fourier space. As pointed out by Cottin-Bizonne et al. (2004) and Ybert et al. (2007) themselves, this numerical method of solution may have limitations that restrict the range of some input values (e.g. accuracy will be significantly lost when the solid fraction becomes smaller than a certain value).

A semi-analytical solution method based on eigenfunction expansions is applied in this study. The Reynolds number in terms of the microscopic length scale is so small that the flow can be assumed to be inertia free, and is called creeping or Stokes flow. For Stokes flow over the two-dimensional microstructures of longitudinal and transverse grooves/grates, the method of eigenfunction expansions and matching has been used previously by Wang (2003), and Ng and Wang (2009) to study the effects of liquid penetration into the grooves. This solution technique is now extended to more complicated flow over the three-dimensional microstructures of posts or holes. Specifically, three-dimensional flow over a periodic array of solid patches on an otherwise no-shear surface, or vice versa, is solved in terms of the primitive variables in the real space. The variables are expressed in terms of Fourier series that naturally satisfy all the boundary conditions except the mixed slip conditions on the composite surface. The point collocation method is then used to determine the Fourier coefficients in order that the mixed boundary conditions are satisfied as well. This solution method is straightforward to apply, and is not subject to the limitations mentioned above.

Posts and holes of circular or square cross section organized on a rectangular lattice are studied in this work. The solid areas may be of no- or partial-slip type, and a unit cell of the lattice may have an aspect ratio different from unity. For various geometries and effects, we compute the effective slip length as a function of the solid fraction. The data points are plotted following the scaling laws proposed by Ybert et al. (2007). Like Ybert et al. (2007), linear regression relationships are derived, but in our case the regression is based on more data points extending over a wider range of the solid fraction, and is geometry specific. We not only refine, but also supplement the linear regression equations obtained by Ybert et al. (2007).

The threshold value of the solid fraction below which posts/pillars (especially those of circular shape) may give rise to larger slippage than grooves/grates is determined. The slippage is also affected by the configuration of the arrangement of different areas in the array. On varying the aspect ratio of a periodic cell, we find that it can be more advantageous to have the pitch (i.e. one length period) being larger in the spanwise direction than in the streamwise direction. This in some sense amounts to adding longitudinal grooves into an array of posts.

2 Mathematical model

Stokes shear flow of a viscous liquid over the envelope of a structured surface composed of posts or holes is considered. From a plan view, the surface features a periodic array of patches organized on a rectangular lattice; see Fig. 1a, b. The Cassie state is assumed: the liquid does not fill the voids, and the flow remains on top of the microstructure. In the case of posts or pillars, the individual patches (area I) represent the liquid/solid interfaces where the no- or partial-slip boundary condition applies. The continuous part (area II) of the surface is then the liquid/void interface on which infinite slip of the liquid holds. In the case of holes, the pattern is interchanged: the discrete areas I are the void surfaces, and the continuous area II is then the solid surface.

Fig. 1
figure 1

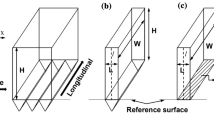
a Side view of liquid flow over the envelope of a structured surface, composed of solid posts (I) embedded in shear-free gas (II), or holes (I) filled with shear-free gas in a solid medium (II). b Plan view of the surface envelope, featuring a periodic array of discrete areas I organized on a rectangular lattice in a continuous area II. The x-axis points in the direction of the flow far above the surface. c Three-dimensional view of a unit domain enclosing one discrete area I at the center on its base, with periodic conditions on the four lateral boundaries, and mixed slip conditions on the surface envelope. The length quantities are normalized with respect to the x-pitch of the periodic structure

Full size image

The patterned surface can be seen as being made up of a rectangular array of unit cells, where one unit cell encloses a single area I centered in the middle. For any unit cell, we define at its center the local rectangular coordinates (x,y), such that the x-axis points in the direction of the flow far above the surface. The area I has a geometry that is symmetrical about the x- and the y-axes. The centers of neighboring cells are separated by a distance (or pitch) L and bL in the x- and y-directions, respectively. Hence, a unit cell has an aspect ratio of b:1.

A unit cell extending into the far field results in a semi-infinite unit volume, which forms the basic domain of our analysis. Figure 1c shows such a unit volume, where the normal z-axis is defined, pointing into the space above the surface. The velocity \({\bf{V}}\equiv (u,v,w)\) and pressure p, which are functions of \({\bf{x}}\equiv (x,y,z),\) are governed by the continuity and Stokes equations

$$ \nabla\cdot{\bf{V}} = 0, $$
(1)
$$ \nabla^2{\bf{V}}=\nabla p, $$
(2)

where the variables x, V, and p have been normalized with respect to L, U, and μU/L, respectively. Here, μ is the dynamic viscosity of the liquid, L is the pitch of the surface pattern in the streamwise x-direction, and U is a velocity scale such that the velocity gradient in the far field is equal to U/L. Our problem is from here on expressed in terms of the normalized variables.

The flow is driven by a unity velocity gradient in the x-direction in the far field as z→∞, where v = w = p = 0 is assumed. By virtue of the forcing and the configuration of the surface pattern, the following symmetry or anti-symmetry properties of the flow field can be anticipated: u is even in both x and y, v is odd in both x and y, while w and p are odd in x but even in y. To observe periodicity, the following conditions on the four lateral boundaries must be satisfied:

$$ {\frac{\partial u} {\partial x}}=v=w=p=0\qquad\hbox{at}\;x=\pm 1/2, $$
(3)
$$ {\frac{\partial u} {\partial y}}=v={\frac{\partial w} {\partial y}}={\frac{\partial p} {\partial y}}=0 \qquad\hbox{at}\;y=\pm b/2. $$
(4)

On the surface z = 0, the vertical velocity component vanishes, w = 0, and mixed boundary conditions are imposed on the horizontal velocity components. Over the void part of the surface, the no-shear or infinite-slip condition applies:

$$ \left.{\frac{\partial (u,v)} {\partial z}}\right|_{z=0}=0. $$
(5)

Over the solid part of the surface, the Navier partial-slip condition applies:

$$ \left.(u, v)_{z=0}=\lambda{\frac{\partial (u, v)} {\partial z}}\right|_{z=0}, $$
(6)

where λ ≥ 0 is the micro- or intrinsic slip length. When λ = 0, the solid surface becomes a no-slip surface.

The basic solutions naturally satisfying the lateral periodic boundary conditions can be expressed in the form of the following eigenfunction expansions:

$$ \begin{aligned} u(x,y,z) & = z+\delta+\sum_{n=1}^{\infty}\hbox{cos}(\alpha_n x) U_{n0}(z) +\sum_{m=1}^{\infty}\hbox{cos}(\beta_m y) U_{0m}(z)\\ &\quad+\sum_{n=1}^{\infty}\sum_{m=1}^{\infty} \hbox{cos}(\alpha_n x) \hbox{cos}(\beta_m y) U_{nm}(z), \end{aligned} $$
(7)
$$ v(x,y,z)=\sum_{n=1}^{\infty}\sum_{m=1}^{\infty} \hbox{sin}(\alpha_n x) \hbox{sin}(\beta_m y) V_{nm}(z), $$
(8)
$$ w(x,y,z)=\sum_{n=1}^{\infty}\hbox{sin}(\alpha_n x) W_{n0}(z) +\sum_{n=1}^{\infty}\sum_{m=1}^{\infty} \hbox{sin}(\alpha_n x) \hbox{cos}(\beta_m y) W_{nm}(z), $$
(9)

and

$$ p(x,y,z)=\sum_{n=1}^{\infty}\hbox{sin}(\alpha_n x) P_{n0}(z) +\sum_{n=1}^{\infty}\sum_{m=1}^{\infty} \hbox{sin}(\alpha_n x) \hbox{cos}(\beta_m y) P_{nm}(z), $$
(10)

where δ is a constant known as the macro-slip length, and U n0, U 0m , U nm , and so on, are functions of z. The eigenvalues are given by

$$ \alpha_n=2n\pi,\quad \beta_m=2m\pi/b\qquad n,m=1,2,\ldots. $$
(11)

The constant δ is also known as the effective or apparent slip length. It amounts to an apparent slip velocity per unit shear rate of the flow near the patterned surface, but at a distance sufficiently far from the microstructure.

Substitution of Eqs. 7–10 into the components of the Stokes equation 2, after matching of terms, gives (for n, m = 1,2,...)

$$ U_{n0}''-\alpha_n^2U_{n0}=\alpha_nP_{n0}, $$
(12)
$$ U_{0m}''-\beta_m^2 U_{0m}=0, $$
(13)
$$ U_{nm}''-\gamma_{nm}^2 U_{nm}=\alpha_n P_{nm}, $$
(14)
$$ V_{nm}''-\gamma_{nm}^2 V_{nm}=-\beta_m P_{nm}, $$
(15)
$$ W_{n0}''-\alpha_n^2W_{n0}=P_{n0}', $$
(16)
$$ W_{nm}''-\gamma_{nm}^2 W_{nm}=P_{nm}', $$
(17)

where \(\gamma_{nm}^2=\alpha_n^2+\beta_m^2.\) Substitution of Eqs. 7–9 into the continuity equation 1 further gives

$$ W_{n0}'-\alpha_n U_{n0}=0, $$
(18)
$$ W_{nm}'-\alpha_n U_{nm}+\beta_m V_{nm}=0. $$
(19)

Using the far-field conditions U n0, U 0m , V nm → 0 as z→∞, and the conditions \(W_{n0}(0)= W_{nm}(0)=0,\) the Eqs. 12–19 can be solved to yield after some algebra:

$$ U_{n0}(z)=A_{1n} \left( \hbox{e}^{-\alpha_n z}-\alpha_n z \hbox{e}^{-\alpha_n z}\right), $$
(20)
$$ U_{0m}(z)=A_{3m} \hbox{e}^{-\beta_m z}, $$
(21)
$$ U_{nm}(z)=B_{1nm} \hbox{e}^{-\gamma_{nm} z}+B_{2nm}z \hbox{e}^{-\gamma_{nm} z}, $$
(22)
$$ V_{nm}(z)=\left( {\frac{\alpha_n} {\beta_m}}B_{1nm}+{\frac{\gamma_{nm}} {\alpha_n\beta_m}}B_{2nm}\right) \hbox{e}^{-\gamma_{nm} z}-{\frac{\beta_m} {\alpha_n}}B_{2nm}z \hbox{e}^{-\gamma_{nm} z}, $$
(23)
$$ W_{n0}(z)=\alpha_n A_{1n} z \hbox{e}^{-\alpha_n z}, $$
(24)
$$ W_{nm}(z)=-{\frac{\gamma_{nm}}{\alpha_n}}B_{2nm} z \hbox{e}^{-\gamma_{nm} z}, $$
(25)
$$ P_{n0}(z)=2\alpha_n A_{1n} \hbox{e}^{-\alpha_n z}, $$
(26)

and

$$ P_{nm}(z)=-2{\frac{\gamma_{nm}} {\alpha_n}}B_{2nm}\hbox{e}^{-\gamma_{nm} z}. $$
(27)

The solutions deduced so far, which contain undetermined constants δ, A 1n , A 3m , B 1nm and B 2nm (n, m = 1,2,...), have yet to satisfy the boundary conditions Eqs. 5 or 6 on the surface z = 0. Let us first truncate each of the series in Eqs. 7–10 to a finite number of terms:

$$ \begin{aligned} u(x,y,z) &= z+\delta+\sum_{n=1}^{N}\hbox{cos}(\alpha_n x) U_{n0}(z) +\sum_{m=1}^{M}\hbox{cos}(\beta_m y) U_{0m}(z)\\ &\quad+\sum_{n=1}^{N}\sum_{m=1}^{M} \hbox{cos}(\alpha_n x) \hbox{cos}(\beta_m y) U_{nm}(z), \end{aligned} $$
(28)
$$ v(x,y,z)=\sum_{n=1}^{N}\sum_{m=1}^{M} \hbox{sin}(\alpha_n x) \hbox{sin}(\beta_m y) V_{nm}(z), $$
(29)

and so on. Then, the no-shear condition 5 gives

$$ \begin{aligned} &2\sum_{n=1}^N\alpha_{n}A_{1n}\hbox{cos}(\alpha_{n}x) +\sum_{m=1}^M\beta_{m}A_{3m}\hbox{cos}(\beta_{m}y)\\ &\quad +\sum_{n=1}^N\sum_{m=1}^M \gamma_{nm}B_{1nm} -B_{2nm}\hbox{cos}(\alpha_n x)\hbox{cos}(\beta_m y)=1, \end{aligned} $$
(30)

and

$$ \sum_{n=1}^N\sum_{m=1}^M\left[ {\frac{\alpha_n\gamma_{nm}} {\beta_m}}B_{1nm} +\left({\frac{\alpha_n} {\beta_m}}+{\frac{2\beta_m} {\alpha_n}}\right) B_{2nm} \right] \hbox{sin}(\alpha_n x)\hbox{sin}(\beta_m y)=0. $$
(31)

The partial-slip condition 6 gives

$$ \begin{aligned} &\delta+\sum\limits_{n=1}^N(1+2\lambda\alpha_n)A_{1n}\hbox{cos}(\alpha_{n}x)+ \sum\limits_{m=1}^M(1+\lambda\beta_m)A_{3m}\hbox{cos}(\beta_m y)\\ &\quad+\sum\limits_{n=1}^N\sum\limits_{m=1}^M(1+\lambda\gamma_{nm})B_{1nm} \hbox{cos}(\alpha_n x)\hbox{cos}(\beta_m y)\\ &\quad-\lambda\sum\limits_{n=1}^N\sum\limits_{m=1}^M B_{2nm}\hbox{cos}(\alpha_{n} x)\hbox{cos}(\beta_m y)=\lambda, \end{aligned} $$
(32)

and

$$ \begin{aligned} &\sum_{n=1}^N\sum_{m=1}^M{\frac{\alpha_n}{\beta_m}} (1+\lambda\gamma_{nm})B_{1nm} \hbox{sin}(\alpha_n x)\hbox{sin}(\beta_m y)\\ &\quad+\sum_{n=1}^N\sum_{m=1}^M{\frac{\gamma_{nm}+\lambda (\alpha_n^2+2\beta_m^2)} {\alpha_n\beta_m}} B_{2nm}\hbox{sin}(\alpha_n x)\hbox{sin}(\beta_m y)=0. \end{aligned} $$
(33)

Now, we need to develop a system of K c  = 1 + N + M + 2N × M equations in order to solve for the same number of unknown coefficients: δ, A 1n , A 3m , B 1nm and B 2nm , where n = 1,...,N, and m = 1,...,M. The method of point collocation is adopted here. The boundary conditions 30 and 31, or 32 and 33, depending on the regions of the surface, are required to be satisfied at a finite number of discrete points distributed over a representative part of the patterned surface. By symmetry of the flow field, it suffices to consider a half-pitch in both x and y. Hence, a convenient computational domain can be the first quadrant: 0 ≤ x ≤ 1/2 and 0 ≤ y ≤ b/2. In our scheme, two different sets of collocation points are selected for the x- and y-components of the boundary conditions. This is to avoid setting points along the four boundaries of the domain for the conditions in terms of v, which is zero on these boundaries. The x-component of the boundary conditions, viz. 30 and 32, are imposed to be satisfied at an IM × JM array of points \(( x_i^{(1)},y_j^{(1)}) =( (i-1)\Updelta x, (j-1)\Updelta y),\) where i = 1,...,IM, j = 1,...,JM, \(\Updelta x=0.5/(IM-1)\) and \(\Updelta y=0.5b/(JM-1).\) For the y-component of the boundary conditions, viz. 31 and 33, they are imposed to be satisfied at an (IM−1) × (JM−1) array of points \(( x_i^{(2)},y_j^{(2)})=( x_i^{(1)}+0.5\Updelta x, y_j^{(1)}+0.5\Updelta y),\) where i = 1,...,IM−1, and j = 1,...,JM−1. Note that the first set of points covers the entire computational domain, while the second set of points only extends to a region that is off the boundaries of the domain by a half grid interval. The total number of collocation points is therefore K p  = IM × JM + (IM−1) × (JM−1), which should be exactly equal to K c in order to form a system with a unique solution. It happens that K c  = K p when IM = N + 1 and JM = M + 1.

Figure 2 shows an example of how the two staggering sets of points are distributed for a case where b = 1, IM = JM = 74, and a circular area I of radius r = 0.25 is considered. Points immediately on the two sides of the interface separating regions I and II are slightly adjusted in position so that they are at an equal distance of Δx/2 from the interface. In this work, we have chosen to use the IMSL-DLSARG high-precision solver to solve the system of equations. Some trial tests have shown that solutions of good accuracy can be obtained when the numbers of the points are as many as IM, JM > 70.

Fig. 2
figure 2

An illustration of the distribution of two staggering sets of collocation points on a composite surface, where the dots and the crosses are, respectively, the points at which satisfaction of the x- and the y-components of the mixed slip conditions are imposed. In this example, b = 1, IM = JM = 74, and a circular area I of radius r = 0.25 is considered. Points immediately on the two sides of the interface separating areas I and II are slightly adjusted in position so that they are at an equal distance of Δx/2 from the interface

Full size image

3 Results

3.1 Flow over posts

Let us first consider flow over a patterned surface made up of solid areas organized on a square lattice (i.e. b = 1), with zero slip on the solid surfaces (i.e. λ = 0). This kind of pattern corresponds to the tops of posts or pillars as a structured surface. The no-slip solid areas can be circular or square in shape. The ratio of solid to total area of the surface, or simply the solid fraction, is denoted by ϕ s . Ybert et al. (2007) have proposed that in the limit of small solid fraction, the macro-slip length for posts is scaled by

$$ \lim_{\phi_s\rightarrow 0}\delta \sim \phi_s^{-1/2}. $$
(34)

They verified this scaling law by showing that their computed slip lengths indeed collapse closely onto a single straight line when plotted against \(\phi_s^{-1/2}.\) They derived that, for some ten data points in the range 0.02 < ϕ s  < 0.3 including circular as well as square solid areas, a linear regression analysis gives the relation \(\delta = 0.325\phi_s^{-1/2}-0.44.\)

Here, in Fig. 3, we re-examine in a more detailed manner the plotting of δ versus ϕ −1/2 s based on our computed values. First, many more data points for each geometry of the solid areas are generated. Second, to obtain a more accurate linear fit reflecting the small limit of ϕ s →0, the solid fraction being considered for linear regression is shifted to a range of smaller limits 0.008 < ϕ s  < 0.25. With these changes, we find that the data points for the two geometries actually fall on slightly different straight lines. These lines are mathematically given by

$$ \delta = 0.34\phi_s^{-1/2}-0.468\quad \hbox{for circular posts}, $$
(35)
$$ \delta = 0.33\phi_s^{-1/2}-0.461\quad \hbox{for square posts.} $$
(36)

One can see that these two lines have slightly greater slopes and lower intercepts than those of the line derived by Ybert et al. (2007). For the same solid fraction, the circular solid areas give rise to a slightly larger effective slip length than the square ones. Nevertheless, the scaling law as proposed by Ybert et al. (2007) is very well followed by either geometry of the solid areas.

Fig. 3
figure 3

Effective slip length, δ, versus the negative half power of the solid fraction, ϕ −1/2 s , for circular (circles and solid line) and square (squares and dashed line) posts, where the symbols are computed results, and the lines are straight lines best fitting the results over the range 0.008 < ϕ s  < 0.25. Other inputs: b = 1, λ = 0. The corresponding theoretical results for stripes oriented parallel and normal to the flow, as given in Eq. 37, are also plotted for comparison. The inset shows the computed results plotted on linear coordinates. The crosses are the experimental results reported by Lee et al. (2008)

Full size image

The inset of Fig. 3 is a plot of the same computed results on linear coordinates. Shown in this inset are also the measured data points recently reported by Lee et al. (2008), who performed rheometry tests with a cone spinning under a constant shear rate over a hydrophobic structured surface exhibiting posts or grates of 50 μm pitch. Apart from some discrepancy, which is probably due to the rotational flow pattern in the rheometry system (Lee et al. 2008), the measured data and the theoretical results show a similar trend of sharp rise of the slip length as the solid fraction tends to zero.

It is also of interest to compare posts with grates. Figure 3 shows also the results corresponding to flow over parallel or normal stripes (i.e. tops of grates). Analytical expressions for the effective slip lengths over these one-dimensional patterns have been obtained by Philip (1972), who considered shear flow over a flat plate with a periodic array of no-shear alternating with no-slip slots:

$$ \delta_{\rm parallel}=2\delta_{\rm normal} ={\frac{1} {\pi}}\ln\left[ \sec\left({\frac{\pi(1-\phi_s)} {2}}\right) \right]. $$
(37)

The figure shows that when the solid fraction is sufficiently small, namely \(\phi_s^{-1/2}>3\) or ϕ s  < 0.11 (say, circular posts of a radius smaller than 0.37 of the half-pitch), the posts will perform better than the parallel grates. The difference is more pronounced as the solid fraction drops further.

3.2 Flow over holes

We next consider flow over a patterned surface made up of holes organized on a square lattice (i.e. b = 1), with no slip on the solid surface (i.e. λ = 0). The holes can also be circular or square in shape. Ybert et al. (2007) argued that holes behave like solid stripes running parallel or normal to the flow, depending on whether ϕ s →1 or ϕ s →0. In the limit ϕ s →0, the right-hand side of the Eq. 37 behaves like \([\ln(2/\pi)-\ln(\phi_s)]/\pi.\) This has motivated Ybert et al. (2007) to propose a scaling law

$$ \lim_{\phi_s\rightarrow 0}\delta\sim -\ln(\phi_s) $$
(38)

for stripes or even holes.

We show in Fig. 4 our computed slip lengths for circular and square holes as functions of \(-\ln(\phi_s).\) For square holes, the numerical method applied by Ybert et al. (2007) can only handle \({\phi_s\geq}0.1.\) Without subject to this constraint, we have computed for square holes of a solid fraction as small as ϕ s  = 0.05. As long as ϕ s  < 0.75, the data points of the slip length of square holes are very closely described by a straight line of the equation:

$$ \delta = -0.115\ln(\phi_s)-0.014\quad \hbox{for square holes}. $$
(39)

Square holes are comparable in effective slip length with normal stripes for an intermediate value of the solid fraction ϕ s ≈ 0.6–0.2. For smaller ϕ s , square holes are outperformed by other geometries.

Fig. 4
figure 4

Effective slip length, δ, versus the negative natural logarithm of the solid fraction, \(-\ln(\phi_s),\) for circular (circles and solid line) and square (squares and dashed line) holes, where the symbols are computed results, and the lines are straight lines best fitting the results over the ranges 0.22 < ϕ s  < 0.75 and 0.05 < ϕ s  < 0.75 for the two geometries. Other inputs: b = 1, λ = 0. The corresponding theoretical results for stripes oriented parallel and normal to the flow, as given in Eq. 37, are also plotted for comparison. The inset shows the computed results plotted on linear coordinates. The circular holes become connected when \(\phi_s<0.22,\) leading to a dramatic increase in the slip length

Full size image

Circular holes arranged on a square lattice remain disconnected when their radius is smaller than the half-pitch of the pattern; the smallest possible solid fraction for isolated circular holes is hence 1−π/4 = 0.215. We find that, in the range 0.22 < ϕ s  < 0.75, the data points of the slip length of circular holes can be fitted, with reasonably good agreement, by a straight line of the equation:

$$ \delta = -0.134\ln(\phi_s)-0.023\quad \hbox{for circular holes}. $$
(40)

Over this range of the solid fraction, circular holes are also comparable in slip length with normal stripes.

Circular holes become connected when their radius is larger than the half-pitch of the pattern. When this happens, the solid part of the surface becomes disconnected instead, and the pattern will tend to behave like posts (i.e., δ increases with ϕ −1/2 s instead of \(-\ln(\phi_s)\)). This explains the dramatic increase in the slip length of circular holes when the solid fraction drops below the threshold value of 0.215. For any given ϕ s , circular holes always give rise to a higher slip length than square holes; the difference is much more pronounced as ϕ s → 0.

In the upper limit ϕ s →1, both circular and square holes behave more like parallel stripes, as has been pointed out by Ybert et al. (2007). On comparing Figs. 3 and 4, one can note that for the same solid fraction posts will in general give rise to a much higher effective slip length than holes.

3.3 Effect of micro-slip

Let us next consider the effect of micro-slip (or “intrinsic slippage”) on the macro-slip length. Obviously, the slip length will be enhanced by finite slippage on the solid areas. Ybert et al. (2007) have put forward the following scaling law for the increase in slip length due to micro-slippage

$$ \Updelta\delta\equiv \delta_{\lambda}-\delta_0\sim {\frac{\lambda} {\phi_s}}, $$
(41)

where λ is the intrinsic slip length, δλ is the effective slip length for a patterned surface with micro-slippage on the solid areas, δ0 is the effective slip length for the same surface, but without micro-slippage. Similar approximate formulas have been proposed by Ng and Wang (2009), who showed that the following phenomenological equation can be used to predict with good accuracy the effect of micro-slippage for the case of flow over grates:

$$ \Updelta\delta \cong {\frac{\lambda} {\phi_s}} \quad \hbox{for solid stripes running parallel or normal to the flow}. $$
(42)

Note that this equation becomes exact, i.e. Δδ = λ, when the surface is wholly solid ϕ s  = 1. Equation 42 leads one to expect that, for any surface patterns, the scaling law (Eq. 41) should have a numerical prefactor nearly equal to unity. Ybert et al. (2007) have reported a factor of 0.165 based on linear regression of some results for square posts. The factor should be rectified to be 1.03, as a factor of 2π had been mistakenly introduced in the horizontal coordinate of their Fig. 3 (Cottin-Bizonne, personal communication, April 3, 2009).

To investigate the relationship in a more thorough manner, we show in Figs. 5 and 6 the increase in the slip length, Δδ, as a function of λ/ϕ s for posts and holes, respectively. Three values of the micro-slip length are considered: λ = 0.5, 0.25 and 0.05. In these plots, the symbols are the calculated results, and the lines are straight lines which best-fit the results. Here, many more data points are used for the line-fitting than was done by Ybert et al. (2007). The equations of these lines-of-best-fit are summarized in Table 1. The following observations can be made. First, individual sets of data points are indeed well described by straight lines with insignificant scattering. The linearity applies virtually to the entire range of the solid fraction 0 < ϕ s  < 1, although the linear fitting is more affected by data of small solid fraction ϕ < 0.1 (i.e. over the range of sparse packing). Second, these lines indeed have slopes close to unity, ranging from 1.006 to 1.048 in the case of posts, and from 1.037 to 1.255 in the case of holes. The slope tends to increase as λ decreases. Third, whether the shape is circular or square is rather unimportant in the case of posts, but can have some finite effects in the case of holes, especially at small micro-slippage. In the case of posts, the data points of the two geometries collapse to nearly the same line for each value of λ. In the case of holes, the micro-slippage tends to have a larger effect on circular holes than on square holes, the difference being more pronounced when ϕ s →0.

Fig. 5
figure 5

The increase in slip length due to micro-slippage, Δδ, versus the ratio of micro-slip length to solid fraction, λ/ϕ s , for circular (circles and solid line) and square (squares and dashed line) posts, where the symbols are computed results, and the lines are straight lines best fitting the results. Other inputs: b = 1, and λ = (a) 0.5, (b) 0.25, (c) 0.05

Full size image
Fig. 6
figure 6

The increase in slip length due to micro-slippage, Δδ, versus the ratio of micro-slip length to solid fraction, λ/ϕ s , for circular (circles and solid line) and square (squares and dashed line) holes, where the symbols are computed results, and the lines are straight lines best fitting the results. Other inputs: b = 1, and λ = (a) 0.5, (b) 0.25, (c) 0.05

Full size image
Table 1 The slope s and the intercept t of the lines Δδ = sλ/ϕ s  + t that best fit the data points for cases shown in Figs. 5 and 6
Full size table

3.4 Effect of aspect ratio

We lastly look into the effect of unequal pitches in the x- and the y-directions (i.e. \(b\,{\not=}\,1\)). We here compare cases in which circular posts are organized on a rectangular lattice with various aspect ratios. Shown in Fig. 7 are again the plots of δ against ϕ −1/2 s for circular solid areas without micro-slippage, but for cases with the y-pitch to x-pitch ratio equal to (i) 2:1, (ii) 1:2, (iii) 1.25:1, (iv) 1:1.25, (v) 1:1, (vi) 0.8:1, and (vii) 0.5:1. Note that the second and the seventh cases, and the fourth and the sixth cases appear to have the same aspect ratios, but they correspond to different scenarios; the length quantities are normalized with respect to the y-pitch in cases (ii) and (iv), but with respect to the x-pitch in cases (vi) and (vii). Compared with the reference case (v), cases (vi) and (vii) are those with the y-pitch shortened, cases (ii) and (iv) are those with the x-pitch lengthened, and cases (i) and (iii) are those with the y-pitch lengthened. By linear regression, the lines that best fit the seven sets of data points (for ϕ s  < 0.25) are found as follows:

$$ \delta = \left\{ \begin{array}{l} 0.475\\ 0.480\\ 0.384\\ 0.376\\ 0.340\\ 0.302\\ 0.240 \end{array} \right\} \phi_s^{-1/2}- \left\{ \begin{array}{l} 0.476\\ 0.697\\ 0.505\\ 0.523\\ 0.468\\ 0.422\\ 0.348 \end{array} \right\}\quad \hbox{for the aspect ratio} \left\{ \begin{array}{l} 2:1\\ 1:2\\ 1.25:1\\ 1:1.25\\ 1:1\\ 0.8:1\\ 0.5:1 \end{array} \right\}. $$
(43)
Fig. 7
figure 7

Effective slip length, δ, versus the negative half power of the solid fraction, ϕ −1/2 s , for circular posts, where the symbols are computed results, and the lines are straight lines best fitting the results over the range 0.0065 < ϕ s  < 0.25, for λ = 0, and y-pitch : x-pitch = 2:1, 1:2, 1.25:1, 1:1.25, 1:1, 0.8:1, 0.5:1

Full size image

Let us consider for instance in case (v) a solid fraction of ϕ s  = 0.05 on a 1:1 lattice. Assuming that the solid area remains unchanged, the solid fraction will increase to 0.0625 in case (vi) when the y-pitch is shortened to 0.8, and decrease to 0.04 in cases (iii) and (iv) when either pitch is lengthened to 1.25. Also, the solid fraction will increase to 0.10 in case (vii) when the y-pitch is shortened to 0.5, and decrease to 0.025 in cases (i) and (ii) when either pitch is lengthened to 2.0. On substituting these values of ϕ s into the equations above, we get δ = 2.53, 2.34, 1.42, 1.36, 1.05, 0.79 and 0.41 for the corresponding seven values of the aspect ratio. Obviously, decreasing the solid fraction will result in a higher slip length, and vice versa. This example shows that a 20–50% reduction in the y-pitch may lead to some 25–61% decrease in the slip length. Also, lengthening the x- and y-pitches by 25–100% may respectively lead to 30–123 and 35–141% increase in the slip length. A further possible change in the configuration is as follows. If the aspect ratio remains 1:1 and the solid area remains the same, the solid fraction will drop to 0.04 when the pitches are each lengthened to \(\sqrt{1.25}.\) Then, with some calculations, one finds that an equal increase of the two pitches will lead to a slip length of 1.38 (31% increase), which is an intermediate value between cases (iii) and (iv). Similarly, when the pitches are each lengthened to \(\sqrt{2},\) the solid fraction drops to 0.025, leading to a slip length of 2.38 (127% increase), which is also an intermediate value between cases (i) and (ii). These results suggest that, for a given solid fraction, it is more advantageous to have the posts spaced farther apart in the y-direction than in the streamwise x-direction. In some sense, widening the gap between rows of posts is equivalent to putting grooves into the structured surface. It is already known that, as given in Eq. 37, longitudinal grooves will give higher effective velocity slip than transverse grooves. This explains why increasing the y-pitch can have a better effect than increasing the x-pitch. This exercise reveals the possibility that a greater slip length can be achieved by a suitable combination of posts and grooves than that by posts or grooves alone.

4 Concluding remarks

A semi-analytical method based on eigenfunction expansions and point collocation has been developed to solve the problem of three-dimensional Stokes flow over a composite surface with mixed boundary conditions. The slip length, which is yielded directly as part of solution, has been computed as a function of the solid fraction, for periodic arrays corresponding to posts or holes. Based on linear regression of calculated results following the scaling laws proposed by Ybert et al. (2007), we have obtained more detailed geometry-specific equations 35, 36, 39, 40, 43, as well as those presented in Table 1, for surfaces with or without micro-slippage. These equations should refine or supplement the counterparts previously deduced by Ybert et al. (2007). To get the dimensional slip length, one has to multiply the normalized slip length by the pitch of the surface pattern. Typical micro-engineered surfaces have a pitch in the order of 10–100 μm. Referring to Fig. 3, one can see that a slip length that is two or three times the pitch can in principle be achieved if the solid fraction is small enough.

While the focus has been largely on arrays organized on a 1:1 square lattice, we have shown that an aspect ratio other than 1:1 may give a better slip effect. For the same solid fraction, it is more advantageous to have a larger pitch in the spanwise direction than in the streamwise direction. In theory, the larger the aspect ratio, the larger the increase in the slip length. There is no finite asymptotic limit for the slip length as the aspect ratio increases. In practice, the absolute maximum pitch is, however, limited by the stability condition depending on the liquid pressure (Lee et al. 2008). We leave the details to a future study to further test the effects of varying the configurations of the arrangement of no-shear and no-slip areas in a periodic unit cell.

Feuillebois et al. (2009) have recently arrived at the conclusion that, on the Hele-Shaw limit of a thin channel, it is an array of longitudinal stripes that will provide the largest possible slip that can be achieved by any texture, whether isotropic or anisotropic. This is opposite to the prediction for thick channels, as considered in this work, where an array of posts will give larger slip than stripes for a sufficiently small solid fraction. One would then question: in what exact manner will the optimum texture change depending on the channel thickness, from an isotropic texture in one limit to an anisotropic texture in another limit? It is very likely that, for a channel of intermediate thickness (i.e. the pattern unit length is comparable with the channel depth), the optimum texture is one made up of certain proportions of the two limits. The details of such an optimum texture as a function of the channel thickness are yet to investigated.