A scaling model for electrowetting-on-dielectric microfluidic actuators

Abstract

A hydrodynamic scaling model of droplet actuation in an electrowetting-on-dielectric (EWD) actuator is presented that takes into account the effects of contact angle hysteresis, drag from the filler fluid, drag from the solid walls, and change in the actuation force while a droplet traverses a neighboring electrode. Based on this model, the threshold voltage, V _T, for droplet actuation is estimated as a function of the filler medium of a scaled device. It is shown that scaling models of droplet splitting and liquid dispensing all show a similar scaling dependence on [t/ε_r(d/L)]^1/2, where t is insulator thickness and d/L is the aspect ratio of the device. It is also determined that reliable operation of a EWD actuator is possible as long as the device is operated within the limits of the Lippmann–Young equation. The upper limit on applied voltage, V _sat, corresponds to contact-angle saturation. The minimum 3-electrode splitting voltages as a function of aspect ratio d/L < 1 for an oil medium are less than V _sat. However, for an air medium the minimum voltage for 3-electrode droplet splitting exceeds V _sat for d/L ≥ 0.4. EWD actuators were fabricated to operate with droplets down to 35pl. Reasonable scaling results were achieved.

1 Introduction

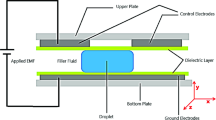
Electrowetting-on-dielectric (EWD) microfluidics is based on the actuation of droplet volumes up to several microliters using the principle of modulating the interfacial tension between a liquid and an electrode coated with a dielectric layer (Berge 1993). An electric field established in the dielectric layer creates an imbalance of interfacial tension if the electric field is applied to only one portion of the droplet, which forces the droplet to move (Pollack et al. 2000). Droplets are usually sandwiched between two parallel plates—the bottom being the chip surface, which houses an addressable electrode array, and the top surface being either a continuous ground plate or a passive top plate (the nature of the top plate is determined by the chip’s characteristics).

The basic EWD device is based on charge-control manipulation at the solution/insulator interface of discrete droplets by applying voltage to control electrodes. The device exhibits bilateral transport, uses gate electrodes for charge-controlled transport, has a threshold voltage, and is a square-law device in the relation between droplet velocity and gate actuation voltage. Thus, the EWD device is analogous to the metal-oxide-semiconductor (MOS) field-effect transistor (FET), not only as a charge-controlled device, but also as a universal switching element (Fair et al. 2001).

MOSFETs are known to scale in dimension according to well-known constant-voltage or constant-field scaling rules for obtaining simultaneous improvements in transistor density, switching speed and power dissipation (Dennard et al. 1974), whereas EWD devices share certain commonalities with MOSFETs and since EWD device development has been largely empirical, it is appropriate to develop a design framework for EWD devices that will guide device scaling into the picoliter region and beyond. This is particularly true now, since most reported EWD devices have operated with liquid volumes in the microliter to tens of nanoliters range (Fair 2007). However, the scaling down of liquid volumes is required for reduced reagent volumes, increased assay throughput, and lower system costs (Mastrangelo et al. 1998).

The EWD parameters that must be considered in scaling actuator dimensions include: (1) threshold voltage for droplet actuation, (2) droplet splitting voltage, (3) droplet dispensing voltage from on-chip reservoirs, (4) voltage dependence of droplet velocity, and (5) droplet mixing times. To address the scaling issues of these device parameters requires an integrated analytical model for the fluidic functions of droplets placed between parallel plates in a EWD actuator. A hydrodynamic model of droplet actuation was constructed in a systematic manner that includes the effects of contact angle hysteresis, drag from the filler fluid, drag from the solid walls, and changes in the actuation force while a droplet traverses one electrode to the next. From this model, we have developed scaling rules for EWD parameters. This model is then applied to EWD actuator scaling. In addition, limits on applied actuator voltages are developed for reliable operation based on conditions for contact-angle saturation.

2 Hydrodynamics of droplet transport

2.1 Force on a droplet

Electrically controlled droplet actuation is undoubtedly complex and not entirely understood. Contributions to droplet transport are made by both electrowetting on dielectric forces and dielectrophoretic forces (Zeng and Korsmeyer 2004). For the purposes of developing a simplified scaling model of a droplet-based actuator, it will be assumed that the driving force for droplet transport is due primarily to a gradient in interfacial tension between the droplet and an insulator surface. When an electric potential is applied between the droplet and an electrode coated with the insulator of thickness t, charges on the surface of the insulator modify the interfacial tension between the droplet and the insulator (Mugele and Baret 2005). Then, the resulting change in contact angle of the droplet is described by the Lippmann–Young equation:

$$ \cos \theta (V) = \cos \theta (0) + \frac{{\varepsilon_{\text{r}} \varepsilon_{\text{o}} V^{2} }}{{2t\gamma_{ \lg } }} $$

(1)

where ε_o (8.85 × 10⁻¹² F/m) is the permittivity of vacuum, ε _r is the dielectric constant of the insulator layer, V is the applied voltage, θ(0) is the non-actuated contact angle, and θ(V) is the droplet contact angle when voltage V is applied. It should be pointed out that Eq. 1 is an approximation that holds at voltages away from contact angle saturation. Also, using Eq. 1 as the basis of a scaling model may introduce simplifications that produce errors in the calculated results. However, the role of a scaling model is to estimate trends in microactuator parameters that provide insight to the designer. Towards this end, we compare scaling model estimates with measured data so the reader can judge the accuracy of the model and the scaling arguments.

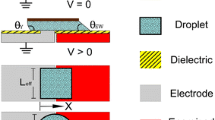
A cross-section of a typical EWD actuator is depicted in Fig. 1. Droplets are placed between two parallel plates with hydrophobic surfaces, and the space between is filled with a medium of air or silicone oil. The electrodes are covered with the insulating layer and connected to an AC or DC voltage source. The droplet, initially stationary, is transported to the right when the neighboring electrode on the right hand side is connected to a voltage exceeding a threshold. When the droplet is completely moved to the neighboring electrode, the droplet becomes stationary with a new contact angle. This results in balances between surface tension forces along the triple line, which is a boundary between solid, liquid, and gas. For a typical droplet diameter of 1 mm, the Bond number, which is the ratio of the gravity force and the capillary force, is small such that the shape of droplet is close to the spheroid cut by two planes. A spherical shape is the optimum energy-minimizing shape of a droplet in the absence of gravity.

Fig. 1

Electrowetting actuator cross-section showing voltage-actuated contact angle changes and key actuator dimensions. The electrodes of pitch, L, are covered with an insulator of thickness, t, and the top and bottom plates are separated by a distance d

The droplet depicted with a dashed line in Fig. 1 indicates a droplet on the non-actuated electrode. It maintains static contact angle θ(0). The droplet depicted with a dash-dot line represents the droplet transported to the next electrode (actuated electrode). The actuated electrode is indicated by a fill pattern. When the droplet is stationary over an electrode, it maintains a static contact angle θ(V). The droplet during transport is illustrated with solid lines. During transport the droplet maintains a dynamic contact angle, θ_d.

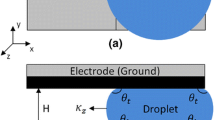
The force balance on a droplet is shown in Fig. 2. When a droplet is in contact with a solid surface, the interaction among molecules of the droplet, the ambient fluid, and the solid can lead to a net force of wetting or non-wetting based on the net of the surface tension forces shown in Fig. 2 (Zeng and Korsmeyer 2004). Under the influence of a wetting force, f _A, a droplet moves and expresses an angle of advancement, ϕ, as shown in Fig. 1. Along the droplet’s triple line the force balance per unit length over the actuated electrode is expressed as (Quinn et al. 2005):

$$ f_{\text{A}} = \gamma_{\text{sg}} - \gamma_{ \lg } \cos \theta_{\text{d}} - \gamma_{\text{sl}} (V) $$

(2)

Fig. 2

The force balance on a droplet’s triple lines in an electrowetting actuator

The force balance per unit length along the droplet’s triple line over the non-actuated electrode is presented as

$$ f_{\text{B}} = \gamma_{\text{sl}} (0) + \gamma_{\lg } \cos \theta_{\text{d}} - \gamma_{\text{sg}} $$

(3)

Then, the driving force per unit length is the sum of these two forces:

$$ f_{\text{m}} = f_{\text{A}} + f_{\text{B}} = \gamma_{\text{sl}} (0) - \gamma_{\text{sl}} (V) $$

(4)

The integration of the driving force per unit length, f _m, over the contact line of a droplet of diameter L, as shown in Fig. 1, yields the total force on the droplet (Ren et al. 2002):

$$ F_{\text{m}} = f_{\text{m}} L\sin \phi $$

(5)

In this simplified analysis only the projected length of the droplet matters, and the actual shape of the triple line does not matter. The effects of irregularities in the triple line shape due to contact-line pinning causing stick-slip motion are not known. The variable angle made where the contact line intersects the adjacent electrode, referenced to the center of the moving droplet, is called the advancement angle, shown in Fig. 1. The angle of advancement ϕ increases from 0 to π as the droplet moves to the next electrode. Therefore, the driving force for the droplet changes as it traverses.

It is known that contact angle hysteresis, caused by random pinning forces, introduces an obstacle to droplet transport manifested as a threshold voltage. In this regard, the receding triple line during droplet transport can maintain a contact angle of θ(0) − α while the advancing triple line can maintain the contact angle of θ(V) + α (Berthier et al. 2007). Thus, the net force on a droplet in Eq. 4 may be written as follows:

$$ f_{\text{m}} = \gamma_{\text{sl}} (0) - \gamma_{\text{sl}} (V) = \gamma_{\lg } \cos \,(\theta (V) + \alpha ) - \gamma_{\lg } \cos \,(\theta (0) - \alpha ) $$

(6)

When V = 0 the concept of contact angle hysteresis is meaningless, since the equilibrium contact angle made along the droplet’s contact line is the same everywhere. Thus, f _m = 0 when V = 0 because α = 0 at equilibrium. Using a trigonometric identity and the Lippmann–Young equation, the driving force per unit length is estimated as:

$$ f_{\text{m}} = \gamma_{\lg } \cos \alpha [\cos \theta (V) - \cos \theta (0)] - \gamma_{\lg } \sin \alpha [\sin \theta (V) + \sin \theta (0)] $$

(7)

$$ f_{\text{m}} = \cos \alpha \frac{{\varepsilon_{\text{r}} \varepsilon_{\text{o}} V^{2} }}{2t} - \gamma_{\lg } \sin \alpha [\sin \theta (V) + \sin \theta (0)] $$

(8)

It is seen that the driving force per unit length is modified by contact angle hysteresis, which highly depends on the combination of the substrate surface, droplet liquid, and the filler fluid. Thus, from Eq. 5 the total estimated force on an actuated droplet becomes:

$$ F_{\text{m}} = L\sin \phi \left\{ {\cos \alpha \varepsilon_{\text{r}} \varepsilon_{\text{o}} V^{2} /2t - \gamma_{\lg } \sin \alpha \left[ {\sin \theta \left( V \right) + \sin \theta \left( 0 \right)} \right]} \right\} $$

(9)

2.2 Drag forces on a droplet

There have been investigations on the drag for the moving droplet. Brochard (1989) indicated that the droplet movement is impeded by a shear force between the droplet and the solid wall, when there is a gradient of interfacial tension on the surface. Depending on the shape of the droplet, the drag was dominated either by the triple line or bulk of the droplet.

Baviere et al. (2008) employed Brochard’s model for the drag of a droplet, but only included the shear stress from the wall. Ren et al. (2002) evaluated the drag for a droplet placed between two plates, while the aqueous droplet was surrounded by a filler fluid. Ren considered the relevant forces including viscous friction force along the contact line, viscous force due to oil, and contact line friction and compared their model with experimental data.

2.2.1 Drag from the filler medium

Stream lines are formed along a droplet moving in a filler fluid. Thus the movement of a droplet is resisted by the shear force from the top and bottom plates and the viscous drag from the filler medium, which is either air or silicon oil. With regard to drag from the filler medium, we assume that the drag of the droplet follows the classical drag model of Beard and Pruppacher (1969) as shown below:

$$ F_{\text{do}} = C_{\text{D}} A_{\text{D}} \frac{1}{2}\rho_{\text{o}} U^{2} $$

(10)

$$ C_{\text{D}} = \frac{24}{Re}\left[ {1 + 0.189Re^{0.632} } \right] $$

(11)

where, Re = 2UR/ν_o is the Reynolds number for the droplet movement, ρ_o is the density of the filler fluid, U is the relative velocity of the droplet, A _D is the projected area of the droplet in the direction of the velocity, and C_D is the drag coefficient. Here the range of Reynolds number is from 21 to 200. When the Reynolds number is smaller than this range, the drag on an unbounded spherical droplet would follow the Stokes drag formula.

$$ C_{\text{D}} = \frac{24}{Re} $$

(12)

Recognizing that droplets in a EWD actuator are confined between two plates, Eq. 12 is only a rough approximation and is useful only to a limited extent. Nevertheless the condition in Eq. 12 is easily satisfied for spherical droplets moving in 1-2cSt silicone oil with velocity < 5 cm/s and with scaled dimensions below 500 μm.

2.2.2 Drag from the plates

In a typical two-plate EWD actuator the droplet is confined between plates separated by a gap, d, with electrodes of pitch L. A moving droplet will have a velocity gradient inside which causes a force balance between the shear stress from the velocity gradient and the gradient in interfacial tension established at the actuator surface. The resulting viscous drag force between the plate and the droplet is expressed as (Brochard 1989; Ren et al. 2002):

$$ F_{\text{dv}} = 2C_{\text{v}} \frac{{\mu_{\text{d}} U}}{d}L^{2} $$

(13)

where C _v is an empirical constant. Depending on the density of the droplet compared to that of the filler fluid, the contribution of the drag from the upper plate and lower plate will change. Here, we assumed that the droplet touches the upper plate and lower plate such that Eq. 13 has a multiplier of 2. Considering Brochard’s analysis (1989), if there exists a strong contribution from the triple line, C _v will be in the range of 10–15. If we assume that the velocity profile of the fluid in the droplet is parabolic, where the velocity reaches maximum at the center, C _v equals 6.

2.2.3 Force balance

Though there is an internal flow and spatial distribution of pressure inside the droplet, the dynamics of steady state droplet movement can be estimated by assuming that the droplet is a solid ball.

The electrowetting force is balanced by the drag from the filler fluid and the drag between the droplet and plate. From Eqs. (9), (10), and (13):

$$ F_{\text{m}} = F_{\text{do}} + F_{\text{dv}} $$

(14)

If we can assume that the droplet diameter is approximately the same as the size of an electrode, L, then in Eq. 10 A _D = Ld, 2R = L and the contact area of droplet and plate could be approximated as L ². Then, there will be two cases. When the Reynolds number is very small, the drag from the filler fluid can be approximated by Stokes drag, and the droplet velocity becomes

$$ U = \frac{{\sin \phi \left\{ {\cos \alpha \frac{{\varepsilon_{\text{r}} \varepsilon_{\text{o}} V^{2} }}{2t} - \gamma_{\lg } \sin \alpha \left[ {\sin \theta (V) + \sin \theta (0)} \right]} \right\}}}{{12\mu_{\text{o}} \frac{d}{L} + 2C_{\text{v}} \frac{{\mu_{\text{d}} }}{d}L}} $$

(15)

The velocity model of Eq. 15 is similar to the simplified model of Baird, which does not take into consideration drag from the filler medium or contact line resistance (Baird and Mohseni 2007).

It is shown that the velocity is proportional to the square of the applied voltage, which agrees with previous observations. Equation 15 also predicts that the droplet velocity will increase with the actuator aspect ratio, d/L, if the viscous drag term dominates over the filler medium drag. This follows since as the gap d increases, the drag on the droplet from the plate surfaces decreases. Such a dependence of droplet velocity on gap height in an air medium has been experimentally observed (Yue et al. 2006). From Eq. 15, we find that there exists an optimum aspect ratio, which would maximize the velocity when the viscosity of the filler fluid is on the same order as that of the droplet fluid:

$$ \left( {\frac{d}{L}} \right)_{\text{opt}} = \left( {\frac{{C_{\text{v}} \mu_{\text{d}} }}{{6\mu_{\text{o}} }}} \right)^{1/2} $$

(16)

If we use a filler fluid which has the same viscosity as the droplet, the optimum aspect ratio would occur for an unconstrained droplet (d/L = 1) with C _v = 6. Thus, we have derived the first scaling rule for a EWD actuator: increasing d/L with all other variables fixed increases droplet velocity up to a maximum, although the dependence on d/L is weak.

For typical values of the parameters in Eq. 15, the droplet velocity changes relatively slowly for d/L > 0.2. This can be seen in Fig. 3, where data of droplet velocity versus voltage for a number of actuators with d/L values 0.2 to 0.6 (Pollack 2001) are plotted. It can be seen that there is no strong dependence of velocity on d/L. However, such dependences may be overshadowed by experimental processing variables of the measured devices.

Fig. 3

Average droplet linear velocity versus voltage for electrodes with different pitch and aspect ratio, d/L (Pollack 2001)

3 Actuator scaling

3.1 Threshold voltage for scaled actuators

The threshold voltage for droplet actuation, V _T, occurs when V = V _T and U = 0 in Eq. 15. Thus, at the threshold of droplet actuation:

$$ V_{\text{T}} = \left\{ {2t\gamma_{\lg } /\varepsilon_{\text{r}} \varepsilon_{\text{o}} \left[ {\tan \alpha (\sin \theta \left( {V_{\text{T}} } \right) + \sin \theta \left( 0 \right)} \right]} \right\}^{1/2} $$

(17)

Equation 17 is similar to the equation for minimum voltage for actuation derived by Berthier (Berthier et al. 2007). If the insulator is a combination of two dielectric layers of thickness t ₁ and t ₂ with relative dielectric constant ε₁ and ε₂, respectively then

$$ t/\varepsilon_{\text{r}} = t_{1} /\varepsilon_{1} + t_{2} /\varepsilon_{2} $$

(18)

Equation 15 can now be written as:

$$ U = \frac{{\sin \phi \varepsilon_{\text{o}} \cos \alpha \left[ {V^{2} - V_{\text{T}}^{2} } \right]}}{{2t/\varepsilon_{\text{r}} \left[ {12\mu_{\text{o}} d/L + 2C_{\text{v}} \mu_{\text{d}} L/d} \right]}} $$

(19)

The effect of the filler medium on V _T can be assessed with the results shown in Fig. 4. Shown are the droplet transfer rates (Hz) in a EWD device, where transport was conducted in an air medium, in a silicone oil medium, and in air after the transport surface had been exposed to volatile silicone oil and then allowed to dry (Pollack 2001). It has been reported that impregnation of Teflon AF with silicone oil reduces the contact angle hysteresis of the surface (Verheijen and Prins 1999). It can be seen that droplet transport in silicone oil is improved (lower V _T) relative to transport in air. These results suggest that the differences are due largely to effects at the solid–liquid interface.

Fig. 4

Comparison of droplet transfer rates in a silicone oil medium, air medium, and air after oil exposure of the transport surface (Pollack 2001)

The contact angle hysteresis for a water droplet in silicone oil is 1.5° < α < 2° and 7° < α < 9° in air (Berthier et al. 2007). To assess the relative contributions to droplet transport in Fig. 4, we start with the assumption that a similar amount of contact angle hysteresis exists for a water droplet in oil and a droplet in air after oil impregnation. Then from Eq. 17, the ratio of V _T in air-after-oil actuation to V _T in oil actuation for a given actuator design is likely dominated by the differences in γ_lg. For silicone oil/water interfacial tension we used γ_lg = 47 mN/m (Reddy and Mathur 1988).

$$\begin{aligned}V_{\text{Tair/oil}} /V_{\text{Toil}} &\sim \left[ {(\gamma_{\lg } \left( {\text{air}} \right)/\gamma_{\lg } \left( {\text{oil}} \right)} \right]^{1/2} \\ & \sim \left[ {72.8\;{\text{mN/m}}/47\;{\text{mN/m}}} \right]^{1/2} = 1.24 \end{aligned}$$

This result compares with the measured ratio in Fig. 4 of about 1.5.

Similarly, the threshold difference between air and air-after-oil actuation is likely dominated by the difference in contact angle hysteresis. Thus, for the ranges given above for contact angle hysteresis, assuming no differences in sinθ(V) for the two systems, the threshold voltage ratio for actuation in air to actuation in oil is:

$$ V_{\text{Tair}} /V_{\text{Toil}} \sim \frac{{\left. {\left[ {\tan \alpha \left( {\text{air}} \right)(\sin \theta \left( {V_{\text{T}} } \right) + \sin \theta \left( 0 \right)} \right]} \right\}^{1/2} }}{{\left. {\left[ {\tan \alpha \left( {\text{oil}} \right) (\sin \theta \left( {V_{\text{T}} } \right) + \sin \theta \left( 0 \right)} \right]} \right\}^{1/2} }} = 1.9 - 2.5 $$

This result compares with the measured ratio of about 1.7. Thus, Eq. 17 gives a reasonable interpretation of the data in Fig. 4.

With regard to scaling V _T for a given filler medium, the dominant variables are insulator thickness and relative dielectric constant. Equation 17 is plotted in Fig. 5 for water droplets in silicone oil. We have used γ_lg (oil) = 47 mN/m, θ(V _T) = 104°, θ(0) = 125°, and α = 2–4° based on OCT measurements of moving droplets (Srinivasan et al. 2003). Threshold voltage data are included for actuators fabricated with parylene C insulators of different thicknesses (0.5, 0.8, 1, and 2 μm) with a thin Teflon overcoat. Reasonable agreement is achieved with experimental results.

Fig. 5

Threshold voltage scaling with insulator thickness (t/ε_r)^1/2 for water droplets in silicone oil and air filler media

For droplet actuation in an air medium, we have included data in Fig. 5 from a number of sources (Cho et al. 2002; Moon et al. 2002; Cooney et al. 2006; Pollack 2001). Equation 17 is plotted in Fig. 5 for γ_lg (air) = 72.8 mN/m, θ(V _T) = 95°, θ(0) = 110°, and α = 9°. Reasonable agreement is achieved with experimental results.

Other factors that have been experimentally observed to affect V _T include the aspect ratio for d/L < 0.2 and silicone oil viscosity (Pollack 2001). The effect of oil viscosity was such that a 75% increase in V _T was associated with a tenfold increase in oil viscosity. Whereas increased oil viscosity would increase drag on a moving droplet, as seen in Eq. 15, the effect on threshold voltage may be associated with thickening of oil entrained beneath a droplet, thus reducing droplet-electrode capacitance. This effect has not been accounted for. On the other hand, the viscosity of the liquid droplet has little effect on V _T (Pollack 2001).

3.2 Scaling droplet splitting

Perhaps the simplest fluidic operations in a EWD device are the splitting of a droplet and the merging of two droplets into one. The minimum splitting arrangement involves three serial electrodes as described by Cho (Cho et al. 2002). Droplet splitting takes place when the two outer electrodes are turned on and the contact angles θ_b2 are reduced, resulting in an increase in the radius of curvature, r ₂. With the inner electrode off, the droplet expands to wet the outer two electrodes. As a result the meniscus over the inner electrode contracts to maintain a constant volume (Fig. 6a). Thus, the splitting process is underway as the liquid forms a neck with radius R ₁. In general, the hydrophilic forces induced by the two outer electrodes stretch the droplet while the hydrophobic forces in the center pinch off the liquid into two daughter droplets (Berthier et al. 2006).

Fig. 6

Droplet configuration for splitting (Cho et al. 2002)

3.2.1 Static splitting model

A static criterion for breaking the neck in Fig. 6a is (Cho et al. 2001):

$$ 1/R_{1} = 1/R_{2} - \left( {\cos \theta_{{{\text{b}}2}} - \cos \theta_{{{\text{b}}1}} } \right)/d $$

(20)

The symbols are indicated in Fig. 6. According to Eq. 20, necking and splitting are facilitated when the gap height, d, is made smaller or the volume of the droplet is increased. The inclusion of contact angle hysteresis described in Eqs. (6) to (8) results in a modification of the condition for splitting in Eq. 20:

$$ 1/R_{1} = 1/R_{2} - \cos \alpha \varepsilon_{\text{r}} \varepsilon_{\text{o}} \left[ {V^{2} - V_{\text{T}}^{2} } \right]/\left( {2{\rm d}t\gamma_{\lg } } \right) $$

(21)

Generalizing splitting to occur over N electrodes (necking occurs over N′ ≥ 1 electrodes, where N = N′ + 2), the minimum voltage required for splitting is approximated by using Ren’s relation for R ₁ (Ren 2004):

$$ V^{2} - V_{\text{T}}^{2} \approx 4\gamma_{\lg } /\varepsilon_{\text{o}} \left[ {t/\varepsilon_{\text{r}} \left( {d/L} \right)} \right]\left[ {1 - 1/\left( {N^{\prime 2} + 1} \right)} \right] $$

(22)

It is assumed that cos α = 1. It can be seen that the static splitting voltage depends on N′ and scales with [t/ε_r(d/L)]^1/2. Equation 22 is shown plotted in Fig. 7 for N′ = 1.

Fig. 7

Comparison between the static splitting model (Eq. 22) and the dynamic splitting model (Eq. 26) plotted above for two effective insulator thicknesses and N′ = 1

3.2.2 Dynamic splitting model

A dynamic view of splitting involves consideration of drag forces on an actuated droplet as it undergoes extension. For this case the splitting mechanism in a EWD actuator can be likened to the breakup of a droplet at a T-junction under two-phase flow. When a droplet in a conduit is pushed into a T-junction by the flowing filler fluid at a velocity U, the droplet is forced into a bidirectional extensional flow (Link et al. 2004).

Droplet splitting in a EWD platform is quite similar to the droplet at a T-junction, since the droplet is forced into a bidirectional extensional flow. Link et al. have shown that droplet breakup is related to a critical capillary number, C _cr, at the droplet’s stability limit (Link et al. 2004). The initial cylindrical droplet having a diameter of w _o and length of l _o is pushed to the T-junction, where the droplet is extended to a droplet having a diameter of w _e and length of l _e. Link et al. (2004) have developed a correlation for the break up in terms of initial amount of extension e_o = l_o/(w _oπ) and the critical capillary number for the droplet break up as below:

$$ C_{\text{cr}} = \mu_{\text{o}} U/\gamma_{\lg } \approx e_{\text{o}} \left( {1/e_{\text{o}}^{2/3} - 1} \right)^{2 } $$

(23)

The capillary number is the relative effect of viscous forces versus surface tension acting across the droplet/filler medium interface. For an electrowetting actuator splitting will occur for N = 3 (N′ = 1). Under this condition, e _o ≅ 3/π and the critical capillary number becomes C _cr > 10⁻³. Thus, the critical capillary number for droplet splitting with N = 3 in a EWD actuator is given as:

$$ C_{\text{cr}} = {\mu_{\text{o}} U/\gamma_{\lg }}= \frac{\sin \phi \cos \alpha \varepsilon_{\text{r}} \varepsilon_{\text{o}} \left[ {V_{\text{cr}}^{2} - V_{\text{T}}^{2} } \right]}{{2t\gamma_{\lg } \left[ {12d/L + 2C_{\text{v}} \left( {\mu_{\text{d}} /\mu_{\text{o}} } \right)L/d} \right]}} \ge 10^{ - 3} $$

(24)

Assuming that ϕ = π/2, α = 1.5° (water droplet in silicon oil), then the voltage for splitting becomes:

$$ \left[ {V^{2} - V_{\text{T}}^{2} } \right] \approx \left[ {2t\gamma_{\lg } /\varepsilon_{\text{r}} \varepsilon_{\text{o}} } \right]\left[ {0.012d/L + 0.002\left( {\mu_{\text{d}} /\mu_{\text{o}} } \right)C_{\text{v}} L/d} \right] $$

(25)

It can be seen that the static model of Eq. 22 yields a direct dependence of [V ² − V _T ²] on t/ε_r(d/L). A similar dependence occurs in Eq. 25 if the term containing C _V is relatively small, indicating a negligible viscous drag force between the plate and the droplet relative to the drag force of the filler medium.

The critical capillary number separates the conditions between breaking and non-breaking droplets. By operating with a larger capillary number, C, we operate with a more affirmative dynamic droplet splitting condition. Assuming arbitrarily a capillary number C that is 10 times C _cr (C > 10⁻²) and a EWD actuator that has no asymmetries, then one might expect uniform splitting to occur. Thus, with C _v = 6, the voltage for splitting becomes:

$$ \left[ {V^{2} - V_{\text{T}}^{2} } \right]^{1/2} \approx \left[ {2t\gamma_{\lg } /\varepsilon_{\text{r}} \varepsilon_{\text{o}} } \right]^{1/2} \left[ {0.12\left( {d/L + \left( {\mu_{\text{d}} /\mu_{\text{o}} } \right)L/d} \right)} \right]^{1/2} $$

(26)

Equation 26 is plotted in Fig. 7 for two values of t/ε_r, and these results are compared with the static model, Eq. 22. Whereas the static model shows splitting voltage increasing linearly with [t/ε_r(d/L)]^1/2 due to lower internal pressure at higher aspect ratio, the dynamic model predicts just the opposite. For a fixed value of t/ε_r, as the aspect ratio increases, the voltage for splitting decreases in Eq. 26 due to reduced plate drag forces. When d/L = 1, the dynamic model curves and the static model curve cross over at common coordinates on the [V ² − V _T ²]^1/2 and [t/ε_r(d/L)]^1/2 axes, corresponding to an unbounded droplet with no plate drag. The general disparity between the static and dynamic models is consistent with experimental observations that time sequencing of electrode voltages influences splitting (Ren 2004).

3.3 Scaling droplet dispensing

Reservoirs can be created on EWD actuators in the form of large electrode areas that allow liquid droplet access and egress (Fair et al. 2003; Wheeler et al. 2004; Srinivasan 2005; Moon et al. 2006). Droplet dispensing requires dynamic application of electrode voltages. To induce a protrusion of liquid from the reservoir requires that the electrowetting force must overcome the pressure gradient caused by curvature differences between the reservoir and the finger front. When the area of the reservoir is much greater than the area of a single electrode, the voltage required to form a liquid protrusion becomes (Fair 2007):

$$ \left( {V^{2} - V_{\text{T}}^{2} } \right)^{1/2} = \left\{ {2\gamma_{\lg } \left[ {t\left( {d/L} \right)} \right]/\varepsilon_{\text{r}} \varepsilon_{\text{o}} } \right\}^{1/2} $$

(27)

Forming a protrusion from a large reservoir requires less voltage than splitting, which is the most demanding operation from a voltage requirement. In addition it can be seen that the voltage for forming a protrusion also scales with [t/ε_r(d/L)]^1/2.

For droplet formation by dispensing from a static reservoir, shown in Fig. 8, the liquid in regions 1 and 3 can be sustained, whereas the liquid in region 2 is unstable. Thus, the liquid in region 2 has a tendency to flow back to region 1. Successful necking occurs when P ₂ > P ₁. Thus, referring to Fig. 8, the pinchoff condition requires that:

Fig. 8

Breaking of the liquid neck to form a droplet of radius R ₃ (Ren et al. 2003a, b)

$$ P_{2} > P_{1} \to 1/r_{2} - 1/r_{1} = \varepsilon_{\text{o}} \varepsilon_{\text{r}} \left( {V^{2} - V_{\text{T}}^{2} } \right)/\left( {2 \gamma_{\lg } td} \right) > 1/R_{1} - 1/R_{2 } $$

(28)

The pressure relations shown in Eq. 28 can be modified by changing droplet size, changing the gap height, d, between the two plates of the actuator, and changing the electrode voltages. Ren has shown that a small aspect ratio (d/L)) and small droplet size are favorable for pinchoff of a droplet (Ren 2004). Thus, the magnitude of the radius of curvature R ₂ (negative) in Fig. 8 can be approximately expressed in terms of droplet radius R ₃ and the number of electrodes in the pinchoff region:

$$ \left| {R_{2} } \right| \approx \left( {N^{\prime 2} + 1} \right)R_{3} /2 $$

(29)

The total number of electrodes in the dispenser is N = N′ + 1. Substituting Eq. 29 into Eq. 28 and assuming R ₃ = L/2 and d/R ₁ ≪ 1 gives the condition for scaling dispensing voltage:

$$ \left( {V^{2} - V_{\text{T}}^{2} } \right)^{1/2} > \left[ {8\gamma_{\lg } /\varepsilon_{o} \left[ {t/\varepsilon_{\text{r}} \left( {d/L} \right)} \right]/\left( {N^{\prime 2} + 1} \right)} \right]^{1/2} $$

(30)

The minimum dispensing voltage, V, in Eq. 30 is plotted in Fig. 9 versus insulator thickness for N′ = 1 and 2. The conditions are for dispensing a water droplet in silicone oil (γ_lg = 47 mN/m). Calculations and data were based on parylene C insulators with a Teflon overcoat with t = 0.5, 1, and 2 μm, an aspect ratio d/L = 0.2, and measured V _T values. Dispensing was performed at both dc and 100 Hz ac electrode voltages. It can be seen that Eq. 30 qualitatively follows the thickness dependence of these data. It also can be seen that low-voltage dispensing is favored at small insulator thicknesses.

Fig. 9

Dispensing voltage versus insulator thickness for d/L = 0.2. Shown is the calculated minimum dispensing voltage and data from actuators with N′ = 2. Dispensing was performed at both dc and 100 Hz ac electrode voltages

Scaling reduces the amount of linear displacement to dispense a droplet. Thus, Eq. 30 reveals that as long as t/ε_r(d/L) is held constant while L is decreased, the same number of dispensing electrodes required is fixed for constant (V ² − V _T ²)^1/2. Therefore, scaling to smaller droplet volumes is favorable for droplet pinchoff with a correspondingly smaller linear displacement of liquid from the reservoir.

3.4 Scaled mixing

Experimental results on mixing times of the contents of two constant volume droplets have been measured as a function of aspect ratio, d/L (Paik et al. 2003a, b). In this study, the volume of the droplets was adjusted to maintain an electrode pitch of L = 1.5 mm, and the insulator thickness was 0.8 μm parylene C. The minimum mixing time was achieved with d/L of about 0.4, after which mixing time increases with increasing d/L.

Mixing in a stationary droplet is controlled by diffusion. Enhanced mixing through electrowetting-induced oscillations has been shown to occur in a droplet in a EWD actuator while the contact angle changes (Mugele et al. 2006). Chaotic advection also enhances mixing by stretching and folding the fluid in a droplet to give rise to an exponential decrease in the striation length (Song et al. 2003). These studies have shown that the mixing time is inversely proportional to the frequency and proportional to the viscosity of the droplet. However, it was noted that there is an inertial effect due to the volume of the droplet and viscosity of the filler fluid and droplet such that a decrease in mixing time occurs as the frequency increases. It is anticipated that if we have a smaller droplet at given frequency, we would have a reduced dependence on inertia.

Song et al. have shown that the time for complete mixing by chaotic advection in a liquid plug moving in a serpentine channel is correlated with the channel dimension, w, flow velocity, U, and diffusion coefficient, D, through the relation (Song et al. 2003):

$$ t_{\text{mix}} \approx aw/U\log \left( {wU/D} \right) $$

(31)

where a is the dimensionless length of the liquid plug. For a EWD actuator, w = L, and similar physical effects can be assumed as in mixing during plug flow. If the actuation frequency is f = U/L, then the mixing time is shown to depend inversely on frequency:

$$ t_{\text{mix}} \sim 1/f\log \left( {L^{2} /Df} \right) $$

(32)

The result above also predicts that mixing time is relatively independent of filler-medium viscosity. Both results agree with experimental results (Paik et al. 2003a, b; Paik 2003). It is also clear that mixing time will decrease as electrode pitch L decreases.

3.5 Combined scaling effects

It has been shown that static models of droplet splitting and dispensing show a similar dependence on [t/ε_r(d/L)]^1/2. As a result, curves for splitting and dispensing with N = 3 electrodes are plotted on the same axes in Fig. 10a and b for actuation in air and in silicone oil respectively. Also plotted is EWD actuator threshold voltage versus [t/ε_r(d/L)]^1/2 for d/L = 1 and the optimum mixing condition. It can be seen that all of the important fluidic operations can be scaled.

Fig. 10

Superimposed scaling of droplet splitting, dispensing, threshold voltage and mixing in a EWD actuator in an oil filler medium (a) and air (b)

Constant voltage scaling with fixed V _T can occur by maintaining constant insulator thickness, t, and d/L. However, the question remains regarding the maximum actuation voltages that can be applied for reliable actuator operation. Instabilities in threshold voltage have been associated with contact angle saturation, insulator charging, and dielectric breakdown (Pollack 2001; Papathanasiou et al. 2008; Verheijen and Prins 1999). Thus scaling to assure reliable operation is now considered.

4 Actuator voltage limits

Experiments show that the Lippmann–Young equation (Eq. 1) is valid for lower voltages, but beyond a critical voltage the contact angle reaches a lower limit, contrary to the prediction of Eq. 1. This phenomenon is known as contact angle saturation (Vallet et al. 1999). Thus for electrode voltages above the voltage at which contact angle saturation occurs, the scaling results presented here are no longer valid. While there have been numerous proposals regarding the origins of contact angle saturation, it still is not certain which effect prevails (Papathanasiou et al. 2008). However, it is clear that the associated mechanism depends on the dielectric material used to insulate the buried electrodes of a EWD actuator and its thickness.

The work of Berry et al. has suggested that increasing the applied voltage until contact angle saturation occurs was damaging to the insulator (Berry et al. 2006; Kedzierski and Berry 2006). Berry et al. later proposed that for a composite insulator consisting of an amorphous fluoropolymer coating of thickness t ₁ on an insulator of thickness t ₂, charge trapping occurs during contact angle saturation (Berry et al. 2007). The onset of charge trapping was proposed to occur when the effective dielectric strength of the fluoropolymer layer, D ₁, is exceeded. The threshold voltage for this condition is given by the expression:

$$ \begin{aligned} V_{\text{tc}} & = \varepsilon_{1} D_{1} t/\varepsilon_{\text{r}} \\ & = D_{1} \left[ { t_{1} + t_{2} \left( {\varepsilon_{1} /\varepsilon_{2} } \right)} \right] \\ \end{aligned} $$

(33)

where ε₁ is the dielectric constant of the amorphous fluoropolymer, and ε₂ is the dielectric constant of the underlying insulator.

For early actuators fabricated in our lab with composite dielectrics of 0.8 μm thick parylene C and 60 nm Teflon AF, it was observed that an actuator’s threshold voltage exhibited a time-dependent increase for applied electrode voltages of 60–100 V (Pollack 2001). However, Eq. 33 predicts that insulator charging at V > 60 Vdc would occur in Pollack’s device at V _tc = 14.1 V. This value of charging voltage falls well below the observed threshold voltages reported by Pollack.

From the standpoint of electrowetting contact angle saturation, it will be assumed that the Lippmann–Young equation (Eq. 1 above) is valid up to V = V _sat at contact angle saturation. Thus, if one knows the contact angles θ (0) and θ (V _sat) for a given EWD droplet system (i.e., water droplet in air or in silicone oil), it is possible to estimate how V _sat changes with aspect ratio, insulator thickness, γ_lg, etc. Therefore, assuming a composite insulator with a fluoropolymer layer over an underlying oxide layer, then at contact angle saturation Eq. 1 can be rewritten as

$$ V_{\text{sat}} = \left\{ {2\gamma_{\lg } /\varepsilon_{o} \varepsilon_{1} \left[ {t_{1} + t_{2} \left( {\varepsilon_{1} /\varepsilon_{2} } \right)} \right]\left[ {\cos \theta \left( {V_{\text{sat}} } \right) - \cos \theta \left( 0 \right)} \right]} \right\}^{1/2} $$

(34)

It can be seen that in Eqs. (33) and (34) V _tc and V _sat each have a different dependence on [t ₁ + t ₂ (ε₁/ε₂)]. As an example of the use of these two equations, we will use the experimental conditions of Berry et al. Berry reported a droplet of 1% SDS in 0.1 M NaCl, the oil phase was dodecane (γ_lg = 5.7 mJ/m²), and the insulator was 6 nm CYTOP on 11 nm oxide. The dielectric strength for CYTOP is D ₁ = 1.1 MV/cm. According to Eq. 33, V _tc = 1.3 V. Experimentally, θ(0) = 160° and contact angle saturation of 60° was observed at about 3.5 V (Fig. 4, Berry et al. 2006). Substituting the experimental conditions into Eq. 33 yields V _sat = 3.24 V, in good agreement with Berry’s measurement.

For EWD actuators fabricated with composite dielectrics of 0.8 μm thick parylene C and 60 nm Teflon AF, contact angle saturation was observed dynamically by OCT to occur just below 60 V, where θ(V _sat) = 63°, θ(0 V) = 125^o, and the oil medium was 1cSt. silicone oil (Srinivasan et al. 2003). According to Eq. 34, the calculated V _sat is about 55.8 V. As a result of obtaining reasonable calculated values for V _sat for two quite different examples, we shall use Eq. 34 to establish the applied voltage operating limits for reliable operation of scaled EWD actuators.

4.1 Air versus oil filler media

Studies of contact angle saturation in air have typically yielded a fairly consistent range of actuation angles for water droplets on Teflon AF/parylene insulators: θ(V _sat) = 70° and θ(0 V) = 110° (Welters and Fokkink 1998; Quinn et al. 2005; Cooney et al. 2006). For operation in a silicone oil we have used θ(V _sat) = 63°, θ(0 V) = 125° (Srinivasan et al. 2003). Thus, based on Eq. 34, calculated saturation voltages versus [t/ε_r]^1/2 are shown in Fig. 11 compared with experimental measurements (Cooney et al. 2006; Welters and Fokkink 1998; Park 2007; Papathanasiou et al. 2008; Baviere et al. 2008; Moon et al. 2002; Quinn et al. 2005; Srinivasan et al. 2003). It can be seen that the saturation voltage is essentially independent of the filler medium (silicone oil with γ_lg(oil) = 47 mN/m and air with γ_lg(air) = 72.8 mN/m), and essentially one curve represents V _sat versus [t/ε_r]^1/2 for a variety of insulator systems.

Fig. 11

Calculated and measured contact angle saturation versus insulator thickness (t/ε_r)^1/2 for water droplets in air and silicone oil media

It can be seen in Fig. 5 that an EWD actuator operating with a silicone oil filler medium has a lower V _T for any given value of [t/ε_r]^1/2. Since similar values of V _sat occur in both systems, an air filler medium will afford a smaller reliable operating voltage range than an oil system. These “safe operating” ranges are plotted in Fig. 12.

Fig. 12

Safe operating ranges for EWD actuators operating with air and oil filler media

4.2 Limits on reliable splitting

As discussed above, estimated droplet minimum splitting voltages exceed the estimated minimum voltages for dispensing and transport. It has also been reported that electrode voltages exceeding the minimum splitting voltage are required to assure splitting a mother droplet into two uniform volume daughter droplets (Fair et al. 2008). Calculated minimum splitting voltages as a function of aspect ratio, d/L, are shown in Fig. 13a for an oil medium, and these splitting voltages are compared with the V _sat curve. It can be seen that the minimum splitting voltage for an actuator with d/L < 1 is always less than V _sat. However, the experimental range for more uniform splitting (d/L = 0.2) is superimposed on Fig. 13a (Fair et al. 2008). This result shows that care must be used in setting conditions for uniform splitting so that V _sat is not exceeded.

Fig. 13

Reliable 3-electrode droplet splitting for values of actuator aspect ratio, d/L. a Oil medium; b air medium

Similar curves are shown in Fig. 13b for an air filler medium. It can be seen that the minimum voltage for 3-electrode droplet splitting exceeds V _sat for d/L ≥ 0.4. This observation implies that reliable splitting in air places tighter limits on the actuator aspect ratio.

4.3 Scaling of fluoropolymer coatings

The requirements for the hydrophobic top coat insulator include low contact angle hysteresis and an acceptable dielectric strength. For a fluoropolymer layer of thickness t ₁ and dielectric constant ε₁ on an insulator of thickness t ₂ and dielectric constant ε₂, an applied voltage, V, will produce an electric field in the fluoropolymer layer. The breakdown voltage of the fluoropolymer film, V _BD1, is related to the dielectric strength of the film, D ₁, as follows:

$$ \begin{aligned} V_{{{\text{BD}}1}} & = \varepsilon_{1} D_{1} t/\varepsilon_{\text{r}} \\ & = D_{1} [t_{1} + t_{2} (\varepsilon_{1} /\varepsilon_{2} )] \\ \end{aligned} $$

(35)

4.3.1 Fluoropolymer on parylene C

Values of D ₁ and ε₁ for Teflon AF are 0.21 MV/cm and 1.93, respectively.¹ Values of D ₁ and ε₁ for CYTOP are 1.1 MV/cm and 2.1, respectively.² Breakdown voltage for Teflon AF and CYTOP overcoats are plotted versus t ₁ in Fig. 14a for a t ₂ = 1 μm thick parylene insulator and in Fig. 14b for a t ₂ = 0.35 μm thick parylene insulator. Also plotted is V _sat versus t ₁. It can be seen that Teflon, with its low dielectric strength, breaks down well below V = V _sat, whereas CYTOP will breakdown if the parylene insulator is too thin. The breakdown voltage for a 1 μm parylene C layer is 224 V. Thus, when the Teflon overcoat breaks down it is likely that all of the voltage is developed across the underlying parylene insulator. However, a 1 μm parylene C layer will not break down over the range of voltages shown in Fig. 14a (dielectric strength of parylene C is 2.24 MV/cm). On the other hand, a 0.35 μm thick parylene C insulator breaks down at 78 V, as shown in Fig. 14b, thus limiting the operating voltage to 78 V. A CYTOP overcoat is preferred for both cases shown in Fig. 14, where V _sat levels can be achieved without breaking down the composite insulator.

Fig. 14

Calculated insulator breakdown voltages for variable thickness fluoropolymer overcoats of Teflon AF and CYTOP on a parylene C insulator showing relative values compared to V _sat. a 1 μm parylene and b 0.35 μm parylene

5 Picoliter scaling demonstration

5.1 Experimental approach

EWD actuators were fabricated on quartz substrates in a single-level metal process. After chrome metal electrode patterning, a gasket layer was formed from SU-8. For devices with L = 60 μm electrodes, the gasket thicknesses were 19 and 7.5 μm. For devices with L = 40 μm electrodes, the gasket thicknesses were 9.2 and 7.5 μm. The electrodes were designed with a round interlocking shape with an interelectrode spacing of 10 μm. Reservoirs were designed to hold 320 nl of water, which gives a capability of dispensing over 9,000 35pl droplets.

The devices were coated with 2 μm of parylene C. A thin layer of 1% Teflon AF was spun on at 2,500 rpm for 45 s and cured at 110°C for 10 min. The devices were then heated to 175°C for 20 min. Finally, a plastic top plate coated with ITO and Teflon AF was created. Holes of approximately 500 μm diameter were drilled in the proper locations to assist in filling the reservoirs. The devices were tested with salt water with blue food dye inserted into the reservoirs. The rest of the chip was filled with 2cSt silicone oil.

5.2 Experimental results

A micrograph showing 105pl droplet dispensing on 60 μm electrodes is shown in Fig. 15. Minimum dispensing voltage was 80 V and d/L = 0.32. Dispensing of 35pl drolets was performed on 40 μm electrodes with d/L = 0.19 (Fair et al. 2008). Minimum dispensing voltage was 65 V. From Fig. 11 above, V _sat = 85 V. Thus, while dispensing was within the safe operating range for the Teflon/parylene C insulator used, the minimum dispensing voltage was well above the 35–50 V one would expect from Fig. 13a. We attribute this result to our design, which brought the gasket edges (not visible in Fig. 15) along the electrodes to an abrupt angle with the reservoir gasket, thus perturbing the pressure relations in the dispensing model of Eq. 27. Additional data taken from these chips are compared to the scaling model in Figs. 5 and 11.

Fig. 15

Image sequence of droplet dispensing and actuation of 105pl droplets on 60 μm electrodes

6 Conclusions

A hydrodynamic scaling model of droplet actuation was constructed in a systematic manner by considering the effects of contact angle hysteresis, drag from the filler fluid, drag from the solid walls, and change in the actuation force while traveling the neighboring electrode. Based on this approximate model, the threshold voltage, V _T, for droplet actuation was estimated as a function of the filler medium of the EWD actuator. With regard to scaling V _T for a given filler medium, the dominant variables are insulator thickness and relative dielectric constant.

Droplet splitting under both static and dynamic conditions was explored. Whereas the static model shows splitting voltage increasing with [t(d/L)]^1/2 due to lower internal pressure at higher aspect ratio, the dynamic model predicts an opposite trend. As aspect ratio increases, the voltage for splitting decreases in Eq. 26 due to reduced plate drag forces. This disparity between the static and dynamic models is related to observations that time sequencing frequency of electrode voltages influences splitting (Ren 2004). However, the static model agrees better with our experimental results obtained under relatively low frequency conditions.

It was shown that static models of droplet splitting and liquid dispensing all show a similar dependence on [t/ε_r(d/L)]^1/2. Scaling reduces the amount of linear displacement to dispense a droplet. Thus, the model shows that as long as t/ε_r(d/L) is held constant while L is decreased, the same number of dispensing electrodes required is fixed for constant (V ² − V _T ²)^1/2. Therefore, scaling to smaller droplet volumes is favorable for droplet pinchoff with a correspondingly smaller linear displacement of liquid from the reservoir.

Based on numerous studies reported in the literature, we conclude that reliable operation of a EWD actuator is possible as long as the device is operated within the limits of the Lippmann–Young equation. The upper limit on applied voltage, V _sat, corresponds to contact-angle saturation. For both silicone oil and air media, the values of V _sat versus (t/ε_r)^1/2 are essentially the same. The estimated minimum 3-electrode splitting voltages as a function of aspect ratio d/L < 1 for an oil medium are less than V _sat. However, it is likely that conditions for uniform droplet splitting may require voltages that exceed V _sat. For an air medium the minimum voltage for 3-electrode droplet splitting exceeds V _sat for d/L ≥ 0.4. This observation implies that reliable splitting in air places tighter limits on the actuator aspect ratio. Similar conclusions also apply to droplet dispensing.